Методика преподавания математики для детей с дцп: Статья “Формы и методы работы на уроках математики, с детьми больными ДЦП
Особенности обучения математике детей с ДЦП
Жукова Наталья Владимировна
Учитель математики МБОУ «Средняя общеобразовательная школа №29 г. Йошкар-Олы»
Особенности обучения математике детей с ДЦП.
(из опыта работы)
Аннотация: Как помочь ребенку-инвалиду с ДЦП? Основными проявлениями ДЦП являются замедленность и несформированность двигательных навыков и умений. У некоторых детей нарушения моторики осложняются насильственными движениями (гиперкинезами) головы, рук, плеч, гримасами лица и т.д., которые особенно усиливаются при волнении, испуге, неожиданном обращении к ребенку, а также при попытках выполнять те или иные целенаправленные действия. Часто у таких детей наблюдается и тремор — дрожание пальцев рук и языка. Он наиболее выражен при целенаправленных движениях (например, при письме). Снижение числа контактов с окружающими приводит к формированию ряда отрицательных черт характера: моральных, волевых. Такие дети не умеют преодолевать трудности, подчинять свои действия определенным требованиям и правилам. Затрудняются организовать свою деятельность, регулировать ее и свое поведение.
Такие дети не умеют преодолевать трудности, подчинять свои действия определенным требованиям и правилам. Затрудняются организовать свою деятельность, регулировать ее и свое поведение.
Дети с ДЦП нуждаются в адаптированных учебных программах по математике, необходимо создать оптимальные условия для занятий в соответствии с их возрастными и индивидуальными особенностями.
Ключевые слова: Обучение детей с ДЦП, адаптированные программы.
Очень часто нарушения опорно—двигательного аппарата являются следствием детского церебрального паралича (ДЦП). Прежде чем начинать обучение детей с таким диагнозом, учителю нужно узнать, что же такое ДЦП.
ДЦП — заболевание, вызывающее нарушение двигательной активности и неестественное положение тела. Оно возникает в результате поражения мозга до рождения ребенка, во время родов или в младенческом возрасте. Поражается не весь мозг, а главным образом отделы, управляющие движением.
Примерно половина детей, страдающих ДЦП, умственно отсталые. Однако нельзя торопиться с выводами. Дети с последствиями ДЦП двигаются неуклюже — либо слишком медленно, либо слишком быстро. Их лица перекашиваются из — за слабости лицевых мышц или затруднения с глотанием, на них появляются гримасы. Поэтому ребенок, обладающий нормальным умственным развитием, может показаться умственно отсталым.[1]
При обучении такого ребенка, необходимо продумать программу преподавания и методы обучения. Каждый урок должен включать в себя не только программный материал, но и элементы психотерапии.
В своей статье я подробнее хочу остановиться на преподавании математики детям с ДЦП.
Проблемы организации педагогического процесса обучения математике детей с ДЦП связаны, прежде всего, с отсутствием адаптированных программ для обучения таких детей, недостаточной методической базой.
Вторая трудность данного процесса – это физиологические особенности ребенка. При ДЦП может быть нарушена координация, речь, зрение, слух, пространственные представления. Эти особенности развития влияют на темп учебной деятельности и заставляют преподавателя тщательно продумывать каждый этап урока, осуществлять индивидуальный подход, учитывая уровень подготовленности учащегося и его психологические особенности. На уроках математики учащиеся с ДЦП испытывают особенные трудности при выполнении рисунков, чертежей, графиков, так как им трудно одновременно держать карандаш и линейку. Их деятельность характеризуется зависимостью от учителя, медленным темпом работы, неустойчивостью внимания, повышенной утомляемостью.
При ДЦП может быть нарушена координация, речь, зрение, слух, пространственные представления. Эти особенности развития влияют на темп учебной деятельности и заставляют преподавателя тщательно продумывать каждый этап урока, осуществлять индивидуальный подход, учитывая уровень подготовленности учащегося и его психологические особенности. На уроках математики учащиеся с ДЦП испытывают особенные трудности при выполнении рисунков, чертежей, графиков, так как им трудно одновременно держать карандаш и линейку. Их деятельность характеризуется зависимостью от учителя, медленным темпом работы, неустойчивостью внимания, повышенной утомляемостью.
Многие из учащихся не могут решать задачи, много писать, быстро устают. Для них необходимо выработать индивидуальный темп работы, выделить больше времени на обдумывание ответов, на осмысление нового материала. Обучающиеся с ДЦП более охотно работают устно, способны воспроизводить теоретический материал. Многие темы приходится адаптировать к особенностям здоровья и возможностям обучающихся.
Для формирования математических умений и навыков лучше использовать устные вычисления, обсуждать готовые решения, использовать правила и формулы по опорным конспектам, в виде схем, рисунков и таблиц, многократно повторять правила и свойства. Одной из особенностей работы с учащимися с ДЦП является то, что им необходимо больше времени для выполнения заданий, чем здоровым детям, поэтому для контроля знаний лучше использовать задачи на готовых чертежах, задачи, в которых уже напечатано условие и начало решения, а ученики остаётся его только закончить, тестовые задания.
Однако особую трудность для учеников с ДЦП представляет процесс овладения материалом по геометрии и тригонометрии. Учет особенностей развития диктует необходимость применения разнообразного наглядного материала, чертежей, схем, рисунков. Очень облегчает занятия использование мультимедийных средств. Во время занятий можно использовать презентации, видеоуроки, готовые программы для построения графиков и их транспонирования. Обучающиеся могут самостоятельно составить презентацию, построить с помощью готовых шаблонов фигуры и описать их свойства. Ребёнку с ДЦП проще нажатием клавиш выполнить чертёж на компьютере, чем это сделать с помощью карандаша и линейки.
Обучающиеся могут самостоятельно составить презентацию, построить с помощью готовых шаблонов фигуры и описать их свойства. Ребёнку с ДЦП проще нажатием клавиш выполнить чертёж на компьютере, чем это сделать с помощью карандаша и линейки.
Ребенку – инвалиду очень важно создавать на уроках ситуацию успеха, наладить контакт учителя и ученика, Чтобы учитель передал знания и опыт ребенку. Следует помнить, что больной ребенок очень остро реагирует на критические замечания, очень тяжело переживает неудачи. На занятиях надо давать ребенку больше самостоятельности в выборе методов решения и ответов — это способствует развитию самостоятельности.
Итак, я считаю, что в основном математический материал ребенку-инвалиду вполне доступен, но некоторые темы приходится адаптировать к особенностям его здоровья и возможностям. Необходимо составить адаптированную программу по математике, соответствующую содержанию обучения математики общеобразовательной школы с учетом индивидуальных способностей конкретного ребёнка, имеющего нарушения развития вследствие ДЦП.
Список литературы:
1. Детский церебральный паралич Хрестоматия /составители Л.М. Шипицына и И.И. Мамайчук. — СПб., «Дидактика Плюс», 2003.
Статья “Обучение математике детей с ДЦП”
Антропова Татьяна Владимировна
Учитель математики МБОУ «Средняя общеобразовательная школа №26 г. Мирный
Республики Саха (ЯКУТИЯ)»
Особенности обучения математике детей с ДЦП.
(из опыта работы)
В последнее время в России наметилась тенденция роста числа детей, имеющих нарушения
опорнодвигательного аппарата. Причин этому много, от биологических до социальных, и
нельзя
друга,
рассматривать
их
отдельно
так как они являются взаимообусловленными.
друг
от
Система общего
образования с проблемами, связанными с особенностями развития детей с
Вследствие
нарушениями опорнодвигательного аппарата,
не справляется.
чего педагогическая адаптация и интеграция таких детей проходит очень
почти «точечный» опыт отдельных
медленно. Имеется лишь локальный,
которые эту проблему пытаются
специалистов,
решать. Второй год, а это шестой класс, я обучаю такого особенного ребенка математике, в
учреждений,
родителей,
текущем учебном году у меня появился еще один ребенокинвалид, обучающийся в 7
классе.
расстройства
Двигательные
у таких детей характеризуются нарушениями скоординированности, темпа движений,
ограничением их объема и силы они приводят к невозможности
осуществления движений скелетномышечной системы во времени и
пространстве. Часто наблюдается дрожание пальцев рук и языка, что наиболее выражено
при целенаправленных движениях (например, при письме). Дети с ДЦП нуждаются в
адаптированных учебных программах по математике, необходимо создать оптимальные
условия для занятий в соответствии с их возрастными и индивидуальными особенностями.
Очень часто нарушения опорно—двигательного аппарата являются следствием детского
церебрального паралича (ДЦП).
Имеется лишь локальный,
которые эту проблему пытаются
специалистов,
решать. Второй год, а это шестой класс, я обучаю такого особенного ребенка математике, в
учреждений,
родителей,
текущем учебном году у меня появился еще один ребенокинвалид, обучающийся в 7
классе.
расстройства
Двигательные
у таких детей характеризуются нарушениями скоординированности, темпа движений,
ограничением их объема и силы они приводят к невозможности
осуществления движений скелетномышечной системы во времени и
пространстве. Часто наблюдается дрожание пальцев рук и языка, что наиболее выражено
при целенаправленных движениях (например, при письме). Дети с ДЦП нуждаются в
адаптированных учебных программах по математике, необходимо создать оптимальные
условия для занятий в соответствии с их возрастными и индивидуальными особенностями.
Очень часто нарушения опорно—двигательного аппарата являются следствием детского
церебрального паралича (ДЦП).

 чувствительности. Проблемы организации педагогического процесса обучения математике детей с ДЦП
связаны, прежде всего, с отсутствием адаптированных программ для обучения таких детей,
недостаточной методической базой.
Необходимо чтобы содержание математики как учебного предмета и его
структура
ограниченными
различных
категорий
детей
для
с
возможностями были ориентированы с учетом не только диагноза, но и
динамики общего и математического развития каждого ребенка в
процессе
обучения. Адаптированная программа по математике соответствует
содержанию обучения математике общеобразовательной школы с учетом индивидуальных
В
способностей детей,
соответствии с медицинскими требованиями к учебной нагрузке в программе
имеющих нарушения развития вследствие ДЦП.
определены следующие
– дать учащимся доступные, количественные пространственные, временные и
задачи:
геометрические представления,
включиться в
трудовую
деятельность;
которые помогут им в дальнейшем
– развивать речь учащихся,
обогащать ее математической терминологией;
– использовать процесс обучения математике для повышения уровня общего
развития и корректировать недостатки в познавательной деятельности и
личностных качествах.
чувствительности. Проблемы организации педагогического процесса обучения математике детей с ДЦП
связаны, прежде всего, с отсутствием адаптированных программ для обучения таких детей,
недостаточной методической базой.
Необходимо чтобы содержание математики как учебного предмета и его
структура
ограниченными
различных
категорий
детей
для
с
возможностями были ориентированы с учетом не только диагноза, но и
динамики общего и математического развития каждого ребенка в
процессе
обучения. Адаптированная программа по математике соответствует
содержанию обучения математике общеобразовательной школы с учетом индивидуальных
В
способностей детей,
соответствии с медицинскими требованиями к учебной нагрузке в программе
имеющих нарушения развития вследствие ДЦП.
определены следующие
– дать учащимся доступные, количественные пространственные, временные и
задачи:
геометрические представления,
включиться в
трудовую
деятельность;
которые помогут им в дальнейшем
– развивать речь учащихся,
обогащать ее математической терминологией;
– использовать процесс обучения математике для повышения уровня общего
развития и корректировать недостатки в познавательной деятельности и
личностных качествах.

 Обучающиеся с ДЦП более охотно
работают устно, способны воспроизводить теоретический материал. Многие темы
приходится адаптировать к особенностям здоровья и возможностям обучающихся.
Для формирования математических умений и навыков часто использую устные
вычисления, обсуждаем готовые решения, используем правила и формулы по опорным
конспектам, в виде схем, рисунков и таблиц, многократно повторяем правила и свойства.
Одной из особенностей работы с учащимися с ДЦП является то, что им необходимо
больше времени для выполнения заданий, чем здоровым детям, поэтому для контроля
знаний лучше использовать задачи на готовых чертежах, задачи, в которых уже напечатано
условие и начало решения, а ученики остаётся его только закончить или выполнить
тестовые задания.
Перед контрольными
работами
проводим
обобщающие уроки по теме, так как
учащихся
сконцентрировать
имеют ослабленную или кратковременную память и урок дает возможность
введенных в
основных упражнениях,
внимание
на
контрольную работу.
Обучающиеся с ДЦП более охотно
работают устно, способны воспроизводить теоретический материал. Многие темы
приходится адаптировать к особенностям здоровья и возможностям обучающихся.
Для формирования математических умений и навыков часто использую устные
вычисления, обсуждаем готовые решения, используем правила и формулы по опорным
конспектам, в виде схем, рисунков и таблиц, многократно повторяем правила и свойства.
Одной из особенностей работы с учащимися с ДЦП является то, что им необходимо
больше времени для выполнения заданий, чем здоровым детям, поэтому для контроля
знаний лучше использовать задачи на готовых чертежах, задачи, в которых уже напечатано
условие и начало решения, а ученики остаётся его только закончить или выполнить
тестовые задания.
Перед контрольными
работами
проводим
обобщающие уроки по теме, так как
учащихся
сконцентрировать
имеют ослабленную или кратковременную память и урок дает возможность
введенных в
основных упражнениях,
внимание
на
контрольную работу.
 Для создания благоприятного психологического климата на уроках (занятиях)
прибегать к сенсорным контактам:
рекомендуется:
находиться поближе к ребенку;
подержать руку, дотронуться до плеча, погладить по голове; взглядом ободрять
ребенка; находиться в позиции лицом к лицу и на уровне глаз детей;
улыбаться каждому ребенку; создавать ему ситуацию успеха; использовать
ласковые, ободряющие интонации; говорить не слишком громко и быстро;
внимательно относиться к инициативным высказываниям учеников, к проявлению
симпатии,
милосердия.
желания
помочь,
опорнодвигательного
не
совершать
Учитывая особенности психофизического развития детей с нарушениями
необходимо:
математики
аппарата
уроках
на
около ребенка
резких
движений;
по
отношению к
приближаться к ребенку тихими шагами и сообщать заранее о своих
действиях
не разговаривать громко возле ребенка, отказаться на уроке от окрика;
оказывать содействие в выполнении задания,
садиться
в случае необходимости
учеником
работает.
Для создания благоприятного психологического климата на уроках (занятиях)
прибегать к сенсорным контактам:
рекомендуется:
находиться поближе к ребенку;
подержать руку, дотронуться до плеча, погладить по голове; взглядом ободрять
ребенка; находиться в позиции лицом к лицу и на уровне глаз детей;
улыбаться каждому ребенку; создавать ему ситуацию успеха; использовать
ласковые, ободряющие интонации; говорить не слишком громко и быстро;
внимательно относиться к инициативным высказываниям учеников, к проявлению
симпатии,
милосердия.
желания
помочь,
опорнодвигательного
не
совершать
Учитывая особенности психофизического развития детей с нарушениями
необходимо:
математики
аппарата
уроках
на
около ребенка
резких
движений;
по
отношению к
приближаться к ребенку тихими шагами и сообщать заранее о своих
действиях
не разговаривать громко возле ребенка, отказаться на уроке от окрика;
оказывать содействие в выполнении задания,
садиться
в случае необходимости
учеником
работает.
 д.;
использовать вариант письма печатными буквами или же письмо на
компьютере;
проверять
дефектологом с целью определения ошибок и определения путей их
самостоятельные
контрольные
работы
учителем
и
с
преодоления.
Итак, я считаю, что в основном математический материал ребенкуинвалиду вполне
доступен, но некоторые темы приходится адаптировать к особенностям его здоровья и
возможностям. Необходимо составить адаптированную программу по математике,
соответствующую содержанию обучения математики общеобразовательной школы с
учетом индивидуальных способностей конкретного ребёнка, имеющего нарушения
развития вследствие ДЦП.
Список литературы: 1. Конвенция ООН о правах инвалидов. Резолюция, принятая Генеральной Ассамблеей
ООН A/RES/61/106, 24 января 2007 г. [Электронный ресурс] // ООН [сайт].
URL: http://www.un.org/ru/documents/decl_conv/conventions/disability.shtml
2. Тихонова С.
д.;
использовать вариант письма печатными буквами или же письмо на
компьютере;
проверять
дефектологом с целью определения ошибок и определения путей их
самостоятельные
контрольные
работы
учителем
и
с
преодоления.
Итак, я считаю, что в основном математический материал ребенкуинвалиду вполне
доступен, но некоторые темы приходится адаптировать к особенностям его здоровья и
возможностям. Необходимо составить адаптированную программу по математике,
соответствующую содержанию обучения математики общеобразовательной школы с
учетом индивидуальных способностей конкретного ребёнка, имеющего нарушения
развития вследствие ДЦП.
Список литературы: 1. Конвенция ООН о правах инвалидов. Резолюция, принятая Генеральной Ассамблеей
ООН A/RES/61/106, 24 января 2007 г. [Электронный ресурс] // ООН [сайт].
URL: http://www.un.org/ru/documents/decl_conv/conventions/disability.shtml
2. Тихонова С. А. Организационноэкономический механизм реализации права на
образование детей с ограниченными возможностями здоровья // Альманах «Наука.
Инновации. Образование». Выпуск 10. – М.: Языки славянской культуры, 2011.
3. Детский церебральный паралич Хрестоматия /составители Л.М. Шипицына и И.И.
Мамайчук. — СПб., «Дидактика Плюс», 2003.
4. Сошникова Т. В. Обучение детей с ДЦП математике в условиях
интегрированного (инклюзивного) образования
//
Научнометодический
электронный журнал «Концепт». – 2015. – Т. 13. – С. 4181–4185. – URL: http://e
koncept.ru/2015/85837.htm.
А. Организационноэкономический механизм реализации права на
образование детей с ограниченными возможностями здоровья // Альманах «Наука.
Инновации. Образование». Выпуск 10. – М.: Языки славянской культуры, 2011.
3. Детский церебральный паралич Хрестоматия /составители Л.М. Шипицына и И.И.
Мамайчук. — СПб., «Дидактика Плюс», 2003.
4. Сошникова Т. В. Обучение детей с ДЦП математике в условиях
интегрированного (инклюзивного) образования
//
Научнометодический
электронный журнал «Концепт». – 2015. – Т. 13. – С. 4181–4185. – URL: http://e
koncept.ru/2015/85837.htm. Калинченко Анна Викторовна – МГПУ
Преподаваемые дисциплиныМетодика обучения математике младших школьников;Методика обучения решению задач в начальной школе;
Преемственность в обучении математике детей 5-11 лет;
Интерактивные технологии в обучении младших школьников математике;
Организация разноуровневой подготовки младших школьников.Научно-преподавательский стаж
18 лет
Заслуги, наградыГрамота департамента образования и науки г. Москвы от 13.08.2020 за значительный вклад в дело подготовки высококвалифицированных педагогических кадров для образовательных организаций города Москвы
Москвы от 13.08.2020 за значительный вклад в дело подготовки высококвалифицированных педагогических кадров для образовательных организаций города Москвы
Образование высшее
Направление подготовки (или специальность)“Олигофренопедагогика”
Общий стаж25 лет
Сведения о повышении квалификации или профессиональной подготовкеПрограмма профессиональной переподготовки «Преподавание в начальной школе» 516 ч. ИДО ГБОУ ВО МГПУ с 13.09.2019 по 08.06.20.2020 г. на ведение профессиональной деятельности в сфере начального общего образования (диплом 330000005954, регистрационный номер ПП 20034/06.
Квалификация Учитель начальных классов
Основные публикации:
Имеет 90 публикаций. Среди них статьи в журналах «Педагогика», «Начальная школа», учебно-методические работы для студентов вуза и педагогов:
1. Методика преподавания начального курса математики: Учебное пособие для студентов учреждений сред. проф. Образования / А.В. Калинченко, Р.Н. Шикова, Е.Н. Леонович.- М.: Издательский центр «Академия», 2017. -208 с. (13 п.л.) ГРИФ ФИРО
проф. Образования / А.В. Калинченко, Р.Н. Шикова, Е.Н. Леонович.- М.: Издательский центр «Академия», 2017. -208 с. (13 п.л.) ГРИФ ФИРО
2. Композиционная структура современного урока математики в начальной школе / А.И. Савенков, М.А. Романова, А.В. Калинченко // Начальная школа. — 2020. — № 8. — С. 44−48
3. Фестиваль «Математика для малышей» как средство стимулирования познавательных интересов младших школьников / А.И. Савенков, А.В. Калинченко, Н.П. Ходакова // Вестник Московского городского педагогического университета. Серия: Педагогика и психология. — 2019.- № 1 (47).- С. 88−94
4. К вопросу об организации обучения студентов педагогического вуза использованию электронных образовательных ресурсов в профессиональной деятельности / А.В. Калинченко // Вестник Московского городского педагогического университета. Серия «Педагогика и психология», 2018. — № 3 (45). — С.84−91.
Являюсь руководителем модуля «Методика обучения математике в начальной школе» по направлению подготовки «Педагогическое образование» в программе бакалавриата и руководителем модуля «Проектирование и реализация образовательных программ начального образования: предметная область «Математика и информатика» в программе магистратуры.
Руковожу НИРМ, курсовыми и выпускными квалификационными работами студентов.
Обучение детей дошкольного и младшего школьного возраста математике;
Поиск эффективных методов и приемов развития математических способностей;
Разработка познавательных заданий с помощью электронных образовательных ресурсов.
Как лечить человека с церебральным параличом
Карен, 1962 г. – 11 лет, ученица 6-го класса. Отсутствуют зубы, чтобы освободить место для скоб. Учится одна в своем специальном классе.
Воспитание детей – это достаточно сложно, не добавляя при этом инвалидности!
Часто учителя пугаются перспективы взять ученика с особыми потребностями.
Они знают, что без правильных знаний, понимания и дальновидности обучение ученика с особыми потребностями может оказаться за пределами их возможностей.
Однако, если вы должным образом подготовлены, обучение ребенка с ограниченными возможностями – наблюдение за его ростом, развитием, достижением своих целей и превосходством всех самых смелых ожиданий – может стать одним из самых успешных событий в вашей карьере учителя.
Как и все в жизни, залог успеха – это правильная подготовка!
3 основных совета по обучению студентов с церебральным параличом
1. Определите особенности инвалидности вашего ученика.
Определите конкретную инвалидность вашего ученика.Независимо от того, является ли он инвалидом или нет, каждый ребенок уникален. Тот факт, что у вашего ученика церебральный паралич, не означает, что он будет чем-то похожим на любого другого ребенка с церебральным параличом.
Постарайтесь понять конкретную инвалидность вашего ученика. Например, если ваш ученик испытывает трудности с математикой (дискалькулия), помните об этом и выделите дополнительное время, чтобы убедиться, что он понимает каждую новую математическую концепцию в том виде, в каком она преподается.
Когда дело доходит до участия в классе, будьте осторожны, когда обращаетесь к своему ученику.Если вы попросите своего ученика ответить на вопрос, который выходит за рамки его текущей глубины, это создаст для него ненужный стресс. Однако, если вы зададите своему ученику вопрос, на который он сможет уверенно ответить, вы подарите ему отличный опыт и значительно повысите самооценку.
Однако, если вы зададите своему ученику вопрос, на который он сможет уверенно ответить, вы подарите ему отличный опыт и значительно повысите самооценку.
Обладая этими знаниями, вы сможете вовлечь учащихся в свою преподавательскую деятельность и позволить им участвовать, повышая их уверенность, самооценку и чувство независимости.
2.Убедитесь, что учащиеся с особыми потребностями не рассматриваются как другие.
Если вы обучаете класс детей и намереваетесь включить в этот класс ребенка с ограниченными возможностями, убедитесь, что ваши нынешние учащиеся понимают, что ребенок с особыми потребностями не должен рассматриваться как разные.
Исследования неизменно показывают, что дети с особыми потребностями чаще подвергаются издевательствам. Дайте понять, что дискриминация недопустима. Дети с особыми потребностями хотят чувствовать себя нормальными и желанными, поэтому лучшее, что вы и ваши ученики можете сделать, – это поговорить с ними и привлечь их, как и любой другой.
3. Расскажите детям об инвалидности их одноклассника.
Чем больше ваши ученики понимают природу инвалидности своего одноклассника, тем больше им понравится их одноклассник. Они с гораздо большей вероятностью будут относиться к ним как к сверстникам и без стеснения вовлекать их в свою социальную деятельность. Чем больше мы сможем обучать друг друга тому, как лечить, включать и заботиться о людях с особыми потребностями, тем больше изменится отношение и образ мышления на благо всех участников.
Ресурсы по поддержке инвалидов для учителей
http://www.teachspeced.ca/cerebral-palsy
Обучающие стратегии для учащихся с церебральным параличом
http://www.mayoclinic.com/health/cerebral-palsy/DS00302
Общие сведения о детском церебральном параличе
http://yourcpf.org/
Фонд, финансирующий исследования и образовательные мероприятия, связанные с церебральным параличом
методов манипуляции с детьми с тяжелыми формами инвалидности для выполнения практических математических задач: робот, направление, руководство
Методы манипуляции с детьми с тяжелыми формами инвалидности для выполнения практических математических заданий: робот, режиссура, руководство
Как правило, изучение первых математических понятий осуществляется путем выполнения практических заданий и обсуждения результатов (Ginsburg, Klein et al. 1998). Однако у детей с физическими и коммуникативными нарушениями могут наблюдаться задержки в освоении математических навыков (например, дети с церебральным параличом в Арпе и Фагарде, 2005 г .; Дженкс, де Моор и др., 2007 г.). Задержки могут быть вызваны факторами окружающей среды, такими как ограниченное время, затрачиваемое на изучение математики (Лайт и Линдсей, 1991; Эрикссон, Веландер и др., 2007), или невозможность физического доступа к объектам манипулирования, используемым в практических занятиях (Дженкс, де Моор и др. 2007). Физическое манипулирование объектами – важный шаг в достижении ранних математических представлений, например, указание на объекты при их подсчете (Ginsburg, Klein et al.1998; Бисанц, Шерман и др. 2005). Детям с физическими ограничениями может быть трудно заниматься подобными видами деятельности из-за ограничений в захвате и перемещении объектов манипулирования с соответствующим разрешением (Eliasson, Krumlinde et al. 2006).
1998). Однако у детей с физическими и коммуникативными нарушениями могут наблюдаться задержки в освоении математических навыков (например, дети с церебральным параличом в Арпе и Фагарде, 2005 г .; Дженкс, де Моор и др., 2007 г.). Задержки могут быть вызваны факторами окружающей среды, такими как ограниченное время, затрачиваемое на изучение математики (Лайт и Линдсей, 1991; Эрикссон, Веландер и др., 2007), или невозможность физического доступа к объектам манипулирования, используемым в практических занятиях (Дженкс, де Моор и др. 2007). Физическое манипулирование объектами – важный шаг в достижении ранних математических представлений, например, указание на объекты при их подсчете (Ginsburg, Klein et al.1998; Бисанц, Шерман и др. 2005). Детям с физическими ограничениями может быть трудно заниматься подобными видами деятельности из-за ограничений в захвате и перемещении объектов манипулирования с соответствующим разрешением (Eliasson, Krumlinde et al. 2006).
Помимо способности манипулировать, важно иметь возможность общаться во время выполнения математических операций, чтобы дети могли «вербализовать, чтобы усвоить» (Bley and Thornton, 1994, стр. 145), просить о помощи или говорить вслух, чтобы учителя могли определить их уровень понимания (Гинзбург, Кляйн и др.1998). Детям, использующим дополнительные методы общения для удовлетворения своих коммуникационных потребностей, может быть трудно обсуждать концепции из-за низкой скорости общения, ограниченного словарного запаса и ограниченного опыта использования и слушания концепций. Знание учителем стратегий включения также было определено как ограничение. В одном исследовании, в котором исследователи обучали учителей стратегиям включения, мальчик посоветовал одноклассникам выбрать объекты для измерения, и он сообщил о результатах (Schlosser, McGhie-Richmond et al.2000). Однако сам он не манипулировал предметами.
145), просить о помощи или говорить вслух, чтобы учителя могли определить их уровень понимания (Гинзбург, Кляйн и др.1998). Детям, использующим дополнительные методы общения для удовлетворения своих коммуникационных потребностей, может быть трудно обсуждать концепции из-за низкой скорости общения, ограниченного словарного запаса и ограниченного опыта использования и слушания концепций. Знание учителем стратегий включения также было определено как ограничение. В одном исследовании, в котором исследователи обучали учителей стратегиям включения, мальчик посоветовал одноклассникам выбрать объекты для измерения, и он сообщил о результатах (Schlosser, McGhie-Richmond et al.2000). Однако сам он не манипулировал предметами.
Были изучены преимущества использования роботов для манипулирования математическими объектами, управляемыми с помощью дополнительных устройств связи (Adams 2011). В серии из трех тематических исследований дети с серьезными физическими и коммуникативными ограничениями использовали свое собственное устройство передачи речи (SGD) для управления роботом LegoTM. Они выполнили математические задания 1-го класса, включающие сравнение, сортировку и упорядочение объектов, и упражнения 2-го уровня, связанные с измерением объектов с нестандартными единицами длины (например,g., соломинки или зубочистки), а затем сравнивая и упорядочивая объекты на основе измерения. У учеников была возможность манипулировать предметами, используя разные режимы: 1) с помощью робота, 2) отвечая на вопросы учителя, такие как «он идет сюда?» пока учитель манипулировал предметами, и 3) один участник руководил учителем, используя свой SGD.
Они выполнили математические задания 1-го класса, включающие сравнение, сортировку и упорядочение объектов, и упражнения 2-го уровня, связанные с измерением объектов с нестандартными единицами длины (например,g., соломинки или зубочистки), а затем сравнивая и упорядочивая объекты на основе измерения. У учеников была возможность манипулировать предметами, используя разные режимы: 1) с помощью робота, 2) отвечая на вопросы учителя, такие как «он идет сюда?» пока учитель манипулировал предметами, и 3) один участник руководил учителем, используя свой SGD.
Члены группы вспомогательных технологий участника были опрошены относительно эффективности использования каждого режима манипуляции.Их коллективное мнение заключалось в том, что использование робота было более эффективным способом «показать то, что знают ученики», чем руководство учителем, поскольку это снимало вопрос о том, кто что делает (участник или учитель). Они чувствовали, что когда участник велел учителю манипулировать с помощью его SGD, это было эффективно, но отнимало много времени и требовало лингвистических усилий для ученика. Они также отметили, что, хотя наблюдение за учителем было наиболее эффективным и имело свое место в классе, преимущества использования робота с точки зрения эффективности в качестве инструмента обучения и удовлетворенности участников (самая высокая с роботом) были важны.
Они также отметили, что, хотя наблюдение за учителем было наиболее эффективным и имело свое место в классе, преимущества использования робота с точки зрения эффективности в качестве инструмента обучения и удовлетворенности участников (самая высокая с роботом) были важны.
Тематические исследования наводят на мысль, что учащиеся могли бы лучше продемонстрировать понимание математических концепций с помощью роботов, но ограничение в исследованиях заключалось в том, что использование различных режимов для манипуляции не применялось последовательно для всех участников и всех видов деятельности. Еще одним ограничением было то, что группа оценки была хорошо знакома со стратегиями участников и вспомогательными технологиями, что не всегда происходит в типичном интегрированном классе.
В этом исследовании был рассмотрен следующий вопрос исследования: когда участники используют три режима манипуляции (управление роботом Lego, ответы на вопросы, задаваемые учителем, и направление учителя) для выполнения задач по измерению математики, воспринимают ли учителя разницу между режимами в эффективности в “показывая то, что знает студент”?
Участники
В исследовании приняли участие те же участники, что и в тематических исследованиях: 12-летняя девочка, 10-летний мальчик и 14-летняя девочка (здесь они называются M01, M02 и M03). У всех был спастический атетоидный квадрипаретический церебральный паралич. Все использовали SGD VanguardTM II, где M01 и M02 использовали полноязыковую систему Unity ™ 45, а M03 использовали Unity 84 Sequenced. Все они активировали свои SGD с помощью двух переключателей в режиме пошагового сканирования, причем переключатели SpecTM были установлены на подголовниках кресел-каталок. M02 и M03 были независимыми коммуникаторами с 5-летним опытом работы с SGD. M01 была контекстно-зависимым коммуникатором, у которого был SGD за 2 года до исследования.
У всех был спастический атетоидный квадрипаретический церебральный паралич. Все использовали SGD VanguardTM II, где M01 и M02 использовали полноязыковую систему Unity ™ 45, а M03 использовали Unity 84 Sequenced. Все они активировали свои SGD с помощью двух переключателей в режиме пошагового сканирования, причем переключатели SpecTM были установлены на подголовниках кресел-каталок. M02 и M03 были независимыми коммуникаторами с 5-летним опытом работы с SGD. M01 была контекстно-зависимым коммуникатором, у которого был SGD за 2 года до исследования.
В оценке эффективности системы участвовали три учителя.Это были учителя начальной школы из местного сообщества, которые ранее не подвергались изучению роботов или специальной подготовке по специальному обучению или вспомогательным технологиям.
Материалы
Рис. 1. Робот Lego с линейкой и ручкой.
Автомобильный робот Lego Mindstorms RCX был адаптирован для выполнения двух практических измерительных задач (рис. 1). Сбоку робота была прикреплена 30-сантиметровая линейка, и участники могли управлять роботом в прямом, обратном, левом и правом направлениях (включая небольшие движения) для измерения длины объектов.Было добавлено перо, чтобы участники могли перемещать его вверх и вниз, чтобы рисовать линии разной длины.
1). Сбоку робота была прикреплена 30-сантиметровая линейка, и участники могли управлять роботом в прямом, обратном, левом и правом направлениях (включая небольшие движения) для измерения длины объектов.Было добавлено перо, чтобы участники могли перемещать его вверх и вниз, чтобы рисовать линии разной длины.
Инфракрасный (ИК) выход SGD использовался для управления роботом. Участники использовали те же командные интерфейсы роботов SGD, что и в тематических исследованиях.
Протокол
Каждый участник присутствовал на двух 60-минутных сеансах. Первая сессия заключалась в повторном ознакомлении с управлением роботом с использованием протокола обучения из тематических исследований.Вторая сессия заключалась в выполнении задач по математическим измерениям. Сессии по математике проводились тем же учителем специального образования, что и в тематических исследованиях, и следовали планам уроков, основанным на материале «Математика имеет смысл, уровень 3, урок 4» (Pearson Education Canada 2009). Вопросы, тема и порядок урока были следующими:
Вопросы, тема и порядок урока были следующими:
- Вопрос 4 a, b и c: начертите линию, чтобы показать, какова длина или высота, и затем измерьте ее (например, «кузнечик может прыгать на 11 см в высоту»).
- Вопрос 3 a, b и c: Измерьте длину каждой формы (e.г., параллелограмм, рисунок 1)
Участник использовал один режим манипуляции для каждого вопроса a, b и c (управляя роботом Lego , отвечая на задаваемых учителем вопросов и направляя учителя ), в произвольном порядке. Были созданы видеоклипы, в которых каждый участник отвечает на каждый вопрос в каждом из трех режимов.
Оценщикам был предоставлен пакет, включающий видеоклипы, описание участников и того, как они общаются, расшифровку слов, сказанных SGD, и копии оригинальных планов уроков.Они просмотрели каждый видеоклип и оценили свое согласие с утверждением «участник может изобразить свой уровень понимания обсуждаемой концепции» по шкале Лайкерта от 1 до 5 (категорически не согласен, не согласен, нейтрально, согласен, категорически Соглашаться). Их попросили прокомментировать каждый видеоклип и сделать какие-либо общие комментарии.
Их попросили прокомментировать каждый видеоклип и сделать какие-либо общие комментарии.
Участники имели переменный успех в режиме «Режиссер-учитель». M02, обладавший самыми продвинутыми лингвистическими способностями, довольно четко выражал свои инструкции.Например, чтобы попросить учителя провести линию, он сказал следующее: «возьмите карандаш и линейку», «положите линейку на стол», «проведите линию от 0 до 11». M03 сказал, что для измерения объектов «линейка рядом с прямоугольником» и «переместите на 0». Однако M01, у которой были наименьшие лингвистические навыки, была настолько разочарована Управлением учителя (даже при сильных подсказках учителя), что попросила прекратить это занятие.
Оценки учителей приведены в таблице 1.
| Режим |
Вопрос 4 |
Вопрос 3 |
||||
|---|---|---|---|---|---|---|
| M01 |
M02 |
M03 |
M01 |
M02 |
M03 |
|
| Учитель-режиссер |
1 (1) |
5 (0) |
4 (1) |
4 (2) |
5 (0) |
4 (1) |
| Под руководством учителя |
3 (2) |
4 (1) |
4 (0) |
5 (1) |
4 (1) |
4 (1) |
| Робот |
3 (3) |
5 (0) |
5 (0) |
4 (2) |
5 (1) |
4 (1) |
Качественный анализ комментариев преподавателя продолжается. Общие комментарии были следующие:
Общие комментарии были следующие:
- Учитель 1 сказал: «Я считаю, что робот – ценный инструмент, в котором легче увидеть, знает ли участник, что делать. участник, чтобы показать, что он / она умеет и умеет “.
- Учитель 2 сказал: «Я думаю, что дети были более точными при использовании робота. Ученики также казались намного более счастливыми при использовании робота».
Учитель 3 не давала общих комментариев, но в ходе обсуждения будут использованы репрезентативные цитаты из ее комментариев относительно видеоклипов.
Из результатов средней оценки видно, что учителя действительно ощущали разницу в эффективности «демонстрации того, что они знают» между различными способами манипуляции при выполнении задач по математическому измерению. Условие «Робот» получило наивысший средний рейтинг один раз и разделило его три раза, в то время как «Режиссер-учитель» разделил наивысший рейтинг дважды, а «Управляемый учителем» получил наивысший средний рейтинг только один раз и поделился им один раз. Следовательно, робот получил или разделил наивысшую оценку в 66% вопросов, а другие режимы получили или разделили наивысшую оценку в 33% вопросов.
Следовательно, робот получил или разделил наивысшую оценку в 66% вопросов, а другие режимы получили или разделили наивысшую оценку в 33% вопросов.
Общие комментарии Учителей 1 и 2 подтверждают, что, по их мнению, использование робота было наиболее эффективным методом. Комментарии учителя 3 к видеоклипу указывают на аналогичные результаты, например, в отношении состояния робота для M01, она сказала: «Участник кажется более способным (или желающим) продемонстрировать понимание, когда она все контролирует».
Вопрос о том, кто и что делает в режиме «Под руководством учителя», прокомментировали учителя. Учитель 1 особо отметил, что «ведущего» участника с роботом было меньше.Учитель 3 сказал, что M01 «мало участвовал в практическом овладении навыком» и что от учителя с M03 было «много наводящих вопросов».
Лингвистические способности, по-видимому, являются фактором, влияющим на то, способствует ли режим манипуляции способности участника изобразить его / ее понимание концепции. M02, обладавший самыми продвинутыми лингвистическими навыками, смог изобразить то, что он знал одинаково хорошо, в условиях режиссера-учителя и робота. Однако M01, у которой были наименьшие лингвистические навыки, получила категорическое несогласие с тем, что она могла изобразить то, что она поняла, руководя учителем в вопросе 4.В вопросе 3 учителя заметили, что условие «Режиссерский учитель» было в основном таким же, как и «управляемый учителем». Следовательно, могло случиться так, что учитель начал компенсировать языковые ограничения участника. Это могло бы объяснить, почему «Направление учителя» не оценивается как низкий для M01 в вопросе 3.
M02, обладавший самыми продвинутыми лингвистическими навыками, смог изобразить то, что он знал одинаково хорошо, в условиях режиссера-учителя и робота. Однако M01, у которой были наименьшие лингвистические навыки, получила категорическое несогласие с тем, что она могла изобразить то, что она поняла, руководя учителем в вопросе 4.В вопросе 3 учителя заметили, что условие «Режиссерский учитель» было в основном таким же, как и «управляемый учителем». Следовательно, могло случиться так, что учитель начал компенсировать языковые ограничения участника. Это могло бы объяснить, почему «Направление учителя» не оценивается как низкий для M01 в вопросе 3.
Ограничением в исследовании является диапазон оценок учителя по Лайкерту для M01 – диапазон был больше единицы для обоих условий робота и одного из других условий.Из комментариев, сделанных для каждого видеоклипа, видно, что учителя иногда оценивали уровень понимания, а не способность изобразить его / ее уровень понимания. Например, один учитель заявил: «Сначала не совсем правильно сообщил об измерении, а затем исправил». Кроме того, низкие языковые навыки M01 по математике и могли затруднить оценку учителей.
Например, один учитель заявил: «Сначала не совсем правильно сообщил об измерении, а затем исправил». Кроме того, низкие языковые навыки M01 по математике и могли затруднить оценку учителей.
В заключение, это исследование подтверждает утверждение из тематических исследований о том, что учащиеся с тяжелыми формами инвалидности могут продемонстрировать понимание математических концепций с помощью робота.Как и группа оценки в тематических исследованиях, учителя в этом исследовании согласились, что робот был наиболее эффективным из трех режимов для участников, чтобы «показать то, что они знают». Как и в тематическом исследовании, учителя в этом исследовании также заметили, что в режиме «Под руководством учителя» проблема в том, кто и что сделал (например, учитель «ведет» участника). Наконец, учителя в этом исследовании оценили «Режиссерский учитель» как эффективный способ изобразить понимание, но только для участников с хорошими языковыми навыками.В случае M01 языковые требования были слишком высоки, чтобы она могла эффективно использовать этот режим. Эффективность (с точки зрения времени) каждого режима и степень удовлетворенности участников были измерены, но здесь не сообщаются. Это важные факторы при рассмотрении использования роботов для выполнения действий.
Эффективность (с точки зрения времени) каждого режима и степень удовлетворенности участников были измерены, но здесь не сообщаются. Это важные факторы при рассмотрении использования роботов для выполнения действий.
Стратегии учителей начальной школы при церебральном параличе
 Они могут проинформировать вас о признаках, на которые следует обратить внимание, о корректировках, которые можно сделать, чтобы уменьшить дискомфорт, и о лучших способах лечения травм, болезней, боли и усталости.
Они могут проинформировать вас о признаках, на которые следует обратить внимание, о корректировках, которые можно сделать, чтобы уменьшить дискомфорт, и о лучших способах лечения травм, болезней, боли и усталости.


 Например, физиотерапевты и логопеды могут помочь вам понять и правильно использовать эффективные материалы и методы общения.
Например, физиотерапевты и логопеды могут помочь вам понять и правильно использовать эффективные материалы и методы общения.

Каковы стратегии обучения ученика с нарушением обучаемости по математике?
Дискалькулия – это инвалидность, связанная с математикой, в результате неврологической дисфункции.У студентов, которым поставлен диагноз дискалькулия, интеллектуальное функционирование в среднем или выше среднего, а также значительное несоответствие между их математическими навыками и нормами их сверстников по хронологическому возрасту. Для диагностики дискалькулии необходимо определить, что дефицит математики не связан просто с такими проблемами, как плохое обучение, плохое зрение, слух или другие физические проблемы, культурные или языковые различия или задержки в развитии.
В разделе «Размещение учащихся-математиков с нарушениями обучаемости» автор Рошель Кеньон перечисляет следующие стратегии обучения учащихся с нарушениями обучаемости, связанными с математикой.
- Избегайте перегрузки памяти. Назначьте управляемый объем работы по мере приобретения навыков.
- Увеличьте удержание, предоставив обзор в течение дня или двух после первоначального изучения сложных навыков.
- Обеспечить контролируемую практику, чтобы не допустить, чтобы учащиеся практиковали заблуждения и «неправильные правила».
- Сделайте новое обучение значимым, связав практику дополнительных навыков с выполнением задания в целом.
- Снижение требований к обработке путем предварительного обучения компонентным навыкам алгоритмов и стратегий.
- Помогите ученикам визуализировать математические задачи с помощью рисунков.
- Используйте наглядные и слуховые примеры.
- Используйте реальные жизненные ситуации, которые делают проблемы функциональными и применимыми к повседневной жизни.
- Решайте математические задачи на миллиметровой бумаге, чтобы числа совпадали.
- Используйте незагроможденные рабочие листы, чтобы не было слишком много визуальной информации.

- Практикуйтесь с соответствующими возрасту играми в качестве мотивационного материала.
- Попросите учащихся отслеживать свои успехи.
- Бросьте вызов критическому мышлению о реальных проблемах с помощью решения проблем.
- Используйте манипуляторы и технические средства, такие как магнитофоны или калькуляторы.
Этот список был адаптирован из следующего источника: Garnett, K., Frank, B., & Fleischner, J. X. (1983). Подход обобщения стратегий к изучению основных фактов (уроки сложения и вычитания, руководство №3; уроки умножения, руководство №5). Научно-исследовательский институт по изучению нарушений обучаемости. Нью-Йорк, Нью-Йорк: Педагогический колледж Колумбийского университета.
Дополнительные ресурсы о том, как сделать математику доступной для учащихся с ограниченными возможностями, см. В статье базы знаний DO-IT. Где я могу найти советы по обеспечению доступности математики для учащихся с ограниченными возможностями?
Для получения дополнительной информации о проблемах, с которыми сталкиваются учащиеся с нарушениями обучаемости по математике, обратитесь к статье базы знаний DO-IT. С какими типичными проблемами сталкиваются учащиеся с нарушениями в обучении, связанными с математикой?
С какими типичными проблемами сталкиваются учащиеся с нарушениями в обучении, связанными с математикой?
Ранние навыки счета при церебральном параличе: обзор и будущие исследования – VAN ROOIJEN – 2011 – Медицина развития и детская неврология
Аббревиатура
-
- SNARC
-
- Пространственная числовая ассоциация кода ответа
Что добавляет эта статья
- •
В нем рассматриваются современные знания о ранней способности детей с врожденным повреждением головного мозга к математике.
- •
Он дает направления для будущих систематических исследований ранних способностей к математике у детей с врожденным повреждением головного мозга, которые могут служить ориентиром для вмешательств в рамках специального образования.

Детский церебральный паралич (ДЦП) – это заболевание, которое в первую очередь влияет на контроль моторики. У детей с диагнозом ДЦП часто наблюдаются дополнительные нарушения чувствительности, восприятия, поведения и общения. 1 Тем не менее, знания о когнитивных способностях и их развитии у детей с ДЦП недостаточны. 2 Это удивительно из-за высокой распространенности проблем с обучением арифметике (26%) и трудностями чтения (19%) у детей с гемиплегическим ДЦП. 3
Было доказано, что ранние арифметические навыки, такие как счет и распознавание чисел, оказывают сильное влияние на последующие академические достижения. 4-7 Кроме того, числа и арифметические навыки играют центральную роль в повседневной жизни. 8, 9 Люди сталкиваются с числовой информацией в повседневной деятельности, например, при поиске нужного автобуса, оплате покупок и назначении свиданий для встречи с друзьями. Удивительно, но исследованиям арифметических способностей уделялось значительно меньше внимания, чем исследованиям способностей к чтению. 10 Это особенно характерно для детей с ДЦП, о чем свидетельствует недавний обзор нейропсихологического функционирования в этой группе, в котором не обсуждались какие-либо исследования развития арифметических способностей. 2
Удивительно, но исследованиям арифметических способностей уделялось значительно меньше внимания, чем исследованиям способностей к чтению. 10 Это особенно характерно для детей с ДЦП, о чем свидетельствует недавний обзор нейропсихологического функционирования в этой группе, в котором не обсуждались какие-либо исследования развития арифметических способностей. 2
Целью данной статьи является рассмотрение темы ранней математической грамотности в CP. Во-первых, мы описываем воплощенную структуру познания, с помощью которой можно систематически изучать развитие арифметических навыков. Во-вторых, мы даем описание современных знаний о развитии числовых и арифметических способностей от младенчества до начальной школы, а затем делаем обзор исследований по ранней математической грамотности у детей с ДЦП. Наконец, мы представляем направления будущих исследований по этой теме.Таким образом, эта статья представляет собой отправную точку для будущих исследований, которые улучшат наше понимание ранних навыков счета после врожденного повреждения мозга (ВП).
Роль воплощенного познания в арифметическом развитии
Один из важнейших вопросов психологии развития – это происхождение и рост знания. Исторически сложилось так, что дискуссия поляризовалась между эмпиризмом и нативизмом как двумя крайностями. 11 Недавно Spencer et al.утверждали, что мы должны оставить в стороне дискуссии между нативистами и эмпириками и сосредоточиться на теориях, которые поддерживают идею о том, что развитие «влечет за собой каскады взаимодействий на множестве уровней причинности, от генов до окружающей среды». 12 (стр. 80) Многообещающая и относительно новая перспектива, сфокусированная на влиянии восприятия в реальном времени и поведения действий на познание, – это теория воплощенного познания. 13-16 Хотя были разработаны различные версии этой точки зрения, центральное предположение состоит в том, что «… разум следует понимать в контексте его отношений с физическим телом, которое взаимодействует с миром». 14 (стр. 625) Как уже было предложено Пиаже, в младенчестве сенсорно-двигательная деятельность имеет фундаментальное значение для развития познания. 17 Другими словами, когда дети приобретут способность ходить, они будут иметь возможность смотреть на мир с другой точки зрения, сталкиваться с другими объектами и в целом сталкиваться с новым опытом обучения. 16 Иначе говоря, локомоция приводит к изменениям в развитии из-за «… переживаний, порождаемых независимой мобильностью». 18 (стр. 151)
14 (стр. 625) Как уже было предложено Пиаже, в младенчестве сенсорно-двигательная деятельность имеет фундаментальное значение для развития познания. 17 Другими словами, когда дети приобретут способность ходить, они будут иметь возможность смотреть на мир с другой точки зрения, сталкиваться с другими объектами и в целом сталкиваться с новым опытом обучения. 16 Иначе говоря, локомоция приводит к изменениям в развитии из-за «… переживаний, порождаемых независимой мобильностью». 18 (стр. 151)
Исследования, посвященные влиянию двигательных способностей на развитие арифметики, в основном сосредоточены на связи между использованием пальцев и счетом. Noël 19 продемонстрировал, что для детей первого класса (средний возраст 6-10 месяцев) гнозия пальцев, а именно распознавание и различение пальцев, является более мощным предиктором комбинированного фактора числовых способностей, такого как тест на ускоренное сложение, чем общие когнитивные год спустя (см. также Fayol et al. 20 ). Более того, методы подсчета пальцев по-прежнему влияют на числовые представления взрослых. Ди Лука и др. 21 исследовали влияние счета на обработку чисел, глядя на скорость набора текста у взрослых. Исходя из предположения, что маленькие числа связаны с левой стороной, а большие числа связаны с правой (также называемое эффектом пространственно-числовой ассоциации кода ответа [SNARC]), можно было бы ожидать, что участники будут быстрее реагировать, когда их пальцы были сопоставлены с клавиатурой, на которой слева направо отображались увеличивающиеся числа.Однако ответы при вводе текста были быстрее, когда сопоставление пальцев и пальцев было похоже на стратегию подсчета пальцев участников (начиная с большого пальца правой руки) по сравнению с другими комбинациями, включая мысленную числовую строку, состоящую из увеличивающихся чисел слева направо. . Таким образом, руки, числа и пространство становятся связанными посредством использования стратегии подсчета пальцев, но точный способ, которым это происходит, все еще неясен.
также Fayol et al. 20 ). Более того, методы подсчета пальцев по-прежнему влияют на числовые представления взрослых. Ди Лука и др. 21 исследовали влияние счета на обработку чисел, глядя на скорость набора текста у взрослых. Исходя из предположения, что маленькие числа связаны с левой стороной, а большие числа связаны с правой (также называемое эффектом пространственно-числовой ассоциации кода ответа [SNARC]), можно было бы ожидать, что участники будут быстрее реагировать, когда их пальцы были сопоставлены с клавиатурой, на которой слева направо отображались увеличивающиеся числа.Однако ответы при вводе текста были быстрее, когда сопоставление пальцев и пальцев было похоже на стратегию подсчета пальцев участников (начиная с большого пальца правой руки) по сравнению с другими комбинациями, включая мысленную числовую строку, состоящую из увеличивающихся чисел слева направо. . Таким образом, руки, числа и пространство становятся связанными посредством использования стратегии подсчета пальцев, но точный способ, которым это происходит, все еще неясен. 22
22
В качестве альтернативы можно было бы предположить, что пальцы представляют собой систему визуального представления, которая позволяет детям отслеживать уже подсчитанные предметы. 23 Следуя этой линии рассуждений, задержка в арифметических способностях детей с ДЦП не связана напрямую с их нарушенными двигательными способностями, но отсутствие репрезентативной системы может косвенно привести к отложенному концептуальному пониманию.
Дополнительная поддержка связи между физической активностью и арифметическими способностями была продемонстрирована Goldin-Meadow et al. в серии экспериментов по изучению роли жестов при решении арифметических задач. 24 Участников попросили объяснить математическую задачу и одновременно запомнить список слов. Задачи по математике должны были быть для участников непростыми. Таким образом, детей (средний возраст 9 лет 11 месяцев) попросили решить задачи сложения (например, 4 + 5 + 3 =… + 3), а взрослым студенческого возраста нужно было решить задачи факторинга (например, x 2 −5 x + 6 = (…) (…)). Дети и взрослые показали значительно лучшие результаты, когда им позволяли «разговаривать» руками при объяснении арифметической задачи, чем когда им не разрешали пользоваться руками.По мнению авторов, «… жест и речь образуют интегрированную и, по сути, синергетическую систему, в которой усилия, затраченные в одной модальности, могут снизить нагрузку на систему в целом». 24 (стр. 521)
Дети и взрослые показали значительно лучшие результаты, когда им позволяли «разговаривать» руками при объяснении арифметической задачи, чем когда им не разрешали пользоваться руками.По мнению авторов, «… жест и речь образуют интегрированную и, по сути, синергетическую систему, в которой усилия, затраченные в одной модальности, могут снизить нагрузку на систему в целом». 24 (стр. 521)
Кроме того, нейровизуализационные исследования показали, что области мозга, активируемые вручную, и области мозга, активируемые вычислениями и обработкой чисел, расположены в непосредственной близости друг от друга во внутрипариетальной борозде. 25 Эти результаты подтверждают предположение, что количественная система (обработка чисел) и система действий (например, схватывание) тесно связаны (поведенческие результаты см. Моретто и ди Пеллегрино 26 ).
В заключение, перспектива воплощенного познания была подтверждена различными исследованиями, которые показали связь между двигательной активностью и познанием. Принимая эту теоретическую основу в качестве отправной точки, можно предположить, что развитие адекватных арифметических способностей скомпрометировано и имеет нетипичную траекторию развития у детей с врожденными двигательными нарушениями (ВП), поскольку их физические недостатки не позволяют им получить необходимый двигательный опыт.
Ранние навыки счета у типично развивающихся детей
В этом разделе мы даем краткий обзор типичного развития арифметических способностей в начальной школе. Более подробные описания были опубликованы в другом месте (см. Geary 27 и Butterworth 8 ).
Одна из самых спорных тем в математическом развитии – есть ли у младенцев врожденная способность обрабатывать числа, что следует из нативистской точки зрения (например,г. Dehaene et al. 28 ). Используя парадигмы привыкания, Сюй и Спелке 29 продемонстрировали, что 6-месячные младенцы могут различать точки в соотношении 1: 2 (8 против 16), но не в соотношении 2: 3 (8 против 12). Кроме того, сообщалось, что 9-месячные младенцы дольше смотрят на неправильные (5 + 5 = 5), чем на правильные (5 + 5 = 10) ответы на простые арифметические задачи. 30 Хотя исследования, подтверждающие врожденную числовую компетентность, впечатляют, несколько важных вопросов остаются. Например, утверждалось, что дети сосредотачиваются не на числах, а на визуально-пространственных характеристиках стимулов. 31
Кроме того, сообщалось, что 9-месячные младенцы дольше смотрят на неправильные (5 + 5 = 5), чем на правильные (5 + 5 = 10) ответы на простые арифметические задачи. 30 Хотя исследования, подтверждающие врожденную числовую компетентность, впечатляют, несколько важных вопросов остаются. Например, утверждалось, что дети сосредотачиваются не на числах, а на визуально-пространственных характеристиках стимулов. 31
Было предложено развивать арифметические способности иерархически, что подразумевает, что первые навыки счета имеют фундаментальное значение для дальнейшего развития. 32 С 2-х лет у детей развивается умение вербально считать. 27 Практически во всех культурах дети разрабатывают стратегии подсчета пальцев, 21 , которые часто используются как строительные леса. 33 Начав считать устно, дети должны усвоить принципы счета.Например, принцип мощности утверждает, что количество подсчитываемых объектов равно значению последнего числа в строке. 34
34
В возрасте от 4 до 5 лет дети обычно полагаются на счетные стратегии для решения простых арифметических задач. Часто они переходят от подсчета всех к отсчету от первого целого числа (2 + 5 = (2), 3, 4 и т. Д.) К отсчету от большей цифры (2 + 5 = (5), 6, 7 ), и в конечном итоге ответы запоминаются по мере того, как дети приобретают арифметические знания.Предполагается, что ассоциации будут развиваться между комбинациями цифр (например, 2 + 4) и их правильными ответами, потому что эти ответы становятся более прочными, а ассоциации между неправильными решениями ослабевают. Дальнейшее арифметическое развитие детей во многом зависит от культуры, в которой они растут, и ее образовательной системы, 8 , что согласуется с акцентом Выготского на роль социальных факторов и факторов окружающей среды. 35
Несколько недавних исследований изучали вклад связанных конструкций в развитие арифметических способностей в начальной школе. Как и ожидалось, было обнаружено влияние общих нейропсихологических факторов высшего порядка, таких как интеллект, рабочая память и исполнительное функционирование (например, De Smedt et al. 36 и Kroesbergen et al. 37 ). Кажется, что рабочая память естественным образом связана с решением математических задач, поскольку необходимо запоминать неполную информацию, а новую информацию необходимо обрабатывать, чтобы прийти к правильному решению. 38 Однако относительно конкретных компонентов модели рабочей памяти 39 Бэдделли и Хитча существует еще больше разногласий.Авторы приходят к выводу, что «… исполнительные и визуально-пространственные навыки могут быть задействованы для изучения и применения новых математических навыков / концепций, тогда как фонологический цикл может вступить в игру после того, как навык будет изучен». 38 (стр. 9) Неопиажеские теории познания (например, Case et al. 40 ) преимущественно обращают внимание на влияние роста объема рабочей памяти на познание.
Как и ожидалось, было обнаружено влияние общих нейропсихологических факторов высшего порядка, таких как интеллект, рабочая память и исполнительное функционирование (например, De Smedt et al. 36 и Kroesbergen et al. 37 ). Кажется, что рабочая память естественным образом связана с решением математических задач, поскольку необходимо запоминать неполную информацию, а новую информацию необходимо обрабатывать, чтобы прийти к правильному решению. 38 Однако относительно конкретных компонентов модели рабочей памяти 39 Бэдделли и Хитча существует еще больше разногласий.Авторы приходят к выводу, что «… исполнительные и визуально-пространственные навыки могут быть задействованы для изучения и применения новых математических навыков / концепций, тогда как фонологический цикл может вступить в игру после того, как навык будет изучен». 38 (стр. 9) Неопиажеские теории познания (например, Case et al. 40 ) преимущественно обращают внимание на влияние роста объема рабочей памяти на познание. 41 Более того, когнитивные способности, зависящие от предметной области, такие как чувство числа, счет и субитизация, также позволяют прогнозировать арифметические способности в школе (например,г. Kroesbergen et al., 37 Desoete et al., 42 и Jordan et al. 43 ).
41 Более того, когнитивные способности, зависящие от предметной области, такие как чувство числа, счет и субитизация, также позволяют прогнозировать арифметические способности в школе (например,г. Kroesbergen et al., 37 Desoete et al., 42 и Jordan et al. 43 ).
Недавно были предприняты попытки объединить общие навыки предметной области (например, рабочая память и исполнительные функции) и особенности предметной области (например, количественно-числовые компетенции) в развитии арифметических способностей с течением времени. 44-46 Bull et al. 44 следили за детьми из дошкольных учреждений, чтобы предсказать математические достижения в первом и третьем классах начальной школы.Их результаты показали, что, хотя рабочая память и навыки управляющих функций были предикторами успеваемости по математике и чтению, зрительно-пространственная кратковременная память была конкретным предиктором успеваемости по математике. В соответствии с этими выводами Simmons et al. 46 обнаружили специфическое влияние визуально-пространственного блокнота на развитие арифметики. Хотя роль зрительно-пространственных способностей не однозначна (например, Gathercole et al. 47 ), способность формировать визуальные представления кажется весьма актуальной для развития математических навыков.
В соответствии с этими выводами Simmons et al. 46 обнаружили специфическое влияние визуально-пространственного блокнота на развитие арифметики. Хотя роль зрительно-пространственных способностей не однозначна (например, Gathercole et al. 47 ), способность формировать визуальные представления кажется весьма актуальной для развития математических навыков.
В целом, хотя развитие арифметических способностей описано подробно, всеобъемлющая теоретическая основа все еще отсутствует. Следовательно, комбинация аспектов из теоретических представлений использовалась исследователями для тщательного изучения развития математических способностей. В частности, влияние Пиаже на сенсорно-моторные переживания для познания и акцент Выготского на окружающей среде и роли языка по-прежнему оказывали влияние. 41
Ранние навыки счета детей с КП
Чтобы просмотреть имеющиеся знания о начальном обучении счету в CP, мы систематически искали в PubMed, Medline, PsychInfo, ERIC и Scopus все статьи по этой теме, опубликованные до 2009 г. включительно.Мы использовали поисковые запросы «умение считать» ИЛИ «числовое понятие» ИЛИ «счет» ИЛИ «субитизирующая арифметика» ИЛИ «математика» ИЛИ «вычисление» ИЛИ «расчет И церебральный паралич» ИЛИ «врожденный» ИЛИ «гемиплегия». Мы решили включить только те исследования, которые были опубликованы в международных журналах, перечисленных в Индексе научного цитирования и написанные на английском языке. После проверки рефератов на релевантность осталось восемь исследований, в которых изучались числовые и арифметические способности детей с врожденным повреждением головного мозга (ВП).Для сравнения: быстрый поиск с использованием PsychInfo привел к более чем 250 статьям, посвященным математическим способностям типично развивающихся детей. Ниже мы дадим краткое изложение немногочисленных исследований, посвященных изучению навыков счета в раннем возрасте у детей с ДЦП (см. Таблицу I).
включительно.Мы использовали поисковые запросы «умение считать» ИЛИ «числовое понятие» ИЛИ «счет» ИЛИ «субитизирующая арифметика» ИЛИ «математика» ИЛИ «вычисление» ИЛИ «расчет И церебральный паралич» ИЛИ «врожденный» ИЛИ «гемиплегия». Мы решили включить только те исследования, которые были опубликованы в международных журналах, перечисленных в Индексе научного цитирования и написанные на английском языке. После проверки рефератов на релевантность осталось восемь исследований, в которых изучались числовые и арифметические способности детей с врожденным повреждением головного мозга (ВП).Для сравнения: быстрый поиск с использованием PsychInfo привел к более чем 250 статьям, посвященным математическим способностям типично развивающихся детей. Ниже мы дадим краткое изложение немногочисленных исследований, посвященных изучению навыков счета в раннем возрасте у детей с ДЦП (см. Таблицу I).
| Исследование | Дизайн a | n (контроль b ) | Средний возраст, г: мес (диапазон) | Тип CP | Арифметическая конструкция | Задание использовано | Результаты |
|---|---|---|---|---|---|---|---|
| Арп и Фагард 49 | Поперечное сечение | 44 (22) | 5:11 и 8: 0 (4–6 и 7–9) | 3 гемиплегии, 19 диплегии, 1 триплегии, 21 тетраплегии | Субитизация | Классическая задача: компьютеризированная, явная, количественная оценочная задача, состоящая из 33 элементов. На экране кратко (250 мс) были представлены предметы, содержащие от одного до шести шариков. Дети должны были оценить количество шариков. Задание на распознавание образов: сначала дети должны были выучить названия шести образов, состоящих из одной-шести точек в порядке, соответствующем случайному условию в классической задаче на субитизацию. Каждый образец был представлен (250 мс) три раза в псевдослучайном порядке. Участников спросили, кто появился на экране. На экране кратко (250 мс) были представлены предметы, содержащие от одного до шести шариков. Дети должны были оценить количество шариков. Задание на распознавание образов: сначала дети должны были выучить названия шести образов, состоящих из одной-шести точек в порядке, соответствующем случайному условию в классической задаче на субитизацию. Каждый образец был представлен (250 мс) три раза в псевдослучайном порядке. Участников спросили, кто появился на экране. |
При разделении заданий на подзадачи детей с ДЦП можно разделить на эффективную (аналогично контролю) и неэффективную (значительно меньшую) группы. |
| Arp et al. 48 | Поперечное сечение | 29 (29 с ) | 6: 6 (4–8) | 3 спастическая гемиплегия (справа), 9 спастическая диплегия, 16 спастическая тетраплегия, 1 атетозная дистония | (1) Субитизация и (2) подсчет | (1) Компьютеризированная, явная задача количественной оценки, состоящая из 33 элементов. На экране кратко (250 мс) были представлены предметы, содержащие от одного до шести шариков. Дети должны были оценить количество шариков. (2) Компьютерное задание, в котором от двух до шести красных шариков показывались один раз без ограничения по времени. Ребенку требовалось назвать количество мячей. На экране кратко (250 мс) были представлены предметы, содержащие от одного до шести шариков. Дети должны были оценить количество шариков. (2) Компьютерное задание, в котором от двух до шести красных шариков показывались один раз без ограничения по времени. Ребенку требовалось назвать количество мячей. |
У детей с ХП был нижний предел субитизации. |
| Dellatolas et al. 56 | Поперечное сечение | 30 (60) | 7: 6 (7–8) | 19 гемиплегий (9 слева, 10 справа), 10 диплегий, 1 триплегия | (1) воспроизведение фигур, (2) встроенные фигуры, (3) счет точек и (4) обратный счет | (1) Сложная геометрическая фигура была представлена в течение 1 мин. Ребенка попросили нарисовать эти фигуры по памяти. (2) Задание с бумагой и карандашом, состоящее из пяти элементов, в котором детям нужно было показать геометрическую фигуру, встроенную в более сложную геометрическую фигуру. (3) Две карточки со случайным образом отображаемыми точками. (10 и 18). Ребенок должен был вслух считать количество точек, одновременно указывая и не указывая. (4) От 22 до 1. Ребенка попросили нарисовать эти фигуры по памяти. (2) Задание с бумагой и карандашом, состоящее из пяти элементов, в котором детям нужно было показать геометрическую фигуру, встроенную в более сложную геометрическую фигуру. (3) Две карточки со случайным образом отображаемыми точками. (10 и 18). Ребенок должен был вслух считать количество точек, одновременно указывая и не указывая. (4) От 22 до 1. |
Корреляция между поражением левой руки и зрительно-пространственными и счетными навыками. |
| Jenks et al. 53 | продольный | 57 (16) | 7: 0 | ЦП группа специального образования: 10 односторонних (4 правых, 6 левых), 29 двусторонних, 2 атаксических. Основная образовательная группа ХП: 12 односторонних (8 правых, 4 левых), 3 двусторонних, 1 атаксическая. Основная образовательная группа ХП: 12 односторонних (8 правых, 4 левых), 3 двусторонних, 1 атаксическая. |
(1) Ранние навыки счета, (2) сложение и (3) вычитание | (1) Ранний тест на математику (van Luit et al. [1994] 54 ). (2) Компьютеризированный тест, состоящий из задач в форме a + b , в которых a и b не являются эквивалентно, как a, , так и b больше 1, а сумма a и b не превышает 10.(3) Компьютеризированная задача, состоящая из задач в форме a – b , в которой 3 < a <11 и 1 < b <8. Оба теста состояли из 28 испытаний. | До школы дети с ДЦП показали более низкие результаты по математике в раннем возрасте, чем при сравнении. В конце первого класса учащиеся с КП в обычном образовании получали столь же высокие баллы, как и в сравнении. Отставали дети с ДЦП в специальном образовании. Отставали дети с ДЦП в специальном образовании. |
| Jenks et al. 52 | продольный | 57 (16) | 7: 0 | ЦП группа специального образования: 10 односторонних (4 правых, 6 левых), 29 двусторонних, 2 атаксических. Основная образовательная группа ХП: 12 односторонних (8 правых, 4 левых), 3 двусторонних, 1 атаксическая. | (1) Сложение и (2) вычитание | Компьютеризированные задачи, состоящие из простого сложения (ответов ≤10), простого вычитания (наибольшее число ≤10) и сложного сложения (ответов ≤100) элементов. | В середине третьего класса группа с ДЦП в специальном образовании была значительно медленнее и менее точна, вероятно, из-за того, что они не знали арифметических фактов. |
| Jenks et al. 51 | продольный | 57 (16) | 7: 0 | ЦП группа специального образования: 10 односторонних (4 правых, 6 левых), 29 двусторонних, 2 атаксических.Основная образовательная группа ХП: 12 односторонних (8 правых, 4 левых), 3 двусторонних, 1 атаксическая. | (1) Сложение и (2) вычитание | Использовались те же задания, что и в исследовании Jenks et al. (2007) 53 | Нет существенных различий между детьми с ДЦП в обычном образовании и сравнениях. Те, у кого ДЦП в специальном образовании, не догнали его к концу второго класса. |
| Jenks et al. 55 | Поперечное сечение | 22 (44) (15 с КП) | 10: 8 | 4 односторонних, 11 двусторонних | (1) арифметическая производительность и (2) скорость вычисления фактов | (1) Голландский стандартизированный групповой тест CITO, предназначенный для измерения уровня арифметических достижений (знаний, понимания и способностей) учащихся.Тестовые задания охватывают сложение, вычитание, умножение и деление в вычислительных задачах и в задачах со словами. (2) Сорок восемь задач на сложение с правильными ответами до 10 и 44 задачи на вычитание в форме a – b (например, что и a , и b были меньше 10). Обе части нужно было завершить за 1 минуту. Обе части нужно было завершить за 1 минуту. |
Группа с расстройствами центральной нервной системы составила в среднем 1 балл.5й отставание по арифметическим достижениям. |
| Kiessling et al. 57 | Поперечное сечение | 16 (13 д ) | (7–14) | 16 гемиплегии (8 справа, 8 слева) | Решение арифметических задач | Оценка с широким диапазоном достижений (Jastak and Jastak [1978] 64 ) | Положительная корреляция между поражением левой руки и оценками по математике. |
- a Дизайн: только указывает, было ли исследование поперечным или продольным.
- b Все контроли соответствовали возрасту, если не указано иное.
- c Дети сравнения не были сопоставлены.
- d Дети сравнения были братьями и сестрами ближайшего возраста.
- ЦИТО, Центральный институт разработки тестов (Centraal Instituut voor Toetsontwikkeling).
Arp et al. 48, 49 сосредоточены на субитизации у детей с ХП. Это возможность определить количество определенного количества предметов, которые представлены за слишком короткое время, чтобы сделать возможным подсчет. 42 Субитизация была выбрана потому, что по сравнению с их сверстниками было показано, что дети с ХП уже задерживают подсчет (например, Арп и Фагард 50 ). Арп и Фагард 49 предположили, что этот недостаток может быть вызван зрительно-пространственной диспраксией, которая приводит к неспособности указать на компоненты дисплея. Это, в свою очередь, помешает детям с ДЦП развить навыки точного счета.
42 Субитизация была выбрана потому, что по сравнению с их сверстниками было показано, что дети с ХП уже задерживают подсчет (например, Арп и Фагард 50 ). Арп и Фагард 49 предположили, что этот недостаток может быть вызван зрительно-пространственной диспраксией, которая приводит к неспособности указать на компоненты дисплея. Это, в свою очередь, помешает детям с ДЦП развить навыки точного счета.
Субитизация была изучена с использованием поперечного дизайна; Установлено, что у 6-летних детей с ХП нижний предел субитизации, т.е.е. максимальное количество элементов, которые они могли правильно оценить, было меньше, чем у сравниваемых детей. Возрастное увеличение пределов субитизации было сопоставимо как для типично развивающихся детей, так и для детей с ХП. На основании этих результатов авторы пришли к выводу, что у детей с ДЦП не наблюдается качественно иной траектории развития, но эта траектория просто задерживается. 48 В связанном исследовании Арп и Фагард 49 изучили причину нарушения способности к субитизации у детей с ХП. Результаты подтвердили гипотезу «зрительно-пространственного дефицита», согласно которой дети с ДЦП имеют затруднения в восприятии и запоминании пространственных паттернов.
Результаты подтвердили гипотезу «зрительно-пространственного дефицита», согласно которой дети с ДЦП имеют затруднения в восприятии и запоминании пространственных паттернов.
Продольные данные об успеваемости детей от 7 лет с КП по простым арифметическим вычислениям доступны из исследований Jenks et al. 51, 52 Они сравнили три группы детей в Нидерландах: дети с ДЦП в обычном русле, дети с ДЦП в специальном образовании и группу сравнения типично развивающихся детей, сопоставимых по возрасту и полу.Голландская система образования такова, что основное и специальное образование существуют параллельно. Первая волна измерений была проведена, когда дети учились в первом классе (средний возраст 7 лет). До того, как началось формальное обучение арифметике, эти три группы значительно отличались друг от друга по начальным навыкам счета (у людей с КП в специальном образовании было меньше навыков, чем у людей с КП в обычном образовании, которые, в свою очередь, обладали меньшими навыками, чем группа сравнения) 53 по результатам теста на умение считать в раннем возрасте. 54 К концу второго класса дети с ДЦП в обычном образовании сравнялись с детьми сравнения по точности арифметики. Однако результаты детей с ДЦП в специальном образовании оставались значительно ниже по арифметическим тестам. Важно отметить, что результаты были аналогичными, когда интеллект был включен в качестве контрольной переменной. Более того, аналогичные результаты были получены в исследовании, в котором участвовала объединенная группа 10-летних детей с ХП и расщелиной позвоночника, у которых было показано отставание 1.5 лет отстает от своих типичных коллег по простым арифметическим операциям. 55
54 К концу второго класса дети с ДЦП в обычном образовании сравнялись с детьми сравнения по точности арифметики. Однако результаты детей с ДЦП в специальном образовании оставались значительно ниже по арифметическим тестам. Важно отметить, что результаты были аналогичными, когда интеллект был включен в качестве контрольной переменной. Более того, аналогичные результаты были получены в исследовании, в котором участвовала объединенная группа 10-летних детей с ХП и расщелиной позвоночника, у которых было показано отставание 1.5 лет отстает от своих типичных коллег по простым арифметическим операциям. 55
Также были исследованы потенциальные факторы, которые могут повлиять на арифметические действия. 53 С этой целью арифметическая точность была связана с вербальным и невербальным интеллектом, визуально-пространственным блокнотом, центральным исполнительным директором, временем обучения в школе и начальными способностями к математике, такими как счет и представление чисел. Интересно, что невербальный интеллект оказался важным предиктором арифметической точности, тогда как вербальный интеллект не имел существенной связи. 51 Кроме того, влияние рабочей памяти было исследовано более тщательно. Из центральных исполнительных компонентов смещение (способность переключаться между задачами) и обновление (способность удерживать информацию) были связаны с математической компетентностью. 52 Таким образом, аналогичные процессы, как у типично развивающихся детей, составляют основу арифметических трудностей у детей с ДЦП. 53
Интересно, что невербальный интеллект оказался важным предиктором арифметической точности, тогда как вербальный интеллект не имел существенной связи. 51 Кроме того, влияние рабочей памяти было исследовано более тщательно. Из центральных исполнительных компонентов смещение (способность переключаться между задачами) и обновление (способность удерживать информацию) были связаны с математической компетентностью. 52 Таким образом, аналогичные процессы, как у типично развивающихся детей, составляют основу арифметических трудностей у детей с ДЦП. 53
Чтобы лучше понять взаимосвязь между ручным трудом (нарушение функции руки; поражение левой или правой руки) и нейропсихологическим функционированием, Dellatolas et al. 56 исследовали детей со спастическим ДЦП, используя расширенную батарею тестов. Не было обнаружено никакой связи между общим когнитивным измерением интеллекта и навыками рук. Однако нарушение работы левой руки положительно коррелировало с навыками арифметических вычислений, тогда как степень исполнения правой рукой положительно коррелировала с фонологическими способностями. Сравнимые результаты были также представлены Kiessling et al., 57 , которые продемонстрировали, что лишенная функция левой руки значительно коррелировала с низкими оценками успеваемости по математике.Эти авторы утверждают, что зрительно-пространственные способности, обычно в сочетании с функцией правого полушария, необходимы для «истинного математического чутья».
Сравнимые результаты были также представлены Kiessling et al., 57 , которые продемонстрировали, что лишенная функция левой руки значительно коррелировала с низкими оценками успеваемости по математике.Эти авторы утверждают, что зрительно-пространственные способности, обычно в сочетании с функцией правого полушария, необходимы для «истинного математического чутья».
Подводя итог, можно сказать, что существующие исследования показывают, что дети с ДЦП регулярно отстают в подсчете, субитализации и простых арифметических операциях по сравнению с их обычно развивающимися сверстниками. Кроме того, продольное исследование Jenks et al. показали, что отстают, в частности, дети с ДЦП в специальном образовании. Однако наш поиск литературы показал недостаток исследований по этой теме по сравнению с типично развивающимися детьми.Следовательно, нельзя сделать общих выводов об антецедентах и траекториях развития арифметических способностей у этих детей. В частности, способности детей с ДЦП в раннем возрасте не изучались в долгосрочном плане. Это особенно примечательно, потому что математика развивается иерархически, и ранние арифметические способности оказались важным требованием для дальнейшего развития. 8
Это особенно примечательно, потому что математика развивается иерархически, и ранние арифметические способности оказались важным требованием для дальнейшего развития. 8
Направления будущего
Арифметические навыки необходимы для большинства повседневных дел и успеваемости в школе.До сих пор исследования упускали из виду важность ранних способностей детей с ДЦП к счету. Однако высокая распространенность проблем с обучением арифметике (26%) у детей с гемиплегической CP 3 требует изучения и вмешательства в этот процесс.
Исследования
В соответствии с Goswami 58 и Karmiloff-Smith, 59 мы предлагаем, чтобы исследования по ранней математической грамотности и CP были направлены на следующие предпосылки.Во-первых, начиная с раннего возраста, за детьми с диагнозом ХП следует наблюдать долгое время. Было обнаружено, что ранние числовые способности позволяют прогнозировать достижения в школьном возрасте типично развивающихся детей. Кроме того, если изучать только конечный результат у детей старшего возраста, многие важные сведения о процессе могут быть упущены. Jenks et al. 51 уже провели лонгитюдное исследование развития арифметических навыков у детей старшего возраста с ДЦП. Однако лонгитюдных данных о раннем развитии математики у детей с ДЦП до сих пор нет.
Кроме того, если изучать только конечный результат у детей старшего возраста, многие важные сведения о процессе могут быть упущены. Jenks et al. 51 уже провели лонгитюдное исследование развития арифметических навыков у детей старшего возраста с ДЦП. Однако лонгитюдных данных о раннем развитии математики у детей с ДЦП до сих пор нет.
Кроме того, следует попытаться отделить поведенческие процессы от лежащих в основе когнитивных процессов. Хорошо известно, что одинаковые поведенческие исходы могут быть результатом разных нейропсихологических процессов. Чтобы иметь возможность оценивать развитие навыков счета у детей с ДЦП, в план исследования должны быть включены группы сравнения, соответствующие когнитивным процессам (математический уровень), а не только поведенческим оценкам (хронологический уровень).
Более того, необходимо провести исследования, чтобы изучить роль факторов окружающей среды, таких как домашняя ситуация и учеба, которые, как было установлено, оказывают влияние на развитие арифметики. 8 Существует острая необходимость в многофакторных исследованиях, объясняющих индивидуальные различия в развитии навыков счета у детей с ДЦП с точки зрения характеристик ребенка, семьи, к которой он принадлежит, и институционального ухода, через который он прошел.
8 Существует острая необходимость в многофакторных исследованиях, объясняющих индивидуальные различия в развитии навыков счета у детей с ДЦП с точки зрения характеристик ребенка, семьи, к которой он принадлежит, и институционального ухода, через который он прошел.
Кроме того, в будущих исследованиях двигательные и когнитивные способности должны быть изучены более подробно. Только Jenks et al. 51 дифференцировали детей с односторонним и двусторонним спастическим ДЦП, и они не обнаружили никаких различий в арифметической точности. Таким образом, влияние типов и локализации КП и арифметической работы далеко не ясно. Более того, более практические аспекты, такие как роль доминирования рук в стратегиях подсчета пальцев, явно не рассматривались.Наконец, интеллект почти всегда используется в качестве критерия включения, когда участвуют дети с ДЦП. Тем не менее, важность невербального интеллекта для развития арифметики требует более тщательного исследования.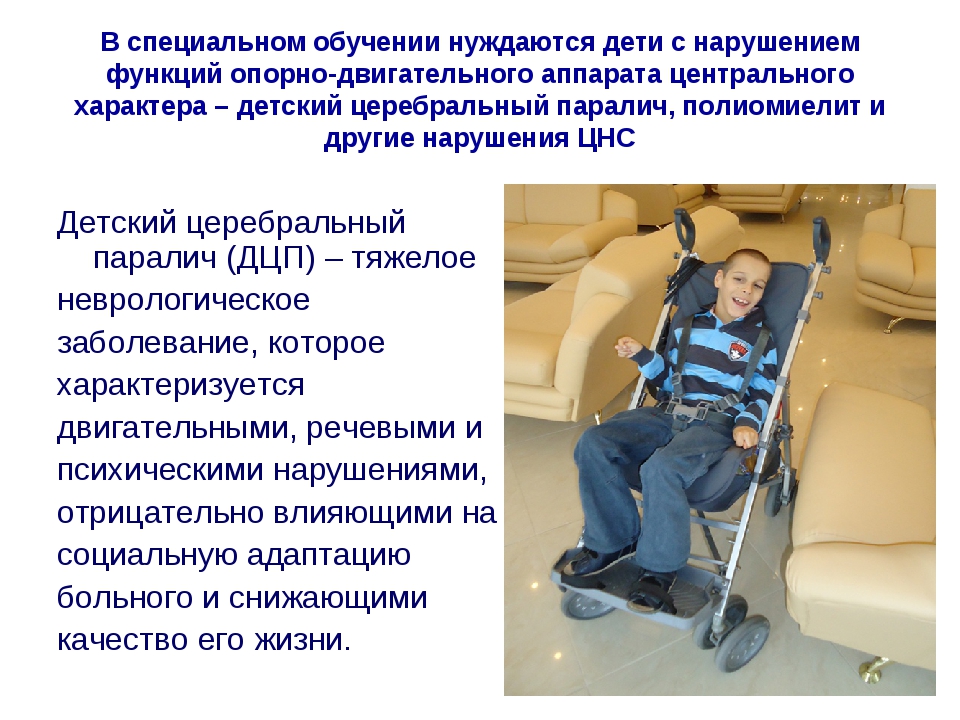
Операция
К сожалению, доступные исследования математического развития детей с ДЦП не предоставляют достаточно информации, чтобы предложить окончательное решение по содержанию программ вмешательства. Принимая во внимание знания типично развивающихся детей, результаты до сих пор подчеркивают влияние ранних способностей, таких как счет и субитизация, а также общих когнитивных факторов предметной области, в частности рабочей памяти. 60 Более того, метаанализ влияния математических вмешательств в специальном образовании пришел к выводу, что обучение базовым навыкам, таким как сложение и вычитание, было наиболее эффективным. 61
Важный вопрос заключается в том, до какой степени можно улучшить развитие навыков счета у детей с ДЦП, следуя воплощенной точке зрения в рамках вмешательства. Кауфман 62 утверждал, что использование пальцев может функционировать как дополнительный инструмент при установлении мысленных представлений чисел и помогать обучаться счету и расчету. Это подтверждается сильной корреляцией, обнаруженной между спонтанным использованием стратегий подсчета пальцев и точностью числовых комбинаций детьми в детском саду. 33 Арифметические процедуры следует выполнять до тех пор, пока они не смогут автоматически выполняться детьми с математическими трудностями. После того, как они получили эти инструкции, у них появляется больше ресурсов для внимания и рабочей памяти, доступных для более конкретных функций математических задач. 32 Таким образом, можно утверждать, что преподавание математики должно быть основано на рассуждении, основанном на воплощении (действие – это обучение), чтобы помочь детям в построении и понимании математики. 63
Это подтверждается сильной корреляцией, обнаруженной между спонтанным использованием стратегий подсчета пальцев и точностью числовых комбинаций детьми в детском саду. 33 Арифметические процедуры следует выполнять до тех пор, пока они не смогут автоматически выполняться детьми с математическими трудностями. После того, как они получили эти инструкции, у них появляется больше ресурсов для внимания и рабочей памяти, доступных для более конкретных функций математических задач. 32 Таким образом, можно утверждать, что преподавание математики должно быть основано на рассуждении, основанном на воплощении (действие – это обучение), чтобы помочь детям в построении и понимании математики. 63
Окончательная перспектива
Подробные отчеты были написаны о развитии арифметических способностей с младенчества (например, Гири 27 ). Однако описание основных факторов и теоретическая база все еще отсутствуют. Описание воплощенного познания предлагает многообещающую перспективу для исследования влияния перцептивного и моторного опыта на когнитивное развитие. Как описано ранее, использование пальцев при счете может функционировать как визуальная репрезентативная система, а жесты могут использоваться для разгрузки познания, т.е.е. снижение нагрузки на рабочую память. Важно отметить, что исследование ранних способностей детей с ДЦП к математике могло не только улучшить наше понимание траекторий развития арифметики у детей с ДЦП в частности, но и расширить наши знания о развитии арифметических способностей детей в целом.
Описание воплощенного познания предлагает многообещающую перспективу для исследования влияния перцептивного и моторного опыта на когнитивное развитие. Как описано ранее, использование пальцев при счете может функционировать как визуальная репрезентативная система, а жесты могут использоваться для разгрузки познания, т.е.е. снижение нагрузки на рабочую память. Важно отметить, что исследование ранних способностей детей с ДЦП к математике могло не только улучшить наше понимание траекторий развития арифметики у детей с ДЦП в частности, но и расширить наши знания о развитии арифметических способностей детей в целом.
Список литературы
- 1
Bax M,
Гольдштейн М,
Розенбаум П.,
Левитон А,
Панет Н.Предлагаемое определение и классификация церебрального паралича, апрель 2005 г.
Dev Med Child Neurol
2005; 47: 571–6.

- 2 Штрауб К., Обрзут Ю. Влияние церебрального паралича на нейропсихологическую функцию. J Dev Phys Disabil 2009; 21: 153–67.
- 3 Фрэмптон I, Юд С, Гудман Р.Распространенность и корреляты конкретных трудностей в обучении в репрезентативной выборке детей с гемиплегией. Br J Educ Psychol 1998; 68: 39–51.
- 4 Дункан Г.Дж., Доусетт CJ, Claessens A, et al. Готовность к школе и последующие достижения. Дев Психол 2007; 43: 1428–46.
- 5
Классенс А,
Дункан Джи,
Энгель М.
 Навыки детского сада и успеваемость в пятом классе: данные ECLS-K.
Econ Educ Rev
2009; 28: 415–27.
Навыки детского сада и успеваемость в пятом классе: данные ECLS-K.
Econ Educ Rev
2009; 28: 415–27.
- 6 Бирнс JP, Васик Б.А. Факторы, предсказывающие успеваемость по математике в детском саду, в первом и третьем классе: анализ возможностей-склонностей. Contemp Educ Psychol 2009; 34: 167–83.
- 7 Лочуняк М.Н., Иордания NC. Использование чувства детского сада для прогнозирования беглости вычислений во втором классе. J Learn Disabil 2008; 41: 451–9.
- 8
Баттерворт Б.Развитие арифметических способностей.
J Детская психическая психиатрия
2005; 46: 3–18.

- 9 Гири, округ Колумбия. От младенчества до взрослой жизни: развитие числовых способностей. Eur Детская подростковая психиатрия 2000; 9: 11–6.
- 10 Hecht SA, Торгесен Ю.К., Вагнера РК, Rashotte CA.Взаимосвязь между способностями фонологической обработки и возникающими индивидуальными различиями в навыках математических вычислений: продольное исследование со второго по пятый класс. J Exp Child Psychol 2001; 79: 192– 227.
- 11 Миллер PH. Теории психологии развития. 4-е изд. Нью-Йорк: Worth Publishers, 2002.
- 12
Спенсер JP,
Блумберг М.
 С.,
МакМюррей Б,
Робинзон С.Р.,
Самуэльсон Л.К.,
Томблин JB.Короткие руки и говорящие яйца: почему мы не должны больше мириться с дебатами нативистов и эмпириков.
Перспектива ребенка-разработчика
2009; 3: 79–87.
С.,
МакМюррей Б,
Робинзон С.Р.,
Самуэльсон Л.К.,
Томблин JB.Короткие руки и говорящие яйца: почему мы не должны больше мириться с дебатами нативистов и эмпириков.
Перспектива ребенка-разработчика
2009; 3: 79–87.
- 13 Barsalou LW. Обоснованное познание. Анну Рев Психол 2008; 59: 617–45.
- 14 Уилсон М.Шесть взглядов на воплощенное познание. Psychon Bull Rev 2002; 9: 625–36.
- 15 Кларк А. Язык, воплощение и когнитивная ниша. Trends Cogn Sci 2006; 10: 370–4.
- 16
Телен Э,
Смит Л.
 Б.
Динамический системный подход к развитию познания и действия.Кембридж, Массачусетс: MIT Press, 1994.
Б.
Динамический системный подход к развитию познания и действия.Кембридж, Массачусетс: MIT Press, 1994.
- 17 Piaget J, Инельдер Б. [Психология ребенка]. (На французском). Париж: Press Universitaires de France, 1966.
- 18 Кампос Дж. Дж., Андерсон Д.И., Барбу-Рот, Массачусетс, Хаббард Э.М., Гертенштейн MJ, Уизерингтон Д. Путешествие расширяет кругозор. Младенчество 2000; 1: 149–219.
- 19 Ноэль М.П. Гнозия пальцев: предсказатель числовых способностей у детей? Детский нейропсихол 2005; 11: 413–30.
- 20
Файол М,
Барруйе П,
Маринт К.
 Прогнозирование арифметических достижений от нервно-психологической деятельности: продольное исследование. Познание
1998; 68: B63– 70.
Прогнозирование арифметических достижений от нервно-психологической деятельности: продольное исследование. Познание
1998; 68: B63– 70.
- 21 Ди Лукас, Granà A, Семенца С, Серон X, Песенти М. Совместимость пальцев и цифр при обработке арабских цифр. Q J Exp Psychol 2006; 59: 1648–63.
- 22 Андрес М, Оливье Э, Бадец А.Действия, слова и числа: моторный вклад в семантическую обработку? Curr Dir Psychol Sci 2008; 17: 313–7.
- 23
Алибали М.В.,
ДиРуссо А.А.
Функция жеста в обучении счету: больше, чем отслеживание.
 Когнитивный разработчик
1999; 14: 37–56.
Когнитивный разработчик
1999; 14: 37–56.
- 24 Голдин-Мидоу С, Нусбаум H, Келли С.Д., Вагнер С.Пояснение к математике: жесты облегчают задачу. Психологические науки 2001; 12: 516–22.
- 25 Саймон О, Мангин Ж.Ф., Коэн Л, Ле Бихан Д, Дехайн С. Топографическое расположение рук, глаз, вычислений и связанных с языком областей в теменной доле человека. Нейрон 2002; 33: 475–87.
- 26 Моретто Дж., ди Пеллегрино Г.Захватывающие числа. Exp Brain Res 2008; 188: 505–15.
- 27
Гири, округ Колумбия.
 Математическое развитие детей. Исследования и практическое применение. Вашингтон, округ Колумбия: Американская психологическая ассоциация, 1994.
Математическое развитие детей. Исследования и практическое применение. Вашингтон, округ Колумбия: Американская психологическая ассоциация, 1994.
- 28 Дехаен С, Пьяцца М, Пинель П, Коэн Л.Три теменных контура для обработки чисел. Cogn Neuropsychol 2003; 20: 487– 506.
- 29 Сюй Ф, Spelke ES. Дискриминация большого числа детей в возрасте 6 месяцев. Познание 2000; 74: B1–11.
- 30 МакКринк К., Винн К.Сложение и вычитание большого числа у 9-месячных младенцев. Психологические науки 2004; 15: 776–81.
- 31
Ньюкомб Н.
 С.
Противоречие между нативистами и эмпириками в контексте недавних исследований пространственного и количественного развития.
Психологические науки
2002; 13: 395–401.
С.
Противоречие между нативистами и эмпириками в контексте недавних исследований пространственного и количественного развития.
Психологические науки
2002; 13: 395–401.
- 32 Аунола К, Лескинен Э., Леркканен М-К, Нурми Дж. Э.Динамика развития успеваемости по математике от дошкольного до 2-го класса. J Educ Psychol 2004; 96: 699–713.
- 33 Иордания NC, Каплан Д, Раминени C, Locuniak MN. Развитие навыка сочетания чисел в раннем школьном возрасте: когда помогают пальцы? Научные разработки 2008; 11: 662–8.
- 34
Акция P,
Desoete A,
Ройерс Х.
 Овладение принципами счета у малышей: важный шаг в развитии подающих надежды арифметических способностей?
Изучите индивидуальные различия
2009; 19: 419–22.
Овладение принципами счета у малышей: важный шаг в развитии подающих надежды арифметических способностей?
Изучите индивидуальные различия
2009; 19: 419–22.
- 35 Выготский Л.С. Разум в обществе: развитие высших психологических процессов. Кембридж, Массачусетс: Издательство Гарвардского университета, 1978.
- 36 Де СмедтБ, Янссен Р, Бувенс К, Verschaffel L, Боетс Б, Гескьер П.Рабочая память и индивидуальные различия в успеваемости по математике: продольное исследование от первого до второго класса. J Exp Child Psychol 2009; 103: 186–201.
- 37
Kroesbergen EH,
Ван Луит JEH,
Ван Лисхаут ECDM,
Ван Лосбрук Э,
Ван де Рийт БАМ.
 Индивидуальные различия в начальных навыках счета: роль исполнительных функций и субитизации. J Psychoeduc Assess
2009; 27: 226–36.
Индивидуальные различия в начальных навыках счета: роль исполнительных функций и субитизации. J Psychoeduc Assess
2009; 27: 226–36.
- 38 Рагхубар КП, Барнс, Массачусетс, Hecht SA. Рабочая память и математика: обзор подходов к развитию, индивидуальных различий и когнитивных подходов. Изучите индивидуальные различия 2010; 20: 110–22.
- 39 Баддели А.Д., Hitch GJ.Рабочая память. В: Г. Бауэр, редактор. Психология обучения и мотивации. Сан-Диего, Калифорния: Academic Press, 1974, стр. 47–90.
- 40
Случай R,
Окамото Y,
Sharon G, et al.
Роль центральных концептуальных структур в развитии детской мысли.
 Monogr Soc Res Child Dev
1996; 61: 295.
Monogr Soc Res Child Dev
1996; 61: 295.
- 41 Госвами У.Когнитивное развитие. Обучающийся мозг. Хоув, Великобритания: Psychology Press, 2008.
- 42 Desoete A, Ceulemans A, Ройерс Х, Хейлбрук А. Субитизация или подсчет в качестве возможных переменных для скрининга неспособности к обучению в математическом образовании или обучении? Educ Res Rev. 2009; 4: 55–66.
- 43
Иордания NC,
Перенасыщение J,
Раминени К.Важность чувства числа для успеваемости по математике в первом и третьем классе.
Изучите индивидуальные различия
2010; 20: 82–8.

- 44 Бык R, Эспи К.А., Wiebe SA. Кратковременная память, рабочая память и исполнительные функции у дошкольников: продольные предикторы математических достижений в возрасте 7 лет. Dev Neuropsychol 2008; 33: 205–28.
- 45 Краевский К, Шнайдер В. Изучение влияния фонологической осведомленности, зрительно-пространственной рабочей памяти и дошкольных количественно-числовых компетенций на успеваемость по математике в начальной школе: результаты трехлетнего лонгитюдного исследования. J Exp Child Psychol 2009; 103: 516–31.
- 46
Симмонс Ф,
Синглтон C,
Хорн Дж.Краткий отчет – фонологическая осведомленность и функционирование визуально-пространственного блокнота предсказывают ранние арифметические достижения: данные лонгитюдного исследования.
 Eur J Cogn Psychol
2008; 20: 711–22.
Eur J Cogn Psychol
2008; 20: 711–22.
- 47 Gathercole SE, Алловей ТП, Уиллис С, Адамс А-М. Рабочая память у детей с нарушениями чтения. J Exp Child Psychol 2006; 93: 265–81.
- 48 Арп S, Таранне П., Фагард Дж. Глобальное восприятие малой численности (субитизации) у детей с церебральным параличом. J Clin Exp Neuropsychol 2006; 28: 405–19.
- 49 Арп S, Фагард Дж. Что нарушает субитизацию у детей с церебральным параличом? Дев Психобиол 2005; 47: 89–102.
- 50
Арп S,
Фагард Дж.
 [Визуально-мануальный дефект и счет у ранее недоношенных детей с церебральным параличом] (на французском языке).
Arobase
2001; 5: 35–42.
[Визуально-мануальный дефект и счет у ранее недоношенных детей с церебральным параличом] (на французском языке).
Arobase
2001; 5: 35–42.
- 51 Дженкс К.М., ван Лисхаут ECDM, де Моор Дж. Связь между медицинскими нарушениями и арифметическим развитием детей с церебральным параличом. J Детский нейрол 2009; 24: 528–35.
- 52 Дженкс К.М., де Моор Дж, van Lieshout ECDM. Арифметические трудности у детей с церебральным параличом связаны с исполнительной функцией и рабочей памятью. J Детская психическая психиатрия 2009; 50: 824–33.
- 53
Дженкс К.
 М.,
де МурДж,
ван ЛисхаутECDM,
Маатуис КГБ,
Кеус I,
Гортер JW.Влияние церебрального паралича на точность арифметики опосредовано рабочей памятью, интеллектом, ранними навыками счета и временем обучения.
Dev Neuropsychol
2007; 32: 861–79.
М.,
де МурДж,
ван ЛисхаутECDM,
Маатуис КГБ,
Кеус I,
Гортер JW.Влияние церебрального паралича на точность арифметики опосредовано рабочей памятью, интеллектом, ранними навыками счета и временем обучения.
Dev Neuropsychol
2007; 32: 861–79.
- 54 Ван Луит JEH, Ван де Рийт БАМ, Пеннингс А.Х. [Тест на раннее счисление]. (На голландском). Doetinchem, Нидерланды: Graviant, 1994.
- 55 Дженкс К.М., ван Лисхаут ECDM, де Моор Дж.Арифметические достижения у детей с церебральным параличом или менингомиелоцеле spina bifida. Remed Spec Educ 2009; 30: 323–9.
- 56
Деллатолас Г,
Филхо Г.
 Н.,
Souza Lg,
Нуньес LG,
Брага LW.
Ручное мастерство, асимметрия навыков рук и выполнение нейропсихологических тестов у школьников со спастическим церебральным параличом.
Боковой: познание мозга асимметрии тела
2005; 10: 161–82.
Н.,
Souza Lg,
Нуньес LG,
Брага LW.
Ручное мастерство, асимметрия навыков рук и выполнение нейропсихологических тестов у школьников со спастическим церебральным параличом.
Боковой: познание мозга асимметрии тела
2005; 10: 161–82. - 57 Кисслинг LS, Денкла МБ, Карлтон М. Доказательства дифференциальной функции полушария у детей с гемиплегическим церебральным параличом. Dev Med Child Neurol 1983; 25: 727–34.
- 58 Госвами У. Почему теории о дислексии развития требуют разработки. Trends Cogn Sci 2003; 7: 534–40.
- 59
Кармилов-Смит А.
Само развитие является ключом к пониманию нарушений развития.
 Trends Cogn Sci
1998; 2: 389–98.
Trends Cogn Sci
1998; 2: 389–98.
- 60 Kroesbergen EH, Ван де Рийт БАМ, Ван Луит JEH.Рабочая память и ранняя математика: возможности раннего выявления нарушений в обучении математике. В: E Scruggs, М.А. Мастропиери, редакторы. Успехи в обучении и нарушениях поведения. Vol. 20: Международные перспективы. Оксфорд, Великобритания: Elsevier, 2007: 1–19.
- 61 Kroesbergen EH, Ван Луит JEH. Математические вмешательства для детей с особыми образовательными потребностями: метаанализ. Remed Spec Educ 2003; 24: 97–114.
- 62
Кауфманн Л.
Дискалькулия: нейробиология и образование.
 Educ Res
2008; 50: 163–75.
Educ Res
2008; 50: 163–75.
- 63 Арцарелло Ф, Робутти О, Баззини Л. Актерское мастерство – это обучение: сосредоточьтесь на построении математических понятий. Camb J Educ 2005; 35: 55–67.
- 64 Ястак Ж.Ф., Ястак С. Тест достижений широкого диапазона. Уилмингтон, Делавэр: Ассоциация Jastak, 1978.
(PDF) Качество арифметического обучения детей с церебральным параличом
Эти результаты следует интерпретировать с осторожностью.Однако кажется вероятным
, что эффективность может быть улучшена за счет
, принимая во внимание сильные и слабые стороны каждого ребенка в таких областях, как
, как рабочая память, исполнительные функции, и подсчитывая навыки
для корректировки учебных материалов и методов
для корректировки. индивидуальные потребности ребенка.
индивидуальные потребности ребенка.
Результаты этого исследования показали, что причина того, что
детей с КП в специальных школах получали на
меньше обучения арифметике в неделю, чем их сверстники в
общеобразовательных школах, не связана, в основном, с отсутствием в школе более
детей. а скорее потому, что запланировано меньшее время обучения
.Поскольку специальные школы для детей с физическими недостатками
в Нидерландах также предоставляют все предписанные
терапевтические процедуры в собственной школе ребенка в течение учебного дня, на образовательные мероприятия на
меньше времени. Кажется вероятным, что
также имеет место в других странах, кроме
Нидерланды. Например, Майк (1995) провел этнографическое исследование
обучения грамоте в школе для
детей с ДЦП в Соединенных Штатах и пришел к выводу, что
было мало времени для ученых из-за
различных методов лечения. что получили студенты.В предыдущих исследованиях этого лонгитюдного проекта
что получили студенты.В предыдущих исследованиях этого лонгитюдного проекта
мы обнаружили, что
детей с ДЦП в специальных школах намного медленнее решали простые арифметические задачи
, чем их сверстники (Jenks
et al., 2009a, b). В результате этим детям фактически нужно на
больше времени, чтобы получить такой же объем практики, как и их
сверстникам в обычных школах. Кроме того, количество времени арифметических инструкций
предсказывало арифметические способности этих детей
(Jenks et al., 2007).
Исследование типов учебных групп
выявило большое разнообразие в специальных школах с небольшим использованием
группового обучения, что может указывать на то, что выбор типа учебных групп
основан на
потребностях учащихся. ребенок. Интересно отметить, что на
больше детей с КП в общеобразовательных школах получили
индивидуального обучения (в сочетании с как минимум
одной другой учебной группой), чем в контрольной группе.
Это может помочь объяснить, почему более ранние исследования в рамках этого лонгитюдного проекта
показали, что арифметические способности
детей в основной группе ХП сопоставимы
с таковыми в контрольной группе (Jenks et al., 2007; Jenks et al.,
2009a, b). Однако, поскольку обучающая группа
не подвергалась экспериментальным манипуляциям, эти результаты
следует интерпретировать с осторожностью.
Мы надеемся, что информация, полученная в этом исследовании относительно
аспектов качества арифметического образования для детей
с КП, будет способствовать достижению цели как улучшения арифметического образования
, так и разработки мероприятий для лечения
трудностей в обучении арифметике в эти дети.
В заключение мы предлагаем школьным властям улучшить
качество IEP для детей с CP, обеспечив
, чтобы IEP включали в себя конкретные, измеримые, привязанные ко времени
арифметические цели на основе углубленной оценки
индивидуальные сильные и слабые стороны ребенка. Результаты
Результаты
тех же самых оценок могут быть использованы для корректировки
методов и материалов обучения в соответствии с потребностями ребенка
, чтобы можно было достичь арифметических целей.Кроме того,
школьные власти и практики должны учитывать возможность
того, что другой баланс в учебный день между
времени для обучения арифметике и других занятий может улучшить арифметические способности этих детей.
Благодарности
Это исследование было частично поддержано грантами двух фондов
: Stichting Bio-Kinderrevalidatie и Dr W.M.
Phelpsstichting voor Spastici.
интересов авторов не имеют конфликта интересов и не получали коммерческой поддержки.
Ссылки
Эшвал С., Руссман Б.С., Бласко П.А., Миллер Г., Сандлер А., Шевелл М., Стивенсон Р.
(2004). Параметр практики: диагностическая оценка ребенка с церебральным параличом
: отчет Подкомитета по стандартам качества Американской академии неврологии
и Практического комитета Общества детской неврологии
. Неврология 62: 851–863.
Неврология 62: 851–863.
Аунио П., Хаутама
Оки Дж., Хейскари П., Ван Луит Дж. Э. (2006). Тест на раннюю смету на финском языке
: детские нормы. Scand J Psychol 47: 369–378.
Bax M, Goldstein M, Rosenbaum P, Leviton A, Paneth N, Dan B и др. (2005).
Предлагаемое определение и классификация церебрального паралича. Дев Мед Чайлд
Neurol 47: 571–576.
Бекунг Э., Хагберг Г (2002). Нейроумерения, ограничения активности и ограничения участия
у детей с церебральным параличом.Дев Мед Чайлд
Neurol 44: 309–316.
De staat van het Onderwijs; Onderwijsverslag 2004/2005 [Состояние образования;
Отчет об образовании 2004/2005] (2006). Гаага, Нидерланды, OBT bv.
Данн Л.М., Данн Л.М. (1997). Словарь Пибоди в картинках. 3-е изд. Circle
Pines, MN: American Guidance Service.
Эванс П.М., Эллиот М., Альберман Э., Эванс SJW (1985). Распространенность и инвалидность
у детей от 4 до 8 лет с церебральным параличом. Arch Dis Child 60: 940–945.
Arch Dis Child 60: 940–945.
Frampton I, Yude C, Goodman R (1998). Распространенность и корреляты специфических трудностей обучения
в репрезентативной выборке детей с гемиплегией
. Br J Educ Psychol 68: 39–51.
Houtveen AAM, Ван де Гриф WJCM, Creemers BPM (2004). Эффективная школа
усовершенствование по математике. Sch Eff Sch Improv 15: 337–377.
Дженкс К.М., де Моор Дж., Ван Лисхаут ECDM, Маатуис КГБ, Кеус И., Гортер Дж. В.
(2007).
Влияние церебрального паралича на точность арифметики опосредовано рабочей памятью, интеллектом, ранними навыками счета и временем обучения. Dev
Neuropsychol 32: 861–879.
Дженкс К.М., ван Лисхаут ECDM, де Моор Дж. (2009a). Арифметические трудности у
детей с церебральным параличом связаны с исполнительной функцией и рабочей памятью
. J Детская психическая психиатрия. [epub перед печатью]
Дженкс К.М., ван Лисхаут ECDM, де Моор Дж. (2009b). Связь между
нарушений здоровья и арифметическим развитием детей с церебральным параличом
. J Child Neurol. 24: 528–535.
J Child Neurol. 24: 528–535.
Майк Д.Г. (1995). Грамотность и церебральный паралич: факторы, влияющие на обучение грамоте
в автономной обстановке. J Прочтите Поведение 27: 627–642.
Палисано Р., Розенбаум П., Уолтер С., Рассел Д., Вуд Е., Галуппи Б. (1997).
Разработка и надежность системы классификации крупной двигательной функции у
детей с церебральным параличом. Дев Мед Чайлд Нейрол 39: 214–223.
Raven JC (1965). Руководство по использованию цветных прогрессивных матриц: наборы A,
,AB и B.Лондон: H.K. Льюис.
Resing WCM, Evers A, Koomen HMY, Pameijer NK, Bleichrodt N, van Boxtel H,
et al. (2002). Показания для направления: условия и инструменты [indicaties-
tell: condities en instrumentarium]. Амстердам: NDC-Boom. стр.224.
Шенкер Р., Костер В.Дж., Паруш С. (2005). Нейроумерения, показатели активности –
человек и участие детей с церебральным параличом – основное направление в
начальных школах. Дев Мед Чайлд Нейрол 47: 808–814.
Дев Мед Чайлд Нейрол 47: 808–814.
Torbeyns J, van den Noortgate W, GhesquieA
´re P, Verschaffel L, van de Rijt BAM,
van Luit JEH (2002). Развитие навыков счета в раннем возрасте у 5-7-летних
детей: сравнение между Фландрией и Нидерландами. Educ Res
Eval 8: 249–275.
Van Luit JEH, Ван де Рийт БАМ, Пеннингс AH (1994). Утрехтсе Getalbegrip Toets
[Тест на раннее счисление]. Doetinchem, Нидерланды: Graviant.
Арифметическое обучение детей с КП Jenks et al.25
Авторские права © Lippincott Williams & Wilkins. Несанкционированное копирование этой статьи запрещено.
5 математических стратегий для поддержки ребенка с трудностями в обучении | Scholastic
На протяжении многих лет я работал учителем математики со многими учениками и обнаружил, что все мы учимся по-разному. У каждого ребенка уникальный стиль обучения, и я считаю своей задачей помочь ученикам понять, как они учатся лучше всего. Как родитель, у меня трое очень разных учеников, и я индивидуально поддерживаю каждого из них. Моей дочери, которая плохо обучается, нужны модели, и она задает много вопросов, чтобы помочь разобраться в проблеме. Мой сын может решать проблемы мысленно, но расстраивается, пытаясь объяснить свои мысли. То, как я помогаю дочери, сильно отличается от того, как я помогаю своему сыну.
Моей дочери, которая плохо обучается, нужны модели, и она задает много вопросов, чтобы помочь разобраться в проблеме. Мой сын может решать проблемы мысленно, но расстраивается, пытаясь объяснить свои мысли. То, как я помогаю дочери, сильно отличается от того, как я помогаю своему сыну.
Учащимся, у которых диагностирована проблема с обучаемостью, требуется дополнительное внимание, когда дело доходит до определения стратегий, которые работают лучше всего. В частности, в математике существует множество различных концепций, и вам может быть сложно поддерживать своего ребенка дома.Наличие необходимых инструментов и приспособлений может иметь огромное значение. Всегда консультируйтесь с учителем математики вашего ребенка, но вот несколько полезных советов, которые вы можете использовать дома с ребенком с ограниченными возможностями обучения.
1. Играйте в математические игры: Всегда старайтесь делать упор на увлекательность математике. Если вашему ребенку не нравится домашнее задание по математике, сделайте перерыв и поиграйте в математическую игру. Или установите таймер, чтобы он закончил свою работу, и, если он завершит ее в отведенное время, он сможет сыграть в математическую игру.Постановка небольших достижимых целей и веселые перерывы могут очень помочь. (Попробуйте домино или игру в кости.)
Или установите таймер, чтобы он закончил свою работу, и, если он завершит ее в отведенное время, он сможет сыграть в математическую игру.Постановка небольших достижимых целей и веселые перерывы могут очень помочь. (Попробуйте домино или игру в кости.)
2. Прочтите и выделите: Прочтите вслух все математические указания и попросите ребенка использовать маркер, чтобы отметить любые важные слова или указания. Это поможет ему сосредоточиться на задаче и не перегружать себя многоэтапными задачами. Дети с ограниченными возможностями в обучении, как правило, испытывают трудности, когда есть несколько разных направлений, поэтому выделение важных ключевых слов очень поможет.
3. Используйте таблицу сотен: Имея в наличии таблицу сотен, подобную приведенной выше, ваш ребенок может использовать ее для выполнения домашних заданий, – это отличный инструмент. Это помогает ему визуализировать и понимать, как располагаются числа. Он также может касаться чисел, чтобы развить их чувство.
4. Решайте четные или нечетные числа: Сидеть неподвижно и уделять внимание деталям может быть особенно трудно для детей с ограниченными возможностями обучения. Если работа по математике занимает очень много времени, спросите учителя вашего ребенка, может ли он решать четные или нечетные числа.Это простое решение, которое вдвое сокращает математическую работу и по-прежнему позволяет вашему ребенку решать различные задачи.
5. Используйте миллиметровую бумагу: Имейте под рукой миллиметровую бумагу для решения проблем. Это очень помогает правильно выстраивать и расставлять числа, а также помогает вашему ребенку улучшить мелкую моторику. К рабочему листу можно прикрепить миллиметровую бумагу, чтобы показать его работу. Вот дополнительная информация о том, как поддержать обучение вашего ребенка с помощью миллиметровой бумаги.
Самое главное – найти то, что лучше всего подходит для вашего уникального ребенка.Все мы учимся по-разному, и нам нужно использовать стратегии, которые помогают нам чувствовать себя успешными.

