Цели урока:
Материал к уроку: учебник, рабочая тетрадь, цифровая касса, веер, поезд с вагонами, домики, смайлики.
Ход урока
I. Организационный момент (мотивация)
У: Придумано кем-то
Просто и мудро.
При встрече здороваться.
Доброе утро!
Доброе утро!
Доброе утро, солнцу и птицам.
Доброе утро, улыбчивым лицам!
Я очень хочу, чтобы у всех сегодня было доброе
утро, добрый день, а особенно, ребята, для вас.
1) Откройте свои цифровые кассы и начнём работу. В результате мы с вами повторим и закрепим изученный материал.
1. Покажите наибольшее однозначное число.
2. Покажите число, которое на 1 меньше этого числа.
3. Покажите число, которое находится между 4 и 6.
4. Покажите цифрой, сколько ножек у стола? А у петуха? На сколько ножек у стола больше?
5. Покажите число, которое предшествует числу 9.
6. Положите карточку с этим числом на парту, а рядом карточку с числом, которое на 1 больше. Какие числа выложили?
7. Сравните эти числа (8< 9, 9 >8).
8. Считаем устно, ответ показываем цифровыми карточками.
7 да 1 6 без 1 3 + 2 7 – 1
9. А теперь решим задачу. (На доске рисунок)
На ветке росло 8 груш.
Мальчик одну грушу сорвал.
Сколько груш осталось на ветке? (Повторяется
условие задачи, вопрос, решение записывают с
помощью карточек, говорят вслух решение и ответ).
10. Составьте задачу по рисунку (по выбору учителя).
11. Ребята, назовём хором все изученные числа. (1, 2, 3, 4, 5, 6, 7, 8, 9)
– Сколько мы изучили чисел? (9)
II. Сообщение темы и цели урока
– Сегодня мы познакомимся с числом 10.
2) Работаем по учебнику с. 28. Рассмотрите верхний рисунок.
– Сколько ребят уже заняли свои места в ряду? (9)
– Которым по счёту будет мальчик? (Десятым)
– Сколько станет зрителей в ряду, когда и он займёт своё место? (10). А записывается это число двумя знаками 1 и 0. Это двузначное число. (Читаю стишок С. Маршака)
– Как получилось число 10? (9 + 1 = 10)
– Сравним эти числа. Что больше 9 или 10? (9 < 10 или 10 > 9)
3) Письмо числа 10.
Работа в тетради.
Объяснение написания числа 10 учителем по таблице в учебнике и на доске.
– Число 10 пишется в двух клеточках. Цифра 1 пишется в правой половинке клеточки, а цифра 0 в левой половинке клеточки.
Запись числа 10 по образцу, данному в учебнике. Показ учителем на доске правильной записи числа 10. Дети пишут в тетради две строки.
4) Физкультминутка.
Вот помощники мои,
С этим братцем кашу ел,
Их как хочешь, назови.
Это пальчики мои!
Пальчик, пальчик, где ты был?
С этим братцем в лес ходил,
С этим братцем щи варил,
С этим братцем песни пел,
Этот пальчик в лес пошел,
Этот пальчик гриб нашел,
Этот пальчик чистить стал,
Этот пальчик жарить стал,
Этот пальчик все съел,
Оттого и потолстел.
Можешь пальцы сосчитать:
Один, два, три, четыре, пять.
Один, два, три, четыре, пять –
Десять пальцев пара рук –
Вот твое богатство, друг.
5) Работа с учебником.
– Рассмотрите внимательно рисунок. Сосчитайте всех героев сказки, подумайте и сделайте вывод, смогут ли они все плыть на паруснике, если он может взять на борт только 10 пассажиров? (Учащиеся считают и делают вывод)
Д: Да, так как сказочных героев всего 10. Послушайте, ребята, отрывок из сказки. Это очень важно.
(Учитель читает отрывок из сказки про Козленка, который учился считать до 10).
“Они мчались сломя голову, не разбирая дороги, и добежали так до речки. А у причала стоял небольшой парусник. На борту парусника они увидели Петуха, Пса, Барана и Кота. Петух был капитаном, Пес – лоцманом, Баран – юнгой, а Кот – корабельным поваром.
– Остановитесь! – закричал Петух, увидав
животных, которые неслись не чуя под собой ног.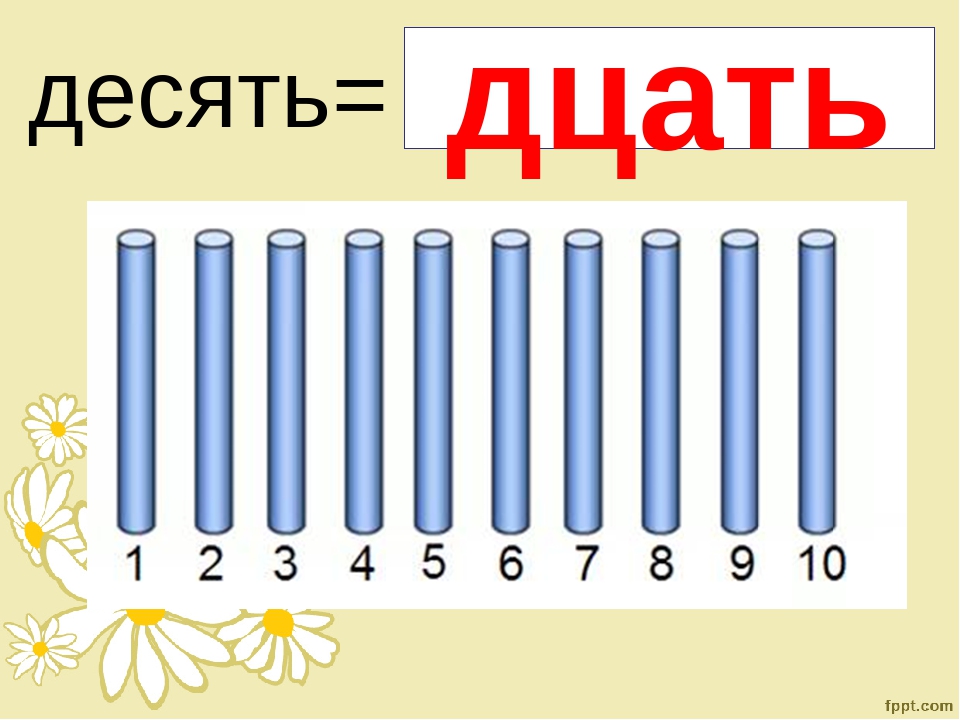
Но
уже было поздно. Козленок оттолкнулся копытцами
от причала и прыгнул на борт парусника. За ним
бросились все остальные. Парусник покачнулся,
заскользил по воде, и его понесло на самое
глубокое место реки. Ох и перепугался же Петух!
– Ку-ка-ре-ку! На помощь! – закричал он не своим голосом. – Парусник тонет! Все так и затряслись от страха! А Петух опять закричал громко-прегромко:
– Кто из вас умеет считать?
– Я умею, – сказал Козленок.
– Тогда пересчитай всех нас поскорее! Парусник может выдержать только 10 пассажиров.
– Скорее считай, скорее! – закричали все хором.
И Козленок начал считать:
– Один-это я, два – это Теленок, три -это Корова, четыре – это Бык, пять – это Конь, шесть – это Свинья, семь – это Кот, восемь – это Пес, девять – это Баран и десять – это Петух.
– Ура Козленку! Ура-а-а-а! – закричали тут все в один голос.
Потом пассажиры переправились через реку и
сошли на берег.
А Козленок с тех пор и остался на
паруснике. Он теперь работает там контролером. И
всякий раз, когда Петух сажает на свой парусник
зверей, Козленок стоит у причала и считает
пассажиров”.
У: Чему учит нас эта сказка?
Д: Надо учиться считать. От этого умения зависит даже жизнь.
6) Сегодня я приглашаю вас в увлекательное путешествие по стране Математика на сказочном поезде, так как нас в классе три раза по десять и мы все не сможем уплыть на паруснике.
– Но чтобы наш поезд тронулся, мы должны прицепить вагончики по порядку. Ответ, решённого примера, будет номером вагончика.
– Чтобы правильно расставить номера вагончиков, давайте повторим счёт.
а) Счёт прямой и обратный.
б) Работа с веером цифр.
– Какое число идёт при счёте за числом 3, 6, 9?
– Какое число идёт перед числом 2, 5,8?
– Покажите “соседей” чисел 4, 7, 9.
– Молодцы! Ну, а теперь нам будет просто найти номера вагончиков.
7) Решаем.
4+1 6+2 3-2 7-1 2+2 9+1 4-2 8-1 2+1 7+2
8) Игра “Составим поезд”.
– Представили, что мы едем в поезде, и чтобы наш поезд не сбился с пути, мы посчитаем до 10. Вот и остановка. И наша первая станция называется.
а) Станция “ Занималкино”. Игра “Засели дом”.
– Молодцы, ребята, справились с заданием!
б). Сели в поезд и едем дальше. Торопится поезд, вагоны стучат, а в этих вагонах ребята сидят. И вот остановка “Смекалкино”.
9) Работа в тетради для самостоятельных работ на с 27 №4. Дорисуй предметы в каждой рамке до десяти. Дополни записи к рисункам. (Задания учащиеся выполняют самостоятельно, по ходу выполнения учитель оказывает индивидуальную помощь).
а) Решить цепочку примеров.
Ответ показать
цифрой. (Примеры записаны на доске).
| 4 + 3 = (7) | 8 – 3 = (5) | 3 + 3 = (6) |
| 7 + 1 = (8) | 5 – 2 = (3) | … (6 – 2 = 4) |
– Что заметили? (Примеры круговые). Дополните своим примером, чтобы круг замкнулся. Разделите на 2 группы.
– Молодцы, ребята, и с этим заданием вы справились!
10) Едем дальше, и чтобы наш поезд не сбился с пути, мы посчитаем обратно от 10 до 0.
Остановка “Задачкино”
Творческие задачи:
1) В комнате зажгли две свечи. Потом одна из них
погасла. Сколько свечей осталось? (2).
2) В хоре 7 кузнечиков песни распевали. Вскоре 5 кузнечиков голос потеряли. Сколько кузнечиков осталось певчих? (2).
Решение задачи по рисунку (на доске нарисовано дерево, на дереве 6 яблок, а 1 яблоко упало).
– Как называется дерево? Почему?
– Составить по увиденному задачу в вопросе которой присутствовали бы слова “Сколько всего…?”
Анализируем задачу и по ходу анализа делаем к задаче рисунок.
– Молодцы, ребята, едем дальше. А вот остановка “Узнавалкино”.
а) Геометрический материал.
Чтобы выйти из леса, вы должны перейти ров.
– какие фигуры видите?
– сколько их?
– переложите 2 палочки, чтобы стало 4 треугольника
– какая ещё фигура получилась?
б) А как называется эта фигура? (Показываю квадрат)
На доске: сколько здесь квадратов, ребята?
А здесь?
Чем отличаются друг от друга ёлочки? В какой ёлочке больше треугольников и на сколько?
– Едем дальше и наша конечная остановка
“Решайкино”.
Письменное задание.
Сравните: >, <, = (по цепочке у доски под диктовку учителя)
7*5 7*4 7*2
6*7 3*7 1*7
(проверить друг друга)
– Молодцы, ребята! Со всеми заданиями вы справились хорошо, этим вы доказали, что уже научились считать. А вот послушайте, как считал один мальчик, тоже первоклассник.
(Стихотворение Б. Заходера “Два и три”)
Пошёл Серёжа в 1 класс.
С Серёжей не шути,
Считать умеет он у нас
Почти до десяти!
Не грех такому мудрецу
Задрать курносый нос,
Вот как-то за столом отцу
И задал он вопрос.
– Два пирожка тут, папа, да? (Два пирожка на тарелке).
А хочешь на пари!-
Я доказать могу всегда,
Что их не два, а три!
Считаем вместе: вот один, (Берёт один и кладёт опять на тарелку).
А вот и два, смотри!
А папа говорит:
– Ну что ж возьму я эти два, (Забирает два пирожка).
А третий ты бери.
– Правильно считал Серёжа, ребята! Мы ещё раз убедились. Как важно правильно считать! А у нас уже все умеют считать правильно. Давайте ещё раз посчитаем до10 и обратно хором.
Итог урока.
– Что узнали сегодня на уроке?
Чему научились!
Оцените урок своими смайликами.
Вопрос с кроссворда
Ответ на вопрос “Число первого десятка “, 6 (шесть) букв:
четыре
Сколько балерин участвует в танце маленьких лебедей в балете Чайковского Лебединое озеро
Цифра
Чертовой дюжиной в Японии считается число…
Столько труб у Титаника
Сколько музыкантов в квартете (цифра прописью)
Столько труб у «Титаника»
Сколько будет 2х2
Толковый словарь русского языка.
Д.Н. Ушаков Значение слова в словаре Толковый словарь русского языка. Д.Н. Ушаков
четырёх, четырём, четырьмя, числит. колич. Число 4; цифра 4. четыре делится на два. Написать четыре. кого-чего. Количество 4. четыре раза ездил в Крым. С четырьмя детьми уехал на дачу. На четырех колесах. Пятилетка в четыре года.
Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова. Значение слова в словаре Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова.
мн. нескл. Оценка успеваемости учащегося по пятибалльной системе, обозначающаяся цифрой “4” и соответствующая оценке “хорошо”; четвёрка. числит. Название числа, состоящего из 4 единиц. Такое количество единиц чего-л. Название цифры, обозначающей такое число.
…
Президент Финляндии Аарне предложил перенести встречу глав четырех держав в Хельсинки, гарантируя обеспечение как условий работы, так и безопасности участников.
Фортен, Леон-Жан, 26 лет, доктор наук, препаратор парижского факультета, получает содержания 150 франков в месяц, живет у родителей в Мезон-Лафите, ездит по делам три, четыре, иногда пять раз в Париж, имеет абонементный билет 3-го класса Западной железной дороги.
В архитектуре этой многопроцессорной векторной ЭВМ, предназначенной в первую очередь для обработки в реальном масштабе времени больших потоков информации, предусмотрены четыре основных части: центральная процессорная часть, аппаратные средства поддержки операционной системы, абонентское сопряжение, специализированная процессорная часть.
Ему хотелось пойти в зрительный зал и погрузиться в ауру, но его четыре абонентских часа в день уже были использованы.
Хотелось бы понаблюдать его в большой хороший телескоп – например, тот, который Хемфри Филд установил четыре года назад на Маунт-Вилсон, с полным набором абсорбентов, поглощающих излишки энергии, так что можно спокойно, часами напролет разглядывать изрытое провалами лицо нашего отца.
Ютака Абэ – наш лидер, ему двадцать четыре года, он из старинного токийского рода и закончил Пирс.
Источник: библиотека Максима Мошкова
Первые десять натуральных чисел — это набор последовательных натуральных чисел от 1 до 10, где 1 — натуральное число, а 10 — наибольшее. Натуральные числа также известны как счетные числа и включают в себя все положительные целые числа от 1 до бесконечности. Набор натуральных чисел в целом представляет собой классификацию большего набора действительных чисел, не включая ноль, дроби, десятичные дроби и отрицательные числа.
В этой статье давайте изучим первые десять натуральных чисел, их сумму, lcm и среднее с формулой и решенными примерами.
| 1. | Список первых десяти натуральных чисел |
| 2. | Сумма первых десяти натуральных чисел |
3. | Среднее значение первых десяти натуральных чисел |
| 4. | НОК первых десяти натуральных чисел |
| 5. | Часто задаваемые вопросы о первых десяти натуральных числах |
Список первых десяти натуральных чисел относится к списку последовательных натуральных чисел, начиная с 1 до 10, который формируется с помощью простой формулы: нам нужно добавить 1 к предыдущему числу, чтобы получить следующее число. Таким образом, можно сделать вывод, что 10 — последнее натуральное число в списке первых десяти натуральных чисел, то есть от 1 до 10, а 1 — наименьшее натуральное число в списке.
Натуральные числа от 1 до 10 — это все те числа в этом диапазоне, которые представляют собой все последовательные числа, начинающиеся от 1 до 10. Список натуральных чисел от 1 до 10 включает 1, 2, 3, 4, 5, 6, 7. , 8, 9и 10.
Первые десять натуральных чисел можно записать как 1, 2, 3, 4, 5…….
10. Ясно, что это образует арифметическую прогрессию (А.П). Применяя формулу арифметической прогрессии суммы п.п., сумму всех натуральных чисел от 1 до 10 можно вычислить по формуле S = n/2[2a + (n − 1) × d], где a — первое член, d — разница между двумя последовательными терминами, а n — общее количество натуральных чисел от 1 до 10. Всего в списке или арифметической прогрессии 10 натуральных чисел, поэтому n = 10,9.0003
Таким образом, a = 1, d = 1 и n = 10
Вычислим сумму первых десяти натуральных чисел.
Сумма А.П: 1, 2, 3, 4,5…….10.
S = n/2[2a + (n − 1) × d]
S = 10/2[2,1 + (10 − 1) × 1]
S = 10/2[2 + 9]
S = 5[11] = 55,
Следовательно, сумма первых десяти натуральных чисел равна 55,
.
Среднее значение первых десяти натуральных чисел соответствует среднему арифметическому чисел от 1 до 10. Среднее значение представляет собой сумму всех чисел в наборе, деленную на количество чисел, присутствующих в наборе.
Другими словами, это отношение суммы всех данных наблюдений к общему количеству наблюдений.
Следовательно, среднее первых десяти натуральных чисел равно 5,5.
НОК первых 10 натуральных чисел — это наименьшее число, которое делится без остатка на все 10 чисел. Так как первые десять натуральных чисел это 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, НОК всех этих чисел есть произведение всех простых множителей, полученных после взятия lcm. Теперь, найдя НОК числа (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) методом деления
В методе деления мы сначала расставляем числа в сетке, а затем делим заданные числа с их простыми делителями до тех пор, пока мы не сможем найти какое-либо простое число для дальнейшего деления данных чисел, не оставляя остатка.
LCM является произведением всех таких общих простых множителей.
Таким образом, НОК первых десяти натуральных чисел равен 2520.
Важные примечания:
Темы, относящиеся к первым десяти натуральным числам
Ознакомьтесь с этими статьями, посвященными понятию первых десяти натуральных чисел.
Первые десять натуральных чисел относятся к списку натуральных чисел от 1 до 10.
Первые десять натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9, и 10. Каждое из двух последовательных чисел имеет разность 1.
Первые десять натуральных чисел можно записать в виде арифметической последовательности – 1, 2, 3, 4, 5…….10. Таким образом, сумму всех натуральных чисел от 1 до 10 можно вычислить по формуле S = n/2[2a + (n − 1) × d], где a — первое слагаемое, d — разность между двумя последовательные члены, а n — общее количество натуральных чисел от 1 до 10. Следовательно, сумма первых десяти натуральных чисел равна 55.
Среднее первых десяти натуральных чисел равно сумме всех чисел в списке (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10), деленной на количество чисел (10 ). Здесь сумма чисел = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55
а количество наблюдений равно 10. Таким образом, среднее равно отношению 55/10 или просто 5,5.
Дисперсия первых десяти натуральных чисел может быть рассчитана по формуле дисперсии \(\sigma^{2}=\frac{\sum\left(x_{i}-\mu\right)^{2}} {N}\).
{t h} \text {term }}{2}\). Таким образом, подставляя значения в формулу, имеем медиана = (6 + 5)/2 = 11/2 = 5,5.
Стандартное отклонение первых десяти натуральных чисел можно рассчитать по формуле стандартного отклонения σ = √var. Мы знаем, что дисперсия первых десяти натуральных чисел равна 8,25. Таким образом, стандартное отклонение σ = √var = √8,25 = 2,87.
Всего в списке первых десяти натуральных чисел 4 простых числа, включая 2, 3, 5 и 7, а всего в списке 10 чисел. Таким образом, процент простых чисел в первых десяти натуральных числах равен (4/10) × 100 = 40%.
В повседневной жизни мы используем числа. Их часто называют цифрами . Мы не можем считать предметы, дату, время, деньги или что-либо еще без чисел. Эти цифры иногда используются для измерения, а иногда для маркировки.
Числа обладают свойствами, позволяющими производить над ними арифметические операции. Эти цифры выражаются как цифрами, так и словами. Например, 3 записывается как три, 33 записывается как тридцать три и так далее. Для дальнейшего изучения учащиеся могут попрактиковаться в написании цифр от 1 до 100 словами.
В математике мы изучаем различные типы чисел. Натуральные и целые числа, нечетные и четные числа, рациональные и иррациональные числа и т. д. — все это примеры. В этой статье мы рассмотрим все разновидности. Кроме того, числа используются в различных приложениях, включая числовые ряды, арифметические таблицы и так далее.
Типы чисел
- Число — это арифметическое значение, которое используется для представления и расчета количества. Числа представлены цифрами, которые представляют собой письменные символы, такие как «2».
- Система счисления — это метод записи чисел, в котором для их представления используются логические цифры или символы.
Система счисления — это система классификации чисел по множествам. В математике есть несколько различных типов чисел:
Для его обозначения используется буква «Р».Натуральные числа — это подмножество системы счисления, которое охватывает все положительные целые числа от 1 до бесконечности и используется для счета. Оно не содержит числа ноль. На самом деле цифры 1,2,3,4,…. часто называют счетными числами.
Натуральные числа — это подмножество действительных чисел, которое включает только положительные целые числа, такие как 1, 2, 3, 4, 5, 6 и т.
д., и не включает ноль, дроби, десятичные дроби и отрицательные числа.
Отрицательные числа и 0 не включаются в натуральные числа.
В этой статье вы узнаете больше о натуральных числах, включая их определение, сравнение с целыми числами, представление на числовой прямой, атрибуты и многое другое.
Примеры Натуральные числа
Положительные целые числа (также известные как неотрицательные целые числа) включены в натуральные числа, и некоторые примеры включают 1, 2, 3, 4, 5, 6,… Натуральные числа, другими словами, представляют собой совокупность всех целых чисел. числа, исключая 0.
103, 42 33, 9999, 101101 и т. д. — все это примеры натуральных чисел.
Так как натуральные числа — это подмножество действительных чисел, которое включает только положительные целые числа, такие как 1, 2, 3, 4, 5, 6 и т. д., и не включает ноль, дроби, десятичные дроби и отрицательные числа.
Таким образом, первые 10 натуральных чисел — это 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10.
