Предлагаю Вам новый раздел со справочной, учебно-методической и разъяснительно-рекомендательной информацией, связанной с запросом репетитор по математике 7 класс. Также здесь будут публиковаться мои заметки об особенностях работы с маленькими учениками (пока отдельные части этой страницы находятся в стадии доработки).
Меня всегда интересовало, зачем в поисковых строчках яндекса или гугла к главной фразе репетитор по математике приписывают еще и 7 класс? Можно подумать, что есть такие репетиторы, которые работают только семиклассниками и больше ни с какими другими возрастами. Да, математика 7 класса – это особый этап освоения предмета, с весьма своеобразными подходами к обучению, отличие которых от работы со старшеклассниками видят все, в том числе и преподаватели, которые в силу своего образования таковыми не являются. Но одно дело — чувствовать эту разницу, а другое дело – уметь следовать заложенным в программе 7 класса морально-методическим принципам. Видимо те немногие родители, кого интересует
Оценивая потребность в информационной поддержке сочетания «репетитор по математике» в паре с «7 классом», я решил изменить традициям и создать практическую страничку, на которой можно было бы соединить дидактический и методический раздел с заданиями и инструкциями по работе преподавателя в 7 классе. Это тесты, перечень тем, изучаемых семиклассниками по разным программам, советы репетитору по работе с математикой 7 класса, родителям по «уходу» за школьниками в младшем и среднем возрасте и др. Читайте, решайте, оценивайте себя или своего ребенка, его репетитора / школьного преподавателя и обращайтесь за помощью в случае необходимости.
Мой тест по алгебре за 7 класс (повышенной сложности):
Пройдите аналогичный тест за 7 класс. Алгебра, уровень «А», учебник Макарычева.
Доступны дополнительные материалы:
Репетитору по математкие для работы в 7 классе. Тест на формулы сокращенного умножения.
Если Вы занимались какое-то время с учеником 7 класса самостоятельно или нанимали ему преподавателя, то наверняка знаете, как тяжело запрягать новую телегу под названием «геометрия». Далеко не всем профессиональным репетиторам по математике удается в 7 классе растолковать маленькому ученику азы этого весьма специфического предмета. Чрезвычайно трудно понять логику доказательства простых и очевидных фактов, тех, которые видны невооруженным глазом и понятны без лишних слов. Тем не менее, репетитор по математике должен довести технику до полного ее осознания и принятия. Пожалуй, это главная проблема, с которой приходится сталкиваться репетитору. Я решаю ее через сочетание целого ряда методов и упражнений, направленных не только на разъяснение новых принципов, но и на запоминание типичных для ранней геометрии логических переходов.
Как мне кажется, правильная работа репетитора по математике с 7 классом по геометрии в самом начале ее изучения должна быть направлена запоминание наиболее часто используемых образцов записей, стандартных схем и даже результатов некоторых обосновании. Она позволяет сформировать у ученика ощущение близости новых для него форм и методов. Дело в том, что ребенок понимает и принимает в свой мир только то, что хорошо помнит и с чем регулярно приходится сталкиваться в жизни. А запоминает то, что его окружает с утра до вечера, в чем он живет.
Конечно, наивно предполагать, что репетитору по математике в 7 классе удастся погрузить подопечного в планиметрию «на полную катушку», но максимально заполнить мир новыми понятиями и заданиями необходимо. Именно с таким расчетом подбираются упражнения, способные притянуть школьника, а не отбросить его от предмета. При наделении меня достаточным количеством временем на начальном этапе изучения геометрии я предлагаю своему подопечному множество заданий развивающего вводного плана (переходного типа), для выполнения которых нужно просто что-то нарисовать, перечислить изображенные объекты, обозначить их, сравнить их размеры, сопоставить рисунки с их символикой. Идет отработка таких понятий, как пересечение, принадлежность, уяснение обозначений и относительного расположения нескольких объектов по отношению друг другу. Надо сказать, что чем проще задание, тем сложнее его разрабатывать, подбирать и оформлять. Важно провести работу над запоминанием терминов, ибо математическая речь, которой владеет Ваш репетитор математике 7 класс, для ученика может оказаться не соответствующей его словарному запасу и смысловой привязке к определенным картинкам.
Терминологическая работа чрезвычайно важна, ибо аккуратные с точки зрения точной математики разъяснения репетитора в 7 классе кажутся детям чем-то космически далеким и непонятным. Однако не стоит увлекаться терминами и не стоит превращать занятия в уроки рисования, ибо суть геометрии в ином.
Проблем с математикой 7 класса хватит на целый сайт, и нет смысла перечислять их все на этой странице.
Преподавание математики в 7 классе принципиально отличается от аналогичной работы в 5 классе и даже в недавно оконченном 6 классе. Главным образом это связано с разделением предмета на геометрию (планиметрию) и алгебру, а также необходимостью заниматься формированием некоего универсального инструмента для решения практических, текстовых или геометрических задач в будущем. Речь идут об умении решать уравнения, а позже и неравенства. Поэтому все усилия репетитора по математике в работе с курсом алгебры 7 класса направляются на изучение буквенных выражений. Некоторых детей это сильно ломает, так как за годы учебы в 5 — 6 классах они привыкают к определенным схемам и правилам изучения математики: а именно к работе с отдельными числами и отдельными арифметическими действиями. В 7 классе репетитор пытается заставить ребенка по-иному взглянуть на буквенные записи и научить оценивать результаты вычислений без их непосредственного выполнения. Например, нужно догадаться, что ни одно число не является корнем уравнения . Заметим, что 6 классе репетитору не приходится разбирать все варианты ответов линейный уравнений.
Есть несколько качеств и профессиональных навыков, которыми должен обладать преподаватель, работающий с семиклассниками.
Репетитор по математике 7 класс – это:
1) Преподаватель, способный грамотно спланировать разделение уроков на алгебру геометрию
2) Репетитор — методист, ориентирующийся сразу в нескольких программах за 7 класс
Учебников для семиклассников больше чем для шестиклассников. Чего стоит перечисление одних только популярных базовых программ: Мордкович ,Алимов, Макарычев. А еще экспериментальные и профильные курсы. Недавно вышел учебник Петерсона для 7 класса. Репетитор по математике обязан знать и уметь работать с их темами именно в том порядке, в котором они расположены, ибо ученик может придти какой угодно.
3) Репетитор – психолог.
В 7 классе дети вплотную подходят к тяжелому переходному возрасту 14-15 лет. Не исключены ранние конфликты на почве учебы с родителями и учителями. Репетитор, обладающий определенными психологическими знаниями и способностью убедить ребенка в том, что нужно учиться, как правило, добивается хороших результатов даже в работе с трудными подростками.
Существует целый рад принципиальных изменений при переходе от программ 5 — 6 класса к 7 классу. Вот они:
1) Изменение подходов к решению текстовых задач. Если шестиклассники сочетают арифметические действия с уравнениями (в примерном соотношении 1:1), то в 7 классе для решения текстовых задач используются только одни уравнения. В 8 — 9 классе они будут только усложняться, в связи с чем на репетитора по математике сваливается работа по изучению одночленов и многочленов во всех мыслимых и немыслимых сочетаниях степеней, слагаемых, скобок и алгебраических действий.
2) Резкое снижение доли практических задач в 7 классе. Это является следствием заполнения программы заданиями, направленными на формирования алгебраической базы школьника.
3) Полное обоснование используемых теорем, тождеств, выводов и алгоритмов. Никогда ранее ученик не сталкивался с таой математикой. Для того, чтобы репетитор в 7 классе не испытывал с учеников проблем с доказательствами (выводами), необходима подготовка их восприятию на материале олимпиадных задач для 5 — 6 класса определенного вида. Они имеются копилке материалов любого хорошего репетитора.
4) Ведение целого ряда новых фундаментальных понятий, таких как функция, тождество, система уравнений и др. В геометрии их еще больше.
5) Увеличение объема записей в тетрадях (по геометрии) и количества типовых заданий (по алгебре). Следствием этого является увеличение физической нагрузки ученика. Она может привести к первым протестам и конфликтам с репетитором по математике и родителями.
Колпаков А.Н. Репетитор по математике для 7 класса.
ankolpakov.ru
Общественный смотр знаний
по математике в 7 классе
Технология использования в обучении игровых методов
Идея урока:
Урок проводится как соревнование между классами в параллели в конце четверти или учебного года для обобщения и систематизации знаний. Классы формируют команду в составе 5 участников и капитана, придумывают математическое название и готовят домашнее задание. В состав жюри смотра приглашаются ученики старших классов, родители и учителя, не преподающие в этих классах. Членам жюри заранее выдаются правильные ответы на задания.
Цель урока:
Обобщение и систематизация знаний в игровой и соревновательной деятельности.
Задачи урока:
Ход урока:
Представление команд. (5 минут)
Обыграть название, защитить выбранную эмблему.
Домашнее задание. (5 минут)
Сдать в жюри найденные высказывания о математике. Обсудить наиболее понравившиеся.
Конкурс капитанов. Древние задачи. (5 минут)
На памятнике древнегреческому ученому Диофанту имеется надпись: «Прохожий! Под этим камнем покоится прах Диофанта, умершего в старости. Шестую часть его жизни заняло детство, двенадцатую – отрочество, седьмую – юность. Затем протекла половина его жизни, после чего он женился. Через 5 лет у него родился сын, а когда сыну исполнилось 4 года, Диофант скончался». Сколько лет прожил Диофант?
Говорят, что на вопрос, сколько у него учеников, древнегреческий математик Пифагор отвечал так: «Половина моих учеников изучает математику, седьмая часть изучает природу, четвертая часть чертит фигуры на песке, а двенадцатая часть проводит время в молчаливом размышлении. Есть еще две девушки, которые занимаются всем понемногу». Сколько учеников было у Пифагора?
Математическое лото. Конкурс для команды без капитана. (5 минут)
Каждой команде нужно сосчитать и сложить карточки лото в ряд так, чтобы ответ предыдущей карточки совпал с первым числом следующей карты.
– + 3, 75 | 3, 55:(0,5) | -7,1-(-)2 | -7,35+(-3)2 | 1,65+ |
2.(-)3 | -+(-)5 | -.2 | -1,75:3,5 | -+(-1,5)2 |
Конкурс «Веселые вопросы» для всей команды (5 минут)
(1 час)
часы. Какое время они показывают на самом деле? (945)
Математические софизмы для всей команды (5 минут)
После обсуждения команда должна объяснить, в чем ошибка преобразований.
4 : 4 = 5 : 5
4 . (1 : 1) = 5 . (1 : 1) Ошибка при вынесении общего множителя. 4 и 5. Не являются общими множителями.
4 = 5
2 . 2 = 5
Пусть, а>b,
а =b+с, тогда а – b –с=0,
а(а-b)=(b+с)(а-b)
а2-аb=аb+ас-b2-bс
а2-аb-ас=аb-b2-bс
а(а-b-с)=b(а-b-с) на 0 делить нельзя! Т.к. а-в-с =0
а=b
Быстрые вопросы по геометрии для команды. (5 минут)
Конкурс задач для всей команды. (10 минут)
(21)
22x ∙2x+5 =2∙22∙23∙…..∙29∙32.(15)
В
А С К
D
Конкурс для команд «Опиши своего классного руководителя математическим языком» (5 минут)
В это время жюри подводит окончательные итоги и готовится награждать победившую команду и лучших игроков и болельщиков.
Конкурсы для болельщиков (во время работы команд)
Болельщики называют команду, за которую они получат дополнительные очки в поддержку.
Под деревом сидят четыре льва. Один ушел, осталось…(3)
Десять ягодок в траве. Я съел пяток. Осталось…(5)
Первая в России печатная книга вышла в свет в Москве в 1653 году. Сколько лет в стране печатаются книги?(361)
Великий русский писатель Л.Н. Толстой прожил 82 года. В 20 веке он прожил 10 лет. Назовите год рождения и год смерти писателя.(1828-1910)
Подведение итогов и награждение.
Диофант Александрийский – выдающийся древнегреческий математик, работавший в Александрии. В его книге «Арифметика» впервые встречается уравнения, решения которых нужно найти на множестве целых чисел. Такие уравнения впоследствии получили название «диофантовыхуравнений».«Арифметика» Диофанта состояла из 13 книг, сохранились только 6 первых. Большая часть труда – это сборник задач с решениями (сохранились 189 задач). На примере решения задач автор демонстрирует общие методы. Диофант исследует системы уравнений 2-го порядка от 2 неизвестных и показывает различные варианты решений одного уравнения. И данные методы используются и для решения уравнений высших степеней.
Диофант был столь известным математиком, что по преданию, даже эпитафия на его могильном камне и та была написана в виде задачи.
Она гласила: «Путник! Под этим камнем покоится прах Диофанта, умершего в глубокой старости. Шестую часть долгой жизни он был ребёнком, двенадцатую – юношей, седьмую – провёл неженатым. Через пять лет после женитьбы у него родился сын, который прожил вдвое меньше отца. Через четыре года после смерти сына уснул вечным сном и сам Диофант, оплакиваемый его близкими. Скажи, если умеешь считать, сколько лет прожил Диофант?»
Задачу можно решить по действиям:
Часть жизни Диофанта, протекшая от его рождения до женитьбы, выразится суммой дробей:
1/6 + 1/12 + 1/7 + 1/2 = 75/84 = 25/28
часть его жизни от женитьбы до смерти выразится разностью
1 – 25/28 = 3/28
и эта часть жизни от женить до смерти равна
5 + 4 = 9
Получаем 9 : 3/28 = 84.
Самый распространенный способ решения данной задачи – составление уравнения:
Примем за х – возраст Диофанта, тогда можем составить уравнение:
х/6 + х/12 + х/7 + 5 + х/2 + 4 + = х;
14х/84 + 7х/84 + 12х/84 + 42х/84 – 84х/84 = -9;
-9х/84 = -9;
х = 84.
Есть ещё один способ решения задачи: обратим внимание на то, что возраст Диофанта должен делиться на 6, 12, и 7. Наименьшее общее кратное этих чисел равно 84. Это и есть возраст, в котором умер Диофант.
Как видим, все способы решения дают один о тот же ответ: возраст Диофанта 84 года. 14 лет Диофант был ребёнком, 7 лет с 14 до 21 года – юношей. Женился Диофант в 33 года, а в 38 лет у него родился сын. Сын Диофанта прожил 42 года и умер, когда отцу было 80 лет.
nsportal.ru
Гаврилова Анна Сергеевна
В 7 классе математика представлена двумя предметами – алгеброй и геометрией.
Алгебра.
Алгебра раздел математики, который можно охарактеризовать как обобщение и расширение арифметики. В арифметике изучаются числа и простейшие (+, −, ×, ÷) действия с ними. В алгебре числа заменяются на переменные (a, b, c, x, y и так далее). Такой подход полезен, потому что:
Особенностью курса является также его практическая направленность, обеспечивающая интерес у учащихся к изучению алгебры и ее приложений и сформированность основных математических навыков.
Алгебра — это важнейший предмет школьной программы, который изучается с начала средних классов и заканчивается сдачей ЕГЭ. Начиная с самых азов изучения алгебры школьнику очень важно хорошо разбираться и знать каждую тему. Поскольку этот предмет имеет эллиптический способ изучения, или «от простого — к сложному», какой-либо пробел даже в самой незначительной теме может сказаться отрицательно на результате сдачи . А ЕГЭ, как известно — это пропуск к получению высшего образования и освоению будущей специальности.
Далеко не всем легко дается алгебра, что вполне объяснимо. И даже если в начальных классах преобладают неплохие результаты по математике, столкнувшись с сухим языком формул и функций, можно легко запутаться и алгебра станет «темным лесом», а обучаться тому предмету, который не понятен, очень тяжело.
По сравнению с другими учебными предметами алгебра, несомненно, выделяется своей трудоемкостью, необходимостью большой самостоятельной, повседневной работы. Надо вдумчиво, ежедневно, серьезно работать, чтобы овладеть алгеброй даже в минимальных размерах, не говоря, уже о более значительных успехах. Со своей стороны учителя, мои основные направлены на формирование у школьников потребности в учебной деятельности, укреплению желания учиться. Также необходимо выработать положительное отношение учеников и родителей к предмету, создавать ситуации успеха, ликвидировать боязнь решения математических задач, формировать у детей уверенность в своих способностях.
Геометрия.
Геометрия – одна из самых древних наук, занимается изучением геометрических фигур. Ранее, в рамках изучения математики в 5-6 классах ученики познакомились с некоторыми геометрическими фигурами и их свойствами. Задача курса – расширить и углубить ранее полученные знания, а также освоить знания о новых геометрических фигурах и их свойствах.
Одна из сложностей в изучении материала – большой объем теоретической части (определения, теоремы и т.п.). Мною, для облегчения усвоения знаний, не вводится обязательное знание доказательств теоретической части, а только знание формулировок.
Следующая сложность – трудность применения полученных теоретических знаний на практике. В геометрии мало действительно однотипных задач, к решению каждой надо подходить взвешенно, «с головой». Я учу детей анализировать условие задачи, понять, на что автор условия нас подталкивает теми вводными, что дает и как мы можем это использовать в итоговом решении.
Таким образом, учитель и родители учеников не должны находиться отрыве друг от друга. Для успешного освоения алгебры и геометрии, несмотря на то, что учащиеся уже не маленькие дети, необходим постоянный контроль родителей и их помощь своим детям.
ext.spb.ru
Открытый урок по алгебре 7 класс
Тема: « Умножение одночлена на многочлен».
Тип урока (мероприятия, занятия): урок обобщения и систематизации знаний.
Цели урока: (образовательные, развивающие, воспитательные)
Образовательные: обобщение и систематизация изученного материала;
создание условий контроля (самоконтроля) усвоения знаний и умений
Развивающие: способствовать формированию умений применять приемы:
обобщения, сравнения, выделения главного, развитию
математического кругозора, мышления, внимания и памяти.
Воспитательные:привитие интереса к математике, активности, организованности, умение общаться.
Задачи урока: повышение интереса к предмету, обобщение знаний и умений по теме «Одночлены и многочлены».
Используемые педагогические технологии, методы и приемы: игровые, здоровьесберегающие, личностно-ориентированные, ИКТ.
Знания, умения ,навыки и качества, которые актуализируют/приобретут/закрепят/др. ученики в ходе урока:
– умение пользоваться опорными знаниями для получения новых знаний;
– умение применять полученные знания при умножении одночлена на многочлен, раскрытие скобок, приведение подобных слагаемых;
– развитие ключевых компетенций само- и взаимоконтроля;
– приобретение компетенции самосовершенствования, саморазвития
Необходимое оборудование и материалы: мультимедиа-проектор, мультимедиа презентация, раздаточный материал к уроку: сигнальные карточки, карточки-задания, карточки для рефлексии.
Дидактическое обеспечение урока : карточки-задания.
Мотивация
Эпиграфом к нашему уроку станут слова
выдающегося французского ученого Блеза Паскаля: «Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным».
А, что может быть занимательнее путешествия? Вы любите путешествовать? Так вот, сегодня на уроке я предлагаю совершить путешествие в космос на планету М и Ф (Математика и Фантазия).
В путешествие лишнее не берут, поэтому у вас на партах (обратите внимание, пожалуйста, возьмите в руки): путевые листы, ручки, документы с заданием из Центра управления полётом. Отложите всё на край парты.
Любое путешествие планируется, давайте мы поставим цель путешествия.
Обратите внимание – это (слайд )- жители планеты МиФ. Что это за жители?
Дети: одночлены и многочлены. Учитель: Правильно. Вы знаете их, обычаи, законы, изучали их на предыдущих уроках и поэтому нам будет интересно с ними общаться!
Как командир корабля, я официально объявляю тему нашего урока – обобщения «Умножение одночлена на многочлен»
Запишите в путевых листах тему урока, подпишите каждый свой лист.
Следить за путешествием будет Цент управления полетами – это наши гости на уроке. В путешествие отправятся только те, кто пройдет комиссию.
Я – капитан корабля и именно я набираю команду.
1 Блиц-разминка (2 мин)
Перед полётом проведём блиц – разминку.
Даю инструкцию: отвечаете с места с помощью сигнальных карточек. «красный» – нет
«зеленый» – да
«желтый» – сомневаюсь
Удачи!
Верно ли утверждение, определение, свойство?
2 Операция «Компьютер» (5 мин)
У: И так, экипаж на борту, но у бортового компьютера требуется проверить «блок памяти».
Решив задания операции « Компьютер», их 9 (показываю) будьте внимательны. Тем самым мы исправим неполадки в его схеме. Решайте в документах ЦУПа, а ответы заносите в путевой лист в соответствующую графу (показываю на путевом листе).
Задание. Запишите в виде степени с основанием а. выполнив задание, расшифруете название нашей ракеты. Ответы записаны в кружках, которым соответствует определенная буква.
Внимание, сверьте свои ответы. А теперь определите как называется ракета на которой мы отправляемся в путешествие? (МНОГОЧЛЕН)
Если ваш ответ правильный, ставьте возле него +, если нет, –
Подведите промежуточный итог по операции компьютер, занесите число плюсов в графу путевого листа.
3.Операция. «Ракета». (5 мин -7 мин)
Мы в полете. Экипаж во время полета находится в ракете и выполняет текущие задачи.
Вам предоставляется выйти в открытый космос к доске.
Начали…
1. Среди следующих одночленов укажите подобные:
1) 9ас; 2) -17; 3) 9ху; 4) -17ас.
2. Какие из выражений не являются многочленами?
1) 3а + в; 2) 7а2 + в + 3; 3) 7а2 · в · 3
3. Запишите многочлен противоположный данному:
а) 8-2а
б) -3в3+4а
в) –св2 –авс +12а
4. Запишите многочлен а3 · а5 – 3а · а · а · + 7а2 в стандартном виде
5. Упростите, раскрыв скобки: 11 + (7а – 11).
6. Упростите: 9а – (3 – 5а).
7. Выполните умножение: 5(а + 1).
8. Выполните умножение: 3а2(7 – а).
Физкультминутка
Детям даётся инструкция: «Сядьте удобнее, закройте глаза. Представьте, что вы лежите на красивой поляне. Сделайте глубокий вдох и медленно делайте выдох, пусть всё напряжение уходит. Вокруг зелёная трава, вдалеке большой лес, поют птицы. Вы чувствуете, какая тёплая земля. Светит яркое солнышко. Один тёплый лучик упал на ваше лицо. Лицо стало тёплым и расслабилось. А луч света пошёл гулять дальше по вашему телу. Вам хорошо и приятно греться на солнышке. Вокруг зелёная трава, вдалеке большой лес, поют птицы. Вы чувствуете, какая тёплая земля. Земля вам даёт силу и уверенность. Сделайте глубокий вдох и медленно делайте выдох, пусть всё напряжение уходит. Ещё раз вдох и выдох… На счёт 5 вы вернётесь обратно. 1 – вы чувствуете, как хорошо лежать и отдыхать. 2,3,4 – у вас открываются глаза, 5 – вы полны сил и уверенности.
ОПЕРАЦИЯ «ОЗЕРО НЕИЗВЕСТНОСТИ»
Итак открыв глаза, мы видим, что находимся на планете МиФ у «Озера неизвестности». В озере плавают «рыбы – уравнения». Их нужно «поймать» то есть решить. Ваши рыбки у вас под вашими космическими креслами!
Проверка ответов по слайду.
Операция. « Мозговой штурм» (самостоятельная работа)
У: Благополучно переплыв озеро неизвестности, мы встречаем новое задание. Чтобы благополучно вернуться домой каждый из нас должен выполнить задания и вернуться домой.
Разноуровневые задания:
Синий цвет | Зеленый цвет |
|
4. 2в3 + в2 – в(2в2 + 1) |
Красный цвет |
4 а3(а2 + а – 1) – а4(а -2) |
После выполнения ребята сдают бланки учителю для последующей проверки.
ИТОГИ УРОКА: повторили раскрытие скобок, умножение одночленов, умножение одночлена на многочлен
Д/3 п5.5 №908.906. 909 а)б)
Если останется время закончить стихотворением.
Среди наук из всех главнейших
Важнейшая всего одна.
Она сложна среди простейших,
Для упрощения дана.
Чтобы решить труднейшую задачу
И знать побольше всех, идя вперед,
Ты ничего не бойся, ищи эту удачу,
И обязательно она тебя найдет.
Учите алгебру, она глава наукам,
Для жизни очень всем нужна,
Ты должен знать её, познай ученья муки,
И будет знанием твоим она покорена.
Когда достигнешь ты наук высоты,
Познаешь цену знаниям своим,
Поймешь, что алгебры красоты,
Для жизни будут кладом не плохим.
nsportal.ru
ПРОЕКТ
«Математика в жизни человека»
Внеклассное мероприятие в 7в классе
МБОУ «Гимназия №125»
Классный руководитель: Церетели Н.К.
Цели:
Вид проекта: исследовательский, практико – ориентированный, групповой, меж предметный, среднесрочный.
Задачи проекта:
1.Ответить на вопросы:
– Как часто люди в жизни сталкиваются с математическими задачами в быту и повседневной жизни?
– Есть ли данная информация в периодической печати?
– Решают ли такие задачи старшеклассники?
2.Отобрать нужные задачи из сборников ОГЭ и ЕГЭ.
3.Издать брошюру с задачами в быту и повседневной жизни.
4.Решить самим предложенные задачи.
5.Подготовить презентацию о проделанной работе.
6.Сделать выводы.
Продукты:
Брошюра «Математика в жизни человека»;
Компьютерная презентация;
Оборудование:
Проектор, экран, компьютер, бумага формата А4, фломастеры, карандаши, степлер
Методы исследования:
Изучение опыта, самостоятельная работа с литературой, эмпирическое исследование (направленное на сбор и анализ данных по проблеме), беседа.
Участники проекта: учащиеся 7в класса.
Ход проекта:
1.этап (подготовительный)
– постановка задач, определение состава групп, определение возможных способов решения поставленных задач
– социологический опрос по определению темы проекта;
– написать эссе
– сбор информации по теме проекта
2.этап (подготовительный)
– обсуждение собранного материала;
– разработка сценария основной части проекта.
3.этап (основной)
– форматирование и печать брошюры
– подготовка компьютерной презентации проекта
– оформление проекта.
4.этап (основной)
– защита проекта с демонстрацией подготовленного материала.
– оформление результатов проекта.
Введение
Кто с детских лет занимается математикой,
тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость
и упорство в достижении цели.
(А. Маркушевич)
Актуальность.
В период бурной информатизации нашего общества нарастает потребность в обучении и воспитании детей, способных жить в открытом обществе, умеющих общаться и взаимодействовать со всем многообразием реального мира, имеющих целостное представление о мире и его информационном единстве. Поэтому для развития детей приобретают значимость умения собирать необходимую информацию и выдвигать гипотезу, делать выводы и умозаключения использовать для работы с информацией новые информационные технологии.
В связи с этим особое внимание уделяется созданию условий для развития творческого личностного потенциала учащихся и расширения возможностей углублённого образования. Бурное развитие новых информационных технологий и внедрение их в нашей стране наложили отпечаток на развитие личности современного ребёнка.
Метод проектов всегда предполагает решение какой-то проблемы, предусматривающей, с одной стороны, использование разнообразных методов, средств обучения, а с другой, интегрирование знаний, умений из различных областей науки, техники, технологии, творческих областей. Использование этого метода делают учебный процесс творческим, а ученика – раскованным и целеустремленным. При работе над проектами царит творческая рабочая обстановка, при которой поощряется любая самостоятельная работа, привлечение нового, не изученного материала, когда идет интенсивное самообучение и взаимообучение, создаются условия для саморазвития творческой индивидуальности человека и раскрытия его духовных потенций.
Проанализировав ситуацию в классах, можно прийти к выводу: Математика начинается вовсе не со счета, что кажется очевидным, а с…загадки, проблемы. Чтобы у учащегося развивалось творческое мышление, необходимо, чтобы он почувствовал удивление и любопытство, повторил путь человечества в познании. Данный проект преследует собой цель пропаганды изучения математики и предлагает новый взгляд на математику в русле важной составляющей для современного человека.
Предлагаемый проект позволяет сформировать у учащихся, проявляющих интерес и склонность к изучению математики, представления о различных методах решения задач и ориентирован на более широкое, выходящее за рамки школьной программы, изучение математики и направлен на подготовку к успешному участию в математических олимпиадах.
Работа со школьными учебниками, сборниками ЕГЭ и ОГЭ позволит помочь школьникам вспомнить, закрепить и повторить материал текстовых задач.
Использование электронных образовательных ресурсов позволяет обеспечить:
Основная часть.
Описание этапов проекта.
На уроках математики нам не хватает времени, чтобы больше узнать о роли математических наук в жизни человека и их связи с различными областями жизнедеятельности, об истории возникновения и развития этой науки, ученых и их достижениях. В результате мы часто задаемся вопросом: «Зачем мы изучаем математику? Какое место в нашей жизни она занимает? Часто ли приходится взрослым решать в повседневной жизни математические задачи?».
Предположили, что если научиться решать задачи с математическим содержанием в быту и повседневной жизни, то это поможет:
Чтобы ответить на эти вопросы, мы:
1. Изучили теорию вопроса.
2. Встретились с людьми разных профессий, беседовали
3. Обработали результаты, полученные в ходе опроса (написали эссе)
4. Собрали информацию о роли математики в разных сферах жизни
Мы распределили задания следующим образом:
1. После социологического опроса, сделали вывод – чаще всего в жизни встречаются задачи на проценты, количественный подсчет, экономические задачи.
2. Собирая задачи с практическим применением в быту и повседневной жизни, которые старшеклассники решают на ОГЭ и ЕГЭ, попробовали решить и сами несколько задач. Нам необходимо научиться решать такие задачи, чтобы удачно сдать выпускные экзамены.
3. Изучив сборники для подготовки к ОГЭ и ЕГЭ, мы выяснили, что это задачи на вычисление и округление, задачи на деление с остатком, задачи на проценты, задачи на проценты и деление с остатком.
Вот некоторые из них:
Решение: 14000-14000*0,13=12180(р.)
Решение:(3500-2800):3500*100=20(%)
5. В процессе выполнения данного этапа мы собирали тексты задач с практическим содержанием, набирали их на компьютере, форматировали тексты, подбирали справочный материал и примеры решения некоторых задач.
6. Все материалы были оформлены в брошюру, которую назвали «Математика в жизни человека».
В результате работы над проектом мы научились оформлять выводы, делать презентацию, проводить опрос, отбирать задачи математического содержания, встречающиеся в быту и повседневной жизни, из сборников ОГЭ и ЕГЭ, распределять работу между собой, оформлять брошюру, выполнять экономические расчеты, оценивать свои результаты.
Заключение.
Данный проект представляется ценным с той точки зрения, что развивает у учащихся, среднего звена, интерес к математике, вызывает стремление глубже изучать математику.
Знания, полученные участниками проекта, позволят авторам выступить в роли консультантов для младших учеников, делясь с ними полученными знаниями.
Рефлексия.
Участники проекта приобрели навыки проектной деятельности, повысилась их самооценка. Отзывы авторов проекта:
Список литературы.
1.Карлин С. Математические методы в теории игр, программировании и экономике.
2.Арутюнян Е.Б., Левитас Г.Г. Занимательная математика
3.Волина В.В. Учимся играя.
4.Лопатина А. М. Как подружиться с математикой.
5. Моисеев Н. Н. Математик задает вопросы.
6.Шаблон VCT –проекта портала Сеть Творческих Учителей
7.Классификация проектных работ: Кукушкин В.С. Теории и методики обучения. Ростов-на- Дону, 2005, С.241.
8. Подготовка и защита реферата, Е.И. Грищук, Л.Д. Мудрова, ВОИПКиРО, 2008 г
9.Дроби и проценты, С,С, Минаева, изд. «Экзамен», Москва, 2012г
10. Материалы интернет ресурсов.
Приложение
Практическая часть.
Математика в кулинарии.
Математика в кулинарии имеет большое значение, так как для приготовления любого блюда должен соблюдаться рецепт. В рецепте указывается точное соотношение продуктов, которое необходимо соблюдать в процессе приготовления. При взвешивании продуктов в кулинарии используются математические величины масса и объём. Ими тоже необходимо уметь пользоваться. Единицы времени играют далеко не последнюю роль в приготовлении блюд. Приготовленные блюда нужно умело делить на порции, в чём нам опять же поможет математика.
Например, для того, чтобы приготовить овощную икру для семьи из 4 человек, используются следующие расчёты: репчатый лук, солёные огурцы и морковь берутся в весовом соотношении 3:4:4. Вымытые, очищенные и порезанные овощи перемешиваются с небольшим количеством томатной пасты и 15 минут тушатся на огне. Подаются в холодном виде.
Математика в торговле.
Математика в торговле важнее всего. Работники торговли должны хорошо знать числа, уметь их складывать и вычитать, умножать и делить. Без этого продавцы не смогли бы сосчитать товар в магазине. Не могли бы вести ведомости расхода и прихода прибыли в магазине. С помощью математических вычислений продавцы считают стоимость приобретённого покупателем товара, отсчитывают сдачу.
Математика в раскрое одежды.
Прежде чем сшить одежду, необходимо снять все мерки с человека, и тут не обойтись без математики. Сантиметровой лентой нужно сделать замеры (длину рукавов, ширину, длину костюма или платья и другое), записывая их в тетрадь. Потом по журналу мод нужно выбрать фасон одежды и по ранее замеренным цифрам мерки рассчитать и начертить выкройку. При помощи математических расчётов оставим запас ткани на припуск и подгиб, только после этого делаем раскрой ткани для шитья из него одежды. Как говорится, семь раз отмерь, один раз отрежь.
Математика в строительстве.
В строительстве без математики никак не обойтись. Посудите сами: Надо уметь измерять высоту, ширину, длину предметов? Надо. Надо уметь вычислять размеры дверей, окон, комнат, квартир? Надо. Как подсчитать количество нужного строительного материала, если не знаешь математику? Никак! Математику применяли ещё задолго до нашей эры. В Древнем Вавилоне при помощи математических расчётов строили водопроводы и подавали в дома воду. В Древнем Египте по математическим расчётам строили пирамиды.
Рассмотрим пример: Строителю заказали покрасить помещение. Для этого ему нужна краска, но тут возникает вопрос, сколько краски нужно купить, чтобы излишне не потратиться и купить чересчур много краски или купить мало краски и не доделать работу. Он знает, сколько краски расходуется на 1 квадратный метр (допустим, что на 1 квадратный метр понадобиться 2 литра). Строителю остается рассчитать площадь стен и потолка. Он знает, что высота одной стены 3 метра, а длина 4 метра. При помощи формулы (S = ab) строитель узнает, что площадь одной стены равна 12 метров в квадрате и узнает, что ему понадобиться 24 литра на одну стену. Те же вычисления он проводит с потолком и другими стенами и едет в магазин.
Так же можно представить, что строителю необходимо поменять пол для последующей укладки паркета. Это требует заливки пола раствором на высоту 10 см. Для этого ему нужно знать объем заливаемого раствора. Длина пола 6 метров, ширина 4 метра. При помощи формулы (S = ab) он узнает, что площадь пола равна 24 квадратных метра. (Формула вычисления объема V=Sh). Он знает, что пол ему надо поднять ровно на 10 сантиметров. За высоту он принимает то расстояние, на которое ему надо поднять пол, то есть на 10 сантиметров. Он узнает, что объем пола составляет 2,4 кубометра.
Математика в спорте.
Прогресс в спорте оценивается ростом результатов (для начинающих) и мировыми достижениями (для профессиональных спортсменов). Зафиксировать, сравнить и записать результат возможно только при помощи математики!
Мы повсюду видим использование натуральных чисел в любых видах спорта. В каждом соревновании ведется счет на время. Без счёта нет и игры. В математике жизнь спорта. Давайте рассмотрим некоторые примеры:
Любой вид соревнований на скорость (бег, плавание, автогонки и др.) подразумевают подсчет результата в часах, минутах, секундах, а время у нас записывается ЦИФРАМИ! Разница между результатами — это простейшие арифметические действия! В игровых видах спорта (футбол, баскетбол, теннис, водное поло и др.) счет идет на очки. В баскетболе, например, заброс мяча в корзину со штрафного даёт 1 очко, с игры из-под кольца- 2 очка, с 6-метровой линии-3 очка. А очки — это тоже ЦИФРЫ! Разница между очками есть математическое вычисление. В таких видах спорта как гимнастика, фигурное катание, прыжки в воду подсчет результата ведется с помощью баллов. Баллы даются судьями за выполнение того или другого элемента. И опять кто набрал больше баллов, помогает определить математика!
Обратимся к самому «математическому» виду спорта – шахматам!. Небольшая шахматная доска является необъятным полем для бесчисленных комбинаций. Достаточно сказать, что в самом начале партии игрок имеет 20 вариантов для первого хода; его партнер может ответить 20 ходами на каждый ход, то есть в распоряжении последнего уже 400 вариантов только для первого хода! Вот простор для математического подхода! Не зря говорят – кто силен в математике – у того сложно выиграть в шахматы. Получается, что спорт без математики никуда!
Математика в музыке и танцах.
Мы посещаем музыкальную школу.
Там мы поём, играем на фортепиано и аккордеоне, изучаем сольфеджио. Начиная разучивать какое-то музыкальное произведение, мы «считаем». Это необходимо, чтобы правильно сыграть произведение, так как ноты могут быть разными по длительности.
Длительность нот — условная продолжительность звуков, измеряемая долями, не зависящая от времени.
Четвертная нота равняется одному удару.
Восьмая нота – это половина от четвертной ноты, следовательно, в одном ударе (шаге) две восьмые ноты. Шестнадцатая нота составляет половину от восьмой ноты, то есть ¼ от четвертной ноты.
Для того чтобы правильно играть, нам нужно отсчитывать эти доли.
Итак, мы выяснили, что без математики невозможно играть на музыкальных инструментах!
Кроме музыкальной школы, мы посещаем танцевальный кружок. Мы танцуем под музыку, а чтобы не сбиться с ритма, нам необходимо опять же «считать». Счёт нужен, чтобы знать, сколько раз нужно сделать одно движение, а сколько раз другое.
Задача 1. Папа купил американский автомобиль, на спидометре которого скорость измеряется в милях в час. Какова скорость автомобиля в км/ч, если спидометр показывает 50 миль в час?
Решение: зная, что 1 американская миля 1км 609 м, увеличим ее в 50 раз, получим ≈80(км/ч)
Задача 2. Счетчик электроэнергии 20 января показывал 32544 киловатт-час, а 20 февраля 32726 киловатт- часов. Сколько рублей нужно заплатить за электроэнергию ?
Решение: 1 киловатт-час стоит 3 рубль 56 коп., поэтому, сначала найдем сколько киловатт-час нагорело, вычитая показания счетчика январские из февральских. Будет 182 киловатт-часа, а затем умножим цену за 1 киловатт-час на 182, будет 647 рубля 92 копейки.
Задача 3.В 50 литрах компота 5 кг сухофруктов и 3 кг 750 г сахара. Сколько % сухофруктов и сколько % сахара в компоте?
Решение: разделим количество каждого продукта на общее количество компота и выразим в процентах. Получим 10% сухофруктов и 7,5 % сахара
Задача 4.Прививку от гриппа в этом году поставили 80% обучающихся в нашей школе. Сколько школьников поставили прививки против гриппа, если в школе 265 обучающихся?
Решение: 80% от 265 составляют 212 школьников
Задача 5.Летом килограмм клубники стоит 100 рублей. Мама купила 3кг 200г клубники. Сколько рублей сдачи она должна получить с 1000 рублей?
Решение:1000-100*3,2=680(руб.)
Задача 6.В школе есть трехместные туристические палатки. Какое наименьшее число палаток нужно взять в поход, в котором участвуют 20 человек?
Решение: 20:3≈7(палаток)
Задача 7.Налог на доходы составляет 13% от заработной платы. Заработная плата Петра Ивановича равна 14 000 рублей. Сколько рублей он получит после удержания налога на доходы?
Решение: 14000-14000*0,13=12180(р.)
Задача 8.Мобильный телефон стоил 3500 рублей. Через некоторое время цену на эту модель снизили до 2800 рублей. На сколько процентов была снижена цена?
Решение:(3500-2800):3500*100=20(%)
Задача 9.Клиент взял в банке кредит на сумму 30 000 рублей с годовой процентной ставкой 14%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?
Решение: 30000*0,14=4200(р.)-14%
30000+4200=34200(р.) – банку за год
34200:12=2850(р.) ежемесячно
nsportal.ru
Задачи:
.
Ход мероприятия
Вступительное слово учителя:
1 слайд Тема: «Математика в жизни человека»
2 слайд Основопологающий вопрос: Нужна ли математика человеку?
3 слайд Проблемные вопросы:
Выступление учащихся:
Чтоб водить корабли, Чтобы в небо взлететь, Надо многое знать, И при этом, и при этом, Вы заметьте-ка, Очень важная наука Ма-те-ма-ти-ка!
Почему корабли Не садятся на мель, А по курсу идут Сквозь туман и метель? Потому что, потому что, Вы заметьте-ка, Капитанам помогает Ма-те-ма-ти-ка!
Чтоб врачом, моряком Или лётчиком стать. Надо прежде всего Математику знать. И на свете нет профессий Вы заметьте-ка, Где бы вам не пригодилась Математика!
4 слайд Как и когда зародилась математика?
Когда речь идёт о чём-нибудь очень простом, понятном, мы часто говорим: «Дело ясно, как дважды два — четыре!».
А ведь прежде чем додуматься до того, что дважды два — четыре, людям пришлось учиться много, много тысяч лет.
Конечно, это учение шло не за партой. Человек постепенно учился жить: строить жилища, находить дорогу в дальних походах, обрабатывать землю.
И одновременно он учился считать.
Потому что даже в самые далёкие времена, когда люди жили в пещерах и одевались в звериные шкуры, они не могли обойтись без счёта и меры.
Многие правила из школьных учебников арифметики и геометрии были известны древним грекам две с лишним тысячи лет назад.
Другие древние народы — египтяне, вавилоняне, китайцы, народы Индии — в третьем тысячелетии до нашего летосчисления имели сведения по геометрии и арифметике, которых не хватает некоторым ученикам пятого или шестого класса.
Ведь всюду, где надо что-то считать, измерять, сравнивать, без математики не обойтись.
А чем дальше, тем больше и точнее нужно было считать.
С каждым десятилетием математика становилась всё нужнее людям. 5 слайд Пифагор
Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Считается, что доказана греческим математиком Пифагором, в честь которого и названа.
Теорема звучит следующим образом: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
6 слайд
В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.
7 слайд
Софья Ковалевская
Девочка из дворянской семьи любила математику и даже ночью прятала под подушку сложный задачник(родители не одобряли её увлечения).
В то время не принято было женщинам поступать в институт, но она поехала против воли родителей в Германию, в университет, и пришла к известному профессору. Он не хотел её брать и, чтобы отделаться, дал несколько им самим составленных задач, сказав, что если она решит, то возьмёт её к себе.
Эти задачи не могли решить даже профессора. Девушка решила за двадцать минут.
Софья Ковалевская закончила университет и стала знаменитым на весь мир математиком
8 слайд
Что может математика?
А ведь с математики начинается всё.
9 слайд
1 пример
Вы стоите на кассе и оплачиваете товар. Вы купили продуктов на 432 рубля, а денег у вас 500 рублей купюрами по 100 рублей . И вам дают сдачу 40 рублей, хотя должны дать 68 рублей. Значит вас обсчитали на 28 рублей!!!
10 слайд
2 пример
Мне нужно быть на даче в 15.40.Я трачу на дорогу 1.40 часа. Сегодня мне нужно заехать в магазин. Когда мне выезжать? Сколько времени я могу провести в магазине?
11 слайд
На дачу!
12 слайд
Решите задачку.
Как при помощи одного действия и пяти единиц получить 100?
13 слайд
14 слайд
Где можно обойтись без математики?
15 слайд
Задача на применение признака равенства треугольников на измерение расстояния между двумя недосягаемыми объектами.
Условие: Бригада по прокладке дорог должна сделать тоннель, но расстояние, которое нужно пробить через гору, не известно. Что должна предпринять бригада, чтобы узнать это расстояние, если известно расстояние от А до С и от В до С (рис. 1)?
Рисунок 1
Решение: Бригада не может проложить дорогу вокруг горы. Поэтому они предприняли небольшую хитрость: на месте входа в еще не прорубленный тоннель поставили человека – (А) и на месте выхода тоже – (В), сбоку горы поставили третьего человека – (С), образовался треугольник ABC. Человек А прокладывает прямую через точку С, и человек В тоже прокладывает прямую через точку С. Проведя прямые и поставив на них на определенном расстоянии еще двух людей – (D, E) так, что CD = AC, а СВ = ЕС.Угол ACB = ECD по свойству вертикальных углов, поэтому треугольник DEC равен треугольнику ABC. Теперь бригада соединяет отрезком на местности точки D и Е. Рабочим остается измерить расстояние от Е до D, которое будет равно искомому расстоянию от А до В.
16 слайд
Нужны ли знания по математике современному человеку?
Стремительно изменяется мир и сама жизнь. В неё входят новые технологии. Только математика и решение задач в традиционном понимании не изменяют себе. Математические законы проверены и систематизированы, поэтому человек в важные моменты может положиться на неё, решить любую задачу. Математика не подведёт.
Но с каждым годом у нас появляется всё больше и больше замечательных машин: сложных станков, различных автоматов. Для того чтобы хорошо работать на таких машинах, надо очень много знаний. Сейчас математика нужна не только ученому или инженеру, но и мастеру, и рабочему на заводе.
Однако ещё несколько десятков лет назад встречалось немало таких задач, решить которые было практически невозможно, хотя математики и знали, как их нужно решать. Бывало, что для решения одной единственной задачи десятки людей работали несколько лет. Вычисления шли медленно. Главные «инструменты» математика были те же, что во времена древних греков — собственная голова и чистый лист бумаги с карандашом.
И вот у математики появился новый могучий помощник, который называется электронно-вычислительной машиной. Существующие быстродействующие компьютеры работают в сотни тысяч раз быстрее человека.
Никогда ещё математика не была настолько всеобъемлющей и такой нужной людям наукой, как сегодня. О том, какой будет математика завтра, говорить трудно. Она развивается сейчас так стремительно, так часто делаются в ней новые открытия, что гадать о том, что будет, пожалуй, бесполезно. Одно можно сказать наверняка: завтра математика станет ещё могущественнее, ещё важнее и нужнее людям, чем сегодня.
multiurok.ru
Изучение математики в 7 классе принципиально отличается от всего того, что предлагалось ранее в 5 — 6 классах. И дело не только в названиях тем и разделении предмета на алгебру и геометрию. Помимо введения новых понятий и правил меняется характер работы с числами и выражениями. Многое из того, что репетитор по математике показывает в 7 классе является обобщением ранее пройденного, но поднимающее использование математики на принципиально новый уровень. Такое продвижение предполагает прочное усвоение вычислительной базы, которое к 7 классу должно быть достигнуто. Должно, но не обязано.
Значительные пробелы отстающих школьников, обращающихся к репетитору по математике в тот или иной период учебы в школе, ставят неразрешимые проблемы перед использованием традиционных методик объяснений, а именно методик прямого изложения материала. Креативный репетитор по математике находится в постоянном поиске новых форм и способов подачи объяснений конкретному ученику. И это очень непросто сделать.
Трудность каждой конкретной темы — весьма относительное понятие. Все зависит от того, с какой стороны к ней подойти и насколько ученик способен воспринимать ту или иную форму объяснений репетитора. Многие сложные понятия упрощаются, если репетитору по математике удается подобрать какое-нибудь простое и лаконичное описание математического процесса, сравнить его с чем-то обыденным и понятным, связать новое с ранее изученным. Это непростая задача, но репетитору нужно стремиться к ее выполнению. В алгебре, при объяснении нового материала, бывает достаточно точно подобрать соответствующие примеры работы правила на числах. У многих учеников 7 класса все еще преобладает тип мышления «от общего к частному», поэтому, стремление репетитора по математике к абсолютной стрости и полноте объяснений (доказательств), к использованию общих форм, рассмотрению всех случаев или педантичной проверке равносильности в переходах может перечеркнуть все усилия по обеспечению понимания.
Важно добиться первоначального понимания, пусть ученику не открывается вся картина происходящего в алгоритме, а лишь приоткрывается некая завеса нового. В некоторых случаях уже одно такое продвижение можно ставить в заслугу репетитору по математике, ибо ребенок начинает хоть что-то решать самостоятельно. Это крайне важно, ибо результаты практической работы помогает осмыслить многие моменты, которые оказались непонятыми.
Иногда репетиторы по математике, особенно начинающие, путают два состояния ученика: не понял и не запомнил. Если ребенок говорит «я не понимаю», — это не всегда означает, что слова репетитора по математике остались не осмысленными. Часто бывает наоборот: заявляет, что все понятно, но на проверку оказывается, что он просто заучил те или иные ходы в решении. Репетитору важно уметь отличать эти два состояния и правильно их использовать.
Как правило, решение систем методом подстановки вызывает у детей 7 класса дикое отвращение и неприязнь. Почему? Процесс, который описывает репетитор по математике на первом уроке по данной теме, очень трудно увязывается с привычным занятием в алгебре 7 класса. Дети настолько привыкают к однострочным одношаговым решениям (какими являются преобразования многочленов). Поэтому, когда репетитор по математике исписывает равносильными системами целую страницу в тетради, ученик почти всегда заявляет: «я не понимаю». «Стоп! Давай разберемся», — говорю я ему. Что именно из этого ты не понял, а что просто не успел запомнить? Если репетитор по математике поставит вопрос именно таким ребром, он переводит деятельность ученика из созерцательной в оценочную. Нужно дать время на то, чтобы привыкнуть к записям и запомнить ходы. Это облегчит оценку того, что именно не понятно. Главное не торопить ученика и дать ему возможность высказаться. Пусть это будут невнятные фразы, лишенные логики. Мастерство репетитора заключается в том, чтобы выявить проблему даже по «обрывкам мыслей» ученика.
Конечно, я описываю ситуацию, в которой репетитор не провел с учеником соответствующую подготовительную работу. А она обязательно нужна.
Нужны задания на проверку конкретных пар чисел для конкретной системы. В процессе выполнения простейших заданий репетитор обкатывает новую терминологию: пара чисел, удовлетворяющая системе, решение системы, проверка пары. Я еще употребляю фразы «вставка чисел», «вставка пары»
Важно убедить ученика в том, что совсем не обязательно искать пару чисел, которая при вставке в начальную систему даст два верных равенства. Мы же ищем саму пару.
Самому слабому ученику достаточно сказать, что при замене одной системы на другую не меняется самое главное — ее ответ, поэтому не важно, какую именно систему решать. Пара, подходящая для одной из них — подойдет и для другой. Это можно просто проверить на конкретных числах. Надо чувствовать ученика и не ввязываться в объяснения равносильности переходов в 7 классе, какими бы точными они не были. Если все-таки репетитор по математике хочет донести до сознания ученика логику алгоритма, это нужно делать после того, как ученик его запомнит.
Если ученик более-менее толковый, репетитор по математике применяет числовую методику проверки равносильности. Покажу ее работу на примере
Пусть задана система линейных уравнений:
Как ее решить — все вы отлично знаете. Но как объяснить это решение слабому учащемуся? Вот она — головная боль для преподавателя. Дети в 7 классе не воспринимают общие математические методы доказательства равносильности, под лупой которых, конечно же, вся логика преобразований оказывается на поверхности.
Какие методики могут быть задействованы в принципе? Обычно репетитор по математике проводит равносильные преобразования по классической схеме: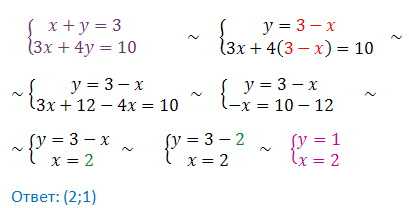
Однако нельзя оставлять такую форму без каких-либо объяснений.
Как правило к моменту изучения темы «метод подстановки», учащиеся 7 класса уже имеют выражать переменную y через переменную x. Будем считать, что репетитор по математике решил эту проблему в теме «графический способ решения систем уравнений». Тогда самый непонятный ход — вставка выражения 3-x во второе уравнение системы на место x.
Как репетитор может объяснить замену игрека на 3-x ?
Я покажу как можно работать со средним учеником по методике числовой проверки ( если ученик сильный — для него вполне подойдут строгие математические обоснования «в обе стороны»). Итак, рассмотрим равносильный переход между системами:
Надо убедить ученика в том, что одна и та же пара чисел (она предоставляется в готовом виде) превращает каждое равенство в верное. Репетитор говорит: «Давай проверим пару (2;1), то есть х=2; y=1. Вставим их на места букв в систему (1).Получим: Эти равенства верные, поэтому пара чисел (2;1) — решение системы (1). Но 1=3-2 и поэтому можно вместо единицы в нижнем уравнении написать в скобках (3-2). От этого при подсчете не изменится результат». Далее репетитор по математике меняет 1 на разность 3 — 2
и спрашивает ученика: “Какая запись получится, если мы задумаем эту же пару (2;1) вставить во вторую систему? Будут ли ее равенства верными? Конечно, ведь мы только что их проверили (в этот момент репетитор по математике показывает на записанную систему №3). Вставка пары (2;1) приводит нас к повторению той же самой записи, к копии уже проверенного равенства. Поэтому пара (2;1) будет еще и решением системы №2. Значит у них одинаковые ответы (понимаю, что вывод не выдерживает никакой критики с точки зрения строгой математики и проверка проведена в одну сторону, но дети проглотят такой маневр репетитора). Поэтому вместо того, чтобы решать первую систему, мы можем решать вторую и через нее искать эту пару (если она неизвестна).
Остальные равносильные преобразования репетитору по математике не составит труда объяснить. В них нет ничего нового. Обычное решение уравнения с одной переменной. Понятно, что икс должен быть корнем уравнения (2). Ученики в 7 классе обычно понимают, что его надо найти.
Замечу, что ответ нужно записывать не в виде x=2; y=1, а в виде пары (2;1). Это будет способствовать скорейшему формированию у ученика представления об ответе, как о некоторой точке координатной плоскости.
Репетитор по математике 7 класс — Колпаков А.Н. Москва, Строгино.
ankolpakov.ru