Математический квадрат 4 класс с ответами: Как решать задачи на магические квадраты в 4-5 классе. Как составлять магические квадраты
Как решать задачи на магические квадраты в 4-5 классе. Как составлять магические квадраты
Магическая константа M – сумма чисел в каждой строке, столбце и на диагоналях.
Для квадрата любой размерности n∙n минимальная магическая константа вычисляется по следующей формуле:
M = n(n2 + 1)/2
I. Магический квадрат 3×3
Для квадрата размера 3×3 минимально возможная магическая константа будет равна:
3(32 + 1)/2 = 3(9 + 1)/2 = 15
Подчеркнём, что 15 – это не единственно возможная магическая константа для квадрата 3×3, а константа, меньше которой других констант для этого квадрата быть не может.
Важное правило, которое вам пригодится при построении магического квадрата 3×3:
Число в центре квадрата 3×3 всегда в три раза меньше магической константы.
То есть, если у нас магическая константа M = 15, то в центре квадрата 3×3 будет стоять
15:3 = 5.
Для дальнейшего составления магического квадрата с магической константой M=15 расставьте по углам чётные числа 2,4,8,6.
Как видим, по сумма чисел на диагоналях квадрата равна 15, то есть магической константе.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Зная магическую константу и по два числа в ряду и столбце, мы можем вписать третье число в ряд и столбец. Определить это число очень просто – надо из магической константы вычесть два числа из ряда или столбца.
Применив этот метод, мы получим полностью заполненный магический квадрат:
Ещё одно важное правило построения магических квадратов:
Если у нас есть один магический квадрат, и мы все числа этого квадрата увеличим на одно и то же число или умножим на одно и то же число, то у нас опять получится квадрат. Это правило достаточно очевидно.
Пример 1. К числам в нашем магическом квадрате с M=15 прибавим 3 и 5
Как видим, у первого квадрата сумма чисел по вертикали, горизонтали и диагонали одинакова и составляет 24 (это и есть его магическая константа), а у второго квадрата магическая константа равна 30.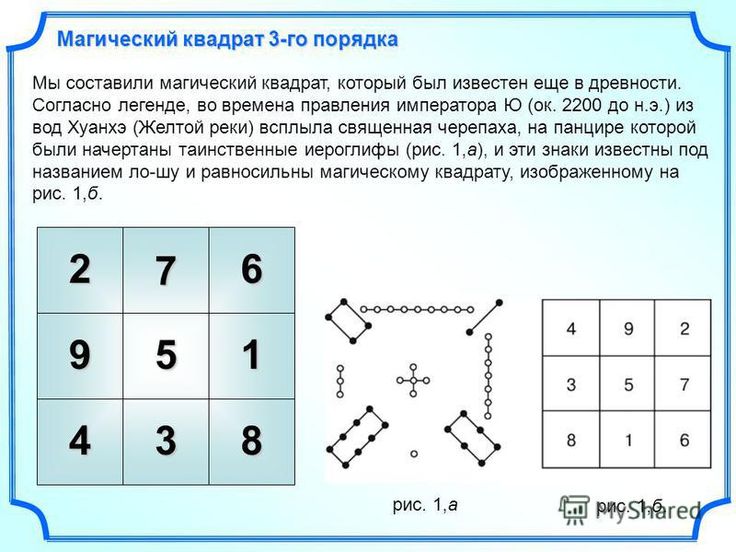
У этих двух квадратов число в центре по прежнему в три раза меньше, чем магическая константа (8 у первого квадрата и 10 у второго).
Пример 2. Числа нашего магического квадрата с M=15 умножим на 2 и на 3
Как видим, в первом случае, после умножения чисел на два, мы получили квадрат с магической константой 30 – та же самая константа, что и после того, как в первом примере мы увеличили все числа на 5. Но при этом, несмотря на то, что у этих двух магических квадратах одинаковые магические константы, числа при этом в клетках разные – а вот число в центральном квадрате одно и то же – это 10.
Так и должно быть, ведь, как было сказано выше, в магическом квадрате 3×3 число в центральной клетке должно быть в три раза меньше магической константы. Т.к. магическая константа у обеих магических квадратов одинаковая, то и центральное число одно и то же.
Задача 1.
Постройте магический квадрат с магической константой 39.
Зная магическую константу, мы легко найдём число, которое должно быть в центральной клетке – нужно магическую константу разделить на 3. 39:3 = 13.
Далее можно или подбирать числа (помня о том, что сумма чисел по диагонали, по горизонтали и по вертикали должна быть равна магической константе) или, для ускорения процесса, воспользоваться знанием чисел магического квадрата с минимальной магической константой M = 15.
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Напомним этот квадрат:
В центре этого квадрата – число 5. В центре того квадрата, который мы должны построить – число 13.
Разница между этими числами составляет 8. И, как следует из правила, которое мы написали выше, если все числа одного магического квадрата увеличить на одно и то же число, то получится другой магический квадрат.
Достаточно запомнить, что в центре минимального магического квадрата – 5, а по углам – чётные числа 2, 4, 6, 8. Таким образом, нам надо увеличить эти числа на 8. Далее будет легко заполнить оставшиеся клетки (числа в них вычисляются как магическая константа минус числа в ряду или столбце).
Таким образом, нам надо увеличить эти числа на 8. Далее будет легко заполнить оставшиеся клетки (числа в них вычисляются как магическая константа минус числа в ряду или столбце).
В итоге получится вот такой квадрат:
Задача 2.
Достройте магический квадрат
В этом квадрате мы знаем число в центральной клетке (9), а, значит, мы знаем магическую константу, которая в 3 раза больше и равна 27. Ну а зная магическую константу и три первоначальных числа, вписать оставшиеся числа в клетки не составит труда.
Решение:
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
II. Магический квадрат 4×4
Мы не будем подробно останавливаться на магических квадратах 4×4 – они почти не встречаются на математических олимпиадах и вступительных экзаменах в физматшколы, но общее представление о них дадим.
Минимально возможная магическая константа вычисляется всё по той же формуле:
M = n(n2 + 1)/2
M = 4(42 + 1)/2 = 34.
У квадрата 4×4 обе стороны чётные, а это значит, что центральной клетки, в отличие от квадрата 3×3, у него нет, и нет соответствующей закономерности, с ним связанной.
Однако, у этого квадрата есть другие закономерности:
Помимо того, что у магического квадрата 4×4 равна сумма числе по диагонали, вертикали и горизонтали, у него сумма чисел в угловых квадратах 2×2 равна магической константе M, сумма чисел в центральном квадрате 2×2 также равна M, и сумма чисел в углах квадрата тоже равна M.
Сумма чисел в левом верхнем квадрате 2×2: 16+3+5+10 = 34. В трёх других угловых квадратах 2×2 сумма также равна магической константе, о чём и сказано выше.
Сумма чисел в центральном квадрате 2×2 также равна магической константе 34: 10+11+6+7 = 34.
Сумма чисел в углах магического квадрата тоже равна магической константе: 16+13+4+1 = 34
Магические квадраты: математические игры от ЛогикЛайк
Математика и логика для детей / Математические игры
Игры с магическими квадратами нравятся всем, кто увлекается головоломками.
Попробуйте занятия на сайте ЛогикЛайк!
Выберите возраст ученика для старта
4-5 лет
6-7 лет
1-2 класс
3-5 класс
6-9 класс
15+ для себя
На платформе Логиклайк
5500 заданий с ответами: задачи, головоломки, занимательные вопросы.
Как решать магические квадраты?
Разгадывать головоломки легче, когда точно понимаешь что нужно сделать и по каким правилам. Для начала нужно разобраться, что особенного в этих квадратных таблицах.
Решить магический квадрат — заполнить пустые ячейки так, чтобы сумма чисел по любой горизонтали, по вертикалям и диагоналям была одинаковой.
Сложите числа в решенной задаче в любой строке, в любом столбце, а также по обеим диагоналям.
Как ни складывай, получаем одну и ту же сумму. Вот где магия, вот почему квадрат — магический!
Проверь себя
Помоги Клапану узнать, какой из 2 квадратов магический.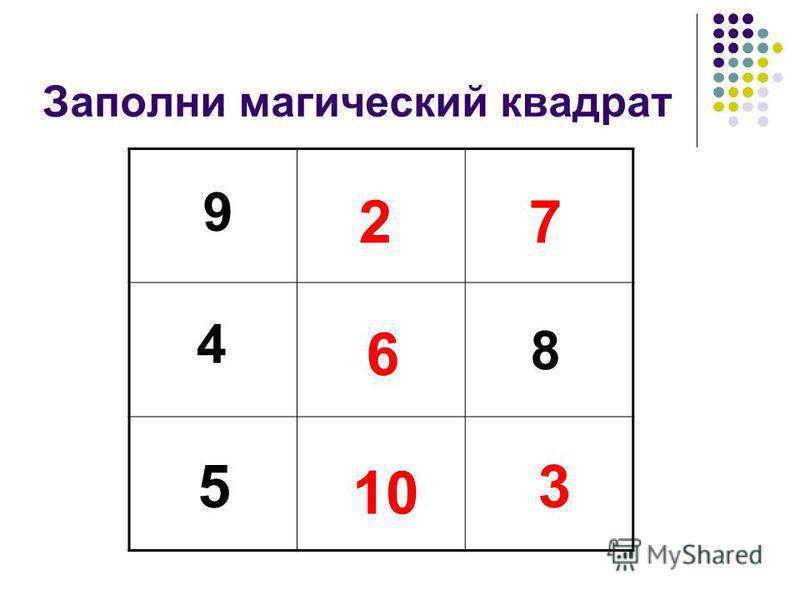
Узнать ответ
Ответ:
Первый, фиолетовый, квадрат.
Решение
В фиолетовом квадрате сумма чисел по всем
направлениям равна 21.
Познакомьтесь с примерами головоломок различного уровня сложности. Несколько заданий мы приводим
с ответами и описанием решения.
Несколько заданий мы приводим
с ответами и описанием решения.
Простые задания взрослый может выполнить в уме. Современным детям нравится решать головоломки и задачи онлайн.
Магические квадраты для 1-2 класса
Подборка заданий из обучающего курса ЛогикЛайк
Определи недостающее число
Чтобы решать задачи, нажмите Начать занятия!
Узнать ответ
Ответ:
5.
Решение
Найти магическое число здесь можно множеством
способов:
В математике это число называется магической константой и в данной головоломке равняется 9.
Находим пропущенное число:
9-2-2=5
или
9-3-1=5.

Чтобы решать задачи, нажмите «Начать занятия»!
Монстрики стерли некоторые числа в магическом квадрате.
Нужно заполнить пустые ячейки так, чтобы квадрат снова стал магическим.
Показать решение
1) Сначала нужно определить магическое число.
Для внимательных ребят это совсем просто:
5+3+1=9.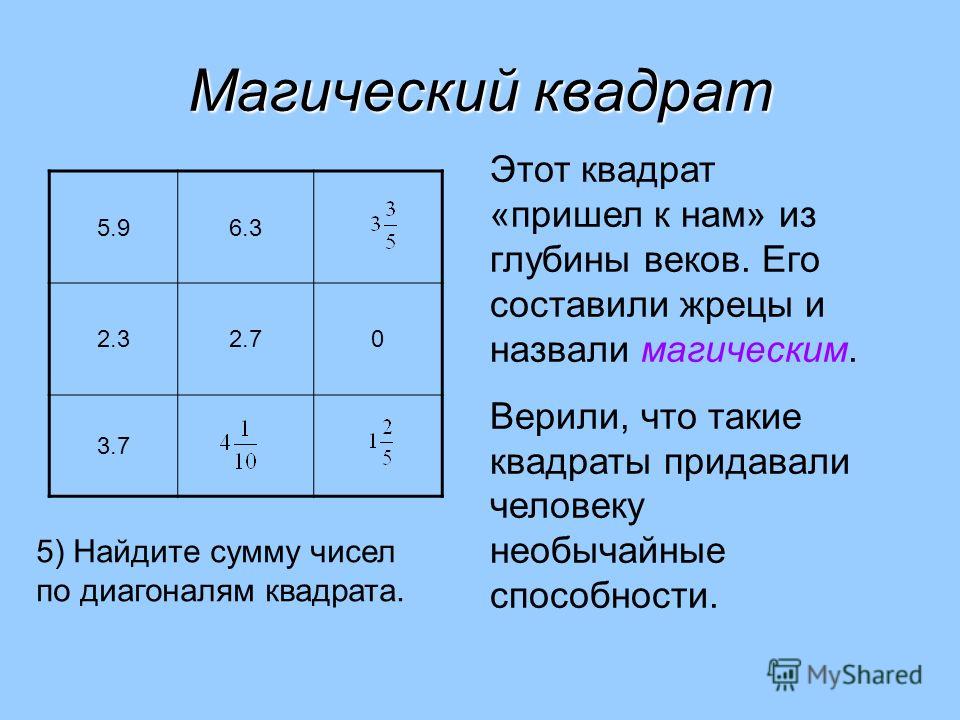
2) Находим недостающее число в первом столбце: 9-5-3=1.
3) Во 2-ой колонке: 9-3-1=5.
4) В 3-ем столбике: 9-1-5=3.
Помоги Иришке сделать квадрат магическим.
Чтобы решать задачи, нажмите «Начать занятия»!
В пустые клетки квадрата вставь числа 2, 3, 4.
Получить подсказку
Подсказка:
Магическое число
= 4 + 3 + 2 = 9.
Интересно, что этот квадрат можно заполнить по правилам
«Судоку».
Чтобы дети развивали логику и мышление с интересом, играючи, мы создали и развиваем онлайн-платформу «ЛогикЛайк».
Магические квадраты для 3-4 класса
Разгадать следующие головоломки в уме будет совсем непросто.
Можно вооружиться бумагой и ручкой или просто посмотреть примеры заданий. Интереснее всего
– играть в магические квадраты онлайн (нажимайте «Начать занятия»).
Чтобы решать, нажмите «Начать занятия»!
Профессор придумал магический квадрат, но из-за своей рассеянности не
заполнил несколько клеток. Осталось заполнить всего 4 пропуска.
Осталось заполнить всего 4 пропуска.
Чтобы решать, нажмите «Начать занятия»!
Монстрикам нужно поставить в пустые ячейки шесть различных чисел так, чтобы квадрат стал магическим.
Чтобы решать, нажмите «Начать занятия»!
Стань волшебником. Вставь в пустые клетки числа 5, 8, 9, 12, 13, 15 и сделай квадрат магическим.
Учим решать любые логические задачи
Более 150 000 детей и родителей со всего мира уже занимаются на сайте ЛогикЛайк. Подключайтесь и развивайте логику и мышление!
Начать обучение! Начать обучение!
Четвертый класс (4 класс) Области вопросов для тестов и рабочих листов
Из них можно создавать печатные тесты и рабочие листы. 4 класс вопроса!
Выберите один или несколько вопросов, установив флажки над каждым вопросом.
Затем нажмите кнопку добавить выбранные вопросы в тест , прежде чем перейти на другую страницу.
4 класс вопроса!
Выберите один или несколько вопросов, установив флажки над каждым вопросом.
Затем нажмите кнопку добавить выбранные вопросы в тест , прежде чем перейти на другую страницу.
Предыдущий Страница 1 из 2 Следующие
Выбрать все вопросыКвадрат имеет периметр 24 дюйма. Какова площадь квадрата?
- 36 квадратных дюймов
- 144 квадратных дюйма
- 12 квадратных дюймов
- 28 квадратных дюймов
Квадрат имеет периметр 88 футов. Какова площадь (в квадратных футах) квадрата?
Какова площадь (в квадратных футах) квадрата?
- 121
- 484
- 1936
- 7744
Площадь показанной фигуры составляет половину периметра. Что может быть правдой?
- площадь 9 периметр 12
- площадь 4 периметр 8
- площадь 25 периметр 50
Чему равна площадь этого прямоугольника, если его размеры 20 на 25 дюймов?
-
450 кв.
 дюймов
дюймов
- 400 кв. дюймов
- 90 кв. дюймов
- 500 кв. дюймов
Размеры большого прямоугольника составляют 15 дюймов x 19 дюймов. Размеры меньшего прямоугольника составляют 10 дюймов x 12 дюймов.
Какова площадь заштрихованной части большего прямоугольника?
- 165 кв. дюймов
-
285 кв.
 дюймов
дюймов
- 95 кв. дюймов
- 120 кв. дюймов
Мэри делала клетку для своей собаки. Она хочет, чтобы у ее собаки было 120 квадратных футов пространства. Какими могут быть ширина (w) и длина (l) клетки?
- ш = 40 футов; л = 2 фута
- ш = 4 фута; l = 30 футов
- ш = 60 футов; л = 3 фута
Фрэнк построил чулан площадью 42 фута. Шкаф шириной 7 футов. Какова длина?
Шкаф шириной 7 футов. Какова длина?
- 35 футов
- 7 футов
- 6 футов
- 49 футов
Чему равна площадь квадрата, если каждая сторона равна 5 см?
- 5 квадратных сантиметров
- 10 квадратных сантиметров
- 20 квадратных сантиметров
- 25 квадратных сантиметров
Прямоугольная гостиная имеет размеры 12 на 10 футов.
Положенный на пол ковер оставляет вокруг себя границу шириной 2 фута.
Какова площадь границы?
- 80 квадратных футов
- 72 квадратных фута
- 40 квадратных футов
- 120 квадратных футов
Чему равна площадь комнаты шириной 8 футов и длиной 12 футов?
- 96 квадратных футов
- 20 квадратных футов
- 128 квадратных футов
- 82 квадратных фута 92[/математика]
Длина умноженная на ширину дает
-
область.
- периметр.
- шкала.
Квадрат имеет длину 34 см и ширину 34 см. Площадь 1158 кв.см.
- Истинный
- ЛОЖЬ
Садовник выкапывает клумбу длиной 6 футов и шириной 3 фута.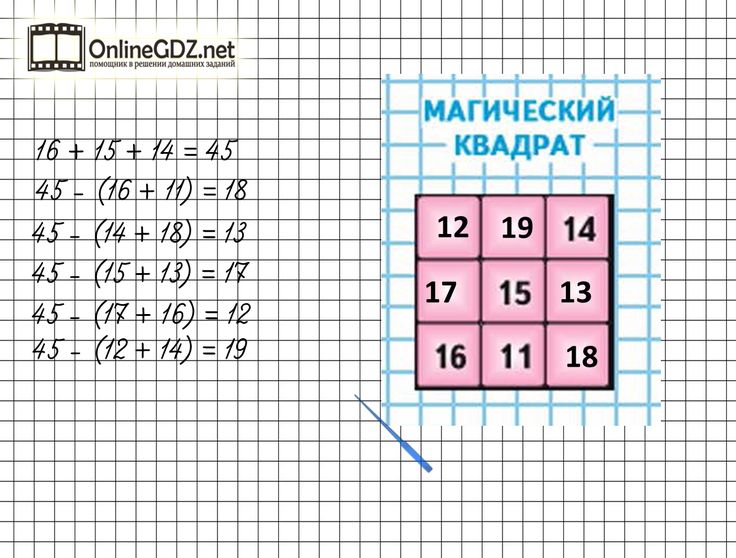 Какова площадь клумбы?
Какова площадь клумбы?
- 81 квадратный фут
- 18 квадратных футов
- 9 квадратных футов
- 15 квадратных футов
Прямоугольник имеет длину 56 см и ширину 12 см. Площадь 634 кв.
- Истинный
- ЛОЖЬ
Мария знает, что ее одеяло имеет площадь 24 квадратных дюйма. Она знает, что длина 6 дюймов. Какова ширина ее одеяла?
Она знает, что длина 6 дюймов. Какова ширина ее одеяла?
- 5 дюймов
- 4 дюйма
- 30 дюймов
- 18 дюймов
Размеры логова Марка составляют 12 на 11 футов. Он хочет выложить пол квадратной плиткой размером 1 фут. Сколько плиток ему понадобится?
- 264
- 46
- 132
- 23
Марк хочет затонировать прямоугольное окно. Если размер окна 4 фута на 2 фута, а стоимость тонировки составляет 5,25 доллара за квадратный фут, сколько будет стоить тонировка окна?
Если размер окна 4 фута на 2 фута, а стоимость тонировки составляет 5,25 доллара за квадратный фут, сколько будет стоить тонировка окна?
- 21 доллар
- $33
- 37 долларов
- 42 доллара
Когда вы находите площадь прямоугольника, вы перемножаете длину и ширину фигуры.
Площадь – это внешнее измерение фигуры.
- Истинный
- ЛОЖЬ
Предыдущий Страница 1 из 2 Далее
У вас должно быть не менее 5 репутации, чтобы голосовать против вопроса. Узнайте, как заработать значки.
Площадь квадрата – формула, как найти площадь квадрата?
Площадь квадрата определяется как количество квадратных единиц, необходимых для заполнения этой фигуры. Другими словами, площадь квадрата — это область, занимаемая в его границах. Когда мы хотим найти площадь квадрата, мы учитываем длину его стороны. Поскольку все стороны фигуры равны, ее площадь равна произведению двух сторон. Общепринятыми единицами измерения площади квадрата являются квадратные метры, квадратные футы, квадратные дюймы и квадратные сантиметры.
Общепринятыми единицами измерения площади квадрата являются квадратные метры, квадратные футы, квадратные дюймы и квадратные сантиметры.
Площадь квадрата можно также рассчитать с помощью других измерений, таких как диагональ и периметр квадрата. Давайте узнаем больше о площади квадрата и формуле площади квадрата на этой странице.
| 1. | Какова площадь квадрата? |
| 2. | Площадь квадрата Формула |
| 3. | Как найти площадь квадрата? |
| 4. | Часто задаваемые вопросы о площади квадрата |
Какова площадь квадрата?
Квадрат представляет собой замкнутую двумерную фигуру с четырьмя равными сторонами и четырьмя равными углами. Четыре стороны квадрата образуют четыре угла при вершинах. Сумма всех длин сторон квадрата — это его периметр, а общее пространство, занимаемое фигурой, — это площадь квадрата. Это четырехугольник, который обладает следующими свойствами.
Это четырехугольник, который обладает следующими свойствами.
- Противоположные стороны квадрата параллельны.
- Все четыре стороны квадрата равны.
- Все углы квадрата равны 90º.
Квадраты можно найти повсюду вокруг нас. Вот некоторые часто встречающиеся объекты, имеющие форму квадрата. Шахматная доска, часы и школьная доска — все это примеры квадрата.
Площадь квадрата Определение
Площадь квадрата – это мера занимаемой им площади или поверхности. Он равен произведению длин двух его сторон. Поскольку площадь квадрата равна произведению двух его сторон, единица измерения площади выражается в квадратных единицах.
Обратите внимание на квадрат, указанный ниже. Он занял 25 кв. Следовательно, площадь квадрата равна 25 квадратных единиц. Из рисунка видно, что длина каждой стороны равна 5 единицам. Следовательно, площадь квадрата равна произведению его сторон. Площадь квадрата = сторона × сторона = 5 × 5 = 25 квадратных единиц.
Квадрат Определение
Квадрат – это четырехугольник, у которого все четыре стороны равны и параллельны друг другу. Все углы в квадрате равны 90 градусов.
Площадь квадрата Формула
Формула площади квадрата, если известна сторона:
Площадь квадрата = сторона × сторона = S 2
Алгебраически площадь квадрата можно найти, возведя число в квадрат представляет собой меру стороны квадрата. Теперь воспользуемся этой формулой, чтобы найти площадь квадрата со стороной 7 см. Мы знаем, что площадь квадрата = Сторона × Сторона. Подставляя длину стороны как 7 см, 7 × 7 = 49. Следовательно, площадь данного квадрата равна 49 см 2 .
Площадь квадрата также можно найти с помощью диагонали квадрата. Формула, используемая для нахождения площади квадрата по диагонали:
Площадь квадрата по диагоналям = Диагональ 2 /2.
Давайте разберемся в выводе этой формулы с помощью следующего рисунка, где «d» — диагональ, а «s» — стороны квадрата.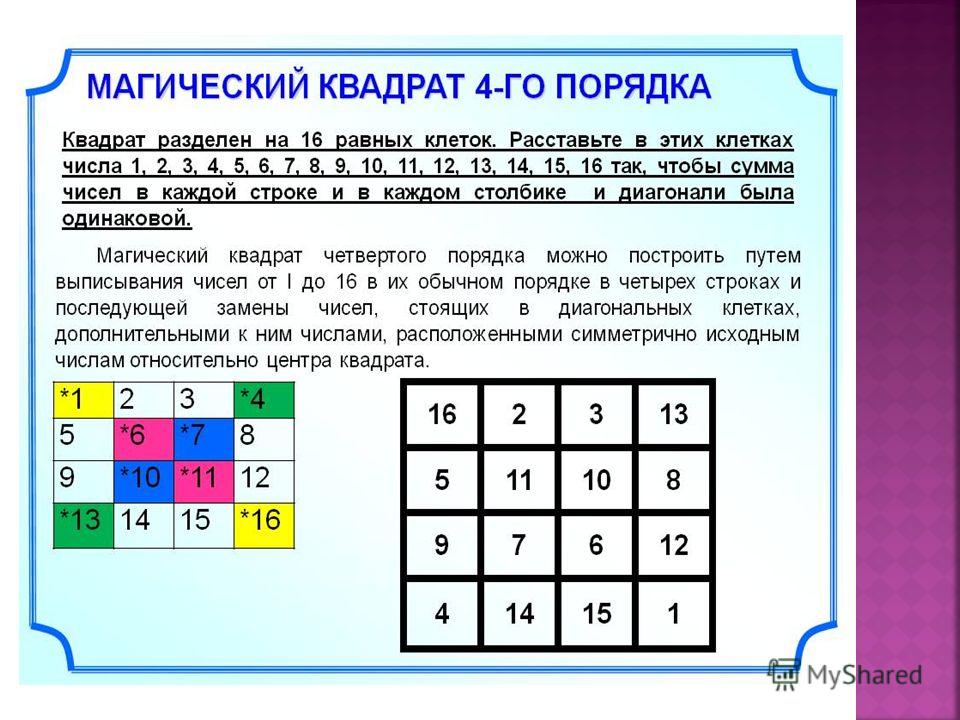
Здесь сторона квадрата ‘s’, а диагональ квадрата ‘d’. Применяя теорему Пифагора, мы имеем d 2 = s 2 + s 2 ; д 2 = 2s 2 ; д = √2с; с = d/√2. Теперь эта формула поможет нам найти площадь квадрата, используя диагональ. Площадь = s 2 = (d/√2) 2 = d 2 /2. Следовательно, площадь квадрата равна d 2 /2.
Как найти площадь квадрата?
Мы можем найти площадь квадрата, используя различные методы в зависимости от значений, которые нам даны. Давайте посмотрим, какими способами мы можем найти площадь квадрата, если известны его периметр, стороны или диагонали.
Площадь квадрата, если известен периметр квадрата
Пример: Найдите площадь квадратного парка, периметр которого равен 360 футов.
Решение:
Дано: периметр квадратного парка = 360 футов
Мы это знаем,
Периметр квадрата = 4 × сторона
⇒ 4 × сторона = 360
⇒ сторона = 360/4
⇒ сторона = 90 футов
Площадь квадрата = сторона 2
Следовательно, Площадь квадратного парка = 90 2 = 90 × 90 = 8100 футов 2
Таким образом, площадь квадратного парка с периметром 360 футов составляет 8100 футов.
Решение:
Дано: Сторона квадрата = 6 см
Мы знаем, что
Площадь квадрата = сторона 2
Следовательно, площадь квадрата = 6 0 2 90 6 = 36 см 2
Площадь квадрата, если известна диагональ квадрата
Пример: Найдите площадь квадрата, диагональ которого равна 12 см.
Решение:
Дано: Диагональ квадрата = 12 см
Мы знаем, что
Формула площади квадрата при заданной диагонали = d 2 /2
Следовательно, площадь квадрата = (12 × 12)/2 = 72 см 2
Советы по нахождению площади квадрата
Обратите внимание на следующие моменты, которые следует помнить при вычислении площади квадрата.
☛ Статьи по теме
- Диагональ квадрата
- Площадь квадратов и прямоугольников Рабочие листы
- Периметр площади
- Площадь поверхности квадратной призмы
- Калькулятор площади квадрата
Cuemath — одна из ведущих мировых платформ для обучения математике, предлагающая онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Площадь квадрата Формула Примеры
-
Пример 1: Какова площадь квадратного бассейна, одна сторона которого равна 8 м?
Решение:
Мы знаем, что одна сторона бассейна равна 8 м, поэтому воспользуемся формулой: Площадь квадрата = сторона × сторона = 8 × 8 = 64 м 2 . Следовательно, площадь бассейна составляет 64 квадратных метра.
-
Пример 2: Площадь квадратной доски составляет 3600 см 2 . Какова длина его стороны?
Решение:
Площадь квадратной доски = 3600 см 2 . Мы знаем, что Площадь = сторона × сторона = сторона 2 . Значит, сторона = √Площадь = √3600 = 60 см.
 Следовательно, сторона доски для каррома равна 60 см.
Следовательно, сторона доски для каррома равна 60 см. -
Пример 3: Найдите площадь квадрата с диагональю 4 фута.
Решение:
Площадь квадрата, если дана его диагональ, равна площади квадрата = диагонали 2 /2. Дано, диагональ (d) = 4 фута. Площадь квадрата = (4 × 4)/2 = 16/2 = 8 квадратных футов. Следовательно, площадь квадрата равна 8 кв.
перейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.
Запись на бесплатный пробный урок
Практические вопросы на площади Square
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади квадрата
Что такое площадь квадрата в геометрии?
Площадь квадрата определяется как количество квадратных единиц, составляющих полный квадрат. Он рассчитывается по формуле площади квадрата: площадь = сторона × сторона, и ответ дается в квадратных единицах.
Он рассчитывается по формуле площади квадрата: площадь = сторона × сторона, и ответ дается в квадратных единицах.
Какова площадь квадратной формулы?
Если известна сторона квадрата, то мы вычисляем площадь квадрата по формуле Площадь квадрата со стороной s: Площадь = s × s = s 2 . Когда дана диагональ ‘d’ квадрата, то формула, используемая для нахождения площади квадрата, такова: Площадь = d 2 /2.
Как вычислить площадь квадрата?
Площадь квадрата рассчитывается по формуле: Площадь = s × s, где s — одна сторона квадрата. Поскольку площадь квадрата является двумерной величиной, она всегда выражается в квадратных единицах. Например, если мы хотим вычислить площадь квадрата со стороной 4 единицы, это будет: A = 4 × 4 = 16 единиц 2 . Проверьте площадь квадратного калькулятора для быстрых расчетов.
Что такое площадь и периметр квадратных формул?
Периметр квадрата представляет собой сумму четырех сторон квадрата, то есть Периметр = 4 × Сторона. Она выражается в м, см, футах и дюймах.
Она выражается в м, см, футах и дюймах.
Площадь квадрата = Площадь = s × s, где s — одна сторона квадрата. Дается в единицах м 2 , см 2 , фут 2 , а в 2 .
Проверка:
- Формулы периметра
- Объемные формулы
- Формулы площади поверхности
- Формулы измерения
Как найти площадь квадрата по диагонали квадрата?
Площадь квадрата также можно найти, если известна его диагональ. В этом случае используется следующая формула: Площадь квадрата по диагоналям = Диагональ²/2. Например, диагональ квадрата равна 6 единицам, Площадь = 6²/2 = 36/2 = 18 квадратных единиц.
Как найти площадь квадрата по периметру квадрата?
Площадь квадрата можно вычислить, если известен его периметр. Поскольку периметр квадрата: P = 4 × сторона, мы можем найти сторону квадрата ‘s’ = периметр/4. После получения стороны площадь квадрата можно вычислить по формуле: A = s × s. Например, если периметр квадрата равен 32 единицам, мы подставим это значение в формулу: P = 4 × сторона. 32 = 4 × стороны. Значит, сторона будет 8 единиц. Теперь мы можем вычислить площадь квадрата со стороной 8 единиц. Площадь = s × s = 8 × 8 = 64 кв.
Например, если периметр квадрата равен 32 единицам, мы подставим это значение в формулу: P = 4 × сторона. 32 = 4 × стороны. Значит, сторона будет 8 единиц. Теперь мы можем вычислить площадь квадрата со стороной 8 единиц. Площадь = s × s = 8 × 8 = 64 кв.
Каковы единицы измерения площади квадрата?
Площадь квадрата является двумерной величиной, поэтому всегда выражается в квадратных единицах. Общие единицы площади квадрата: м 2 , дюймы 2 , см 2 и футы 2 .
Какова площадь квадрата, вписанного в окружность?
Если квадрат вписан в круг, то диагональ квадрата равна диаметру круга. Итак, если диаметр круга дан, это значение можно использовать как диагональ квадрата, а площадь квадрата можно рассчитать по формуле: Площадь квадрата с использованием диагоналей = Диагональ²/2.
Найдите сторону квадрата, площадь которого равна 36 квадратных единиц.
Если площадь квадрата составляет 36 квадратных единиц, сторону квадрата можно рассчитать по той же формуле, подставив заданное значение.
