Конспект открытого занятия по математике в подготовительной группе
«Путешествие на планету Математика»
Выполнила: воспитатель Шишкина Юлия Александровна
Образовательные области: “Познание”, “Социализация”, “Коммуникация”, “Здоровье”.
Цель: Закрепление математических знаний и умений посредством игры – путешествия.
Задачи:
Образовательные:
– Упражнять в счёте в пределах 10 в прямом и обратном порядке;
– закрепить понятия: «предыдущее», «последующее», «соседи» названного числа;
– Закрепить знания о последовательности дней недели, времён года,
– Закрепить умение ориентироваться на плоскости.
– Закрепить умение различать понятия: выше – ниже, шире – уже, длиннее – короче, толще – тоньше, старше – младше.
– Формировать навык полных ответов на вопросы.
Развивающие:
– Создать условия для развития логического мышления, сообразительности, внимания,
– Развивать смекалку, зрительную память, воображение, мелкую моторику рук.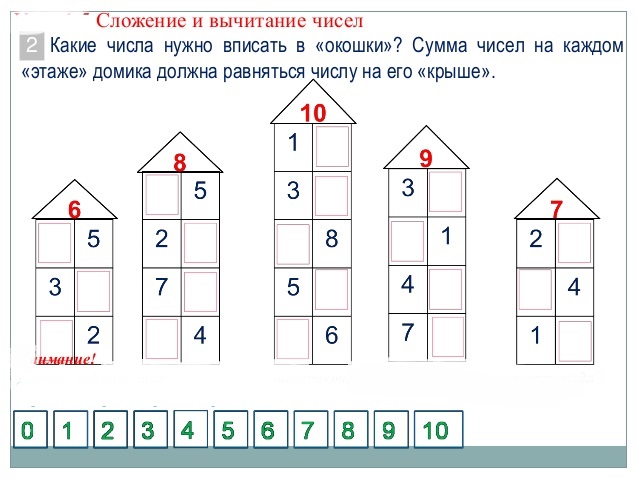
– Способствовать формированию мыслительных операций, развитию речи, умению аргументировать свои высказывания.
Речевые:
– Развивать речь, умение аргументировать свои высказывания, рассуждать, доказывать.
Воспитательные :
– Воспитывать самостоятельность, умение понимать учебную задачу и выполнять её самостоятельно.
– Воспитывать интерес к математическим занятиям.
– Воспитывать дружеские взаимоотношения между детьми, привычку заниматься вместе.
Предварительная работа с детьми:
Отгадывание загадок, решение логических задач, решение простых арифметических задач, наблюдение за календарём, индивидуальные занятия
Методические приёмы:
Игровой: использование сюрпризных моментов.
Наглядный: использование карточек, экран.
Словесный: напоминание, указание, вопросы, индивидуальные ответы детей.
Поощрение, анализ занятия.
Оборудование: компьютер, цифры, тетради, счётные палочки, мяч.
Демонстрационный материал: карточки с изображением фигур из счетных палочек.
Раздаточный материал: математические наборы, тетради, карандаши, счетные палочки, геометрические фигуры.
Ход занятия:
I – Ребятки, к нам на занятие пришли гости, давайте подарим им свои улыбки, поприветствуем их. На занятии постараемся быть внимательными и хорошо отвечать на вопросы. А теперь красиво сели, ножки поставили вместе, спинка прямая. Занятие начнем со стихотворения.
Чтоб врачом, моряком
Или лётчиком стать.
Надо, прежде всего
Математику знать.
И на свете нет профессий,
Вы заметьте-ка,
Где бы вам не пригодилась
Математика!
– «Ребята, как вы думаете, а какое у нас сейчас будет занятие? Сегодня у нас с вами необычное занятие. Мы отправимся в космос на планету Математики. Там нас ждут большие трудности, но я думаю, что вы с ними справитесь»
– «А на чем мы с вами отправимся? Перед вами листок бумаги, а на ней цифры.
Соединив цифры по порядку, мы узнаем, на чем мы с вами полетим». – «Так на чем мы с вами полетим? Что у нас получилось?» (Ракета)
II – Но, чтобы поднялась наша ракета, нам надо правильно нажать нужные кнопки от 1 до 10.
Игра с мячом «Назови число» Воспитатель спрашивает: – Какое число называется предыдущим (то, которое стоит перед названным) и какое последующим? (то, которое стоит после названного). Воспитатель бросает мяч каждому ребенку индивидуально: – «Я буду бросать мяч и называть число, вы, бросая, мне мяч обратно, будете называть предыдущее и последующее числа».
Молодцы. Справились с заданием, а теперь займите свои места, приготовьте пальчики.
Пальчиковая гимнастика
Луно, луно, луноход
Отправляется в полет.
На старт, внимание, зажигание
10,9,8,7,6,5,4,3,2,1,0
Взлет!
III – « Мы полетели (слайд №1). А пока мы с вами летим, чтобы не было скучно, я загадаю вам загадки. Слушайте внимательно:
1) Яблоки в саду поспели,
Мы отведать их успели:
8 румяных, наливных,
1 с кислинкой.
Сколько их?(8)
2) На дереве сидят 4 птицы: 2 воробья, остальные вороны.
Сколько ворон?(2)
3) Мурка кошка-мышеловка
Съела трех мышей в кладовке,
И сейчас к норе подкралась.
Цап! Еще одна попалась,
Вот так Мурка! Сколько ей
Удалось поймать мышей. (4)
4) Пять ворон на крышу сели,
Две еще к ним прилетели.
Отвечайте быстро, смело
Сколько всех их прилетело? (7)
5) С неба звездочка упала,
В гости к детям забежала.
Две кричат вослед за ней:
«Не забудь своих друзей!»
Сколько ярких звезд пропало,
С неба звездного упало? (3)
6) Я сегодня ночью встала,
Звёзды все пересчитала:
Три— на окошке,
Две— на перинке,
Одна в колпачке
На зеленом сундучке.
Я считала, я трудилась,
Но потом со счета сбилась.
Помогите мне опять
Звёзды все пересчитать! (6 звёзд)
7) Загадали нам загадку,
Сосчитаем по порядку:
2 звезды и 3 кометы
В космосе гуляют где-то
Кто поможет отгадать, что за цифра это? (5)
IV- « Ребята, мы и не заметили, как мы с вами быстро долетели.
1 задание: «Что лишнее и почему?» (слайд №3-6)
все цифры и одна буква и наоборот;
все четырёхугольники и один пятиугольник;
все фигуры зеленые, одна красная;
– Если ответ правильный, лишняя картинка исчезнет. Главное! Не забудьте доказать, почему именно эта картинка лишняя.
Зарядка для глаз.
Солнышко с тучками в прятки играло,(закрыть, открыть глаза)
Солнышко тучки – летучки считало.
Серые тучки направо,
Черные тучки налево,
Легких – две штучки, (глаза наверх)
Тяжелых – три штучки, (глаза вниз)
Тучки попрощались, тучек не стало, (закрыть глаза ладонями)
Солнце на небе вовсю засияло. (широко открыть глаза)
2 задание: «Найди и покажи 5 треугольников и 1 четырехугольник»
(слайд №7)
3 задание: «Математический диктант».
(слайд № 8)
Под диктовку указаний дети раскладывают геометрические фигуры в разные части листа.
– В верхнем правом углу прямоугольник
– В левом верхнем углу квадрат
– В правом нижнем углу овал
– В левом нижнем углу треугольник
– А посередине круг
После выполнения задания дети проверяют правильность его выполнения, проговаривая каждое действие.
– Молодцы! А сейчас мы немного отдохнём.
ФИЗМИНУТКА.
(Исходное положение: стоя врассыпную)
Раз, два – стоит ракета.
(поднять руки через стороны вверх, ладони соединить над головой)
Три, четыре – самолёт.
(руки в стороны, слегка покачать прямыми руками)Раз, два – хлопок в ладоши. (хлопаем в ладоши)
А потом на каждый счёт: (шагаем на месте)
Раз, два, три, четыре – (хлопаем в ладоши)
Руки выше, плечи шире, (руки вверх-вниз)
Раз, два, три, четыре – (хлопаем в ладоши)
И на месте походили.
(шагаем на месте)
Как пружинки все присели
И на место разом сели.
4 задание «Назови задуманное число» (слайд № 9)
– У каждого из вас свой набор цифр. Я задаю вопрос, вы думаете, ответ показываете цифрой.
– это число больше 5 на 1
– это число меньше 7 на 1
– Это число стоит между цифрами 6 и 8
– Соседи этого числа цифры 1 и 3
5 задание «Запомни и сделай» (счетные палочки).
Воспитатель поочередно показывает карточки с изображением фигурок из счетных палочек. Дети считают, сколько потребуется палочек. Затем рисунок убирается, дети по памяти воспроизводят фигуру.
V – Все задания выполнены, а теперь пора нам возвращаться домой. Но чтобы лететь назад, нам нужно найти другие кнопки.
Игра «ОТГАДАЙ КОД»
– Я возьму молоточек, а вам надо сосчитать, сколько раз он ударит и назвать цифру. Педагог ударяет молоточком, при этом дети называют цифру и по очереди выставляют цифры на столе: 3 5 9 1 8 6 .
– Молодцы!
– Говорим наш волшебный код и отправляемся в космос – 3 5 9 1 8 6 !
Пуск! Полетели!
VI « А пока мы с вами летим – небольшая «Умственная разминка»
– Какое сейчас время года? А месяц?
– Сколько дней в неделе? (семь)
– Назовите их.
– Сегодня вторник, а завтра?
– Какие арифметические знаки вы знаете?
– Если линейка длиннее карандаша, то карандаш…?
– Если стол выше стула, то стул…?
– Если дорога шире тропинки, то тропинка?
– Если сестра старше брата, то брат…?
VII.- Подведение итогов.
– Мы приземлились! Дети, вам понравилось наше путешествие?
Что мы делали? Что больше всего понравилось?
Мне очень понравилось, как вы сегодня занимались! Вы были настойчивыми, внимательными, сообразительными и поэтому вам удалось выполнить все задания. Спасибо! Давайте себе похлопаем. Мы молодцы!
ЛИТЕРАТУРА
1. «Подготовительная к школе группа в детском саду».
( книга для воспитателей, Москва, «Просвещение», 2001 г.
2. «Программа воспитания и обучения в детском саду» под редакцией М. А. Васильевой, В. В. Гербовой, Т. С. Комаровой. Издательский дом «Воспитание дошкольника», Москва, 2004 г.
3. Тарабарина Т.И., Ёлкина Н.В. И учёба, и игра: Математика. – Ярославль: «Академия развития», 1997.
4. Белоусова Л.Е. Ура я научился! Сборник игр и упражнений для дошкольников: Методическое пособие для воспитателей ДОУ.- СПб.: «ДЕТСТВО-ПРОГРЕСС», 2004
Структурное подразделение МОУ «СОШ №82»
Октябрьского района г. Саратова
«Детский сад «Совенок»
Конспект НОД
по ФЭМП
Тема: «Путешествие на планету Математика»
Подготовительная группа
Составил воспитатель:
Шишкина Юлия Александровна
г. Саратов 2018 год
Конспект занятия по математике в подготовительной группе по ФГОС
Составила: Педченко А.
В.
Цель: Создать условия продолжения умения формирования детей составлять и решать простые арифметические задачи, на сложение и вычитание в пределах 10.
Задачи: формировать умение детей составлять и решать простые арифметические задачи, на сложение и вычитание в пределах 1;закреплять счет в пределах 10 в прямом и обратном порядке, развивать слуховое внимание и координацию движений; логическое мышление детей; совершенствовать знания о геометрических фигурах и ориентировку на плоскости; умение быстро ориентироваться в пространстве на ограниченной плоскости.
Предварительная работа:
Дидактические игры на сенсорное развитие: «Составь пейзаж», «Построй дворец», «Придумай сказочную птицу».
Дидактические игры: «Живая неделя», «Ручеек», «Что, где?», «Покажи животное» или «Кто внимательный».
Материалы: 2 письма (и посылка) Царицы Математики, геометрические фигуры разных цветов и размеров; лист ватмана; клеящие карандаши; счетные палочки; наглядный материал для решения арифметических задач; мяч; буквенно-числовые карточки от 1 до 10; картонные золотые медали «Юному математику», шоколадные конфеты.
Ход занятия:
Воспитатель: «Ребята, сегодня у нас много гостей…»
В группу входит воспитатель соседней группы с конвертом в руках и говорит: «Вам письмо».
Воспитатель: «Большое спасибо. Сейчас посмотрим…»
Рассматривает конверт и удивленно говорит: «Ребята, это письмо нам прислала сама Царица Математика. Вот, послушайте, что она пишет». Читает письмо.
Конверт с письмом оформлен цифрами, знаками, геометрическими фигурами.
1. Письмо Царицы Математики: «Здравствуйте, дорогие ребята! Пишет вам Царица Математика. Мне очень нужна ваша помощь. Дело в том, что в мое математическое царство забрался двоечник и хулиган. Он сотворил ужасные вещи: разрушил геометрические фигуры в моем городе, совершенно не знает цифр. Этот двоечник испортил узоры из счетных палочек, решил задачи с ошибками!
Все нарушилось в моем математическом царстве-государстве! Жители моей страны страшно напуганы, и некому нам помочь.
Дорогие ребята, если вы смелые, сообразительные, внимательные и не боитесь трудностей, поспешите к нам на помощь! Математическое царство в опасности.
Ваш друг Царица Математика».
«Ну, что, ребята, поможем Царице Математике навести порядок в ее математическом царстве-государстве?»
Дети: «Да, да, поможем!»
Воспитатель: «Но попасть в это царство совсем не просто, для этого нужно пройти пароль.
Помните, чтобы справиться со всеми трудностями, вы должны быть сообразительными, смелыми, внимательными и наблюдательными. Но самое главное, что вернуться мы сможем только в том случае, если справимся со всеми заданиями. Ну, что, не передумали? Тогда в путь!»
Прохождение пароля.
Цель: закреплять у детей образное мышление и восприятие, умение воспринимать задание на слух, считать в уме, развивать сообразительность и быстроту реакции.
Ход: Дети выстраиваются в колонну и по очереди отвечают на вопросы воспитателя:
Воспитатель: «Молодцы, ребята, вы успешно прошли пароль, и теперь мы с вами в математической стране. А вот и первое задание: вам предстоит стать спасателями и строителями. Разрушился целый город, который состоит из геометрических фигур, но мы его восстановим. Давайте вспомним, из чего состоит город».
Дети: «Из домов, жителей, транспорта, деревьев, животных, птиц, растений».
Задание «Построй город из геометрических фигур»
Цель: закреплять умение составлять коллективную аппликацию в виде города из геометрических фигур; работать сообща, быстро и аккуратно наклеивать фигуры, создавая из готовых форм изображения людей, домов, транспорта, деревьев и т.д.
Материал: ватман, геометрические фигуры из цветной бумаги разных форм и размеров, клеящие карандаши.
Ход: дети выполняют аппликацию на ватмане из геометрических фигур, т.е. «восстанавливают» разрушенный город: дома, деревья, транспорт, людей, животных, птиц.
Работа проходит в быстром темпе.
Воспитатель: «Молодцы, ребята! Вы оказались замечательными строителями. Ожила математическая страна, но впереди у нас еще много дел! Сейчас нам предстоит вспомнить, как мы составляем число 10 из двух чисел».
Игровое задание со счетными палочками.
Цель: закреплять знания детей о геометрических фигурах, воспринимать задание на слух, выкладывать из счетных палочек узоры; видеть и называть фигуры, составляющие узоры.
Материалы: счетные палочки.
Ход: воспитатель дает детям задание:
Воспитатель: «Молодцы, ребята, вы прекрасно справились с заданием! А теперь проверим, кто из вас самый ловкий и внимательный».
Игра «Что, где?»
Цель: закреплять умение детей ориентироваться в пространстве, различать правую и левую стороны, употреблять слова и предлоги (справа, слева, впереди, позади; над, под, между); развивать ловкость, быстроту реакции.
Составление и решение арифметических задач
Цель: закреплять умение детей составлять простейшие арифметические задачи на сложение и вычитание в пределах 10, записывать решение в виде примеров, самостоятельно выбирая нужный знак ( «плюс» или «минус).
Материал: демонстрационный счетный материал на ковролине.
Ход: воспитатель показывает демонстрационный материал и задает тему: «Составьте задачу про кораблики» (рыбок, яблоки, грибы, морковки и т.д.).
6+3 – в море плавало 6 корабликов, к ним приплыло еще 3. Сколько стало корабликов?
4+5 (рыбки) – в аквариуме плавало 4 рыбки, купили еще 5 рыбок. Сколько стало рыбок?
10-6 (яблоки) – в вазе было 10 яблок, 6 яблок съели. Сколько яблок осталось?
2+8 (грибы) – на полянке было 2 грибочка, после дождя выросло еще 8.Сколько стало грибов?
10-5 (морковки) – на грядке росло 10 морковок, 5 морковок вытащили.
Сколько морковок осталось?
Дети самостоятельно записывают решение задач и объясняют, почему поставили «плюс» или «минус»
Воспитатель: «Молодцы, ребята! Вы прекрасно справились с трудным заданием! А теперь вам предстоит проверка на слух и внимание».
Игра «Кто самый внимательный»
Цель: закреплять умение детей воспринимать задание на слух (количество хлопков), сопоставлять действия со словами; развивать внимание и быстроту реакции.
Ход: воспитатель объясняет детям правила игры, на один хлопок дети ходят по комнате, на два хлопка – встают в позу аиста, на три хлопка – в позу лягушки. Побеждает тот, кто ни разу не ошибся, т.е. самый внимательный.
Воспитатель: «Молодцы, ребята, вы все очень внимательные! Вы прекрасно справились со всеми заданиями. Ну, а теперь, последнее задание. Пожалуй, оно самое сложное и необычное, ведь это пароль на выход из математической страны.
Вам нужно выложить числовой ряд от 1 до 10 в обратном порядке. Если вы правильно расставите числа, то узнаете пароль и сможете его прочесть».
Прохождение пароля на выход из волшебной страны.
Цель: закреплять умение детей выкладывать числовые карточки в обратном порядке (от 10 до 1), читать по слогам.
Материал: буквенно-числовые карточки, на которых с одной стороны цифры (от 1 до 10), а с другой – буквы.
Ход: карточки лежат на ковре в хаотичном порядке цифрами вверх. Дети по очереди подходят и берут по одной карточке, выкладывая числовой ряд в обратном порядке (от 10 до 1), после чего воспитатель просит детей закрыть глаза и переворачивает карточки на другую сторону. Дети читают «пароль» (на обратной стороне написано слово «Математика»).
По просьбе воспитателя дети хором по слогам читают «пароль» и «возвращаются» домой.
Воспитатель: «Ну вот мы и дома, в детском сад… Все математические приключения позади. Ребята, а теперь скажите, вам было очень трудно?»
Дети: «Совсем нетрудно, а даже интересно!»
Входит воспитатель соседней группы и говорит: «Вам письмо с посылкой».
Воспитатель: «Большое спасибо. Кто бы это мог быть?»
2. Письмо Царицы Математики: «Дорогие друзья! Огромное вам спасибо за оказанную помощь! Вы прекрасно справились со всеми заданиями. Вы не просто спасли математическую страну, вы создали прекрасный город из геометрических фигур, он стал лучше прежнего. В моем математическом царстве царит абсолютная точность и порядок.
Вам, мои юные математики, в благодарность от всех жителей моей страны и от меня лично, вручаются золотые медали и самые вкусные конфеты! Надеюсь, они вам понравятся. Приятного вам чаепития».
Воспитатель зачитывает детям письмо, в котором Царица Математика благодарит детей за оказанную помощь и в качестве награды присылает им конфеты и золотые медали с надписью «Юному математику».
Воспитатель: «Ребята, благодаря знаниям, полученным в детском саду, вы оказали помощь математической стране и ее жителям. Скоро вы пойдете в школу и узнаете там много интересного».
Звучит фонограмма песни «Чему учат в школе»
| < Предыдущая | Следующая > |
|---|
Конспект занятия по математике
«ЗАНИМАТЕЛЬНАЯ МАТЕМАИКА»
Цель: закреплять знания по элементарным математическим представлениям.
Задачи:
– развивать умение ориентироваться на листе;
– воспитывать желание работать сообща, сотрудничать, починяться дисциплине;
– учить оценивать правильность выполнения задания;
-упражнять в решении примеров, задач;
-развивать логическое мышление, смекалку, воображение.
3. Тип занятия: закрепление знаний и выработки навыков и умений по практическому применению знаний.
4. Форма занятия: групповая, фронтальная.
5. Продолжительность: 30 минут.
6. Участники: воспитанники – дети, воспитатель.
7. Возраст детей: 6-7 лет.
8. Оборудование и материалы: таблички с цифрами от 1 до 9; таблички с математическим знаками; набор карточек с графическими заданиями, набор карточек с примерами с пропущенным математическими знаками, счетные палочки, математические наборы, цветные карандаши.
9. Предварительная подготовка:
– заучивание дней недели;
– решение подобных задач и примеров;
– изготовление атрибутов для занятия.
10. Методы и приемы работы с детьми: практический метод – выполнение практических действий: использование дидактического материала, выработка навыков счета; самостоятельная работа с раздаточным материалом, игровые упражнения.
11. Структура занятия:
Приветствие. Объяснение правил.Разминка.
5 минут
Основная часть
1. Игра «Кто быстрее» с графическими изображениями
2. Разложить числовой ряд от 1 до 9
3. Математические задачи в стихах
3. «Живые цифры» подвижная игра
4. «Неделька» подвижная игра
5. Игра «Поставь правильно знаки»
6. Игра «Волшебники»
20 минут
Заключительная часть
Подсчет звездочек
Рефлексия.
5 минут
12. Ход занятия.
Здравствуйте, ребята! Сегодня у нас необычное занятие по математике! Посмотрите, перед вами лежит листочек, на котором выбудете после каждого правильно выполненного задания ставить звездочку.
Только честно! В конце занятия вы подсчитаете количество звездочек а своих листочках и мы узнаем победителя сегодняшнего занятия!
Начнем с разминки! Отвечать можно хором!
– Сколько дней в неделе?
– Корова в детстве?
– Сказочный мальчик с деревянным носом?
– Прибор для измерения времени?
– Соседи числа 6?
– Назовите осенние месяцы.
Молодцы!
Итак, первое задание. Дети получают листочки с графическим изображением сложных геометрических фигур.
– Ребята, посмотрите на свои листочки: вам нужно выложить счетными палочками такие же фигуры. Кто выполнит задание правильно самый первый сможет нарисовать себе две звездочки! Начали!
Педагог проверяет правильность выполнения задания.
– Молодцы ребята! Кто выполнил правильно, ставьте звездочки оценочный лист.
– Сейчас я порошу вас разложить числовой ряд от 1 до 9 из математических наборов.
– Слушайте внимательно условие задачи, выбирайте нужную цифру, правильный ответ показывайте мне. За каждый правильный ответ – звездочка! Количество задач может меняться в зависимости от заинтересованности детей.
Задачи
Как то ночью под кусточком
Грибы выросли опять.
Два гриба и три грибочка
А всего их ровно (5)
Над рекой летели птицы:
Голубь, щука, две синицы.
Сколько птиц? Ответь скорее! (3)
У животного: две правые ноги,
Две левые ноги,
Две ноги спереди,
Две ноги сзади.
Сколько ног у животного? (4)
Под кустами у реки
Жили майские жуки:
Дочка, сын, отец и мать-
Кто их сможет сосчитать? (4)
Яблоки в саду поспели.
Мы отведать их успели:
Пять румяных наливных,
Три с кислинкой. Сколько их? (8)
А теперь немного разомнемся! Поиграем в игру «Соседи числа». Выходят два ребенка. На доске висит цифра, детям нужно найти из предложенных цифр-карточек соседние числа предложенного числа и встать с правильной стороны от заданного числа.
– Поиграем с вами в игру «Неделька». Выходите, пожалуйста семь человек. Педагог предлагает выбрать из стопки карточек каточку с цифрой. Дети выбирают, называют цифру. Педагог играет в бубен, «дни недели» бегают врассыпную. Как только музыка заканчивается, дети должны встать по порядку от 1 до 7.
– Дни недели, назовитесь!
Дети называют дни недели. Кто правильно все сделал, ставит себе звездочку в оценочный лист.
– Следующее задание! На доске висят карточки с примерами, нужно вставить правильный знак.
Педагог вызывает детей по одному к доске, дети вставляют знаки. За правильный ответ – звездочка в оценочный лист. Количество карточек варьируется в зависимости от заинтересованности детей.
-И последнее задание! Сейчас вы станете самыми настоящими волшебниками! Вы будете превращать геометрические фигуры в животных! Дети получают листочки с простыми геометрическими фигурами. Итак, волшебники, творите волшебство!
Педагог проверяет выполнение работ. Хвалит детей!
А теперь давайте подсчитаем ваши звездочки! Дети считают свои звездочки, называют количество звездочек. Педагог может добавить звездочек за честность, за хорошую работу на занятии и другое.
А теперь давайте вспомним, чем мы занимались на этом занятии. Можно использовать управляемый диалог, если дети не устали. Педагог задает вопросы по теме занятия, дети отвечают или проявляют инициативу и отвечают самостоятельно.
Спасибо вам за то, что так замечательно работали сегодня! Давайте поблагодарим друг друга улыбками и аплодисментами!
С П И С О К Л И Т Е Р А ТУ Р Ы
1.
Белоус, Т.К. и др. Организация работы по математике в малокомплектном детском саду./ Т.К. Белоус. // Дошк. воспитание, 1999, № 10.
2. Березина, Р.И. Обучение детей подготовительной группы измерению. / Р.И. Березина. // Дошк. воспитание, 1999, № 10.
3. Веракса, Н.С. Формирование единых временно-пространственных представлений. / Н.С. Веракса. // Дошк. воспитание, 1996, № 5.
4. Водопьянов, Е.Н. Формирование начальных геометрических понятий у дошкольников. / Е.Н. Водопьянов. // Дошк. воспитание, 2000, № 3.
5. Воспитание детей в игре: Пособие для воспитателя дет.сада / Сост. А.К. Бондаренко, А.И. Матусик. – 2-е изд., перераб. И доп. – М.: Просвещение, 1983.
7. Давайте поиграем. Математические игры для детей 5-6 лет. – Под ред. А.А.Столяра. – М.: Просвещение, 1991).
8. Данилова, В.В. Математическая подготовка детей в дошкольных учреждениях. – М.: Просвещение, 1987.
9. Дидактические игры и упражнения но сенсорному воспитанию дошкольников: Пособие для воспитателя детского сада.
– Под ред. Л. А. Венгера. 2-е изд., перераб. и доп. – М.: Просвещение, 1998.
10. Дьяченко, О.М., Агаева, Е.Л. Чего на свете не бывает? – М.: Просвещение, 1991.
11. Ерофеева, Т.И., Павлова, Л.Н., Новикова, В.П. Математика для дошкольников: Кн. Для воспитателя дет. сада. – М.: Просвещение, 1992.
12. Житомирский, В. Г., Шеврин, Л. Н. Геометрия для малышей. – М.: 1996.
13. Каразану, В.Н. Ориентирование в пространстве (старший дошкольный возраст). / В.Н. Каразану. // Дошк. воспитание, 2000, № 5.
14. Корнеева, Г. А., Мусеибова, Т. А. Методические указания к изучению курса «Формирование элементарных математических представлении у детей дошкольного возраста». – М., 2000.
15. Корнеева, Г. А. Роль предметных действий в формировании понятия числа у дошкольников. / Г.А. Корнеева. // Вопр. психологии, 1998, № 2.
Муниципальное казенное общеобразовательное учреждение
Байкальская средняя общеобразовательное школа
Болотнинского района Новосибирской области
Конспект НОД по ФЭМП в подготовительной группе
по теме «Путешествие по математическому городку »
Тоичкина Людмила Степановна –
воспитатель дошкольной разновозрастной группы
Байкал, 2018 год.
Организация непрерывной непосредственно образовательной деятельности детей в подготовительной группе
по теме «Путешествие по математическому городку ».
Цель: Закрепление математических знаний – через игру.
Приоритетная образовательная область: «Познание»
Задачи:
Образовательные:
Формировать умение детей группировать предметы, вести счет до 20 и обратно.
Формировать временные представления (дни недели)
Закрепить умение соотносить количество предметов с цифрой;
Развивающие:
Развивать логическое мышление
Закреплять знания о составе числа
Воспитательные:
Воспитывать умение работать в коллективе, усидчивость, умение понимать и самостоятельно выполнять задания воспитателя
Воспитывать доброе, уважительное отношение к окружающим, самостоятельно работать с раздаточным материалом.
Материал к НОД: Кружочки разного цвета по 10 шт одного цвета и 10 шт другого, для каждого ребенка. Карта с заданиями. Задания. Презентация, проектор. Музыка для путешествия. Задания на листочках по количеству детей.
Ход занятия.
Организационный момент.
В. – Здравствуйте ребята.
-Встаньте, пожалуйста, подойдите ко мне. Давайте мы возьмемся за руки с вами и друг – другу улыбнемся. А теперь садимся на места тихонько-тихонько как мышки.
В.- Сегодня мы с вами совершим путешествие по городу «Математика», нам будут встречаться различные задания, которые мы должны будем с вами выполнять чтобы увидеть красивые места этого городка.
В.- Смотрите вот перед нами карта (на доске прикреплена карта, на ней задания под номерами, конверты с заданиями у воспитателя) по ней мы с вами и будем путешествовать, а конечная остановка это – детский сад.
В.- Прежде чем начнем наше путешествие, нам нужно усвоить некоторые правила поведения.
Я буду начинать говорить правило, а вы будете его заканчивать.
– Ты сиди за партой стройно и веди себя … (ДОСТОЙНО)
– Парта – это не кровать и на ней нельзя… (ЛЕЖАТЬ)
– Ответить хочешь – не шуми, а только руку… (ПОДНИМИ)
– Хорошо все вспомнили наши правила поведения на занятии.
В.- Прежде чем мы отправимся в «математический городок» немного разомнемся.
-Согласны?
Дети- Да.
В.- Тогда отвечаем быстро
Вопросы:
-Какой сегодня день недели?
-Сколько месяцев в году?
-Какое сейчас время года?
-Сколько дней в неделе?
-Сколько сезонов в году?
-Какой по счёту день недели четверг, суббота, пятница?
– Какой день идет перед вторником, пятницей, воскресеньем?
В.- Молодцы, вы справились с заданием.
В.- Ну, что готовы?
Д.-Да.
(Звучит музыка из мультфильма «Паровозик из Ромашкова», дети закрывают глаза.
Открывают)
В.- Вот и первое наше с вами задание.
Первое задание. Счёт от 1 до 20. Вставь пропущенные числа.
В.- Нужно посчитать от 1 до 20 и обратно.
-Готовы.
Д.- Да.
В.- Смотрите, цепочка, но что- то с ней не так.
(У детей лежат листики с цепочкой, и там пропущенные числами, нужно вставить числа по своим местам)
Д.- Здесь не все цифры.
В.- Правильно. Вам нужно их дописать.
(Дети дописывают недостающие цифры, у себя на листиках, а один ребенок у доски.)
(1..34..5678…11..1314….17..1920)
В.- Молодцы , мы свами с правились с заданием. Смотрите, какой красивый вид открывается перед нами. Это парк цветов.
В.- Прогуляемся?
Дети- Да.
В.- Закрывайте глазки и представьте себе много-много разных, красивых цветов. (Звучит музыка «Вальс цветов»). Давайте мы их посчитаем. ( Дети вместе с воспитателем считают до 20 и открывают глаза.
)
В.- Посмотрите, какой красивый музей перед нами, но чтобы нам в него попасть нам нужно будет посчитать.
Второе задание. Расставь знаки:≤.
На доске прикреплены таблички, где нужно поставить знаки (больше, меньше или равно). Дети выходят по одному, и выполняют задание.
5 8 9 4 7 7
4 1 10 10 5 2
7 2 9 8 4 4
6 6 5 3 9 2
В.- Молодцы, мы справились с этим заданием.
А теперь посмотрите на доску (с помощью мультимидийного проектора, на доске показывается презентация о музее.)
Дети смотрят презентацию, воспитатель рассказывает. (После просмотра презентации.)
В.- Смотрите мы прошли весь музей и вышли на центральную площадь, где нас поджидает еще одно задание.
В.- Прежде чем мы с вами приступи к выполнению следующего задания мы немного отдохнем.
Физкультминутка. Дети встают.
Руки ставим все вразлёт:
Появился необычный самолет
Мах крылом туда-сюда,
Делай «раз» и делай «два».
Раз и два, раз и два!
Руки в стороны держите,
Друг на друга посмотрите.
Раз и два, раз и два!
Опустили руки вниз,
И на место все садись!
(Дети повторяют движения за воспитателем 2 раза)
В.- Молодцы. Отдохнули. Приступаем к выполнению задания.
Третье задание. Из каких чисел состоит.?
Жители городка «Математики», не могут решить, как можно раскладывать числа на меньшие числа.
У детей на столиках лежат листочки с заданием. Из каких чисел состоит?
Дети самостоятельно выполняют задание. А когда все выполнят, подходят и крепят свой листик к доске. (у всех детей разные числа).
(2,3,4,5,6,7,8,9,10)
В.- Молодцы, теперь жители городка научаться делить числа пополам и у них уже не будет споров.
-Ну, а мы с вами продолжаем наше путешествие и сейчас отправимся к следующему заданию на автобусе.
(дети закрывают глаза, звучит музыка машин.)
В.
– Вот мы с вами и добрались до следующего задания.
-Смотрите, какие красивые здания стоят, но почему- то не во всех окнах горит свет. Давайте спросим у жителей городка почему?
Дети- Давайте узнаем.
В.- Оказывается еще не все «соседи» смогли найти свои квартиры, поэтому они и пустуют.
-Поможем жителям расселиться по квартирам?
Дети –Да.
Четвёртое задание. «Впиши в пустые окошечки соседей чисел»
На доске прикреплены одноэтажные домики с пустыми окошками. Дети по одному выходят и вписывают соседей чисел которые уже есть.
В.- Молодцы.
– Ну что у нас с вами осталась последнее задание, и задание, чтобы пройти в нашу группу.
-Готовы?
Дети – Да.
В.- Следующее задание, будет трудным, но мы с ним справимся. Правда?
Дети – Да.
В.
– Мы уже умеем решать задачи?
Дети –Да.
В.- Посмотрите, по краям дороги растут деревья и на них висят задание с задачами.
-Сможем решить?
Дети –Да.
В. –Я буду читать , а вы у себя на столе с помощью кружков будете выкладывать решение. Хорошо?
Дети –Да.
Пятое задание. «Реши задачи»
На поляне росли пять ёлок и четыре сосны. Сколько всего деревьев росло на поляне?
На праздник надули семь шариков. Два из них лопнули. Сколько шариков осталось целых?
На тарелке лежало шесть яблок. Два яблока взяли. Сколько яблок осталось лежать на тарелке.
На поляне росло три гвоздики и пять ромашек. Сколько цветов всего росло на поляне?
В вазе лежало три конфеты и две шоколадки. Сколько сладостей всего лежало в вазе?
На поляне сидели четыре зайчика, к ним прискакали ещё два. Сколько зайчиков было на полянке?
У Алеши было семь карандашей, три из них сломались.
Сколько карандашей осталось у Алеши?
Дети решают у себя за столиками с помощью кружков. А кто первый решит, выходит к доске и записывает решение.
В.- Молодцы и с этим задание вы справились.
– У нас осталось последнее задание, и мы возвращаемся в детский сад, в нашу группу.
Я буду читать вам задание ,а вы будете мне говорить ответ. Хорошо?
Дети –Да.
Шестое задание. «Математические загадки».
-Сколько углов в квадрате?(4)
-Сколько хвостов у пяти коров?(5)
-Сколько лап у двух гусей?(4)
-Сколько ушей у трех мышей?
-Сколько лап у двух медвежат?
-Сколько углов в квадрате?(4)
-Если линейка длиннее карандаша , то карандаш?…(короче линейки)
-Если стол выше стол, то стул ?…(Ниже стола)
-Если дорога шире тропинки, то тропинка?… (Уже дороги)
-Назовите соседей числа5,7
-Какое число идёт за числом 4, 6
-Какое число перед числом 8, 2
В.
– Молодцы и с этим заданием вы справились. Пора возвращаться в детский сад.
-Закрывайте глазки.
(Звучит музыка из мультфильма «Паровозик из Ромашкова», дети закрывают глаза. Открывают)
В.- Вот теперь мы с вами и в нашей группе.
Рефлексия:
-Понравилось путешествие?
-Что было трудным?
-Что было самым интересным?
-Что больше всего запомнилось?
Ребята, посмотрите что это? Сундук. Откуда интересно он взялся. Вам интересно
узнать, что внутри. Давайте откроем его и посмотрим что в нем. Посмотрите, а в нем
письмо:
«Здравствуйте, друзья! Меня зовут обезьянка Анфиса. Я вырастила необычное
растение и хочу вам его показать. Очень жду в гости»
Интересно, ребята, какое же растение вырастала обезьянка. Хотите узнать?
А как же мы узнаем где она живет?
Посмотрите, здесь и карта есть?
А на чем мы можем отправиться? Как вы думаете синий цвет это что?
Сегодня мы с вами отправимся в гости к обезьянке, что бы к ней попасть мы
должны пройти все удивительные геометрические острова, где познаем много
интересного.
А на чём же мы отправимся в путешествие? (поплывём на корабле).
Верно, сейчас каждый из вас соединит цифры в правильном порядке (от 1 до 10) и
у вас получатся кораблики, на которых мы отправимся в путешествие.
Воспитатель: Вижу, все у всех получились кораблики, мы отправляемся в путь.
2. Основная часть
Воспитатель: Вот мы приплыли к первому острову, который
называется «Разминка».
Какой он формы? А цвета?
Дети: Квадратной, жёлтого цвета.
Дидактическая игра «Передай якорь». А для этого нужно ответить на вопросы.
1. Вспомнить порядковый счёт от 1 до 10, от 10 до 20.
2. Вспомнить обратный счёт от 10 до 1, от 10 до 20
3. Посчитайте от 1 до 5, от 5 до 10, от 10 до 15, от 15 до 20
4. Посчитайте от 20 до 15, от 15 до 10, от 10 до 5, от 5 до 1
6. Угадай число, живущее между числами 5 и 7, 4 и 6, 9 и 7, 16 и 18
7. Какое число больше 3 или 4, 7 или 8, 12 или 13
8. Какое число меньше 1 или 3, 10 или 6, 15 или 19
Молодцы! Справились с первым заданием.
Поплывём на следующий остров.
И вот мы приплыли на второй остров.
Какой он формы? А цвета?
Дети: Круглой, синего цвета.
Правильно! А называется он «Островов Рыболовов»
Здесь мы будем ловить рыбок и отвечать на вопросы, которые они нам
приготовили
Воспитатель читает вопросы на рыбках, дети отвечают.
Бурлият Ахмедпашаева
Конспект НОД «Математическое развитие» в подготовительной группе.
НОД «Математическое развитие » в подготовительной группе .
Тема : «Путешествие в сказку»
Цель :
– Развитие воображения , сообразительности, смекалки, внимания;
Учить воспринимать информацию на слух.
Обучающие задачи :
1)Упражнять в решении примеров на сложение и вычитание, в решении арифметических задач.
2)Закрепить навыки счета в пределах 10.
4)Закрепить умения различать и называть геометрические фигуры.
5)Закрепить знания о временах и месяцах года.
Развивающие задачи :
1)Развитие внимания , памяти, творческого воображения, логического мышления.
2)Способствовать формированию и выражению своих мыслей.
3)Развивать речь .
Воспитательные задачи :
1) Воспитывать самостоятельность, выдержку, умение
выслушать вопрос воспитателя до конца.
2) Воспитывать дружеские взаимоотношения, умение работать в коллективе.
Интегрируется с образовательными областями :
Социализация
Коммуникация
Безопасность
Здоровье
Материал :
Простые карандаши, тетради, набор цифр, игровой материал «Палочки Кюизера» , изображения кукол, рисунки с изображением героев сказки «Приключения Буратино» для раскраски, мольберт для воспитателя, фланелеграф,карточки с изображением Буратино и карточки с изображением Карабаса.
(Звучит музыка из сказки «Приключения Буратино» ).
Воспитатель : «Дети, кто-то стучит в дверь!» (Открывает дверь, в группу входит почтальон c сумкой на плече).
Почтальон : «Дети я принес вам письмо из Сказочного города. Пишет вам Буратино. (Почтальон отдает письмо воспитателю) . До свидания, ребята! (Почтальон уходит) .
Воспитатель : – Ребята, вы смотрели сказку про Буратино? (Да)
Давайте прочитаем письмо от Буратино. Воспитатель открывает конверт и читает письмо : «Дорогие ребята! Меня схватил Карабас – Барабас. Он не хочет меня отпускать, пока я не выполню задания, а я затрудняюсь их выполнить. Помогите мне, пожалуйста. Я очень хочу попасть в новый кукольный театр».
Ребята, вы согласны помочь Буратино и отправиться в Сказочный город? (Да)
Воспитатель : Первое наше задание называется «Веселый счет» .
1. Проводится разминка :
Прямой и обратный счет в пределах 10; (Дети передают мяч друг другу и называют числа от 1 до 10 и обратно) .
Воспитатель называет числа 5,6,7, а дети – «соседей этого числа» , показать соответствующие цифры и объяснить свой ответ;
Воспитатель называет числа от 1 до 8; от 1 до 5; от 1 до 6, а дети считают от этого числа до10;
Сравнить числа 4 и 6, 2 и 9, 7 и 7;
Дети, вы очень быстро справились с этим заданием.
2. Ориентировка на листе бумаги. «Графический диктант» .
Воспитатель :
Дети, смотрите! Девочка с голубыми волосами – Мальвина. Она убежала от
Карабаса и заблудилась. Она хочет попасть в новый кукольный театр. Поможем ей найти дорогу?
Дети открывают тетради. От отмеченной точки дети рисуют по указанию воспитателя : 1 клетка направо, 3 вверх, 1 направо, 3 вниз, 1 направо, 1 вверх, 1 направо и т. д.
Молодцы, дети! Вот мы и показали Мальвине дорогу.
3. Третье задание. Решение простых арифметических задач.
На фланелеграфе появляются изображения кукол Карабаса.
Воспитатель :
Ребята, как звали кукол Карабаса?
У Карабаса было 7 кукол. Он поймал и забрал к себе Буратино. Больше или меньше стало кукол у Карабаса? (ответы детей) Сколько стало? Какое в этой задаче условие? Какой вопрос? (ответы детей)
4. Физкультминутка
Воспитатель :
Ребята, вы, наверное устали?
Ну, тогда давайте все вместе встанем.
Буратино потянулся
Раз – нагнулся.
Два – нагнулся.
Руки в стороны развел .
(Выполнять движения в соответствии с текстом)
Ключик, видно, не нашел
(жест сожаления) .
Чтобы ключик
(повороты влево – вправо)
Нам достать
(руки вверх)
Нужно на носочки встать
(подъем на носочки) .
5 задание. Решите быстро и правильно примеры (устно)
(На фланелеграфе появляются изображения кукол.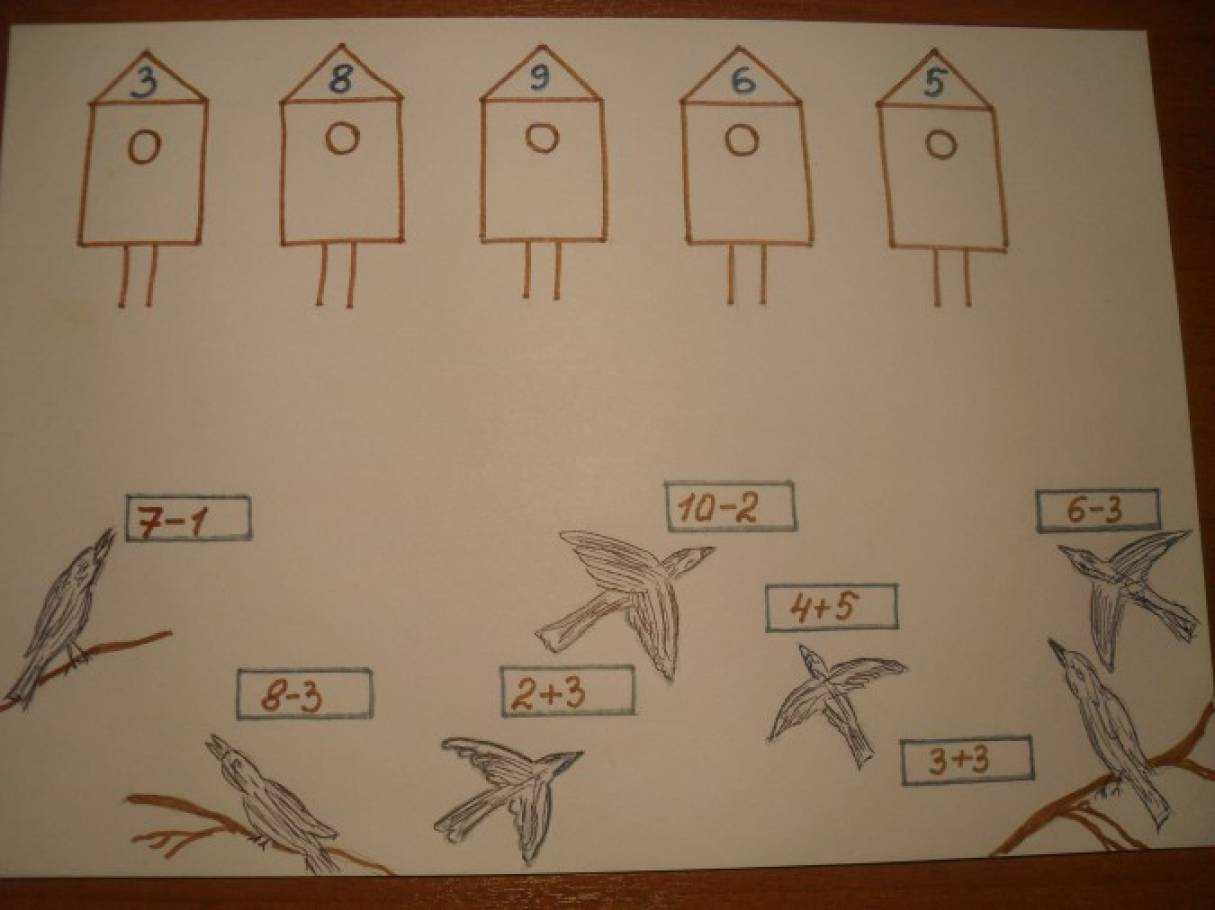
Дети выставляют нужное количество кукол и решают примеры).
Ребята сколько было кукол? (3) Сколько надо взять еще? (4) Сколько стало? и. т. д.
Мы справились и с этим заданием.
6 задание.
Воспитатель :
А сейчас, дети, мы попали в театр Геометрических фигур. Вам нужно посмотреть и рассказать по рисунку сколько и какие фигуры вы видите.
7 задание.
Воспитатель :
Еще одно задание нам нужно выполнить в театре Геометрических Фигур. Нам
нужно отгадать загадки и составить фигуры.
1. Три вершины тут видны
Три угла, три стороны,
Ну, пожалуй, и довольно! –
Что ты видишь? – (треугольник) .
2. Из него мы строим дом.
И окошко в доме в доме том.
За него в обед садимся,
В час досуга веселимся.
Ему каждый в доме рад
Кто же он? Наш друг –(квадрат) .
3. Обведи кирпич мелком
На асфальте целиком,
И получится фигура –
Ты, конечно, с ней знаком (прямоугольник)
Воспитатель :
Дети, вам надо составить эти три фигуры и назвать их.
8. «Тренировка»
Воспитатель :
Сейчас у нас тренировка для глаз.
(Дети выполняют движения в соответствии с текстом)
Раз – налево, два – направо,
Три – наверх, четыре – вниз.
А теперь по кругу смотрим,
Чтобы лучше видеть мир.
Тренируя мышцу глаз.
Видеть скоро будем лучше,
Убедитесь вы сейчас!
А теперь нажмем немного
Точки возле своих глаз.
Сил дадим им много-много,
Чтоб усилить в сотню раз!
(Посмотреть влево. Посмотреть вправо.
Круговые движения глазами : налево – вверх – направо – вниз – вправо – вверх – влево – вниз.
Поднять взгляд вверх. Опустить взгляд вниз.
Быстро поморгать)
9 задание.
Закреплять знания о временах и месяцах года.
Воспитатель :
Сейчас, дети, отгадайте загадки.
1. Солнце печет, липа цветет
Рожь поспевает, когда это бывает? (летом) .
2. Кто поляны белит белым.
И на стенах пишет мелом.
Шьет пуховые перины.
Разукрасил все витрины? (зима) .
3. Тает снежок, ожил лужок
День прибывает
Когда это бывает? (весной) .
4. Пусты поля, мокнет земля,
Дождь поливает,
Когда это бывает? (осенью) .
Ребята, с какого месяца начинается год?
Каким месяцем заканчивается?
Какие времена года вы знаете?
Из каких месяцев состоит осень (лето, весна, зима? (Ответы детей)
Воспитатель : Молодцы, дети!
Вот мы и выполнили задания. Буратино сможет освободиться от Карабаса и попасть со своими друзьями в новый кукольный театр, который находится за заветной дверцей, за очагом, потому что вы все активно участвовали и все выполнили правильно.
Ребята, давайте сообщим эту новость Буратино, напишем ему письмо.
(Воспитатель вместе с детьми пишут письмо и отправляют) .
Ребята, где вы сегодня побывали? А вам понравилось ваше путешествие? Что вам было наиболее трудно? Что вам показалось интересным? В следующий раз вы отправитесь в
путешествие в другой сказочный город, где вас встретят другие сказочные герои.
А кто там нас встретит – это секрет.
Ребята, а какое у вас настроение? Если хорошее, то поднимите карточку с изображением Буратино, а если плохое, то карточку с изображением Карабаса. (Дети показывают карточки) . Я вижу, что у всех настроение хорошее.
Стук в дверь. Воспитатель открывает дверь. Появляется Буратино.
Буратино :
Cпасибо большое, ребята, за помощь! Я освободился от Карабаса – Барабаса и спешу со своими друзьями в новый кукольный театр. На память я хочу подарить вам картины с изображением своих друзей. До свидания, дети.
Конспект НОД по математическому развитию в подготовительной к школе группе
Задачи:
Обучающие:
закреплять умение ориентироваться на плоскости;
закреплять умение классифицировать множества по трём свойствам цвет, форма, размер.
Развивающие:
развивать навык порядного счета в пределах 20;
развивать логическое мышление, умения находить сходство и отличия;
развивать зрительное внимание, общую, тонкую моторику, творческое воображение;
поощрять стремление ребенка выражать свои мысли и суждения при помощи точной, ясной речи.
Воспитательные:
поддерживать интерес к интеллектуальной деятельности, желание играть в игры математического содержания, проявлять настойчивость, целеустремленность, воображение, сообразительность, аналитическое восприятие, взаимопомощь.
Предварительная работа: чтение сказки «Гуси- лебеди», беседа с воспитателем, по сказке.
Оборудование:
мультимедийное оборудование,
магнитофон,
три обруча (красный, зелёный, желтый),
учебно-игровое пособие «Блоки Дьенеша»,
схемы знаков-символов, обозначающие свойства предметов;
картинки яблок разных форм и размера и цвета,
цифровая «Да – нетка»,
картинки (яблоня, речка, ёжик, печка),
альбомный лист с точками, пронумерованными в порядке возрастания для игрового упражнения «Соедини точки»,
плоскостные яблоки с примерами для игрового упражнения «Собери яблоки»,
карточка ЛГЕУБЕСДИИ,
счётные палочки,
листочки в клеточку, карандаши.
Ход НОД:
1. Организационный момент:
Дети входят в группу вместе с воспитателем, встают на ковёр вокруг воспитателя.
2. Мотивационная часть
Воспитатель: – Сегодня нам предстоит большое путешествие с приключениями, с заданиями на смекалку и сообразительность. А поможет нам в этом сказка. Вы узнаете её название, если прочитаете сначала все красные, а потом чёрные буквы.
ЛГЕУБЕСДИИ – «Гуси- лебеди»
3. Основная часть
Воспитатель: – Предлагаю вам начать путешествие…. С чего начинается сказка? Сколько было гусей-лебедей? – Внимание. Загадка в стихах:
Два гуся летят над нами,
Два гуся за облаками.
Три спустились за ручей.
Сколько было всех гусей? (Семь)
Давайте составим, число 7 из двух меньших чисел, все возможные варианты. 6 и 1; 5 и 2; 4 и З; З и 4; 2 и 5; 1 и 6.
Воспитатель: – Вернёмся к сказке. Прибежала девочка, посмотрела – нет брата.
Побежала девочка искать брата, бежит и видит… А что она увидела, вы узнаете, если правильно соедините числа от 1 до 12 (Дети соединяют)
Воспитатель: – Правильно, ПЕЧКА. Печка, печка скажи, куда гуси-лебеди полетели?
Печка: – Достань пирожки и посчитай, сколько их у меня испеклось? А поможет мне в этом игра «Да-нетка».
Правила игры:
Воспитатель раскладывает на столе в ряд карточки с цифрами 1-9 и загадывает какую-либо цифру.
Дети угадывают ее, задавая вопросы, на которые можно ответить «Да» или «Нет».
Воспитатель: – А теперь представим, что пирожков много и они в виде геометрических фигур.
Разложите пирожки в три корзинки (в первую корзинку – все круглые, во вторую – все
желтые, в третью – большие фигуры).
Проводится игра с «Блоками Дьенеша», дети раскладывают фигуры в три обруча.
Воспитатель: – Показала печка девочке дорогу. И я вам сейчас покажу дорогу, а вы запомните
её, и потом выложите такую же дорогу при помощи счётных палочек, учитывая цвет и количество.
Сколько палочек зелёного цвета?
Сколько красного?
Сколько палочек нужно взять?
Воспитатель: – Побежала девочка по дорожке и вдруг видит ЯБЛОНЮ.
«Яблоня, яблоня, куда гуси-лебеди полетели?» – спрашивает девочка. Выполните мое задание, тогда скажу.
Задание: Соберите яблочки в корзину по схемам, которые лежат на столе. Дети по схемам находят фигуры- яблочки и складывают в корзину (на одном яблоке – пример, на другом – ответ; необходимо подобрать яблоки правильно).
Физминутка
Руки подняли и помахали –
Это деревья в лесу.
Локти согнули, кисти встряхнули-
Ветер сбивает росу.
В стороны руки, плавно помашем –
Это к нам птицы летят.
Как они сядут – тоже покажем:
Крылья сложили назад.
Речка, речка, куда гуси лебеди полетели? – спросила девочка.
Скажу тогда, когда нарисуешь русло реки. А поможет в этом графический диктант.
От точки 3 клеточки вниз и 3 клеточки вправо, 2 клеточки вниз и 2 вправо, 4 вниз и 1
вправо, 1 вверх и 1 вправо, 1 вверх и 1 вправо, 2 вверх и 2 вправо, 2 вверх и 5 влево.
Воспитатель: – Показала речка путь до избушки Бабы-Яги. Теперь, дети, предстоит вам помочь девочке Алёнушке забрать Иванушку из дома Бабы- Яги. Как это можно сделать?
Предполагаемые ответы детей:
1. Напугать Бабу-Ягу, одевшись, как она.
2. Вылечить от злобы.
3. Пригласить в гости погостить.
4. Предложить ей стать человеком.
4. Заключительная часть
Алёнушка освободила братика, и они прибежали домой. Родители приехали из города, привезли гостинцев детям и вам за то, что вы помогли справиться Алёнушке со всеми заданиями.
Конспект НОД по математическому развитию в подготовительной к школе группе «Морское путешествие».
Воспитатель: Самосудова Т.В.
Задачи: Продолжать формировать у детей конструктивное мышление, учить строить сложные геометрические фигуры по заданной схеме. Продолжать упражнять в счете в пределах 20 в прямом и обратном порядке, в умении различать количественный и порядковый счет в пределах 20.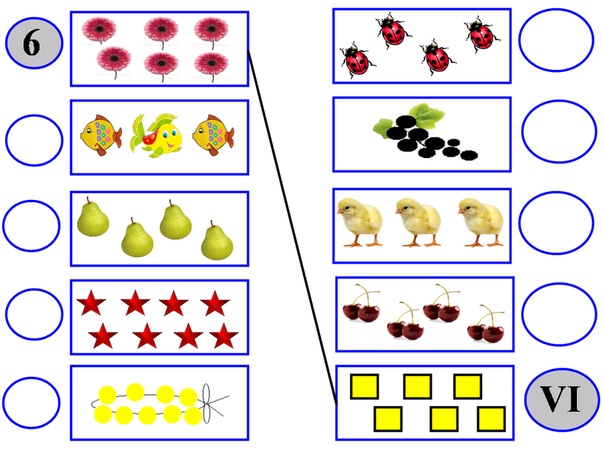
Закрепить знания детей о составе чисел в пределах 10 из двух меньших чисел. Закрепить знания детей о последовательности дней недели, времен года, месяцев года. Закрепить умение ориентироваться на листе бумаги в клетку. Воспитывать самостоятельность, умение понимать и принимать учебную задачу и выполнять её самостоятельно. Воспитывать интерес к математическим заданиям.
Предварительная работа: Отгадывание загадок, решение логических и конструктивных задач, наблюдение за календарем, индивидуальная работа с детьми по развитию математических представлений.
Демонстрационный материал: Телеграмма, ребус, длинная веревка, иллюстрация замка, замок, сундук с книгами, чашка, бокал, крупа.
Раздаточный материал: Карточки с заданиями и числовыми домиками, конверты с геометрическими фигурами, чашки, крупа, шнуры.
Ход
Оргмомент.
Воспитатель: Ребята, сегодня утром нам доставили телеграмму от Феи из страны Математики: «Дорогие дети, я приглашаю вас в путешествие по морю к острову чудес на поиски сокровищ.
В пути вас ждут интересные задания. Вы должны будете показать свои знания, умения, сообразительность и смекалку. Желаю удачи!»
Воспитатель: Перед путешествием необходимо размяться.
Проведем разминку: Если стол выше стула, то стул? (ниже стола).
Если дорога шире тропинки, то тропинка? (уже дороги).
Если линейка длиннее карандаша, то карандаш? (короче линейки).
Если веревка толще нитки, то нитка? (тоньше линейки).
Если сестра старше брата, то брат? (младше сестры).
Воспитатель: Молодцы! Команда готова. А на чем мы отправимся в плаванье?
Дети: Надо построить корабль.
Воспитатель: достаньте геометрические фигуры из конвертов.
Сколько у вас геометрических фигур?
Сколько у вас треугольников?
Сколько у вас четырехугольников?
Воспитатель: Приступаем к строительству.
(Дети работают за столами.По заданной схеме собирают из геометрических фигур корабль).
Воспитатель: Молодцы! Вот и готов волшебный корабль. Вы оказались умелыми строителями, отправляемся. Приготовьте пульты управления. Начинаем отсчет.
(Дети показывают и называют цифры от 1 до 20 и обратно).
Воспитатель: И вот мы уже в море. (Раздается телефонный звонок.Педагог «принимает» сообщение).
Воспитатель: Дети, я получила сообщение с другого корабля. Послушайте внимательно:
«Вот такая канитель –
Наш корабль сел на мель,
И матросы всю неделю
Карамель на мели ели»,
Надо матросам поесть на обед что-нибудь по питательнее, например, кашу. Но вот беда, у них сломались весы, и повар не может узнать, сколько крупы взять. Помогите ему. У нас есть пакеты, в которые нужно насыпать по два больших бокала крупы. Но имеется, к сожалению, только один большой бокал, но перед каждым стоит маленькая чашечка. Две таких чашечки составляют бокал.
(Воспитатель демонстрирует, что в 1 бокал вмещается 2 маленькие чашки крупы.
Дети самостоятельно выполняют задание).
Воспитатель: Молодцы, ребята. К нашему кораблю спешат и другие корабли. Они и доставят им крупу. А мы отправляемся дальше.
Ой, на море опустился туман времени. Чтобы выйти из тумана, надо ответить на вопросы:
Сколько дней матросы сидели на мели? (7).
Почему вы так думаете? (В неделе 7 дней).
Какой день недели сегодня?
Какой день недели был вчера?
Какой день недели будет завтра?
Какой день недели между понедельником и средой?
Воспитатель: Я буду называть день недели, а вы отвечайте, какой он по счету (четверг, пятница, вторник).
Сколько времен года вы знаете?
Физминутка.
В году четыре времени, и все они дружны.
Эти четыре времени ребята знать должны!
Зимой год начинается, все снегом покрывается.
Весною продолжается, листочки появляются.
Летом солнце греет, и листья зеленеют.
Осенью листва желтеет, ветер ее по полям развеет.
А после осени опять зима год будет продолжать.
Воспитатель: Сколько месяцев в каждом времени года? (Ответы детей).
Назовите осенние, зимние, весенние, летние месяцы.
Какое время года сейчас? Какой сейчас месяц?
Молодцы, мы быстро двигаемся вперед. Мы уже у острова. Надо бросить якорь. Но неизвестно, хватит ли якорной цепи, чтобы зацепить якорь за дно?
(Дети получают одинаковые по длине шнуры, но для их измерения разные мерки.У каждого карточка, обозначающая нужное количество мерок).
Сколько раз уложилась мерка по длине цепи? Почему получились разные числа? (Дети отвечают).
Воспитатель: Молодцы, ребята. Посмотрите, на острове растут необыкновенные цветы. На каждом цветке – задание, загадки Феи. Ребята, давайте отгадаем загадки:
У бабушки Даши – внучка Маша,
Кот Пушок, собака Дружок.
Сколько у бабушки внуков? (1).
На дереве сидят 4 птицы: 2 воробья, остальные вороны.
Сколько ворон? (2).
Воспитатель: Следующее задание Феи – помочь жителям Числограда. Дома в этом городе необычные: на каждом этаже живут числа-соседи, которые в сумме дают число дома. Заселите домики числами. (В домике числа «6» находятся пары: 1 и 5, 2 и 4, 3 и 3).
Воспитатель: Мы справились еще с одним заданием Феи и оказались перед замком. Где же нам искать сокровища? Ведь замок такой большой. В этом нам поможет ребус, давайте его расшифруем. (ребус «ПО 2 Л» – подвал).
Правильно, ребята, но дверь в подвал охраняет невидимый страж, нам необходимо узнать, кто этот страж и назвать его.
Математический диктант:
2- вверх 6- вправо 3- вниз
2- вправо 2- вверх 1- влево 1- влево
вверх 1- вправо 3- вверх 3- вниз
вправо 8- вниз 4- влево 1- влево
вверх 1- влево 3- вниз 6- вверх
вправо 3- вверх 1- влево 2- влево
4- вниз 1- влево 3- вверх
Воспитатель: Кто же охраняет замок? (Собака).
Вы справились со сложным заданием, потому что были настойчивы и внимательны, дружны. Я горжусь вами! Осталось открыть дверь, но на двери висит замок. Надо разгадать код замка. Если к задуманному числу прибавить 2, то получится 8. Какой код у дверного замка? (Число 6).
Итог.
Воспитатель: Молодцы! Открываем сундук, а в нем книги по математике. Это очень важные книги. По ним вы научитесь решать задачи, примеры. Мы справились со всеми заданиями и нашли сокровище. Фея благодарит вас за хорошую игру. А нам пора в детский сад. Возьмите пульты управления и дадим обратный отсчет от 20 до 1. Закройте глаза. Вот мы и вернулись в свою группу. Все вы молодцы!
Занятие по математике в подготовительной группе “Путешествие в страну математики”
Описание занятия : данное занятие предназначено для воспитателей, работающих с детьми подготовительной группы (возраст детей 6-7 лет).
Мольберт, презентация к занятию.Звучит загадочная музыка. В группу влетает шар, к ниточке которого привязан конверт. В конверте письмо и разрезная картинка «Профессор Математик»
Воспитатель : Ребята, посмотрите, что это такое? Обращает внимание детей на воздушный шарик, с привязанным конвертом. Конверт не подписан. Странный конверт какой то, на нём ничего не написано, только цифры и геометрические фигуры.
Я предлагаю открыть конверт и узнать от кого мы его получили (открывает конверт, в нём разрезная картинка и письмо).
Что надо сделать, чтобы узнать от кого это письмо пришло к нам?
Дети: собрать картинку.
Воспитатель : как вы думаете, кто это? (ответы детей) всё ясно! Это написал нам профессор Математик! Нужно скорее прочитать его, может там что- то важное!
Воспитатель читает письмо:
«Здравствуйте, дорогие ребята! Я знаю, что вы уже многому научились. Я приготовил вам интересные задания! За каждое выполненное задание вы будите получать карточки с буквами.
Только смелые и дружные ребята пройдут все испытания! Вы готовы к путешествию? (ответы детей.) Тогда удачи! Даю вам подсказку: План-схема по выполнению заданий.
Воспитатель показывает детям схему выполнения заданий.
Какое первое задание? Что расположено в верхнем левом углу? (геометрические фигуры) Наше первое задание называется «Весёлые фигуры»
Воспитатель показывает фигуры на доске. Как называются эти фигуры? Назовите к каждой из фигур предметы такой же формы.
После выполнения задания дети получают карточку с буквой. Вы молодцы!
Поставим карточку на доску и отправимся выполнять второе задание.
Посмотрите на схему. Как вы думаете какое второе задание?(ответы детей)
Воспитатель предлагает детям сесть за столы. Откройте тетради. Наше следующее задание « Математический диктант» Дети работают в тетрадях в клетку под диктовку воспитателя. Что у нас получилось? Сравните с образцом. Воспитатель показывает увеличенный образец. Правильно у нас получилась собачка.
Дети оценивают свои работы и работы товарищей. Молодцы! Вы заработали вторую карточку!
Прежде чем перейти к следующему заданию, предлагаю вам математическую разминку. Игра »Верно не верно»
Воспитатель : если вы услышите, то, что считаете правильным, хлопайте в ладоши, если же, то, что неправильно –топайте ногами.
– утром солнышко встаёт
-по утрам нужно делать зарядку
– нельзя умываться по утрам
– днём ярко свети луна
– утром дети идут в детский сад
-ночью люди обедают
-в неделе семь дней
– за понедельником следует среда
-после субботы идёт воскресенье
-перед пятницей стоит четверг
-всего пять времён года
– весна наступает после лета.
Воспитатель : молодцы ребята! Но нас ждёт следующее задание!
Давайте посмотрим на нашу схему.
Так всё понятно! Вы знаете, что у каждого числа есть соседи слева и справа? Сейчас я буду показывать вам карточки с цифрами, а вы по очереди называйте их соседей. Игра» Назови соседей»
Воспитатель: вот какие молодцы и с этим заданием справились! Получайте карточку с буквой!
Воспитатель: а теперь снова посмотрим на схему с заданиями.
Что это за знаки? Математические знаки забыли, как называются и потеряли своё место. Поможем им?
Присаживайтесь за стол. Вам нужно сравнить числа на карточках и поставить нужные знаки.
Молодцы! Вы справились с этим заданием профессора и получаете от него карточку с буквой.
Продолжим дальше. Что показывает наша схема? Стрелочки разного цвета и противоположного направления! Профессор Математик предлагает вам поиграть в игру «Скажи наоборот».
Игра проводится с мячом. Воспитатель кидает мяч ребёнку и называет одно из математических понятий.
Большой-маленький
Длинный-короткий
Высокий-низкий
Широкий-узкий
Толстый-худой
Далеко-близко
Вверху-внизу
Слева-справа
Вперёд-назад
Лёгкий-тяжёлый
Воспитатель: и с этим заданием вы справились! Вот ваша карточка!
Посмотрите ребята на схему. Стрелочка опять показывает на левый верхний угол. Мы вернулись к изображению геометрических фигур. Как вы думаете каким буде наше задание? (ответы детей) Да, правильно наше задание будет связано с геометрическими фигурами.
Профессор просит сделать ему необычный ковёр из фигур. Подходите к столу. Все вместе разложите геометрические фигуры на листе бумаги, а потом приклейте их.
Вот какой интересный и красивый ковёр получился! Вы все старались! За это занятие профессор Математик даёт вам сразу две карточки!
Воспитатель : вот мы и собрали все карточки с буквами. Какое слово получилось из букв? (МОЛОДЦЫ). Воспитатель спрашивает, какие задания понравились, что показалось трудным. (Ответы детей)
Ребята, мы возвращаемся из нашего волшебного путешествия! А ковёр с геометрическими фигурами мы отправим на волшебном шаре профессору Математику во время прогулки!
Занятие заканчивается.
Государственное бюджетное дошкольное образовательное учреждение детский сад №9 комбинированного вида Колпинского района Санкт-Петербурга
Конспект НОД
по математике в подготовительной группе
«Веселая математика»
Составила:
Афанасьева В.
Г.
2017г
Тема: Число 7 и его состав, ориентировка на листе бумаги, ориентировка во времени, логические задачи с математическим содержанием, сравнение двух чисел.
Закрепить прямой счет до 10, обратный от 10 до 0;
-закрепить представления о числовом ряде,уметь называть соседей числа, последующее и предыдущее число. -познакомить с образованием числа 7; – закреплять умения решать простые примеры на сложение и вычитание;
– закреплять умение решать логические задачи на основе зрительно воспринимаемой информации;
– закрепить знания о днях недели, весенних месяцах;
– формировать умение понимать поставленную задачу и решать её самостоятельно;
– уметь сравнивать два числа с помощью знаков. – развивать умение ориентироваться на листе бумаги в клетку.
Материал: ИКТ,презентация,карточки с заданиями, карточки монетки разного цвета, листы бумаги в клеточку, карточки с цифрами, музыкальное сопровождение.
План занятия.
I. Вводная часть.
II.
Основная часть.
Д/и «Цифры потерялись».
Логическая задача «Какая фигура лишняя в ряду?»
Логические задачи – шутки.
Физминутка.
Познакомить с числом 7. Учить составлять число 7 из двух меньших чисел.
Решение примеров на сложение и вычитание.
Пальчиковая гимнастика.
Графический диктант.
III. Заключительная часть.
Подведение итогов занятия.
Ход занятия.
Ребята,здравствуйте, давайте встанем с вами в круг и поприветствуем друг друга. Повернемся направо и улыбнемся соседу, а теперь повернемся налево и улыбнемся соседу слева. А теперь скажем всевместе
Здравствуйте!!!
(1 слайд.На ИКТ появляется изображение Незнайки,который говорит:
«Дорогие ребята, я пошел в школу,а для того чтобы хорошо учиться в школе, надо много знать, уметь, думать, догадываться. А также решать необычные задачи, выполнять задания на смекалку и сообразительность. Мне так много всего задают, а помочь некому… Помогите мне, пожалуйста».
Ребята, давайте поможем Незнайке.
1 задание. Ответьте на вопросы:
2 слайд. Изображение весны.
Какое время года? (весна)
Назовите весенние месяцы (март, апрель, май)
Какой месяц сейчас идёт? (март)
Сколько дней в недели? (семь)
Назови их;
Какой сегодня день недели? (четверг)
Какой четверг по счету? (четвертый)
Вчера какой был день недели? (среда)
Завтра какой будет день недели? (пятница)
2 задание. – Ребята, Незнайка предлагает нам поиграть в игру «Цифры потерялись»
3 слайд. Цифры разбросаны..
Предложить детям подходить к доске и передвигать цифры на место…
Посчитайтесь по порядку, а теперь в обратном порядке.
Назови предыдущее и последующее число, числа 5,7,9,8,
сравни числа 5 и 3;
Сравни числа 4 и 4;
Какие бывают числа? (четные и нечетные)
Вы справились с заданием.
3 задание. Решить логическую задачу «Какая фигура лишняя в ряду?»
4 слайд.
Изображены 2 ряда геометрических фигур)
Какая фигура лишняя, почему ты так думаешь?
Вы справились и с этим заданием Незнайки.
4 задание. «Друзья, все предыдущие логические задачи были серьезные, а есть еще и задачки – шутки. Будьте внимательны и вы обязательно справитесь с ними».
5 слайд. Игра «Задачи – ловушки».
Воспитатель читает задачи, дети отвечают и объясняют.
Вот медведица идет,
Медвежат своих ведет.
Сколько здесь всего зверей?
Сосчитай-ка поскорей! (3)
Вот грибочки на лужайке
В жёлтых шапочках стоят.
2 грибочка, 3 грибочка.
Сколько вместе будет?..? (5)
Из дупла выглядывало 8 беличьих хвостов. Сколько бельчат сидело в дупле? (8)
На яблоне висели 5 яблок и 3 груши. Сколько всего плодов висело на яблоне? (5 яблок)
В вазе 3 тюльпана и 4 нарцисса. Сколько тюльпанов в вазе? (3 тюльпана)
Наступила долгожданная зима. Сначала зацвела 1 яблоня, а потом – ещё 3 сливы. Сколько деревьев зацвело? (зимой деревья не цветут).
У стула 4 ножки. Сколько ножек у 2-х стульев? (8 ножек)
В.- Молодцы! Решив все задачи…
Физминутка. «Зарядка» на ИКТ звучит бодрая музыка
Раз – согнуться, разогнуться.
Два – нагнуться, потянуться.
Три – в ладоши три хлопка,
Головою три кивка.
На четыре – руки шире.
Пять, шесть – тихо сесть.
5 задание. Какой состав числа 7?
6 слайд. Изображение кинотеатра.
Чтобы ответить на этот вопрос Незнайки, мы сегодня познакомимся с составом числа 7.
Незнайке нужно купить билет -стоит 7 монеток. На столе лежат карточки на них нарисованы кружки двух цветов. – это монетки. Подберите монетки так, что бы у вас было 7 монеток. (Дети работают с карточками и показывают результат)
Вопросы детям:
Выложите по порядку все варианты состава числа семь у себя на столах.
Как только дети закончат работу, еще раз предложите им рассказать, как можно составить число семь из двух меньших чисел.
Молодцы! Спасибо! Из каких же двух чисел можно получить число 7?
6+1, 5+2, 4+3 и 7 единиц)
Молодцы, теперь Незнайка,обязательно попадет в кино!
6 задание.
Решите примеры
7 слайд. На доске записаны примеры, предложить решить примеры устно.
5+2=? 3+4=? 9+1=?
8-1=? 6-3+? 7-2=?
Пальчиковая гимнастика.
Как-то маленький удав
Захотел залезть под шкаф
Он под шкафом растянулся,
А потом в клубок свернулся.
7 задание. А теперь Незнайка приготовил вам графический диктант.
8 слайд. Изображение Незнайки, он читает задание, а дети выполняют сидя на своих местах.
Поставьте карандаш на точку и рисуйте: семь клеток направо,три клетки вниз, семь клеток налево, три клетки вверх.
Посмотрите и сравните получившийся у вас рисунок с образцом
9 слайд. На ИКТ появляется изображение прямоугольника
Воспитатель: Молодцы, ребята!
Рефлексия: -Вот и выполнили вы все задания Незнайки. Что же мы сегодня нового узнали? Какие задания с вами выполняли? (ответы детей).
Опубликовано: 27 сентября, 2018
Все учителя хотят, чтобы уровень успеваемости своих учеников повысился. Обучение в малых группах и совместное обучение оказывают значительное влияние на успеваемость учащихся (Hattie, 2009) и широко используются в начальных классах. Многие учителя средних и старших классов все чаще используют эти структуры в других предметных областях.Однако перед тем, как приступить к обучению в малых группах, у учителей часто возникают вопросы, на которые нужно ответить.
(Сьюзан Ван Зант и Нэнси Вольпе, старшие специалисты по образовательным услугам, CORE, Inc. )
Когда обычно следует проводить обучение в малых группах?
Обучение в малых группах обычно следует за инструкциями всей группы для закрепления или повторного обучения определенным навыкам и концепциям и обеспечивает меньшее соотношение учеников и учителей. Небольшие группы обычно составляют от четырех до шести учеников.
Каковы основные преимущества обучения в малых группах?
Обучение в малых группах дает четыре основных преимущества:
Как организованы небольшие группы?
На основе частого постоянного мониторинга успеваемости (и некоторой диагностической) оценки учащиеся часто группируются и перегруппируются из-за общего дефицита навыков.Однако время от времени учитель может формировать кооперативную группу учеников с разными способностями для совместной работы в течение независимого рабочего времени. В этом случае учитель может выбрать для более успешного ученика роль сторонника сверстников.
А как насчет учеников, которые не работают напрямую с учителем?
Задача обучения в малых группах состоит в том, чтобы управлять другими учащимися, которые должны выполнять значимые задания во время самостоятельной работы, в то время как учитель работает с небольшой группой.Это время следует использовать, чтобы укрепить понимание ключевых навыков и стратегий грамотности или математики и развить ответственность за выполнение заданий. Организация увлекательных и дифференцированных заданий и мероприятий, направленных на закрепление навыков, которым обучают во время группового обучения, является ключом к успешному управлению временем независимой работы.
Для того, чтобы время самостоятельной работы было эффективным, следует выбирать задания и виды деятельности, которые предназначены для непосредственного закрепления концепций, изучаемых во время обучения грамоте или математике в группе.Эти действия и задания должны быть значимыми, а не просто «занятой работой», и их следует обновлять и изменять по мере обучения новым концепциям и навыкам, позволяющим использовать различные возможности для практики. Все материалы должны быть организованы, а расходные материалы должны быть легкодоступными. Чтобы материалы оставались организованными и учащиеся могли возвращать материалы в назначенные места, преподаватель должен маркировать материалы и назначенные им места для хранения и объяснять учащимся ожидания по управлению этими материалами и их возврату.
Как ввести и организовать независимое рабочее время?
Перед тем, как организовать обучение в малых группах, учителя должны сначала научить ожиданиям и предоставить распорядок практики для самостоятельной работы. Это методическое обучение и практика обеспечат лучший успех для всех студентов. Каждое задание или действие следует вводить по одному. Учитель должен моделировать, что ученики должны делать и как они должны себя вести на каждом рабочем месте. Перед тем, как приступить к другому виду деятельности, необходимо отработать и четко определить процедуры посещения рабочего места, использования материалов и того, что делать с готовой работой.Чтобы эффективно управлять независимым рабочим временем, учитель может захотеть получить доступ к 21-дневному планировщику обучения в малых группах CORE, который можно найти на веб-сайте CORE.
Заставить обучение в малых группах работать не всегда может быть легкой задачей, но при условии приверженности и последовательности учителя обнаружат, что такая структура является ценным распределением учебного времени. Время и усилия на подготовку окупятся, когда учитель увидит мощные возможности, предоставляемые каждому ученику, а также общий рост успеваемости учеников.Независимо от текущего уровня успеваемости, хорошо продуманное обучение в малых группах может иметь большое значение для каждого ученика.
Список литературы
Хэтти, Дж. (2009). Видимое обучение: синтез более 800 метаанализов, относящихся к достижению . Лондон: Рутледж.
Узнайте больше об услугах профессионального обучения CORE.
Чтобы получать будущие выпуски этого блога по электронной почте, добавьте свое имя в список рассылки.
Стратегия обучения – это метод, который вы используете для передачи информации своим ученикам. Может быть особая стратегия, которая хорошо работает с вашей группой студентов в течение одного года, но не будет работать с вашими студентами в следующем году. По этой причине важно иметь в своем арсенале множество обучающих стратегий. Вот некоторые из лучших идей, которые вы можете использовать.
Рассказав ученикам, что делать, важно точно показать им , как это делать . Независимо от того, насколько ясны ваши указания, неплохо смоделировать, как вы ожидаете, что они выполнят задание, чтобы они точно понимали, что они должны делать. Это будет особенно полезно для ваших учеников, которые учатся наглядно.
Например, если вы назначаете научную лабораторию, физически продемонстрируйте каждый этап лаборатории, прежде чем ученики сделают это самостоятельно.
То же самое касается фактического пошагового решения математической задачи на доске перед тем, как попросить учащихся решить аналогичные задачи самостоятельно.
Или, скажем, вы учитель английского языка, который хочет, чтобы ваши ученики активно комментировали назначенное им чтение каждую ночь. Было бы легко дать им ключ и пример, например:
Но также очень полезно продемонстрировать аннотирование отрывка в классе, чтобы учащиеся имели представление о том, как самостоятельно комментировать отрывок.
Это отличное видео по демонстрации аннотаций:
Если вы когда-нибудь случайно написали на доске слово неправильно, вы знаете, что студенты любят выявлять ошибки. Когда вы обучаете новому навыку, попробуйте привести пример, в котором есть ошибки. Позвольте ученикам попрактиковаться в этом навыке, выявляя и исправляя ошибки за вас.
Например, многие студенты съеживаются при изучении грамматики с помощью традиционных упражнений и уроков, но многие могут выявлять ошибки органически, даже если не знают, как их исправить.Попробуйте раздать задание и обсудить, включая грамматические ошибки, обсудить задание в классе и посмотреть, что учащиеся могут уловить. Затем обсудите , почему ошибки могут быть неправильными, и посмотрите, что могут придумать учащиеся, а затем проведите мини-урок по имеющимся грамматическим ошибкам.
Устранение ошибок гораздо более значимо для учащихся, когда есть более широкий контекст. Также действительно здорово создать атмосферу в классе, в которой ошибки являются частью учебного процесса и учащихся, что меньше пугает учащихся тем, с которыми они могут столкнуться с трудностями.
Студенты не всегда знают, хорошо ли они выполняют свою работу, без вашего ведома.
Регулярно предоставляйте письменную или устную обратную связь для индивидуальных или групповых заданий и сделайте это частью вашей школьной культуры.
Помните, что учащиеся часто не знают , почему что-то не так, , поэтому по возможности и если позволяет время, уделите несколько минут, чтобы объяснить, почему вы отметили что-то «неправильным» в тестах и заданиях.
Также неплохо проводить регулярные сеансы «групповой обратной связи» на основе шаблонов, которые вы наблюдаете в работе своих учеников. Если изрядная доля ваших учеников, кажется, испытывает затруднения с концепцией, часто бывает более полезным создать урок, нацеленный на эту тему, и обсудить закономерности, которые вы видели в классной работе в целом.
Не забудьте, конечно, предоставить множество положительных отзывов , а также отзывы, указывающие, где ученику есть куда расти или что ученик должен делать по-другому.Поощрение помогает поддерживать моральный дух, вдохновение и стремление учащихся.
И, наконец, иногда может быть полезно перевернуть столы. Пусть студенты поделятся с вами своим мнением , чтобы вы тоже узнали, как у вас дела. Вы можете сделать это в форме обсуждения, провести опросы в классе (на которые можно ответить анонимно или нет) или попросить студентов отправить вам электронное письмо с отзывами.
Фотография Defne Goncu
Студенты эффективно учатся, когда они работают вместе.Планируйте занятия, которые требуют от учащихся совместной работы и обучения друг у друга. В процессе они также приобретут навыки критического мышления, коммуникативные навыки, навыки решения проблем и многое другое.
Студенты учатся на практике, поэтому создайте для них опыт, чтобы увидеть концепции в действии. Позвольте им практиковать эти концепции в безопасной среде. Затем им следует поразмышлять над полученным опытом и обсудить, что они из него извлекли. Классные занятия, которые вы могли бы использовать для экспериментального обучения, включают веселые игры, эксперименты или симуляции.
Когда ученики становятся учителями в течение дня, они изучают вещи, которые иначе они бы не узнали. Вы можете попросить студентов обучать в группе или работать в группах, чтобы преподавать новую тему. Вы обнаружите, что другие ученики тоже будут учиться на уникальном подходе своих сверстников к предметам.
Еще один способ обучения студентов – обсуждения в классе. По мере того как учащиеся по очереди обсуждают предмет, вы можете оценить их знания и выяснить, какие учащиеся понимают концепции и в какой степени.
Задавая вопросы и работая вместе над решением проблем, учащиеся вовлекаются в процесс обучения. Класс может работать вместе, чтобы определить ответ и сообщить о нем. По мере того, как учащиеся работают над поиском ответов самостоятельно, они лучше и полнее запоминают концепции.
Вместо того, чтобы позволять ученикам самостоятельно определять, что им следует изучать, просто скажите им.Четко сформулируйте цели или задачи вашего урока. Вы можете объявить об этом в классе или написать на доске. Просто сделайте это простым и понятным для всех ваших учеников. Затем они знают, над чем они работают и что им следует знать к концу урока. Это также действительно помогает снизить беспокойство студентов во время экзаменов.
Фото Джимми
Graphic кратко резюмируют информацию. Используя блок-схему, диаграмму Венна или Интернет, учащиеся могут увидеть информацию в новом свете.Это помогает им систематизировать информацию в уме, чтобы они могли лучше понять новые концепции.
Математика – это все вокруг маленького ребенка с первого дня. Сколько тебе лет? Через час ты пойдешь в школу. Вы родились 2го числа.
Само число не может быть определено, и понимание числа вырастает из опыта работы с реальными объектами, но со временем они становятся абстрактными идеями. Это одно из самых абстрактных понятий, с которыми сталкивался человеческий разум.Никакие физические аспекты объектов никогда не могут предложить идею числа. Способность считать, вычислять и использовать числовые отношения – одни из самых значительных достижений человека. Концепция числа – это не вклад одного человека, а продукт постепенной социальной эволюции. Система счисления, которая создавалась на протяжении тысячелетий, является абстрактным изобретением. Все началось с осознания одного, а затем и нескольких. Замечательно видеть, насколько ребенок понимает ту же самую концепцию.
Арифметика имеет дело с формой, пространством, числами, их отношениями и атрибутами с помощью чисел и символов. Это наука о моделях, включающая в себя все виды закономерностей, например числовые узоры, абстрактные узоры, узоры формы и движения. В классе Монтессори ребенку представлены пять семей с математикой: арифметика, геометрия, статистика и исчисление. Точнее, понятия, охватываемые классом Primary, – это нумерация, десятичная система, вычисления, арифметические таблицы, целые числа, дроби и положительные числа.Мы предлагаем арифметику ребенку в последние два года на первом месте развития от четырех до пяти и шести лет.
Арифметика – это наука о вычислениях с использованием положительных действительных чисел. Это, в частности, процесс сложения, вычитания, умножения и деления. Материалы начальной школы Монтессори также представляют сенсорный опыт по геометрии и алгебре.
Маленьких детей естественным образом привлекает наука о числах.Математика, как и язык, является продуктом человеческого интеллекта.
Следовательно, это часть природы человека. Математика возникает из человеческого разума, когда он вступает в контакт с миром и когда он рассматривает вселенную и факторы времени и пространства.
Он поддерживает стремление человека понять мир, в котором он живет. Эту математическую предрасположенность проявляют все люди, даже маленькие дети. Поэтому можно сказать, что человечество обладает математическим умом.
Монтессори заимствовал идею о том, что у человека есть математический ум, от французского философа Паскаля. Мария Монтессори сказала, что математический ум – это «вид ума, который построен с точностью». Математический ум имеет тенденцию оценивать, ему необходимо количественно определять идентичность, сходство, различие и закономерности, устанавливать порядок и последовательность и контролировать ошибки.
Младенец и ребенок младшего возраста наблюдает и переживает чувственный мир. На основе этого опыта ребенок абстрагируется от понятий и качеств вещей в окружающей среде.Эти концепции позволяют ребенку создавать мысленный порядок. Ребенок составляет мысленную карту, которая поддерживает адаптацию к окружающей среде и изменениям, которые могут в ней произойти.
Для мышления используются ясные, точные, абстрактные идеи. Растущие познания ребенка в окружающей среде позволяют ему чувствовать себя в пространстве. Численность также связана с особой ориентацией. На первом плане развития человеческая тенденция к порядку вместе с чувствительным периодом к порядку поддерживает точность, с которой ребенок классифицирует восприятие мира.Материалы Монтессори помогают ребенку выстроить точный порядок. В классе ребенку предлагают материал и опыт, которые помогут ему навести внутренний порядок. Это внутренний порядок, который позволяет ребенку хорошо функционировать в окружающей среде. За порядком скрывается сила рассудка и способность адаптироваться к изменениям в окружающей среде.
Каждая культура функционирует в этом обществе по своему образцу. Этот образец усваивается ребенком и становится основой, на которой ребенок строит свою жизнь.Этот культурный образец является контекстом для класса Монтессори. Практическая жизнь. Упражнения – это повседневная задача домашней культуры, включающая в себя вежливость, с которой люди общаются. Ребенка привлекают эти занятия, потому что они – обычаи его людей. Его привлекает настоящая цель, в которой задействован его интеллект. Когда он начинает работать с практическими жизненными упражнениями, его все больше и больше привлекают требуемые порядок и точность. Участие в этих мероприятиях помогает ребенку стать членом общества сверстников в классе.Ребенок не подозревает, что эти действия закладывают закономерности в нервной системе. Повторение задает эти шаблоны и ведет к облегчению усилий.
Сенсорный материал – это математический материал. Это точно. Он преподносится с точностью и точно будет использоваться ребенком. Эти упражнения требуют точности, чтобы ребенок мог соприкоснуться с изолированными концепциями и, повторяя их, извлекать из сути каждого и иметь четкую абстракцию.Эти понятия помогают ребенку упорядочить свой ум. Он умеет классифицировать опыт. Четкое восприятие и умение классифицировать позволяет делать точные выводы. Сенсорная работа – это подготовка к изучению последовательности и развития. Это помогает ребенку строить пространственные представления величин и формировать изображения их величин, такие как Розовая башня.
Разговорный язык используется для выражения абстрактных концепций и передачи их другим. Помимо разговорного языка, людям понадобился язык для выражения количественного опыта, и отсюда появился язык математики.
К четырем годам ребенок уже готов к языку математики. Был проведен ряд приготовлений. Сначала в ребенке наведен внутренний порядок. Во-вторых, у ребенка развиты точные движения. В-третьих, у ребенка сформировалась рабочая привычка. В-четвертых, ребенок может следить за рабочим циклом и выполнять его. В-пятых, у ребенка есть способность концентрироваться. В-шестых, ребенок научился следовать процессу. В-седьмых, ребенок использовал символы. Все это предшествующее развитие привело ребенка к зрелости ума и готовности к работе.Конкретный материал для арифметики – это материализованные абстракции.
Это подходящие с точки зрения развития способы для ребенка изучить арифметику. Ребенок получает сенсорные впечатления от математических понятий, а движение поддерживает процесс обучения. Материал начинается с конкретных переживаний, но приближает ребенка к абстрактному. Есть также прогрессирование сложности. В подаче материала соблюдается шаблон. Он используется во всех арифметических упражнениях.Для изложения математических понятий ребенок сначала знакомится с количеством отдельно, и ему дается название. Затем вводится символ отдельно, и ему также дается имя. Затем ребенку предоставляется возможность связать количество и символ. Последовательность дана попутно во всей работе. Различные упражнения требуют от ребенка установления последовательности.
Математический материал дает ребенку собственный математический опыт и дает возможность приступить к самостоятельной работе.Существуют некоторые виды деятельности под руководством учителя, но за ними следуют занятия для отдельных лиц. Некоторая работа начинается с уроков в малых группах, они также будут направлены на самостоятельную индивидуальную работу.
Упражнения по арифметике сгруппированы. Есть некоторая последовательная работа и некоторая параллельная работа. Первая группа – это числа до десяти. Опыт в этой группе последовательный. Когда ребенок полностью понимает числа до десяти, можно ввести вторую группу, десятичную систему.
Основное внимание здесь уделяется иерархии десятичной системы и принципам ее функционирования. Он также запускает ребенка в упражнениях по простым вычислениям, которые являются операциями арифметики. Третья группа будет запущена, когда десятичная система будет в полном разгаре.
С этого момента эти упражнения будут даваться параллельно с продолжением десятичной системы. В эту третью группу, «Счет за пределами десяти», входят подростки, десятки, линейный и пропускающий счет. Четвертая группа – это запоминание арифметических таблиц.Эта работа может начаться, пока продолжаются более поздняя работа с десятичной системой и счет сверх десяти упражнений. Пятая группа – это переход к абстракции. Упражнения в этой группе требуют, чтобы ребенок понимал процесс каждой формы арифметики и знал таблицы каждой операции. Опять есть совпадение.
Ребенок, который знает процесс и таблицы для сложения, может начать выполнять сложение для этой группы. Он может все еще работать над изучением таблиц для других операций, и они не будут использоваться, пока он не будет готов.Упражнения в группе для перехода к абстракции позволяют ребенку отказаться от использования материала по мере его готовности. Затем он может начать все больше и больше работать с символами на бумаге, не используя материал для поиска ответов. Шестая группа материалов, фракции, может работать параллельно с группой создания абстракций, и ранняя работа с фракциями может начаться даже раньше. Сенсорную работу с дробным материалом можно проводить параллельно с другими группами арифметики.Запись дробей и операции с дробями могут выполняться по мере того, как ребенок продвигается к переходу к абстракции.
Взрослый несет ответственность за окружающую среду и переживания ребенка в ней. Перед изучением важно провести косвенную подготовку опыта работы с числами. По мере того, как ребенок готов, необходимо внимательно подавать арифметические материалы. Монтессори подчеркнула, что маленькие дети получают огромное удовольствие от работы с числами. Поэтому важно, чтобы взрослый не привносил какой-либо негативный оттенок в арифметический опыт ребенка.Эти упражнения представлены с большим энтузиазмом. Их нужно бережно и четко давать ребенку. В этой работе директрисе также важно наблюдать за работой ребенка. На основании наблюдений руководитель узнает, понимает ли ребенок концепции или требуется дополнительная помощь. Как всегда, взрослый поощряет повторение и обеспечивает самостоятельную работу, которая приведет к мастерству.
Когда ребенок готов, усвоение происходит так же легко и естественно, как и в других областях знаний.Это воодушевляет и выводит ребенка на уровень уверенности и радости на другом культурном пути. Абстрактная природа человека не является абстракцией, если взрослый понимает развитие ребенка.
Поделитесь своим опытом с
Слушайте этот пост как подкаст:
Когда я работал с учениками-учителями над разработкой эффективных планов уроков, я всегда просил их пересмотреть фразу «Мы обсудим.”
Обсудим видео.
Обсудим рассказ.
Обсудим наши результаты.
Каждый раз, когда я видел это в плане урока, я добавлял пометку: «Какой формат вы будете использовать? Какие вопросы вы зададите? Как вы обеспечите участие всех студентов? » Я был почти уверен, что Мы обсудим на самом деле означало, что учитель будет говорить большую часть времени; Он задавал пару вопросов, например: «Так что ты думаешь о видео?» или «Какова была тема рассказа?» и несколько студентов ответили, что привело к чему-то, что выглядело как обсуждение, но в конечном итоге было просто беседой между учителем и горсткой студентов-экстравертов; классический пример обучения «рыбий глаз».
Проблема была не в них; в большинстве классов, где они сидели как ученики, именно так и выглядела классная дискуссия. Других «форматов» они не знали. Я сам был знаком лишь с некоторыми из них. Но когда недавно учителя начали связываться со мной с просьбой составить более полный список, я понял, что пора провести серьезное исследование.
Итак, вот они: 15 форматов для структурирования обсуждения в классе , чтобы сделать его более увлекательным, организованным, более справедливым и более сложным с академической точки зрения.Если вы изо всех сил пытались найти эффективные способы развития навыков речи и слушания учащихся, это ваш счастливый день.
Я разделил стратегии на три группы. Первый пакет содержит стратегий более высокой подготовки , форматы, которые требуют от учителей заранее планировать или собирать материалы. Затем идут стратегии с низкой подготовкой , которые можно использовать на лету, когда у вас есть несколько дополнительных минут или вы просто хотите, чтобы ваши ученики стали более активными.Обратите внимание, что это не строгие категории; безусловно, можно упростить или добавить больше мяса к любой из этих структур и при этом заставить их работать. Последняя группа – это текущих стратегий . Это небольшие техники, которые можно интегрировать с другими учебными стратегиями, и они не являются самостоятельными. Для каждой стратегии вы найдете список других названий, которые она иногда использует, описание ее базовой структуры и объяснение существующих вариаций, если таковые имеются. Чтобы увидеть каждую стратегию в действии, щелкните ее название, и откроется новое окно с видео, демонстрирующим ее.
Наслаждайтесь!
Галерея Walk>или чат-станции
Базовая структура: Станции или плакаты устанавливаются вокруг класса, на стенах или на столах. Небольшие группы студентов вместе путешествуют от станции к станции, выполняя какое-то задание или отвечая на подсказку, что приведет к разговору.
Варианты: Некоторые прогулки по галерее соответствуют термину галерея , когда группы студентов создают информативные плакаты, затем выступают в качестве гидов или доцентов, давая другим студентам краткую презентацию своего плаката и проводя вопросы и ответы по этому поводу.В классе старшей школы Старр Сакштейн ее станции состояли из видеоуроков, созданных самими учениками. До того, как я узнал термин «Прогулка по галерее», я поделился стратегией, похожей на него, под названием «Станции чата», где учитель готовит подсказки для обсуждения или задачи, связанные с контентом, и размещает их по комнате, чтобы ученики могли посещать их небольшими группами.
Философские стулья>a.k.a. Континуум значений, принудительные дебаты, физический барометр, тот или иной
Базовая структура: Утверждение с двумя возможными ответами – согласен или не согласен – зачитывается вслух.В зависимости от того, согласны они или не согласны с этим утверждением, студенты переходят в одну сторону комнаты или в другую. С этого места студенты по очереди отстаивают свои позиции.
Варианты: Часто дебаты на философских кафедрах основываются на тексте или группе текстов, которые студенты прочитали заранее; Студенты должны приводить текстовые свидетельства в поддержку своих утверждений и обычно держат тексты в руках во время обсуждения. Некоторые учителя устанавливают одно горячее сиденье, чтобы представлять каждую сторону, и ученики должны сидеть на сиденье по очереди.В менее формальных вариантах (которые требуют меньшей подготовки) учитель может просто зачитывать провокационные утверждения, с которыми ученики могут не согласиться, и дебаты могут происходить спонтанно без текста, на который можно сослаться (в моем классе я называю этот вариант тем или другим сообщением о ледоколах ). Учителя также могут предложить целый ряд вариантов, начиная от «Полностью согласен» с одной стороны комнаты до «Совершенно не согласен» с другой, и предлагать учащимся расположить себя в этом континууме в зависимости от силы их взглядов. убеждения.
Базовая структура: Студенты делятся на 4 группы. Три из этих групп назначены для представления определенных точек зрения. Члены четвертой группы называются «провокаторами», которым поручено следить за тем, чтобы дискуссия продолжалась и оставалась сложной. По одному человеку из каждой группы («выступающий») сидит за столом напротив выступающих из других групп, поэтому они образуют квадрат в центре комнаты. За каждым выступающим сидят остальные члены группы: двое сразу за говорящим, затем трое за ними и так далее, образуя своего рода треугольник.Сверху это будет похоже на вертушку. Четыре докладчика представляют и обсуждают вопросы, которые они заранее подготовили (эта подготовка проводится с их группами). По прошествии некоторого времени новые ученики переходят с мест за спикером на центральные места и продолжают разговор.
Варианты: Когда учительница английского языка в средней школе Сара Браун Весслинг представила эту стратегию в показанном видео (нажмите «Обсуждение вертушки» выше), она использовала ее как средство для разговора о литературе, где каждая группа представляла своего автора плюс одну провокаторскую группу. .Но в комментариях, которые следуют за видео, Весслинг добавляет, что она также использует стратегию в отношении научной литературы, когда студенты представляют авторов различных текстов научной литературы или им поручают взглянуть на проблему с разных точек зрения.
Сократический семинар>он же Сократовские круги
Базовая структура: Учащиеся готовятся, читая текст или группу текстов и записывая некоторые вопросы для обсуждения более высокого порядка по тексту.В день семинара студенты садятся в круг, и преподаватель или ведущий обсуждения студентов задает вводный открытый вопрос. После этого студенты продолжают беседу, побуждая друг друга подтвердить свои утверждения текстовыми доказательствами. Нет особого порядка в том, как студенты говорят, но их поощряют уважительно делить слово с другими. Обсуждение должно происходить естественно, и учащимся не нужно поднимать руки, чтобы говорить. В этом обзоре Сократического семинара с веб-сайта «Встреча с историей и самим собой» представлен список соответствующих вопросов, а также дополнительная информация о том, как подготовиться к семинару.
Варианты: Если ученики являются новичками, учитель может написать вопросы для обсуждения, или создание вопроса может быть совместным усилием. Для больших классов учителям может потребоваться организовать семинары в форме аквариума, разделив студентов на один внутренний круг, который будет участвовать в обсуждении, и один внешний круг, который молча наблюдает, делает заметки и может в конечном итоге поменяться местами с те, кто находится во внутреннем кругу, иногда все сразу, а иногда «подключаясь», когда их охватывает побуждение.
, также известное как Affinity Diagramming
Базовая структура: Задайте студентам широкий вопрос или задачу, которая может привести к появлению множества различных идей, например: «Каковы были последствия Великой депрессии?» или «Какие литературные произведения следует читать каждому?» Предложите учащимся генерировать ответы, записывая идеи на стикерах (одна идея на заметку) и размещая их в произвольном порядке на стене, доске или диаграмме.Когда будет создано множество идей, попросите учащихся начать группировать их по аналогичным категориям, затем обозначить категории и обсудить, почему идеи вписываются в них, как категории соотносятся друг с другом и т. Д.
Варианты: Некоторые учителя заставляют учеников выполнять большую часть этого упражнения – записывать свои идеи и распределять их по категориям – без сначала говорить. В других вариантах участников просят повторно объединить идеи в новые, разные категории после первого раунда организации.Часто это упражнение служит хорошим упражнением перед написанием, после которого студенты напишут какой-то анализ или позиционный документ.
или Скоростное Свидание
Базовая структура: Учащиеся формируют два круга, один внутренний круг и один внешний круг. Каждый студент внутри находится в паре со студентом снаружи; они смотрят друг на друга. Учитель задает вопрос всей группе, и пары обсуждают свои ответы друг с другом.Затем учитель дает ученикам знак по очереди: ученики на внешнем круге перемещаются на одно деление вправо, чтобы они стояли перед новым человеком (или сидели, как на видео). Теперь учитель задает новый вопрос, и процесс повторяется.
Варианты: Вместо двух кругов ученики могут также образовать две прямые линии, обращенные друг к другу. Вместо того, чтобы «вращаться» для смены партнеров, одна линия просто скользит по одному месту, и оставшийся человек в конце движется к началу линии.Некоторые учителя используют эту стратегию, чтобы ученики преподали один фрагмент материала своим сокурсникам, делая это не столько стратегией обсуждения, сколько форматом взаимного обучения. Фактически, многие из этих протоколов можно использовать и для взаимного обучения.
Базовая структура: Еще одна замечательная идея Сары Браун Весслинг – это стратегия обсуждения в малых группах, которая дает учащимся возможность познакомиться с большим количеством идей их сверстников и предотвращает застой, который может произойти, когда в группе нет правильная химия.Учащиеся делятся на несколько групп по 4-6 человек в каждой, и им дается вопрос для обсуждения. По прошествии достаточного времени для развития обсуждения один или два студента из каждой группы переходят в другую группу, в то время как другие члены группы остаются на своих местах. Попав в новую группу, они обсудят другой, но связанный вопрос, а также могут поделиться некоторыми ключевыми моментами из беседы в последней группе. Для следующей смены могут быть выбраны ученики, которые не менялись раньше, в результате чего группы будут постоянно развиваться.
Базовая конструкция: Два ученика сидят лицом друг к другу в центре комнаты; остальные студенты садятся вокруг них. Два центральных ученика беседуют на заранее заданную тему и часто используют определенные навыки, которые практикует класс (например, задают уточняющие вопросы, перефразируют или развивают точку зрения другого человека). Студенты со стороны наблюдают, делают заметки или выполняют какое-либо другое задание, связанное с дискуссией, назначенное учителем.
Варианты: Один из вариантов этой стратегии позволяет ученикам из внешнего круга поменяться местами с теми, кто находится в аквариуме, проводя своего рода обсуждение в стиле эстафеты, или они могут периодически «тренировать» говорящих в аквариуме со стороны. Учителя также могут выбрать, чтобы ученики из внешнего круга оценивали беседу участников с помощью критериев, а затем оставляли отзывы о том, что они увидели, в ходе подведения итогов, как указано в представленном видео.
Базовая структура: Один ученик берет на себя роль книжного персонажа, значимого исторического персонажа или концепта (например, торнадо, животного или Титаник ).Сидя перед остальным классом, ученик отвечает на вопросы одноклассников, сохраняя при этом характер в этой роли.
Варианты: Предоставьте большему количеству студентов возможность быть в центре внимания, увеличивая при этом участие всех за счет того, что учащиеся проводят горячие дискуссии в небольших группах, где один человек в группе выступает в роли «персонажа», а трое или четверо других задают им вопросы . В другом варианте несколько учеников могут сформировать группу из разных персонажей, вместе отвечать на вопросы класса и взаимодействовать друг с другом, как гости в телевизионном ток-шоу.
a.k.a. Обсуждение пирамиды
Базовая структура: Учащиеся начинают в парах, отвечая на вопросы обсуждения только с одним партнером. После того, как каждый человек поделится своими идеями, пара присоединяется к другой паре, создавая группу из четырех человек. Пары делятся своими идеями с парой, к которой они только что присоединились. Затем группы из четырех человек объединяются в группы по восемь человек и так далее, пока весь класс не объединится в одно большое обсуждение.
Варианты: Эту структуру можно просто использовать для обмена идеями по теме, или от студентов может потребоваться достижение консенсуса каждый раз, когда они присоединяются к новой группе.
В то время как другие форматы в этом списке имеют отличную форму – конкретных действий , которые вы выполняете со студентами, – стратегии в этом разделе больше похожи на плагины, рабочие обсуждения в других учебных мероприятиях и улучшение качества и охвата существующих разговоров.
Одним из ограничений обсуждения является то, что насыщенные личные беседы могут происходить только тогда, когда доступны все стороны, поэтому мы ограничены временем, которое у нас есть в классе. С таким инструментом, как Voxer, эти ограничения исчезают. Подобно частному голосовому почтовому ящику, который вы настраиваете только для одного человека или группы (но ТАКЖЕ намного проще), Voxer позволяет пользователям общаться в любое время, наиболее удобное для каждого участника. Таким образом, группа из четырех учеников может «обсуждать» тему с 15:00 до отхода ко сну – асинхронно – каждый участник вносит свой вклад всякий раз, когда у них есть момент, и если учитель становится частью группы, она может слушать, предлагать отзывы или вносить свой вклад собственные точки для обсуждения.Voxer также бесценен для совместной работы над проектами и для индивидуальных бесед со студентами, родителями и вашими коллегами. Как и многим другим педагогам, Питеру ДеВитту потребовалось время, чтобы по-настоящему понять потенциал Voxer, но в этой статье EdWeek он объясняет, что его перевернуло.
Обратный канал – это диалог, который происходит одновременно с другим действием. Впервые я увидел обратный канал в действии во время моей первой неконференции: в то время как те из нас, кто был в аудитории, слушали выступающих и смотрели несколько коротких видеоклипов, рядом с главным экраном находился отдельный экран, проецирующий что-то под названием TodaysMeet (обновление: TodaysMeet закрылся.Используйте YoTeach! Вместо этого.) Это было очень похоже на те чаты прошлого, в основном пустой экран, на котором люди вносили несколько строк текста, строки складывались одна за другой, никаких других наворотов. Любой в комнате мог участвовать в этом разговоре на своем телефоне, ноутбуке или планшете, задавая вопросы, предлагая комментарии и делясь ссылками на связанные ресурсы, не прерывая поток презентаций. Этот вид инструментов позволяет вести совершенно бесшумную дискуссию, не требующую сверхбыстрого темпа, и дает студентам, которые могут неохотно высказываться или которые обрабатывают свои мысли медленнее, возможность внести свой вклад в полной мере.Для более глубокого обсуждения того, как можно использовать этот вид инструментов, прочтите этот вдумчивый обзор использования дискуссий по обратному каналу в классе от Edutopia’s Beth Holland.
a.k.a. Accountable Talk
Разговорные движения – это фреймы предложений, которые мы предоставляем нашим ученикам, которые помогают им выражать идеи и взаимодействовать друг с другом уважительным, академически приемлемым способом. От детского сада до колледжа учащиеся могут извлечь пользу из подробного обучения навыкам резюмирования аргументов другого человека, прежде чем представлять альтернативную точку зрения, задавать уточняющие вопросы и выражать согласие или частичное согласие с позицией другого участника.Ход обсуждения может быть включен в любой из других форматов обсуждения, перечисленных здесь.
Whole Brain Teaching – это комплекс методов обучения и управления классом, популярность которых выросла за последние 10 лет. Одним из основополагающих методов WBT является Teach-OK , стратегия взаимного обучения, которая начинается с того, что учитель тратит несколько минут на представление концепции классу. Далее учитель говорит: Учите! , класс отвечает Хорошо! , и пары студентов по очереди заново учат друг друга этой концепции.Это немного похоже на обмен мыслями в паре, но он более быстрый, он больше ориентирован на повторное обучение, чем на общий обмен мнениями, и учащимся рекомендуется использовать жесты, чтобы оживить обсуждение. Хотя WBT наиболее популярен в начальных школах, на этом видео показано, как создатель WBT, Крис Биффл, довольно успешно использует его со студентами колледжей. Я также использовал Teach-OK со студентами колледжа, и большинство моих студентов сказали, что они были рады изменениям от сидячей и слушающей беседы, к которой они привыкли в классных комнатах колледжа.
Старое, но полезное средство «Think-Pair-Share» можно использовать в любое время, когда вы хотите добавить интерактивности в урок: просто попросите учащихся подумать над своим ответом на вопрос, сформируйте пару с другим человеком, обсудите их ответ, затем делятся с большей группой. Поскольку я считаю, что у этой стратегии так много применений и она может быть намного мощнее, чем мы думаем, я посвятил целый пост теме «Думай-пара-делись»; все, что вам нужно знать об этом, прямо здесь.
С момента написания этого поста я узнал еще о двух стратегиях обсуждения, которые учителя считают невероятно эффективными и мощными для побуждения учащихся к разговору, особенно о книгах и других текстах:
В этом протоколе учащиеся придумывают свои собственные мыслей , удерживая вопросов и богоявлений из заданного чтения. Учителя, которые использовали этот метод, говорят, что он породил одни из самых насыщенных разговоров, которые они когда-либо слышали от учеников!
Эта стратегия позволяет учащимся беседовать один на один, побуждая их лучше выучить имена друг друга и записывать то, о чем они говорили.Отлично подходит для классов, где вы хотите оценить для обсуждения и помочь учащимся привыкнуть друг к другу.
Так что еще у вас есть? Я хотел бы думать, что это довольно полный список, но я уверен, что есть и другие стратегии. Если вы используете стратегию обсуждения, не упомянутую здесь, поделитесь ею ниже.
Согласно прогнозам рабочей силы, Техас будет иметь второй по величине процент будущих рабочих мест в области STEM в стране.
Чтобы наши студенты были подготовлены к этой будущей рабочей силе, Образовательное агентство Техаса разработало STEM Framework для округов, чтобы использовать руководство по программированию STEM, и работает над созданием Texas EcosySTEM – совместными усилиями, объединяющими различные заинтересованные стороны для работать над достижением общей цели – расширить доступ молодых людей к богатой STEM учебной среде, чтобы они были вовлечены и овладели необходимыми навыками для успеха в карьере STEM.
STEM (наука, технология, инженерия и математика) – это метод практического преподавания и обучения, при котором студенты учатся применять академический контент, творчески решая реальные проблемы с инновационным мышлением, основанным на дизайне, чтобы подготовить студентов к будущему. карьерные возможности.
Структура STEM Education Framework предоставляет определение, теорию действий и цели для внедрения STEM-образования в Техасе.Структура включает стратегии для достижения успеха, дифференцированные модели реализации STEM , основанные на исследованиях методы обучения и высококачественные индикаторы STEM . Заинтересованные стороны смогут использовать эту структуру в качестве руководства при создании своих индивидуальных программ STEM. Дополнительные ресурсы предоставляются в наборе инструментов STEM и должны использоваться вместе со структурой STEM.
Техас
EcosySTEM
Texas EcosySTEM объединяет сообщества, бизнес, школы и семьи.
Бенджамин Браун, главный редактор, Университет Кентукки; Присцилла Бремзер, редактор, Колледж Миддлбери; Арт Дюваль, редактор, Техасский университет в Эль-Пасо; Элиза Локвуд, редактор, штат Орегон; и Дайана Уайт, редактор, Колорадский университет в Денвере.
Примечание редактора. Это первая статья из серии, посвященной активному обучению на курсах математики.Остальные статьи этой серии можно найти здесь.
«… если бы анализируемые здесь эксперименты проводились как рандомизированные контролируемые испытания медицинских вмешательств, они могли быть остановлены ради преимущества».
Свидетельства, подтверждающие положительный эффект активных методов обучения на курсах математики и естествознания после среднего образования, настолько убедительны, что Фриман и другие сделали заявление выше в своей статье Слушаний Национальной академии наук (PNAS) за 2014 год. Активное обучение увеличивает количество учащихся. Успехи в области естественных наук, инженерии и математики .Тем не менее, принятие преподавателями стратегий активного обучения стало узким местом в продвижении обучения математике в послесреднем учебном заведении. Вдохновленные вышеупомянутой статьей PNAS, знаменательным метаанализом 225 исследований о положительных эффектах активного обучения, мы посвятим серию постов теме активного обучения на курсах математики.
Непосредственная проблема, которая возникает при обсуждении активного обучения математике, заключается в том, что фраза «активное обучение» не имеет четкого определения.Преподаватели математики интерпретируют эту фразу в широком диапазоне: от полностью неструктурированной работы в малых группах до периодического использования студентами системы реагирования (например, кликера) на больших лекциях. В этой статье мы обсуждаем несколько описаний из литературы, в том числе то, что мы будем считать нашим рабочим пониманием в этой серии сообщений, обсуждаем важные соображения при адаптации таких методов и выделяем некоторые важные аспекты статьи PNAS.
Что такое активное обучение?
Основной принцип активного обучения заключается в том, что предоставление учащимся возможности активно взаимодействовать с контентом во время занятий приводит к положительным результатам обучения.В математике фразы «активное обучение» и «обучение на основе запроса» (IBL) тесно связаны, хотя мнения расходятся относительно того, в какой степени они связаны или пересекаются. Вот некоторые особенно содержательные описания активного обучения и IBL из литературы.
Активное обучение обычно определяется как любой метод обучения, который вовлекает учащихся в процесс обучения. Короче говоря, активное обучение требует от учащихся осмысленной учебной деятельности и размышлений о том, что они делают.Хотя это определение может включать традиционные действия, такие как домашнее задание, на практике активное обучение относится к действиям, которые вводятся в класс. Основными элементами активного обучения являются активность учащихся и участие в учебном процессе. Активное обучение часто противопоставляется традиционной лекции, где студенты пассивно получают информацию от преподавателя.
– Работает ли активное обучение? Обзор исследований, Майкл Принс, J. Engr. Образование, 93 (3), 223-231, 2004В контексте математики подходы IBL вовлекают студентов в исследование математических проблем, выдвижение и проверку гипотез, разработку доказательств или решений и объяснение своих идей.По мере того как учащиеся изучают новые концепции посредством аргументации, они также начинают рассматривать математику как творческое человеческое усилие, в которое они могут внести свой вклад. В соответствии с текущими социально-конструктивистскими взглядами на обучение, методы IBL делают упор на построение индивидуальных знаний, поддерживаемых социальным взаимодействием сверстников.
– Оценка долгосрочных эффектов обучения на основе запросов: пример из математического колледжа, Марина Коган и Сандра Л. Лаурсен, Innov High Educ (2014) 39: 183–199Подход к обучению, ориентированный на студента, уделяет меньше внимания передаче фактической информации от преподавателя и соответствует сдвигу в моделях обучения от получения информации (середина 1900-х годов) к построению знаний (конец 1900-х годов).Этот подход включает
- больше времени потрачено на привлечение учащихся к активному обучению во время занятий;
- частое формирующее оценивание для предоставления студентам и преподавателям обратной связи об уровнях концептуального понимания студентов; и
- в некоторых случаях – внимание к метакогнитивным стратегиям студентов, когда они стремятся усвоить материал курса.
– Исследования в области образования на основе дисциплин: понимание и улучшение обучения в области естественных наук и инженерии, С.Р. Сингер, Н. Р. Нильсен и Х. А. Швайнгрубер (редакторы), Национальный исследовательский совет, The National Academies Press, 2012 г.
Авторы PNAS не пытаются дать определение активного обучения, а вместо этого рассматривают в своем анализе «документы, представляющие широкий спектр активных учебных действий, включая неопределенно определенные« совместные групповые действия в классе », рабочие листы в классе, кликеры, тематические задания. обучение (PBL) и студийные классы с интенсивностью от 10% до 100% учебного времени.”
В соответствии с общей картиной, нарисованной только что приведенными описаниями, наш подход состоит в том, чтобы использовать фразу «активное обучение» для обозначения любой стратегии в классе, которая предоставляет учащимся возможность напрямую взаимодействовать с контентом во время урока, индивидуально или совместно со сверстниками. . Избегание единичного определения активного обучения увеличивает риск того, что преподаватели, администраторы и другие заинтересованные стороны «заговорят друг с другом». Однако, когда мы обсудим дальше, мы считаем важным подчеркнуть разнообразие подходов к повышению вовлеченности учащихся и подчеркнуть необходимость ясного языка при обсуждении различных условий в классе.
Важно отметить, что исследователи математического образования десятилетиями изучали влияние активных методов обучения на учащихся математики, особенно на уровне K-12. См. Статью Энтони «Активное обучение в конструктивистской среде», приведенную в справочной литературе, в качестве примера из середины 1990-х годов, который содержит хорошее изложение различных интерпретаций «активного обучения». В этой статье мы хотим подчеркнуть, что эффекты активного обучения выходят за рамки дисциплин и что педагогические методы, ориентированные на учащихся, в настоящее время являются предметом широкого обсуждения в различных науках.
Важные замечания
При реализации или поддержке стратегий активного обучения необходимо учитывать следующие три фундаментальных вопроса. Эти проблемы усложняют нашу способность вести последовательный национальный диалог по вопросам преподавания математики после окончания средней школы и являются частым источником путаницы среди различных заинтересованных сторон в сфере высшего образования на национальном, региональном и местном уровнях.
Классная среда : Часто в результате факторов, не зависящих от отдельных преподавателей (или даже кафедр), учебная среда сильно различается от учреждения к учреждению.«Типичный» размер класса может составлять от пятнадцати до шестисот с различными уровнями поддержки при выставлении оценок. В среде, где курсы часто преподаются гибридным образом, что означает сочетание времени личного общения и онлайн-модулей, время контакта структурировано иначе, чем в традиционной структуре классных встреч продолжительностью от трех до пяти часов в неделю. Все эти и другие соображения влияют на выбор активных стратегий обучения, доступных для курса или учебного заведения, как через ограничения на тип доступного прямого взаимодействия, так и за счет обогащения типа доступного взаимодействия, основанного на технологиях.
Преподавательская среда : На математическом факультете невероятно разнообразны условия трудоустройства. В отличие от общепринятых стереотипов преподавательского состава с постоянным сроком пребывания в научно-исследовательских учреждениях, учителя математики с высшим образованием включают как преподавателей с длительным сроком службы, так и преподавателей с неполной или дополнительной занятостью, с постоянным и непостоянным сроком пребывания, с множеством различных требований к административным должностям и различными уровни поддержки педагогических инноваций. Такой диапазон профилей преподавателей создает столь же широкий спектр потребностей в отношении того, как осуществляется педагогическая подготовка и наставничество, и поднимает такие вопросы, как: сколько времени на подготовку доступно преподавателям? Рассматриваемые курсы преподаются опытными преподавателями или теми, кто преподает впервые или во второй раз? Зависит ли оценка работы преподавателей и / или продление работы от неизменно удовлетворительных оценок студентов? Имело ли данное учреждение какое-либо историческое внимание в отношении подготовки преподавателей для новых сотрудников?
Цели курса / студента : Результаты обучения по курсам и сопровождающие их ожидания студентов сильно различаются между преподавателями, курсами и учреждениями.Например, курсы, которые в первую очередь служат частью общего образования или компонента количественной грамотности, обычно имеют принципиально другие цели и ожидания для студентов, чем курсы, которые в первую очередь служат для перехода к специальностям STEM. У отдельных преподавателей часто есть различные модели обучения студентов, начиная с точки зрения преподавания / обучения как передачи знаний и фактов, и заканчивая точкой зрения на развитие у студентов способности решать новые проблемы и / или бороться с новыми идеями и развивать их понимание.Многие преподаватели имеют разные ожидания от студентов в отношении уровня познавательных задач, которые они должны выполнять, и часто эти ожидания неявно связаны с тем, как они структурируют свой курс, а не напрямую сообщаются студентам и сверстникам.
Аспекты, связанные с эффективностью и государственной политикой
Несколько дополнительных вопросов непосредственно затронуты в статье PNAS. Сила их результатов привела к тому, что авторы PNAS предположили, что «преподаватели STEM могут начать сомневаться в продолжении использования традиционных лекций в повседневной практике.Сказав это, они отмечают, что на сегодняшний день активное обучение осуществляется в основном преподавателями, заинтересованными в экспериментах с новыми педагогическими стратегиями. Что не ясно, так это то, будут ли наблюдавшиеся до сих пор высокие уровни эффективности методов активного обучения, если они будут реализованы почти всеми математическими факультетами. Мы считаем, что это ключевой вопрос, особенно если использование активных стратегий обучения предписано без надежной системы поддержки / вознаграждения и полного признания того, что переход к новым педагогическим методам никогда не бывает плавным и легким процессом.Также было бы целесообразно сравнить эффективность различных методов активного обучения математике по аналогии с работой Принса, приведенной в справочных материалах.
Наконец, авторы PNAS отмечают, что усиление обучения студентов в результате активных методов обучения приведет к увеличению успеваемости студентов, что приведет к меньшему количеству повторений курсов математики и естествознания. Это может значительно сэкономить студентам время и плату за обучение. Также было обнаружено, что активное обучение оказывает непропорционально благоприятное влияние на членов меньшинств в областях STEM, показывая, что фундаментальные проблемы, касающиеся справедливости, уже под рукой.Помимо этических и моральных вопросов, которые эти вопросы поднимают перед сообществом преподавателей математики, эти качества активного обучения привлекают внимание людей, занимающихся защитой интересов студентов, государственной политикой, финансированием грантов и стипендий и смежными областями. Мы считаем, что следует приветствовать усиление поддержки и внимания к успеху наших студентов со стороны людей, не входящих в математическое преподавательское сообщество, и что всестороннее обсуждение того, как лучше всего помочь студентам изучать математику на глубоком уровне, приведет к более богатому обучению и опыту обучения. для всех.
A Предварительный просмотр
В оставшихся статьях этой серии мы исследуем, как разные задачи несут различные уровни когнитивных требований со стороны учащихся, и предоставим примеры активных методов обучения, которые обращаются к этим уровням в различных учебных и классных средах. Мы поделимся своим личным опытом как учителя, которые экспериментировали с педагогическими стратегиями, и рассмотрим сложный вопрос поиска баланса между предоставлением студентам времени для изучения и предоставлением студентам прямой обратной связи и инструкций.Наконец, мы обсудим возможные точки противоречия между научным обучением математике исследовательского уровня и научным развитием педагогических стратегий и методов.
Список литературы
Гленда Энтони
Активное обучение в конструктивистских рамках
Образовательные исследования по математике, Vol. 31, No. 4 (декабрь 1996 г.), стр. 349-369
Скотт Фриман, Сара Л. Эдди, Майлз МакДонаф, Мишель К. Смит, Ннадози Окороафор, Ханна Джордт и Мэри Пэт Вендерот
Активное обучение повышает успеваемость учащихся в области естественных наук, инженерии и математики
Proc.Natl. Акад. Sci. США 2014 111 (23) 8410-8415
Марина Коган и Сандра Л. Лаурсен
Оценка долгосрочных эффектов обучения на основе запросов: пример из математического колледжа
Innov High Educ (2014) 39: 183–199
Майкл Принс
Работает ли активное обучение? Обзор исследований
Engr. Образование, 93 (3), 223-231, 2004
Р. Сингер, Н. Р. Нильсен и Х. А. Швайнгрубер (ред.)
Исследования в области дисциплинарного образования: понимание и совершенствование обучения в области бакалавриата и инженерии
Национальный исследовательский совет, The National Academies Press, 2012
50 7 /
.Сью получает базовый оклад в размере 90 долларов в неделю плюс 12% комиссионных со всех продаж. На этой неделе у Сью было продано 3000 долларов. Сколько она всего заработала?
1. C: Уравнение x -0,10 x -0,15 ( x -0,10 x ) = 306, может использоваться для решения проблемы. Решение относительно x дает 0,90 x – 0,15 x + 0,015 x = 306, где x = 400. Таким образом, первоначальная цена составляла 400 долларов.
2. B: Уравнение можно решить, сначала распределив y по выражению, x – 1, в левой части уравнения. Это дает: x y – y = Z .Добавление y к обеим сторонам уравнения дает: x y = Z + y . Наконец, деление обеих частей уравнения на y дает: x = ( Z + y ) / y или x = Z / y +1.
3. B: Эта задача иллюстрирует свойство распределения умножения над сложением. Распределяемый коэффициент не может измениться.
4. D: Размер третьего угла треугольника равен 180 ° – (15 ° + 85 °) или 80 °.
5. C: Поскольку в 2 фунтах 32 унции (16 унций = 1 фунт), можно записать следующую пропорцию: 5/140 = 32/ x . Решение x дает x = 896. Таким образом, в 2 фунтах мяса содержится 896 граммов.
6. E: Наибольшее количество детей, посещающих уроки плавания в течение одного года, составляло 500 в 1995 году.
7. C: Единственное уменьшение количества детей, посещающих уроки плавания, произошло с 1992 по 1993 год. , с уменьшением на 200 детей.
8. B: Среднее значение можно записать как (200 + 250 + 400 + 200 + 300 + 500) / 6, что составляет примерно 308.
9. A: Перемещение десятичной запятой на два разряда слева дает 0,0593.
10. C: Для решения задачи можно использовать следующую пропорцию: 1/20 = 6,2 / x . Решение относительно x дает x = 124, так что на самом деле между двумя городами есть 124 мили.
11. A: На правильном графике должен быть показан отрезок прямой между 1 и 4, включая точки 1 и 4.
12. D: Объем олова 972 дюйма. Объем каждой выдумки – 27 дюймов. 972 ÷ 27 = 36.
13. B: Для решения задачи может использоваться следующая система уравнений: ( с = 2 b @ с – b = 15). Подставив во втором уравнении 2 b вместо s , получим: 2 b – b = 15, где b = 15. Младшему брату 15 лет.
14. C: Умножение числителя и знаменателя данной дроби на 5 дает дробь 25/30, что эквивалентно.
15. B: После преобразования футов в ярды размеры можно переписать как 4 ярда на 6 2/3 ярда. Таким образом, площадь этажа составляет 26 2/3 ярда. Умножение этой площади на стоимость квадратного ярда дает выражение 26 2/3? 8,91, что равно 237,6. Таким образом, стоимость составляет 237,60 долларов.
16. C: Следующее уравнение может быть решено для x : 6000 = 1/2 x .Решение относительно x дает x = 12000. Таким образом, сумма розыгрыша призов составила 12 000 долларов.
17. D: Расстояние можно определить, записав и решив следующее уравнение для c : 50 2 +120 2 = c 2 . c = 130, следовательно, расстояние составляет 130 футов.
18. D: Средняя стоимость поездки туда и обратно – это общее пройденное расстояние, деленное на общее время в пути.Пройденное расстояние = 2x. Время прохождения = x / 10 + x / 8 = 4x / 40 + 5x / 40 = 9x / 40. Средняя скорость = 2xx9x / 40 = (2xx40) / 9x = 80/9 = приблизительно 8,9 миль в час.
19. E: Длина равна 216 дюймам. Ширина равна 36 дюймам. Таким образом, длина может быть покрыта 18 12-дюймовыми камнями, а ширина может быть покрыта 3 12-дюймовыми камнями. Всего на один слой нужно 42 камня, а на два – 84 камня. Умножение 84 на 2,32 доллара дает 194,88. Таким образом, общая стоимость составляет 194,88 доллара.
20. E: Уравнение можно решить для x , сначала вычтя 6 x из обеих частей уравнения. Это дает -3 x = -15, где x = 5. Подстановка 5 вместо x во второе выражение дает 5 + 8, что равно 13.
21. B: Есть 1000 миллилитров. в 1 л.
22. D: Задачу можно смоделировать с помощью уравнения, 6.50 = 5.00 + 0.50 x , где x представляет количество пассажиров.Решение для x дает x = 3. Таким образом, было 3 пассажира плюс 1 водитель, всего в автомобиле было 4 человека.
23. C: Эту проблему можно представить как 1/9 . 9, что равняется 1.
24. D: Если взять по три каждого цвета, то у него будет по одному каждого цвета. Таким образом, ему нужно вынуть всего 9 шариков.
25. E: 0,20% = 0,002 и 1/500 = 0,002.
26. D: Увеличение от срока к сроку вдвое превышает увеличение по сравнению с двумя предыдущими сроками.Таким образом, увеличение с 19 до пропущенного члена будет 20, или вдвое больше, чем 10. Таким образом, пропущенный член равен 19 + 20, или 39.
27. C: Решение может быть смоделировано следующим образом: выражение 0,25 (2490). Таким образом, в ее бюджете в апреле 2001 года было предусмотрено 622,50 доллара на жилье.
28. E: Среднее значение может быть представлено как (0,10 (2578) +0,10 (2432) +0,10 (2668) +0,10 (2490) +0,10 ( 2622) +0.10 (2555)) / 6, что упрощается как (257.80 + 243.20 + 266.80 + 249.00 + 262.20 + 255.50) / 6 или 255.75. Средняя сумма бюджета на одежду за первые шесть месяцев 2001 года составила 255,75 долларов.
29. A: Сэкономленную ею сумму можно представить выражением 0,25 (2622) – 0,20 (2622), что равно 131,10. Таким образом, она сэкономила 131,10 доллара.
30. B: Задачу можно смоделировать с помощью уравнения: 1/40 + 1/30 + 1/24 = 1/ t . Решение для t дает t = 10. Таким образом, работая вместе, они могут напечатать один и тот же документ за 10 минут.
31. D: Дробь 3/5 равна 0,6, что меньше 2/3.
32. C: Соотношение можно записать как 6/14, что сокращается до 3/7.
33. B: Заработанную ею сумму можно представить выражением 90 + 0,12 x , где x представляет собой сумму продаж. Замена 3000 на x дает 90 + 0,12 (3000), что равняется 450. Итак, на этой неделе она заработала 450 долларов.
34. A: Во-первых, измерение периметра может быть преобразовано в футы.Умножение 25 1/3 ярда на 3 дает эквивалент 76 футов. Таким образом, можно записать следующее уравнение: 76 = 2 (22) + 2 w , что упрощается до 76 = 44 + 2 w , где w = 16.