Формирование навыков устного счета у учащихся начальной школы
Математика является одним из важнейших предметов обучения детей с интеллектуальными нарушениями, и именно с ней они встречаются каждый день в своей жизни.
Поэтому главная общеобразовательная задача обучения математике – добиться овладения учащимися системой доступных математических знаний, умений и навыков, необходимых в повседневной жизни и в будущей профессии, так прочно, чтобы они стали достоянием учащихся на всю жизнь. Приобретение умений считать, устно и письменно вычислять, измерять, решать арифметические задачи, ориентироваться во времени и пространстве, распознавать геометрические фигуры позволит учащимся более успешно решать жизненно-практические задачи.
Но у обучающихся с нарушением интеллекта в процессе усвоения программного материала возникают определенные трудности в связи с особенностями и несовершенствами восприятия (узость, фрагментарность, нецеленаправленность и слабая активность), в том числе зрительного (зрительного анализа и синтеза) и слухового, нарушениями моторики и координации движений, чрезвычайно слабо развитыми способностью к обобщению математических отношений, действий и объектов, способностью к быстрой перестройке направленности мыслительного процесса, математической памятью (обобщенная память на математические отношения, методы решения задач), такими процессами логического мышления, как анализ, синтез, сравнение.
У детей с нарушением интеллекта наблюдается более простой вид обобщений – движение от частного к известному общему, подвести частный случай под общее правило. Способность к оперированию числовой и знаковой символикой детям даётся нелегко. Математическая память находится на низком уровне. Дети с большим трудом запоминают цифры, знаки, определения, формулировки, компоненты действий, общие схемы рассуждений, алгоритмы математических действий. Путаются в операциях «сложения» и «вычитания», «умножения» и «деления».
На низком уровне находится уровень развития гибкости мыслительных процессов. Им очень трудно переключаться от одной умственной операции к другой. Утомляемость этих детей повышена, поэтому нужен периодический отдых.
Учащиеся с нарушением интеллекта плохо ориентируются в новых условиях, не умеют найти наиболее рациональные пути решения поставленных задач, у них отсутствует понимание связи теории с практикой, нет уверенности в своих силах, а между тем по окончанию школы умственно отсталого школьника ждет работа в обществе, в быту, где часто возникает потребность в устном вычислении.
Все эти особенности математических знаний учащихся с нарушением интеллекта подтверждают практическую значимость упражнений в устном счете на уроках математики.
Они должны служить развитию и укреплению навыков устного счета, возбуждать в детях интерес к вычислениям, воспитывать сообразительность и находчивость, развивать внимание, укреплять память. Ведь все эти стороны личности у учащихся коррекционных школ развиты очень слабо. В ходе упражнений по устному счету хорошо организуется коллектив класса; укрепляются и расширяются познавательные интересы, обеспечивается усвоение нового материала. Устный счет также оказывает огромное влияние на продвижение умственно отсталых учащихся в общем развитии.
В задачи учителя, работающего с детьми с нарушением интеллекта, входит формирование у учащихся сознательных и прочных вычислительных навыков, преодоление инертности, а самое главное – помощь в социальной и трудовой адаптации.
Каждый учитель знает, как важно, чтобы урок с самого начала задался, и чтобы ученики были активны с первых минут урока.
А задания, подобранные с расчетом пробудить у учащихся интерес, подготовят детей к восприятию нового материала или к решению далее предложенных задач и упражнений.
Устный счет является неотъемлемой частью почти каждого урока математики. Устный счет может проводиться не обязательно в начале урока, но в середине, конце, в зависимости от целей устного счета на уроке.
Так как устные упражнения или устный счёт – это этап урока, то он имеет свои задачи:
1) воспроизводство и корректировка определённых ЗУН учащихся, необходимых для их самостоятельной деятельности на уроке или осознанного восприятия объяснения учителя;
2) контроль учителя за состоянием знаний учащихся;
3) мониторинг психологического состояния класса;
4) психологическая подготовка учащихся к восприятию нового материала.
Устные упражнения в коррекционной школе имеют ряд преимуществ:
1.
Дают возможность охватить большой объем материала за короткий промежуток времени.
2. Позволяют по реакции класса в тот или иной мере судить об усвоении материала, готовят к изучению нового, помогают выявить ошибки.
3. Если даются в начале урока, то дисциплинируют учащихся, помогают настроиться на работу.
4. Если предлагаются в середине или в конце урока, то служат переключением внимания, интересной, своеобразной разрядкой после напряжения и усталости, вызванной письмом или практической работой, при этом обеспечивается самостоятельность выполнения заданий.
5. Больше учащихся получают возможность ответить, проверить правильность решений.
6. Каждый ученик по мере своих возможностей может ответить на тот или иной вопрос или задание.
Устный счет тесно связан с темой и основной обучающей задачей урока. Однако в устный счет могут включаться и такие упражнения, которые ставят целью выработать беглость счета, закрепить те или иные вычислительные приемы.
Устный счет нередко ставит целью подготовить учащихся к восприятию новых знаний. Устный счет включает несколько форм упражнений и заданий: это могут быть устные арифметические и геометрические задачи, упражнения вычислительного характера, задания на закрепление нумерации, различение фигур, повторение их свойств и т.д. Длительность этого этапа урока не должна превышать 10-12 минут, т.к. устный счет требует от учащихся максимальной отдачи умственных сил. Устный счет, как правило, проходит в быстром темпе, происходит довольно частое переключение с одного вида деятельности на другой, с одной формы упражнений на другую. Как известно, такого рода переключения чрезвычайно полезны для развития мыслительных процессов, но трудны для обучающихся с нарушением интеллекта.
Упражнения для устного счета предъявляются как в устной, так и в письменной форме. Нередко вместо записи на доске учитель пользуется различными таблицами с краткой записью содержания задач, с записью чисел, арифметических знаков, выражений.
Задания для устного счета необходимо подбирать с учетом индивидуальных особенностей каждого ребенка. Это позволит вести фронтальную работу и включить в активную учебную деятельность всех учащихся класса.
При устном счете важно установить обратную связь между учителем и учащимися. С этой целью использую различные средства, например, сигнальные карточки, «светофор», использование табличек с цифрами, из которых ученики составляют числа ответов и т.д. После проведения устного счета подводится итог, учитель оценивает активность класса, правильность их ответов, успехи отдельных учеников.
Задания по устному счету строятся на числовом материале, который подбирается в соответствии с программой, с учетом математических способностей каждого класса и отдельного ученика. Для достижения правильности и беглости устных вычислений на каждом уроке математики отводится 5-10 минут для проведения упражнений в устных вычислениях.
Есть разные взгляды на методы подбора, цели и задачи устных упражнений.
Устные упражнения должны находиться в тесной связи с основной темой урока, подчиняться его целевой установке. Они должны дополнять ту часть урока, которой подчинены.
Устный счет может иметь целью:
-закрепление пройденного или нового материала;
-актуализация знаний учащихся с целью подготовки к восприятию нового материала;
-повторение пройденного материала.
Учитель определяет цели и задачи устного счета с учетом темы урока и психо-физических особенностей учащихся класса.
Для развития интереса у детей к устному счету учитель должен разнообразить виды упражнений. Целесообразно устным заданиям придавать занимательный характер, шире использовать дидактические игры математического содержания.
Правильное проведение устного счета немыслимо без настойчивой работы по развитию математической речи.
Необходимо требовать от учащихся склонение числительных, полных ответов, умения объяснять ход решения задачи или примера. Нужно чтобы учащиеся сознательно владели хотя бы минимумом пространственных представлений, понятиями о величине и форме предметов, о расстоянии между ними и т. п.
При обучении детей устному счету необходимо осуществлять индивидуальный подход к учащимся, т.к. один ученик считает быстро и правильно, другой считает быстро, но ошибается, третий считает верно, но медленно, четвертый медленно и допускает ошибки.
При планировании учитель должен учитывать, что основными целями данного этапа урока является:
достижение поставленных целей урока;
развитие вычислительных навыков;
развитие устной речи учащихся, приучение их к умению вести дискуссии;
расширение знаний учащихся об окружающем мире;
воспитание чувства товарищества и взаимовыручки; формирование навыков культурного поведения.
Кроме того, при проведении устного счета каждый учитель придерживается следующих требований:
упражнения для устного счета выбираются не случайно, а целенаправленно;
задания должны быть разнообразными;
тексты упражнений, чертежей и записей должны быть приготовлены заранее;
к устному счету должны привлекаться все ученики;
при проведении устного счета должны быть продуманы критерии оценки.
Для эффективного использования устных упражнений нужно правильно определить их место в системе формирования понятий и навыков.
Для проведения устного счета можно подобрать задания следующего характера.
Виды упражнений для устных вычислений:
Задания на тему «Нумерация»
Назвать пропущенные в числовом ряду числа:
16, …, 18, 19, …
Назвать число, которое стоит перед числами:
…, 15 …, 7 …, 18
Назвать число, которое следует за числами:
13, … 9, … 4, …
Назовите число, в котором:
-1 десяток, 5 единиц
-2 десятка , 0 единиц
2) Сравнение чисел и математических выражений
Эти упражнения имеют ряд вариантов.
Дан ряд чисел.
5, 9,2,10,17,3, 20
Назвать числа в порядке возрастания (убывания):
Могут быть даны два выражения, а надо установить, равны ли их значения, а если не равны, то какое из них больше или меньше.
Например: 10+7…10+5 или 2х8…3х3
Главная цель таких упражнений – способствовать усвоению теоретических знаний об арифметических действиях, их свойствах, о равенствах, о неравенствах и др. Также они помогают выработке вычислительных навыков.
3) Нахождение значений математических выражений
Предлагается в той или иной форме математическое выражение, требуется найти его значение. Эти упражнения имеют много вариантов. Можно предлагать числовые математические выражения и буквенные, при этом буквам придают числовые значения и находят числовое значение полученного выражения, например:
– найдите разность чисел 4 и 2
– найдите сумму чисел 5 и 5
Выражения могут предлагаться в разной словесной форме:
– из 10 минус 9; 10 минус 9;
– уменьшаемое 10, вычитаемое 9, найдите разность;
– найти разность чисел 10 и 9
– уменьшить 10 на 9 и т.
д.
Эти формулировки использует не только учитель, но и ученики.
Выражения можно давать и в форме таблицы:
Уменьшаемое | 120 | 104 | 133 | 144 |
Вычитаемое | 80 | 14 | 10 | 20 |
Разность | ? | ? | ? | ? |
На доске пишут несколько примеров. Ответ первого примера служит первым числом второго, ответ второго примера – первым числом третьего и т.д.
20 : 5 = ? х4 = ? : 2 = ? : 4 = ? х 10 = ? : 5 х 2 = 8
На доске записаны примеры:
20-5= 10+ 3= 5-1=
Учитель задает задания:
Найдите пример, в ответе которого 1 десяток и 5 единиц.
Число 10 увеличить на 3. Найдите пример с таким ответом.
Число, которое стоит между числами 3 и 5. Найдите пример с таким ответом.
.
Игра «Светофор»
Учитель предлагает учащимся решить примеры (на таблицу умножения, примеры на деление, на сложение, на вычитание). Один ученик отвечает, а остальные «сигналят» светофором (показывают карточку красного или зеленого цвета).
Основная цель использования упражнений на нахождение значений выражений – выработать у учащихся твердые вычислительные навыки.
Простые арифметические задачи
Они включаются в устный счет с целью выработки умений решать задачи.
Текстовые задачи
В парке растут 12 берез и 8 рябин. На сколько больше растет в парке берез, чем рябин?
Задачи в стихах
Книги свои он расставил на полки:
Девять книжек на одной
И восемь на другой.
Сколько на двух полках
Книжек у Егорки?
Занимательные задачи
Задания на развитие восприятия, пространственного воображения
Посчитайте, сколько линий.
Задания на развитие наблюдательности:
Учащимся предлагается запомнить несколько чисел:
1, 2, 5, 8, 4.
Далее числа закрываются и учащиеся вспоминают и называют числа в том же порядке. Можно попросить назвать в порядке возрастания (убывания).
Далее можно убрать (добавить) какое-то число и спросить: «Какое число потерялось (добавилось)?»
Задания на развитие внимания, памяти
Найдите, что лишнее?
Использую презентации:
Например, игра попади в ворота мячом, собери в лукошко и т.
п.
В целом, устный счет по внешним формам может быть разделен на 3 группы:
Счет в уме, когда учащиеся воспринимают данные числа на слц23уух, ничего не записывают и не пользуются пособиями. Это слуховые упражнения.
Запись учителем примеров на доске, в то время как учащиеся решают их устно и записывают ответы в тетрадь. Это зрительные упражнения.
Устный счет при помощи таблиц, плакатов, фигур и других наглядных пособий. Учитель читает и иллюстрирует примеры пособиями. Это зрительно-слуховые упражнения.
У детей с умственной отсталостью наблюдаются нарушения тех или иных анализаторов, память ослаблена, внимание не сосредоточено. Для большей эффективности занятия по устному счету нужно использовать зрительно-слуховые упражнения.
Таким образом, устный счет активизирует познавательную деятельность учащихся на уроке, способствует общему развитию ученика.
При их выполнении активизируется и развивается память, речь, внимание, способность воспринимать сказанное на слух, быстрота реакции. Он помогает учителю (помимо прямой задачи – проверка знаний), во-первых, переключить ученика с одной деятельности на другую, во-вторых, подготовить учащихся к изучению новой темы, в-третьих, в устный счет можно включить задания на повторение и обобщение пройденного материала и, в-четвертых, он повышает интерес обучающихся к математике.
Вывод. Помимо того, что устный счет на уроках математики способствует развитию и формированию прочных вычислительных навыков и умений, он также играет немаловажную роль в привитии и повышении у детей познавательного интереса к урокам математики, как одного из важнейших мотивов учебно-познавательной деятельности, развития мышления и развития личностных качеств ребенка с нарушением интеллекта. Вызывая интерес и прививая любовь к математике с помощью различных видов устных упражнений, учитель помогает ученикам активно действовать с учебным материалом, пробуждать у них стремление совершенствовать способы вычислений и решения задач, менее рациональные заменять более совершенными.
А это – важнейшее условие сознательного усвоения материала.
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа р.п. Озинки»
Озинского района Саратовской области
СТАТЬЯ
«Устный счет, как средство развития устных вычислительных навыков на уроках математики в начальной школе»
Составила учитель начальных классов
МОУ «СОШ р.п. Озинки»
Афанасьева Татьяна Евгеньевна
2020 – 2021 год
Введение
Одна из важнейших задач обучения школьников математике – формирование у них вычислительных навыков, основой которых является осознанное и прочное усвоение приемов устных и письменных вычислений.
Вычислительные навыки необходимы как в практической жизни каждого человека, так и в учении. Ни один пример, ни одну задачу по математике, нельзя решать, не обладая элементарными способами вычислений.
Но было бы ошибкой решать эту задачу только путем зазубривания таблиц сложения и умножения и использования при выполнении однообразных тренировочных упражнений. Не менее важная задача современной школы – развитие у учащихся в процессе обучения познавательной самостоятельности, творческой активности, потребности в знаниях.
Вычислительная культура формируется у учащихся на всех этапах изучения курса математики, но основа ее закладывается в начальной школе. В этот период школьники обучаются именно умению осознанно использовать законы математических действий (сложение, вычитание, умножение, деление). Позже полученные умения и навыки совершенствуются и закрепляются в процессе изучения алгебры, физики и других предметов.
Данная тема актуальна, так как устные вычисления необходимы в жизни каждому человеку.
Математика является одной из важнейших наук на земле, и именно с ней человек встречается каждый день в своей жизни. Поэтому необходимо формировать у детей вычислительные навыки, используя различные виды устных упражнений.
Основная часть
Цели и задачи устного счёта
Цели:
1) развитие вычислительных навыков;
2) развитие математической культуры, речи;
3) умение обобщать и систематизировать, переносить полученные знания на новые задания.
Так как устные упражнения или устный счёт это этап урока, то он имеет свои задачи:
1) Воспроизводство и корректировка определённых знаний, умений и навыков учащихся, необходимых для их самостоятельной деятельности на уроке или осознанного восприятия объяснения учителя.
2) Контроль учителя за состоянием знаний учащихся.
3) Психологическая подготовка учащихся к восприятию нового материала.
4) Повышение познавательного интереса.
Требования к проведению устного счёта
При проведении устного счета каждый учитель придерживается следующих требований:
Упражнения для устного счета выбираются не случайно, а целенаправленно.
Задания должны быть разнообразными, предлагаемые задачи не должны быть легкими, но и не должны быть «громоздкими».
Тексты упражнений, чертежей и записей, если требуется, должны быть приготовлены заранее.
К устному счету должны привлекаться все ученики.
При проведении устного счета должны быть продуманы критерии оценки (поощрение).
Устный счет может быть построен в следующей форме:
Задания на развитие и совершенствование внимания.
Такие как: найди закономерность, продолжи ряд, что лишнее?)
Задания на развитие восприятия, пространственного воображения. Например, нарисуйте орнамент, узор.
Устные упражнения с использованием дидактических игр.
Презентации.
Формы восприятия устного счета
1) Беглый слуховой (читается учителем) – при восприятии задания на слух большая нагрузка приходится на память, поэтому учащиеся быстро утомляются. Однако такие упражнения очень полезны: они развивают слуховую память.
2) Зрительный (таблицы, плакаты, карточки, записи на доске, интерактивной доске) – запись задания облегчает вычисления (не надо запоминать числа). Здесь идет работа на скорость.
3) Комбинированный.
обратная связь (показ ответов с помощью карточек, взаимопроверка, угадывание ключевых слов, проверка с помощью компьютерной программы Microsoft Power Point).
задания по вариантам (обеспечивают самостоятельность).
Для развития у учащихся сознательных и прочных вычислительных навыков я использую различные методические приемы и формы, например, устный счет по цепочке, игры «Пассажиры», «Футболисты», «Рыбаки», «Хоккеисты», «Запомни числа», «Пропусти число», «Исправляем ошибки Незнайки», тесты «Проверь себя сам», математические диктанты, презентации,
Варианты работы в 1 полугодии
Игра «Пассажиры». Ученики «по цепочке» решают примеры по карточке. Если ответ ученика – неверный, то наехал на кочку.
Игра «Футболисты». Делимся на 2 команды, неверный ответ – гол.
Игра «Рыбаки». Карточка с примерами – это удочка, сколько ученик решил примеров правильно, столько он поймал рыбы.
Игра «Хоккеисты». Карточка – это хоккейное поле, сколько правильных ответов – столько забитых голов.
Презентации.
Варианты работы во 2 полугодии
Игра «Запомни числа». Условия игры. Я называю какое-либо число. Первый ученик повторяет это число и называет свое. Каждый следующий повторяет ранее названные числа и называет свое. Интерес игры в ее соревновательном характере: кто сможет запомнить больше чисел. Игра продолжается до первой ошибки.
Эту игру можно использовать в самом начале урока, так как она помогает ученикам настроиться на рабочий лад, создать хорошее настроение.
Игра «Пропусти число». Условия игры. Учитель предлагает учащимся по очереди называть вслух в порядке возрастания (убывания) четные (нечетные) числа, начиная с 8 (16, 7, 29). Ученик, назвавший запрещенное число, выбывает. Побеждает тот, кто остается последним.
Эту игру хорошо использовать в начале урока вместо опроса.
Игра «Исправляем ошибки Незнайки».
Условия игры. Все учащиеся класса делятся на несколько команд. Каждой команде выдают одни и те же задания с математическими выражениями и определениями, в которых допущены ошибки, с таким расчетом, чтобы число заданий было равно числу участников каждой из команд. Командам дается некоторое время для нахождения ошибки и подготовки к ответу. Та команда, которая первой успела подготовиться, дает свою версию ошибки. Если ее ответ был неверным, с точки зрения других команд или жюри, то другим командам дается возможность доказать свою точку зрения. За верный ответ команде присваивается балл (или несколько баллов в зависимости от сложности задания). Побеждает та команда, которая наберет больше баллов. Данную игру можно использовать при проведении повторительно-обобщающих уроков.
Важно, чтобы при подготовке данной игры использовать картотеку типичных ошибок. В моей практике, по результатам контрольных работ, – это «Вычитание чисел с переходом через десяток», «Порядок действий в выражениях», «Письменное вычисление».
Презентации.
Вывод
Вычислительный навык – это высокая степень овладения вычислительными приёмами. Приобрести вычислительные навыки – значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия и выполнять эти операции достаточно быстро.
Полноценный вычислительный навык характеризуется правильностью, осознанностью, рациональностью, обобщённостью, автоматизмом, прочностью.
Правильность – ученик правильно находит результат арифметического действия, то есть правильно выбирает и выполняет операции, составляющие приём.
Осознанность – ученик осознаёт, на основе каких знаний выбраны операции и установлен порядок их выполнения, в любой момент может объяснить, как он решал и почему так может решать.
Рациональность – ученик выбирает для данного случая более рациональный приём, то есть выбирает те из возможных операций, выполнение которых легче других и быстрее приводит к результату.
Обобщённость – ученик может применить приём вычисления к большому числу случаев, то есть способен перенести приём вычисления на новые случаи.
Автоматизм – ученик выполняет и выделяет операции быстро и в свёрнутом виде, но всегда может вернуться к объяснению выбора системы операций. Высокая степень автоматизации должна быть достигнута по отношению к табличным случаям сложения и вычитания, умножения и деления.
Прочность – ученик сохраняет сформированные вычислительные навыки надолго.
Помимо того, что устный счет на уроках математики способствует развитию и формированию прочных вычислительных навыков и умений, он также играет немаловажную роль в привитии и повышении у детей познавательного интереса к урокам математики, как одного из важнейших мотивов учебно-познавательной деятельности, развития логического мышления, и развития личностных качеств ребенка. На мой взгляд, вызывая интерес и прививая любовь к математике с помощью различных видов устных упражнений, учитель будет помогать ученикам активно действовать с учебным материалом, пробуждать у них стремление совершенствовать способы вычислений и решения задач, менее рациональные заменять более совершенными.
А это – важнейшее условие сознательного усвоения материала.
Используемая литература
Зайцева О.П. Роль устного счёта в формировании вычислительных навыков и в развитии личности ребёнка // Начальная школа, 2001 г.
Зимовец К.А., Пащенко В.А. Интересные приемы устных вычислений. // Начальная школа. 1990 г.
Волошина М.И. Активизация познавательной деятельности школьников на уроках математики. //Начальная школа. 1992 г.
Зимина С.В. Как развивается интерес к математике? // Начальная школа. // 1999 г.
Иванова Т. Устный счёт. // Начальная школа. 1999 г.
Интернет ресурсы.
Коваленко В.П. Дидактические игры на уроках математики.
Куличкова О.П., Уланова К. Формирование вычислительных навыков в процессе игры. // Начальная школа. 2000 г.
Узорова О.В. Устный счёт и математические диктанты для начальной школы. // Просвещение 2001г.
Распечатать ресурс
Функция печати в настоящее время несовместима с Firefox.
ДРЕМЕ ТЕ
Распечатать ресурс
Функция печати в настоящее время несовместима с Firefox.
Дети развивают повседневную математику
Контекст и обзор
Маленькие дети, даже младенцы, развивают в основном невербальные базовые понятия количества: больше/меньше, порядок, то же и сложение/вычитание.
Дети учатся большинству этих вещей самостоятельно, без особой помощи взрослых. Дети часто используют эти понятия в повседневной жизни, например, чтобы определить, у кого больше или меньше мороженого. Детские концепции и процедуры полезны при определенных условиях, но их необходимо обогатить. (Возможно, поэтому было изобретено число: пастуху нужно знать не только, что у него много овец, но и сколько именно.) Это то, что знают дети и что им нужно усвоить примерно в возрасте трех, четырех и пяти лет.
Больше/меньше
Дети должны видеть, что здесь больше предметов, чем там. Они часто решают эту проблему не счетом, а внешним видом. «Эта стая гусей в небе должна быть больше, потому что она покрывает большую площадь, чем другая стая». Такой подход часто адекватен, но может привести к неверным ответам и путанице.
Приказ
Для многих целей достаточно суждений о большем или меньшем, но иногда необходимо провести сравнение между более чем двумя вещами.
Маленькие дети склонны слишком полагаться на внешность при решении проблем.
Тот же номер
Идея того же номера развивается, даже без помощи взрослых, через несколько стадий:
Идея добавить как результат больше и вычесть меньше
Дети узнают, что :
Последующие инструкции должны основываться на всех этих идеях, когда вводятся письменные числа.
Учимся считать слова
Контекст и обзор
В повседневной жизни мы все время используем слова для счета, выбирая продукты в супермаркете («нам нужны два банана») или играя в «10, девять, восемь, … взлетай!» Дети любят считать как можно больше, как и взрослые. Их может даже заинтересовать название самого большого числа.
Свободное владение счетными словами помогает в дальнейшем вычислении.
Механическая память плюс
Сначала дети запоминают счетные слова примерно от 1 до 10 или около того. Но их обучение включает не только память. Дети также узнают некоторые идеи и правила о числах, а именно, что правильный порядок важен; цифры отличаются от букв; и вы не должны пропускать или повторять числа, когда считаете.
Структура
Позже дети усваивают основную структуру числа: десять — это основная единица (20, 30 и т. д.), и мы присоединяем единицы к десяткам ( двадцать один и т. д.). Правила произношения английских счетных слов от одиннадцать до девятнадцать особенно трудно выучить, потому что они плохо разработаны. Одиннадцать должно быть «десять один», точно так же, как двадцать один . Пятнадцать должно быть “десять пять”, как двадцать пять . Языки Восточной Азии понимают это правильно, но английский и многие другие языки этого не делают.
Напротив, английский довольно хорошо разработан для числовых слов, начинающихся с 9.0053 двадцать
Считаем вещи: сколько их?
Контекст и обзор
Представления детей о том же, больше, меньше и порядке сильно зависят от восприятия и их собственной несовершенной логики (например, то, что выглядит больше, значит больше).
Принципы, необходимые для понимания перечисления
Перечисление относится к использованию счетных слов для определения количества объектов. (Это включает в себя любой объект, от воображаемых монстров до шариков.) Дети должны научиться следовать нескольким правилам и принципам точного перечисления. Этот набор правил является фундаментальным:
Учитывая эти правила и принципы, существует несколько способов точного подсчета. Дети должны уметь:
Дети должны научиться использовать эти подходы в соответствующих ситуациях. Например, если есть только два объекта, субитизация может быть полезной, но если их девять, то может быть указано отодвигание объектов в сторону.
Понимание количества элементов
Детям, которые точно перечисляют, также необходимо понимать полученный результат.
Предположим, ребенок точно считает пять вещей. Само по себе правильное перечисление еще не означает, что ребенок понимает кардинальность. На вопрос, сколько их, ребенок может просто пересчитать предметы в другой раз. Для этого ребенка ответ на вопрос о количестве просто активирует процедуру счета, но не дает понимания результата. Дети должны узнать несколько вещей о кардинальном числе. Основная идея состоит в том, что правильное перечисление дает кардинальное значение множества. Последнее числовое слово относится не к последнему подсчитанному объекту, а ко всему набору в целом. Когда мы считаем, единица относится к первому объекту; два относится не ко второму подсчитанному объекту, а к двум объектам в новой группе и так далее. Кроме того, когда ребенок определил, что в наборе пять предметов, уже не имеет значения, спрятаны ли они или предметы просто переставлены (скажем, из прямой линии в круг). Есть еще пять объектов. это
Распространенные ошибки или заблуждения
При подсчете дети часто слишком полагаются на внешний вид, точно так же, как они делали это при определении больше или меньше .
Одна из целей обучения должна заключаться в том, чтобы помочь детям понять, что разум должен преобладать над внешностью. Детям необходимо абстрактно мыслить о материальных вещах. В конце концов, им нужно внедрить понимание кардинального числа (например, абстрактную идею о том, что здесь есть пять объектов) в более крупную систему счисления, например, что пять идет после четырех и составляет половину от 10.
Ежедневное сложение и вычитание чисел
Контекст и обзор
Далее нам нужно понять, как понятия больше/меньше, порядок, то же самое, сложение и вычитание без точного числа (зная, что добавление означает увеличение набора, даже если вы не знаете точное число), и перечисление разрабатываются для создания числового сложения и вычитания. Кое-что из этого дети узнают сами, но взрослые могут и должны помочь.
Понимание сложения
Эти понятия необходимо изучить, чтобы понять сложение (вычитание аналогично):
Стратегии, используемые для сложения (или вычитания)
Дети часто начинают с использования конкретных предметов и пальцев для сложения, но постепенно учатся считать в уме и запоминают некоторые суммы.
Дополнительные функции числового сложения и вычитания
Чувство числа
Контекст и обзор
Детям необходимо развивать чувство числа, понятие, которое, как известно, трудно определить простым и эксклюзивным способом. Мне нравится думать об этом как о математической уличной смекалке, которую можно использовать практически в любой области чисел, включая те, что обсуждались выше. Чувство числа, помогающее ребенку осмысливать мир, состоит из нескольких компонентов, каждый из которых проходит процесс развития.
Думать вместо того, чтобы считать
Восприятие чисел включает в себя использование основных идей, чтобы избежать вычислительной рутины, например, когда ребенок знает, что если вы сложите два и три и получите пять, то вам не нужно считать, чтобы получить ответ на три -и два.
Используйте то, что удобно
Чувство чисел включает в себя разбиение чисел на удобные части, которые облегчают вычисления, например, когда мы мысленно складываем 5 + 5 + 1 вместо 5 + 6.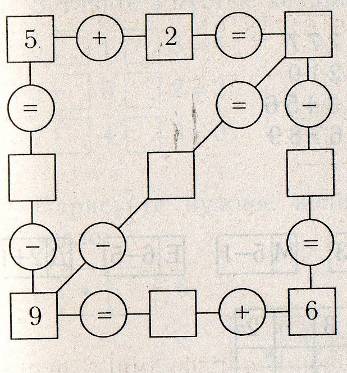
Знание того, что правдоподобно, а что невозможно может включать «чувство» чисел в смысле знания того, являются ли определенные числа правдоподобными ответами на определенные проблемы (если вы складываете два и три, вы знаете, что ответ должен быть больше трех; все, что меньше, не только неправдоподобно, но и невозможно) .
Понимание взаимосвязей
Чувство чисел включает интуитивные представления об отношениях между числами. (Например, “это намного больше, чем это”.)
Беглость
Восприятие чисел включает свободное владение числами, например, когда ребенок сразу знает, что восемь больше, чем четыре, или видит, что есть три животных без приходится считать.
Оценка
Это включает в себя определение приблизительного количества группы объектов и связано с понятием правдоподобных ответов.
Переход к письменной, символической математике
Контекст и обзор
Формальная, символическая математика может дать детям более мощные инструменты и идеи, чем те, которые даются им через неформальную повседневную математику.
Формальная математика (и использование символов) развивалась в нескольких культурах и теперь практически универсальна. Дети должны этому научиться.
Повседневное происхождение и формальная математика
Дети сталкиваются с математическими символами в повседневной жизни: номера лифтов, номера автобусов, телевизионные каналы и уличные знаки. Часто родители, телевидение и деятельность с программным обеспечением вводят некоторые простые символические математические действия, такие как чтение цифр, написанных по телевизору или на игральных картах.
В школах обязательно должны преподавать формальную математику. Но сделать это непросто. Даже если они компетентны в повседневной математике, у детей могут возникнуть проблемы с осмыслением и увязкой своих неформальных знаний с тем, чему учат в школе. Учителя часто не преподают символизм эффективно. Если дети встают не с той символической ноги, результатом может быть неприятное падение с образовательной лестницы.
Таким образом, цель учителей состоит в том, чтобы помочь детям, начиная с дошкольного возраста, понять, почему используются символы, и осмысленно использовать их, чтобы связать уже известную неформальную математику с формальной символической математикой. Учителю необходимо «математизировать» бытовую, личную математику детей; то есть помочь детям связать их неформальную систему с формальной математикой, которую преподают в школе. Не является опрометчивым или неуместным с точки зрения развития знакомить маленьких детей с символами, если это занятие мотивирует и имеет смысл. Наоборот, крайне важно, чтобы обучение символам начиналось как можно раньше, но опять же, если и только если это делается осмысленным образом.
Вот ключевые проблемы, связанные с введением формальной математики для маленьких детей:
Маленьким детям трудно связать цифры и символы арифметики (+ и -) с их собственной повседневной математикой
Они могут хорошо складывать, но быть смущает выражение 3 + 2.
Ребенок как бы живет в альтернативных реальностях: повседневном мире и «академическом» (в уничижительном смысле) мире. Повседневный мир имеет смысл, а школьный мир — нет. В первом вы думаете сами, а во втором делаете то, что вам говорят.
Знак равенства (=) представляет собой сложную задачу
Учитель намеревается научить знаку равенства как “эквивалентному” и думает, что у нее есть, но ребенок усваивает его как “делает” (например, 3 + 2 делает 5). Это история о том, как детский эгоцентризм встречается с эгоцентризмом учителя, но ни один из них не разговаривает с другим.
Решение
Мы не должны избегать обучения символам, но должны осмысленно вводить их. Это означает учет того, что дети уже знают, и соотнесение введения символов с этим предшествующим знанием. Это также означает мотивацию использования символов. Таким образом, если вы хотите сказать другу, сколько кукол у вас дома, вам нужно сосчитать их числовыми словами (символами), а затем использовать устные слова («У меня пять кукол»), письменные слова («У меня пять кукол », написанное на листе бумаги или на экране компьютера), или написанные символы (5) для сообщения результата.
Манипуляторы могут помочь
Использование манипуляторов может быть эффективным в обучении символизму и формальной математике, но они часто используются плохо. Цель состоит не в том, чтобы заставить ребенка играть с конкретными предметами, а в том, чтобы использовать эти предметы, чтобы помочь ребенку усвоить абстрактные идеи. Цель манипулятивных действий — избавиться от них, заложив их в голову ребенка, чтобы использовать по мере необходимости в мышлении. Например, предположим, что ребенок учится представлять десятки и единицы с помощью блоков с основанием десять. Учитывая задачу на сложение в уме 13 плюс 25, ребенок может понять, что каждое число состоит из десятков (квадратов 10 на 10) и некоторых единиц (отдельных блоков), и что решение задачи включает сложение одной десятки и еще двух, что легко, а затем выяснить количество единиц. Мысленные образы десятков и единиц обеспечивают основу для ее вычислений, часть которых может быть выполнена по памяти (один плюс два равно трем), а часть может быть выполнена путем счета на пальцах (пять пальцев и еще три дают восемь).
).
Заключение
Основы числа интересны и глубоки. Хотя маленькие дети развивают удивительно компетентные повседневные математические способности, им есть чему поучиться, и учителя могут помочь.
Тип ресурса
Раздаточный материал
Математические советы и стратегии для развития чувства числа до 20 в детском саду и первом классе: Включен обширный список заданий и ресурсов для изучения числа: книги, материалы, математические манипуляции и БЕСПЛАТНЫЕ занятия!
Математические советы и стратегии, необходимые для развития чувства числа до 20, находятся прямо здесь. У вас будет все, что вам нужно, чтобы быстро внедрить множество заданий, игр и центров, связанных с числами, в свой класс или домой.
Занятия, книги, предложения ресурсов (включая БЕСПЛАТНУЮ) охватывают множество концепций числового смысла и идеально подходят для детского сада и первого класса.
Кроме того, вы найдете ценные материалы по численному смыслу и манипулятивные предложения, а также бесплатные подарки, которые вы можете получить уже сегодня! Предупреждение: он ДЛИННЫЙ, но в нем так много всего, что вы не захотите ничего пропустить!
Детям нужны возможности изучать числа и знакомиться с ними. Научиться считать, определять числа и понимать количество — это лишь некоторые из основных понятий. Повторяющийся опыт способствует пониманию и свободному обращению с числами. Этот опыт помогает расширить знания и узнать новые идеи. Сильное чувство числа жизненно важно для будущего понимания более сложных математических тем.
Приведенные ниже действия успешно использовались. Используйте их так, как они описаны, или адаптируйте их к своим потребностям. Быть гибким. Обсуждайте числа и поощряйте вопросы. Когда есть возможность заказать, посчитать, сопоставить или описать вместе с ребенком, дерзайте! Им выгодно видеть числа естественным и плавным образом.
Каждый день уделяйте время веселым и увлекательным занятиям с числами и наблюдайте, как развивается беглость речи.
Очень важно считать с детьми каждый день. Повторяющийся устный счет помогает им услышать, как звучат числа, и запомнить их порядок. Использование математических манипуляций, таких как подсчет фишек, может помочь установить связь с вербальным счетом и счетом объектов. Этот счет один к одному является важным навыком, который необходимо часто практиковать.
Поставьте небольшие группы предметов в центре, чтобы их можно было сосчитать.Предоставьте детям материалы для счета и связи с предметами и числами. Это побуждает детей видеть, что цифры — это больше, чем слова. Объясните детям, что числа имеют множество представлений, таких как точки, пальцы, счетчики, цифры, предметы, десять рамок и т. д.
Когда дети видят числа разными способами одновременно и многократно, их чувство числа развивается.
Выберите число дня, начинающееся с единицы, и проанализируйте его во время математического блока.
Предоставьте детям возможность упорядочивать числа.
Располагая числа или объекты с числами в правильном порядке, они считают и развивают чувство числа.
Вырежьте произвольно кусочки и торгуйте с партнером. Снова соберите пазл для практики.Обучение детей разрядному значению должно начинаться с обучения их видеть десять разными способами. Перейдите к иллюстрированию чисел с помощью десятичных блоков.
Сделайте много примеров, где дети должны использовать и считать кубики. Используйте диаграмму, чтобы помочь сосчитать блоки. Дети постоянно окружены числами в своем окружении. Они быстро учатся распознавать отдельные цифры от 0 до 9 с помощью различного опыта. Продолжайте поощрять это знакомство, размещая цифры на стене. Плакаты, числовые строки и календари являются полезными инструментами.
Используйте все свое тело, чтобы совершать действия или рисовать в воздухе.Научите детей читать числовые слова, пока они учатся читать. Учите каждое числовое слово по одному и произносите их фонетически (если применимо).
д.).Научите детей считать от числа вперед и назад, чтобы подготовить детей к сложению и вычитанию.
Предоставьте детям множество возможностей угадать, сколько вещей они видят в своей повседневной жизни.
Задавайте наводящие вопросы, чтобы стимулировать это мышление. Убедитесь, что дети знают, что они оценивают и что это всего лишь догадки. Подчеркните, что оценки не обязательно должны быть точными, но они должны быть продуманными. С большей практикой оценки должны стать ближе к фактическому количеству объектов.
Быстро покажите партнера, а затем спрячьте его. Они делают оценку, а затем вы вместе считаете, чтобы проверить.По мере того, как растет знакомство с числами, растет и способность сравнивать числа друг с другом. Обеспечьте возможность сравнивать числа ежедневно. Задавайте вопросы о том, какое число больше, меньше или одинаково.
Аллигатор съедает большую башню.Действия, представленные в этом посте, можно найти в следующих ресурсах, которые можно найти на сайте «Учителя платят учителям».
Числа до 5 для детского сада
Числа до 10 для детского сада
Числа от 11 до 20 для детского сада
Учебная программа Mindful Math для детского сада
Числа до 10 для первоклассников
Числа до 20 для первоклассников
Учебная программа Mindful Math для первоклассников
Подготовьте этот забавный набор числовых головоломок для своих учебных центров и помогите детям построить свое число смысл!
Возьмите 20 БЕСПЛАТНЫХ числовых головоломок с разными изображениями на каждой части, щелкнув изображение ниже .
I Spy Numbers Jean Marzollo
1,2,3 Peas от Кита Бейкера
Chicka Chicka 1,2,3 от Bill Martin Jr.
Splash! Энн Джонас (счет)
Очень голодная гусеница Эрик Карл (счет)
Как динозавры считают до 10? Джейн Йолен
Число повсюду Эллиот Кауфман
10 черных точек Дональд Крюс
Сколько жуков в коробке? Дэвид Картер
Сколько улиток? Пол Гиганти-младший.
Десять хитрых пираний, Уильям Уайз.
Нет числа, Оливер Джефферс.0029 «Больше или меньше» Стюарта Мерфи
«Талли О’Мэлли» Стюарта Мерфи
«Местное значение» Дэвида Адлера
«Что такое местное значение» Ширли Дьюк
«Крякай и считай» Кита Бейкера
Спорим! Стюарт Дж. Мерфи
Прочитайте о программе Mindful Math и о том, как она может изменить ваш математический блок в лучшую сторону! Эта всеобъемлющая учебная программа по математике доступна для детского сада, первого и второго класса.