Тема: Плоскость. Прямая. Луч. ( Дата 19.09 Класс 5а )
Тип урока: изучение нового материала
Цели:
Предметные
– познакомить учащихся с геометрическими фигурами : плоскость. прямая. луч ;
– научить распознавать на рисунках эти фигуры, а в окружающем мире – объекты, для которых плоскость. прямая. луч являются моделями.
Личностные
– проявлять интерес к изучению темы и желание применять приобретённые знания и умения.
Метапредметные
– формировать умение видеть математическую задачу в контексте проблемной ситуации, в окружающей жизни.
Планируемые результаты: учащиеся научаться распознавать на чертежах геометрические фигуры: плоскость. прямая. луч.
Основные понятия: плоскость. прямая. луч.
Организационная структура урока.
1.
Ну-ка, проверь, дружок!
Готов ли ты начать урок?
Всё ль на месте? Всё ль в порядке?
Книжка, ручка и тетрадка…
Проверили? Вот здорово!
К уроку всё готово!
2 Активизация знаний обучающихся.
Верным помощником на уроке у нас будет самая маленькая геометрическая фигура
“Весёлая точка”.
№1 Прочитайте числа: 180000509, 300001700, 608600005003(фронтально)
№2 Какое число нужно вписать в последнюю клетку?(индивидуально по цепочке)
№3 Выразите в дециметрах: 50 см, 230 см, 67 м, 800 м. (фронтально)
Выразите в метрах : 600
см, 30 дм, 2 км, 12000 мм.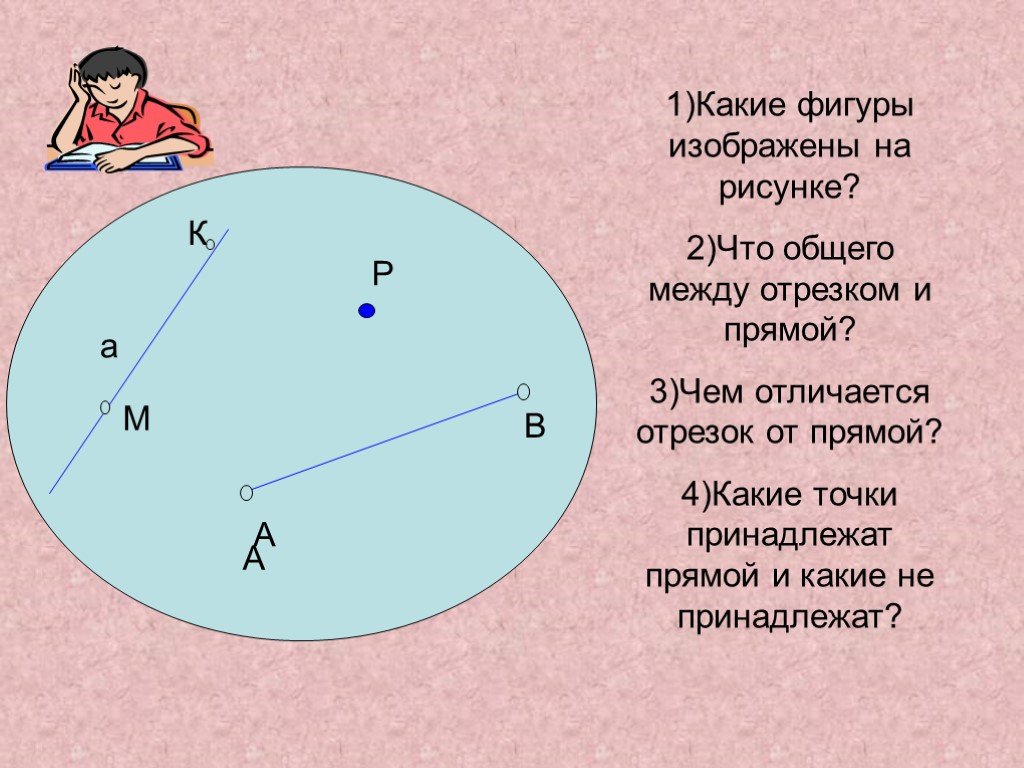
3. Мотивация урока. Анаграммы. Просмотр презентации.
Расшифруйте слова: КОСТЬПЛОС, МАЯПРЯ, РЕЗООТК, КАТОЧ, ЧУЛ, ТКИНИ.
-Это слова”плоскость”, «прямая», «отрезок», «точка», «луч», «нитки».
-Все ли расшифрованные слова вам знакомы?
-А где вы с ними встречались?
(На уроке математики, а нитки на уроке труда).
-Какое слово лишнее?
(Нитки. Они не относятся к уроку математики).
-Но все эти слова сегодня помогут нам сделать открытие.
Сообщение темы и цели урока.
-Рассмотрите фигуры на доске.
– Какую из этих фигур вы уже знаете?(отрезок)
– В какие группы фигуры можно объединить?
(В ходе рассуждения можно разбить на 3 группы: мы рассмотрим «отрезки» )
-Но возникает проблема: куда можно отнести фигуры 1, 3 и 4?
4. Изучение нового материала.
– понятие плоскости (с. 27-28 рассмотреть на окружающих примерах)
– Сравните фигуры с уже известными нам отрезком
-Что можно сказать?
-Можно ли эту фигуры назвать отрезком? Почему?
-Тогда давайте выполним одну операцию.
-В руках у меня 2 катушки тесьмы. Мы раздвигаем их в разные стороны.
-Что заметили?
(Это прямая линия, только в воздухе)
-Можно ли её продолжить в обоих направлениях?
-А эту прямую можно изобразить на доске?
(Чертим на доске, а дети в тетради).
А
а
В
Без начала и без края линия прямая,
Хоть 100 лет по ней идти,
Не найдёшь конца пути.
(Эта геометрическая фигура – прямая)
– У людей есть имена, у животных клички.
-А прямую линию можно обозначить одной или двумя буквами.
– Предложите имя прямой линии.
Вывод: У прямой линии нет ни начала, ни конца.
Мы можем изобразить только маленькую часть прямой линии. Её можно продолжить.
-Наша Весёлая Точка поможет нам ещё
поработать с прямой линией.
-Поставьте точку, проведите через неё прямую линию.
-Можно ещё провести линию через эту точку?
-Сколько прямых линий можно провести через одну точку?
-Поставьте 2 точки. Через эти точки проведите прямую линию. Можно ли ещё провести?
А К
Вывод: Через одну точку можно провести сколько угодно линий, а через 2 точки – только одну.
-Теперь нашу прямую линию я разрежу.
(К месту разреза прикреплю Солнышко).
-Что получилось?
-На что похоже?
(Луч солнца)
О новой фигуре разносится весть
Конца пусть в ней нет,
Начало-то есть!
И солнце, тихонько взойдя из-за туч,
Сказало: «Друзья, назовём его луч!»
-Можно ли продолжить луч со стороны разреза?
(Нет, мешает круг и нечего продолжать)
-А с другой стороны?
(Можно продолжить до бесконечности)
СРАВНИТЕ: Луч и прямую линию.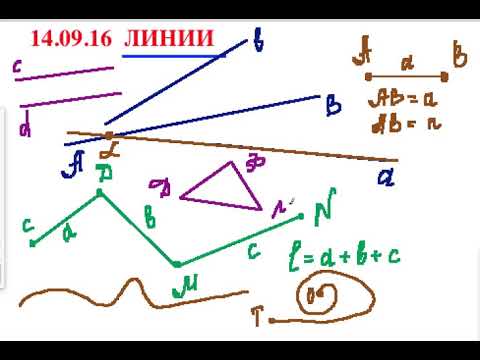
(Прямую линию можно продолжить в обе стороны, а луч только в одну. Луч имеет начало)
-Начертите луч на доске и в тетради
-Луч обозначается двумя прописными буквами.
На первом месте всегда указывается начало луча.
-Поставьте точку, проведите луч, а ещё можно провести из этой точки, ещё…
-Какие лучи бывают?
(Солнечные лучи, лампа, фонарик и т.д.)
Вывод: Луч – это прямая линия, ограниченная с одной стороны. Из одной точки можно провести бесконечное множество лучей.
-У луча я отрезаю ту часть, которую можно продолжить…и прикреплю ещё одну точку.
-Что получилось?
(Отрезок)
-Линия, ограниченная с двух сторон.
СРАВНИТЕ: Луч и отрезок.
-У луча есть только начало, а отрезок имеет и начало и конец.
-Можно отрезок изобразить на доске и в тетради?
Точки две поставь в тетради,
Чтоб потом нарисовать между ними
Под линеечку – прямую,
И окажется, мой друг,
Что отрезок вышел вдруг,
Только точкам имена дать ты
Не забудь!
-Отрезок обозначается двумя буквами,
но порядок при чтении и записи не имеет значения.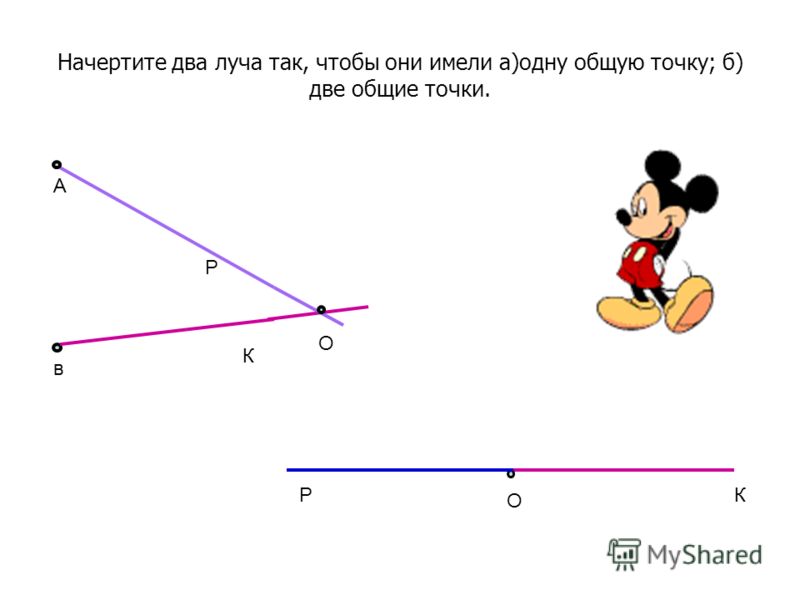
Вывод: Отрезок – это прямая, ограниченная с двух сторон.
-Что нового узнали об этих фигурах?
Вывод: Луч, прямая – это геометрические фигуры.
Работа с учебником $ 4 с.17-28.
5. Физкультминутка.
Раз, два, три, четыре, пять,-
Все умеем мы считать,
Отдыхать умеем тоже,
Руки за спину заложим,
Голову поднимем выше
И легко – легко подышим,
Раз – подняться, потянуться,
Два – согнуться, разогнуться,
Три – в ладоши три хлопка,
На четыре – руки шире,
Пять – руками помахать,
Шесть – за парту тихо сесть.
6. Первичное закрепление нового материала.
(На доске изображены геометрические фигуры)
-Найдите отрезок, луч, прямую.
-Обоснуйте свой ответ.
-Можно ли сказать, что они пересекающиеся?
-А могут ли они пересечься?
Учебник: №85, 87(устно), 88(устно), 90, 91 – фронтально
Рабочая тетрадь: № 32, 34, 35, 36 – индивидуально(обучающая самостоятельная работа)
№ 33- работа в парах
Повторение: № 105
7.
Обучающая самостоятельная работа.
8. Домашнее задание.
На дом вам будет дано следующее задание: $ 4, № 86, 89, 106, доп. № 111.
9. Подведение итогов урока. Рефлексия.
Вопросы : 1-7 с. 29.
– Соедините названия фигуры с фигурой.
Подберите правильное название.
ОТРЕЗОК ЛУЧ ПРЯМАЯ линия ПЛОСКОСТЬ
ПРЯМАЯ линия – не имеет начала и конца; можно обозначать одной или двумя буквами; через одну точку можно провести сколько угодно линий, через две – только одну.
ЛУЧ– прямая, ограниченная с одной стороны; продолжать можно только в одну сторону; из одной точки можно провести сколько угодно лучей; лучи бывают разные.
ОТРЕЗОК – прямая линия, ограниченная с двух сторон; на одной прямой может быть несколько отрезков; любую прямую можно превратить в отрезок.
ПЛОСКОСТЬ – воображаемая
геометрическая модель; модели части плоскости: тетрадь, крышка стола, пол,
стены, поле, море и т.
д. Плоскость бесконечна, её нельзя изобразить.
Нарисовать свое настроение в виде солнышка в конце урока. «Лестница успеха».
-Вы сегодня дружно и творчески работали (Оценивается работа обучающихся).
-Спасибо всем! Урок окончен.
Разработки уроков (конспекты уроков)
Основное общее образование
Линия УМК А. Г. Мерзляка. Математика (5-6)
Математика
Данный план урока является частью сервиса “Классная работа”*
Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.
Цель урока
Закрепить навыки работы с чертежами и геометрических построений.
Задачи урока
Виды деятельности
Ключевые понятия
| № | Название этапа | Методический комментарий |
|---|---|---|
| 1 | Актуализация знаний | |
| 2 | Обобщение и систематизация знаний |
№ 98. Если отметить точку на прямой, то тем самым задаются два луча. Для фронтальной работы на уроке рекомендуем задания из учебника: № 92, 94, 95, 98, 99. Для парной работы на уроке рекомендуем задания: № 1, 4. Для индивидуальной работы на уроке рекомендуем задания: № 2, 3, 5.
|
| 3 | Контроль и коррекция знаний | |
| 4 | Повторение | Для повторения можно использовать задание из учебника. |
| 5 | Рефлексия учебной деятельности | Для подведения итогов урока можно предложить учащимся ответить на вопросы. |
| 6 | Информация о домашнем задании | Для индивидуальной работы дома рекомендуем: § 4, № 93, 100, 108. |
Данный план урока является частью сервиса “Классная работа”*
Используйте презентациюВнесите нужные вам правки: в технологическую карту урока или в презентацию, если требуется.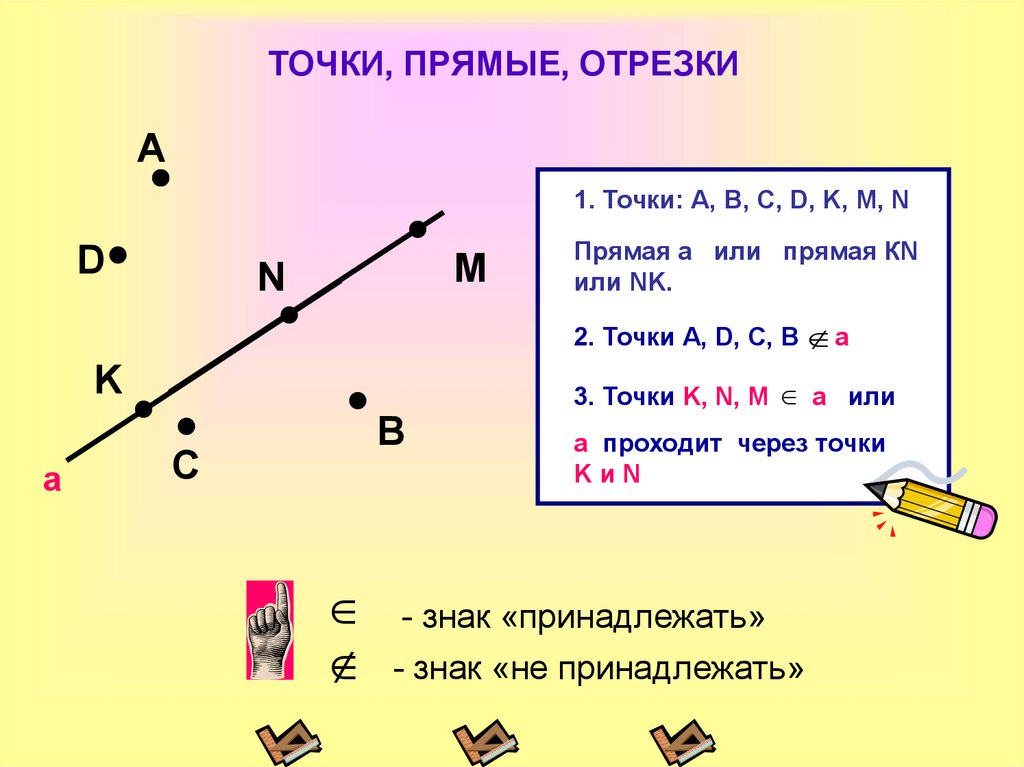
Хотите сохранить материал на будущее? Отправьте себе на почту
в избранноеТолько зарегистрированные пользователи могут добавлять в избранное.
Войдите, пожалуйста.
Назад к методической помощи по линии Линия УМК А. Г. Мерзляка. Математика (5-6)
Для оценки работы вам необходимо авторизоваться на сайте
Войти или зарегистрироваться
Для доступа к материалу требуется регистрация на сайте
Войти или зарегистрироваться
Нужна помощь?
Балки — это горизонтальные элементы, используемые для поддержки вертикальных нагрузок, приложенных к проему. В более общем смысле это элементы конструкции, которые внешние нагрузки имеют тенденцию изгибаться или искривляться.
Обычно термин «балка» применяется к элементам, вершина которых непрерывно соединена с низом по всей их длине, а элементы, вершина и низ которых соединены с интервалами, называются фермами. См. также Структурная система, ст. 1.7.
Существует множество способов поддержки балок. Некоторые из наиболее распространенных методов показаны на рис. с 5.11 по 5.16.
Балка на рис. 5.11 называется свободно опертой, или простой балкой. На концах он имеет
опор, которые удерживают его только от вертикального движения. Концы балки могут свободно вращаться. Когда нагрузки имеют горизонтальную составляющую или когда изменение длины балки из-за температуры может иметь важное значение, опоры также должны предотвращать горизонтальное движение. В этом случае, как правило, достаточно горизонтального закрепления на одной опоре.
Расстояние между опорами называется пролетом. Нагрузка, которую несет каждая опора, называется реакцией.
Балка на рис. 5.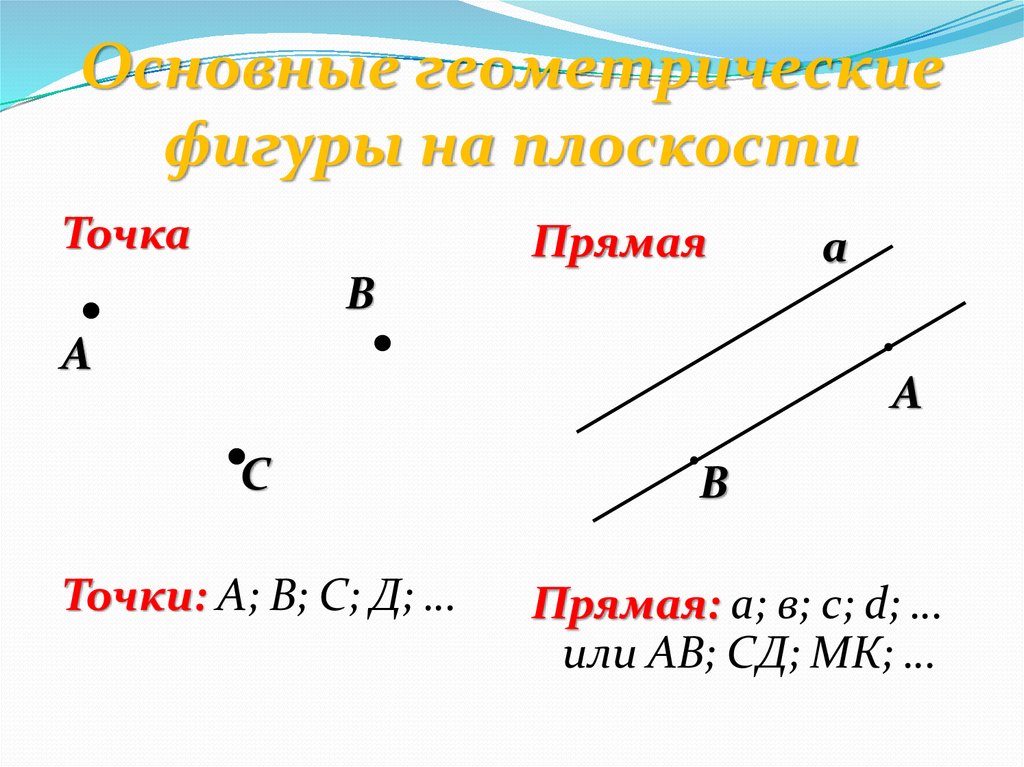
12 является консольной. У него есть только одна опора, которая удерживает его от вращения или перемещения по горизонтали или вертикали на этом конце. Такая опора называется фиксированным концом.
Если под свободный конец консоли поставить простую опору, получится подпирающая балка на рис. 5.13. У него один конец зафиксирован, один конец просто поддерживается.
Балка на рис. 5.14 закреплена с обоих концов. На обоих концах не может происходить вращение или вертикальное движение. На практике редко удается получить полностью фиксированный конец.
Обычно допускается некоторый поворот концов балки. Большинство условий опоры являются промежуточными между условиями для простой балки и для балки с фиксированным концом.
На рис. 5.15 показана балка, выступающая за обе простые опоры. У выступов есть свободный конец, как у консоли, но опоры допускают вращение.
Когда балка проходит через несколько опор, она называется неразрезной балкой (рис. 5.16).
Реакции для балок на рис.
5.11, 5.12 и 5.15 можно найти из уравнений равновесия. По этой причине они классифицируются как статически определяемые балки.
Уравнений равновесия, однако, недостаточно для определения реакции балок на рис. 5.13, 5.14 и 5.16. Для этих балок неизвестных больше, чем уравнений. Дополнительные уравнения должны быть получены на основе допустимых деформаций; на знании, например, что фиксированный конец не допускает вращения. Такие балки относятся к статически неопределимым. Методы нахождения напряжений в этом типе балки приведены в ст. 5.10.4, 5.10.5, 5.11 и 5.13.
В качестве примера применения уравнений равновесия (ст. 5.2.1) для определения реакций статически определимой балки вычислим реакции балки длиной 60 футов с выступами в Рис. 5.17. Эта балка выдерживает равномерную нагрузку в 200 фунтов на фут·фут по всей длине и несколько сосредоточенных нагрузок. Расстояние между опорами – 36 футов.
Чтобы найти реакцию R1, возьмем моменты относительно R2 и приравняем сумму моментов нулю (вращение по часовой стрелке считается положительным, против часовой стрелки – отрицательным):
Поскольку балка находится в равновесии под действием приложенных к ней сил, очевидно, что в каждом сечении действуют внутренние силы, препятствующие движению.
Например, предположим, что мы разрезаем луч на рис. 5.17 вертикально справа от его центра. Если мы суммируем внешние силы, включая реакцию, слева от этого разреза (см. рис. 5.18а), мы обнаружим, что существует неуравновешенная направленная вниз нагрузка в 4000 фунтов. Очевидно, в разрезе внутренняя сила, действующая вверх 4000 фунтов должны присутствовать для поддержания равновесия. Опять же, если мы возьмем моменты внешних сил относительно сечения, мы найдем неуравновешенный момент в 54 000 футо-фунтов. Таким образом, для поддержания равновесия должен действовать внутренний момент в 54 000 футо-фунтов.
Этот внутренний или сопротивляющийся момент создается парой, состоящей из силы C, действующей на верхнюю часть балки, и равной, но противоположной силы T, действующей на нижнюю часть (рис. 18b). Верхняя сила является результатом сжимающих напряжений, действующих на верхнюю часть балки, а нижняя сила является результатом растягивающих напряжений, действующих на нижнюю часть. Поверхность, на которой напряжения изменяются от сжатия к растяжению, где напряжение равно нулю, называется нейтральной поверхностью.
s переход от сжатия к растяжению, где str
Неуравновешенная внешняя вертикальная сила в сечении называется сдвигом. Он равен алгебраической сумме сил, лежащих по обе стороны сечения. Силы, действующие вверх слева от сечения, считаются положительными, силы, действующие вниз, отрицательными; знаки меняются местами для сил справа.
Диаграмма, на которой сдвиг в каждой точке по длине балки отображается в виде ординаты, называется диаграммой сдвига. Диаграмма сдвига для балки на рис. 5.17 показана на рис. 5.19.б.
Диаграмма построена, начиная с левого конца. Нагрузка в 2000 фунтов была отложена в удобном масштабе.
Затем определялся сдвиг при следующей сосредоточенной нагрузке левой опоры.
Это равно 2000 – 200 x 12 или -4400 фунтов. Однако при переходе от сусла слева от опоры к точке справа сдвиг изменяется на величину реакции. Следовательно, на
с правой стороны левой опоры сдвиг равен -4400 + 14 000, или 9600 фунтов.
При следующей сосредоточенной нагрузке сдвиг равен 9600 – 200 x 6, или 8400 фунтов. Однако при прохождении нагрузки в 4000 фунтов сдвиг меняется на 8400 – 4000, или 4400 фунтов. Продолжая таким образом до правого конца балки, мы заканчиваем сдвигом 3000 фунтов, что равно нагрузке на свободный конец.
Следует отметить, что диаграмма сдвига при равномерной нагрузке представляет собой прямую линию с наклоном вниз вправо (см. рис. 5.21). Поэтому диаграмма сдвига была завершена путем соединения нанесенных точек прямыми линиями.
Диаграммы сдвига для часто встречающихся условий нагружения приведены на рис. 5.30 до 5.41.
Неуравновешенный момент внешних сил относительно вертикального сечения балки называется изгибающим моментом. Он равен алгебраической сумме моментов относительно сечения внешних сил, лежащих по одну сторону сечения. Моменты по часовой стрелке считаются положительными, моменты против часовой стрелки отрицательными, когда рассматриваемые силы лежат слева от сечения.
Таким образом, когда изгибающий момент положительный, нижняя часть балки находится в напряжении.
Диаграмма, на которой изгибающий момент в каждой точке по длине балки нанесен по оси ординат, называется диаграммой изгибающего момента.
На рис. 5.20в представлена диаграмма изгибающих моментов для балки, нагруженной сосредоточенными нагрузками только на рис. 5.20а. Изгибающий момент на опорах для этой свободно опертой балки, очевидно, равен нулю. Между опорами и первой нагрузкой изгибающий момент пропорционален расстоянию от опоры, поскольку он равен произведению реакции на расстояние от опоры. Следовательно, диаграмма изгибающего момента для этой части балки представляет собой наклонную прямую линию.
Изгибающий момент под нагрузкой в 6000 фунтов на рис. 5.20а с учетом только силы слева составляет 7000 x 10, или 70 000 фут-фунтов. Таким образом, диаграмма изгибающего момента между левой опорой и первой сосредоточенной нагрузкой представляет собой прямую линию, восходящую от нуля на левом конце балки до 70 000 футо-фунтов, построенную в удобном масштабе под 6000 фунтов.
нагрузка.
Изгибающий момент под нагрузкой в 9000 фунтов, учитывая силы слева от нее, составляет 7000 x 20 – 6000 x 10, или 80 000 футо-фунтов. (Его можно было бы легче получить, рассматривая только силу справа, обращая соглашение о знаках:
8000 x 10 = 80 000 ft-lb.) Поскольку между двумя сосредоточенными нагрузками нет нагрузок, диаграмма изгибающего момента между двумя секциями представляет собой наклонную прямую линию.
Если известны изгибающий момент и поперечный момент в каком-либо сечении балки, можно рассчитать изгибающий момент в любом другом сечении при условии, что между двумя сечениями нет неизвестных сил. Правило:
Изгибающий момент в любом сечении балки равен изгибающему моменту в любом сечении слева, плюс сдвиг в этом сечении, умноженный на расстояние между сечениями, за вычетом моментов промежуточных нагрузок. Если раздел с известным моментом и долей находится справа, соглашение о знаках должно быть изменено на противоположное.
Например, изгибающий момент под нагрузкой в 9000 фунтов на рис.
5.20а также мог быть получен из момента под нагрузкой в 6000 фунтов и сдвига справа от нагрузки в 6000 фунтов, указанных на диаграмме сдвига ( рис. 5.20б). Таким образом, 80 000 = 70 000 + 1000 x 10. Если бы между двумя сосредоточенными нагрузками были какие-либо другие нагрузки, момент этих нагрузок на секцию под нагрузкой в 9000 фунтов был бы вычтен.
Диаграммы изгибающих моментов для часто встречающихся условий нагружения приведены на рис. 5.30 до 5.41. Они могут быть объединены для получения изгибающих моментов для других нагрузок.
Когда балка несет равномерную нагрузку, диаграмма изгибающего момента не состоит из прямых линий. Рассмотрим, например, балку на рис. 5.21а, которая несет равномерную нагрузку по всей своей длине. Как показано на рис. 5.21c, диаграмма изгибающего момента для этой балки представляет собой параболу.
Наклон кривой изгибающего момента для любой точки балки равен сдвигу в этой точке; то есть
Одним из наиболее полезных инструментов для решения задач, связанных с переменными или подвижными нагрузками, является линия влияния.
В то время как диаграммы сдвига и моментов оценивают влияние нагрузок на все участки конструкции, линия влияния показывает воздействие на заданное сечение единичной нагрузки, приложенной в любой точке конструкции.
Например, чтобы построить линию влияния изгибающего момента в некоторой точке A на балке, единичная нагрузка приложена в некоторой точке B. Изгибающий момент A из-за единичной нагрузки в B отображается как ордината для удобного масштаб в B. Та же самая процедура выполняется в каждой точке вдоль луча, и через полученные таким образом точки проводится кривая.
На самом деле единичную нагрузку нет необходимости размещать в каждой точке. Уравнение линии влияния можно определить, поместив нагрузку в произвольную точку и вычислив изгибающий момент в общих чертах. (См. также ст. 5.10.5.)
На рисунке 5.22b показана линия влияния изгибающего момента в центре балки. По внешнему виду она напоминает диаграмму изгибающих моментов для нагрузки в центре балки, но ее значение совершенно иное.
Каждая ордината указывает момент в середине пролета для нагрузки в соответствующем месте. Это указывает на то, что если единичная нагрузка помещена на расстоянии xL от одного конца, она создает изгибающий момент 1–2 xL в центре пролета.
На рис. 5.22c показана линия влияния сдвига в четверти балки.
Когда нагрузка находится справа от точки четверти, сдвиг положительный и равен левой реакции. Когда нагрузка направлена влево, сдвиг отрицателен и равен правой реакции.
На диаграмме показано, что для обеспечения максимального сдвига в точке четверти нагрузки должны быть размещены только справа от точки четверти, при этом наибольшая нагрузка должна быть в точке четверти, если это возможно. При равномерной нагрузке максимальный сдвиг возникает, когда нагрузка простирается от правого конца балки до точки четверти.
Предположим, например, что балка представляет собой балку крана с пролетом 60 футов. Нагрузки на колеса составляют 20 и 10 тысяч фунтов соответственно и расположены на расстоянии 5 футов друг от друга.
Для максимального сдвига в точке четверти колеса должны располагаться так, чтобы колесо на 20 кипов было расположено в этой точке, а колесо на 10 килов – справа от него. Соответствующие ординаты линии влияния (рис. 5.22c) равны 3×4 и 40×45 x 3×4. Следовательно, максимальный сдвиг составляет 20 x 3×4 + 10 x 40×45 x 3×4 = 21,7 тысячи фунтов.
На рис. 5.22d показаны линии влияния изгибающего момента в нескольких точках балки. Примечательно, что вершины диаграмм приходятся на параболу, показанную пунктирной линией. Это указывает на то, что максимальный момент, создаваемый в любом заданном сечении одной сосредоточенной нагрузкой, движущейся поперек балки, возникает, когда нагрузка находится в этом сечении. Величина максимального момента увеличивается, когда сечение перемещается к середине пролета, в соответствии с уравнением, показанным на рис. 5.22d для параболы.
Когда на пролет действует более одной нагрузки, линия влияния полезна при разработке критерия для определения положения нагрузок, при которых изгибающий момент является максимальным в данном сечении.
Максимальный изгибающий момент будет возникать в сечении C простой балки, когда нагрузки перемещаются поперек него, когда одна из нагрузок находится в точке C. Надлежащей нагрузкой для приложения C является та, для которой выражение Wa /a Wb /b (рис. 5.23) меняет знак при переходе нагрузки с одной стороны C на другую.
Когда несколько нагрузок перемещаются по простой балке, максимальный изгибающий момент, создаваемый в балке, может быть вблизи, но не обязательно в середине пролета. Чтобы найти максимальный момент, сначала определите положение нагрузок для максимального момента в середине пролета. Затем перемещайте нагрузки до тех пор, пока нагрузка Р2, находившаяся в центре балки, не окажется на таком же расстоянии от середины пролета, как равнодействующая всех нагрузок на пролет находится на другой стороне середины пролета (рис. 5.24). Максимальный момент будет иметь место при P2.
Когда другие нагрузки перемещаются по пролету или за его пределы во время смещения P2 от середины пролета, может потребоваться исследовать момент под одним из других
загружается, когда он и результирующая равноудалены от середины пролета.
Чтобы вывести обычно используемую формулу изгиба для расчета изгибающих напряжений в балке, мы должны сделать следующие предположения:
1. Единичное напряжение в точке в любой плоскости, параллельной нейтральная поверхность балки пропорциональна единичной деформации в плоскости в точке.
2. Модуль упругости при растяжении такой же, как и при сжатии.
3. Общая и единичная осевая деформация в любой плоскости, параллельной нейтральной поверхности, пропорциональны расстоянию этой плоскости от нейтральной поверхности. (Плоские сечения до изгиба остаются плоскими после изгиба. Это требует, чтобы все плоскости имели одинаковую длину перед изгибом, таким образом, чтобы балка была прямой.)
4. Нагрузки действуют в плоскости, содержащей центральную ось балки. и перпендикулярны этой оси. Кроме того, нейтральная поверхность перпендикулярна плоскости нагрузок. Таким образом, плоскость нагрузок должна содержать ось симметрии каждого поперечного сечения балки.
(Формула изгиба не применяется к балке, нагруженной несимметрично. См. ст. 5.5.18 и 5.5.19..)
5. Балка рассчитана таким образом, чтобы исключить предварительное разрушение или серьезную деформацию в результате скручивания, местного коробления, сдвига или любой другой причины, кроме изгиба.
Приравнивая изгибающий момент к моменту сопротивления из-за внутренних напряжений в любом сечении балки, получаем, что M – изгибающий момент в сечении, Æ’ – нормальное единичное напряжение в плоскости на расстоянии c от нейтральной оси (рис. 5.25), а I — момент инерции поперечного сечения относительно нейтральной оси
. Если Æ’ указано в фунтах на квадратный дюйм (psi), I в дюймах4, а c в дюймах, то M будет выражено в дюйм-фунтах. Для максимального единичного напряжения c – это расстояние до самого дальнего волокна. См. также Искусство. 5.5.11 и 5.5.12.
Нейтральная ось в симметричной балке совпадает с центральной осью;
, т. е. в любом сечении нейтральная ось расположена так, что
Значения I для нескольких распространенных типов поперечного сечения приведены на рис.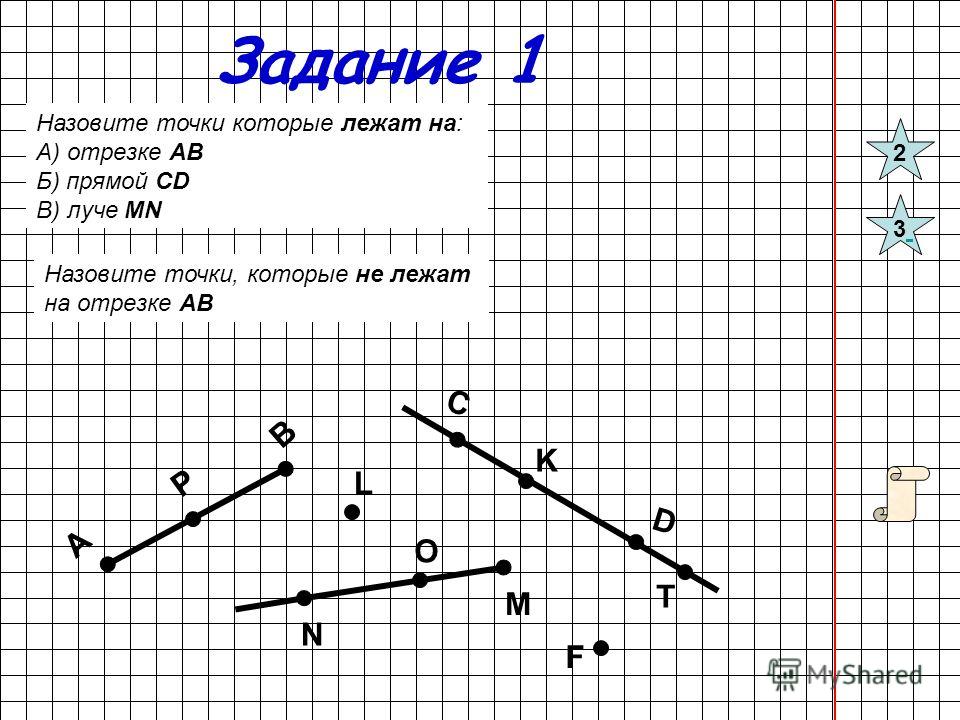
5.26. Значения для сечений из конструкционной стали представлены в руководствах Американского института стальных конструкций, Чикаго, штат Иллинойс. Когда требуются моменты инерции сечений других типов, их можно вычислить непосредственно с помощью уравнения. (5.56) или разбивая сечение на составляющие, для которых известен момент инерции.
Если I — момент инерции относительно нейтральной оси, A — площадь поперечного сечения, а d — расстояние между этой осью и параллельной осью в плоскости поперечного сечения, то момент инерции относительно параллельной оси равен
С помощью этого уравнения известный момент инерции компонента сечения относительно нейтральной оси компонента может быть перенесен на нейтральную ось полного сечения. Затем суммирование переданных моментов инерции для всех компонентов дает момент инерции всего сечения.
Когда моменты инерции площади относительно любых двух перпендикулярных осей известны, момент инерции относительно любой другой оси, проходящей через точку пересечения двух осей, может быть получен с помощью
две перпендикулярные оси, проходящие через точку, относительно которой моменты инерции максимальны и минимальны, называются главными осями.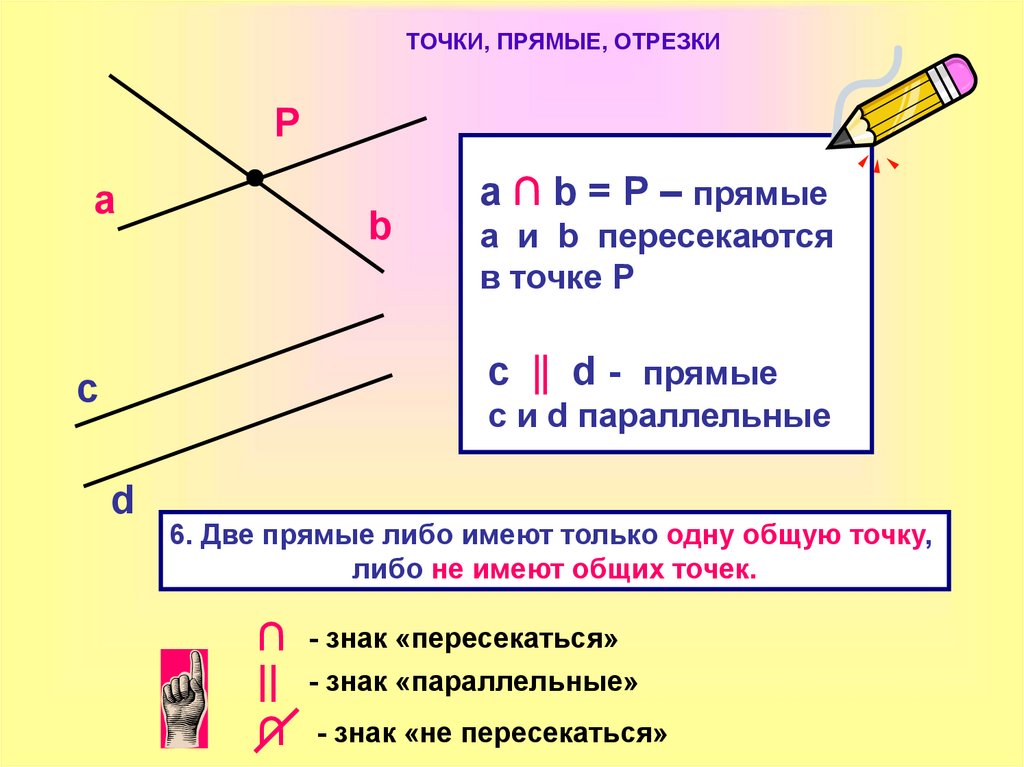
Произведения инерции равны нулю для главных осей.
Отношение S I /c в уравнении. (5.54) называется модулем сечения. I — момент инерции поперечного сечения относительно нейтральной оси, а c — расстояние от нейтральной оси до самого дальнего волокна. Значения S для распространенных типов сечений приведены на рис. 5.26.
Вертикальному сдвигу в любом сечении балки сопротивляются неравномерно распределенные вертикальные единичные напряжения (рис. 5.27). В каждой точке сечения также существует горизонтальное единичное напряжение, равное по величине вертикальному единичному касательному напряжению [см. (5.34)].
На любых расстояниях y от нейтральной оси как горизонтальное, так и вертикальное единичные напряжения сдвига равны
То есть максимальное напряжение сдвига на 50% больше, чем среднее напряжение сдвига по сечению. Точно так же для круглого луча максимальное значение на одну треть больше среднего.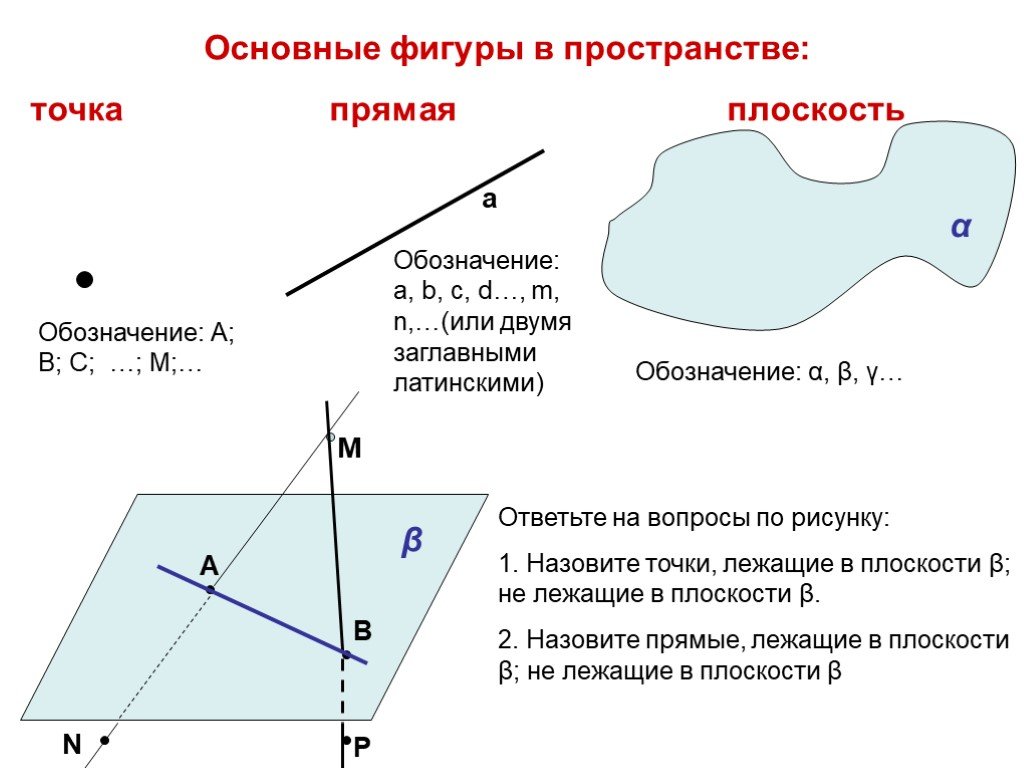
Однако для двутавровой балки максимальное напряжение сдвига в стенке ненамного превышает среднее значение только для сечения стенки, если предполагается, что полки не испытывают сдвиг.
Для глубоких балок на коротких пролетах и балок из низкопрочных материалов иногда необходимо определить максимальное напряжение Æ’ на наклонной плоскости, вызванное сочетанием напряжения сдвига и изгиба v и Æ’ соответственно. Это напряжение Æ’, которое может быть растяжением или сжатием, больше нормального напряжения. Его значение может быть получено путем применения круга Мора (ст. 5.3.6), как показано на рис. 5.10, но с Æ’y = 0 и равно
Тангенциальное отклонение t точки на кривой упругости представляет собой расстояние этой точки, измеренное в направлении, перпендикулярном исходному положению балки, от касательной, проведенной в какой-либо другой точке на упругая кривая.
Уравнение (5.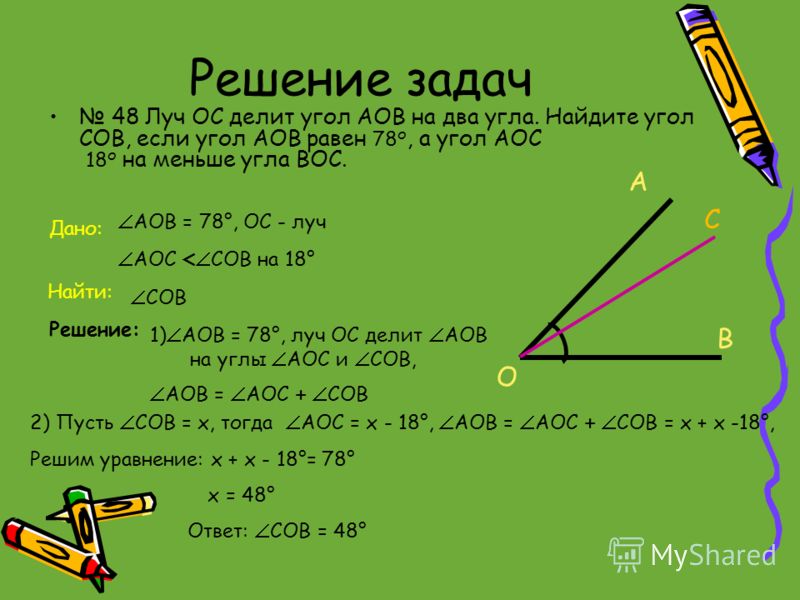
64) показывает, что тангенциальное отклонение любой точки по отношению ко второй точке кривой упругости равно моменту относительно первой точки диаграммы M/EI между двумя точками. Метод момент-площадь для определения отклонения балок – это метод, в котором уравнения. (5.63) и (5.64).
Предположим, например, что прогиб в середине пролета должен быть рассчитан для балки однородного поперечного сечения с сосредоточенной нагрузкой в центре (рис. 5.28).
Поскольку прогиб в середине пролета для этой нагрузки является максимальным для пролета,
наклон кривой упругости в центре балки равен нулю; т. е. касательная параллельна неотклоненному положению луча. Следовательно, отклонение любой опоры от касательной середины пролета равно отклонению в центре балки. Тогда по теореме момент-площадь [уравнение. (5.64)], прогиб yc определяется моментом относительно любой из опор области диаграммы M/EI, заключенной между ординатой в центре балки и этой опорой.
В общем случае это справедливо для всех простых балок независимо от типа нагрузки.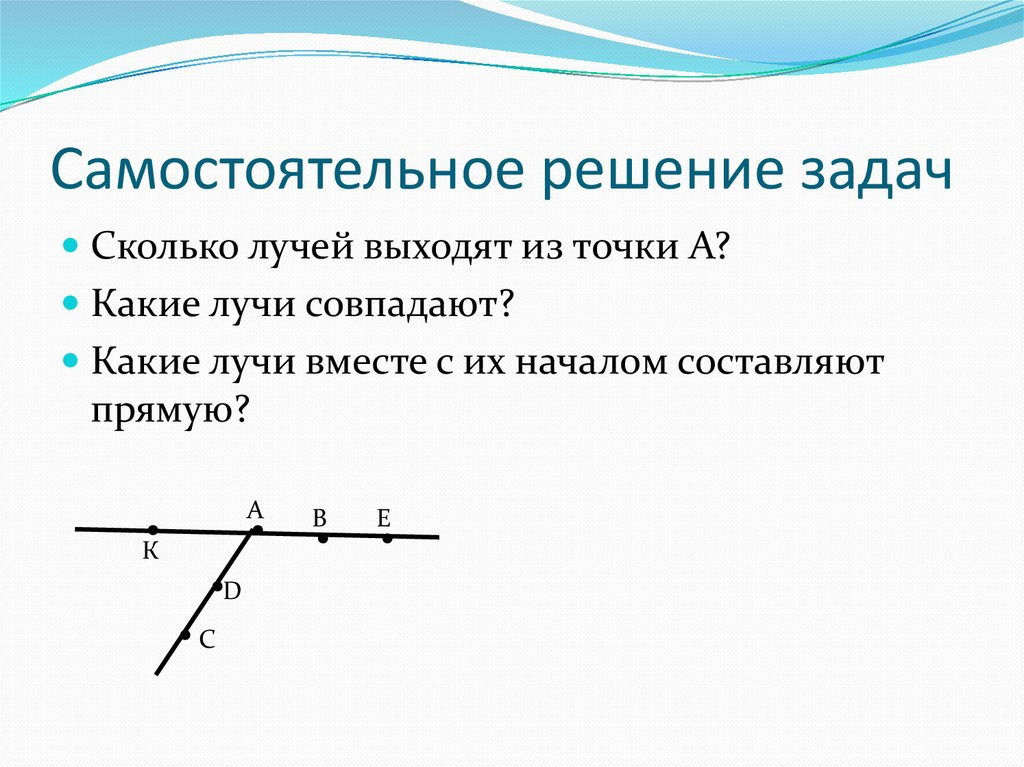
Процедура применения уравнения. (5.65) для прогиба нагруженной балки на рис. 5.28 эквивалентно нахождению изгибающего момента в D с диаграммой M / EI, служащей диаграммой нагрузки. Метод применения диаграммы M/EI в качестве нагрузки и определения прогиба в виде изгибающего момента известен как метод сопряженной балки.
Сопряженный луч должен иметь ту же длину, что и заданный луч; он должен быть в равновесии с нагрузкой M/EI и реакциями, вызываемыми нагрузкой; а изгибающий момент в любом сечении должен быть равен прогибу данной балки в соответствующем сечении. Последнее требование эквивалентно требованию, чтобы сдвиг на любом сечении сопряженной балки с нагрузкой М/ЭИ был равен наклону кривой упругости на соответствующем сечении данной балки. Рисунок 5.29показаны сопряжения для различных типов балок.
Прогибы для нескольких видов нагружения простых балок приведены на рис. 5,30–5,35, а для выступающих балок и консолей на рис. 5,36 до 5,41.
Когда балка несет несколько нагрузок разных типов, наиболее удобный метод расчета ее прогиба, как правило, состоит в том, чтобы найти прогибы отдельно для равномерных и сосредоточенных нагрузок и сложить их.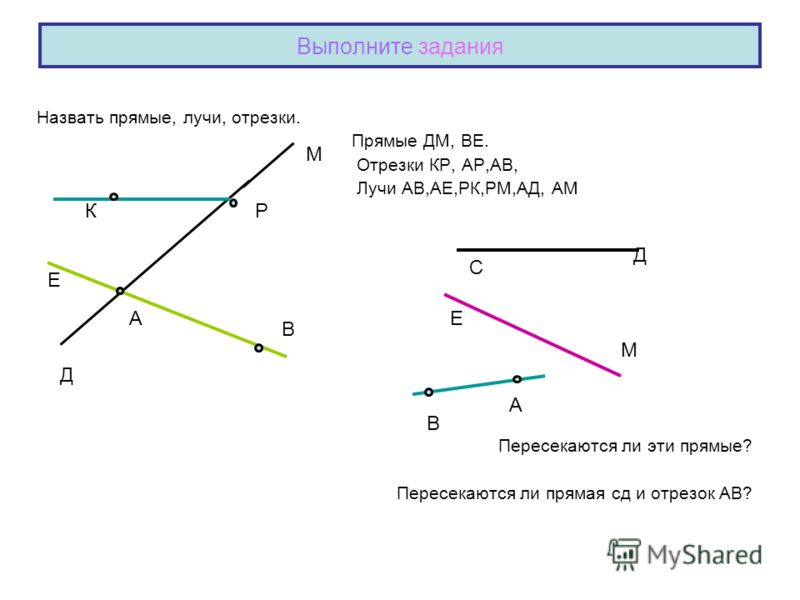
Для нескольких сосредоточенных нагрузок самым простым решением является применение теоремы взаимности (статья 5.10.5). Согласно этой теореме, если к балке в точке A приложена сосредоточенная нагрузка, прогиб, который она производит в точке B, равен прогибу в A для той же нагрузки, приложенной в B (dAB дБA).
Предположим, например, что необходимо вычислить прогиб середины пролета. Затем предположим , что каждая нагрузка по очереди приложена к центру балки, и вычислите отклонение в точке, где она первоначально была приложена, по уравнению упругой кривой , приведенному на рис. 5.33. Сумма этих прогибов является полным прогибом в середине пролета.
Еще один способ расчета прогибов балок представлен в ст. 5.10.4. Этот метод также может применяться для определения отклонения балки из-за сдвига.
Для жестких балок, подвергающихся как поперечной, так и осевой нагрузке, напряжения задаются по принципу суперпозиции, если отклонением из-за изгиба можно пренебречь без серьезной ошибки.
То есть полное напряжение задается с достаточной точностью в любом сечении суммой осевого напряжения и напряжения изгиба. Максимальное напряжение равно
Когда отклонение из-за изгиба велико, а осевая нагрузка вызывает изгиб
напряжений, которыми нельзя пренебречь, максимальное напряжение определяется как
Внецентренная продольная нагрузка в плоскости симметрии создает изгибающий момент Pe, где e – расстояние нагрузки от центральной оси. Суммарная единица
На рисунке 5.26 приведены значения радиуса инерции для некоторых часто используемых поперечных сечений.
Для осевой сжимающей нагрузки, если в поперечном сечении не должно быть растяжения, e не должно превышать r2 /c. Следовательно, для прямоугольного сечения шириной b и глубиной d эксцентриситет должен быть меньше b/6 и d/6; т. е. нагрузка не должна прикладываться за пределами средней трети. Для круглого поперечного сечения диаметром D эксцентриситет не должен превышать D/8.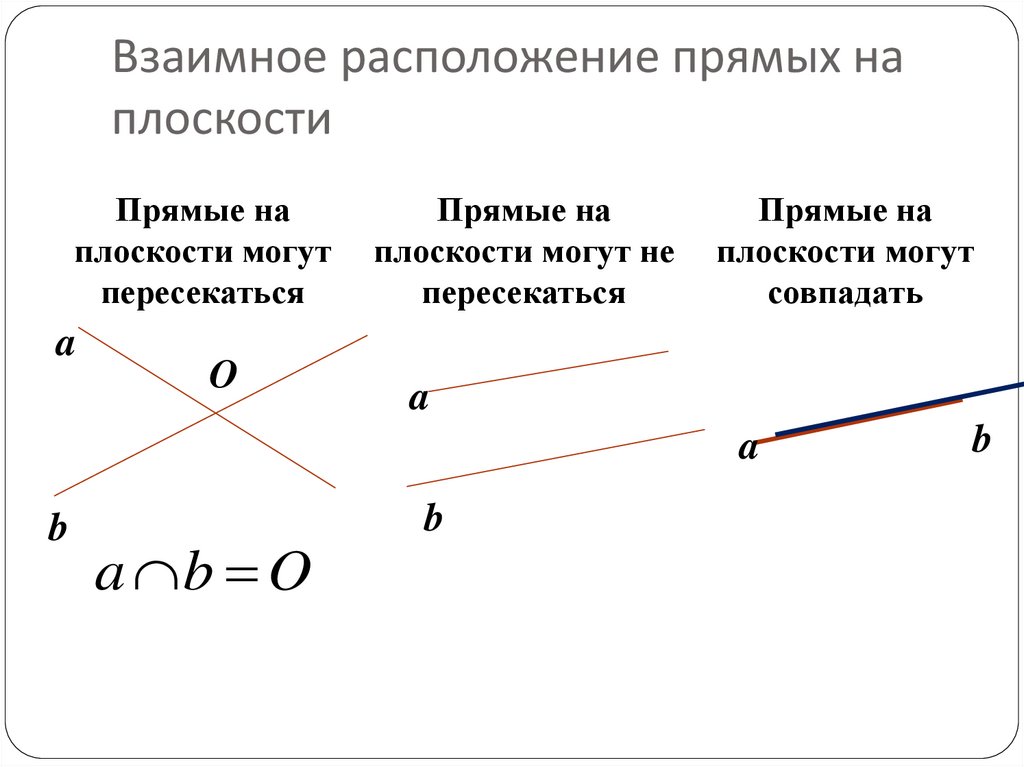
Когда внецентренная продольная нагрузка вызывает прогиб слишком большой, чтобы им можно было пренебречь при расчете изгибающего напряжения, необходимо учитывать дополнительный изгибающий момент Pd, где d – прогиб. Это отклонение может быть вычислено с помощью уравнения (5.62) или приблизительно
Главные оси — это две перпендикулярные оси, проходящие через центр тяжести, для которых моменты инерции максимальны или минимальны и для которых произведения инерции равны нулю.
Изгиб, вызванный нагрузками, которые не лежат в плоскости, содержащей главную ось каждого поперечного сечения балки, называется несимметричным изгибом. Если ось изгиба балки лежит в плоскости нагрузок, для исключения кручения (см. ст. 5.4.1), а если нагрузки перпендикулярны оси изгиба, для исключения осевых составляющих, напряжение в любой точке в поперечное сечение определяется как
При выводе формулы изгиба Æ’ = Mc/I [уравнение.
(5.54)] делается допущение, что балка изгибается без кручения в плоскости нагрузок и что нейтральная поверхность перпендикулярна плоскости нагрузок. Эти допущения верны для балок с поперечными сечениями, симметричными относительно двух осей, когда плоскость нагрузок содержит одну из этих осей. Они не обязательно верны для лучей, которые не являются дважды симметричными. Причина в том, что в пучках, дважды симметричных
метрическая ось изгиба совпадает с центральной осью, тогда как в несимметричных сечениях две оси могут быть отдельными. В последнем случае, если плоскость нагрузок содержит центральную ось, но не ось изгиба, балка будет подвергаться как изгибу, так и кручению.
Ось изгиба может быть определена как продольная линия в балке, через которую должны проходить поперечные нагрузки, чтобы предотвратить скручивание балки при ее изгибе. Точка в каждом сечении, через которую проходит ось изгиба, называется центром сдвига или центром кручения. Центр сдвига также является центром вращения сечения при чистом кручении (ст.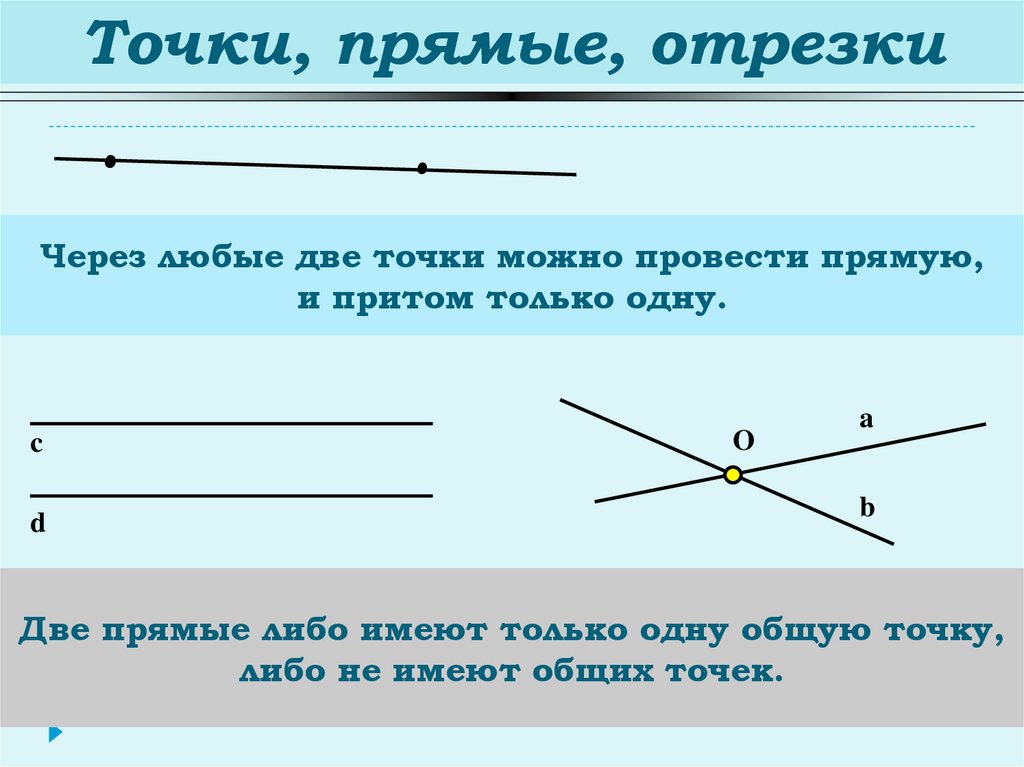
5.4.1).
Вычисление напряжений и деформаций в элементах, подвергающихся как изгибу, так и кручению, затруднено, поскольку необходимо учитывать деформацию поперечного сечения и коробление. Предпочтительно, скручивание следует предотвращать с помощью раскосов или избегать путем выбора соответствующих форм для элементов, а также путем размещения и направления нагрузок, проходящих через ось изгиба.
(Ф. Блейх, Прочность металлических конструкций на разрыв, издательство McGraw-Hill Publishing Company, Нью-Йорк.)
исследования
человек
курсы
блог
Чтобы рассчитать напряжение (и, следовательно, деформацию), вызванное изгибом, нам нужно понять, где находится нейтральная ось балки, и как рассчитать второй момент площади для данного поперечного сечения.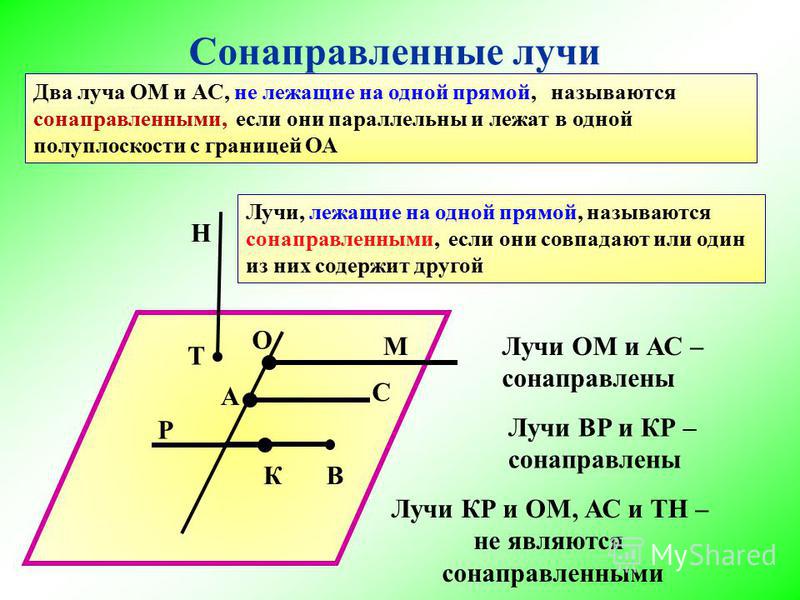
Начнем с того, что представим себе произвольное поперечное сечение — что-то не круглое, не прямоугольное и т. д.
На изображении выше произвольная форма имеет площадь, обозначенную A . Мы можем посмотреть на небольшую дифференциальную область dA , которая существует на расстоянии x и y от начала координат. Мы можем посмотреть на первый момент площади в каждом направлении из следующих формул:
Первый момент площади — это интеграл длины по площади — это означает, что он будет иметь единицы длины в кубе [L 3 ]. Это важно, потому что помогает нам найти центр тяжести объекта. Центроид определяется как «среднее 9 0274 x (или y ) позиции области”. Математически это утверждение выглядит так:
Крайняя правая часть приведенных выше уравнений будет очень полезна в этом курсе — она позволяет нам разбить сложную фигуру на простые формы с известными площадями и известным расположением центроидов.
В большинстве инженерных сооружений есть хотя бы одна ось симметрии — и это позволяет значительно упростить нахождение центроида. Центроид должен располагаться на оси симметрии . Например:
Для поперечного сечения слева мы знаем, что центроид должен лежать на оси симметрии, поэтому нам нужно найти только центроид вдоль оси y . Поперечное сечение справа еще проще — поскольку центроид должен совпадать с осями симметрии, он должен быть в центре объекта.
Теперь, когда мы знаем, как найти центр тяжести, мы можем обратить внимание на второй момент площади. Как вы, возможно, помните из предыдущего раздела о кручении, это определяется как:
И, наконец, иногда нам нужно будет определить второй момент площади относительно произвольной оси x или y , которая не соответствует центроиду. В этом случае мы можем использовать теорему о параллельных осях для его вычисления. В этом случае мы используем второй момент площади относительно центроида плюс термин, который включает расстояния между двумя осями.
Это уравнение называется теоремой о параллельных осях . Это будет очень полезно на протяжении всего курса. Как описано во вступительном видео к этому разделу, вычисление второго момента площади простой формы может быть простым. Для более сложных форм нам потребуется вычислить I путем вычисления отдельных I для каждой простой формы и объединения их вместе с использованием теоремы о параллельных осях.
Диаграммы сдвига и момента Поперечная нагрузка относится к силам, которые перпендикулярны длинной оси конструкции. Эти поперечные нагрузки вызовут изгибающий момент M , который вызывает нормальное напряжение , и поперечную силу V , которая вызывает касательное напряжение . Эти силы могут и будут варьироваться по длине балки, и мы будем использовать диаграммы сдвига и момента (диаграмма VM) для извлечения наиболее подходящих значений.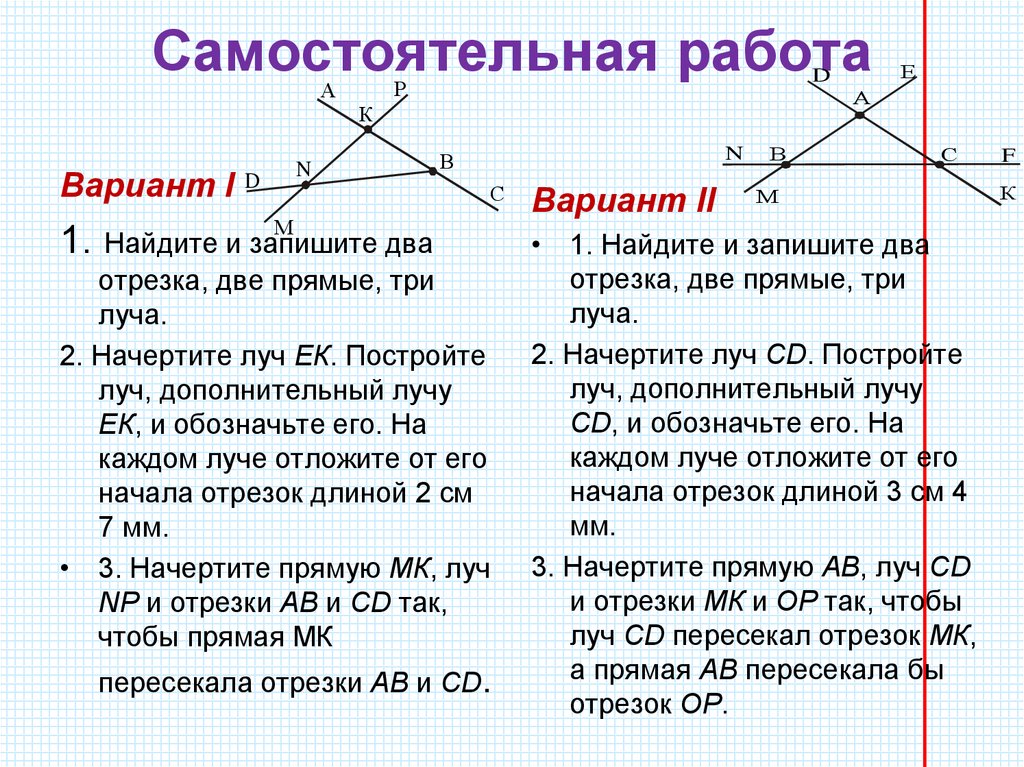
Построение этих диаграмм должно быть вам знакомо по статике , но мы рассмотрим их здесь. При исследовании балки с поперечной нагрузкой необходимо учитывать два важных момента:
Знание нагрузок и опор позволит вам начертить качественную диаграмму V-M, а затем статический анализ свободного тела поможет вам определить количественное описание кривых. Начнем с того, что вспомним наши соглашения о знаках .
Эти соглашения о знаках должны быть знакомы. Если сдвиг вызывает вращение против часовой стрелки, он положительный. Если момент изгибает луч таким образом, что луч изгибается в «улыбку» или U-образную форму, он положительный. Лучший способ вспомнить эти диаграммы — это проработать пример.
Начните с этой консольной балки — отсюда вы можете переходить к более сложным нагрузкам.
Во многих отношениях изгиб и кручение очень похожи. Изгиб возникает из-за приложенной пары или изгибающего момента M . Как и при кручении, при чистом изгибе в материале есть ось, на которой напряжение и деформация равны нулю. Это называется нейтральной осью . И, как и при кручении, напряжение уже не одинаково по сечению конструкции — оно меняется. Давайте начнем с того, что рассмотрим момент о z – ось изгибает конструкцию. В данном случае мы не будем ограничиваться круглыми сечениями – на рисунке ниже рассмотрим призматическое сечение.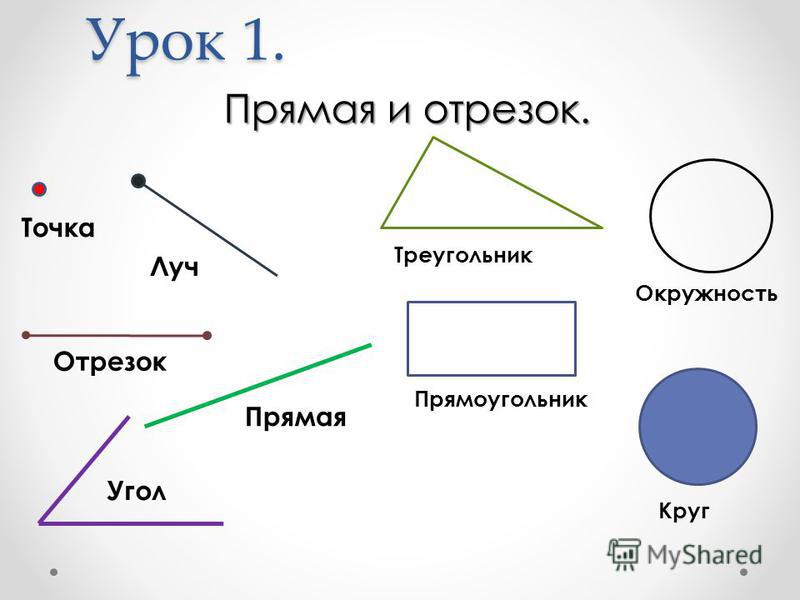
Прежде чем мы углубимся в математику изгиба, давайте попробуем понять его концептуально. Возможно, лучший способ увидеть, что происходит, — наложить изогнутую балку поверх оригинальной прямой балки.
Теперь вы можете заметить, что нижняя поверхность луча стала длиннее, а верхняя поверхность луча стала короче. Также по центру луча длина вообще не изменилась – соответствует нейтральной оси. Повторяя это язык этого класса, мы можем сказать, что нижняя поверхность находится под напряжением, а верхняя поверхность находится под сжатием. Кое-что, что является немного более тонким, но все еще можно наблюдать из наложенного выше изображения, заключается в том, что смещение луча изменяется линейно сверху вниз, проходя через ноль на нейтральной оси. Помните, это именно то, что мы видели и при кручении — напряжение линейно менялось от центра к центру. Мы можем посмотреть на это распределение напряжений по поперечному сечению балки немного более явно:
Теперь мы можем найти математическую связь между приложенным моментом и напряжением внутри балки.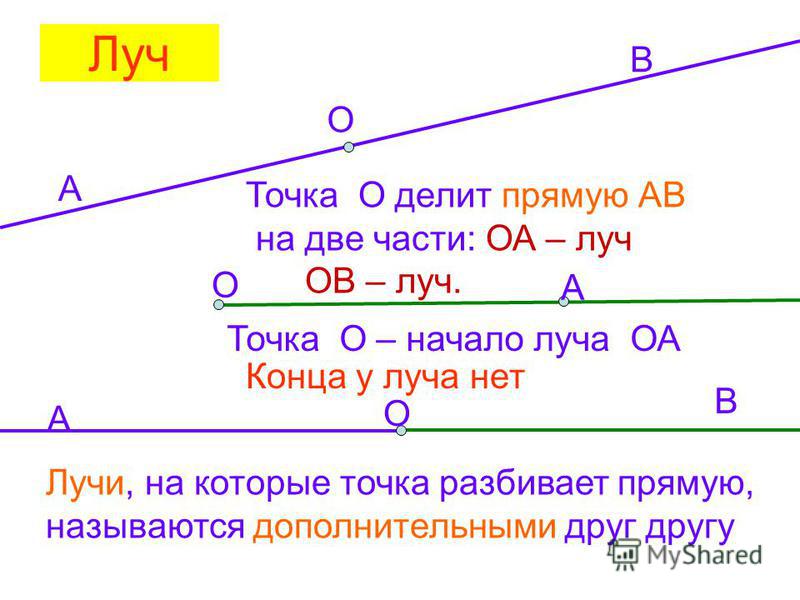
Мы уже упоминали, что балка деформируется линейно от одного края к другому — это означает, что деформация в направлении x увеличивается линейно с расстоянием вдоль оси y- (или по толщине балки). Таким образом, деформация будет максимальной при растяжении при y = -c (поскольку y=0 находится на нейтральной оси, в данном случае в центре балки), и будет максимальной при сжатии при y=c . Мы можем записать это математически следующим образом:
Теперь это говорит нам кое-что о деформации, что мы можем сказать о максимальных значениях напряжения? Начнем с умножения обеих частей уравнения на E , модуль упругости Юнга. Теперь наше уравнение выглядит так:
Используя закон Гука, мы можем связать эти величины с фигурными скобками под ними с напряжением в направлении x и максимальным напряжением. Что дает нам это уравнение для напряжения в направлении x-:
Наш последний шаг в этом процессе — понять, как изгибающий момент связан с напряжением.
Для этого вспомним, что момент — это произведение силы на расстояние. Если мы можем представить себе, что смотрим только на очень маленький элемент в луче, дифференциальный элемент, то мы можем записать это математически как:
Поскольку в нашем уравнении есть дифференциалы, мы можем определить момент M , действующий на площадь поперечного сечения балки, путем интегрирования обеих частей уравнения. И если мы вспомним наше определение напряжения как силы на единицу площади, мы можем написать:
Последний член в последнем уравнении — интеграл по y в квадрате — представляет второй момент площади относительно оси z (из-за того, как мы определили наши координаты). В декартовых координатах этот второй момент площади обозначается I (в цилиндрических координатах, помните, обозначался J ). Теперь мы можем, наконец, записать наше уравнение для максимального напряжения и, следовательно, напряжения в любой точке вдоль оси y , как:
Важно отметить, что нижние индексы в этом уравнении и направление вдоль поперечного сечения (здесь оно измеряется вдоль y ) будут меняться в зависимости от характера проблемы, то есть направления момента — по какой оси находится луч.
сгибаясь? Мы основывали наши обозначения на изображении изогнутой балки на первом изображении этого урока.
Помните, в начале раздела я упомянул, что изгиб и кручение на самом деле очень похожи? На самом деле мы очень ясно видим это в последнем уравнении. В обоих случаях напряжение (нормальное для изгиба и сдвиговое для кручения) равно пар/момент ( M для изгиба и T для кручения), умноженных на положение вдоль поперечного сечения. , , потому что напряжение неравномерно по поперечному сечению (с декартовыми координатами для изгиба и цилиндрическими координатами для кручения), все делится на второй момент площади поперечного сечения.
Сводка На этом уроке мы узнали о моментах площади и диаграммах момента сдвига . Из первого момента площади поперечного сечения мы можем вычислить центроид .
Мы узнали, как вычислить 90 266 секундный момент площади 90 267 в декартовых и полярных координатах, и мы узнали, как теорема о параллельной оси позволяет нам вычислить второй момент площади относительно центра тяжести объекта — это полезно для разбиения сложного поперечного сечения на несколько простых фигур и объединение их вместе. Мы пересмотрели концепцию диаграммы сдвига и момента из статики. Эти диаграммы будут необходимы для определения максимальной силы сдвига и изгибающего момента вдоль сложно нагруженной балки, что, в свою очередь, потребуется для расчета напряжений и прогнозирования разрушения. Наконец, мы узнали о нормальном напряжении от изгиба балки. И напряжение, и деформация изменяются по поперечному сечению балки, при этом одна поверхность растягивается, а другая сжимается. Плоскость, проходящая через центр тяжести, образует нейтральную ось — вдоль нейтральной оси нет напряжений или деформаций. Напряжение является функцией приложенного момента и второго момента площади относительно оси, вокруг которой находится момент.