Министерство образования и науки Российской Федерации
Областное государственное образовательное учреждение
Новосибирский педагогический колледж №1 им.А.А.Макаренко
КОНСПЕКТ
ЗАНЯТИЯ ПО МАТЕМАТИКЕ
В старшей группе д/с №33
Длительность: 25 – 30 мин.
Дата проведения:
Провела: Сухина Наталья Александровна
студентка 506 группы
Новосибирск, 2008г.
КОНСПЕКТ ЗАНЯТИЯ ПО МАТЕМАТИКЕ
ТЕМА:
Числа и цифры 1,2,3, 4, 5, 0, знак -, логическая задача на установление закономерностей, геометрические фигуры, знакомство с названием месяца – ноябрь.
ЗАДАЧИ:
– учить решать математическую задачу, записывать решение с помощью знаков, цифр;
-познакомить со знаком «минус»;
ХОД ЗАНЯТИЯ
Вопросы.
Предложите детям составить задачу про птичек. Если дети затрудняются, составьте ее сами. На ветке сидели четыре птички, а затем четыре улетели. Сколько птичек осталось на ветке? (Ни одной.)
Скажите, что если в задаче кто-то улетает, уходит, уезжает, то пишется знак«-» (Он написан в правом уголке.)
Прочитайте стихотворение о знаке «минус».
Я – минус,
Тоже добрый знак.
Ведь не со зла я отнимаю,
А роль свою лишь выполняю.
Дайте задание записать решение задачи: 4 – 4.
Уточните, что на нижней ветке нет ни одной птички. Это можно записать цифрой 0.
2. Знакомство с цифрой 0
Прочитайте стихотворение И. Блюмкина:
Цифру ноль ты раньше знал:
Это круг или овал.
Задания.
3. Физкультминутка «Теремок».
Кисти рук подняты на уровень шеи, концы пальцев соединены, изображают крышу.
Стоит в поле теремок, (Пальцы раздвинуты в стороны.)
На двери висит замок. (Пальцы переплетены в замок.)
Открывает его волк (Движения сомкнутыми кистями влево-вправо.)
Дерг-дерг, дерг-дерг. (Движения сомкнутыми кистями к себе, от
себя.)
Пришел Петя-Петушок (Пальцы размыкаются, руки занимают
исходное положение.
)
И ключом открыл замок.
4. Игровое упражнение «Дорисуй листья на деревьях»
Перед тем как детям будет предложено выполнить задание, загадайте им загадку:
Черное поле белым стало,
А еще похолодало,
Мерзнет в поле озимь ржи,
Что за месяц, подскажи?
(Ноябрь)
Спросите, как называются два других осенних месяца. (Сентябрь, октябрь.)
Уточните, что в каждом времени года три месяца.
Предложите детям назвать осенние месяцы по порядку (сентябрь, октябрь, ноябрь).
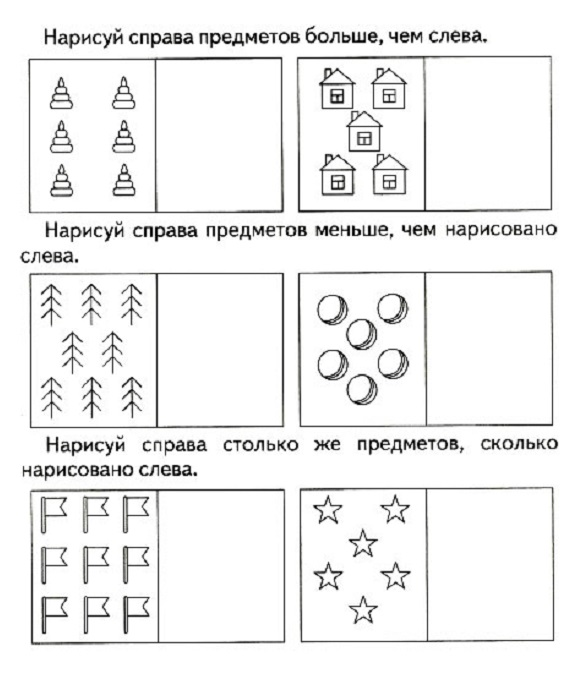
Дайте задание нарисовать столько листьев на деревьях, сколько их было в каждом осеннем месяце (в сентябре много, в октябре поменьше, в ноябре мало).
5. Игра «Найди в группе предметы, похожие на геометрические фигуры».
Предложите детям походить и найти предметы, которые похожи на геометрические фигуры.
(Окна и двери, крышки у стола, книги, коробки похожи на прямоугольник, выключатели – на квадрат, мячи, шары – на круг и т.д.)
6. Игра «Преврати геометрические фигуры в предметы»
Задания.
7. Самоконтроль и самооценка выполненной работы.
Можно использовать два вида самоконтроля и самооценки:
По образцу и по словесной инструкции. Желательно их чередовать
ПО ОБРАЗЦУ:
Покажите детям заранее приготовленную правильно выполненную работу и предложите сравнить свою работу с образцом. Если работа ребенка соответствует образцу, попросите нарисовать внизу зеленый кружок, если есть одна, две ошибки – желтый, если ошибок три и более – красный.
Скажите детям, то эти цвета символизируют светофор: зеленый – все в порядке, можно переходить к следующей страничке; желтый – надо поработать над небольшим количеством ошибок; красный – материал усвоен недостаточно хорошо и прежде, чем перейти к следующей страничке, надо еще поработать над этим заданием.
Образовательная область: «Познавательное развитие» (ФЭМП).
Интеграция образовательных областей: «Речевое развитие (Развитие речи)».
Тип ООД: Познавательно-развивающая.
Возраст детей: 5-6 лет.
Форма проведения ООД: Занятие-путешествие.
Форма организации: Подгрупповая.
Виды детской деятельности: ответы на вопросы, высказывание предположений, выводы.
Дидактические игры: «Сосчитай замки», «Подбери ключ к замку», «Открой крышку сундука», «Сосчитай запасы», «Собери бусы».
Физкультминутка: «Мы устали засиделись».
Цель: закрепление и обобщение полученных знаний.
Задачи:
Образовательные:
Развивающие:
Воспитательные:
Оборудование: магнитная доска, ноутбук.
Демонстрационный материал: сказочные цифры от 1 до10, изображение 8 орехов, 9 грибов, геометрические фигуры (круги, треугольники, квадраты) с точками от 1 до 10.
Раздаточный материал: головоломка «Монгольская игра» на каждого ребенка, геометрические фигуры треугольной (квадратной, круглой) формы, красного (зеленого, синего и желтого цвета) с цифрами от 1 до 10, картинки с предметами от 5 до10, карточки с цифрами то 1 до 10, 6 каштанов,3 желудя, 3 ореха фундука.
Ход занятия
1. Введение ситуациюВоспитатель собирает детей возле себя, в руках держит игрушку белочку.
Воспитатель: Дети, посмотрите, к нам в гости пришла Белочка. Здравствуй, пушистая Белочка. Давайте поздороваемся с Белочкой и скажем ей добрые слова.
Дети здороваются и говорят добрые слова (добрая, ласковая, красивая, пушистая, мягкая и т.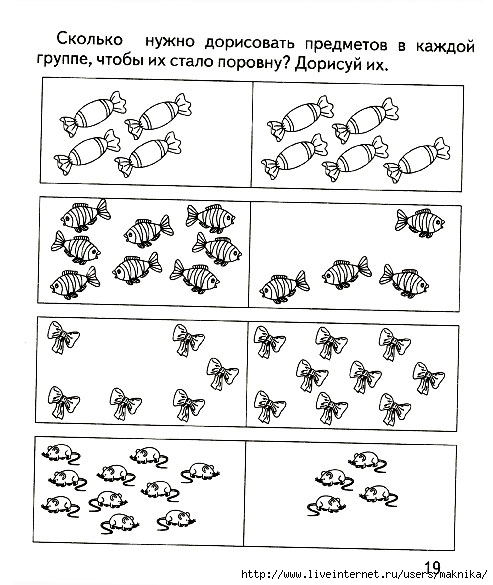
д.)
Белочка: Здравствуйте, ребята. Спасибо вам за добрые слова, присаживайтесь на мои стульчики. Хотела пригласить вас в свой сказочный лес, но на волшебной двери закрылись все замки.
2. Совместная деятельность2.1 Игра «Сосчитай замки»
На магнитной доске геометрические фигуры (круги, треугольники, квадраты) с точками от 1 до 10.
Воспитатель: Чтобы войти в сказочный лес, нам надо узнать, сколько замков открыть.
– Сколько замков получится, если считать с правой стороны? (10)
– Сколько замков получится, если считать с левой стороны? (10)
– Я знаю математический секрет. Если мы хотим узнать, сколько предметов, то не имеет значение, откуда начинать счёт, главное при счете не пропускать ни один предмет и ничего не считать два раза.
– На каком месте справа (слева) находится замок треугольной формы 6-ю кругами?
– На каком месте справа (слева) находится замок круглой формы с двумя кругами? и
т.
д.
– Есть ещё один математический секрет, если надо узнать, на каком месте находится предмет, надо договориться, с какой стороны вести счёт.
– Замки мы сосчитали, а сейчас попробуем их открыть.
2.2. Игра «Подбери ключ к замку»
На столе лежат «ключи» геометрические фигуры треугольной (квадратной, круглой) форм.
– Возьмите каждый по одному ключу. Чтобы открыть замок, надо найти соответствующий ключ и прикрепить его под замком.
Дети выполняют задание самостоятельно.
– Давайте, рассмотрим, все ли замки открыты.
– Рассмотрим первый замок и ключ.
– Какой формы замок и ключ? (Треугольной, круглой, квадратной).
– Какого цвета ключ и круги на замке? (Красного, синего, желтого, зеленого).
– Соответствует ли количество кругов на замке, цифре на ключе. (На замке столько же кружков, сколько показывает цифра на ключе).
– Возьмите свои ключи, чтобы никто не закрыл снова замки.
Белочка: Ой, все замки открылись! Можно войти в мой лес.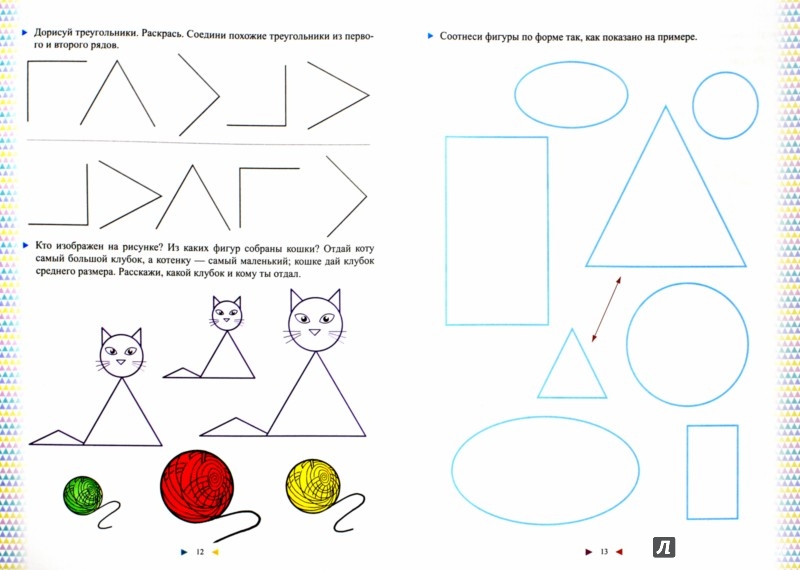
– Раз-два повернитесь, в сказочном лесу очутитесь.
На доске цифры «Веселый счет» С.Я.Маршак
Воспитатель: Ой, и, правда, какой сказочный лес! Посмотрите, какие здесь необычные цифры!
– Сравните свою цифру со сказочной цифрой и поставьте её внизу под сказочной.
– Наши цифры черные строгие, а белочкины сказочные, интересные. Белочка, а мы про твои цифры стихотворение знаем.
Дети читают стихотворение «Веселый счет» С.Я.Маршак.
– Идём дальше.
2.3 Игра «Открой крышку сундука»
На экране изображение закрытого сундука.
Белочка: А вот мой сундук. Там все мои запасы на зиму. Сейчас я вас угощу.
– Ой, а сундук захлопнулся, а замок на сундуке кодовый, помогите мне его раскодировать.
Воспитатель: Надо собрать ключ из частей головоломки «Монгольская игра».
Дети собирают по контуру.
Воспитатель: Если вы правильно расположите все геометрические фигуры, сундук
откроется.
После того как все дети положили фигуры, на экране меняется картинка, появляется изображение открытого сундучка.
Воспитатель: Посмотрите, сундучок открылся.
Белочка: Ребята, помогите сосчитать мои запасы.
2.4. Игра «Сосчитаем запасы»
Дети садятся за столы, на которых находятся листы с нарисованными на них предметами (каштаны, яблоки, ягоды, желуди, грибы, орехи) в количестве от 5 до 10 и карточки с числами от 1 до 10.
Воспитатель: Это сундучок, в котором в коробках лежат запасы Белочки.
– Сколько коробок в сундуке? (6).
– Нужно пересчитать, что лежит в каждой коробке, и рядом поставить соответствующее число.
Дети считают предметы по очереди, согласовывая числительное с существительным. Ставят каждой картинке карточку с соответствующим числом.
На доске у воспитателя 8 орехов и 9 грибов.
Воспитатель: А сколько орехов (грибов) у меня? (8, 9)
– Чего больше (меньше) орехов или грибов?
– На сколько грибов больше чем орехов?
– Как сделать, чтобы орехов и грибов было поровну? Ответы детей.
Физкультминутка «Мы устали, засиделись»
Мы устали, засиделись,
Нам размяться захотелось. Повороты головы
То на стенку посмотрели,
То в окошко поглядели.
Вправо, влево поворот,
А потом наоборот.
Вправо, влево поворот,
А потом наоборот. Повороты корпусом.
Приседанья начинаем,
Ноги до конца сгибаем.
Вверх и вниз, вверх и вниз,
Приседать не торопись! Приседания.
И в последний раз присели,
А потом на место сели. Дети садятся.
Воспитатель: Давайте для белочки сделаем подарок красивые бусы.
2.5 Игра «Собери бусы»
Дети садятся за столы, на столе, на двоих детей находятся 6 каштанов, 3 желудя, 3 ореха фундука.
Воспитатель: Какую геометрическую фигуру напоминают нам каштаны? (Круг)
– Какую геометрическую фигуру напоминают нам орехи? (Круг)
– Чем они похожи? (Формой)
– Чем они отличаются? (Размером)
– Какую геометрическую фигуру напоминают нам желуди? (Овал)
– Возьмите в одну ладошку 3 одинаковых любых плода и столько же одинаковых плодов в другую ладошку.
Положите эти плода на стол перед собой. Выложите бусы, чередуя плоды.
Дети самостоятельно выкладывают бусы.
Воспитатель: Скажите, какие у вас получились бусы? (Ответы детей).
– Вот, Белочка, тебе подарок от нас, а нам пора возвращаться в детский сад.
Белочка: Спасибо вам, ребята.
Воспитатель
Дети собираются около воспитателя.
Приложение 1
Приложение 2
Приложение 3
Список литературы
В.Колесникова. – М.: Сфера, 2015. – 112 cсобытие
01 сентября 2022 г. | 00:00 – 30 апреля 2023 г. | 12:00
В 2022-2023 учебном году в Школе будет
специальная программа по приложениям динамики в теории чисел и
Алгебраическая геометрия. Тамар Циглер из Еврейского университета в г.
Иерусалим будет заслуженным приглашенным профессором…
Читать далее
событие
01 сентября 2021 г. | 00:00 – 30 апреля 2022 г. | 12:00
В 2021-22 учебном году в Школе пройдет специальная программа на h-принципе и ее приложения к задачам в анализ и геометрия, организованная Камилло Де Леллисом и Ласло Székelyhidi Jr., который будет почетным гостем…
Читать далее
событие
01 сентября 2020 г. | 9:00 – 30 апреля 2021 г. | 9:00
В 2020-2021 учебном году в Школе прошла акция программа по геометрической и модульной теории представлений. Джорди Уильямсон из Сиднейского университета был выдающимся Посещая профессора.
Подтвержденные старшие участники для семестра I…
Читать далее
событие
01 сентября 2019 г.
| 00:00 – 30 апреля 2020 г. | 00:00
Особый год возглавил Санджив Арора, Чарльз Фицморрис, профессор компьютерных наук в Принстоне университета, с двойным назначением в ИАС в 2017-2019 (Визитная профессор) и 2019-2020 (заслуженный приглашенный профессор).
Особый год…
Читать далее
событие
01 сентября 2018 г. | 12:00 – 30 апреля 2019 г.| 00:00
В течение 2018-19 учебного года Школа была специальная программа по Вариационным методам в Геометрия. Фернандо Кода Маркес из Принстонского университета был заслуженным приглашенным профессором.
Подтвержденные старшие участники первого семестра: Айлана…
Читать далее
событие
01 сентября 2017 г.
| 00:00 – 30 апреля 2018 г. | 12:00
В течение учебного года было проведено два семинара. Термин я мастер-класс «Мотивы, Представления Галуа и когомологии вокруг Ленглендса программа», состоялась 6-10 ноября 2017 года. Семестр II семинара “Теория представлений и…
Читать далее
событие
01 сентября 2016 г. | 00:00 – 30 апреля 2017 г. | 00:00
Изображение Аилсы Китинг, использовано с разрешения Тема программа в контексте
HMS начался с ICM-адреса Концевича 1994 года. К настоящему времени это самостоятельная зрелая область математики, но все же та, которая может можно подойти из многих…
Читать далее
событие
01 сентября 2015 г.
| 00:00 – 30 апреля 2016 г. | 12:00
В 2015-16 учебном году Школа математики провел специальную программу по геометрическим структурам на трехмерных многообразиях. Программу вел заслуженный приглашенный профессор Ян Агол из Калифорнийский университет в Беркли.
Читать далее
событие
01 сентября 2014 г. | 01:00 – 01 августа 2015 г. | 12:00
Топология алгебраических многообразий, 2014-15
Клэр Вуазен, Институт математики де Жюссье, была Заслуженный приглашенный профессор школы в 2014-15 гг. академический год. Профессор Вуазен вел специальную программу «The Топология…
Читать далее
событие
01 сентября 2013 г. | 01:00 – 01 августа 2014 г. | 12:00
Неравновесная динамика и случайные матрицы, 2013-14
За последние несколько десятилетий был достигнут значительный прогресс
в математическом анализе равновесной статистической механики.
Однако неравновесная динамика пока находится на начальной стадии…
Читать далее
событие
24 сентября 2012 г. | 00:00 – 15 августа 2013 г. | 00:00
Соорганизаторы:
Стив Авуди (IAS/CMU),
Тьерри Кокан (IAS/Университет Гётеборга) и
Владимир Воеводский (IAS).
Участники программы Программа
Описание Важные даты
10 лет воздействия Выписка
Читать далее
событие
19 сентября 2011 г. | 00:00 – 15 августа 2012 г. | 00:00
Математическая теория динамических систем предоставляет инструменты для
понимать сложное поведение многих важных физических систем.
Особый интерес представляют гамильтоновы системы. Начиная с Пуанкаре
фундаментальный вклад многие математические инструменты.
..
Читать далее
событие
Читать далее
событие
01 сентября 2009 г. | 00:00 – 30 июня 2010 г. | 00:00
В 2009-2010 учебном году Энрико Бомбьери из Школа и Питер Сарнак из Принстонского университета/Института Advanced Study вел программу по аналитической теории чисел.
В программе особое внимание уделялось аналитическим аспектам и особенно…
Читать далее
событие
01 сентября 2008 г. | 00:00 – 30 июня 2009 г. | 00:00
Организатор: Элис Чанг ( Принстон Университет )
Специальная программа на 2008-09 учебный год была запущена
геометрическое УЧП.
Акцент был сделан на нелинейный частичный дифференциал
уравнения с приложениями к задачам дифференциальных, конформных
и…
Читать далее
событие
01 сентября 2007 г. | 01:00 – 01 июня 2008 г. | 00:00
В 2007-08 учебном году Роман Безрукавников из Массачусетского технологического института руководил специальная программа по алгебраической геометрии и физике в теория представлений.
Основное внимание в этом году было уделено последним событиям в теория представлений, алгебраическая геометрия…
Читать далее
событие
01 сентября 2007 г. | 01:00 – 01 января 2008 г. | 12:00
Мини-конференция 10-12 декабря
В течение I семестра, Преподаватель школы Жан Бурген
и Ван Ву из Университета Рутгерса вели программу по арифметике.
комбинаторика. Ниже представлена предварительная информация о
программа.
Добавка…
Читать далее
событие
01 сентября 2006 г. | 01:00 – 01 июня 2007 г. | 00:00
В 2006-07 учебном году в Школе математики было специальная программа по алгебраической геометрии. В центре внимания не было ни один аспект, а скорее стремился иметь множество разновидностей алгебраического представлена геометрия и ее приложения, в том числе…
Читать далее
событие
01 сентября 2005 г. | 01:00 – 01 мая 2006 г. | 00:00
В последние годы появились новые и важные связи
между дискретными подгруппами групп Ли, автоморфными формами и
арифметика с одной стороны и вопросы дискретной математики,
комбинаторика и теория графов с другой. Один из.
..
Читать далее
событие
02 сентября 2004 г. | 01:00 – 01 мая 2005 г. | 12:00
В 2004-2005 учебном году Школа математики вел программу о гипотезе Блоха-Като, касающейся
K-теории Милнора и этальных когомологий. Деятельность программы включал два или более еженедельных курса, охватывающих…
Читать далее
событие
01 сентября 2003 г. | 00:00 – 30 июня 2004 г. | 00:00
Основное внимание уделялось последним разработкам в области нелинейных УЧП. и соответствующий анализ. Сюда входят такие темы, как дисперсионный Уравнения Гамильтона с критической нелинейностью, структура формации особенностей для НУШ и обобщенного КДВ…
Читать далее
событие
01 сентября 2002 г.
| 00:00 – 30 июня 2003 г. | 12:00
В 2002-2003 учебном году ИАС провела программу в статистические модели турбулентности. Weinan E и Грегори Фалькович находились в резиденции в течение года, и в смежных областях Джон Болл был также в институте.
Хотя проблема 3…
Читать далее
событие
01 сентября 2001 г. | 00:00 – 30 июня 2002 г. | 00:00
Целью программы было изучение различных аспектов теория голоморфных кривых и их взаимодействия. Специальный акцент был сделан на приложениях к симплектической геометрии в низкоразмерная топология.
Еженедельные мероприятия
Читать далее
событие
01 сентября 2000 г.
| 00:00 – 30 июня 2001 г. | 00:00
Читать далее
событие
01 сентября 2000 г. | 01:00 – 01 июня 2001 г. | 12:00
В 2000-2001 учебном году Школа математики провел специальную программу по теории вычислительной сложности в Институт перспективных исследований. Несколько старших научных сотрудников находились в проживания в институте на год, а также…
Читать далее
событие
01 сентября 2000 г. | 00:00 – 30 июня 2001 г. | 00:00
Джеймс Артур из Университета Торонто находился в резиденции в институт за 2000-01 учебный год и дал повышенную курс по формуле следа и приложениям. Кроме того, Роберт Коттвиц, Дайана Шелстад, М.-Ф. Виньерас, Г. Хенниарт…
Читать далее
событие
01 сентября 1999 г.
| 00:00 – 30 июня 2000 г. | 12:00
Семинар по комбинаторике и теоретической информатике в Институт перспективных исследований проходил каждый понедельник в 11 часов утра. в комнате 101, помещение для семинаров в зале Симони.
Читать далее 91$-гомотопическая теория — это гомотопическая теория алгебраических разновидностей и, в более общем плане, для схем, основанных на аналогия между аффинной прямой и единичным интервалом. Во время этого специальный год мы сосредоточились на двух темах. Один был…
Читать далее
событие
01 сентября 1999 г. | 00:00 – 30 июня 2000 г. | 00:00
В этом учебном году Хенрик Иванец и Петер Сарнак были
в резиденции в Институте перспективных исследований и был
программа с целью объединения специалистов в области аналитики
теория чисел и специалисты по аналитической теории.
..
Читать далее
событие
01 сентября 1999 г. | 00:00 – 30 июня 2002 г. | 00:00
Мероприятия
Лекции о кросс-функторах
Владимир Воеводский,
Ср. 11:00 в Dilworth Room (первая лекция 10 октября)
Для любой категории $C$ с продуктами из волокна и…
Читать далее
событие
01 сентября 1998 г. | 01:00 – 01 сентября 1999 г. | 00:00
В 1998-99 учебном году Джордж Люстиг был Заслуженный приглашенный профессор школы и руководил программой в геометрические методы в теории представлений. Хираку Накадзима был в проживания хотя бы часть года.
Читать далее
событие
01 сентября 1998 г.
| 01:00 – 01 сентября 1999 г. | 12:00
Ниже приводится список семинаров, которые были проведены в первом семестре. и термин II:
Читать далее
событие
01 сентября 1997 г. | 12:00 – 30, 19 июня98 | 12:00
В 1997-98 учебном году действовала годовая программа в геометрическом PDE в институте. Карен Ухлебек была в резиденции в качестве заслуженного приглашенного профессора в течение года, и она служила в качестве Главный организатор программы.
Ниже приведены …
Читать далее
событие
01 сентября 1997 г.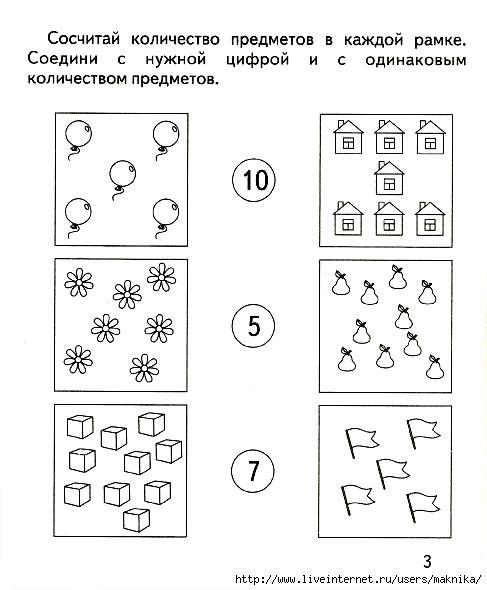
| 00:00 – 31 декабря 1997 г. | 00:00
Деятельность в области комбинаторики и теоретической информатики в Институте перспективных исследований возобновился в понедельник, сентябрь 29.
Он проходил по понедельникам и включал:
Семинар по комбинаторике и теории сложности – понедельник 11:00,
начиная…
Читать далее
событие
01 сентября 1997 г. | 00:00 – 30 июня 1998 г. | 00:00
МАТЕМАТИКА И ФИНАНСЫ
конференция по математическим проблемам в финансах
В течение 1997/98 учебного года, преимущественно в течение первого семестр, когда Майкл Айзенман, Дэниел Фишер и Томас Спенсер был в резиденции, была небольшая программа по…
Читать далее
событие
01 сентября 1996 г.
| 00:00 – 30 июня 1999 г. | 12:00
Программа по квантовой теории поля для математиков прошла в Институт повышения квалификации в течение учебного года 1996-97. Участники и лекторы подготовили конспекты лекций и задачи. наборы (и некоторые решения задач) по…
Читать далее
Получайте подобные истории прямо на свой почтовый ящик. Подпишитесь на информационный бюллетень 74
Согласно опубликованным сегодня утром результатам национальных тестов, два десятилетия роста числа американских учащихся в чтении и математике были сведены на нет всего двумя годами обучения, нарушенного пандемией.
Унылые выпуски Национальной оценки образовательного прогресса (NAEP), часто называемые «табель успеваемости нации», в последние годы стали традицией, которую выдают два раза в год, поскольку академический прогресс сначала застопорился, а затем пошел на спад как в четвертом, так и в восьмом классе.
Но сегодняшняя публикация, отслеживающая долгосрочные академические тенденции для 9-летних с 1970-х годов по настоящее время, включает первую федеральную оценку того, как COVID-19 повлиял на обучение.
Картина, которую он предлагает, мрачная. В специальном наборе данных, объединяющем баллы с начала 2020 года, непосредственно перед тем, как школы начали закрываться, с дополнительными результатами зимы 2022 года, отчет показывает, что средняя долгосрочная успеваемость по математике впервые за всю историю упала; по чтению показатели упали больше всего за 30 лет. И в другом известном развитии событий снижение было намного больше для учащихся с более низкими уровнями успеваемости, что увеличило и без того огромное неравенство в обучении между высокими и низкими успевателями в стране.
Пегги Карр Результаты в некоторой степени отражают опубликованные прошлой осенью оценки для 13-летних, которые также выявили беспрецедентные отклонения в обучении на долгосрочном экзамене. Но эти данные были собраны только осенью 2019 года; последние данные показывают дальнейший вред, нанесенный младшим школьникам в последующие годы.
Пегги Карр, комиссар Национального центра статистики образования, заявила по телефону с журналистами, что «отрезвляющие» выводы иллюстрируют потери в обучении, вызванные длительным закрытием школ и перемещением учащихся.
«Понятно, что COVID-19 потряс американское образование и ошеломил академический рост этой возрастной группы учащихся», — сказал Карр. «Мы не делаем это заявление легкомысленно».
Средние результаты по математике для 9-летних упали на ошеломляющие семь баллов в период между 2020 и 2022 годами, это единственное такое снижение с тех пор, как в 1973 году впервые был проведен долгосрочный тест. чем математика, а потому теоретически защищены от пандемического шока, — упали на пять пунктов.
Неизбежно это означает, что меньшее число учащихся достигли эталонных показателей теста, чем два года назад. Что касается математики, то процент 9-летних детей, набравших 250 баллов и выше (определяемых как «численные операции и решение простых задач»), в этом году снизился с 44% тестируемых до 37%; число тех, кто набрал 200 баллов и выше («начальные навыки и понимание»), сократилось с 86 до 80 процентов; даже подавляющее большинство набрало самый базовый порог в 150 баллов («простые арифметические факты») немного сократилось, с 9от 8 до 97 процентов за два периода тестирования.
Ни в одной демографической подгруппе не наблюдалось прироста по тесту, но существовали различия в темпах снижения. Например, успеваемость по математике у белых 9-летних детей снизилась на пять баллов, а у их испаноязычных и афроамериканских сверстников ущерб был еще больше (8 баллов и 13 баллов соответственно). В результате разрыв в математических достижениях между белыми и афроамериканцами увеличился на статистически значимую величину.
При чтении оценки афроамериканцев, выходцев из Латинской Америки и белых были на шесть пунктов ниже, оставив относительный разрыв без изменений. Оценки азиатских студентов снизились всего на один балл.
Примечательно, что оценка долгосрочной тенденции несколько отличается от основного теста NAEP, проводимого каждые два года. Он следует за успеваемостью студентов за полвека и сделан с помощью бумаги и карандаша, а не в цифровом виде. По большей части элементы тестирования не изменились с начала 1970-х годов, оценивая больше базовых навыков грамотности и вычислений, чем обычно можно увидеть в основном NAEP.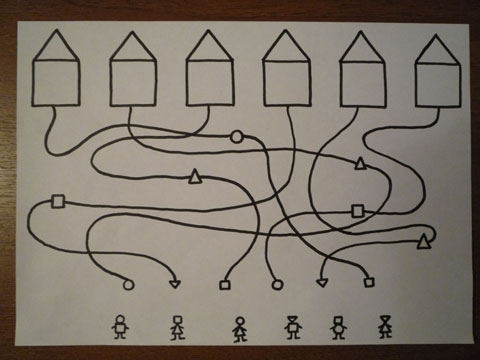
Связанный
Широкая линия тренда была положительной на протяжении всего экзамена, и даже в самом последнем выпуске оценки учащихся по обоим предметам намного выше, чем при первом измерении. Но Дэн Голдхабер, исследователь и давний наблюдатель за успеваемостью студентов, сказал, что поразительно видеть, как быстро испаряется восходящий импульс.
«Если посмотреть на период в 40 или 50 лет, в образовании есть что-то вроде скрытой истории — прогресс, достигнутый учащимися, и непропорциональный прогресс, которого добились исторически маргинализированные учащиеся», — сказал Гольдхабер, Центр анализа продольных данных в исследованиях в области образования (CALDER) Американских институтов. «Мы видим, что многое из этого очень долгосрочного прогресса полностью стирается в течение пары лет».
Одним из наиболее последовательных и неизменно тревожных результатов предыдущих раундов NAEP было резкое разобщение учащихся на обоих концах шкалы успеваемости.
На протяжении более полувека учащиеся с высокими баллами обычно с каждой итерацией теста справлялись на один или два балла лучше или, по крайней мере, оставались на том же уровне, в то время как учащиеся с низкими баллами наблюдали падение своих результатов.
Похожие
Феномен растущего разрыва в результатах снова проявляется в пост-COVID-результатах, хотя и принимает несколько иную форму. На всех уровнях успеваемости по обоим предметам у 9-летних детей наблюдалось статистически значимое снижение баллов; но даже при идентичной нисходящей траектории борющиеся студенты потеряли так много позиций, что неравенство все еще увеличивалось.
По чтению 9-летние дети, набравшие в 2022 году 90-й процентиль всех тестируемых, потеряли два балла по сравнению со своими предшественниками в 2020 году.
Но учащиеся, набравшие намного меньше среднего, 10-го процентиля, упали на 10 баллов.
Следовательно, средний разрыв в чтении между детьми 90-го и 10-го процентиля вырос со 103 до 110 баллов всего за два года. По математике за тот же период расхождение выросло с 95 до 105 пунктов.
Goldhaber сказало что тенденции видимые в представлении NAEP больш dovetailed с теми, котор он и другие исследователя определили использующ счеты испытания от испытания КАРТОЧКИ, котор вводят группа оценки NWEA. Он утверждал, что из нескольких источников данных стало ясно, что последствия пандемии были непропорционально негативными для уже борющихся и находящихся в неблагоприятном положении детей.
«Дело не только в потерях, мы наблюдаем потери в тестах по математике и чтению, и они непропорционально в нижней части тестового распределения», — сказал он. «Таким образом, пандемия обращает вспять долгосрочную тенденцию к сокращению разрыва в достижениях. Это особенно плохо, на мой взгляд».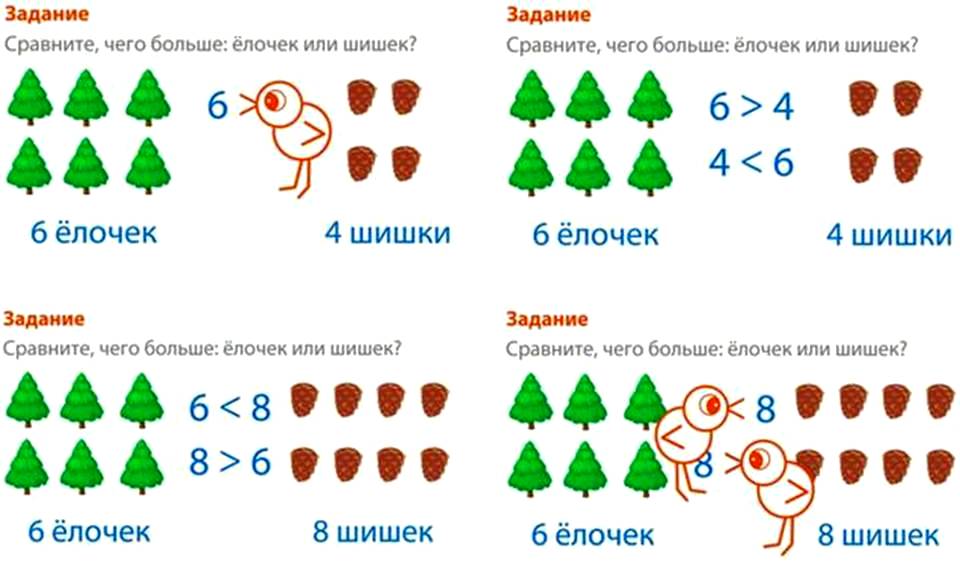
Тот факт, что потери так сильно сконцентрированы среди студентов с самыми низкими баллами, может помочь объяснить то, что Гольдхабер назвал «разрывом срочности»; ни штаты, ни школьные округа, ни даже семьи, похоже, не стремились принять меры по обучению поколений — от резкого удлинения учебного года до широко распространенного индивидуального обучения — чего требуют масштабы потерь в обучении. Одним из показателей является то, что миллиарды долларов федеральной помощи школам в связи с COVID остаются неизрасходованными более чем через год после того, как они были впервые выделены.
Это может измениться после выпуска NAEP. В то время как предыдущие исследования указывали на аналогичные и столь же несправедливые потери в обучении за последние несколько лет с использованием данных MAP и государственных стандартизированных тестов, Национальный табель успеваемости считается авторитетным показателем эффективности для американских школ K-12. Как отметил комиссар NCES Карр, в сегодняшнем выпуске представлены первые общенациональные репрезентативные результаты, измеряющие достижения до и после пандемии.