Демонстрационный материал · Изучение цифр · Карточки для детей · Математика в детском саду
Карточки с цифрами до пяти в среднюю группу детского сада. Такие карточки можно использовать как: Демонстрационный материал, предварительно распечатав на листах формата А4. Для оформления…
Демонстрационный материал · Изучение цифр · Карточки для детей · Математика в детском саду
В 4-5 лет воспитанники детского сада уже умеют считать до 10 и сопоставлять количество предметов соответствующей цифре. «Цифры для детей 4-5 лет» — это карточки…
Демонстрационный материал · Математика в детском саду
Карточки с примерами для создания демонстрационного материала по математике. Можно использовать на открытых занятиях, а также в качестве повседневного материала для проведения занятий с детьми…
Демонстрационный материал · Изучение цифр · Математика в детском саду · Учимся считать
Счет чисел по предмету в детском саду используется в качестве основы для проведения занятий и дидактических игр по математике в младшей и средней группе.
Демонстрационный материал · Изучение цифр · Математика в детском саду
Демонстрационный материал для младшей и средней группы детского сада «Число и количество предметов» — это яркие карточки для печати на листах А4 и дальнейшего использования…
Демонстрационный материал · Изучение цифр · Карточки для детей · Математика в детском саду · Учимся считать
Сравнение предметов и чисел в виде красочных картинок с демонстрационным материалов в детский сад. Данная картотека пригодится для проведения математических занятий в средней группе, когда…
Демонстрационный материал · Изучение цифр · Карточки для детей · Учимся считать
Большие карточки в виде демонстрационного материала для изучения цифр в детском саду. Цифры для детского сада имеют красочное оформление и яркий окрас соответствующих цифрам предметов….
Демонстрационный материал · Изучение цифр · Презентации для детей в детском саду
Презентация «Цифры» для дошкольников в детский сад, а также для воспитателей дошкольных образовательных учреждений.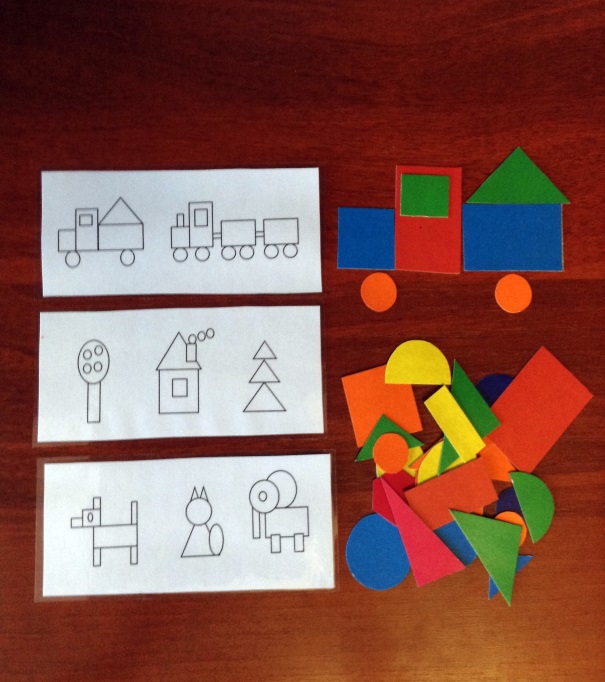
Презентация выполнена в виде отдельных листов с цифрами. Каждый лист, кроме…
Демонстрационный материал · Дидактические игры для детей · Математика в детском саду
Демонстрационный материал по математике для детей дошкольного возраста. Состоит из карточек, которые можно использовать также в качестве элементов дидактической игры. Как использовать примеры с ответами…
Демонстрационный материал · Дидактические игры для детей · Картотека дидактических игр
Дидактическая игра «Назови одним словом» для детей в детском саду. Такая игра благоприятно влияет на развитие сообразительности, мышления, внимания. Также данный материал можно использовать как…
Понравилось? Расскажи друзьям:
|
ДИАГНОСТИКА МАТЕМАТИЧЕСКИХ СПОСОБНОСТЕЙ На основе 16 тестов в картинках для определения математических способностей ребенка, который скоро собирается идти в школу, родители смогут определить уровень знаний ребенка без помощи профессиональных психологов и педагогов.
ДИАГНОСТИКА ПОЗНАВАТЕЛЬНЫХ ПРОЦЕССОВ ДЕТЕЙ 5-6 ЛЕТНЕГО ВОЗРАСТА Диагностика памяти (методика опосредованного запоминания) Нужно подобрать 10—15 слов, которые будут предложены для запоминания детям, а также набор карточек с картинками (20—30). Картинки не должны быть прямой иллюстрацией к запоминаемым словам. Слова для запоминания: обед сад дорога поле молоко свет одежда ночь ошибка лошадь птица ученье стул лес мышь В наборе карточек должны быть изображены: хлеб, яблоко, шкаф, часы, карандаш, самолет, стол, кровать, сани, лампа, корова, кошка, грабли, гнездо, ножик, дерево, земляника, рубашка, автомобиль, телега, луна, диван, здание школы, чашка, велосипед, дом, тетрадь, фонарь. ИНСТРУКЦИЯ РЕБЕНКУ: «Сейчас я буду зачитывать слова, а ты, чтобы лучше запомнить, будешь выбирать соответствующую карточку с рисунком, которая тебе поможет вспомнить названное мною слово». Первым произносится слово, например, молоко. Для того, чтобы запомнить это слово, ребенок должен выбрать карточку с рисунком коровы и т. д. На выбор карточки к каждому слову отводится 30 секунд. Многие дети осуществляют этот выбор раньше. После каждого выбора следует расспросить ребенка, почему он сделал этот выбор. Затем следует занять ребенка на 15 минут какой-нибудь другой игрой. По истечении этого времени ребенку демонстрируются картинки, которые были выбраны им для опосредованного запоминания. Количество правильно названных слов может свидетельствовать о развитии у ребенка логических связей в процессе запоминания. Диагностика распределения внимания Ход выполнения задания Педагог предлагает испытуемым следующие задания: а) написать числа от 1 до 10, одновременно считая вслух от 10 до 1. б) считать вслух от 1 до 20, но ребенок не должен называть числа, включающие тройку или кратные трем, вместо этих чисел он должен говорить: “Не собьюсь”. Например: “Один, два, не собьюсь, четыре, пять, не собьюсь” и т.д. Обработка результатов Подсчитать ошибки: максимум —7, минимум – 0. Принято считать, что: хорошее распределение внимания – от 0 до 2 ошибок; среднее – от 3 до 5; плохое – от 6. Образец правильного счета: 1, 2, -, 4, 5, —, 7, 8, -, 10, 11, -, 14, -, 16, 17, -, 19, 20 (черта замещает числа, которые нельзя произносить). Диагностика зрительной памяти дошкольников по методике Векслера Ребенку предлагается 4 рисунка. На каждую из картинок ребенку разрешается посмотреть в течение 10 секунд. Затем он их должен воспроизвести на чистом листе бумаги. Результаты опыта: 1. Две перекрещенные линии и два флажка — 1 балл; правильно расположенные флажки — 1 балл; правильный угол пересечения линий — 1 балл; максимальная оценка этого задания — 3 балла. 2. Большой квадрат, разделенный на 4 части двумя линиями — 1 балл; четыре маленьких квадрата в большом .— 1 балл; две пересекающиеся линии и 4 мелкие квадрата — 1 балл; четыре точки в квадратах — 1 балл; точность в пропорциях — 1 балл; максимальная оценка этого задания — 5 баллов. 3. Большой прямоугольник с маленьким в нем — 1 балл; все вершины внутреннего прямоугольника соединены с вершинами внешнего прямоугольника — 1 балл; маленький прямоугольник точно размещен в большом — 1 балл.) Максимальная оценка — 3 балла. 4. Открытый прямоугольник с правильным углом на каждом краю — 1 балл; центр и левая и правая стороны воспроизведены правильно — 1 балл; фигура правильная за исключением одного неправильно воспроизведенного угла — 1 балл. Максимальная оценка — 3 балла. Максимальный результат — 14 баллов. О хорошей зрительной памяти свидетельствует результат — 10 и выше баллов, о средней – 9 – 6 баллов, о низкой – 5 – 0 баллов. Диагностика коммуникативных умений ребенка Шкалы: умение договариваться, взаимный контроль, отношение к результату деятельности, взаимопомощь, рациональное использование средств совместной деятельности. Тестируем: Межличностные отношения. Назначение теста: изучение коммуникативных умений детей. Процедура тестирования: I. Двум детям одного возраста дают по одному изображению рукавички и просят украсить их, но так, чтобы они составили пару, были одинаковые. Поясняют, что сначала договориться, какой узор рисовать, а потом приступать к рисованию. Дети получают по одинаковому набору карандашей. II. Детям предлагают сделать то же, но дают один набор карандашей, предупреждая, что карандашами нужно делиться. Далее проводится эксперимент, в котором участвуют дети разного возраста. Важно, чтобы дети выполняли задание самостоятельно. Оценка результатов теста: анализируют, как протекало взаимодействие детей в каждой серии, по следующим признакам:
Определяют, как зависят эти показатели от возрастного состава пар испытуемых. Делают выводы о сформированности коммуникативных умений у детей. Диагностика образной памяти ребенка Данная методика предназначена для изучения образной памяти. Сущность методики заключается в том, что испытуемому предлагается в течение 30 секунд запомнить 12 образов, которые предлагаются в виде таблицы. Задача испытуемого — после того как убрали таблицу, нарисовать или выразить словесно те образы, которые он запомнил. Оценка результатов тестирования проводится по количеству правильно воспроизведенных образов. МЕТОДИКА “Какой Я?” Методика “Какой Я?” предназначена для определения самооценки ребенка 6-9 лет. Экспериментатор, пользуясь представленным далее протоколом, спрашивает у ребенка, как он сам себя воспринимает и оценивает по десяти различным положительным качествам личности. Оценки, предлагаемые ребенком самому себе, предоставляются экспериментатором в соответствующих колонках протокола, а затем переводятся в баллы. Оценка результатов: ответы типа “да” оцениваются в 1 балл, ответы типа “нет” оцениваются в 0 баллов, ответы типа “не знаю” или “иногда” оцениваются в 0,5 балла. Уровень самооценки определяется по общей сумме баллов, набранной ребенком по всем качествам личности. Выводы об уровне развития самооценки: Протокол методики “Какой я”
10 баллов – очень высокий; 8-9 баллов – высокий; 4-7 баллов – средний; 2-3 балла – низкий; 0-1 балл – очень низкий
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ, ЗАДАЧИ В СТИХОТВОРНОЙ ФОРМЕ, ЛОГИЧЕСКИЕ ЗАДАЧИ Математика для маленьких детей довольно сложная наука, которая может вызвать трудности во время обучения в школе. Занимательные задачи, задачи в стихотворной форме Логические задачи
ЗАДАЧИ-ШУТКИ, ГОЛОВОЛОМКИ, ЗАДАНИЯ НА СООБРАЗИТЕЛЬНОСТЬ
Загадки
Логические концовки
ДИДАКТИЧЕСКИЕ ИГРЫ Дидактические игры Дидактические игры по математике Игры, упражнения на развитие познавательных процессов Игры шашечного хода Игры с карточками
ПРАВИЛА РАБОТЫ ХУДОЖЕСТВЕННЫМИ МАТЕРИАЛАМИ Как работать акварелью. Акварель — краска легко разводимая водой, и главное ее достоинство — прозрачность. Просвечивая через тонкий слой краски, бумага как бы освещает акварельный цвет изнутри.
МАТЕРИАЛЫ ДЛЯ РАЗВИТИЯ РЕЧИ Скороговорки Скороговорки для развития речи и звукопроизношения Стихи-загадки про буквы алфавита Стихи для заучивания Стихи о буквах Считалки, стихи-шутки
ФИЗКУЛЬТМИНУТКИ Разминки и физкультминутки Сборник физминуток для детей Физкультминутки (математика)
ИГРЫ Цепочка примеров Цель: упражнять детей в умении производить арифметические действия. Ход игры: две группы участников садятся на стулья – одна против другой. Один ребенок берет мяч, называет простой арифметический пример: 3 + 2 – и бросает мяч кому-нибудь из другой группы. Тот, кому брошен мяч, дает ответ и бросает мяч игроку из первой группы. Поймавший мяч продолжает пример, в котором надо произвести действие с числом, являющимся ответом в первом примере. Участник игры, давший неверный ответ или пример, выбывает из игры. Выигрывает группа детей, у которой осталось больше игроков (предлагается для детей 6 – 7 лет, успешно усвоившими арифметические действия). Отгадай число Цель: закрепить умение детей сравнивать числа. Ход игры: по заданию ведущего ребенок должен быстро назвать число (числа) меньше 8, но больше 6; больше 5 , но меньше 9 и т.д. Ребенок, выполнивший условия игры, получает флажок. При делении детей на 2 группы ответивший неправильно выбывает из игры. Только одно свойство Для игры необходимо изготовить специальный набор геометрических фигур. Цель: закрепить знание свойств геометрических фигур, развивать умение быстро выбирать нужную фигуру, описывая ее. Ход игры: у двоих играющих детей по полному набору фигур. Один (тот, кто начинает игру) кладет на стол любую фигуру. Второй играющий должен положить рядом фигуру, отличающуюся от нее только по одному признаку. Так, если первый положил желтый большой треугольник, то второй кладет желтый большой квадрат или синий большой треугольник и т.д. Неправильным считается ход, если второй играющий положит фигуру, не отличающуюся от нее более чем на один признак. Игра строится по типу домино. По ходу игры требуется быстрая ориентировка играющих в цвете, форме, размере фигур, отсюда и воздействие на развитие логики, обоснованности мышления и действий. Числовой ряд (для детей старшего дошкольного возраста) Цель: закрепить знание последовательности чисел в натуральном ряду. Ход игры: двое детей раскладывают перед собой лицевой стороной вниз карточки с цифрами то 1 до 10. При этом каждому из детей дается определенное количество карточек с цифрами (например, до 13). Некоторые из цифр встречаются в наборе дважды. Каждый играющий в порядке очередности берет карточку с цифрой, открывает ее и кладет перед собой. Затем первый играющий открывает еще одну карточку. Если обозначенное на ней число меньше числа открытой им ранее карты, ребенок кладет карточку левее первой, если больше – правее. Назови число Цель: упражнять детей в умении производить устные вычисления. Ход игры: взрослый или старший ребенок говорит: «я могу отгадать число, которое ты задумал. Задумай число, прибавь к нему 6, от суммы отними 2, затем еще отними задуманное число, к результату прибавь 1, у тебя получилось число 5». В этой несложной задаче на смекалку задуманное число может быть любым, но для решения ее нужно уметь устно вычислять. Сколько взять конфет? Цель: упражнять детей в соотнесении условия задачи с результатом. Ход игры: предлагается условие задачи: «в вазе лежало 3 яблоко. Мама угостила ими трех девочек. Каждая из девочек получила по одному яблоку, и одно осталось в вазе. Как это получилось?» к ответу решающей задачу приходит вследствие размышления, соотнесения условий с результатом.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дети начинают развивать свои математические навыки еще в младенчестве, исследуя окружающую среду, и продолжают это в дошкольном возрасте.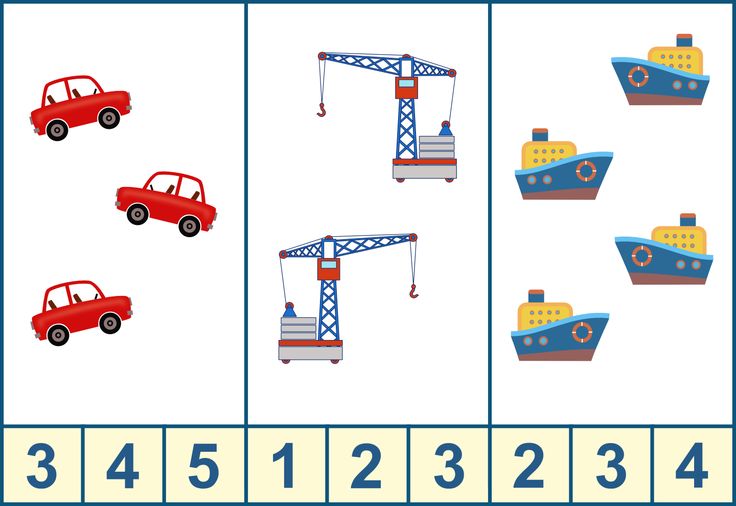
К тому времени, когда они изучают формальные математические понятия в первом классе, основа для успеха уже заложена.
Вот несколько советов о том, как преподавать математику дошкольникам в школе или дома с помощью практическая деятельность и последующий конкретно-графический-абстрактный подход.
Что такое ранние математические навыки?Ранняя математика относится к математическим понятиям и навыкам, которые ребенок формирует неформально в течение первых нескольких лет. Их также называют предварительными математическими навыками или навыками раннего счета .
Очень важно сначала разработать их, прежде чем пытаться ввести слишком сложные математические концепции.
Знакомя ребенка с математикой, вы можете сразу подумать о цифрах и начать с 9.0015 считая , распознавая числа и добавляя или вычитая их .
Хотя научиться считать до 10 весело для маленьких детей, понимание значения этих чисел и того, что они обозначают, является продвинутым навыком.
Если вы попросите очень маленького ребенка сосчитать 5 предметов, прикасаясь к ним по одному, вы можете увидеть, как они считают один и тот же предмет дважды или пропускают некоторые из них.
Важно сначала понять, как дети усваивают математические понятия, а затем помочь им развить ранние математические навыки .
Как дети изучают математику: конкретный иллюстрированный абстрактный подходТри стадии изучения любой математической концепции: конкретная, графическая и абстрактная .
Конкретная сценаНа конкретной стадии дети должны физически испытать концепцию . Им нужно развить понимание одного предмета, удерживая один блок.
По игра с бетонными предметами , дети формируют представление о том, что может быть один объект , несколько объектов , меньше объектов , больше объектов, и т.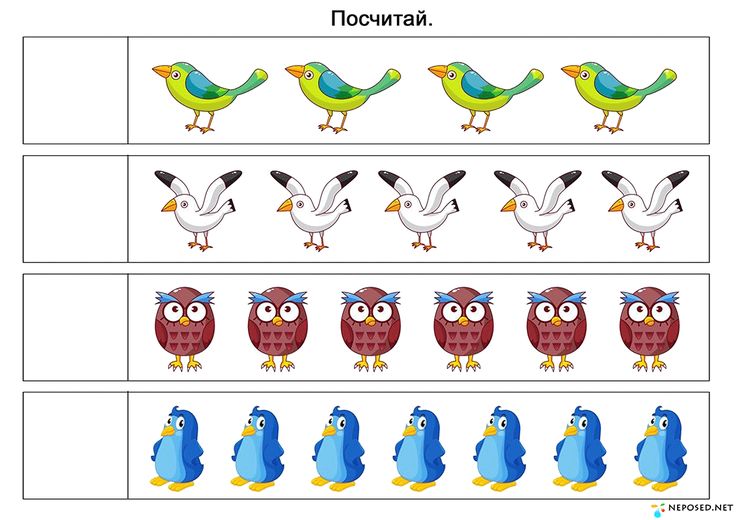
д.
Многие математические процессы происходят, пока дети строят башню из блоков или сделать глиняные лепешки в песочнице. Они изучают такие понятия, как больше, меньше, еще один, недостаточно, сколько, много, меньше, убрать и добавить .
Дети сравнивают предметы и узнают, что значение может быть присвоено объектам .
Наглядный этапНа изобразительном этапе, который следует за конкретным этапом, дети могут видеть изображения предметов и понимать, что они представляют реальные предметы.
Например, ребенок может посмотреть на картинку и понять, что 4 листа представляют собой 4 настоящих листа.
Позже ребенок может увидеть игральную кость с 4 точками и присвоить значение 4 , зная, что точки гипотетически могут представлять любой объект.
Затем они смогут сложить 4 точки на одном кубике с 3 точками на другом и сказать, что всего 7 точек.
Это последняя стадия понимания математической концепции. Это означает, что ребенок может посмотреть на сумму, например. 4 + 3 , записанные числовыми символами , и сложить их без конкретных предметов или картинок.
Ребенок достаточно созрел, чтобы понять, что символов 4 и 3 представляют количество объектов , которые необходимо добавить.
Этот пост содержит партнерские ссылки на образовательные продукты, которые я лично рекомендую. Если вы покупаете через один из них, я получаю комиссию без каких-либо дополнительных затрат для вас. Прочтите условия для более подробной информации.
Дошкольники находятся на конкретной, изобразительной или абстрактной стадии?Дошкольники в основном находятся на конкретной стадии .
На самом деле, вплоть до третьего или четвертого класса любой достойный учитель будет по-прежнему познакомьте с новым понятием конкретным образом, прежде чем переходить к книгам или рабочим листам с примерами для решения.
Когда дети понимают понятие конкретно, им намного легче решать абстрактные задачи.
Это означает, что в дошкольном возрасте пытаться подтолкнуть ребенка считать изображения предметов или понимать значение цифровых символов преждевременно и вызовет разочарование.
Возможно, вы захотите познакомить ребенка с числами (например, играя с деревянными числами, подобными этим, или с магнитными плитками с числами) или с рифмами, обучающими счету, но не ожидайте, что ваш ребенок еще поймет значение этих чисел.
Как научить дошкольника математике: 15 простых заданийЛучший метод обучения математике в раннем детстве – это основное средство обучения – игра.
Это означает, что в эти ранние годы детям не нужны формальные уроки, рабочие листы и рабочие тетради. Математика для дошкольников должна быть связана с развлечением.
Вот список лишь нескольких основных повседневных занятий, которые идеально подходят для дошкольных занятий по математике.
Игра с фигурками из пенопласта или дерева знакомит вашего ребенка с основными геометрическими фигурами, а также с их свойствами. Учит распознавать формы.
Вырежьте основные фигуры из цветной бумаги и сделайте из них картинку. Дети учатся соединять 2D-формы вместе, чтобы создавать разные формы.
Танграмы (такие как эти) отлично подходят для создания изображений с фигурами.
Головоломки отлично развивают зрительное восприятие и улучшают понимание ребенком геометрии.
Выбирайте качественные деревянные пазлы с деревянным подносом.
Прищепки — еще одно отличное занятие для развития математических навыков у дошкольников. Они развивают представления о числах и геометрические знания.
Это может показаться не математическим заданием, но строительство фортов и других сооружений и лазание внутри них — это первый шаг ребенка к изучению пространства и формы.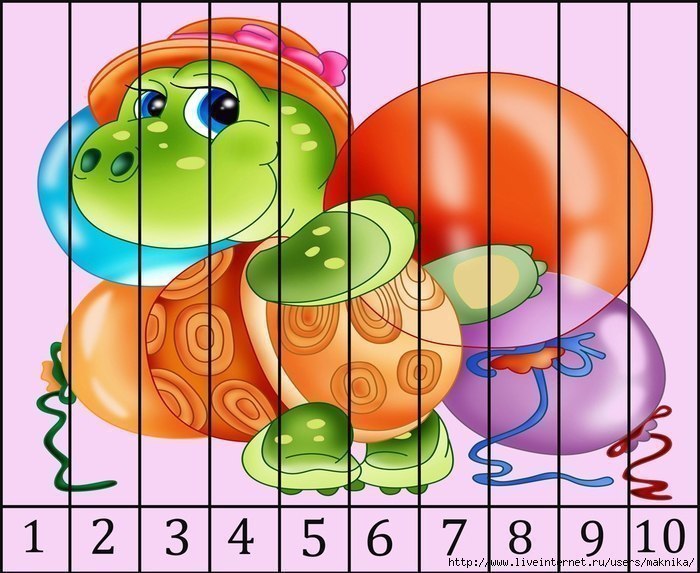
Эти ранние игровые сессии являются обязательными.
Игра с кубиками дает так много преимуществ, что дети должны иметь возможность ежедневно играть с кубиками и всевозможными манипуляторами.
Предлагаем бусины, фишки и предметы для игры с незакрепленными частями. Есть также много преимуществ Lego и других игрушек-конструкторов.
Игра с кубиками — это первый шаг в построении представления о числах, и у каждого ребенка дома должен быть хороший набор деревянных кубиков. Этот набор отлично подойдет для занятий в классе или дома.
Когда дети играют в песочнице и делают пироги из грязи и другие конструкции, они начинают использовать такие термины, как «Мне нужно сделать еще один», «Есть 3 пирога» или — Я сделал по одному для каждого из нас.
Песенки для счета — это интересный способ для маленького ребенка научиться считать в прямом и обратном порядке.
Это известно как механический счет.
Они также узнают об увеличении и уменьшении количества песен, таких как Пять зеленых бутылок .
Пусть ваш ребенок поиграет с пенопластовыми, резиновыми, деревянными или пластиковыми цифрами в ванночке или на магнитной доске. Поскольку это физические объекты, ваш ребенок может прикоснуться к ним и почувствовать их форму.
Для маленького ребенка это гораздо важнее, чем просмотр цифр на странице активности. Со временем они естественным образом научатся распознавать их и знать, как они формируются.
Playdough — одно из лучших веществ, обладающее удивительными преимуществами.
Попросите детей вылепить цифры из пластилина. Эта сенсорная деятельность отпечатает числа в памяти вашего ребенка гораздо быстрее, чем попытка написать числа на бумаге.
Подготовьте контейнеры разных размеров и форм, чтобы ваш ребенок открыл для себя основы вместимости, развлекаясь в ванне или песочнице.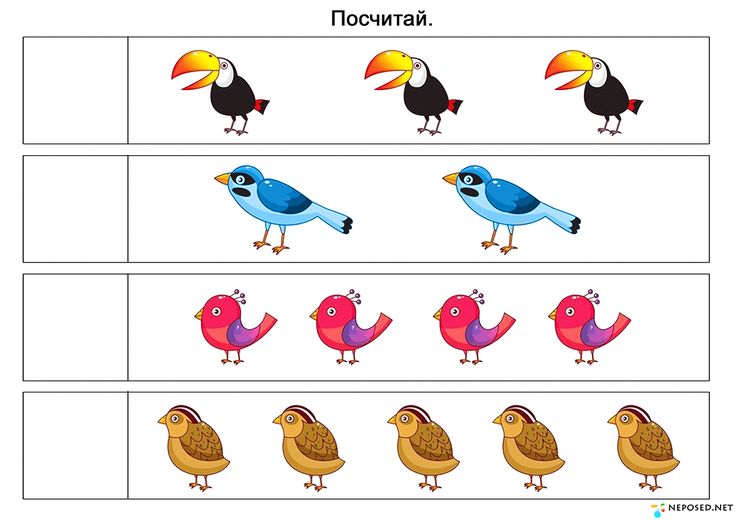
Выпечка — это большой математический опыт. Пусть ваш ребенок будет участвовать в измерении ингредиентов, чтобы познакомить их с единицами измерения и количествами.
Попросите ребенка измерить определенные предметы, например книгу, стол или комнату, используя части тела, такие как руки или ноги, а затем предметы, такие как блок или книга.
Дети должны сначала научиться измерять длину с помощью нестандартных предметов, прежде чем их можно будет познакомить со стандартными измерениями.
Ежедневно находите возможности поговорить о времени. Используйте распорядок дня в качестве отправной точки.
Обсудите такие понятия, как время суток (утро, день), а также время на часах («Я заеду за тобой в 12 часов после рассказа»).
Дайте детям разные предметы и попросите их почувствовать, какие из них тяжелые, а какие легкие, и сравнить вес разных предметов.
Используйте балансировочные весы (или сделайте сами) и положите на них различные предметы домашнего обихода.
Решение задач может быть самой, гм… проблематичной из всех математических задач! Дети в классах часто изо всех сил пытаются визуализировать проблемы и то, что они на самом деле означают.
Они часто прибегают к угадыванию (например, там написано больше , так что я должен добавить), не имея ни малейшего представления о том, в чем проблема на самом деле и почему при визуализации решение обычно оказывается таким логичным.
Лучший способ подготовить детей к решению проблем — постоянно давать возможность на самом деле решить настоящие проблемы .
Поощряйте детей развивать навыки критического мышления .
Вам не обязательно давать математические задачи, достаточно общих задач, которые требуют тренировки мозга, чтобы мыслить нестандартно.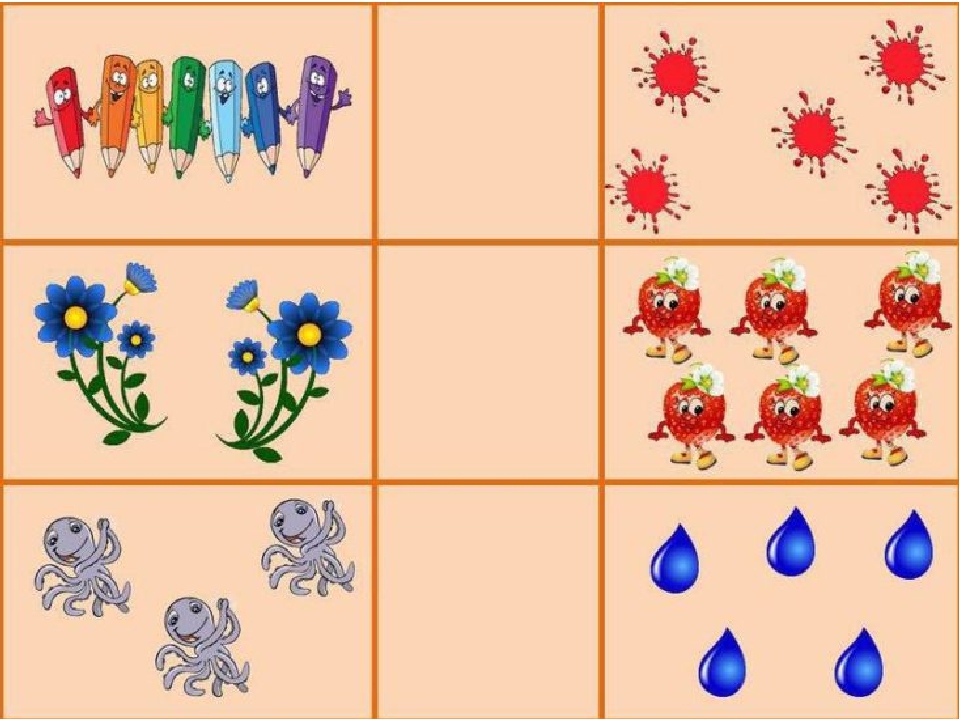
Много возможностей:
Как видите, в большинстве игр есть скрытые возможности для изучения математики.
Научитесь распознавать их и использовать для сознательного обучения определенным навыкам. Не забудьте ввести новый словарь и постоянно задавать вопросы во время игры.
Введите такие слова, как: тяжелее, легче, длиннее, короче, раньше, позже, больше, меньше, больше, чем, меньше, меньше, больше, недостаточно, совсем, осталось, другой, полный, пустой, соответствующий, такой же , другой.
Надеюсь, вам понравилось читать эту статью и у вас есть новые идеи, которые можно попробовать.
Присоединяйтесь к программе Empowered Parents +, и вы получите загружаемый набор из печатных головоломок, игр и рассказов , а также набор «Обучение через игру» , который включает целый год занятий для детей от 3 до 6 лет.
Бесплатный доступ навсегда.
Регистрация бесплатной учетной записи Grow выполняется быстро и легко и позволит вам добавлять в закладки статьи для последующего чтения на этом веб-сайте, а также на многих веб-сайтах по всему миру, использующих Grow .
Если вы выросли, наблюдая за сериалом «Соседство мистера Роджерса », вы, возможно, помните Picture Picture, кинопроектор и слайд-проектор, который Фред Роджерс использовал, чтобы объяснить, например, как изготавливаются цветные карандаши, с помощью наглядных пособий.
Эта визуальная процедура хорошо сработала для юной аудитории, и многие учителя продолжают использовать картинки со старшими учениками, чтобы улучшить свои уроки, как я часто делаю на уроках математики. Как и дети, которые оценили Picture Picture, наши ученики могут увлечься математикой с картинками и изображениями, а использование изображений меняет тех, кто воспринимается как хорошо разбирающийся в математике: мы можем показать ученикам, что математика — это не просто алгоритмы и ярлыки видеть закономерности и применять то, что мы знаем, к увиденному.
Особенно сейчас, когда виртуальные уроки становятся все более популярными в образовании, использование изображений очень привлекает детей. Основное внимание уделяется не тому, кто быстрее всех вычисляет ответы, а истинному пониманию. Мы должны помочь нашим ученикам увидеть математику вокруг себя.
Словесные задачи и счет могут быть трудными, и учителя уже давно используют картинки как еще один способ доступа к числовым данным.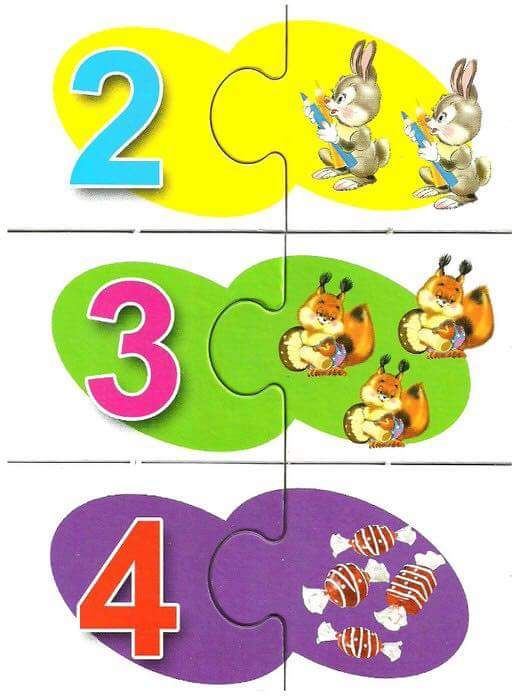
Чтобы помочь учащимся понять математику, которую вы от них просите, используйте изображения поддающихся количественному измерению объектов, чтобы создать простые точки входа.
Взгляните на фото коробки с яйцами выше. Что ты заметил? Что вам интересно?
Теперь покажите фотографию учащимся и спросите их, что они замечают и удивляются. Они могут сказать, что это коробка для яиц, и что некоторых яиц не хватает. Затем спросите: “Как бы вы сосчитали яйца на картинке?” Предложите им озвучить, как они считают яйца. Один учащийся может увидеть пять яиц вверху, четыре в середине и пять внизу (добавление 5 + 4 + 5 = 14 яиц). Другой учащийся может увидеть яйца в виде четырех столбцов по три с дополнительными двумя яйцами сбоку. Третий учащийся может увидеть на этой картинке всего 18 яиц, при этом четыре яйца отсутствуют. С помощью этой одной картинки вы можете охватить стратегии сложения, вычитания и умножения.
Эта стратегия помогает создать много точек входа для всех желающих.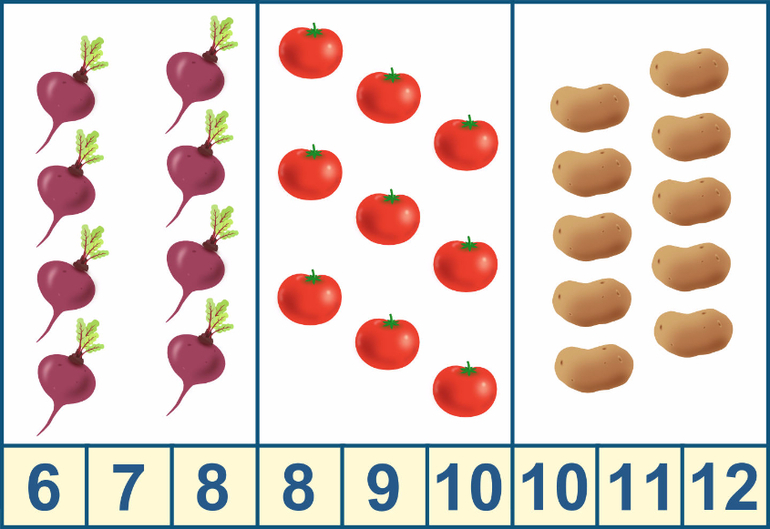
Каждый ученик будет считать яйца по-своему, и вы можете использовать различные картинки, чтобы получить представление о подходе каждого ученика к счету.
Начальные классы: Поскольку основное внимание уделяется счету, сложению и вычитанию, идеально подходят картинки, в которых отсутствуют части или пробелы. Найдите картинки, на которых разбросаны предметы. Вы также можете использовать одни и те же картинки для разных оценок. Если учащиеся видели картинку в предыдущем классе, попросите их найти как можно больше различных способов найти ответ. Они найдут дополнительные способы считать предметы, потому что их числовое чувство усиливается с каждым годом.
Старший элементарный: Умножение и деление являются основным направлением, поэтому изображения с массивами будут работать. Не забудьте расширить разговор, чтобы он включал вопросы о разделении. Например, покажите изображение 44 бобов и пяти чашек.
Спросите, сколько бобов попадет в каждую чашку и сколько останется, если положить в каждую чашку одинаковое количество.
Дроби: Изучение дробей и десятичных знаков может быть непростой задачей. Изображения измерительной ленты или мерных чашек полезны для обучения дробям (и изображения с несколькими компонентами также подходят для того, чтобы спрашивать о частях).
Предоставлено Кристен Акоста
Вопрос к вашим ученикам: Каковы некоторые стратегии подсчета этих монет?
Десятичные дроби: Деньги — главный источник разговоров о десятичных дробях. Поэтому картинки, ориентированные на счет денег, пригодятся для процентов и десятичных дробей.
Процент: Понятие процента идет рука об руку с покупками. Когда на табличке написано “Скидка 40 %”, что это значит? Когда знаки говорят: «Купи одну, получи другую бесплатно», вы действительно получаете что-то бесплатно? Торговые вывески — идеальный способ понять проценты.
Соотношения/коэффициенты: Эта тема средней школы гораздо более привлекательна для учащихся, если им нужно сравнивать разные объекты. Использование реальной рекламы продуктового магазина в качестве способа обучения расценкам привлекает учащихся средних классов. Это показывает, как взрослые используют тарифы, чтобы найти лучшее предложение при совершении покупок.
Геометрия: Формы, линии и углы легко найти в нашей повседневной жизни. Картинки с различными формами могут помочь учащимся понять, что мы постоянно пользуемся математикой и геометрией. От парковки автомобилей до строительства домов геометрия легко доступна через изображения.
Найти картинки для уроков математики проще, чем вы думаете. Вот несколько советов:
Эти мини тесты по математике для дошкольников в картинках позволят развить логическое мышление и математические навыки и умения.
Если он сразу начинает сбиваться – у него слабое распределение внимания;
д.;
Кроме того, далеко не все дети имеют математический склад ума, и не у всех есть природная тяга к точным наукам. Поэтому развитие у дошкольника интереса к математике в раннем возрасте значительно облегчит ему обучение в школе. Ведь современная школьная программа довольна насыщенна и далеко не проста даже для первоклашки. Овладение дошкольником навыками счета и основами математики в игровой и занимательной форме поможет ему в дальнейшем быстрее и легче усваивать сложные вопросы школьного курса.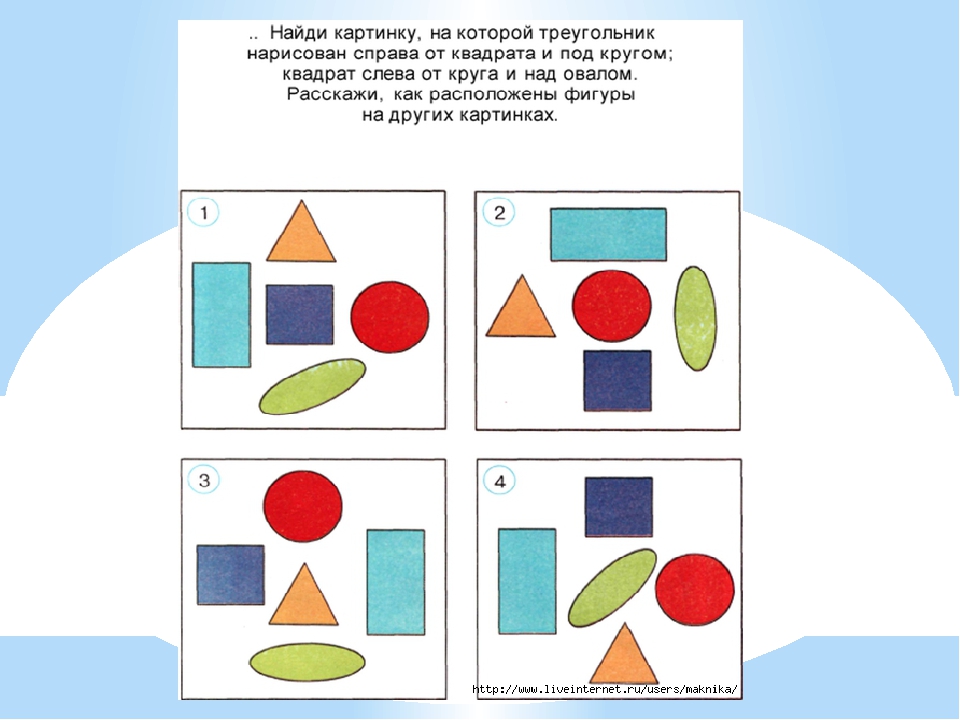
Сколько шло человек? (8 человек)
Почему? (они наблюдали за дождем из окна; у каждого был зонт или плащ)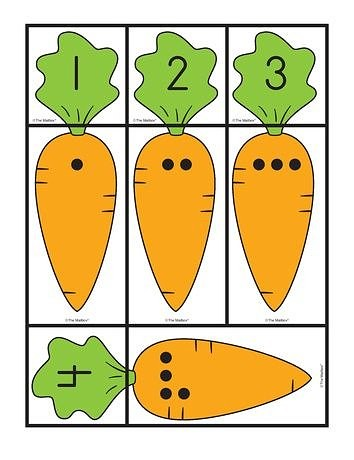
Сколько рисунков получил дедушка? (4 рисунка)
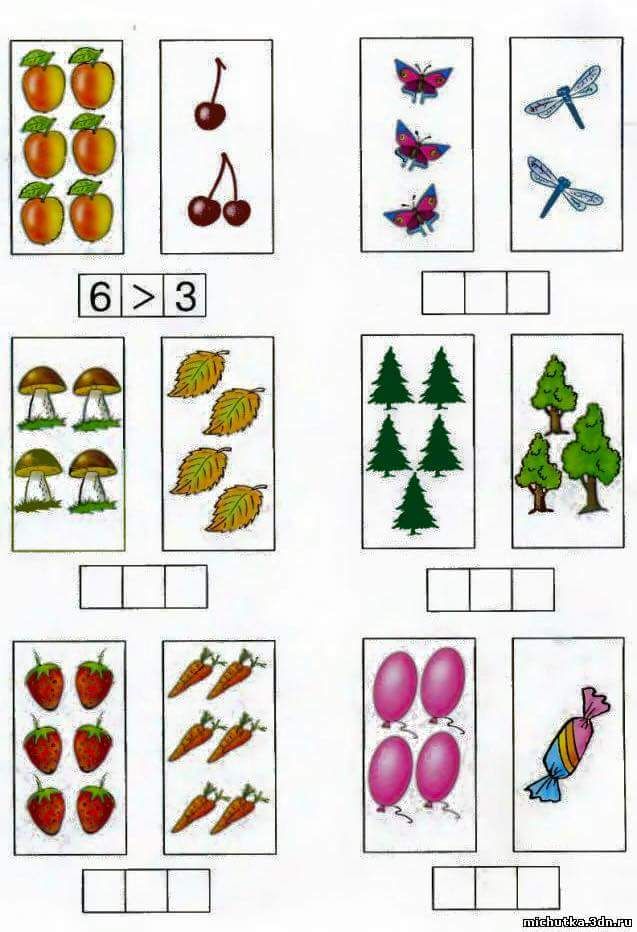Как удалить из середины самый длинный карандаш, не трогая его? (переложить один из тех, что короче)
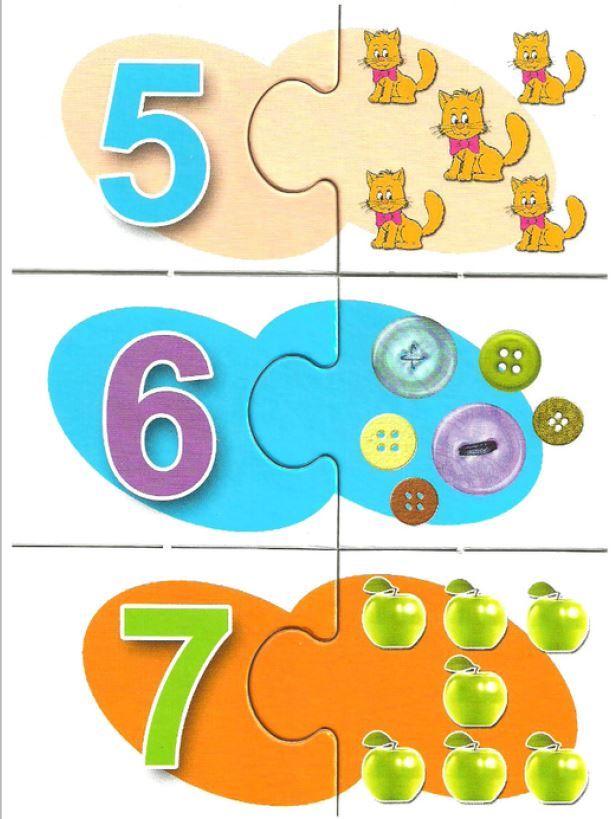(Перчатка)
(Веник)
Это придает акварели необычную воздушность и звучность. Другим отличительным свойством акварели является большая ее подвижность. Благодаря воде, кисть легко наполняется красящим пигментом, и краска свободно сходит на бумагу, оставляя на ней заметный след. Поэтому акварель требует особенно хорошего, выразительного рисунка…читать далее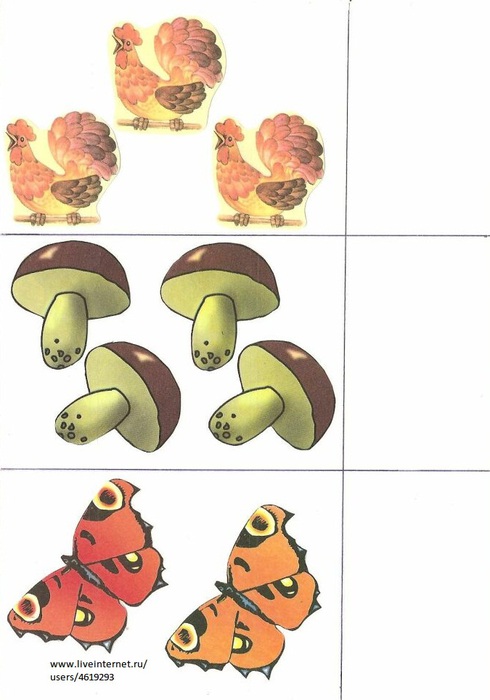 
В него входят 4 фигуры (круг, квадрат, треугольник и прямоугольник) четырех цветов (красного, синего, желтого и белого), маленького размера. В этот же набор включается такое же количество перечисленных фигур указанных цветов, но больших по размеру. Таким образом, для игры (на одного участника) необходимо 16 маленьких геометрических фигур четырех видов и четырех цветов и столько же больших.
В этом случае фигуру у игрока забирают. Проигрывает тот, кто первый останется без фигур. (Возможны варианты.)
Если же возьмет карту с числом уже открытым, то возвращает ее на место, а право ходе переходит соседу. Выигрывает тот кто первый выложит свой ряд.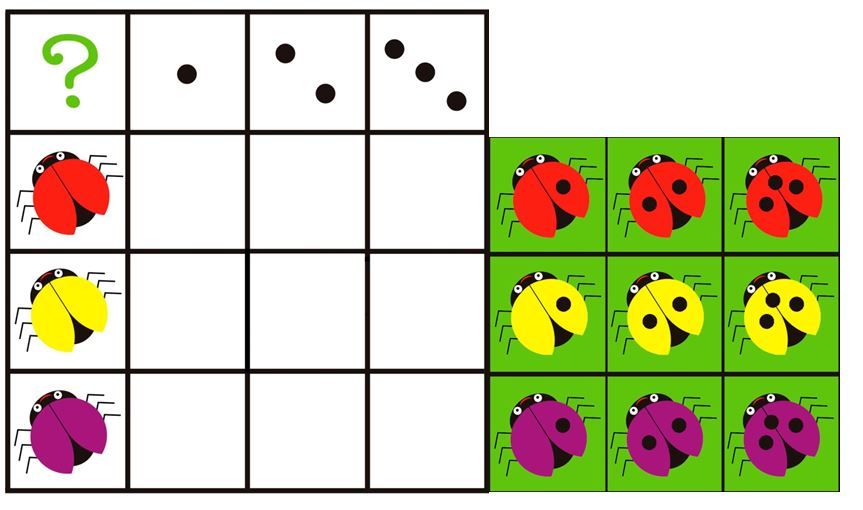
(одна девочка взяла яблоко вместе с вазой).