Контрольная работа подобие фигур 9 класс: Контрольная работа по геометрии на тему “Подобие фигур” 9 класс
Контрольная работа по геометрии на тему “Подобие фигур” 9 класс
КОНТРОЛЬНАЯ РАБОТА .
Подобие фигур.
1 ВАРИАНТ.
№ 1. У подобных треугольников АВС и А1В1С1 А = 270, АВ = 3м, ВС = 4м, В1С1 = 20м. Чему равны А1 и сторона А1В1?
№ 2. У треугольников АВС и А1В1С1, А = А1, В = В1 АВ=20см, ВС=3см, А1В1=4см, А1С1 = 10см. Найдите остальные стороны треугольников.
№ 3. Длина тени фабричной трубы равна 80м; в это же время вертикально воткнутый в землю столб высотой 7м дает тень длиной 4м. Найдите высоту трубы.
№ 4. Диагонали трапеции АВСD пересекаются в точке Е.
№ 5. Углы В и В1 треугольников АВС и А1В1С1 равны. Стороны треугольника АВС, прилежащие к углу В в 4 раза больше сторон треугольника А1В1С1, прилежащих к углу В1. Найдите А1С1, если АС = 30 м.
_____________________________________________________________________________
КОНТРОЛЬНАЯ РАБОТА .
Подобие фигур.
2 ВАРИАНТ.
№ 1. У подобных треугольников АВС и А1В1С1 А = 350, АВ = 4м, ВС = 5м, В1С1 = 25м. Чему равны А1 и сторона А1В1?
№ 2. У треугольников АВС и А1В
1С1, А = А1, В = В1 АВ=18см, ВС=5см, А1В1=3см, А1С1 = 12см.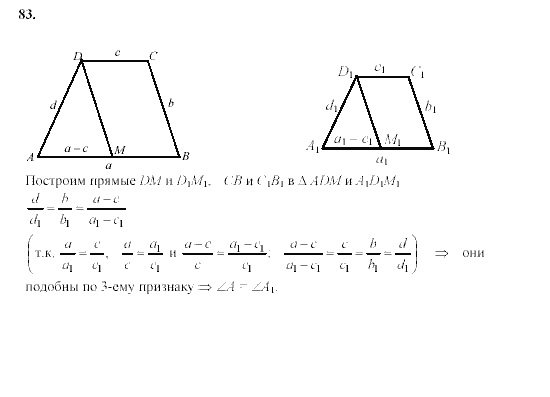 Найдите остальные стороны треугольников.
Найдите остальные стороны треугольников.
№ 3. Длина тени фабричной трубы равна 100м; в это же время вертикально воткнутый в землю столб высотой 6м дает тень длиной 3м. Найдите высоту трубы.
№ 4. Диагонали трапеции АВСD пересекаются в точке Е. Найдите длины диагоналей, если основания АD = 15 дм и ВС = 3дм, а отрезки DЕ = 10дм и ЕС = 4дм.
№ 5. Углы В и В1 треугольников АВС и А1В1С1 равны. Стороны треугольника АВС, прилежащие к углу В в 2 раза больше сторон треугольника А1В1С1, прилежащих к углу В1. Найдите А1С1, если АС = 15 м.
_____________________________________________________________________________
КОНТРОЛЬНАЯ РАБОТА .
Подобие фигур.
3 ВАРИАНТ.
№ 1. У подобных треугольников АВС и А1В1С1 А = 430, АВ = 5м, ВС = 8м, В1С1 = 32м. Чему равны А1 и сторона А1В1?
Чему равны А1 и сторона А1В1?
№ 2. У треугольников АВС и А1В1С1, А = А1, В = В1 АВ=15см, ВС=4см, А1В1=5см, А1С1 = 9см. Найдите остальные стороны треугольников.
№ 3. Длина тени фабричной трубы равна 48м; в это же время вертикально воткнутый в землю столб высотой 12м дает тень длиной 6м. Найдите высоту трубы.
№ 4. Диагонали трапеции АВСD пересекаются в точке Е. Найдите длины диагоналей, если основания АD = 16 дм и ВС = 8дм, а отрезки DЕ = 12дм и ЕС = 3дм.
№ 5. Углы В и В1 треугольников АВС и А1В1С1 равны. Стороны треугольника АВС, прилежащие к углу В в 5 раза больше сторон треугольника А1В1С1, прилежащих к углу В1. Найдите А1С1, если АС = 42м.
Найдите А1С1, если АС = 42м.
КОНТРОЛЬНАЯ РАБОТА .
Подобие фигур.
4 ВАРИАНТ.
№ 1. У подобных треугольников АВС и А1В1С1 А = 560, АВ = 6м, ВС = 20м, В1С1 = 60м. Чему равны А1 и сторона А1В1
№ 2. У треугольников АВС и А1В1С1, А = А1, В = В1 АВ=21см, ВС=6см, А1В1=3см, А1С1 = 14см. Найдите остальные стороны треугольников.
№ 3. Длина тени фабричной трубы равна 69м; в это же время вертикально воткнутый в землю столб высотой 8м дает тень длиной 3м. Найдите высоту трубы.
№ 4. Диагонали трапеции АВСD пересекаются в точке Е. Найдите длины диагоналей, если основания АD = 18 дм и ВС = 6дм, а отрезки DЕ = 15дм и ЕС = 5дм.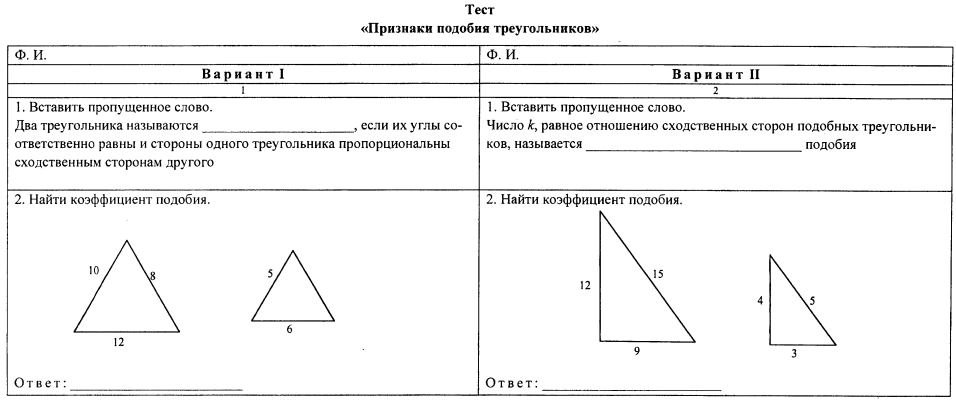
№ 5. Углы В и В1 треугольников АВС и А1В1С1 равны. Стороны треугольника АВС, прилежащие к углу В в 3 раза больше сторон треугольника А1В1С1,
прилежащих к углу В1. Найдите А1С1, если АС = 18 м._____________________________________________________________________________
Контрольная Работа Подобие Треугольников 9 Класс – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
Контрольная Работа Подобие Треугольников 9 Класс
Контрольная работа по геометрии “Признаки подобия треугольников” 9 класс
Геометрия 9 класс. А.В. Погорелов. Н.И. Кулида п. 106.
Контрольная работа по геометрии № 1 «Признаки подобия треугольников»
Цель: выявление знаний учащихся и степени усвоения ими приёмов решения задач на
применение признаков подобия треугольников.
I. Домашнее задание: п.103 – 106 повторить; принести циркуль.
II. Организация учащихся на проведение работы.
III. Выполнение контрольной работы.
2. В треугольнике ABC проведена прямая BD
так, что ∠ABD=∠ACB. Найдите AD и CD, если AB=2
2. В треугольнике ABC проведена прямая AD
так, что ∠BAD=∠BCA. Найдите DB и DC, если AB=2
3. Основания трапеции 1,8 см и 1,2 см.
Боковые стороны, имеющие длины 1,5 см и 1,2 см,
продолжены до взаимного пересечения. Найдите, на
сколько сантиметров продолжены боковые
основаниями 1,8 м и 1,2 м, продолжены до
взаимного пересечения соответственно на 3 м и 2,4
м. Найдите длины боковых сторон трапеции.
1. Докажите подобие треугольников ABC и
1. Докажите подобие треугольников ABC и
2. В треугольнике ABC проведена прямая CD
так, что ∠ACD=∠ABC. Найдите AD и DB, если AC=2
2. В треугольнике ABC проведена прямая BD
так, что ∠CBD=∠CAB. Найдите AD и CD, если BC=2
Найдите AD и CD, если BC=2
3. Основания трапеции 1,5 см и 1,2 см.
Боковые стороны, имеющие длины 1,8 см и 2 см,
продолжены до взаимного пересечения. Найдите, на
сколько сантиметров продолжены боковые
основаниями 1,5 м и 1,2 м, продолжены до
взаимного пересечения соответственно на 7,2 м и 8
м. Найдите длины боковых сторон трапеции.
прямоугольного треугольника проведена прямая,
перпендикулярная гипотенузе ВС и пересекающая
её в точке М. Найдите BC, если AC = 20 см, KM = 8 см,
2. Через точку М стороны KP треугольника
FPK проведена прямая, параллельная стороне FK и
пересекающая сторону FP в точке Т. Найдите TM,
если FK = 52 см, FT = 12 см, TP = 36 см.
3. Стороны параллелограмма KMPT равны 9
см и 13,5 см. Сумма его высот MA и MB, проведённых
из вершины тупого угла M, равна 15 см. Найдите
3. Диагонали трапеции ABCD пересекаются в
т.O. Основания AD и BC равны соответственно 7,5 см
и 2,5 см, BD = 12 см. Найдите BO и OD.
Найдите BO и OD.
Геометрия 9 класс. А.В. Погорелов. Н.И. Кулида п. 106.
Ответы к задачам контрольной работы
1. Белобрысова Т.С. Планирование и контрольные работы по геометрии в VIII и IX классах //
Математика в школе. – М.: «Школьная пресса», 2005. – № 6, 7, 10.
2. Берёзина М.Ю. Методика преподавания геометрии в 7-9 классах. –М. Просвещение, 1989.
3. Гусев В.А., Медяник Ф.И. Дидактические материалы по геометрии. 9 класс.- М:
4. Карнацевич Л.С., Грузин А.И. Изучение геометрии в 7 класс: Из опыта работы. Пособие для
учителя. Под ред. И.Ф. Тысенко. – М.: «Просвещение», 1983.
5. Купорова Т.И. Геометрия IX класс: поурочные планы по учебнику А.В. Погорелова.-
6. Погорелов А. В. Геометрия 7-9 классы. Учебник для общеобразовательных учреждений. –
7. Электронный учебник-справочник «Планиметрия» – ЗАО КУДИЦ, 1998 г.
Геометрия 9 класс. А.В. Погорелов. Н.И. Кулида п. 106.
Контрольная работа по геометрии № 1 «Признаки подобия треугольников»
прямая BD так, что ∠ABD=∠ACB. Найдите AD и
Найдите AD и
прямая AD так, что ∠BAD=∠BCA. Найдите DB и
3. Основания трапеции 1,8 см и 1,2 см.
Боковые стороны, имеющие длины 1,5 см и 1,2
см, продолжены до взаимного пересечения.
основаниями 1,8 м и 1,2 м, продолжены до
взаимного пересечения соответственно на 3 м
и 2,4 м. Найдите длины боковых сторон
Контрольная работа по геометрии № 1 «Признаки подобия треугольников»
прямая CD так, что ∠ACD=∠ABC. Найдите AD и
прямая BD так, что ∠CBD=∠CAB. Найдите AD и
3. Основания трапеции 1,5 см и 1,2 см.
Боковые стороны, имеющие длины 1,8 см и 2
см, продолжены до взаимного пересечения.
основаниями 1,5 м и 1,2 м, продолжены до
взаимного пересечения соответственно на 7,2
м и 8 м. Найдите длины боковых сторон
Контрольная работа по геометрии № 1 «Признаки подобия треугольников»
прямоугольного треугольника проведена
прямая, перпендикулярная гипотенузе ВС и
пересекающая её в точке М. Найдите BC, если
Найдите BC, если
параллельная стороне FK и пересекающая
сторону FP в точке Т. Найдите TM, если
FK = 52 см, FT = 12 см, TP = 36 см.
равны 9 см и 13,5 см. Сумма его высот MA и
MB, проведённых из вершины тупого угла M,
пересекаются в т.O. Основания AD и BC равны
соответственно 7,5 см и 2,5 см, BD = 12 см.
Геометрия – еще материалы к урокам:
Copyright © 2013-2020 “Учителя.com” | Обратная связь: [email protected]
Контрольная работа по геометрии “Признаки подобия…”
Контрольная работа по геометрии в 9 классе
Контрольная работа по геометрии для 9 класса | Тренажёр по…
Подобие фигур – КОНТРОЛЬНЫЕ РАБОТЫ – ГЕОМЕТРИЯ
Контрольная работа по геометрии “Подобие треугольников”
День Солнца Сочинение
Структура Привлеченных Средств Коммерческого Банка Реферат
Примеры Сочинения Рассуждения По Русскому Языку
Самостоятельные И Контрольные Работы Илекса
Сочинение Фильм Онлайн
Персональный сайт – Анисимова Е.
 В. (алгебра, геометрия)
В. (алгебра, геометрия)
Домашнее задание по математике с 18.05 по 22.05
Домашнее задание по математике с 18.05 по 22.05 5 класс
18.5 – Повторение. Угол. №1189(измерить все углы и записать), 1190, 1191, 1192.
19.05 – Повторение. Среднее арифметическое. №1041, 1044, 1047, 847.
20.05 – Итоговая контрольная работа в 10.00.
21.05 – Работа над ошибками.
21.05 -Решение заданий ОГЭ. Карточка.
22.05 – Решение заданий ОГЭ. Карточка.
Домашнее задание по математике с 18.05 по 22.05 8 класс
18.05 – А. Повторение. Графики. №882, 886, 360, 917.
19.05 – А. Повторение. 840, 932, стр.203 №11,12(решить задачи).
Г. Повторение. Подобие треугольников. №829, 832, 834
20.05 – А. Итоговая контрольная работа по алгебре в 10.00.
21.05 – Г. Итоговая контрольная работа по геометрии в 10.00.
22.05 – А. Демоверсия ОГЭ.
Домашнее задание по математике с 18.05 по 29.05 9 класс
18.05 – А. Повторение. Комбинаторные задачи. №583, 585, 593, 595, 597.
19.05 – Г. Повторение. Правильные многоугольники. №856, 859, 860, 863.
20.05 – А. Повторение. Теория вероятностей.№1011, 1014, 657, 658.
21.05 – А. Обобщающее повторение. Карточка.
22.05 – А. Итоговая контрольная работа по алгебре в 10.00.
Г. Повторение. Декартовы координаты. №867, 870, 873, 875.
25.05 – Г. Повторение. Векторы. Геометрические преобразования. №893, 894, 897, 898, 905.
26.05 – Г. Итоговая контрольная работа по геометрии в 10.00.
27.05 – Тренировочные работы ОГЭ.28.05 – Тренировочные работы ОГЭ.
29.05 – Тренировочные работы ОГЭ.
29.05 – Тренировочные работы ОГЭ.
Домашнее задание с 11.05 по 15.05 5 класс
11.05 – Повторение. Решение задач на движение. №1152, 1153, 1154, 1155.
12.05 – Повторение. Решение задач на движение по реке. №1163, 1164, 1165, 1166, 1167.
13.05 – Повторение . Решение задач на нахождение дроби от числа. №1174, 1175, 1176, 1177, 1178.
14.05 – Повторение. Решение задач на нахождение числа по его дроби. №1181, 11892, 1183, 1184, 1185, 1186, 1187.
15.05 – Повторение. Решение геометрических задач. №1197, 1201, 1202, 1203.
Домашнее задание с 11.05 по 15.05 8 класс
11.05 – А. Повторение. Квадратный корень. №898, 899, 900, 902, 903.
12.05 – А. Повторение. Квадратный корень. №904, 905, 906.
Г. Обобщение и систематизация ученого материала. § 15-23. Тест 3 (стр.134), тест 4 (стр.166), повторить все правила после тестов.
13.05 – А. Повторение. Решение уравнений. №890, 922.
14.05 – А. Повторение. Решение уравнений. №929, 930.
15.05 – 10.00 Контрольная работа №5 “Решение прямоугольных треугольников”
Контрольная работа №6 “Площадь многоугольника”
Домашнее задание с 11. 05 по 15.05 9 класс
05 по 15.05 9 класс
11.05 – А. Повторение. Арифметическая прогрессия. №1017, 1019, 1020, 1021, 1031(1,2).
12.05 – Г. 10.00. Контрольная работа №4 “Векторы”,
Контрольная работа №5 “Геометрические преобразования” ( выполняем на двойных листках).
13.05 – А. Повторение. Сумма n первых членов арифметической прогрессии. №1022, 1026, 1030, 1031, 1033.
14.05 – А. Повторение. Геометрическая прогрессия. №1037, 1039.
15.05 – А. Повторение. сумма n первых членов геометрической прогрессии. №1041, 1042.
Г. Повторение. Решение треугольников. №832, 833, 836, 840, 853.
Домашнее задание 11 класс с 11.05 по 29.05
11.05 – Г. Повторение . Площади и объемы многогранников. Решение задач по материалам ЕГЭ . Карточка.
13. 05 – А. Обобщающее повторение. Подготовка к итоговой к/р. Карточка.
05 – А. Обобщающее повторение. Подготовка к итоговой к/р. Карточка.
13.05 – А. Обобщающее повторение. Подготовка к итоговой к/р. Карточка.
18.05 – Г. Обобщающее повторение. Подготовка к итоговой к/р. Карточка.
20.05 – Итоговая контрольная работа
20.05 – Итоговая контрольная работа
25.05 – Диагностическая работа ЕГЭ
28. 05 – Диагностическая работа ЕГЭ
05 – Диагностическая работа ЕГЭ
28.05 – Диагностическая работа ЕГЭ
Домашнее задание по математике с 4.05 по 8.05.
5 класс
4.05 – Повторение. Среднее арифметическое. Проценты. Карточка.
5.05 – Повторение. Решение задач на проценты. Карточка.
6.05 – Контрольная работа №9
7.05 – Повторение. Действия с десятичными дробями. № 1123 (10,12, 13, 15, 18), 1123 (19,21,22- заменить обыкновенную дробь на десятичную, где это необходимо и возможно)
8.05 – Повторение. Решение уравнений. № 1128 (1,3,5,6,8,10,12,13,16,18), 1129 (1,3,4,6,9)
8 класс
4.05 -А. Повторение. Рациональные выражения. № 847, 843(5-12), 850(5,6,7).
5.05 -А. Повторение. Рациональные выражения. №867(делать по действиям).
Г. – §23. Площадь трапеции. №773,774, 776, 777, 778.
№773,774, 776, 777, 778.
6.05 – А. Повторение.§8,9 Степень. №872, 876, 877(7-12)
7.05 – А. Повторение. §12,16 Корень. №888, 889(2.3,6), 891(4,6,7,8), 892.
8.05 – Г. §23. Площадь трапеции. №780, 782, 783, 784, 786.
9 класс
4.05 – А. Повторение. Системы уравнений с двумя переменными. №985.
5.05 – Г. §20 Гомотетия. Подобие фигур.(стр.178-180) №745, 746, 748, 757, 762,773.
6.05 – А. Повторение. Решение задач. №988, 989, 990,991.
7.07 – А. Повторение. Решение задач. №992, 993, 994, 995.
8.05 – А.Повторение. Решение задач. №996, 997, 998, 999, 1001, 1002, 1003.
Г. Обобщение и систематизация учебного материала. Глава 4. Тест 4 (стр.145) и правила, Глава 5. Тест №5 (стр. 193) и правила.
Домашнее задание по математике на 27.04 – 30.04
5 класс
27.04 – §37. Нахождение процентов от числа. № 1080, 1081, 1082, 1083, 1084, 1085, 1086
29. 04 – §38. Нахождение числа по его проценту. № 1093, 1094, 1095, 1096, 1097, 1098, 1099,1100,1101.
04 – §38. Нахождение числа по его проценту. № 1093, 1094, 1095, 1096, 1097, 1098, 1099,1100,1101.
30.04 – §38. Нахождение числа по его проценту. № 1103, 1104, 1105, 1106, 1107, 1108, 1109, 1110, 1111, 1112, 1113, 1114, 1115.
8 класс
27.04 – А. Решение задач ОГЭ (на работу) карточка
28, 29.04 – А. Обобщение и систематизация учебного материала §19-24. № 627, 689, 716, 731, 754(3,6,9), 756(3), 758(3), 776(3), 782(3), 788(4).
30.04 – А. Контрольная работа №5 “Квадратные уравнения”, контрольная работа №6 “Рациональные уравнения”
9 класс
27.04 – А. Повторение. Решение квадратных неравенств (§12) № 976, 977.
29.04 – А. Повторение. Решение систем неравенств № 978(1, 8), 979, 980.
30.04 – А. Повторение. Решение систем уравнений с двумя переменными. № 983(2, 3), 984(1, 3, 5, 7, 9)
Домашнее задание 11 класс с 27.04 по 6.05
27.04 – Г. Повторение. Параллельность прямых и плоскостей (скрещивающиеся прямые). Карточка.
Карточка.
29.04 – А. Геометрический смысл производной. Касательная. Карточка.
29.04 – А. Применение производной. Исследование функции. Карточка.
4.05 – Г. Повторение. Перпендикулярность прямых и плоскостей (теорема о трех перпендикулярах). Карточка
6.05 – А. Повторение. Первообразная. Интеграл. Площадь криволинейной трапеции. Карточка.
6.05 – А. Комбинаторные задачи. Теория вероятностей. Карточка.
|
Контрольная работа по геометрии 8 класс 1 вариант
а) Докажите, что AO : OC = BO : OD. б) Найдите AB, если OD=15 см, OB=9 см, CD=25 см. 2. Найдите отношение площадей треугольников ABC и KMN, если AB=8 см, BC=12 см, AC=16 см, KM=10 см, MN=15 см, NK=20 см. 3. Стороны треугольника равны 10 см, 17 см и 21 см. Периметр подобного ему треугольника равен 72 см. Найдите стороны второго треугольника.
|
Контрольная работа по геометрии 8 класс 2 вариант
а) Докажите, что AB : BM = CB : BN. б) Найдите MN, если AM=6 см, BM=8 см, AC=21 см. 2. Даны стороны треугольников PQR и ABC: PQ=16 см, QR=20 см, PR=28 см и AB=12 см, BC=15 см, AC=21 см, KM=10 см, MN=15 см, NK=20 см. Найдите отношение площадей этих треугольников. 3. Стороны треугольника относятся как 3:2:4. Периметр подобного треугольника равен 108 см. Найдите стороны второго треугольника.
|
пособие для учителей общеобразовательных организаций. Сост. Т. А. Бурмистрова
%PDF-1.6 % 378 0 obj > endobj 380 0 obj > endobj 377 0 obj >stream application/pdf
 Сост. Т. А. Бурмистрова
Сост. Т. А. Бурмистрова -5Rz4\{}qՌ'(j6KH77R)D68[@’u>8lEsZ
s\U%YQnk\(tnat
-5Rz4\{}qՌ'(j6KH77R)D68[@’u>8lEsZ
s\U%YQnk\(tnat|
№ |
Тема урока |
Кол- во уроков |
Дата проведения. |
Причина и дата пропуска и дата ликвидации |
Тип урока, Форма контроля |
Требования общеобразовательного минимума знаний , умения |
Использование ИКТ |
|
|
1 триместр. |
|
|
||||
|
|
Подобие фигур |
16 |
|
|
|
|
|
|
1 |
Преобразование подобия, п. |
1 |
07.09 |
|
Изуч. нов. мат. |
Знать: – определения гомотетии, подобия, коэффициентов гомотетии и подобия, формулировку теоремы; – определение подобных фигур, формулировки признаков подобия фигур; – признаки подобия прямоугольных треугольников. Уметь: – доказывать сохранение углов при преобразованиях подобия при изучении текущего материала; – воспроизводить доказательства признаков в ходе изучения текущего материала, применять признаки подобия при решении задач; – применять признаки подобия прямоугольных треугольников при решении задач. |
Презент. |
|
2 |
Свойства преобразования подобия п.101 |
1 |
09. |
|
Комбин. |
Презент. |
|
|
3 |
Подобие фигур., п.102 |
1 |
14.09 |
|
Изуч. нов. мат. |
|
|
|
4 |
Признак подобия треугольников по двум углам п.103 |
1 |
16.09 |
|
Комб. |
|
|
|
5 |
Признак подобия треугольников по двум сторонам и углу между ними., п.104 |
1 |
21. |
|
Комбин. |
|
|
|
6 |
Признак подобия треугольников по трем сторонам п.105 |
1 |
23.09 |
|
Комбин. |
|
|
|
7 |
Решение задач |
1 |
28.09 |
|
Обобщ. |
|
|
|
8 |
Подобие прямоугольных треугольников, п.106 |
2 |
30. |
|
Изуч. нов. мат. |
|
|
|
9 |
Подобие прямоугольных треугольников, п.106 |
|
05.10 |
|
Закреп. |
|
|
|
10 |
Контрольная работа №1 |
1 |
07.10 |
|
Контр. |
|
|
|
11 |
Углы, вписанные в окружность, п. |
2 |
12.10 |
|
Изуч. нов. мат. |
Знать: – понятие плоского угла, дополнительных углов; – определения центрального угла, дуги окружности, градусной меры дуги окружности, угла, вписанного в окружность; – формулировку теоремы о связи градусных мер центрального и вписанного углов; – свойство вписанных углов в окружность. Уметь: – по чертежу определять дополнительные углы, центральные и вписанные в окружность; – строить центральный и вписанный в окружность углы; – записывать пропорциональность отрезков хорд и секущих окружности.
|
|
|
12 |
Углы, вписанные в окружность, п.107 |
|
14. |
|
Обобщ. |
|
|
|
13 |
Пропорциональность отрезков хорд и секущих окружности, п.108 |
3 |
19.10 |
|
Изуч. нов. мат. |
|
|
|
14 |
Пропорциональность отрезков хорд и секущих окружности, п.108 |
|
21.10 |
|
Закреп. |
|
|
|
15 |
Пропорциональность отрезков хорд и секущих окружности, п. |
|
26.10 |
|
Обобщ. |
|
|
|
16 |
Контрольная работа №2 |
1 |
28.10 |
|
Контр. |
|
|
|
|
Решение треугольников |
9 |
|
|
|
|
|
|
17 |
Теорема косинусов, п. |
2 |
09.11 |
|
|
Знать: – формулировки теоремы косинусов и следствий из нее, утверждения о свойстве диагоналей параллелограмма; – формулировки теоремы синусов и следствия из нее о соотношении между сторонами и углами треугольника;
Уметь: – доказывать теорему косинусов, записывать в виде равенства теорему косинусов применительно к данному треугольнику, по трем данным сторонам находить его углы, по данным двум сторонам треугольника и углу между ними находить третью сторону, применять теорему косинусов и следствия из нее к решению задач; – доказывать теорему синусов, записывать ее формулировку символически и составлять пропорции для сторон и углов данного треугольника, решать задачи; – для каждой из трех основных задач проводить решение в общем виде и для конкретных треугольников.
|
|
|
18 |
Теорема косинусов, п.109 |
|
11.11 |
|
|
|
|
|
19 |
Теорема синусов п.110 |
2 |
16.11 |
|
|
|
|
|
20 |
Теорема синусов п.110 |
|
18.11 |
|
|
|
|
|
21 |
Соотношение между углами и противолежащими сторонами треугольника п. |
1 |
23.11 |
|
|
|
|
|
22 |
Решение треугольников, п.112 |
3 |
25.11 |
|
|
|
|
|
23 |
Решение треугольников, п.112 |
|
30.11 |
|
|
|
|
|
|
2 триместр. |
|
|
|
|
|
|
|
24 |
Решение треугольников, п. |
|
02.12 |
|
|
|
|
|
25 |
Контрольная работа №3 |
1 |
07.12 |
|
|
|
|
|
|
Многоугольники |
13 |
|
|
|
|
|
|
26 |
Ломаная, п. |
1 |
09.12 |
|
|
Знать: – что длина ломаной не меньше длины отрезка, соединяющего ее концы; – что сумма углов выпуклого n-угольника равна 180º∙(n-2), а сумма внешних углов выпуклого n-угольника равна 360º; – определения правильного многоугольника, многоугольника, вписанного в окружность, многоугольника, описанного около окружности; – что для каждого правильного многоугольника существует окружность, вписанная в него, и окружность, описанная около него, и что такие окружности имеют общий центр, который находится в точке пересечения биссектрис правильного многоугольника; – формулы, связывающие радиус описанной окружности и радиус вписанной окружности со стороной a правильного n-угольника для n=3,4,6; – что периметры правильных n- угольников относятся как радиусы описанных (вписанных) окружностей, отношение длины окружности к ее диаметру одно и тоже (π), формулу длины окружности; – что такое радианная мера угла, какой центральный угол является углом в 1 радиан, что радианная мера угла 180º равна π радианам. Уметь: – изображать ломаную, называть по рисунку ее элементы, проводить доказательство теоремы; – чертить многоугольник (выпуклый), строить его диагонали, внешние углы, доказывать теорему о сумме углов выпуклого n-угольника, решать задачи; – проводить доказательство теоремы; – выводить формулы для R, r, конкретизировать их для правильного многоугольника с заданным числом сторон, выводить частные случаи этих формул для n=3,4,6 без использования общей формулы, решать задачи; – применять формулу длины окружности для решения задач; – строить некоторые правильные многоугольники с помощью циркуля и транспортира; – составлять пропорцию, связывающую градусную и радианную меры угла, и использовать ее для перевода градусной меры угла в радианную и наоборот.
|
|
|
27 |
Выпуклые многоугольники п.114 |
1 |
14. |
|
|
|
|
|
28 |
. Правильные многоугольники п.115 |
1 |
16.12 |
|
|
|
|
|
29 |
Формулы для радиусов вписанных и описанных окружностей правильных многоугольников, п.116 |
3 |
21.12 |
|
|
|
|
|
30 |
Формулы для радиусов вписанных и описанных окружностей правильных многоугольников, п. |
|
23.12 |
|
|
|
|
|
31 |
Формулы для радиусов вписанных и описанных окружностей правильных многоугольников, п.116 |
|
28.12 |
|
|
|
|
|
32 |
Построение некоторых правильных многоугольников, п.117 |
1 |
11.01 |
|
|
|
|
|
33 |
Подобие правильных выпуклых многоугольников, п. |
1 |
13.01 |
|
|
|
|
|
34 |
Длина окружности п.119 |
1 |
18.01 |
|
|
|
|
|
35 |
Радианная мера угла, п.120 |
1 |
20.01 |
|
|
|
|
|
36 |
Решение задач |
2 |
25. |
|
|
|
|
|
37 |
Решение задач |
|
27.01 |
|
|
|
|
|
38 |
Контрольная работа №4 |
1 |
01.02 |
|
|
|
|
|
|
Площади фигур |
19 |
|
|
|
|
|
|
39 |
Понятие площади. |
1 |
03.02 |
|
|
Знать: – свойства площади простой фигуры, формулу площади прямоугольника, параллелограмма, трапеции, треугольника; – площади подобных фигур относятся как квадраты их соответствующих линейных размеров, что с увеличением (уменьшением) линейных размеров фигуры в k раз ее площадь увеличивается (уменьшается) в kраз; – определение круга, формулу площади круга. Что такое круговой сектор и круговой сегмент. Уметь: – вывести формулу площади прямоугольника для случая, когда длины сторон – рациональные числа; – провести доказательство справедливости формул для параллелограмма, трапеции, треугольника, применять их для решения задач; – использовать формулы площади треугольника через синус, Герона, радиуса описанной и вписанной окружностей при решении задач; – находить отношение площадей подобных фигур по известным длинам пары соответствующих элементов этих фигур; – вычислять площади круга, кругового сектора и кругового сегмента. |
|
|
40 |
Площадь прямоугольника п.122 |
1 |
08.02 |
|
|
|
|
|
41 |
Площадь параллелограмма, п.123 |
2 |
10.02 |
|
|
|
|
|
42 |
Площадь параллелограмма, п.123 |
|
15.02 |
|
|
|
|
|
43 |
Площадь треугольника, п. |
1 |
17.02 |
|
|
|
|
|
44 |
Формула Герона п.125 |
1 |
22.02 |
|
|
|
|
|
45 |
Решение задач на нахождение площади треугольника |
1 |
24.02 |
|
|
|
|
|
|
3 триместр. |
|
|
|
|
|
|
|
46 |
Площадь трапеции, п. |
2 |
01.03 |
|
|
|
|
|
47 |
Площадь трапеции, п.126 |
|
03.03 |
|
|
|
|
|
48 |
Решение задач по теме |
1 |
10.03 |
|
|
|
|
|
49 |
Контрольная работа №5 |
1 |
15. |
|
|
&am |
Гимназия 3
ТРИМЕСТРЫ:
I триместр:
с 01.09.2021 по 30.11.2021
II триместр:
с 01.12.2021 по 28.02.2022
III триместр:
1-4 классы с 01.03 по 27.05.2022
5-8 классы с 01.03 по 31.05.2022
10 класс с 01.03 по 10.06.2022
9, 11 классы с 01.03 по 20.05.2022
КАНИКУЛЫ:
Осенние:
26. 10.2021 по 07.11.2021
10.2021 по 07.11.2021
Зимние:
31.12.2021 по 09.01.2022
Весенние:
21.03.2022 по 27.03.2022
Летние:
1 – 4 классы – 28.06.2022 по 31.08.2022
5 – 8 классы – 01.06.2022 по 31.08.2022
10 класс – 30.06.2022 по 31.08.2022
Дополнительные (для 1-х классов):
14.02.2022 по 20.02.2022
Окончание учебного года:
1 – 4 классы – 27.05.2022
5 – 8 классы – 31.05.2022
10 классы – 30. 06.2022
06.2022
9,11 классы – по окончании ГИА
Похожие фигурки
Говорят, что две фигуры похожий если они одинаковой формы. Говоря более математическим языком, две фигуры похожи, если их соответствующие углы равны конгруэнтный , а отношения длин соответствующих сторон равны.
Это общее отношение называется масштаб .
Символ ∼ используется для обозначения сходства.
Пример 1:
На рисунке ниже пятиугольник А B C D E ∼ пятиугольник V W Икс Y Z .
(Обратите внимание, что порядок, в котором вы пишете вершины, имеет значение; например,
пятиугольник
А
B
C
D
E
является
нет
похож на пятиугольник
V
Z
Y
Икс
W
. )
)
Пример 2:
Два цилиндра похожи. Найдите масштабный коэффициент и радиус второго цилиндра.
Высота цилиндра справа составляет 1 3 высота цилиндра слева.Итак, коэффициент масштабирования равен 1 3 .
Чтобы получить радиус меньшего цилиндра, разделите 1,8 к 3 .
1,8 ÷ 3 знак равно 0,6
Итак, радиус меньшего цилиндра равен 0,6 см.
Обратите внимание, что двухмерная фигура похожа на другую, если вторая может быть получена из первой последовательностью вращения , размышления , переводы , а также дилатации .
Пример 3:
На рисунке выше шестиугольник
А
1
B
1
C
1
D
1
E
1
F
1
переворачивается по горизонтали, чтобы получить
А
2
B
2
C
2
D
2
E
2
F
2
.
Тогда шестиугольник А 2 B 2 C 2 D 2 E 2 F 2 переводится, чтобы получить А 3 B 3 C 3 D 3 E 3 F 3 .
Шестиугольник А 3 B 3 C 3 D 3 E 3 F 3 расширяется на коэффициент масштабирования 1 2 получить А 4 B 4 C 4 D 4 E 4 F .
Обратите внимание, что
А
1
B
1
C
1
D
1
E
1
F
1
∼
А
2
B
2
C
2
D
2
E
2
F
2
∼
А
3
B
3
C
3
D
3
E
3
F
3
∼
А
4
B
4
C
4
D
4
E
4
F
4
.
То есть все четыре шестиугольника похожи. (Фактически, первые три совпадают.)
Пример 4:
Рассмотрим пятиугольник п Q р S Т на координатной плоскости.
Ротация 180 ° о происхождении берет пятиугольник, чтобы п ‘ Q ‘ р ‘ S ‘ Т ‘ .
Теперь, расширение начала координат с помощью масштабного коэффициента. 2 занимает пятиугольник п ‘ Q ‘ р ‘ S ‘ Т ‘ к п ‘ ‘ Q ‘ ‘ р ‘ ‘ S ‘ ‘ Т ‘ ‘ .
Обратите внимание, что
п
Q
р
S
Т
∼
п
‘
Q
‘
р
‘
S
‘
Т
‘
∼
п
‘
‘
Q
‘
‘
р
‘
‘
S
‘
‘
Т
‘
‘
. То есть все три пятиугольника похожи. (И первые два совпадают.)
То есть все три пятиугольника похожи. (И первые два совпадают.)
открытых учебников | Сиявула
Математика
Наука
-
- Читать онлайн
-
Учебники
-
Английский
-
Класс 7A
-
Марка 7Б
-
7 класс (A и B вместе)
-
-
Африкаанс
-
Граад 7А
-
Граад 7Б
-
Граад 7 (A en B saam)
-
-
-
Пособия для учителя
-
- Читать онлайн
-
Учебники
-
Английский
-
Марка 8A
-
Сорт 8Б
-
Оценка 8 (вместе A и B)
-
-
Африкаанс
-
Граад 8А
-
Граад 8Б
-
Граад 8 (A en B saam)
-
-
-
Пособия для учителя
-
- Читать онлайн
-
Учебники
-
Английский
-
Марка 9А
-
Марка 9Б
-
9 класс (A и B вместе)
-
-
Африкаанс
-
Граад 9А
-
Граад 9Б
-
Граад 9 (A en B saam)
-
-
-
Пособия для учителя
-
- Читать онлайн
-
Учебники
-
Английский
-
Класс 4A
-
Класс 4Б
-
Класс 4 (вместе A и B)
-
-
Африкаанс
-
Граад 4А
-
Граад 4Б
-
Граад 4 (A en B saam)
-
-
-
Пособия для учителя
-
- Читать онлайн
-
Учебники
-
Английский
-
Марка 5А
-
Марка 5Б
-
Оценка 5 (вместе A и B)
-
-
Африкаанс
-
Граад 5А
-
Граад 5Б
-
Граад 5 (A en B saam)
-
-
-
Пособия для учителя
-
- Читать онлайн
-
Учебники
-
Английский
-
Марка 6A
-
Марка 6Б
-
6 класс (A и B вместе)
-
-
Африкаанс
-
Граад 6А
-
Граад 6Б
-
Граад 6 (A en B saam)
-
-
-
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете делать ксерокопии, распечатывать и распространять их сколь угодно часто. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Вы можете делать ксерокопии, распечатывать и распространять их сколь угодно часто. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без марочного обозначения)
Эти небрендовые версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, изменять или дополнять их любым способом, с единственным требованием – дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
похожих треугольников – доказательство, определение и теоремы (видео)
Подобные треугольники (определение, доказательство и теоремы)
Сходство в математике не означает того же, что сходство в повседневной жизни.Подобные треугольники – это треугольники одинаковой формы, но с разными размерами сторон.
- Определение похожих треугольников
Определение похожих треугольников
Мороженое с шоколадной крошкой и мороженое с шоколадной крошкой похожи, но не одинаковы. Слово «подобный» используется в повседневной жизни, но не так, как мы используем его в математике.
В геометрии две формы похожи , если они одинаковой формы, но разных размеров.У вас может получиться квадрат со сторонами 21 см и квадрат со сторонами 14 см; они были бы похожи. Равносторонний треугольник со сторонами 21 см и квадрат со сторонами 14 см не похожи друг на друга, потому что это разные формы.
Подобные треугольники легко идентифицировать, потому что к треугольникам можно применить три теоремы. Эти три теоремы, известные как Угол – Угол (AA) , Сторона – Угол – Сторона (SAS) и Сторона – Сторона – Сторона (SSS) , являются надежными методами определения сходства в треугольниках.
- Угол – Угол (AA)
- Сторона – Угол – Сторона (SAS)
- Сторона – Сторона – Сторона (SSS)
Соответствующие углы
В геометрии соответствие означает, что конкретная часть одного многоугольника точно соответствует аналогичной части другого. Даже если два треугольника ориентированы по-разному друг от друга, если вы можете повернуть их таким же образом и увидеть, что их углы одинаковы, вы можете сказать, что эти углы совпадают.
Три теоремы подобия в треугольниках зависят от соответствующих частей. Вы смотрите на один угол одного треугольника и сравниваете его с таким же углом другого треугольника.
Вы смотрите на один угол одного треугольника и сравниваете его с таким же углом другого треугольника.
Пропорции
Сходство связано с пропорцией. Треугольники легко оценить на предмет пропорциональных изменений, которые делают их похожими. Их сравнительные стороны пропорциональны друг другу; их соответствующие углы идентичны.
Вы можете установить отношения для сравнения длин сторон двух треугольников.Если отношения совпадают, соответствующие стороны подобны друг другу.
Уголок в комплекте
Включенный угол относится к углу между двумя парами соответствующих сторон. Вы не можете сравнить две стороны двух треугольников, а затем перепрыгнуть на угол, который не находится между этими двумя сторонами.
Доказательство треугольников аналогично
Вот два равных треугольника. Чтобы облегчить вам жизнь, мы сделали их оба равносторонними треугольниками.
△ FOX сравнивается с △ HEN.Обратите внимание, что ∠O на △ FOX соответствует ∠E на △ HEN.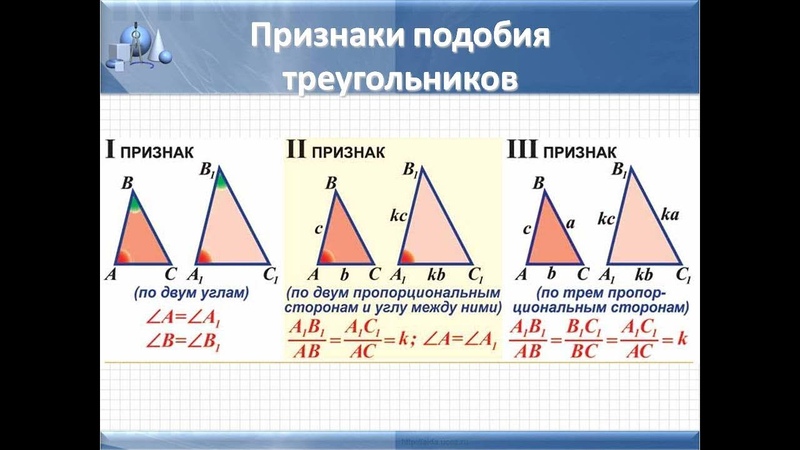 Оба ∠O и ∠E – это включенных углов между сторонами FO и OX на △ FOX и сторонами HE и EN на △ HEN.
Оба ∠O и ∠E – это включенных углов между сторонами FO и OX на △ FOX и сторонами HE и EN на △ HEN.
Side FO конгруэнтен боковому HE; сторона OX конгруэнтна стороне EN, а ∠O и ∠E – входящие конгруэнтные углы.
Два равносторонних треугольника одинаковые, за исключением букв. Они одинакового размера, поэтому представляют собой одинаковых треугольника . Если бы они оба были равносторонними треугольниками, но сторона EN была бы вдвое длиннее стороны HE, это были бы аналогичные треугольники .
Теоремы подобия треугольника
Угол-угол (AA) Теорема
Угол-угол (AA) говорит, что два треугольника подобны, если у них есть две пары соответствующих углов, которые совпадают. Два треугольника могут быть на больше, чем на , чем аналогичные; они могли быть идентичными. Для AA все, что вам нужно сделать, это сравнить две пары соответствующих углов.
Примерка Угол-Угол
Вот два разносторонних треугольника △ JAM и △ OUT. Мы уже отметили два внутренних угла каждого треугольника с помощью сокращения геометрии для сравнения: маленьких косых черт. Одна косая черта для внутреннего A и такая же косая черта для внутреннего ∠U означает, что они совпадают. Обратите внимание, что ∠M совпадает с ∠T, потому что на каждом из них есть две маленькие косые черты.
Мы уже отметили два внутренних угла каждого треугольника с помощью сокращения геометрии для сравнения: маленьких косых черт. Одна косая черта для внутреннего A и такая же косая черта для внутреннего ∠U означает, что они совпадают. Обратите внимание, что ∠M совпадает с ∠T, потому что на каждом из них есть две маленькие косые черты.
Поскольку A конгруэнтно U, а ∠M конгруэнтно ∠T, теперь у нас есть две пары конгруэнтных углов, поэтому теорема AA утверждает, что эти два треугольника подобны.
Уловки торговли
Остерегайтесь уловок из учебников, онлайн-заданий и учителей математики.Иногда треугольники ориентированы по-разному, когда вы на них смотрите. Возможно, вам придется повернуть один треугольник, чтобы увидеть, сможете ли вы найти две пары соответствующих углов.
Еще одна проблема: два угла измеряются и идентифицируются на одном треугольнике, но два разных угла измеряются и идентифицируются на другом.
Поскольку каждый треугольник имеет только три внутренних угла, по одному каждому из идентифицированных углов должен быть конгруэнтным. Вычитая измеренные идентифицированные углы каждого треугольника из 180 °, вы можете узнать меру недостающего угла.Затем вы можете сравнить любые два соответствующих угла для сравнения.
Вычитая измеренные идентифицированные углы каждого треугольника из 180 °, вы можете узнать меру недостающего угла.Затем вы можете сравнить любые два соответствующих угла для сравнения.
Боковой угол-сторона (SAS) Теорема
Вторая теорема требует точного порядка: сторона, затем включенный угол, затем следующая сторона. Теорема Side-Angle-Side (SAS) утверждает, что если две стороны одного треугольника пропорциональны двум соответствующим сторонам другого треугольника, и их соответствующие включенные углы совпадают, эти два треугольника подобны.
Попытка бокового угла
Вот два треугольника, расположенных бок о бок и ориентированных одинаково.△ RAP и △ EMO определили стороны размером 37 дюймов на △ RAP и 111 дюймов на EMO, а также стороны 17 на △ RAP и 51 дюйм на EMO. Обратите внимание, что угол между обозначенными измеренными сторонами одинаков для обоих треугольников: 47 °.
Отношение 37/111 совпадает с соотношением 17/51? Да; эти два соотношения пропорциональны, так как каждое из них упрощается до 1/3. Эти два треугольника схожи с одинаковым углом между ними.
Эти два треугольника схожи с одинаковым углом между ними.
Теорема Сторона-Сторона-Сторона (SSS)
Последняя теорема – Side-Side-Side или SSS .Эта теорема утверждает, что если два треугольника имеют пропорциональные стороны, они подобны. Это может показаться большим скачком, игнорирующим их углы, но подумайте об этом: единственный способ построить треугольник со сторонами, пропорциональными сторонам другого треугольника, – это скопировать углы.
Попытка сторона-сторона-сторона
Вот два треугольника: FLO и △ HIT. Обратите внимание, мы не определили внутренние углы. Стороны △ FLO имеют длину 15, 20 и 25 см. Стороны △ HIT имеют длину 30, 40 и 50 см.
Вам необходимо задать соотношения соответствующих сторон и оценить их:
1530 = 12
2040 = 12
2550 = 12
Все они имеют одинаковое соотношение при упрощении. Их всех 12. Итак, даже не зная внутренних углов, мы знаем, что эти два треугольника похожи, потому что их стороны пропорциональны друг другу.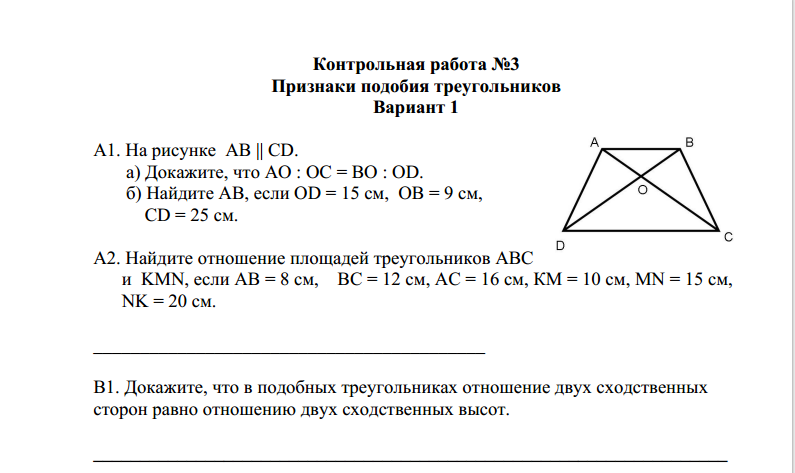
Краткое содержание урока
Теперь, когда вы изучили этот урок, вы можете определять и идентифицировать похожие фигуры, и вы можете описать требования к треугольникам, чтобы они были похожими (они должны иметь либо две конгруэнтные пары соответствующих углов, либо две пропорциональные соответствующие стороны с включенными соответствующими угол конгруэнтный, или все соответствующие стороны пропорциональны).
Вы также можете применить три теоремы подобия треугольников, известные как Угол – Угол (AA), Сторона – Угол – Сторона (SAS) или Сторона – Сторона – Сторона (SSS), чтобы определить, похожи ли два треугольника.
Следующий урок:
Постулаты конгруэнтности треугольника
похожих треугольников
Два треугольника подобны, если разница только в размере (и, возможно, в необходимости перевернуть или перевернуть один треугольник).
Все эти треугольники похожи:
(равные углы отмечены таким же количеством дуг)
Некоторые из них имеют разные размеры, а некоторые перевернуты или перевернуты.
Для одинаковых треугольников:
Все соответствующие углы равны
и
Все соответствующие стороны имеют одинаковое соотношение
Также обратите внимание, что соответствующие стороны обращены к соответствующим углам. Например, стороны, обращенные к углам с двумя дугами, соответствуют друг другу.
Соответствующие стороны
В подобных треугольниках соответствующие стороны всегда находятся в одинаковом соотношении.
Например:
Треугольники R и S похожи. Равные углы обозначены одинаковым количеством дуг.
Какова соответствующая длина?
- Длины 7 и a соответствуют (они обращены к углу, отмеченному одной дугой)
- Длины 8 и 6,4 соответствуют (они обращены к углу, отмеченному двумя дугами)
- Длины 6 и b соответствуют (они обращены к углу, отмеченному тремя дугами)
Расчет длин соответствующих сторон
Иногда мы можем вычислить длины, которых еще не знаем.
- Шаг 1: Найдите отношение соответствующих сторон
- Шаг 2: Используйте это соотношение, чтобы найти неизвестную длину
Пример: Найдите длины a и b треугольника S
Шаг 1. Найдите соотношение
Мы знаем все стороны треугольника R и
Мы знаем сторону 6.4 треугольника S
6.4 обращен к углу, отмеченному двумя дугами, как и сторона длиной 8 в треугольнике R .
Таким образом, мы можем сопоставить 6.4 с 8 , и поэтому отношение сторон в треугольнике S к треугольнику R будет:
от 6,4 до 8
Теперь мы знаем, что длины сторон в треугольнике S равны 6,4 / 8, умноженным на длины сторон в треугольнике R .
Шаг 2: Используйте соотношение
a обращен к углу с одной дугой, как и сторона длиной 7 в треугольнике R .
a = (6.4/8) × 7 = 5,6
b обращен к углу с тремя дугами, как и сторона длиной 6 в треугольнике R .
b = (6,4 / 8) × 6 = 4,8
Готово!
% PDF-1.4
%
407 0 объект
>
эндобдж
xref
407 172
0000000016 00000 н.
0000004969 00000 н.
0000005054 00000 н.
0000005292 00000 н.
0000006643 00000 п.
0000006690 00000 н.
0000006736 00000 н.
0000006784 00000 н.
0000006831 00000 н.
0000006878 00000 н.
0000006925 00000 н.
0000006972 00000 н.
0000007018 00000 н.
0000007066 00000 н.
0000007113 00000 п.
0000007161 00000 н.
0000007209 00000 н.
0000007257 00000 н.
0000007305 00000 н.
0000007353 00000 н.
0000007401 00000 п.
0000007454 00000 н.
0000007501 00000 н.
0000007579 00000 п.
0000007655 00000 н.
0000007949 00000 п.
0000008269 00000 н.
0000008653 00000 н.
0000009046 00000 н.
0000009402 00000 п.
0000009449 00000 н.
0000009497 00000 н.
0000009543 00000 н.
0000009590 00000 н.
0000009637 00000 н.
0000009684 00000 п.
0000009730 00000 н.
0000009776 00000 н. 0000009823 00000 п.
0000009870 00000 н.
0000009917 00000 н.
0000018043 00000 п.
0000026086 00000 п.
0000026163 00000 п.
0000026522 00000 п.
0000026965 00000 п.
0000034115 00000 п.
0000038738 00000 п.
0000043063 00000 п.
0000047778 00000 п.
0000048067 00000 п.
0000048522 00000 н.
0000048875 00000 п.
0000049142 00000 п.
0000049491 00000 п.
0000049697 00000 п.
0000050480 00000 п.
0000050586 00000 п.
0000051197 00000 п.
0000051307 00000 п.
0000051371 00000 п.
0000051762 00000 п.
0000051959 00000 п.
0000052252 00000 п.
0000052633 00000 п.
0000053294 00000 п.
0000053672 00000 п.
0000054181 00000 п.
0000054846 00000 н.
0000054897 00000 п.
0000054934 00000 п.
0000055646 00000 п.
0000055721 00000 п.
0000062114 00000 п.
0000062893 00000 п.
0000063065 00000 п.
0000063235 00000 п.
0000063586 00000 п.
0000063768 00000 п.
0000064030 00000 п.
0000064291 00000 п.
0000068847 00000 п.
0000070669 00000 п.
0000072951 00000 п.
0000076190 00000 п.
0000077145 00000 п.
0000009823 00000 п.
0000009870 00000 н.
0000009917 00000 н.
0000018043 00000 п.
0000026086 00000 п.
0000026163 00000 п.
0000026522 00000 п.
0000026965 00000 п.
0000034115 00000 п.
0000038738 00000 п.
0000043063 00000 п.
0000047778 00000 п.
0000048067 00000 п.
0000048522 00000 н.
0000048875 00000 п.
0000049142 00000 п.
0000049491 00000 п.
0000049697 00000 п.
0000050480 00000 п.
0000050586 00000 п.
0000051197 00000 п.
0000051307 00000 п.
0000051371 00000 п.
0000051762 00000 п.
0000051959 00000 п.
0000052252 00000 п.
0000052633 00000 п.
0000053294 00000 п.
0000053672 00000 п.
0000054181 00000 п.
0000054846 00000 н.
0000054897 00000 п.
0000054934 00000 п.
0000055646 00000 п.
0000055721 00000 п.
0000062114 00000 п.
0000062893 00000 п.
0000063065 00000 п.
0000063235 00000 п.
0000063586 00000 п.
0000063768 00000 п.
0000064030 00000 п.
0000064291 00000 п.
0000068847 00000 п.
0000070669 00000 п.
0000072951 00000 п.
0000076190 00000 п.
0000077145 00000 п. 0000083365 00000 п.
0000083417 00000 п.
0000087989 00000 п.
00000
0000083365 00000 п.
0000083417 00000 п.
0000087989 00000 п.
00000
00000 п.
0000100881 00000 н.
0000100933 00000 н.
0000103749 00000 п.
0000103932 00000 н.
0000105456 00000 п.
0000105566 00000 н.
0000105865 00000 н.
0000106378 00000 п.
0000106449 00000 н.
0000106535 00000 н.
0000106639 00000 н.
0000106778 00000 н.
0000106855 00000 н.
0000106926 00000 н.
0000107039 00000 п.
0000107128 00000 н.
0000107217 00000 п.
0000107377 00000 н.
0000108027 00000 н.
0000108140 00000 п.
0000108259 00000 н.
0000108821 00000 н.
0000109112 00000 н.
0000109523 00000 п.
0000109975 00000 н.
0000110381 00000 п.
0000110800 00000 н.
0000111222 00000 н.
0000111685 00000 н.
0000111783 00000 н.
0000113641 00000 п.
0000113929 00000 н.
0000114090 00000 н.
0000116031 00000 н.
0000116322 00000 н.
0000116696 00000 н.
0000161518 00000 н.
0000161557 00000 н.
0000202953 00000 н.
0000202992 00000 н.
0000203521 00000 н.
0000203669 00000 н.
0000204198 00000 н.
0000204348 00000 н. 0000207020 00000 н.
0000207350 00000 н.
0000207562 00000 н.
0000207765 00000 н.
0000208063 00000 н.
0000208325 00000 н.
0000208580 00000 н.
0000208953 00000 н.
0000210725 00000 н.
0000215659 00000 н.
0000215828 00000 н.
0000216691 00000 п.
0000217559 00000 н.
0000220496 00000 н.
0000220719 00000 н.
0000220929 00000 н.
0000221514 00000 н.
0000222497 00000 н.
0000223001 00000 п.
0000224684 00000 н.
0000225868 00000 н.
0000228083 00000 н.
0000229475 00000 н.
0000232134 00000 н.
0000233329 00000 н.
0000235895 00000 н.
0000236507 00000 н.
0000237847 00000 н.
0000240918 00000 п.
0000241732 00000 н.
0000243947 00000 н.
0000245214 00000 н.
0000249340 00000 н.
0000249878 00000 н.
0000250120 00000 н.
0000250332 00000 н.
0000250588 00000 н.
0000003736 00000 н.
трейлер
] / Назад 2423198 >>
startxref
0
%% EOF
578 0 объект
> поток
ч T {PU? ~ ! $ g [1 $ d; KhLBMC 0D * -d: 0B: 9MDG; s {~
0000207020 00000 н.
0000207350 00000 н.
0000207562 00000 н.
0000207765 00000 н.
0000208063 00000 н.
0000208325 00000 н.
0000208580 00000 н.
0000208953 00000 н.
0000210725 00000 н.
0000215659 00000 н.
0000215828 00000 н.
0000216691 00000 п.
0000217559 00000 н.
0000220496 00000 н.
0000220719 00000 н.
0000220929 00000 н.
0000221514 00000 н.
0000222497 00000 н.
0000223001 00000 п.
0000224684 00000 н.
0000225868 00000 н.
0000228083 00000 н.
0000229475 00000 н.
0000232134 00000 н.
0000233329 00000 н.
0000235895 00000 н.
0000236507 00000 н.
0000237847 00000 н.
0000240918 00000 п.
0000241732 00000 н.
0000243947 00000 н.
0000245214 00000 н.
0000249340 00000 н.
0000249878 00000 н.
0000250120 00000 н.
0000250332 00000 н.
0000250588 00000 н.
0000003736 00000 н.
трейлер
] / Назад 2423198 >>
startxref
0
%% EOF
578 0 объект
> поток
ч T {PU? ~ ! $ g [1 $ d; KhLBMC 0D * -d: 0B: 9MDG; s {~
Ошибка
Прыгать в. ..
Перейти к … План курсаКалендарь курсаРекомендуемые профессиональные репетиторы по математикеГлава 1 Ключ к ответу в рабочей тетрадиГлава 1 Ключ к ответу на обзорГлава 2 Обзор 2.1 Ключ к ответу на рабочем листе по моделированию квадратов и кубов2.2 Выражение числа в качестве ключа ответа 2.3 Разнообразное выражение числа Ключ ответа2 .4 Рабочие листы 1 и 2 для умножения и деления степеней Ключ ответа 2.5 Комбинирование сил 2 Ключ ответа Глава 2.1 – 2.5 Проверка ключа ответа Отрицательные показатели степени Ответ 2.6 Вычисление с помощью степеней Ключ ответа Глава 2 Обзор ответа Ключ Глава 3 Обзор 3.2 Определение сходства 3.3 Масштабный коэффициент 3.4 Рисование аналогичных многоугольников Ключ ответа 3.4 Рисование похожего многоугольника 3.5 Решение проблем Глава 3 Обзор ответа Ключ Глава 4 Обзор 4.1 Примечания 4.1 Рабочий лист Ключ ответа 4.2 Примечания 4.3 Примечания 4.3 Ключ к ответу на листе 4.4 Примечания Глава 4 Ключ к ответу на обзор Глава 5 Обзор 5.1 Примечания 5.
..
Перейти к … План курсаКалендарь курсаРекомендуемые профессиональные репетиторы по математикеГлава 1 Ключ к ответу в рабочей тетрадиГлава 1 Ключ к ответу на обзорГлава 2 Обзор 2.1 Ключ к ответу на рабочем листе по моделированию квадратов и кубов2.2 Выражение числа в качестве ключа ответа 2.3 Разнообразное выражение числа Ключ ответа2 .4 Рабочие листы 1 и 2 для умножения и деления степеней Ключ ответа 2.5 Комбинирование сил 2 Ключ ответа Глава 2.1 – 2.5 Проверка ключа ответа Отрицательные показатели степени Ответ 2.6 Вычисление с помощью степеней Ключ ответа Глава 2 Обзор ответа Ключ Глава 3 Обзор 3.2 Определение сходства 3.3 Масштабный коэффициент 3.4 Рисование аналогичных многоугольников Ключ ответа 3.4 Рисование похожего многоугольника 3.5 Решение проблем Глава 3 Обзор ответа Ключ Глава 4 Обзор 4.1 Примечания 4.1 Рабочий лист Ключ ответа 4.2 Примечания 4.3 Примечания 4.3 Ключ к ответу на листе 4.4 Примечания Глава 4 Ключ к ответу на обзор Глава 5 Обзор 5.1 Примечания 5. 1 Ключ к ответу на листе 5.2 Примечания 5.2 Ключ к ответу на обзор 5.3 Примечания 5.4 Введение 5.4 Ключ к ответу на листе 25 .1-5.4 Контрольный ответ 5.6 Примечания и рабочие листы Ключ ответа 5.8 Примечания Глава 5 Контрольный ответ Ключ 5 Обзор ответа Глава 6 Схема 6.1 Моделирование с помощью многочленов 6.3 Сбор похожих терминов 6.4 Добавление многочленов 6.4 Ключ рабочего листа 6.5 Вычитание Многочлены 6.7 Умножение одночлена на многочлен 6.7 Деление многочлена на одночлен 6.7 Умножение и деление многочленов 6.7 Биномиальные произведения Глава 6 Обзор Таблица умножения и деления одночленов Ключевые слова Биономные продукты Рабочий лист Ответ Ключ Вопросы) Ключ свойства хорды Записанные углы и центральные углы KeyCentral Вписанный ключ свойства Ключ свойства полукруга (страница 2) Ключ свойства Tangent Radius Ключ свойства равного касания Ключ свойства тангенса Ключ от внешней точки Циклические четырехугольники KeyGeometry Unit Примечания Ответ KeyGeometry Review Package # 1 Anspter KeyGeometry Review Package # 2 Answer KeyChaometry Review Package # 1 Anspter KeyGeometry Review Package # 2 Answer KeyChapter 10 Примечания Буклет Ответ Ключевой Буклет Примечания Часть 1 Буклет t Примечания Часть 2 Ключевой буклет с ответамиОбзор финального экзамена 1Проверка финального экзамена 2Практика финального экзамена 2Практика финального экзамена 2Ключ ответа
1 Ключ к ответу на листе 5.2 Примечания 5.2 Ключ к ответу на обзор 5.3 Примечания 5.4 Введение 5.4 Ключ к ответу на листе 25 .1-5.4 Контрольный ответ 5.6 Примечания и рабочие листы Ключ ответа 5.8 Примечания Глава 5 Контрольный ответ Ключ 5 Обзор ответа Глава 6 Схема 6.1 Моделирование с помощью многочленов 6.3 Сбор похожих терминов 6.4 Добавление многочленов 6.4 Ключ рабочего листа 6.5 Вычитание Многочлены 6.7 Умножение одночлена на многочлен 6.7 Деление многочлена на одночлен 6.7 Умножение и деление многочленов 6.7 Биномиальные произведения Глава 6 Обзор Таблица умножения и деления одночленов Ключевые слова Биономные продукты Рабочий лист Ответ Ключ Вопросы) Ключ свойства хорды Записанные углы и центральные углы KeyCentral Вписанный ключ свойства Ключ свойства полукруга (страница 2) Ключ свойства Tangent Radius Ключ свойства равного касания Ключ свойства тангенса Ключ от внешней точки Циклические четырехугольники KeyGeometry Unit Примечания Ответ KeyGeometry Review Package # 1 Anspter KeyGeometry Review Package # 2 Answer KeyChaometry Review Package # 1 Anspter KeyGeometry Review Package # 2 Answer KeyChapter 10 Примечания Буклет Ответ Ключевой Буклет Примечания Часть 1 Буклет t Примечания Часть 2 Ключевой буклет с ответамиОбзор финального экзамена 1Проверка финального экзамена 2Практика финального экзамена 2Практика финального экзамена 2Ключ ответа
Пропорции решения и приложения с аналогичными фигурами – Элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Решить пропорции
- Решите аналогичные фигуры приложений
Прежде чем начать, пройдите тест на готовность.
Если вы пропустили проблему, вернитесь в указанный раздел и просмотрите материал.
- Решить.
Если вы пропустили эту проблему, просмотрите (рисунок). - Периметр треугольного окна составляет 23 фута. Длина двух сторон – десять и шесть футов. Какова длина третьей стороны?
Если вы пропустили эту проблему, просмотрите (рисунок).
Решить пропорции
Когда два рациональных выражения равны, уравнение, связывающее их, называется пропорцией .
Уравнение представляет собой пропорцию, потому что две дроби равны. Соотношение читается как «1 – 2, 4 – 8».
Пропорции используются во многих приложениях для «увеличения» объемов. Мы начнем с очень простого примера, чтобы вы могли увидеть, как работают пропорции. Даже если вы сразу сможете найти ответ на этот пример, убедитесь, что вы также научились решать его, используя пропорции.
Предположим, директор школы хочет иметь 1 учителя на 20 учеников. Она могла использовать пропорции, чтобы найти количество учителей на 60 учеников.Допустим, что x будет количеством учителей для 60 учеников, а затем установим пропорцию:
Она могла использовать пропорции, чтобы найти количество учителей на 60 учеников.Допустим, что x будет количеством учителей для 60 учеников, а затем установим пропорцию:
Мы внимательно следим за тем, чтобы единицы числителей и знаменатели совпадали: учителя в числителях, ученики в знаменателях.
Поскольку пропорция – это уравнение с рациональными выражениями, мы будем решать пропорции так же, как мы решали уравнения в Solve Rational Equations. Мы умножим обе части уравнения на ЖК-дисплей, чтобы очистить дроби, а затем решим полученное уравнение.
Итак, давайте закончим решение проблемы директора. Мы не будем записывать единицы до последнего шага.
Умножьте обе стороны на ЖК-дисплей, 60. |
|
| Упростить. | |
| Директору нужны 3 учителя на 60 учеников. |
Теперь мы рассмотрим несколько примеров решения числовых пропорций без каких-либо единиц. Затем будем решать аппликации с использованием пропорций.
Решите пропорцию:
Решите пропорцию:
Решите пропорцию:
Когда мы работаем с пропорциями, мы исключаем значения, которые делали бы любой знаменатель равным нулю, точно так же, как мы делаем для всех рациональных выражений. Какие значения следует исключить для пропорции в следующем примере?
Решите пропорцию:
Решите пропорцию:
Решите пропорцию:
Решите пропорцию:
Решите пропорцию:
Решите пропорцию:
Решить:
Решить:
Решить:
Чтобы решать приложения с пропорциями, мы будем следовать нашей обычной стратегии решения приложений. Но когда мы устанавливаем пропорцию, мы должны убедиться, что единицы измерения правильные – единицы в числителях должны совпадать, а единицы в знаменателях должны совпадать.
Но когда мы устанавливаем пропорцию, мы должны убедиться, что единицы измерения правильные – единицы в числителях должны совпадать, а единицы в знаменателях должны совпадать.
Когда педиатры назначают детям парацетамол, они назначают 5 миллилитров (мл) парацетамола на каждые 25 фунтов веса ребенка. Если Зоя весит 80 фунтов, сколько миллилитров парацетамола пропишет ее врач?
Педиатры прописывают 5 миллилитров (мл) парацетамола на каждые 25 фунтов веса ребенка.Сколько миллилитров парацетамола врач пропишет Эмилии, которая весит 60 фунтов?
На каждый 1 килограмм (кг) веса ребенка педиатры назначают 15 миллиграммов (мг) жаропонижающего средства. Если Изабелла весит 12 кг, сколько миллиграммов жаропонижающего средства пропишет педиатр?
В холодном карамельном макиато весом 16 унций 230 калорий. Сколько калорий в холодном макиато с карамелью на 24 унции?
В ресторане быстрого питания шоколадный коктейль на 22 унции содержит 850 калорий. Сколько калорий в шоколадном коктейле на 12 унций? Ваш ответ округлите до ближайшего целого числа.
Сколько калорий в шоколадном коктейле на 12 унций? Ваш ответ округлите до ближайшего целого числа.
Янели любит конфеты Starburst, но хочет, чтобы количество закусок не превышало 100 калорий. Если 8 штук конфет содержат 160 калорий, сколько штук она может съесть в перекусе?
Джозия отправился в Мексику на весенние каникулы и обменял 325 фунтов стерлингов на мексиканские песо. В то время курс обмена был равен 12,54 мексиканских песо.Сколько мексиканских песо он получил за поездку?
Юрианна едет в Европу и хочет обменять 800 долларов на евро. По текущему обменному курсу 1 доллар США равен 0,738 евро. Сколько евро у нее будет на поездку?
Кори и Николь едут в Японию, и им нужно обменять 600 фунтов стерлингов на японские иены. Если каждый доллар составляет 94,1 иены, сколько иен они получат?
В приведенном выше примере мы связали количество песо с количеством долларов, используя пропорцию. Можно сказать, что количество песо пропорционально долларам. Если две величины связаны между собой пропорцией, мы говорим, что они пропорциональны.
Можно сказать, что количество песо пропорционально долларам. Если две величины связаны между собой пропорцией, мы говорим, что они пропорциональны.
Приложения для решения аналогичных фигур
Когда вы уменьшаете или увеличиваете фотографию на телефоне или планшете, определяете расстояние на карте или используете выкройку для создания книжного шкафа или шитья платья, вы работаете с похожими фигурами. Если две фигуры имеют одинаковую форму, но разные размеры, они считаются похожими. Одно – это масштабная модель другого. Все их соответствующие углы имеют одинаковые размеры, и их соответствующие стороны находятся в одинаковом соотношении.
Подобные фигурки
Две фигуры подобны, если размеры их соответствующих углов равны и их соответствующие стороны находятся в одинаковом соотношении.
Например, два треугольника на (Рисунок) похожи. Каждая сторона в 4 раза длиннее соответствующей стороны.
Это суммируется в свойстве подобных треугольников.
Собственность подобных треугольников
Если аналогично, то их соответствующие угловые меры равны и их соответствующие стороны находятся в одинаковом соотношении.
Для решения приложений с похожими фигурами мы будем следовать стратегии решения проблем для геометрических приложений, которую мы использовали ранее.
Решайте геометрические приложения.
- Прочтите задачу и сделайте так, чтобы все слова и идеи были понятны. Нарисуйте фигуру и напишите на ней указанную информацию.
- Определите , что мы ищем.
- Назовите то, что мы ищем, выбрав переменную для его представления.
- Переведите в уравнение, написав соответствующую формулу или модель для ситуации. Подставьте в данную информацию.

- Решите уравнение , используя хорошие методы алгебры.
- Проверьте ответ в проблеме и убедитесь, что он имеет смысл.
- Ответьте на вопрос полным предложением.
похож на. Даны длины двух сторон каждого треугольника. Найдите длины третьих сторон.
похож на. Длины двух сторон каждого треугольника указаны на рисунке.
Найдите длину стороны.
похож на. Длины двух сторон каждого треугольника указаны на рисунке.
Найдите длину стороны.
В следующем примере показано, как похожие треугольники используются на картах.
На карте Сан-Франциско, Лас-Вегас и Лос-Анджелес образуют треугольник, стороны которого показаны на рисунке ниже. Если фактическое расстояние от Лос-Анджелеса до Лас-Вегаса составляет 270 миль, найдите расстояние от Лос-Анджелеса до Сан-Франциско.
На карте Сиэтл, Портленд и Бойсе образуют треугольник, стороны которого показаны на рисунке ниже. Если фактическое расстояние от Сиэтла до Бойса составляет 400 миль, найдите расстояние от Сиэтла до Портленда.
Используя карту выше, найдите расстояние от Портленда до Бойсе.
Мы можем использовать аналогичные цифры, чтобы найти высоты, которые мы не можем измерить напрямую.
Рост Тайлера 6 футов. Однажды поздно вечером его тень была 8 футов в длину. В то же время тень от дерева была длиной 24 фута. Найдите высоту дерева.
Телефонный столб отбрасывает тень длиной 50 футов. Рядом находится дорожный знак высотой 8 футов, отбрасывающий тень длиной 10 футов. Какой высоты у телефонного столба?
Сосна отбрасывает тень высотой 80 футов рядом со зданием высотой 30 футов, которое отбрасывает тень высотой 40 футов.Насколько высока сосна?
Ключевые понятия
- Собственность подобных треугольников
- Если аналогично, то их соответствующие размеры углов равны и их соответствующие стороны находятся в одинаковом соотношении.
- Если аналогично, то их соответствующие размеры углов равны и их соответствующие стороны находятся в одинаковом соотношении.
- Стратегия решения проблем для геометрических приложений
- Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте фигуру и напишите на ней указанную информацию.
- Определите , что мы ищем.
- Назовите то, что мы ищем, выбрав переменную для его представления.
- Переведите в уравнение, написав соответствующую формулу или модель для ситуации. Подставьте в данную информацию.
- Решите уравнение , используя хорошие методы алгебры.
- Проверьте ответ в проблеме и убедитесь, что он имеет смысл.
- Ответьте на вопрос полным предложением.
Практика ведет к совершенству
Решить пропорции
В следующих упражнениях решите.
Педиатры прописывают 5 миллилитров (мл) парацетамола на каждые 25 фунтов веса ребенка.Сколько миллилитров парацетамола врач пропишет Джоселин, которая весит 45 фунтов?
Брианна, которая весит 6 кг, только что получила укол, и ей нужно обезболивающее. Детям обезболивающее назначают в дозе 15 миллиграммов (мг) на каждый 1 килограмм (кг) веса ребенка. Сколько миллиграммов пропишет врач?
Ветеринар прописал Санни, собаке весом 65 фунтов, антибактериальное лекарство на случай, если после чистки зубов появится инфекция.Если дозировка составляет 5 мг на каждый фунт, сколько лекарства было дано Санни?
Белль, 13-фунтовая кошка, страдает от боли в суставах. Сколько лекарства должен прописать ветеринар, если дозировка составляет 1,8 мг на фунт?
Сколько лекарства должен прописать ветеринар, если дозировка составляет 1,8 мг на фунт?
Новый энергетический напиток рекламирует 106 калорий на 8 унций. Сколько калорий в 12 унциях напитка?
Одна банка газировки объемом 12 унций содержит 150 калорий. Если Джозия выпьет большую порцию в 32 унции из местного мини-маркета, сколько калорий он получит?
Рекламируется, что новый ледяной напиток с лимоном на 7 унций содержит всего 140 калорий.Сколько унций могла бы выпить Салли, если бы она хотела выпить всего 100 калорий?
Риз любит пить здоровые зеленые смузи. Порция смузи на 16 унций содержит 170 калорий. Риз выпивает 24 унции этих смузи за день. Сколько калорий смузи он потребляет за день?
Дженис едет в Канаду и обменяет 250 фунтов стерлингов на канадские доллары. По текущему обменному курсу 1 фунт США равен 1,01 канадского фунта. Сколько канадских долларов она получит за поездку?
Тодд отправляется в Мексику и ему нужно обменять 450 фунтов стерлингов на мексиканские песо. Если каждый доллар стоит 12,29 песо, сколько песо он получит за поездку?
Если каждый доллар стоит 12,29 песо, сколько песо он получит за поездку?
Стив обменял 600 фунтов на 480 евро. Сколько евро он получил за каждый доллар США?
Марта обменяла 350 фунтов стерлингов на 385 австралийских долларов. Сколько австралийских долларов она получила за каждый доллар США?
Во время поездки в Великобританию Бетани обменяла свои 900 фунтов стерлингов на 570 британских фунтов. Сколько фунтов она получила за каждый американский доллар?
Миссионер, направленный в Южную Африку, должен был обменять свои 500 фунтов стерлингов на южноафриканский ранд, который стоит 12.63 на каждый доллар. Сколько Ранд было у него после обмена?
Рональду нужен утренний завтрак, который даст ему не менее 390 калорий. В одной чашке апельсинового сока 130 калорий. Сколько чашек ему нужно выпить, чтобы достичь своей цели по калориям?
Сара выпивает энергетический напиток объемом 32 унции, содержащий 80 калорий на 12 унций. Сколько калорий она выпила?
Сколько калорий она выпила?
Элизабет возвращается в Соединенные Штаты из Канады. Она меняет оставшиеся 300 канадских долларов на 230 фунтов стерлингов.05 в американских долларах. Сколько стоит? 1 в канадских долларах?
Бену нужно конвертировать 1000 фунтов стерлингов в японские иены. Один американский доллар стоит 123,3 иены. Сколько иен у него будет?
Золотистый ретривер весом 85 фунтов страдает диареей. Его лекарство прописано из расчета 1 чайная ложка на 5 фунтов. Сколько лекарства ему нужно дать?
Пятилетнюю Лейси ужалила пчела. Дозировка противозудной жидкости составляет 150 мг на ее вес 40 фунтов.Какая дозировка на фунт?
Карен съедает чашку овсянки, которая дает 2 балла по ее программе похудания. Ее муж, Джо, может съесть 3 порции овсянки на завтрак. Сколько овсянки он может съесть?
стакан
Рецепт овсяного печенья требует стакана масла, чтобы приготовить 4 дюжины печенья. Хильде нужно сделать 10 дюжин печенья для продажи. Сколько стаканов масла ей понадобится?
Хильде нужно сделать 10 дюжин печенья для продажи. Сколько стаканов масла ей понадобится?
Приложения для решения аналогичных фигур
В следующих упражнениях аналогичен.Найдите длину указанной стороны.
В следующих упражнениях аналогичен.
Найдите длину стороны d .
Найдите длину стороны q .
В следующих двух упражнениях используйте показанную карту. На карте Нью-Йорк, Чикаго и Мемфис образуют треугольник, стороны которого показаны на рисунке ниже. Фактическое расстояние от Нью-Йорка до Чикаго составляет 800 миль.
Найдите фактическое расстояние от Нью-Йорка до Мемфиса.
Найдите фактическое расстояние от Чикаго до Мемфиса.
В следующих двух упражнениях используйте показанную карту. На карте Атланта, Майами и Новый Орлеан образуют треугольник, стороны которого показаны на рисунке ниже. Фактическое расстояние от Атланты до Нового Орлеана составляет 420 миль.
Фактическое расстояние от Атланты до Нового Орлеана составляет 420 миль.
Найдите фактическое расстояние от Нового Орлеана до Майами.
Найдите фактическое расстояние от Атланты до Майами.
Собака высотой 2 фута отбрасывает тень 3 фута, в то время как кошка отбрасывает тень длиной в фут. Какого роста кошка?
фут
Ларри и Том стояли рядом друг с другом на заднем дворе, когда Том предложил Ларри угадать, какого он роста. Ларри знал, что его собственный рост – 6,5 футов, и когда они измерили их тени, тень Ларри была 8 футов, а Тома – 7,75 футов в длину. Какой рост у Тома?
Башня ветряной мельницы имеет высоту 212 футов.Человек шести футов ростом, стоящий рядом с башней, отбрасывает семифутовую тень. Какова длина тени мельницы?
Высота Статуи Свободы 305 футов. Николь, стоящая рядом со статуей, отбрасывает 6-футовую тень, а ее рост – 5 футов. Какой длины должна быть тень статуи?
Повседневная математика
Пульс В тренажерном зале Кэрол измеряет пульс в течение 10 секунд и считает 19 ударов.
- ⓐ Сколько это ударов в минуту?
- ⓑ Достигла ли Кэрол своей целевой частоты пульса 140 ударов в минуту?
Частота пульса Кевин хочет поддерживать частоту пульса 160 ударов в минуту во время тренировки.Во время тренировки он насчитывает 27 ударов за 10 секунд.
- ⓐ Сколько это ударов в минуту?
- ⓑ Достиг ли Кевин своей целевой частоты пульса?
Стоимость поездки Автомобиль Джесси получает 30 миль за галлон бензина.
- ⓐ Если Лас-Вегас находится в 285 милях от отеля, сколько галлонов бензина необходимо, чтобы добраться туда, а затем домой?
- ⓑ Если бензин стоит 3,09 евро за галлон, какова общая стоимость газа для поездки?
Стоимость поездки Дэнни хочет поехать в Феникс, чтобы увидеть своего дедушку.Феникс находится в 370 милях от дома Дэнни, а его машина проезжает 18,5 миль на галлон.
- ⓐ Сколько галлонов бензина понадобится Дэнни, чтобы добраться до Феникса и обратно?
- ⓑ Если бензин стоит? 3,19 за галлон, какова общая стоимость бензина, чтобы увидеть его дедушку?
Удобрение для газона Фил хочет удобрить свой газон. Каждый мешок с удобрениями покрывает около 4000 квадратных футов газона. Лужайка Фила составляет примерно 13 500 квадратных футов. Сколько мешков удобрений ему придется купить?
Краска для дома Эйприл хочет покрасить фасад своего дома.Один галлон краски покрывает около 350 квадратных футов, а площадь дома составляет около 2000 квадратных футов. Сколько галлонов краски ей придется купить?
Приготовление Рецепт пасты Натальи требует 2 фунта пасты на 1 литр соуса. Сколько фунтов пасты следует приготовить Наталье, если у нее 2,5 литра соуса?
Топочный мазут Топливный бак емкостью 275 галлонов стоит 400 фунтов стерлингов за заполнение. Сколько будет стоить заполнение масляного бака на 180 галлонов?
Письменные упражнения
Марисоль вычисляет пропорцию «перекрестным умножением», поэтому ее первый шаг выглядит так: «Объясните, чем это отличается от метода решения, показанного на (Рисунок)».
Найдите распечатанную карту, а затем напишите и решите прикладную задачу, подобную (Рисунок).
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
.


 100
100 09
09 09
09 09
09 107
107 10
10 108
108 109
109
 111
111 112
112 113
113
 12
12 116
116 118
118 01
01 , п.121
, п.121
 124
124 126
126 03
03