На прошлых уроках мы узнали:
· Алфавитом языка называется набор всех различных символов, которые используются для представления информации на этом языке.
· Любой алфавит характеризуется своей мощностью, так называется количество символов, которые в него входят.
· Мощность двоичного алфавита – всего два символа.
· Двоичным кодированием называется запись информации с помощью символов двоичного алфавита, а двоичным кодом – код информации, получившийся в результате двоичного кодирования.
· Двоичное кодирование универсально, это означает, что с помощью двоичного кода можно представить любую информацию.
· На компьютере любая информация хранится в виде двоичных кодов.
Вопросы:
· Алфавитный подход к измерению информации.
· Информационный вес символа.
· Информационный
объём сообщения.
· Единицы измеряется информации.
Как мы помним, информация для человека – это набор сигналов, которые человек получает из различных источников. Человек, каким-то образом их воспринимает и интерпретирует, придёт им какое-то значение. Однако разные люди могут интерпретировать сигналы по-разному. Так одно и то же сообщение, то есть один и тот же набор сигналов, может нести разным людям совершенно разную информацию. Как же тогда можно измерить информацию?
Всего существует два
подхода к измерению информации. Первый подход – содержательный. Как ясно
из названия, он оценивает содержание информации. А как же можно оценить
содержание информации? Универсально оценить содержание любой информацию
позволяют её свойства: объективность, достоверность полнота, актуальность,
полезность и понятность. Однако, часть свойств информации субъективна, то есть
для разных людей информация может быть по-разному полезна, понятна или
актуальна.
Измерить информацию независимо от её содержания позволяет алфавитный подход. Рассмотрим его подробнее. Прежде чем что-нибудь выразить количественно, необходимо установить, для этого единицу измерения. Так расстояние измеряется в метрах, а время в секундах. А в чём же измеряется информация? В алфавитном подходе считается, что каждый символ алфавита, который использован для записи информации, имеет некоторый информационный вес. Это означает, что он несёт некоторое количество информации. Все символы одного и того же алфавита имеют одинаковый информационный вес. Информационный вес каждого из символов алфавита зависит от мощности этого алфавита. Минимальная единица измерения информации – это информационный вес одного символа двоичного алфавита. Эта величина получила название
Слово бит на английском языке (Bit)
произошло как результат сокращения словосочетания «Binary
digit», что в переводе
на русский язык, означает «двоичный символ».Почему же именно один бит был принят в качестве минимальной единицы измерения информации? Как мы помним из прошлого урока, любую информацию можно записать в виде её двоичного кода, то есть представить её как совокупность двоичных символов. В то же время меньшей информационной единицы, чем один бит просто не существует. Наверняка у вас возник вопрос, почему? Вспомним, чем является любой алфавит. Любой алфавит – это знаковая система. А какая знаковая система минимальна? Сколько символов она содержит? 2. Так как 1 символ, вне знаковой системы не может нести информацию. То есть двоичный алфавит – это минимальная знаковая система.
Раньше мы узнали, что
алфавит любого языка, естественного или формального можно заменить двоичным
алфавитом.
Для этого всем символам алфавита можно присвоить уникальные двоичные
коды одинаковой разрядности. Причём минимальная разрядность двоичного кода, необходимая,
для кодирования одного символа алфавита,
зависит от мощности кодируемого алфавита. Запишем выражение для этой
зависимости. Мощность алфавита обозначим латинской буквой «М», а минимальную
необходимую разрядность двоичного кода – буквой «i».
Тогда M = 2i,
или перемноженной последовательности из i
двоек. При этом, если мощность алфавита нельзя получить простым перемножением
двоек, то она увеличивается до числа, которое можно получить таким образом. Это
делается потому, что иначе двоичный код с меньшей разрядностью не сможет
уникальным образом закодировать все символы алфавита.
Информационным весом
символа называется, количество информации, которое он несёт в
рамках своего алфавита. Она равна минимальной разрядности двоичного кода,
необходимой для равномерного кодирования алфавита этого символа.
Информационный
вес символа, как и любая информация измеряется в битах.
Задача: алфавит русского языка содержит:
· тридцать три буквы,
· десять арабских цифр,
· одиннадцать знаков препинания,
· и пробел.
Вычислить информационный вес одного символа из алфавита русского языка.
В начале нужно найти
мощность русскоязычного алфавита M.
Для этого посчитаем общее число всех символов: букв – 33, количество цифр – 10,
количество знаков препинания – 11 и добавим ещё 1, то есть пробел. M
= 33 + 10 + 11+ 1 = 55. Общая мощность русского алфавита равна 55 символам.
Теперь найдём, какая разрядность двоичного кода потребуется, чтобы закодировать
1 символ алфавита мощностью 55 символов. Информационный вес символа будет равен
этой разрядности. То есть M
= 55 = 2i. Число 55 мы не можем
получить простым перемножением двоек.
Поэтому увеличим число до 64-х. Для того,
чтобы получить 64, нужно перемножить 6 двоек или 26. i
= 6. Мы можем дать ответ: информационный вес одного символа русского алфавита –
6 бит.
Таким образом мы научились измерять информацию, которую несёт 1 символ алфавита. Однако в действительности информация передаётся целыми сообщениями, которые складываются из множества символов. Как же измерить такую информацию? Размер информации, которую несёт сообщение, называется его
Задача: сообщение
содержит 296 бит информации.
Его длина – 37 символов. Какова максимальная
мощность алфавита, с помощью символов которого записано это сообщение?
Так как мы знаем информационный объём сообщения и его длину – мы можем найти информационный вес одного его символа. Информационный вес символа равен информационному объёму сообщения делённому на длину сообщения, i = V / L. 296 / 37 = 8 бит. Информационный вес одного символа нашего алфавита – восемь бит. Так как мы знаем информационный вес каждого символа алфавита, то есть разрядность двоичного кода символа такого алфавита, мы можем найти его максимальную мощность. Максимальная мощность равна двум в степени информационного веса символа. M = 2i = 28 = 256. Мы можем дать ответ: максимальная мощность алфавита – 256 символов.
Итак, минимальная единица
измерения информации один бит, и мы можем выразить с помощью этой величины
любой объём информации, но всегда ли это удобно? Ведь текст на компьютере может
содержать десятки и даже сотни тысяч символов, а звуки и изображения
представляются миллиардами символов двоичного кода.
Первая из них – байт, рассмотрим, как же он появился и чему равен. В самом начале большая часть информации на компьютерах была текстовой. Для набора информации использовалось несколько алфавитов, или кодировок. Большинство из них содержало по 256 символов. Это означает что информационный вес одного символа в таком алфавите был 8 бит. Так же именно 8 бит информации могли одновременно обрабатывать процессоры того времени. Эта величина и была названа байтом.
Так же существуют и ещё
более крупные единицы информации, например килобайты (Кб). Некоторые из вас
могут подумать, что в 1 килобайте 1000 байт, так же как в 1 килограмме – 1000
грамм. Однако это не верно. Для более удобного измерения информации на
компьютере 1 килобайт содержит не 1000, а 1024 байта. Почему именно 1024?
Потому, что 1024 = 2 10. Есть и ещё более крупные величины.
Так один
мегабайт (Мб) содержит 1024 Кб. Ещё десять лет назад информация, содержащаяся на
компьютере, измерялась в гигабайтах. Один гигабайт (Гб) содержит 1024 Мб. Сейчас
на одном домашнем компьютере могут храниться терабайты (Тб) информации, и в 1 Тб
– сколько, как вы думаете? – Правильно: 1024 Гб.
Задача: на заводе работает автоматическая система учёта рабочего времени. По приходу на работу, и при уходе с работы сотрудник вставляет свою карту-пропуск в специальное устройство и оно заносит в память сообщение, которое состоит из 2 частей: уникального двоичного кода сотрудника и текущего времени. Найти минимальный информационный объём, который устройство внесло в память за день, если известно, что:
· всего на заводе работает 714 сотрудников;
· на работу вышло 698 сотрудников;
· часть сообщения, которая содержит текущее время, имеет информационный объём 3 байта;
· все
уникальные двоичные коды сотрудников имеют одинаковую разрядность.
Итак, минимальный информационный объём – Vобщ., который устройство занесло в память в течение дня можно найти, умножив информационный объём одного сообщения Vсообщ. на количество сообщений Nсообщ. Количество сообщений Nсообщ. равно количеству сотрудников Nсотр., которые вышли на работу в течение дня, умноженному на 2, так как на каждого сотрудника приходится 2 сообщения: одно – когда он приходит на работу, а второе – когда уходит. Nсообщ. = Nсотр. × 2 = 1396 сообщений за день.
Информационный объём
одного сообщения состоит из информационного объёма уникального двоичного кода
сотрудника Vкода и
информационного объёма времени, который равен 3 байтам. Теперь нам нужно найти
информационный объём уникального двоичного кода сотрудника. Мы можем
представить всех сотрудников, которые работают на заводе, в качестве алфавита
мощностью 714 символов.
Нам остаётся найти информационный вес одного символа.
Как мы помним это можно
сделать по формуле M=2i.
Мы не можем получить 714 путём перемножения двоек, зато мы можем так получить
число 1024. 1024 = 210. Значит информационный объём Vкода
= 10 бит. Теперь найдём информационный объём Vсообщ.
он состоит из 10 бит уникального двоичного кода и 3 байт времени. Переведём 3
байта в биты, для этого умножим число 3 на 8. 3 × 8 = 24 бита и 10 бит
кода. Информационный объём одного сообщения Vсообщ. =
24 + 10 = 34 бита. Теперь остаётся лишь найти информационный объём Vобщ.
Для этого информационный объём одного сообщения Vсообщ.
умножим на количество сообщений Nсообщ.
34 × 1396 = 47 464 бита. Для удобства переведём в более крупные величины.
47 464 / 8 = 5933 байта, 5933 / 1024 = 5,8 Кб. Ответ: За день в память
устройства поступило 5,8 Кб информации.
Важно запомнить:
· Алфавитный подход позволяет измерить объём информации не зависимо от её содержания. При этом каждый символ несёт, некоторое количество информации, имеет информационный вес (i).
· Минимальная единица измерения информации – 1 бит.
· Мощность алфавита равна двум в степени, равной информационному весу символа (M = 2i).
· Информационный объём сообщения равен произведению информационного веса одного символа и длины сообщения (V = i × L).
· 1 байт = 8 бит.
· Байты, килобайты (Кб), мегабайты (Мб), гигабайты (Гб), терабайты (Тб) – единицы измерения информация. Каждая следующая больше предыдущей в 1024 раза.
Процесс познания окружающего мира приводит к накоплению информации в форме знаний.
Как же узнать, много её получено или нет? Важно понимать, хватит ли места на носителе, чтобы сохранить нужную информацию, и как много времени необходимо для того, чтобы передать её по каналу связи. На этом уроке учащиеся рассмотрят алфавитный, или объёмный, подход к измерению информации, узнают, есть ли связь между алфавитным подходом к измерению информации и содержанием информации, а также выяснят, в каких единицах измеряется объем письменного или печатного текста.
Вопросы занятия:
· алфавитный (объёмный) подход к измерению информации;
· связь между алфавитным подходом к измерению информации и содержанием информации;
· единицы измерения объёма письменного или печатного текста.
Процесс познания
окружающего мира приводит к накоплению информации в форме знаний.
Как же
узнать, много получено информации или нет?
Из прошлых уроков вы знаете, что информацию можно собирать, обрабатывать, хранить, и передавать.
Но тогда очень важно понимать хватит ли места на носителе, чтобы сохранить нужную информацию. Или сколько времени нужно, чтобы передать информацию по каналу связи.
Как вы понимаете, нам просто необходимо научиться измерять информацию.
В компьютерных (цифровых) системах хранения и передачи информации применяется алфавитный подход к измерению информации. Здесь используется двоичный способ кодирования информации и важен только размер или объём хранимого и передаваемого кода. Именно поэтому алфавитный подход также называют объёмным.
Мы уже говорили о том, что разрядность двоичного кода i и количество возможных кодовых комбинаций или мощность алфавита N связаны соотношением:
Например,
Рассмотрим систему
кодирования английского алфавита.
Английский алфавит состоит из 26 букв. Добавляем сюда же пробел, точку, запятую, вопросительный и восклицательный знаки, тире, то есть ещё 6 символов. Тогда расширенный алфавит состоит из 32 символов.
Так как 32 = 25 значит, все символы можно закодировать пятиразрядными двоичными кодами от пяти нулей до пяти единиц.
Мы уже встречали такой пятиразрядный код, когда изучали телеграфные аппараты, появившиеся в девятнадцатом веке. Помните код Бодо?
В двоичном коде каждая двоичная цифра несёт одну единицу информации, которую называют один бит. Именно бит является единицей измерения информации.
Длина двоичного кода, с помощью которого кодируется символ алфавита, называется информационным весом символа. Так, например, информационный вес символа расширенного английского алфавита равен пяти битам.
Информационный объем
текста складывается из информационных весов всех символов,
составляющих текст.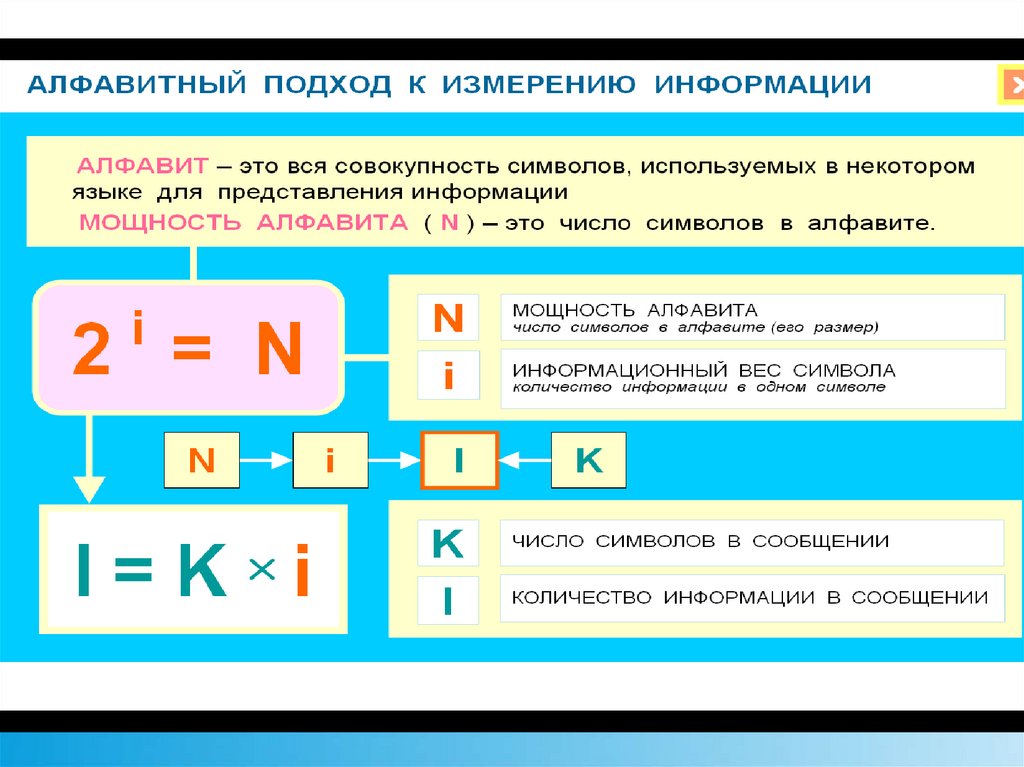
Например, английский текст из тысячи символов в телеграфном
сообщении будет иметь информационный объем пять тысяч бит.
Теперь рассмотрим систему кодирования русского языка. Русский алфавит состоит из 33 букв. Добавляем к нему те же 6 дополнительных символов, что и для английского алфавита, получаем набор из 39 символов.
Понятно, что пятиразрядного кода нам уже не хватает. Попробуем шестиразрядный код.
Так как 26 = 64, остаются свободные 25 символов, которые можно, использовать, например, для кодирования цифр, скобок и знаков математических операций.
Соответственно, информационный вес символа в расширенном русском алфавите будет равен 6 бит. А текст, состоящий из 1000 символов будет иметь объем 6000 бит.
Данное следствие можно записать в виде формулы:
информационный объём
сообщения I равен произведению количества
символов К в сообщении умноженному на информационный вес символа алфавита i.
Измерять количество информации через длину двоичного кода придумал выдающийся российский математик Андрей Николаевич Колмогоров. Он решил, что количество информации, содержащийся в тексте, определяется минимально возможной длиной двоичного кода, необходимого для представления этого текста.
Зная ряд целых степеней двойки можно быстро определить информационный вес символа.
Если N – это мощность алфавита, оказывается не целой степенью двойки, тогда находят ближайшее к N значение во второй строке таблицы, но большее чем N. Причём значение i в первой строке будет равно информационному весу символа.
Рассмотрим пример. Необходимо определить информационный вес символа испанского алфавита, включающего в себя 54 строчные и прописные буквы; 10 цифр; 10 знаков препинания, скобок, кавычек.
Итак, сначала узнаем общее количество всех символов. Для этого нужно сложить все символы.
Теперь посмотрим на
таблицу степеней двойки.
Это означает, что все 74 символа можно закодировать семиразрядными двоичными кодами.
В современных компьютерах чаще всего применяется восьмиразрядный код для двоичного представления текстов. Восьмиразрядный двоичный код позволяет получить 256 различных кодовых комбинаций, то есть 28 = 256.
Такой код содержится, например, в операционной системе Windows в кодовой таблице ANSI. Он включает в себя английские и русские буквы – прописные и строчные, цифры, знаки препинания, знаки арифметических операций, скобки и другое.
Для измерения информационного объёма памяти компьютера используются байты. Причём, 1 байт = 8 бит.
Рассмотрим пример.
Пользователь компьютера, хорошо владеющий навыками ввода информации с
клавиатуры, может вводить в минуту 100 знаков. Мощность алфавита, используемого
в компьютере равна 256 символов. Нужно определить какое количество информации в
байтах может ввести пользователь в компьютер за одну минуту.
Также для измерения информации используются кратные единицы.
Вся информация в компьютере представляется в виде двоичного кода. Это и тексты, и звуки, рисунки, видео и многое другое.
Объем информации любого вида, выраженный в битах равен длине двоичного кода, в котором эта информация представлена.
Рассмотрим пример. Учебник содержит 160 страниц. На каждой странице – 60 строк. В каждой строке 70 символов (включая пробелы). Нужно найти информационный объем текста, если используется восьмиразрядная кодировка.
Bтоги урока.
В компьютерных (цифровых) системах хранения и передачи информации применяется алфавитный подход измерения информации. Здесь используется двоичный способ кодирования информации и важен только размер или объём хранимого и передаваемого кода. Именно поэтому алфавитный подход также называют объёмным.
Информационный объем
текста складывается из информационных весов всех символов,
составляющих текст.
Объем информации равен длине двоичного кода
Основная единица: 1 бит — один разряд двоичного кода. А также применяются производные единицы: байт, Кб, Мб, Гб и Тб.
Предыдущий урок 3 История технических способов кодирования информации
Следующий урок 5 Измерение информации. Содержательный подход
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Главная » Блог » Математика » Видео, обучающие детей измерениямАвтор: Энджи Олсон
2,0 К акции
3KИзмерение – это одна из тех тем, которую некоторым учащимся может быть довольно сложно понять. Общая тема измерения охватывает массу информации, и даже будучи взрослой, я считаю, что удержать все это может быть ошеломляюще! Поиск способов увлечь детей и сделать ваши уроки измерения веселыми и увлекательными имеет решающее значение для понимания учащихся. Вот почему я люблю использовать измерительные видео!
Хорошее математическое видео может заинтересовать ученика, помочь ему глубже понять концепцию и добавить тот «веселый» фактор, который поддерживает желание детей учиться дальше! Следующие видеоролики представляют собой коллекцию моих любимых видеороликов на YouTube, основанных на измерениях. Некоторые из них содержат запоминающиеся песни и стишки, в то время как другие предлагают отличные объяснения и соответствующую графику или анимацию. Независимо от того, какие видео из этого списка вы решите показать своим ученикам, я обещаю, что все они будут «соответствовать»!
Прежде чем мы перейдем к видео, вот несколько ресурсов Lucky Little Learners, которые можно добавить к инструкции по измерению.
Это подробное видео об измерениях – отлично подходит для ознакомления с единицей измерения или повторения понятия на ходу. Он начинается с объяснения того, что такое измерение, зачем оно нам нужно, и реальных применений измерений. Видео продолжает объяснять широкий спектр измерений, таких как вес, длина, скорость, температура и рост. Мне нравится, как видео выделяет определенную лексику и дает четкое определение.
Вторая половина видео оформлена как игра – отличная возможность для интерактивного обсуждения!!
Этот, вероятно, больше подходит для более молодой аудитории.
Дополнительное задание : После просмотра видео скажите учащимся: «Теперь давайте выясним, как вы буквально соответствуете». Студенты измерят десять друзей и создадут линейный график с вопросами о данных. Им понравятся руки на активности и перерыв в движении.
Получить этот ресурс ЗДЕСЬ
Это короткое, милое и по делу видео! К концу этого урока ваши дети полностью поймут, как пользоваться линейкой для измерения! Несмотря на то, что он короткий, он отлично помогает вовлечь аудиторию и заинтересовать ваших учеников!
Дополнительное задание : Проведите этот урок о том, как измерять в дюймах, и используйте совместные и независимые практические занятия для закрепления знаний.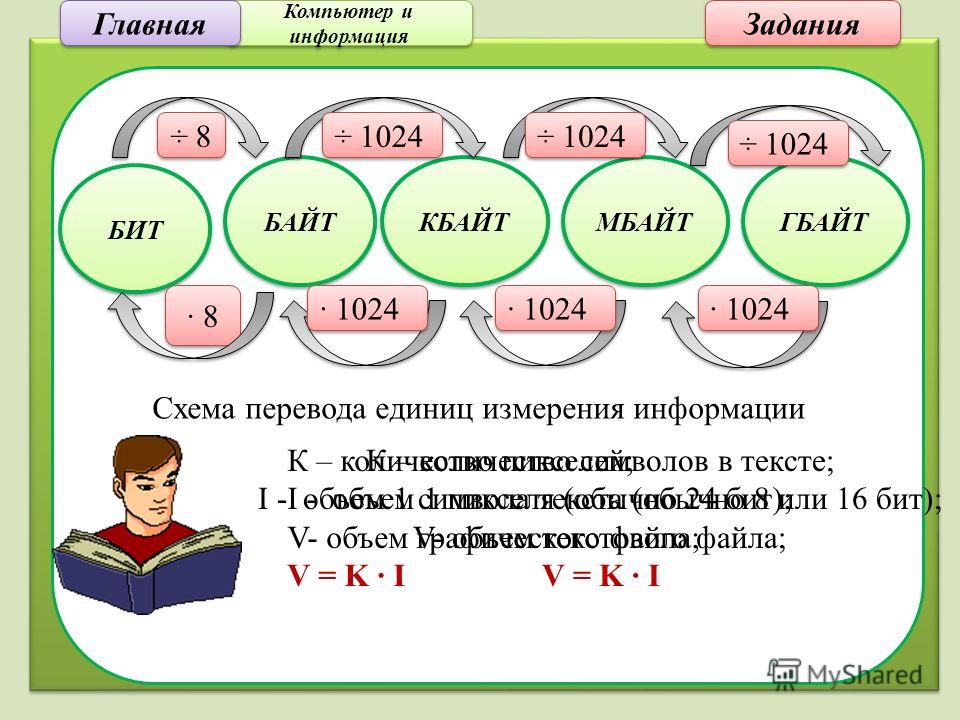
Получите урок и задания ЗДЕСЬ
Это видео отлично подойдет для детей младшего возраста! Симпатичный главный герой Сид ясно объясняет, как пользоваться линейкой, и развивает эту концепцию, исследуя, как измерять действительно большие предметы, например, синего кита! Он отлично справляется с ответами на вопросы о том, почему измерения полезны, и о многих целях обучения измерениям.
youtube.com/embed/VzW2sdCe228?feature=oembed” allow=”accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share” allowfullscreen=””> Это видео короткое, но мне оно нравится, потому что оно действительно увлекает детей, задавая им вопросы — отличное место, чтобы нажать на паузу и принять участие в обсуждении в классе. В этом коротком, но эффективном видео идея нестандартного измерения становится простой!
Дополнительное задание : Познакомьте учащихся с нестандартными единицами измерения с помощью этого урока, который включает в себя цифровые обучающие слайды, мини-урок, варианты дифференциации и партнерские/независимые занятия.
Уроки и упражнения ЗДЕСЬ
Вы не ошибетесь, взглянув на это видео, которое предлагает множество примеров различных типов измерений.
Я всегда обнаруживаю, что детям трудно понять, как связаны между собой измерения — например, 3 фута равняются 1 метру. Благодаря успокаивающей мелодии и четкой графике это видео действительно улучшит понимание вашими учениками этой концепции. Он охватывает все виды измерений – длину, вес и объем.
Нужно добавить к инструкции еще несколько одобренных учителем видео? Взгляните на список ниже.
Наша учебная программа Lucky to Learn Math уже полюбилась учителям благодаря простоте планирования и реализации. Студентам нравятся различные игры с партнерами и практические занятия. Загрузите Модуль 7: Измерение нашего мира ниже, чтобы повысить уровень своего математического блока.
Получите этот ресурс ЗДЕСЬ
Если вы нашли этот пост полезным и хотели бы сохранить его для дальнейшего использования, не стесняйтесь использовать изображение ниже, чтобы прикрепить его к своей доске Pinterest.
2,0 К акции
Учебные программы от дошкольного возраста до 12 класса должны позволить каждому учащемуся—
Pre-K–2 Ожидания: В Pre-K–2 классе каждый ученик должен –
- распознавать атрибуты длины, объема, веса, площади и времени;
- сравнивать и упорядочивать объекты по этим признакам;
- понимать, как измерять в нестандартных и стандартных единицах;
- выберите соответствующую единицу измерения и инструмент для измеряемого атрибута.
3–5 классы Ожидания: В 3–5 классах каждый учащийся должен–
- понимать такие атрибуты, как длина, площадь, вес, объем и размер угла, и выбирать соответствующий тип единицы измерения каждого атрибута;
- понять необходимость измерения в стандартных единицах и ознакомиться со стандартными единицами в обычной и метрической системах;
- выполнять простые преобразования единиц измерения, например, из сантиметров в метры, в системе измерения;
- понимать, что измерения являются приблизительными и как различия в единицах измерения влияют на точность;
- исследуйте, что происходит с измерениями двумерной формы, такими как ее периметр и площадь, когда форма каким-либо образом изменяется.
6–8 классы Ожидания: В 6–8 классах каждый ученик должен –
- понимать как метрическую, так и общепринятую систему измерения;
- понимать отношения между единицами и преобразовывать одну единицу в другую в рамках одной и той же системы;
- понимать, выбирать и использовать единицы соответствующего размера и типа для измерения углов, периметра, площади, площади поверхности и объема.
9–12 классы Ожидания: В 9–12 классах каждый ученик должен –
- принимать решения о единицах и шкалах, которые подходят для проблемных ситуаций, связанных с измерением
Pre-K–2 Ожидания: В подготовительном классе до 2 класса каждый учащийся должен –
- мера с несколькими копиями единиц одного размера, таких как скрепки, уложенные встык;
- использовать повторение одной единицы для измерения чего-то большего, чем единица, например, для измерения длины комнаты с помощью одной метровой палки;
- использовать инструменты для измерения;
- разработать общие референсы для измерений для проведения сравнений и оценок.
3–5 классы Ожидания: В 3–5 классах каждый ученик должен –
- разработка стратегий оценки периметров, площадей и объемов неправильных форм;
- выбрать и применить соответствующие стандартные единицы и инструменты для измерения длины, площади, объема, веса, времени, температуры и величины углов;
- выбирать и использовать контрольные точки для оценки измерений;
- разрабатывать, понимать и использовать формулы для нахождения площади прямоугольников и связанных с ними треугольников и параллелограммов;
- разработка стратегий для определения площади поверхности и объема прямоугольных тел.
