Единицы измерения информации самостоятельная работа 8 класс: Самостоятельная работа “Единицы измерения количества информации” 8 класс скачать
Самостоятельная работа по теме “Единицы измерения информации”. Информатика. 8 класс.
Гулина Наталия Степановна
МОУ «Средняя школа № 1» г. Кимры Тверской области
Учитель информатики
___________________________________________________________________
Урок информатики в 8 классе
Самостоятельная работа
«Единицы измерения количества информации»
Вариант № 1
Переведите в биты:
256 Мбайт
2048 байт
Переведите в байты:
128 Мбит
512 Кбит
Сколько байт (без кавычек) занимает сообщение «Люблю грозу в начале мая!».
Посчитать объем книги, если известно, что в ней 250 страниц и на каждой странице 25 строчек по 50 символов.
Самостоятельная работа
«Единицы измерения количества информации»
Вариант № 2
Переведите в биты:
64 Гбайт
512 байт
Переведите в байты:
256 Мбит
64 Гбит
Сколько бит (без кавычек) в следующей фразе: «Я учусь в первой школе».
Сколько музыкальных файлов размеров 3 Мбайта может поместиться на одном CD-диске размером 700 мегабайт?
Самостоятельная работа
«Единицы измерения количества информации»
Вариант № 3
Переведите в биты:
512 Мбайт
32 Кбайт
Переведите в байты:
32 Мбит
1024 Кбит
Сколько байт (без кавычек) занимает сообщение «Ура! Скоро каникулы!».
Сколько фотографий размером 2 Мбайта может поместиться на флешке размером 4 гигабайт?
Самостоятельная работа
«Единицы измерения количества информации»
Вариант № 4
Переведите в биты:
128 Кбайт
64 Мбайт
Переведите в байты:
256 Кбит
16 Гбит
Сколько бит (без кавычек) в следующей фразе: «Сегодня замечательная погода!».
У Вас есть флешка объемом 4 Гб, но на ней уже занято 3,8 Гб. Сколько нужно освободить места, чтобы поместить на нее файл размером 380 Мб?
Самостоятельная работа
«Единицы измерения количества информации»
Вариант № 5
Переведите в биты:
256 Мбайт
1024 байт
Переведите в байты:
128 Мбит
512 Кбит
Сколько байт (без кавычек) необходимо для кодирования фразы: «КАЗНИТЬ НЕЛЬЗЯ, ПОМИЛОВАТЬ. »?
»?
Посчитать объем книги, если известно, что в ней 300 страниц и на каждой странице 30 строчек по 40 символов.
Самостоятельная работа
«Единицы измерения количества информации»
Вариант № 6
Переведите в биты:
64 Гбайт
256 байт
Переведите в байты:
256 Мбит
64 Гбит
Сколько бит информации содержится в фразе: “Доброе утро!”.
Сколько файлов размеров 2 Мбайта может поместиться на флешке размером 8 гигабайт?
Самостоятельная работа
«Единицы измерения количества информации»
Вариант № 7
Переведите в биты:
512 Мбайт
64 Кбайт
Переведите в байты:
32 Мбит
1024 Кбит
Сколько байт (без кавычек) необходимо для кодирования фразы: «Сколько байт в килобайте?».
У Вас есть флешка объемом 16 Гб, но на ней уже занято 15,7 Гб. Сколько нужно освободить места, чтобы поместить на нее файл размером 2048 Кб?
Самостоятельная работа
«Единицы измерения количества информации»
Вариант № 8
Переведите в биты:
512 Кбайт
64 Мбайт
Переведите в байты:
256 Кбит
16 Гбит
Сколько бит необходимо для кодирования словосочетания: ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ.
Сколько фотографий размеров 4 Мбайта может поместиться на флешке размером 16 гигабайт?
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/138889-samostojatelnaja-rabota-po-teme-edinicy-izmer
Самостоятельная работа по теме “Единицы измерения количества информации. Определение количества информации” (8 класс, Угринович Н.Д., п.1.3)
Вариант 1
В какой из последовательностей единицы измерения указаны в порядке возрастания?
А) гигабайт, килобайт, мегабайт, байт
Б) гигабайт, мегабайт, килобайт, байт
В) мегабайт, килобайт, байт, гигабайт
Г) байт, килобайт, мегабайт, гигабайт
Что больше
А) 1 килобайт или Б) 1000 байт?
512 байт – это:
А) ½ килобайта
Б) 64 байта
В) 256 байт
Г) 50 бит
1 мегабайт – это:
А) 1000 килобайт
Б) 8 бит
В) 1024 бита
Г) 1024 килобайта
В марафоне участвует 256 спортсменов.
 Определите количество информации, которое несёт сообщение о победителе марафона.
Определите количество информации, которое несёт сообщение о победителе марафона.Проходит конференция школьников. Сообщение о следующем выступающем школьнике на конференции несет 6 бит информации. Определите количество школьников, которые будут выступать на конференции.
Вариант 2
В какой из последовательностей единицы измерения указаны в порядке возрастания?
А) бит, байт, килобайт, мегабайт
Б) гигабайт, мегабайт, килобайт, байт
В) байт, килобайт, мегабайт, гигабайт
Г) бит, байт, гигабайт, мегабайт
Что больше
А) 1 мегабайт или Б) 1000 килобайт?
512 килобайт – это:
А) 64 байта
Б) ½ мегабайта
В) 256 килобайт
Г) 50 байт
1 килобайт – это:
А) 1000 байт
Б) 8 бит
В) 1024 байта
Г) 1024 бита
В коробке лежали 64 фломастера.
 Все фломастеры разных цветов. Определите количество информации, которое несёт сообщение о том, что из нее достали красный фломастер.
Все фломастеры разных цветов. Определите количество информации, которое несёт сообщение о том, что из нее достали красный фломастер.Проходит соревнование конькобежцев. Сообщение о победителе соревнования несет 7 бит информации. Определите количество участников соревнования.
Контрольная работа №1 по теме «Измерение информации» ФГОС 8 класс
Контрольный урок №1 по теме «Измерение информации»
Вариант1
B. 2
C. 3
D. 4
1. Сообщение, уменьшающее неопределенность в 2 раза,
несет… информации.
А. 1 Мбайт
B. 1 байт
C. 1бит
D. 1Кбайт
2. Осуществите перевод из одних единиц измерения в
другие 5 Кбайт=…
А. 5120 байт
B. 5000 байт
C. 500 байт
D. 5120 бит
3. В шкафу на полке стоит 64 книги. Сколько бит
информации несет сообщение о том, что с полки взяли
одну книгу?
А. 6
B. 5
C.4
D.7
4. Алфавит некоего народа состоит из 8 символов.
Сколько бит информации несет сообщение, написанное с
помощью этого алфавита, содержащее 56 букв?
А. 64
B. 56
C.
 1 Кбайт
B. 1 Мбайт
C. 1бит
D. 1байт
2. Осуществите перевод из одних единиц измерения в
другие 1,4Мбайт=…
А. 1400 Кбайт
B. 1433,6 Кбайт
C. 1240 Кбайт
D. 1433,6 байт
3. При угадывании числа из диапазона от 1 до N было
получено 7 бит информации. Чему равно N?
А. 64
B. 17
C. 127
D. 128
4. Алфавит некоего народа состоит из 16 символов.
Сколько бит информации несет сообщение, написанное с
помощью этого алфавита, содержащее 32 букв?
А. 128
B. 48
C. 148
D. 512
5. Сообщение занимает 3 страницы по 25 строк. В каждой
строке записано по 60 символов. Сколько символов в
используемом алфавите, если всё сообщение содержит
1125 байтов?
А. 2
B. 4
C. 6
D. 8
Контрольный урок №1 по теме «Измерение информации»
Вариант2
1. Минимальная единица измерения количества
информации –
А. 1 Кбайт
B. 1 Мбайт
C. 1бит
D. 1байт
2. Осуществите перевод из одних единиц измерения в
другие 1,4Мбайт=…
А. 1400 Кбайт
B. 1433,6 Кбайт
C. 1240 Кбайт
D. 1433,6 байт
3. При угадывании числа из диапазона от 1 до N было
получено 7 бит информации.
1 Кбайт
B. 1 Мбайт
C. 1бит
D. 1байт
2. Осуществите перевод из одних единиц измерения в
другие 1,4Мбайт=…
А. 1400 Кбайт
B. 1433,6 Кбайт
C. 1240 Кбайт
D. 1433,6 байт
3. При угадывании числа из диапазона от 1 до N было
получено 7 бит информации. Чему равно N?
А. 64
B. 17
C. 127
D. 128
4. Алфавит некоего народа состоит из 16 символов.
Сколько бит информации несет сообщение, написанное с
помощью этого алфавита, содержащее 32 букв?
А. 128
B. 48
C. 148
D. 512
5. Сообщение занимает 3 страницы по 25 строк. В каждой
строке записано по 60 символов. Сколько символов в
используемом алфавите, если всё сообщение содержит
1125 байтов?
А. 2
B. 4
C. 6
D. 8
Контрольный урок №1 по теме «Измерение информации»
Вариант2
1. Минимальная единица измерения количества
информации –
А. 1 Кбайт
B. 1 Мбайт
C. 1бит
D. 1байт
2. Осуществите перевод из одних единиц измерения в
другие 1,4Мбайт=…
А. 1400 Кбайт
B. 1433,6 Кбайт
C. 1240 Кбайт
D. 1433,6 байт
3. При угадывании числа из диапазона от 1 до N было
получено 7 бит информации.
 896
C. 33
D. 140
5. В эстафете участвует 32 спортсмена. Специальное
устройство регистрирует прохождение каждым
участником промежуточного этапа, записывая его номер
с использованием минимально необходимого количества
бит. (подсказка: найдите каким количеством бит
кодируется номер каждого спортсмена). Каков
информационный объем сообщения, записанного
устройством, после прохождения промежуточного
финиша 20-ти спорсменами?
А. 32 бита С. 100 бит
B. 20 бит D. 31 бит
Контрольный урок №1 по теме «Измерение информации»
Вариант3
1. Для кодирования 1 символа компьютерного алфавита
требуется:
А. 1 Кбайт
B. 1 Мбайт
C. 1бит
D. 1байт
2. Осуществите перевод из одних единиц измерения в
другие 256Мбайт=…
А. 256 байт
B. 262144 Кбайт
C. 0,2 Гбайт
D. 266144 байт 3. Сообщение о том, что почтальон опустил письмо в
ящик квартиры №34, несет 6 бит информации. Сколько
квартир в доме?
А. 64
B. 34
C. 128
D. 40
4. Алфавит некоего народа состоит из 32 символов.
896
C. 33
D. 140
5. В эстафете участвует 32 спортсмена. Специальное
устройство регистрирует прохождение каждым
участником промежуточного этапа, записывая его номер
с использованием минимально необходимого количества
бит. (подсказка: найдите каким количеством бит
кодируется номер каждого спортсмена). Каков
информационный объем сообщения, записанного
устройством, после прохождения промежуточного
финиша 20-ти спорсменами?
А. 32 бита С. 100 бит
B. 20 бит D. 31 бит
Контрольный урок №1 по теме «Измерение информации»
Вариант3
1. Для кодирования 1 символа компьютерного алфавита
требуется:
А. 1 Кбайт
B. 1 Мбайт
C. 1бит
D. 1байт
2. Осуществите перевод из одних единиц измерения в
другие 256Мбайт=…
А. 256 байт
B. 262144 Кбайт
C. 0,2 Гбайт
D. 266144 байт 3. Сообщение о том, что почтальон опустил письмо в
ящик квартиры №34, несет 6 бит информации. Сколько
квартир в доме?
А. 64
B. 34
C. 128
D. 40
4. Алфавит некоего народа состоит из 32 символов.
 В.
С.
D.
Проверк
а
Оценка ____
Учитель Киян И.В.
Контрольный урок №1 по теме «Измерение информации»
Вариант___
Дата_______________
Фамилия____________________ Имя________________ Класс_______________
Учитель Киян И.В.
БЛАНК ОТВЕТОВ
Задание
1
Задание
2
Задание
3
Задание
4
Задание
5
А.
В.
С.
D.
Провер
ка
Оценка ____
Учитель Киян И.В.
Контрольный урок №1 по теме «Измерение информации»
Вариант___
Дата_______________
Фамилия____________________ Имя________________
Класс_______________
БЛАНК ОТВЕТОВ
Задание
1
Задание
2
Задание
3
Задание
4
Задание
5
А.
В.
С.
D.
Провер
ка
Оценка ____
В.
С.
D.
Проверк
а
Оценка ____
Учитель Киян И.В.
Контрольный урок №1 по теме «Измерение информации»
Вариант___
Дата_______________
Фамилия____________________ Имя________________ Класс_______________
Учитель Киян И.В.
БЛАНК ОТВЕТОВ
Задание
1
Задание
2
Задание
3
Задание
4
Задание
5
А.
В.
С.
D.
Провер
ка
Оценка ____
Учитель Киян И.В.
Контрольный урок №1 по теме «Измерение информации»
Вариант___
Дата_______________
Фамилия____________________ Имя________________
Класс_______________
БЛАНК ОТВЕТОВ
Задание
1
Задание
2
Задание
3
Задание
4
Задание
5
А.
В.
С.
D.
Провер
ка
Оценка ____Проверочная работа по теме «Единицы измерения информации»
1) Напишите буквами последовательность, в которой объемы памяти будут расположены в порядке возрастания: а)2045 байт, б) 62 бит, в) 1026 байт, г) 72 бит, д) 8 байт, е) 2Кб.
2) Переведите
40 байт = бит
5 Мб= Кб
87 Кб= байт
7 Мб = бит
42 байт = Кб
700000 бит = Кб
3) Сообщение, записанное буквами из 64 символьного алфавита, содержит 90 символов.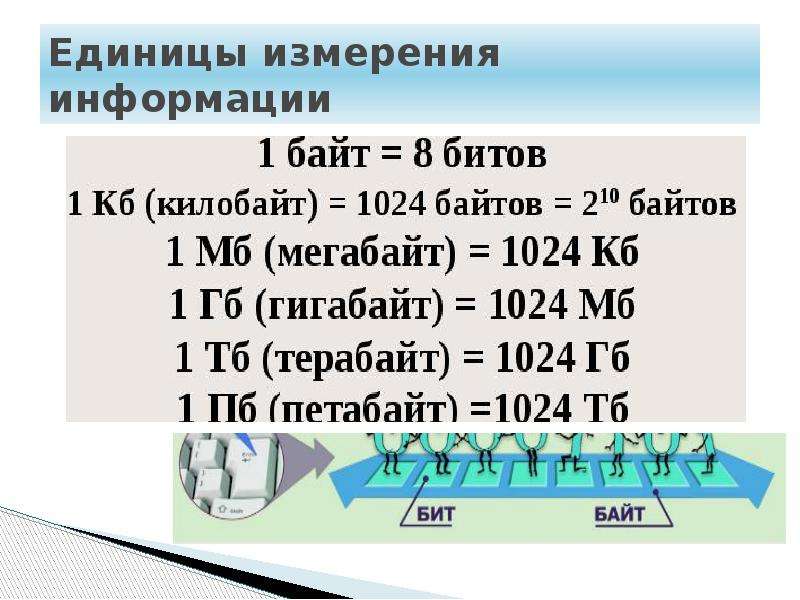 Какой объем информации в битах оно несет?
Какой объем информации в битах оно несет?
4) Сколько символов содержит страница учебника, если размер алфавита, с помощью которого её печатали, равен 16, а объем текста на ней составляет 3 Кбайта.
5) Определить мощность используемого алфавита, если 2048 символов заняли 1/512 часть мегабайта?
6) Сообщение, записанное при помощи 32-х символьного алфавита, содержит 80 символов, а сообщение, записанное с помощью 64-х символьного алфавита – 70 символов. Сравните объемы информации, содержащейся в этих сообщениях.
7) Найти значение х. 512 х-3 Кб= 128 х Кбит
Ответы
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| бгдвае | 320 5120 89088 58720256 0,04 85,4 | 540 | 6144 | 256 | 1<2, на 20 | 12 |
КОНТРОЛЬНАЯ РАБОТА ПО ПРЕДМЕТУ «ИНФОРМАТИКА и ИКТ» 7 класс по теме «ЕДИНИЦЫ ИЗМЕРЕНИЯ ИНФОРМАЦИИ»
Всероссийский дистанционный конкурс для учителей физики и информатики
«Контрольная работа в формате теста»
МБОУ «О(С)ОШ» |
Всероссийский дистанционный конкурс для учителей физики и информатики «Контрольная работа в формате теста» |
Лобанов Алексей Александрович |
05. |
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КОНТРОЛЬНОЙ РАБОТЕ ПО ТЕМЕ
«Информация и информационные процессы»
Автор: | Лобанов Алексей Александрович, учитель информатики МБОУ «О(С)ОШ» г. Ангарск | ||||||||||||||||||||||||||||||
Класс | 7 класс | ||||||||||||||||||||||||||||||
Предмет | информатика | ||||||||||||||||||||||||||||||
Продолжительность выполнения теста | 30 – 40 минут | ||||||||||||||||||||||||||||||
Структура и содержание заданий | Задания разработаны в соответствии с требованиями ФГОС ООО к системе оценки достижений планируемых результатов освоения основной образовательной программы по УМК Л. | ||||||||||||||||||||||||||||||
Число заданий в работе | 9 | ||||||||||||||||||||||||||||||
Уровни сложности | В работе представлены задания разного уровня сложности: базового (8 заданий) и повышенного (1 задание). Задания базового уровня включены в первую часть работы (заданий с выбором ответа). Это простые задания, проверяющие усвоение наиболее важных понятий темы. Задания повышенного уровня направлены на проверку умения использовать полученные знания в рамках курса информатики по данной теме. | ||||||||||||||||||||||||||||||
Цель работы | Проверка сформированности знаниевых компетенций по теме «Единицы измерения информации» и универсальных учебных действий у учащихся. | ||||||||||||||||||||||||||||||
Планируемый результат | Знание единиц измерения информации и свободное оперирование ими. Оценивать количественные параметры информационных объектов и процессов. | ||||||||||||||||||||||||||||||
Умения | Определять информационный вес символа произвольного алфавита Определить информационный объём сообщения, состоящего из некоторого количества символов алфавита Соотносить результаты измерения количества информации, выраженные в разных единицах. | ||||||||||||||||||||||||||||||
Сформированность УУД | |||||||||||||||||||||||||||||||
Регулятивные | составление плана и последовательности деятельности; контролировать правильность и полноту выполнения изученных способов действий | ||||||||||||||||||||||||||||||
Познавательные | построение логической цепи рассуждений | ||||||||||||||||||||||||||||||
Личностные | навыки концентрации внимания | ||||||||||||||||||||||||||||||
Требования к уровню подготовки учащихся по теме за курс 7 класса | |||||||||||||||||||||||||||||||
Система оценивания работы | За правильный ответ на задания ставится 1 балл, за неверный ответ или его отсутствие – 0 баллов. За правильный ответ задания повышенного уровня -2 балла | ||||||||||||||||||||||||||||||
Критерии выставления оценок: |
| ||||||||||||||||||||||||||||||
Эталоны ответов |
|
КОНТРОЛЬНАЯ РАБОТА ПО ПРЕДМЕТУ «ИНФОРМАТИКА и ИКТ» 7 класс
по теме «ЕДИНИЦЫ ИЗМЕРЕНИЯ ИНФОРМАЦИИ»
ИНСТРУКЦИЯ
На тестировании не разрешается: Общаться друг с другом. Вставать с места без разрешения учителя. Передавать что-либо друг другу.
Вставать с места без разрешения учителя. Передавать что-либо друг другу.
После получения теста вы должны их подписать (фамилию и имя, класс)
Работать вы должны самостоятельно. Вопросы, связанные с содержанием заданий, задавать не следует.
Внимательно читайте инструкцию и каждое задание. Отвечайте на вопрос только после того, как вы его поняли.
Выполняйте задания в том порядке, в котором они даны. Если какое-то задание вызывает у вас затруднение, пропустите его. К пропущенным заданиям можно будет вернуться, если у вас останется время.
Не забывайте записывать ответы в бланк ответов и все решения в специально оставленные места в тесте. Без решения и оформления данные задания не будут засчитаны.
При ошибочной записи ответа на задание необходимо зачеркнуть неправильный ответ и, отступив в той же строчке указать новый вариант ответа.
Фамилия, Имя учащегося | |
Класс |
ВАРИАНТ №1
Установите соответствие: где N- мощность алфавита, i-информационный вес символа алфавита.
1. N=4 | А) i=2 | |
2. i=3 | Б) N=8 | |
3. N=32 | В) i=5 | |
4. i=6 | Г) N=64 |
Установите соответствие:
1. 88 бит | А) 1 Мбайт | |
2. 1024 Кбайт | Б) 11 байт | |
3. 3 байта | В) 0,5 Кбайт | |
4. | Г) 24 бита |
3. Отсортируйте в порядке возрастания величины: А) 1 байт; Б) 7 бит; В) 1025 байт; г) 1 Кбайт
4. Получено сообщение ВАПРАПСАПМАПЮТ, в котором использованы все символы алфавита, определите информационный вес символа в полученном сообщении.
Дано: | Формула(ы) | Решение | |
-? | Ответ: | ||
Информационное сообщение объёмом 1 Кбайт состоит из 8192 символов. Каков информационный вес символа этого сообщения и сколько символов содержит алфавит, с помощью которого записано сообщение. В ответ запишите сумму полученных ответов.
В ответ запишите сумму полученных ответов.
Дано: | Формула(ы) | Решение | |
-? | Ответ: | ||
6. Найдите наибольшую величину среди предложенных: А) 88 бит, Б)1 Мбайт; В) 1025 Кбайт; Г) 11 байт.
7. Заполните пропуски 4Мбайт =___ Кбайт =___________ байт = ___________ бит. В ответ запишите степень полученного числа с основанием два.
8. Получено сообщение ТОАМИШЫН, в котором использованы все символы данного алфавита, определите информационный объём полученного сообщения.
Дано: | Формула(ы) | Решение | |
-? | Ответ: | ||
9*.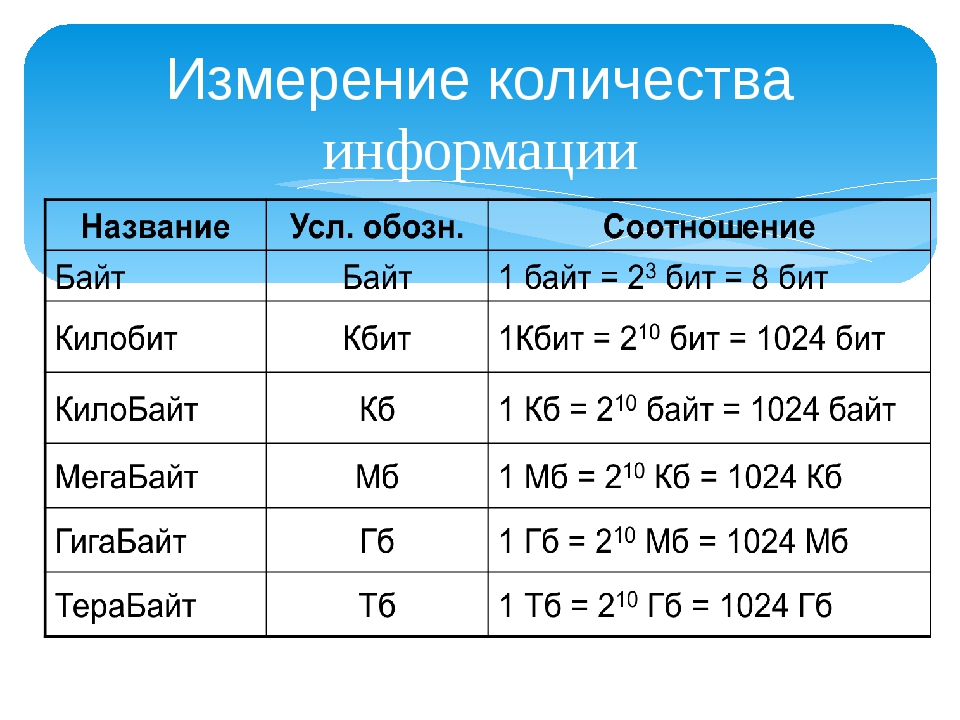 Решите предложенное уравнение 16х битов=128Кбайт
Решите предложенное уравнение 16х битов=128Кбайт
БЛАНК ОТВЕТОВ
Номер задания | ОТВЕТ | Вес задания | Отметка о правильности выполнения |
1 | 1 балл | ||
2 | 1 балл | ||
3 | 1 балл | ||
4 | 1 балл | ||
5 | 1 балл | ||
6 | 1 балл | ||
7 | 1 балл | ||
8 | 1 балла | ||
9 | 2 балла | ||
ИТОГО БАЛЛОВ | баллов | ||
Оценка за работу | |||
КОНТРОЛЬНАЯ РАБОТА ПО ПРЕДМЕТУ «ИНФОРМАТИКА и ИКТ» 7 класс
по теме «ЕДИНИЦЫ ИЗМЕРЕНИЯ ИНФОРМАЦИИ»
ИНСТРУКЦИЯ
контрольная работа информатика
DOCX / 366.
 78 Кб
78 КбНа тестировании не разрешается: Общаться друг с другом. Вставать с места без разрешения учителя. Передавать что-либо друг другу.
После получения теста вы должны их подписать (фамилию и имя, класс)
Работать вы должны самостоятельно. Вопросы, связанные с содержанием заданий, задавать не следует.
Внимательно читайте инструкцию и каждое задание. Отвечайте на вопрос только после того, как вы его поняли.
Выполняйте задания в том порядке, в котором они даны. Если какое-то задание вызывает у вас затруднение, пропустите его. К пропущенным заданиям можно будет вернуться, если у вас останется время.
Не забывайте записывать ответы в бланк ответов и все решения в специально оставленные места в тесте. Без решения и оформления данные задания не будут засчитаны.
При ошибочной записи ответа на задание необходимо зачеркнуть неправильный ответ и, отступив в той же строчке указать новый вариант ответа.
Фамилия, Имя учащегося | |
Класс |
ВАРИАНТ №2
Установите соответствие: где N- мощность алфавита, i-информационный вес символа алфавита.
1. N=2 | А) i=1 | |
2. i=4 | Б) N=16 | |
3. N=64 | В) i=6 | |
4. i=7 | Г) N=128 |
Установите соответствие:
1. | А) 2 Мбайт | |
2. 2048 Кбайт | Б) 12 байт | |
3. 4 байта | В) 0,25 Кбайт | |
4. 256 байт | Г) 32 бита |
3. Отсортируйте в порядке убывания величины: А) 1 байт; Б) 9 бит; В) 1023 байт; г) 1 Кбайт
4. Получено сообщение ЯАХРАХСАХМАХЮТ, в котором использованы все символы алфавита, определите информационный вес символа в полученном сообщении.
Дано: | Формула(ы) | Решение | |
-? | Ответ: | ||
5. Информационное сообщение объёмом 128 Кбайт состоит из 1024 символов. Каков информационный вес символа этого сообщения и сколько символов содержит алфавит, с помощью которого записано сообщение. В ответ запишите сумму полученных ответов.
Информационное сообщение объёмом 128 Кбайт состоит из 1024 символов. Каков информационный вес символа этого сообщения и сколько символов содержит алфавит, с помощью которого записано сообщение. В ответ запишите сумму полученных ответов.
Дано: | Формула(ы) | Решение | |
-? | Ответ: | ||
6. Найдите наибольшую величину среди предложенных: А) 88888 бит, Б) 1025 Кбайт; В) 1Мбайт; Г) 1111 байт.
7. Заполните пропуски 2Мбайт =___ Кбайт =___________ байт = ___________ бит. В ответ запишите степень полученного числа с основанием два.
8. Получено сообщение ПУЕРПУЕР, в котором использованы все символы данного алфавита, определите информационный объём полученного сообщения.
Дано: | Формула(ы) | Решение | |
-? | Ответ: | ||
9*. Решите предложенное уравнение 16х битов=8Кбайт
БЛАНК ОТВЕТОВ
Номер задания | ОТВЕТ | Вес задания | Отметка о правильности выполнения |
1 | 1 балл | ||
2 | 1 балл | ||
3 | 1 балл | ||
4 | 1 балл | ||
5 | 1 балл | ||
6 | 1 балл | ||
7 | 1 балл | ||
8 | 1 балла | ||
9 | 2 балла | ||
ИТОГО БАЛЛОВ | баллов | ||
Оценка за работу | |||
Лобанов А.А. учитель информатики МБОУ «О(С)ОШ» г. Ангарск Страница 8
Контрольная работа по информатике по теме «Измерение информации» в 8 классе
Контрольная работа по теме «Измерение информации» 8 класс
Вариант №1
1. Сообщение, записанное буквами из 128-символьного алфавита, содержит 80 символов. Какой объем информации оно несет?
2. Сколько байтов составляет сообщение, содержащее 4416 бит?
3. Сколько бит составляет сообщение, содержащее 0,25 Кбайт?
4. Информационное сообщение объёмом 14 Кбайт содержит 16384 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение?
5. Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1,25 Кбайта?
6. Для записи текста использовался 4-символьный алфавит. Каждая страница содержит 30 строк по 70 символов в строке. Какой объем информации содержат 5 страниц текста?
7. Сообщение занимает 4 страницы по 40 строк и содержит 7200 байтов информации. Сколько символов в строке, если при составлении этого сообщения использовали 64-символьный алфавит?
Контрольная работа по теме «Измерение информации» 8 класс
Вариант №2
1. Сообщение, записанное буквами из 64-символьного алфавита, содержит 120 символов. Какой объем информации оно несет?
2. Сколько килобайтов составляет сообщение, содержащее 16384 бит?
3. Сколько бит составляет сообщение, содержащее 0,5 Кбайт?
4. Информационное сообщение объёмом 5 Кбайт содержит 8192 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение?
5. Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1,75 Кбайта?
6. Для записи текста использовался 32-символьный алфавит. Каждая страница содержит 40 строк по 50 символов в строке. Какой объем информации содержат 6 страниц текста?
7. Сообщение занимает 3 страницы по 40 строк и содержит 2100 байтов информации. Сколько символов в строке, если при составлении этого сообщения использовали 128-символьный алфавит?
Контрольная работа по теме “Измерение информации”
Панафидина Л.М. МБОУ «СОШ №17» г. Новомосковск
Контрольная работа
по теме «Единицы измерения количества информации»
7 класс
I вариант
1. Перевести в биты:
А) 128 байт;
Б) 1,5 Кбайт;
В) 0,5 Байт;
Г) 0,2 Кбайт.
2. Перевести в байты:
А) 256 бит;
Б) 0,5 Мбайт;
В) 12 бит;
Г) 1,25 Кбайт.
3. Сравнить:
А) 24 байта и ;
Б) 0,5 Кбайт и 212 бит;
В) 128 Кбайт и 2 7 Мбайт;
Г) и 213 бит.
4. Решить задачу:
Сколько символов содержит сообщение, записанное с помощью 256 символьного алфавита, если его объём составил 1/16 часть мегабайта?
II вариант
1. Перевести в биты:
А) 45 байт;
Б) 0,5 Кбайт;
В) 80 байт;
Г) 0,001 Мбайт.
2. Перевести в байты:
А) 128 бит;
Б) 0,5 Мбайт;
В) 88 бит;
Г) 1,5 Кбайт.
3. Сравнить:
А) 64 байта и ;
Б) 1 Кбайт и 223 бит;
В) 25 Мбайт и 128 Кбайт;
Г) и 64 бит.
4. Решить задачу:
В сообщении, записанном с помощью 64 символьного алфавита, содержится 2048 символов. Найдите информационный объем этого сообщения. (ответ выразить в Кбайтах).
III
1. Перевести в биты:
А) 16 байт;
Б) 0,5 Кбайт;
В) 1,5 Байт;
Г) 0,1 Кбайт.
2. Перевести в байты:
А) 1024 бит;
Б) Мбайт;
В) 24 бит;
Г) 1,05 Кбайт.
3. Сравнить:
А) 32 бит и ;
Б) 1 Кбайт и 210 бит;
В) 256 Кбайт и 28 Мбайт;
Г) и 128 бит.
4. Решить задачу:
Сколько символов содержит сообщение, записанное с помощью 16 символьного алфавита, если его объём составил 1/128 часть мегабайта?
IV вариант
1. Перевести в биты:
А) 64 байт;
Б) 0,02 Кбайт;
В) 1,05 байт;
Г) 1 Кбайт.
2. Перевести в байты:
А) 12 бит;
Б) Мбайт;
В) 240 бит;
Г) 1,2 Кбайт.
3. Сравнить:
А) 16 бит и ;
Б) 1 Кбайт и 215 бит;
В) 256 Кбайт и 210 Мбайт;
Г) и 64 бит.
4. Решить задачу:
В сообщении, записанном с помощью 256символьного алфавита, содержится 4096 символов. Найдите информационный объем этого сообщения. (ответ выразить в Кбайтах).
ОТВЕТЫ:
| Номер задания: | I вариант | II вариант | III вариант | IV вариант |
| 1 | А) 1024 Б) 12288 В) 4 Г) 1638,4 | А) 360 Б) 4096 В) 640 Г) 8388,608 | А) 128 Б) 4096 В) 12 Г) 819,2 | А) 512 Б) 163,84 В) 8,4 Г) 8196 |
| 2 | А) 32 Б) 524288 В) 1,5 Г) 1280 | А) 16 Б) 524288 В) 11 Г) 1536 | А) 128 Б) 4096 В) 3 Г) 1075,2 | А) 1,5 Б) 2048 В) 30 Г) 1228,8 |
| 3 | А) Б) = В) Г) | А) Б) В) Г) = | А) = Б) В) Г) | А) Б) В) Г) = |
| 4 | 65 536 символов | 1,5 Кбайт | 16 384 символов | 4 Кбайта. |
Иллюстративное пособие по математике для 8-го класса – Учителя
Рассказ
Ученики начинают 8-й класс с трансформационной геометрии. Они изучают жесткие преобразования и конгруэнтность, затем растяжения и подобие (это дает основу для понимания наклона линии в координатной плоскости). Затем они основывают свое понимание пропорциональных отношений с 7 класса, чтобы изучить линейные отношения. Они выражают линейные отношения с помощью уравнений, таблиц и графиков и устанавливают связи между этими представлениями.Они расширяют свои возможности работы с линейными уравнениями с одной и двумя переменными. Основываясь на своем понимании решения уравнения с одной или двумя переменными, они понимают, что подразумевается под решением системы уравнений с двумя переменными. Они узнают, что линейные отношения – это пример особого вида отношений, называемых функцией. Они применяют свое понимание линейных отношений и функций к контекстам, включающим данные с изменчивостью. Они расширяют определение показателей степени, включая все целые числа, и в процессе кодифицируют свойства показателей.Они узнают о порядках величин и научных обозначениях, чтобы представлять и вычислять очень большие и очень маленькие величины. Они впервые сталкиваются с иррациональными числами и неформально расширяют рациональную систему счисления до действительной системы счисления, мотивированные своей работой с теоремой Пифагора.
Раздел 1: Жесткие преобразования и сравнение
Работа с преобразованиями плоских фигур в 8 классе опирается на более ранние работы с геометрией и геометрическими измерениями.Учащиеся начали изучать двумерные и трехмерные формы в детском саду и продолжили эту работу в 1 и 2 классах, составляя, разлагая и идентифицируя формы. Работа студентов с геометрическим измерением началась с длины и продолжилась площадью. Студенты научились «структурировать двумерное пространство», то есть видеть прямоугольник с целочисленными длинами сторон, состоящий из массива единичных квадратов или состоящий из повторяющихся строк или повторяющихся столбцов единичных квадратов. В 3 классе ученики различали периметр и площадь.Они соединили площадь прямоугольника с умножением, понимая, почему (для целых сторон) умножение длин сторон прямоугольника дает количество единичных квадратов, которые покрывают прямоугольник. Они использовали диаграммы с областями для представления экземпляров распределительного свойства. В 4 классе учащиеся применяли формулы площади и периметра для прямоугольников для решения реальных и математических задач и научились использовать транспортиры. В 5 классе ученики распространили формулу площади прямоугольников на прямоугольники с дробными длинами сторон.В 6 классе учащиеся объединили свои знания геометрии и геометрических измерений, чтобы составить формулы для площади параллелограммов и треугольников, используя эти формулы для определения площади поверхности многогранников. В 7 классе ученики работали с масштабированными копиями и масштабными чертежами, узнав, что размеры углов сохраняются в масштабированных копиях, но площади увеличиваются или уменьшаются пропорционально квадрату масштабного коэффициента. Их изучение масштабированных копий ограничивалось парами фигур с одинаковым вращением и зеркальной ориентацией.С точки зрения 8-го класса масштабированная копия – это расширение и перемещение, а не вращение или отражение другой фигуры.
В 8-м классе ученики распространяют свои рассуждения на плоские фигуры с разным вращением и зеркальной ориентацией.
Благодаря упражнениям, разработанным и упорядоченным, чтобы позволить учащимся осмыслить проблемы и упорно их решать (MP1), учащиеся используют и расширяют свои знания геометрии и геометрических измерений. Они начинают раздел с просмотра пар мультфильмов, каждый из которых иллюстрирует перевод, поворот или отражение.Учащиеся своими словами описывают, как переместить одну мультяшную фигуру на другую. По мере продвижения модуля они укрепляют свое понимание этих преобразований, повышают точность своих описаний (MP6) и начинают использовать связанную терминологию, распознавая, что определяет каждый тип преобразования, например, две точки определяют перевод.
На первых уроках учащиеся сталкиваются с примерами преобразований на плоскости без добавления структуры сетки или координат.Причина этого выбора состоит в том, чтобы избежать ограничения схемы учащихся, показывая наименее ограничительные примеры преобразований. В частности, ученики видят примеры переводов в любом направлении, поворотов на любой угол и отражений над любой произвольной линией. Благодаря этим примерам они начинают понимать особенности этих преобразований, не ограничивая свое понимание, например, горизонтальным или вертикальным перемещением или поворотом только на 90 или 180 градусов. Кроме того, благодаря использованию прозрачных пленок, учащиеся на начальном этапе понимают, что такое трансформации, и предполагает перемещение всей плоскости, а не просто перемещение определенной фигуры.Поскольку все преобразования являются преобразованиями плоскости, учащимся рекомендуется сначала столкнуться с примерами, которые включают перемещение всей плоскости.
Они идентифицируют и описывают смещения, вращения и отражения, а также их последовательности. При описании изображений фигур при жестких преобразованиях на квадратной сетке и вне ее, а также на координатной плоскости учащиеся используют термины «соответствующие точки», «соответствующие стороны» и «изображение». Студенты узнают, что углы и расстояния сохраняются при любой последовательности перемещений, вращений и отражений, и что такая последовательность называется «жестким преобразованием».\ circ \). Последний будет использован в следующем блоке 8-го класса по сходству и расширению. На протяжении всего модуля учащиеся обсуждают свои математические идеи и откликаются на идеи других (MP3, MP6).
Многие уроки этого раздела просят студентов поработать над геометрическими фигурами, не относящимися к реальному контексту. Этот выбор дизайна учитывает значительную интеллектуальную работу по рассуждению о местности. Задачи, поставленные в контексте реального мира, иногда являются надуманными и скорее мешают, чем помогают пониманию.Более того, математические контексты – это законные контексты, заслуживающие изучения. У студентов действительно есть возможности в отделении для решения реальных приложений. В завершающей стадии занятия студенты исследуют и создают различные узоры, образованные плоскими фигурами. Это возможность для них применить то, что они узнали в модуле (MP4).
В этом разделе несколько планов уроков предполагают, что каждый ученик имеет доступ к набору геометрических инструментов . Они содержат кальку, миллиметровую бумагу, цветные карандаши, ножницы, линейку, транспортир и учетную карточку для использования в качестве линейки или для обозначения прямых углов, что дает учащимся возможность развивать свои способности для выбора подходящих инструментов и стратегического использования их для решения задач. (MP5).Обратите внимание, что даже учащиеся в классе с цифровым расширением должны иметь доступ к таким инструментам; приложения и моделирование следует рассматривать как дополнение к их инструментам, а не как замену физическим инструментам.
Развитие дисциплинарного языка
В этом разделе учителя могут предвидеть, что ученики будут использовать язык в математических целях, таких как описание, обобщение и обоснование. \ circ \) (Урок 8)
Обосновать
- , могут ли жесткие преобразования создать изображение (Урок 7)
- , конгруэнтны ли формы (Урок 11)
- , конгруэнтны ли многоугольники (Урок 12)
- совпадают ли овалы (Урок 13)
- , можно ли создавать треугольники из заданных угловых измерений (Урок 15).
Кроме того, ожидается, что студенты объяснят и интерпретируют инструкции по преобразованию фигур и о том, как применять преобразования для поиска определенных изображений.Студентов также просят использовать язык для сравнения поворотов линейного сегмента и сравнения периметров и площадей прямоугольников. В ходе этого модуля учителя могут поддерживать математическое понимание учащихся, расширяя (а не упрощая) язык, используемый для всех этих целей, по мере того, как учащиеся демонстрируют и развивают идеи.
В таблице показаны уроки, на которых впервые вводится новая терминология, в том числе когда ожидается, что учащиеся будут понимать слово или фразу восприимчиво, и когда ожидается, что учащиеся произнесут слово или фразу в своей речи или письме.Термины из глоссария выделены жирным шрифтом. Учителя должны продолжать поддерживать использование учащимися нового термина на уроках, следующих за тем, в котором он был впервые введен.
| урок | новая терминология | |
|---|---|---|
| приемный | продуктивная | |
| 8.1.1 |
вершина плоскость измерение направление |
слайд поворот |
| 8.1,2 | по часовой стрелке против часовой стрелки отражение вращение перемещение |
напротив |
| 8.1.3 |
изображение угол поворота центр (вращения) линия отражения |
вершина |
| 8.1.4 |
последовательность преобразований расстояние |
по часовой стрелке против часовой стрелки отразить повернуть переместить |
| 8.1,5 |
координатная плоскость точка отрезок координаты \ (x \) – ось \ (y \) – ось |
|
| 8.1.6 | многоугольник | угол поворота центр (вращения) линия отражения |
| 8.1.7 |
жесткое преобразование соответствует измерений сохранить |
отражение вращение перемещение измерение точка |
| 8.1,8 | середина | сегмент |
| 8.1.9 |
вертикальные углы параллельно пересекаются |
расстояние |
| 8.1.10 |
изображение жесткое преобразование средняя точка параллельно |
|
| 8.1.11 |
конгруэнтный периметр площадь |
|
| 8.1.12 |
прямой угол \ (x \) – ось \ (y \) – ось площадь |
|
| 8.1,13 | соответствует | |
| 8.1.14 | переменные внутренние углы поперечные |
вертикальных углов конгруэнтных дополнительных углов |
| 8.1.15 | прямой угол | |
| 8.1.16 | переменные внутренние углы поперечные прямые |
|
| 8.1,17 |
мозаика симметрия |
|
Блок 2: Расширения, сходство и вводный наклон
Работа с преобразованиями плоских фигур в 8-м классе основана на более ранней работе с геометрией и геометрическими измерениями, основанной на знакомстве учащихся с геометрическими фигурами, их знании формул для площадей прямоугольников, параллелограммов и треугольников, а также их умении пользоваться линейками и транспортиры. Особенно актуальна 7 класс работа с масштабированными копиями.Эта работа была ограничена парами фигур с одинаковым вращением и зеркальной ориентацией (то есть, которые не являются вращениями или отражениями друг друга). В 8 классе ученики изучают пары масштабированных копий, которые имеют разное вращение или зеркальное отражение, исследуя, как один член пары может быть преобразован в другой, и описывая эти преобразования. Первоначально они рассматривают преобразования как перемещение одной фигуры в плоскости на другую фигуру в плоскости. По мере продвижения отряда они начинают рассматривать преобразования как перемещение всей плоскости.
Благодаря упражнениям, разработанным и упорядоченным, чтобы позволить учащимся осмыслить проблемы и упорно их решать (MP1), учащиеся используют и расширяют свои знания геометрии и геометрических измерений. Учащиеся начинают первый урок этого модуля с просмотра вырезанных фигур, сначала сравнивая их визуально, чтобы определить, являются ли они копиями друг друга в масштабе, затем представляют фигуры на диаграмме и, наконец, представляют их на круговой сетке с радиальными линиями. . Они сталкиваются с термином «масштабный коэффициент» (знакомым по 7-му классу) и новыми терминами «расширение» и «центр расширения».На следующем уроке ученики снова используют круговую сетку с радиальными линиями, чтобы понять, что при расширении изображение круга представляет собой круг, а изображение линии – линию, параллельную исходной. Во время остальной части модуля ученики рисуют изображения фигур в растяжениях на квадратной сетке и вне ее, а также на координатной плоскости. При описании соответствий между фигурой и ее расширением они используют термины «соответствующие точки», «соответствующие стороны» и «изображение». Учащиеся узнают, что размеры углов сохраняются при растяжении, но длина изображения умножается на коэффициент масштабирования.Они изучают определение «похожего»: две фигуры считаются подобными, если существует последовательность перемещений, вращений, отражений и растяжений, которая переводит одну фигуру в другую. Они используют определение «сходства» и свойства подобных фигур, чтобы оправдать заявления о сходстве или несходстве и аргументировать подобные фигуры (MP3). Используя эти свойства, студенты приходят к выводу, что если два треугольника имеют два общих угла, то треугольники должны быть похожими. Студенты также приходят к выводу, что частное пары длин сторон в треугольнике равно частному соответствующих длин сторон в аналогичном треугольнике.Этот вывод используется в следующем уроке: учащиеся изучают термины «наклон» и «наклонный треугольник» и используют сходство наклонных треугольников на одной линии, чтобы понять, что любые две различные точки на прямой определяют один и тот же наклон (MP7 ). На следующем уроке учащиеся используют свои знания об уклоне, чтобы найти уравнение для прямой. Они будут строить эту первоначальную работу с уклоном в следующем блоке 8-го класса по линейным отношениям. На протяжении всего модуля учащиеся обсуждают свои математические идеи и откликаются на идеи других (MP3, MP6).
Многие уроки этого раздела просят студентов поработать над геометрическими фигурами, не относящимися к реальному контексту. Этот выбор дизайна учитывает значительную интеллектуальную работу по рассуждению о местности. Задачи, поставленные в контексте реального мира, иногда являются надуманными и скорее мешают, чем помогают пониманию. Более того, математические контексты – это законные контексты, заслуживающие изучения. У студентов действительно есть возможности в отделении для решения реальных приложений. На завершающем этапе занятия студенты исследуют тени, отбрасываемые объектами на Солнце.Это возможность применить то, что они узнали о похожих треугольниках (MP4).
В этом разделе несколько планов уроков предполагают, что каждый ученик имеет доступ к набору геометрических инструментов . Каждый набор инструментов содержит кальку, миллиметровую бумагу, цветные карандаши, ножницы, линейку, транспортир и учетную карточку для использования в качестве линейки или для обозначения прямых углов, что дает учащимся возможность развивать свои способности выбирать подходящие инструменты и стратегически использовать их для решения проблемы (MP5).Обратите внимание, что даже учащиеся в классе с цифровым расширением должны иметь доступ к таким инструментам; приложения и моделирование следует рассматривать как дополнение к их инструментам, а не как замену физическим инструментам.
Развитие дисциплинарного языка
В этом разделе учителя могут предвидеть, что ученики будут использовать язык в математических целях, таких как описание, объяснение, представление и обоснование. На протяжении всего модуля учащиеся извлекут пользу из рутин, разработанных для развития прочного дисциплинарного языка, как для их собственного осмысления, так и для построения общего понимания со сверстниками.Учителя могут сформировать формативную оценку того, как учащиеся используют язык таким образом, особенно когда учащиеся используют язык для:
Описать
- наблюдения о масштабированных прямоугольниках (Урок 1)
- наблюдений о расширенных точках, кругах и многоугольниках (Урок 2)
- последовательностей преобразований (Урок 6)
- наблюдений о длинах сторон в подобных треугольниках (Урок 9)
Объяснить
- как применять дилатацию для поиска определенных изображений (Урок 5)
- как определить, совпадают ли треугольники, схожи или нет (Урок 8)
- стратегии поиска недостающих длин сторон (Урок 9)
- как применять растяжения для поиска определенных изображений точек (Урок 12)
- аргументы в пользу гипотезы (Урок 13)
Представлять
- растяжения с использованием заданных масштабных коэффициентов и координат (Урок 4)
- фигур с использованием специфических преобразований (Урок 6)
- графиков линий с использованием уравнений (Урок 12)
Кроме того, ожидается, что учащиеся будут использовать язык для интерпретации указаний для расширения фигур и для создания треугольников; сравнить расширенные многоугольники и методы определения сходства; критика рассуждений об углах, сторонах и сходстве; обосновать, похожи ли полигоны; и обобщить информацию о точках на прямой и подобных треугольниках.
В таблице показаны уроки, на которых впервые вводится новая терминология, в том числе когда ожидается, что учащиеся будут понимать слово или фразу восприимчиво, и когда ожидается, что учащиеся произнесут слово или фразу в своей речи или письме. Термины из глоссария выделены жирным шрифтом. Учителя должны продолжать поддерживать использование учащимися нового термина на уроках, следующих за уроком, на котором он был впервые введен.
| урок | новая терминология | |
|---|---|---|
| приемный | продуктивная | |
| 8.2,1 |
коэффициент масштабирования масштабная копия масштабирование |
|
| 8.2.2 |
дилатация центр дилатации дилатация |
|
| 8.2.4 | центр расширения масштабный коэффициент |
|
| 8.2.6 | аналогичный | расширять |
| 8.2.7 | расширение | |
| 8.2,9 | частное | |
| 8.2.10 | аналогичный |
наклон наклон треугольника |
| 8.2.11 | подобие \ (x \) – координата \ (y \) – координата уравнение прямой |
частное |
| 8.2.13 | оценка приблизительная / приблизительно |
|
Блок 3: Линейные отношения
Работа с линейными отношениями в 8 классе основана на более ранней работе со ставками и пропорциональными отношениями в 7 классе, а работа 8 класса с геометрией.В конце предыдущего раздела, посвященного расширению, учащиеся выучили термины «наклон» и «треугольник наклона», использовали сходство треугольников наклона на одной линии, чтобы понять, что любые две различные точки на линии определяют один и тот же наклон, и нашли уравнение для прямой с положительным наклоном и вертикальным пересечением. В этом модуле учащиеся получают опыт работы с линейными отношениями и их представлениями в виде графиков, таблиц и уравнений с помощью заданий, разработанных и упорядоченных, чтобы позволить им понять смысл проблем и упорно их решать (MP1).Из-за этой зависимости этот блок и предыдущий нужно выполнять по порядку.
Модуль начинается с пересмотра различных представлений пропорциональных отношений (графиков, таблиц и уравнений), а также роли константы пропорциональности в каждом представлении и того, как ее можно интерпретировать в контексте (MP2).
Затем учащиеся анализируют взаимосвязь между количеством чашек в данной стопке чашек и высотой стопки – взаимосвязь, которая является линейной, но не пропорциональной, – чтобы ответить на вопрос «Сколько чашек необходимо, чтобы подняться на высоту». 50 см? » Их не просят решать эту проблему определенным образом, что дает им возможность выбирать и использовать стратегически (MP5) представления, которые появились ранее в этом блоке (таблица, уравнение, график) или в предыдущем блоке (уравнение, график).Студенты знакомятся с «скоростью изменения» как способом описать скорость на 1 в линейной зависимости и отмечают, что ее числовое значение совпадает с наклоном линии, которая представляет собой взаимосвязь. Учащиеся анализируют другую линейную зависимость (высота воды в цилиндре по сравнению с количеством кубиков в цилиндре) и находят способ вычисления наклона линии из любых двух различных точек на линии с помощью повторных рассуждений (MP8). Они изучают третий способ получить уравнение для линейной зависимости, рассматривая график линии в координатной плоскости как вертикальное перемещение пропорциональной зависимости (MP7).
Пока что в блоке задействованы только линии с положительным наклоном и \ (y \) – пересечениями. Затем учащиеся рассматривают график линии с отрицательной точкой пересечения \ (y \) и уравнения, которые могут ее представить. Они рассматривают ситуации, представленные линейными отношениями с отрицательной скоростью изменения, составляют их график (MP4) и интерпретируют координаты точек на графиках в контексте (MP2).
Модуль завершается двумя уроками, которые включают построение графиков двух уравнений с двумя неизвестными, а также поиск и интерпретацию их решений (MP2).Это включает рассмотрение соответствий между различными представлениями (MP1), в частности, что означает, что пара значений является решением уравнения, и соответствие между координатами точек на графике и решениями уравнения.
В этом разделе несколько планов уроков предполагают, что каждый ученик имеет доступ к набору геометрических инструментов . Каждый набор инструментов содержит кальку, миллиметровую бумагу, цветные карандаши, ножницы, линейку, транспортир и учетную карточку для использования в качестве линейки или для обозначения прямых углов, что дает учащимся возможность выбирать подходящие инструменты и использовать их стратегически для решения задач (MP5) .Обратите внимание, что даже учащиеся в классе с цифровым расширением должны иметь доступ к таким инструментам; приложения и моделирование следует рассматривать как дополнение к их инструментам, а не как замену физическим инструментам.
Об использовании терминов соотношение, ставка и пропорция. В этих материалах величина – это величина, которая является или может быть указана числом и единицей измерения, например, 4 апельсина, 4 сантиметра, «мой рост в футах» или «мой рост» (при том понимании, что необходимо выбрать единицу измерения).Термин отношение используется для обозначения связи между двумя или более величинами, а дроби \ (\ frac {a} {b} \) и \ (\ frac {b} {a} \) никогда не называются отношениями. Дроби \ (\ frac {a} {b} \) и \ (\ frac {b} {a} \) идентифицируются как «удельные ставки» для отношения \ (a: b \). Слово «за» используется со студентами при интерпретации удельной стоимости в контексте, например, «\ 3 доллара за унцию» и «по той же ставке» используется для обозначения ситуации, характеризующейся эквивалентными соотношениями.
В 6–8 классах учащиеся записывают расценки без сокращенных единиц, например, «3 мили в час» или «3 мили за каждый 1 час».3 \).
Пропорциональное отношение – это набор эквивалентных соотношений. В старшей школе – после изучения соотношений, показателей и пропорциональных соотношений – ученики отбрасывают термин «единичная ставка», имея в виду от \ (a \) до \ (b \), \ (a: b \) и \ ( \ frac {a} {b} \) как «отношения».
Пропорциональная связь между двумя величинами, представленными \ (a \) и \ (b \), связана с двумя константами пропорциональности : \ (\ frac {a} {b} \) и \ (\ frac {b} {а} \). На протяжении всего модуля принято, что если \ (a \) и \ (b \) представлены столбцами в таблице, а столбец для \ (a \) находится слева от столбца для \ (b \), то \ (\ frac {b} {a} \).- константа пропорциональности для отношения, представленного в таблице.
Развитие дисциплинарного языка
В этом разделе учителя могут предвидеть, что ученики будут использовать язык в математических целях, таких как представление, обобщение и объяснение. На протяжении всего модуля учащиеся извлекут пользу из рутин, разработанных для развития прочного дисциплинарного языка, как для их собственного осмысления, так и для построения общего понимания со сверстниками. Учителя могут сформировать формативную оценку того, как учащиеся используют язык таким образом, особенно когда учащиеся используют язык для:
Представляют
- ситуации, связанные с пропорциональными отношениями (Урок 1)
- константы пропорциональности по-разному (Урок 3)
- наклон с использованием выражений (Урок 7)
- линейных отношений с использованием графиков, таблиц, уравнений и словесных описаний (Урок 8)
- ситуаций с отрицательными наклонами и нулевыми наклонами (Урок 9)
- ситуаций путем построения линий и записи уравнений (Урок 12)
- ситуаций, связанных с линейными отношениями (Урок 14)
Обобщить
- категорий для графиков (Урок 2)
- об уравнениях и линейных связях (Урок 7)
- , чтобы делать прогнозы относительно наклона линий (Урок 10)
Объяснить
- как построить график пропорциональных отношений (Урок 3)
- как использовать график для определения информации о линейной ситуации (уроки 5 и 6)
- как построить график линейных отношений (Урок 10)
- как наклон соотносится с изменениями в ситуации (Урок 11)
Кроме того, ожидается, что учащиеся опишут наблюдения, касающиеся уравнения переведенной линии, и опишут особенности уравнения, которые могут облегчить или усложнить решение одной переменной, чем другой.Студенты также будут иметь возможность использовать язык для интерпретации ситуаций, связанных с пропорциональными отношениями, интерпретации графиков с использованием различных шкал, интерпретации наклонов и пересечений линейных графиков, обоснования рассуждений о линейных отношениях, обоснования соответствий между различными представлениями и обоснования того, какие уравнения соответствуют графикам горизонтальных и вертикальные линии.
В таблице показаны уроки, на которых впервые вводится новая терминология, в том числе когда ожидается, что учащиеся будут понимать слово или фразу восприимчиво, и когда ожидается, что учащиеся произнесут слово или фразу в своей речи или письме.Термины из глоссария выделены жирным шрифтом. Учителя должны продолжать поддерживать использование учащимися нового термина на уроках, следующих за тем, в котором он был впервые введен.
| урок | новая терминология | |
|---|---|---|
| приемный | продуктивная | |
| 8.3.1 | представляют масштаб этикетка |
коэффициент пропорциональности |
| 8.3,2 | уравнение | |
| 8.3.3 | скорость изменения | уравнение |
| 8,3,5 |
линейная зависимость постоянная скорость |
уклон |
| 8.3.6 |
вертикальная точка пересечения \ (y \) – точка пересечения |
|
| 8.3.7 | начальная (стоимость или сумма) | постоянная скорость |
| 8.3,8 | относятся | |
| 8,3,9 | точка пересечения по горизонтали \ (x \) – точка пересечения |
|
| 8.3.10 | точка пересечения |
скорость изменения точка пересечения по вертикали \ (y \) – точка пересечения |
| 8.3.11 | ограничение | горизонтальная линия вертикальная линия |
| 8.3.12 |
решение уравнения с двумя переменными переменная комбинация набор решений |
|
Раздел 4: Линейные уравнения и линейные системы
В этом модуле учащиеся, опираясь на свои 6 и 7 классы, работают с эквивалентными выражениями и уравнениями с одним вхождением одной переменной, изучают алгебраические методы решения линейных уравнений с несколькими вхождениями одной переменной.Учащиеся учатся использовать алгебраические методы для решения систем линейных уравнений с двумя переменными, опираясь на свои 7 и 8 классы работы с графиками и уравнениями линейных отношений. Понимание линейных отношений, в свою очередь, основано на понимании пропорциональных отношений, разработанных в 7 классе, которые связывали отношения и показатели с помощью линий и треугольников.
Раздел начинается с урока, посвященного «головоломкам с числами», в которых учащимся показывают диаграмму с числовыми линиями, на которой отображаются числовые изменения (например,g., как в 7 классе работа с числами со знаком) и попросили написать описания ситуаций и уравнения, которые могла бы отображать диаграмма. Затем студентам дается описание ситуаций, в которых неизвестная величина линейно связана с комбинацией известных величин, и их просят определить неизвестные величины любым доступным им способом, например, с помощью диаграмм или написания уравнений.
Во втором и третьем разделах модуля учащиеся пишут и решают уравнения, абстрагируясь от контекстов (MP2), чтобы представить проблемную ситуацию, указывая значения символов, которые представляют неизвестные (MP6), определяя предположения, такие как постоянная скорость (MP4) , выбор методов и представлений для использования при получении решения (MP5), обоснование для получения решения (MP1), интерпретация решений в контекстах, из которых они возникли (MP2), и запись их с соответствующими единицами (MP6), передача своих рассуждений другие (MP3) и определение соответствий между словесными описаниями, таблицами, диаграммами, уравнениями и графиками, а также между различными подходами к решению (MP1).
Второй раздел посвящен линейным уравнениям с одной переменной. Учащиеся анализируют «схемы подвесок», на которых изображены две совокупности форм, уравновешивающих друг друга. Предполагая, что одинаковые формы имеют одинаковый вес, они решают, какие действия по добавлению или удалению весов сохранят этот баланс. Имея диаграмму подвески, которая показывает один тип формы с неизвестным весом, они используют диаграмму и свое понимание баланса, чтобы найти неизвестный вес. Абстрагируя действия по добавлению или удалению весов, сохраняющих баланс (MP7), учащиеся формулируют аналогичные действия для уравнений, используя их вместе со своим пониманием эквивалентных выражений для разработки алгебраических методов решения линейных уравнений с одной переменной.Они анализируют группы линейных уравнений с одним неизвестным, отмечая, что они делятся на три категории: без решения, ровно одно решение и бесконечно много решений. Они узнают, что любое такое уравнение является ложным, истинным для одного значения переменной или (используя свойства операций) истинным для всех значений переменной. Получив описания реальных ситуаций, студенты пишут и решают линейные уравнения с одной переменной, интерпретируя решения в контексте, из которого возникли уравнения.
Третий раздел посвящен системам линейных уравнений с двумя переменными.Он начинается с заданий, призванных напомнить учащимся, что точка лежит на графике линейного уравнения тогда и только тогда, когда ее координаты делают уравнение истинным. Получив описание двух линейных отношений, учащиеся интерпретируют точки на своих графиках, включая точки на обоих графиках. Учащиеся классифицируют пары линейных уравнений, нанесенных на одни и те же оси, отмечая, что есть три категории: нет пересечения (прямые и параллельные, нет решения), ровно одно пересечение (прямые не параллельны, ровно одно решение) и одна и та же линия (бесконечно много решения).
Развитие дисциплинарного языка
В этом разделе учителя могут предвидеть, что ученики будут использовать язык для математических целей, таких как критика, обоснование и обобщение. На протяжении всего модуля учащиеся извлекут пользу из рутин, разработанных для развития прочного дисциплинарного языка, как для их собственного осмысления, так и для построения общего понимания со сверстниками. Учителя могут сформировать формативную оценку того, как учащиеся используют язык таким образом, особенно когда учащиеся используют язык для:
Критика
- стратегии решения головоломок (Урок 1)
- рассуждения о поддержании баланса в уравнениях (Урок 3)
- решений линейных уравнений (Уроки 4 и 5)
- рассуждения о структуре систем уравнений (Урок 14)
- объяснения решений (Урок 16)
Обосновать
- стратегии решения головоломок (Уроки 1 и 5)
- прогнозов о поддержании баланса (Урок 2)
- прогнозов о решениях линейных уравнений (Урок 6)
Обобщить
- о структурах уравнений, имеющих одно, бесконечное и не имеющее решений (уроки 7 и 8)
- о структурах систем уравнений (Уроки 14 и 15)
Кроме того, ожидается, что студенты будут использовать язык для представления и интерпретации ситуаций, связанных с системами линейных уравнений, сравнения решений линейных уравнений и описания графиков систем линейных уравнений.
В таблице показаны уроки, на которых впервые вводится новая терминология, в том числе когда ожидается, что учащиеся будут понимать слово или фразу восприимчиво, и когда ожидается, что учащиеся произнесут слово или фразу в своей речи или письме. Термины из глоссария выделены жирным шрифтом. Учителя должны продолжать поддерживать использование учащимися нового термина на уроках, следующих за тем, в котором он был впервые введен.
| урок | новая терминология | |
|---|---|---|
| приемный | продуктивная | |
| 8.4,1 | представительство | |
| 8.4.2 | выражение | |
| 8.4.3 | решение уравнения распределить |
|
| 8.4.4 | заменитель | уравнение |
| 8,4,5 |
термин аналогичные термины распределительное свойство коэффициент |
|
| 8.4.6 |
термин одинаковых терминов распределить общий знаменатель |
|
| 8.4,7 | нет решения (только) одно решение |
|
| 8,4,8 |
постоянный член коэффициент линейное уравнение бесконечно много решений |
выражение переменная |
| 8.4.11 | заказанная пара | |
| 8.4.12 |
система уравнений решение системы уравнений |
|
| 8.4,13 | замена | заменить нет решения (только) одно решение бесконечно много решений |
| 8.4.14 | алгебраически | |
| 8.4.15 |
система уравнений подстановка |
|
Блок 5: Функции и объем
В этом модуле учащиеся знакомятся с концепцией функции как отношения между «входами» и «выходами», в которых каждый допустимый вход определяет ровно один выход.В первых трех разделах модуля учащиеся работают с отношениями, знакомыми по предыдущим оценкам или модулям (формулы периметра, пропорциональные отношения, линейные отношения), выражая их как функции. В остальных трех разделах модуля учащиеся опираются на свои знания формулы для объема правой прямоугольной призмы из 7-го класса, изучая формулы для объемов цилиндров, конусов и сфер. Учащиеся выражают функциональные взаимосвязи, описываемые этими формулами, в виде уравнений.Они используют эти отношения, чтобы рассуждать о том, как изменяется объем фигуры при изменении другого ее измерения, преобразуя алгебраические выражения для получения необходимой информации (MP1).
Первый раздел начинается с примеров «правил ввода-вывода», таких как «делить на 3» или «если даже, то. . . ; если нечетное, то. . . В этих примерах входные данные (неявно) являются числами, но студенты отмечают, что некоторые входные данные недопустимы для некоторых правил, например, \ (\ frac 12 \) не является четным или нечетным.Затем учащиеся работают с таблицами, в которых перечислены пары входов и выходов для правил, заданных «диаграммами входа-выхода», отмечая, что конечный список пар не обязательно определяет уникальное правило входа-выхода (MP6). Затем учащихся знакомят с термином «функция», описывающим взаимосвязь, при которой каждому допустимому входу назначается ровно один выход.
Во втором разделе учащиеся связывают термины «независимая переменная» и «зависимая переменная» (которые они выучили в 6 классе) с входами и выходами функции.Они используют уравнения для выражения зависимой переменной как функции независимой переменной, рассматривая формулы из более ранних оценок (например, \ (C = 2 \ pi r \)) как определяющие функции. Они работают с таблицами, графиками и уравнениями для функций, изучая соглашение, согласно которому независимая переменная обычно отображается на горизонтальной оси. Они работают с словесным описанием функции, возникающей из реальной ситуации, идентифицируют таблицы, уравнения и графики, которые представляют функцию (MP1), и интерпретируют информацию из этих представлений с точки зрения реальной ситуации (MP2).
Третий раздел посвящен линейным и кусочно-линейным функциям. Учащиеся используют линейные и кусочно-линейные функции для моделирования отношений между величинами в реальных ситуациях (MP4), интерпретируя информацию из графиков и других представлений в терминах ситуаций (MP2). Уроки по линейным функциям дают студентам возможность координировать и синтезировать свое понимание новых и старых терминов, описывающих аспекты линейных и кусочных функций.Работая с пропорциональными отношениями в 7 классе, учащиеся выучили термин «константа пропорциональности» и что любую пропорциональную взаимосвязь можно представить уравнением вида \ (y = kx \), где \ (k \) – постоянная пропорциональность, что его график лежит на линии, проходящей через начало координат, которая проходит через Квадрант I, и что константа пропорциональности указывает крутизну линии. В предыдущем блоке 8-го класса учащиеся познакомились с «скоростью изменения» как способом описания коэффициента на 1 в линейной зависимости и отметили, что его числовое значение такое же, как и наклон линии, которая представляет собой взаимосвязь. .В этом разделе учащиеся связывают свое понимание «увеличения» и «уменьшения» из предыдущего раздела с их пониманием линейных функций, отмечая, например, что если линейная функция возрастает, то ее график имеет положительный наклон, и что ее скорость изменения положительная. Точно так же они связывают свое понимание \ (y \) – перехвата (изученного в предыдущем разделе) с новым термином «начальное значение», отмечая, например, когда числовая часть начального значения функции задается \ (y \) – пересечение его графика (MP1).
В остальных трех разделах модуля учащиеся работают с объемом, используя навыки, полученные ранее при работе с геометрией и геометрическими измерениями.
Работа учащихся с геометрией началась в детском саду, где они определили и описали двух- и трехмерные формы, включая конусы, цилиндры и сферы. Они продолжили эту работу в 1 и 2 классах, составляя, разлагая и идентифицируя двух- и трехмерные формы.
Работа студентов с геометрическим измерением началась с длины, а затем продолжилась с площади и объема.Студенты научились «структурировать двумерное пространство», то есть видеть прямоугольник с целочисленными длинами сторон, состоящий из массива единичных квадратов или состоящий из повторяющихся строк или повторяющихся столбцов единичных квадратов. В 3 классе ученики соединили площадь прямоугольника с умножением, понимая, почему (для целых сторон) умножение длин сторон прямоугольника дает количество единичных квадратов, которые составляют прямоугольник. Они использовали модели площадей для представления экземпляров распределительной собственности.В 4 классе учащиеся использовали формулы площади и периметра прямоугольников для решения реальных и математических задач. В 5 классе ученики распространили формулу площади прямоугольников на прямоугольники с дробными длинами сторон. Они нашли объемы правильных прямоугольных призм, рассматривая их как слои массивов кубов, и использовали формулы для вычисления этих объемов как произведений длин ребер или произведений площади основания и высоты. В 6 классе ученики распространили формулу объема правой прямоугольной призмы на правильные прямоугольные призмы с дробными длинами сторон и использовали ее для решения задач.Они расширили свои рассуждения о площади, включив в нее фигуры, не состоящие из прямоугольников, и объединили свои знания геометрии и геометрических измерений для создания формул для площадей параллелограммов и треугольников, используя эти формулы для определения площадей поверхности многогранников. В 7 классе ученики анализировали и описывали поперечные сечения призм (включая призмы с многоугольным, но непрямоугольным основанием), пирамид и многогранников, а также использовали формулу для объема правой прямоугольной призмы (объем – это площадь основания, умноженная на высоту. призмы) для решения задач, связанных с площадью, площадью поверхности и объемом.
В этом модуле для 8 класса учащиеся расширяют свое понимание объема от правых прямоугольных призм до правых цилиндров, правых конусов и сфер. Они начинают с исследования объема воды в градуированном цилиндре в зависимости от высоты воды и наоборот. Они исследуют изображения цилиндра, призмы, сферы и конуса, чтобы развить свои способности определять радиусы, основания и высоту этих объектов. Они оценивают объемы призм, цилиндров, конусов и сфер, чтобы укрепить идею о том, что измерение объема указывает количество пространства внутри объекта.Учащиеся используют свои способности для определения радиусов, оснований и высот вместе с геометрическими способностями, развитыми в более ранних классах, чтобы воспринимать аналогичную структуру (MP7) в формулах для объема прямоугольной призмы и объема цилиндра – оба являются продуктом базы и высоты. После ознакомления с формулой объема цилиндра и ее использования для решения задач учащиеся воспринимают аналогичную структуру (MP7) в формуле объема конуса.
Пятый раздел начинается с изучения функциональных соотношений между двумя величинами, которые иллюстрируются изменениями в масштабе трехмерных фигур.Например, если радиус цилиндра увеличивается втрое, его объем становится в девять раз больше. Эта работа сочетает в себе работу 7-го класса по масштабам и пропорциональным отношениям. В 7 классе ученики изучали масштабированные копии двумерных фигур, узнавая, что длины масштабируются с помощью масштабного коэффициента, а площади – с помощью квадрата масштабного коэффициента, и применяли свои знания для масштабирования чертежей, например, карт и планов этажей. В своем исследовании пропорциональных отношений учащиеся 7-го класса решали задачи, поставленные в контекстах, обычно связанных с пропорциональными отношениями, такими как постоянная скорость, цена за единицу и преобразование единиц измерения, и узнали, что любое пропорциональное отношение может быть представлено уравнением формы \ (y = kx \), где \ (k \) – коэффициент пропорциональности.В этом разделе учащиеся используют свои знания о масштабе, пропорциональных отношениях и объеме, чтобы понять, как изменяется объем призмы, конуса или цилиндра при изменении другого измерения.
В последнем разделе раздела студенты рассуждают о том, как изменяется объем сферы при изменении ее радиуса. Они рассматривают ситуацию, в которой вода течет в цилиндр, конус и сферу с одинаковой постоянной скоростью. Информация о высоте воды в каждом контейнере отображается в виде уравнения, графика или таблицы, что позволяет учащимся использовать ее стратегически (MP5) для сравнения высоты воды и вместимости контейнеров.
Развитие дисциплинарного языка
В этом разделе учителя могут предвидеть, что ученики будут использовать язык в математических целях, таких как обобщение, обоснование и сравнение. На протяжении всего модуля учащиеся извлекут пользу из рутин, разработанных для развития прочного дисциплинарного языка, как для их собственного осмысления, так и для построения общего понимания со сверстниками. Учителя могут сформировать формативную оценку того, как учащиеся используют язык таким образом, особенно когда учащиеся используют язык для:
Обобщить
- о том, что происходит с входными данными для каждого правила (Урок 1)
- о габаритах цилиндров (Урок 14)
- о соотношении объемов цилиндров и конусов (Урок 15)
- о размерах конусов (Урок 16)
- об объемах сфер, конусов и цилиндров в зависимости от их радиусов (Урок 21)
Обосновать
- утверждает, что можно определить на основе предоставленной информации (Урок 2)
- утверждений об объемах кубов и сфер на основе графиков (Урок 7)
- утверждает приблизительно линейные отношения (Урок 10)
- рассуждения об объемах сфер и конусов (Урок 21)
Сравнить
- различные представления функций (Урок 3)
- особенности графиков, уравнений и ситуаций (Урок 4)
- особенности ситуации с особенностями графика (Урок 6)
- температуры показаны на графике с различными температурами, приведенными в таблице (Урок 7)
- объемы конусов с объемами цилиндров (Урок 16)
- Методы определения и аппроксимации объема сферы как функции ее радиуса (Урок 20)
Кроме того, студенты должны интерпретировать представления функций объема цилиндров, конусов и сфер; описывать количество в ситуации; описывать объемные измерения и особенности трехмерных фигур; описать влияние различных размеров прямоугольных призм и конусов на их объем; и описывают и представляют приблизительно линейные отношения.Студенты также должны использовать язык для представления взаимосвязей между объемом и переменной длиной стороны прямоугольной призмы и взаимосвязей между объемом и переменной высотой цилиндра; объясните и изобразите, как связаны высота и объем цилиндров; и объясните рассуждения о нахождении объема цилиндра и о соотношении между объемами полусфер и объемами ящиков, цилиндров и конусов.
В таблице показаны уроки, на которых впервые вводится новая терминология, в том числе когда ожидается, что учащиеся будут понимать слово или фразу восприимчиво, и когда ожидается, что учащиеся произнесут слово или фразу в своей речи или письме.Термины из глоссария выделены жирным шрифтом. Учителя должны продолжать поддерживать использование учащимися нового термина на уроках, следующих за тем, в котором он был впервые введен.
| урок | новая терминология | |
|---|---|---|
| приемный | продуктивная | |
| 8.5.1 | вход выход |
|
| 8.5.2 | функция | вход выход зависит от |
| 8.5,3 | независимая переменная зависимая переменная радиус |
|
| 8.5.5 | предсказание | |
| 8.5.7 |
объем куб |
|
| 8,5,8 | функциональная связь линейная функция |
функция |
| 8,5,9 | математическая модель | предсказание |
| 8.5,10 | кусочно-линейная функция | линейная функция постоянная скорость |
| 8.5.11 |
цилиндр трехмерный |
|
| 8.5.12 |
конус сфера размер |
цилиндр куб кубический сантиметр прямоугольная призма |
| 8.5.13 | основание (цилиндра или конуса) приближение для \ (\ pi \) |
|
| 8.5,14 |
радиус основание (цилиндра или конуса) |
|
| 8.5.16 | конус | |
| 8.5.19 | полусфера | |
| 8.5.20 | сфера | |
| 8.5.21 | сферический | объем |
| 8.5.22 | приблизительный диапазон | |
Раздел 6: Связи в данных
В этом разделе учащиеся анализируют двумерные данные – используя точечные диаграммы и подогнанные линии для анализа числовых данных, а также используя двусторонние таблицы, гистограммы и сегментированные гистограммы для анализа категориальных данных.
Блок начинается с исследования таблицы данных. Измерения ноги и периметра равнобедренного прямоугольного треугольника показаны в каждой строке, но записи столбцов расположены не по порядку, что затрудняет различение закономерностей. Учащиеся манипулируют данными, чтобы найти закономерности в таблице (MP7), а затем исследуют диаграмму рассеяния тех же данных. Это мотивирует необходимость использовать разные представления одних и тех же данных для поиска и анализа любых закономерностей.
Второй раздел начинается с исследования двух вопросов: «Всегда ли старшие школьники выше?» и «У более высоких учеников руки больше?» Учащиеся собирают данные (измерения размаха рук, размаха рук и роста каждого учащегося) и записывают измерения каждого учащегося вместе с его возрастом в месяцах.Они составляют диаграмму рассеяния для зависимости роста от размаха рук и выбирают свои собственные методы для отображения данных о высоте (MP5).
Второй раздел посвящен использованию диаграмм рассеяния и аппроксимирующих линий для анализа числовых данных. Учащиеся составляют и изучают диаграммы рассеяния, интерпретируя точки в терминах представленных величин (MP2) и выявляя диаграммы рассеяния, которые могут представлять словесные описания ассоциаций между двумя числовыми переменными (MP1). Они видят примеры использования линии для моделирования связи между измерениями, отображаемыми на диаграмме рассеяния, и сравнивают значения, предсказанные линейной моделью, с фактическими значениями, приведенными на диаграмме рассеяния (MP4).Они рисуют линии, чтобы соответствовать данным, отображаемым на диаграммах рассеяния, и неформально оценивают, насколько хорошо линия соответствует, судя о близости точек данных к линиям (MP4). Учащиеся сравнивают диаграммы разброса, которые показывают различные типы ассоциаций (MP7), и учатся определять эти типы, устанавливая связи между общей формой облака точек и тенденциями в представленных данных, например, диаграмма разброса цены подержанного автомобиля по сравнению с пробегом. показывает облако точек, которое спускается слева направо, и цены на подержанные автомобили снижаются с увеличением пробега (MP2).Они устанавливают связи между общей формой облака точек, наклоном подобранной линии и тенденциями в данных, например, «линия, соответствующая данным, имеет отрицательный наклон, а диаграмма рассеяния показывает отрицательную связь между ценой подержанный автомобиль и его пробег ». Выбросы неформально идентифицируются на основе их относительного расстояния от других точек на диаграмме рассеяния. Учащиеся изучают диаграммы разброса, которые показывают линейные и нелинейные ассоциации, а также некоторые наборы данных, которые показывают кластеризацию, описывая их различия (MP7).Они возвращаются к данным о росте и размахе рук, собранным в начале блока, описывают связь между ними и подходят к данным (MP4).
Третий раздел посвящен использованию двусторонних таблиц для анализа категориальных данных (MP4). Учащиеся используют двухстороннюю таблицу частот, чтобы создать таблицу относительной частоты, чтобы проверить проценты, представленные на каждом пересечении категорий, чтобы найти какие-либо связи между категориями. Студенты также изучают и создают гистограммы и сегментированные гистограммы для визуализации любых ассоциаций.
Модуль заканчивается уроком, в котором учащиеся собирают и анализируют числовые данные с помощью диаграммы рассеяния, затем классифицируют данные на основе порогового значения и анализируют категории на основе двусторонней таблицы (MP4).
Развитие дисциплинарного языка
В этом разделе учителя могут предвидеть, что ученики будут использовать язык для математических целей, таких как объяснение, представление и интерпретация. На протяжении всего модуля учащиеся извлекут пользу из рутин, разработанных для развития прочного дисциплинарного языка, как для их собственного осмысления, так и для построения общего понимания со сверстниками.Учителя могут сформировать формативную оценку того, как учащиеся используют язык таким образом, особенно когда учащиеся используют язык для:
Объяснить
- как оценить с использованием имеющихся данных (Урок 1)
- как использовать таблицы и диаграммы разброса для оценок и прогнозов (Урок 3)
- значение наклона для ситуации (Урок 6)
- как использовать линии для отображения ассоциаций, выявления выбросов и ответов на вопросы (Урок 8)
Представлять
- данные в организованном порядке (Урок 1)
- данных с использованием двусторонних таблиц, гистограмм и сегментированных гистограмм (уроки 9 и 10) Данные
- с использованием точечной диаграммы (Урок 11)
Интерпретировать
- ситуации и графики с двумерными данными (Урок 2)
- таблиц и точечных диаграмм двумерных данных (Урок 3)
- таблиц, точечных диаграмм, уравнений и ситуаций с двумерными данными (Урок 4)
Кроме того, ожидается, что учащиеся будут сравнивать различные представления одной и той же ситуации, описывать и сравнивать особенности графиков разброса, обосновывать, подходят ли линии для ситуации, и обосновывать связи между двумерными данными.У студентов также есть возможность использовать язык для обобщения того, что делает линия подходящей для набора данных, и обобщения о категориях для сортировки графиков разброса.
В таблице показаны уроки, на которых впервые вводится новая терминология, в том числе когда ожидается, что учащиеся будут понимать слово или фразу восприимчиво, и когда ожидается, что учащиеся произнесут слово или фразу в своей речи или письме. Термины из глоссария выделены жирным шрифтом. Учителя должны продолжать поддерживать использование учащимися нового термина на уроках, следующих за тем, в котором он был впервые введен.
| урок | новая терминология | |
|---|---|---|
| приемный | продуктивная | |
| 8.6.1 | диаграмма рассеяния | |
| 8.6.2 | отображение данных атрибут |
числовые данные категориальные данные |
| 8.6.4 |
выброс прогноз переоценка недооценка линейная модель |
|
| 8.6,5 |
положительная ассоциация отрицательная ассоциация линейная ассоциация |
|
| 8.6.6 | нелинейная ассоциация без ассоциации подогнанная линия |
|
| 8.6.7 | кластер | |
| 8.6.8 |
независимая переменная зависимая переменная положительная связь отрицательная связь линейная связь |
|
| 8.6,9 | сегментированная гистограмма относительная частота двусторонняя (частотная) таблица |
|
| 8.6.11 |
диаграмма рассеяния выброс кластер |
|
Раздел 7: Показатели и научная нотация
Учащиеся были ознакомлены с обозначением экспонент в 6 классе. Они работали с выражениями, которые включали круглые скобки и положительные целочисленные показатели с целым числом, дробью, десятичным основанием или переменным основанием, стратегически используя свойства экспонент, но не формулировали правила использования экспонентов.п \).
Третья часть единицы возвращается к степеням 10 как прелюдия к введению научных обозначений. Учащиеся рассматривают различия в величине степени 10 и используют степень 10 и кратность степени 10 для описания величин, например, расстояния от Земли до Солнца или населения России. Первоначально они работают с большими величинами, располагая на числовой прямой степени 10 и целые положительные числа, кратные степени 10. Большинство из этих кратных – произведение однозначных чисел и степени 10.6 \), и что некоторые формы могут быть более полезными при поиске местоположений на числовой прямой. На следующем уроке студенты проделывают аналогичную работу с небольшими количествами.
На оставшихся пяти уроках учащиеся записывают оценки величин в виде целых или нецелых кратных степеней 10 и используют свои знания экспоненциальных выражений для решения задач, например, сколько метровых палочек нужно, чтобы равняться массе Луна? Они знакомятся с термином «научная нотация», практикой отличия научной нотации от других, и используют научную нотацию (с не более чем тремя значащими цифрами) для проведения аддитивных и мультипликативных сравнений пар величин.Они вычисляют суммы, разности, произведения и частные чисел, записанных в научной системе счисления (некоторые из которых содержат до четырех значащих цифр), используя такие вычисления для оценки количеств. Они выполняют преобразования измерений, которые включают степени десяти, например, конвертируют байты в килобайты или гигабайты, выбирают подходящие единицы измерения и выражают их в экспоненциальной нотации.
Развитие дисциплинарного языка
В этом разделе учителя могут предвидеть, что ученики будут использовать язык в математических целях, таких как критика, представление и обоснование.На протяжении всего модуля учащиеся извлекут пользу из рутин, разработанных для развития прочного дисциплинарного языка, как для их собственного осмысления, так и для построения общего понимания со сверстниками. Учителя могут сформировать формативную оценку того, как учащиеся используют язык таким образом, особенно когда учащиеся используют язык для:
Критика
- рассуждения о полномочиях (Урок 3)
- рассуждения о нулевых показателях (Урок 4)
- приложений экспонентных правил (Урок 7)
- рассуждения о научных обозначениях (Урок 15)
Представлять
- ситуаций с использованием экспонент (Урок 1)
- больших и малых чисел с использованием числовых линий, показателей степени и десятичных знаков (Урок 9–11)
- ситуаций сравнения величин, выраженных в экспоненциальном представлении (Урок 14)
Обосновать
- рассуждения об умножении степеней 10 (Урок 2)
- рассуждения о полномочиях (Урок 3)
- рассуждения о делении степеней 10 (Урок 4)
- , эквивалентны ли выражения экспоненциальным выражениям (Урок 6)
- рассуждения о ситуациях, сравнивающих степени 10 (Урок 12)
Кроме того, ожидается, что учащиеся будут использовать язык для обобщения рассуждений о повторном умножении и обобщения закономерностей при умножении различных оснований и показателей; опишите, как отрицательная степень 10 влияет на расстановку десятичных знаков; и интерпретировать ситуации, сравнивая величины, выраженные в научных обозначениях.Студенты также имеют возможность сравнивать соответствия между экспоненциальными выражениями и диаграммами с основанием десяти; сравнивать выражения в научном представлении с другими выражениями; объясните, как упростить выражения с отрицательной степенью 10; и объясните, как размещать и заказывать большие числа в числовой строке.
В таблице показаны уроки, на которых впервые вводится новая терминология, в том числе когда ожидается, что учащиеся будут понимать слово или фразу восприимчиво, и когда ожидается, что учащиеся произнесут слово или фразу в своей речи или письме.Термины из глоссария выделены жирным шрифтом. Учителя должны продолжать поддерживать студентов & rsqup; использование нового термина в уроках, следующих за тем, в котором он был впервые введен.
| урок | новая терминология | |
|---|---|---|
| приемный | продуктивная | |
| 8.7.1 |
показатель степени степень коэффициент обратный |
повторное умножение |
| 8.7,2 | степени 10 | |
| 8.7.3 |
основание (экспоненты) степень степеней |
|
| 8.7.4 | развернутая положительная экспонента нулевая экспонента |
|
| 8.7.5 | отрицательная экспонента | положительный показатель |
| 8.7.6 |
экспонента основание (экспоненты) степень нулевая экспонента |
|
| 8.7,7 |
обратный оценить |
коэффициент мощность степеней отрицательный показатель |
| 8.7.8 | квадрат (из ряда) | |
| 8.7.9 | млрд трлн кратное |
|
| 8.7.10 | целое | |
| 8.7.12 | , кратное | |
| 8.7,13 | в научном обозначении | целое |
| 8.7.14 | степени 10 миллиардов триллионов |
|
| 8.7.15 | в научном обозначении | |
Раздел 8: Теорема Пифагора и иррациональные числа
Работа по этому модулю предназначена для развития и объединения знаний учащихся о геометрии и числовых выражениях.Раздел начинается с описания алгебраических и геометрических аспектов теоремы Пифагора и стратегий ее доказательства. Студентам показывают три квадрата и просят сравнить площадь самого большого квадрата с суммой площадей двух других квадратов. Сравнение может быть выполнено путем подсчета квадратов сетки и сравнения подсчетов – когда три квадрата находятся на сетке, их стороны находятся на линиях сетки, а вершины – на пересечении линий сетки – используя понимание измерения площади, установленное в 3-м классе.Сравнение также можно провести, показав, что существует фигура, которую можно разложить и переставить, чтобы сформировать самый большой квадрат или два самых маленьких квадрата. Учащимся предоставляется возможность использовать и обсуждать обе стратегии.
Во втором разделе учащиеся работают с фигурами, изображенными на сетках, используя сетки для оценки длины и площади в единицах сетки, например, оценивая длины сторон квадрата, возводя свои оценки в квадрат и сравнивая их с оценками, полученными путем подсчета сетка квадратов.Термин «квадратный корень» вводится как способ описания отношения между длиной стороны и площадью квадрата (измеряется в единицах и квадратных единицах соответственно) вместе с обозначением \ (\ sqrt {} \). Студенты продолжают работать с длинами сторон и площадями квадратов. Они изучают и используют определения «рационального числа» и «иррационального числа». Они наносят на числовую прямую рациональные числа и квадратные корни. Они используют значение «квадратного корня», понимая, что если данное число \ (p \) является квадратным корнем из \ (n \), то \ (x ^ 2 = n \).Студенты узнают (без доказательств), что \ (\ sqrt 2 \) иррационально. Они понимают два доказательства теоремы Пифагора – алгебраическое доказательство, которое включает манипулирование двумя выражениями для одной и той же области, и геометрическое доказательство, которое включает разложение и перестановку двух квадратов. Они используют теорему Пифагора в двух и трех измерениях, например, для определения длины диагоналей прямоугольников и прямоугольных призм, а также для оценки расстояний между точками в координатной плоскости.
В третьем разделе учащиеся работают с длинами граней и объемами кубов и других прямоугольных призм.2 \) находится между \ (m \) и \ (p \), а \ (x \) находится между \ (\ sqrt {m} \) и \ (\ sqrt {p} \).
В четвертом разделе учащиеся работают с десятичными представлениями рациональных чисел и десятичными приближениями иррациональных чисел. В 7 классе они использовали длинное деление, чтобы записывать дроби как десятичные, и узнали, что такие десятичные дроби либо повторяются, либо заканчиваются. Они основываются на своем понимании десятичных дробей, чтобы делать последовательные десятичные приближения \ (\ sqrt 2 \) и \ (\ pi \), которые они наносят на числовые линии.
Развитие дисциплинарного языка
В этом модуле учителя могут предвидеть, что ученики будут использовать язык в математических целях, таких как объяснение, обоснование и сравнение. На протяжении всего модуля учащиеся извлекут пользу из рутин, разработанных для развития прочного дисциплинарного языка, как для их собственного осмысления, так и для построения общего понимания со сверстниками. Учителя могут сформировать формативную оценку того, как учащиеся используют язык таким образом, особенно когда учащиеся используют язык для:
Объяснить
- стратегии поиска местности (Урок 1)
- стратегий приближения и нахождения квадратных корней (Урок 4)
- стратегий для определения длин сторон треугольника (Урок 6)
- прогнозов о ситуациях, связанных с прямоугольными треугольниками, и стратегии для проверки (Урок 10)
- стратегии нахождения расстояний между точками на координатной плоскости (Урок 11)
- стратегий для приближения значения кубических корней (Урок 13)
Обосновать
- , у каких квадратов длина сторон находится в заданном диапазоне (Урок 1)
- упорядочивание иррациональных чисел (Урок 5)
- Порядок длин гипотенузы (Урок 9)
Сравнить
- рациональные и иррациональные числа (Урок 3)
- длин диагоналей в прямоугольных призмах (Урок 10)
- стратегий приближения иррациональных чисел (Урок 15)
Кроме того, ожидается, что студенты будут использовать язык для обобщения площади квадратов, квадратных корней и приближений длин сторон, а также для обобщения расстояния между любыми двумя парами координат; критика рассуждений о приближении квадратного корня и критика стратегии представления повторяющихся десятичных разложений в виде дробей; описать наблюдения о взаимосвязях между длинами сторон треугольников и описать гипотенузы и длины сторон для данных треугольников; интерпретировать диаграммы, состоящие из квадратов и прямоугольных треугольников; интерпретировать уравнения и приближения для значений квадратных и кубических корней; и представляют отношения между длинами сторон и площадями.
В таблице показаны уроки, на которых впервые вводится новая терминология, в том числе когда ожидается, что учащиеся будут понимать слово или фразу восприимчиво, и когда ожидается, что учащиеся произнесут слово или фразу в своей речи или письме. Термины из глоссария выделены жирным шрифтом. Учителя должны продолжать поддерживать использование учащимися нового термина на уроках, следующих за тем, в котором он был впервые введен.
| урок | новая терминология | |
|---|---|---|
| приемный | продуктивная | |
| 8.8,2 | корень квадратный | квадрат (из ряда) |
| 8.8.3 |
иррациональное число символ квадратный корень |
рациональное число |
| 8.8.4 | диагональ десятичное приближение |
|
| 8.8.5 |
корень квадратный символ квадратный корень |
|
| 8.8.6 | Теорема Пифагора гипотенуза катетов |
прямоугольный треугольник |
| 8.8,9 | обращение теоремы Пифагора | Теорема Пифагора |
| 8.8.10 | длина кромки | гипотенуза ножек |
| 8.8.12 | кубический корень | |
| 8.8.13 |
кубический корень длина ребра |
|
| 8.8.14 |
повторяющееся десятичное представление десятичное представление конечное десятичное представление |
|
| 8.8,15 | бесконечное десятичное разложение | иррациональное число десятичное повторение |
Раздел 9: Собираем все вместе
На этих факультативных уроках учащиеся решают сложные задачи. На первых нескольких уроках они рассматривают мозаику плоскости, понимая и используя термины «мозаика» и «регулярная мозаика» в своей работе, а также используя свойства форм (например, сумма внутренних углов четырехугольника равна 360 градусов), чтобы делать выводы о регулярной мозаике.Эти уроки необходимо пройти после того, как будет выполнен раздел 8.1. На более поздних уроках они исследуют взаимосвязь температуры и широты, климата, сезона, облачности или времени суток. В частности, они используют диаграммы рассеяния и линии наилучшего соответствия для исследования вопроса моделирования температуры как функции широты. Эти уроки нужно проводить после того, как будут изучены разделы 8.5 и 8.6.
Развитие дисциплинарного языка
В этом разделе учителя могут предвидеть, что ученики будут использовать язык в математических целях, таких как описание, представление и обоснование.На протяжении всего модуля учащиеся извлекут пользу из рутин, разработанных для развития прочного дисциплинарного языка, как для их собственного осмысления, так и для построения общего понимания со сверстниками. Учителя могут сформировать формативную оценку того, как учащиеся используют язык таким образом, особенно когда учащиеся используют язык для:
Описать
- мозаики (Урок 1)
- связей в двумерных данных (Урок 5)
Представлять
- взаимосвязь между широтой и погодой (Урок 5)
Обосновать
- утверждения о формах, которые можно и нельзя использовать для создания обычных мозаик (Урок 2)
В таблице показаны уроки, на которых впервые вводится новая терминология, в том числе когда ожидается, что учащиеся будут понимать слово или фразу восприимчиво, и когда ожидается, что учащиеся произнесут слово или фразу в своей речи или письме.Термины из глоссария выделены жирным шрифтом. Учителя должны продолжать поддерживать использование учащимися нового термина на уроках, следующих за тем, в котором он был впервые введен.
| урок | новая терминология | |
|---|---|---|
| приемный | продуктивная | |
| 8.9.1 |
мозаика узор |
|
| 8.9.2 | обычная мозаика | правильный многоугольник |
| 8.9,6 | математическая модель | |
Обучение Измерению | Лучшие виды деятельности по измерению
Измерение – один из тех математических навыков, которые мы используем практически каждый день. Итак, когда мы обучаем измерению, очень важно дать нашим ученикам возможность осмысленно поработать над своими навыками измерения. Более того, эти измерения должны быть интересными и увлекательными!
Сделайте ваш класс шумным! Подпишитесь на Teach Starter и получите доступ к тысячам ресурсов, соответствующих учебной программе, и инструментам цифрового обучения.Начало работы
Вы изо всех сил пытаетесь найти время, чтобы написать свой неформальный план единицы измерения? Не бойтесь, наши опытные учителя начальных классов сделали это за вас! Они разработали пять планов единиц , которые помогут вам обучать измерению и помогут вашему классу научиться измерять объем, площадь, массу и длину с использованием неформальных единиц.
Важно помнить:
Когда мы обучаем измерению, может возникнуть соблазн думать исключительно об использовании неформальных или формальных измерительных инструментов.Однако также важно создать возможности для ваших учеников изучать и использовать следующие навыки:
- выбор соответствующих неформальных единиц
- определение измеримых атрибутов, включая длину, вместимость и вес
- развитие языка, связанного с измерением
- оценка с использованием неформальные единицы.
В этом блоге я собираюсь распаковать наш всеобъемлющий анализ длины для младших лет с планом единиц неформальных единиц и поделиться лучшими неформальными измерениями на блоке.
Этот блок включает в себя 5 увлекательных уроков и оценочное задание, чтобы вы могли контролировать понимание учащимися. Он был создан для проведения либо как отдельная неделя уроков по измерению, либо как часть более широкого многоступенчатого плана.
Каждый урок начинается с увлекательного урока и включает в себя инструкции учителя, управляемые или независимые измерения и идеи для завершения урока. Вы также найдете предложения о способах расширения знаний и понимания для более уверенных учащихся и о том, как оказать поддержку менее уверенным учащимся.
Урок 1
Давали ли вы когда-нибудь своему классу возможность измерить длину объектов с помощью следов динозавра ? В Уроке 1 этого замечательного модуля ученики заполняют Рабочий лист «Измерение со следами динозавров» и многократно используют следы динозавров (повторное использование одного и того же устройства) для измерения длины различных объектов в классе. Записав свои результаты, студенты сравнивают их со сверстниками, которые использовали большие и меньшие следы динозавров, а также с теми, кто использовал неформальные единицы такого же размера.
Урок 2
В Уроке 2 учащиеся начинают с прямого сравнения белого медведя и предметов в классе, развивая язык измерений. Затем учащиеся получают практический опыт поиска предметов разной длины в классе и их измерения с помощью неформальных единиц измерения, например блоки, Неформальные единицы Правители , Медвежьи квадраты .
Не забывайте о важности предоставления вашему классу возможности развивать язык, связанный с измерением! Не стоит недооценивать влияние создания видеостены для измерения показателей в вашем классе.Выберите список слов, соответствующий потребностям вашего класса, с помощью нашей настраиваемой стены слов Measurement Word .
Дополнительные идеи и информацию об использовании математической терминологии можно найти в нашем блоге «Важность использования математической терминологии».
Урок 3
Измерение, сравнение и упорядочивание высоты с использованием неформальных единиц – это название игры в Уроке 3. Учащиеся узнают, что высота – это измерение объекта от его основания до его вершины, и выбирают неформальные единицы для измерения своей высоты. рост.Следующим шагом этого измерения является определение роста трех одноклассников, а также их собственного, от самого низкого человека до самого высокого человека. Заключительная и крайне важная часть этого урока – размышление, которое побуждает ученика анализировать свои результаты и развивать свой язык измерения.
Есть ли в вашем классе ученики, которым нужна задача? Если да, то все наши планы уроков включают идеи о том, как расширить свои знания. На этом уроке более уверенным ученикам предлагается оценить высоту перед ее измерением и изучить возможность пропуска подсчета для завершения измерений.
Урок 4
Важно включать исследований по математике при обучении измерению и всем областям математики. Урок 4 дает вашему классу возможность применить свои знания и понимание измерения длины с использованием неформальных единиц измерения в реальной ситуации. В этом расследовании директору школы нужно найти помощников, чтобы подать сигнал, чтобы он не шуметь во время собраний. Сборки проходят на большом пространстве, поэтому ему нужны люди с длинными пальцами, чтобы каждый действительно мог видеть сигнал!
Этот учебный ресурс включает:
- заметки учителя, детализирующие ряд важной информации о расследовании
- подробное описание расследования для студентов, включая пошаговые инструкции
- сбор и запись данных рабочий лист
- отражение вопросов.
время исследования математики!
Урок 5
Что может быть лучше для начала предпоследнего урока этого устройства, чем с Ballard of Dizzy D . Это видео на YouTube – отличный способ узнать, как объекты могут быть измерены с помощью неформальных единиц, и развить язык, связанный с измерением.
После начала урока 5 продолжается повторное рассмотрение использования неформальных инструментов измерения. Все, что вам нужно сделать, это настроить 3 рабочих места и следить за своими учениками, когда они демонстрируют свои знания и понимание! Три сменных действия включают:
- Упорядочивание группы объектов (10-15) от самого короткого до самого длинного.
- Измерение длины нескольких предметов в классе с помощью неформальных единиц, например кубики, Неформальные единицы Линейки, Медвежьи квадраты. Запишите длину.
- Трехкратное измерение роста другого ученика с использованием отпечатка динозавра разного размера каждый раз.
Урок 6
После выполнения этих действий по измерению ваш класс обязательно будет готов выполнить задание по оценке. Чтобы облегчить вам жизнь, мы создали рабочий лист, который напрямую связан с уроками в этом модуле и идеально подходит для использования в качестве задания по оценке.В этом задании учащиеся измеряют объекты квадратами, сравнивают их длину, а затем отсортировывают объекты от самых коротких до самых длинных. Более того, также был включен лист для ответов.
Вот и все! Этот мини-блок включает в себя некоторые из лучших методов измерения и ставит галочки во многих ячейках.
Я надеюсь, что вы оцениваете по ощущениям готовые и подготовленные шкалы для вашей следующей неофициальной единицы измерения.
Сообщите нам, какие упражнения по измерению больше всего нравятся вашему классу, на странице комментариев и отзывов.
Сделайте ваш класс шумным! Подпишитесь на Teach Starter и получите доступ к тысячам ресурсов, соответствующих учебной программе, и инструментам цифрового обучения. Начало работы
Измерение 2-го класса | Общее Ядро Королевства
Измерение – большая тема для второго класса. Многое нужно для обучения второклассным стандартам измерения Common Core, и вы можете использовать множество увлекательных и интерактивных занятий. Вот несколько полезных советов по обучению второклассников.
Что нужно знать первоклассникам
Ученики должны поступать во 2 класс со следующими навыками:
- Заказать 3 предмета по длине. (Например, книга самая длинная, бумага вторая по длине, а карандаш самый короткий.)
- Сравните длину двух объектов, используя третий объект. (Ластик длиннее скрепки. Я знаю это, потому что использую карандаш в качестве измерительного инструмента.)
- Определите длину объекта как целое число единиц длины, наложив несколько более коротких объектов встык.
- Поймите, что для определения длины объекта единицы одинакового размера должны охватывать его без зазоров и перекрытий
Учащиеся, поступающие во 2-й класс, могут или не могут полностью понять эти концепции. Учащимся, которые начинают отставать, может потребоваться дополнительная помощь в небольших группах, но не обязательно заново учить концепции первого класса.
Обучение измерению общего ядра во 2-м классе
ЭталоныCommon Core 2-го класса основываются друг на друге, поэтому они помогают обучать этим стандартам по порядку.Вот каждый из стандартов Common Core Measurement для 2-го класса вместе с некоторыми обучающими советами, которые помогут сделать эту тему интересной и эффективной.
Преподавание измерения для второго класса: 2.MD.A.1
Измерьте длину объекта, выбрав и используя соответствующие инструменты, такие как линейки, мерки, измерительные стержни и измерительные ленты.
Обратите внимание на следующие инструменты измерения
Учащиеся с большей вероятностью усвоят концепции измерения, если они не перегружены слишком большим количеством инструментов.Важно обучать различным инструментам, но сосредоточение внимания на приведенных ниже инструментах позволит учащимся понять концепции измерения, не будучи перегруженными.
- Рулетка :
- Гибкий – Используется для измерения одежды и круглых предметов
- Выдвижной – используется для измерения больших расстояний, например, комнаты
- Метрическая палочка – Используется для измерения предметов длиннее линейки при измерениях в метрах, сантиметрах или миллиметрах.
- Yardstick – Используется для измерения предметов длиннее линейки при измерении в ярдах, футах, дюймах
- Линейка – Используется для измерения небольших объектов, например ластика
День 1:
- Открытие: Выделите время (10 минут) для исследования. Убедитесь, что в каждой группе есть много инструментов, чтобы учащиеся могли их изучить. По мере изучения инструментов попросите их записывать любые наблюдения, которые они делают в своем математическом дневнике.
- Мини-урок: Соберите студентов, а затем познакомьте их с различными инструментами измерения.Составьте диаграмму привязки всех различных инструментов, единиц измерения для каждого инструмента и типов объектов, которые они измеряют.
Таблица привязки средств измерения 2-го класса для 2.MD.A.1.
- Самостоятельная работа: Попросите учащихся заполнить рабочие листы, требующие выбора соответствующих инструментов измерения. (Их можно найти в моей измерительной единице здесь.)
- Закрытие: Просмотрите таблицу привязки измерений. Попросите учащихся обобщить то, что они узнали. Используйте такие вопросы, как:
-
- Какой инструмент вы бы использовали, чтобы измерить рост Сэма?
- Какой инструмент вы бы использовали для измерения длины стола?
- Какой инструмент вы бы использовали для измерения мяча?
День 2:
- Открытие: Просмотрите (10 минут) график привязки за предыдущий день.Обсудите различные инструменты, затем задайте обзорные вопросы о том, какой инструмент лучше всего подходит для измерения конкретных объектов.
- Какой инструмент вы бы использовали для измерения веса собаки?
- Какой инструмент вы бы использовали для измерения длины маркера?
- Какой инструмент вы бы использовали, чтобы измерить чью-то талию?
- Модель: Покажите учащимся каждый инструмент измерения и способы его использования.
- Обязательно покажите, как начать с «0» на любом инструменте измерения длины, который не обязательно всегда находится в начале инструмента.
- Покажите, как округлить до ближайшего целого числа в большую или меньшую сторону. Укажите полудюймовую линию на линейке и объясните, что если она идет перед полудюймом, вы берете число перед ней. Если он равен или превышает половину единицы, он переходит к следующему числу. Обратите внимание: округление – очень сложное понятие для многих второклассников. Многие не сразу поймут, и это нормально. Не ждите, что они сразу овладеют им. Требуется много практики. Кроме того, цель этого урока – выбрать подходящие измерительные инструменты и начать экспериментировать с измерениями.
- Партнерская работа: Попросите учащихся поработать вместе с ними, чтобы отправиться на охоту за мусором в классе. Они должны найти предметы по комнате и определить подходящий измерительный инструмент и единицу измерения. Затем они должны попытаться измерить каждый объект.
- Пока партнеры работают над охотой за мусором, чередуйте каждую группу, чтобы прояснить неправильные представления или помочь им с использованием инструментов измерения. Следите за учениками, которые действительно испытывают трудности и могут нуждаться в обучении в небольших группах или один на один.
- Окончание: После охоты за мусором ученики приходят к месту сбора, чтобы ознакомиться с результатами. Я говорю студентам, что на сегодня это нормально, если их измерения будут немного отклоняться. Затем студенты делятся своими результатами. Если в какой-либо группе есть серьезные расхождения, я моделирую, как измерить объект.
- В конце каждый студент должен заполнить 2.MD.A.1 Exit Tickets для измерений (щелкните, чтобы получить доступ к этому бесплатному ресурсу). Выходные билеты – еще одна быстрая проверка, чтобы узнать, каким учащимся на следующий день потребуется помощь в небольшой группе или индивидуально.
День 3:
Перед тем, как перейти к следующему стандарту, выделите дополнительный день, чтобы студенты попрактиковались в измерениях.
- Открытие: Начните с краткого обзора обычных и метрических систем. Не ждите, что ученики запомнят различные системы. Цель состоит в том, чтобы показать им разницу и причину, по которой они могут видеть разные единицы. Создайте якорную диаграмму, показывающую обычную и метрическую системы, и попросите учащихся поместить ее в свои журналы.Также важно подчеркнуть, как ученики обычно должны использовать маленькие единицы для измерения небольших объектов и более крупные единицы для измерения более длинных или более крупных объектов.
- Время работы: Как упоминалось выше, второклассников важно научить округлять свои измерения до ближайшей единицы. Объекты из реальной жизни не всегда будут иметь точные единицы измерения, поэтому второклассники должны понимать, как округлять в большую или меньшую сторону. Найдите время сегодня, чтобы студенты попрактиковались в измерении реальных объектов в классе.Студенты могут работать в партнерстве или самостоятельно. В моем пакете измерений есть страница, которую студенты могут использовать для отслеживания своего обучения. Пока студенты работают (вместе или самостоятельно), я собираю небольшую группу студентов, которые не справились с уроком предыдущего дня.
- Окончание: Просмотрите, что узнали учащиеся. Это прекрасное время для выдачи следующего выходного билета на измерение.
Преподавание второго класса Измерение: 2.MD.A.2
Измерьте длину объекта дважды, используя единицы длины разной длины для двух измерений; опишите, как эти два измерения соотносятся с размером выбранной единицы.
День 4 и День 5:
В этом стандарте учащиеся должны узнать, как разные единицы сравниваются друг с другом. Например, сантиметр короче дюйма, поэтому, если вы измеряете объект обеими единицами измерения, вы должны использовать больше сантиметров, чем дюймов. У второклассников очень часто возникает неправильное представление о том, что вы бы использовали больше единиц большего размера, чем меньшего. Чтобы исправить это заблуждение, студентам необходимо много попрактиковаться в измерении объектов с использованием различных единиц измерения.
-
Я моделирую сравнение измерений, используя студентов в качестве примеров.
Модель: Модель измерения одного и того же объекта в разных единицах измерения. Обычно я начинаю с измерения роста ученика в дюймах и футах, а затем моделирую с другими предметами в классе.
- Работа в группе: Попросите партнеров или группы измерить объекты в комнате с помощью двух разных единиц измерения.
- Самостоятельная работа: Студенты заполняют практические листы из пакета мер, чтобы сравнить единицы.
- Окончание: Просмотрите, что узнали учащиеся. Вы можете оценить их самостоятельную работу как оценку, чтобы выявить учащихся, которым на следующий день потребуется дополнительная помощь.
2.MD.A.3
Измерьте и оцените длину в дюймах, футах, сантиметрах и метрах.
Для оценки длины учащиеся должны иметь контрольные точки, которые помогут им визуализировать размер каждой единицы. Студенты, как правило, легко понимают критерии тела для оценки.Контрольные показатели тела – это части вашего тела, которые примерно равны размеру каждой единицы. Проблема в том, что все люди разного размера, поэтому не все тесты тела точны для всех. Вы также можете использовать стандартные объектные тесты. Вот список примеров для каждого:
День 6 и 7:
- Модель: Введите термин «оценка». Объясните: когда мы что-то оцениваем, мы получаем не точный ответ, а приблизительное предположение. Скажите студентам, что для того, чтобы помочь нам сделать оценки измерений, лучше всего придумать эталон, который поможет нам визуализировать размер чего-либо.Смоделируйте несколько примеров. Например, «кончик моего пальца около сантиметра, поэтому я могу по кончику пальца оценить длину карандаша в сантиметрах, если бы у меня не было линейки». Измерьте кончик пальца, чтобы установить ориентир, затем измерьте карандашом. Наконец, измерьте карандаш линейкой, чтобы сравнить свою оценку с фактическим измерением.
- Время работы: Попросите учащихся обнаружить свои собственные контрольные показатели, выполнив Benchmark Scavenger Hunt.Студенты должны начать с создания контрольных показателей. Попросите их сесть с несколькими измерительными инструментами, чтобы узнать длину своих пальцев, предплечий и ступней. Затем они должны найти объекты по комнате и попытаться измерить каждый объект с помощью контрольных точек.
- Пока партнеры работают над охотой за мусором, чередуйте каждую группу, чтобы прояснить неправильные представления или помочь им с использованием тестов и оценок. Следите за учениками, которые действительно испытывают трудности и могут нуждаться в обучении в небольших группах или один на один.
- Окончание: После охоты за мусором ученики приходят к месту сбора, чтобы ознакомиться с результатами. Студенты делятся своими результатами. Если в какой-либо группе есть серьезные расхождения, я моделирую, как измерить объект.
- Завершите урок быстрым обзором и выходным талоном для измерений.
Студентам нужно много повторяющейся практики. Вот образец оценочного листа из моего пакета измерений для студентов, которые могут выполнять независимую практику.
Обучение измерению во втором классе: 2.MD.A.4
Измерение, чтобы определить, насколько длиннее один объект, чем другой, выражая разницу в длине в единицах стандартной длины.
В этом стандарте учащиеся сравнивают длину различных предметов. Этот стандарт по-разному встречается во многих общих основных стандартах математики для 2-го класса (задачи сравнения слов (2.OA.A.1), построение графиков (2.MD.D.10) и задачи с денежными словами (2.MD.C. 8).
Важно, чтобы учащиеся глубоко понимали, что означает сравнение.Студенты должны видеть связь между этими проблемами во всех этих стандартах. Их методы решения этих проблем в разных стандартах также будут одинаковыми.
«Сравнение» означает нахождение отличия. Чтобы сравнить две длины (или любые другие числа), вы можете убрать меньшую длину из более длинной (вычитание a-b = c). Вы также можете добавить от наименьшей длины к большей длине (b + c = a). Если учащиеся действительно понимают концепцию фактических семей, сравнение их длины будет иметь смысл.
День 8 и 9
- Модель: Модель, как сравнивать длины двух разных объектов. Объясните: мы сравниваем их размеры, чтобы определить, насколько один из них длиннее другого. Еще раз возьмем для примера рост ученика. Это действительно привлекает студентов, потому что они любят моделировать для класса. Во-первых, смоделируйте, как найти разницу между высоким и низким учеником. Затем выберите двух учеников, чтобы измерить свой рост и рост другого ученика, а затем вместе выясните, насколько вы выше этого ученика.Затем смоделируйте, как найти разницу между двумя меньшими объектами на бумаге, которые будут иметь более точные измерения.
- Групповая работа: Затем попросите учащихся поработать в группах или с партнерами, чтобы сравнить длину двух объектов. Вы можете использовать для этого одну из моих таблиц измерений, но мой любимый способ побудить студентов сотрудничать – это создать плакат, на котором сравниваются два объекта. Заранее создайте по одному плакату для каждой группы, после чего учащиеся смогут измерить и выполнить задание как группа.После этого каждая группа может поделиться своими выводами с классом.
- Самостоятельная работа: Наконец, студенты практикуются в самостоятельном сравнении измерений. Таблицы из моего пакета измерений доступны здесь. В то время как большинство студентов работают независимо, собирают небольшие группы или отдельных лиц, которым требуется дополнительная помощь.
- Окончание: В конце каждого дня собирайте студентов, чтобы повторить то, что они узнали. После того, как вы убедитесь, что большинство студентов усвоили этот стандарт, вы можете дать им выходной билет для проведения измерений за 2.MD.A.4.
Обучение измерению второго класса: 2.MD.B.5
Используйте сложение и вычитание в пределах 100 для решения словесных задач, связанных с длинами, указанными в тех же единицах.
Надеюсь, что до того, как вы представите этот стандарт, студенты уже знакомы с задачами со словами (2.OA.A.1). Студентам важно понимать, что задачи с измерением слов ничем не отличаются от обычных задач со словами. Студентам, как правило, не требуется выполнять измерения для задачи с измерением слов.Представляя этот стандарт, он помогает уйти от предыдущего стандарта и придерживаться словесных задач, которые сравнивают измерения. Сравнение словесных задач измерения, как правило, является одним из самых сложных для учащихся; однако студенты склонны относиться к тому, что они узнали в предыдущем стандарте. После некоторой практики объедините все типы задач измерения слов.
1.3 Язык физики: физические величины и единицы
Точность, прецизионность и значащие числа
Наука основана на экспериментах, требующих точных измерений.Достоверность измерения можно описать с точки зрения его точности и точности (см. Рис. 1.19 и рис. 1.20). Точность – это насколько измерение близко к правильному значению для этого измерения. Например, предположим, что вы измеряете длину стандартного листа бумаги для принтера. На упаковке, в которой вы приобрели бумагу, указано, что ее длина составляет 11 дюймов, и предположим, что указанное значение верное. Вы трижды измеряете длину бумаги и получаете следующие размеры: 11.1 дюйм, 11,2 дюйма и 10,9 дюйма. Эти измерения довольно точны, потому что они очень близки к правильному значению 11,0 дюймов. Напротив, если бы вы получили размер в 12 дюймов, ваше измерение не было бы очень точным. Вот почему измерительные приборы калибруются на основе известного измерения. Если прибор постоянно возвращает правильное значение известного измерения, его можно безопасно использовать для поиска неизвестных значений.
Рис. 1.19. Механические весы с двумя чашами используются для сравнения различных масс.Обычно объект неизвестной массы помещается в одну чашу, а объекты известной массы – в другую. Когда стержень, соединяющий две посуды, расположен горизонтально, массы в обеих посудах равны. Известные массы обычно представляют собой металлические цилиндры стандартной массы, например 1 грамм, 10 грамм и 100 грамм. (Серж Мелки)
Рисунок 1.20. В то время как механические весы могут считывать массу объекта только с точностью до десятых долей грамма, некоторые цифровые весы могут измерять массу объекта с точностью до ближайшей тысячной доли грамма.Как и в других измерительных приборах, точность шкалы ограничивается последними измеренными цифрами. Это сотые доли в изображенной здесь шкале. (Splarka, Wikimedia Commons)
«Точность» указывает, насколько хорошо повторные измерения чего-либо дают одинаковые или похожие результаты. Следовательно, точность измерений означает, насколько близки друг к другу измерения, когда вы измеряете одно и то же несколько раз. Один из способов анализа точности измерений – определение диапазона или разницы между самым низким и самым высоким измеренными значениями.В случае размеров бумаги для принтера наименьшее значение составляло 10,9 дюйма, а максимальное значение – 11,2 дюйма. Таким образом, измеренные значения отклонялись друг от друга не более чем на 0,3 дюйма. Эти измерения были достаточно точными, потому что они варьировались всего на долю дюйма. Однако, если бы измеренные значения были 10,9 дюймов, 11,1 дюймов и 11,9 дюймов, тогда измерения не были бы очень точными, потому что есть много отклонений от одного измерения к другому.
Измерения в бумажном примере точны и точны, но в некоторых случаях измерения точны, но неточны, или они точны, но неточны.Давайте рассмотрим систему GPS, которая пытается определить местоположение ресторана в городе. Думайте о расположении ресторана как о самом центре мишени в яблочко. Затем представьте, что каждая попытка GPS определить местонахождение ресторана – это черная точка в яблочко.
На рис. 1.21 вы можете видеть, что измерения GPS разнесены далеко друг от друга, но все они относительно близки к фактическому местоположению ресторана в центре цели. Это указывает на низкую точность измерительной системы с высокой точностью.Однако на Рисунке 1.22 измерения GPS сосредоточены довольно близко друг к другу, но они находятся далеко от целевого местоположения. Это указывает на высокую точность измерительной системы с низкой точностью. Наконец, на рис. 1.23 GPS является точным и точным, что позволяет определить местонахождение ресторана.
Рис. 1.21. Система GPS пытается определить местонахождение ресторана в центре мишени. Черные точки представляют каждую попытку определить местоположение ресторана. Точки расположены довольно далеко друг от друга, что указывает на низкую точность, но каждая из них находится довольно близко к фактическому местоположению ресторана, что указывает на высокую точность.(Темное зло)
Рис. 1.22 На этом рисунке точки сосредоточены близко друг к другу, что указывает на высокую точность, но они довольно далеко от фактического местоположения ресторана, что указывает на низкую точность. (Темное зло)
Рисунок 1.23 На этом рисунке точки сосредоточены близко друг к другу, что указывает на высокую точность, и они находятся близко к фактическому местоположению ресторана, что указывает на высокую точность. (Темное зло)
Неопределенность
Точность и прецизионность измерительной системы определяют неопределенность ее измерений.Неопределенность – это способ описать, насколько ваше измеренное значение отклоняется от фактического значения, которое имеет объект. Если ваши измерения не очень точны или точны, то неопределенность ваших значений будет очень высокой. В более общем плане неопределенность можно рассматривать как отказ от ответственности за ваши измеренные значения. Например, если кто-то попросил вас указать пробег вашего автомобиля, вы можете сказать, что это 45 000 миль, плюс-минус 500 миль. Сумма плюс или минус – это неопределенность в вашей стоимости.То есть вы указываете, что фактический пробег вашего автомобиля может составлять от 44 500 миль до 45 500 миль или где-то между ними. Все измерения содержат некоторую неопределенность. В нашем примере измерения длины бумаги мы можем сказать, что длина бумаги составляет 11 дюймов плюс-минус 0,2 дюйма или 11,0 ± 0,2 дюйма. Неопределенность измерения, A , часто обозначается как δA («дельта A »),
.Факторы, способствующие неопределенности измерения, включают следующее:
- Ограничения измерительного прибора
- Навык человека, производящего измерение
- Неровности в измеряемом объекте
- Любые другие факторы, влияющие на результат (в значительной степени зависящие от ситуации)
В примере с бумагой для принтера неточность может быть вызвана: тем фактом, что наименьшее деление на линейке равно 0.1 дюйм, человек, использующий линейку, имеет плохое зрение или неуверенность, вызванную бумагорезательной машиной (например, одна сторона бумаги немного длиннее другой). Хорошей практикой является тщательное рассмотрение всех возможных источников неопределенности в измерение и уменьшение или устранение их,
Процент неопределенности
Один из методов выражения неопределенности – это процент от измеренного значения. Если измерение A выражается с неопределенностью δ A , неопределенность в процентах составляет
1.2% неопределенность = δAA × 100%.% Неопределенность = δAA × 100%.Рабочий пример
Расчет процента неопределенности: мешок яблок
В продуктовом магазине продаются 5-фунтовые пакеты с яблоками. Вы покупаете четыре пакета в течение месяца и каждый раз взвешиваете яблоки. Вы получите следующие размеры:
- Неделя 1 Вес: 4,8 фунта 4,8 фунта
- Вес 2 недели: 5,3 фунта 5,3 фунта
- Вес 3 недели: 4,9 фунта 4,9 фунта
- 4 неделя вес: 5.4 фунта 5,4 фунта
Вы определили, что вес 5-фунтового мешка имеет погрешность ± 0,4 фунта. Какова погрешность в процентах от веса мешка?
Стратегия
Во-первых, обратите внимание, что ожидаемое значение веса мешка, AA, составляет 5 фунтов. Неопределенность этого значения, δAδA, составляет 0,4 фунта. Мы можем использовать следующее уравнение для определения процентной неопределенности веса
% Неопределенности = δAA × 100%.% Неопределенности = δAA × 100%.Решение
Подставьте известные значения в уравнение
% Неопределенности = 0.4 фунта5 фунтов × 100% = 8%.% Погрешности = 0,4 фунта5 фунтов × 100% = 8%.Обсуждение
Мы можем сделать вывод, что вес мешка с яблоками составляет 5 фунтов ± 8 процентов. Подумайте, как изменился бы этот процент неопределенности, если бы мешок с яблоками был вдвое меньше, но неопределенность в весе осталась бы прежней. Совет для будущих расчетов: при вычислении процентной погрешности всегда помните, что вы должны умножить дробь на 100 процентов. Если вы этого не сделаете, у вас будет десятичная величина, а не процентное значение.
Неопределенность в расчетах
Есть неопределенность в любом вычислении на основе измеренных величин. Например, площадь пола, рассчитанная на основе измерений его длины и ширины, имеет неопределенность, потому что и длина, и ширина имеют неопределенности. Насколько велика неопределенность в том, что вы вычисляете умножением или делением? Если измерения в расчетах имеют небольшую погрешность (несколько процентов или меньше), то можно использовать метод сложения процентов.В этом методе говорится, что процент неопределенности в величине, вычисленной путем умножения или деления, представляет собой сумму процентных погрешностей в элементах, использованных для выполнения расчета. Например, если пол имеет длину 4,00 м и ширину 3,00 м с погрешностями 2 процента и 1 процент соответственно, то площадь пола составляет 12,0 м 2 и погрешность составляет 3 процента ( выраженная как площадь, это 0,36 м 2 , которое мы округляем до 0,4 м ( 2 , поскольку площадь пола дается с точностью до одной десятой квадратного метра).
Для быстрой демонстрации точности, прецизионности и неопределенности измерений, основанных на единицах измерения, попробуйте это моделирование. У вас будет возможность измерить длину и вес стола, используя единицы измерения в миллиметрах и сантиметрах. Как вы думаете, что обеспечит большую точность, точность и неопределенность при измерении стола и блокнота в моделировании? Подумайте, как природа гипотезы или вопроса исследования может повлиять на точность измерительного инструмента, необходимого для сбора данных.
Прецизионность измерительных инструментов и значащих цифр
Важным фактором точности измерений является точность измерительного инструмента. В общем, точный измерительный инструмент – это инструмент, который может измерять значения с очень маленькими приращениями. Например, рассмотрите возможность измерения толщины монеты. Стандартная линейка может измерять толщину с точностью до миллиметра, а микрометр может измерять толщину с точностью до 0,005 миллиметра. Микрометр – более точный измерительный инструмент, потому что он может измерять очень небольшие различия в толщине.Чем точнее измерительный инструмент, тем точнее и точнее могут быть измерения.
Когда мы выражаем измеренные значения, мы можем перечислить только столько цифр, сколько мы первоначально измерили с помощью нашего измерительного инструмента (например, линейки, показанные на рисунке 1.24). Например, если вы используете стандартную линейку для измерения длины палки, вы можете измерить ее дециметровой линейкой как 3,6 см. Вы не можете выразить это значение как 3,65 см, потому что ваш измерительный инструмент не был достаточно точным, чтобы измерить сотую долю сантиметра.Следует отметить, что последняя цифра в измеренном значении была определена каким-то образом лицом, выполняющим измерение. Например, человек, измеряющий длину палки линейкой, замечает, что длина палки находится где-то между 36 и 37 мм. Он или она должны оценить значение последней цифры. Правило состоит в том, что последняя цифра, записанная в измерении, является первой цифрой с некоторой погрешностью. Например, последнее измеренное значение 36,5 мм состоит из трех цифр или трех значащих цифр.Количество значащих цифр в измерении указывает на точность измерительного инструмента. Чем точнее инструмент измерения, тем большее количество значащих цифр он может сообщить.
Рисунок 1.24 Показаны три метрические линейки. Первая линейка измеряется в дециметрах и может измерять до трех дециметров. Вторая линейка имеет длину в сантиметрах и может измерять три целых шесть десятых сантиметра. Последняя линейка в миллиметрах и может измерять тридцать шесть целых пять десятых миллиметра.
нулей
Особое внимание уделяется нулям при подсчете значащих цифр.Например, нули в 0,053 не имеют значения, потому что они всего лишь заполнители, которые определяют местонахождение десятичной точки. В 0,053 есть две значащие цифры – 5 и 3. Однако, если ноль встречается между другими значащими цифрами, нули имеют значение. Например, оба нуля в 10.053 значимы, поскольку эти нули были фактически измерены. Таким образом, заполнитель 10.053 содержит пять значащих цифр. Нули в 1300 могут иметь значение, а могут и не иметь значения, в зависимости от стиля написания чисел.Они могут означать, что число известно до последнего нуля, или нули могут быть заполнителями. Итак, 1300 может иметь две, три или четыре значащих цифры. Чтобы избежать этой двусмысленности, запишите 1300 в экспоненциальном формате как 1,3 × 10 3 . Только значащие цифры приведены в множителе x для числа в экспоненциальном представлении (в форме x × 10yx × 10y). Таким образом, мы знаем, что 1 и 3 – единственные значащие цифры в этом числе. Таким образом, нули имеют значение, за исключением случаев, когда они служат только в качестве заполнителей.В таблице 1.4 приведены примеры количества значащих цифр в различных числах.
| Номер | Значимые цифры | Обоснование |
|---|---|---|
| 1,657 | 4 | Нет нулей, и все ненулевые числа всегда значимы. |
| 0,4578 | 4 | Первый ноль – это только местозаполнитель для десятичной точки. |
| 0,000458 | 3 | Первые четыре нуля – это заполнители, необходимые для представления данных с точностью до десятитысячных. |
| 2000,56 | 6 | Три нуля здесь значимы, потому что они встречаются между другими значащими цифрами. |
| 45 600 | 3 | Без подчеркивания или научного обозначения мы предполагаем, что последние два нуля являются заполнителями и не имеют значения. |
| 15895 00 0 | 7 | Два подчеркнутых нуля значимы, а последний ноль – нет, так как он не подчеркнут. |
| 5,457 × 10 13 | 4 | В экспоненциальном представлении все числа перед знаком умножения являются значащими |
| 6.520 × × 10 –23 | 4 | В экспоненциальном представлении все числа, указанные перед знаком умножения, значимы, включая нули. |
Значимые цифры в расчетах
При объединении измерений с разной степенью точности и точности количество значащих цифр в окончательном ответе не может быть больше количества значащих цифр в наименее точном измеренном значении. Есть два разных правила: одно для умножения и деления, а другое – для сложения и вычитания, как описано ниже.
-
Для умножения и деления: Ответ должен иметь такое же количество значащих цифр, что и начальное значение с наименьшим количеством значащих цифр.Например, площадь круга можно вычислить по его радиусу, используя A = πr2A = πr2. Посмотрим, сколько значащих цифр будет у площади, если в радиусе всего две значащие цифры, например, r = 2,0 м. Тогда, используя калькулятор, который хранит восемь значащих цифр, вы получите
A = πr2 = (3,1415927 …) × (2,0 м) 2 = 4,5238934 м2. A = πr2 = (3,1415927 …) × (2,0 м) 2 = 4,5238934 м2.Но поскольку радиус состоит только из двух значащих цифр, вычисленная площадь имеет значение только до двух значащих цифр или
, даже если значение ππ имеет значение не менее восьми цифр.
-
Для сложения и вычитания : ответ должен иметь такие же числовые разряды (например, разряды десятков, разряды единиц, разряды десятков и т. Д.), Что и наименее точные начальные значения. Предположим, вы купили в продуктовом магазине 7,56 кг картофеля, измеренного по шкале с точностью 0,01 кг. Затем вы бросаете в свою лабораторию 6,052 кг картофеля, измеренного по шкале с точностью до 0,001 кг. Наконец, вы идете домой и добавляете 13,7 кг картофеля, измеренное на весах с точностью до 0.1 кг. Сколько у вас сейчас килограммов картошки и сколько значащих цифр уместно в ответе? Масса находится простым сложением и вычитанием:
7,56 кг − 6,052 кг + 13,7 кг_ 15,208 кг 7,56 кг − 6,052 кг + 13,7 кг_ 15,208 кгНаименее точное измерение – 13,7 кг. Это измерение выражается с точностью до 0,1 десятичного знака, поэтому наш окончательный ответ также должен быть выражен с точностью до 0,1. Таким образом, ответ следует округлить до десятых, получая 15,2 кг. То же верно и для недесятичных чисел.Например,
6527,23 + 2 = 6528,23 = 6528,6527,23 + 2 = 6528,23 = 6528.Мы не можем указать десятичные разряды в ответе, потому что 2 не имеет значимых десятичных знаков. Следовательно, мы можем отчитаться только до одного места.
Рекомендуется оставлять лишние значащие цифры при вычислении и округлять до правильного числа значащих цифр только в окончательных ответах. Причина в том, что небольшие ошибки из-за округления при вычислении иногда могут привести к значительным ошибкам в окончательном ответе.В качестве примера попробуйте вычислить 5,098– (5.000) × (1010) 5,098– (5.000) × (1010), чтобы получить окончательный ответ только на две значащие цифры. Удержание всего значимого во время расчета дает 48. Округление до двух значащих цифр в середине расчета изменяет его до 5 100 – (5.000) × (1000) = 100, 5 100 – (5.000) × (1000) = 100, что является способом выключенный. Точно так же вы бы избегали округления в середине вычислений при подсчете и ведении бухгалтерского учета, когда нужно аккуратно сложить и вычесть много маленьких чисел, чтобы получить, возможно, гораздо большие окончательные числа.
Значимые цифры в этом тексте
В этом учебнике предполагается, что большинство чисел состоит из трех значащих цифр. Кроме того, во всех проработанных примерах используется постоянное количество значащих цифр. Вы заметите, что ответ, данный для трех цифр, основан на вводе как минимум трех цифр. Если на входе меньше значащих цифр, в ответе также будет меньше значащих цифр. Также уделяется внимание тому, чтобы количество значащих цифр соответствовало создаваемой ситуации.В некоторых темах, таких как оптика, будет использоваться более трех значащих цифр. Наконец, если число является точным, например 2 в формуле, c = 2πrc = 2πr, оно не влияет на количество значащих цифр в вычислении.
Рабочий пример
Приближение огромных чисел: триллион долларов
Федеральный дефицит США в 2008 финансовом году был немногим больше 10 триллионов долларов. Большинство из нас не имеют представления о том, сколько на самом деле стоит даже один триллион.Предположим, вам дали триллион долларов банкнотами по 100 долларов. Если вы составили стопки по 100 купюр, как показано на рис. 1.25, и использовали их для равномерного покрытия футбольного поля (между концевыми зонами), сделайте приблизительное представление о том, насколько высокой станет стопка денег. (Здесь мы будем использовать футы / дюймы, а не метры, потому что футбольные поля измеряются в ярдах.) Один из ваших друзей говорит, что 3 дюйма, а другой говорит, что 10 футов. Как вы думаете?
Рис. 1.25. Банковская стопка содержит сто банкнот по 100 долларов и стоит 10 000 долларов.Сколько банковских стеков составляет триллион долларов? (Эндрю Мэджилл)
Стратегия
Когда вы представляете себе ситуацию, вы, вероятно, представляете себе тысячи маленьких стопок по 100 завернутых банкнот по 100 долларов, которые вы могли бы увидеть в фильмах или в банке. Поскольку это величина, которую легко оценить, давайте начнем с нее. Мы можем найти объем стопки из 100 купюр, узнать, сколько стопок составляют один триллион долларов, а затем установить этот объем равным площади футбольного поля, умноженной на неизвестную высоту.
Решение
- Рассчитайте объем стопки из 100 купюр. Размеры одной банкноты составляют примерно 3 на 6 дюймов. Пачка из 100 штук имеет толщину примерно 0,5 дюйма. Таким образом, общий объем стопки из 100 купюр равен объем стопки = длина × ширина × высота, объем стопки = 6 дюймов × 3 дюйма × 0,5 дюйма, объем стопки = 9 дюймов. 3. объем стопки = длина × ширина × высота, объем стопки = 6 дюйма × 3 дюйма × 0,5 дюйма, объем стопки = 9 дюймов 3.
-
Подсчитайте количество стопок.Обратите внимание, что триллион долларов равен 1 × 1012 $ 1 × 1012, а стопка из ста 100-долларовых банкнот равна 10000, 10000 долларов или 1 × 104 доллара 1 × 104. Количество стопок у вас будет
. 1,3 $ 1 × 1012 (триллион долларов) / 1 × 104 доллара на стек = 1 × 108 стеков. 1 доллар × 1012 (триллион долларов) / 1 × 104 доллара на стек = 1 × 108 стеков. -
Вычислите площадь футбольного поля в квадратных дюймах. Площадь футбольного поля составляет 100 ярдов × 50 ярдов 100 ярдов × 50 ярдов, что дает 5 000 ярдов 25 000 ярдов2.Поскольку мы работаем в дюймах, нам нужно преобразовать квадратные ярды в квадратные дюймы
. Площадь = 5000 ярдов2 × 3 фут1 ярд × 3 фут1 ярд × 12 дюймов 1 фут × 12 дюймов 1 фут = 6 480 000 дюймов 2, Площадь ≈6 × 106 дюймов 2 Площадь = 5000 ярдов2 × 3 фут1 ярд × 3 фут1 ярд × 12 дюймов 0,1 фут × 12 дюймов 1 фут = 6 480000 дюймов 2, Площадь ≈6 × 106 дюймов 2.Это преобразование дает нам 6 × 106 дюймов 26 × 106 дюймов 2 для площади поля. (Обратите внимание, что в этих расчетах мы используем только одну значащую цифру.)
- Рассчитайте общий объем купюр.Объем всех стопок по 100 долларов составляет 9 дюймов 3 / стопка × 108 стопок = 9 × 108 дюймов 39 дюймов / стопка × 108 стопок = 9 × 108 дюймов 3
- Рассчитайте высоту. Чтобы определить высоту купюр, используйте следующее уравнение
объем купюр = площадь поля × высота денег Высота денег = объем купюр Площадь поля Высота денег = 9 × 108 дюймов 36 × 106 дюймов 2 = 1,33 × 102 дюймов Высота денег = 1 × 102 дюйма = 100 дюймы объем купюр = площадь поля × высота денег Высота денег = объем купюр площадь поля Высота денег = 9 × 108 дюймов36 × 106 дюймов 2 = 1,33 × 102 дюйма Высота монеты = 1 × 102 дюйма = 100 дюймов
Высота денег будет около 100 дюймов. Преобразование этого значения в футы дает
. 100 дюймов × 1 фут 12 дюймов = 8,33 футов ≈ 8 футов 100 дюймов × 1 фут 12 дюймов = 8,33 футов ≈ 8 футов
Обсуждение
Окончательное приблизительное значение намного выше, чем ранняя оценка в 3 дюйма, но другая ранняя оценка в 10 футов (120 дюймов) была примерно правильной. Как это приближение соответствует вашему первому предположению? Что это упражнение может сказать вам с точки зрения приблизительных оценок, и тщательно рассчитанных приближений?
В приведенном выше примере окончательное приблизительное значение намного выше, чем ранняя оценка первого друга в 3 дюйма.Однако ранняя оценка другого друга в 10 футов (120 дюймов) была примерно верной. Как это приближение соответствует вашему первому предположению? Что это упражнение может предложить о значении приблизительных оценок по сравнению с тщательно рассчитанными приближениями?
Что ваш ребенок узнает в восьмом классе – HCPSS
Введение
«Что будет изучать ваш ребенок» – это обзор целей и ожиданий учащихся на протяжении восьмого учебного года. Конкретные студенческие программы могут отличаться в зависимости от учебных потребностей.
Направления обучения:
Искусство английского языка
Классы по английскому языку обеспечивают обучение на основе строгих требований Common Core College и стандартов готовности к карьере, которые отражены в блоках HCPSS, посвященных анализу жанра и темы. Примерные единицы для 8-го класса включают:
- Любовь и дружба.
- Свобода.
- Изучение неизвестного.
Стандарты привязки к колледжу и профессиональной подготовке (Common Core) для изучения английского языка
Стандарты охватывают четыре основные категории с подтемами, как указано ниже.Конкретные описания каждой подтемы можно найти на сайте www.corestandards.org/ELA-Literacy.
Стандарты якоря для чтения (художественный и информационный текст)
Учащиеся будут развиваться в своей способности понимать сложный текст, делать выводы и устанавливать связи между текстами.
- Ключевые идеи и детали.
- Ремесло и конструкция.
- Интеграция знаний и идей.
- Диапазон чтения и уровень сложности текста.
Стандарты привязки для письма
Учащиеся будут писать разными способами в соответствии с данными, полученными при их чтении и исследованиях.
- Типы и назначение текстов (аргумент, пояснение, повествование).
- Изготовление и распространение письменности.
- Исследования для создания и представления знаний.
- Диапазон письма.
Как помочь ребенку писать
Стандарты якоря для разговора и аудирования
Учащиеся будут развиваться в своей способности общаться в формальных и неформальных ситуациях, одновременно развивая навыки межличностного общения, необходимые для эффективного сотрудничества.
- Понимание и сотрудничество.
- Презентация знаний и идей.
Стандарты привязки для языка
Студенты будут правильно и эффективно использовать язык и расширять свои знания по предметной и общей академической лексике.
- Условные обозначения стандартного английского языка.
- Знание языка.
- Пополнение и использование словарного запаса.
Запись
Студенты выполняют задания в различных режимах, например:
- Пояснительная, включая анализ как печатных, так и непечатных текстов.
- Аргумент с использованием доказательств в поддержку иска.
- Повествование.
Все студенты, изучающие английский язык, поддерживают письменные портфолио, чтобы оценить и повысить свой писательский рост.
Семинар по чтению
Учащиеся, которым требуется помощь в расшифровке или понимании, записываются в классы семинара по чтению. Дифференцированное обучение проводится в небольшой группе. Эти классы предоставляются школам в зависимости от потребностей учащихся.Для каждого класса предлагаются семинары по чтению.
Семинар по искусству английского языка
Студенты имеют возможность изучать и применять стратегии чтения, письма и овладения языком, которые напрямую связаны с результатами обучения в English Language Arts 8. Преподаватель English Language Arts Seminar проводит инструктаж в небольших группах, чтобы учащиеся могли продемонстрировать и применить свои знания языковые навыки и концепции и успешно прошли курс изучения английского языка.
Одаренные и талантливые
Учащиеся отвечают требованиям учебной программы по английскому языку 8, а также приобретают особые навыки критического чтения, письма и мышления, необходимые для продолжения успешной учебы в старшей школе. Кроме того, сжатие учебной программы позволяет мотивированным учащимся свернуть материал и извлечь пользу из более удобной для учащихся аудитории. Учитель предоставляет учащимся возможность ответить на задания, аналогичные тем, что были на экзамене College Board по английскому языку и сочинению на продвинутом уровне.
Как помочь своему ребенку с языковыми искусствами
К началу ↑
Программа инноваций и запросов
Программа исследований и инноваций предоставляет учащимся межучебные возможности для взаимодействия с интересными, актуальными, заслуживающими доверия и разнообразными ресурсами, поскольку они разъясняют свое собственное мышление с учетом фактов, мнений, достоверности и актуальности источников при установлении реальных связей. Учащиеся взаимодействуют с различными СМИ и задают зондирующие и вдумчивые вопросы.Студенческое любопытство – это путь к рассмотрению возможностей, побуждающий студентов увидеть причину для проведения исследования и создания продукта. Создавая связь с реальным миром, студенты изучают и практикуют навыки, собирают и представляют информацию, а также решают проблемы. В течение каждого девятинедельного курса студенты углубляют понимание темы в каждом конкретном блоке.
Еда будущего
Студенты рассказывают о том, как правительственные директивы по питанию, а также региональные и культурные факторы влияют на выбор продуктов питания.
Кафе писателя
Учащиеся развивают понимание того, как творческое самовыражение, особенно мемуары и стихи, дает писателям возможность понять себя и отреагировать на окружающий мир.
Максимально эффективное обучение в средней школе и за ее пределами
Учащиеся обращаются к личным сильным сторонам, талантам и ценностям и изучают связи между учебными программами средней школы и карьерными соображениями и путями.
Развивайте мозг
Учащиеся развивают понимание связи между развитием мозга и поведением подростков и принятием решений.
Гражданин в действии
Студенты считают, что навыки, необходимые для того, чтобы быть активными, информированными гражданами, которые ценят разнообразие и способствуют культурному взаимопониманию.
К началу ↑
Математика
Стандарты математической практики
«Стандарты математической практики» описывают различные виды знаний, которые преподаватели математики на всех уровнях будут стремиться развить у своих учеников.
- Разбирайтесь в проблемах и настойчиво их решайте.
- Размышляйте абстрактно и количественно.
- Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
- Модель с математикой.
- Стратегически используйте соответствующие инструменты.
- Четко и точно сообщайте математические проблемы и решения, используя соответствующие символы, определения и степени точности.
- Ищите и используйте структуру.
- Ищите и выражайте закономерность в повторяющихся рассуждениях.
Стандарты математического содержания
Приведенные ниже стандарты содержания математики (основной учебный план) разработаны для обеспечения сбалансированного сочетания процедуры и понимания.Ожидания, начинающиеся со слова «понять», часто являются особенно хорошей возможностью связать математические методы с содержанием. Стандарты содержания, которые устанавливают ожидание понимания, являются потенциальными точками пересечения между Стандартами математического содержания и математическими практиками.
Блок 1: Система счисления и экспоненты
Знайте, что есть числа, которые не являются рациональными, и округлите их рациональными числами.
- Знайте, что есть числа, которые не являются рациональными, и округлите их рациональными числами.
- Знайте, что нерациональные числа называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показывают, что десятичное расширение в конечном итоге повторяется, и преобразует десятичное расширение, которое в конечном итоге повторяется в рациональное число.
- Используйте рациональные приближения иррациональных чисел, чтобы сравнить размер иррациональных чисел, расположить их приблизительно на числовой линейной диаграмме и оценить значение выражений (например,3 = p , где p – положительное рациональное число. Вычислите квадратные корни из маленьких полных квадратов и кубические корни из маленьких идеальных кубов. Знайте, что √2 иррационально.
- Используйте числа, выраженные в виде одной цифры, умноженной на целую степень 10, чтобы оценить очень большие или очень маленькие количества и выразить, во сколько раз одно больше другого.
- Выполнять операции с числами, выраженными в экспоненциальном представлении, включая задачи, в которых используются как десятичные, так и экспоненциальные представления.Используйте научную нотацию и выбирайте единицы подходящего размера для измерений очень больших или очень малых количеств (например, используйте миллиметры в год для растекания по морскому дну). Интерпретируйте научные обозначения, созданные с помощью технологий.
Блок 2: Геометрия
Понять и применить теорему Пифагора.
- Объясните доказательство теоремы Пифагора и ее обращения.
- Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальных и математических задачах в двух и трех измерениях.
- Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.
Поймите соответствие и сходство с помощью физических моделей, прозрачных пленок или программного обеспечения для работы с геометрией.
- Проверить экспериментально свойства вращения, отражения и перемещения:
- Линии превращаются в линии, а сегменты линий – в сегменты одинаковой длины.
- Углы отсчитываются до углов той же меры.
- Параллельные прямые заменяются параллельными.
- Поймите, что двухмерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью вращений, отражений и перемещений; учитывая две совпадающие фигуры, опишите последовательность, демонстрирующую соответствие между ними.
- Опишите эффект расширения, сдвига, поворота и отражения на двумерные фигуры, используя координаты.
- Поймите, что двухмерная фигура похожа на другую, если вторая может быть получена из первой последовательностью вращений, отражений, перемещений и растяжений; для двух одинаковых двумерных фигур опишите последовательность, демонстрирующую сходство между ними.
- Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образованных, когда параллельные прямые пересекаются трансверсалью, и о критерии подобия треугольников угол-угол.
Раздел 3: Анализ функций и уравнений
Определение, оценка и сравнение функций.
- Поймите, что функция – это правило, которое назначает каждому входу ровно один выход. График функции – это набор упорядоченных пар, состоящих из входа и соответствующего выхода.
- Сравните свойства двух функций, каждая из которых представлена по-разному (алгебраически, графически, численно в таблицах или словесных описаниях).
Поймите связь между пропорциональными отношениями, линиями и линейными уравнениями.
- График пропорциональных отношений, интерпретируя единицу расхода как наклон графика. Сравните два разных пропорциональных отношения, представленных по-разному. Примечание: опирайтесь на понимание учащимися константы пропорциональности, чтобы лучше понять наклон.
- Используйте похожие треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя разными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для линии, проходящей через начало координат, и уравнение y = mx + b для линии, пересекающей вертикальную ось в точке b .
Определение, оценка и сравнение функций.
- Интерпретируйте уравнение y = mx + b как определяющее линейную функцию, график которой представляет собой прямую линию; приведите примеры функций, которые не являются линейными.
Используйте функции для моделирования отношений между количествами.
- Создайте функцию для моделирования линейной зависимости между двумя величинами. Определите скорость изменения и начальное значение функции из описания взаимосвязи или из двух значений (x, y) , включая считывание их из таблицы или графика. Интерпретируйте скорость изменения и начальное значение линейной функции в терминах моделируемой ситуации, а также в терминах ее графика или таблицы значений. Примечание: просмотрите концепции независимых и зависимых переменных.
- Опишите качественно функциональную взаимосвязь между двумя величинами, анализируя график (например, где функция увеличивается или уменьшается, линейная или нелинейная). Нарисуйте график, демонстрирующий качественные характеристики функции, которая была описана устно.
Анализируйте и решайте линейные уравнения и пары одновременных линейных уравнений.
- Решите линейные уравнения с одной переменной.
- Приведите примеры линейных уравнений с одной переменной с одним решением, бесконечным множеством решений или без решений. Покажите, какая из этих возможностей имеет место, путем последовательного преобразования данного уравнения в более простые формы, пока не получится эквивалентное уравнение в форме x = a , a = a или a = b (где a и b – разные номера).
- Решайте линейные уравнения с рациональными числовыми коэффициентами, включая уравнения, решения которых требуют расширения выражений с использованием свойства распределения и сбора похожих членов.
- Анализируйте и решайте пары одновременных линейных уравнений.
- Поймите, что решения системы двух линейных уравнений с двумя переменными соответствуют точкам пересечения их графиков, потому что точки пересечения удовлетворяют обоим уравнениям одновременно.
- Решите системы двух линейных уравнений с двумя переменными алгебраически и оцените решения, построив уравнения. Решайте простые случаи путем осмотра.
- Решайте реальные и математические задачи, приводящие к двум линейным уравнениям с двумя переменными.
Раздел 4: Модели ассоциации
Изучите закономерности ассоциации в двумерных данных.
- Постройте и интерпретируйте графики рассеяния для данных двумерных измерений, чтобы исследовать закономерности связи между двумя величинами. Опишите шаблоны, такие как кластеризация, выбросы, положительная или отрицательная ассоциация, линейная ассоциация и нелинейная ассоциация.
- Знайте, что прямые линии широко используются для моделирования отношений между двумя количественными переменными.Для диаграмм рассеяния, которые предполагают линейную связь, неформально установите прямую линию и неформально оцените соответствие модели, судя о близости точек данных к линии.
- Используйте уравнение линейной модели для решения проблем в контексте данных двумерных измерений, интерпретируя наклон и точку пересечения.
- Поймите, что закономерности ассоциации также можно увидеть в двумерных категориальных данных, отображая частоты и относительные частоты в двусторонней таблице.Постройте и интерпретируйте двустороннюю таблицу, суммирующую данные по двум категориальным переменным, собранным от одних и тех же субъектов. Используйте относительные частоты, рассчитанные для строк или столбцов, чтобы описать возможную связь между двумя переменными.
Блок 5: Объемы твердых фигур
Решение реальных и математических задач, связанных с объемом цилиндров, конусов и сфер.
- Знать формулы объемов конусов, цилиндров и сфер и использовать их для решения реальных задач.
Выше класса и одаренные / талантливые восьмиклассники
Студенты, обучающиеся по математике высшего уровня, будут обучаться по учебной программе, изложенной в Алгебре I. Студенты, обучающиеся по математике G / T, будут обучаться по учебной программе, изложенной для Геометрии GT. Для получения дополнительной информации об учебной программе этих курсов посетите http://hcpssfamilymath.weebly.com.
Как помочь ребенку с математикой
К началу ↑
Наука
Введение
Научная программа системы государственных школ округа Ховард направлена на поддержку всех учащихся в развитии научной грамотности.Как описано в «Основах естественнонаучного образования для школьников до 12 лет», научная грамотность означает, что учащиеся понимают природу науки и обладают достаточными знаниями и навыками в практической деятельности в области науки и техники, чтобы они могли участвовать в публичных обсуждениях научных и технологических вопросов, будьте осторожны потребители научно-технической информации, относящейся к их повседневной жизни, продолжают изучать науку вне школы и делают карьеру по своему выбору, включая карьеру в области науки, техники и технологий.В средней школе учащиеся развивают научную грамотность, работая в качестве учащихся-ученых. В восьмом классе учащиеся используют научные методы для исследования и понимания физических и химических систем, включая материю и ее взаимодействия, силы и их взаимодействия, энергию и ее передачу, а также волны и их применение в технологиях передачи информации. Опыт обучения экологической грамотности, который включает в себя образовательный опыт осмысленного водораздела, вплетен в учебную программу средней школы по естествознанию.
Практика науки и техники
В средней школе учащиеся естественнонаучных дисциплин будут развивать свои навыки практического применения естественных наук. Каждый год студенты будут применять эти навыки в лабораторных и полевых исследованиях. Эти методы, описанные в «Основах естественнонаучного образования для K – 12», включают:
- Задайте научные вопросы, которые можно проверить эмпирически
- Использование и построение моделей, таких как диаграммы, чертежи, математические взаимосвязи, аналогии, компьютерное моделирование и физические копии, для представления идей и объяснений
- Планировать и проводить научные исследования в полевых условиях или в лаборатории
- Анализируйте и интерпретируйте данные с помощью различных инструментов
- Представление физических переменных и их взаимосвязей с использованием основных инструментов математики и вычислений
- Составьте пояснительные отчеты о мире, используя доказательства
- Рассуждения и аргументы, основанные на доказательствах, для определения лучшего объяснения природного явления или лучшего решения проектной проблемы
- Получать, оценивать и передавать информацию ясно и точно
Содержание курса
Учебная программа 8-го класса состоит из трех больших вопросов, которые обеспечивают контекст и мотивацию к обучению.Вот эти вопросы:
- Как ученые работают вместе, чтобы разработать и построить автомобили, отвечающие определенным критериям?
- Как ученые используют энергию и изменения в энергии для разработки решений проблем?
- Как ученые работают вместе, чтобы понять и улучшить качество воздуха?
В поисках ответов на эти вопросы учащиеся участвуют в тщательно упорядоченных, соответствующих с точки зрения развития процессах обучения, которые поддерживают глубокое понимание.К концу восьмого класса учащиеся будут в состоянии соответствовать ожиданиям по физическим наукам, установленным в соответствии с требованиями стандартов Мэриленда в средней школе.
Программа для одаренных и талантливых ученых
По программе G / T science в восьмом классе учащиеся более глубоко и независимо исследуют содержание и практику науки, решая дополнительные задачи обучения и завершая углубленные исследования с использованием творческих методов решения проблем.Исследование включено в учебный план и проводится в течение длительного периода времени, чтобы обеспечить сбор и анализ достоверных данных.
Как помочь своему ребенку с наукой
К началу ↑
Общественные науки
Обзор
Это первая часть двухлетней программы по истории США. Эта программа дает студентам возможность развить понимание исторических навыков, концепций и содержания, связанных с историей нашей нации.Этот курс также предоставляет ценную справочную информацию для подготовки учеников 10-го класса к американскому правительству. Ежеквартально проводятся местные аттестации на уровне округа.
Навыки социальных исследований
Эти и другие навыки включены в учебную программу:
- Чтение, построение и интерпретация карт.
- Пространственный анализ и интерпретация.
- Навыки исторического мышления.
- Решение проблем / критическое мышление
- Роли, права и обязанности гражданства.
- Стратегическое чтение текста обществознания.
- Принятие экономических решений.
- Составление пояснений и аргументов.
- Информационная грамотность
- Анализ и оценка первичных и вторичных источников.
- Анализ и интерпретация данных.
Содержание курса
В восьмом классе обществознания четыре отделения. Ниже приводится краткое изложение некоторых ключевых целей.
Часть I: Исторический процесс и путь к независимости
- Определите и найдите первоначальные тринадцать британских колоний.
- Объясните, как география этих регионов привела к политическим, экономическим и культурным различиям.
- Дайте определение меркантилизму и объясните его влияние на американские колонии.
- Объясните рост рабского труда в британских колониях.
- Приведите примеры, как события в Европе ускорили борьбу за империю в Северной Америке.
- Объясните, как война между французами и индейцами и Парижский договор 1763 года заложили основу американской революции.
- Изучите британскую экономическую и политическую политику 18-го века по отношению к американским колониям и реакцию Америки на эту политику, чтобы объяснить причины независимости Америки.
- Обобщите содержание Декларации независимости.
- Рассмотрите Декларацию независимости как обоснование революции и утверждение американских принципов правления.
Часть II: Создание новой нации
- Оцените готовность американцев и британцев накануне американской революции.
- Опишите роли ключевых политических и военных лидеров во время войны за независимость.
- Проанализируйте взгляды, жизни и вклад простых американцев во время войны за независимость.
- Объясните ключевые события американской войны за независимость.
- Опишите роль географии и экономики в победе Америки.
- Определите результаты и подчеркните важность Парижского договора.
- Определите сильные и слабые стороны Статей Конфедерации.
- Определите причины начальных экспериментов с конфедеративной формой правления.
- Определите и объясните несколько ключевых компромиссов, которые были достигнуты при разработке Конституции.
- Кратко изложите содержание и структуру Конституции, включая преамбулу, статьи и Билль о правах.
- Объясните принципы управления, закрепленные в Конституции.
- Проанализируйте аргументы федералистов и антифедералистов за и против ратификации Конституции.
- Сопоставьте основные различия между строгим и вольным толкованием Конституции.
- Проанализировать современные проблемы, демонстрирующие эволюционный характер Конституции.
Часть III: Рост нации
- Определите и опишите трудности и основные достижения администраций Джорджа Вашингтона и Джона Адамса.
- Объясните, как продолжающийся конфликт между Великобританией и Францией повлиял на внутреннюю и внешнюю политику Соединенных Штатов.
- Сравните политические и экономические различия между федералистами и республиканцами-демократами.
- Проследите корни аннулирования на примерах резолюций Кентукки и Вирджинии.
- Оцените, как Марбери против Мэдисона усилил роль судебной системы.
- Объясните шаги, предпринятые администрацией Джефферсона и Конгрессом для сохранения американского нейтралитета, и оцените успех этих действий.
- Проанализируйте взгляды, жизни и вклад простых американцев во время второй войны за американскую независимость.
- Объясните факторы, которые привели к появлению Доктрины Монро, и проанализируйте влияние Доктрины Монро на внешнюю политику Соединенных Штатов.
- Оцените факторы, способствовавшие росту секционализма в начале 19 века.
- Опишите изменения в американской политической системе во время джексоновской эры.
- Оцените влияние политики Джексона на коренных американцев.
Часть IV: Союз в разъединении
- Сравните региональные различия между Севером и Югом.
- Объясните взаимосвязь между расширением на запад и углублением конфликта между Севером и Югом.
- Проанализируйте опыт свободных и порабощенных афроамериканцев в Соединенных Штатах с начала до середины 1800-х годов.
- Изучите причины, использовавшиеся для противодействия или поддержки рабства в Америке с начала до середины 19 века.
- Опишите различные усилия по реформированию американского общества.
- Определите и опишите события, которые усилили враждебность отдельных групп.Оцените роль Верховного суда в отношении института рабства в Америке с начала до середины 1800-х годов.
- Объясните, как результаты выборов 1860 года вызвали отделение южных штатов.
- Проанализируйте взгляды, жизни и вклад простых американцев во время Гражданской войны в США.
- Объясните и опишите значение ключевых событий Гражданской войны в США.
- Опишите роль географии и экономики в победе Союза.
- Сравните цели и политику различных планов реконструкции.
- Объясните, как 13-я, 14-я и 15-я поправки расширили гражданские права афроамериканцев за счет отмены смертной казни, предоставления гражданства и права голоса.
- Опишите законные и незаконные действия, использованные для отказа афроамериканцам в гражданских правах после Гражданской войны.
- Объясните, почему выборы 1876 г. ознаменовали конец эпохи реконструкции.
- Оцените успех Реконструкции.
Одаренные и талантливые
учащихся G / T завершают «Исследования G / T Research» в течение школьных лет.Эти исследования основаны на содержании конкретных разделов и могут принимать форму разработанных учителем исторических или географических исследований, заданий по оценке результатов, разработанных округом, или утвержденных округом вопросов на основе документов. По желанию студенты могут принять участие в программе Национального дня истории.
Специальные программы
Управление средних социальных исследований поддерживает несколько специальных программ, доступных для учащихся средних школ. Конкурс «День истории» – это соревнование на местном, государственном и национальном уровнях, которое способствует изучению истории, знаниям и пониманию среди учащихся средних школ.День истории поощряет развитие исследовательских навыков, анализ и интерпретацию первичных и вторичных исходных материалов, а также возможность для творческого самовыражения. Ежегодно HCPSS спонсирует крупный региональный конкурс, в котором принимают участие до 300 студентов из наших государственных и частных школ. Эта программа обычно входит в состав учебной программы, но зависит от школьных интересов. Конкурс «Черная сага» – это соревнование в масштабе штата, которое ставит под сомнение знания учащихся об опыте афроамериканцев.Средние и начальные школы со всего штата соревнуются за призы и награды. Это мероприятие очень зависит от интереса школы и поддержки общества, так как это внеклассная программа.
Как помочь своему ребенку в изучении социальных наук
К началу ↑
Изобразительное искусство
Применяйте различные стратегии, концепции и средства массовой информации к:
- Создавайте и развивайте идеи для личного самовыражения в производстве произведений искусства.
- Экспериментируйте с различными инструментами, материалами, процессами, методами и идеями, чтобы систематизировать знания в производстве произведений искусства.
- Давать и получать обратную связь / конструктивную критику и настойчиво совершенствовать личные решения для художественных работ.
- Анализируйте и защищайте личный выбор и выбор предметов или произведений искусства для презентации или выставки.
- Изучите, как и почему люди собирают, представляют и сохраняют предметы и идеи, которые имеют личное, культурное или историческое значение.
- Воспринимать, интерпретировать и реагировать на идеи, опыт и окружающую среду с помощью изобразительного искусства.
- Анализировать и интерпретировать влияния, намерения и значения произведений искусства.
- Оценить произведение искусства на основе выбранных критериев.
- Соедините личный опыт и знания с созданием искусства.
- Понимать искусство как важный аспект истории и человеческого опыта.
При выходе из средней школы учащиеся смогут:
- Применяйте различные средства массовой информации, стратегии и концепции для генерации инновационных идей для решения художественных задач.
- Поддерживайте коллекцию идей, демонстрирующих личную заинтересованность и рост.
- Осознавать и применять сложную природу, силу и историю искусства, чтобы общаться с другими, рассказывать истории, записывать увиденное, связывать личные идеи или делать видимым то, что вы вообразили.
- Быть комфортным и применять различные стратегии, когда нет четкого пути или решения проблемы.
- Работайте в рамках заданных ограничений для решения сложных художественных задач.
- Создавайте лично значимые решения.
- Настойчиво решайте проблемы, оценивая незавершенную работу, чтобы определять области, нуждающиеся в улучшении, и альтернативные решения.
- Сотрудничайте с коллегами для достижения консенсуса и решений.
Как помочь своему ребенку с помощью изобразительных искусств
К началу ↑
Науки о семье и потребителей
Продовольствие и питание
- Обсудите краткосрочные и долгосрочные преимущества и риски, связанные с выбором питания.
- Создать рекомендации по выбору более здорового питания в ресторанах быстрого питания и быстрого питания.
- Проанализировать записи о его / ее диете, чтобы оценить выбор продуктов и возможные последствия для здоровья.
- Изучить, как особенности географических и культурных регионов, включая климат, социальные системы, религиозные обычаи и физическую географию, влияют на выбор продуктов питания, пищевые обычаи и основные продукты питания.
- Приготовьте и подайте традиционные блюда из различных культурных / этнических регионов, демонстрируя знание мировых кухонь и пищевых обычаев.
- Применять знания в области питания и навыки в приготовлении пищи, управлении кухней, безопасности и санитарии при приготовлении здоровых и привлекательных блюд и закусок.
- Опишите и продемонстрируйте термины и приемы рецепта, относящиеся к нарезке, смешиванию и приготовлению ингредиентов.
- Измените рецепты для достижения результатов в области питания, включая снижение содержания жиров, сахара и натрия и увеличение количества клетчатки, кальция и питательных веществ.
- Изучите возможности карьерного роста, уделяя особое внимание тем, кто работает в сфере общественного питания и гостеприимства.
Финансовая грамотность
- Применяйте аргументы финансовой грамотности для принятия информированных и ответственных с финансовой точки зрения решений.
- Свяжите выбор в отношении своего образования и карьерного роста с потенциалом заработка.
- Развивайте навыки эффективного планирования и управления деньгами путем определения финансовых целей и разработки планов расходов.
- Развивайте навыки для принятия обоснованных решений о взыскании долгов и поддержании кредитоспособности.
- Развивайте навыки планирования и достижения долгосрочных целей, связанных со сбережениями и инвестированием, с целью создания финансовой безопасности и богатства.
- Развивайте навыки финансового планирования, чтобы минимизировать финансовые неудачи.
Как помочь своему ребенку в вопросах семьи и потребительских наук
К началу ↑
Одаренные и талантливые
Программа G / T предоставляет ряд услуг в дополнение к классам G / T. Преподаватели G / T в средней школе инструктируют учащихся, которые участвуют в учебных семинарах G / T и исследованиях, развитии талантов и возможностях исследований, доступных для всех заинтересованных учащихся.
Санитарное просвещение
Национальные стандарты санитарного просвещения
Эти навыки включены в учебную программу:
- Студенты будут понимать концепции, связанные с укреплением здоровья.
- Студенты проанализируют влияние семьи, сверстников, культуры, средств массовой информации, технологий и других факторов на поведение в отношении здоровья.
- Студенты продемонстрируют способность получать доступ к достоверной информации, а также к продуктам и услугам для улучшения здоровья.
- Студенты продемонстрируют способность использовать навыки межличностного общения для улучшения здоровья и предотвращения или снижения рисков для здоровья.
- Студенты продемонстрируют способность использовать навыки принятия решений для улучшения здоровья.
- Учащиеся продемонстрируют способность практиковать укрепляющее здоровье поведение и избегать или снижать риски для здоровья.
- Студенты продемонстрируют способность защищать личное, семейное и общественное здоровье.
Безопасность, первая помощь и предотвращение травм
- Обобщите и оцените стратегии предотвращения и вмешательства в проблемы безопасности.
- Обобщите стратегии предотвращения и вмешательства в жестокое обращение с детьми.
- Опишите составляющие здоровых отношений.
- Используйте навыки разрешения конфликтов для предотвращения насилия.
Социальное и эмоциональное здоровье
- Изучите источники стресса и беспокойства.
- Изучите эффекты стресса, включая депрессию и самоубийство.
- Изучите стратегии совладания и вмешательства при стрессе, депрессии и самоубийстве.
- Используйте навыки разрешения конфликтов для предотвращения насилия.
Сексуальное здоровье
- Опишите компоненты сексуальности, включая биологические, психологические, культурные и этические.
- Обзор анатомии и физиологии мужской и женской репродуктивной системы.
- Опишите профилактику, симптомы и лечение ИППП, включая ВИЧ / СПИД.
- Опишите различные противозачаточные средства и их эффективность в снижении риска беременности.
- Определите источники поддержки сексуального здоровья.
- Определите модели поведения, поддерживающие сексуальное здоровье.
Табак, алкоголь и другие наркотики
- Различайте здоровое и нездоровое употребление рецептурных и безрецептурных лекарств.
- Проанализировать физические, психологические, социальные, экономические и правовые последствия злоупотребления наркотиками.
- Продемонстрировать навыки, способствующие личному стремлению оставаться свободным от наркотиков.
Как помочь своему ребенку с санитарным просвещением
К началу ↑
Учебные технологии
Учебная технология в 8-м классе соответствует стандартам ISTE 2016 для учащихся. Эти стандарты подчеркивают навыки и качества, которые государственные школы округа Ховард ценят для всех учащихся, что позволяет им участвовать и преуспевать в объединенном цифровом мире.Стандарты ISTE нацелены на преобразование обучения с использованием технологий на протяжении всей академической карьеры студента путем развития этих навыков. Учителя округа Ховард по всем направлениям учебной программы работают, чтобы умело наставлять и вдохновлять учащихся расширять обучение с помощью технологий и побуждать их быть проводниками собственного обучения.
Усиленный ученик
- Студенты используют технологии, чтобы ставить цели, работать над их достижением и демонстрировать свои знания. Например, студенты будут
- ставить личные цели обучения и разрабатывать стратегии с использованием технологий для их достижения.
- создает сети и учебную среду таким образом, чтобы поддерживать обучение.
- используют технологии, чтобы продемонстрировать свое обучение различными способами.
- понимают концепции технологических операций, могут выбирать и использовать текущие технологии, а также передавать свои знания новым технологиям.
Цифровой гражданин
- Студенты понимают права, обязанности и возможности жить, учиться и работать во взаимосвязанном цифровом мире.Например, студенты будут
- управляют своей цифровой идентичностью и репутацией и осознают постоянство своих действий в цифровом мире.
- должны вести себя позитивно, безопасно, законно и этично при использовании технологий.
- уважает права на использование и передачу интеллектуальной собственности.
- управляют своими личными данными, чтобы поддерживать цифровую конфиденциальность и безопасность.
Конструктор знаний
- Студент критически выбирает, оценивает и синтезирует цифровые ресурсы в коллекцию, которая отражает мои знания и расширяет мои знания.Например, студенты будут
- использовать эффективные исследовательские стратегии для поиска информации и других ресурсов.
- оценивает точность, перспективу, достоверность и актуальность информации, средств массовой информации, данных или других ресурсов.
- собрать информацию с цифровых ресурсов, чтобы сделать выводы
- накапливает знания, исследуя реальные проблемы и проблемы.
Инновационный конструктор
- Студенты решают задачи, создавая новые творческие решения, используя различные цифровые инструменты.Например, студенты будут
- использовать преднамеренный процесс проектирования для генерации идей и решения подлинных проблем.
- использует цифровые инструменты для планирования и управления процессом проектирования.
- разрабатывает, тестирует и дорабатывает прототипы.
- демонстрируют способность работать с открытыми проблемами.
Вычислительный мыслитель
- Студенты выявляют подлинные проблемы, работают с данными и используют пошаговый процесс для автоматизации решений.Например, студенты будут
- формулировать определения проблемы, подходящие для методов с технологической поддержкой
- собирать данные, использовать цифровые инструменты для анализа и представления данных различными способами
- разбивает проблемы на составные части, извлекает ключевую информацию и разрабатывает модели для облегчения решения проблем.
- использует алгоритмическое мышление для разработки последовательности шагов для создания и тестирования автоматизированных решений.
Creative Communicator
- Студенты эффективно общаются и творчески выражают свои мысли, используя различные инструменты, стили, форматы и цифровые носители.Например, студенты будут
- выбрать подходящие инструменты для достижения желаемых целей
- создавать оригинальные работы или ответственно перепрофилировать или преобразовывать цифровые ресурсы в новые творения.
- общаться четко и эффективно, используя различные цифровые объекты
- публикуют или представляют контент, соответствующий их целевой аудитории.
Глобальный сотрудник
- Студенты стремятся расширить кругозор, понять других и эффективно работать в командах, используя цифровые инструменты.Например, студенты будут
- использовать цифровые инструменты для связи с учащимися из разных слоев общества и культур, чтобы расширить взаимопонимание и обучение.
- использует технологии совместной работы для работы с другими.
- вносят свой вклад в проектные команды, выполняя различные роли для достижения общей цели.
- исследует локальные и глобальные проблемы и использует технологии совместной работы для поиска решений.
Как помочь своему ребенку с помощью обучающих технологий
К началу ↑
Процесс запроса
- Определите информационные потребности.
- Создавайте, уточняйте и используйте критерии для руководства исследовательским процессом.
- Следуйте систематическим шагам по решению проблем, используя процесс Big6.
Найдите и оцените ресурсы и источники
- Выявление и использование самых разных ресурсов.
- Используйте каталог медиацентра библиотеки, чтобы найти источники для удовлетворения информационных потребностей.
- Оцените потенциальные источники информации.
- Используйте текстовые функции для выбора подходящих источников.
- Определите и соблюдайте Политику округа 8080: Ответственное использование технологий и социальных сетей.
- Научитесь применять безопасные методы в Интернете.
Поиск, создание, запись и систематизация данных / информации
- Используйте ключевые слова для поиска ответов на вопросы.
- Используйте эффективные стратегии поиска для сбора релевантной информации из источников.
- Используйте технологические инструменты для поиска, записи и систематизации данных / информации в источниках.
- Различайте факты и мнения.
- Избегайте плагиата, правильно записывая соответствующую информацию и отслеживая использованные источники.
- Используйте различные форматы для записи и организации данных / информации.
- Создайте список источников, используя принятый стиль цитирования.
- Сопоставьте соответствующий формат с содержанием, которое необходимо организовать.
Интерпретировать записанные данные / информацию
- Определите основные идеи записанной информации.
- Применяйте критическое мышление и стратегии решения проблем.
- Создать новое понимание и знания, связанные с потребностями в информации.
Поделиться Результаты / выводы
- Используйте различные форматы для обмена полученной информацией.
- Применяйте добросовестное использование, законы об авторском праве и указание авторства Creative Commons.
- Обдумайте и поделитесь своим мнением о процессе исследования и информационном продукте.
Признание литературы и непрерывное обучение
- Читайте, слушайте, просматривайте и обсуждайте истории, отражающие человеческий опыт.
- Установите связь между литературой и собой, с другой литературой, с мультимедиа и с миром.
- Используйте библиотеки для личных или назначенных нужд.
- Используйте процедуры и правила обращения библиотеки для доступа к материалам для чтения.
- Найдите и выберите литературу и / или мультимедиа в различных жанрах.
- Осознайте связь между чтением и непрерывным обучением.
Как помочь ребенку с библиотечными материалами
К началу ↑
Музыка
Создание:
- Imagine – генерируйте музыкальные идеи для различных целей и контекстов.
- Plan and Make – отбирайте и развивайте музыкальные идеи для определенных целей и условий.
- Evaluate and Refine – выберите музыкальные идеи для создания музыкального произведения, отвечающего соответствующим критериям.
- Present – поделитесь творческими музыкальными произведениями, которые передают замысел, демонстрируют мастерство и оригинальность.
Выполнено:
- Select – выберите разнообразные музыкальные произведения для представления на основе интересов, знаний, технических навыков и контекста.
- Анализировать – анализировать структуру и контекст различных музыкальных произведений и их значение для исполнения.
- Интерпретировать – разработать личные интерпретации, учитывающие намерения авторов.
- Rehearse, Evaluate and Refine – оценивайте и улучшайте личные и коллективные выступления, индивидуально или в сотрудничестве с другими.
- Настоящее – выступать выразительно, с соответствующей интерпретацией и технической точностью, в манере, соответствующей аудитории и контексту.
Ответ:
- Select – выберите музыку, подходящую для определенной цели или контекста.
- Анализировать – анализировать, как структура и контекст различных музыкальных произведений влияют на отклик.
- Интерпретация – поддержка интерпретаций музыкальных произведений, отражающих выразительные намерения создателей / исполнителей.
- Оценить – поддержать их личную оценку музыкальных произведений и исполнений на основе анализа, интерпретации и установленных критериев.
Как помочь ребенку с музыкой
К началу ↑
Физическая культура
Двигательные навыки и паттерны движений
- Обходит и принимает предметы во время бега, грамотно меняя направление и скорость в небольшой игре.
- Ведет мяч доминирующими и недоминантными руками и ногами в игре с малыми сторонами.
- Ударяет предметом орудие в открытое пространство в небольшой игре.
Концепции и стратегии
- Выполняет по крайней мере три из следующих атакующих тактик для создания открытого пространства: перемещается в открытое пространство без мяча, использует различные передачи и подделки или использует уступки с партнером.
- Переход от нападения к защите или защиты к нападению за счет быстрого восстановления, общения с одноклассниками и использования преимуществ.
- Уменьшает пространство в поле, работая с одноклассниками для максимального охвата.
Физическая активность и фитнес
- Определяет пять компонентов фитнеса, связанного со здоровьем, и объясняет связь между фитнесом и общим физическим здоровьем.
- Понимает важность участия в различных самостоятельно выбранных аэробных упражнениях вне школы, таких как ходьба, бег трусцой, езда на велосипеде, катание на коньках, танцы и плавание.
Личное и социальное поведение
- Принимает на себя ответственность за повышение собственного уровня физической подготовки.
- Соответствующим образом реагирует на этичное и неэтичное поведение участников во время физической активности.
Признает ценность физической активности
- Разрабатывает план действий по физической активности и принимает соответствующие решения в зависимости от текущего уровня физической подготовки.
- Обсуждает, как можно увеличить удовольствие от выбранной пользователем физической активности.
- Демонстрирует уважение к себе, прося о помощи и помогая другим в различных ситуациях.
Как помочь своему ребенку с физическим воспитанием
К началу ↑
Школьное консультирование
Академическое развитие
- Определите личные сильные стороны и развивайте навыки, необходимые для постановки и достижения академических целей.
- Определите требования к окончанию, чтобы понять академическую подготовку, необходимую для выбора из широкого диапазона существенных вариантов послесреднего образования, включая колледж.
Развитие карьеры
- Определите личные сильные стороны, навыки, интересы и способности и соотнесите их с возможными вариантами карьеры.
- Выберите курсовую работу в средней школе, которая связана с карьерными интересами.
Личное / социальное развитие
- Применяйте знания о личных сильных сторонах для более здорового принятия решений и позитивного взаимодействия со сверстниками.
Как помочь своему ребенку с помощью школьного консультирования
К началу ↑
Инженерно-техническое образование
Студенты разовьют понимание того, как технологические системы работают вместе для решения проблем.Студенты участвуют в инженерном проектировании, чтобы понять, как критерии, ограничения и процессы влияют на проектирование. Мозговой штурм, визуализация, моделирование, конструирование, тестирование и доработка проектов предоставляют учащимся возможность из первых рук понять технологические системы. Студенты также будут развивать навыки поиска информации, передачи информации о дизайне и отчетности о результатах.
Природа технологий
- Объясните сущность, характеристики и область применения техники.
- Объясните основные концепции технологии.
- Объясните взаимосвязь между технологиями и взаимосвязь между технологиями и другими областями обучения.
Влияние технологий
- Оцените влияние продуктов и систем.
- Опишите культурные, социальные, экономические и политические эффекты технологий.
- Изучите влияние технологий на окружающую среду.
Процесс инженерного проектирования и разработки
- Обозначьте атрибуты дизайна.
- Изучить инженерный проект.
- Примените процесс проектирования.
- Правильно и безопасно выбирайте и используйте инструменты и оборудование.
Базовые технологии, составляющие конструируемого мира
- Объяснять функционирование и применение основных технологий, применяемых в общих технологических системах.
- Исследование материаловедения.
Крупные предприятия, производящие товары и услуги созданного мира
- Понимание информационных и коммуникационных технологий.
Как помочь своему ребенку с инженерно-техническим образованием
К началу ↑
Мировые языки (французский или испанский)
Общайтесь на французском или испанском
Межличностный (французский)
- Поговорите о развлечениях, досуге, спорте и местах, где можно прогуляться по городу.
- Описывать блюда и заказывать в кафе.
- Опишите одежду и спортивный инвентарь.
- Поговорим о повседневных делах.
- Опишите комнаты и мебель в доме.
Межличностный (испанский)
- Поговорите о развлечениях, досуге, спорте и местах, где можно прогуляться по городу.
- Заказать еду в ресторане.
- Опишите членов семьи и домашних животных.
- Поговорим о повседневных делах.
- Опишите комнаты и мебель в доме.
- Опишите одежду и аксессуары.
Устный
- Понимайте простые повседневные разговоры на знакомые темы, используя аутентичные записи, передачи и видео.
- Определять значение слов на основе контекстных подсказок, родственных слов, производных слов и использования других ресурсов.
- Используйте стратегии «до», «во время» и «после» для улучшения понимания письменной и устной речи.
Презентационный
- Примените компоненты черт письма для сочинения в различных форматах.
- Составьте и проведите официальные устные презентации на изучаемом языке.
Получите знания и понимание других культур
Практики
Продемонстрировать знание и понимание образа жизни других людей и взаимосвязи между их образцами поведения и основными убеждениями и ценностями, которыми они руководствуются.
Продукты
Продемонстрировать знание и понимание взаимосвязи между продуктами, убеждениями и ценностями культур, использующих изучаемый язык.
Связь с другими дисциплинами и получение информации
Межучебная
Пополнять и углублять знания по другим дисциплинам с помощью мирового языка.
Развивайте понимание природы языка и культуры
Язык
Изучите элементы изучаемого языка и сопоставимые элементы на английском языке.
Культура
Сравните концепции изучаемых культур с собственными.
Участвуйте в многоязычных сообществах
- Используйте язык как в школе, так и за ее пределами.
- Используйте язык для личного удовольствия и обогащения в качестве ученика на протяжении всей жизни.
Как помочь своему ребенку с мировыми языками
К началу ↑
8 класс | Средняя школа MLK
Факультативы
Учащиеся седьмого и восьмого классов выбирают один факультатив, который они будут изучать в течение учебного дня.Обратите внимание, что некоторые факультативы рассчитаны только на семестр; другие требуют полного учебного года.
Вернувшиеся ученики получают пакет зачисления на факультатив весной 7-го класса. Они выбирают из предложенных факультативов, указывая первый, второй и третий варианты. Они увидят свой факультатив в списке курсов, который они получат на Welcome Fair до начала школы.
Новые учащиеся получат пакет для зачисления на факультативы, когда зарегистрируются в школе.Они должны заполнить первую страницу и вернуть ее в то время.
Учащиеся восьмого класса могут выбрать работу в качестве независимого помощника по опыту работы (IWE) у конкретного учителя или для работы в главном офисе или библиотеке. Приложения IWE доступны у заместителей директора.
Вопросы по элективной программе следует направлять заместителю директора по классу учащегося.
Годовые курсы
Годичные курсы предназначены для того, чтобы дать студентам углубленный опыт в одной области, в отличие от семестровых курсов.
Средний уровень испанского
Чтобы записаться на средний уровень испанского, вы должны были сдать курс «Начальный испанский» в 7-м классе. После прохождения двух лет обучения в средней школе по испанскому языку вы сможете перейти в старшую школу Беркли на уровень 2 испанского. В течение двух лет учащиеся овладевают всеми четырьмя направлениями языка; разговор, понимание, чтение и письмо. Учащиеся с предшествующим языковым опытом и носители культурного наследия могут пройти тестирование в классах испанского более высокого уровня в старшей школе.
AVID
Программа AVID (Продвижение через индивидуальное определение) помогает отточить навыки студентов, чтобы они могли стать конкурентоспособными в четырехлетних колледжах. Студенты AVID изучают возможности колледжа и карьеры, развивают навыки постановки вопросов на более высоком уровне с помощью совместных обучающих программ, практикуют стратегии организации и учатся делать заметки. На занятиях AVID проводятся экскурсии, на которых освещаются возможности колледжа, а также выступают различные приглашенные докладчики.
Независимый опыт работы (IWE) 8
учащихся IWE помогают сотрудникам в различных мероприятиях в их классах, офисе или в школе.В форме запроса на выбор вы можете записаться на должность IWE в офисе, библиотеке, компьютерном классе, саду или попросить поработать с учителем. Пожалуйста, напишите всем учителям, с которыми вы заинтересованы в работе, прежде чем подписываться, чтобы узнать, хотят ли они получить IWE. Если вы не имеете в виду конкретного учителя, мы можем вам помочь.
S.T.E.M. – Наука, технологии, инженерия и математика
Исследуйте науку, технологии, инженерию и математику с помощью проектов и множества практических занятий! В этом классе вы можете узнать больше о дизайнерском мышлении, разобрать устройство, поиграть с роботами или создать интерактивную схему из медной ленты и найденных предметов.Этот класс для всех, кто любит возиться и исследовать!
Драма
Студенты будут изучать многие аспекты драмы: как адаптировать рассказы для сцены; как писать и ставить собственные пьесы / рассказы / сцены / монологи и другие возможности. «Риск и уважение» – это девиз класса, который способствует созданию атмосферы, в которой все студенты чувствуют себя комфортно, рискуя и поддерживая других, когда мы исследуем волшебный мир театра.
7 и 8 классы, семестр
Семестровые курсы
Семестровые курсыразработаны, чтобы дать студентам разнообразный опыт.Семестровые занятия парные, и вы должны пройти оба курса в паре.
Компьютеры (1 семестр) и Искусство (1 семестр)
Компьютеры: исследуйте информатику с помощью программирования, дизайна, создания интерактивных проектов, игр и многого другого! В этом классе вы можете узнать больше о процессе проектирования, создать веб-игру с использованием javascript или построить игру из схемы, которую вы узнаете, как программировать на code.org!
Искусство: В художественном классе мы будем учиться ИЗГОТОВЛЕНИЮ.Мы изучим различные медиа и техники, включая рисование, живопись, коллаж, гравюру и лепку из глины, картона, найденных предметов и папье-маше. Многие из наших проектов будут вдохновлены работами художников из разных культур, традиций и периодов времени.
Киноведение (1 семестр) и Искусство (1 семестр)
Киноведение: этот факультатив посвящен изучению искусства и ремесла видео-повествования. Работайте над каждым аспектом видеопроизводства, от написания сценария, игры на экране, работы с камерой и звуком до редактирования конечного продукта.
Искусство: В художественном классе мы будем учиться ИЗГОТОВЛЕНИЮ. Мы изучим различные медиа и техники, включая рисование, живопись, коллаж, гравюру и лепку из глины, картона, найденных предметов и папье-маше. Многие из наших проектов будут вдохновлены работами художников из разных культур, традиций и периодов времени.
4 Оценивание для поддержки изучения математики | Измерение того, что имеет значение: концептуальное руководство для оценки по математике
обычно путем подсчета количества вопросов, на которые даны правильные ответы, и сравнения баллов одного человека с баллами другого на основании их относительного процентильного ранга.Так называемые оценки с привязкой к норме уже много лет беспокоят педагогов. Хотя высказывались различные критические замечания по поводу ссылок на нормы, основная проблема образования заключается в том, что такая информация недостаточно полезна для улучшения обучения и обучения и может, фактически, иметь контрпродуктивные образовательные последствия. В классе учителя и ученики должны знать, что ученики понимают хорошо, что они понимают хуже, и какими должны быть следующие шаги обучения. Относительные рейтинги протестированных студентов могут быть использованы вне контекста класса, но в этом контексте необходимы формы результатов, полезные для процесса преподавания и обучения.
|
Программы оценки должны информировать учителей и учеников о том, что ученики узнали, как они учатся и что они думают о математике. |
Например, чтобы спланировать свое обучение, учителя должны знать о текущем понимании каждым учеником того, что будет преподавать. Таким образом, программы оценки должны информировать учителей и учеников о том, что ученики узнали, как они учатся и как они думают о математике.Чтобы эта информация была полезной для учителей, она должна включать анализ конкретных сильных и слабых сторон понимания учащимся, а не только оценок вне контекста.
Чтобы обучение было эффективным, результаты оценки должны быть своевременными. 35 Учебе учащихся не способствуют компьютерные распечатки, отправляемые учителям после окончания занятий в течение года и учебы учащихся, а также учителя, которые уделяют слишком много времени оценке оценок.В частности, необходимо найти новые способы дать учителям и ученикам более непосредственные знания об успеваемости учеников по оценкам, предписанным внешними властями, чтобы эти оценки, а также собственные оценки учителя могли использоваться для улучшения обучения. Даже если основной целью оценки является определение достижений школы, штата или страны, оценка должна предоставлять учащимся и учителям отчеты об их успеваемости. Школьное время дорого.Когда учащимся не сообщают об их ошибках и заблуждениях, не говоря уже о том, чтобы помочь их исправить, оценка может как усилить недопонимание, так и потратить драгоценное учебное время впустую.
Когда форма оценивания незнакома, учителя несут особую ответственность перед своими учениками, чтобы сообщить им заранее.
.
 11.2020
11.2020 Л. Босовой учебной дисциплины «Информатика и ИКТ».
Л. Босовой учебной дисциплины «Информатика и ИКТ».

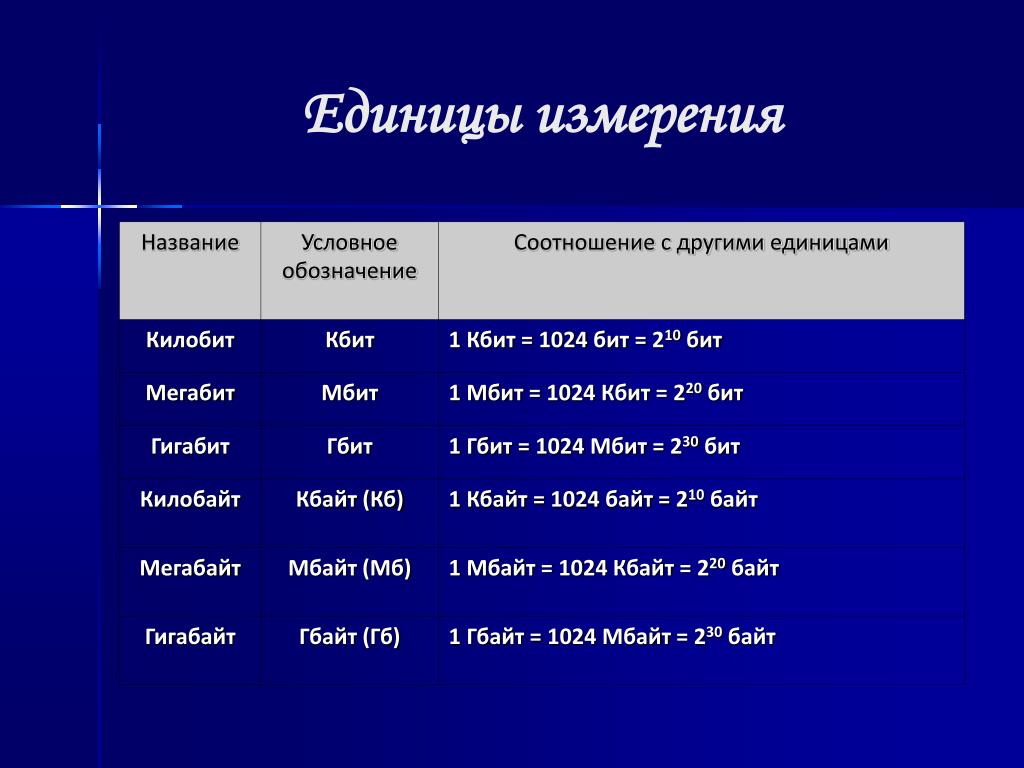 512 байт
512 байт 96 бит
96 бит