Конспект по математике 6 класс: Математика 6 класс: все темы, правила и формулы
Математика 6 класс: все темы, правила и формулы
Математика 6 класс: все темы, правила и формулы.
Краткий курс математики за 6 класс.
«Математика 6 класс: все темы, правила и формулы» — это краткое повторение математики за 6 класс (основные понятия, формулы и определения). Вся информация, самое главное и всё, что нужно знать вкратце. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского) — М.: Просвещение, 2014.
Делимость чисел
- Пусть а и b — натуральные числа и при делении а на b в частном получается q и в остатке r. Тогда а = bq + r, где q и r — натуральные числа или нули, причём r < b.
 Например:
Например:
- Если натуральное число а делится на натуральное число b, то а называют кратным b, а b — делителем а. Это означает, что а = bq, где q — натуральное число. Например, 62 кратно 31, 31 — делитель 62, так как 62 = 31 • 2.
- Простым числом называется такое натуральное число, которое имеет только два делителя — единицу и само это число. Составным числом называется такое натуральное число, которое имеет более двух делителей.
Например, числа 2, 7, 43, 109 — простые, а числа 4, 12, 35 — составные. Число 1 не является ни простым, ни составным. Всякое составное число можно разложить на простые множители, и притом единственным способом. Например, 630 = 2 • 32 • 5 • 7.
- Чтобы найти
наименьшее общее кратное (НОК) нескольких чисел, надо разложить эти числа на простые множители и найти произведение всех получившихся простых множителей, взяв каждый из них с наибольшим показателем.
 Например, 72 = 23 • 32; 180 = 22 • 32 • 5 и 600 = 23 • 3 • 52. Наименьшее общее кратное чисел 72, 180 и 600 равно 23 • 32 • 52 = 1800.
Например, 72 = 23 • 32; 180 = 22 • 32 • 5 и 600 = 23 • 3 • 52. Наименьшее общее кратное чисел 72, 180 и 600 равно 23 • 32 • 52 = 1800.
Чтобы найти наибольший общий делитель (НОД) нескольких чисел, надо разложить эти числа на простые множители и найти произведение общих простых множителей, взяв каждый из них с наименьшим показателем. Например, наибольший общий делитель чисел 72, 180 и 600 равен 22 • 3, т. е. числу 12.
- Если число оканчивается цифрой 0 или цифрой 5, то оно делится на 5. Если число оканчивается любой другой цифрой, то оно не делится на 5.
- Если число оканчивается чётной цифрой, то оно делится на 2. Если число оканчивается нечётной цифрой, то оно не делится на 2.
- Если сумма цифр числа делится на 3, то и число делится на 3. Если сумма цифр числа не делится на 3, то число не делится на 3.
- Если сумма цифр числа делится на 9, то и число делится на 9.
 Если сумма цифр числа не делится на 9, то и число не делится на 9.
Если сумма цифр числа не делится на 9, то и число не делится на 9.
Обыкновенные дроби
- Правильной дробью называется дробь, у которой числитель меньше знаменателя. Неправильной дробью называется дробь, у которой числитель больше знаменателя или равен ему.
- Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
- Чтобы привести дроби к наименьшему общему знаменателю , надо найти наименьшее общее кратное знаменателей дробей; вычислить дополнительные множители, разделив наименьшее общее кратное на каждый знаменатель; умножить числитель и знаменатель каждой дроби на соответствующий дополнительный множитель. Например, приведём к наименьшему общему знаменателю дроби 1/6, 7/12, 5/18. Наименьший общий знаменатель равен 36:
- При сложении дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби и оставляют тот же знаменатель.
 При вычитании дробей с одинаковыми знаменателями из числителя первой дроби вычитают числитель второй дроби и оставляют тот же знаменатель. Например,
При вычитании дробей с одинаковыми знаменателями из числителя первой дроби вычитают числитель второй дроби и оставляют тот же знаменатель. Например,
При сложении и вычитании дробей с разными знаменателями сначала их приводят к общему знаменателю.
- Чтобы перемножить две дроби, надо перемножить отдельно их числители и знаменатели; первое произведение сделать числителем, а второе — знаменателем. Чтобы разделить одну дробь на другую, надо делимое умножить на дробь, обратную делителю.
Например,
Десятичные дроби
- При округлении десятичной дроби до какого-нибудь разряда все следующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их отбрасывают. Если первая следующая за этим разрядом цифра 5, б, 7, 8 или 9, то к последней оставшейся цифре прибавляют 1. Если первая следующая за этим разрядом цифра 0, 1, 2, 3 или 4, то последнюю оставшуюся цифру не изменяют.

Например, 4,376 ≈ 4,4; 2,8195 ≈ 2,820; 10,1425 ≈ 10,14.
- Сложение и вычитание десятичных дробей выполняют поразрядно. При этом дроби записывают одну под другой так, чтобы запятая оказалась под запятой.
Например:
- Чтобы умножить одну десятичную дробь на другую, надо выполнить умножение, не обращая внимания на запятые, а затем в полученном произведении отделить запятой справа столько цифр, сколько их стоит после занятой в обоих множителях вместе.
- Чтобы разделить десятичную дробь на десятичную, надо в делимом и делителе перенести запятые вправо на столько цифр, сколько их после запятой в делителе, а затем выполнить деление на натуральное число.
Например:
- Чтобы умножить десятичную дробь на 10n, надо в этой дроби перенести запятую на n цифр вправо. Чтобы разделить десятичную дробь на 10n, надо в этой дроби перенести запятую на n цифр влево.

Например, 8,373 • 100 = 837,3; 3,4 : 1000 = 0,0034.
Положительные и отрицательные числа
- Модулем положительного числа и нуля называется само это число. Модулем отрицательного числа называется противоположное ему положительное число. Модул
Математика – 6 класс – Конспекты
Выберите категорию: Все категорииАнглийский языкБиологияВнеурочная деятельностьВсеобщая историяГеографияДиректору, завучуДоп. образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураМатематикаМузыкаНемецкий языкОБЖОбществознаниеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФранцузский языкШкольному психологуДругое
Выберите класс: Все классы1 класс2 класс3 класс4 класс5 класс6 класс
Выберите учебник:
Все учебники”Испанский язык”, Анурова И.

Выберите тему:
Опорные конспекты по математике 6 класс | План-конспект занятия по алгебре (6 класс) на тему:
Муниципальное бюджетное общеобразовательное учреждение
«Покровская средняя общеобразовательная школа»
Рузского района Московской области
ОПОРНЫЕ КОНСПЕКТЫ
ПО МАТЕМАТИКЕ
6 КЛАСС
Учитель математики и физики
Александрова Татьяна Валентиновна
2015 год
ОК-1 Признаки делимости на 2, на 5, на 10
На 10: число оканчивается 0.
На 5: число оканчивается 0 или 5.
Четные цифры (делятся без остатка на 2) : 0, 2, 4, 6, 8
Нечетные цифры ( при делении на 2 дают остаток 1): 1, 3, 5, 7, 9
На 2: число оканчивается четной цифрой.
ОК-2 Взаимно обратные числа
Два числа, произведение которых равно единице, называют взаимно обратными.
и взаимно обратны, при , т.к. 1
Если одно из двух взаимно обратных чисел – правильная дробь, то другое – неправильная дробь.
и взаимно обратны
– правильная дробь правильная дробь
Число 1 взаимно обратно самому себе, а число 0 – не имеет обратного себе числа.
Задание: найдите число, обратное данному:
- → ∙ = 1
- →
- = → = 1
ОК-3 Сокращение дробей
Сокращение дроби – деление числителя и знаменателя дроби на их общий делитель, не равный 1.
3 и 5 – взаимно простые числа – несократимая дробь
Дробь, у которой числитель и знаменатель являются взаимно простыми числами, называется несократимой.
Способы сокращения дробей:
- Подбор общих делителей числителя и знаменателя, пока не получится несократимая дробь.

= (: 7) =
- Разделить числитель и знаменатель на их НОД.
42 = 2 ∙ 3 ∙ 7
70 = 2 ∙ 5 ∙ 7
НОД (42; 70) = 2 ∙ 7 = 14
- Разложить числитель и знаменатель на простые множители и вычеркнуть одинаковые множители.
ОК – 4 Нахождение дроби от числа
Дробь используют, чтобы кратко обозначить часть некоторой целой величины.
Часть Целое
«Остается пройти пути» → Весь путь
Задача 1: Маша собирает коллекцию камней. Всего в Машиной коллекции уже камней, из них составляют аметисты. Сколько аметистов в Машиной коллекции?
Решение:
60 ∙ аметистов
Ответ: 36 аметистов.
Задача 2: Палисадник занимает всего земельного участка. Участок, засаженный колокольчиками, занимает палисадника. Какую часть всего земельного участка занимает участок засаженный колокольчиками?
Какую часть всего земельного участка занимает участок засаженный колокольчиками?
Решение:
=
Ответ:.
Задача 3: Дачнику нужно высадить саженцев плодовых деревьев. В первый день он высадил от всех, саженцев. Сколько саженцев высадил дачник за первый день?
Решение:
20 ∙ 0,6 = 20 ∙ = = 12
Ответ: 12 саженцев.
Задача 4: Приусадебный участок занимает сотки. Цветами засажено 35% этого участка. Какова площадь засаженного цветами участка?
Решение: 4 ∙ = = = = 1
Ответ: 1 сотки.
Чтобы найти дробь (часть) от числа, нужно умножить число на данную дробь.
ОК-5 Дробные выражения
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
= 1 : 2 числитель
=
знаменатель
Чтобы найти значение дробного выражения, нужно:
- найти по отдельности значения его числителя и знаменателя;
- затем первый результат разделить на второй.

Пример 1. =
Пример 2. = = 2
Пример 3. Выражение не имеет значения!
Пример 4. Найти значение выражения при
=
ОК-6 Длина окружности
Длина окружности прямо пропорциональна длине ее диаметра.
Отношение длины окружности к длине ее диаметра является одним и тем же числом для любой окружности.
– длина окружности
– диаметр окружности
С =
длина окружности
C = R
S = – площадь круга
ОК-7 Применение распределительного закона умножения
Распределительное свойство умножения относительно сложения:
Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения.
Распределительное свойство умножения относительно вычитания:
Для того чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.
Чтобы умножить смешанное число на натуральное число, можно:
1) умножить целую часть на натуральное число;
2) умножить дробную часть на это натуральное число;
3) сложить полученные произведения.
Чтобы умножить смешанное число на смешанное число, можно:
- перевести одно смешанное число в неправильную дробь;
- умножить целую часть второго множителя на неправильную дробь;
- умножить дробную часть второго множителя на неправильную дробь;
- сложить полученные результаты.
Пример 1:
Пример 2: =
Пример 3:
Пример 4: х + х = х
Пример 5: у + у = у
ОК-8 Координаты на прямой
Координатная прямая – это прямая, на которой выбрано начало отсчёта; единичный отрезок.
Стрелкой обозначено положительное направление.
В А
-4 -3 -2 -1 0 1 2 3 4
отрицательные положительные
не положительное,
не отрицательное
Координата точки – число, показывающее положение точки на координатной прямой.
В(-3), А(2)
ОК-9 Модуль числа
Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а).
В О А
-2 0 2
Модуль числа 2 равен 2, т.к. точка А(2) удалена от начала отсчета на 2 единицы.
Модуль числа -2 равен 2, т.к. точка В(-2) удалена от начала отсчета на 2 единицы.
Пишут: │2│= 2, │-2│= 2, │0│= 0
Модуль числа не может быть отрицательным!
Модулем положительного числа и числа 0 является само число, модулем отрицательного числа – противоположное ему число.
Противоположные числа имеют одинаковые модули.
│-а│ = │а │
ОК-10 Пропорции
Пропорция – это равенство двух отношений.
Крайние
a : b = c : d ↔ =
средние
Основное свойство пропорции:
В любой верной пропорции произведение крайних членов равно произведению средних членов пропорции.
Признак пропорции:
Если произведение крайних членов равно произведению средних членов
a · d = b · c, то пропорция a : b = c : d верна.
=
Пример 1. Верна ли пропорция ?
30 ∙ 7 = 210
5 ∙ 42 = 210 верна
Если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны.
=
Используя основное свойство пропорции, можно найти неизвестный член пропорции, если все остальные члены известны.
Пример 2. Решите уравнение
1,5 ∙ у = 21,6 ∙ 0,25
Ответ: у = 3,6
ОК – 11 Шар
Шар – простейшее геометрическое тело.
Сфера – поверхность шара.
Радиус шара – отрезок, соединяющий любую
точку сферы с центром шара.
Диаметр шара – отрезок, соединяющий две
точки сферы и проходящий через центр шара.
O – центр шара
ОА = ОВ = R – радиус
CD = D – диаметр
D = 2R
———————————————————————————————–
ОК-12 Дробные выражения
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
= 1 : 2 числитель
=
знаменатель
Чтобы найти значение дробного выражения, нужно:
- найти по отдельности значения его числителя и знаменателя;
- затем первый результат разделить на второй.
Пример 1. =
Пример 2. = = 2
Пример 3. Выражение не имеет значения!
Пример 4. Найти значение выражения при
Найти значение выражения при
=
ОК-13 Перпендикулярные прямые
Прямой угол – это угол, Две прямые, образующие
градусная мера которого при пересечении прямые
равна 90о . углы, называются
перпендикулярными.
Е
900 А
В
F
AB ┴ EF
А
Опорные конспекты по математике 6 класс | План-конспект занятия по алгебре (6 класс) на тему:
Муниципальное бюджетное общеобразовательное учреждение
«Покровская средняя общеобразовательная школа»
Рузского района Московской области
ОПОРНЫЕ КОНСПЕКТЫ
ПО МАТЕМАТИКЕ
6 КЛАСС
Учитель математики и физики
Александрова Татьяна Валентиновна
2015 год
ОК-1 Признаки делимости на 2, на 5, на 10
На 10: число оканчивается 0.
На 5: число оканчивается 0 или 5.
Четные цифры (делятся без остатка на 2) : 0, 2, 4, 6, 8
Нечетные цифры ( при делении на 2 дают остаток 1): 1, 3, 5, 7, 9
На 2: число оканчивается четной цифрой.
ОК-2 Взаимно обратные числа
Два числа, произведение которых равно единице, называют взаимно обратными.
и взаимно обратны, при , т.к. 1
Если одно из двух взаимно обратных чисел – правильная дробь, то другое – неправильная дробь.
и взаимно обратны
– правильная дробь правильная дробь
Число 1 взаимно обратно самому себе, а число 0 – не имеет обратного себе числа.
Задание: найдите число, обратное данному:
- → ∙ = 1
- →
- = → = 1
ОК-3 Сокращение дробей
Сокращение дроби – деление числителя и знаменателя дроби на их общий делитель, не равный 1.
3 и 5 – взаимно простые числа – несократимая дробь
Дробь, у которой числитель и знаменатель являются взаимно простыми числами, называется несократимой.
Способы сокращения дробей:
- Подбор общих делителей числителя и знаменателя, пока не получится несократимая дробь.
= (: 7) =
- Разделить числитель и знаменатель на их НОД.
42 = 2 ∙ 3 ∙ 7
70 = 2 ∙ 5 ∙ 7
НОД (42; 70) = 2 ∙ 7 = 14
- Разложить числитель и знаменатель на простые множители и вычеркнуть одинаковые множители.
ОК – 4 Нахождение дроби от числа
Дробь используют, чтобы кратко обозначить часть некоторой целой величины.
Часть Целое
«Остается пройти пути» → Весь путь
Задача 1: Маша собирает коллекцию камней. Всего в Машиной коллекции уже камней, из них составляют аметисты. Сколько аметистов в Машиной коллекции?
Решение:
60 ∙ аметистов
Ответ: 36 аметистов.
Задача 2: Палисадник занимает всего земельного участка. Участок, засаженный колокольчиками, занимает палисадника. Какую часть всего земельного участка занимает участок засаженный колокольчиками?
Решение:
=
Ответ:.
Задача 3: Дачнику нужно высадить саженцев плодовых деревьев. В первый день он высадил от всех, саженцев. Сколько саженцев высадил дачник за первый день?
Решение:
20 ∙ 0,6 = 20 ∙ = = 12
Ответ: 12 саженцев.
Задача 4: Приусадебный участок занимает сотки. Цветами засажено 35% этого участка. Какова площадь засаженного цветами участка?
Решение: 4 ∙ = = = = 1
Ответ: 1 сотки.
Чтобы найти дробь (часть) от числа, нужно умножить число на данную дробь.
ОК-5 Дробные выражения
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
= 1 : 2 числитель
=
знаменатель
Чтобы найти значение дробного выражения, нужно:
- найти по отдельности значения его числителя и знаменателя;
- затем первый результат разделить на второй.

Пример 1. =
Пример 2. = = 2
Пример 3. Выражение не имеет значения!
Пример 4. Найти значение выражения при
=
ОК-6 Длина окружности
Длина окружности прямо пропорциональна длине ее диаметра.
Отношение длины окружности к длине ее диаметра является одним и тем же числом для любой окружности.
– длина окружности
– диаметр окружности
С =
длина окружности
C = R
S = – площадь круга
ОК-7 Применение распределительного закона умножения
Распределительное свойство умножения относительно сложения:
Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения.
Распределительное свойство умножения относительно вычитания:
Для того чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.
Чтобы умножить смешанное число на натуральное число, можно:
1) умножить целую часть на натуральное число;
2) умножить дробную часть на это натуральное число;
3) сложить полученные произведения.
Чтобы умножить смешанное число на смешанное число, можно:
- перевести одно смешанное число в неправильную дробь;
- умножить целую часть второго множителя на неправильную дробь;
- умножить дробную часть второго множителя на неправильную дробь;
- сложить полученные результаты.
Пример 1:
Пример 2: =
Пример 3:
Пример 4: х + х = х
Пример 5: у + у = у
ОК-8 Координаты на прямой
Координатная прямая – это прямая, на которой выбрано начало отсчёта; единичный отрезок.
Стрелкой обозначено положительное направление.
В А
-4 -3 -2 -1 0 1 2 3 4
отрицательные положительные
не положительное,
не отрицательное
Координата точки – число, показывающее положение точки на координатной прямой.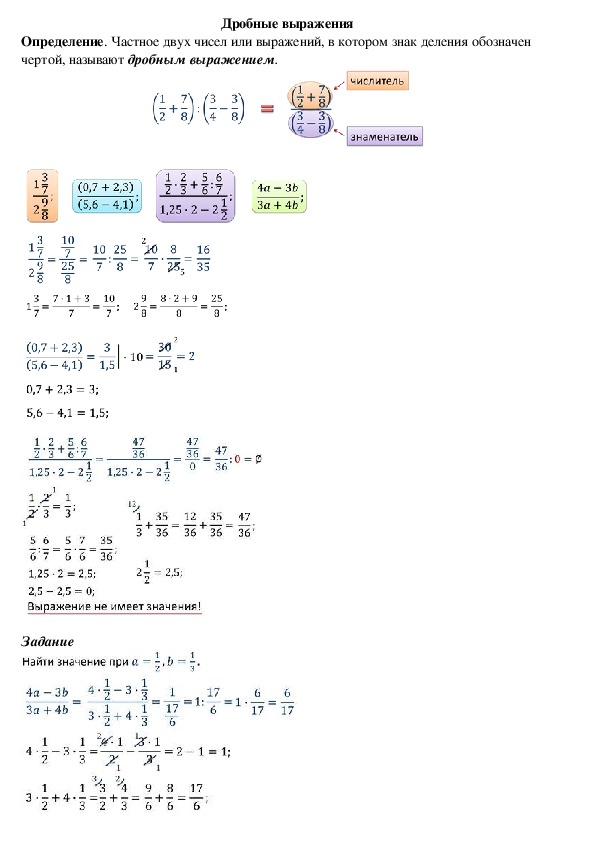
В(-3), А(2)
ОК-9 Модуль числа
Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а).
В О А
-2 0 2
Модуль числа 2 равен 2, т.к. точка А(2) удалена от начала отсчета на 2 единицы.
Модуль числа -2 равен 2, т.к. точка В(-2) удалена от начала отсчета на 2 единицы.
Пишут: │2│= 2, │-2│= 2, │0│= 0
Модуль числа не может быть отрицательным!
Модулем положительного числа и числа 0 является само число, модулем отрицательного числа – противоположное ему число.
Противоположные числа имеют одинаковые модули.
│-а│ = │а │
ОК-10 Пропорции
Пропорция – это равенство двух отношений.
Крайние
a : b = c : d ↔ =
средние
Основное свойство пропорции:
В любой верной пропорции произведение крайних членов равно произведению средних членов пропорции.
Признак пропорции:
Если произведение крайних членов равно произведению средних членов
a · d = b · c, то пропорция a : b = c : d верна.
=
Пример 1. Верна ли пропорция ?
30 ∙ 7 = 210
5 ∙ 42 = 210 верна
Если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны.
=
Используя основное свойство пропорции, можно найти неизвестный член пропорции, если все остальные члены известны.
Пример 2. Решите уравнение
1,5 ∙ у = 21,6 ∙ 0,25
Ответ: у = 3,6
ОК – 11 Шар
Шар – простейшее геометрическое тело.
Сфера – поверхность шара.
Радиус шара – отрезок, соединяющий любую
точку сферы с центром шара.
Диаметр шара – отрезок, соединяющий две
точки сферы и проходящий через центр шара.
O – центр шара
ОА = ОВ = R – радиус
CD = D – диаметр
D = 2R
———————————————————————————————–
ОК-12 Дробные выражения
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
= 1 : 2 числитель
=
знаменатель
Чтобы найти значение дробного выражения, нужно:
- найти по отдельности значения его числителя и знаменателя;
- затем первый результат разделить на второй.
Пример 1. =
Пример 2. = = 2
Пример 3. Выражение не имеет значения!
Пример 4. Найти значение выражения при
Найти значение выражения при
=
ОК-13 Перпендикулярные прямые
Прямой угол – это угол, Две прямые, образующие
градусная мера которого при пересечении прямые
равна 90о . углы, называются
перпендикулярными.
Е
900 А
В
F
AB ┴ EF
А
М В
Если ∠ АМВ = 900, то АМ ⏊ МВ.
И наоборот:
Если АМ ⏊ МВ, то ∠ АМВ = 900
Через любую точку плоскости можно провести единственную прямую, перпендикулярную данной.
Отрезки (или лучи), лежащие на перпендикулярных прямых называются перпендикулярными.
ОК-14 Параллельные прямые
ПРЯМЫЕ
пересекаются не пересекаются
а m k
M
c m k
Две непересекающиеся прямые на плоскости называются параллельными.
k t d
M k t
t d
k
Если две прямые на плоскости параллельны третьей прямой, то они параллельны.
k t
a k ⏊ a
k t
t ⏊ a
Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны.
Через каждую точку плоскости, не лежащую на данной прямой, можно провести единственную прямую, параллельную данной.
Отрезки (или лучи), лежащие на параллельных прямых называются параллельными.
ОК-15 Сложение и вычитание чисел
- Сложение отрицательных чисел
Чтобы сложить два отрицательных числа, нужно:
- Перед результатом поставить знак « – » ,
- Сложить модули чисел.
Пример: – 9 + (- 45) = – ( 9 + 45) = – 54
- Сложение чисел с разными знаками
Чтобы сложить два числа с разными знаками, нужно:
- Поставить перед результатом знак того слагаемого, модуль которого больше,
- Из большего модуля слагаемых вычесть меньший модуль.
Примеры:
- 9 + (- 3) = 9 – 3 = 6
- 9 + (-12) = – ( 12 – 9) = – 3
- Вычитание чисел
Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.
a – b = a + (–b)
Любое выражение, содержащее лишь знаки сложения и вычитания, можно представить в виде суммы.
Примеры:
- -12 – 13 = -12 + (-13) = – (12 + 13) = – 25
- 7 – 16 = 7 + (- 16) = – (16 – 7) = – 9
- 6 – (- 5) = 6 + 5 = 11
Разность двух чисел положительна, если уменьшаемое больше вычитаемого: а b ⟹ a – b
Разность двух чисел отрицательна, если уменьшаемое меньше вычитаемого: а ⟹ a – b
Если уменьшаемое и вычитаемое равны, то их разность равна нулю
а = b ⟹ a – b =
Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.
А( -6), В(8) ⟹ АВ = 8 – (-6) = 8 + 6 = 14
ОК-16 Деление чисел
- Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.
Пример : ( – 14) : ( – 2) = 14 : 2 = 7
- При делении чисел с разными знаками надо:
– поставить перед результатом знак « – »;
– разделить модуль делимого на модуль делителя.
Примеры: (- 4,8) : 4 = – (4,8 : 4) = – 1,2
0,33 : (- 1,1) = – (0,33 : 1,1) = – 0,3
( – ) : ( – ) = ( + )
( – ) : ( + ) = ( – )
( + ) : ( – ) = ( – )
- На нуль делить нельзя!
- При делении нуля на любое число получается нуль.
0 : а = 0
- При делении любого числа на 1 получается то же число.
а : 1 = а
- При делении любого числа на ( -1) получается противоположное число.
а : ( – 1) = – а
ОК-17 Координатная плоскость
О – начало координат
х – абсцисса
у – ордината
(х; у) – координаты
Координаты точки (х; у) на плоскости – это пара чисел, в которой на первом месте стоит абсцисса (х), а на втором – ордината (у) этой точки.
Оси координат разбивают плоскость на 4 части – 4 четверти.
I четверть: х > 0, у > 0
II четверть: х 0
III четверть: х
IV четверть: х > 0, у
Координаты можно указать для любой точки координатной плоскости: для этого надо из точки провести перпендикуляры на координатные оси и определить, какому числу координатной оси соответствует основание перпендикуляра.
Как найти координаты точки:
1. Провести из точки перпендикуляр к оси ОХ.
2. Провести из точки перпендикуляр к оси ОУ.
3. Записать координаты точки (х; у).
Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса и ордината.
Наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
Точки любой прямой, перпендикулярной оси абсцисс, имеют одну и ту же абсциссу.
Точки любой прямой, перпендикулярной оси ординат, имеют одну и ту же ординату.
а ⏊ ОХ ⟹ А(4; 3), В(4; – 4)
b⏊ ОУ ⟹ С(- 2; – 3), D(3; – 3)
Если точка лежит на оси ОХ, то ее ордината равна 0 (у = 0).
Если точка лежит на оси ОУ, то ее абсцисса равна 0 (х = 0).
у
А(0; 4)
М (4; 0)
Х
ОК-18 Умножение положительных и отрицательных чисел
- Чтобы перемножить два числа с разными знаками, надо перемножить модули чисел и перед полученным результатом поставить знак « – ».
Примеры: – 5 ∙ 2 = – (5 ∙ 2) = – 10
0,2 ∙ ( – 1,5) = ( – 0,2 ∙ 1,5) = – 0,3
- Произведение двух отрицательных чисел равно произведению их модулей.
Примеры: – 2 ∙ ( – 3) = 2 ∙ 3 = 6 ( – ) ∙ ( + ) = ( – )
– 4 ∙ ( – 0,3) = 4 ∙ 0,3 = 1,2 ( – ) ∙ ( – ) = ( + )
- Свойства 0 и 1 при умножении сохраняются:
а ∙ 0 = 0 а ∙ 1 = а
- При умножении на ( – 1) число меняется на противоположное.
а ∙ (- 1) = – а
ОК-19 Координаты на прямой
Координатная прямая – это прямая, на которой выбрано начало отсчёта; единичный отрезок.
Стрелкой обозначено положительное направление.
В А
-4 -3 -2 -1 0 1 2 3 4
отрицательные положительные
не положительное,
не отрицательное
Координата точки – число, показывающее положение точки на координатной прямой.
В(-3), А(2)
МАТЕМАТИКА
Урок № 1. Тема. Делители натурального числа. Простые и составные числа |
Поурочные разработки по Математике 6 класс
ГЛАВА I. ОБЫКНОВЕННЫЕ ДРОБИ
§ 1. ДЕЛИМОСТЬ ЧИСЕЛ (20 ч)
ДЕЛИТЕЛИ И КРАТНЫЕ (3 ч)
Урок 1. Делители и кратные
Урок 2. Делители и кратные
Урок 3. Делители и кратные
ПРИЗНАКИ ДЕЛИМОСТИ НА 10, НА 5, НА 2 (3 ч)
Урок 4. Признаки делимости на 10, на 5, на 2
Урок 5. Признаки делимости на 10, на 5, на 2
Урок 6. Признаки делимости на 10, на 5, на 2
ПРИЗНАКИ ДЕЛИМОСТИ НА 9 И НА 3 (2 ч)
Урок 7. Признаки делимости на 9 и на 3
Урок 8. Признаки делимости на 9 и на 3
ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА (2 ч)
Урок 9. Простые и составные числа
Урок 10. Простые и составные числа
РАЗЛОЖЕНИЕ НА ПРОСТЫЕ МНОЖИТЕЛИ (2 ч)
Урок 11. Разложение на простые множители
Урок 12. Разложение на простые множители
НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ. ВЗАИМНО ПРОСТЫЕ ЧИСЛА (3 ч)
Урок 13. Наибольший общий делитель
Урок 14. Наибольший общий делитель. Взаимно простые числа
Урок 15. Наибольший общий делитель. Взаимно простые числа
НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ (4 ч)
Урок 16. Наименьшее общее кратное
Урок 17. Наименьшее общее кратное
Урок 18. Наименьшее общее кратное
Урок 19. Наименьшее общее кратное
Урок 20. Контрольная работа № 1
§ 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ (22 ч)
ОСНОВНОЕ СВОЙСТВО ДРОБИ (2 ч)
Урок 21. Основное свойство дроби
Урок 22. Основное свойство дроби
СОКРАЩЕНИЕ ДРОБЕЙ (3 ч)
Урок 23. Сокращение дробей
Урок 24. Сокращение дробей
Урок 25. Сокращение дробей
ПРИВЕДЕНИЕ ДРОБЕЙ К ОБЩЕМУ ЗНАМЕНАТЕЛЮ (3 ч)
Урок 26. Приведение дробей к общему знаменателю
Урок 27. Приведение дробей к общему знаменателю
Урок 28. Приведение дробей к общему знаменателю
СРАВНЕНИЕ, СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ (6 ч)
Урок 29. Сравнение дробей с разными знаменателями
Урок 30. Сравнение дробей с разными знаменателями
Урок 31. Сравнение, сложение и вычитание дробей с разными знаменателями
Урок 32. Сравнение, сложение и вычитание дробей с разными знаменателями
Урок 33. Сравнение, сложение и вычитание дробей с разными знаменателями
Урок 34. Сравнение, сложение и вычитание дробей с разными знаменателями
Урок 35. Контрольная работа № 2
СЛОЖЕНИЕ И ВЫЧИТАНИЕ СМЕШАННЫХ ЧИСЕЛ (6 ч)
Урок 36. Сложение и вычитание смешанных чисел
Урок 37. Сложение и вычитание смешанных чисел
Урок 38. Сложение и вычитание смешанных чисел
Урок 39. Сложение и вычитание смешанных чисел
Урок 40. Сложение и вычитание смешанных чисел
Урок 41. Сложение и вычитание смешанных чисел
Урок 42. Контрольная работа № 3
§ 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ (32 ч)
УМНОЖЕНИЕ ДРОБЕЙ (5 ч)
Урок 43. Умножение дробей
Урок 44. Умножение дробей
Урок 45. Умножение дробей
Урок 46. Умножение дробей
Урок 47. «Счастливый случай» (урок-игра)
НАХОЖДЕНИЕ ДРОБИ ОТ ЧИСЛА (4 ч)
Урок 48. Нахождение дроби от числа
Урок 49. Нахождение дроби от числа
Урок 50. Нахождение дроби от числа
Урок 51. Нахождение дроби от числа
ПРИМЕНЕНИЕ РАСПРЕДЕЛИТЕЛЬНОГО СВОЙСТВА УМНОЖЕНИЯ (5 ч)
Урок 52. Применение распределительного свойства умножения
Урок 53. Применение распределительного свойства умножения
Урок 54. Применение распределительного свойства умножения
Урок 55. Применение распределительного свойства умножения
Урок 56. Применение распределительного свойства умножения
Урок 57. Контрольная работа № 4
ВЗАИМНО ОБРАТНЫЕ ЧИСЛА (2 ч)
Урок 58. Взаимно обратные числа
Урок 59. Взаимно обратные числа
ДЕЛЕНИЕ (5 ч)
Урок 60. Деление
Урок 61. Деление
Урок 62. Деление
Урок 63. Деление
Урок 64. Деление
Урок 65. Контрольная работа № 5
НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ (5 ч)
Урок 66. Нахождение числа по его дроби
Урок 67. Нахождение числа по его дроби
Урок 68. Нахождение числа по его дроби
Урок 69. Нахождение числа по его дроби
Урок 70. Нахождение числа по его дроби
ДРОБНЫЕ ВЫРАЖЕНИЯ (3 ч)
Урок 71. Дробные выражения
Урок 72. Дробные выражения
Урок 73. Дробные выражения
Урок 74. Контрольная работа № 6
§ 4. ОТНОШЕНИЯ И ПРОПОРЦИИ (19 ч)
ОТНОШЕНИЯ (3 ч)
Урок 75. Отношения
Урок 76. Отношения
Урок 77. Отношения
ПРОПОРЦИИ (4 ч)
Урок 78. Пропорции
Урок 79. Пропорции
Урок 80. Пропорции
Урок 81. Пропорции
Урок 82. Повторение, обобщение и закрепление материала, пройденного за I полугодие
ПРЯМАЯ И ОБРАТНАЯ ПРОПОРЦИОНАЛЬНАЯ ЗАВИСИМОСТИ (3 ч)
Урок 83. Прямая и обратная пропорциональная зависимости
Урок 84. Прямая и обратная пропорциональная зависимости
Урок 85. Прямая и обратная пропорциональная зависимости
Урок 86. Контрольная работа № 7
МАСШТАБ (2 ч)
Урок 87. Масштаб
Урок 88. Масштаб
ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА (2 ч)
Урок 89. Длина окружности и площадь круга
Урок 90. Длина окружности и площадь круга
ШАР (2 ч)
Урок 91. Шар
Урок 92. Шар
Урок 93. Контрольная работа № 8
ГЛАВА II. РАЦИОНАЛЬНЫЕ ЧИСЛА
§ 5. ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ ЧИСЛА (13 ч)
КООРДИНАТЫ НА ПРЯМОЙ (3 ч)
Урок 94. Координаты на прямой
Урок 95. Координаты на прямой
Урок 96. Координаты на прямой
ПРОТИВОПОЛОЖНЫЕ ЧИСЛА (2 ч)
Урок 97. Противоположные числа
Урок 98. Противоположные числа
МОДУЛЬ ЧИСЛА (2 ч)
Урок 99. Модуль числа
Урок 100. Модуль числа
СРАВНЕНИЕ ЧИСЕЛ (3 ч)
Урок 101. Сравнение чисел
Урок 102. Сравнение чисел
Урок 103. Сравнение чисел
ИЗМЕНЕНИЕ ВЕЛИЧИН (2 ч)
Урок 104. Изменение величин
Урок 105. Изменение величини
Урок 106. Контрольная работа № 9
§ 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ (11 ч)
СЛОЖЕНИЕ ЧИСЕЛ С ПОМОЩЬЮ КООРДИНАТНОЙ ПРЯМОЙ (2 ч)
Урок 107. Сложение чисел с помощью координатной прямой
Урок 108. Сложение чисел с помощью координатной прямой
СЛОЖЕНИЕ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ (2 ч)
Урок 109. Сложение отрицательных чисел
Урок 110. Сложение отрицательных чисел
СЛОЖЕНИЕ ЧИСЕЛ С РАЗНЫМИ ЗНАКАМИ (3 ч)
Урок 111. Сложение чисел с разными знаками
Урок 112. Сложение чисел с разными знаками
Урок 113. Сложение чисел с разными знаками
ВЫЧИТАНИЕ (3 ч)
Урок 114. Вычитание
Урок 115. Вычитание
Урок 116. Вычитание
Урок 117. Контрольная работа № 10
§ 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ (12 ч)
УМНОЖЕНИЕ (3 ч)
Урок 118. Умножение
Урок 119. Умножение
Урок 120. Умножение
ДЕЛЕНИЕ (3 ч)
Урок 121. Деление
Урок 122. Деление
Урок 123. Деление
РАЦИОНАЛЬНЫЕ ЧИСЛА (2 ч)
Урок 124. Рациональные числа
Урок 125. Рациональные числа
СВОЙСТВА ДЕЙСТВИЙ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ (3 ч)
Урок 126. Свойства действий с рациональными числами
Урок 127. Свойства действий с рациональными числами
Урок 128. Свойства действий с рациональными числами
Урок 129. Контрольная работа № 11
§ 8. РЕШЕНИЕ УРАВНЕНИЙ (15 ч)
РАСКРЫТИЕ СКОБОК (3 ч)
Урок 130. Раскрытие скобок
Урок 131. Раскрытие скобок
Урок 132. Раскрытие скобок
Урок 133. Повторение и обобщение материала за III четверть (урок-игра)
КОЭФФИЦИЕНТ (2 ч)
Урок 134. Коэффициент
Урок 135. Коэффициент
ПОДОБНЫЕ СЛАГАЕМЫЕ (3 ч)
Урок 136. Подобные слагаемые
Урок 137. Подобные слагаемые
Урок 138. Подобные слагаемые
Урок 139. Контрольная работа № 12
РЕШЕНИЕ УРАВНЕНИЙ (4 ч)
Урок 140. Решение уравненийк
Урок 141. Решение уравнений
Урок 142. Решение уравнений
Урок 143. Решение уравнений
Урок 144. Контрольная работа № 13
§ 9. КООРДИНАТЫ НА ПЛОСКОСТИ (13 ч)
ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ (2 ч)
Урок 145. Перпендикулярные прямые
Урок 146. Перпендикулярные прямые
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ (2 ч)
Урок 147. Параллельные прямые
Урок 148. Параллельные прямые
КООРДИНАТНАЯ ПЛОСКОСТЬ (3 ч)
Урок 149. Координатная плоскость
Урок 150. Координатная плоскость
Урок 151. Координатная плоскость
СТОЛБЧАТЫЕ ДИАГРАММЫ (2 ч)
Урок 152. Столбчатые диаграммы
Урок 153. Столбчатые диаграммы
ГРАФИКИ (3 ч)
Урок 154. Графики
Урок 155. Графики
Урок 156. Графики
Урок 157. Контрольная работа № 14
Ресурсы по математике STAAR | Техасское образовательное агентство
Перейти к основному содержаниюМега Меню
-
О ЧАЕ
- Добро пожаловать и обзор
- Агентство Финансы
- Свяжитесь с нами
- Законы и правила
- Лидерство
- Отношения с государством и правовые вопросы
- Новости и мультимедиа
- Другие услуги
-
Школы Техаса
- Основная информация
- Подотчетность
- Чартерные школы
- Районные инициативы
- Здоровье, безопасность и дисциплина
- Школьные доски
- Поддержка школ и студентов из группы риска
- Отказы
-
Академики
- Колледж, карьера и военная подготовка
- Стандарты учебной программы
- Дошкольное образование
- Информация об окончании
- Учебные материалы
- Поддержка обучения и программы
- Особые группы студентов
- Тематические области
-
Финансы и гранты
- Финансовая ответственность
- Финансовое соответствие
- Гранты
- Государственное финансирование
- Фонд постоянной школы Техаса
-
Отчеты и данные
- Подача данных
- Данные преподавателя
- Финансовые отчеты
- Законодательная информация
- Оценка программы
- Данные школы
- Школьное представление
- Данные студентов
-
Оценка учащихся
- Тестирование
- Свидетельство об эквивалентности средней школы (TxCHSE)
- Счет за дом 3906
- Мониторинг и вмешательства
-
Педагоги Техаса
- Сертификация
- Система оценки и поддержки преподавателей
- Образовательные инициативы
- Расследования
- Подготовка и непрерывное образование
- Заработная плата и послужной список
Популярные приложения
- Спросите TED
- ЭКОС для преподавателей
- Возможности гранта
- Безопасные приложения
- TEAL Войти
- TSDS
Меню
Приложения
Поиск
Поиск
Утилита
- Индекс A – Z
- Связаться с нами
- Занятость
- Подпишитесь на обновления
- ЧАЙ Переписка
Переключить навигацию
Основная навигация
-
О ЧАЕ
-
Добро пожаловать и обзор
- Стратегический план
- Индекс A – Z
- Календари
- Занятость
- Глоссарий сокращений
-
Агентство Финансы
- Контракты и закупки
- Запрос на законодательные ассигнования
-
Свяжитесь с нами
- Жалобы и расследования
- Справочник отделов
- Равные возможности для получения образования
- Общий запрос
- Справочник персонала
-
Законы и правила
- Правила комиссара (TAC)
- Правила SBEC (TAC)
- Правила SBOE (TAC)
- Правила и положения специального образования
-
Лидерство
- Комиссар
- Заместители комиссара
- Государственный совет образования
- Государственный совет по сертификации педагогов
-
Отношения с государством и юридические
- Консультативные комитеты законодательного собрания 86-го созыва
- Правительственные отношения
- Слушания и апелляции
- Дом Bill 3
- Публичная информация
- Разрешение споров в сфере специального образования
-
Добро пожаловать и обзор
Тест по математике в шестом классе
Перед началом распечатайте свой тест по математике для шестого класса.Постарайтесь ответить на все вопросы.
Имя __________________ Дата: __________________
Решите следующие задачи
1.
В приведенном ниже уравнении, каково значение x
20 = x + (2 × 8) – 6
2.
У Сары 30 карандашей. У ее подруги Сильвии на k карандашей меньше. Какое выражение показывает количество карандашей у Сильвии?
A. 30 + к B. k – 30 C. 30 – k D. 30 – 2k
3.
Треугольник ABC подобен треугольнику DEF
Какова длина DF?
A. 2 дюйма B. 1 дюйм C. 3 дюйма D. 1,5 дюйма
4.
Какое значение имеет приведенное ниже выражение?
5 3
A. 15 B. 8 C. 25 D. 125
5.
Используйте следующий список, чтобы найти среднее или среднее значение, медиану, моду и диапазон
10, 15 , 5, 8, 6, 6, 2
Среднее значение = ___________
Медиана = __________
Режим = ___________
диапазон = __________
6.
-5 – 8 = _______
5-8 = _______
-8-5 = ______
7.
Нарисуйте систему координат в пространстве ниже, а затем постройте (2,5) и (-4, 2)
8.
Найдите периметр и площадь прямоугольника ниже:
Периметр = _____________ единиц
Площадь = __________________ квадратных единиц
9.
Возьмите кубик и бросьте его.
Различные исходы: __________________________
Напишите вероятность получения четного числа ____________
Напишите вероятность получения нечетного числа ____________
Напишите вероятность получения простого числа ____________
10.
Сложите 3/5 и 2/7 _____________
11.
Для числа 76.2345 значение цифры 4 будет
A. 4 десятков B. 4 десятых C. 4 тысячных D. 4 десятитысячных
12.
Если 9450 / x равно 21, что такое x? ________________
13.
Поместите следующие числа в порядке от меньшего к большему
-1/4, 7/4, 0.90, -2/4, 0.20, 3/4, 1.50, -0.50,
_____, ______, ______, ______, ______, _______, ______, _______
14.
a. Вы хотите сэкономить на покупке велосипеда. Вы начинаете с 50 долларов и экономите 4 доллара каждый день. Какое выражение показывает, сколько денег у вас будет через x дней?
50 – 4x
4x – 50
4x + 50
50 + 4 × 10
б. Сколько денег у вас будет через 20 дней?
А. 120 долларов Б. 130 долларов C. 110 долларов D. 200 долларов
15.
a. Запишите все составные числа больше 10 и меньше 20 (Подсказка: их 5
_________, __________, __________, ____________, ____________,
Выберите составное число и запишите все множители в поле под
б) Запишите все простые числа больше 10 и меньше 20 (Подсказка: их 4
_________, __________, ___________, ____________
16.
Сколько линий симметрии у квадрата? ____________
17.
Диаметр круга 8 дюймов
Периметр и площадь:
A. P = 4 пи и A = 12 пи B. P = 16 пи и A = 8 пи C. P = 8 пи и A = 16 пи D. P = 16 пи и A = 4 пи
18.
У Джона и Питера вместе 40 долларов. Если у Джона в 4 раза больше денег, чем у Питера.Сколько денег у каждого? (Подсказка: попробуйте методом проб и ошибок)
У Джона есть ____________ долларов
У Питера ____________ долларов
19.
Машина производит 5000 единиц товара за 6 минут. Какая пропорция не может быть использована для определения количества минут для производства 15000 изделий?
A. 5000/6 = 15000 / x B. 5000/6 = x / 15000 C. 6 / x = 5000/15000 D. 6/5000 = x / 15000
20.
Вы идете в ресторан и покупаете еду на 120 долларов. Ресторан требует чаевых 15%. Какая у вас сумма?
21.
На карте 1 дюйм означает 30 миль. Сколько дюймов покажет расстояние в 120 миль? __________
22.
Ящик содержит 6 синих шариков, 4 желтых шарика и 10 красных шариков.
Какова вероятность выбора красного мрамора?
А. 4/20 B. 3/20 C. 6/20 D. 10/20
Какой цвет будет выбран с меньшей вероятностью? ___________
23.
а. Напишите краткое определение конгруэнтности
Сделайте рисунок, чтобы показать две конгруэнтные формы
b. Напишите краткое определение сходства
Нарисуйте на рисунке две одинаковые формы
24.
Покрутите каждый счетчик один раз и перечислите все возможные результаты (Подсказка: один результат равен 2 и белый)
Какова вероятность получить 1 и красное? __________
25.
Оцените числовое выражение ниже:
(8 + 2) [(7 – 3) × 5]
A. 100 B. 150 C. 300 D. 200
26.
Какова сумма углов в пятиугольнике? (Подсказка: разделите пятиугольник на треугольники. Треугольник равен 180 градусам)
27
a. Сколько дюймов в 3 и 1/2 футах?
г. Сколько метров в 500 сантиметрах?
28.
Каков объем и площадь поверхности следующей прямоугольной призмы?
Объем = _______________
Площадь поверхности = ______________
29.
a. Форма бассейна больше похожа на
A. Прямоугольная призма B. Круг C. пирамида D. Сфера
b. Поищите футбольное поле в Интернете.Затем найдите 4 геометрические фигуры
_________, __________, ____________, __________
30.
Вы идете по магазинам и видите знак с надписью: «Купите 1 футболку и получите скидку 20% на вторую футболку. Футболка стоит 30 долларов, и вы покупаете 2 футболки. Какова ваша сумма? __________
Примечание : результат 25 или более баллов на этом тесте по математике в шестом классе является хорошим показателем того, что большинство навыков преподается в Были освоены 6-й класс
Если вы много боролись с этим тестом по математике в 6-м классе, попросите кого-нибудь помочь вам
Хотите получить решение для этого теста? Добавьте в корзину и приобретите Подробное 18-СТРАНИЦНОЕ РЕШЕНИЕ и ПРЕВОСХОДНЫЕ ОБЪЯСНЕНИЯ с PayPal.
Я изо всех сил старался сделать этот тест по математике для 6-го класса в соответствии с национальными стандартами
Чтобы распечатать этот тест по математике для 6-го класса, нажмите здесь
К этому тесту по математике для 6-го класса относится тест по математике для 5-го класса
-
Введение в физику
18 ноя, 20 13:20
Первоклассное введение в физику. Универсальный ресурс для глубокого понимания важных концепций физики
Подробнее
Новые уроки математики
Ваша электронная почта в безопасности.Мы будем использовать его только для информирования вас о новых уроках математики.
XII. Математика, 6 класс – Скачать PDF бесплатно
1 XII. Математика, 6 класс
Тест по математике для 2-х классов Весной 1-го класса тест по математике для 6-го класса был основан на учебных стандартах по пяти основным направлениям учебной программы по математике штата Массачусетс (000), перечисленным ниже.Номера страниц для 5 классов 6 Стандартные стандарты обучения указаны в скобках. Смысл чисел и операции (Framework, страницы 5 6) Шаблоны, отношения и алгебра (Framework, страница 34) Геометрия (Framework, страница 4) Измерение (Framework, страница 50) Анализ данных, статистика и вероятность (Framework, страница 58) Структура учебной программы по математике доступна на веб-сайте факультета в разделе «Математика». Результаты тестов представлены в пяти категориях отчетности MCAS, которые идентичны пяти направлениям содержания структуры, перечисленным выше.Тестовые сессии Тест по математике для 6 класса включал в себя две отдельные тестовые сессии. Каждая сессия включала вопросы с множественным выбором, короткие и открытые ответы. Примерно половина общих тестовых заданий показана на следующих страницах в том виде, в котором они представлены в тестовых буклетах. Справочные материалы и инструменты Каждому ученику, сдававшему тест по математике для 6 класса, была предоставлена пластиковая линейка и справочный лист по математике для 6 класса. Копия справочного листа следует за последним вопросом в этой главе.Изображение правителя в данной публикации не воспроизводится. Использование двуязычных дословных словарей было разрешено только для нынешних и бывших студентов, изучающих английский язык, во время обеих тестовых сессий по математике. Использование калькуляторов, других справочных инструментов или материалов не разрешалось. Информация о перекрестных ссылках В таблицах в конце этой главы указаны категории отчетности для каждой выпущенной и невыпущенной общей позиции и стандарт обучения, который она оценивает. Правильные ответы на выпущенные вопросы с множественным выбором и краткие ответы также отображаются в таблице выпущенных элементов.195
3 Математика. Занятие 1 Вы можете использовать свой справочный лист и линейку MCAS во время этого занятия. Вы не можете использовать калькулятор во время этого сеанса. НАПРАВЛЕНИЯ Это занятие содержит девять вопросов с несколькими вариантами ответов, два вопроса с кратким ответом и один вопрос с открытым ответом. Отметьте свои ответы на эти вопросы в полях в вашем буклете для ответов учащегося.ID: _AR1.eps Обычный 1 Джиллиан работает на горнолыжном курорте. Она записала количество сноубордов, которые были взяты напрокат каждый день в течение двух недель, на участке стеблей и листьев ниже. Количество сноубордов, арендуемых каждый день ID: 99675 C Обычный Что из следующего эквивалентно выражению ниже? 6 5 A B C D. 5 6 Обозначение 6 3 представляет 63 Каков режим данных на графике «стебель-лист»? А. 53 Б. 66 С. 75 D
4 Математика Сессия 1 ID: 17541 RJR015-scale.eps [stem_01 C Common 3 Шкала, показанная ниже, сбалансирована. Основываясь на этой шкале, что из следующего показывает правильное соотношение между массой одного куба и массой сфер? ID: 9001 D Common 4 В июне и июле Йонас продал 319 чашек лимонада. В июне он продал 136 чашек лимонада. Что из перечисленного соответствует количеству чашек лимонада, проданных Джонас в июле? А Б В Г А. Б. С. Д. 197
5 Математика Сессия 1 ID: 7187 CMC18_graphs.eps [opt_a0 B Common 5 На каком из следующих графиков показана постоянная скорость изменения между переменными x и y? A. y C. y x x B. y D. y x x 198
6 Математика Сессия 1 Вопросы 6 и 7 – это вопросы с короткими ответами. Напишите свои ответы на эти вопросы в полях в буклете для ответов учащегося. Не записывайте свои ответы в этот тестовый буклет. Вы можете делать свои расчеты в тестовом буклете.ID: 8894 Обычный 6 Что такое 5% в простейшей форме? D: 65897 Общий 7 Каково значение выражения ниже, когда 5?
7 Математика. Занятие 1 Отметьте ответы на вопросы с несколькими вариантами ответов с 8 по 11 в отведенных местах в буклете для ответов учащегося. Не записывайте свои ответы в этот тестовый буклет. Вы можете делать свои расчеты в тестовом буклете.ID: _AR1.eps B Общий 8 На графике ниже показано количество миль, которые Майкл проезжал на велосипеде каждую неделю в течение четырех недель. Miles Ridden y 0 15 Количество миль x Номер недели Какова взаимосвязь между количеством миль, которые Майкл проехал на велосипеде, и номером недели? A. Количество миль в неделе номер 5 B. Количество миль в неделе номер 5 C. Количество миль в неделе номер 5 D. Количество миль в неделе номер 5 00
8 Математика, сессия 1 ID: 17519 PB00017_Numberline.eps A Общий 9 Какое из следующих уравнений лучше всего представлено в числовой строке ниже? A. (4) B. () 0 C. 4 () D. 0 () ID: 864 D Обычный 10 Вики написала уравнение, показанное ниже, в своей записной книжке. x 9 6 Какое из следующих уравнений также должно быть истинным, чтобы уравнение Вики было верным? A. x 9 6 B. x 9 6 C. x 6 9 D. x
9 Математика Сессия 1 ID: 8883 ME007_negative_number_lin B Общие 11 точек A, B, C и D показаны в числовой строке ниже.A B C D Какая точка находится на числовой прямой? A. точка A B. точка B C. точка C D. точка D 0
10 Математика Сессия 1 Вопрос 1 – это открытый вопрос. ОБЯЗАТЕЛЬНО ОТВЕТИТЕ И ПОМЕТИТЕ ВСЕ ЧАСТИ ВОПРОСА. Покажите всю свою работу (диаграммы, таблицы или вычисления) в буклете для ответов учащегося. Если вы делаете работу в уме, объясните письменно, как вы ее проделали.Напишите свой ответ на вопрос 1 в отведенном для этого месте в буклете для ответов учащегося. ID: 8475 AL86140_scale_stem_01.ep Обычный 1 января использует карту для планирования двухдневного похода. Масштаб карты, которую она использует, показан ниже. Масштаб 1 дюйм: 1 миля a. Расстояние, которое Ян преодолеет в первый день, равно 1 дюйму на карте. Какое фактическое расстояние в милях Ян преодолеет в первый день? Покажите или объясните, как вы получили свой ответ. б. Фактическое расстояние, которое Ян преодолеет во второй день, составляет 5 миль.Какое расстояние на карте в дюймах соответствует 5 1 милям? Покажите или объясните, как вы получили свой ответ. c. Судя по шкале, которую использовал Ян, сколько футов соответствует 1 дюйму на карте? Покажите или объясните, как вы получили свой ответ. (1 миля футов) 03
11 Математическое занятие Во время этого занятия вы можете использовать свой справочный лист и линейку MCAS. Вы не можете использовать калькулятор во время этого сеанса.НАПРАВЛЕНИЯ Это занятие содержит семь вопросов с несколькими вариантами ответов, один вопрос с кратким ответом и один вопрос с открытым ответом. Отметьте свои ответы на эти вопросы в полях в вашем буклете для ответов учащегося. ID: 6467 C Common 13 В таблице ниже показано расстояние в милях, которое мистер Кляйн проезжал каждый день в течение 5 дней. Дистанция проезда г-на Кляйна Количество миль в день Какое среднее количество миль в день проезжал г-н Кляйн за 5 дней? ID: 865 C Обычные 14 коробок Джин и Клинт на складе.Джин складывает 50 коробок в час. Клинт складывает 60 коробок в час. Какое из следующих выражений представляет общее количество ящиков, которые Жан и Клинт складывают в h часов, где h – любое количество часов? A. 50h 60 B h C. 50h 60h D. 50 h 60 h A. 76 B. 98 C. 104 D
12 Идентификатор сеанса математики: 66109 AL661108_fraction_options D Общий 15 Что из следующего представляет часть рисунка X, которая закрашена? Рисунок X A.1 Б. 3 С. 4 5 Д
13 Идентификатор сеанса математики: 7175 CMC06_table.eps, [opt_a0 B Common 16 Джо хочет принять участие в гоночной игре. Участие в первой гонке стоит 5 долларов. Участие в каждой дополнительной гонке стоит $. В какой из следующих таблиц правильно представлена стоимость участия в гонках в игре? A. Стоимость гоночной игры Количество гонок Стоимость 1 $ 4 3 $ 6 4 8 $ C. Стоимость гоночной игры Количество гонок Стоимость 1 $ 5 10 $ 3 15 4 $ 0 B.Стоимость гоночной игры Количество гонок Стоимость 1 5 долларов 7 долларов 3 9 4 11 долларов D. Стоимость гоночной игры Количество гонок Стоимость 1 5 долларов США 1 3 19 долларов 4 6 долларов США 06
14 Математика Вопрос 17 сессии – это вопрос с коротким ответом. Напишите свой ответ на этот вопрос в поле в буклете для ответов учащегося. Не пишите свой ответ в этом тестовом буклете. Вы можете делать свои расчеты в тестовом буклете.ID: 8349 mjb130_crackers.eps Common 17 Коробка с крекерами имеет форму прямоугольной призмы и ее размеры показаны на схеме ниже. 6 см 0 см 15 см Какова площадь поверхности коробки с крекерами в квадратных сантиметрах? 07
15 Математика Вопрос 18 сессии – открытый вопрос. ОБЯЗАТЕЛЬНО ОТВЕТИТЕ И ПОМЕТИТЕ ВСЕ ЧАСТИ ВОПРОСА. Покажите всю свою работу (диаграммы, таблицы или вычисления) в буклете для ответов учащегося.Если вы делаете работу в уме, объясните письменно, как вы ее проделали. Напишите свой ответ на вопрос 18 в отведенном для этого месте в буклете для ответов учащегося. ID: 51347 Обычный 18 Мисс Диас работает в зоопарке. Она создала выставку с животными, перечисленными в таблице ниже. Тип животного Экспонат Число животных слон 8 жираф 1 носорог 4 a. Какая часть животных – жирафы? Упростите свой ответ до самых низких терминов. Покажите или объясните, как вы получили свой ответ. Г-жа Диас планирует добавить на выставку больше животных.Она добавит еще слонов. Она добавит еще жирафов и носорогов, чтобы соотношение слонов к другим животным было таким же, как и раньше. б. Какое новое общее количество животных будет на выставке? Покажите или объясните, как вы получили свой ответ. 08
16 Урок математики Отметьте ответы на вопросы с несколькими вариантами ответов с 19 по 1 в отведенных местах в буклете для ответов учащегося.Не записывайте свои ответы в этот тестовый буклет. Вы можете делать свои расчеты в тестовом буклете. ID: 89 D Обычный 19 У мисс Джарман была коробка с 10 карандашами. Она дала каждому ученику в классе по 6 карандашей. Остался 1 карандаш. Мисс Джарман выбрала n, чтобы обозначить количество учеников в ее классе. Она написала уравнение ниже, чтобы представить эту ситуацию. 6 n 1 10 Какое значение n делает уравнение мисс Джарман верным? A. 6 B. 10 C. 1 D. 18 ID: 51458 WDN058_intersection.eps B Общий 0 Мишель нарисовала на листе бумаги показанные ниже отрезки линий.K E I G Какая из следующих пар отрезков кажется перпендикулярной? A. GH и KL B. GH и IJ C. EF и KL D. EF и GH F J H L ID: 17478 A Common 1 Какая из следующих трехмерных форм имеет 1 прямоугольную грань и 4 треугольные грани? A. прямоугольная пирамида B. треугольная пирамида C. прямоугольная призма D. треугольная призма 09
17 Массачусетс Департамент НАЧАЛЬНОЙ И ВТОРИЧНОЙ СИСТЕМЫ Y Массачусетская комплексная система оценивания 6-й класс Справочный лист по математике ФОРМУЛЫ ПЕРИМЕТРА ФОРМУЛЫ ОБЪЕМА расстояние по периметру 5 вокруг прямоугольной призмы….. V 5 lwh квадрат P 5 4s прямоугольник P bh OR P lw треугольник P abc ФОРМУЛ ОБЛАСТИ куб V sss (длина ребра s 5) ФОРМУЛЫ КРУГА C 5 πr ИЛИ C 5 πd A πr квадрат A ss прямоугольник A 5 bh OR A 5 lw параллелограмм ….. A 5 bh треугольник A 5 1 bh круг A πr 10
Математика, 18 класс, Весна 01 Выпущенные задания: Категории отчетов, стандарты и правильные ответы * Пункт №Номер страницы Категория отчета Стандартный правильный ответ (MC / SA) * Анализ данных, статистика и вероятность 6.D.1 Смысл и операции 196 чисел 6.N.1 C Шаблоны, отношения и алгебра 6.P.5 C Смысл числа и операции 6.N.9 D Паттерны, отношения и алгебра 6.P.7 B Смысл числа и операции 6.N Паттерны, отношения и алгебра 6.P Паттерны, отношения и алгебра 6.P.6 B 9 01 Смысл чисел и операции 6.N.10 A Паттерны, отношения и алгебра 6.P.3 D 11 0 Смысл чисел и операции 6.N.6 B 1 03 Измерение 6.M Анализ данных, статистика и вероятность 6.D.1 C Паттерны, отношения и алгебра 6.P.4 C Смысл числа и операции 6.N.4 D Паттерны, отношения и алгебра 6 .P.4 B Измерение 6.M Смысл чисел и операции 6.N, 00 квадратных сантиметров Шаблоны, отношения и алгебра 6.P.5 D 0 09 Геометрия 6.G.3 B 1 09 Геометрия 6.G. A * Ответы предоставляются здесь только для вопросов с несколькими вариантами ответов и вопросов с короткими ответами. Образцы ответов и рекомендации по выставлению оценок для вопросов с открытым ответом, которые обозначены затененными ячейками, будут размещены на веб-сайте Департамента в конце этого года.11
19 Класс 6 Математика Весна 01 Невыпущенные общие элементы: Категории и стандарты отчетности № элемента Категория отчета Стандартные шаблоны, отношения и алгебра 6.P.4 3 Значение и операции с числами 6.N.5 4 Значение и операции с числами 6.N .7 5 Смысл чисел и операции 6.N.14 6 Паттерны, отношения и алгебра 6.P.4 7 Геометрия 6.G.1 8 Паттерны, отношения и алгебра 6.P. 9 Геометрия 6.G.9 30 Измерение 6.M.1 31 Измерение 6.M.6 3 Измерение 6.M.4 33 Паттерны, взаимосвязи и алгебра 6.P.6 34 Определение числа и операции 6.N Смысл чисел и операции 6.N.8 36 Смысл чисел и операции 6.N.4 37 Геометрия 6.G.4 38 Паттерны, отношения и алгебра 6.P.5 39 Смысл чисел и операции 6.N.7 40 Число Смысл и операции 6.N Смысл числа и операции 6.N.13 4 Анализ данных, статистика и вероятность 6.D. 1
12 класс Математика | Образ мышления Изучите
класс 12 по математике | Образ мышления учиться- Математика
- 12 класс Математика
Редакция видео
Редакция видео
Редакция видео
Редакция видео
Редакция видео
Редакция видео
Редакция видео
Редакция видео
