Все геометрические фигуры мы изображаем на листе бумаги карандашом, на школьной доске мелом или маркером. Часто летом мелом или белым камушком мы рисуем фигуры на асфальте. И всегда, прежде чем начинать рисовать задуманное, мы оцениваем, хватит ли нам места. А так как мы редко знаем точные размеры нашего будущего рисунка, то всегда места нужно взять с запасом, и лучше с большим запасом. Обычно мы не боимся, что место для рисования кончится, если поле для рисования во много раз больше, чем сам рисунок. Так асфальта во дворе вполне хватит, чтобы начертить поле для прыганья. Тетрадного листа достаточно, чтобы посредине начертить два пересекающихся отрезка.
В математике таким полем, на котором мы все изображаем, является плоскость (рис. 1).
Рис. 1. Плоскость
Она обладает двумя качествами:
1. На ней можно изобразить любую фигуру, про которую мы уже говорили, или еще будем говорить.
2. Мы не дойдем до края. Ее размеры можно считать намного большими, чем размеры рисунка.
То обстоятельство, что мы никогда не доходим до края плоскости, можно понимать как отсутствие краев вообще. Нам не нужны ее края, вот мы и договорились считать, что их нет (рис. 2).
Рис. 2. Плоскость бесконечна
В этом смысле плоскость бесконечна в любую сторону.
Мы можем представлять ее как большой лист бумаги, большую ровную асфальтовую площадку или огромную доску для рисования.
Геометрических фигур бесконечное множество, и изучить их все совершенно невозможно. Но геометрия устроена во многом как конструктор. Есть несколько видов основных деталей, из которых можно построить все остальное, любую самую сложную постройку.
Этот принцип можно сравнить со словами и буквами: мы знаем все буквы, но не знаем всех слов. Встретив незнакомое слово, мы сможем его прочитать, так как знаем, как буквы пишутся и как произносятся соответствующие звуки.
Так и в математике – существует совсем немного основных геометрических фигур, которые нам с вами нужно хорошо знать.Рассмотрим отрезок (рис. 3). Отрезок – это кратчайшая линия, соединяющая две точки.
Рис. 3. Отрезок
Продолжим отрезок в обе стороны до бесконечности. Продолжать будем тоже прямо.
Что значит «прямо»? Рассмотрим отрезки и (рис. 4).
Рис. 4. Отрезки и
Продолжим их в обе стороны. Верхняя линия прямая, а нижняя нет (рис. 5).
Рис. 5. Прямая линия и непрямая линия
Добавим еще по одной точке на верхнюю и нижнюю линию и (рис. 6). Часть верхней линии между точками и тоже является отрезком, а часть нижней линии между точками и отрезком не является, так как он не соединяет эти точки по самому короткому пути.
Рис. 6. Продолжение линий и
Прямая – это линия, продолжающаяся бесконечно в обе стороны, любая часть которой, ограниченная двумя точками, является отрезком.
Прямая – это тип линии, и, как любая линия, прямая является фигурой. И, как для любой линии, данная точка либо принадлежит данной прямой, либо нет (рис. 7).
Рис. 7. Точки и , принадлежащие прямой, и точки и , не принадлежащие прямой
1. Прямая делит плоскость на две части, на две полуплоскости. На рисунке 8 точки и лежат в одной полуплоскости, а и – в разных полуплоскостях.
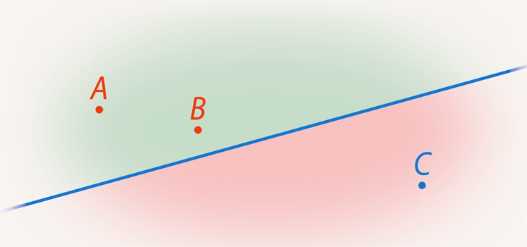
Рис. 8. Две полуплоскости
2. Через две точки всегда можно провести прямую, причем только одну (рис. 9).
Рис. 9. Прямая, проведенная через две точки
Прямую, как и любую линию, можно отметить одной строчной буквой латинского алфавита или последовательностью точек, которые на ней лежат. Чтобы обозначить прямую через точки, лежащие на ней, достаточно двух точек.
Продлив отрезок в обе стороны до бесконечности, получили прямую. Если так же продлить отрезок, но всего лишь в одну сторону до бесконечности, получим фигуру, которая называется луч (рис. 10). Этот геометрический луч очень похож на световой луч, поэтому он так и называется. Если взять в руки лазерную указку, то луч света будет начинаться в указке и уходить в бесконечность по прямой.
Рис. 10. Луч
Точка называется началом луча. Обозначается луч .
Если на прямой отметить точку , то она делит эту прямую на два луча (рис. 11). Оба луча имеют начало в точке , но направлены в разные стороны. Два этих луча составляют прямую, являются ее половинами. Поэтому луч часто еще называют «полупрямая».
Рис. 11. Точка делит прямую на два луча
Рассмотрим рисунок 12.
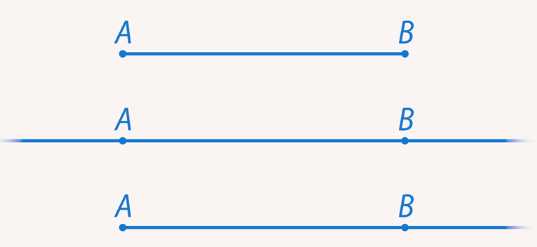
Рис. 12. Отрезок, прямая и луч
Разберемся, в чем похожи и не похожи друг на друга отрезок, прямая и луч:
– отрезок и луч легко достраиваются до прямой, отрезок для этого нужно продолжить в обе стороны, а луч в одну;
– на прямой всегда можно выделить отрезок или луч;
– точка делит прямую на два луча, на две полупрямые;
– точки и ограничивают на прямой отрезок ;
– все эти фигуры: отрезок, луч, прямая – являются «прямыми линиями». Различаются они наличием концов. У отрезка их два, у луча один, у прямой ни одного. Иначе можно сказать еще так: и луч, и отрезок являются частью прямой;
– нам известно, что у отрезка можно измерить его длину. Два отрезка можно сравнить, выяснить, какой из них длиннее;
– прямая же бесконечно продолжается в обе стороны, луч – в одну сторону. По этой причине невозможно измерить длину прямой или луча, также невозможно сравнить по длине две прямых или два луча. Они все одинаково бесконечны.
Два луча, имеющие свои начала в одной точке, образуют еще одну геометрическую фигуру из основного набора – угол. Точка, начало обоих лучей, называется вершиной угла. Сами лучи называются сторонами угла.
Итак, угол – это фигура, состоящая из двух лучей, выходящих из одной точки (рис. 13).
Рис. 13. Угол
Обозначают угол одной буквой, соответствующей обозначению вершины. В данном случае угол можно назвать угол (рис. 14). Чтобы было понятно, что речь идет именно об угле, а не о точке, перед его названием надо написать слово «угол» или поставить специальный знак угла («»).
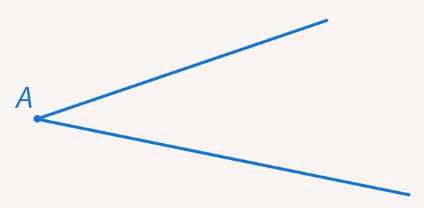
Рис. 14. Угол
Если по вершине сложно понять, о каком именно угле идет речь, как на рисунке 15, то используют еще две точки на обеих сторонах угла.
Если просто назвать угол на этом рисунке, то непонятно, о каком конкретно идет речь, ведь с вершиной в точке мы видим несколько у
interneturok.ru
Немецкий учений Гильберт как-то сказал на эту тему, что “точкой можно назвать хоть стул”, тем самым говоря, что вся наша модель строится на некоторых условностях.
С этим пониманием приступим к первой теме урока.
Для начала нам нужно понять, что такое поверхность.
Есть много строгих математических формулировок, но они уместны скорее в высших учебных заведениях, пока будет достаточно обиходного понятия поверхности.
Будем понимать под поверхностью непрерывное множество точек, границу, отделяющую геометрическое тело от внешнего пространства.
Представьте себе поверхность рабочего стола, футбольного мяча или любого другого предмета.
Также известно, что некоторые поверхности, например, рабочего стола, плоские.
Так мы подходим к понятию плоскости. Плоскость – плоская, бесконечная поверхность.
Плоская в данном случае обозначает, что если через любые две точки, принадлежащие этой плоскости, провести прямую, то она будет лежать в этой плоскости.
В самом деле, если нарисовать две точки на поверхности стола и соединить их прямой, то эта прямая будет лежать в плоскости стола.
Если же отметить две точки на шаре, то (тут нужен некоторый мысленный эксперимент) прямая, соединяющая их, будет проходить внутри шара, а не по его поверхности. Таким образом, поверхность шара не плоская, не является плоскостью.
Сейчас очень важно понять, что плоскость – это некоторое математическое понятие, соответствующее нашим бытовым плоским поверхностям с главным отличием в том, что у плоскости нет края.
Обычно на рисунках плоскость обозначается конечной, в крайнем случае лист бумаги или экран компьютера конечен.
Но это лишь обозначения, сама плоскость бесконечна
Поверхности и плоскости принято обозначать двумя способами: с помощью трех латинских букв, соответствующих трем точкам плоскости, или одной греческой.
Выше изображена четырехугольная пирамида. В ней можно насчитать 5 плоскостей:
Согласись, две точки слишком мало, чтобы обозначить плоскость: на данном рисунке, например, есть две плоскости, проходящие через точки A и E, а четыре точки уже несут избыточную информацию, поэтому плоскости обозначают тремя точками.
Иногда плоскость обозначают одной строчной греческой буквой, например, так:
ladle.ru
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике – это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка – две граничные точки.
На рисунке мы видим следующее: отрезки [A;C],[C;D],[D;M],[M;F],[F;E] и [E;T], а также две точки B и S.
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая – это отрезок, который не имеет двух концов.
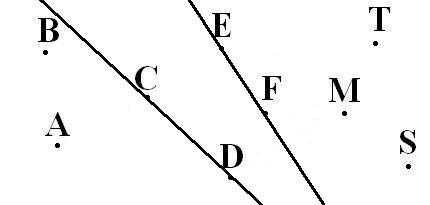
На рисунке изображены две прямые: CD и EF.
Что же такое луч? Определение луча в математике: луч – часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
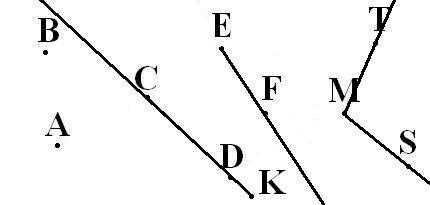
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD – один луч, т.к. у них общее начало.
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
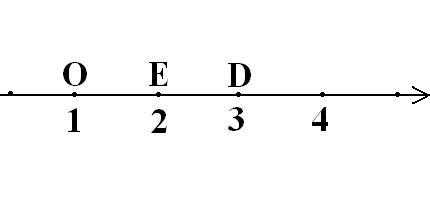
На рисунке изображена числовая прямая, а также луч OD и ED
Все неприличные комментарии будут удаляться.
www.nado5.ru
ПЛАН-КОНСПЕКТ УРОКА
Прямая.Луч.Отрезок.
ФИО (полностью)
Борсук Наталия Сергеевна
Место работы
МБОУ СОШ № 35 г.Симферополь
Должность
Учитель
Предмет
Математика
Класс
5
Тема урока в теме
Прямая. Луч. Отрезок.
Цели урока:
Цель урока: формировать представление о прямой, отрезке и луче, развивать умение решать геометрические задачи.
Задачи:
– образовательные (формирование познавательных УУД):
Выявить и сформировать умения распознать различия между прямой, лучом и отрезком. Научить стороить данные фигуры в различных условиях.
– развивающие (формирование регулятивных УУД)
умение обрабатывать информацию и ранжировать ее по указанным основаниям; планировать свою деятельность в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Учить устанавливать единые и общие признаки;
Учить классифицировать факты, делать обобщающие выводы
– воспитательные (формирование коммуникативных и личностных УУД):
умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, воспитывать ответственность и аккуратность.
Воспитание мотивов учения, положительного отношения к знаниям
Тип урока: Комбинированный.
Формы работы учащихся: Фронтальная, групповая, индивидуальная
Необходимое оборудование: Компьютер, проектор, учебники по математике, электронная презентация, выполненная в программе Power Point.
Ход урока
Задачи урока: повторить понятия прямой и отрезка и ввести понятие луча, закрепить умение строить прямые, отрезки и лучи. Развивать умение решать геометрические задачи.
Отработать навыки построения геометрических фигур.
Воспитание дисциплинированности;
Формировать умения выделять главное;
Учить преодолевать трудности при достижении поставленной цели;
Развивать умения владеть собой, выдержку, самообладания;
Развивать умения действовать самостоятельно.
Обучающиеся должны:
Иметь представление о прямой, отрезке и луче;
Уметь:
уметь распознавать данные фигуры;
строить прямую, отрезок, луч;
отражать в письменной форме результаты деятельности;
проводить информационно смысловой анализ прочитанного текста;
решать текстовые задачи с разными условиями постановки задачи;
рассуждать, обобщать аргументировано отвечать на вопросы собеседников, вести диалог.
1. Организационный момент.(1 слайд)
Проверка готовности класса, организация внимания.
Устный счет.
Актуализация знаний: вспомнить понятия точки, прямой, отрезка, полученные ранее.
Отработка пройденного материала. Решение упражнений
и отметьте на нем точку O. Запишите все получившиеся отрезки.
2.Физминутка.
Закрепление изученного материала, решение практических заданий:
1.Какие точки лежат на прямой АС?
2.Какие точки не лежат на прямой АС?
3.Какие точки лежат на луче ВА?
4.Какие точки не лежат на луче ВА?
5.Определите, пересекаются ли:
Луч OD и прямая TM
Отрезок КС и луч OD
Прямая ТМ и отрезок КС
5. Подведение итогов урока.
– Оценивается работа класса и отдельных учащихся
– Достигли бы цели, которую ставили в конце урока?
– Все ли было понятно?
– Понравился ли вам урок?
Домашняя работа: №382,383,385 п.2.3
№
Этапы 1 урока
Название используемых ЭОР
Деятельность учителя
(с указанием действий с ЭОР, например, демонстрация)
Деятельность ученика
Время
(в мин.)
Формируемые УУД
Познаватель-
ные
Регулятивные
Коммуникатив-
ные
Личност-
ные
1
2
3
5
6
7
8
9
10
11
1
Организационный момент
1 слайд
Приветствие учащихся; проверка учителем готовности класса к уроку; организация внимания.
2
Осознанное и произвольное построение речевого высказывания
Прогнозирование своей деятельности
Умение слушать и вступать в диалог
Умение выделять нравственный аспект поведения
2
Актуализация знаний
Устный счет
2,3,4 слайды
5 слайд (тема урока)
6-7
Повторение
теоретических знаний
Вспомнить понятия точки, прямой, отрезка, полученные ранее.
Задает учащимся наводящие вопросы
Участвуют в работе по повторению, в беседе с учителем, отвечают на поставленные вопросы,
7
Анализ объектов с целью выделения признаков.
Выделение и осознание того, что уже пройдено.
Постановка цели учебной задачи.
Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог
Установление связи между целью деятельности и ее мотивом
3
Отработка пройденного материала. Решение упражнений.
Осмысление и закрепление знаний
8,9,10 слайды
Вместе с учениками определяет тему урока.
Задает вопросы, подводящие к определению понятий.
Учащиеся записывают тему урока в тетрадь.
Выполняют задание, отвечая на вопросы
проверяют правильность выполнения.
3
10
Поиск и выделение необходимой информации.
Структурирование знаний.
Подведение под понятие
Целеполагание, выдвижение гипотез
Планирование своей деятельности для решения поставленной задачи
Умение слушать и вступать в диалог
Коллективное обсуждение проблем (при необходимости)
Проявление терпения и аккуратности при построении чертежей
Физминутка
11 слайд
Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.
Учащиеся сменили вид деятельности (отдохнули) и готовы продолжать работу.
2
Осознание ценности здоровья
4
Закрепление изученного материала, решение практических заданий
12-14 слайды
Комментирует, направляет работу учащихся.
Постановка проблемного вопроса.
Один ученик у доски, остальные в тетради .
7
Выделение и формулирование познавательной цели, рефлексия способов и условий действия.
Решение у доски заданий
Со слайдов 12-14
10
Анализ объектов и синтез
Контроль изученного материала
Умение с достаточной полнотой и точностью выражать свои мысли
Проявление доброжелательности в дискуссии, доверия к собеседнику
5
Подведение итогов
15 слайд
Вносит корректировку в ответы учащихся Дает возможность самим ученикам оценить себя, затем оценивает учащихся с комментированием.
Рефлексия.
Подводят итог урока, оценивают себя своих товарищей
3
Осознанное и произвольное построение речевого высказывания
Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог
Ориентация в межличностных отношениях
6
Домашнее задание
16 слайд
Задаёт домашнее .
Записывают домашнее задание в дневник №382,383,385 п.2.3
1
www.metod-kopilka.ru
На этом уроке мы познакомимся с понятиями «отрезок», «прямая», «луч» и «плоскость». Рассмотрим расположение точек, отрезков, прямых и лучей в плоскости.
На прошлом уроке мы разобрались, как строить отрезок. Мы уже знаем, что отрезок – это прямая линия, ограниченная двумя точками.
Определение
Давайте начертим отрезок MN. Если продлить этот отрезок неограниченно за точку N, то мы получим новую фигуру, которая называется луч. У нас получился луч MN.
Точку М называют началом луча.
Если бы мы продлевали отрезок MN неограниченно за точку М, то у нас бы получился луч NМ, у которого точка N – начало луча.
Заметьте: обозначается луч большими заглавными буквами латинского алфавита, первой буквой записывают его начало, а затем букву, обозначающую какую-либо другую точку луча.
Обратите внимание, что луч имеет начало, но не имеет конца, т. е. он бесконечен в одну сторону.
Для того чтобы представить луч в окружающей среде, достаточно сфотографировать след от самолёта в безоблачном небе, где сам самолёт – это начальная точка, а след, оставленный на небе, – это прямая линия, которая бесконечна.
Либо солнечный луч, где начальная точка – это солнце, а конечной точки нет.
Определение
Если отрезок MN неограниченно продлевать в обе стороны – как за точку М, так и за точку N, то у нас получится фигура, которая называется прямой.
На рисунке у нас получилась прямая MN, также её можно назвать и прямая NМ. Как кому больше нравится!
Заметьте, что прямая не имеет ни начала, ни конца.
Любая точка прямой разделяет её на 2 луча.
В нашем случае точка О разделяет прямую MN на луч ОМ и луч ОN. Лучи, на которые точка разбивает прямую, называют дополнительными друг другу.
Представление о прямой можно получить, если сложить лист бумаги (линия, которая получилась при сгибе, и будет прямой) или туго натянуть верёвку.
В математике прямая представляется идеально ровной и бесконечной в обе стороны.
Прямую можно обозначить двумя вариантами.
1-й вариант: двумя заглавными буквами латинского алфавита, например MN. В таком случае говорят: «Прямая MN».
2-й вариант: прямую обозначают одной малой буквой, например m, и говорят: «Прямая m».
Давайте попробуем провести ещё одну прямую через эти же две точки.
У нас это не получится. Через любые две точки можно провести только одну прямую!
Точки, отрезки, лучи и прямые располагаются в плоскости. Примеры плоскостей в жизни мы встречаем каждый день. Представление о плоскости дают поверхности стола, оконного стекла или замёрзшего водоёма.
Только эти поверхности имеют границы, а плоскость в математике безгранична во всех направлениях. Мы рисуем фигуры на «кусках» плоскости, например в тетрадном листе или на школьной доске.
Теперь давайте рассмотрим расположение точек, отрезков, прямых и лучей в плоскости.
На рисунке изображены прямая EF и точки А, L, P и T. Точки А, E, F лежат на отрезке EF, а точки L, P, T не лежат на этом отрезке. Посмотрите, как это записывается.
Точки А, E, F лежат на луче EF, а точки А, E, F, Т лежат на луче FЕ. Посмотрите запись этих утверждений.
Точки А, E, F, Т лежат на прямой EF, а точки А, P, L – на прямой PL.
Обозначается это так:
Точка А лежит между точками Е и F. Точка L не лежит между точками Е и F, она находится вне отрезка EF. Точка Е лежит между точками А и Т, а точка А – между точками P и L.
На следующем рисунке изображены прямая a и прямая b.
Если две прямые имеют одну общую точку, то говорят, что они пересекаются в этой точке. В нашем примере прямые а и b пересекаются в точке О. Точка О делит каждую прямую на две части. Точка О – точка пересечения прямых.
Посмотрите на взаимное расположение прямых m и n:
Они не имеют общих точек. Если прямые не имеют общих точек, то говорят, что они параллельны.
Запомните!
· Прямая бесконечна.
· Отрезок ограничен.
· Луч имеет начало, но не имеет конца.
· Плоскость бесконечна.
Итоги
Итак, на уроке мы с вами разобрались в отличиях понятий «отрезок», «прямая», «луч». Научились их строить. Узнали, что такое плоскость, а также рассмотрели расположение точек, отрезков, прямых и лучей в плоскости.
videouroki.net
Дата: 13.11.2017
Учитель: Кольцова Н.А.
Тема:
Прямая, луч, отрезок
Тип урока:
Урок усвоения новых знаний, умений и навыков
Место урока в разделе:
Первый урок в теме «Измерение величин»
Оборудование:
Мультимедийный комплекс
Формы работы на уроке
Фронтальная, групповая, индивидуальная
Цели:
обучающие
(ориентированные на достижение предметных результатов обучения)
Ввести понятия “плоскость”, “луч”, “прямая”, “отрезок”; установить свойства изучаемых объектов; научить строить и распознавать данные фигуры.
развивающие (ориентированные на достижение метапредметных результатов обучения)
Развивать внимание, память, образное мышление; формировать самостоятельность и коммуникативность; создавать условия для проявления познавательной активности.
воспитательные (ориентированные на достижение личностных результатов обучения)
Воспитывать умение слушать, вступать в диалог, участвовать в коллективном обсуждении проблем;
УУД:
познавательные
Поиск и выделение необходимой информации;
анализ объектов с целью выделения признаков; выделение и формулирование познавательной цели, рефлексия способов и условий действий.
регулятивные
Прогнозирование своей деятельности; планирование своей деятельности для решения поставленной задачи.
коммуникативные
Умение слушать и вступать в диалог; умение с достаточной полнотой и точностью выражать свои мысли.
личностные
Установление связи между целью деятельности и ее мотивом; проявление внимания и терпения; проявление доброжелательности в дискуссии, доверия к собеседнику.
Приветствие учителя, проверка готовности учащихся к уроку.
II. Мотивация учебной деятельности
1. Сообщение темы (устный счет).
Решив все примеры и расположив ответы в порядке возрастания, вы сможете прочитать три слова, которые являются темой нашего урока (прямая, луч, отрезок).
2. Формулирование цели урока.
3. Актуализация опорных знаний, полученных в начальной школе.
(Вспомнить понятия точки, прямой, отрезка)
III. Восприятие и первичное осознание нового материала
1. Определение плоскости.
Поверхность стола, стена, классная доска, оконное стекло могут служить примером части плоскости. Всю плоскость невозможно изобразить потому, что она бесконечна, но ее можно представить себе (привести примеры части плоскости).
2. Определение и обозначение прямой.
– прямая не имеет ни начала, ни конца – она бесконечна;
– прямую обозначают одной строчной латинской буквой или двумя заглавными;
– через любые две точки можно провести только одну прямую;
– две прямые на плоскости могут пересекаться или быть параллельными.
3. Определение луча.
Точка А, лежащая на прямой, делит ее на две части. Каждую их этих частей называют лучом с началом в точке А, обозначают луч двумя заглавными буквами.
4. Определение отрезка.
– определение отрезка;
– обозначение отрезка;
– определение равных отрезков.
IV. Первичное применение новых знаний
Решение упражнений №342, 354, 355, 356, 359.
V. Физминутка
VI. Применение знаний в стандартных условиях с целью усвоения навыков
1. Фронтальный опрос (1 группа):
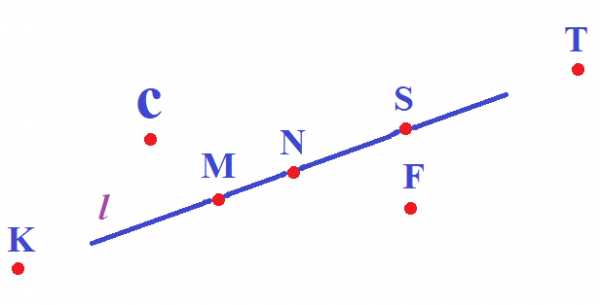
– Какие точки лежат на прямой l ?
– Какие точки не лежат на прямой l ?
– Назовите все лучи с вершиной в точках M, N, S?
– Какие точки не лежат на луче MS?
– Перечислите все отрезки, изображенные на рисунке.
2. Индивидуальная работа по карточкам (2 группа):
Тест (Приложение 1).
Начало формы
Конец формы
VII. Итог урока.
Сообщение домашнего задания:
Прочитать п.2.1. стр. 77-79, выполнить №353,357 – 1 группа;
№
infourok.ru
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:Презентация по математике 5 класс Н.А. Кольцова, Учитель математики МБОУ Ишунский УВК
2 слайд
Описание слайда:Решив все примеры и расположив ответы в порядке возрастания, вы сможете прочитать три слова, которые являются темой нашего урока. 15х0= (П) 44+150= (Р) 120:2= (Л) 32:32= (Р) 16-14= (Я) 25х4= (Ч) 160-80= (У) 90:10= (М) 11х10= (О) 920-800= (Т) 12+18= (А) 1000х15= (К) 1000:2= (О) 90-35= (Я) 50х4= (Е) 450-150= (З)
3 слайд
Описание слайда:Тема: Прямая. Луч. Отрезок Цель урока: Ввести понятия “плоскость”, “луч”, “прямая”, “отрезок”; установить свойства изучаемых объектов; научиться строить и распознавать данные фигуры.
4 слайд
Описание слайда:Актуализация опорных знаний Какие геометрические фигуры вы изучали в начальной школе? Что такое точка? Как она обозначается? Что такое прямая? Что называют отрезком?
5 слайд
Описание слайда:A Точки обозначаются большими буквами латинского алфавита
6 слайд
Описание слайда:Изучение нового материала: Плоскость
7 слайд
Описание слайда:Прямая
8 слайд
Описание слайда:Две прямые на плоскости могут пересекаться или быть параллельными
9 слайд
infourok.ru