Что изучают по математике в 5 классе: Рабочая программа по математике 5 класс | Рабочая программа по математике (5 класс) на тему:
Раздел | № урока | Тема урока | Кол-во часов | Форма проведения | Дата | Корр | По разделу | ||
Планируемые результаты | Контроль | Учебно-методическое обеспечение | |||||||
Глава 1 . Натуральные числа (20 часов) | 1 | Ряд натуральных чисел | 2 | Лекция практикум | 01. | натуральное число, ряд натуральных чисел | ИндивидуальноУстный опрос по карточкам. | П.1,№ 1 – 4 № 8 – 10 Презентация по теме урока | |
2 | 02.09 | ||||||||
3 | Цифры. Десятичная запись натуральных Чисел. | 3 | Лекция практикум | 03.09 | Цифры как символы для записи чисел, способ записи натуральных чисел с помощью позиционной системы «класс», «разряд», позиция цифры в десятичной записи многозначного числа | ИндивидуальноУстный опрос по карточкам. | П.2, № 19, 22, 25 № 26, 28, 30 № 32, 35 Презентация по теме урока | ||
4 | 04.09 | ||||||||
5 | 07.09 | ||||||||
6 | Отрезок. Длина отрезка | 4 | 08.09 | Отрезок, концы отрезка, длина отрезка, расстояние между точками Различные единицы измерения длины Ломаная, звенья ломаной, её длина | § 3, № 44, 46 № 50, 54, 57 № 60, 62 № 65, 69 | ||||
7 | 09. | ||||||||
8 | 10.09 | ||||||||
9 | 11.09 | ||||||||
10 | Плоскость. Прямая. Луч. | 3 | 14.09 | Представление о плоскости как поверхности, прямая, луч, начало луча | § 4, № 86, 89 № 93, 97, 100 | ||||
11 | 15.09 | ||||||||
12 | 16.09 | ||||||||
13 | Шкала. | 3 | 17.09 | Шкала, координатный луч, координата точки, единичный отрезок | § 5, № 114, 116, 119 № 122, 124, 126 № 130, 132, 134 | ||||
14 | 18.09 | ||||||||
15 | 21.09 | ||||||||
16 | Сравнение натуральных чисел | 3 | 22.09 | Наименьшее и наибольшее Что значит «сравнить» Меньше-левее, больше-правее, «Лежать между…» | § 6, № 145, 147, 149 № 152, 154, 160, 162 № 158, 164 | ||||
17 | 23. | ||||||||
18 | 24.09 | ||||||||
Раздел | № урока | Тема урока | Кол-во часов | Форма проведения | Дата | Корр | По разделу | ||
Планируемые результаты | Контроль | Учебно-методическое обеспечение | |||||||
Глава 1 . Натуральные числа (20 часов) | 19 | Повторение и систематизация учебного материала по теме «Натуральные числа» | 1 | 25. | . | Стр. 47, проверь себя, № 1 – 12 | |||
20 | Контрольная работа № 1 по теме«Натуральные числа» | 1 | 28.09 | Повтор правила | |||||
Глава II. Сложение и вычитание натуральных чисел (33 часа) | 21 | Сложение натуральных чисел. Свойства сложения. | 4 | 29. | Формулировать свойства сложения и вычитания натуральных чисел, записывать эти свойства в виде формул | § 7, № 168, 170, 172 № 174, 176, 178 № 180, 183, № 181, 194 | |||
22 | 30.09 | ||||||||
23 | 01.10 | ||||||||
24 | 02.10 | ||||||||
25 | Вычитание натуральных чисел | 5 | 05.10 | § 8, № 198, 200, 204 № 207, 210, 209 № 213, 215, 217 № 219, 221,223 | |||||
26 | 06. | ||||||||
27 | 07.10 | ||||||||
28 | 08.10 | ||||||||
29 | 09.10 | ||||||||
30 | Числовые и буквенные выражения | 3 | 12.10 | Приводить примеры числовых и буквенных выражений, формул. Составлять числовые и буквенные выражения по условию задачи. | § 9, № 244, 246, 248 № 250, 252, 254 № 256, 258, 260 | ||||
31 | 13. | ||||||||
32 | 14.10 | ||||||||
33 | Контрольная работа № 2 по теме: «Сложение и вычитание натуральных чисел» | 1 | 15.10 | Повторить правила | |||||
34 | Уравнения | 3 | 16.10 | Решать уравнения на основании зависимостей между компонентами действий сложения и вычитания. | § 10, № 270, 268(1), № 272 № 274, 277 | ||||
35 | 19. | ||||||||
36 | 20.10 | ||||||||
Раздел | № урока | Тема урока | Кол-во часов | Форма проведения | Дата | Корр | По разделу | ||
Планируемые результаты | Контроль | Учебно-методическое обеспечение | |||||||
Глава II. Сложение и вычитание натуральных чисел (33 часа) | 37 | Угол. Обозначение углов. | 2 | 21. | Изображают и обозначают углы, их вершины и стороны. | § 11, № 284, 286, 289 | |||
38 | 22.10 | § 12, № 287, 288, 294 | |||||||
39 | Виды углов. Измерение углов | 5 | 23.10 | Сравнивают углы. Изображают и распознают прямые углы с помощью чертежного треугольника Распознают острые и тупые углы, измеряют углы | № 299, 300, 303 | ||||
40 | 02. | № 304, 308, 309 | |||||||
41 | 03.11 | № 302, 305, 307 | |||||||
42 | 04.11 | № 310, 314, 318 | |||||||
43 | 05.11 | ||||||||
44 | Многоугольники. Равные фигуры. | 2 | 06. | Изображают и обозначают многоугольники, их вершины и стороны. Распознают на чертежах и рисунках углы, многоугольники, в частности треугольники, прямоугольники. Распознавать в окружающем мире модели этих фигур | § 13, № 324, 326, 328 | ||||
45 | 09.11 | № 329, 327, 329 | |||||||
46 | Треугольник и его виды. | 3 | 10.11 | Измеряют с помощью инструментов и сравнивают длины отрезков и величины углов треугольников. Распознавать в окружающем мире модели этих фигур. Называют фигуры обладающие осью симметрии. | § 14, № 340, 342, 345 | ||||
47 | 11.11 | № 347, 349, 351 | |||||||
48 | 12.11 | § 15, № 360, 362, 364 | |||||||
49 | Прямоугольник. Ось симметрии фигуры | 3 | 13.11 | № 366, 368, 369 | |||||
50 | 16. | § 15, № 375, 373,379 | |||||||
51 | 17.11 | ||||||||
52 | Повторение и систематизация знаний по теме «Уравнения» | 1 | 18.11 | Стр. 102, проверь себя, № 5 – 10 | |||||
53 | Контрольная работа № 3 по теме: «Уравнения» | 1 | 19.11 | Демонстрируют умение изображать заданные геометрические фигуры | карточка | ||||
Основные правила математики (кратко). 5 класс — Сайт учителя математики Косыхиной Н.В.
5 класс — Сайт учителя математики Косыхиной Н.В.
Основные правила математики (кратко). 5 класс
Содержание
- Натуральные числа
- Сравнение натуральных чисел
- Свойства сложения
- Формула пути
- Корень уравнения
- Правила решения уравнений
- Отрезок, прямая, луч
- Угол, биссектриса угла
- Углы: развернутый, прямой, острый, тупой
- Многоугольники. Равные фигуры
- Треугольники: остроугольный, прямоугольный, тупоугольный
- Треугольники: равнобедренный, равносторонний, разносторонний
- Прямоугольник. Квадрат. Периметр
- Умножение. Свойства умножения
- Деление. Деление с остатком
- Площадь. Площадь квадрата, прямоугольника
- Объем. Объем прямоугольного параллелепипеда, куба
- Дроби: правильная, неправильная, сравнение дробей
- Сложение и вычитание дробей с одинаковыми знаменателями
- Сложение и вычитание смешанных чисел
- Преобразование неправильной дроби в смешанное число
- Преобразование смешанного числа в неправильную дробь
- Десятичные дроби: свойства, сравнение, округление
- Десятичные дроби: сложение, вычитание
- Десятичные дроби: умножение, деление
- Среднее арифметическое
- Процент
Натуральные числа
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.
д., которые используют при счете предметов, называют натуральными.
Сравнение натуральных чисел
Число меньше любого натурального числа.
Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.
Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр.
Свойства сложения
Переместительный закон:
Сочетательный закон:
Формула пути
,
где — пройденный путь, — скорость движения, — время, за которое пройден путь .
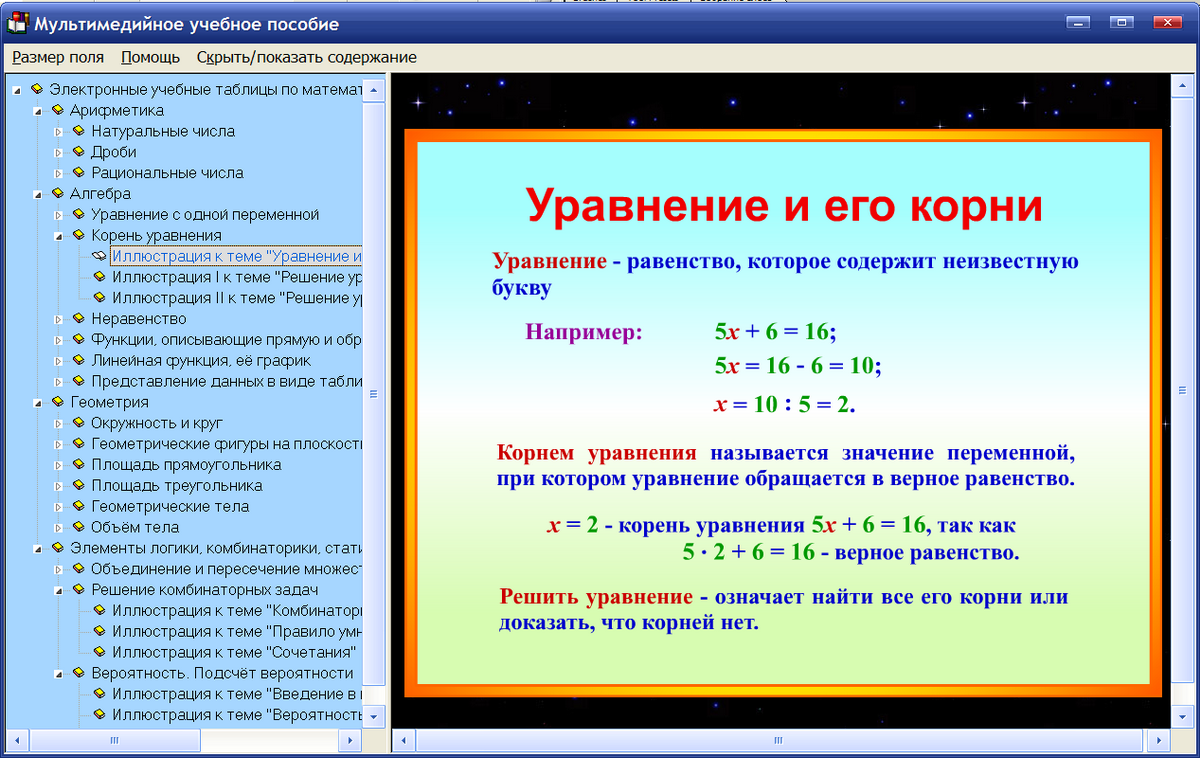
Корень уравнения
Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.
Что значит «Решить уравнение»
Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.
Правила решения уравнений
- Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
- Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
- Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
- Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
- Чтобы найти неизвестное делимое, надо делитель умножить на частное.
- Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Отрезок, прямая, луч
Отрезок
Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)
Свойство длины отрезка
Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .
Равные отрезки
Два отрезка называют равными, если они совмещаются при наложении.
Свойство прямой
Через две точки проходит только одна прямая.
Измерить отрезок
Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается
Ломаная
Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом
Луч
Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча. В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
Угол, биссектриса угла
Угол
Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.
Равные углы
Два угла называют равными, если они совмещаются при наложении.
Свойство величины угла
Если между сторонами угла провести луч , то градусная мера угла равна сумме градусных мер углов и , то есть .
Биссектриса угла
Луч, который делит угол на два равных угла, называется биссектрисой угла.
Углы: развернутый, прямой, острый, тупой
Развернутый угол
Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.
Прямой угол
Угол, градусная мера которого равна 90°, называют прямым.
Острый угол
Угол, градусная мера которого меньше 90°, называют острым.
Тупой угол
Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.
Многоугольники. Равные фигуры
Равные многоугольники
Равные фигуры
Две фигуры называют равными, если они совмещаются при наложении.
Треугольники: остроугольный, прямоугольный, тупоугольный
Остроугольный треугольник
Если все углы треугольника острые, то его называют остроугольным треугольником.
Прямоугольный треугольник
Если один из углов треугольника прямой, то его называют прямоугольным треугольником.
Тупоугольный треугольник
Если один из углов треугольника тупой, то его называют тупоугольным треугольником.
Треугольники: равнобедренный, равносторонний, разносторонний
Равнобедренный треугольник
Если две стороны треугольника равны, то его называют равнобедренным треугольником.
Равносторонний треугольник
Если три стороны треугольника равны, то его называют равносторонним треугольником.
Периметр равностороннего треугольника
Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле
Разносторонний треугольник
Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.
Прямоугольник. Квадрат. Периметр
Прямоугольник
Если в четырехугольнике все углы прямые, то его называют прямоугольником.
Свойство прямоугольника
Противоположные стороны прямоугольника равны.
Периметр прямоугольника
Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле
Квадрат
Прямоугольник, у которого все стороны равны, называют квадратом.
Периметр квадрата
Если сторона квадрата равна , то его периметр вычисляют по формуле .
Умножение. Свойства умножения
Умножение
Свойства умножения
- Переместительный закон умножения:
- Сочетательный закон умножения:
- Распределительное свойство умножения относительно сложения:
- Распределительное свойство умножения относительно вычитания:
Деление. Деление с остатком
Деление с остатком
Деление
Для натуральных чисел равенство является правильным, если является правильным равенство
В равенстве число называют делимым, число — делителем, число и запись — частным от деления, отношением, долей.
На ноль делить нельзя.
Для любого натурального числа правильными являются равенства:
,
Деление с остатком
, где — делимое, — делитель, — неполное частное, — остаток, .
Если остаток равен нулю, то говорят, что число делится нацело на число .
Площадь. Площадь квадрата, прямоугольника
Свойства площади фигуры
Равные фигуры имеют равные площади;
Площадь фигуры равна сумме площадей фигур, из которых она состоит.
Площадь прямоугольника
Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.
Площадь квадрата
,
где — площадь квадрата, — длина его стороны.
Объем. Объем прямоугольного параллелепипеда, куба
Свойства объема фигуры
Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.
Объем прямоугольного параллелепипеда
,
где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;
,
где — площадь основания параллелепипеда, — его высота.
Объем куба
,
где — объем куба, — длина его ребра.
Дроби: правильная, неправильная, сравнение дробей
Правильная дробь
Дробь, числитель которой меньше знаменателя, называют правильной
Неправильная дробь
Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.
Сравнение дробей
- Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.
- Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.

- Все правильные дроби меньше единицы, а неправильные — больше или равны единице.
- Любая неправильная дробь больше любой правильной дроби.
Сложение и вычитание дробей с одинаковыми знаменателями
- Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
- Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
Сложение и вычитание смешанных чисел
- Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.
- Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Преобразование неправильной дроби в смешанное число
Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно
- числитель разделить на знаменатель;
- полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.
Преобразование смешанного числа в неправильную дробь
Чтобы преобразовать смешанное число в неправильную дробь нужно
- целую часть числа умножить на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- эту сумму записать как числитель неправильной дроби;
- в его знаменателе записать знаменатель дробной части смешанного числа.
Десятичные дроби: свойства, сравнение, округление
Свойства десятичной дроби
Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.
Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.
Сравнение десятичных дробей
Из двух десятичных дробей больше та, у которой целая часть больше.
Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо
- с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
- после чего сравнить полученные дроби поразрядно.

Округление десятичных дробей
Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо
- все следующие за этим разрядом цифры отбросить.
- если при этом первая из цифр, которые отбрасывают равна 0, 1, 2, или 4, то последнюю из цифр, которые оставляют, не меняют;
- если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8 или 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.
Десятичные дроби: сложение, вычитание
Сложение десятичных дробей
Чтобы найти сумму двух десятичных дробей, нужно:
- уравнять количество цифр после запятых;
- записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
- сложить полученные числа так, как складывают натуральные числа;
- поставить в полученной сумме запятую под запятыми.
Вычитание десятичных дробей
Чтобы найти разность двух десятичных дробей, нужно:
- уравнять количество цифр после запятых;
- записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
- выполнить вычитание так, как вычитают натуральные числа;
- поставить в полученной разности запятую под запятыми.

Десятичные дроби: умножение, деление
Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, надо:
- перемножить их как натуральные числа, не обращая внимания на запятые;
- в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.
Деление десятичных дробей
Чтобы разделить десятичную дробь на десятичную, надо:
- перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
- выполнить деление на натуральное число.
Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.
д. цифры.
Среднее арифметическое
Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.
Процент
Процентом называют сотую часть величины или числа 1%=
Данная информация взята из УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир
ГДЗ по математике за 5 класс, решебник и ответы онлайн
Решение есть!-
1 класс
- Математика
- Английский язык
- Русский язык
- Музыка
- Литература
- Окружающий мир
-
2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Технология
-
3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Казахский язык
-
4 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Казахский язык
Предметы в 5 классе (список школьных предметов по программе)
Закончив 4 класс, многие дети – кто с радостным нетерпением, кто с опаской – ждут важного события в своей жизни – перехода из младшей школы в среднюю.
Содержание
Какие предметы в 5 классе
О чем предметы, изучаемые в 5 классе
Факультативные предметы в пятом классе
А ждать пятиклассникам есть чего:
- встречи сразу с несколькими новыми преподавателями вместо одной хорошо знакомой учительницы начальных классов;
- возможности взглянуть на недоступные прежде и давно привлекающие своими экспонатами кабинеты физики или биологии;
- знакомства с новыми предметами, а предметы в 5 классе поражают своим разнообразием.
Последний вопрос, касающийся списка предметов 5 класса, особенно волнует родителей юных школьников, поскольку они хотят как можно лучше подготовить своих детей к новому учебному году.
Какие предметы в 5 классе
Обычно школьников ждут следующие предметы в 5 классе:
- Русский язык
- Иностранный язык (чаще всего английский)
- Литература
- Информатика
- История древнего мира
- Математика
- Обществознание
- Музыка
- ОДНКНР
- Технология (труд)
- Природоведение
- Основы безопасности жизнедеятельности
- География
- ИЗО (рисование)
- Физическая культура
Сколько предметов в 5 классе, теперь не сложно посчитать. Их 15.
Их 15.
Кроме перечисленных обязательных предметов, в отдельных образовательных учреждениях программа 5 класса, как, впрочем, и любого другого, может быть дополнена и иными, разрешенными Министерством образования. Например, в некоторых школах преподают такие школьные предметы, как краеведение и граждановедение. Также в некоторых школах уже с 5 класса начинаются уроки биологии, хотя обычно ученики знакомятся с этим предметом в 6 классе.
О чем предметы, изучаемые в 5 классе
Наверняка, многим родителям будет интересно узнать, чему конкретно призваны обучить их детей перечисленные в списке предметы пятого класса.
Литература
На уроках литературы пятиклассники познакомятся с русским фольклором и мифами Древней Греции, а также с наиболее известными детскими произведениями выдающихся русских и зарубежных писателей и биографией этих авторов. Не обойдется и без заучивания наизусть стихотворений известных русских поэтов. Кроме того, ученики начнут понемногу знакомиться с теоретическими сведениями по литературе.
Кроме того, ученики начнут понемногу знакомиться с теоретическими сведениями по литературе.
Литература – единственный предмет, по которому школьникам дают задание на лето в виде списка произведений, которые необходимо прочитать к новому учебному году. Поэтому стоит поинтересоваться у учителя литературы, какие книги будущие пятиклассники должны успеть прочитать за лето.
Информатика
На занятиях по информатике ученики пятого класса узнают, как устроен компьютер и что он умеет, а также научатся работать с основными компьютерными программами. Так, пятиклассники узнают, как набирать и форматировать текст в текстовом редакторе (Word), создавать простые рисунки в графическом редакторе (Paint), а также познакомятся с другими полезными программами, такими как MS Excel и MS PowerPoint.
ОДНКНР и обществознание
Оба предмета были введены в программу для 5 класса совсем недавно.
ОДНКНР (основы духовно-нравственной культуры народов России) – предмет, призванный развивать общую культуру школьников, дать представление о народах, проживающих на территории России, а также научить школьников уважению к другим народам. На уроках по этому предмету ученики будут изучать происхождение и особенности различных религий и культур, а также будут обсуждать нравственные ценности человека.
На уроках по этому предмету ученики будут изучать происхождение и особенности различных религий и культур, а также будут обсуждать нравственные ценности человека.
На занятиях по обществознанию речь будет идти о человеке как части общества. Пятиклассники познакомятся с основами правовой системы России, а также получат общее представление об экономике и политике. Этот предмет полезен тем, что уже с юного возраста учит школьников быть юридически грамотными и иметь активную гражданскую позицию.
Технология (труд)
По технологии уроки в 5 классе впервые будут проводиться раздельно для мальчиков и для девочек. Девочки в 5 классе получают основные знания по кулинарии, учатся обращаться со швейной машинкой и шьют какое-нибудь изделие (чаще всего фартук), а также учатся вязать или вышивать. Мальчики же учатся обращаться с различными инструментами и делают поделки из дерева.
Музыка
Раньше этот предмет назывался просто – «пение». И если раньше на уроках по этому предмету от детей требовалось только петь, то сейчас все серьезнее. На занятиях по музыке современные школьники не только разучивают разные песни и поют их под аккомпанемент учителя, но и знакомятся с музыкальной историей, с биографиями известных композиторов и их наиболее известными произведениями. Кроме того, школьники изучают основы нотной грамоты.
И если раньше на уроках по этому предмету от детей требовалось только петь, то сейчас все серьезнее. На занятиях по музыке современные школьники не только разучивают разные песни и поют их под аккомпанемент учителя, но и знакомятся с музыкальной историей, с биографиями известных композиторов и их наиболее известными произведениями. Кроме того, школьники изучают основы нотной грамоты.
ИЗО
На уроках изобразительного искусства дети не только учатся рисовать, но и получают значительный объем теоретической информации. Например, ученики изучают историю декоративно-прикладного искусства, учатся видеть разницу между разными жанрами изобразительного искусства, а также знакомятся с наиболее выдающимися работами знаменитых художников, скульпторов, архитекторов и прочих деятелей искусства.
Факультативные предметы в пятом классе
Кроме обязательных предметов в школе могут быть предусмотрены так называемые факультативы – предметы, на которые ученики ходят по собственному выбору. К таким предметам относятся, например, риторика, краеведение, правоведение, философия, и др. В 5 классе среди таких предметов может быть проектирование и основы религиозных культур и светской этики. Кроме того, в каждой школе могут быть введены собственные факультативные занятия.
К таким предметам относятся, например, риторика, краеведение, правоведение, философия, и др. В 5 классе среди таких предметов может быть проектирование и основы религиозных культур и светской этики. Кроме того, в каждой школе могут быть введены собственные факультативные занятия.
К факультативам можно также отнести классный час – еженедельное занятие, обычно перед началом уроков, на котором ученики вместе с классным руководителем обсуждают актуальные проблемы.
В целом, предметы в 5 классе не выглядят слишком сложными для ребенка, только что расставшегося с начальной школой. В конце концов, 5 класс можно назвать подготовительным этапом перед средней школой, так как за этот год ученики осваиваются в новой обстановке, привыкают к новым учителям и большой учебной нагрузке.
Учебники и тетради 5 класса
9 стратегий мотивации учащихся к математике
Мотивация учащихся к тому, чтобы они были с энтузиазмом восприимчивыми, является одним из наиболее важных аспектов обучения математике и критическим аспектом любой учебной программы. Эффективные учителя сосредотачивают внимание на менее заинтересованных учениках, а также на мотивированных. Вот девять методов, основанных на внутренней и внешней мотивации, которые можно использовать для мотивации учащихся средних школ к математике.
Эффективные учителя сосредотачивают внимание на менее заинтересованных учениках, а также на мотивированных. Вот девять методов, основанных на внутренней и внешней мотивации, которые можно использовать для мотивации учащихся средних школ к математике.
Внешняя и внутренняя мотивация
Внешняя мотивация включает в себя вознаграждения, которые возникают вне контроля учащегося.Сюда могут входить символические экономические вознаграждения за хорошую работу, признание хороших результатов коллегами, избежание «наказания» за хорошую работу, похвалу за хорошую работу и так далее.
Тем не менее, многие студенты демонстрируют внутреннюю мотивацию в своем желании понять тему или концепцию (связанное с задачей), превзойти других (связанное с эго) или произвести впечатление на других (связанное с обществом). Последний гол находится между внутренним и внешним.
Имея в виду эти базовые концепции, существуют определенные методы, которые можно расширить, приукрасить и адаптировать к личности учителя и, прежде всего, сделать подходящими для уровня способностей и среды ученика. Стратегии – это важные части, которые следует запомнить – примеры приведены только для того, чтобы помочь понять техники.
Стратегии – это важные части, которые следует запомнить – примеры приведены только для того, чтобы помочь понять техники.
Стратегии повышения мотивации учащихся по математике
1. Обращайте внимание на пробел в знаниях студентов: Выявление студентам пробелов в их понимании основывается на их желании узнать больше. Например, вы можете представить несколько простых упражнений со знакомыми ситуациями, за которыми следуют упражнения с незнакомыми ситуациями на ту же тему.Чем ярче вы обнаружите разрыв в понимании, тем эффективнее будет мотивация.
2. Покажите последовательное достижение: Тесно связано с предыдущей техникой, когда студенты понимают логическую последовательность понятий. Этот метод отличается от предыдущего тем, что зависит от желания учащихся расширить, а не дополнить свои знания. Одним из примеров последовательного процесса является то, как особые четырехугольники переходят один в другой с точки зрения их свойств.
3. Откройте для себя закономерность: Создание надуманной ситуации, которая побуждает учащихся обнаруживать закономерность, часто может быть весьма мотивирующим, поскольку они получают удовольствие от поиска, а затем воплощения идеи в жизнь. Примером может быть сложение чисел от 1 до 100. Вместо того, чтобы складывать числа последовательно, учащиеся складывают первое и последнее (1 + 100 = 101), а затем второе и предпоследнее (2 + 99 = 101 ), и так далее. Затем все, что им нужно сделать, чтобы получить требуемую сумму, – это решить 50 × 101 = 5 050.Это упражнение подарит студентам поучительный опыт с действительно длительным эффектом. Существуют шаблоны, которые могут быть мотивирующими, особенно если они обнаруживаются учеником – конечно, под руководством учителя.
4. Представьте задачу: Когда учащиеся сталкиваются с интеллектуальными проблемами, они реагируют с энтузиазмом. При выборе задачи необходимо проявлять особую осторожность. Проблема (если это тип вызова) обязательно должна вести к уроку и быть в пределах досягаемости учащихся.Следует проявлять осторожность, чтобы задача не отвлекала от урока, а фактически приводила к нему.
Проблема (если это тип вызова) обязательно должна вести к уроку и быть в пределах досягаемости учащихся.Следует проявлять осторожность, чтобы задача не отвлекала от урока, а фактически приводила к нему.
5. Соблазните класс математическим результатом «ну и дела»: В области математики есть много примеров, которые часто противоречат здравому смыслу. Эти идеи по самой своей природе могут быть мотивирующими. Например, чтобы мотивировать основную веру в вероятность, очень эффективной мотивацией является обсуждение в классе известной проблемы дня рождения, которая дает неожиданно высокую вероятность совпадения дней рождения в относительно небольших группах.Его удивительный – даже невероятный – результат вызовет трепет у класса.
6. Укажите полезность темы: Предложите классу практическое применение, представляющее неподдельный интерес, в начале урока. Например, в средней школе по геометрии ученика могут попросить найти диаметр пластины, где вся информация, которую он имеет, представляет собой сечение пластины меньше полукруга. Выбранные приложения должны быть краткими и несложными, чтобы мотивировать урок, а не отвлекать от него.
Выбранные приложения должны быть краткими и несложными, чтобы мотивировать урок, а не отвлекать от него.
7. Используйте развлекательную математику: Рекреационная мотивация включает головоломки, игры, парадоксы, школьное здание или другие близлежащие строения. Эти устройства должны быть краткими и простыми, а не только выбираться с учетом их конкретной мотивационной выгоды. Эффективное выполнение этого приема позволит школьникам без особых усилий завершить отдых. Еще раз, с удовольствием, которое приносят эти развлекательные примеры, нужно обращаться осторожно, чтобы не отвлекать от последующего урока.
8. Расскажите соответствующую историю: Рассказ об историческом событии (например, рассказ о том, как Карл Фридрих Гаусс сложил числа от 1 до 100 за одну минуту, когда ему было 10 лет в 1787 году) или надуманная ситуация может мотивировать студентов. Учителя не должны спешить, рассказывая историю – поспешная презентация сводит к минимуму потенциальную мотивацию стратегии.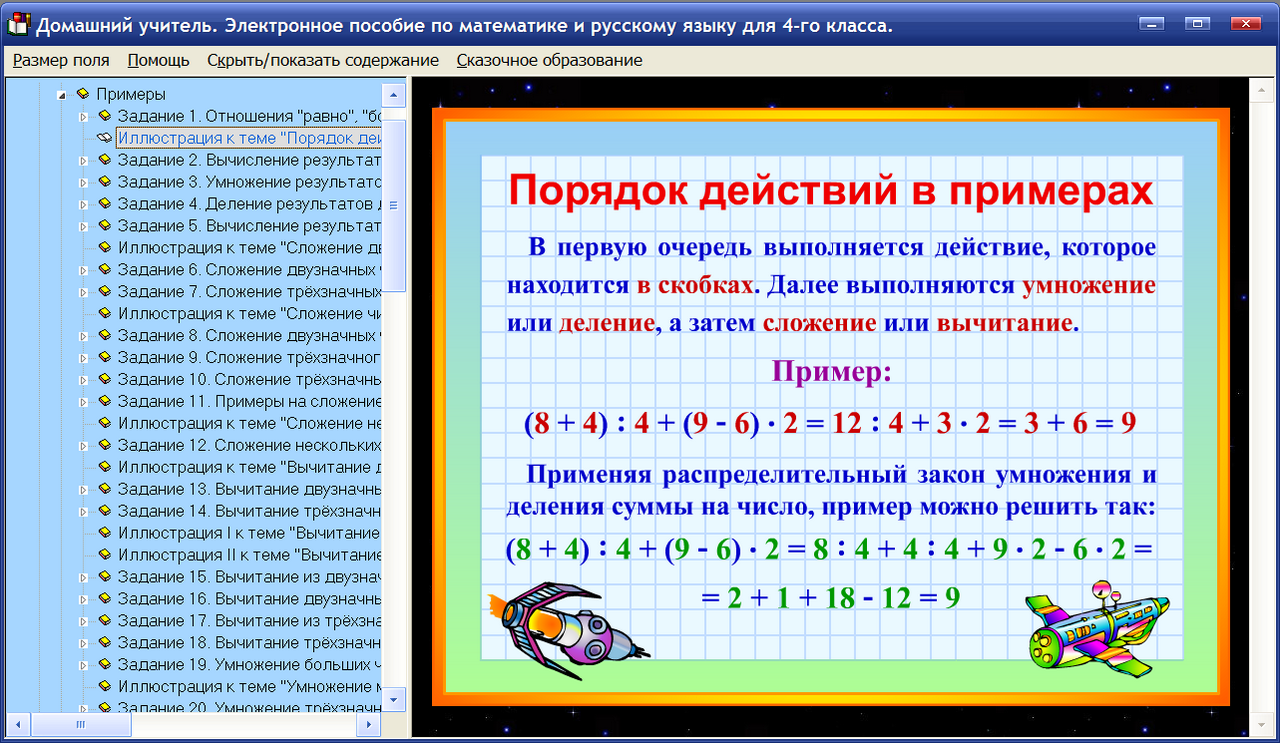
9. Активно вовлекайте студентов в обоснование математических любопытств: Один из наиболее эффективных методов мотивации студентов – это попросить их обосновать один из многих уместных математических курьезов, например, тот факт, что когда сумма цифр числа равна делится на 9, исходное число также делится на 9.Студенты должны быть знакомы с математическим любопытством и чувствовать себя комфортно, прежде чем вы бросите им вызов.
Учителя математики должны понимать основные мотивы, уже присутствующие в их учениках. Затем учитель может использовать эти мотивы для максимального вовлечения и повышения эффективности учебного процесса. Использование мотивации и склонности студентов может привести к созданию искусственных математических задач и ситуаций. Но если такие методы вызывают неподдельный интерес к теме, они в высшей степени справедливы и желательны.
Вы можете найти больше примеров того, как использовать эти стратегии, в моей книге со Стивеном Круликом, Эффективные методы мотивации по математике, инструкция .
EM4 в домашних условиях 5 класс
EM4 дома Оценка 5
Выберите подразделение
- Раздел 1 Площадь и объем
- Модуль 2 Целочисленное значение места и операции
- Блок 3 Понятия дроби, сложение и вычитание
- Раздел 4 Десятичные понятия; Координатные сетки
- Блок 5 Операции с дробями
- Блок 6 Исследования в области измерения; Десятичное умножение и деление
- Блок 7 Умножение смешанных чисел; Геометрия; Графики
- Блок 8 Приложения измерения, вычислений и построения графиков
Поиск номеров модуля и уроков
Математика на каждый день разделен на блоки, которые делятся на уроки. В верхнем левом углу Home Link вы должны увидеть такой значок:
В верхнем левом углу Home Link вы должны увидеть такой значок:
Номер модуля – это первое число, которое вы видите на значке, а номер урока – второе число. В этом случае учащийся работает над Модулем 5, Урок 4. Чтобы получить доступ к справочным ресурсам, вы должны выбрать «Модуль 5» из приведенного выше списка, а затем найти строку в таблице с пометкой «Урок 5–4».
Математика на каждый день для родителей: Что нужно знать, чтобы помочь своему ребенку добиться успеха
Проект математики школы Чикагского университета
Издательство Чикагского университета
Подробнее >>
Ссылки по теме
Повседневная математика Онлайн
Используя логин, предоставленный учителем вашего ребенка, вы получите доступ к ресурсам, которые помогут вашему ребенку с домашним заданием или освежить свои математические навыки.
Понимание Повседневная математика для родителей
Узнайте больше об учебной программе EM и о том, как помочь своему ребенку.
учебных программ (CG) для 1–12 классов (SY 2019-2020)
Обновленные руководства по учебной программе (CG) DepEd для 1-12 классов для SY 2018-2019 Сейчас (2019-2020)
Знание, чему учить и когда – частый источник беспокойства среди начинающих учителей. Многие штаты, округа и школы помогают учителям рассчитывать время уроков с помощью руководства по учебной программе.Хотя эти инструменты иногда и являются строгими, они могут сделать обучение более целенаправленным.
Что такое учебный план?
Учителя не входят в класс, не зная, чему и когда учить. Если бы образование работало таким образом, это был бы хаос! Вместо этого штаты, округа и отдельные школы помогают определить, какой материал учителя охватывают, создавая учебный план , руководство, в котором излагаются материалы, которые учителя должны освоить. Хотя руководство по учебной программе может варьироваться от очень конкретного до общего плана, учителя от дошкольного образования до профессионального мира используют их для руководства при планировании.
В зависимости от учебного заведения руководство по учебной программе может быть привязано к предмету и / или классу. Например, в начальной школе могут быть руководства по математике, естественным наукам, обществознанию и языковым искусствам для каждого класса от детского сада.
В рамках каждого предмета в руководстве излагаются цели или стандарты, которым учащиеся должны соответствовать к концу установленного периода времени, обычно учебного года. Некоторые руководства являются конкретными и содержат подробную информацию о том, чему и когда следует учить, а также о том, как должны выглядеть инструкции.Например, руководство по учебной программе по математике может направить учителя обучать дробям в ноябре, а затем разбить содержание на ежедневные инструкции по числителям и знаменателям. Он может даже содержать шаги для инструктирования учителя и возможные задачи для практики и оценки.
Источник: study.com
Обновленные руководства по учебной программе K-12 для всех классов
| Руководство по учебной программе для детского сада | Загрузить |
| Araling Panlipunan Curriculum Guide | Download |
| Arts Curriculum Guide | Download | Загрузить |
| EPP, TLE Curriculum Guide | Download |
| Download | |
| Health Curriculum Guide with tagged math equipment | Загрузить | MathDownload |
| Mother Tongue Curriculum Guide | Download |
| Music Curriculum Guide | Download |
| Physical Education Curriculum Guide | Download |
| Руководство по учебной программе с пометкой SCI-оборудования | Загрузить |
Руководства по учебной программе для старших классов
SHS APPLIED TRACK SUBJECTS
| SHS Applied Empowerment Technologies (for the Strand) | Download | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| SHS Applied English for Academic and Professional Purposes CG | Download | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| SHS Applied Entrepreneurship | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Download (Akademik) CG | Загрузить | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Филиппинский SHS (Isports) CG | Загрузить | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Филиппинский SHS Прикладной (Sining) CG | Загрузить | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| SHS Tech | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Загрузить | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прикладные исследования, исследования и погружения в SHS CG | Загрузить | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прикладные исследования SHS 1 CG | Загрузить | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прикладные исследования SHS 2 CG | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Базовая литература SHS 21 века с Филиппин и всего мира CG | Скачать | ||
| SHS Core Contemporary Philippine Arts from the Regions CG | Download | ||
| SHS Core Готовность к бедствиям и снижение риска | CG 90 | ||
| SHS Core Earth and Life Science CG с помеченным научным оборудованием | Загрузить | ||
| SHS Core Earth Science CG | Загрузить | ||
| SHS Core General Math CG | Загрузить | ||
| Скачать | |||
| SHS Core Komunikasyon и Pananaliksik sa Wika и Kulturang Pilipino CG | Download | ||
| SHS Core Media and Information Literacy Communication CG | SHS Core | Download | CoreЗагрузить |
| SHS Core Pagbasa и Pagsusuri ng Iba’t-Ibang Teksto Tungo Sa Pananaliksik CG | Download | ||
| SHS Core PE and Health CG | Download | ||
| Core Personal Development CG SHS Core Physical Science CGс помеченным научным оборудованием | Скачать | ||
| SHS Core Reading and Writing CG | Download | ||
| SHS Core Statistics and Probability CG | Download | ||
| SHS Core Understanding Culture | Download |
СПЕЦИАЛИЗИРОВАННЫЕ ПРЕДМЕТЫ SHS (ACADEMIC TRACK)
Бухгалтерский учет, бизнес и менеджмент (ABM STRAND)
ABM Strand Рекомендуемое расписание предметов (пересмотрено 16 июня 2015 г. ) ) | Загрузить | |||||||
| ABM Applied Economics CG | Загрузить | |||||||
| ABM Business Ethics and Social Responsibility CG | Business | Business Ethics and Social Responsibility CG | Business | Business | Business | Business | Финансы CG | Загрузить |
| ABM Business Math CG | Загрузить | |||||||
| ABM Culminating Activity Business Enterprise Simulation CG | Загрузить | |||||||
| ABM Fundamentals of ABM 1143 CG | ABM 2 CGЗагрузить | |||||||
| ABM Organization and Management CG | Загрузить | |||||||
| ABM Principles of Marketing CG | Загрузить |
Science, Technology, Engineering and Mathematics
Гуманитарные и социальные науки (HUMSS 9000 STRAND)
HUMSS Strand Рекомендуемое расписание предметов (от 16 июня 2015 г.) Скачать HUMSS Community Engagement, Solidarity and Leadership CG Download CG Creative Writing CG HUMSS Creative 9014S Скачать HUMSS Culminating Activity CG Скачать HUMSS Дисциплины и идеи в социальных науках CG Скачать HUMSS 9014 Вероисповедание 904 Введение в мир HUMSS Philippine Politics and Governance CG Download HUMSS Trends, Networks and Critical Thinking in the 21st Century CG Download
Программа профессионально-технического обеспечения средств к существованию
СЕЛЬСКО-РЫБНОЕ ХОЗЯЙСТВО
Производство сельскохозяйственных культур (NC I) Загрузить Производство сельскохозяйственных культур (NC II) Загрузить Производство сельскохозяйственных культур (NC III) Загрузить Управление здоровьем животных (NC III) Загрузить Животноводство (птица-курица) (NC II) Загрузить Животноводство (жвачные животные) (NC II) Загрузить Животноводство (свиньи) (NC II) Загрузить Аквакультура (NC II) Загрузить Искусственное осеменение (жвачные животные) (NC II) Загрузить Искусственное осеменение ( ) (NC143) Загрузить Fish Capture (NC II) Загрузить Ремонт и обслуживание рыболовных снастей (NC III) Загрузить Упаковка для рыбных продуктов (NC II) Загрузить Fish Wharf Operation (NC I) Загрузить Пищевая промышленность (NC II) Загрузить Horticulture (NC III) Download Установка и обслуживание ландшафта (NC II) Download Organic Agriculture (NC II) Download Pest Management (NC II) Download Обработка риса (NC II) Загрузить Обработка резины (NC II) Загрузить Производство резины (NC II) Загрузить Убойные операции (NC II) Загрузить
Home Economics
Информационные и коммуникационные технологии (ИКТ)
Анимация (NC II) Загрузить Установка широкополосного доступа (фиксированные беспроводные системы) (NC II) Загрузить Компьютерное программирование (. 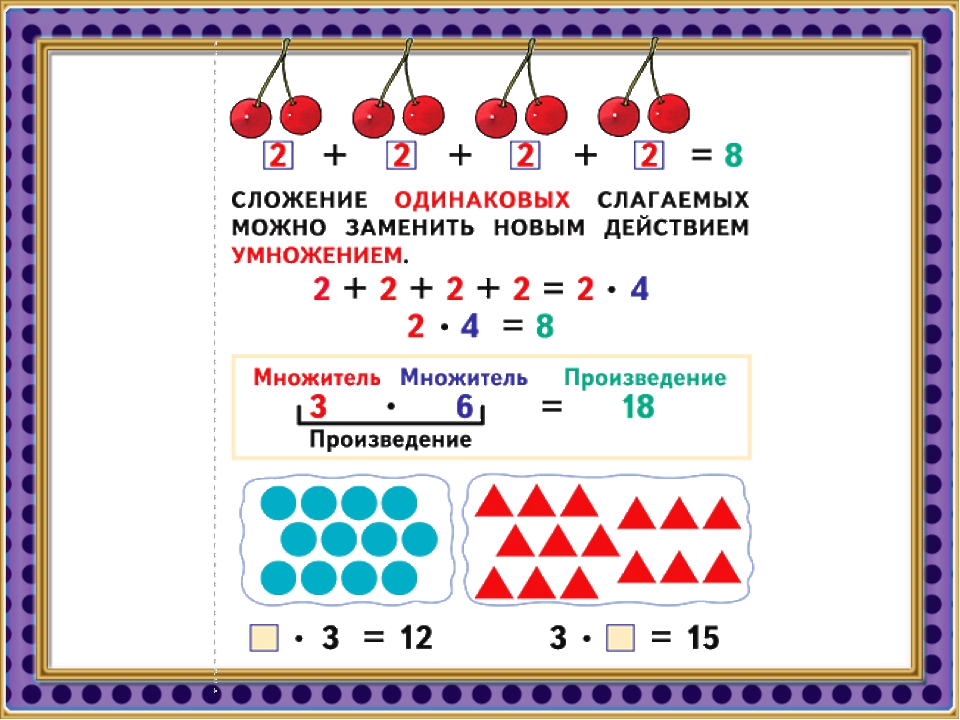 net Technology) (NC III)
net Technology) (NC III) Загрузить Компьютерное программирование (Java) (NC III) Загрузить Компьютерное программирование (Oracle Database) (NC III) Загрузить Обслуживание компьютерных систем (NC II) Загрузить Услуги контактного центра (NC II) Загрузить Иллюстрация (NC II) Загрузить Медицинская справка (NC II) Загрузить Технический проект (NC II) Загрузить Установка OSP Telecom и абонентской линии (медный кабель / POTS и DSL) (NC II) Загрузить Установка OSP Telecom (оптоволоконный кабель) (NC II) Загрузить
Industrial Arts
Автомобильное обслуживание (NC I) Загрузить Автомобильное обслуживание (NC II) Загрузить Плотницкие работы (NC II) Загрузить III Карп III Загрузить Строительная окраска (NC II) Загрузить Обслуживание бытового холодильного оборудования и кондиционирования воздуха (DOMRAC) (NC II) Загрузить Электрический монтаж и обслуживание (NC II) Привод (NC II) Загрузить Загрузить Строительство линии распределения электроэнергии (NC II) Загрузить Сборка и обслуживание электронных изделий (NC II) Загрузить Изготовление мебели ( Окончательная обработка) (NC II) Download Instrumentation and Control Servi cing (NC II) Загрузить Дуговая сварка металла в газовой среде (GMAW) (NC II) Загрузить Дуговая сварка вольфрамовым электродом (GTAW) (NC II) Загрузить Обработка ( NC I) Загрузка Обработка (NC II) Загрузка Кладка (NC II) Загрузка Мотоцикл Обслуживание двигателя (NC II) Обслуживание мехатроники (NC II) Мотоцикл Загрузить Сантехника (NC I) Загрузить Сантехника (NC II) Загрузить Холодильное оборудование и кондиционирование воздуха (агрегатный блок кондиционирования воздуха [PACU ] / Торговое холодильное оборудование [CRE]) Сервисное обслуживание (NC III) Загрузить Дуговая сварка экранированного металла (NC I) Загрузить 90 143 Дуговая сварка экранированного металла (NC II) Загрузить Установка плитки (NC II) Загрузить Установка и обслуживание линии передачи (NC II) Загрузить


 09
09
 09
09 Координатный луч
Координатный луч 09
09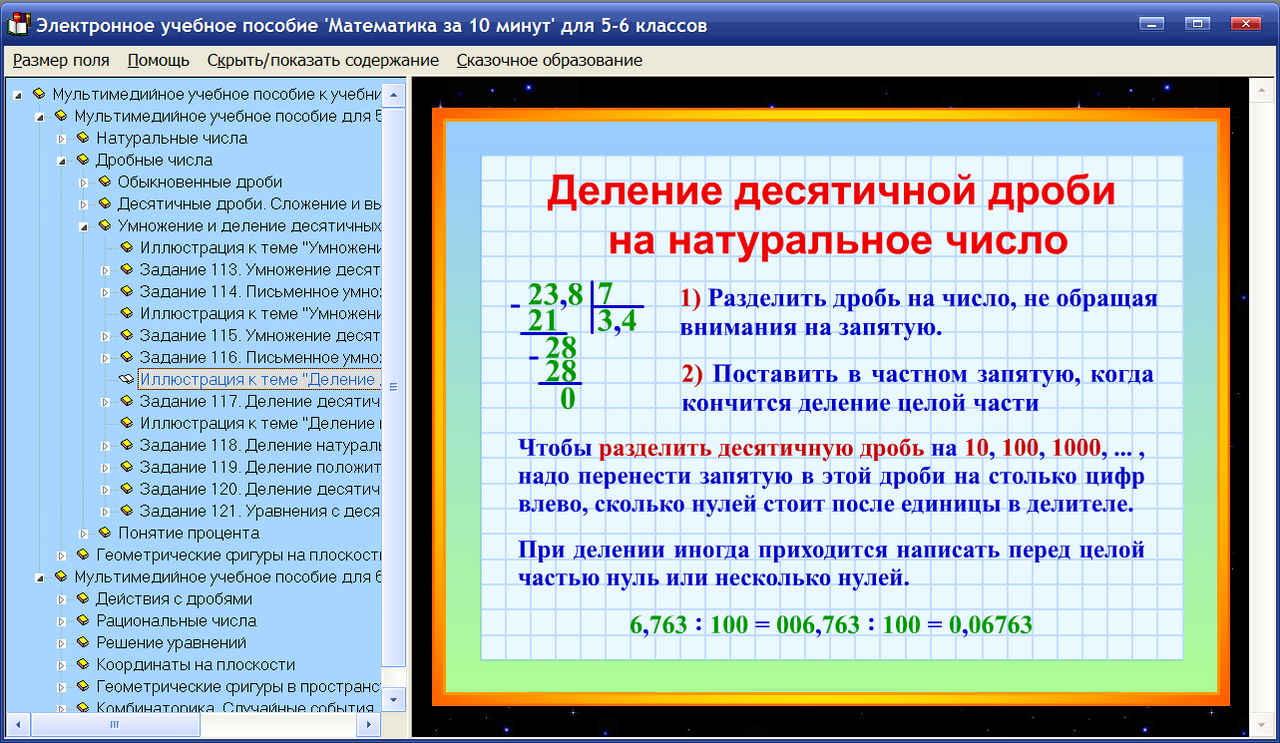 09
09 09
09 10
10 10
10 10
10 10
10 11
11 11
11 Выделяют равные треугольники.
Выделяют равные треугольники. 11
11