Рабочая программа логика 4 класс: Рабочая программа курса внеурочной деятельности «Интеллект. Мышление. Логика». 4 класс
Рабочая программа курса внеурочной деятельности «Интеллект. Мышление. Логика». 4 класс
Рабочая программа курса внеурочной деятельности «Интеллект. Мышление. Логика» разработана на основе авторской программы Э.Кочуровой «Интеллект. Мышление. Логика» общеинтеллектуальной направленности рассчитана на 4 учебных года, ориентирована на обучающихся 4 класса.
Количество часов: 34.
Данная программа включает в себя пояснительную записку, общую характеристику курса внеурочной деятельности, описание места курса в учебном плане, описание ценностных ориентиров содержания курса, личностные и метапредметные результаты освоения курса, содержание курса внеурочной деятельности, тематическое планирование и описание материально-технического обеспечения курса внеурочной деятельности.
Предлагаемый курс предполагает применение коллективных форм организации занятий и использование современных средств обучения, создание на занятиях ситуаций активного поиска, предоставление возможности сделать собственное «открытие», знакомство с оригинальными путями рассуждений, овладение элементарными навыками исследовательской деятельности.
В программе курса предусмотрено значительное увеличение активных форм работы, направленных на вовлечение обучающихся в динамичную деятельность, на обеспечение понимания ими математического материала и развития интеллекта, приобретение практических навыков самостоятельной деятельности.
Курс внеурочной деятельности «Интеллект. Мышление. Логика» представляет собой комплекс специально разработанных игровых заданий, упражнений, тренингов, логических задач.
В соответствии с планом внеурочной деятельности 1-4 классов, реализующих образовательную программу начального общего образования на курс внеурочной деятельности «Интеллект. Мышление. Логика» предусмотрено в 4 классе 34 часа в год (34 учебных недели по 1 часу в неделю).
Всего на изучение курса «Интеллект. Мышление. Логика» с 1 по 4 класс отводится 135 часов.
Количество страниц в документе: 14.
Содержание рабочей программы
Пояснительная записка
Общая характеристика курса внеурочной деятельности
Описание места курса внеурочной деятельности в учебном плане
Описание ценностных ориентиров содержания курса внеурочной деятельности
Личностные и метапредметные результаты освоения курса внеурочной деятельности
Содержание курса внеурочной деятельности
Тематическое планирование с определением основных видов учебной деятельности обучающихся
Описание учебно-методического и материально-технического обеспечения образовательной деятельности курса внеурочной деятельности
Колонки календарно-тематического планирования
№ занятия
Дата (план/факт)
Тема занятия
Количество часов
Характеристика деятельности обучающегося
Скачать рабочую программуРабочие программы
Положение о рабочей программе МБОУ “Лицей”
Русский язык и литература
Рабочая программа по русскому языку 8 класс (учитель – Сисякина А. А.)
А.)
Рабочая программа по русскому языку 9 А класс (учитель – Сисякина А.А.)
Рабочая программа по русскому языку 10 класс (учитель – Сисякина А.А.)
Рабочая программа по литературе 5 Б класс (учитель – Сисякина А.А.)
Рабочая программа по литературе 8 класс (учитель – Сисякина А.А.)
Рабочая программа по литературе 9 А класс (учитель – Сисякина А.А.)
Рабочая программа по литературе 10 класс (учитель – Сисякина А.А.)
Рабочая программа элективного курса по русскому языку «Русское правописание: орфография и пунктуация» 10 класс (учитель – Сисякина А.А.)
Рабочая программа по русскому языку 5 А кл. (учитель – Лебедева Е.В.)
Рабочая программа по русскому языку 7 Б кл. Лебедева Е.В. (учитель – Лебедева Е.В.)
Рабочая программа по литературе 5 А кл.
 Лебедева Е.В. (учитель – Лебедева Е.В.)
Лебедева Е.В. (учитель – Лебедева Е.В.)
Рабочая программа по литературе 6б кл. Лебедева ЕВ. (учитель – Лебедева Е.В.)
Рабочая программа по литературе 7 Б кл. Лебедева Е.В (учитель – Лебедева Е.В.)
Рабочая программа ВУД «Посиделки у Грамматейки», 5 а кл. (учитель – Лебедева Е.В.)
Рабочая программа по родному языку 8 Б кл. (учитель – Лебедева Е.В.)
Рабочая программа по родной литературе 8 Б кл. (учитель – Лебедева Е.В.)
Рабочая программа по литературе 8 Б кл. (учитель – Лебедева Е.В.)
Рабочая программа по русскому языку 8 Б кл. (учитель – Лебедева Е.В.)
Рабочая программа по математике 1 класс (учитель – Басова О.В.)
Рабочая программа элективного курса по математике в 9 классе (учитель – Довлатбегян В.В)
Рабочая программа по математике в 5 классе (учитель – Довлатбегян В. В)
В)
Рабочая программа по алгебре в 9 классе (учитель – Довлатбегян В.В)
Рабочая программа по геометрии в 9 классе (учитель – Довлатбегян В.В)
Рабочая программа элективного курса “Что таит модуль” (учитель – Довлатбегян В.В)
Рабочая программа по алгебре (8 класс) (учитель – Савченкова М.В.)
Рабочая программа по геометрии (8 класс) (учитель – Савченкова М.В.)
Астрономия:
Рабочая программа по астрономии (Ларионов В.В.)
Информатика:
Рабочая программа по информатике (БУ) 7 класс (учитель -Савченкова М.В.)
Рабочая программа по информатике (БУ) 8 класс (учитель – Савченкова М.В.)
Рабочая программа по информатике (БУ) 9 класс (учитель – Савченкова М.В.)
Рабочая программа по информатике (Профильный уровень) (учитель – Савченкова М.В.)
Рабочая программа по информатике и ИКТ (БУ) 11 класс (учитель -Савченкова М. В.)
В.)
Биология:
Рабочая программа по биологии 11 класс (учитель – Володина Г.В.)
Рабочая программа по биологии 10 класс (учитель – Володина Г.В.)
Рабочая программа по биологии 8 класс (учитель – Володина Г.В.)
Рабочая программа по биологии 7 класс (учитель – Володина Г.В.)
Рабочая программа по биологии 6 класс (учитель – Володина Г.В.)
Химия:
Рабочая программа по химии 11 класс (учитель – Назарова Е.А.)
Рабочая программа по химии 10 класс (учитель – Назарова Е.А.)
Рабочая программа по химии 9 класс (учитель – Назарова Е.А.)
Рабочая программа по химии 8 класс (учитель – Назарова Е.А.)
Иностранные языки:
Английский язык:
Рабочая программа по английскому языку 2 А класс (учитель – Морозова К. С.)
Рабочая программа по английскому языку 3 класс (учитель – Морозова К. С.)
С.)
Рабочая программа по английскому языку 4 Б класс (учитель – Морозова К. С.)
Рабочая программа по английскому языку 5 А класс (учитель – Морозова К. С.)
Рабочая программа по английскому языку 6 Б класс (учитель – Морозова К. С.)
Рабочая программа по английскому языку 7 класс (учитель – Морозова К. С.)
Рабочая программа по английскому языку 8 Б класс (учитель – Морозова К. С.)
Рабочая программа по английскому языку 9 Б класс (учитель – Морозова К. С.)
Рабочая программа по английскому языку 11 класс (учитель – Морозова К. С.)
Немецкий язык:
Рабочая программа по немецкому языку 7,9 классы (учитель – Гараева Э.Р.)
Рабочая программа по немецкому языку 6,8 классы (учитель – Гараева Э.Р.)
ОБЖ
Рабочая программа по ОБЖ 10 класс (учитель Казакова С.А.)
Рабочая программа по ОБЖ 11 класс (учитель Казакова С.А.)
Рабочая программа по ОБЖ 9 класс (учитель Казакова С. А.)
А.)
Рабочая программа по ОБЖ 8 класс (учитель Казакова С.А.)
Окружающий мир:
Рабочая программа по окружающему миру (человек, природа, общество) 1 класс(учитель Казакова С.А.)
Рабочая программа по окружающему миру (человек, природа, общество) 2 класс (учитель Казакова С.А.)
Рабочая программа по окружающему миру (человек, природа, общество) 3 класс (учитель Казакова С.А.)
Рабочая программа по окружающему миру (человек, природа, общество) 4 класс (учитель Казакова С.А.)
Технология:
Рабочая программа по технологии 5 класс ( учитель -Караваевой Л.И.)
Рабочая программа по технологии 6 класс (учитель – Караваевой Л.И.)
Рабочая программа по технологии 7 класс ( учитель -Караваевой Л.И.)
Физическая культура:
Рабочая программа по физической культуре 5-7 классы (учитель -Лысенко Е.
Рабочая программа учителя по физической культуре 8-9 классы (учитель -Лысенко Е.А.)
Рабочая программа по физической культуре 10-11 юноши (учитель -Лысенко Е.А.)
Рабочая программа по физической культуре 11 класс девушки (учитель -Лысенко Е.А.)
ИЗО:
Рабочая программа по изобразительному искусству 5 класс (учитель – Желудкова Е.Е.)
Рабочая программа по изобразительному искусству 6 класс (учитель – Желудкова Е.Е.)
Рабочая программа по изобразительному искусству 7 класс (учитель – Желудкова Е.Е.)
Музыка:
Рабочая программа “Музыка” (1 класс) (учитель – Визгалова А.В.)
Рабочая программа “Музыка” (2 класс) (учитель – Визгалова А.В.)
Рабочая программа “Музыка” (3 класс) (учитель – Визгалова А.В.)
Рабочая программа “Музыка” (4 класс) (учитель – Визгалова А.В.)
Рабочая программа “Музыка” (5-7 класс) (учитель – Визгалова А. В.)
В.)
Рабочая программа “Музыка” (8 класс) (учитель – Визгалова А.В.)
Внеурочная деятельность:
Рабочая программа кружка внеурочной деятельности “Русский язык и культура речи” 10 класс (учитель – Сисякина А.А.)
Рабочая программа по внеурочной деятельности в 5 классе (учитель – Довлатбегян В.В)
Рабочая программа внеурочной деятельности “Полезное программирование”, 10 класс, ФГОС ООО (учитель – Савченкова М.В.)
Рабочая программа “Робототехника” (3-4 класс) (учитель Савченкова М.В.)
Рабочая программа внеурочной деятельности “Город, компьютеры, программа, роботы (7 класс) (учитель – Савченкова М.В.)
Рабочая программа внеурочной деятельности “Город, компьютеры, программа, роботы” (5 класс) (учитель – Савченкова М.В.)
Рабочая программа внеурочной деятельности “Мультстудия” (учитель Караваева Л.И.)
Рабочая программа внеурочной деятельности Здоровое питание” (3-4 класс) (учитель – Караваева Л. И.)
И.)
Рабочая программа внеурочной деятельности «Здоровое питание» (1-2 класс) (учитель – Караваева Л.И.)
Рабочая программа по внеурочной деятельности «Жизненные навыки» 1 класс (учитель -Рохман Е.О.)
Рабочая программа по внеурочной деятельности «Жизненные навыки» 2 класс (учитель -Рохман Е.О.)
Рабочая программа по внеурочной деятельности «Жизненные навыки» 6 класс (учитель -Рохман Е.О.)
Рабочая программа по внеурочной деятельности«Логика» 3 класс (учитель -Рохман Е.О.)
Программа внеурочной деятельности “ОСНОВЫ МИРОВОЙ ХУДОЖЕСТВЕННОЙ КУЛЬТУРЫ” (учитель – Желудкова Е.Е.)
Рабочая программа внеурочной деятельности “Все узнаю, все смогу” (учитель – Басова О.В.)
Рабочая программа внеурочной деятельности “Логика” (учитель – Басова О.В.)
Рабочая программа внеурочной деятельности “Театр “Лицедеи” (учитель – Басова О.В.)
Рабочая программа ГТО- 10класс (учитель -Лысенко Е. А.)
А.)
Рабочая программа ГТО 8-9 классы (учитель -Лысенко Е.А.)
Рабочая программа “Спортивные игры” 5-6 класс (учитель- лысенко Е.А.)
Рабочая программа “Экология растения” 6 класс(учитель – Володина Г.В.)
Рабочая программа “Биохимия” 10 класс (учитель – Казакова С. А.)
Рабочая программа “Экология человека” 8 класс (учитель – Володина Г.В.)
Рабочая программа “Разговор о здоровье” (1-2 класс) (учитель – Караваева Л.И.)
Рабочая программа “Разговор о здоровье” (3-4 класс) (учитель – Караваева Л.И.)
Рабочая программа “Мультстудия” (5-6 класс) (учитель – Караваева Л.И.)
Рабочая программа “Азбука смекалки” (3 класс) (учитель – Богданова Н.А.)
Рабочая программа “Азбука смекалки” (1 класс) (учитель – Богданова Н.А.)
Рабочая программа “Логика” (3 класс) (учитель – Богданова Н.А.)
Рабочая программа “Все цвета, кроме черного” (3 класс) (учитель – Богданова Н. А.)
А.)
Рабочая программа “НОУ Жираф” (3 класс) (учитель – Богданова Н.А.)
Рабочая программа “Логика” (1 класс) (учитель – Купряшина О.А.)
Рабочая программа “Звонкий голосок” (1 класс) (учитель – Визгалова А.В.)
Рабочая программа “Звонкий голосок” (2 класс) (учитель – Визгалова А.В.)
Рабочая программа “Звонкий голосок” (3 класс) (учитель – Визгалова А.В.)
Рабочая программа “Звонкий голосок” (4 класс) (учитель – Визгалова А.В.)
Рабочая программа “Занимательная математика” (6 а класс) (учитель – Рыбакова Е.А.)
Рабочая программа “Лаборатория математического моделирования” (7 класс) (учитель – Рыбакова Е.А.)
Рабочая программа “За страницами учебника” (8 класс) (учитель – Рыбакова Е.А.)
Рабочая программа “Замечательные уравнения и неравенства, их обоснование и применение” (9 класс) (учитель – Рыбакова Е.А.)
Рабочая программа “Биохимия” (10 класс) (учитель – Казакова С. А.)
А.)
Рабочая программа “Читательская грамотность” (6 А класс) (учитель – Лебедева Е.В.)
Рабочая программа “Читательская грамотность” (7 Б класс) (учитель – Лебедева Е.В.)
Рабочая программа “Читательская грамотность” (8 Б класс) (учитель – Лебедева Е.В.)
Рабочая программа “Биохимия” (11 класс )(учитель – Володина Г.В.)
Рабочая программа “Основы биоиндикации” (7 класс )(учитель – Володина Г.В.)
Рабочая программа “Экология человека” (8 класс )(учитель – Володина Г.В.)
Рабочая программа “Основные алгоритмы решения цитологических и генетических задач” (9 класс )(учитель – Володина Г.В.)
Рабочая программа “Спортивные игры” (7 класс)(учитель – Лысенко Е. А.)
Рабочая программа “Спортивные игры” (6 класс)(учитель – Лысенко Е. А.)
Рабочая программа “Спортивные игры” (5 класс)(учитель – Лысенко Е. А.)
Рабочая программа “Готовимся к сдаче ГТО” (9 класс)(учитель – Лысенко Е. А. )
)
Рабочая программа “Готовимся к сдаче ГТО” (10 класс)(учитель – Лысенко Е. А.)
Рабочая программа “Готовимся к сдаче ГТО” (11 класс)(учитель – Лысенко Е. А.)
Рабочая программа “Русский язык и культура речи” 10 класс (учитель – Сисякина А.А.)
Рабочая программа “Русский язык и культура речи” 11 класс (учитель – Сисякина А.А.)
Рабочая программа “В мире английского языка” (5 класс) (учитель – Ульюк В.И.)
Рабочая программа “В мире английского языка” (10 класс) (учитель – Ульюк В.И.)
Рабочая программа “На пути к проекту” (6 класс) (учитель – Караваева Л.И.)
Рабочая программа “Разговоры о здоровье” (1 – 2 класс) (учитель – Караваева Л.И.)
Рабочая программа “Разговоры о здоровье” (3 – 4 класс) (учитель – Караваева Л.И.)
Рабочая программа “Живая природа Московской области” (6 класс )(учитель – Володина Г.В.)
Рабочая программа «БИОХИМИЯ (ХИМИЯ)» 10-11 класс (учитель – Назарова Е. А.)
А.)
Рабочая программа «Первые шаги в химии» 8 класс (учитель – Назарова Е.А.)
Рабочая программа «Экспериментальное решение задач по химии» 9 класс (учитель – Назарова Е.А.)
Рабочая программа по английскому языку 8 класс (учитель – Морозова К. С.)
Рабочая программа по английскому языку 1 класс (учитель – Морозова К. С.)
Кружки:| Рабочая программа по русскому языку | 1-4 классы | Файл (PDF; 792Кб) | |
| Рабочая программа по литературному чтению | 1-4 классы | Файл (PDF; 584Кб) | |
| Рабочая программа по математике и информатике | 1-4 классы | Файл (PDF; 532Кб) | |
| Рабочая программа по окружающему миру | 1-4 классы | Файл (PDF; 947Кб) | |
| Рабочая программа по изобразительному искусству | 1-4 классы | Файл (PDF; 704Кб) | |
| Рабочая программа по технологии | 1-4 классы | Файл (PDF; 984Кб) | |
| Рабочая программа по математике | 5-11 классы | Файл (ZIP; 7Мб) | |
| Рабочая программа по русскому языку | 5-9 классы | Файл (ZIP; 1Мб) | |
| Рабочая программа по истории | 5-11 классы | Файл (ZIP; 7Мб) | |
| Рабочая программа по литературе | 5-9 классы | Файл (ZIP; 886Кб) | |
| Рабочая программа по музыке | 1-8 классы | Файл (ZIP; 642Кб) | |
| Рабочая программа по изобразительному искусству | 5-8 классы | Файл (ZIP; 191Кб) | |
| Рабочая программа по технологии (девочки) | 5-8 классы | Файл (ZIP; 289Кб) | |
| Рабочая программа по технологии (мальчики) | 5-8 классы | Файл (PDF; 1Мб) | |
| Рабочая программа по физике | 7-8 классы | Файл (ZIP; 302Кб) | |
| Рабочая программа по химии | 10-11 классы | Файл (ZIP; 741Кб) | |
| Рабочая программа по астрономии | 10 класс | Файл (PDF; 967Кб) | |
| Рабочая программа по физической культуре | 1-11 классы | Файл (ZIP; 3Мб) | |
| Рабочая программа по Истории Сибири | 11 класс | Файл (PDF; 373Кб) | |
| Рабочая программа по литературе | 10-11 класс | Файл (PDF; 684Кб) | |
| рабочая программа по математике (профильная) | 10-11 классы | Файл (PDF; 1Мб) | |
| Рабочая программа по МХК | 10-11 классы | Файл (PDF; 707Кб) | |
| Рабочая программа по ОБЖ | 5-11 классы | Файл (ZIP; 221Кб) | |
| Рабочая программа по обществознанию | 5-9 классы | Файл (DOC; 377Кб) | |
| Рабочая программа по обществознанию | 10-11 классы | Файл (PDF; 795Кб) | |
| Рабочая программа по русскому языку | 10-11 классы | Файл (PDF; 780Кб) | |
| Рабочая программа по химии | 8-9 классы | Файл (PDF; 1Мб) | |
| Рабочая программа по английскому языку | 2-4 классы | Файл (ZIP; 1Мб) | |
| Рабочая программа по английскому языку | 5-11 классы | Файл (ZIP; 2Мб) | |
| Рабочая программа по ОРКСЭ | 4 класс | Файл (PDF; 492Кб) | |
| Рабочая программа по физике | 10-11 классы | Файл (ZIP; 428Кб) | |
| Рабочая программа по географии | 10-11 классы | Файл (PDF; 585Кб) | |
| Рабочая программа по географии | 5-9 классы | Файл (PDF; 2Мб) | |
| Рабочая программа по биологии | 5-9 классы | Файл (PDF; 1Мб) | |
| Рабочая программа по биологии | 10-11 классы | Файл (PDF; 918Кб) | |
Программа внеурочной деятельности. Курс “Подготовка к сдаче норм ГТО” Курс “Подготовка к сдаче норм ГТО” | 5-9 классы | Файл (PDF; 625Кб) | |
| Программа внеурочной деятельности. Курс “Калейдоскоп наук” | 4 классы | Файл (PDF; 470Кб) | |
| Программа внеурочной деятельности. Курс “Английский для малышей” | 1 класс | Файл (PDF; 730Кб) | |
| Программа внеурочной деятельности. Курс “Я-гражданин” | 1-4 классы | Файл (PDF; 898Кб) | |
| Программа внеурочной деятельности. Курс “Подготовка к сдаче комплекса ГТО” | 9 класс | Файл (PDF; 802Кб) | |
| Программа внеурочной деятельности. Курс ” Вокальная студия” | 5-11 класс | Файл (PDF; 527Кб) | |
| Программа внеурочной деятельности. Курс “Общая физическая подготовка” | 5-8 классы | Файл (PDF; 445Кб) | |
| Программа внеурочной деятельности. Курс “Вожатский отряд “Пеликан” | Файл (PDF; 488Кб) | ||
Программа внеурочной деятельности. Курс “Занимательная математика” Курс “Занимательная математика” | 1 класс | Файл (PDF; 707Кб) | |
| Программа внеурочной деятельности. Курс “Логика” | 1-4 классы | Файл (PDF; 547Кб) | |
| Программа внеурочной деятельности. Курс “Логика | 1-4 классы | Файл (PDF; 547Кб) | |
| Элективный курс “Подготовка к ЕГЭ по биологии” | 10-11 классы | Файл (PDF; 965Кб) | |
| Элективный курс “Экология животных” | 7 класс | Файл (PDF; 840Кб) | |
| Внеурочная деятельность. Курс “ОБЖ.Островок безопасности” | 1 класс | Файл (PDF; 670Кб) | |
| Внеурочная деятельность. Курс “Чтение. Работа с текстом” | 1-4 классы | Файл (PDF; 760Кб) | |
| Рабочая программа по математике | 5 | Файл (PDF; 1Мб) | |
| Рабочая программа по математике | 6 класс | Файл (PDF; 1Мб) | |
| Внеурочная деятельностью Курс “Олимпиадный русский язык” | 1-4 классы | Файл (PDF; 1Мб) | |
Внеурочная деятельность. Курс “Исследовательская и проектная деятельность” Курс “Исследовательская и проектная деятельность” | 7 класс | Файл (PDF; 452Кб) | |
| Внеурочная деятельность. Курс “Исследовательская и проектная деятельность” | 8 класс | Файл (PDF; 813Кб) | |
| Дополнительная общеобразовательная общеразвивающая программа “Преемственность. Подготовка к школе” | 6 лет | Файл (PDF; 1Мб) | |
| Дополнительная общеобразовательная общеразвивающая программа по английскому языку “Страноведение” | Файл (PDF; 1Мб) | ||
| Дополнительная общеобразовательная общеразвивающая программа по французскому языку “Французский в перспективе” | Файл (PDF; 583Кб) | ||
| Рабочая программа по французскому языку | 5-9 классы | Файл (ZIP; 652Кб) | |
| Рабочая программа по немецкому языку | 5-9 классы | Файл (RAR; 607Кб) | |
| Рабочая программа по физике | 9 класс ФГОС | Файл (RAR; 111Кб) | |
| Адаптированная рабочая программа по биологии | 5 класс | Файл (PDF; 1Мб) | |
| Адаптированная рабочая программа по географии | 5 класс | Файл (PDF; 939Кб) | |
| Рабочая программа факультатива “Познавательная география” | 6 класс | Файл (PDF; 359Кб) | |
| Программа курса “Проектная деятельность по географии” | 8 класс | Файл (PDF; 359Кб) |
| Study.
 com
com
Продолжительность
2–2,5 часа
Стандарты учебной программы
- CCSS.ELA-LITERACY.RST.11-12.3
Точно следовать сложной многоступенчатой процедуре при проведении экспериментов, проведении измерений или выполнении технических задач; анализировать конкретные результаты на основе объяснений в тексте.
Материалы
- Компьютер с проектором
- Копии викторины урока
- Листы с головоломками судоку – по 2 на каждую пару учеников
- Бумага для принтера
- Правители
- Прозрачность логической головоломки
Инструкция
- В начале урока расскажите своим ученикам, что есть много разных головоломок.Они могли решать простые головоломки с картинками, когда были моложе. Есть головоломки посложнее, которые требуют использования логики.
- Объясните своим ученикам, что они узнают больше о решении логических головоломок, посмотрев видеоурок «Использование логики и стратегии для решения головоломок».

- Проиграйте урок для своих учеников и периодически приостанавливайте его для обсуждения.
- Начните видео с самого начала и остановите его на 0:55, затем спросите и обсудите следующее:
- Что такое судоку?
- Какие числа должны быть в подсетке головоломки судоку?
- Что такое логические головоломки?
- Что вам дают, чтобы решать логические задачи?
- Продолжите воспроизведение видео и снова приостановите его на 2:40, затем спросите и обсудите:
- Что такое логика?
- Сколько раз можно использовать число в строке или столбце в головоломке судоку?
- Как сетка помогает решать логические задачи?
- Продолжите воспроизведение видео и снова остановите его на 3:58, затем спросите и обсудите следующее:
- Что такое стратегия?
- Какова стратегия решения головоломок судоку?
- Что такое стратегия решения логических головоломок?
- Продолжите воспроизведение оставшейся части видео, а затем ответьте на любые вопросы, которые могут возникнуть у ваших учеников.

- Проецируйте прозрачность логической головоломки на доску.
- Решите логическую головоломку всем классом. Убедитесь, что вы ответили на любые вопросы или неясности при решении головоломки .
Судоку
- Объедините учеников в пары
- Дайте каждой паре по 2 головоломки судоку
- Объясните своим ученикам, что они должны собирать головоломки вместе. Они должны записывать свою стратегию решения головоломки по мере ее решения.Стратегия должна быть пошаговой.
- Каждая пара должна предоставить вам свои головоломки, а также свои пошаговые стратегии для проверки.
Создайте свой собственный судоку
- Раздайте каждой паре учащихся несколько листов бумаги для принтера и линейку
- Объясните своим ученикам, что они будут вместе создавать свои собственные головоломки судоку.
- После того, как пары создадут свои головоломки, пусть они передают свои головоломки паре слева от них, чтобы они могли ее решить.

- После того, как они будут решены, пары должны передать головоломки паре, которая их создала для них, чтобы проверить ее на точность.
Оценка
- Дайте каждому учащемуся контрольную работу на уроке
- Просмотрите ответы викторины после того, как все учащиеся завершили свои викторины
Как участвовать в процессе доказательной практики
Теперь, когда мы рассмотрели основные подходы к практическому оцениванию в группах, нам нужно представить инструмент, используемый во многих организациях социальной работы, логическую модель.До сих пор вы читали о целях и задачах, а также о показателях процесса и результата. Часто организации социального обеспечения используют так называемые «логические модели», чтобы объединить цели, задачи и меры.
Эти логические модели ориентированы на одну конкретную программу, обслуживающую группу клиентов с особыми потребностями. Однако логические модели не используются для индивидуального отслеживания клиентов. Основная функция логической модели – наметить процесс программы, чтобы информировать об оценке практики.
Основная функция логической модели – наметить процесс программы, чтобы информировать об оценке практики.
Универсальные по своей природе логические модели могут использоваться не только для оценки практики планирования. Действительно, эти модели можно использовать для разработки новой программы или отслеживания реализации (т. е. внедрения) новой программы. С другой стороны, логические модели можно использовать для планирования программы, чтобы ее можно было объяснить новым социальным работникам, чтобы облегчить участие спонсоров программы или для общения с другими заинтересованными сторонами организации. Подводя итог, можно сказать, что просмотр логической модели может помочь людям увидеть, как различные элементы программы сочетаются друг с другом, достигая кульминации в том, как успех измеряется на этапе результата.
Модели Logic бывают разных форматов и конструкций. Ниже, на рис. 5.1, мы представляем общий формат логических моделей в организациях, связанных с социальной работой. После четкого определения целей и задач организация может документировать входные данные, мероприятия и результаты программы, а также показатели результатов в краткосрочной, среднесрочной или долгосрочной перспективе.
После четкого определения целей и задач организация может документировать входные данные, мероприятия и результаты программы, а также показатели результатов в краткосрочной, среднесрочной или долгосрочной перспективе.
|
|||||
|
|||||
Рисунок 5. 1 Пример шаблона логической модели
1 Пример шаблона логической модели
В логической модели под входами следует понимать отдельные типы инвестиций, которые вносятся в программу. Часто входные данные включают финансы, отработанные часы или пожертвованное пространство. Виды деятельности документируют действия, предпринимаемые организацией, и на кого ориентированы эти действия.
Выходы — это определенные элементы, отслеживаемые в этом процессе. А что касается показателей результатов, мы полагаем, что к этому моменту вы уже в курсе, что это такое! Некоторые люди рассматривают краткосрочные и среднесрочные меры как результаты, тогда как долгосрочные меры — как воздействия.Кроме того, хотя шаблон, показанный на рис. 5.1, имеет только два показателя результата, нет правила, согласно которому вы не можете использовать больше показателей!
Чтобы понять, как работает логическая модель, давайте вернемся к нашему социальному работнику в области психического здоровья, который работает над улучшением симптомов психического здоровья своих клиентов (см. рис. 5.2).
рис. 5.2).
|
|||||
|
|||||
|
|||||
|
|
||||
|
|
|
|
||
|
|
||||
|
|
|
|
||
Рисунок 5. 2 Шаблон логической модели для оценки амбулаторного центра психического здоровья
2 Шаблон логической модели для оценки амбулаторного центра психического здоровья
Как вы помните, наш социальный работник разбил эту клиническую цель на измеримые задачи, включая уровень тревоги и частоту раздражительности. Каждая из этих целей может быть измерена в процессе терапевтического вмешательства, чтобы отслеживать прогресс клиента, но также может быть рассмотрена во время или после того, как клиент завершил лечение, на этот раз в качестве меры результата. Цель сбора информации о процессе отличается от цели сбора информации о результатах, даже если меры те же.
Теперь, когда мы рассмотрели логическую модель, ориентированную на клиническую практику, давайте посмотрим на наш пример организации сообщества, чтобы поддержать тех из вас, кто занимается макросоциальной работой (см. рис. 5.3).
Если мы вернемся к предыдущим главам, то вспомним, что повышение чувства гордости за общество является целью города, нанимающего социального работника для организации сообщества. Однако наш социальный работник осознал необходимость разработки измеримых задач, которые вместе составляют эту цель.В этом случае задачи включают сбор информации о том, остается ли стабильным намерение граждан оставаться в сообществе или испытывают ли граждане чувство гордости за свой местный парк.
Однако наш социальный работник осознал необходимость разработки измеримых задач, которые вместе составляют эту цель.В этом случае задачи включают сбор информации о том, остается ли стабильным намерение граждан оставаться в сообществе или испытывают ли граждане чувство гордости за свой местный парк.
|
|||||
|
|||||
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|||
|
|
|
|
|
|
Рисунок 5. 3 Пример шаблона логической модели для оценки проекта организации сообщества
3 Пример шаблона логической модели для оценки проекта организации сообщества
Таким образом, логические модели являются полезными инструментами для понимания того, как все части программы сочетаются друг с другом. Полезные в качестве ориентира, логические модели могут также помочь привлечь спонсоров программы к цели дальнейшего финансирования. Многим социальным работникам никогда не понадобится создавать логическую модель, но они должны знать, как интерпретировать логические модели своих собственных программ.
Вопросы для обсуждения к главе 5:
- Как дизайн исследования связан с логическим моделированием?
- Объясните разницу между выводом и результатом.
- Опишите различные варианты использования логической модели для организации социальной работы.
- Как может выглядеть логическая модель программы, над которой вы работаете/стажируетесь?
- Предположим, вы оцениваете программу обучения социальным и эмоциональным навыкам для 3 учащихся rd .
 Вы хотите определить свои входы, действия, выходы, результаты и воздействия. Определите каждый из списка ниже:
Вы хотите определить свои входы, действия, выходы, результаты и воздействия. Определите каждый из списка ниже: - Улучшение социальных и эмоциональных навыков
- Грант для вашего проекта социальных и эмоциональных навыков
- Количество учащихся, участвовавших в проекте социального и эмоционального обучения
- Использование говорящей палочки для обучения социальным и эмоциональным навыкам.
Логический стиль обучения | Time4Learning
Посмотрите наши демонстрации уроков! Какой тип учащихся обладает способностью логически мыслить и может исследовать закономерности? Логические учащиеся преуспевают, используя порядок, шаги и логику. Эти учащиеся могут легко устанавливать связи и распознавать закономерности, а также хорошо работать с числами. У них очень систематический подход к обучению, и они отлично справляются с организацией. Уроки с большим количеством текста могут быть не идеальными для логических учеников; они предпочитают перейти к делу и сосредоточиться на фактах.
На этой странице вы узнаете больше о логическом стиле обучения, советы, которые помогут им достичь своих целей в обучении, и многое другое.
Каковы характеристики логического стиля обучения?
Чтобы объяснить логический стиль обучения, нам нужно понять некоторые характеристики этих учащихся, этих учеников:
- Любите хранить подробные планировщики и органайзеры
- Наслаждайтесь игрой в стратегии
- Очень любознательны и любопытны
- Предпочитайте визуальные эффекты словам
- Очень целеустремленные
- Поиск правил и процедур
- Май с трудом пишет творчески
- Может иметь проблемы с просмотром больших изображений
Учебные советы для логических учащихся
Мы знаем, что логико-математические ученики обычно методичны и думают линейно.Будучи заинтересованными, мотивированными и активно создающими и проектирующими свои собственные визуальные эффекты, эти учащиеся помогают запоминать важную информацию и создают легкий ориентир для будущего обучения.
Поэтому, чтобы удовлетворить их, мы собрали несколько советов по обучению для логических учащихся, которые помогут повысить их успеваемость.
- Учащиеся с логико-математическим стилем обучения лучше всего учатся, используя наглядные материалы, ноутбуки и выполняя практические задания.
- Не забудьте предоставить структуру с набором правил, целей и процедур для них, так как эти учащиеся иногда могут бороться с двусмысленностью.
- Цели могут быть краткосрочными, но обязательно поощряйте ребенка мыслить масштабно и ставить долгосрочные цели на месяц или даже на учебный год. Вы можете инвестировать в планировщик, где они могут планировать дни, недели и / или месяцы, чтобы отслеживать прогресс.
- Поработайте со своим ребенком, чтобы узнать, в каком порядке он хотел бы работать над своими предметами, и создайте календарь, на который он может легко ссылаться и которому будет легко следовать.
- Маркеры могут быть очень полезны для логических учеников, чтобы определить наиболее важные части во время чтения.

- Для таких занятий, как история, которые содержат большое количество текста, временные шкалы со списком фактов — отличный способ заинтересовать вашего логического учащегося. Четкая структура и последовательная организация позволяют им легко усваивать информацию.
- Поощряйте вашего ученика выбирать общие темы и закономерности в истории; позвольте им творчески использовать это распознавание образов и попросите их попытаться предсказать будущее!
- Старайтесь поощрять обучение как решение проблем и поиск решений.Если ваш ученик застрял, задайте ему вопросы, чтобы подтолкнуть его к обучению, или предложите ему найти ответ среди «доказательств».
- Везде, где это возможно, старайтесь использовать категоризацию или классификации, чтобы помочь логическим учащимся достичь своих целей обучения. Например, для географии вы можете использовать языки, этнические группы и региональные категории, чтобы преподавать этот предмет своим ученикам.
- Попросите ребенка разбить большие объемы информации на диаграммы и графики.
 Логико-математические учащиеся любят составлять и рассматривать карты, диаграммы, схемы и графики.
Логико-математические учащиеся любят составлять и рассматривать карты, диаграммы, схемы и графики. - Ученикам, которые не умеют писать, предлагается составить план самостоятельно. Это поможет им превратить мелкие детали в общие идеи.
Математика и естествознание, как правило, являются предметами, в которых ученики, изучающие логику и математику, преуспевают из-за подробного, основанного на процедурах характера этих предметов. Тем не менее, логические учащиеся могут испытывать затруднения в этих предметах, когда им даются сложные словесные задачи. Обязательно разбивайте большие абзацы на более мелкие части, которые учащимся будет легко разбить.
Вы также можете ознакомиться с советами по обучению, которые мы составили для кинестетиков, так как логические и кинестетические учащиеся процветают благодаря практическим действиям.
Как Time4Learning работает для логических учащихся
Как только вы узнаете, как ваш ученик учится лучше всего, вы сможете помочь ему улучшить свои знания во многих областях. Традиционные учебные программы на дому часто разрабатываются так же, как учебные программы в классе, и просто не удовлетворяют потребности учащихся, изучающих логику/математику.
Традиционные учебные программы на дому часто разрабатываются так же, как учебные программы в классе, и просто не удовлетворяют потребности учащихся, изучающих логику/математику.
Time4Learning обеспечивает идеальную среду, в которой логические учащиеся могут изучать новые вещи, практиковаться и исследовать.Каждый предмет представлен в мультимедийном формате, который является очень интерактивным и увлекательным. Учебная программа Time4Learning:
- Предлагает пошаговые инструкции в организованном, последовательном порядке.
- Включает в себя множество интерактивных заданий и рабочих листов, которые разбивают обучение на более мелкие фрагменты информации.
- Включает в себя фантастическую систему отслеживания, которая упорядочивает и составляет списки заданий, которые понравятся ученикам, изучающим логику и математику!
- Предлагает возможность ставить цели и отслеживать прогресс, что дает учащимся простую информацию о том, какие задания необходимо выполнить и когда.

- Имеет дополнительные инструкции для наших членов, такие как модульные исследования, которые учат детей интересным концепциям с использованием временных шкал и маркеров.
Подпишитесь на Time4Learning и получите доступ к разнообразным учебным материалам, которые помогут вашему ребенку добиться успеха. Сделайте Time4Learning частью своего набора инструментов для образовательных ресурсов для обучения вашего уникального логического ученика.
Дополнительная информация о стилях обучения
The Logic of English Essentials
The Logic of English Essentials Курс был написан для учащихся в возрасте от семи лет и старше, которым нужна структурированная интегрированная программа для обучения чтению, правописанию и грамматике.Его можно использовать после курса Foundations того же автора или другой вводной фонетической программы. (Основы не являются обязательным условием.) Учащиеся, которые не прошли предварительный инструктаж, могут начать с Essentials , если они проходят предварительные уроки, описанные ниже.
Второе издание Essentials содержит два больших руководства для учителей и две рабочие тетради для учащихся. Оба тома необходимы для курса, и на прохождение каждого тома уйдет не менее семестра.
Второе издание учебника Essentials существенно переработано по сравнению с первым изданием и включает три уровня инструкций. Это позволяет учителям удовлетворять потребности учащихся, работающих на разных уровнях в семье или классе, а также дает возможность циклически проходить всю программу два или три раза для учащихся, которым требуется повторение основ, но с повышением уровня сложности. Большая часть каждого урока адресована «Всем», но некоторые сегменты урока определены для использования с уровнями A, B или C.Руководство для учителя включает в себя вступительный тест. Уровень A предназначен для второклассников или учащихся старшего возраста, испытывающих затруднения, уровень B лучше всего подходит для учащихся третьего или четвертого класса, а уровень C подходит для учащихся пятого класса и старше. Essentials могут быть выполнены учащимися старшего возраста всего за три-четыре месяца.
Essentials могут быть выполнены учащимися старшего возраста всего за три-четыре месяца.
Первые десять уроков в Essentials являются «предварительными уроками», которые повторяют или обучают (в зависимости от уровня навыков учащегося) фонематическому восприятию, фонограммам, смешению и основам письма.Эти необязательные уроки следует использовать с учащимися, которым необходимо начать с самого начала, прежде чем переходить к обычным урокам, которые начинаются на уровне, который можно считать вторым классом или выше. Вы должны уделять столько времени, сколько вам нужно, для работы над предварительными уроками. Курс Logic of English Rhythm of Handwriting рекомендуется для тех, кто все еще нуждается в обучении письму. Уроки этого курса коррелируют с предварительными уроками в Essentials .
Essentials первый из обычных уроков начинается с краткого обзора основных фонограмм (включая qu вместе с отдельными буквами), а затем продолжается занятиями по орфографии, грамматике, диктовке, словарному запасу, чтению и сочинению. .Очевидно, что это требует некоторого предварительного развития навыков либо на предварительных уроках, либо на других инструкциях, поскольку темп будет слишком быстрым для тех, кто не прошел никакой предварительной подготовки.
.Очевидно, что это требует некоторого предварительного развития навыков либо на предварительных уроках, либо на других инструкциях, поскольку темп будет слишком быстрым для тех, кто не прошел никакой предварительной подготовки.
Методология
Essentials объединяет чтение, правописание, сочинение и грамматику, используя мультисенсорные обучающие упражнения и игры, что делает его комплексной программой языковых искусств. Основанный на методологии Ортона-Гиллингема, Essentials использует интенсивный фонетический подход, обучая правилам, которые охватывают около 98% слов в английском языке (согласно Essentials ). Essentials обучает каждой фонограмме и представляет все ее звуки вместе (например, O говорит /ŏ – ō – ö/ как в слове стоп, иди, делай), а не обучает различным звукам фонограммы изолированно друг от друга. К концу программы учащиеся узнают все возможные варианты написания каждого звука (например, о, оа, оэ и оо для долгого звука о).
Essentials использует фонограммы и другие наглядные пособия как неотъемлемую часть учебного процесса. Индуктивные методы иногда используются в Essentials , чтобы учащиеся обнаруживали правила или закономерности, а не рассказывали, что они из себя представляют.
Уроки преподаются из руководств учителя и требуют прямого обучения. Преподавательские инструкции — как в том, чему учат студентов, так и в боковых панелях для учителя — являются более подробными и обширными, чем во многих других программах. Например, в дополнение к базовым инструкциям программа использует частые диктовки, учит осознавать движения рта и языка, необходимые для произнесения звуков, и подчеркивает важность изучения правил слоговой лексики.
В то время как некоторые другие программы, основанные на методологии Ортона-Гиллингема, требуют, чтобы учащиеся создавали свои собственные тетради, записывая все правила, фонограммы, правописание слов и т. д., Essentials предоставляет учащимся рабочие тетради, но при этом использует отдельные записные книжки, в которых учащиеся будут писать под диктовку или составлять свои собственные фразы и предложения. Рабочие тетради делают объем письма более управляемым, и это может быть особенно важно для учащихся, которые борются с мелкими моторными навыками или имеют другие трудности в обучении.
Рабочие тетради делают объем письма более управляемым, и это может быть особенно важно для учащихся, которые борются с мелкими моторными навыками или имеют другие трудности в обучении.
Essentials очень всеобъемлющий. Гиды учителя огромны. Том 1 состоит из 632 страниц и весит около пяти фунтов! Несмотря на то, что пособия для учителей такие объемные, дополнительный материал во втором издании действительно облегчает преподавание курса.В то время как первая рабочая тетрадь для учащихся содержит более 300 страниц, она крупная и не перегружена, так что каждая страница выглядит очень удобной.
В каждом томе 15 уроков. Каждый урок разделен на пять разделов, и каждый раздел должен занимать от 30 до 45 минут в день. Уроки следуют типичному потоку в течение каждой недели с обучением фонограммам, чтению, правописанию, словарному запасу, грамматике и диктанту. Орфографический анализ является ключевой функцией Essentials . Это последовательный процесс, в ходе которого учащимся предлагается применить свои знания о звуках и фонограммах для определения правописания каждого слова. Учащиеся записывают слова в своих рабочих тетрадях, подчеркивая те или иные фонограммы, делая это сначала по указанию учителя, а затем постепенно самостоятельно.
Учащиеся записывают слова в своих рабочих тетрадях, подчеркивая те или иные фонограммы, делая это сначала по указанию учителя, а затем постепенно самостоятельно.
Учебный материал для уровней A, B и C включает в себя списки анализа орфографии для каждого уровня с более сложными словами, а также более сложные инструкции по грамматике и словарному запасу. Материал диктанта также привязан к разным уровням.
На протяжении всего курса учителю необходимо проводить уроки, в первую очередь с доской и карточками.Учащиеся отвечают устно, выполняют письменные работы в своих рабочих тетрадях и тетрадях, а иногда и в играх. В курс встроено множество обзоров и периодических оценок.
Руководства для учителя Essentials содержат пошаговые планы уроков, написанные по сценарию, чтобы учитель точно знал, что говорить и делать. Это облегчает родителям и учителям подготовку и проведение уроков.
Помимо руководств для учителей и рабочих тетрадей для учащихся вам понадобится ряд других предметов: Флэш-карты с базовой фонограммой, Logic of English Spelling Journal , Флэш-карты с правилами правописания, Флэш-карты с грамматикой, Флэш-карты с расширенной фонограммой, Фонограмма Игровые карты, карточки с морфемами, игровые плитки с фонограммами и карточки для анализа правописания. Они включены в полный пакет.
Они включены в полный пакет.
Extras
Те, кто использует Essentials для восстановления, могут также захотеть приобрести дополнительный Essentials Reader с сопровождающим его руководством по обучению и тетрадью для учащихся. Это обеспечивает фоническую практику чтения и развитие навыков.
Вы также можете прочитать книгу автора Дениз Эйде, Раскрывая логику английского языка , в которой она представляет основы и философию программы, а также методологию и таблицы правил и шаблонов.
Хотя обучение не требуется, некоторые родители и учителя действительно хотят пройти обучение и получить более глубокое понимание того, как работает программа. С этой целью автор Дениз Эйде создала дополнительное видео-обучение. Доступ к видео можно получить по адресу https://www.logicofenglish.com/loe-training. Это обширное обучение, которое включает в себя введение и обзор методологии, а также подробную информацию о фонограммах, правилах правописания, орфографических диктантах, инструкциях по письму, стилях обучения, развитии морфологии/словарного запаса, развитии языка, исследованиях чтения, фонематическом восприятии и многом другом. .
.
Резюме
Essentials предлагает комплексное обучение словесности, основанное на исследованиях и тщательной методологии. Его можно легко использовать со студентами в широком возрастном диапазоне. Essentials требует некоторого предварительного прочтения и подготовки со стороны родителей или учителей, но не требует учебных занятий или другой серьезной подготовки учителей. Ознакомившись с вводной информацией о программе, вы сможете проводить большинство уроков без значительных затрат времени на подготовку к уроку.Этот фактор делает Essentials особенно практичным выбором для многих родителей, которые хотят использовать методологию такого типа.
Вам не нужно хорошо разбираться в математике, чтобы научиться кодировать
Я не одобряю обучение программированию, если она действительно этого не хочет. Я считаю, что вы должны следовать своему счастью с точки зрения карьеры, потому что большинство вещей, которые вы купите на все деньги, которые вы заработаете как программист, не сделают вас счастливыми. Кроме того, если единственная причина, по которой вы учитесь программировать, заключается в том, что вы хотите стать журналистом, и считаете, что это единственный способ прорваться в эту область, это неверно.
Кроме того, если единственная причина, по которой вы учитесь программировать, заключается в том, что вы хотите стать журналистом, и считаете, что это единственный способ прорваться в эту область, это неверно.
Другими словами, я полностью за то, чтобы люди не становились программистами, пока они принимают это решение по правильным причинам. «У меня плохо с математикой» — неправильная причина.
Математика имеет очень мало общего с программированием, особенно на ранних стадиях. На самом деле, я даже не уверен, почему люди смешивают эти два понятия. (Возможно, это связано с тем, что в обеих областях доминируют мужчины.)
Виктория Файн, Директор по стратегии Slate , на этой неделе рассказала, как научилась программировать, несмотря на то, что ненавидит математику.Ее секрет? Много-много гугления.
Как и любой хороший запрос Google, успешный ответ зависел от правильного вопроса. Вопрос «Как сделать веб-сайт красным» оказался далеко не таким успешным вопросом, как «Цветовые значения CSS HEX red» в сочетании с «Цвет фона CSS».
Я провел много времени, изучая Google как профессионал. Я тщательно изучил словарь HTML, поэтому знал, о чем говорю, когда спрашивал ответы в Интернете.
Опыт Файна типичен для программистов-самоучек и напоминает мое собственное приключение по обучению кодированию марш смерти .В начале вы запоминаете некоторые основные понятия, например, как работает Интернет, что делает код, как использовать FTP и так далее. Затем вы опираетесь на эти знания — в первую очередь с помощью поиска в Google, проб и ошибок — по мере изучения выбранного вами языка (языков).
Чтобы понять, что должна говорить ваша программа, вам потребуются некоторые базовые логические навыки. Вам также необходимо уметь копировать и вставлять элементы из онлайн-репозиториев и слегка их настраивать. Но гуманитарии, только что написавшие пачки курсовых работ, вероятно, более талантливы в этом, чем математики.
Я знаю множество людей со степенью бакалавра, магистра и даже доктора философии или международных отношений, которые научились программировать. Это правда, что некоторые типы кода немного похожи на уравнения. Но вам на самом деле не нужно их решать, просто знайте, куда они идут и что они делают. Программист и предприниматель Эмма Малкуини хорошо выразилась:
Это правда, что некоторые типы кода немного похожи на уравнения. Но вам на самом деле не нужно их решать, просто знайте, куда они идут и что они делают. Программист и предприниматель Эмма Малкуини хорошо выразилась:
В большинстве случаев вы видите, что сложную математику (физическую и геометрическую) выполняет либо компьютер, либо кто-то другой.Хотя расчеты происходят и необходимы для успешного выполнения программы, программисту не нужно знать, как они выполняются.
Людям, которые программируют видеоигры, наверное, нужно больше математики, чем среднему веб-дизайнеру. Но если вы просто хотите кодировать что-то, что появляется в Интернете, вы получите всю математику, которая вам понадобится, когда вы пройдете последний уровень Math Blaster. (Вот хороший обзор математических навыков, необходимых для начального уровня программирования. Самое сложное — это теорема Пифагора.)
По моему опыту, единственное, что вам нужно при обучении кодированию, — это способность подавлять свой гнев, когда компьютеры не делают того, что вы хотите. Вот почему, увы, я плохой кодер.
Вот почему, увы, я плохой кодер.
Использование логических моделей для планирования и оценки программ – творческие исследовательские решения
На любом вводном курсе по оценке программ вы, скорее всего, узнаете о логических моделях. Возможно, вы не знакомы с логическими моделями или у вас могут возникнуть вопросы о том, почему и как можно использовать логические модели для помощи в планировании или оценке вашей программы.Цель этой статьи — описать логические модели, цель использования логических моделей, а также предоставить некоторые советы и ресурсы для разработки логической модели для вашей программы. Создание логической модели может показаться трудоемким процессом, который вы можете пропустить. Надеюсь, к концу этой статьи я прояснил логические модели, что они влекут за собой, и упростил процесс создания ваших собственных.
Логическая модель — это инструмент планирования, который используется для визуализации входных данных и действий для программы, а также ожидаемых результатов программы. Он показывает, как работает программа. Логические модели обычно имеют следующие шесть категорий: входы, действия, выходы, краткосрочные результаты, промежуточные результаты и долгосрочные результаты. Представьте себе гипотетическую программу общественного здравоохранения, предназначенную для повышения уровня здорового питания среди молодежи, при чтении компонентов логической модели и приведенных ниже примеров.
Он показывает, как работает программа. Логические модели обычно имеют следующие шесть категорий: входы, действия, выходы, краткосрочные результаты, промежуточные результаты и долгосрочные результаты. Представьте себе гипотетическую программу общественного здравоохранения, предназначенную для повышения уровня здорового питания среди молодежи, при чтении компонентов логической модели и приведенных ниже примеров.
- Входы: включает любые ресурсы, необходимые для работы программы или инициативы (например, финансирование, помещения для проведения собраний)
- Стратегии/мероприятия: все программные мероприятия и мероприятия (напр.г. разработать учебный план, набрать участников)
- Результаты: непосредственные материальные продукты программной деятельности (например, шесть еженедельных кулинарных курсов)
- Краткосрочные результаты: Ожидаемые изменения сразу после завершения программы (например, изменения в знаниях о приготовлении здоровой пищи)
- Промежуточные результаты: промежуточные результаты программы, которые могут проявиться в течение нескольких недель или месяцев (например, увеличение потребления фруктов и овощей, потеря веса или поддержание веса)
- Долгосрочные результаты: долгосрочных результата, которые происходят в течение нескольких месяцев или лет (например,г.
 снижение развития хронических заболеваний)
снижение развития хронических заболеваний)
Существует много преимуществ использования логической модели для планирования вашей программы и помощи в оценке. Логические модели, по сути, обеспечивают план, который позволяет планировщикам программ, оценщикам и другим заинтересованным сторонам связывать программные процессы с программными результатами. Поэтому он полезен для оценки результатов, поскольку показывает, как компоненты программы приводят к изменению поведения или, по крайней мере, к изменению поведения, которое вы предполагаете на основе теоретической основы вашей программы.При оценке процессов можно использовать логическую модель для оценки того, были ли программные действия реализованы так, как предполагалось. Создание логической модели часто представляет собой совместный процесс, и ее создание на этапах планирования программы позволяет оценщику участвовать в процессе раньше, а не оценивать программу в конце.1
Вы уже находитесь на этапе реализации своей программы, но никогда не создавали логическую модель? Я работал с несколькими программами, которые впервые создали свою логическую модель намного позже того, как их программа была запущена и запущена. На данный момент еще не поздно создать свою логическую модель. На самом деле полезно убедиться, что оценщик осведомлен обо всех существующих компонентах программы и ожидаемых результатах.
На данный момент еще не поздно создать свою логическую модель. На самом деле полезно убедиться, что оценщик осведомлен обо всех существующих компонентах программы и ожидаемых результатах.
Поддержание логического потока
Ваша логическая модель должна двигаться слева направо. Каждый вход должен быть связан с определенной деятельностью, которая затем связана с определенным выходом и, наконец, с конкретным результатом. Это позволяет планировщикам визуализировать, как каждый аспект их программы протекает и соединяется, чтобы в конечном итоге достичь намеченных результатов программы.Преимущество создания логической модели таким образом заключается в том, что она позволяет увидеть, насколько каждый компонент важен для результатов программы. Если в процессе произошел сбой, намеченные результаты могут быть не достигнуты. Таким образом, логическая модель позволяет разработчикам исследовать любые сбои в реализации программы таким образом, чтобы показать, что могло привести к недостаткам в результатах программы.
Использование материального реквизита
Наконец, существует множество онлайн-инструментов и шаблонов для создания логических моделей.Однако при совместной работе в группе создание логической модели с использованием карточек для заметок, стикеров или других материальных маркеров является простым способом манипулирования различными частями модели. Например, попробуйте использовать стикеры для визуализации каждого раздела и его элементов, используя стикеры разного цвета для каждого раздела. Наклейки можно легко перемещать по мере разработки логической модели перед созданием окончательной логической модели в электронном виде.
Пересмотрите свою логическую модель
Наконец, логические модели не являются статическими документами, они могут меняться со временем.По мере роста и развития вашей программы эти изменения должны отражаться в вашей логической модели. Выделите время, чтобы вернуться к своей логической модели и подумать о новых разработках или направлениях в программе.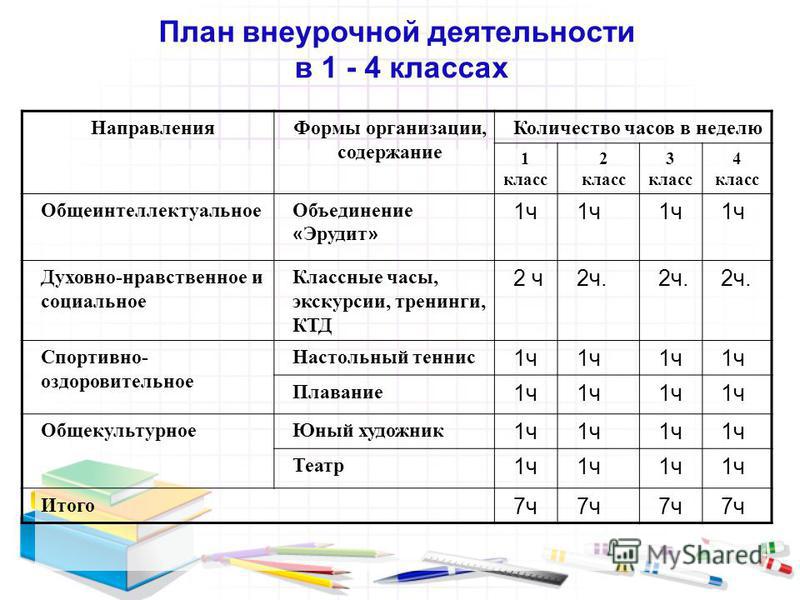 Я рекомендую пересматривать логические модели ежегодно.
Я рекомендую пересматривать логические модели ежегодно.
Ниже приведены некоторые дополнительные ресурсы по созданию логических моделей.
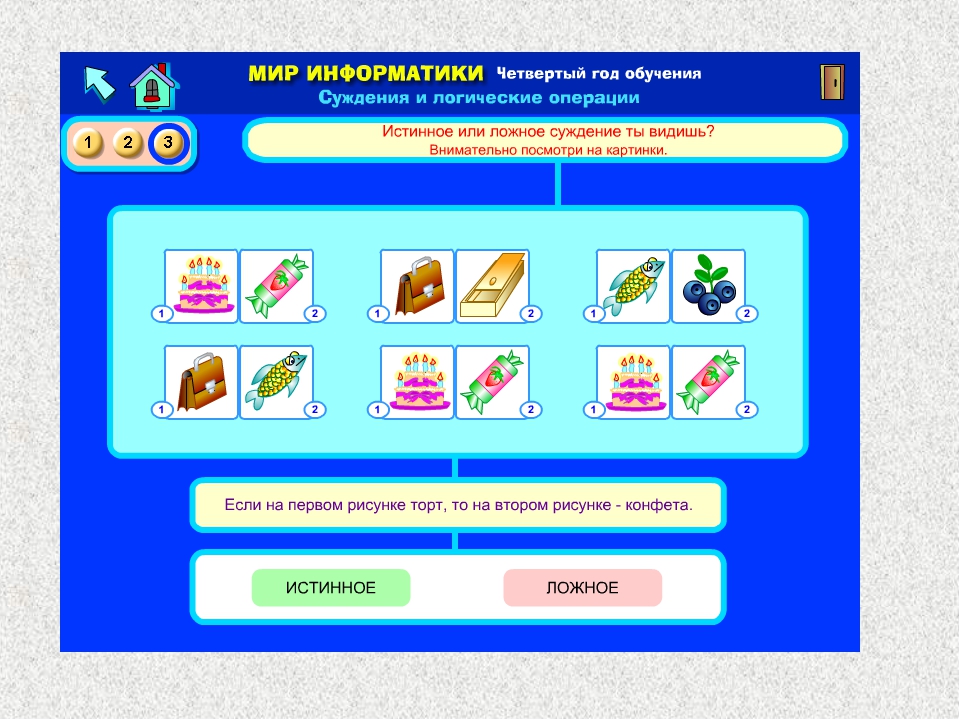
1.1 Логические операции
Математика обычно включает в себя объединение истинных (или гипотетически истинных) утверждения различными способами для получения (или доказательства) новых истинных утверждений.Начнем с разъяснения некоторых из этих фундаментальных идей.
Под предложением мы подразумеваем утверждение, имеющее определенное истинностное значение , истина (T) или ложь (F) — например,
«В 1492 году Колумб плыл по синему океану». (T)
«Наполеон выиграл битву при Ватерлоо». (Ф)
В более общем смысле под формулой мы подразумеваем
утверждение, возможно, с некоторыми переменными, которое либо истинно, либо
false всякий раз, когда мы присваиваем определенные значения каждой из переменных.2+y = 12$”, то $P(2,8)$ и $P(3,3)$
верно, а $P(1,4)$ и $P(0,6)$ ложны. Если $Q(x,y,z)$ равно “$x+y
Если $Q(x,y,z)$ равно “$x+y
Является ли предложение истинным или ложным, обычно зависит от того, что мы говорят о том, что одно и то же предложение может быть истинным или ложным в зависимости от по контексту; например, формула $x|y$ означает, что `$x$ делит $у$’. То есть $x|y$, если существует некоторый $z$ такой, что $y=x\cdot z$. В настоящее время, правда ли, что $3|2$? Это зависит: если мы говорим о целых числах, ответ – нет; если мы говорим о рациональных числах, то ответ да, потому что $2=3\cdot(2/3)$.(Конечно, если $x\not=0$ и $y$ любых рациональных чисел, затем $x|y$, так что это не очень полезное понятие. При обычном использовании внешний вид формулы “$x|y$” подразумевает , что $x$ и $y$ являются целыми числами.)
Вселенная дискурса для конкретной области математики представляет собой набор, который
содержит все, что представляет интерес для этой темы. Когда мы
изучение математических формул типа «$x$ делит $y$» на переменные
предполагается, что они принимают значения в любом дискурсивном универсуме
подходит для конкретного предмета. Вселенная дискурса
обычно ясно из обсуждения, но иногда нам нужно будет
идентифицируйте его явно для ясности.
Вселенная дискурса обычно обозначается $U$.
Вселенная дискурса
обычно ясно из обсуждения, но иногда нам нужно будет
идентифицируйте его явно для ясности.
Вселенная дискурса обычно обозначается $U$.
Сложные предложения и формулы составляются из более простых, используя небольшое количество логических операций . Просто горстка этих операций позволит нам сказать все, что мы должны сказать в математика.
Если $P$ — это формула, то «не $P$» — это другая формула. формула, которую мы символически запишем как $\lnot P$.Конечно, $\lне P$ ложно, если $P$ истинно, и наоборот, например,
«6 не является простым числом» или «Неверно, что 6 премьер” или “$\lnot(\hbox{6 простое число})$” (T)
«Рональд Рейган не был президентом». (Ф)
Предположим, что $P$ и $Q$ — формулы. потом «$P$ и $Q$» — это формула, записанная символически как $P\land Q$, называемое соединением из $P$ и $Q$. Чтобы $P\land Q$ были истинными как $P$, так и $Q$ должно быть истинным, иначе оно ложно, например,
“5$=6$ и 7$=8$. ” (Ф)
” (Ф)
«Сиэтл находится в Вашингтоне, а Бойсе — в Айдахо». (T)
«Толстой был русским, а Диккенс был Французский.” (Ф)
Если $P$ и $Q$ являются формулами, то формула “$P$ или $Q$” записывается символически как $P\lor Q$, называемая дизъюнкция $P$ и $Q$. это важно отметить, что это включительно или, то есть, “либо или оба”. Итак, если $P$, $Q$ или оба $P$ и $Q$ верны, то же самое и с $P\lor Q$. Единственный случай, когда $P\lor Q$ может быть ложным, состоит в том, что оба $P$ и $Q$ ложны, например,
«Вашингтон находится в Канаде, а Лондон — в Англии.” (Т)
“$5
«Ленин был испанцем или Ганди был итальянцем». (Ф)
Если $P$ и $Q$ – формулы, то “если $P$, то $Q$”
или “$P$ означает, что $Q$” написано
$P\подразумевает Q$, используя условное обозначение ,
$\подразумевает$. Не очевидно (по крайней мере, для большинства людей), под чем
обстоятельства $P\имеет Q$ должно быть правдой. Отчасти это потому, что
«if… then» используется в обычном английском языке более чем одним способом, однако
нам нужно исправить правило, которое позволит нам точно знать, когда $P\ подразумевает
Q$ верно. Конечно, если $P$ истинно, а $Q$ ложно, $P$ не может
подразумевают $Q$, поэтому $P\implis Q$ в этом случае ложно. Чтобы помочь нам с
в других случаях рассмотрим следующее утверждение:
Конечно, если $P$ истинно, а $Q$ ложно, $P$ не может
подразумевают $Q$, поэтому $P\implis Q$ в этом случае ложно. Чтобы помочь нам с
в других случаях рассмотрим следующее утверждение:
«Если $x$ меньше 2, то $x$ меньше 4».
Это утверждение должно быть верным независимо от значения $x$. (при условии, что вселенная дискурса является чем-то знакомым, например целые числа). Если $x$ равно 1, оно оценивается как $\rm T\имплицитно T$, если $x$ равно 3, оно становится $\rm F\implis T$, а если $x$ равно 5, становится $\rm F\ подразумевает F$.Таким образом, оказывается, что $P\implis Q$ истинно, если только $P$ истинно, а $Q$ ложно. Это правило, которое мы принимаем.
Наконец, бикондиционал , записанный как $\Leftrightarrow$, соответствует фраза «если и только если» или «если» коротко. Таким образом, $P \Leftrightarrow Q$ истинно, когда и $P$, и $Q$ имеют одинаковое истинностное значение, иначе оно ложно.
Пример 1.1.2 Предположим, что $P(x,y)$ равно “$x+y=2$” и $Q(x,y)$
равно “$xy>1$”. Тогда, когда $x=1$ и $y=1$,
$\lnot P(x,y)$, $P(x,y)\land Q(x,y)$, $P(x,y)\lor Q(x,y)$,
$P(x,y)\имеет Q(x,y)$ и $P(x,y)\Leftrightarrow Q(x,y)$
имеют значения истинности F, F, T, F, F соответственно, а когда
$x=2$ и $y=3$ имеют истинностные значения
Т, Ф, Т, Т, Ф соответственно.$\квадрат$
Тогда, когда $x=1$ и $y=1$,
$\lnot P(x,y)$, $P(x,y)\land Q(x,y)$, $P(x,y)\lor Q(x,y)$,
$P(x,y)\имеет Q(x,y)$ и $P(x,y)\Leftrightarrow Q(x,y)$
имеют значения истинности F, F, T, F, F соответственно, а когда
$x=2$ и $y=3$ имеют истинностные значения
Т, Ф, Т, Т, Ф соответственно.$\квадрат$
Используя операции $\lnot$, $\land$, $\lor$, $\implies$,
$\Leftrightarrow$, мы можем построить составных выражений, таких как
$$
(P\land (\lnot Q))\ подразумевает ((\lnot R)\lor ((\lnot P)\land Q)).
$$
Как показывает этот пример, иногда необходимо
включать много круглых скобок, чтобы группировать термины
в формуле ясно. Как и в алгебре, где
умножение имеет приоритет перед сложением, мы можем
убрать некоторые скобки
согласование определенного порядка, в котором логически
операции выполняются.Мы
будет применять операции в этом порядке, начиная с
от первого к последнему: $\lnot$, $\land$, $\lor$, $\implies$
и $\Leftrightarrow$. Так
$$A\подразумевает B\или C\land\lnot D
$$
сокращение от
$$A\подразумевает (B\или (C\land (\lnot D))). $$
Как и в алгебре, часто разумно включать
несколько дополнительных скобок, чтобы убедиться, что предполагаемый смысл понятен.
Большую часть информации, которую мы обсудили, можно обобщить в таблицах истинности . Например, таблица истинности для
$\lnot P$:
$$
Как и в алгебре, часто разумно включать
несколько дополнительных скобок, чтобы убедиться, что предполагаемый смысл понятен.
Большую часть информации, которую мы обсудили, можно обобщить в таблицах истинности . Например, таблица истинности для
$\lnot P$:
В этой таблице две строки, потому что есть только две возможности для истинное значение $P$.Другие логические операции используют две переменные, поэтому им требуется 4 строки в их таблицах истинности.
| $P$ | $Q$ | $P\land Q$ | $P\lor Q$ | $P\Rightarrow Q$ | $P\Leftrightarrow Q$ |
|---|---|---|---|---|---|
| Т | Т | Т | Т | Т | Т |
| Ф | Т | Ф | Т | Т | Ф |
| Т | Ж | Ж | Т | Ж | Ж |
| Ф | Ф | Ф | Ф | Т | Т |
Любое составное выражение имеет таблицу истинности. п$
строки в таблице, потому что есть много разных способов назначить
T и F для $n$ простых формул в составном выражении.
Таблица истинности для $(P\land Q)\lor \lnot R$ такова:
п$
строки в таблице, потому что есть много разных способов назначить
T и F для $n$ простых формул в составном выражении.
Таблица истинности для $(P\land Q)\lor \lnot R$ такова:
| $P$ | $Q$ | $R$ | $P \land Q$ | $\lnot R$ | $(P \land Q)\lor\lnot R$ |
|---|---|---|---|---|---|
| Т | Т | Т | Т | Ф | Т |
| Ф | Т | Т | Ф | Ф | Ф |
| Т | Ж | Т | Ж | Ж | Ж |
| Ф | Ф | Т | Ф | Ф | Ф |
| Т | Т | Ж | Т | Т | Т |
| Ф | Т | Ф | Ф | Т | Т |
| Т | Ж | Ж | Ж | Т | Т |
| Ф | Ф | Ф | Ф | Т | Т |
Обратите внимание, как включение промежуточных шагов облегчает работу с таблицей. посчитай и прочитай.
посчитай и прочитай.
Тавтология — это логическое выражение, которое всегда оценивается как T, то есть последний столбец его таблицы истинности состоит только из Т. Иногда говорят, что тавтология действительна ; хотя «действительный» используется в других контекстах как ну, это не должно вызывать путаницы. Например, $(P\land Q)\lor P\Leftrightarrow P$ является тавтологией, поскольку ее таблица истинности такова:
| $P$ | $Q$ | $P\land Q$ | $(P\land Q)\lor P$ | $(P\land Q)\lor P\Leftrightarrow P$ |
|---|---|---|---|---|
| Т | Т | Т | Т | Т |
| Ж | Т | Ж | Ж | Т |
| Т | Ж | Ж | Т | Т |
| Ф | Ф | Ф | Ф | Т |
Мы перечисляем несколько важных тавтологий в следующей теореме.
Теорема 1. 1.3. Справедливы следующие утверждения.
1.3. Справедливы следующие утверждения.
а) $P\стрелка влево \lnot\lnot P$
б) $P\lor Q\Leftrightarrow Q\lor P$
c) $P\land Q\Стрелка влево Q\land P$
d) $(P\land Q)\land R\Стрелка влево P\land(Q\land R)$
e) $(P\lor Q)\lor R\Стрелка влево P\lor(Q\lor R)$
f) $P\land (Q\lor R)\Leftrightarrow (P\land Q)\lor (P\land R)$
g) $P\lor (Q\land R)\Стрелка влево (P\lor Q)\land (P\lor R)$
ч) $(P\подразумевает Q)\стрелка влево (\lnot P\или Q)$
i) $P\подразумевает (P\или Q)$
j) $P\land Q\подразумевает Q$
k) $(P\стрелка влево Q)\стрелка влево ((P\подразумевает Q)\land (Q\подразумевает P))$
l) $(P\подразумевается Q)\стрелка влево (\lnot Q\подразумевается \lnot P)$
Доказательство. Доказательства оставлены в качестве упражнений. $\qed$
Заметим, что (b) и (c) — коммутативные законы, (d) и (e) —
ассоциативные законы и (е) и (ж) говорят, что $\land$
и $\lor$ распределяются друг над другом. Это говорит о том, что существует
форма алгебры для логических выражений, аналогичная алгебре
для числовых выражений. Этот предмет называется Булева алгебра и имеет множество применений.
особенно в информатике.
Это говорит о том, что существует
форма алгебры для логических выражений, аналогичная алгебре
для числовых выражений. Этот предмет называется Булева алгебра и имеет множество применений.
особенно в информатике.
Если две формулы всегда принимают одно и то же истинностное значение независимо от того, элементы из вселенной дискурса, которые мы заменяем различными переменные, то мы говорим, что они эквивалентны .Стоимость эквивалента формулы в том, что они говорят одно и то же. Это всегда правильный шаг в доказательстве заменить некоторую формулу эквивалентной. Кроме того, многие тавтологии содержат важные идеи для построения доказательств. За например, (k) говорит, что если вы хотите показать, что $P\Leftrightarrow Q$, это можно (и часто целесообразно) разбить доказательство на два части, одна из которых доказывает импликацию $P\implis Q$, а вторая доказывая обратное , $Q\имеет P$.
Читая теорему 1.1.3 у вас может быть
заметил, что $\land$ и $\lor$ обладают многими схожими свойствами. Они называются «двойственными» понятиями — для любого свойства
один, есть почти идентичное свойство, которому удовлетворяет другой,
экземпляры двух операций поменялись местами. Это часто
означает, что когда мы доказываем результат, включающий одно понятие, мы получаем
соответствующий результат для своего двойственного без дополнительной работы.
Они называются «двойственными» понятиями — для любого свойства
один, есть почти идентичное свойство, которому удовлетворяет другой,
экземпляры двух операций поменялись местами. Это часто
означает, что когда мы доказываем результат, включающий одно понятие, мы получаем
соответствующий результат для своего двойственного без дополнительной работы.
Джордж Буль. Буль
(1815–1864) имел только обычное школьное образование, хотя и выучил
Греческий и латынь самостоятельно.Он начал свою карьеру в качестве элементарного
школьным учителем, но решил, что ему нужно больше узнать о
математики, поэтому он начал изучать математику, а также
языки, необходимые ему для чтения современной литературы на
математика. В 1847 году он опубликовал короткую книгу «Математический анализ».
Анализ логики , который, можно справедливо сказать, лег в основу исследования.
математической логики. Ключевой вклад работы заключался в
переопределить «математику» так, чтобы она означала не просто «изучение чисел и
величина», но изучение символов и манипулирование ими в соответствии с
к определенным правилам. Важность этого уровня абстракции для
будущее математики трудно переоценить. Вероятно, на
Благодаря этой работе он перешел на должность в Куинс-колледж в Корке.
Важность этого уровня абстракции для
будущее математики трудно переоценить. Вероятно, на
Благодаря этой работе он перешел на должность в Куинс-колледж в Корке.
В «Исследовании законов мысли» , опубликованном в 1854 г.,
Буль установил настоящую формальную логику, развивая то, что сегодня называется
Булева алгебра или иногда алгебра множеств . Он использовал символы для
сложение и умножение как операторы, но в совершенно абстрактном
смысл.Сегодня эти символы все еще иногда используются в булевых выражениях.
алгебре, хотя символы `$\land$’ и `$\lor$’, и `$\cap$’ и
`$\cup$’ также используются. Буль применил алгебраическую манипуляцию к
процесс рассуждения. Вот простой пример типа
манипуляцию, которую он проделал: уравнение $xy=x$ (которое сегодня можно было бы записать
$x\land y = x$ или $x\cap y = x$) означает, что «все вещи, удовлетворяющие
$x$ удовлетворяет $y$’, или, говоря нашим языком, $x\имеет y$. Если также $yz=y$ (что
есть $y\implis z$), то подстановка $y=yz$ в $xy=x$ дает
$x(yz)=x$ или $(xy)z=x$. 2+bD+c=0$, обработка
$D$ как номер , предоставляет информацию о решениях для
дифференциальное уравнение.
2+bD+c=0$, обработка
$D$ как номер , предоставляет информацию о решениях для
дифференциальное уравнение.
Информация здесь взята из A History of Mathematics, by Карл Б. Бойер, Нью-Йорк: John Wiley and Sons, 1968. Подробнее информацию см. в Lectures on Ten British Mathematicians , by Александр Макфарлейн, Нью-Йорк: John Wiley & Sons, 1916.
Упражнения 1.1
Пример 1.1.1 Постройте таблицы истинности для следующих логических выражений:
а) $(P\land Q)\lor \lnot P$
б) $P\имеет (Q\land P)$
c) $(P\land Q)\Стрелка влево (P\lor \lnot R)$
d) $\lnot P\имеет в виду \lnot(Q\lor R)$
Пример 1.1.2 Проверьте тавтологии в теореме 1.1.3.
Пример 1.1.3 Предположим, что $P(x,y)$ — это формула «$x+y=4$», а $Q(x,y)$ — это формула “$x
$P(x,y)\land Q(x,y)$, $\lnot P(x,y)\lor Q(x,y)$,
$P(x,y)\подразумевает \lnot Q(x,y)$, $\lnot(P(x,y)\Leftrightarrow Q(x,y))$,
, используя значения:
| a) $x=1, y=3$ | c) $x=1, y=2$ |
| b) $x=3, y=1$ | 910 $x=2, y=1$
Пример 1. 1.4
1.4
а) Найти таблицы истинности для $$ P\land (\lnot Q)\land R, \quad\quad (\lnot P)\land Q\land (\lnot R) $$
b) Используйте их, чтобы найти таблицу истинности для $$ (P\land (\lnot Q)\land R)\lor ((\lnot P)\land Q\land (\lnot R)) $$
c) Используйте метод, предложенный в частях (a) и (b) найти формулу со следующей таблицей истинности.
| $P$ | $Q$ | $R$ | ??? |
|---|---|---|---|
| Т | Т | Т | Т |
| Ф | Т | Т | Ф |
| Т | Ж | Т | Ж |
| Ж | Ж | Т | Ж |
| Т | Т | Ф | Т |
| Ф | Т | Ф | Т |
| Т | Ж | Ж | Ж |
| Ф | Ф | Ф | Ф |
г)
Используйте метод, предложенный частями (a)-(c), чтобы
объясните, почему любой список из $2^n$ T и F является
последний столбец таблицы истинности для некоторой формулы из $n$ букв.
