Ответ: 3 года
Задача 2
Запиши число 7 при помощи четырех троек и знаков действий.
Найди несколько решений.
Ответ: (7 = 3 : 3 + 3 + 3, 7 = 3 + 3 + 3 : 3, 7 = 3 + 3 : 3 + 3)
Задача 3
Речь пойдёт про единицы времени. Что можно узнать, данным произведением 60 х 60 х 24 х 7?
Ответ: Количество секунд в неделю
Задача 4
На пароме помещается или 6 грузовиков, или 10 легковушек.
В четверг паром, полностью загруженный, 5 раз пересек реку и переправил 42 машины.
Сколько было среди них грузовиков?
Ответ: 12
Задача 5
В гости к Игорю пришли друзья.
Сколько их было, если каждый из них сложил из даты своего рождения число и номер месяца и получил 35? Причём даты рождения у всех гостей разные.
Ответ: 8
Задача 6
Ребята измеряли шагами длину игровой площадки.
У Лизы получилось 25 шагов, у Полины – 27, у Максима – 22, а у Юры – 24.
У кого из ребят самый короткий шаг?
Ответ: У Полины
Задача 7
У сороконожки 90 ножек. Она купила 13 пар сапожек. Но при этом 16 ног остались босыми.
Сколько пар старых сапожек было на сороконожке до покупки новых сапожек?
Ответ: 24
Задача 8
Из 64 маленьких кубиков составили большой куб. Синей краской покрасили пять граней большого куба.
Назови количество маленьких кубиков с тремя синими гранями.
Ответ: 4 – по углам
Задача 9
Расставь скобки так, чтобы получилось верное равенство 211 – 126 – 74 · 8 = 88
Ответ: (211 – 126 – 74) · 8 = 88
Задача 10
Если самое большое трехзначное число уменьшить на самое большое двузначное число, полученный результат разделить на 4, а затем вычесть 25, то получится возраст мудреца-звездочета.
Сколько лет звездочету?
Решение:
1. 999 – 99 = 900
2. 900 : 4 = 225
3. 225 – 25 = 200
Ответ: 200 лет
Задача 11
Длина прямоугольного бассейна в 5 раз больше его ширины, причем ширина на 20 м меньше.
Найдите площадь дна бассейна.
Решение:
1. 20 : 4 = 5 (м) составляет 1 часть, и является шириной бассейна
2. 5 * 5 = 25 (м) длина бассейна
3. 25 * 5 = 125 (м2) площадь дна бассейна
Ответ: площадь бассейна равна 125 м2
Задача 12
Степа Смекалкин задумал число. Потом он уменьшил это число на 19 и к произведению прибавил 19. В ответе у него тоже получилось 19. Какое число задумал Степа?
Ответ: 0
Размер | Толщина | Фон | ||
| Скрыть ответы | +шрифт –шрифт | +жирн –жирн | White Cyan LGreen GYellw DpSkBl Coral DPink1 DPink2 SkBlue Orange OlivD1 OlivD2 LBlue PGreen Yellow Gold Blue Green Wheat Chocol Salmon Red HPink DPink Pink VioRed Magent Violet Plum Purple OrRed Bisque Bisqu2 LemC1 LemC2 Corns2 Honey2 Turqu1 Turqu2 SGrn1 SGrn2 Orchi1 Orang1 Gray golrod | |
Как вы думаете, если полста разделить на половину, то сколько в итоге получится?
Получится не 25, как многие могут подумать, а 100.
Так как если 50 разделить на 1/2, то это равносильно умножению на 2.
Если три десятка умножить на четыре десятка, то сколько получится?
Получится не 12 десятков, а 120 десятков. То есть : 30 * 40 = 1200.
Можете ли вы обосновать, почему почти во всех странах мира канализационные крышки у люков имеют только круглую форму? (Квадратные крышки люков бывают лишь тогда, когда они дополнительно крепятся шарнирами).
Если крышки люков будут квадратными, то они могут легко провалиться в люк, т.к. диагональ квадрата больше стороны квадрата. Поэтому их если и делают, то только прикрепив к люку шарнирами. У круглых крышек люков нет диагонали и стороны, а только диаметр, который у крышки всегда больше отверстия люка.
Как вы думаете, какой знак следует поставить между 0 и 1, чтобы было получено число больше 0, но меньше 1?
Этот знак является запятой.
То есть 0,1. Это число больше 0, но меньше 1.
Как вы думаете, сколько граней имеет шестигранный карандаш, который ни разу не затачивали?
Шестигранный карандаш, если не подвергался заточке будет иметь 8 граней. 6 большие грани и 2 торцевые.
Трехлитровый сосуд полностью заполнен тремя литрами воды. Вам необходимо за 2 переливания заполнить два пустых сосуда на 1 и 2 литра, чтобы в каждом из них было по 1 литру воды. При этом больше нельзя пользоваться ни чем, кроме этих трех сосудов.
Из полного сосуда наливаем в двухлитровый пустой ровно два литра, т.е. до краев. Далее из этого сосуда выливаем в однолитровый ровно литр воды (т.е. до краев).
Как вы думаете, существуют ли линии отличные от окружности, на которых все точки будут равноудалены от какой-то одной точки?
Равноудаленностью всех точек обладает любая линя, лежащая на поверхности шара.
Как вы думаете, какой предмет будет иметь одинаковое изображение при рисовании его с любой точки зрения?
Этим свойством обладает только шар.
Попробуйте сообразить, какой из выводов, указанных ниже, верный :
А) Здесь три ложных вывода.
Б) Здесь один ложный вывод.
В) Здесь два ложных вывода.
Г) Здесь пять ложных выводов.
Д) Здесь четыре ложных вывода.
Правильный вариант Д – здесь четыре ложных вывода. В связи с тем, что один является верным, а остальные не верные.
Попробуйте догадаться сколько стоит книга, если книга стоит доллар плюс пол книги.
Книга стоит 2 доллара. Решение : полкниги стоит доллар, значит вся книга стоит 2 доллара.
Поделитесь с друзьями: |
Ответьте, сколько сейчас времени, если оставшаяся часть суток в два раза превышает прошедшую?
Сейчас восемь часов.
Некий бизнесмен захотел привезти в Японию для продажи 10 000 пар первоклассных дорогих кроссовок. Но в Японии на такие кроссовки накладываются очень большие пошлины. Подумайте и скажите, как же хитроумный бизнесмен смог ввезти все эти кроссовки в Японию, при этом заплатил только очень небольшие деньги? (Никакой коррупционной и преступной составляющей здесь нет).
Бизнесмен поступил очень хитро. Он разделил каждую пару кроссовок и отправил весь объем двумя партиями. То есть в одной партии были только кроссовки на левую ногу, во второй только на правую ногу. Одну партию он отправил в Токио, другую в Осака. В каждом из городов бизнесмен не заплатил пошлину и товары были конфискованы и выставлены на аукционе. В связи с тем, что никому не была нужна партия кроссовок только на одну ногу, то бизнесмен выкупил сам обе партии за мизерные деньги.
5 рыбаков съели 5 карпов за 5 дней.
Как вы думаете, а за сколько дней 15 рыбаков съедят 15 карпов?
15 рыбаков съедят 15 карпов тоже за 5 дней. Если 5 рыбаков съедают 5 карпов за определенный промежуток времени, то у 15 рыбаков скорость поедания карпов в 3 раза больше, следовательно за 5 дней они съедят 15 карпов.
В мешке имеется 9 кг сахара. Есть также и две гири по 50г и 200г. Подумайте, как за три взвешивания на чашечных весах отвесить 2кг сахара?
Сперва необходимо на чашечных весах разделить содержимое мешка пополам на 4,5кг в каждой чашке. Далее одну чашу опустошаем, и снова 4,5кг делим пополам и получаем в каждой чаше весов по 2,25кг. В третье взвешивание уже нужно опустошить обе чаши, но из одной чаши 2,25кг сахара положить в отдельный мешок. И далее при помощи гирек в 200г и 50г (итого 250г) отвесить из пакета с 2,25кг ровно 250г. Тогда в пакете останется ровно 2 кг.
Два колхозника решили узнать, у кого больше овец.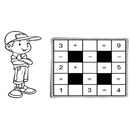
Первый из них сказал : «если ты дашь мне свою козу, то у меня будет их в два раза больше, чем у тебя». Второй ему говорит : «А давай лучше ты мне дашь свою одну овцу, тогда у меня овец будет столько же, сколько и у тебя». Сколько же овец у каждого из колхозников? (Передачи овец пока еще не было).
У первого колхозника 7 овец, у второго только 5. Если первый колхозник отдает одну овцу второму и их становится поровну, то значит, что изначально у первого их на 2 больше. Если же второй колхозник отдает овцу первому, то их становится у первого в 2 раза больше, такое возможно, только если у первого изначально было 7 овец, а у второго 5.
В одном классе всего 36 учеников. Девочек на 3 больше, чем мальчиков. Сколько мальчиков и девочек в этом классе?
Если разделить 36 пополам, то получим 18, т.е. две половины класса по 18 человек. Если из первой половины добавить школьника в другую, то получится разница в 2 человека.
Можете ли вы записать число 1000 при помощи только восьми восьмерок и арифметических знаков суммы?
Получится равенство : 888 + 88 + 8 + 8 + 8 = 1000.
На столе лежат 4 монеты, из которых одна сделана из другого металла и отличается по весу, хотя внешне они все одинаковые. Как определить эту монету за 2 взвешивания на чашечных весах?
Варианты взвешиваний : 1) ложем на весы 1 и 2 монеты, если они равны по весу, то одну монету заменяем на третью. Далее если они равны, то отличная монета 4-я, если не равны, то 3-я монета отличная от остальных. 2) ложем на весы 1 и 2 монеты, если они не равны по весу, то вместо одной монеты ложем 3-ю. Если уравновешиваются, то отличная убранная монета, если не уравновешиваются, то отличная от других монет оставшаяся на весах старая монета.
Как так могло оказаться, что половина числа 12 стало равно 7 ?
Нужно написать число 12 римскими цифрами : IIX , далее провести посередине линию. Верхняя половина будет в виде VII, что соответствует цифре 7.
На праздничном столе горят 7 свечей. 3 из них потушили. Сколько свечей останется?
Останутся 3 потушенные свечи, т.к. остальные 4 сгорят полностью.
Поделитесь с друзьями: |
«Папа у Васи силен в математике, папа решает, а Вася сдает!» – этот детский стишок из юмористического фильма знаком не одному поколению школьников. Однако, сколько бы не смеялись над строчками «цветы жизни», но факт остается фактом: для большинства детей математика – это темный лес.
Математические головоломки для 4 класса покажут, что цифры и теоремы могут быть разные. Здесь нет ничего сверхъестественного. Нужно всего лишь посмотреть на учебу глазами ребенка. Любое «надо» вызывает отторжение. С другой стороны, если «надо» превратить в «слабо», то детвора наперегонки броситься выполнять задание. Такой же принцип действует и в Головоломках по математике 5 класс. Как бы ваши чадо не отнекивалось от выполнения домашней работы, загадки всегда идут на ура.
Головоломки по математике 4 класс разработаны специально для того, чтобы развить интерес к счету у детей 10-11 лет. Сложность будет нарастать постепенно, когда ребенок уже получит определенный набор знаний из предыдущих уровней. Шанс вернуться назад не будет наталкивать на мысли о бесконечных пересдачах, которые существуют в школьном образовании. Математические головоломки для 5 класса станут плавным переходом в более серьезные задачи, но ничего заумного и отталкивающего ученик по-прежнему не обнаружит. Знакомство с математикой не будет скучным и однообразным. Множество непохожих друг на друга заданий сделают очевидным все то, что обычно не входит в систему школьных знаний. Нелогичность вопроса «зачем мне математика» будет очевидна, поскольку именно математика станет тем ключом, который откроет дальнейшие миссии.
Головоломки по математике 6 класс помогут подготовится не только к обычным урокам, но и станут отличной подготовительной площадкой для олимпиад. Нестандартные решения, закрученные подсказки, хитросплетения логики и арифметики – все это поможет почувствовать себя настоящим гением в мире тайн и секретов. Математические головоломки для 2 класса станут отличным стартом для малышей, только вступающих на стезю математических открытий, головоломки по математике 1 класс только приоткроют завесу перед будущими студентами, но поверьте – более удачного репетитора просто не найти. Смело спорьте с сыном или дочкой, что математика интереснее многих игр. А когда у вас потребуют доказательств, просто установите Ребусы и головоломки по математике. Этот спор будет выигран вами!
Вторая Олимпиада, 14.01.2018
Задача №1
Разделите фигуру вдоль линий сетки на три равные по форме и размеру части.
Задача №2
Антон, Боря, Вася, Гога и Даня встали в ряд.
Подпишите имена мальчиков, если известно, что:
Боря стоит рядом с Антоном.
Задача №3
На чёрно-белую вечеринку пришли ребята или в полностью черном костюме, или в полностью белом. Когда в финальном танце все встали в круг и взялись за руки, то выяснилось, что:
Кого на вечеринке больше девочек или тех, кто в белом? На сколько?
Напишите ответ и объяснение.
Задача №4
Мистер Кот гуляет по роялю. Сначала он вступает на первую клавишу, потом на четвертую (первая плюс три), потом на девятую (четвертая плюс пять) и так дальше он прибавляет последовательные нечётные числа.
Когда не хватает клавиш, кот спрыгивает вниз. На какую последнюю клавишу вступит Мистер Кот, если у рояля 57 клавиш? Напишите ответ и объяснение.
Задача №5
Петя и Аня решали головоломки. В конце занятия Оксана Евгеньевна спросила, сколько головоломок решили ребята. Петя ответил: «Я решил половину количества головоломок, которые решила Аня, да ещё 10 штук». Аня сказала: «Я решила столько же, сколько Петя, да ещё 20 штук». Сколько всего головоломок решили Аня и Петя в сумме? Напишите ответ и объяснение.
Задача №6
Расставьте на шахматной доске 16 коней, чтобы каждый бил ровно 4 других.
Задача №7
Аня и Петя придумали по натуральному числу. Оказалось, что если их сложить, то получится 1345. Если Аня к концу своего числа припишет цифру 3, а Петя на конце своего числа вычеркнет цифру 2, то получившиеся числа будут одинаковые. Найдите задуманные числа. Напишите ответ и решение.
Задача №8
В кружочки расставлены числа как на картинке.
За один ход можно взять три числа в вершинах какого-нибудь треугольника со сторонами, идущими по линиям, и прибавить к ним по 1. Можно ли такими операциями сделать все числа равными? Если можно, напишите как это сделать (алгоритм), если нельзя, объясните почему.
Интеллектуальные шахматы — это постоянная «пища» для ума, которую необходимо поддерживать. Тренировки являются оптимальным вариантом для тех, кто хочет не забывать азы, постигать новые уникальные техники и совершенствоваться в своей деятельности. Решать задачи по шахматам может далеко не каждый. Для этого нужно интересоваться этой игрой, иметь большое желание тренироваться в интеллектуальном плане и получать новые знания, а также проверять старые. Чтобы постигать новые решения, необязательно покупать какие-то методические пособия и справочники. Можно решать задачи в режиме реального времени, что не только сэкономит ваши свободные минуты, но и приведет к поразительным результатам развития в области шахматных реалий.
Задачи по шахматам онлайн
В режиме реального времени можно воспользоваться самыми увлекательными, сложными и универсальными задачами, чтобы обеспечить скорейший переход на более высокий уровень познаний в области этой занимательной игры. Задачи по шахматам — играть, решать их можно постоянно и при этом постоянно совершенствовать свои знания практического и теоретического уклона. Всегда интересно проверить, пригодились ли вам вчерашние занятия, или урок прошел незамеченным. Можно воплощать интересные и увлекательные идеи, реализовывать их в игровом формате, что очень продуктивно и занимательно.
Решение задач по шахматам онлайн — ценный вариант тренировки ума, если необходимо не забывать основные партии и ходы, правила и особенности этой популярной игры. Доступ к задачам в режиме реального времени позволяет получать новые и интересные задания, проверять свое развитие в режиме онлайн. В дальнейшем это поможет сориентироваться в своих навыках игры в шахматы, понять, что нужно немного подучить или освоить заново.
Современные виртуальные технологии позволяют не ограничивать себя и заниматься тем, что и правда интересно. Для тех, кто живет в зоне интернет-доступа прекрасной возможностью станет индивидуальное решение задач в режиме онлайн.
Учитесь решать задачи по шахматам онлайн
Интересные, увлекательные и полезные задачи по шахматам для начинающих помогут получить максимум пользы от онлайн-обучения. Непростые, логические задания направлены на развитие памяти и мышления, запоминание основных шахматных фигур и нестандартных приемов. Можно ежедневно решать несколько задачек, чтобы не потерять навык и получать положительные результаты. С помощью задач онлайн вы точно сможете тренироваться, даже не выходя из дома. Для их решения не нужен противник, ведь он — виртуальный. Можно выбирать сложные и простые варианты. Обязательное решение задач по шахматам сделает свое дело, поможет начинающим и опытным шахматистам чему-то научиться или не утратить бесценные знания. Постоянные тренировки логического мышления всегда дают положительные результаты.
Поэтому стоит ориентироваться на занятия онлайн в большей степени. Это удобно и весьма продуктивно.
Примеры математических ребусов: 1 класс, 2 класс, 3 класс, 4 класс, в картинках, с ответами
Родина ребуса — Франция. Именно в этой стране в 16 веке был издан первый сборник ребусов, составленный Этьеном Туаро. В переводе с латинского rebus означает — «при помощи вещей». К настоящему времени техника составления ребусов дополнилась множеством новых приемов, от чего ребусы стали еще более захватывающими и увлекательными, а разгадывать их одинаково интересно как детям, так и взрослым.
Не хуже ребусов тренируют память, сообразительность и логическое мышление математические кроссворды, зашифрованные примеры и загадки. Такие задания вызывают у детей интерес, так как проходят в игровой форме.
1. Разгадайте кроссворд, разгадав ребус после примера.Номер клеточки в кроссворде соответствуют результату решенного примера.
Решение зашифрованных примеров тоже потребует наличие логического мышления и внимательности. В данном примере под буквами скрыты цифры, попробуйте расшифровать их.
УСЛОВИЕ: в данном примере используются только шесть цифр от 0 до 5. Одинаковыми буквами зашифрованы одинаковые цифры, а разными — разные.
ВОПРОС: Какая цифра скрывается за словом «ЛАЙ«?
РЕШЕНИЕ.
Известно, что если от числа отнять равное ему число, то получим 0.Для решения, используем данный тезис. Л — Л = Й, значит из этого следует, что Й = 0.
Самая большая цифра в примере — это 5. Из условия нам известно, что У = 4, значит Е = 5, А = 1. За буквами Л и М зашифрованы оставшиеся цифры 2 и 3. М > Л, соответственно, М = 3, а Л = 2.
Получается: 352 − 142 = 210
ОТВЕТ: 210
Пример №4 – задача на деление, сложение и вычитание
Условие.
В магазине спортивных товаров продаются наборы из нескольких предметов.
Первый набор включает в себя: 10 мячей, 2 обруча и 10 скакалок. Его цена – 120 условных единиц.
Второй комплект включает: 7 мячей, 1 обруч и 6 скакалок. Его стоимость – 77 условных единиц.
Определите цену третьего комплекта, если он включает в себя: 2 мяча и 1 скакалку.
Решение и ответ. Для начала необходимо определить разницу в стоимости между первым и вторым набором (120-77=43). Получается, что 43 условных единицы – это стоимость 3 мячей, 1 обруча и 4 скакалок.
Интересно! Логические задачи по математике для 1 класса
Теперь отнимем эту цифру от стоимости 2 набора (77-43=34). Так мы узнаем цену 4 мячей и 2 скакалок. Следовательно, стоимость 2 мячей и 1 скакалки будет составлять 17 условных единиц (34÷2=17).
Математические ребусы
Среди логических задач по математике для 3 класса иногда встречаются ребусы. Задачи такого типа помогают ребенку развивать умение рассуждать и мыслить последовательно.
Приведем пример.
Задача – математический ребус-таблица с фруктами
Условие. Рассмотрите предложенную таблицу. В ней указана общая цена фруктов по горизонтали и вертикали. Известно, что одинаковые фрукты имеют одинаковую цену. Определите стоимость персика.
Решение и ответ. Для начала необходимо внимательно рассмотреть таблицу на наличие одинаковых фруктов в столбцах и строках. Мы видим, что во второй строке находится 3 яблока общей стоимостью в 9 условных единиц. Узнаем цену 1 яблока (9÷3=3). Теперь обращаем внимание на второй столбец. Мы можем найти стоимость клубники (11-3х2=5). Теперь мы можем определить цену граната в нижней строке (18-3х5=3). Наконец, настало время выяснить, сколько стоит персик. Для этого решаем следующее выражение 26-(3+3+5)=15. Получается, что стоимость персика равняется 15 условным единицам.
Задачи на определение истины
Умение мыслить и логически рассуждать – именно эти качества тренируют задачи на определение истины. Предлагаем вашему вниманию два примера подобного типа заданий.
Одно простое, а второе – олимпиадного уровня.
Пример №1 – простая задача
Условие. Фокусник, выступающий в цирке, вынес из-за кулис 3 коробки с надписями (смотрите фотографию). Он заявил, что совсем скоро собравшиеся зрители увидят собачек, голубей и кроликов. Определите, из какого ящичка фокусник достанет кроликов, если нам известно, что каждая из надписей на коробках – неправда.
Решение и ответ. Мы знаем, что фокусник пытается нас запутать, поэтому надпись «В первой коробке кролики» означает, что их там точно нет. Возле второй коробки находится надпись «Кролики». Это значит, что кролики точно не во втором ящике. У нас остается только один вариант. Получается, что кролики прячутся в коробке № 3.
Пример № 2 – задача для 3 класса повышенной сложности
Условие. Бабушка, дедушка и их внучка живут в одном подъезде трехэтажного дома, но на разных этажах. Известно, что бабушка проживает выше дедушки, внучка не на третьем этаже, а дедушка на 1 на не на 3 этаже.
Кто на каком этаже живет, если известно, что одно из утверждений – ложь.
Решение и ответ. Утверждение, связанное с дедушкой является неправдивым. Дедушка живет на первом этаже, внучка на втором этаже, а бабушка – на третьем.
Классические задачи на логику
Школьная программа построена таким образом, что в 3 классе дети уже могут работать с числами: вычитать, складывать, делить и умножать их. Предлагаем вашему вниманию несколько интересных логических задач по математике.
Интересно! Объемные цветы из бумаги делаем пошагово
Решение и ответ. Следует понимать, что при распиле стержня на пять частей, количественно прибавляется 4 куска. В общей сложности добавилось 24 кусочка (33-9=24). Теперь мы можем определить, что профессор распилил 6 стержней (24÷4=6).
Пример №2
Условие. Мальчик играл в компьютерную игру, в которой ему нужно быть победить монстрика с помощью пистолета. Изначально у игрока было в запасе 9 выстрелов. Но по правилам игры, за каждое попадание в цель, мальчик получал еще 3 дополнительных выстрела.
Определите, сколько раз парень попал в монстрика, если известно, что в общей сложности он выстрелил 30 раз и израсходовал при этом все выстрелы.
Решение и ответ. 30-9=21. Именно столько выстрелов мальчик получил дополнительно за попадания по монстрику. Известно, что за каждое попадание прибавлялось еще 3 попытки, значит, теперь мы можем найти общее количество попаданий 21÷3=7.
Надеемся, что логические задачи по математике для 3 класса с ответами и решениями, приведенные в статье, помогут вашему ребенку лучше разобраться в данном предмете и получать только лучшие оценки в школе.
29 января – 4 февраля
2019 года
Математика
Участники 1-11 классы
СтатусИтоги подведены
Перейти к мероприятиям этого года
Конкурс «Занимательная математика» для тех, кто, конечно же, любит математику.
А те, кто думает, что математика – это только скучные примеры, убедятся в обратном! Занимательная математика – это логические головоломки и занимательные сюжетные задачи, необычные математические игры и шифровки. В общем, математика – это занимательно и весело! Убедись в этом сам!
В этом конкурсе будет уделено особое внимание следующим темам:
1-2 классы
1. Логические задачи (алгоритмы, продолжение ряда, нахождение общего свойства или лишнего предмета, умозаключения, сравнение объектов).
2. Счёт, сложение, вычитание в пределах от 1 до 100. Сравнение чисел.
3. Математические определения, термины.
4. Геометрические фигуры.
5. Математические игры и головоломки.
6. Задача Эйнштейна.
3-4 классы
1. Логические задачи (алгоритмы, продолжение ряда, нахождение общего свойства или лишнего предмета, умозаключения, сравнение объектов).
2. Арифметические действия с числами в пределах от 1 до 1000. Сравнение чисел.
3. Математические определения, термины.
4. Применение союза «и», союза «или» и частицы «не» в математике.
5. Математические игры и головоломки.
6. Задача Эйнштейна.
5-6 классы
1. Логические задачи (алгоритмы, продолжение ряда, нахождение общего свойства или лишнего предмета, умозаключения, сравнение объектов).
2. Арифметические действия с числами от 1 до 10000. Сравнение чисел.
3. Математические определения, термины.
4. Работа с информацией: чтение таблиц и диаграмм.
5. Применение союза «и», союза «или» и частицы «не» в математике.
6. Математические игры и головоломки.
7. Задача Эйнштейна.
7-8 классы
1. Логические задачи (нахождение общего свойства или лишнего предмета, умозаключения, сравнение объектов).
2. Математические определения, термины.
3. Математические игры и головоломки.
4. Арифметические действия с числами.
5. Применение союза «и», союза «или» и частицы «не» в математике.
6. Задача Эйнштейна.
9-11 классы
1. Логические задачи (нахождение общего свойства или лишнего предмета, умозаключения, сравнение объектов).
2. Текстовые сюжетные задачи.
3. Математические определения, термины.
4. Математические игры и головоломки.
5. Задача Эйнштейна.
Особенности конкурса:
* Конкурс проводится для учащихся 1-2, 3-4, 5-6, 7-8, 9-11 классов.
* При создании конкурсных заданий учитывается временной промежуток, отведённый на их выполнение, — 7 дней.
* Для каждого конкурсного задания определено среднее время его выполнения, что позволяет участнику выбрать индивидуальный темп выполнения конкурсных заданий: можно сразу выполнить все конкурсные задания или разделить выполнение заданий на несколько дней.
* Задания конкурса повышают мотивацию к изучению к изучению предметной области «Математика».
* Конкурс предусматривает самостоятельную работу с дополнительной литературой и интернет-источниками.
* Конкурс развивает УУД: выбор наиболее эффективных способов решения задач, самостоятельное создание алгоритмов деятельности при решении заданий творческого и поискового характера, построение логической цепи рассуждений, эффективное представления результатов своей деятельности.
Дата проведения: 29 января — 4 февраля 2019 года
Завершился XII Международный конкурс «Занимательная математика». Пора подводить итоги! В мероприятии приняли участие 545 человек, 53 из которых заняли места победителей и лауреатов. Поздравляем!
Вы решали занимательные задачки, составляли и рисовали карты сокровищ, решали задачи вместе с героями-пиратами и выполняли много других увлекательных заданий! Да! Математика – занимательная наука!
С каждым из вас очень приятно работать! Для вас, чем больше неизвестности и новизны, тем креативнее и вдумчивее будут ваши ответы! Не останавливайтесь на достигнутом! Желаем вам удачи и новых простых ответов к непростым задачам!
Победители и лауреаты
1 – 2 классы
I место Ким Николай, Образовательный центр «Эрудит», Россия, Московская область, г.
Подольск, 2 класс
II место Гриценко Екатерина, МБОУ «Школа № 60», Россия, Ростовская область, г. Ростов-на-Дону, 2 класс
II место Крупа Анатолий, КГУ «Урицкая школа-лицей отдела образования акимата Сарыкольского района», Республика Казахстан, Костанайская область, Сарыкольский район, п. Сарыколь, 2 класс
II место Турнина Анна, МБУ ДО «ЦДТ», Россия, Республика Татарстан, Алексеевский район, п. г. т. Алексеевское, 1 класс
III место Ивлев Даниил, МБОУ Гимназия «Интеллект», Россия, Ставропольский край, г. Ессентуки, 2 класс
III место Соловьева Татьяна, МАОУ Лицей № 6 «Перспектива», Россия, Красноярский край, г. Красноярск, 2 класс
III место Портянкина Александра, МБОУ «Лицей № 5», Россия, Липецкая область, г. Елец, 2 класс
III место Гордеев Максим, Школа при Посольстве России в Кувейте, Кувейт, Эль-Асима, г. Эль-Кувейт, 1 класс
III место Балыбердина Альбина, МБОУ Лицей информационных систем и технологий № 73, Россия, Пензенская область, г.
Пенза, 2 класс
III место Каневский Тиберий, МАОУ «Лицей № 9», Россия, Новосибирская область, г. Новосибирск, 1 класс
Лауреат Казакова Алина, КОГОАУ «Кировский физико-математический лицей», Россия, Кировская область, г. Киров, 2 класс
Лауреат Чижикова Даниэла, МБОУ «СОШ № 26», Россия, Иркутская область, г. Братск, 1 класс
Лауреат Ожегова Валерия, КОГОАУ «Кировский физико-математический лицей», Россия, Кировская область, г. Киров, 2 класс
Лауреат Колотырин Богдан, МАОУ «Лицей № 36», Россия, Саратовская область, г. Саратов, 2 класс
Лауреат Чукавин Тимофей, МБОУ «ИТ- лицей № 24», Россия, Удмуртская Республика, г. Ижевск, 1 класс
Лауреат Шайкина Дарья, МОУ «СОШ № 23», Россия, Ярославская область, г. Рыбинск, 1 класс
Лауреат Курилин Сергей, МБОУ «Лицей № 5», Россия, Липецкая область, г. Елец, 2 класс
Лауреат Никеев Сергей, МБУ ОО СОШ № 1, Россия, Хабаровский край, г. Советская Гавань, 2 класс
Лауреат Грейцер Валерия, МБОУ Гимназия «Интеллект», Россия, Ставропольский край, г.
Ессентуки, 2 класс
Лауреат Баранова Арина, БОУ г. Омска «СОШ № 83», Россия, Омская область, г. Омск, 1 класс
3 – 4 классы
Победитель Рублёва Анастасия, МБОУ СОШ № 207, Россия, Новосибирская область, г. Новосибирск, 4 класс
Победитель Воронина Василиса, МАОУ «СОШ № 102», Россия, Свердловская область, г. Екатеринбург, 4 класс
Лауреат Петухова Анастасия, МБОУ «Кингисеппская гимназия», Россия, Ленинградская область, г. Кингисепп, 4 класс
Лауреат Тарасенко Антон, МБОУ г. Мурманска СОШ № 41, Россия, Мурманская область, г. Мурманск, 4 класс
Лауреат Аниферов Ярослав, МБОУ «Булдеевская ООШ», Россия, Чувашская Республика, Цивильский район, д. Булдеево, 3 класс
Лауреат Кашина Софья, МБОУ СОШ № 1, Россия, Московская область, г. Чехов, 4 класс
Лауреат Холдеева Александра, МОУ СОШ № 47, Россия, Московская область, г. Люберцы, 3 класс
Лауреат Рат Эрик, Семейная форма образования, Россия, Кемеровская область, г.
Киселёвск, 3 класс
5 – 6 классы
I место Сугакова Влада, МБОУ «СОШ № 84», Россия, Томская область, г. Северск, 6 класс
I место Ефремова Дарья, БОУ г.Омска «Лицей № 92», Россия, Омская область, г. Омск, 5 класс
II место Дульянинова Ангелина, МАОУ «СОШ № 46», Россия, Республика Бурятия, г. Улан-Удэ, 6 класс
II место Ефимова Екатерина, МБОУ Гимназия № 7, Россия, Московская область, г. Красногорск, 6 класс
III место Шушпанова Ангелина, КГУ «ОСШ им. Абая», Республика Казахстан, Восточно-Казахстанская область, Бородулихинский район, с. Бородулиха, 6 класс
III место Воронин Владимир, ФГКОУ «Екатеринбургское суворовское военное училище» МО РФ, Россия, Свердловская область, г. Екатеринбург, 6 класс
III место Соловьева Наталья, МАОУ Лицей № 6 «Перспектива», Россия, Красноярский край, г. Красноярск, 5 класс
III место Иванющенко Эрик, МБОУ СОШ № 207, Россия, Новосибирская область, г.
Новосибирск, 5 класс
III место Письменко Андрей, МБОУ «Мирновская средняя школа», Россия, Республика Крым, п. Мирный, 6 класс
Лауреат Поединок Вероника, МБОУ «Мирновская средняя школа», Россия, Республика Крым, п. Мирный, 6 класс
Лауреат Ложников Сергей, БОУ г. Омска «Лицей № 92», Россия, Омская область, г. Омск, 5 класс
Лауреат Ложников Дмитрий, БОУ г. Омска «Лицей № 92», Россия, Омская область, г. Омск, 5 класс
Лауреат Казанцева Евлалия, БОУ г. Омска «Лицей № 92», Россия, Омская область, г. Омск, 5 класс
Лауреат Носар Карина, МБОУ «Лицей № 2», Россия, Иркутская область, г. Братск, 5 класс
Лауреат Кутбидинова Самира, LOGOS, Узбекистан, Ферганская область, Фергана, 5 класс
7 – 8 классы
Победитель Лишик Ксения, ГУО «Средняя школа № 61 г. Минска», Республика Беларусь, Минская область, г. Минск, 8 класс
Победитель Потапов Станислав, МБОУ Лицей № 4, Россия, Московская область, г.
Чехов, 7 класс
Лауреат Исакова Инна, МБОУ СОШ № 49, Россия, Ростовская область, г. Шахты, 8 класс
Лауреат Золкина Ольга, МАОУ Гимназия № 9, Россия, Свердловская область, г. Екатеринбург, 7 класс
Лауреат Верховская Карина, МБОУ «Булдеевская ООШ», Россия, Чувашская Республика, Цивильский район, д. Булдеево, 7 класс
Лауреат Лоскутникова Ксения, МАОУ г. Иркутска СОШ № 69, Россия, Иркутская область, г. Иркутск, 8 класс
Лауреат Приходько Дарья, ГУО «СОШ № 11», Республика Беларусь, Гомельская область, Гомельский район, г. Гомель, 8 класс
9 – 11 классы
Победитель Проценко Никита, МБОУ Озерновская СОШ № 47, Россия, Красноярский край, Енисейский район, с. Озерное, 9 класс
Лауреат Филиппенко Вероника, МБОУ Озерновская СОШ № 47, Россия, Красноярский край, Енисейский район, с. Озерное, 9 класс
Лауреат Попова Анастасия, МАОУ Турасская СОШ, Россия, Тюменская область, Уватский район, п.
Туртас, 9 класс
Поздравляем с заслуженной победой!
Общие основные математические кроссворды для 4-го класса
NEW – Математические кроссворды для 4-х классов Интерактивные онлайн-кроссворды
Эти кроссворды с математическим составом для 4-х классов можно распечатать. Учителя, родители и ученики могут распечатать их и сделать копии.Эти математические кроссворды с математическим составом для 4-х классов сосредоточены на ключевой академической математической лексике, которую должны знать все учащиеся. Математическая лексика в этих кроссвордах – это словарь Common Core Math Vocabulary для 4-го класса. В каждом из этих математических кроссвордов для 4-х классов используется 18 общих основных математических терминов.
Математический кроссворд для 4-го класса 1
Математический кроссворд для 4-го класса 1 ответы
Математический кроссворд для 4-го класса 2
Математический кроссворд для 4-го класса 2 ответов
Математический кроссворд для 4-го класса 3
Математический кроссворд для 4-го класса 3 ответа
Математический кроссворд для 4-го класса 4
Математический кроссворд для 4-го класса 4 ответа
Математический кроссворд для 4-го класса 5
Математический кроссворд для 4-го класса 5 ответов
Математический кроссворд для 4-го класса 6
Математический кроссворд для 4-го класса 6 ответов
Математический кроссворд для 4-го класса 7
Математический кроссворд для 4-го класса 7 ответов
Перейти к поиску слов по математике для 4-го класса
Перейти к 4-му классу Словарь кроссвордов словарный запас
Перейти к урокам правописания со звуком для 4-го класса и к тестам по правописанию со звуком
Перейти к другим кроссвордам по математике
Перейти к рабочим листам по математике
Задания по математике для 4-х классов
Уроки математики в 4 классе
Видеоуроки математики для 4-х классов
___________________________________________________
Cogat (Тест на познавательные способности) 100 практических вопросов БЕСПЛАТНО!
Gate Test 100 практических вопросов БЕСПЛАТНО!
ITBS (Iowa Test of Basic Skills) Тест 100 практических вопросов БЕСПЛАТНО!
Тест для одаренных и талантливых, Нью-Йорк 100 практических вопросов БЕСПЛАТНО!
OLSAT (школьные способности Отиса-Леннона) Тест 100 практических вопросов БЕСПЛАТНО!
Тест NNAT-2 (тест на невербальные способности Наглиеры) 100 практических вопросов БЕСПЛАТНО!
CCAT (Canadian Cognitive Abilities) Тест 100 практических вопросов БЕСПЛАТНО!
TerraNova Tests 100 практических вопросов БЕСПЛАТНО!
ТестWISC (Детская шкала Векслера) 100 практических вопросов БЕСПЛАТНО!
Тест SCAT (Scholastic and College Ability) 100 практических вопросов БЕСПЛАТНО!
Тест Стэнфорда-Бине 100 практических вопросов БЕСПЛАТНО!
WPPSI Test 100 практических вопросов БЕСПЛАТНО!
ТестISEE (Независимый вступительный экзамен в школу) 100 практических вопросов БЕСПЛАТНО!
Тест творческого мышления Торранса 100 практических вопросов БЕСПЛАТНО!
Тесты Вудкока Джонсона 100 практических вопросов БЕСПЛАТНО!
Выбранные английские головоломки призваны помочь в развитии навыков письма, правописания, словарного запаса, памяти и логических рассуждений.
Эти 45 математических головоломок увлекут и стимулировать способность вашего ребенка решать проблемы путем сложения, вычитания и умножения здоровой пищи.
🍎 🍐 🍍 🍋 🍊 🍏 В дошкольном образовании было продемонстрировано, что существует корреляция между уровнем математических способностей ребенка и их будущими академическими успехами.Наблюдалась и обратная ситуация, когда дети, отстающие от математических навыков своих сверстников, продолжают отставать в будущих исследованиях (Pelkowski, et al., 2019). Кроме того, в литературе хорошо известно, что чем больше математика, тем больше математика. Возможности обучения, которым открывается ребенок, тем больший рост он получит в области математических знаний (Piasta, et al.
, 2015).
В наш век информации очень важно научить учащихся критическому мышлению и навыки логического мышления, позволяющие эффективно расшифровать и осмыслить большие объемы информации (Fitzgerald, 2005).Логические рассуждения помогают в построении концепций и знаний в процессе обучения (Ongcoy, 2016). В эту книгу входят логические головоломки, способствующие когнитивному развитию, и логические рассуждения для улучшения их успеваемости в старших классах и за ее пределами (Bouhnik, Giat, 2009)! Шейер и Адей (1993) обнаружили, что по завершении 2-летней научной программы, разработанной для развития формального оперативного мышления, на Британских национальных экзаменах были замечены улучшения в математике, английском и естественных науках.
📚 📚Какое домино завершает ряд?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 2Какое число завершает последовательность?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 3Какая буква отсутствует в следующая последовательность букв?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 4Какой номер нужен завершить пирамиду?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Какая следующая фигура в узоре?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Логическая головоломка 6Какой недостающий номер в этой головоломке?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Логическая головоломка 7Какое однозначное число заменяет А в этой головоломке?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 8Какое число будет следующим в этой последовательности?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Логическая головоломка 9Какое число завершается шаблон ?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 10Какое однозначное число отсутствует?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 11Какие 4 числа завершат эту сложную головоломку?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 12Какая буква отсутствует в этой последовательности?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Который час на 4-х часах?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 14Какого числа не хватает?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 15Какой номер нужен завершить последовательность?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Brain teaser 16Какая буква отсутствует?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 17Какое число завершает последовательность?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 18Какая буква отсутствует?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 19Какой номер нужен завершить этот узор?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 20Какие 4 фигуры и комбинации цифр необходимо заполнить коробка формы?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Какое число завершает числовой узор?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 22Какое письмо завершает эта головоломка?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Логическая головоломка 23Какой недостающий номер в этой головоломке?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 24Какое недостающее число завершает узор?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Головоломка 25Какое число нужно добавить к пирамиде?
Нажмите здесь, чтобы узнать ответ и распечатать этот пазл.
Все наши головоломки доступны для печати и представлены в Powerpoint версии .
Нажмите на загадку, чтобы перейти на страницу с ответами, и здесь вы найдете PDF-файл для печати и Powerpoint.
файлы.Наши головоломки имеют 4 уровня сложности: Уровень 1,
Уровень 2,
Уровень 3,
и Уровень 4.
На каждом уровне есть 100 головоломок.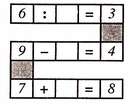
Наши головоломки IQ созданы как для студентов-математиков, так и для тех, кто любит решать числовые и логические головоломки. Решение математических и числовых головоломок – идеальный способ стимулировать и повысить свой уровень интеллекта. Решение головоломок помогает улучшить связь между клетками мозга, скорость мысли, концентрация и мыслительный процесс. IQ и логические головоломки – отличный способ улучшить математическую точность, навыки решения проблем и краткосрочная память.
В то время, когда многие люди привязаны к своим компьютерам и телефонам, это очень важно. чтобы продолжать стимулировать свой мозг. The MathinАнглийский Головоломки IQ – отличный инструмент для развития вашего мозга.
Разделенные на 5 уровней сложности, наши головоломки IQ подходят для всех возрастов и уровней способностей.
Пазлы IQ на этой странице, наши головоломки уровня 1, представляют собой сборник числовых и математических головоломок,
головоломки с фигурами, головоломки с последовательностью фигур для детей, головоломки с кубиками и домино, головоломки на время, головоломки с буквами и логика.
Математические и буквенные головоломки по сложности эквивалентны математическим классам от 1 до 3.
Не стесняйтесь загружать наши бесплатные книги-головоломки IQ, которые можно найти в ответах на головоломки.
Разгадать научные загадки и головоломки с семьей – это увлекательное и познавательное занятие.
Поощрение детей к разгадыванию научных загадок – отличный способ научить их мыслить нестандартно.Научные загадки также могут помочь детям запомнить важные научные факты – это и ежу понятно!
Здесь представлены 50 лучших научных загадок с ответами, которые понравятся вам и вашим детям. Мы разделили наши научные загадки на категории по биологии, химии и физике. Удачного разгадывания загадок!
Научные загадки – всегда отличный способ воспитать маленьких Эйнштейнов. Вот лучшие загадки по физике, которые поразят вас.
1. Многие слышали это, но никто никогда не видел.Он не ответит, пока к нему не заговорят. Что это? Эхо.
2. Я скала больше Венеры, но меньше Урана. Что я? Земля.
3. Вы не видите меня, меня нельзя трогать, вы не чувствуете меня, но я могу приготовить ваш обед. Что я? Микроволновая частица.
4. Что такое центр тяжести? Буква «V».
5. Когда-то я был массивной звездой и скоро стану ярким газовым облаком. На данный момент я – мощный взрыв. Что я? Сверхновая.
6. Что жрецу больше всего нравится в физике? Масса
7. У какой планеты самый короткий год? Меркурий, как наиболее близкий к Солнцу.
8. Что тяжелее: фунт перьев или фунт кирпичей? Оба они весят одинаково.
9. Я живу миллионы лет, но мне всего месяц. Что я? Луна.
10. Что дырявое, но все еще выдерживает критику? Губка.
11. Какой период времени имеет наименьшее значение? Световой год.
12. Я самое горячее тело в солнечной системе и согреваю всех. Кто я? Солнце.
13. Я – три четверти Вселенной, и обо мне почти ничего не известно. Что я? Темная материя.
14. Я могу спешить, мне может быть жарко, мне может быть холодно, я могу быть твердым, я могу проскользнуть через что угодно. Что я? Воды.
15. Меня невозможно создать, и меня нельзя уничтожить, я могу только изменить форму. Что я? Энергия.
16. Я туннель, ярлык, соединяющий места в пространстве и времени.Что я? Червоточина.
17. Вы не видите меня, но я вижу вас; Чтобы быть более конкретным, я вижу насквозь. Что я? Рентген.
Вместо того, чтобы устраивать беспорядочный химический эксперимент, попробуйте одну из этих загадок, вдохновленных химией. Дети любят их так же сильно, как любят устраивать беспорядок!
18. Что можно съесть много железа и не заболеть? Ржавчина.
19. Что можно измерить, но не имеет ширины, длины или высоты? Температура.
20. Дай мне еды, и я буду жить. Дай мне воды, и я умру. Что я? Огонь.
21. Какие только два периодических элемента имеют жидкое состояние? Бром и ртуть.
22. Какой периодический элемент пироманьяки любят больше всего? Мышьяк.
23. Я газ и линейка с неоном. Я также дом супергероя. Что я? Криптон.
24. Какой химический элемент не любит следовать? Вести.
25. Я твердая как скала, но в горячей воде сразу таю.Что я? Кубик льда.
26. Что такое черное, когда вы покупаете, красное, когда вы его используете, и серое, когда вы его выбрасываете? Уголь.
27. Какие два периодических элемента излечивают вместе? Гелий и алюминий (HE + AL)
28. Я бог, планета и могу измерять тепло. Что я? Меркурий.
29. В каком состоянии я время от времени ассоциируюсь с вонючими вещами? Газ.
30. У вас есть стакан молока и стакан воды. Вам нужно налить их в одну емкость, чтобы две жидкости были разделены и могли быть разделены.Как ты это делаешь? Влить воду, заморозить, затем влить молоко.
Эти научные загадки на тему биологии – отличный способ побудить ваших детей полюбить науку.
31. Какие три «Р» поддерживают чистоту нашей планеты? Повторное использование, переработка, сокращение.
32. Я газ, который помогает растениям, но его нельзя купить на заправке. Что я? Углекислый газ.
33. Я тверд как камень, но ты можешь найти меня на теле. Что я? Зубья
34.Какое животное дольше всего живет в зоопарках? Черепахи.
35. На какие десять вещей вы всегда можете рассчитывать? Пальцы.
36. Что есть у собак, чего нет у других животных? Щенки.
37. Что можно удерживать не дольше нескольких секунд? Твое дыхание.
38. Когда-то я был эмбрионом, но сейчас прошел восемь недель развития. Что я? Плод.
39. Я под вашим лицом и вне вашего разума. Что я? Ваш череп.
40. Я нужен для полета, но не могу летать самостоятельно.Что я? Перья.
41. Я люблю бродить, но всегда остаюсь дома. Если бы ты нес то, что нес я, ты сломал бы себе спину. Что я? Улитка.
42. Я могу быть для тебя хорошим, я могу быть плохим. Вы можете найти меня по всему телу. Что я? Бактерии.
43. У меня отличный вкус, но ужасный запах. Что я? Язык.
44. Что не является ни водой, ни землей, но всегда насквозь промокло? Водно-болотные угодья.
45. Каждый из ваших родителей дал вам двадцать три нитевидных нити, которые сделали вас тем, кем вы являетесь сегодня.Кто они такие? Хромосомы.
Математика – это не совсем наука, но без нее наука была бы ничем! Вот лучшие научные загадки на математическую тематику, которые мы смогли найти.
46. Сколько сторон у круга? Два, внутренний и внешний.
47. Две курицы несут по два яйца каждые две минуты. Сколько всего кур откладывают 500 яиц за 500 минут? Две курицы.
48. Если взять четыре года, сколько всего дней получается? 1461, (365 х 4) + 1 из-за високосного года.
49. Я в четыре раза старше моего сына. Через 20 лет я буду вдвое старше его. Сколько нам сейчас лет? Мне 40 лет, моему сыну 10.
50. Если я 90 см плюс половина моего роста, какой я рост? 180см.
Если вы хотите прочитать другие интересные статьи по загадкам после научных загадок, вы можете проверить загадки с водой.
Четвероклассники лучше читают и любят словесные игры.Вы можете использовать эти поисковые запросы для 4-х классов, чтобы помочь своим детям и ученикам познакомиться с правописанием слов, практикой понимания прочитанного, научной лексикой, контрольными словами и т. Д.
Учащиеся 4-х классов становятся более сложными мыслителями по мере расширения их мировоззрения. Они практикуют рассуждение с помощью математических задач со словами, дробей и деления в столбик. Практические эксперименты, научные выставки, проекты и введение в периодическую таблицу элементов придают им более сильное чувство науки.Они учатся лучше понимать мир через уроки истории, культуры и географии и становятся лучшими читателями и писателями. Эти бесплатные печатные поисковые запросы для 4-го класса – отличные упражнения на правописание или словарный запас в дополнение к любым предметам, а также могут быть отличным занятием для вашего класса.
Ищете другие рабочие листы для 4-го класса? Хотите ли вы использовать рабочие листы для 4-го класса или попрактиковаться в научных проектах для 4-го класса, вы можете создавать свои собственные кроссворды, поисковые запросы и рабочие листы с помощью наших трех простых в использовании сайтов, ссылки на которые приведены ниже.
Просмотрите и распечатайте поисковые запросы для 4-го класса ниже.
ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ: каждое задание для печати 4-го класса выполнялось пользователями My Word Search. Они не проверялись на актуальность или точность. Мы настоятельно рекомендуем вам убедиться, что головоломка для 4-го класса соответствует вашим стандартам, прежде чем использовать ее в классе.
Конфиденциальность очень важна для нас. Все пользователи My Word Search, которые хотят сохранить их частные головоломки могут добавить пароль к своим головоломкам на экране головоломки, при входе в систему.Каждая головоломка, созданная с помощью My Word Search, является исключительной собственностью автора головоломки, и My Word Search не зарабатывает деньги на работе своих пользователей.
В своих дневниках Бенджамин Баннекер (математик и ученый-самоучка) писал и собирал математические головоломки, написанные стихами. Математика в этом журнале состоит из шести головоломок и двух страниц математических сочинений.Шесть загадок Баннекера были опубликованы в его прекрасной биографии, написанной Сильвио Бедини. Насколько мне известно, я впервые могу воспроизвести здесь три головоломки Баннекера, написанные его настоящим почерком. i
Головоломки Бенджамина Баннекера могут решить ученики средних и старших классов. Баннекер не использовал символическую алгебру для решения этих задач, и они показывают, что некоторые проблемы легче всего решить без алгебры! Математический факультет моей средней школы спонсировал конкурс, посвященный этим головоломкам.Каждой оценке была поставлена задача решить, и одна проблема была открыта для всех учащихся. У студентов было несколько недель на решение задач, и сберегательные облигации были присуждены случайно выбранным правильным записям. Мы распределили задачи по четырем уровням следующим образом:
Девятый класс
Десятый класс
Одиннадцатый класс
Двенадцатый класс
Все марки
Головоломка №3: «Разделите 60 на четыре такие части… »
Головоломка №1: «Джентльмен послал своего слугу …»
Головоломка №2: «Допустим, лестница длиной 60 футов …»
Головоломка №4: «А, В и С, рассуждая о своем возрасте …»
Головоломка № 6: «Головоломка собаки и зайца»
Banneker использовал методы одинарного и двойного положения, которые являются ранними методами решения проблем, которые трудно преобразовать в уравнения.Следующее определение взято из книги Дэниела Адамса 1802 года The Scholar’s Arithmetic or Federal Accountant :
“Позиция – это правило, которое по ложным или предполагаемым числам, взятым по желанию, обнаруживает истинное требуемое. Оно бывает двух видов: одинарное и двойное. Одинарное положение – это работа с одним предполагаемым числом, как если бы оно было истинным. один, чтобы найти истинное число.
Правило:
Доказательство
Этот метод предполагает, что выражение близко или точно линейно. Используя указанное выше правило, вызовите x 1 предположение (предполагаемое число) и y 1 результат применения правила к x 1 .Если y 2 – это «заданная сумма», то правило диктует следующее:
Это верно, если выражение является линейным, и почти истинным, если оно приблизительно линейно.
В переводе этот метод предполагает первое предположение о решении проблемы. Если это предположение неверно, то предположение должно быть умножено на отношение желаемого результата к этому неверному результату, которое профессор Лампкин (1996) назвал «поправочным коэффициентом», чтобы получить правильное решение.
Двойная позиция предполагает использование двух предположений для нахождения значения, которое делает выражение равным нулю.После правила 1 Адамс заявляет: «2. Поместите каждую ошибку напротив ее соответствующей позиции или предполагаемого номера; если ошибка слишком велика, отметьте ее знаком +; если слишком маленькая – знаком -. 3. Умножьте их крест-накрест, первая позиция – последней ошибкой, а последняя позиция – первой ошибкой. 4. Если они похожи, то есть оба больше или оба меньше заданного числа, разделите разницу продуктов на разницу ошибок, и частное будет ответом; но если ошибки различны, разделите сумму произведений на сумму ошибок, и частное будет ответом.«
Опять же, это основано на предположении, что выражение является либо линейным, либо приблизительно линейным. По сути, метод вычисляет точку пересечения x линии, проходящей через две предполагаемые точки. Предположим, что предположение x 1 дает результат y 1 , а это предположение x 2 дает результат y 2 . Пусть x будет «истинным» ответом, который делает выражение равным 0.Тогда, установив одинаковые уклоны, получим:
Например, с g ( x ) = x 2 – 5, пусть ( x 1 , y 1 ) = (3, 4) и пусть ( x 2 , y 2 ) = (1, -4). Тогда:
Если ( x 2 , y 2 ) изменить на (2, -1), то оценка для интервала x будет:
Правильный ответ – 2.2361.
Джентльмен послал своего слугу со 100 фунтами стерлингов, чтобы купить 100 голов крупного рогатого скота, с приказом дать 5 фунтов стерлингов за каждого буллока, 20 шиллингов за коров и один шиллинг за каждую овцу, вопрос состоит в том, какое количество каждой породы он принес своему хозяину.
Асвер
| 19 Буллоков по 5 фунтов стерлингов | £ 95 |
| 1 Корова на 20 С. | 1 |
| 80 Овцы с шагом 1 сек | 4 |
| 100 проба | 100 |
Примечание: шиллинг равен 1/20 фунта (£).
Ответ: Используя очевидные переменные, получаем:. Этот набор диофантовых уравнений имеет только один набор положительных целочисленных решений: B = 19, C = 1 и S = 80.
Предположим, что лестница длиной 60 футов размещена на Улице так, чтобы дойти до окна на одной стороне высотой 37 футов, и, не двигая ее внизу, она достигнет другого окна на другой стороне Улицы, которое имеет высоту 23 фута, требовалась ширина улицы.
Нижняя часть 60-футовой лестницы находится на улице. Если верхнюю часть повернуть на одну сторону улицы, она достигнет окна высотой 37 футов. Если верх, не сдвигая низ, повернуть на другую сторону улицы, он достигнет окна высотой 23 фута.Насколько широкая улица?
Ответ: Используя теорему Пифагора, мы получаем выражения, показанные на этом снимке экрана:
И поэтому ширина улицы 102,65 фута.
Вопрос от Ellicott Geographer General
Разделите 60 на четыре Такие части, чтобы первая была увеличена на 4, вторая уменьшилась на 4, третья умножилась на 4, четвертая часть разделена на 4, что сумма, разница, продукт, а коэффициент должен быть одним и тем же числом.
| Ans | ||
| первая часть 5.6 увеличена на 4 | 9,6 | |
| Вторая часть 13,6 уменьшена на 4 {is} | 9,6 | |
| третья часть 2,4 умноженная на 4 | 9,6 | |
| четвертая часть 38,4 разделить на 4 | 9.6 | |
| 60,0 | ||
Ответ: Используя метод единой позиции, угадайте «то же число». Угадаем 16.
Тогда первая часть – 12 (12 + 4 = 16),
вторая часть – 20 (20-4 = 16),
третья часть – 4 (4 x 4 = 16),
и четвертая часть – 64 (64/4 = 16).
Эти четыре части в сумме дают 12 + 20 + 4 + 64 = 100.
Следовательно, поправочный коэффициент равен 60/100 или 3/5.
Таким образом, ответ – предположение, умноженное на 16 и поправочный коэффициент 3/5; 9,6 – это значение для «того же числа». Таким образом, четыре части равны 5,6, 13,6, 2,4 и 38,4 – их сумма составляет 60, желаемый результат.
Single Position работает здесь, потому что, поскольку предположение дает слишком большой результат, он уменьшается на поправочный коэффициент, основанный на отношении желаемого ответа к неправильному ответу.
A, B и C, рассуждая об их возрасте, говорит A, если из удвоения кубического корня из возраста B удвоить биквадратный корень из возраста C, а остаток будет равен корню Sursolid из моего возраста, говорит B. , квадратный корень из моего возраста равен одной четвертой части A, и говорит C, что квадратный корень из моего возраста на единицу больше, чем квадратный корень из B, требуется их несколько возрастов.
| А | 32 Корень Sursolid которого равен 2 | |
| B’s | { Возраст } | 64 Кубический корень из которого равен 4 |
| C | 81 Биквадратный корень которого равен 3. |
Примечания: «Биквадрат» означает квадрат квадрата.«Sursolid» означает пятую степень.
На современном языке:
Три человека – назовите их A, B и C – рассказывают о своем возрасте.
A гласит: Если я вычту дважды корень четвертой степени возраста C из дважды кубического корня возраста B, я получу корень пятой степени возраста.
B утверждает: квадратный корень из моего возраста равен одной четвертой возраста A.
C утверждает: Квадратный корень из моего возраста на единицу больше квадратного корня из возраста Б.
Сколько лет A, B и C?
Ответ: Следующие уравнения:.
Баннекер правильно предположил, что (1) каждый возраст был целым числом и (2) поскольку использовался корень пятой степени возраста A, единственным разумным значением A было 32 (Lumpkin 1996). Это дает значение 64 из второго уравнения для B и, таким образом, значение 81 из третьего уравнения для C. Проверяя эти значения в первом уравнении, мы получаем:.
Эта головоломка приписывается Баннекеру и первоначально была опубликована в биографии Баннекера в середине девятнадцатого века, написанной Мартой Тайсон.
Купер и винодел сели поговорить,
Оба были настолько вялыми, что ни один не мог ходить;
Сказал Купер виноделу: «Я первый в своем деле. туннель к жабре “.
«Тогда, – говорит винодел, – ты для меня мужчина».
Сделай мне сосуд, если мы можем согласиться.
Верхний и нижний диаметры определяют,
Чтобы выдержать эту пропорцию как пятнадцать к девяти,
Тридцать – пять дюймов – это как раз то, чего я жажду,
Не больше и не меньше на глубине у меня будет;
Всего тридцать девять галлонов в этом сосуде,
Тогда я награжу тебя серебром или золотом, –
Дай мне свое обещание , мой честный старый друг.”
” Я сделаю это завтра, чтобы вы могли положиться! ” посохи, что сделало его слишком маленьким,
И затем проклял сосуд, винодела и всех остальных.
Он ударил себя в грудь: «Силой» он поклялся
Он никогда больше не будет работать в своем ремесле.
Так вот, мой друг достойный, узнай, если сможешь,
Размеры сосуда, утешай человека!
Примечания:
Бочка – большая бочка, часто используемая для вина.В Англии бочка вмещает 252 галлона вина.
«Жабры»: в пинте четыре жабры.
Соотношение диаметров верха и низа 15/9. Эта фраза также подразумевает, что верх и низ являются кругами.
Высота судна 35 дюймов. Емкость составляет 39 галлонов. В США галлон равен 231 дюйм. 3 . Британский имперский галлон равен 277,42 дюйма 3 . В 1854 году Бенджамин Хэллоуэлл из Александрии, штат Вирджиния, предложил решение этой проблемы на собрании Исторического общества Мэриленда.Его решение о диаметрах 24,745 дюйма и 14,8476 дюймов основано на размере галлона эля галлона, который составлял 288 дюймов. 3 .
Ответ: Я предположил, что сосуд имел форму усеченного конуса. Пусть h – высота отрезанной части конуса; затем аналогичными треугольниками, так что h = 52,5. Я использовал британские имперские галлоны, что дало объем 39 x 277,42 = 10819,36 дюйма. 3 . Пусть k представляет собой константу пропорциональности радиусов верха и низа, объем усеченного конуса – это разность между объемами двух конусов:
Устанавливая эту разницу равной 10819.36 дюймов 3 дает k = 0,81815, что дает диаметры 24,5445 и 14,7267 дюймов.
Когда ворсистые небеса покрыли землю
С белой мантией вокруг
Затем с серой собакой Снежная ярмарка
В молочно-белых полях мы Курсили Зайца
Просто посреди шампанского
Мы поставили ее , прочь она убежала,
Собака, я думаю, была от нее тогда
Всего тридцать прыжков или три раза по десять
О, было приятно видеть
Как Заяц действительно так пугливо бежал
Но все же так быстро, что я
Думал, что она это сделала не бегать, но летать
Когда Собака была почти за ней по пятам
Она быстро повернула и по полям
Она снова побежала с полной Карьерой
И ‘прибыль, которую она повернула на то место, где была
На каждом повороте она бросалась ‘d of land
На столько ярдов, сколько борзая
Может прыгнуть трижды, и Она сделала,
Всего шесть, если я не ошибаюсь,
Четыре раза Она прыгнула за собак три
Но двое из собак прыгнули согласен
С тремя из них, не молись и объявляй
Сколько прыжков он сделал, чтобы поймать зайца.
(ответ)
Всего семьдесят два, которые я предположил,
Отсюда возник ложный ответ,
Я удвоил сумму семидесяти двух,
Но все же я обнаружил, что это не годится,
Я смешал их числа,
которые Было так ясно, что Я принесу Клятву,
Восемьсот прыжков, которые совершила Собака,
И Шестьдесят четыре, Заяц, чтобы взять
Примечания:
Допущение: арифметика Баннекера в конце эквивалентна решению пропорции, которая дает x = 864. Это иллюстрирует метод ложной позиции.
Ответ: Баннекер начал с 72 в качестве предположения и получил значение 4 вместо желаемых 48 (эквивалентная фору для зайца).Баннекер, должно быть, вычислил, как далеко пробежит заяц (в собачьих прыжках), если собака пробежит 72 собачьих прыжка, и получил ответ 68. Это означало, что если бы у зайца было преимущество в 4 собачьих прыжка, собака бы догнала заяц в 72 прыжка. Затем он использовал правильное значение форы 48, чтобы получить ответ 864. К сожалению, Баннекер допустил ошибку. Собака бежит на 9/8 так же быстро, как заяц, и поэтому, когда собака пробегает 72 прыжка собаки, заяц пробегает расстояние в 64 прыжка, оставляя разницу в 8. Замена «4» в вычислении Баннекера на 8 дает правильный ответ на загадку 432 прыжков собаки.
Другой метод поддерживается последними восемью строками, которые озаглавлены «Ответить». Автор, предположительно Баннекер, начинает с предположения 72 и получает «ложный ответ». Затем 72 удваивается, чтобы получить 144, но «это не годится». «Я смешал оба числа» – это иллюстрация метода двойной позиции. Предполагая, что собака делает 72 прыжка, заяц, двигаясь на 8/9 быстрее собаки, преодолевает расстояние в 64 прыжка собаки. Заяц также имеет фору в 48 прыжков. Таким образом, в конце 72 прыжков собаки заяц будет (64 + 48) – 72 = 40 собак прыгает впереди собаки.Предполагая, что собака делает 144 прыжка, заяц, двигаясь на 8/9 быстрее собаки, преодолевает расстояние в 128 прыжков собаки. Заяц также имеет фору в 48 прыжков. Таким образом, в конце 144 прыжков собаки заяц на (128 + 48) – 144 = 32 собака прыгает впереди собаки. В современных обозначениях это гласит правило двойной позиции. Полагая ( x 1 , y 1 ) = (72, 40) и ( x 2 , y 2 ) = (144, 32), получаем.
Адамс, Дэниел.Ученые Арифметика или Федеральный бухгалтер . Леоминстер, Массачусетс, 1802 г.
Бедини, Сильвио А. Жизнь Бенджамина Баннекера: первый афроамериканский ученый . 2-е изд. Балтимор, Мэриленд: Историческое общество Мэриленда, 1999.
Ассоциация Бенджамина Баннекера. http://www.mth.msu.edu/banneker/about.html.
Эглаш, Рон. «Африканское наследие Бенджамина Баннекера». Социальные науки . Vol. 27, нет.2 (апрель 1997 г.).
Фазанелли, Флоренс Д. «Жизнь и математика Бенджамина Баннекера: Сеть истины? Легенды как факты; Человек против легенды», доклад, сделанный 8 января 2004 года на встрече MAA / AMS в Фениксе, штат Аризона.
Лумпкин, Беатрис. «От Египта до Бенджамина Баннекера: африканские истоки ложных решений». В Vita Mathematica, Historical Research and Integration with Teaching . Примечания МАА, т. 40 (1996).
Лумпкин, Беатрис. “Математические головоломки и упражнения из Рукописного журнала Баннекера.”Из неопубликованной рукописи. Доктор Лампкин преподавал в колледже Малкольма Икс в Чикаго.
Махони, Джон Ф. «Математические головоломки Бенджамина Баннекера». В NCTM Учитель математики . Vol. 96, нет. 2 (февраль 2003 г.).
Махони, Джон Ф. «Бенджамин Баннекер и единственная позиция», в программе NCTM «Преподавание математики в средней школе ». Vol. 10, вып. 7 (март 2004 г.).
Махони, Джон Ф. «Бенджамин Баннекер и закон синусов», статья в процессе рецензирования для NCTM’s Mathematics Teacher .
Тайсон, Марта Э. Баннекер, Афро-американский астроном . Книжная ассоциация друзей Филадельфии, 1884 г. (Копия в Историческом обществе Мэриленда).
i Я нашел микрофильмированную копию журнала Баннекера в Историческом обществе Мэриленда в Балтиморе. Качество воспроизведения было плохим, но мне помогла кропотливая и точная ретушь фотографий, сделанная г-ном Омаром Руми из Куала-Лумпура, Малайзия, и моим сыном Куинном, студентом Массачусетского технологического института.
0 = 44-44
1 = 44/44 или (4 + 4) / (4 + 4) или (4/4) / (4/4) или ((4! – 4) / 4) – 4
2 = 4/4 + 4/4
3 = (4 + 4 + 4) / 4
4 = 4 × (4-4) + 4
5 = (4 × 4 + 4) / 4
6 = 4 × 0,4 + 4,4
7 = 44/4 – 4
8 = 4 + 4,4 – 0,4
9 = 4/4 + 4 + 4
10 = 44 / 4,4
11 = 4 / 0,4 + 4/4
12 = (44 + 4) / 4
13 = 4! – 44/4
14 = 4 × (4 – 0,4) – 0,4
15 = 44/4 + 4
16 =.4 × (44-4)
17 = 4/4 + 4 × 4
18 = 44 × 0,4 + 0,4
19 = 4! – 4 – 4/4
20 = 4 × (4/4 + 4)
21 = (4,4 + 4) /. 4
22 = 44 × √4 / 4
23 = (4 × 4! – 4) / 4
24 = 4 × 4 + 4 + 4
25 = (4 × 4! + 4) / 4
26 = 4 / .4 + 4 × 4
27 = 4 – 4/4 + 4!
28 = 44 – 4 × 4
29 = 4 / .4 / .4 + 4
30 = (4 + 4 + 4) / .4
31 = (4! + 4) / 4 + 4!
32 = 4 × 4 + 4 × 4
33 = (4 – 0,4) /. 4 + 4!
34 = 44 – 4 / .4
35 = 44/4 + 4!
36 = 44-4-4
37 = (√4 + 4!) / √4 + 4!
38 = 44 – 4! / 4
39 = (4 × 4 -.4) /. 4
40 = 44 – √ (4 × 4)
41 = (√4 + 4!) /. 4-4!
42 = √4 + 44 – 4
43 = 44 – 4/4
44 = 44,4 – 0,4
45 = 4/4 + 44
46 = 44 – √4 + 4
47 = 4! + 4! – 4/4
48 = 4 × (4 + 4 + 4)
49 = (4! – 4,4) / 0,4
50 = 4! / 4 + 44
БОНУС! 51 на 100, но у нас есть пробелы. Вы можете их заполнить?
51 = (4! – 4 + .4) / .4
52 = 44 + 4 + 4
53
54 = 4! + 4! + (4! / 4)
55
56 = 44 + 4! / √4
57
58 = 4! + 4! + 4 /.√4 × √4
73
74 = 4! + 4! + 4! + √4
75 = (4! + √4 + 4) / .4
76 = 4! × 4 – 4! + 4
77
78
79
80 = 4! × 4 – 4 × 4
81
82 = 4! / .4 + 4! – √4
83
84 = 4! × 4 – 4! / √4
85
86 = 4! × 4 – 4 / .4
87
88 = 4! × 4 – 4 – 4
89 = 4! + (4! + √4) / 0,4
90 = 4! × 4 – 4! / 4
91 = 4 × 4! – √4 / .4
92 = 4! × (√4 + √4) – 4
93
94 = 4! × 4-4 / √4
95 = 4! × 4 – 4/4
96 = 4! × 4 + 4-4
97 = 4! × 4 + 4/4
98 = 4! × 4 + 4 / √4
99
100 = 4! × 4 + √4 + √4
(Примечание: людям удалось сделать это для тысяч чисел)
.