Тема:
«Таблица умножения и денения с числом 6 »
3 класс
УРОК МАТЕМАТИКИ
(технология деятельностного метода обучения)
Тип урока: усвоение новых знаний
Тема: «Таблица умножения и деления с числом 6».
Цель: составить и выучить таблицу умножения и деления на 6.
Задачи
1) формировать умения применять таблицу умножения и деления на 6.
2) закреплять умения выполнять вычисления по алгоритмам, заданным блок-схемами.
3) закреплять умения решать задачу разными способами и уметь выбирать наиболее рациональный способ решения.
4) воспитывать культуру общения, умение работать индивидуально и коллективно.
Оборудование:
Ход урока
Все расселись по местам, никому не тесно,
По секрету скажу вам: «Будет интересно!
Будем мы считать, писать, и решать задачи,
Чтоб сегодня, как всегда, в руки шла удача.
– Ребята, на доске девиз нашего урока: «С хорошим настроением принимайся за работу!»
Работа в тетрадях:
– Запишите в тетрадях число. Классная работа.
Минутка чистописания
6+6+6+6+6+6+6+6+6+6+9=
Заменим умножением 6*10+9
– Давайте повторим правильное написание цифры 6.
(После объяснения и показа учителем, дети прописывают, чередуя число 6 с числом 69, устно дают характеристику написанным числам)
На прошлом уроке мы с вами составляли таблицу умножения на 2,3,4,5 и деления с эти числом, а дома вы должны были их выучить. Сегодня мы с вами проверим и закрепим знание уже изученной таблицы умножения.Но урок будет не обычный. Мы отправимся в сказку.
Но прежде чем мы туда попадем, нужно проверить, насколько вы готовы к путешествию. Проверим, как вы выполнили домашнее задание, вам нужно было решить примеры на порядок действий. Если все совпадает, ставьте рядом знак «+», а если вы у себя нашли ошибку, зачеркните карандашом, а потом разберетесь, в чем ошиблись, и исправите.
А ну-ка послушайте:
Я на балу никогда не бывала
Чистила, мыла, варила и пряла
Когда же случилось попасть мне на бал
То голову принц от любви потерял.
Как вы думаете кто это?
Золушка
– Да это сказка «Золушка» Шарля Перро. Шарль Перро был придворным поэтом. Но очень любил сказки, поэтому начал сам писать их. На экране высвечиваются слова: придворные, стражники, карета, кучер, упряжка. Дети сами объясняют слова. На прошлом уроке я предложила вам прочитать эту сказку. Вы с ней уже знакомы
Мы сегодня на уроке будем не только учениками, а станем волшебниками. Потому, что только волшебники творят чудеса. И мы должны обязательно помочь Золушке для этого нам нужно выполнить все задания Мачехи.
– Посмотрите, Золушка встревожена. Она беспокоится: «Успею ли я на королевский бал?»
– Не волнуйся, Золушка ребята тебе помогут.
– Правда, ребята? (Да)
– На уроке мы будем закреплять полученные знания по теме « Табличное умножение и деление», cоставим таблицу умножения и деления на 6.
закреплять умения выполнять вычисления по алгоритмам, заданным блок-схемами.
Будем закреплять умения решать задачи разных видов и уметь выбирать наиболее рациональный способ решения.
Продолжим работу над воспитанием культуры общения, умение работать индивидуально и коллективно
IV. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.
– Составьте из чисел 2,6 и12 3,6 и 18 4,6 и 24 5,6 и 30 все возможные равенства.
2*6=12 6*2=12 12:6=2 12:2=6
(Перестановка множителей, нахождение неизвестного множителя)
(Учитель открывает на доске эталон.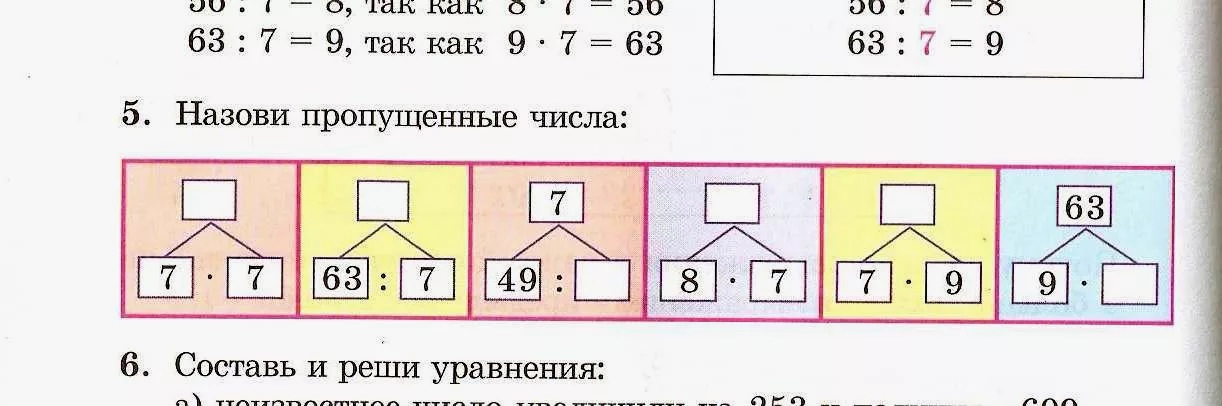
)
– Повторите эти правила, проверьте в паре друг друга.
(Учитель открывает на доске задание)
3*6=18 6*3=18 18:6=3 18:3=6
4*6=24 6*4=24 24:6=4 24:4=6
5*6=30 6*5=30 30:6=5 30:5=6
6+6
V.Работа по теме:
– Прочитайте выражения. Что в них общего? (Во всех выражениях один их компонентов равен 6.)
(Последнее, так как во всех выражениях действие умножение, а в этом выражении – действие сложения.)
Учитель:
(Выслушиваются разные гипотезы детей (6 ∙ 5+ 6)
Учитель:
(обратное действие умножению ) 36:6=
Учитель:
Составление выражений
6*7= : 6=7
7*6= :7=6
Дружно с вами мы считали и про числа рассуждали,
А теперь мы дружно встали, свои косточки размяли.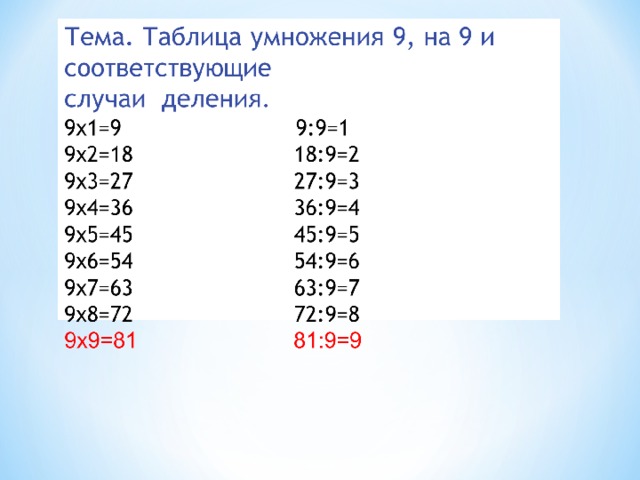
На счет раз кулак сожмем, на счет два в локтях сожмем.
На счет три – прижмем к плечам, на 4- к небесам
Хорошо прогнулись, и друг другу улыбнулись
Про пятерку не забудем – добрыми всегда мы будем.
На счет шесть прошу всех сесть.
Числа, я, и вы, друзья, вместе дружная 7-я (семья)
Постановка проблемы. Построение проекта выхода из затруднения (открытие нового знания).
– Работаем в учебнике, заполняем таблицу умножения и деления на 6
( с комментированием )
– Какую цель вы поставите перед собой на уроке? («Открыть» таблицу умножения и деления на «6»)
(6 умножить на 5, будет 30.)
)-Какие еще таблицы можем составить? (деления на 6, деления с ответом 6)
(Учащиеся проверяют свои ответы по эталону – по таблице умножения)
( Мы все «открыли» правильно, верно составили таблицу умножения и деления на «6».)
VI.Закрепление изученного.
Золушка мечтает о красивом наряде, но без вашей помощи ей не обойтись. Решите задачи, и тогда Золушка сможет отправиться на бал.
посажено в один ряд?
каждое платье. Сколько жемчужинбыло пришито?
Золушка поблагодарив Крестную фею , спешит на бал.
Какое предостережение сделала ей Фея? (ответы детей)
Что необходимо помнить Золушке, что бы не ошибиться? И почему?
( электронные часы- ночь 24.00 )
Своей «волшебной работой» мы помогли создать для Золушки из
тыквы карету, из мышек – лошадей, из крысы – кучера.
Помоги Золушке добраться до королевского дворца.
Для этого необходимо найди , чему равно расстояние, если известно что расстояние между точками равно 8 км?
8х5= 40 (км)
Самоконтроль с самопроверкой.
Сам король вышел навстречу Золушке. Ей нужно поскорее подняться по ступенькам, а вам правильно найти корни уравнений.
1 уровень :у х 6=2448:х=6
2 уровень : 6 х У=54-69х4:У=6
3 уровень : 25:5 хУ=54-24(284-236):У=6
(Учащиеся выполняют самостоятельную работу .Проверка организуется на доске.)
Мы все хорошо потрудились.
VII. Рефлексия учебной деятельности на уроке.Какова была цель сегодняшнего урока?
(Составить таблицу умножения и деления на 6.
)
– трудолюбива,
– добра
– почтительна
– ласкова
– Ребята, а какое у вас настроение сейчас?
Дерево успеха
VIII. Домашнее задание:
– Дома сделайте задание – № 5, стр.106, № 7*, стр. 107
III. Постановка учебной задачи Словесный: беседа Словесный: синтез плана. | 5 мин. | – Ребята, посмотрите все на доску. 7 · 6 3 · 2 2 · 8 15 : 3 – Что здесь лишнее? – Для чего нужно знать таблицу умножения? (Ответы детей.) – Что мы будем закреплять сегодня на уроке? – Какая тема нашего урока? – Поставьте цель урока. | – Выражение на деление лишнее, потому что все остальные на умножение. – Таблицу умножения. – Таблица умножения. Закрепление. – Закрепить таблицу умножения и деления. | Р.: принятие и сохранение учебной задачи, сличение с образцом, оценка работы К.: построение монологического высказывания; развитие речи К.: планирование учебного сотрудничества с учителем и со сверстниками, согласованно выполнять совместную деятельность |
VII. Включение в систему знаний, повторение. Словесный: беседа Практический: работа с упражнением | 7 мин. | – А сейчас мы с вами устроим небольшие соревнования! За верный ответ я буду давать вам фишку. Победители получат небольшие призы. – Первое задание называется «Быстрый круг». Вам необходимо решить примеры по кругу и записать ответ, задание выполняется на скорость, кто справится быстрее и выполнит задание верно получит 1 фишку. (Ответы будут на доске) – Второе задание. «Верный ответ». Вам нужно дать верный ответ на пример, если ответ неверный, задание переходит к другому участнику, ответ нужно давать быстро. 5·9, 42:7, 6·9, 36:6, 72:8, 7·8, 4·5, 64:8. – Третье задание. «Логическая задача». Вам нужно найти верный ответ на задачу, если ответ неверный, задание переходит к друглому. По дорожке бежали 6 кошек. Сколько всего у них ножек? (24) – Четвертое задание называется «Собери грибы». – Вначале давайте вспомним с вами, какие числа называются чётными, а какие нечётными. (Ответы детей). На улице зима, а вы сейчас отправитесь собирать грибы. 1 человеку нужно собрать грибы, в результате которых получатся чётные числа, а 2 грибы – в результате которых нечётные числа. (Каждый получает предметные картинки с изображением грибов, на шляпках которых записаны примеры на умножение и деление). Кто выполнит это задание правильно и быстро? – Сейчас вам необходимо выйти к доске и прикрепить на магниты, выбранные вами грибы. – Последнее задание «Уравнения». Вам нужно решить представленные на доске уравнения. Кто справится быстрее поднимает руку. Если ученик даёт неверный ответ, задание переходит к другому участнику. х * 6 = 48 7 * х = 42 40 : х = 8 х : 7 = 7 Сейчас посчитайте сколько фишек получилось у каждого. Побеждает… Победители по очереди подойдите ко и выберите одну наклейку. Все остальные возвращаются на свои места. – Итак ребята, какой мы можем сделать вывод после наших соревнований? Важно ли хорошо знать таблицу умножения? – Сейчас мы выполним самостоятельную работу. Подпишите листы. На работу у вас 15 минут. 1 вариант 24 : 4 =___ 72 : 8 =___ 5 · 5 =___ 12 : 2 =___ 3 · 4 =___ 42 : 6 =___ 45 : 9 =___ 6 · 8 =___ 3 · 6 =___ 7 · 8 =___ 24 : 3 =___ 7 · 7 =___ 8 · 8 =___ 35 : 7 =___ 27 : 3 =___ 2 вариант 7 · 3 =___ 24 : 4 =___ 5 · 5 =___ 12 : 2 =___ 3 · 4 =___ 4 · 8 =___ 6 · 8 =___ 45 : 9 =___ 18 : 2 =___ 7 · 8 =___ 24 : 3 =___ 36 : 4 =___ 35 : 7 =___ 8 · 8 =___ 7 · 9 =___ – Заканчиваем работу, передаём листы на 1 парту. – Открываем учебники на стр. 68. Прочитайте задачу № 2. – О чем говорится в задаче? – Что нам нужно найти? – Можем ли мы ответить на вопрос задачи? – Что нужно сделать чтобы мы смогли ответить на вопрос задачи? – Что будем делать первым действием? 1) 54 : 9 = 6 (ч. 2) 5 * 6 = 30 (ч.) – в 5 наборах. 1) 60 : 6 = 10 наборов. – Читаем внимательно задачу № 3. – Вслух читает … – О чём говорится в задаче? (О свёклах) – Кто мне скажет, что известно в задаче, а что нужно найти? (Один ученик отвечает и решает у доски.) В корзине – 5 кг св. во ? раз больше В 6 ящиках – 60 кг св.
(60 : 6) : 5 = 2 (р.) Ответ: в 2 раза больше было свёклы в одном ящике, чем в корзине. Молодец, садись. (Оценка.) | 1 вариант 6 * 4 = 24, 6 * 8 = 48, 6 * 2 = 12, 6 * 6 =36, 6 * 6 = 36, 6 * 5 = 30, 6 * 9 = 54, 6 * 3 = 18, 6 * 7 = 42. 2 вариант 7 * 4 = 28, 7 * 8 = 56, 7 * 2 = 14, 7 * 6 = 42, 7 * 5 = 35, 7 * 9 = 63, 7 * 3 = 21. 5 * 9 = 45 42 : 7 = 6 6 * 9 = 54 36 : 6 = 6 72 : 8 = 9 7 * 8 = 56 4 * 5 = 20 64 : 8 = 8 – 24 – 18 – 9 – 28 3 * 7 = 21 5 * 8 = 40 9 * 4 = 36 64 : 8 = 8 3 * 5 = 15 56 : 8 = 7 7 * 7 = 49 45 : 9 = 5 8 6 5 49 – Таблицу умножения знать важно. 1 вариант 24 : 4 = 6 72 : 8 = 9 5 · 5 = 25 12 : 2 = 6 3 · 4 = 12 42 : 6 = 7 45 : 9 = 5 6 · 8 = 48 3 · 6 = 18 7 · 8 = 56 24 : 3 = 8 7 · 7 = 49 8 · 8 = 64 35 : 7 = 5 27 : 3 = 9 2 вариант 7 · 3 = 21 24 : 4 = 6 5 · 5 = 25 12 : 2 = 6 3 · 4 = 12 4 · 8 = 32 6 · 8 = 48 45 : 9 = 5 18 : 2 = 9 7 · 8 = 56 24 : 3 = 8 36 : 4 = 9 35 : 7 = 5 8 · 8 = 64 7 · 9 = 63 1) 54 : 9 = 6 (ч.) – в одном наборе 2) 5 * 6 = 30 (ч.) – в 5 наборах. 1) 60 : 6 = 10 наборов. В корзине – 5 кг св. во ? раз больше В 6 ящиках – 60 кг св.
(60 : 6) : 5 = 2 (р.) | К.: выражение мысли в соответствии с задачами и условиями коммуникации Р.: принятие и сохранение учебной задачи, П.: установление причинно-следственных связей, анализ объекты с целью выделения общих признаков, подведение под понятие. К.: построение речевых высказываний П.: восприятие информации. Р.: принимать и сохранять задачу К.: планирование учебного сотрудничества с учителем и со сверстниками, согласованно выполнять совместную деятельность |
Мистер Математика Блог
Спасибо за пожертвование! Каждая мелочь помогает мне помочь вам! 🙂
Модель Периметр – Урок 11.1
Найти периметр – Урок 11.2
Найти неизвестные боковые длины – Урок 11.3
Область понимания – Урок 11,4
. Модели – Урок 11.6
Решение задач – Площадь прямоугольников – Урок 11.7
Область комбинированных прямоугольников – Урок 11,8
То же периметр – Разное область – Урок 11,9
Той и та же область – Различная периметр – Урок 11.10
Глава 11 Обзор для тестирования по периметру и области
Ваше небольшое пожертвование помогает мне поддерживать вас.
Спасибо! 🙂
Пожалуйста, пожертвуйте, если вы постоянный клиент!
Ссылка для пожертвований находится ниже. Спасибо!!
Описание плоских фигур – Урок 12.1
Опишите углы в форме плоскости – Урок 12.2
Идентификация полигонов – Урок 12.3
Опишите стороны полигонов – Урок 12.4
Классифицируйте четырехборы – Урок 12.5
Нарисовать квадратторов.
Описание треугольников — Урок 12.7
Глава 12 Проверка задания на выполнение теста
Решение задач — Сравнение дробей — Урок 9.1
Сравните фракции с тем же знаменателем – Урок 9.2
Сравните фракции с тем же числителем – Урок 9.3
Фракции – Урок 9.4
Сравнение и закачные фракции – Урок 9.5
. – Урок 9.6
Равные дроби – Урок 9.7
Разделить на 2 – Урок 7.1
Разделить на 10 – Урок 7.
Разделение на 3 – Урок 7.4
Разделение на 4 – Урок 7.5
Разделение на 5 – Урок 7.6
Средняя чапотера 7 Контрольная точка по фактам дивизии и стратегии
Разделение 7- 7.7
Разделите на 8 – Урок 7.8
Divide на 9 – Урок 7.9
Решение проблем – двухэтапные проблемы – Урок 7.10
Орден операций – Урок 7.11
Размер равных групп – Урок Урок 6,2
Количество равных групп — Урок 6.3
Модель (деление) с моделью стержня — Урок 6.4
Отношение вычитания и деления — Урок 6.5 Урок 6.6
Связь умножения и деления — Урок 6.7
Запись связанных фактов — Урок 6.8
Правила деления на 1 и 0 — Урок 6.9
Умножьте на 2 и 4 – Урок 4.1
Умножение с 5 и 10 – Урок 4.
2
Умножение с 3 и 6 – Урок 4.3
Распределительное свойство – Урок 4.4
Умножение с 7 – урок 4.5
Свойство умножения — Урок 4.6
Образцы в таблице умножения — Урок 4.7
Умножить на 8 — Урок 4.8
Умножить на 9 — Урок 4.9
Повторить тест по главе 4
Найти неизвестные факторы – Урок 5.2
Решение проблем: использование распределительного свойства – Урок 5.3
Стратегии умножения с множеством 10 – Урок 5.4
Множественные множественные числа 10 на 1 цифры – Урок 5.5
Глава 5 Обзор фактов умножения
Онлайн-класс по математике
Численные закономерности — Урок 1.1
Округление до ближайших десятков или сотен — Урок 1.2
Расчет суммы — Урок 1.3
Ментальные математические стратегии для дополнения – Урок 1.4
Используйте свойства для добавления – Урок 1.5
Используйте стратегию Break Apart, чтобы добавить – Урок 1.
6
– Урок 1.8
Стратегии вычитания в уме – Урок 1.9
Использование разрядных значений для вычитания – Урок 1.10
Объединение разрядных значений для вычитания – Урок 1.11
равные части целого – Урок 8.1
равные акции – Урок 8.2
Единые фракции целого – Урок 8.3
Фракции целого – Урок 8.4
Фракции на номере – уроки 8.5
Соотношение дробей и целых чисел – Урок 8.6
Дроби группы – Урок 8.7
Количество равных групп – урок 3.1
Связь с добавлением и умножением – Урок 3.2
Счет пропуска по чисел -линии – Урок 3.3
Решение проблем 3.5
Коммутативное свойство умножения — Урок 3.6
Умножение на 1 и 0 — Урок 3.7
Решение задач — Систематизация данных — Урок 2.1
Использовать графики изображений – Урок 2.2
Сделать графики изображения – Урок 2.
3
Использовать гистограммы – Урок 2.4
Сделайте гистограмму – Урок 2.5
Решайте проблемы с использованием данных – Урок 2.6
и Создание линейных графиков — Урок 2.7
Время до минуты — Урок 10.1
A.M. и П.М. – Урок 10.2
Измерение временных интервалов – Урок 10.3
Использование временных интервалов – Урок 10.4
Решение проблем – интервалы времени – Урок 10.5
Длина измерения – Урок 10.6
Оценка и измерения объема жидкости – Урок 10.7
Оценка и измерение массы – Урок 10.8
*Привязать к области
Большая идея: Многие модели можно использовать для умножения.
| Основные иллюстрации/упражнения:
|
Словарь глав: пропуск, точка, числовая линия, переместительное свойство умножения, ассоциативное свойство умножения, мультипликативное свойство единицы, мультипликативное свойство нуля, модель массива, модель площади
Предварительный просмотр урока:
|
из Math in Focus Curriculum
Обучающие видео: | Ссылки на обучение: |
| Глава 6 Фоновое видео для родителей
| ||||||||
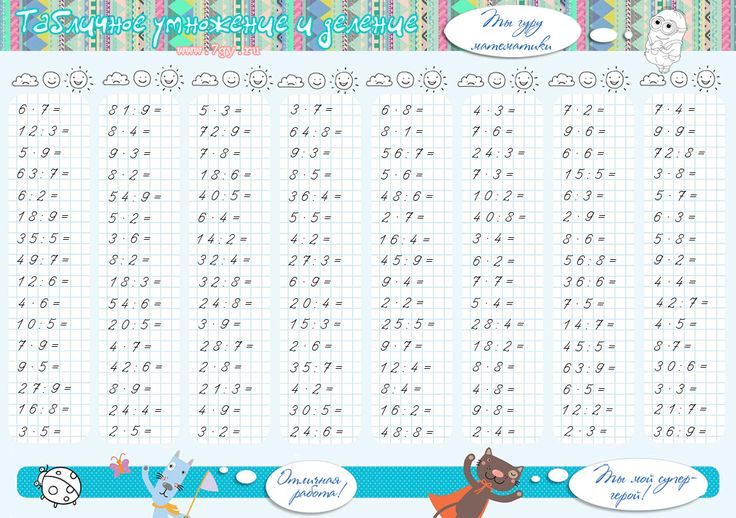
Практика умножения фактов: 6-9 – Игры с таблицами умножения:
 ation. d25 логинов!) Свойства игр на умножение:
| Видео с рабочими тетрадями (от Daniel Lu):
Сайт Даниэля Лу для рабочей тетради |
Операции и алгебраическое мышление:
Представлять и решать задачи на умножение и деление.
CONTENT.3.OA.A.3 Понимать свойства умножения и связь между умножением и делением.
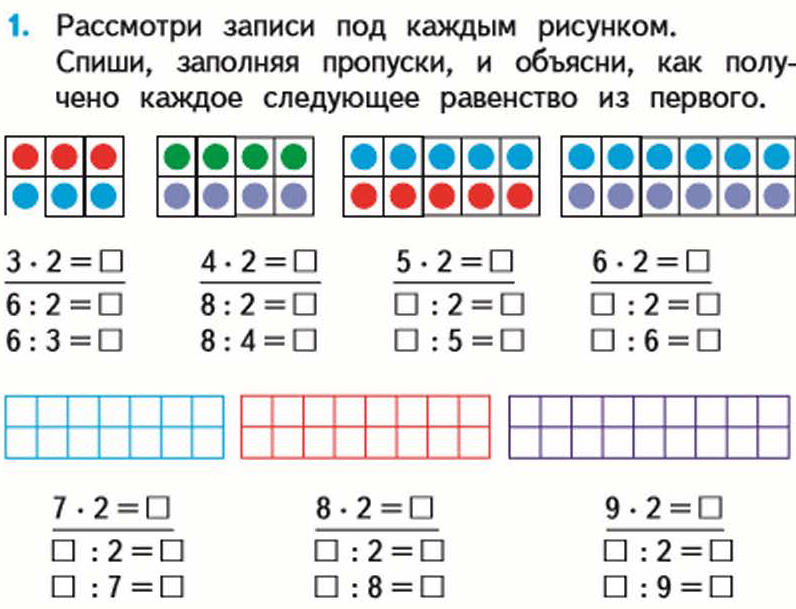Грибы у нас тоже необычные – зимние, цвета белого-белого снега и ясного морозного неба.
Вам нужно решить 15 примеров без использования таблицы умножения, всё убрали на край стола. Каждый работает сам.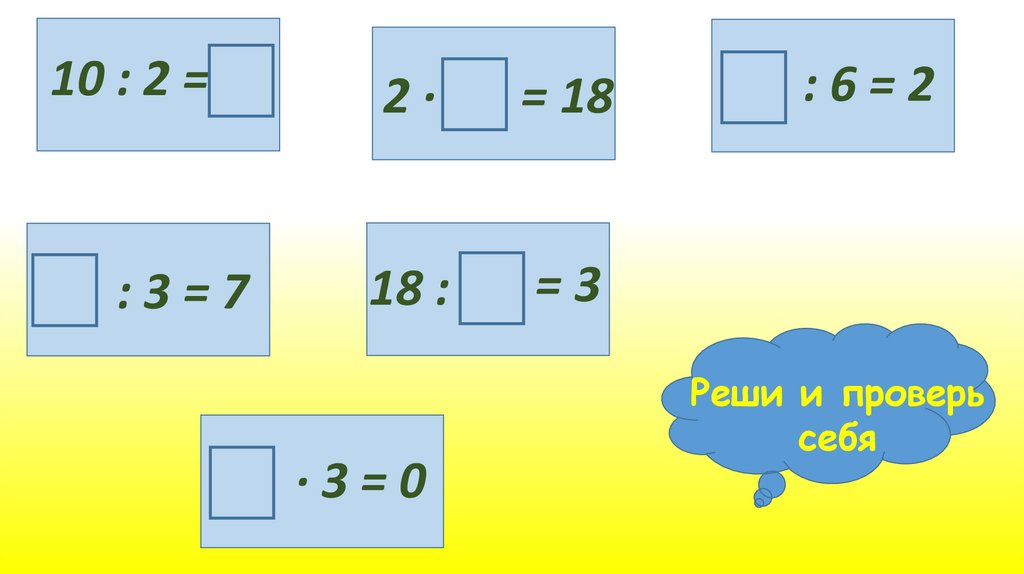
) – в одном наборе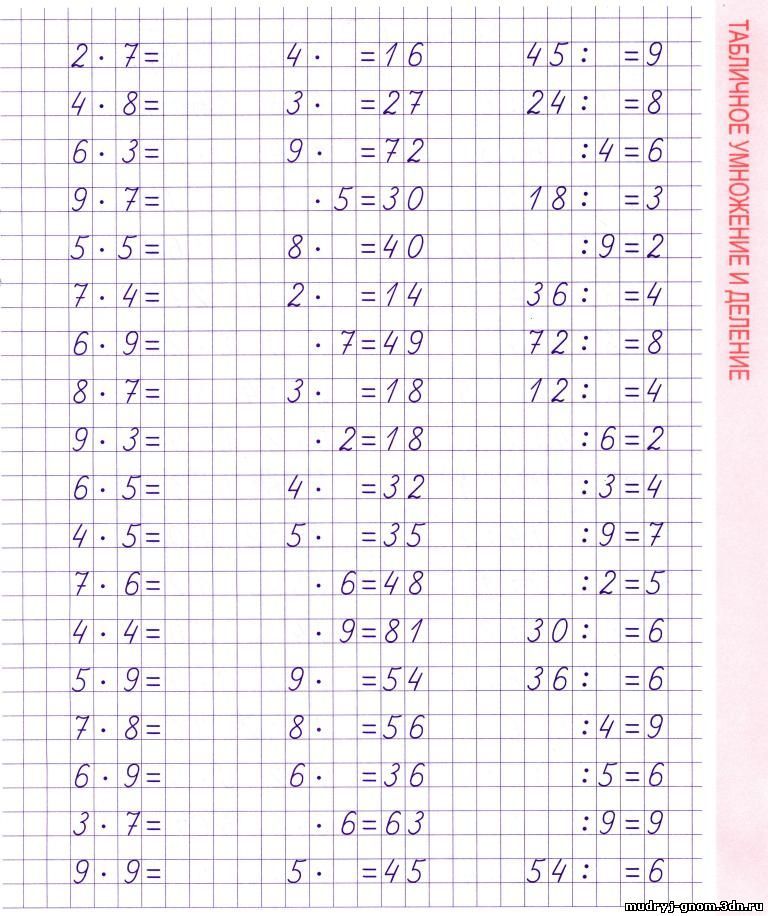
1 Свойства умножения
в разделе «Подведение итогов» ниже!
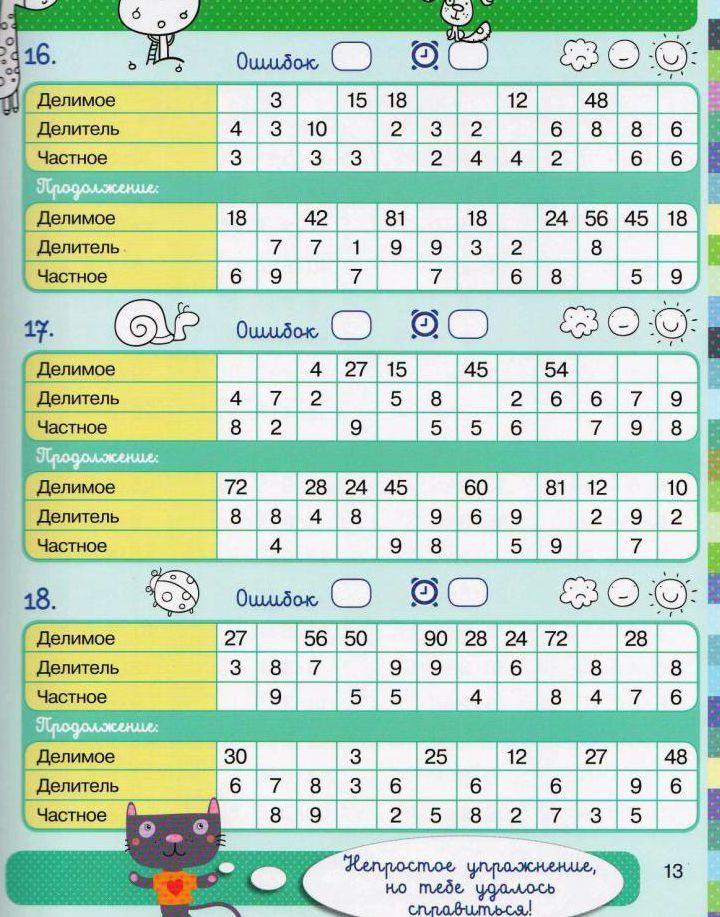
105-106