Презентация таблица умножения и деления с числом 4 3 класс: Презентация по математике на тему “Таблица умножения и деления с числом 4”
Урок 12. таблица умножения и деления с числом 4. таблица пифагора – Математика – 3 класс
Математика, 3 класс
Урок №12. Таблица умножения и деления с числом 4.
Таблица Пифагора
Перечень вопросов, рассматриваемых в теме:
– Какая закономерность в составлении таблицы умножения с числом 4?
– Что представляет собой таблица Пифагора?
Глоссарий по теме:
В таблице умножения с числом 4 произведение чисел увеличивается на 4.
Значения таблицы умножения чисел 2, 3, 4 можно оформить в виде таблице.
В результате получится таблица умножения.
Впервые таблицу составил древнегреческий учёный Пифагор, живший до нашей эры.
Основная и дополнительная литература по теме урока
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с.34-35
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 3 класс.
с. 17-18.
Теоретический материал для самостоятельного изучения
Четыре в комнате угла.
Четыре ножки у стола.
И по четыре ножки
У мышки и у кошки.
Известно детям в целом мире,
Что дважды два равно четыре.
Наша задача: составить таблицу умножения и деления с числом 4.
Заполним таблицу, зная таблицу умножения числа 2.
В первой строке записаны числа от 1 до 9. Умножим число 2 на каждое и запишем ответы во второй строке.
Добавим третью строку с числом 3. Умножим число 3 на каждое число из первой строчки.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
2 | 4 | 6 | 8 | 10 | 12 |
14 | 16 | 18 |
3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
Добавим в таблицу четвертую строку с числом 4.
Но заполнить строку с числом 4 труднее, так как не знаем таблицу умножения с числом 4.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
4 |
Для составления можно воспользоваться рисунком.
Начнём составлять таблицу умножения с числом 4 со случая
4 ∙ 4, так как знаем
4 ∙2 = 8
4∙3 = 12
4 ∙ 4 – число 4 нужно взять 4 раза и получится 16
4 ∙ 5 – число 4 нужно взять 5 раз, получится 20.
Произведение
увеличивается на 4.
Значит при умножении на 6, произведение равно 24, на 7 – 28, на 8 – 32, на 9 – 36.
4 ∙ 4 = 16
4 ∙ 5 = 20
4 ∙ 6 = 24
4 ∙ 7 = 28
4 ∙ 8 = 32
4 ∙ 9 = 36
Зная правило: от перестановки множителей произведение не меняется, составим таблицу умножения на 4. А правило: если произведение разделить на один множитель, то получим другой, поможет нам составить таблицу деления с числом 4.
5 ∙ 4 = 20 20 : 4 = 5 20 : 5 = 4
6 ∙ 4 = 24 24 : 4 = 6 24 : 6 = 4
7 ∙ 4 = 28 28 : 4 = 7 28 : 7 = 4
8 ∙ 4 = 32 32 : 4 = 8 32 : 8 = 4
9 ∙ 4 = 36 36 : 4 = 9 36 : 9 = 4
Теперь можно заполнить четвёртую строку в таблице.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
Таким образом, мы можем заполнить таблицу умножения числа 5, 6, 7, 8, 9.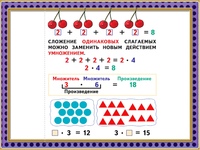
Получится таблица умножения, которую впервые составил древнегреческий учёный Пифагор.
Пифагор жил в 6 веке до нашей эры. Пифагор родился на греческом острове Самос в Эгейском море и, по сохранившимся преданиям, много путешествовал.Жил Пифагор в Египте, Вавилоне, совершал путешествие в Индию, знакомился с достижениями науки этих стран. Потом он поселился на юге нынешней Италии, где основал пифогорейский союз – общество философов. Философы пифагорейского союза много занимались наукой, особенно математикой. Ими создана таблица умножения, они разделили все числа на чётные и нечётные.
Сегодня таблицей Пифагора пользуются на уроках математике, по ней учат таблицу умножения.
Попробуем воспользоваться таблицей Пифагора и найти значения выражений.
2 ∙ 5; 3 ∙ 9; 4 ∙ 7;
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
Задания тренировочного модуля.
1. Вычислите устно. Значения, каких выражений равно 4.
36 : 9;
4 ∙ 8;
16: 4 ∙ 1;
24 : 8;
(6 ∙ 2) :3
Правильный ответ:
36 : 9;
16 : 4 ∙ 1;
(6 ∙ 2) : 3
Презентация на тему: “Таблица умножения и деления с числом 8”
библиотека
материалов
Содержание слайдов
Номер слайда 1
Здравствуйте, ребята!
Номер слайда 2Восемь жёлтеньких цыплят,Восемь пухленьких зайчат,Восемь лис и восемь кошек. Дружно выстроили в ряд. Сосчитайте все игрушки?По траве бежал котёнок,А за ним бежал щенок. Кто, ребята, сосчитает,Сколько там бежало ног?Мышка зёрна собирала,По два зёрнышка таскала. Принесла восьмой то раз. Каков у мышки стал запас?(8 4) = 32(2 4) = 8(2 8) = 16
Дружно выстроили в ряд. Сосчитайте все игрушки?По траве бежал котёнок,А за ним бежал щенок. Кто, ребята, сосчитает,Сколько там бежало ног?Мышка зёрна собирала,По два зёрнышка таскала. Принесла восьмой то раз. Каков у мышки стал запас?(8 4) = 32(2 4) = 8(2 8) = 16
56:7 = 6 7 = 54:6 = 16:2 = 36:6 = 32:4 = 35:5 = 80:10 = 5 7 = 3 7 =842986821 7 3588
Номер слайда 4
«Таблица умножения и деления с числом 8»
Номер слайда 58 2 =8 3 =8 4 =8 5 =8 6 =8 7 = 162432404856 8 8 = 64
Номер слайда 6
Как можно вычислить: 8 8 8+8+8+8+8+8+8+8 = 64 8 7 + 8 = 6456 + 8
В хоровод встал серый зайка, И поёт: «Я был зазнайкой, А теперь могу считать – Раз, два, три. Прибавляю, отнимаю- Математику, я знаю. И поэтому с утра, Я кричу: «Ура! Ура!»
Прибавляю, отнимаю- Математику, я знаю. И поэтому с утра, Я кричу: «Ура! Ура!»
Номер слайда 8
Номер слайда 9
{284 E427 A-3 D55-4303-BF80-6455036 E1 DE7}Количество рыбок в одном аквариуме Количество аквариумов. Общее количество рыбок 27 шт.54 шт. ?6 шт.? (Одинаковое)
Общее количество рыбок 27 шт.54 шт. ?6 шт.? (Одинаковое)
Номер слайда 10
Проверка:1). 54:6= 9 (р.) – в одном аквариуме.2). 27:9= 3 (ак.). Ответ: 3 аквариума занимают 27 рыбок.
Номер слайда 11
Номер слайда 12
Номер слайда 13
X- 27 = 54 X= 54+27 X= 81 81-27= 54 54=54 100- X= 63 X= 100- 63 X= 37 100-37= 63 63=63 X+ 18 = 67 X= 67- 18 X= 49 49 + 18= 67 67=67
Номер слайда 14
8 9= 7228:7= 416 + 20:4= 213 8 = 2432:8 = 4
Номер слайда 15
Всем спасибо за урок!!! До свидания!
Название этапа |
Деятельность учителя |
Деятельность учащихся |
I. Организация начала урока |
Начинается урок, |
Проверяют готовность Садятся на места. |
| II. Актуализация опорных знаний, устный счет
|
Чтоб работать быстро и ловко, Нам нужна для ума тренировка. Поэтому наш урок начнем с устного счета. 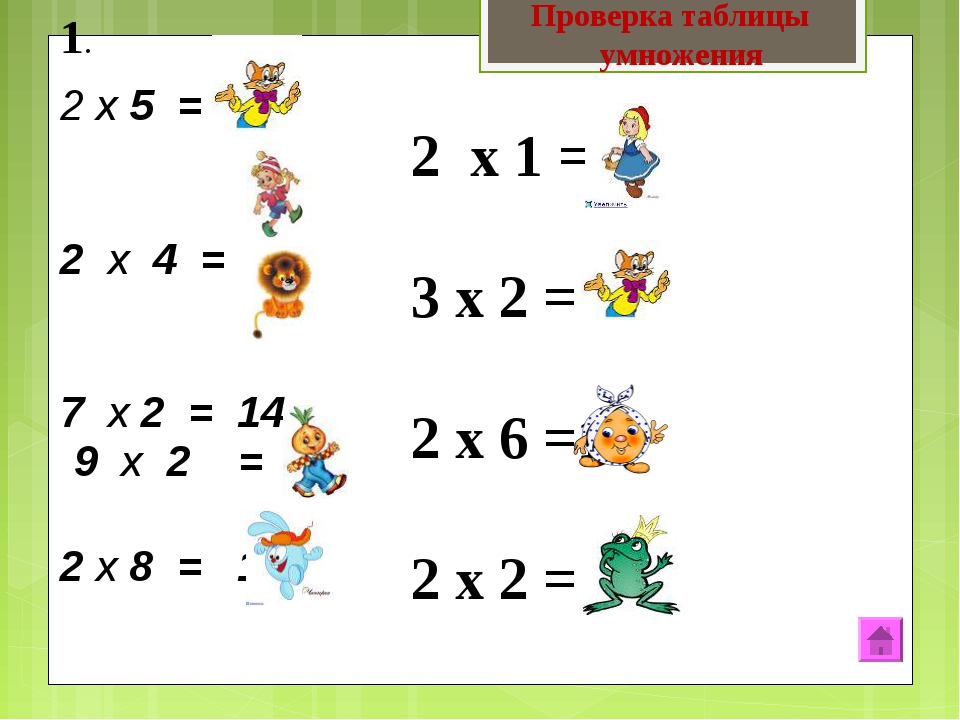 |
Слушают учителя. |
| Произведение каких чисел равно 15? | 3 и 5 | |
| Первый множитель 6, второй 3. | 18 | |
| Найдите произведение: 7 х 3. | 21 | |
| Какое число надо умножить на 8, чтобы получить 16? | 2 | |
| 18 : 9. | 2 | |
| Чтобы найти неизвестное слагаемое, надо… | Из суммы вычесть известное слагаемое | |
| Чтобы найти неизвестный множитель, надо… | Произведение разделить на один из известных множителей | |
| Чтобы найти неизвестное уменьшаемое, надо… | К вычитаемому прибавить значение разности | |
| Чтобы найти неизвестное делимое, надо… | Делимое умножить на частное. |
|
Расставьте порядок действий и найдите значения выражения. (60 – 30) : 10 ∙ 5 = 15 12 : 2 + 3 ∙ 4 + 17=35 90 – 2 ∙ 5 + 13 + 0 =93 |
|
|
| III. Постановка учебной проблемы, сообщение темы
|
На доске выражение: 4 + 4 + 4 + 4 + 4 = – Вычисли. Можно ли посчитать быстрее? Что для этого нужно знать? |
Значение этого выражения удобнее всего найти при помощи умножения, для этого надо знать таблицу умножения на 4 или умножить слагаемое 4 на количество всех слагаемых. |
| Совершенно верно. Предположите, чему будем учиться на уроке? | Выдвигают предположения, среди которых есть «умножению и делению на 4. | |
Сформулируйте задачи урока. |
Формулируют задачи урока: составить таблицу умножения и деления на 4, закрепить знания об умножении и делении на другие числа (например, 2 и 3) и т. |
|
| IV. Изучение нового материала
|
Открываем тетради, записываем число, классная работа. Открываем учебники на стр.34. |
|
| Смотрим на таблицу Вычисли и запомни! – Как вы думаете, почему эту таблицу начали с примера 4*4? |
Потому что 4*1,4*2,4*3 мы уже знаем. | |
| – Посмотрите на первый множитель в 1 столбике, что вы о нём скажите? | Первый множитель везде один и тот же. | |
| – На второй? | Второй увеличивается на 1. | |
| – На произведение? | Произведение увеличивается на 4. | |
| – Записываем первый столбик в тетрадь с комментированием. | Комментируют и записывают. | |
– Составим и запишем таблицу умножения на 4. Что для этого нужно сделать? Что для этого нужно сделать? – Выполняем с комментированием. |
Переставить множители местами. Записывают с комментированием. |
|
– Составим таблицу деления. – Каким правилом вы будете пользоваться для составления таблицы деления? – Составляем таблицу деления на 4, записываем. Составляем таблицу деления с частным 4. |
Если произведение разделить на один из множителей, то получится другой множитель. |
|
V. Динамическая пауза |
– Настало время отдохнуть. |
Встают возле парт. |
| VI. Первичная проверка усвоения знаний | Решите
весёлые задачи на закрепление таблицы умножения на 4. Четыре милых свинки |
16 |
| Четыре учёных мартышки Ногами листали книжки На каждой ноге – пять пальцев Четырежды пять… |
20 | |
| Шла на парад кошка в мундире: Четырежды шесть… |
24 | |
| Цыплят считают под осень: Четырежды семь… |
28 | |
| У Бабы Яги сломалась ступа: Четырежды восемь… зуба! |
32 | |
| Без зубов ей нечем есть: Четырежды девять… |
36 | |
Гуляли сорок сорок, |
40 |
|
VII. Закрепление знаний, решение задачи, уравнений Закрепление знаний, решение задачи, уравнений
|
– Сейчас вы поработаете в парах. – У вас на столах лежат карточки с задачей, прочитайте, обсудите и запишите решение на карточке. – Кому нужна будет моя помощь поднимите руку. |
Работают в парах. |
– Проверяем, заслушаем… – Подводим итог: |
Несколько пар рассказывают ход решения.
|
|
| №5 решить уравнения 1 вариант – 1 строчка 2 вариант -2 строчка |
Самостоятельно решают уравнения. | |
VIII. Информация о домашнем задании |
С.34 №1, №3, учить таблицу умножения и деления с числом 4. |
Слушают пояснения учителя и записывают домашнее задание. |
| IX. Подведение итогов. Рефлексия
|
Наш урок подходит к концу. – С чем мы познакомились на уроке? |
– Мы изучали таблицу умножения и деления с числом 4. |
– Какое задание показалось трудным? Спасибо за урок! |
– Мы повторили таблицу умножения на 2 и 3, нахождение значений числовых выражений в два действия, решали задачу на нахождение количества по известным цене и стоимости. |
Таблица умножения и деления на 4 (3 класс)
Математика3 класс
Тема: Таблица умножения и деления на
4.
Составил учитель начальных классов :Шило Е.
 А.
А.Приветствие учеников:
С добрым утром. Начат день,
Первым делом гоним лень.
На уроке не зевать,
А работать и читать.
На уроке будь старательным,
Будь спокойным и внимательным.
Всё пиши, не отставая,
Слушай, не перебивая.
Говорите чётко, внятно,
Чтобы было всё понятно.
Если хочешь отвечать
Надо руку поднимать
Сегодня у нас необычный урок! Мы не
только будем сами учиться, но и помогать
учиться маленьким Миньонам! Очень им
хочется тоже быть грамотными!
Привет, ребята! Поможете
сосчитать рыбок в двух
аквариумах?
А в трех? Сможете?
Совсем растерялись
миньоны! Поспешим им на
помощь! Реши
математическую цепочку.
10 : 2 = 5
2 · 9 = 18
:3=7
18 : 6 = 3
21
0 ·3=0
12
:6=2
Открываем тетради,записываем.
12 ноября
Классная работа
Таблицы умножения и деления с числом 4
Составим таблицу умножения с числом 4
4 · 4=
4 · 5=
4 · 6=
4 · 7=
4 · 8=
4 · 9=
16
20
24
28
32
36
4+4+4+4 = 16
4+4+4+4+4= 20
4+4+4+4+4+4 = 24
4+4+4+4+4+4+4 = 28
4+4+4+4+4+4+4+4 = 32
4+4+4+4+4+4+4+4+4 = 36
Можно по-разному группировать слагаемые
например:
4 * 7 = 4 * 5 + 4 * 2 = 20 + 8 = 28
Можно переставлять множители
например:
4 * 5 = 5 * 4 = 5 + 5 + 5 + 5 + 5 =20
Это нужно помнить.

Используя таблицу умножения и рисунок,
составь таблицу деления с числом 4
Таблица деления с числом 4
16 : 4 = 4
20 : 4 = 5
24 : 4 = 6
28 : 4 = 7
32 : 4 = 8
36 : 4 = 9
Открываем учебники на странице 34
и записываем примеры №1.
Теперь будем решать задачу, которая содержит
такие ключевые слова:
цена,количество,стоимость.Вспомним как
решаются такие задачи.Перейди к следующему
слайду.
• Чтобы найти ЦЕНУ, стоимость делим на количество;
Ц=С:К
• Чтобы найти КОЛИЧЕСТВО, стоимость делим на цену;
К=С:Ц
•Чтобы найти СТОИМОСТЬ, цену умножаем на количество;
С=Ц·К
Цена
4 р.
Количество Стоимость
?
32 : 4 = 8 (р.)
Ответ: 8 ручек продали.
32 р.
Домашнее задание:
Учебник: стр. 34 №3,
выучить таблицу
умножения 4.
Спасибо
вам,
ребята!
Слайды «Умножение и деление» для 3-го и 4-го классов
Слайды «Умножение и деление» для 3-го и 4-го классов помогут учащимся развить навыки счета. Эти слайды можно использовать в классе со своими учениками или загрузить в цифровой класс для дистанционного обучения.
Эти слайды можно использовать в классе со своими учениками или загрузить в цифровой класс для дистанционного обучения.
Есть готовые слайды и слайды с редактируемыми вопросами . Это позволяет различать, а также позволяет дублировать слайды, чтобы создавать больше вопросов для ответов учащихся.Загрузите на Google Диск или в Класс и поручите учащимся заполнить и отправить.
Навыки, представленные на этих слайдах;
- Skip Counting By TWOS
- Пропустить отсчет по плитам
- пропустить отсчет по десяткам
- пропустить отсчет по тремя
- пропустить счет на четвертый
- пропустить счет на шестерся
- пропустить подсчет по сетью
- Пропустить счет на восемь
- Пропустить счет девятками
- Использование массивов для умножения
- Использование массивов для деления
- Связывание фактов умножения и деления (предварительно составленное + ввод собственного)
- Умножение как многократное сложение -made + введите свой собственный)
- Запишите таблицу умножения (таблицы умножения на 2–12)
- Стратегия умножения десятков и десятков единиц (заранее подготовленный + введите свой собственный)
- Использование известных фактов умножения для решения задач на деление
Если у вас есть какие-либо вопросы, используйте Q & A или напишите мне по адресу talesfrommissd@gmail. ком.
ком.
Похожие товары
раз
раза столовые слайды
год 3 и 4 дополнения и вычитания слайдов
год 3 и 4 всей номера слайдов
дополнение и вычитание слов задача MATS
Маты для задач на умножение и деление
Ресурсы для дистанционного обучения
Заработайте кредит на будущие покупки:
Просто перейдите на страницу «Мои покупки».Рядом с каждой покупкой вы увидите кнопку «Оставить отзыв». Нажмите на нее, и вы попадете на страницу, где вы можете поставить оценку и оставить комментарий к продукту.
Узнай первым о моих товарах и распродажах!
Нравится то, что вы видите? Найдите зеленую звезду в верхней части любой страницы моего магазина и нажмите на нее, чтобы стать подписчиком. Затем вы будете получать индивидуальные обновления по электронной почте об этом магазине!
Связь между делением и умножением
Это полный урок с обучением и упражнениями о связи между умножением и делением, предназначенный для третьего класса. Это противоположные операции, и обе они имеют отношение к группам одинакового размера. Учащиеся пишут предложения на умножение и деление по одной и той же картинке. В более поздних упражнениях они записывают факт деления, соответствующий заданному умножению, и наоборот. Наконец, учащиеся используют свои знания о фактах умножения для решения задач на деление.
Это противоположные операции, и обе они имеют отношение к группам одинакового размера. Учащиеся пишут предложения на умножение и деление по одной и той же картинке. В более поздних упражнениях они записывают факт деления, соответствующий заданному умножению, и наоборот. Наконец, учащиеся используют свои знания о фактах умножения для решения задач на деление.
|
Мы получаем как , так и факт умножения и факт разделения с той же картинки: |
|
||||||
Умножение и деление очень тесно связаны. они противоположны
операции. они противоположны
операции. Можно сказать, что деление «наоборот». умножение. |
|||||||
1. Заполните пропуски.
|
а. Два группы по 6 это 12. 2 × 6 = 12 12 разделены на групп по 6 две группы. 12 ÷ 6 = 2 |
б.
Пять групп по 2 это _____. ____ × 2 = ____ ____ разделен на группы по 2 _____ ÷ 2 = ____ |
|
с.
Одна группа из 4 равна 4.
____ × 4 = ____ 4 разделены на групп по 4 составляют одну группу. _____ ÷ 4 = ____ |
д. ____ группы по 3 это _____.
____ группы по 3 это _____.
____ × ____ = ____ ___ разделен на группы по 3 _____ ÷____ = ____ |
|
эл.
Пять групп по 1 равны 5.
____ × 1 = ____ 5 разделены на групп по 1 _____ ÷ 1 = ____ |
ф. ____ групп ____ является _____.
____ × ____ = ____ ___ разделен на групп по 2 _____ ÷____ = ____ |
2. Создавайте группы. Затем запишите факты деления и умножения, которые картинки иллюстрируют.
3.Теперь нарисуйте палочки или
круги и сделать картину самостоятельно.
Напишите деление
и умножение предложений.
|
|
|
|||||||||
|
|
|
|||||||||
|
|
|
4.Для каждого факта умножения запишите также факт деления. Считать про группы!
|
а. ______ ÷ 2 = _____ |
б.
12 × 2 = _____ ______ ÷ 2 = _____ |
в.
8 × 5 = _____ ______ ÷ 5 = _____ |
|
д. 6 × 7 = _____ ______ ÷ ____ = _____ |
эл.
7 × 7 = _____ ______ ÷ ____ = _____ |
ф.
11 × 3 = _____ ______ ÷ ____ = _____ |
|
г. 9 × 8 = _____ ______ ÷ ____ = _____ |
час.
1 × 5 = _____ ______ ÷ ____ = _____ |
я.
7 × 9 = _____ ______ ÷ ____ = _____ |
|
Вы можете решить задачу на деление, подумав о
соответствующее умножение .
Итак, поскольку вы уже знаете таблицу умножения, делить будет легко! |
5.Для каждого деления подумайте о соответствующем умножении и решать.
|
а. 14 ÷ 2 = ______ ____ × 2 = 14 |
б.
18 ÷ 2 = ______ ____ × 2 = ______ |
в.
21 ÷ 7 = ______ ____ × 7 = ______ |
|
д. 54 ÷ 6 = ______ ____ × ____ = ______ |
эл. 24 ÷ 4 = ______
24 ÷ 4 = ______ ____ × ____ = ______ |
ф.
30 ÷ 3 = ______ ____ × ____ = ______ |
|
г. 32 ÷ 4 = ______ ____ × ____ = ______ |
час.
56 ÷ 7 = ______ ____ × ____ = ______ |
я.
55 ÷ 5 = ______ ____ × ____ = ______ |
6. Разделить. Опять думаю умножения.
| а. | б. | в. | д. |
|
24 ÷ 4 = ______ 16 ÷ 2 = ______ 20 ÷ 2 = ______ 36 ÷ 9 = ______ |
15 ÷ 5 = ______ 35 ÷ 5 = ______ 49 ÷ 7 = ______ 54 ÷ 9 = ______ |
32 ÷ 8 = ______ 40 ÷ 8 = ______ 50 ÷ 5 = ______ 42 ÷ 6 = ______ |
48 ÷ 6 = ______ 56 ÷ 8 = ______ 81 ÷ 9 = ______ 100 ÷ 10 = ______ |
|
Подумайте об умножении и решите.
|
Этот урок взят из книги Марии Миллер Math Mammoth Division 1 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторское право © Мария Миллер.
Умножение и деление: введение в умножение
Урок 1: Введение в умножение
Что такое умножение?
Когда вы умножаете , вы в основном добавляете определенное число более одного раза. Например, если вы съели 4 конфеты, затем съели еще 4, затем еще 4, вы можете сказать, что вы умножили на количество съеденных конфет.
Например, если вы съели 4 конфеты, затем съели еще 4, затем еще 4, вы можете сказать, что вы умножили на количество съеденных конфет.
В реальной жизни умножение происходит постоянно. Например, рассмотрим ситуацию ниже.
-
Представьте, что вы покупаете 6 банок газировки. У вас есть 1 набор из 6 банок.
-
В терминах умножения мы бы сказали, что у вас есть 1 x 6 банок. Вы можете прочитать это как один раз шесть .
-
Что делать, если вы покупаете 2 упаковки по 6 штук?
-
Теперь у вас есть 2 комплекта по 6 банок или 2 x 6 банок. Это 2 умножить на столько банок, сколько было раньше!
-
Это может продолжаться вечно. Как насчет 3 x 6 банок или 3 умножить на банок?
-
Теперь у вас есть 8 x 6 банок. Это 8 раз столько банок, сколько у вас было в начале.
-
Важно знать, что числа в выражении умножения можно записывать в любом порядке.

-
Таким образом, 8 x 6 также можно записать как 6 x 8.
-
Другими словами, 6 x 8 = 8 x 6.
-
Итак, если вы купили 6 комплектов по 8 банок в каждом… это будет тот же , что и 8 комплектов по 6 банок в каждом. У вас будет точно такое же количество банок.
Запись выражения умножения
Как вы только что видели, выражение умножения на записывается так:
2 х 6
Вы можете прочитать это выражение как два раза по шесть .Символ умножения (x) также можно назвать символом умножения на . Помните, вы всегда ставите между числами, которые хотите умножить.
Многие жизненные ситуации можно выразить с помощью умножения. Например, представьте, что вы хотите испечь три торта. В рецепте сказано, что на каждую лепешку понадобится два яйца. Другими словами, вам нужно 3 х 2 яйца.
Попробуйте это!
Запишите следующие ситуации в виде выражений умножения. Пока не пытайтесь их решить.
Пока не пытайтесь их решить.
У вас есть шесть пар по два носков в каждой.
Вам необходимо принимать по две таблетки по четыре раза в день.
Каждый пакет содержит девять пончиков. Вы покупаете три пакета .
Решение задач на умножение
Вы можете использовать счет и сложение для решения небольших простых задач на умножение. Например, на последней странице мы пытались вычислить, сколько яиц нам понадобится, чтобы испечь три торта.На каждый торт требовалось два яйца, поэтому мы записали задачу так:
.3 х 2
Как вы уже знаете, это выражение означает три раза по два , или 3 лепешки по 2 яйца в каждой. Это простая проблема. Чтобы решить ее, вы можете либо сосчитать яиц, либо добавить их: 2 + 2 + 2. В любом случае ответ равен 6. Мы знаем, что 3 x 2 = 6.
В то время как это работает для небольших задач, подсчет больших чисел может занять много времени — и это тоже довольно скучно. По этой причине большинство людей запоминают общих задач на умножение, чтобы быстро их решать. Если это звучит сложно, не волнуйтесь. Чем больше вы будете практиковать , тем легче вам будет запоминать ответы на задачи.
По этой причине большинство людей запоминают общих задач на умножение, чтобы быстро их решать. Если это звучит сложно, не волнуйтесь. Чем больше вы будете практиковать , тем легче вам будет запоминать ответы на задачи.
До тех пор вы можете решать задачи на умножение с помощью таблицы умножения . Ее также называют таблицей умножения на . Таблица умножения — это таблица с ответами на все задачи на умножение, в которых используются числа от 1 до 12.Это просто в использовании. Нажмите на слайд-шоу ниже, чтобы узнать, как это сделать.
-
Это таблица раз .
-
В верхней части таблицы умножения вы можете найти числа от 1 до 12. Они идут в порядке от слева направо.
-
Каждое из чисел сверху находится в начале столбца . Например, это столбец, который идет с 5. Все числа в этом столбце кратны из 5. Это означает, что все эти числа можно получить, умножив 5.

-
Вы также можете найти числа от 1 до 12 в левой части таблицы умножения. Здесь числа идут по порядку от сверху до снизу.
-
Каждое из этих чисел является началом строки . Эта строка содержит числа, кратные 4.
-
Попробуем решить задачу с таблицей умножения. Начнем с 7 x 3.
-
В 7 x 3 найдите первое число, на которое мы умножаем, слева от знака времени.Это 7.
-
Найдите 7 вверху таблицы.
-
Далее, посмотрите на второе число, на которое мы умножаем, справа от знака времени. В 7 x 3 это 3.
-
Найдите цифру 3 сбоку от таблицы.
-
Ответ будет в квадрате, где столбец 7 и ряд 3 встречаются и перекрываются.
-
Это квадрат, 21. Итак, 7 x 3 равно 21.
-
Попробуем еще раз. На этот раз мы решим 5 х 9.
-
Во-первых, для 5 x 9 мы находим столбец 5.
-
Далее, для 5 x 9, мы найдем 9-й ряд.

-
Наконец, мы находим квадрат, где встречаются столбец и строка. Это 45. Итак, 5 x 9 = 45.
Вы могли заметить, что в таблице умножения нет строки 0 . Это потому, что ноль, умноженный на что-либо, — это просто ноль . Например, 5 х 0 = 0 и 0 х 100 = 0,
.Попробуйте это!
Решите следующие задачи на умножение.При необходимости вы можете использовать таблицу умножения в качестве справочной информации. Проверьте свой ответ, введя его в поле.
Практика!
Практика умножения с этими задачами. Если хотите, можете использовать таблицу умножить на . Есть 3 наборов задач. В каждом наборе 5 задач.
Набор 1
Набор 2
Набор 3
/en/multiplicationdivision/умножение двух- и трехзначных чисел/содержание/
Умножение — Элементарная математика
Как с картинкой, так и с выражениями 4 × 3 = 3 × 4 — не что иное, как чудо. Дети, конечно, могут переставлять объекты, сгруппированные как 3 + 3 + 3 + 3, чтобы показать эквивалентность 4 + 4 + 4, но это требует перестановки и не является «очевидным».
Дети, конечно, могут переставлять объекты, сгруппированные как 3 + 3 + 3 + 3, чтобы показать эквивалентность 4 + 4 + 4, но это требует перестановки и не является «очевидным».
Но если одно и то же печенье разложить на подносе рядами и столбцами, то совершенно очевидно, что как бы мы ни держали поднос, количество печенья одинаково. Даже если у нас есть предпочтения в отношении того, как мы обозначаем первые две картинки ниже (настаивая, например, на том, что одна имеет размер 4 × 3, а другая — 3 × 4, чего математики не делают), у нас нет способа сделать такое изображение. задание для последнего лотка.4 × 3 просто равно 3 × 4, хотя обозначения не совпадают.
Если мы описываем картинку «три тарелки, по четыре печенья на каждой», используя повторяющееся выражение сложения, то 4 + 4 + 4 более «естественно» использовать, чем 3 + 3 + 3 + 3. Но если мы опишем эту картинку с помощью выражение умножения, 3 × 4 и 4 × 3 одинаково правильно; нет математически предпочтительного порядка записи выражений умножения. [1].
[1].
Для младших школьников полезно и возможно развить представление об умножении, которое выдержит переход от целых чисел к дробям и десятичным дробям.Конечно, также полезно увидеть, как умножение может упростить вычисление, которое в противном случае потребовало бы повторного сложения, но оно не должно быть первичным образом умножения и, по этой причине, предпочтительно не его первым образом.
В Подумай о математике! умножение связано прежде всего с рядами и пересечениями, а довольно рано связано с «сочетаниями» (в том числе и простыми парами) вещей: улицами и проспектами, гласными и согласными в двухбуквенных словах и т. д.Идея повторного сложения также представлена, но позже, как пример другой задачи, которую решает умножение.
Учитывая количество строк и столбцов в прямоугольном массиве, умножение сообщает нам, сколько элементов находится в массиве, не заставляя нас считать их один за другим или многократно добавлять (или пропускать счет) элементы в каждой строке или столбце. Когда элементы в строках и столбцах представляют собой квадраты, выровненные из стороны в сторону, умножение подсчитывает эти квадраты и, следовательно, дает нам площадь прямоугольника.Это изображение отлично работает даже для дробей и объясняет алгоритм умножения дробей.
Когда элементы в строках и столбцах представляют собой квадраты, выровненные из стороны в сторону, умножение подсчитывает эти квадраты и, следовательно, дает нам площадь прямоугольника.Это изображение отлично работает даже для дробей и объясняет алгоритм умножения дробей.
Если прямоугольник размером три на четыре разместить «на уровне» в одну сторону, он будет состоять из 3 строк и 4 столбцов ; если мы повернем его на 90 градусов, строки станут столбцами, а столбцы станут строками, поэтому в нем будет 4 строки и 3 столбца . Если он держится под наклоном, нет правила, указывающего, какие строки называть, а какие столбцы, но в любом случае это не имеет значения; количество квадратов внутри него одинаково.Также не имеет значения, в каком порядке мы обозначаем ширину и длину прямоугольника: 3 × 4 и 4 × 3 обозначают один и тот же прямоугольник, независимо от того, как прямоугольник держат. Два выражения, 3 × 4 и 4 × 3, называют одно и то же число. Комбинации: сколько возможных блоков можно составить ровно из трех цветов и четырех форм? (Предположим, что каждый блок одного цвета и все блоки одного размера. ) Вопросы такого рода предполагают другой образ (и использование) умножения.
) Вопросы такого рода предполагают другой образ (и использование) умножения.
На самом деле умножение подходит для любой ситуации, в которой элементы одного набора соединяются по порядку с элементами другого набора.Здесь элементы одного набора являются началами «слов», а элементы другого набора — окончаниями.
Намек на связь с алгоритмом умножения.
См. статью об умножении и делении для полной разработки алгоритма многоразрядного умножения, показывающего, как он является точной записью показанных здесь моделей пересечения/площади.
В отличие от сложения, которое объединяет только одинаковые количества (сотни с сотнями, единицы с единицами), умножение образует все пары (3 × 7, 3 × 40, 3 × 200, 80 × 7, 80 × 40, 80 × 200)
Для целей выполнения многоразрядного умножения изображение «пересечения», показанное выше, неудобно, потому что оно рассеивает частичные произведения таким образом, что это мешает последнему обязательному шагу сложения. Для понимания того, как организовать вычисления, удобнее использовать табличное представление комбинаций, а также знакомит с моделью массива/площади.
Для понимания того, как организовать вычисления, удобнее использовать табличное представление комбинаций, а также знакомит с моделью массива/площади.
Такой взгляд на многозначное умножение лежит в основе ведического умножения в Индии. Это может быть увлекательной культурной побочной темой для учащихся, которые научились умножать многозначные числа.
Массивы и таблица умножения
В начале второго класса дети могут решать такие задачи и получать от них удовольствие.
Вот две красные буквы и три синие буквы: A, I, S, N, T . Сколько двухбуквенных слов вы можете составить, начиная с красной буквы и заканчивая синей буквой?
Сколько двухблочных башен именно такой формы можно построить из этих блоков?
Вот два примера: . Сколько других вы можете сделать?
Дети могут проводить опыты, создавая актуальные комбинации, а также изобретать собственную систему записи этих комбинаций.В случае двухбуквенных слов достаточно просто написать слова. Что касается башен, дети могут нарисовать их или указать сочетания цветов более абстрактным способом. Когда количество вариантов достаточно мало, как в случае с двухбуквенными словами, второклассники быстро находят все варианты.
Что касается башен, дети могут нарисовать их или указать сочетания цветов более абстрактным способом. Когда количество вариантов достаточно мало, как в случае с двухбуквенными словами, второклассники быстро находят все варианты.
Перекрестки как модель для составления организованного списка
Когда количество вариантов больше, как в задаче о блочной башне, дети, как правило, пропускают комбинации или записывают их дважды, если только они не систематизированы.
Вот один из способов визуализировать пары в этих двух экспериментах. Каждое пересечение представляет собой комбинацию. Сам символ × связан с изображением пересечения, пересечением линий.
Дети могут «провести» пальцем вдоль «улицы А» и «проспекта N» и обозначить светофор на этом перекрестке «ан». например, с красным верхом. Когда второклассники впервые проводят эти эксперименты, они учатся составлять систематические списки, а не умножать.Но мы видим, к чему это ведет: пересечения сами по себе перечисляют комбинации, которые ищут дети, и помогают им понять, как организовать эти списки; количество пересечений можно найти путем умножения, и дети получают предварительный просмотр этих идей умножения.
Таблицы как модель для составления упорядоченного списка
Таблицы одинаково хороши для представления комбинаций и организации задачи их перечисления. Ячейки внутри таблицы (старательно избегая путаницы с ячейками «заголовка» над каждым столбцом и слева от каждой строки) снова показывают, как умножение отвечает на вопрос «сколько пар можно составить?»
Математика широко использует обе структуры — таблицы и пересекающиеся линии.
Умножение часто представляется в виде массивов смежных квадратов — «модель площади» умножения — или массивов точек или других мелких объектов. Первые визуально больше похожи на внутренности столов; последние визуально больше похожи на перекрестки.Якорь
Построение основных фактов
Первые шаги
Когда мы видим одинаковые тройки цифр — 3, 5, 15; 4, 3, 12; 2, 5, 10; 6, 4, 24 — всплывающие в разных контекстах, они начинают казаться знакомыми еще до каких-либо сознательных усилий по их запоминанию. На самом деле, сфокусированные, преднамеренные усилия, которые кажутся необходимыми для некоторых троек (например, 7, 8, 56), могут быть связаны именно с тем, что существует очень мало естественных контекстов, в которых эти тройки иначе появляются. Многие внешкольные занятия помогают построить таблицу умножения на 5: опыт определения времени в минутах на часах, обращения с монетами, наблюдения за своими руками. Следующие идеи представляют несколько контекстов для одних и тех же основных фактов, чтобы разнообразить практику (чтобы она оставалась интересной и создавала богатое разнообразие образов), чтобы к тому времени, когда дети пытаются запомнить факты умножения, они уже были хорошо знакомы с наиболее распространенными. те, что знают их «на холодную», а количество оставшихся фактов, требующих заучивания, совсем невелико (всего пятнадцать!).
На самом деле, сфокусированные, преднамеренные усилия, которые кажутся необходимыми для некоторых троек (например, 7, 8, 56), могут быть связаны именно с тем, что существует очень мало естественных контекстов, в которых эти тройки иначе появляются. Многие внешкольные занятия помогают построить таблицу умножения на 5: опыт определения времени в минутах на часах, обращения с монетами, наблюдения за своими руками. Следующие идеи представляют несколько контекстов для одних и тех же основных фактов, чтобы разнообразить практику (чтобы она оставалась интересной и создавала богатое разнообразие образов), чтобы к тому времени, когда дети пытаются запомнить факты умножения, они уже были хорошо знакомы с наиболее распространенными. те, что знают их «на холодную», а количество оставшихся фактов, требующих заучивания, совсем невелико (всего пятнадцать!).
Удвоение и деление пополам
В первом классе дети учатся удваивать ([[умственная арифметика|мысленно]) все целые числа до 12. Второклассники практикуют эти базовые удвоения, используя их вместе с развивающимися представлениями о разрядности для удвоения (мысленно) целые числа до 50. В этих классах дети также учатся находить половину четных чисел, получающихся в результате такого удвоения.
В этих классах дети также учатся находить половину четных чисел, получающихся в результате такого удвоения.
Малые массивы
В Подумай о математике! , вторая половина второго класса дает учащимся большой опыт работы с небольшими массивами, из которых они могут запоминать небольшие факты умножения.В одном из упражнений учитель может поднять такой массив и спросить: «Сколько строк? Сколько столбцов? Сколько маленьких квадратиков?»
Учащиеся, которые еще не владеют навыком сложения, могут использовать сложение или пропустить счет, чтобы определить количество квадратов. Связь размеров массива — количества строк и столбцов — с количеством маленьких квадратов устанавливает факт умножения.
Затем учитель может держать тот же массив в этой ориентации и задавать те же вопросы.
Строки и столбцы меняются местами, но количество квадратов остается прежним.
Преподаватель может устроить из этого веселую игру, меняя набор поддерживаемых элементов (2×3, 3×3, 4×5 и т. д., но не более 5 строк или столбцов, потому что большие числа слишком сложны для понимания). распознавать без утомительного подсчета), и учащиеся довольно быстро запоминают, сколько квадратов в этих знакомых прямоугольниках.
д., но не более 5 строк или столбцов, потому что большие числа слишком сложны для понимания). распознавать без утомительного подсчета), и учащиеся довольно быстро запоминают, сколько квадратов в этих знакомых прямоугольниках.
Тот факт, что прямоугольник, расположенный горизонтально или вертикально, имеет одинаковое количество маленьких квадратов внутри, дает наглядное представление о том, почему умножение является коммутативным.
Пересекающиеся вертикальные и горизонтальные линии дают еще один образ для умножения — 2 вертикальные линии пересекают 3 горизонтальные линии в 6 пересечениях — и еще один контекст для репетиции фактов. Они могут рисовать их или играть с прозрачными картами, сначала пытаясь предсказать количество пересечений, а затем перекрывая прозрачные пленки, чтобы непосредственно подсчитать их предсказания. С картами с прорезями в них тоже интересно играть. Дети выбирают пару и, как и в случае с диапозитивами, пытаются изобразить количество пересечений, прежде чем они начнут экспериментировать, кладя одну карточку поверх другой, чтобы убедиться, что их предсказание было верным. Если карту с 2 вертикальными слотами положить поверх карты с 5 горизонтальными слотами, мы сможем видеть сквозь двойной слой только на 10 пересечениях.
Если карту с 2 вертикальными слотами положить поверх карты с 5 горизонтальными слотами, мы сможем видеть сквозь двойной слой только на 10 пересечениях.
Перекрестки для разъяснения умножения на 0 и 1. «Представьте себе крошечный городок с тремя дорогами, идущими с востока на запад…» Проведите пальцем по воздуху горизонтально, чтобы объяснить, что означает «восток-запад». Затем «нарисуйте» еще две дороги с востока на запад прямо в воздухе, чтобы дети могли представить их в уме. Позже вы или ребенок нарисуете их на доске.«…и только одна дорога, идущая с севера на юг».
В воздухе указать пальцем дорогу с севера на юг.
«Давайте нарисуем карту этого крошечного городка. Вот дороги с востока на запад.
Нарисуйте неправильную границу города, а на ней проведите три параллельные горизонтальные линии от одной стороны города к другой (и немного выходящие за границу города, чтобы показать, что они продолжают идти в соседние регионы).
«На карте дороги выглядят как три горизонтальные линии. Кто хотел бы нарисовать дорогу с севера на юг?»
Кто хотел бы нарисовать дорогу с севера на юг?»
Вы можете снова указать направление пальцем в воздухе, но не прямо на карте. Пригласите кого-нибудь порисовать.
«Город поставил светофор на каждом перекрестке (указать на перекрестки). Сколько там светофоров?»
Играйте с изображением.
«А что, если бы город построил еще одну дорогу с востока на запад? Сколько пересечений получится?»
Умножение любого числа на 1 дает это число; умножение любого числа на 0 дает 0.Дети, которых учат этим просто правилам для запоминания, без некоторого понимания, часто искажают правила, путая их друг с другом. (Что дает 1 умножение числа на 1 или число?) Изображение крошечного городка помогает понять, почему 1 умножение на любое число дает это число. (При использовании только одной вертикальной линии количество пересечений будет таким же, как и количество горизонтальных линий.)
Карты с 0-5 слотами также могут быть особенно полезными. Когда карта с одним вертикальным слотом помещается поверх карты с тремя горизонтальными слотами, три пересечения появляются как единственные «окна» через пару карт. Изменение того, какая карта находится сверху или какая вертикальная, а какая горизонтальная, не имеет значения. Если одна карта имеет один слот, количество пересечений будет соответствовать количеству слотов на другой карте, когда они наложены друг на друга (и другие слоты перпендикулярны одному слоту). Изображение слота особенно ясно показывает, почему умножение на 0 всегда дает 0.
Изменение того, какая карта находится сверху или какая вертикальная, а какая горизонтальная, не имеет значения. Если одна карта имеет один слот, количество пересечений будет соответствовать количеству слотов на другой карте, когда они наложены друг на друга (и другие слоты перпендикулярны одному слоту). Изображение слота особенно ясно показывает, почему умножение на 0 всегда дает 0.
Этот урок дает прекрасную возможность использовать слова «горизонтальный» и «вертикальный» в контексте и связать их использование в качестве направлений на картах с востоком, западом, севером и югом в качестве направлений на земле.(См. Горизонтальный и вертикальный, чтобы узнать о распространенных заблуждениях относительно идей, которые представляют эти слова.)
Построение таблицы умножения
Проект учащегося для второго класса: учащиеся используют сетку, устроенную как таблица умножения, но не имеющую строки или столбца для нуля. Используя лист бумаги в форме буквы L, они выбирают часть сетки; в правом нижнем углу выделения они пишут количество захваченных квадратов (что равно площади прямоугольника, если каждый маленький квадрат представляет собой одну квадратную единицу площади).
Обратите внимание, что число вверху, ближайшее к синей границе, указывает ширину зеленого прямоугольника, количество столбцов квадратов; число слева, ближайшее к синей границе, дает высоту зеленого прямоугольника и количество строк в нем.
Если мы переместим границу прямо вниз на один шаг, мы добавим новую строку без изменения количества клеток в строке.
Этот способ мышления говорит, что 6 (количество квадратов в предыдущем прямоугольнике, 2×3) плюс 3 (количество квадратов в новом ряду) равно 9 (количество квадратов в новом прямоугольнике).Другой способ описать новый прямоугольник — 3×3. Итак, 2×3 + 3 = 3×3.
Этот прямоугольник имеет одинаковую ширину и высоту, так что это квадрат. Поэтому число в углу (количество крошечных квадратов внутри него) называется квадратным числом.
Ход по диагонали — один шаг «на юг» и один шаг «на восток» (или один шаг вниз и один шаг вправо) — дает другое квадратное число.
Два шага по диагонали на юго-восток дают еще один квадратный номер.
Интересно, если начать с квадратного числа (в данном случае 16) и сделать один шаг на северо-восток
или юго-запад
полученное число ровно на 1 меньше квадратного числа, с которого вы начали. Этот пример показывает, что прямоугольник 3×5 содержит на один квадрат меньше, чем прямоугольник 4×4. См. статью о разнице квадратов, чтобы узнать больше об этом интригующем шаблоне и еще одном особенно эффективном способе для студентов практиковать факты, развивая новые и полезные математические идеи.
Симметрия таблицы умножения
Подсчет квадратов в прямоугольниках позволяет понять, почему 3×4 = 4×3. Оба способа описания этого прямоугольника . И даже если мы решим зарезервировать одну из этих нотаций для , а другую нотацию для , они все равно будут равны.
Поскольку умножение является коммутативным, то есть поскольку 2×6 = 6×2 и 3×5 = 5×3 и т. д., таблица умножения симметрична относительно диагонали северо-запад-юго-восток.Эта диагональ, желтая на этих иллюстрациях, содержит квадратные числа.
Избавившись от отвлекающих цифр и стрелок, мы видим три области: диагональ с квадратными цифрами, зеленую область с другими товарами и белую область с теми же номерами, что и в зеленой области.
Это очень хорошая новость для тех, кто пытается запомнить факты умножения! (См. Сколько фактов нужно выучить? ниже.)
Умножение на 10 и 100
Строится: 7 стержней это 70 маленьких кубиков
Умножение на 5 и 50
Дети, которые могут умножить на 10 и взять половину, могут затем использовать эти навыки, чтобы умножить на 5.Например, 7×5 — это половина 7×10, значит, это 35. В конечном счете, 7×5 следует признать само по себе — один из «основных фактов», — но двухшаговая процедура (умножение на 10 и затем взять половину результата) также полезно знать и установить хорошую связь с 5-кратными фактами. Точно так же, зная, что 50 — это половина 100, мы можем увидеть, что 50 семерок — это половина 100 семерок, поэтому 50 × 7 — это половина 100 × 7: мы можем умножить любое число на 50, умножив его на 100, а затем взяв половину. Дети, хорошо усвоившие это, могут легко умножить в уме 18×5, подумав «половина от 180».” Поскольку умножение и деление можно выполнять в любом порядке с одинаковым результатом, мы могли бы сначала взять половину (от 18), а затем умножить на 10.
Точно так же, зная, что 50 — это половина 100, мы можем увидеть, что 50 семерок — это половина 100 семерок, поэтому 50 × 7 — это половина 100 × 7: мы можем умножить любое число на 50, умножив его на 100, а затем взяв половину. Дети, хорошо усвоившие это, могут легко умножить в уме 18×5, подумав «половина от 180».” Поскольку умножение и деление можно выполнять в любом порядке с одинаковым результатом, мы могли бы сначала взять половину (от 18), а затем умножить на 10.
Сколько фактов нужно узнать?
Если умножение на ноль и единицу понятно, эти факты (голубые) не нужно запоминать. Если симметрия таблицы понятна (3 × 4 = 4 × 3, коммутативное свойство умножения), эти факты (темно-синие) не нужно запоминать. К тому времени, когда дети работают над фактической практикой, квадратные числа (желтые) уже выучены, а «простые» факты (розовые) уже выучены (удвоение, умножение на 10 и умножение на 5).К этому моменту осталось запомнить только 15 фактов — те, что отмечены зеленым.
Умножение и деление: Введение в деление
Урок 4: Знакомство с Подразделением
/en/multiplicationdivision/video-multiplication/content/
Что такое деление?
Подразделение делит что-то поровну. Например, допустим, у вас есть 10 лотерейных билетов, и вы хотите поделиться ими с 5 друзьями.
Например, допустим, у вас есть 10 лотерейных билетов, и вы хотите поделиться ими с 5 друзьями.
Вы делите билетов между своими друзьями.Каждый друг получает равное количество билетов.
Видите, у каждого из них по 2 билета? Когда вы делите 10 билетов между пятью друзьями, вы создаете 5 равных групп по 2 билета.
Дивизиячасто случается в реальной жизни. Например, рассмотрим ситуацию ниже.
Запись выражений деления
В слайд-шоу вы видели, что мы разделили шесть кексов на две равные группы. Чтобы вычислить количество кексов в каждой группе, вы можете написать выражение деления следующим образом:
6 / 2
Вы также можете написать выражение следующим образом:
6 ÷ 2
Любое выражение можно прочитать как шесть разделить на два .Знак деления (/ или ÷) означает, что что-то делится. Поэтому мы всегда ставили после первого числа — было 6 кексов, и мы разделили их на 2 группы.
Многие жизненные ситуации можно выразить делением. Например, представьте, что вы расставляете 15 банок на 3 полках. Вы можете разделить, чтобы убедиться, что вы поставили одинаковое количество банок на каждой полке. Другими словами, 15 банок, разделенных тремя полками, или 15/3.
Попробуйте это!
Попробуйте настроить эти ситуации как выражения деления.Пока не пытайтесь их решить.
У учительницы есть 16 карандашей, которые она распределяет поровну между 4 учениками.
У флориста есть 18 роз, и он делит их поровну между 3 вазами.
У вас есть 6 угощений, которыми вы поровну делитесь с 3 собаками.
Решение задач на деление
Вы можете использовать , считая , для решения простых задач на деление. Например, допустим, у нас есть 12 саженцев. Решаем посадить их в два ровных ряда. Сколько растений в каждом ряду? Мы могли бы написать этот вопрос так:
12/2
Помните, это выражение означает 12 разделить на два , или 12 саженцев разделить на 2 ряда. Это простая проблема. Чтобы решить ее, вы можете разделить саженцы на две группы, а затем подсчитать , сколько растений в каждой группе. Ответ 6. Мы знаем, что 12/2 = 6.
Это простая проблема. Чтобы решить ее, вы можете разделить саженцы на две группы, а затем подсчитать , сколько растений в каждой группе. Ответ 6. Мы знаем, что 12/2 = 6.
В то время как подсчет работает для задач, которые начинаются с маленьких чисел, задача, которая начинается с большого числа , может занять много времени, чтобы решить ее с помощью подсчета. По этой причине большинство людей запоминают общих задач на деление, чтобы быстро их решать. Если это звучит сложно, не волнуйтесь.С некоторой практикой вы сможете быстро запомнить ответы.
В разделе «Введение в умножение» вы познакомились с таблицей умножения на . На этом уроке вы использовали его для решения задач на умножение. Вы также можете использовать таблицу умножения для решения задач на деление.
Давайте начнем с проблемы, с которой мы уже знакомы. Как бы мы решили задачу о ростке с таблицей умножения?
Нажмите на слайд-шоу ниже, чтобы узнать, как это сделать.
-
Помните, что каждое число в верхней части таблицы умножения находится в начале столбца .
-
Например, это столбец, который идет с 7.
-
Каждое число в левой части таблицы умножения является началом строки . Этот ряд идет с 9.
-
Давайте попробуем решить задачу о ростке: 12 / 2.
-
Сначала найдите число, на которое вы делите, справа от знака деления.В 12/2 мы делим на 2.
-
Найдите столбец 2.
-
Затем найдите число, которое вы делите, слева от знака деления. В 12/2 это 12.
-
Найдите 12 в колонке 2.
-
Найдите число в начале ряда, которое перекрывает 12. В данном случае это 6-й ряд.
-
Итак, ответ или частное для 12/2 равно 6.
-
Попробуем еще раз.На этот раз мы решим 15 / 5.
-
Сначала мы найдем 5-й столбец, так как мы делим на 5.

-
Затем мы найдем 15 в 5-м столбце, так как это число, которое мы делим.
-
Наконец, мы найдем число в начале ряда, которое перекрывает 15. Это 3. Итак, 15/5 = 3.
Попробуйте это!
Решите эти задачи на деление. Если вам нужна помощь, вы можете использовать таблицу умножения.
Остаток
На предыдущих страницах мы делили числа поровну.Например, в начале урока мы разделили 10 билетов поровну между 5 людьми. Каждый получил по 2 билета. Что происходит, когда число нельзя разделить поровну?
Например, рассмотрим ситуацию ниже.
Из слайд-шоу видно, что остаток (1) меньше, чем число, на которое мы делили (3). Так будет всегда, когда у проблемы есть остаток. Например, посмотрите на каждую из этих проблем ниже:
21/5 = 4 р1
Остаток от 1 меньше 5.
76/6 = 12 р4
Остаток от 4 меньше 6.
Если остаток больше, это означает, что остаток слишком велик. Вам нужно будет попробовать разделить еще раз. Например, если у вас 4 друга и осталось 7 билетов, вы знаете, что каждый друг может получить как минимум еще один билет.
Вам нужно будет попробовать разделить еще раз. Например, если у вас 4 друга и осталось 7 билетов, вы знаете, что каждый друг может получить как минимум еще один билет.
Практика!
Практика разделения с этими проблемами. Если хотите, можете воспользоваться таблицей умножить на . Имеется 3 наборов задач по 5 задач в каждом.
Набор 1
Набор 2
Набор 3
/en/multiplicationdivision/long-division/content/
Факты умножения PowerPoint – таблицы умножения на семь
CCSS.MATH.CONTENT.3.OA.A.1
Интерпретируйте произведения целых чисел, например, интерпретируйте 5 × 7 как общее количество объектов в 5 группах по 7 объектов в каждой. Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7.
- 3 класс
- Стандарты математической практики
- Операции и алгебраическое мышление
- Представлять и решать задачи на умножение и деление
CCSS.
 МАТЕМАТИЧЕСКОЕ СОДЕРЖАНИЕ.3.OA.A.3
МАТЕМАТИЧЕСКОЕ СОДЕРЖАНИЕ.3.OA.A.3 Используйте умножение и деление в пределах 100 для решения текстовых задач в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например, используя рисунки и уравнения с символом для неизвестного числа для представления проблемы.
- 3 класс
- Стандарты математической практики
- Операции и алгебраическое мышление
- Представлять и решать задачи на умножение и деление
CCSS.МАТЕМАТИЧЕСКОЕ СОДЕРЖАНИЕ.3.OA.A.4
Определите неизвестное целое число в умножении или уравнении деления, связывающем три целых числа. Например, определите неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ?
- 3 класс
- Стандарты математической практики
- Операции и алгебраическое мышление
- Представлять и решать задачи на умножение и деление
CCSS.
 МАТЕМАТИЧЕСКОЕ СОДЕРЖАНИЕ.3.OA.C.7
МАТЕМАТИЧЕСКОЕ СОДЕРЖАНИЕ.3.OA.C.7 Свободно умножайте и делите в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная, что 8 × 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать на память все пр…
- 3 класс
- Стандарты математической практики
- Операции и алгебраическое мышление
- Умножение и деление в пределах 100
CCSS.MATH.СОДЕРЖАНИЕ.4.OA.A.1
Интерпретируйте уравнение умножения как сравнение, например, интерпретируйте 35 = 5 × 7 как утверждение, что 35 в 5 раз больше, чем 7, и в 7 раз больше, чем 5. Представьте вербальные утверждения мультипликативных сравнений в виде уравнений умножения.
- 4 класс
- Стандарты математической практики
- Операции и алгебраическое мышление
- Используйте четыре операции с целыми числами для решения задач
CCSS.
 МАТЕМАТИЧЕСКОЕ СОДЕРЖАНИЕ.4.OA.A.2
МАТЕМАТИЧЕСКОЕ СОДЕРЖАНИЕ.4.OA.A.2 Умножьте или разделите, чтобы решить текстовые задачи, включающие мультипликативное сравнение, например, используя рисунки и уравнения с символом неизвестного числа для представления проблемы, отличая мультипликативное сравнение от аддитивного сравнения.
- 4 класс
- Стандарты математической практики
- Операции и алгебраическое мышление
- Используйте четыре операции с целыми числами для решения задач
Математика 3.4(Ф)
Вспомнить факты, чтобы умножить до 10 на 10 с автоматизмом и вспомнить соответствующие факты деления;
- TEKS Math
- TEKS Math 3
- Math 3.4
Math 3.
 4(K)
4(K) Решайте одноэтапные и двухэтапные задачи, включающие умножение и деление в пределах 100 с использованием стратегий на основе объектов; живописный модели, включая массивы, модели областей и равные группы; свойства операций; или вспомнить факты.
- TEKS Math
- TEKS Math 3
- Math 3.4
Математика 3.5(С)
Опишите выражение умножения как сравнение, такое как 3 x 24, представляет собой 3 раза больше, чем 24;
- TEKS Math
- TEKS Math 3
- Math 3.5
Math 4.4(D)
Используйте стратегии и алгоритмы, в том числе
стандартный алгоритм умножения четырехзначного числа на однозначное
число и умножение двузначного числа на двузначное число. Стратегии
может включать ментальную арифметику, частичные произведения, а…
Стратегии
может включать ментальную арифметику, частичные произведения, а…
- TEKS Math
- TEKS Math 4
- Math 4.4
Math 4.4(H)
Бегло решать одно- и двухшаговые задачи включая умножение и деление, включая интерпретацию остатков.
- TEKS Math
- TEKS Math 4
- Math 4.4
Math 5.3
Число и операции. Студент подает заявку стандарты математических процессов для разработки и использования стратегий и методов вычисления с положительными рациональными числами для эффективного решения задач и точность.Ожидается, что студент…
- TEKS Math
- TEKS Math 5
Свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная, что 8 5 = 40, известно, что 40 5 = 8) или свойства операций.
 К концу 3 класса знать наизусть все произведения двух однозначных чисел.
MAFS.3.OA.3.7 — бегло умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (т.г., зная, что 8 5 = 40, известно 40 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.
К концу 3 класса знать наизусть все произведения двух однозначных чисел.
MAFS.3.OA.3.7 — бегло умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (т.г., зная, что 8 5 = 40, известно 40 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.
Веб-сайт несовместим с используемой версией браузера. Не все функции могут быть доступны. Пожалуйста, обновите ваш браузер до последней версии.
Свободно умножайте и делите в пределах 100, используя такие приемы, как взаимосвязь между умножением и делением (например,г. , зная, что 8 × 5 = 40, известно 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.
, зная, что 8 × 5 = 40, известно 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.
Пояснения
Ожидания беглости или примеры достижения стандартовУчащиеся бегло умножают и делят в пределах 100.К концу 3 класса они знают по памяти все произведения двух однозначных чисел. Умножение и деление являются новыми в 3 классе и соответствуют стандарту беглости умножения и деления. 3.OA.3.7 с пониманием составляет основную часть работы учащихся 3-го класса.
Примеры возможностей для углубленного изучения
Нахождение однозначных произведений и связанных с ними частных является обязательным требованием для 3-го класса.
Достижение свободного владения языком у многих студентов займет большую часть года. Эти навыки и
понимание, которое их поддерживает, имеет решающее значение; учащиеся будут полагаться на них долгие годы, когда будут учиться умножать и делить многозначные целые числа, а также складывать, вычитать, умножать и делить дроби. После того, как ситуации с умножением и делением были установлены, рассуждения о закономерностях в произведениях (например, произведениях с делителями 5 или 9) могут помочь учащимся запомнить определенные произведения и частные. Упражняться
— и, при необходимости, дополнительная поддержка — должна продолжаться в течение всего года для тех, кто нуждается в ней для достижения свободного владения языком.
Эти навыки и
понимание, которое их поддерживает, имеет решающее значение; учащиеся будут полагаться на них долгие годы, когда будут учиться умножать и делить многозначные целые числа, а также складывать, вычитать, умножать и делить дроби. После того, как ситуации с умножением и делением были установлены, рассуждения о закономерностях в произведениях (например, произведениях с делителями 5 или 9) могут помочь учащимся запомнить определенные произведения и частные. Упражняться
— и, при необходимости, дополнительная поддержка — должна продолжаться в течение всего года для тех, кто нуждается в ней для достижения свободного владения языком.
Общая информация
Предметная область: Математика
Класс: 3
Домен-поддомен: Операции и алгебраическое мышление
Кластер: Уровень 1: Отзыв
Кластер: Умножить и разделить в пределах 100. (Основной кластер) –
(Основной кластер) – Кластеры не следует сортировать от основных к вспомогательным, а затем обучать в этом порядке. Это лишило бы связность математических идей и упустило бы возможность улучшить основную работу класса с помощью поддерживающих кластеров.
Дата принятия или пересмотра: 14 февраля
Дата последней оценки: 14.02
Статус: Утвержден Государственным советом
Оценено: Да
Спецификации объекта испытаний
- Пределы оценки:
Все значения в пунктах не могут превышать целое число, умноженное на 10 x 10 или соответствующие факты разделения.
- Калькулятор:
Нет
- Контекст:
Без контекста
Образцы тестовых заданий (2)
- Тестовый образец #: Образец 2
- Вопрос:
А.Какое число, умноженное на 7, равно 42?
B. Число 42, разделенное на какое число, равно 7?
- Сложность: Н/Д
- Тип: EE: Редактор уравнений
Связанные точки доступа
Альтернативная версия этого теста для учащихся с серьезными когнитивными нарушениями.
Связанные ресурсы
Проверенные ресурсы, которые преподаватели могут использовать для обучения концепциям и навыкам в этом эталонном тесте.
Уроки STEM – Активность по моделированию
Плавающий плот Rift: В этом пуле плавучих плотов учащиеся будут делиться, чтобы найти стоимость каждого плавсредства. Затем они должны определить, какой плот лучше всего подходит для общественного пользования, исходя из стоимости, гарантии и сборки. Студенты отправят письмо клиенту, объясняющее их процедуру ранжирования плавучих устройств.
Затем они должны определить, какой плот лучше всего подходит для общественного пользования, исходя из стоимости, гарантии и сборки. Студенты отправят письмо клиенту, объясняющее их процедуру ранжирования плавучих устройств.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для того, чтобы выявить мысли учащихся о концепциях, внедренных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Спин Бейблэйд: Студенты смогут оценить данные и создать процесс, для которого бейблейд будет «лучшим» для мистера Блэка.Магазин игрушек Брауна. Данные будут включать отзывы клиентов, цену, стиль и количество оборотов в минуту. Студенты будут применять понимание разделения в решении проблем. Они напишут письмо с объяснением своей процедуры, используя языковые соглашения, соответствующие их классу.
Они напишут письмо с объяснением своей процедуры, используя языковые соглашения, соответствующие их классу.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для того, чтобы выявить мысли учащихся о концепциях, внедренных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Формирующие оценки MFAS
Оригинальные учебники для учащихся по математике – классы K-5
День рождения дома: беглость умножения и деления, часть 1: Джалия готова отпраздновать свой день рождения и использовать стратегии удвоения и деления пополам, а также связывания умножения и деления, чтобы бегло знакомиться с фактами умножения и деления в этом интерактивном учебном пособии.
Это первая часть из двух частей. Нажмите ЗДЕСЬ, чтобы просмотреть вторую часть.
День рождения дома: беглость умножения и деления, часть 2:Помогите Джалии продолжать планировать вечеринку по случаю ее дня рождения и свободно владеть математическими фактами, используя уже известные ей полезные факты и взаимосвязь между умножением и делением в части 2 этого интерактивного руководства.
Это вторая часть серии из двух частей. Нажмите ЗДЕСЬ, чтобы просмотреть часть 1.
Ресурсы для учащихся
Проверенные ресурсы, которые учащиеся могут использовать для изучения концепций и навыков в этом эталонном тесте.
Оригинальные учебные пособия для студентов
День рождения дома: беглость умножения и деления, часть 2:Помогите Джалии продолжать планировать вечеринку по случаю ее дня рождения и свободно владеть математическими фактами, используя уже известные ей полезные факты и взаимосвязь между умножением и делением в части 2 этого интерактивного руководства.
Это вторая часть серии из двух частей. Нажмите ЗДЕСЬ, чтобы просмотреть часть 1.
Тип: оригинальное учебное пособие для учащихся
День рождения дома: беглость умножения и деления, часть 1: Джалия готова отпраздновать свой день рождения и использовать стратегии удвоения и деления пополам, а также связывания умножения и деления, чтобы бегло знакомиться с фактами умножения и деления в этом интерактивном учебном пособии.
Это первая часть из двух частей. Нажмите ЗДЕСЬ, чтобы просмотреть вторую часть.
Тип: оригинальное учебное пособие для учащихся
Образовательные игры
Арифметическая тренировка:Этот учебник поможет вам освежить свои навыки умножения, деления и факторизации в этой захватывающей игре.
Тип: обучающая игра
Sundae Times: игра на умножение целых чисел:
Вы пытаетесь построить самый высокий рожок мороженого, умножив 2 целых числа! Будь осторожен! Вы соревнуетесь с другими детьми! Иди так быстро, как только можешь, но используй особые способности, которые помогут тебе продвинуться вперед!
Тип: обучающая игра
Таблицы умножения – Соответствующие карты: Эта интерактивная флэш-версия знакомой игры «Концентрация» («пельманизм» в Великобритании) помогает одному пользователю тренировать беглость и запоминание фактов умножения. Игрок может выбрать массив из 16, 20 или 24 карт, которые появляются лицевой стороной вниз. Цель состоит в том, чтобы перевернуть две карты за раз, чтобы максимально эффективно сопоставить все пары факторов с их продуктами. Функция подсчета очков препятствует случайным угадываниям. Пользователи могут выбрать работу с факторами в трех диапазонах. Выбирая 2x-10x, игра отвечает части стандарта: к концу 3 класса учащиеся будут знать наизусть все произведения двух однозначных чисел. Печатные версии игровых карт доступны для скачивания.
Игрок может выбрать массив из 16, 20 или 24 карт, которые появляются лицевой стороной вниз. Цель состоит в том, чтобы перевернуть две карты за раз, чтобы максимально эффективно сопоставить все пары факторов с их продуктами. Функция подсчета очков препятствует случайным угадываниям. Пользователи могут выбрать работу с факторами в трех диапазонах. Выбирая 2x-10x, игра отвечает части стандарта: к концу 3 класса учащиеся будут знать наизусть все произведения двух однозначных чисел. Печатные версии игровых карт доступны для скачивания.
Тип: обучающая игра
Онлайн-ресурс для практики умножения: Это простое поле для умножения 10 на 10, представленное в простой в использовании онлайн-настройке. Все ответы даны как нагромождение кусочков головоломки. Он имеет таймер и ведет счет правильных ответов. Неправильные ответы просто не «прилипают» к сетке.
Он имеет таймер и ведет счет правильных ответов. Неправильные ответы просто не «прилипают» к сетке.
Тип: обучающая игра
Продуктовая игра (множители и коэффициенты):Эта интерактивная игра для двух игроков развивает беглость учащихся с фактами умножения, их понимание взаимосвязи между факторами и продуктами, а также их стратегическое мышление.На доске, отображающей все факторы с номерами от 1 до 9, игроки по очереди перемещают маркеры в списке факторов и забирают свои продукты. Выигрывает тот, кто первым наберет четыре подряд.
Тип: обучающая игра
Образовательное программное обеспечение/инструмент
Арифметическая викторина: В этом упражнении учащиеся решают арифметические задачи, включающие целые числа, целые числа, сложение, вычитание, умножение и деление. Это задание позволяет учащимся отслеживать свои успехи в изучении арифметических действий с целыми числами и целыми числами. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Это задание позволяет учащимся отслеживать свои успехи в изучении арифметических действий с целыми числами и целыми числами. Это задание включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и исследовательские вопросы для использования с апплетом Java.
Тип: Образовательное программное обеспечение/инструмент
Деятельность студенческого центра
Edcite: Математика 3 класс: Учащиеся могут практиковаться в ответах на математические вопросы по различным темам. Имея учетную запись, учащиеся могут сохранять свою работу и отправлять ее учителю по завершении.
Имея учетную запись, учащиеся могут сохранять свою работу и отправлять ее учителю по завершении.
Тип: деятельность студенческого центра
Руководство
Умножение 2- и 3-значных чисел: Этот учебник для студенческой аудитории поможет учащимся углубить свое понимание умножения с использованием таблицы умножения.Студенты смогут перемещаться по учебной части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется. В 5-м разделе учебника учащимся предлагаются дополнительные практические задачи для самопроверки.
Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется. В 5-м разделе учебника учащимся предлагаются дополнительные практические задачи для самопроверки.
Тип: Учебник
Виртуальный манипулятор
Арифметика: Учащимся будут даны задачи на умножение и деление, на которые они должны ответить.У них также есть возможность получить число, а затем указать факторы того, как это число было получено, с помощью умножения или деления.
Тип: виртуальный манипулятор
Ресурсы для родителей
Проверенные ресурсы, которые воспитатели могут использовать, чтобы помочь учащимся освоить концепции и навыки в рамках этого теста.
Образовательная игра
Alien Munchtime – Игра «Разделение»: Это онлайн-игра, в которой учащиеся изучают факты о делении, кормя голодных инопланетян. Пользователь может установить количество семейств фактов, с которыми он хочет играть, от 2 до 12.
Пользователь может установить количество семейств фактов, с которыми он хочет играть, от 2 до 12.
Тип: обучающая игра
Задача решения проблем
Боулинг для чисел: Цель этой игры — помочь учащимся гибко мыслить о числах и операциях и записывать несколько операций, используя соответствующие обозначения.Студенты, стремящиеся сбить все булавки, быстро развивают шаблоны в своих выражениях. Они могут повторно использовать части выражения, возможно, изменяя только последнюю операцию.
Тип: Задача решения проблем
Руководство
Умножение 2- и 3-значных чисел: Этот учебник для студенческой аудитории поможет учащимся углубить свое понимание умножения с использованием таблицы умножения.Студенты смогут перемещаться по учебной части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется. В 5-м разделе учебника учащимся предлагаются дополнительные практические задачи для самопроверки.
В 5-м разделе учебника учащимся предлагаются дополнительные практические задачи для самопроверки.
Тип: Учебник
Виртуальные манипуляторы
Игра «Умножение»:Эта забавная игра позволяет учащимся использовать свои навыки умножения, чтобы победить компьютер.И учащийся, и компьютер по очереди перемещают по одному маркеру за раз. Выиграет тот, кто первым соберет 4 подряд.
Тип: виртуальный манипулятор
Быстрая математика: Эта интересная игра требует, чтобы учащиеся быстро думали и нажимали на правильный символ, чтобы завершить уравнение как можно быстрее.
Тип: виртуальный манипулятор
Загрузка….
.

 3-й класс
3-й класс  д.
д.

 Ничья
27 палочек.
Ничья
27 палочек.  Ничья
8 палочек.
Ничья
8 палочек.  7 × 2 = _____
7 × 2 = _____ 
