«План-конспект урок математики 3 класс »
Тема урока Деление суммы на число
Тип урока урок усвоения новых знаний и способов действий
Цель урока:
Обучающая: организовать деятельность детей по изучению и первичному применению знаний и способов действий по теме «Деление суммы на число» в результате чего учащиеся будут знать правило деления суммы на число; уметь применять данное правило деления при решении числовых выражений и составных задач, сравнении числовых выражений.
Развивающая: содействовать развитию аналитического мышления через организацию исследовательских ситуаций, направленных на анализ, сравнение, обобщение, умение делать выводы, строить рассуждение ;
Воспитательная: способствовать формированию навыков учебного взаимодействия, доброжелательного отношения друг к другу.
Тип урока: урок усвоения новых знаний и способов действий.
Ход урока
I.Организационно-мотивационный этап.
Друзья мои, я очень рада
Войти в приветливый ваш класс,
И для меня уже награда,
Вниманье ваших умных глаз.
– Ребята! Я очень рада встрече с вами. И мне хотелось бы разделить эту радость с вами. Я запишу это так:
Радость : 22 =
Почему я разделила на 22? Назовите компоненты деления в этом примере. (Делимое- радость, делитель – 22). Что получится в частном? (Радость).
– Если мы разделим радость, её станет больше или меньше? Объясните.( Вешаю на доску слово радость)
-В таком случае, я предлагаю разделить радость вам друг с другом, выразив её улыбкой. Подарить её мне, друг другу, гостям. И в хорошем настроении начать урок.
-Вы, наверное, догадались, что я не просто так заговорила о делении. Сегодня мы откроем новый способ деления. Для начала подготовим тетради к работе и запишем дату, классная работа.
II.Актуализация знаний учащихся
– Давайте проверим, хорошо ли вы знаете табличные случаи деления?
1) Посмотрите на доску, я записала ряд чисел 18, 36,7, 35, 42, 48, 28,49, 56, 60, а ваша задача- выписать только те, которые делятся:
1вариант – на 6 2 вариант на – 7.
– Время выполнения задания одна минута. (песочные часы)
– Давайте проверим выполнение задания, сверим с ответами на слайде:
18, 36,42,48,60. 7, 35, 28,42,49, 56.
– Запишите под каждым числом результат деления на это число.
-Проверим ответы: На слайде
18, 36,42,48,60. 7, 28, 42, 35, 49, 56.
3, 6, 7, 8, 10. 1, 4, 6, 5, 7 , 8.
– Поднимите руки, кто справился правильно со всеми примерами на деление?
– Перед вами лежат оценочные листы. В левом столбике написаны задания, которые вы будете выполнять, далее максимальный балл, которым оценивается задание. А в последнюю колонку вы будете вносить свои результаты.
– Этим ребятам нужно обязательно ещё повторять таблицу деления и умножения.
– Давайте поддержим тех, кто справился с ошибками и поделимся с ними своей удачей. Как же это сделать? (пожелать удачи, пожать за руку, тронуть за плечо)
Вывешиваю слово удача на доску в это время. – Пусть удача сопутствует вам в дальнейшей работе на уроке.
2) Постановка темы и цели урока.
– А сейчас, ребята, я предлагаю рассмотреть два буквенных выражения (вывешиваю карточки):
(а+в):с
(а+в) · с
-Кто может прочитать их, пользуясь математическими терминами.
– Какое из этих буквенных выражений вам знакомо? Какое свойство умножения вы знаете? Кто может объяснить это свойство? (Выходит ученик и дописывает =а·с+в·с)
– Давайте сравним два выражения: -Что у них общего? (сумма) – А чем отличается?
– Может кто-то сможет прочитать запись «математическим» языком? (деление суммы на число)
-Вы догадались, чему мы будем учиться на уроке?
III. Этап усвоения новых знаний и способов действий
– Я вам предлагаю придумать задачу по рисунку на слайде:
(Трое детей хотят разделить поровну 18 ирисок и 12 леденцов.
Сколько конфет получит каждый?)
– Предлагаю вам найти способ решения этой задачи, объединитесь в группы и запишите решение на больших листах. Время на обсуждение и запись решения – 2 минуты.
(Записи на листах вывешивают на доске, представители групп объясняют способ решения). Возможно это будет по действиям, тогда предложу детям составить выражения.
(18+12):3= 30:3=10 18:3+12:3= 6+4=10
– У нас получилось два способа решения задачи.– Можно ли поставить знак равенства между двумя способами,если ответ получился одинаковый? Слайд
– Давайте запишем в тетради:(18+12):3=18:3+12:3
– Как можно разделить сумму на число?
– Сраните свой вывод с выводом учебника на с.18 Прочитаем хором.
– Кто из вас сможет записать способ деления суммы на число в виде буквенного выражения?
– Чем это правило отличается от правила умножения суммы на число?
– Ребята,мы сейчас вместе открыли правило. А что нам в этом помогло? (совместная работа или сотрудничество)
Сотрудничество.
Физминутка
– Вы очень хорошо потрудились , поэтому я предлагаю отдохнуть.
IV. Этап первичной проверки понимания изученного
– А теперь, ребята, давайте проверим, насколько хорошо вы запомнили правило деления суммы на число и вместе решим примеры №1 с. ( 2 примераскомментированием у доски)… Кто пойдёт к доске?
(8+4) : 2 = 8: 2 + 4 : 2 = 6
– Ребята поднимите руки,кто понял задание и может применить способы решения самостоятельно? Тогда я предлагают разделиться на варианты: 1 вариант выполнит 1 сроку, 2 вариант – 2 строку самостоятельно. – Может кто-то хочет это задание выполнить у доски с обратной стороны.( выходят 2 ученика)
– Если кому- то будет не понятно, я могу оказать вам помощь , только поднимите руку. ( В этот момент вывешиваю слово помощь на доску).
-Давайте сверим выполнение задания на доске и в ваших тетрадях . Первый вариант проверяет Васю, а второй вариант Петю. (Самопроверка?) Оцените себя в оценочном листе.
– Пришлось ли вам воспользоваться моей помощью или помощью друг друга?
V. Этап закрепления новых знаний и способов деятельности
– А сейчас, ребята я вам предлагаю решить ещё одну задачу – №5. с. 19 учебника. – Давайте прочитаем задачу вслух
– Что известно в задаче? Какой вопрос?
– Выберите схему к задаче. -Какие слова в задаче подсказывают выбор схемы? ( в 3 раза больше –это 3 равных отрезка у Милы,1 отрезок у Тимы)
– Вывешиваю схему на доске .
– Что обозначает число 4? (на столько больше слив съела Мила)
-Сколько частей занимают эти 4 сливы на схеме?(2 части)
– Можно ли найти в таком случае 1 часть? Каким действием? (4:2=2)
– Значит одна часть равна 2 сливам. – У кого две сливы? ( У Тимы)
-А как узнать сколько слив у Милы? Можно ли использовать другой способ решения? ( 2·3=6 или 2+4=6)
Давайте составим план решения:
2 способа:
4
2
?
4
?
Запишите решение задачи самостоятельно с пояснением любым способом.
– Я бы хотела у вас спросить , а если Мила не съест сливы, а решит поделиться с Тимой, то сколько ей надо отдать Тиме слив? ( предположение детей)
– Как можно это показать на схеме?( переставить одну часть)
– Как это характеризует Милу? (Не жадная, а по другому – щедрая)
Вывешиваю слово щедрость на доску.
VI. Этап контроля и самоконтроля знаний и способов действия.
– Давайте вспомним с каким правилом познакомились? Как действует правило?
– Предлагаю вам задание для самостоятельной работы. Время выполнения 2 мин.
Задание на карточках:
1вариант: 2 вариант:
Вычисли, используя правило деления суммы на число:
(16+12):4= (24+ 36):6 =
(30 +19) : 7= (50+14):8=
– Смогли вы заметить «ловушку»? В каком примере?
– Как вы справились с последним примером? ( применили другой способ) – Какой вывод сделаем? Всегда ли можно при делении суммы на число применить новое правило? (Каждое слагаемое обязательно должно делиться на число).
Предлагаю вам творческое задание – самим подобрать подходящие слагаемые.
На доске 1вариант – (…+…) : 7 2 вариант (…+…) : 8 =
– Оцените себя.
Предлагаю по желанию выставить отметки в дневники.
VII. Этап подведения итогов учебного занятия
Задание со знаком? с19.
– Какой пример соответствует теме сегодняшнего урока?
– Какое правило узнали?(правило деления суммы на число)
– При каких условиях действует?(если каждое слагаемое делится на число)
VIII. Этап информации о домашнем задании
– Вы сможете закрепить применение этого правила выполнив задание № 1,с. 19
– А на закрепление умения решать задачу предлагаю выбрать ещё №2 по желанию.
ІХ. Этап рефлексии
Обратимся к оценочному листу … и делаем выводы.
– А что ещё мы сегодня с вами смогли разделить между собой? (радость, удача, сотрудничество, помощь)
– Я думаю, что если вы будете так продолжать делить друг с другом все чувства и дела, то у вас будет очень дружный и крепкий класс.
Сегодня у нас начинается грандиозная стройка. Мы будем строить новый дом «Дом-Знаний». И от того каким он будет зависит только от вас. Каждое выполненное задание на сегодняшнем уроке – это этаж нашего дома. Готовы? Начинаем!
А что нужно заложить прежде, чем строить дом?
. Закладка фундамента.
Устный счет.
– Начнем наш урок с веселого счета.
перед вами цифро- гусеница.
Как быстрее посчитать сумму всех чисел, из которых она состоит? (ищем способ решения данного выражения)
9 * 8 + 6 * 3 + 1 + 8 = 72 + 18 + 9 = 99
1. В одном ряду сидели 23 ученика, в другом – на 5 учеников меньше. Сколько учеников сидело во втором ряду? (18 учеников)
2. 8 пар танцуют польку,
А всех танцоров сколько? (16)
3. После того как 19 человек ушли в поход, в отряде осталось 7 человек.
Сколько всего человек в отряде? (12 человек)
1. Ребята, давайте вспомним, что такое умножение? ( одно из основных арифметических действий, при котором одно число умножается на другое).
Другими словами умножение- это математическая операция, которая заключается в сложении одинаковых слагаемых, определённое количество раз.
2. Как называются компоненты действия умножения? (вывешиваю таблицы)
Дети: Умножаемое- множитель-произведение
3. Какое математическое действие можно назвать обратным действию умножению? (деление)
4. Как называются компоненты действия деления?
Дети: Делимое-делитель-частное
Строительство 1 этажа.
Информационный центр.
Ребята, как вы думаете какая тема сегодняшнего урока??
Какие цели поставим себе на урок??
Работа над задачей
Да, ребята, верно, мы будем учиться решать задачи на умножение и деление.
Открываем тетради, записываем число и классная работа.
Мальчик и девочка принесли 27 морковок для кроликов и разложили поровну по 9 штук в каждую клетку. Во сколько клеток дети разложили морковку? . Объяснение на наглядной основе.
–О ком говорится в условии? (О мальчике и девочке)
– Что они делали? (Принесли морковку для кроликов)
– Что они сделали с морковкой? (Разложили кроликам в клетки)
– А что значит разложили?
– Как разложили морковь? (Поровну в каждую клетку, по 9 штук)
– Что обозначает число 27? 9
-Сможем ответить на вопрос задачи?
– При помощи какого действия решим задачу?
Составляем краткую запись и у доски решает ребенок.
Итак, информационный центр построен, пора переходить к строительству следующего этажа.
Открываем учебник на стр.109. №1
V.Строительство 2 этажа.
Решение задач
1) А сейчас мы попробуем решить следующую задачу.
Прочитайте её и обсудите в парах.
Обратите внимание у вас есть схема к данной задаче, на нее вы можете опираться при решении задачи.
Проверка(фронатально)
Что нам известно в задаче?
Что значит сорвали с 4 клумб по 6 цветков?
Что надо узнать?
Что надо знать, чтобы ответить на вопрос задачи?
Что будем узнавать сначала? Каким действием? ( обратитесь к схеме задачи)
Что узнаем потом? Каким действием?
Записываем решение задачи в тетрадь.
2) Решаем задачу под № 2 С.110 (самостоятельно)
Проверка(фронтально)
Прочитайте задачу. Посмотрите на схему к задаче и на запись, которая находится под задачей в зеленой рамке.
Что нам известно в задаче?
Что надо узнать?
Как мы узнаем сколько кг винограда в 1 ящике? Что нужно сделать?
А как узнать сколько кг винограда в 3 таких ящиках?
Ученик записывает решение
на доске .
Итак, строительство идет полным ходом, но нам с вами нужно передохнуть.
Все встали смотрим внимательно и выполняем вместе со мной.
Быстро встали, улыбнулись,
Выше-выше подтянулись.
Ну-ка плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали, сели, встали,
И на месте побежали.
Закончили, все тихо- тихо сели. Продолжаем…
VI. Строительство 3 этажа.
Составление задач по таблице.
Построили 2 этажа нашего дома. А чтобы построить следующий этаж дома нужно научиться составлять задачи по таблице и решать их.
С.110 № 3 (а,б)
По вариантам выполняем
проверка (фронтально)
Дети составляют задачу. Итак посмотрите на первую линию задачи .
-Что нам известно, что дано? ( известно, что цена апельсина 60 тг за 1 шт., и количество апельсинов 4 штуки)
-А что необходимо узнать? ( стоимость 4 апельсинов)
– Как мы узнаем стоимость апельсинов? ( цену умножим на количество)
Верно.
Обратите внимание на вторую строку задачи
-Что нам здесь известно? ( количество бананов 3 шт)
– Посмотрите внимательно, а еще нам что-нибудь известно? ( да, стоимость, ведь она одинаковая и для апельсинов и для бананов)
– Как мы узнаем сколько стоит 1 банан? ( стоимость поделим на количество)
Записываем таблицу в тетрадь, решает ученик у доски
Подводим детей к обобщению что
По цене и количеству предметов можно узнать их стоимость, по стоимости и цене узнать количество, по стоимости и количеству — цену.
Б) Разбор задачи аналогичен разбору предыдущей задачи .
Подводим детей к обобщению что
По общей массе и количеству можно узнать массу 1 предмета, по массе 1 предмета и общей массе можно узнать количество предметов, по массе 1 предмета и по количеству можно узнать общую массу.
VII. Строительство 4 этажа.
Чтобы построить 4 этаж нашего дома нужно выполнить…
Задание на С.110 № 4 (3-4 ст)
2 ученика работают у доски, остальные в тетрадях
Пока выполняем задание
В это время С/р на листочках (выбранные ученики 5 детей).
VIII. Возводим крышу.
Домашнее задание: откройте дневники, запишите домашнее задание на следующий урок математики стр.110 № 3 (в)
ИЛИ
№ 8 на стр.111
Глядя на построенный дом, давайте вспомним что мы сегодня делали на уроке?
-Что повторили?
-Чему научились?
– Какие задания на сегодняшнем уроке показались вам наиболее сложными, интересными?
На партах у каждого лежат смайлики, поднимите тот смайл, который характеризует ваше отношение к сегодняшнему уроку.
Вы считаете, что урок прошёл для вас плодотворно, с пользой.
Вы научились и можете помочь другим.
Вы считаете, что научились решать задачи на умножение и деление, но вам ещё нужна помощь.
Вы считаете, что было трудно на уроке.
Спасибо за работу!
Урок окончен!
Конспект урока по математике
Дата______________.
Тема:. Меры времени:час,сутки.
Цель урока: Сформировать представление о единицах времени.
Задачи:
обучающие: познакомить с новой единицей времени: часом; сутками, совершенствовать вычислительные навыки;
развивающие: развивать умение наблюдать, сравнивать;
воспитательные: воспитание самостоятельности.
Тип урока: изучение нового материала.
Формировать познавательные, коммуникативные, регулятивные, личностные УУД.
Оборудование: учебник, счетный материал., часы.
Ход урока
Вступительная часть
Орг.момент
НПП
Давайте, ребята, учиться считать,
Чтобы скорей математиком стать.
Ему по плечу любая работа,
Но прежде разучим правила счёта.
Звонок прозвенел. Он позвал на урок.
Пора! Тишина! К нам наука идёт…
3. Минутка чистописания.
– Если внимательно послушаешь загадку, то узнаешь какую цифру нужно написать.
Вьется по ветру коса,
А средь спинки полоса.
(Цифра 7)
-Запиши в тетради одну строчку цифры 7.
Проверка домашнего задания
Основная часть
Актуализация знаний обучающихся
– Какое сейчас время года?
– Какой месяц?
– Какой день недели?
– Какое сегодня число?
Устный счет.
– Давайте вспомним какие числа вы уже знаете.
Считаем от 1 до 20, от 20 до 1.
Считаем по цепочке от 10 до 20 и обратно.
Назовите соседей числа 10, 15, 18.
Назовите предшествующее число числу 11, 14, 19.
Назовите последующее число 12, 17, 19.
Сравнить числа 10 и 11; 19 и 9; 12 и 14.
Сообщение темы и цели урока.
Видеоролик меры времени
Работа по теме
-Что всегда идет, а с места не сойдет?
-Правильно, это часы.
Знакомство со строением часов.
Рассмотрим моделб циферблата и настоящие часы.
Две сестрицы друг за другом
Пробегают круг за кругом.
Коротышка только раз,
Та, что выше, каждый час.
– О чем здесь идет речь? (О стрелках часов.)
– Что за коротышка бегает по кругу? (Часовая стрелка.)
– А сестрица, что повыше? (Минутная стрелка.)
-Почему длинную стрелку называют минутной, а короткую – часовой?
-Одинаково ли двигаются по кругу минутная и часовая стрелки?
-Какая быстрее?
– Какая медленнее?
-Какая единица времени больше, час или минута?
– Сколько минут проходит минутная стрелка за один час?
– За один час минутная стрелка пройдет 60 минут.
В наше время началом суток считается полночь. Когда начинаются новые сутки? (0 часов 0 минут – полночь).
Рассмотрите макет часов. Сколько цифр на часах?
Сколько часов отсчитывает часовая стрелка, проходя один круг? Два круга?
За сутки часовая стрелка дважды обходит циферблат.
1 сутки = 24 часа
За сутки, то есть 24 часа, наша планета Земля успевает сделать один виток вокруг своей оси.
Мы запомнили все враз:
60 минуток – это …(час)
Я твержу сестре Анюте:
60 секунд в … ( 1 минуте)
Повторение соотношений между единицами времени
год = 12 месяцев (повторение по порядку «цепочкой»), 365 или 366 дней
месяц = 28(29), 30 или 31 день
неделя = 7 дней (по порядку «цепочкой»)
сутки = 24 часа
Работа по учебнику _________________
Физкультминутка
Продолжение этапа закрепления полученных знаний.
Упражнение в решении примеров _________
Домашнее задание:
Рефлексия:
Интересно, ребята, вам было на уроке?А что вызвало ваш интерес, какие задания? Были ли у вас затруднения? В чем?Продолжите предложения:
Я научился …
Мне было трудно, когда…
Мне было интересно….
Подвести итоги .
Оценить работу на уроке.
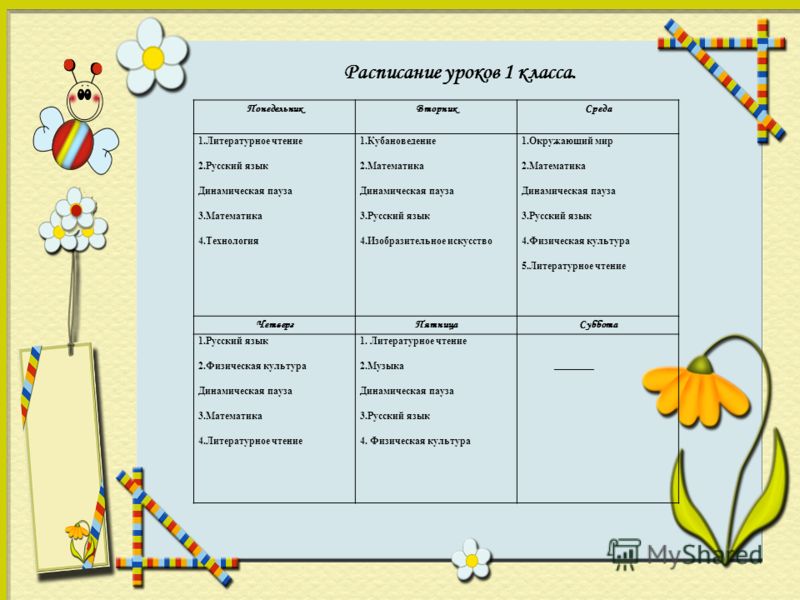
1 класс
1 урок – 08.30ч. – 09.05ч.
2 урок – 09.15ч. – 09.50ч.
3 урок – 10.05ч. -10.40ч.
4 урок – 10.55ч. – 11.30ч.
5 урок 11.40ч. – 12.15ч.
2-4 классы
1 урок – 08.30ч.- 09.15ч.
2 урок – 09.25ч. – 10.10ч.
3 урок – 10.25ч. – 11.10ч.
4 урок – 11.25ч. – 12.10ч.
5 урок – 12.20ч. – 13.05ч.
6 урок – 13.15ч. – 14.00ч.
7 урок – 14.10ч. – 14.55ч.
5-7 классы
1 урок – 08.00ч. – 08.45ч.
2 урок – 09.
00ч. – 09.45ч.
3 урок – 09.55ч. – 10.40ч.
4 урок – 10.55ч. – 11.40ч.
5 урок – 12.00ч. – 12.45ч.
6 урок – 12.55ч. – 13.40ч.
7 урок – 13.50ч. – 14.35ч.
8 урок – 14.45ч. – 15.25ч.
8-11 классы
1 урок – 08.15ч. – 09.00ч.
2 урок – 09.10ч. – 09.55ч.
3 урок – 10.10ч. – 10.55ч.
4 урок – 11.10ч. – 11.55ч.
5 урок – 12.10ч. – 12.55ч.
6 урок – 13.05ч. – 13.55ч.
7 урок – 14.00ч. – 14.45ч.
8 урок – 14.55ч. – 15.35ч.
Отъезд:
Понедельник, пятница – 14.55ч.
Вторник, среда, четверг – 15.45ч.
Школа, школа – пристань века! Школа, школа – наш причал! Школа – дом для человека и начало всех начал!!!
Этап урока | Деятельность учителя | Деятельность учащихся |
Мотивация к учебной деятельности. Приём: высказывание добрых пожеланий учащимся. | Цель: включение учащихся в деятельность на личностно-значимом уровне; создание положительного эмоционального настроя. Вдохнём три раза глубоко, Весною дышится легко. Все друг другу улыбнитесь, За парту правильно садитесь. – Откройте тетради и запишите число. Слайд 1 | Цель: самоорганизация. Приветствуют учителя. Проверяют готовность к уроку. Записывают в тетради дату |
Актуализация знаний и метапредметных умений. Метод: подводящий диалог, самооценка. | Цель: актуализация изученных способов действий, достаточных для построения новых знаний и их обобщения. -Посмотрите на числовые выражения (Слайд2) 2 + 2 + 2 + 2+ 2 4 + 4 + 4 + 4+4 5 + 5 + 55 + 5 6 + 6 + 6 -Найдите лишнее выражение. -Почему вы выбрали именно третье выражение? -Что общего во всех выражениях? -Каким действием можно заменить сумму одинаковых слагаемых? – Замените, запишите в тетрадь только произведения. -Считая устно, проверьте, все ли равенства являются верными.
| |
Постановка проблемы. | У вас на партах лежат конверты. Проанализируйте содержимое конвертов, что из этого для вас является известным, а что вы уже знаете. То, что знаете, положите обратно в конверт. А то, что для вас является новым, оставьте перед собой. Слайд 4 -Что тогда необходимо будет узнать? Что такое переместительное свойство умножения? Что произойдет, если поменять местами множители. – Чему мы тогда с вами будем учиться? | |
Открытие новых знаний. | Поиграем в солдатиков. Работать будем в парах.У вас на столах в конвертах лежат солдатики Первый вар раскладывает солдатиков в 2 шеренги по 5 солдатиков, второй вар в 5 рядов по 2 солдатика. -Проверка со слайда. Запишите выражение соседнего ряда. – Сравните и сделайте вывод, число солдатиков на 1 ряду и на 2ом ряду разное или одинаковое? -Какой знак поставим между произведениями? 5*2=2*5 -Что вас удивило? Это какое свойство? А у вас на карточках, как оно называется? (коммуникативное) (Множители поменялись местами, а значение произведений одинаковое. ) | Учащиеся выполняют задание в парах – В 2 шеренги по 5 солдатиков в каждой. – В 5 рядов по 2 солдатика в каждом. Записывают задание в тетради: 5х2 2х5 Ответы детей: -Значение этих произведений должны быть равны, так как количество солдатиков не изменилось. Работают в парах. 5х2=5+5=10 2х5=2+2+2+2+2=10 -Правы оба. -Вывод: от перестановки множителей значение произведения не меняется |
Первичное закрепление. Метод: самооценка. Приём: «столкновение разных мнений». | -Мы исследователи! Проверим, верно ли это свойство для других выражений? 7•2 2•7 Слайд 8 -Можно ли утверждать, что значения этих произведений равны? Почему? Запишите соответствующее равенство двух выражений. 7•2 = 2•7 -Проверьте справедливость этого равенства, вычислив значение каждого из произведений с помощью сложения. 7 • 2 = 7 + 7 = 14 2 • 7 = 2 + 2 + 2 + 2 + 2+2+2= 14 -Какой вывод сделали? От перестановки множителей значение произведения не изменяется. (Слайд 9) -Закройте глаза и проговорите это правило про себя. ЗАРЯДКА ДЛЯ ГЛАЗ Слайд 10 | Цель: проверить выполнение переместительного свойства для действия умножения, сформулировать вывод. |
Включение нового знания в систему знаний. Метод: самооценка. | Цель: создать условия для включения нового знания в систему знаний. Задание из учебника №2 – Каким свойством вы пользовались при выполнении этого задания? | Цель: учиться применять полученные знания при выполнении типовых заданий. Учащиеся решают задания. Самопроверка, самооценка. Ответы детей: переместительным свойством умножения. |
Самостоятельная работа. Методы: самооценка, самоконтроль. | Цель: закрепление умений, отработка вычислительных навыков с применением – Пользуясь полученными знаниями. Выполните задание, самостоятельно. – Восстановите равенства, используя правило перестановки множителей. (Слайд 11) 2 • 8 = 8 • 2 9 • 4 = 4 • 9 5 • 3 = 3 • 5 8 • 4 = 4 • 8 5 • 9 = 9 • 5 3 • 7 = 7 • 3 САМОПРОВЕРКА Слайд 12 | Цель: самооценка полученных результатов. Учащиеся выполняют задание самостоятельно. Фронтальная проверка. |
Закрепление нового материала. | Цель: закрепление и применение полученных знаний. Работа с заданиями в учебнике №3 | |
Рефлексия деятельности. Итог урока. Метод: словесный | Цель: подвести итог успешности владения содержанием урока, самооценка результатов деятельности. – Какую задачу ставили на уроке? Удалось достичь поставленной цели? – Какие получили результаты? Кому нужно поработать над этой темой? – Где можно применить новое знание? Оцените свою работу Слайд 13 | Цель: выявление степени соответствия поставленной цели и результатов деятельности, определение цели последующей деятельности, самооценка. |
Проверим, правильно ли сформулировали правило на других выражениях.
Откройте учебник на странице 62.
Задание 202. под цифрой. 1) 8∙6 как найти значение выражения?
Найдите значение выражения.
6∙8 как найти значение выражения?
Какие значения выражений получились?
В чем убедились?
Выполните задание под цифрой 2 самостоятельно.
6∙3 3∙6
Какой значение получилось?Посмотрите задание под цифрой 5. Как будем вычислять значение произведения?
1 ученик у доски.
Найдите значение выражений под цифрами 6 и 7 самостоятельно.
Под цифрами 8 и 9 выполним устно.
0∙12 Замените сложением
12∙0
Почему?
15∙1
Почему?
1∙15
Какой вывод можно сделать?
Прочитайте правило, которое написано в учебнике.
Повторите несколько раз. Его нужно выучить.
Задание 204. Прочитайте задание, что нужно сделать?
Прочитайте первое выражение.
Запишите в тетради, а я на доске. Что нужно сделать, для того, чтобы выполнить умножение?
А удобно заменять? Почему?
Что нужно сделать, чтобы было удобно умножать?
Что для этого нужно использовать?
Почему можно использовать переместительное свойство?
Запишем 2∙14=14∙2
Как умножить?
14+14=28
Запишем результат умножения:
14∙2=28
Значит 2∙14 сколько получится?
Следующее выражение у доски.
Отступите 3 клеточки от первого решения и запишите следующее.
Первый вариант находит значение выражения 4∙20, второй вариант 5∙15. Проверить. Назовите произведение.
Для того чтобы найти значение этих выражений, чем нужно пользоваться?
Значит, когда будем пользоваться переместительным свойством умножения?
Сейчас будем применять переместительное свойство умножения для сравнения выражений.
На листочках. (записано на доске).
1 ученик у доски. Прочитайте первое выражение.
прочитайте второе выражение.
Как называются выражения слева и справа?
Какие слагаемые в сумме слева? а права?
Как можно заменить сложение одинаковых слагаемых?
Как заменить сумму слева?
Почему?
Запишите во второй строке, как заменить выражение справа.
Прочитайте выражение, которое получили.
Какой знак нужно поставить?
Почему?
Поставьте знак, между выражениями.
1 человек у доски с объяснением самостоятельно.
Сравните остальные выражения самостоятельно.
Проверить.
8 взять слагаемым 6 раз.
8∙6=48 8+8+8+8+8+8=48
6 взять слагаемым 8 раз.
6∙8 6+6+6+6+6+6+6+6
48, одинаковые значения.
От перестановки множителей значение произведения не изменяется.
18.
С помощью калькулятора.
12∙14=168
14∙12=168
6) 297
7) 126
0+0+0+0+0+0+0+0+0+0+0+0=0
Получится 0.
При умножении любого числа на 0 получается 0.
При умножении любого числа на единицу получится то число, которое умножали.
1+1+1+1+1+1+1+1+1+1+1+1+1+1+1
Читают правило.
Найти значение выражений.
2∙14
Заменить сложением.
Нет. Много слагаемых.
Нужно переставить множители, чтобы второй множитель был меньше первого.
Переместительное свойство умножения.
От перестановки множителей значение произведения не изменится.
Заменить умножение сложением.
2∙14=14∙2
14+14=28
14∙2=28
2∙14=28
Записывают в тетради.
28.
Записывают решение.
5∙13=13∙5
13+13+13+13+13=65
13∙5=65
5∙13=65
4∙20=20∙4
20+20+20+20=80
20∙4=80
4∙20=80
Переместительным свойством умножения.
При вычислении значения произведения. При умножении однозначного числа на двузначное.
9+9
2+2+2+2+2+2+2+2+2
Суммы.
Одинаковые.
Умножением.
9∙2.
9 повторили слагаемым 2 раза.
2∙9 2 повторить слагаемым 9 раз.
9∙2 и 2∙9.
Равно.
От перестановки множителей значение произведения не изменяется.
2) = 3)= 4)> 5)=
Конспект урока математики в 3 классе
Сочетательное свойство умножения
Цели: ввести понятие сочетательного свойства умножения и учить его использовать; обобщать и закреплять навыки умножения многозначных чисел; развивать мышление, познавательную активность, память; воспитывать аккуратность, внимательность, ответственность, активность, формировать интерес к изучению математики.
Оборудование: учебник по математике, доска, мел, карточки с заданиями, компьютер, мультимедийный проектор.
Ход урока
Организационное начало.
– Ребята, чем мы занимаемся на уроках математики?
– Для чего нам нужна математика?
– Где можем применить эти знания в будущем? Значит, наша цель какая?
– Тема нашего урока: «Сочетательное свойство умножения».
– Вы что-нибудь об этом знаете? Чтобы узнать, давайте повторим ранее изученное.
2. Основная часть.
1) Устные упражнения.
500 · 2 100· 8 200 · 7 400 ·7 500· 9
600 · 3 500 · 4 700 · 9 500 · 5 600 · 8
800· 4 900 · 8 500 · 8 400 · 6 900 · 4
300 · 5 400 · 4 600 ·6 700 · 3 600 · 9
Вывод:
– Давайте сделаем вывод, как мы умножаем многозначное круглое число на однозначное? Сотни умножаются на число так же, как и единицы.
2) Решение задач (устно).
а)В корзине 40 груш, а на тарелке – в 5 раз меньше. Сколько груш на тарелке?
б)Ласточка живет 14 лет, а скворец – на 4 года дольше. Сколько лет живет скворец?
в)Отцу 45 лет, а сын в 5 раз моложе. Сколько лет сыну?
г)В одной коробке 16 конфет, во второй – на 4 конфеты больше. Сколько конфет во второй коробке?
Основная часть.
– Как можно вычислить число кубиков в этом квадрате?( можно посчитать число кубиков, умножить число кубиков по вертикали на число кубиков по горизонтали и наоборот ) СЛАЙД 1
– Как называется это свойство умножения? ( переместительное свойство умножения )
На доске запись: 6 · 5 = 5 · 6
а · б = б · а – переместительное свойство умножения.
– Сегодня мы познакомимся с сочетательным свойством умножения.
– Посмотрите на конструкцию, составленную из кубиков. СЛАЙД 2
– Как можно вычислить число кубиков в этой конструкции? Давайте представим ее состоящей из столбиков по 3 кубика. Число таких кубиков легко найти, перемножив числа 4 и 5.
3 · ( 4 · 5) = 60
– А можно вычислить и по – другому, воспользовавшись тем, что в каждом из 5 слоев 12 кубиков.
( 3 · 4) · 5 = 60
На доске запись: 3 · ( 4 · 5) = ( 3 · 4) · 5
а · (б · с) = (а · б) ·с – сочетательное свойство умножения.
– Чем похожи выражения в левой и правой части? (одинаковые множители)
– Чем отличаются? (по – разному стоят скобки)
Чтение правила на стр. 87
– А теперь давайте попробуем применить сочетательное свойство умножения при решении примеров № 285
– В данных выражениях расставьте скобки так, чтобы упростить вычисление значений этих выражений.
9 · (2 · 5) = 90 (4 · 5) · 7 = 140 8 · (25 ·4) = 800 9 · (4 · 5) = 180
(25 · 2) · 4 = 200 (4 · 5) · 6 = 120 (5 · 4) · 8 = 160 2 · (5 · 10) = 100
– Какое свойство применили при решении примеров?
Решение задачи № 291
Запиши с помощью произведения трех множителей число учеников в классе, если в каждом классе стоят парты в 3 ряда по 5 парт в каждом, а за каждой партой сидит по 2 ученика. Вычисли удобным способом.
1) 2 · 5 = 10 (уч.) – в одном ряду.
2) 3 · 10 = 30 (уч.)
2. ( 2 · 5) · 3 = 30 (уч.)
3. 2 · ( 5 · 3) = 30 (уч.)
Ответ: в классе 30 учеников.
Вывод : сочетательное свойство умножения применяется и при решении задач.
Физминутка.
– Используя сочетательное свойство умножения, запишите выражение, значение которого равно значению данного выражения.
(5 · 8) · 2= __ · (__ __)
(25 · 5) · 2 = __ · (__ __)
(5 · 7) · 10= __ · (__ __)
(8 · 5) · 10= __ · (__ __)
Нужно выражения расставить так, чтобы между ними можно было поставить знак равенства.
На доске:
15 · (10 · 6) (20 · 5) · 3 (15 ·10) · 6
18 ·(5 · 8) 20 · (5 · 3) (18 · 5) · 8
3.Заключительная часть.
1)Подведение итогов.
– Что нового узнали на уроке?
– С каким новым понятием познакомились?
– Что для вас было сложно?
– Что было легко?
2) Оценивание.
ПРОЕКТ УРОКА в 3 классе
по Математике
ФИО Федотовских Галины Олеговны
Тема: «Переместительное свойство умножения»
Образовательная программа: Давыдов-Эльконин
Тип урока: Урок формирования новых знаний
Тема урока: Переместительное свойство умножения
Цель: Сформировать умение использовать переместительное свойство умножения
Задачи урока
Образовательная:
– Знать переместительное свойство умножения
– Уметь применять переместительное свойство умножения
– Понимать переместительное свойство умножения и использовать его в учебной деятельности
Воспитательная:
– Воспитывать интерес к изучению математики, показать важность изучения математики, связь данного предмета с другими
Развивающая:
– Развивать вычислительные навыки, математическую речь, умение анализировать, выделять главное, обобщать, доказывать, развивать навыки контроля, самоконтроля и взаимоконтроля
ПРОЕКТ УРОКА в 3 классе
по Математике
ФИО Федотовских Галины Олеговны
Тема: «Переместительное свойство умножения»Образовательная программа: Давыдов-Эльконин
Тип урока: Урок формирования новых знаний
Тема урока: Переместительное свойство умножения
Цель: Сформировать умение использовать переместительное свойство умножения
Задачи урока
Образовательная:
– Знать переместительное свойство умножения
– Уметь применять переместительное свойство умножения
– Понимать переместительное свойство умножения и использовать его в учебной деятельности
Воспитательная:
– Воспитывать интерес к изучению математики, показать важность изучения математики, связь данного предмета с другими
Развивающая:
– Развивать вычислительные навыки, математическую речь, умение анализировать, выделять главное, обобщать, доказывать, развивать навыки контроля, самоконтроля и взаимоконтроля
Основное содержание темы, термины и понятия
Содержание темы предполагает:
Умение применять переместительное свойство умножения
Организация образовательного пространства
Межпредметные связи:
Оборудование:
Презентация, доска, учебник
Ресурсы:
Интернет
Учебник за 3 класс
Формы работы:
И
. ю
ндивидуальная формаПланируемые результаты
Личностные | Метапредметные | Предметные | ||
Познавательные | Регулятивные | Коммуникативные | ||
Мотивация к обучению и познанию | Делать выводы в результате совместной работы учителя и класса | Умение работать по предложенному учителем плану | Умение оформлять свои мысли в устной форме | Умение использовать переместительное свойство умножения |
Технология изучения темы
Этап I. Самоопределение к деятельности
Цель | № | Ситуативные задания (Деятельность учителя) | Деятельность учащихся | Форма работы |
– Устный счет! 740 – 240 + 5 = 76000 : 1000 = 840 – 40 : 8 = 9600 х 10 = 120 – 20 + 4 х 5 = 500 : 100 х 5 = 70 : 7 + 42 : 6 = 300 : 10 : 10 = 66 – 6 х 9 +1 = |
Этап II. Изучение нового содержания
Цель | № | Учебные задания и методы работы с информацией (Деятельность учителя) | Деятельность учащихся | Форма работы |
– Молодцы, вы все справились с заданием! – Посмотрите на доску. А такое вы сможете решить? 3756 x 2 -Откройте свои тетради, запишите число. Классная работа! – Вычислите у себя в тетрадях – Кто готов поднимите руки. – Кто выйдет к доске и решит? – Посмотрите внимательно. У всех ли так же записано?! – Есть ли у вас вопросы? – Хорошо, я и не сомневалась, что вы решите его. – А как вы поступите если нужно вычислить такое произведение? 2 x 3756 – С помощью сложения найти результат можно но не удобно -Тогда у меня возникает вопрос, будут ли равны произведения? 3756 x 2 и 2 x 3756 – И чтобы ответить на вопрос, нужно сравнить способы действия при измерении. Для этого начертите такую схему |
Этап III. Диагностика качества освоения темы
Цель | № | Варианты заданий (Деятельность учителя) | Деятельность учащихся | Форма работы |
– 2 раза – Какую величину мы измерили? (площадь) – Мы измерили ее разными способами, а значит ли это что: a • b = b • а Хорошо. Тогда скажите равны ли произведение 3756 x 2 и 2 x 3756 Действительно. Поэтому мы с полной уверенностью можем сказать что 3756 x 2 = 7512 a • b = b • а – Это и есть переместительное свойство умножения ( ОТ ПЕРЕСТАНОВКИ МНОЖИТЕЛЕЙ ПРОИЗВЕДЕНИЕ НЕ МЕНЯЕТСЯ) – Запишите это в тетрадь! |
Этап IV. Интеллектуально-преобразовательная деятельность
№ | Варианты заданий (Деятельность учителя) | Деятельность учащихся | Форма работы | |
– Откройте свои учебники на стр. 50, посмотрите на № 106 – Прочитайте задание. – Решите его самостоятельно. Через % минут буду проверять! – Кто пойдет к доске и объяснит 1е (2е, 3е) равенство? a + b = b + а– переместительное свойство сложения a • b = b • а – переместительное свойство умножения a – b = b – а – вычитание. Как вы думаете, почему оно будет неверным? a : b = b : а – тоже не верно. Почему? – Перейдем к заданию № 107 – Выберете мерку и покажите на схеме с помощью выражения 3•8 – Сравните величины. Какие они? Почему? |
Этап V. Рефлексивная деятельность
Цель | № | Варианты заданий (Деятельность учителя) | Самоанализ и самооценка ученика | Форма работы |
– Что нового вы узнали? – Было ли вам трудно? Где? Придя домой, что вы расскажите родителям об уроке? Спасибо за урок! |
Цель: учить упрощать выражение, содержащее только действия умножения.
Задачи (Слайд 2):
Тип урока: изучение нового материала.
План урока:
1. Организационный момент.
2. Устный счёт. Математическая разминка.
Строка чистописания.
3. Сообщение темы и задач урока.
4. Подготовка к изучению нового маериала.
5. Изучение нового материала.
6. Физкультминутка
7. Работа по закреплению н. м. Решение задачи.
8. Повторение пройденного материала.
9. Итог урока.
10. Рефлексия
11. Домашнее задание.
Оборудование: карточки с заданием, наглядный материал (таблицы), презентация.
ХОД УРОКА
I. Организационный момент
Прозвенел и смолк звонок.
Начинается урок.
Вы зa парты тихо сели
На меня все посмотрели.
II. Устный счёт
– Посчитаем устно:
1) «Весёлые ромашки» (Слайды 3-7 таблица умножения)
2) Математическая разминка. Игра «Найди лишнее» (Слайд 8)
Строка чистописания. Прописать в тетради
числа, чередуя: 45 22
670 9
– Подчеркнуть самую аккуратную запись числа
III. Сообщение темы и задач урока. (Слайд 9)
– Запишите число, тему урока.
– Прочитайте задачи нашего урока
IV. Подготовка к изучению нового материала
а) Верно ли выражение
На доске запись:
(23 + 490 + 17) + (13 + 44 + 7) = 23 + 490 + 17 + 13 + 44 + 7
– Назовите используемое свойство сложения. (Сочетательное)
– Какую возможность даёт сочетательное
свойство?
Сочетательное свойство даёт возможность записывать выражения, содержащие только сложение, без скобок.
43 + 17 + (45 + 65 + 91) = 91 + 65 + 45 + 43 + 17
– Какие свойства сложения мы применяются в данном случае?
Сочетательное свойство даёт возможность записывать выражения, содержащие только сложение, без скобок. При этом вычисления можно выполнять в любом порядке.
– В таком случае как называется ещё одно свойство сложения? (Переместительное)
(2 * 6) * 3 = 12 * 3
– Вызывает ли это выражение затруднение? Почему?(Мы не умеем умножать двузначное число на однозначное)
V. Изучениенового материала
1) Если мы будем выполнять умножение в том порядке, в каком записаны выражения, то возникнут трудности. Что же поможет нам снять эти трудности?
(2 * 6) * 3 = 2 * 3 * 6
2) Работа по учебнику с. 70, № 305 (Выскажи своё предположение о результатах, которые получат Волк и Заяц. Проверь себя, выполнив вычисления).
3) № 305. Проверь, равны ли значения выражений. Устно.
Запись на доске:
(5 • 2) • 3 и 5 • (2 • 3)
(4 • 7) • 5 и 4 • (7 • 5)
4) Сделай вывод. Правило.
Чтобы произведение двух чисел умножить на
третье число, можно первое число умножить на
произведение второго и третьего.
– Расскажите сочетательное свойство умножения.
– Объясните сочетательное свойство умножения на
примерах
5) Коллективная работа
На доске: (8 • 3) • 2, (6 • 3) • 3, 2 • (4 • 7)
VI. Физминутка
1) Игра «Зеркало». (Слайд 10)
Свет мой зеркальце, скажи,
Да всю правду доложи.
Мы ль на свете всех умнее,
Всех забавней и смешнее?
Повторяйте все за мной
Веселые движения физминутки озорной.
2) Физминутка для глаз «Зоркие глазки».
– Закройте глаза на 7 секунд, посмотрите направо, затем налево, вверх, вниз, затем сделайте глазами 6 кругов по часовой стрелке, 6 кругов против часовой стрелки.
VII. Закрепление изученного
1) Работа по учебнику. решение задачи. (Слайд 11)
(с. 71, № 308) Прочитайте текст. Докажите, что это
задача. (Есть условие, вопрос)
– Выделите условие, вопрос.
– Назовите числовые данные. (Три, 6,
трёхлитровые)
– Что они обозначают? (Три ящика. 6 банок, в
каждой банке по 3 литра сока)
– Какая это задача по структуре? (Составная
задача, т. к. нельзя сразу ответить на вопрос
задачи или для решения требуется составление
выражения)
– Тип задачи? (Составная задача на
последовательные действия))
– Решите задачу без краткой записи составлением
выражения. Для этого используйте следующую
карточку:
Карточка-помощница
• ( • )
– В тетради решение задачи можно оформить следующим образом: (3 • 6) • 3
– Можем ли мы решить задачу в таком порядке?
Решение.
(3 • 6) • 3 = (3 • 3) • 6 = 9 • 6 = 54 (л).
3 • (3 • 6) = (3 • 3) • 6 = 9 • 6 = 54 (л )
Ответ: 54 литра сока во всех ящиках.
2) Работа в парах (по карточкам): (Слайд 12)
– Поставь знаки, не вычисляя:
(15 * 2) *4 15 * (2 * 4) (–Какое свойство?)
(8 * 9) * 6 7 * (9 * 6)
(428 * 2) * 0 1 * (2 * 3)
(3 * 4) * 2 3 + 4 + 2
(2 * 3) * 4 (4 * 2) * 3
Проверка: (Слайд 13)
(15 * 2) * 4 = 15 * (2 * 4)
(8 * 9) * 6 > 7 * (9 * 6)
(428 * 2) * 0 < 1 * (2 * 3)
(3 * 4) * 2 > 3 + 4 + 2
(2 * 3) * 4 = (4 * 2) * 3
3) Самостоятельная работа (по учебнику)
(с. 71, № 307 – по вариантам)
1 в. (8 • 2) • 2 = (6 • 2) • 3 = (19 • 1) • 0 =
2 в. (7 • 3) • 3 = (9 • 2) • 4 = (12 • 9) • 0 =
Проверка:
1 в. (8 • 2) • 2 = 32 (6 • 2) •3 = 36 (19• 1) • 0 = 0.
2 в. (7 • 3) • 3 = 63 (9 • 2) • 4 = 72 (12 • 9) • 0 = 0
Свойства умножения: (Слайд 14).
– Зачем нужно знать свойства умножения? (Слайд 15).
VIII. Повторение пройденного материала. «Ветряные мельницы». (Слайд 16, 17)
485
+ 38
523583
+ 38
621681
+ 38
719583
– 38
545545
– 38
507507
– 38
469
Учащиеся выполняют задания по вариантам (двое учащихся решают задания на дополнительных досках).
Взаимопроверка.
IХ. Итог урока
– Чему учились сегодня на уроке?
– В чём же заключается смысл сочетательного
свойства умножения?
Х. Рефлексия
– Кто считает, что понял смысл сочетательного
свойства умножения? Кто доволен своей работой на
уроке? Почему?
– Кто знает, над чем ему еще надо поработать?
– Ребята, если вам урок понравился, если вы
довольны своей работой, то поставьте руки на
локти и покажите мне ладошки. А если вы были
чем-то расстроены, то покажите мне обратную
сторону ладошки.
XI. Информация о домашнем задании
– Какое домашнее задание вы бы хотели получить?
По выбору:
1. Выучить правило с. 70
2. Придумать и записать выражение на новую тему с
решением
Оценки за урок.
181. Заполните пропуски.
1) Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего.
2) В буквенном виде сочетательное свойство умножения записывают так: (ab)c=a(bc).
3) Чтобы число умножить на сумму двух чисел, можно умножить это число на каждое слагаемое и полученные произведения сложить.
4) В буквенном виде распределительное свойство умножения записывают так: a(b+c)=ab+аc.
5) Справедливо распределительное свойство умножения относительно вычитания: если b>с или b=с, то а(b-c)=ab-аc.
182. Вычислите удобным способом.
1) 4*23*25=(4*25)*23=100*23=2300
2) 2*417*5=(2*5)*417=10*417=4170
3) 4*46*5=(4*5)*46=20*46=920
4) 125*729*8=(125*8)*729=1000*729=729000
183. Упростите выражение.
1) 2а*14=(2*14)а=28а
2) 7*6м=42м
3) 4а*9b=(4*9)*(аb)=36аb
4) 5х*3у*4z=(5*3*4)*(хуz)=60хуz
184. Вычислите значение выражения, использую распределительное свойство умножения.
1) 427*74+427*26=(74+26)*427=100*427=42700
2) 716*384+284*384=(716+284)*384=1000*384=384000
3) 918*1235-918*1225=(1235-1225)*918=10*918=9180
4) 56*68+56*19-56*87=(68+19-87)*56=0*56=0
185. Проверьте, верно ли раскрыты скобки. Если задание выполнено неверно, приведите верное решение.
1) 3(а+7)=3а+21 – неверно
2) (8-b)*5=40-5b – неверно
3) 4(2m+3n)=8m+12n – верно
4) 10(17х-11у)=170х-110у – неверно
186. Упростите выражение.
1) 3а+6а=9а
2) 15b+9b=24b
3) 14х+х=15х
4) 18у-5у=13у
5) 10с-с=9с
6) 2а+7а+9а=18а
7) 12к-8к+16к=20к
8) 13d+4d+15=17d+15
187. Упростите выражение и найдите его значение.
1) 25а*4, если а=39
25*39*4=(25*4)*39=100*39=3900
2) 5m*20n, если m=12, n=7
5*12*20*7=(20*5)*(12*7)=100*84=8400
3) 125с*8d, если с=16, d=34
125*16*8*34=(125*8)*(16*34)=1000*544=544000
188. Упростите выражение и вычислите его значение при указанном значении переменной:
1) 17р+43р, если р=18
17*18+43*18=(17+43)*18=60*18=1080
2) 62а-43а, если а=56
(62-43)*56=28*56=1568
3) 38m+17m-44m+m, если m=210
(38+17-44+1)*210=12*210=2520
4) 46с-25с+с+184, если с=25
(46-25+1+)*25+184=22*25+184=550+184=734
189. Вычислите удобным способом.
1) 32*25=8*4*25=(4*25)*8=100*8=800
2) 125*64=125*8*8=(125*8)*8=1000*8=8000
3) 68*50=34*2*50=34*(2*50)=34*100=3400
4) 75*24=75*4*6=(75*4)*6=300*6=1800
190. Вычислите значение выражения, используя распределительное свойство умножения.
1) 82*7=(80+2)*7=80*7+2*7=560+14=574
2) 97*9=(100-3)*9=100*9-3*9=900-27=873
3) 63*8=(60+3)*8=60*8+3*8=480+24=504
4) 78*6=(80-2)*6=80*6-2*6=480-12=468
До сих пор вы много умножали.
Вы что-то заметили?
Умножение – это всего лишь правил!
Правила облегчают изучение умножения! 😎
В этом уроке мы собираемся изучить свойства умножения.
Свойства умножения дают вам правила, которые помогут вам быстро умножать числа.
Вы это уже знаете! Это как-то связано с номером 1.
Вы помните, что происходит с числом, когда оно умножается на 1?
Верно!
Остается прежним.
Свойство идентичности умножения говорит, что число, умноженное на 1 , даст такое же число. Ничего не меняется.
1 x 1 = 1
10 x 1 = 10
25 x 1 = 25
160 x 1 = 160
2,000 x 1 = 2,000
Когда вы видите число, умноженное на 1, вы уже знаете ответ.
Каким бы большим он ни был, ответ все тот же номер! 😎
Какое самое большое число вы знаете?
Умножьте на 1.
Какой ответ?
Это тот же номер!
Посмотрите на эти уравнения.
3 x 4 = 12
4 x 3 = 12
Что вы заметили?
Да, оба уравнения имеют одно и то же произведение.
Эти уравнения показывают нам коммутативность умножения.
Коммутативное свойство говорит, что когда два числа умножаются вместе, они всегда будут давать один и тот же продукт, независимо от того, как они расположены.
Итак, если …
4 x 6 = 24
Что такое …
6 x 4 = ?
Это тоже 24!
Совет: коммутативный звук похож на слово «добираться», что означает «передвигаться».
👉Коммутативность составляет всего около , перемещая вокруг факторов.
Когда вы думаете о коммутативности, подумайте о близнецах!
Благодаря свойству коммутативности количество известных вам фактов умножения просто удвоилось! 😎
Это свойство также связано с порядком номеров.
Ассоциативное свойство говорит, что при умножении 3 или более чисел не имеет значения, как они сгруппированы.
Ассоциативное свойство означает, что продукт останется таким же, даже если порядок группировки будет изменен с использованием круглой скобки .
Если умножить это …
(4 x 2) x 5 = ?
Вы можете сначала умножить это …
4 x 2 = 8
Тогда это…
8 x 5 = 40
👉 Другой способ решения выглядит так …
Обратите внимание, как числа сгруппированы по-разному?
4 x (2 x 5) = ?
Итак, вы сначала умножите это …
2 x 5 = 10
Затем мы умножаем его на первый множитель.
4 x 10 = 40
Смотрите! Оба ответа – 40, даже если группировки были разными.
😀 Совет: когда мы говорим об ассоциативном свойстве, мы используем скобки () , чтобы сгруппировать числа, которые мы умножаем в первую очередь.
( 4 x 2 ) x 5 то же самое, что 4 x ( 2 x 5 )
( 4 x 2 ) x 5 = 4 x ( 2 x 5 )
Произведение этих двух чисел будет умножено на последнее число.
А теперь попробуй потренироваться! 💪
Что такое распределительное свойство? Вы обсуждали определение распределительной собственности в школе, но до сих пор не знаете, что это такое и почему это важно?
Дистрибутивность – это ключевое математическое свойство, которое вам нужно знать для решения многих задач алгебры. В этом руководстве мы подробно объясняем, что такое распределительное свойство, почему оно важно, когда вы должны его использовать, какие еще математические правила вам нужно знать для него, а также прорабатываем несколько примеров, чтобы вы могли увидеть распределительное свойство в действие.
Распределительное свойство, иногда известное как распределительное свойство умножения, говорит нам, как решать определенные алгебраические выражения, которые включают как умножение, так и сложение. Буквальное определение свойства распределения состоит в том, что умножение числа на сумму аналогично выполнению каждого умножения отдельно.
В форме уравнения распределительное свойство выглядит следующим образом: $ a (b + c) = ab + ac $
(Помните, что в математике, когда два числа / множителя находятся рядом друг с другом, это означает их умножение.)
Как и многие другие математические определения, свойство распределения легче понять, если взглянуть на несколько примеров. Вот простой:
$$ 5 (2 +7) $$
Обычно, если у вас возникает такая проблема, вы складываете 2 и 7 вместе, чтобы получить 9, затем вы умножали 5 на 9, чтобы получить 45. Это самый простой способ решить уравнение, и он также следует порядок операций, который говорит вам сначала упростить то, что указано в круглых скобках, прежде чем переходить к другим операциям, таким как умножение.
Решение этого уравнения с использованием свойства распределения будет выглядеть так:
$$ 5 (2 + 7) $$
Свойство распределения означает выполнение умножения перед сложением в круглых скобках, поэтому мы распределили 5 на оба значения в круглых скобках:
$$ 5 (2) + 5 (7) $$
Определите умножение:
$$ 10 + 35 $$
Затем сложите два числа:
$$ 10 + 35 = 45 $$
Мы получаем тот же ответ, что и при решении проблемы с помощью первого метода, который показывает, что свойство распределения работает.
Итак, зачем вам использовать свойство distributive, если оно заняло больше времени, чем первый метод? Свойство распределения пригодится, когда в скобках указаны термины, которые нельзя складывать вместе, , например это уравнение: $ {3/4} (a + 2b) $. Поскольку речь идет о переменных, нет простого способа упростить $ a + 2b $.
В этих более сложных уравнениях свойство распределения может помочь нам привести уравнение в форму, упрощающую его упрощение или решение.Мы увидим примеры того, как это сделать позже в этом руководстве.
Когда вы используете свойство распределения, вам часто придется использовать или знать другие математические правила и свойства, чтобы решать или упрощать уравнения. Вот три наиболее важных из них.
Коммутативные законы гласят, что вы можете менять местами числа при сложении или умножении и при этом получать тот же ответ.
Итак, $ x + y = y + x $ и $ x (y) = y (x) $
К настоящему моменту они, вероятно, интуитивно понятны для вас, но они являются важной частью распределительного свойства, которое не работало бы без них. Вы можете использовать их, когда вам нужна помощь в упрощении определенных уравнений, чтобы привести их в более работоспособную форму.
Когда у вас есть сложное уравнение, которое выглядит так, как будто его можно упростить несколькими способами, порядок операций дает вам правильный способ работы с этими операциями.Аббревиатура PEMDAS позволяет легко запомнить, над какими операциями нужно работать в первую очередь. От первого до последнего, вот порядок, в котором вы должны отработать операции:
Круглые скобки
Экспоненты
Умножение и деление (делайте это одновременно, работая слева направо)
Сложение и вычитание (выполняйте это одновременно, работая слева направо)
Порядок операций важно знать, потому что вам часто придется помнить его при упрощении уравнений, включающих множество различных операций.2 + bx + c = 0 $ , чтобы можно было использовать квадратное уравнение для решения для $ \ bi x $ .
В этом разделе мы рассмотрим три примера упрощения задач с использованием свойства распределенности. Вы заметите, что каждая из них содержит переменные в круглых скобках, что является ключевым признаком того, что свойство дистрибутива необходимо.
$$ \ bo4 \ bi x (\ bo5 \ bi x + \ bo6) = – \ bo7 $$
Во-первых, мы собираемся распределить 4 доллара между 5 и 6 долларами.2+ 24x +7 = 0 $$
Это уравнение теперь находится в правильной формуле для решения относительно $ x $ с использованием квадратичной формулы (x будет равняться $ -0,7 $ и $ -0,5 $), или вы могли бы сохранить уравнение в этой форме, если бы вы просто просят упростить его.
$$ \ bo3 \ bi x (\ bi x- \ bo4) + \ bo5 (\ bo4 \ bi x + \ bo6) $$
Для этого уравнения есть два набора круглых скобок, поэтому нам нужно использовать свойство распределения дважды. 2- 12x + 30 $$
$$ – \ bo7 (\ bi x + \ bo4) + \ bo8 (\ bo2 – \ bo4 \ bi x) $$
Этот пример немного сложнее, потому что перед 7 стоит отрицательный знак.Если значение сразу за круглыми скобками отрицательное, отрицательный знак должен быть распределен по каждому члену в скобках.
Распределите -7 по его набору круглых скобок и 8 к его набору круглых скобок:
$$ (- 7) (x) + (-7) (4) + (8) (2) + (8) (- 4x) $$
Умножаем те:
$$ – 7x -28 + 16 – 32x $$
Теперь упростим:
$$ – 39x – 12 $$
Что такое распределительная собственность? Дистрибутивное свойство умножения утверждает, что $ a (b + c) = ab + ac $.Его часто используют для уравнений, когда термины в круглых скобках нельзя упростить, поскольку они содержат одну или несколько переменных. Используя свойство распределения, вы можете упростить или решить уравнения, с которыми в противном случае было бы сложно работать.
При использовании свойства распределения не забывайте размещать отрицательные знаки, если они указаны перед круглыми скобками, и помните о других важных математических правилах, таких как формула квадратов, порядок операций и коммутативные свойства.
Вы изучаете логарифмы и натуральные логарифмы на уроках математики? У нас есть руководство по всем правилам естественного ведения журнала, которые вам необходимо знать.
Что такое динамическое равновесие и какое отношение оно имеет к ржавым автомобилям? Узнайте, прочитав наше полное руководство по динамическому равновесию.
Рациональные числа – еще одна важная математическая концепция, которую вы должны понимать. Прочтите наше руководство по рациональным числам, чтобы узнать все, что вам нужно о них!
Переход от обучения вычитанию и сложению к обучению умножение – одна из самых сложных задач, с которыми ученики сталкиваются в школе.
Проблемы с предметом возникают не только у учащихся. При обучении умножению преподаватели часто начинают с неправильных концепций или слишком быстро проводят уроки. Это может отпугнуть и запугать учащихся, что в конечном итоге может отрицательно сказаться на результатах обучения. К счастью, существуют известные стратегии, позволяющие избежать этих препятствий. Используйте приведенное ниже руководство, чтобы узнать, как упростить преподавание и обучение умножению за шесть простых шагов, которые будут привлекать и находить отклик у учащихся. Эта статья разбита на два раздела:Раздел A Шестиступенчатое руководство по обучению умножению ✔ Узнайте, как вводить ключевые понятия и как научить детей учить и запоминать Таблица умножения! |
Раздел B Интересные способы научиться умножению ✔ Список забавных идей для обучения умножению ваших учеников! |
2 x 2 совпадает с 2 + 2
или
3 x 4 совпадает с 4 + 4 + 4
n + 0 = n
Затем объясните, что при умножении любое число , умноженное на ноль, также равно нулю:nx 0 = 0
Предложите учащимся открыть для себя примеры нулевое имущество в комнате.Например, если в классе 25 стульев, на каждом из которых не сидят обезьяны, это означает, что в классе нет обезьян. По желанию, один забавный пример увлекательного математического упражнения для развлечения ваших учеников включает в себя придумывание забавных примеров этого свойства, например 0 x один миллион = 0 … или … 0 x бутерброд с ветчиной = 0. Источник изображения: Переход во второй класс [/ caption] Умножение на единицу: свойство идентичности Короче говоря, свойство идентичности утверждает, что произведение данного числа на единицу и есть само это число: n x 1 = n. Как и в случае с нулевым свойством, выделите в своем классе, что умножение числа на единицу дает то же значение. Чтобы обосновать свойство в контексте реальной жизни, предложите вашему классу подумать об экземплярах свойства идентичности в классе. Например,( a x b ) x c = a x ( b x c )
или
(1 x 2) x 3 = 1 x (2 x 3)
Ваши ученики могут понять эту концепцию, связав ее со сложением столбцов, посредством чего они группируют слагаемые, чтобы найти сумму.Студенты также могут научиться группировать факторы любым удобным для них способом в поисках ответа. Вы можете объяснить это правило как расширение указанного выше коммутативного свойства. Распределительное свойство Распределительное свойство обозначено как a (b + c) = (ab) + (ac) Это может показаться учащимся сложным, но часто это так. уже используют свойство само по себе как мысленный математический трюк для решения более сложных фактов умножения.Проще говоря, свойство распространяется – или, как следует из названия, распределяет – значение a поровну до b, и c. Например, для 6 x 8 они могут использовать свойство распределения, чтобы думать: (6 x 5) + (6 x 3) или 30 +18 Чтобы объяснить свойство визуальным или тактильным учащимся, позвольте детям изучить свойство распределения с такими материалами, как чашки и бобы или сетка. Раздел B: Интересные способы научить умножать Играть в классные математические игры Классные математические игры могут избавить от страха перед умножением.Рассмотрим эти два примера, специализирующихся на умножении: Константы калькулятора Если калькуляторы в вашем классе имеют постоянную функцию, поощряйте своих учеников использовать их, чтобы находить кратные любого числа, чтобы найти связь между умножением и сложением. Как это работает:Оценка: 03
CCSS.Math.Content.3.OA.A.1
Интерпретируйте произведения целых чисел, например, интерпретируйте 5 × 7 как общее количество объектов в 5 группах по 7 объектов в каждой. Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7.
Оценка: 03
CCSS.Math.Content.3.OA.A.4
Определите неизвестное целое число в уравнении умножения или деления, связывающего три целых числа. Например, определить неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 ×? = 48, 5 = _ ÷ 3, 6 × 6 =?
Класс: 04
CCSS.Math.Content.4.NBT.A.2
Чтение и запись многозначных целых чисел с использованием десятичных цифр, числовых имен и расширенной формы. Сравните два многозначных числа на основе значений цифр в каждом месте, используя символы>, = и
Класс: 04
CCSS.Math.Content.4.NBT.B.5
Умножьте целое число до четырех цифр на однозначное целое число и умножьте два двузначных числа, используя стратегии, основанные на разрядах и свойствах операций. Проиллюстрируйте и объясните расчет с помощью уравнений, прямоугольных массивов и / или моделей площадей.
Класс: 04
CCSS.Math.Content.4.OA.A.1
Интерпретируйте уравнение умножения как сравнение, например, интерпретируйте 35 = 5 × 7 как утверждение, что 35 в 5 раз больше 7 и 7 раз больше 5. Представьте словесные утверждения мультипликативных сравнений как уравнения умножения.
Класс: 04
CCSS.Math.Content.4.OA.A.2
Умножайте или делите для решения словесных задач, включающих мультипликативное сравнение, например, используя рисунки и уравнения с символом неизвестного числа для представления проблемы, отличая мультипликативное сравнение от аддитивного.
Класс: 04
CCSS.Math.Content.4.OA.C.5
Создайте рисунок числа или фигуры, который следует заданному правилу. Определите очевидные особенности шаблона, которые не были явными в самом правиле. Например, учитывая правило «сложить 3» и начальное число 1, сгенерируйте термины в результирующей последовательности и обратите внимание, что термины кажутся чередующимися между нечетными и четными числами. Неформально объясните, почему числа будут и дальше меняться таким образом.
Оценка: 05
CCSS.Math.Content.5.NBT.A.2
Объясните закономерности в количестве нулей в произведении при умножении числа на степень 10 и объясните закономерности в расположении десятичной точки при умножении десятичной дроби или делении десятичной дроби на степень 10.Используйте целые числа для обозначения степени 10.
4 марта 2009 г. · Г-н Эскаланте и г-жа Тернер планируют записать свои музыкальные классы на музыкальное ревю. Билеты стоят 6 долларов каждый. Классу мистера Эскаланте нужно 22 билета, а классу миссис Тернер – 26 билетов. Используйте свойство распределения, чтобы написать предложение, чтобы выразить, как найти общую стоимость билетов двумя способами. Хорошо, это вопрос, который я просто не могу понять, пожалуйста, помогите мне !!! если ты мне просто поможешь…
Свойство распределения Вы можете использовать свойство распределения, чтобы умножить сумму или разницу на число. Вы можете использовать свойство распределения для умножения некоторых чисел с помощью математических вычислений. Например, 102 можно представить как 100 +2, а 98 – как 100 -2. Упрощение числового выражения Используйте свойство распределения, чтобы упростить 34 (102).
Распределительная собственность. 1. Распределительное свойство – это: A) процесс распределения числа за пределами круглых скобок для каждого члена внутри.
Дистрибутивность позволяет нам переписывать алгебраические выражения без использования скобок. Умножение можно распределить как на сложение, так и на вычитание. Распределительное свойство умножения над сложением позволяет нам преобразовать произведение, содержащее сумму, в сумму произведений.
Свойство распределения позволяет разбить один из факторов на меньшие числа. 😀 Меньшие числа умножать легче, чем большие числа. Обычно мы выделяем более крупный из двух факторов.👉 Мы выберем 12.
В математике свойство распределения двоичных операций обобщает закон распределения из булевой алгебры и элементарной алгебры. В логике высказываний под распределением понимаются два действительных правила замены. Правила позволяют переформулировать союзы и дизъюнкции в рамках логических доказательств.
Распределительное свойство умножения над сложением позволяет нам исключить символ группировки, обычно в форме круглых скобок. После распределения вычтите обе части на 3 и разделите на – \, 6 с обеих сторон уравнения, чтобы прийти к окончательному ответу.
Распределительная собственность. 1. Распределительное свойство – это: A) процесс распределения числа за пределами круглых скобок для каждого члена внутри.
DreamBox – это цифровая математическая программа для K-8, разработанная для дополнения вашей математической программы в классе или дома. Наши строгие и интерактивные уроки адаптируются к каждому ученику, обеспечивая максимально индивидуальный опыт обучения.Доступно на английском и испанском языках!
Попробуйте примеры уроков
DreamBox динамически адаптируется на основе текущих инструментов формирующей оценки, которые определяют, как учащиеся решают задачи, предоставляя мощные данные для выявления пробелов и индивидуализированных способов обучения.Наша цифровая программа помогает школам и округам знакомиться с учащимися там, где они находятся, независимо от условий дистанционного обучения, и дает эффективную информацию для планирования.
Узнайте, как DreamBox может помочь вашему округу
DreamBox предлагает более 2000 уроков, разработанных учителями математики и соответствующих государственным стандартам, и помогает сформировать концептуальное понимание, повысить беглость процедур и повысить успеваемость учащихся.Мы объединили строгие, соответствующие стандартам уроки с профессиональным развитием, чтобы поддерживать эффективные реализации и дополнять инструкции, где бы они ни проходили. DreamBox доступен на английском и испанском языках, потому что каждый ребенок лучше всего учится на своем основном языке.
Посмотрите, как это работает
Поддерживайте интерес детей и помогайте им учиться на платформе, которая им понравится.DreamBox дополняет график дистанционного обучения вашего ребенка и, как доказано, повышает успеваемость по математике. Независимо от того, является ли ваш ученик гением математики или ему нужна помощь в заполнении пробелов, DreamBox предлагает индивидуальные инструкции и вселяет уверенность.
Получите DreamBox дома
Ресурсы для домашнего обучения
Получите лучшее представление о федеральных, государственных и местных фондах, доступных вашему округу, с помощью нашей шпаргалки по финансированию EdTech.Это руководство включает описание каждого типа финансирования, для каких программ они могут использоваться и как использовать их для покупки DreamBox Math.
Загрузить Руководство по финансированию
Мы считаем, что позитивный настрой имеет большое значение. Учащиеся приобретают уверенность в математике по мере того, как они укрепляют свои социально-эмоциональные навыки – навыки, которые включают твердость, настойчивость и постановку целей. Поскольку этой осенью многие школы перейдут к дистанционному обучению, DreamBox предлагает три простых совета, которые помогут вашему ребенку развить уверенность в математике из дома.
Узнать больше
С DreamBox Math преподаватели могут использовать данные об учащихся в реальном времени для измерения успеваемости, решения проблемы незавершенного обучения путем выявления пробелов и создания дифференцированных заданий, соответствующих целям их летней программы, при этом встречаясь с учащимися прямо там, где они находятся.
Подробнее о DreamBox для летней школы
Predictive Insights for K-5 – это новый инновационный инструмент для составления отчетов, который может прогнозировать будущий уровень владения математикой в конце учебного года в течение учебного года.Получите более глубокое понимание того, где находятся студенты, независимо от условий дистанционного обучения.
Узнать больше
Возможности нового продукта предоставляют преподавателям важнейшие инструменты для взаимодействия, связи и мотивации учащихся, независимо от того, учатся ли они в классе или удаленно.
Узнать больше
Математиков часто интересует, обладают ли определенные множества определенные свойства при данной операции.Одна из причин, по которой математики интересовались этим, заключалась в том, что они могли определить, когда уравнения будут иметь решения. Если набор при данной операции имеет определенные общие свойства, то мы можем, например, решать линейные уравнения в этом наборе.
Есть несколько важных свойств, которые может или не может удовлетворить при определенной операции. Свойство – это определенное правило , которое содержит , если для верно все элементы набора по данной операции и свойство выполняет , а не , если есть хотя бы одна пара элементов , которые не следуйте свойству в данной операции.
Говорить о свойствах таким абстрактным образом пока нет никакого смысла, поэтому давайте рассмотрим несколько примеров свойств , чтобы вы могли лучше понять, что это такое. В этой лекции мы узнаем о свойстве закрытия.
Собственность закрытияНабор имеет свойство закрытия под конкретным операция , если результат операции всегда является элементом в наборе. Если набор имеет свойство закрытия при конкретной операции , тогда мы говорим что набор закрыт в рамках операции .
Намного легче понять свойство, глядя на примеры, чем просто говоря о нем абстрактно, поэтому давайте перейдем к рассмотрению примеров, чтобы вы могли точно понять, о чем мы говорим, когда говорим, что набор имеет свойство закрытия:
Сначала давайте рассмотрим несколько бесконечных множеств с операциями, которые нам уже знакомы:
a) Набор из целых чисел – это , закрытый при операции из сложение , потому что сумма любых двух целых чисел всегда является другим целым числом и, следовательно, в наборе целых чисел.
b) Набор из целых чисел – это , а не , закрытый в рамках операции из деления , потому что когда вы делите одно целое число на другое, вы не всегда получаете другое целое число как ответ. Например, 4 и 9 являются целыми числами, но 4 9 = 4/9. 4/9 является , а не целым числом, поэтому в наборе целых чисел это , а не !
, чтобы увидеть больше примеров бесконечных множеств, которые удовлетворяют и не удовлетворяют закрытие собственности .
c) Набор из рациональных чисел – это , закрытый при операции умножения , потому что произведение любых двух рациональных чисел всегда будет другим рациональное число, и поэтому будет в наборе рациональных чисел. Это связано с тем, что умножение двух дробей всегда дает в результате другую дробь, поскольку произведение двух дробей a / b и c / d в результате даст вам ac / bd. Единственный возможный способ, при котором ac / bd не может быть дробью, – это если bd равно 0.Но если a / b и c / d являются дробями, это означает, что ни b, ни d не равны 0, поэтому bd не может быть 0.
d) Набор из натуральных чисел – это , а не , закрытый при операции из вычитания , потому что, когда вы вычитаете одно натуральное число из другой, вы не всегда получаете другое натуральное число. Например, 5 и 16 – натуральные числа, но 5 16 = 11. 11 является , а не натуральным числом, поэтому в наборе натуральных чисел это , а не . числа!
e) Набор {1,2,3,4} – это , а не закрыто под операция сложения, потому что 2 + 3 = 5, а 5 – это , а не элемент набора {1,2,3,4}.
Мы можем увидеть это также, посмотрев на операционную таблицу для набор {1,2,3,4} под операцию дополнения:
+ | 1 | 2 | 3 | 4 |
1 | 2 | 3 | 4 | 5 |
2 | 3 | 4 | 5 | 6 |
3 | 4 | 5 | 6 | 7 |
4 | 5 | 6 | 7 | 8 |
Набор {1,2,3,4} – не закрыт при операции +, потому что есть хотя бы один результат (все результаты заштрихованы оранжевым цветом), который является , а не элементом набора {1,2,3,4}.В диаграмма содержит результаты 5, 6, 7 и 8, нет из которых являются элементами набора {1,2,3,4}!
f) set {a, b, c, d, e} имеет следующую таблицу операций для операции *:
* | б | c | д | e | |
б | c | e | а | д | |
б | д | а | c | б | e |
c | c | д | б | e | а |
д | а | e | д | c | б |
e | e | б | а | д | c |
Набор {a, b, c, d, e} равен , закрыт в рамках операции *, потому что все результаты (заштрихованные оранжевым цветом) являются элементами набора {a, b, c, d, e}.
в см. другой пример.
g) Набор {a, b, c, d, e} имеет следующую таблицу операций для операции $:
$ | б | c | д | e | |
б | f | e | а | ч | |
б | д | а | c | ч | e |
c | c | д | б | г | а |
д | г | e | д | c | б |
e | e | б | ч | д | c |
Набор {a, b, c, d, e} равен , а не закрыт ниже операция $, потому что есть хотя бы один результат (все результаты заштрихованы оранжевым), что означает , а не элемент набора {а, б, в, г, д}.
| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 08-11-2018 |
конспект урока по математике 3 класс контрольная работа 2 – Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail” data-nosubject=”[No Subject]” data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Конспект урока «Контрольная работа №1» конспект ы-уроковрф/nachalnaya Cached Контрольная работа по математике за 1 четверть по теме “Умножение и деление”, 3 класс по программе “Планета знаний” Контрольные работы за 3 класс по математике, по Моро за 1, 2 mathematics-testscom/matematika- 3 -klass-new/ Cached Контрольная работа №13 ( 3 четверть) “Внетабличное умножение и деление чисел от 1 до 100 (часть 2 )”, “Текстовые задачи” Конспект урока по математике на тему “Контрольная работа по infourokru/konspekt-uroka-po-matematike-na-temu Cached › Конспекты › Конспект урока по математике на тему ” Контрольная работа по теме “Нумерация многозначных чисел” 4 класс Конспект Урока По Математике 3 Класс Контрольная Работа 2 – Image Results More Конспект Урока По Математике 3 Класс Контрольная Работа 2 images Конспект урока «Входная контрольная работа по математике 4 класс» конспект ы-уроковрф/matem/4 Cached Проверка знаний учащихся, по итогам третьего года обучения Конспект урока «Входная контрольная работа по математике 4 класс » Конспект по математике 3 класс на тему:Контрольная работа №1 infourokru/konspekt-po-matematike-klass-na Cached Конспект урока по математике 3 класс на тему: Входная контрольная работа по математике 15102016 602 Математика 3 класс Поурочные планы по учебнику Петерсон ЛГ allengorg/d/math/math2126htm Cached Математика 3 класс Итоговая контрольная работа за 3 класс 356 ГДЗ по математике Контрольная работа Тема “Сложение и вычитание в столбик” 3 класс pedportalnet/nachalnye-klassy/matematika/ Cached Контрольная работа по математике по теме “Сложение и вычитание многозначных чисел” 4 класс 2 четверть УМК “Школа России” Контрольные работы по математике 3 класс “Школа России” urokimatematikiru/kontrolnie-raboti-po Cached Итоговая контрольная работа по математике 3 класс 01122016 4236 0 Олимпиада по математике 3 класс Конспект урока по математике в 1 классе по теме “Числа 1,2,3 pedportalnet/nachalnye-klassy/matematika/ Cached Контрольная работа по математике в 3 классе по теме “Числа от 1 до 1 000 Сложение и вычитание” Багатикова Нелли Васильевна План-конспект урока по математике (3 класс) по теме: Уроки nsportalru//2012/08/15/uroki-matematiki- 3 -klass Cached План- конспект урока по математике ( 3 класс ) по теме: КОНТРОЛЬНАЯ РАБОТА № 9 задание № 2 v Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox – the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 36,400 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
то можно прийти к результату
Лицей “ЭКУС” – это школа с углубленным изучением математики, русского языка, английского языка, информатики, а также предметов по выбору: физики, обществознания, истории, биологии, химии, литературы, географии.
В учебных планах Лицея «ЭКУС» предусмотрены учебные часы по предметам не вошедших в образовательные стандарты – риторика (5 – 8 кл.), черчение (8-9кл.), программирование (5-8кл), компьютерная графика (5-8кл.)
С 9 класса осуществляется предпрофильная и профильная подготовки по выбору учащихся по направлениям менеджмент, лингвистика (перевод), программирование и прикладная информатика, юриспруденция.
В каждой школе есть своя “изюминка”. В нашем Лицее это, конечно же, содружество талантливых и очень любящих свое дело педагогов, трудолюбивых, способных учеников и замечательных интеллигентных родителей. Мы понимаем друг друга, поэтому нам достаточно просто достичь намеченной цели – дать хорошее разностороннее образование нашим детям и подготовить их к успешной карьере.
Лицей «ЭКУС» уже много лет имеет лучшие в г. Подольске и одни из лучших в Московской области результаты ОГЭ и ЕГЭ. Ученики Лицея ежегодно становятся призерами и победителями предметных олимпиад и конкурсов разного уровня. Из года в год наши талантливые ученики становятся лауреатами именных стипендий Президента России и Губернатора Московской области.
Выпускники Лицея «ЭКУС» поступают в ведущие ВУЗы России – МГУ, МФТИ, МГТУ им. Баумана, МИФИ, Высшую школу экономики, Российскую академию народного хозяйства и государственной службы при Президенте РФ, Финансовый университет при Правительстве РФ, Санкт-Петербургский университет, ГУУ и др. Некоторые наши выпускники продолжают свое обучение за рубежом.
В Лицее «ЭКУС» созданы прекрасные условия для обучения детей. Лицей располагает собственным зданием с комфортными учебными и бытовыми помещениями, а также собственной благоустроенной территорией. Все кабинеты Лицея «ЭКУС» оборудованы ПК и устройствами для визуального восприятия информации (Проекторы, led-панели, электронные доски). Все помещения оснащены системой доступа к Интернет ресурсам
Учебная программа по математике Time4Learning доступна для учащихся от дошкольных учреждений до двенадцатых классов. Родители могут ожидать, что они увидят охватываемые темы, включая определение трансформаций и симметрии, демонстрацию дробей, решение проблем и многое другое.
Подробные планы уроков, представленные ниже, содержат подробный список учебной программы Time4Learning по математике для третьего класса.
Участникичасто используют эту страницу как ресурс для более подробного планирования, как руководство, помогающее выбрать конкретные занятия с помощью средства поиска занятий или сравнить нашу учебную программу с государственными стандартами и законами о домашнем обучении.
Учащиеся, обучающиеся по математической программе третьего класса Time4Learning, будут иметь доступ к урокам как второго, так и четвертого класса в рамках своего членства, так что они смогут продвигаться вперед или делать повторения в своем собственном темпе.
Преобразует числа, содержащие от двух до шести цифр, из стандартной формы в развернутую и наоборот.
Записывайте числа до шести цифр, используя устные и письменные подсказки.
Заказывайте номера до шести цифр и сравнивайте номера с помощью символов <,> и =.
Округлите числа с точностью до десятков тысяч до ближайшего десятка. Используйте числовые линии и знание разрядов.
Округлите числа до десятков тысяч до ближайшей сотни.Используйте числовые линии и знание разрядов.
Округлите числа до ближайшей десятки, до ближайшей сотни и до ближайшей тысячи.
Добавьте три или более однозначных слагаемых. (свойство группировки) Добавьте 2- и 3-значные числа. (с перегруппировкой и без)
Вычтите 2- и 3-значные числа. (с перегруппировкой) Вычтите 2- и 3-значные числа, если minuend имеет несколько нулей. (с перегруппировкой)
Оцените суммы и разницы, используя округление.
Введение в умножение (0-12 x 0-12), включая умножение на 0 и 1, с использованием массивов и таблиц.
Определите и перечислите кратные данного числа (1-10). Изучите умножение как повторяющееся сложение и массивы.
Умножение двух целых чисел с перегруппировкой и без нее, в котором один множитель является однозначным числом, а другой – двузначным числом. Умножьте мысленно на 10, 100 и 1000.
Умножайте однозначные целые числа на кратные 10 в диапазоне 10–90, используя стратегии, основанные на разрядах и свойствах операций.
Введение в простые задачи деления, включая деления с использованием 0 и 1 и деления с использованием остатков с использованием таблиц и других манипуляций.
Распознайте и используйте основные факты деления на 100 ÷ 10, а также определите дивиденд, делитель и частное. Опишите эти свойства деления: вы не можете делить на 0, и любое число, деленное на 1, равняется этому числу.
Представлять и решать задачи, связанные с разделением. Интерпретируйте частные целого числа либо как количество объектов в каждой доле, если объекты разделены поровну, либо как количество долей.
Представлять и решать задачи, связанные с разделением. Используйте деление в пределах 100 для решения словесных задач в ситуациях с участием равных групп, используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.
Разделите двузначные дивиденды на однозначные делители с остатками и без них.
Определите арифметические шаблоны с помощью таблицы сложения.
Определите арифметические шаблоны с помощью таблицы умножения и объясните их, используя свойства операций.
Решите многоступенчатую задачу со словами, используя умножение и деление.
Поймите разделение как проблему с неизвестным фактором.
Разберитесь в умножении и используйте стратегии для плавного умножения в пределах 100.
Понимание деления и использование стратегий для плавного деления в пределах 100.
Распознавайте дроби как часть целого и понимайте значение числителя и знаменателя.
Определите дробь, обозначенную точкой на числовой прямой, и узнайте, как записать дробь на числовой прямой.
Считайте две дроби эквивалентными, если они одного размера или имеют одну и ту же точку на числовой прямой.
Сравните две дроби с одним и тем же числителем или одним знаменателем, используя модели дробей.
Обозначает части множества и части целого с эквивалентными дробями со знаменателем до 10.
Укажите эквивалентные дроби. (1/2 = 2/4)
Порядок дробей с одинаковыми знаменателями и сравнение дробей с помощью символов <,> и =.
Изучите взаимосвязь между дробями и десятичными знаками. (десятые и сотые)
Укажите десятичные дроби с точностью до сотых. Считайте и запишите десятичные дроби с точностью до сотых.
Упорядочивайте десятичные дроби до сотых и сравнивайте десятичные дроби, используя символы <,> и =.
Подсчет коллекции монет и купюр до 50 долларов. Сложите и вычтите суммы в долларах. (доллар и центы)
Решайте словесные задачи, связанные со стоимостью монет, банкнот и сдачей.
Решение проблем, связанных с ценой за единицу товара.
Выявление и расширение повторяющихся шаблонов и применение правил шаблонов с использованием форм, цветов и чисел.
Идентифицируйте и расширяйте шаблоны и применяйте правила шаблонов, используя последовательность связанных чисел.
Примените соответствующее правило, чтобы заполнить диаграмму, включая таблицы ввода / вывода.
Представлять и оценивать письменные отношения в виде числовых выражений.
Определите неизвестное целое число в уравнении умножения, связывающем три целых числа.
Определите неизвестное целое число в уравнении деления, связывающем три целых числа.
Найдите неизвестную величину в уравнении. Пример: 3 + __ = 7. (Пример: пропущенное слагаемое или отсутствующий множитель)
Поймите свойства умножения и примените эти свойства как стратегии умножения.
Поймите свойства деления и примените эти свойства как стратегии деления.
Используйте свойства порядка (коммутативность) и группировки (ассоциативность) сложения и умножения, чтобы найти эквивалентные выражения или уравнения, содержащие неизвестную величину.
Опишите линейные сегменты, линии и пары линий.
Определяет и классифицирует углы как прямые, острые или тупые.
Определение атрибутов многоугольников (стороны и углы) и сортировка по конкретным характеристикам плоской фигуры.
Определите атрибуты твердых фигур (ребра, вершины и грани), такие как кубы, прямоугольные призмы, прямоугольные пирамиды, конусы, цилиндры и сферы, и выполните сортировку по определенным характеристикам.
Определяет и создает двумерное представление трехмерной фигуры.
Найдите расстояние по горизонтали или вертикали между двумя точками на координатной сетке.
Нанесите точку на координатную сетку с учетом упорядоченной пары и запишите упорядоченную пару точек, показанных на координатной сетке.
После получения навигационных указаний от начальной точки определите упорядоченную пару конечной точки.
Для плоской фигуры определите конгруэнтную форму и создайте конгруэнтную форму, используя другие плоские фигуры.
Примените скольжение, переворот или поворот к плоской фигуре и спрогнозируйте результат. Определите изображение плоской фигуры как слайд, переворот или поворот.
Используйте линейную и точечную симметрию для определения и создания симметричных фигур.
Определите, скажите и покажите время с точностью до часа, получаса и четверти часа. Определите, расскажите и покажите время для 5- и 1-минутных интервалов.
Найдите прошедшее время в минутах, часах, днях и неделях. Развивайте навыки измерения и демонстрируйте понимание концепций, связанных с измерением времени.
Решите проблемы с истекшим временем, используя числовую строку.
Расшифровка расписания с использованием минут, часов, дней и недель.
Определите единицы длины. (дюйм, фут, ярд, миля) Оцените и сравните длину. Измерьте с точностью до полудюйма.
Определите единицы мощности. (чашка, пинта, кварта, галлон) Оцените и сравните вместимость.
Определите единицы веса. (унция, фунт) Оцените и сравните вес.
Считайте показания термометра с точностью до ближайшего 5-градусного интервала.
Определите единицы длины. (сантиметр, дециметр, метр) Оцените и сравните длину. Измерьте с точностью до сантиметра.
Определите единицы мощности. (миллилитры, литры) Оцените и сравните емкость.
Определите единицы массы. (граммы, килограммы) Оцените и сравните массу.
Считайте показания термометра с точностью до ближайшего 5-градусного интервала.
Оцените объемы объектов в литрах и миллилитрах путем сравнения с эталонными объектами.
Решение реальных задач, связанных с массой в килограммах и граммах и объемом в литрах.
Измерьте площадь прямоугольника с помощью единичных квадратов.
Найдите площадь фигуры, считая единичные квадраты.
Найдите площадь прямоугольника, укладывая плитку и умножая длины сторон.
Интерпретировать y = mx + b как линейную функцию.
Найдите площадь прямоугольника, умножив длину и ширину.
Найдите площадь прямоугольника, разделив его на два меньших прямоугольника.
Найдите область, разложив составные формы на прямоугольники и добавив области.
Найдите периметр, считая единицы измерения и складывая длины. Измерьте, чтобы найти периметр. Выберите соответствующую метку для измерения.
Найдите область, считая единицы. Умножьте, чтобы найти площадь. Выберите соответствующие метки измерения.
Сравните периметр и площадь.
Отображение и интерпретация данных в виде пиктограмм.
Отображение и интерпретация данных в виде вертикальных и горизонтальных гистограмм.
Отображение и интерпретация данных в таблицах, включая таблицы подсчетов, данных и частот.
Отображение и интерпретация данных в частотных таблицах с использованием двух атрибутов.
Определите достоверность, вероятность и справедливость событий.
Определите и перечислите все возможные исходы события.
Используйте четырехэтапный метод Polya для решения двухэтапных задач со словами с использованием четырех операций. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестное.
Решите двухэтапные задачи со словами, используя четыре операции. Оцените разумность ответов с помощью мысленных вычислений и стратегий оценки, включая округление.
Объем и последовательность Авторские права. © 2017 Edgenuity, Inc. Все права защищены.
Инструмент для поиска занятий – один из многих полезных инструментов, которые Time4Learning предлагает своим участникам. Средство поиска занятий – это ярлык, с помощью которого родители могут легко просмотреть уроки или найти дополнительную практику для своего ребенка.
Каждому уроку в учебной программе присвоен уникальный номер занятия, который в планах уроков называется «номером LA». Эти номера можно найти либо на страницах содержания и последовательности, либо в планах уроков на родительской информационной панели.
Для получения дополнительной информации посетите наш раздел подсказок и помощи, в котором есть более подробная информация о поисковике действий.
Если вас интересуют планы уроков математики для третьего класса, вас также могут заинтересовать:
Если вы только изучаете Time4Learning, мы рекомендуем сначала посмотреть наши интерактивные демонстрации уроков.
Зарегистрируйтесь на Time4Learning и получите доступ к разнообразным образовательным материалам, которые увлекут и побудят вашего ребенка добиться успеха. Сделайте Time4Learning частью ресурсов для домашнего обучения ваших детей.
Что такое математика для 3-го класса?
Класс 3 фокусируется на четырех ключевых достижениях предыдущих лет: (1) развитие понимания и беглости умножения и деления в пределах 100; (2) развитие понимания дробей, особенно единичных дробей; (3) развитие понимания прямоугольных массивов и площади; и (4) описание и анализ двумерных форм.
Как мы заказывали агрегаты?
В блоке 1 «Разрядное значение, округление, сложение и вычитание» учащиеся полагаются на свою основную работу во 2-м классе по разряду, чтобы развить понимание округления. Затем они развивают беглость сложения и вычитания в пределах 1000. Наконец, они используют оба вышеупомянутых навыка для решения одно- и двухэтапных задач со словами, включающих сложение и вычитание, используя округление для оценки разумности своих ответов.Хотя содержание, преподаваемое в этом модуле, не является основной работой для 3-го класса, как это определено Общими основными государственными стандартами, оно служит основой для дальнейшей работы, такой как оценка разумности всех типов двухэтапных задач со словами и умножение одно- цифры числа, кратные десяти. Таким образом, он служит введением в курс.
В , Части 2 и 3, Умножение и деление, части I и II , студенты знакомятся с двумя другими основными операциями, умножением и делением.Они приходят к пониманию умножения как нахождения общего количества объектов в определенном количестве групп равного размера, а деление как нахождения либо размера группы, либо количества групп. Учащиеся стремятся к беглости всех фактов умножения и деления в пределах 100, полагаясь на свойства и шаблоны, чтобы помочь, в частности, с трудными фактами 6, 7, 8, 9. Учащиеся решают одноэтапные задачи умножения и деления слов с участием равных групп и массивы и решать двухэтапные задачи со словами, включающие все четыре операции.Они также исследуют бесчисленные связи с умножением и делением, в том числе исследуют закономерности, в том числе закономерности в последовательности подсчета пропусков, а также масштабированные изображения и гистограммы.
В уроке 4 , Площадь ученики определяют площадь как количество квадратных единиц, необходимых для покрытия двумерного пространства. Первоначально они находят площадь прямоугольников, считая единичные квадраты или пропуская счет по строкам и столбцам. Затем, увидев связь между подсчетом пропусков и умножением, которая была построена в предыдущих двух разделах, учащиеся применяют недавно приобретенную беглость речи с умножением, чтобы вычислить площадь прямоугольника, и использовать свою беглость с добавлением, чтобы найти площадь составных двух частей. размерные формы.В качестве шага к овладению всеми типами словесных задач, ожидаемых от учащихся 3-х классов, они также знакомятся с одностадийными задачами со словами, затрагивающими область в этом разделе.
В , Блок 5, Формы и их периметр , учащиеся начинают с изучения конкретного атрибута периметра и приходят к тому, чтобы различать периметр и площадь как разные измерения. Затем они исследуют двухмерные формы в разных категориях, видя, что формы в этих категориях имеют общие атрибуты.
В уроке , блок 6, дроби , учащиеся на основе своей работы разбивают круги и прямоугольники во 2 классе, чтобы изучать дроби. Они строят более сложные дроби из единичных дробей и начинают понимать дроби как числа, а не как части фигур. Для этого учащиеся проводят обширную работу, помещая дроби на числовую линию, что является полезным представлением для сравнения и поиска эквивалентных дробей. Учащиеся также изучают линейные графики с дробными измерениями, что является ключевым достижением по сравнению со вторым классом работы с линейными графиками, которые связаны с их работой с дробями.
В Блок 7, Измерение студенты изучают время, а также объемы и массы жидкости. Учащиеся учатся считать время с точностью до минуты и используют свою работу с числовыми линиями в блоке 1 (с округлением) и блоке 5 (с дробями) для решения задач, связанных с истекшим временем. Они также полагаются на свою работу с числовыми линиями для считывания шкал измерений и используют эти измерения для решения одношаговых задач со словами во всех четырех операциях с объемами и массами жидкости.
Этот курс соответствует рамкам учебной программы штата Массачусетс 2017 года, которые включают Общие основные государственные стандарты 2010 года.Кроме того, мы полагаем, что ежедневная беглость речи и практика применения являются важной частью обучения элементарной математике, но не включены в наши математические единицы. Все ученики 3-х классов получают около 45 минут практики в этих областях во время других блоков.
НАЗВАНИЕ УРОКА: Дробь как число в числовой строке
УЧИТЕЛЬ: Деондра М. Симон, Ассоциация учителей Орискани
ТЕМА: Математика
КЛАСС: 3
ВРЕМЕННЫЕ РАМКИ: 4 дня
ПЛАНИРОВАНИЕ И ПОДГОТОВКА:
Перед уроками учащиеся разовьют понимание дробей, начиная с единичных дробей; 3.NF.1. Студенты должны рассматривать дроби в целом как построенные из единичных дробей и использовать дроби вместе с визуальными моделями дробей для представления частей целого. Используя 3.NF.2a и b, учащиеся поймут: дроби – это числа, которые могут быть представлены на числовой прямой, а целые числа могут быть разделены на равные части.
МАТЕРИАЛЫ УРОКА:
Размышления учителя о развитии урока:
ССЫЛКИ ПО ТЕМЕ:NYSED Классные видео:
Департамент образования штата Нью-Йорк предлагает учебные видеоролики по английскому языку (3 начальных, 1 среднее), математике (2 начальных, 2 средних) и урок европейской истории.Видео представлены в неотредактированном виде и отформатированы, чтобы выделить конкретные стандарты обучения штата Нью-Йорк по мере их внедрения.
Зайдите в EngageNY, чтобы просмотреть видео.
Планирование и подготовка:
Необходимые материалы / оборудование:
Стандарты обучения:
Общие основные стандарты обучения: 3.NF2a и b
2. Считайте дробь числом на числовой прямой; представляют дроби на числовой линейной диаграмме.
а. Изобразите дробь 1 / b на числовой линейной диаграмме, определив интервал от 0 до 1 как целое и разделив его на b равных частей. Помните, что каждая часть имеет размер 1 / b и что конечная точка части, основанная на 0, находится на числовой строке с номером 1 / b.
г. Изобразите дробь a / b на числовой линейной диаграмме, отметив длину 1 / b от 0.Помните, что результирующий интервал имеет размер a / b и что его конечная точка находит число a / b в числовой строке.
Смены по общим стандартам:
Этот урок включает в себя все педагогические смены, требуемые Стандартными государственными стандартами
.Цели содержания:
Перед уроками учащиеся разовьют понимание дробей, начиная с единичных дробей; 3.NF.1. Студенты должны рассматривать дроби в целом как построенные из единичных дробей и использовать дроби вместе с визуальными моделями дробей для представления частей целого. Используя 3.NF.2a и b, учащиеся поймут: дроби – это числа, которые могут быть представлены на числовой прямой, а целые числа могут быть разделены на равные части.
Основные вопросы:
Академический словарь:
Дифференцированная инструкция:
Дифференциация будет использоваться в течение каждого дня урока для всех учащихся, включая изучающих английский язык и учащихся с ограниченными возможностями.Учащиеся будут работать в группах в соответствии с их уровнем знаний дробей, как видно из предварительной оценки.
Последовательность занятий:
День 1: Предварительная оценка (15 мин.)
День 2: многоуровневые групповые занятия (50 мин.)
День 3: Технологические мероприятия (40 мин.)
http://www.visualfractions.com/IdentifyLines/identifylines.html ,
http: // www.conceptuamath.com/fractions/ordering-fractions-number-line.html , и приложение Number Line .
День 4: Постеры с цифрами (40 мин.)
ОЦЕНКА:
Формирующие оценки
Суммарные оценки
ОТРАЖЕНИЕ:
Процесс:
Этот урок был выбран, поскольку третьеклассники должны развивать понимание дробей как чисел.Это одна из четырех важнейших областей учебного времени по общей основной математике для третьего класса.
При написании этого урока я решил, что ученики должны заниматься, используя следующее: моделирование, дифференциация, технологии и ведение дневника.
Применение этих процедур для выполнения математических сдвигов может быть трудным для некоторых преподавателей. Возможно, им придется изменить свой «способ» обучения, но, в конце концов, это улучшит усвоение нашими учащимися и понимание концепций.
Ресурсы Библиография:
Элизабет Б.Стоун, начальная школа Святой Марии, округ Энн Арундел, штат Мэриленд, и
Шелби Лейлич, Школа для глухих штата Мэриленд
Math-Aids.com
Супер учитель Worsheets.com
Скотт Маккиннон, начальная школа Харлана, Флоренция
ID плана урока: 26348
Черил начала урок с чтения Спагетти и фрикадельки для всех! вслух классу. По сюжету мистер и миссисКомфортно пригласите 32 члена семьи и друзей на встречу и установите восемь квадратных столов, чтобы разместить по четыре человека за каждым, по одному в стороне. По мере того, как приходят гости, у всех есть свои идеи о том, как переставить столы, чтобы группы разного размера могли сидеть вместе. Миссис Комфорт протестует, зная, что позже возникнут проблемы с сиденьем, но ее протесты игнорируются. Вечеринка превращается в веселую смесь переставленных столов, стульев, тарелок, стаканов и еды. Однако в конце концов все сработает, когда миссисВ конце концов, комфорт оказался правильным.
Когда Шерил закончила читать рассказ, она спросила класс: «О чем беспокоилась миссис Комфорт?»
Николь сначала ответила: «Здесь не будет достаточно места, потому что, когда вы складываете столы вместе, вы теряете стулья», – сказала она.
“Что ты имеешь в виду?” – спросила Черил.
«Это как если вы сложите два стола вместе, вы потеряете места там, где они соприкасаются. Это трудно объяснить.” Николь нарисовала в воздухе два стола, указывая на стороны, где они встретились.Черил нарисовала на доске два квадрата, нарисовав стрелку там, где стороны касались друг друга. “Вы имеете в виду потерять стулья здесь?” она спросила. Николь кивнула. (См. Рисунок 1).
Выслушав идеи других студентов о проблеме миссис Комфорт, Черил сказала: «Давайте использовать цветные плитки, чтобы изучить различные способы расстановки всего четырех столов. Начнем всего с четырех столов ».
Черил дала классным указаниям по расстановке квадратных «столов». «Когда плитки соприкасаются, – сказала она, – они должны касаться всей стороны.Прикосновение к частям сторон или только к углам недопустимо ». Она продемонстрировала на диапроекторе. (См. Рисунок 2.)
Шерил также разместила плитки таким образом, чтобы не следовать ее правилу, и попросила учеников объяснить, почему. (См. Рисунок 3.)
Затем она выполнила инструкции. «В своей группе поделитесь плитками, которые я положил на ваш стол, и найдите разные способы расставить четыре плитки. Обязательно следуй моему правилу ». Черил разложила около 70 плиток для каждой группы из четырех учеников.
Пока ученики работали, Черил ходила по классу, наблюдая за учениками и отвечая на вопросы по мере необходимости. Когда у всех была возможность поработать над проблемой, она прервала студентов и попросила их внимания.
“Что вы сделали?” – спросила Черил. «Кто бы хотел описать расположение, чтобы я мог построить его из плиток наверху?»
«Вы можете провести прямую линию», – сообщил Брэндон.
«Как это?» – спросила Черил, складывая четыре плитки в прямоугольник размером 1 на 4.Брэндон кивнул.
«Сделайте квадрат со всеми четырьмя из них», – сказала Рахиль. Черил построила квадрат из четырех плиток.
«Я сделала тройку и одну», – сказала Николь.
“Что ты имеешь в виду?” – спросила Черил.
«Один маленький столик, как у Натана, – пояснила Николь, – а затем столик 1 на 3».
«Вы можете сделать четыре отдельных стола», – сказал Натан.
«Ты мог бы поставить Т», – сказал Зак. «Положите три в ряд и один под средним».
«Я тоже сделал это, но мой перевернут», – сказал Эрик.
Шерил построила аранжировку Эрика под руководством Зака и указала классу, что когда вы можете перевернуть, повернуть или сдвинуть фигуру, чтобы она точно соответствовала другой фигуре, фигуры совпадают. «Мы будем считать конгруэнтные формы одинаковыми», – пояснила она.
Когда расположение студентов заполнило накладные расходы, Черил спросила: «Что, если бы мы использовали только отдельные прямоугольные столы, сделанные из четырех плиток? Какие формы мы должны удалить? ”
«Я предложил четыре отдельные таблицы, – сказал Натан.
Рифка добавила: «И та, которая похожа на букву Т».
«Вы также должны снять мою», – сказала Николь. “Это не один прямоугольник”.
Когда Малкия предложила убрать квадрат, разговор разгорелся. Некоторые ученики помнили, что квадрат – это прямоугольник, а другие – нет. Черил пояснила: «Квадрат – это особый вид прямоугольника, потому что все его стороны имеют одинаковую длину. Но, как и прямоугольник, квадрат по-прежнему имеет четыре угла в 90 градусов, а противоположные стороны параллельны.”
Шерил хотела убедиться, что ученики умеют маркировать построенные ими прямоугольники. Она нарисовала на доске прямоугольник размером 1 на 4. «Я могу записать это двумя способами», – сказала она и записала под прямоугольником:
Затем Черил нарисовала квадрат 2 на 2 и пометила его.
Черил указала на квадратный стол 2 на 2 и спросила: «Если один человек сидит сбоку от небольшого квадратного стола, и никто не сидит по углам или в щелях между столами, сколько людей может сидеть здесь? ”
«Легко, восемь», – ответила Николь.«Просто сосчитайте по два человека с каждой стороны, умноженные на четыре стороны».
«Когда вы подсчитываете количество людей, которые могут сесть за стол, вы фактически находите его периметр», – объяснила Шерил. «Это потому, что каждый человек сидит по одну сторону от меньшего квадрата и занимает одну единицу длины. Таким образом, периметр прямоугольника 2 на 2 составляет 8 единиц ».
«Периметр стола размером 1 на 4 равен 10», – заметил Эрик.
Черил попросила остальных проверить показания Эрика, а также изобразить периметр нескольких других прямоугольников.Затем она представила другую проблему.
– Давайте вспомним вечеринку мистера и миссис Комфорт, – начала Черил. «Предположим, миссис Комфорт решила, что все 32 человека должны сесть за один большой массивный прямоугольный стол, и она хотела выяснить, сколько маленьких квадратных столов можно арендовать. Посмотрите, сможете ли вы найти все возможные прямоугольные столы разных размеров и форм, на которых могут разместиться 32 человека ».
«Должен ли каждый стол вмещаться ровно 32?» JT хотел знать.
«Да», – ответила Черил.
«Сколько плиток мы используем?» – спросила Малкия.
«Это будет зависеть от столов, которые вы построите», – ответила Черил.
«Можем ли мы работать с партнером?» – спросила Николь.
«Да, – ответила Черил, – но веди свой личный учет».
Больше вопросов не было. Черил дала последнее указание. «Используйте плитки, но нарисуйте свои решения на листе бумаги. Обязательно запишите размеры каждого стола и количество людей, за которыми он может разместиться ».
Остаток урока Черил наблюдала за учениками за работой и при необходимости оказывала помощь.
Она наблюдала, как Кэтлин составляла прямоугольник 16 на 2. «Хм, – громко сказала Кэтлин, работая, – давайте посмотрим, 32 человека. Это должно сработать, потому что 16 умножить на 2 будет 32 ». Кэтлин сосредоточенно нахмурилась, считая стороны квадратов. Затем она с удивлением посмотрела на Шерил.
«Я не понимаю», – сказала она. «Я насчитал 36 мест. Но в этом нет смысла, потому что 16 умножить на 2 равно 32. Может, я неправильно посчитал ». Она снова сосчитала стороны.
«Еще 36. Ага». Кэтлин пожала плечами, перемешала 16 плиток обратно в стопку в центре стола и начала строить еще один прямоугольник.
«Что ты делаешь?» – спросила ее Шерил.
«Что ж, я, должно быть, напортачила, потому что первая, которую я сделал, не сработала, поэтому я попробую что-нибудь еще», – ответила Кэтлин.
«Что ты собираешься попробовать?» – спросила Черил.
«Не знаю. Я просто собираюсь повозиться и посмотреть, что будет », – сказала она.
Черил наблюдала, как Кэтлин начала складывать плитки в длинный ряд шириной в один квадрат. Она продолжала считать стороны одну за другой каждый раз, когда добавляла новую плитку.Наконец она улыбнулась.
«Это работает! Этот вмещает 32 человека. Это 1 на 15. А теперь записать это ». Кэтлин начала рисовать прямоугольник на бумаге.
Алекс сидел напротив Кэтлин. «Я тоже нашел это», – сказал он. «Теперь я пробую что-то вдвое».
«О», – ответила Кэтлин и начала строить прямоугольник шириной в четыре квадрата.
Натан подошел к Шерил. «Я не рисую на бумаге прямоугольники, как все, – сказал он. «Вместо этого я решил использовать Xs.Но Люк сказал мне, что это неправильно. Разве я не могу нарисовать крестики, если захочу? ” Натан показал Шерил свою газету.
Черил попросила Натана объяснить, что он сделал. Удовлетворенная тем, что он понимает, что делает, Шерил сказала: «То, что вы сделали, имеет для меня смысл».
Натан вернулся к Люку. «Я сказал вам, что она скажет, что все в порядке», – сказал он.
Черил пошла по классной комнате. К концу периода она увидела, что все студенты нашли некоторые прямоугольники, а некоторые нашли их все.Она попросила детей убрать плитку и собрала их бумаги. Шерил планировала продолжить урок на следующий день.
На следующее утро Черил дала классу возможность подумать над расширением. «Какой самый дешевый способ разместить 32 человека за одним большим прямоугольным столом? А какой самый дорогой способ? Чтобы ответить, некоторым из вас нужно будет найти дополнительные расстановки столов ».
Примерно через 10 минут Черил прервала учеников, чтобы начать обсуждение в классе.«Какие варианты есть у Comforts, чтобы посадить всех 32 человека за один стол?» – спросила Черил. Руки студентов вскинулись.
«У них будет группа, точнее, восемь», – сказала Рэйчел. Большинство студентов кивнули или пробормотали свое согласие.
«Может ли кто-нибудь описать размеры таблиц, которые будут работать?» – спросила Черил. «Я запишу их на доске».
Эрик сообщил: «Один раз-15, 2-раз-14, 3-раз-13, 4-раз-12, 5-раз-11, 6-раз-10, 7-раз-9 и-8-раз-8». . » После того, как Шерил записала размеры, она вернулась и зарисовала каждый соответствующий прямоугольник.
«О, я вижу закономерность!» – сказала Анферни. “Могу я показать это?” Черил кивнула, и Анферни подошла к доске. Она сказала, указывая: «Сверху вниз идет 1, затем 2, затем 3, затем 4, затем 5 и так далее, вплоть до 8».
«А другая сторона идет вниз», – добавила Анн Мария.
«О да, я этого не видела», – сказала Анферни. «Ага, 15, 14, 13 и так далее». Он снова сел.
«Разве список не должен продолжаться?» – спросила Черил. “Разве не следует прямоугольник 9 на 7?” (См. Рисунок 6.)
«Этот у тебя уже есть», – сказала Малкия.
«Да, 9 на 7 и 7 на 9 – это одно и то же, – добавила Николь.
«Все числа после 8-умножить на 8 – это повторения, – сказала Кирстен, – так что вы не можете их сосчитать».
«Давайте подумаем, сколько квадратных столов придется арендовать мистеру и миссис Комфорт на каждый большой прямоугольник», – сказала Шерил. «Сколько им придется арендовать за стол размером 15 на 1?»
«Пятнадцать. Легко, – ответили несколько студентов.
«А как насчет 2 на 14?» Черил продолжила.«Сколько столов придется арендовать Comforts для такой договоренности?»
«Двадцать восемь», – звали многие дети.
«А как насчет расположения 3х13?» – спросила Черил. Класс быстро понял, чем занимается Шерил.
«Вы просто размножаетесь», – сказала Рифка. «Просто сделай это для всех – 28, 39, 48, 55, 60, 63 и 64».
«Что вы заметили в форме столов?» Затем спросила Черил.
Малкия сказала: «Размер 8 на 8 – квадрат, а все остальные – прямоугольники.”
«Но ведь размер 8 на 8 тоже прямоугольник, помнишь?» Эрин напомнила Малкию.
«Смотрите, – сказал Брэндон. «Если они устроят длинный тонкий прямоугольник для 32 человек, то они смогут сделать это всего с 15 столами. Так дешевле всего.
«И они также сэкономили бы место, поскольку 1-умноженный на 15 занимает меньше всего места», – добавил Шарнет.
«Но вам понадобится длинная комната, – добавила Николь, – как для королевского банкета».
Затем Шерил остановила беседу и дала письменное задание оценить мышление каждого ученика.Она написала на доске три вопроса, чтобы дети могли ответить:
Учащиеся работали над заданием на оставшуюся часть класса.
Первые 20 уроков предназначены для детей с небольшими математическими навыками или без них.Дети изучают основные навыки работы с числами, включая распознавание чисел, числовые слова и счет. Персонажи Mathseeds во главе с Манго вводят ряд навыков, включая распознавание формы каждого числа 0-10 и взаимно-однозначное соответствие. Детей также знакомят с четырьмя основными 2D-формами: кругом, квадратом, треугольником и прямоугольником, цветами и некоторыми простыми понятиями размера: большой, маленький, короткий, высокий и т. Д.
Уроки 21–50 развивают математические навыки. Дети учатся уверенно считать вперед и назад до двадцати.Они используют ряд техник, включая десять рамок и числовые линии. Они также учат числовые слова до двадцати. Вводится сложение, и дети складывают до десяти и удваивают до пяти. Манго и другие персонажи Mathseeds представляют концепции прохождения времени, жизненных циклов и дней недели во время этих уроков. Дети развивают свое понимание 2D-форм, сортируя их в соответствии с их свойствами. Они также знакомятся с четырьмя трехмерными формами: сферой, кубом, конусом и цилиндром.
Обзор уроков в детском садуMathseeds Уроки 51–100 основаны на навыках, которые дети приобрели ранее в программе.Дети учатся считать до 100, заказывать числа и определять порядковые числа до 10-го. Развивается понимание разрядов, в том числе торговых на десятки. Дети идентифицируют деньги США и исследуют дроби, уделяя особое внимание целым, половинным и четвертым. Вводится вычитание, и дети сначала складывают и вычитают до 10, а затем с точностью до 100. Они также учатся решать задачи на вычитание с неизвестным слагаемым. Стратегии включают в себя расчет, обратный отсчет, близкое к удвоению и использование семейств числовых фактов.Дети учатся пропускать счет на 2, 5 и 10, а также овладевают навыками раннего умножения и деления группирования и совместного использования. На этих уроках вводятся понятия площади и объема, и дети продолжают исследовать атрибуты 2D-форм и 3D-объектов. Дети следуют простым указаниям в определенное место и учатся считать цифровые и аналоговые часы с точностью до получаса. Представлены таблицы подсчета и простые графические изображения. Дети также работают с концепцией случая и вероятности происходящего.
Обзор уроков 1 классаMathseeds Уроки 101–150 знакомят с рядом новых концепций и закрепляют ранее полученные навыки. Дети учатся считать до 1000, определять нечетные и четные числа и округлять до ближайших 10 и 100. Они продолжают развивать навыки числового значения; сложение и разложение чисел до 999. Стратегии сложения и вычитания получают дальнейшее развитие, включая методы «перехода» и «разделения», а также вертикальное сложение и вычитание.Дети продолжают практиковать группирование, совместное использование и использование знаков умножения и деления. Их также учат, как находить части коллекции предметов. Дети исследуют длину, и им показывают, как измерять в метрах и сантиметрах. Они исследуют, как движутся и отражаются 2D-формы, а также как строятся 3D-объекты. Дети называют время с точностью до четверти часа и ближайших 5 минут и используют календарь для определения конкретных дат. Они создают счетные диаграммы и простые графические изображения и интерпретируют данные различными способами.
Обзор уроков 2 классаMathseeds Уроки 151–200 охватывают ряд тем, связанных с математикой, которые преподаются в 3 классе. Дети учат числа до 10 000, считая вперед и назад в тысячах, сотнях и десятках и упорядочивая большие числа от меньшего к большему. Они будут исследовать углы, вертикальные и горизонтальные линии симметрии и определять изображения в окружающей среде, которые являются симметричными. Детей также познакомят с единицами измерения L и мл, и они научатся читать приращения на мерных кувшинах, чтобы определять количество жидкости.Они также научатся считать квадраты для измерения площади и умножать длину на ширину, чтобы найти площадь в квадратных единицах. Изучаются стратегии умножения и деления, включая таблицы умножения и связанные с ними факты деления. Дети будут более подробно изучать денежные единицы, а также дроби, углубляя свое понимание роли верхних и нижних чисел в дробях, используя термин «знаменатель».
Обзор уроков 3-го классаМатематика на каждый день разделен на блоки, которые делятся на уроки.В верхнем левом углу Home Link вы должны увидеть такой значок:
Номер модуля – это первое число, которое вы видите на значке, а номер урока – второе число. В этом случае учащийся работает в Разделе 5, Урок 4. Чтобы получить доступ к справочным ресурсам, вы должны выбрать «Раздел 5» из списка выше, а затем найти строку в таблице с пометкой «Урок 5–4».
Повседневная математика для родителей: Что нужно знать, чтобы помочь своему ребенку добиться успеха
Проект математики школы Чикагского университета
Издательство Чикагского университета
Подробнее >>
Используя логин, предоставленный учителем вашего ребенка, вы получите доступ к ресурсам, которые помогут вашему ребенку с домашним заданием или освежить свои математические навыки.
Узнайте больше об учебной программе EM и о том, как помочь своему ребенку.
– Проверка со слайда (слайд 3) -Назовите компоненты при умножения?-Что обозначает первый множитель?А второй?
Первый ряд запишите в виде произведения число солдатиков. Второй ряд запишите число солдатиков в виде произведения. Слайды 5-7
Применение знаний.
