15.03.1982| alexxlab| 0 Comment

Конспект урока по математике 3 класс множество и его элементы петерсон: “3 класс Математика Петерсон Л.Г. Математика 3 класс Т. Е. Демидова.”. Скачать бесплатно и без регистрации.

Содержание

Тема урока “Множество. Элементы множества. Изображение множеств.”

Раздел долгосрочного планирования:

5.3C Множества

Школа: Коржинкольская СШ

Дата:

ФИО учителя: Тимофеенко С.Ю.

класс: 5, 1 урок

Участвовали:

Не участвовали:

Тема урока

Множество. Элементы множества.
Изображение множеств.

Цели обучения, достигаемые на этом уроке

5. 4.1.1 усвоить понятия множества и его элементов, пустого множества;

5.5.3.8 использовать символы , ,  при работе с множествами.

Цель урока

– знать понятия множества и его элементов, пустого множества,

– использовать символы , ,  при работе с множествами

Критерии оценивания

– все учащиеся знают понятия множества и его элементов, пустого множества;

– большинство учащихся используют символы , ,  при работе с множествами и записывают результаты, используя , , 

– некоторые учащиеся используют диаграмму Эйлера – Вена для решения заданий

Языковые задачи

Учащиеся будут:

– формулировать понятия множества и его элементов;
– комментировать использование символов , ,  при работе с множествами.

Словарный запас и термины:

– множество;

– элементы множества;

– изображение множеств;

– принадлежать множеству;

– пустое множество.

Сочетания, используемые для диалога и письма:

Множества – это группа ….., обозначаются заглавными буквам…

Множество, содержащее хотя бы один элемент, называется ….

Воспитание ценностей

Национальное единство, мир и согласие в обществе

через групповую и парную работу, оценивание, решение заданий, применение знаний

Уровень мыслительных навыков

знание, понимание, применение, анализ, синтез

Межпредметная связь

История – через историческую справку, английский язык – через физминутку

Предыдущие знания

Правила работы с десятичными дробями и действия над нами

Ход урока

Запланированные этапы урока

Виды упражнений, запланированных на урок:

Ресурсы

I.

Начало урока

1 мин;

Фронтальная работа

3 мин

1 мин

1 мин

Эпиграф урока: «В математике, когда что-нибудь или кто-нибудь собираются вместе, говорят одно и то же слово – множество».

Л.Г.Петерсон

Готовность к уроку Психологический настрой

Прием «Подари комплимент».

Учитель: – добрый день, ребята. Давайте встанем в круг. У меня конфеты, возьмите в коробочке конфету и подарите ее тому, кто стоит напротив, но обязательно со словами: «Я дарю тебе эту конфетку, потому что ты самый…». Спасибо, молодцы.

Давайте постараемся сегодня поработать так, чтобы урок не оказался трудным и скучным. Удачи вам, ребята.

Актуализация опорных знаний:

«Устный счет».

Учащиеся стоят в кругу. Игра «Мяч». Учитель зачитывает со слайда пример, а первый ученик, ответивший правильно, ловит от учителя мяч. Далее этот обучающийся выбирает товарища, и ему задает пример, и если ученик отвечает правильно, то ему кидают мяч, а если неверно, то кидают мяч первому ответившему ученику.

Обратная связь.

Ребята вы что-нибудь заметили интересного в вопросах

А как вы думаете? Почему?

Давайте теперь составим критерии, по которым мы будем оценивать себя и других на уроке.

Учащиеся предлагают свои варианты критериев оценки. Совместно их обсуждают.

(Разбаловка от 1 до 6 баллов).

Каждому учащемуся раздаётся индивидуальный оценочный лист, в котором он будет выставлять свою оценку за каждый этап работы

ФИ ученика____________________

Устный счет

1 станция

2 станция

3

станция

4

станция

5

станция

Сам работа

Раб по учеб

Итого

По 1 баллу

1-4 балла

1-4 балла

1-4 балла

1-4 балла

1-4 балла

1-4 балла

(Все задания на листах)

Стадия вызова

Определение цели урока

Посмотрите на слайды (Работа с презентацией).

Давайте сформулируем тему и цель нашего урока;

Дети делают предположения, что тема урока множество чисел; Формулируем цель урока.

Значит тема нашего урока: «Множество. Элементы множества. Изображение множеств» (записываю тему на доске)

Интерктивная доска, проектор, презентация к уроку, индивидуальные оценочные листы

Мяч, конфеты

Работа с презентацией

Слайды 1-2

Слайды


слайд

П

Середина урока

Изучение нового материала

8 мин

Закрепление

Групповая работа

ФО

15 мин;

1 мин

1 мин

1 мин

Парная работа

5 мин

Индивидуальная работа

5 мин

ФО

Применение знаний

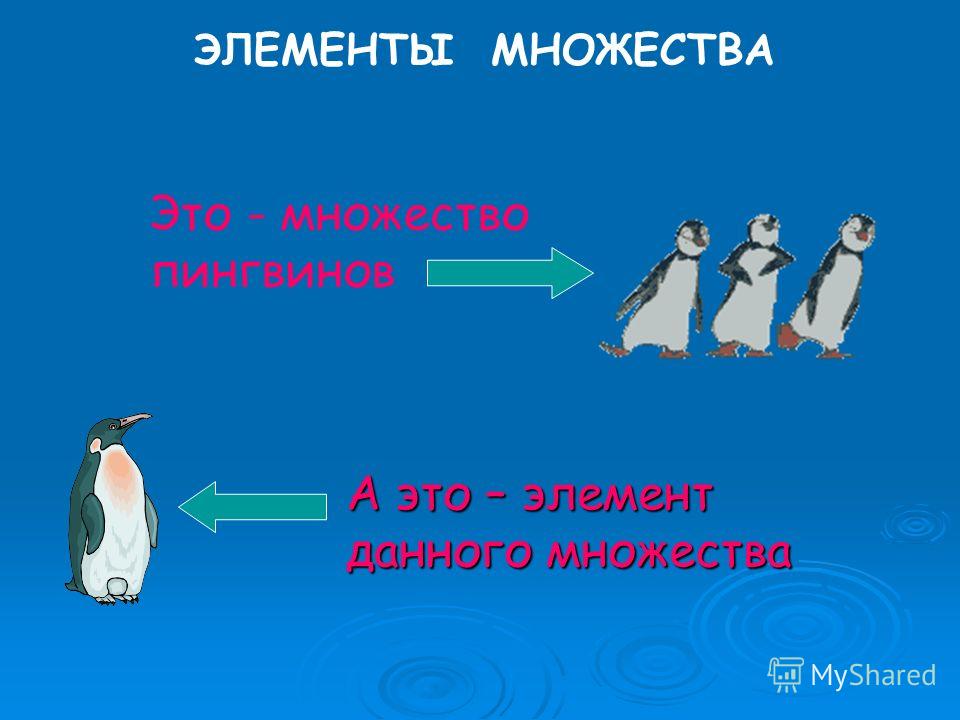
1. Введение понятий «множество», «элемент множества»

Начинаем изучение новой темы с вопроса: От какого слова происходит слово “множество”? Дети отвечают: От слова “много” и в этот момент надо пояснить, что “множество” обозначает необязательно большую группу предметов или существ, оно может включать совсем немного предметов, или очень-очень много предметов, или же вовсе ничего (тогда это будет “пустое множество”).

Историческая справка: Георг Кантор считается основателем теории множеств.

В 1860 году Георг закончил с отличием реальное училище в Дармштадте; учителя отмечали его исключительные способности к математике, в частности, к тригонометрии.

Далее предлагается найти в классе множество предметов, имеющих одно и то же имя:

множество учеников;

множество столов;

множество стульев;

множество окон;

и т.д.

Попрошу встать:

множество мальчиков,

затем множество девочек

похлопайте множество 5 класса.

Формативное оценивание. Приём «Большой палец»

Ответы учащихся оцениваются жестами:

«Палец вверх» – ответ правильный.

«Палец влево» – ответ неточный.

«Палец вниз» – неверный ответ.

Следовательно, делаем вывод: “Множество – это группа предметов или существ, объединенных общим признаком, действием или именем”.

Игра “Из какого множества”. Учитель перечисляет, а ученики дают название множеству перечисляемых объектов: принадлежит и непринадлежит знаки.

Принтер, монитор, мышь, процессор – устройства компьютера;

Волгоград, Муром, Тверь, Омск, Москва – города России;

Подснежники, ландыши, мать и мачеха, василек – полевые цветы;

Лиза, программа, картошка, сказка, лужа – слова заканчиваются на “а”.

— Значит, в нём нет ни одного элемента. Про такое множество говорят что это пустое множество, т.е пустое множество это множество в котором нет ни одного элемента. Изображение множеств.

Деление учащихся на 2 группы:

Учащиеся выбирают висящие на доске стикеры на обратной стороне у них нарисованы геометрический фигуры (квадрат, треугольник, окружность), выбирают название коменды и капитана.

Метод Карусель; Команды представляются, и садятся на свою станцию. Решают задание своей станции, записывают ответ в маршрутный лист. Время работы на каждой станции 3 минуты. Взаимопрверка ответов по командам. Обратная связь По истечению времени звучит сигнал. группы всем составом по часовой стрелке переходят от одной станции к другой, пока все станции не будут пройдены.

Критерий оценивания

Задание группам:

1 станция «Определение»: Составь определение множества, элементов множества (из слов на бумаге) (клеят)

ФО: Учитель на слайде показывает правильный ответ и учащиеся проводят взаимопроверку

Обратная связь: Каждая группа комментирует свои оценки.

Учитель; Ребята, те кто допустил ошибки, что вам нужно повторить?

2 станция «Соответствия»:

Семга, форель, карп, окунь, щука

Сапоги, ботинки, сандалии, кроссовки, туфли

Мяч, обруч, скакалка, ракетка, клюшка

Найдите соответствие – рыбы, – обувь, – спортивные снаряды.

ФО: Учитель на слайде показывает правильный ответ и учащиеся проводят взаимопроверку

Обратная связь: Учитель: – Ребята, кто допустил ошибки, что вам нужно повторить?

Каждая группа комментирует свои оценки.

3 станция «Игра»

Игра1 для всех «Найди лишнее»

1) Тюльпан, лилия, фасоль, ромашка.
2) Река, озеро, мост, море.
4) Курица, петух, орёл, гусь.
5) Саша, Витя, Петров, Коля.

Игра 2 для учащегося с особыми потребностями

«Дай название множеству»

1) Окунь, карась, щука –
2) Дерево, цветок, трава – 
4) Слон, муравей, пингвин – 
5) Шляпа, фуражка, кепка –

ФО: Учитель на слайде показывает правильный ответ и учащиеся проводят взаимопроверку

Обратная связь: Каждая группа комментирует свои оценки.

Учитель; Ребята, кто допустил ошибки, что вам нужно повторить?

4 станция «Задания»:

Задание

1) Пусть А – множество четных чисел. Является ли элементом данного множества число:

  1. 5;

  2. 12;

  3. 34.

Дескриптор: Обучающийся

– определяет принадлежность числа заданному множеству.

ФО: Учитель на слайде показывает правильный ответ и учащиеся проводят взаимопроверку

Обратная связь: Каждая группа комментирует свои оценки.

Учитель; Ребята, кто допустил ошибки, что вам нужно повторить?

5 станция «Определить истинность утверждения»:

Задание

Определите истинность утверждений:

Истина

Ложь

Множества обозначаются заглавными буквами латинского алфавита.

Любое множество содержит минимум один элемент.

Все элементы множества можно обозначить заглавными буквами латинского алфавита.

Множество, содержащее хотя бы один элемент, называется непустым множеством.

Дескриптор: Обучающийся

– указывает истинные утверждения на основе определений, связанные с понятием «множество».

ФО: Учитель на слайде показывает правильный ответ и учащиеся проводят взаимопроверку

Обратная связь: Каждая группа комментирует свои оценки.

Учитель: – Ребята, кто допустил ошибки, что вам нужно повторить?

ФО: по окончании работы учащиеся обсуждают работу товарищей и выставляют баллы за работу в группе

– Как вы справились с заданиями?

ФО: Приём «Большой палец»

Учащиеся поднимают большой палец руки вверх, если хорошо справились с заданиями

Учащиеся отводят большой палец руки в сторону, если были затруднения при выполнении заданий

Учащиеся опускают большой палец руки вниз, если совсем не справились с работой

Обратная связь:

– Какое задание вызвало наибольшие трудности?

– Какое задание было лёгким?

– Объясните почему?

Физминутка: «Танцующий скелет»

(песня на английском языке)

Деление учащихся на пары.
Учащиеся выбирают висящие на доске стикеры на обратной стороне которых нарисованы геометрический фигуры (квадрат, треугольник, окружность (фигур по 2 шт) и т д)

Каждой паре учеников предлагаются карточки с тремя дифференцированными заданиями из учебника. На карточках учащиеся подписывают имя и фамилию, и выполняют вычисления.

Дифференцированые задания

(учащиеся самостоятельно выбирают уровень, но могут советоваться в паре по решению задания)

Работа по учебнику стр 94-95.

Уровень А № 1017 стр 95-оценка «3»

Уровень В № 1019 – оценка «4»

Уровень С № 1026 – оценка «5»

ФО: Учитель на слайде показывает правильный ответ и учащиеся проводят взаимопроверку

ФО: Приём «Большой палец»

Учащиеся поднимают большой палец руки вверх, если хорошо справились с заданиями

Учащиеся отводят большой палец руки в сторону, если были затруднения при выполнении заданий

Учащиеся опускают большой палец руки вниз, если совсем не справились с работой

Обратная связь

– Что в заданиях вызывало у вас затруднения?

Самостоятельная работа

Учащиеся самостоятьельно выполняют задания.

Критерий оценивания Обучающийся

Применяет соответствующие символы при работе с множествами

Задание

Запишите выражение, используя символы , , 

  1. элемент а принадлежит множеству А;

  2. пустое множество;

  3. число 1,5 не принадлежит множеству N;

Дескриптор: Обучающийся

– записывает выражение, используя символы объединения / – записывает выражение, используя символы принадлежности;

– записывает выражение, используя символ пустого множества.

ФО: Учитель на слайде показывает правильный ответ и учащиеся проводят взаимопроверку

Обратная связь

– Что в заданиях вызывало у вас затруднения?

Историческая справка

Слайд

Слайд

Слайд

Слайд

Слайд

Маршрутные листы с названием станций

Видеоролик

https://www;youtube

III.

Конец урока

1 мин

1 мин

1 мин

Проверка результатов и подведение итогов урока;

ФО: Учащиеся выполняют подсчет общего колличества баллов и выставляют в индивидуальный оценочный лист.

Обратная связь

– Что мы повторили сегодня на уроке?

– Какие задания вам понравились?

– Какие задания вызывали затруднения?

Домашнее задание 1 мин.

Дифференцированые задания

(учащиеся самостоятельно выбирают уровень)

Уровень А № 1017 стр 95

Уровень В № 1019

Уровень С Со­ставь­те 3 за­да­чи на мно­же­ство и его эле­мен­ты(творческое задание).

Рефлексия: Стратегия «Лестница успеха».

ФО: Каждый учащийся должен отметить на какой ступеньки он находится на данном этапе урока и крепт свой стикер на лестницу

Лист оценивания

Учебник «Математика5»

Алматы: Мектеп

Стикеры

Дифференциация – каким способом вы хотите больше оказывать поддержку? Какие задания вы даете ученикам более способным по сравнению с другими?

Оценивание – как Вы планируете проверять уровень усвоения материала учащимися?

Охрана здоровья и соблюдение техники безопасности

На уроке используются дифференцированные задания с учетом индивидуальных способностей учащихся, задания на урок подобраны по принципу «От простого к сложному». Для работы в группе учащимся предлагаются задания трех уровней сложности, чтобы каждый ученик выбрал себе посильное задание.

На этапе проверки знаний учащихся применяется приём мяч, оценивание проходит при помощи задания устного счета, групповой работы оцениваются при помощи индивидуального оценочного листа.

На уроке проводится подвижная физминутка; Происходит смена видов деятельности для снижения утомляемости учащихся, перед уроком проветривается помещение.

Рефлексия по уроку

Была ли реальной и доступной цель урока или учебные цели?

Все ли учащиесы достигли цели обучения? Если ученики еще не достигли цели, как вы думаете, почему? Правильно проводилась дифференциация на уроке?

Эффективно ли использовали вы время во время этапов урока? Были ли отклонения от плана урока, и почему?

Используйте данный раздел урока для рефлексии. Ответьте на вопросы, которые имеют важное значение в этом столбце.

Итоговая оценка

Какие две вещи прошли действительно хорошо (принимайте в расчет, как преподавание, так и учение)?

1:

2:

Какие две вещи могли бы улучшить Ваш урок (принимайте в расчет, как преподавание, так и учение)?

1:

2:

Что нового я узнал из этого урока о своем классе или об отдельных учениках, что я мог бы использовать при планировании следующего урока?

Урок 2. Способы задания множеств

1

Условие:

Решение:

Советы:

Найди, что общего между всеми предметами на одной картинке

2

Условие:

Решение:

Советы:

Когда  какие-нибудь  объекты  собирают  вместе,  в  математике  используют для их названияобщее слово — множество.

3

Условие:

Решение:

Советы:

Прежде чем выполнять это задание, прочитай стихотворение С.  Я.  Маршака

4

Условие:

Решение:

Советы:

Загляни к себе в портфель, чтобы перечислить множество предметов, которые лежат у тебя в портфеле

5

Условие:

Решение:

Советы:

Подумай и ответь на вопросы, как ты сам думаешь

6

Условие:

Решение:

Советы:

Придумывая множество с конечным числом элементов, внимательно посмотри вокруг себя, например, дома, ты можешь найти кучу примеров для решения этой задачи.

7

Условие:

Решение:

Советы:

Найди общее среди элементов множества

8

Условие:

Решение:

Советы:

Множество  задано,  если  определены  его  элементы,  то  есть  о  любом объекте  можно  точно  сказать,  является  ли  он  элементом  этого множества или нет.

9

Условие:

Решение:

Советы:

Вспомни правила, которые проходили ранее

10

Условие:

Решение:

Советы:

Если используем предлог "в", то значит умножаем или делим, если же предлог "на", то вычитаем или складываем.

11

Условие:

Решение:

Советы:

Нужно пройти от одной стены класса к другой и посчитать шаги.

12

Условие:

Решение:

Советы:

1м=100см
1дм=10см

13

Условие:

Решение:

Советы:

Прежде чем вычислять, убедись, что у тебя везде одинаковые единицы измерения

14

Условие:

Решение:

Советы:

Чтобы выполнить проверку, нужно из суммы вычесть одно из слагаемых, если получилось другое слагаемое, значит пример решен верно

15

Условие:

Решение:

Советы:

Соединяй точки последовательно

16

Условие:

Решение:

Советы:

перечисли все трехзначные числа, где встречаются только цифры 3 и 6

Петерсон математика 3 клас 4 частина відповіді

Скачать петерсон математика 3 клас 4 частина відповіді djvu

4 класс. Математика. Петерсон Л.Г. Автор: Петерсон Л.Г. Издательство: Ювента Решебник (ГДЗ) для 4 класса по математике ФГОС часть 1, часть 2, часть 3. Авторы учебника: Петерсон Л.Г Содержит в себе полные и подробные ответы на все упражнения онлайн на пять фан.

ГДЗ к учебнику по математике за 4 класс Петерсон Л.Г. (Учусь учиться). ГДЗ к рабочей тетради по математике за 4 класс Петерсон Л.Г. (Учусь учиться). ГДЗ к самостоятельным и контрольным работам по математике за 4 класс Петерсон Л.Г. (Учусь учиться). Часть 1. страницы учебника. 1. ГДЗ математика 3 класс учебник Петерсон. автор: Петерсон Л.Г. ГДЗ к рабочей тетради по математике за 3 класс Петерсон можно смотреть здесь.

Часть 1 (учебник). Урок 1. Множество и его элементы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Урок 2. Задание множества перечислением и свойством: 1 2 3 4 5 6 7 8 9 10 11 12 Урок 3. Равные множества. Пустое множество: 1 2 3 4 5 6 7 8 9 10 11 12 Урок 4. Диаграмма Венна. Знаки G и £: 1 2 3 4 5 6 7 8 9 10 11 12 Урок 5. Диаграмма Венна. Знаки G и £: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Урок 6. Подмножество: 1 2 3 4 5 6 7 8 9 10 11 Урок 7. Решение задач: 1 2 3 4 5 6 7 8 9.

Авторы: Петерсон Л.Г. Ваш ребёнок перешёл в 3-й класс, а математика осталась для него загадкой? Не упустите этот важный момент его развития, садитесь за учебник и занимайтесь вместе. В помощь всем заботливым родителям – сборник ГДЗ по математике к учебнику Л. Г. Петерсон. Школьный курс направлен на решение простых примеров, задач на логику, быстрый счёт. В этом возрасте ваш ребёнок должен дружить с цифрами, применять их на практике и не бояться незнакомых символов.

Только вместе с решебником вы найдёте простой способ объяснить школьнику неведанное и новое. ГДЗ учебник по математике 3 класс Петерсон. ГДЗ Математика 3 класс Петерсон. авторы: Петерсон. издательство: “Ювента” год. Задачи. Математика. 1 – 4 классы. Математика 4 клас 3 частина л.г.петерсон страница 80 №4.

1. Смотреть ответ.  Новые вопросы в Математика. Найти экцентириситет эллипса. Если: 9x²+15y²=а)E=0,6б)E=0,7в)E=0,9.

Математика, 3 класс, Л.Г. Петерсон. 3 КЛАСС. Решебник по математике для 3 класса. Авторы: Петерсон Л.Г. Издательство: Ювента Темы учебника. Часть 1. Урок 1. Множества и элементы. Урок 2. Способы задания множеств.

Урок 3. Равные множества. Пустое множество. Решение задания 1 урока 4 к учебнику по математике за 3 класс автора Петерсон часть 3.  ГДЗ(готовые домашние задания), решебник онлайн по математике за 3 класс автор Петерсон часть 3 урок 4, задание 1 – вариант решения задания 1.

Часть 1: Урок 1: 1 2 3 4 5 6 7 8 9 10 11 12 13 Урок 2: 1 2 3 4 5 6 7 8 9 10 11 Урок 3: 1 2 3 4 5 6 7 8 9 10 11 Урок 4: 1 2 3 4 5 6 7 8 9 10 11 Урок 5: 1 2 3 4 5 6 7 8 9 10 11 12 13 1-класс 2-класс 3-класс 4-класс 5-класс 6-класс 7-класс 8-класс 9-класс класс класс.

Решебники для 4-го класса. Учебники для 4-го класса. Учебники за 4 класс > Математика > Л.Г. Петерсон. Учебник Математика 4 класс Л.Г. Петерсон ( год) Часть 3. Авторы: Л.Г. Петерсон. Год: |. Класс: 4 |. Предмет: Математика |. Похожие учебники (2) +. Математика 4 класс Л.Г. Петерсон ( год) Часть 1. Математика 4 класс Л.Г. Петерсон ( год) Часть 2. Решебник: Математика 4 класс Л.Г. Петерсон ( год) Часть 3. Читать онлайн. Скачать учебник.

Урок 1. Сравнение угловстр. 1 – 4.

rtf, PDF, txt, txt

Похожее:

  • Різдвяна історія пісня
  • Гдз 4 клас українська мова 2 частина вправа 65
  • Презентація на тему гриби в біосфері та житті людини
  • Фізика 10 клас ненашев збірник
  • Англійська мова 5 клас робочий зошит о м павличенко
  • Рідна мова 5 клас плани-конспекти уроків
  • Урок 11 клас проголошення незалежності україни
  • Алгебра геометрія 7 клас зошит для контрольних і самостійних робіт корнес

    • Гдз математика петерсон росток 3 клас

    Скачать гдз математика петерсон росток 3 клас txt

    Условия правильного использования ГДЗ по математике за 3 класс, Петерсон. Каждый ребенок – индивидуален, и способности у учеников разные. Сложности в понимании математических правил периодически возникают почти у всех младшеклассников.  качественней готовиться к урокам, глубже изучить и понять материал, пройденный в классные часы; уверенней чувствовать себя на самостоятельной или контрольной работе, во время прохождения тестов.

    Родителям важно объяснить детям, что ГДЗ по математике для 3 класса от Петерсон используется не для бездумного списывания верных ответов, а для комплексной подготовки номеров домашнего задания. Главная» Решебники, ГДЗ» ГДЗ – Математика. 3 класс – Петерсон Л.Г.

    ГДЗ – Математика. 3 класс – Петерсон Л.Г. cкачать в PDF. В пособии выполнены и в большинстве случаев подробно разобраны задания и упражнения из учебника “Математика. 3 класс”. В 3-х частях. Пособие адресовано родителям, которые смогут проконтролировать детей, а в случае необходимости помочь им в выполнении домашней работы по математике.

    Рубрика: Решебники, ГДЗ / Математика. Автор: Петерсон Л.Г. Год: Для учеников: 3 класс. Язык учебника: Русский. Формат: PDF. Петерсон Л.Г. ГДЗ к учебнику математике за 3 класс. АВТОР: Петерсон Л.Г., У нас вы найдете ответы к учебнику по математике за третий класс авторов Петерсон Л.Г. года выпуска. Мы собрали для вас только самые лучшие решебники и ГДЗ по математике.

    Ответы. Ответы на задания по математике за третий класс к учебнику Петерсон Л.Г. Часть 1. Урок 1: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Урок 2: 1 2 3 4 5 6 7 8 9 10 11 12 Урок 3: 1 2 3 4 5 6 7 8 9 10 11 12 Урок 4: 1 2 3 4 5 6 7 8 9 10 11 12 Урок 5: 1 2 3. 4 5 6 7 8 9 10 11 12 13 14 Урок 6: 1 2 3 4 5 6 7 8 9 10 11 Урок 7: 1 2 3 4 5 6 7 8. Урок 2 Задание 10 – ГДЗ по математике 3 класс (Петерсон Л.Г.) Часть 1.

    UrokiTV. UrokiTV. • Текущее видео. Урок 2 Задание 11 – ГДЗ по математике 3 класс (Петерсон Л.Г.) Часть 1. UrokiTV. Готові домашні завдання (ГДЗ) спеціально для підручника “Математика”, 3 клас автором якої являється Л.Г. Петерсон. Завдяки нам та своєю роботою з даним сайтом ви завжди будете отримувати найвищі бали за зроблені домашні завдання. Тільки у нас ГДЗ онлайн і безкоштовно, що головне, у теперішній важкий час.

    CHELIK Войдите: Отправить.

    Рабочая тетрадь по математике за 3 класс автора Петерсон Л.Г. года издания. Первая часть тетради содержит 34 урока на 64 страницах. Ученики 3 класса найдут готовые решения по следующим темам: множество и его элементы, многозначные числа, умножение на 10//, деление на 10//, единицы длины, единицы массы и т.д. Школьникам будут предложены готовые решения по таким видам заданий, как примеры, задачи, сравнение чисел, уравнение, работа с множествами, поиск решений с помощью рисунков, поиск суммы разрядных слагаемых и пр.

    УМК Математика 3 класс Петерсон. Математика. Петерсон Л.Г. 3. 1-класс 2-класс 3-класс 4-класс 5-класс 6-класс 7-класс 8-класс 9-класс класс класс. Решебники для 3-го класса. Учебники для 3-го класса. Решебники за 3 класс > Математика > Л.Г. Петерсон. Решебник (ГДЗ) Математика 3 класс Л.Г. Петерсон ( год) Часть 1. Авторы: Л.Г. Петерсон. Год: |. Класс: 3 |. Предмет: Математика |. Похожие ГДЗ (2) +. Математика 3 класс Л.Г. Петерсон ( год) Часть 2.

    Математика 3 класс Л.Г. Петерсон ( год) Часть 3. Учебник: Математика 3 класс Л.Г. Петерсон ( год) Часть 1. Урок 1. Множество и его элементы№ Петерсон Л.Г. ГДЗ к учебнику математике за 3 класс. АВТОР: Петерсон Л.Г., У нас вы найдете ответы к учебнику по математике за третий класс авторов Петерсон Л.Г. года выпуска. Мы собрали для вас только самые лучшие решебники и ГДЗ по математике. Ответы. Ответы на задания по математике за третий класс к учебнику Петерсон Л.Г.

    Часть 1. Урок 1: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Урок 2: 1 2 3 4 5 6 7 8 9 10 11 12 Урок 3: 1 2 3 4 5 6 7 8 9 10 11 12 Урок 4: 1 2 3 4 5 6 7 8 9 10 11 12 Урок 5: 1 2 3. 4 5 6 7 8 9 10 11 12 13 14 Урок 6: 1 2 3 4 5 6 7 8 9 10 11 Урок 7: 1 2 3 4 5 6 7 8.

    PDF, EPUB, EPUB, doc

    Похожее:

  • Контрольна робота з математики 6 клас мерзляк варіант 2
  • Біологія планування 11 клас
  • Відповіді на зошит з хімії 7 клас титаренко
  • Яке значення має повітря презентація
  • Мова як етноформуюча ознаки етносу
  • Рамка українська вишивка
  • Усі уроки хімії 10 клас відповіді
  • Українська мова 5 клас для шкіл з російською мовою навчання

    • ch07.indd

    % PDF-1.6 % 699 0 объект / M (D: 20110125145506-06’00 ‘) / Имя (ARE Acrobat Product v8.0 P23 0002337) / ByteRange [0 116 9650 2583256] / Ссылка [> / Data 699 0 R / TransformMethod / UR3 / Type / SigRef> >] / Prop_Build> / App> / PubSec >>> / Type / Sig >>>> / Metadata 778 0 R / AcroForm 774 0 R / Pages 689 0 R / Type / Catalog / PageLabels 687 0 R >> эндобдж 700 0 объект > эндобдж 778 0 объект > поток PScript5.dll версии 5.2.22011-01-25T14: 55: 06-06: 002011-01-25T08: 23: 13-08: 002011-01-25T14: 55: 06-06: 00application / pdf

  • ch07.indd
  • пользователь
    • Acrobat Distiller 8.1.0 (Windows) uuid: fff082e9-29c8-4cc8-abf3-538c9d05b7efuuid: ed82956f-4e87-4a9c-96a4-46a3710a0004 конечный поток эндобдж 774 0 объект > / Кодировка >>> / SigFlags 2 >> эндобдж 689 0 объект > эндобдж 687 0 объект > эндобдж 688 0 объект > эндобдж 690 0 объект > эндобдж 691 0 объект > эндобдж 692 0 объект > эндобдж 693 0 объект > эндобдж 694 0 объект > эндобдж 695 0 объект > эндобдж 534 0 объект > эндобдж 541 0 объект > эндобдж 547 0 объект > эндобдж 552 0 объект > эндобдж 559 0 объект > эндобдж 566 0 объект > эндобдж 568 0 объект > поток h ބ Vn6} ẈTh% E) @C “* tq,> / u1” p̙3_ “A E2igh9gT] I} ^ D: ($ q | L * I & Vkhq j (uZ1) NP: g ## b9ZF3Vgw> (3d? T8t? OȨpi $ m 0CxMa3xh¼} W -> – jefr / 2PUN% Q) ILq ܪ ev # b2 {b

    IJ [uƭ # – ɋ! X8pxMQ3 .XμL9Π9DЮyhWCpcj> T 猈 uH (܇` X72KA.Vş> 4 ~ $ BKilsy ه (gM @ TT8dOe> Ś2Drs ~ vL_m [> {ԝp! B: + w5: WÉz’u \>; iSwTR5 ‘) T2 S’Otevq W _ :! ԕ5 # U! FjuUVX [jmЧ% 9Dyo06) q`fjZ

    Самореализующиеся пророчества в классе: ожидания учителей, отзывы учителей и достижения учеников

    https://doi.org/10.1016/j. learninstruc.2019.101296Получить права и контент

    Основные моменты

    •

    Ранние ожидания учителя предсказывают, что ученики будут учиться в первый год обучения.

    •

    Эффект ожидания учителя сильнее в чтении, чем в математике.

    •

    Различия в ожиданиях учителей приводят к разным отзывам учителей.

    •

    Отзывы учителей не оказывают существенного влияния на ожидаемые результаты учителей.

    Реферат

    В этом исследовании изучалась связь между ожиданиями учителя и обучением учащихся, опираясь на лонгитюдные данные из 64 классных комнат и 1026 учеников первого класса в Германии. Далее, на основе подвыборки из 19 классных комнат с 354 учениками, мы исследовали посредническую роль трех характеристик отзывов учителей, оцениваемых в видеозаписях школьных уроков.Результаты показали, что ожидания учителей были в некоторой степени неточными; то есть они не полностью согласны с текущими достижениями, общими когнитивными способностями и мотивацией учащихся. Кроме того, эта неточность в ожиданиях учителя в значительной степени предсказывала достижения учащихся в конце учебного года, даже после предыдущих достижений, учитывались общие когнитивные способности, мотивация и характеристики учащегося. В частности, неточно завышенные ожидания учителя были связаны с более высокими достижениями в чтении и математике, в то время как неточно низкие ожидания учителей были связаны с более низкими достижениями только в чтении.Кроме того, отзывы учителей значительно варьировались в зависимости от неточных ожиданий учителей, но не оказали существенного влияния на ожидаемые результаты учителей.

    Ключевые слова

    Самоисполняющееся пророчество

    Ожидания учителя

    Отзывы учителей

    Взаимодействие учителя и ученика

    Видеография

    Рекомендуемые статьиЦитирующие статьи (0)

    © 2020 Авторы. Опубликовано Elsevier Ltd.

    Рекомендуемые статьи

    Цитирующие статьи

    Наблюдение в классе – цели наблюдения в классе, ограничения наблюдения в классе, новые направления – студенты, исследования, учителя и преподавание

    Систематическое наблюдение в классе – это количественный метод измерения поведения в классе на основе прямых наблюдений, который определяет как события или поведения, которые необходимо наблюдать, так и то, как они должны быть записаны.Как правило, данные, собранные с помощью этой процедуры, фокусируются на частоте, с которой определенные поведения или типы поведения проявляются в классе, и измеряют их продолжительность. Есть несколько элементов, которые являются общими для большинства систем наблюдений.

    • Цель наблюдения
    • рабочих определений всех наблюдаемых моделей поведения
    • процедур обучения наблюдателей
    • особый объект наблюдения
    • установка
    • единица времени
    • график наблюдений
    • метод записи данных
    • – метод обработки и анализа данных (Stallings and Mohlman, pp.469–471)

    До использования систематических методов наблюдения исследования эффективного обучения обычно состояли из субъективных данных, основанных на личных и анекдотических отчетах об эффективном обучении. Чтобы разработать научную основу для обучения, исследователи начали использовать более объективные и надежные методы систематического наблюдения в классе. В последней четверти двадцатого века несколько сотен различных систем наблюдений были разработаны и использовались в классных комнатах.Аналогичным образом с 1970-х годов были проведены сотни исследований, в которых использовались системы наблюдения в классе.

    Несмотря на то, что существует несколько типов процедур или методов наблюдения, которые использовались для проверки эффективного обучения (например, диаграммы, рейтинговые шкалы, контрольные списки и повествовательные описания), наиболее широко используемой процедурой или методом исследования было систематическое наблюдение в классе, основанное на интерактивном системы кодирования. Эти интерактивные системы кодирования позволяют наблюдателю записывать практически все, что студенты и учителя делают в течение заданного промежутка времени.Эти системы взаимодействия очень объективны и обычно не требуют от наблюдателя делать каких-либо серьезных выводов или суждений о поведении, которое они наблюдают в классе. Другими словами, эти системы наблюдения с низким уровнем логического вывода обеспечивают конкретное и легко идентифицируемое поведение, которое наблюдатели могут легко кодировать. Некоторые из наиболее часто используемых инструментов наблюдения – это система диадического взаимодействия Брофи-Гуда, система наблюдения за сваливанием и расписание наблюдений в классе. Все они широко использовались в исследованиях и в проектах повышения квалификации учителей, направленных на улучшение обучения в классе.

    Некоторые из основных преимуществ использования наблюдения в классе позволяют преподавателям делать следующее: (1) разрешать исследователям изучать процессы обучения в естественных условиях; (2) предоставлять более подробные и точные доказательства, чем другие источники данных; и (3) стимулировать изменения и убедиться, что изменение произошло. Также было обнаружено, что описания учебных мероприятий, предоставляемые этим методом, приводят к лучшему пониманию и лучшим моделям для улучшения обучения.

    Последней сильной стороной этого метода исследования является то, что результаты этих наблюдательных исследований предоставили последовательную, хорошо обоснованную базу знаний об эффективном обучении.Многие обзоры и резюме исследований по наблюдению в классе, такие как исследование Херба Уолберга (1991, 1995), неизменно указывают на то, что некоторые виды поведения в классе в значительной степени связаны с академической успеваемостью учащихся. Было обнаружено, что некоторые аспекты обучения в классе, такие как проведение ежедневных обзоров, представление нового материала, проведение управляемой практики, предоставление отзывов и исправлений, проведение независимой практики и проведение еженедельных и ежемесячных обзоров, в значительной степени связаны с академической успеваемостью учащихся.Другими словами, исследования с использованием систематических наблюдений в классе предоставили нам существенную базу знаний, которая помогла нам понять эффективное преподавание.

    Цели наблюдения в классе

    Наблюдение в классе преследует множество важных и важных образовательных целей. В этом разделе резюмируются три важные цели или области, в которых систематическое наблюдение в классе широко использовалось: (1) описание учебных практик; (2) исследование неравенства в обучении для разных групп студентов; и (3) улучшение обучения учителей в классе на основе обратной связи от индивидуальных профилей в классе или школе.

    Описание учебных процессов. Одной из фундаментальных целей исследования в классе является описание текущего статуса учебной практики и выявление учебных проблем. По словам Тома Гуда, «одна из задач наблюдательного исследования – описать то, что происходит в классных комнатах, чтобы очертить сложные практические проблемы, с которыми сталкиваются практикующие» (стр. 337). Было проведено множество наблюдательных исследований, специально разработанных для описания конкретных образовательных явлений.Например, крупномасштабные обсервационные исследования, такие как Кен Сиротник и Херш Ваксман, Шву-Йонг Хуанг и Иоланда Падрон, изучали методы обучения в начальной и средней школах. Сиротник обследовал 1000 начальных и средних классов и обнаружил, что практика преподавания по предметам и классам очень незначительна. Он обнаружил, что большая часть учебного времени проводилась либо с учителем, читающим лекции классу, либо с учениками, выполняющими письменные задания. Ваксман, Хуанг и Падрон наблюдали за девяносто шестыми и восьмыми классами шестнадцати городских средних школ и обнаружили результаты, аналогичные результатам Сиротника.Студенты обычно участвовали в обучении в классе и не общались ни со своим учителем, ни с другими учениками. Учащиеся редко выбирали свои собственные учебные занятия и, как правило, были очень пассивны в классе, часто просто наблюдая или слушая учителя, хотя было обнаружено, что они выполняли задание около 94 процентов времени. Результаты наблюдения учителей показали, что учителя обычно сосредотачивались на содержании задачи или задания, реагировали на сигналы учеников, передавали процедуры задания и проверяли работу учеников.Было замечено, что учителя тратят очень мало времени, общаясь с учениками по личным вопросам, поощряя учеников к успеху, проявляя личное уважение к ученикам и проявляя интерес к работе учеников.

    Другой пример описательных наблюдательных исследований касается степени использования технологий в классе. Хотя было проведено большое количество исследований, посвященных изучению использования технологий в школах, большинство из них основывались на данных самоотчетов администраторов, учителей или учеников.Однако эти типы данных часто ненадежны и имеют тенденцию иметь тенденцию к увеличению в сторону завышения фактического объема использования технологий. Таким образом, важно наблюдать за фактической степенью использования технологий в классных комнатах и ​​конкретно смотреть на технологии, используемые в классе и используемые отдельными учащимися. В одном из таких исследований Ваксман и Хуанг (1995) использовали систематическое наблюдение в классе, чтобы изучить, в какой степени компьютерные технологии были интегрированы в учебную программу 200 городских классов начальной и средней школы.Они обнаружили, что не было интеграции (то есть использования) компьютерных технологий в классах начальной школы, и что ученики работали с компьютерами только 2 процента учебного времени в классах средней школы. Хуанг и Ваксман (1996) также провели систематические наблюдения за 1315 учениками средней школы из 220 классов математики, чтобы изучить количество используемых технологий. Описательные результаты показали, что ученики наблюдали за использованием калькуляторов около 25 процентов учебного времени, но они использовали компьютеры менее 1 процента учебного времени на уроках математики.

    Некоторые другие применения описательных наблюдательных исследований заключались в оценке программ и, более конкретно, в оценке точности или степени выполнения программ; исследовать, в какой степени в школах делается упор на мыслительные процессы более высокого уровня; и изучить, в какой степени многокультурное образование уделяется в городских классах. Последнее важное использование включает исследования эффективности школы, такие как исследование Waxman et al. 1997 г., в котором данные наблюдений в классе использовались для исследования наблюдаемых различий между эффективными и неэффективными школами.Ваксман и Хуанг (1997), например, наблюдали за более чем 700 учениками из четырех эффективных и четырех неэффективных городских начальных школ, которые обслуживали преимущественно афроамериканских учеников, и обнаружили, что значительно больше учеников из эффективных школ работали в индивидуальной обстановке, взаимодействуя друг с другом. со своим учителем и работая над письменными заданиями. С другой стороны, учащиеся из неэффективных школ, наблюдаемые в условиях целого класса, значительно меньше взаимодействовали со своим учителем, взаимодействовали с другими, читали и работали с манипулятивными материалами, чем учащиеся из эффективных школ.

    Расследование неравенства в обучении. Несколько исследований, таких как исследование Элизабет Феннема и Пенелопа Петерсон, показали, что некоторые группы или типы учеников по-разному рассматриваются учителями в классах, и что эти несправедливые модели взаимодействия учителя и ученика в классах приводят к разным результатам обучения для учеников. Например, было проведено множество исследований, которые выявили гендерный дисбаланс в моделях взаимодействия учителей в классе. Обзор исследования Джера Брофи и Тома Гуда в 1974 году показал, что в классах существуют устойчивые гендерные различия в моделях взаимодействия учителей.Например, мальчики, как правило, получают больше похвалы и критики в классе, чем девочки. Они также обнаружили, что учителя больше взаимодействуют с мальчиками в поведенческих, процедурных и академических вопросах, чем с девочками. Было также установлено, что мальчики задают больше вопросов в классе, а учителя задают мальчикам больше вопросов. Гуд и его коллеги (1987,1988) также провели несколько наблюдательных исследований, в ходе которых изучали, почему учащиеся с низкой успеваемостью в средних школах задают меньше вопросов, чем ученики с высокими достижениями.Они также обнаружили, что учащиеся начальной школы с доходом от среднего класса задавали больше вопросов, чем ученики из школ с низким средним классом.

    В других исследованиях изучались как половые, так и этнические различия в классе. Харт исследовал взаимосвязь между взаимодействием учителя и ученика и успеваемостью по математике в разбивке по расе и полу. Она обнаружила следующие различия: (1) белые и черные ученики мужского пола чаще общались в классе, чем студенты из других групп; (2) различия в типах взаимодействия между белыми и черными студентами; и (3) мальчики участвовали в большем общении с учителями, чем девочки.Другими словами, похоже, что модели взаимодействия учителя и ученика могут зависеть не только от пола ученика, но и от его этнической принадлежности.

    Падрон, Ваксман и Хуанг наблюдали различия в поведении учащихся между устойчивыми (т.е. успешными) и неустойчивыми (т.е. менее успешными) учащимися начальной школы из низкого социально-экономического положения. Они обнаружили, что устойчивые ученики тратят значительно больше времени на взаимодействие с учителями в учебных целях, тогда как неустойчивые ученики проводят больше времени, взаимодействуя с другими учениками в социальных или личных целях.Устойчивые студенты также наблюдали или слушали значительно чаще, чем неустойчивые студенты, тогда как последние наблюдались чаще, не уделяя внимания заданию. Процент времени, в течение которого устойчивые ученики наблюдались за выполнением задания (85%), был намного выше, чем у неустойчивых учеников (61%). Масштабы этих различий были как статистически, так и образовательно значимыми и иллюстрируют образовательное неравенство, существующее в классах.

    Совершенствование педагогической практики.Исследования с использованием методов наблюдения дали важную информацию, которая имеет практическое значение для улучшения практики преподавания. Одной из традиционных проблем, мешающих учителям проводить занятия в классе, было отсутствие достоверной и точной информации, которую учителя могли бы использовать для содействия своему профессиональному росту. Многие учителя, даже опытные, не всегда осознают характер своего взаимодействия с отдельными учениками. Следовательно, одной из наиболее важных целей систематического наблюдения в классе является улучшение работы учителей в классе.Было обнаружено, что обратная связь с профилями отдельных классов, полученная в результате систематических наблюдений, помогает учителям понять свои сильные и слабые стороны и, следовательно, позволяет им значительно улучшить свое обучение. Благодаря обратной связи учителя могут узнать, как функционирует их класс, и, таким образом, внести желаемые изменения. Этот процесс обычно включает в себя систематическое наблюдение за учителями и их учениками в классах подготовленных наблюдателей, а затем предоставление учителям информации об их инструкциях на клинических занятиях.Этот подход основан на предположении, что учителя ценят точную информацию, которую они могут использовать для улучшения своего обучения.

    Появляется все больше свидетельств того, что обратная связь с систематическими наблюдениями может быть использована для улучшения обучения. Несколько исследований, таких как исследование Джейн Столлингс, показали, что учителя могут положительно изменить свое отношение и поведение по отношению к ученикам после получения обратной связи от наблюдений в классе. «Исследование лечения» Гуд и Брофи в 1974 году служит примером такого рода исследований.В этом исследовании учителям была дана обратная связь, основанная на сорокачасовом наблюдении в классе. В результате этого одноразового интервью, на котором была дана обратная связь, изменились модели взаимодействия учителей, а также изменилось их отношение к отдельным ученикам. Столлингс, Ховард Эбмайер, Гуд и Гуд и Дуглас Гроус использовали аналогичные стратегии в других проектах. В этих исследованиях учителям были представлены индивидуальные отзывы относительно их обучения в классе, а затем было обнаружено, что они изменили свое поведение желаемым образом.Все эти исследования показали, что учителя могут улучшить свои занятия в классе, если учесть соответствующие отзывы и предложения по улучшению.

    Общие результаты этих исследований показывают, что обратная связь с наблюдениями в классе является жизнеспособным и эффективным механизмом для предоставления учителям необходимой информации об их поведении в классе. Эта обратная связь предназначена для создания «дисбаланса» в восприятии учителями своего поведения. Этот дисбаланс возникает всякий раз, когда учителя обнаруживают, что их отношение или восприятие их обучения отличается от взглядов подготовленных наблюдателей.Учителя в таком состоянии «неуравновешенности» мотивированы что-то делать со своим поведением, чтобы восстановить равновесие. Аналогичное представление заключается в том, что самосознание увеличивает контроль учителей над своими действиями и возможность их изменения. В 1995 году Ваксман, Хуанг и Падрон предоставили общешкольные отзывы учителям средних школ, которые сравнили их школьный профиль по учебному поведению в классе с общим средним показателем того же поведения по округу.Отзывы из этих профилей использовались для стимулирования диалога и обсуждения сильных и слабых сторон преподавания в школе. Профили также помогли инициировать обсуждение конкретных учебных областей, которые необходимо улучшить в школе. Следует отметить, что эти профили содержали некоторые рекомендации для практики, и они не были попыткой указывать учителям, что им делать. Эти профили предоставляют учителям концепции и критерии, которые они могут использовать для размышлений о своем собственном обучении.Сессия обратной связи не рассматривалась как та, где результаты исследования должны быть применены к конкретным правилам или руководящим принципам, которым должны следовать учителя. Скорее, обратная связь по результатам наблюдений была предназначена для использования в качестве руководства для учителей, с помощью которого они и их коллеги могли бы самостоятельно поразмышлять о своей практике и решить, какие действия предпринять. Профессиональные услуги и университетские курсы – это некоторые из возможностей, которые учителя могли бы выбрать, если бы они хотели продолжить сотрудничество с исследователями, чтобы помочь им улучшить свое обучение.Таким образом, использование обратной связи с наблюдениями в классе представляется действенной стратегией, которая может улучшить учебное поведение в определенных классах и школах.

    Ограничения наблюдения в классе

    По словам Сары Деламонт и Дэвида Гамильтона, также было несколько критических замечаний и предостережений, связанных с использованием методов структурированного наблюдения. Критические замечания и ограничения использования методов структурированного наблюдения разделены на три подраздела: (1) теоретическая и эпистемологическая критика; (2) методологические проблемы; и (3) прагматические соображения.Этот раздел также включает краткое обсуждение значения наблюдения в классе и некоторых новых направлений.

    Теоретическая и эпистемологическая критика. Несмотря на то, что в результате наблюдательного исследования был получен значительный объем важных результатов, которые могут привести к улучшению практики преподавания, по-прежнему отсутствует консенсус или неуверенность в отношении исследования. Было много теоретических и эпистемологических критических замечаний в адрес классных наблюдательных исследований процессов и продуктов, таких как исследование Мориса Гальтона в 1988 году.Некоторые критики, например, утверждали, что это исследование лишено теории и, следовательно, не может объяснить, почему некоторые виды учебного поведения влияют на успеваемость учащихся. Есть также связанные с этим опасения относительно того, почему некоторые переменные выбраны для наблюдения при исключении других переменных. Поскольку в основе исследования нет модели или теории, критики утверждают, что нет никаких оснований для выбора переменных или значимости, связанных с интерпретацией результатов. Они также утверждают, что выбор событий или поведения может быть непонятен никому, кроме наблюдателя или разработчика прибора.Другими словами, исследования в классе не касались теоретических предположений о том, почему определенный стиль преподавания или набор учебных переменных влияет на обучение учащихся.

    Том Попкевиц, Роберт Табачник и Кеннет Цайхнер (1979) заявляют, что этот исследовательский подход имеет бихевиористскую ориентацию, которая поддерживает «можно идентифицировать, контролировать и манипулировать конкретными результатами обучения, изменяя отдельные аспекты открытого поведения учителя» ( стр.52).Они также утверждают, что обучение рассматривается, как «предполагается, что сумма дискретного поведения и изменение одного или нескольких из них влияет на качество обучения в целом» (стр. 52). Однако их самый яростный аргумент касается представления о том, что такое поведение при обучении «часто рассматривается независимо от учебного контекста, с которым связаны методы» (стр. 52). Они обеспокоены тем, что наблюдатели обычно сосредотачиваются на изолированном поведении, не заботясь о предшествующем и последующем поведении, которое, по их мнению, обеспечивает контекст и значение поведения.Другая проблема заключается в том, что большинство систем наблюдения обычно ограничены – они могут использоваться только для наблюдения за скрытым поведением, которое можно измерить количественно. Кроме того, эти системы наблюдения затрудняют запись сложных учебных действий.

    Методологические проблемы. Большинство методов наблюдения имеют ограничения. Некоторые из этих опасений или ограничений связаны с методологическими проблемами, которые могут помешать сделать обоснованные выводы. Одна из основных методологических проблем или источников недействительности, которую необходимо решить в отношении использования методов систематического наблюдения, связана с навязчивостью метода.Эффект наблюдателя может возникать, потому что учителя и ученики знают, что за их поведением наблюдают. Присутствие наблюдателя может изменить поведение учителя или ученика, что может привести к реактивным эффектам. Беспокойство учителя или менее высокая успеваемость учителя, чем обычно, могут помешать составлению обоснованных выводов о том, что обычно происходит в классе. С другой стороны, есть также некоторые свидетельства того, что обучение учителей может быть немного лучше, чем обычно, когда за ними наблюдают.Хотя некоторые исследователи, такие как Дональд Медли, Гомер Кокер и Роберт Соар, утверждают, что эффекты наблюдателя не вызывают серьезного беспокойства, вероятность того, что это угрожает достоверности и надежности собранных данных, существует.

    Существует ряд методологических проблем, которые необходимо решить аналогичным образом. Надежность и достоверность систем наблюдений является первоочередной задачей. Хотя многие системы сообщают о согласии между экспертами или о точности наблюдателя, в них не указывается надежность, поскольку она относится к стабильности поведения учителя или к внутренней согласованности шкалы.Действительность – еще одна важная проблема, которую необходимо решить. Например, конструктивная валидность, которая фокусируется на «теоретической целостности» поведения, особенно важна. Связанная с критериями валидность или степень, в которой меры наблюдения относятся к критериальной мере, редко сообщается, а одновременная валидность или степень, в которой конкретный инструмент связан с другими инструментами, также обычно отсутствует.

    Существуют и другие методологические проблемы, связанные с фактическим количеством времени, которое необходимо для получения действительного периода наблюдения, а также с соответствующим количеством наблюдений, необходимых для получения надежных и обоснованных мер обучения.Аналогичным образом существует ряд методологических проблем, связанных с анализом данных. Большинство из этих проблем связано с вопросом о том, какой соответствующий уровень анализа (например, студент, класс или студенты в классе) следует использовать при анализе данных наблюдений. Учащиеся размещаются внутри классов, а классы – внутри школ. Предыдущие исследования эффективности учителей часто объединяли данные для анализа на уровне класса, который может недооценивать важность процессов в классах, потому что все различия внутри класса теряются.Последние аналитические разработки, такие как иерархическое линейное моделирование (HLM), позволяют исследователям распутать эти вложенные эффекты и исследовать гипотезы о влиянии факторов внутри и между школой или классом на обучение в классе или восприятие учащимися своей учебной среды. Расширенные статистические модели, такие как HLM, позволяют исследователям идентифицировать и отделить индивидуальные эффекты от групповых эффектов после статистического контроля других независимых переменных. Такие многоуровневые модели могут оценить, как переменные на уровне группы (например,g. характеристики класса или школы) влияют на то, каким образом переменные индивидуального уровня (например, поведение учащихся в классе) влияют на успеваемость учащихся.

    Еще одна проблема, связанная с предыдущими исследованиями в классе, заключается в том, что они обычно носят общий характер (т. Е. Обобщают по уровням классов и областям содержания), а не сосредотачиваются на данном уровне обучения и / или предметной области. Точно так же содержание урока часто игнорируется, как и качество записываемого взаимодействия.

    Прагматические опасения. Последняя категория ограничений, связанных с наблюдением в классе, – это прагматические соображения, которые сосредоточены на практичности проведения наблюдательных исследований. Одна из основных прагматических проблем наблюдательных исследований состоит в том, что их проведение дорого, поскольку требует обширной подготовки и времени. Некоторые учебные программы для наблюдателей, например, требуют целых семи полных дней интенсивного обучения, прежде чем наблюдения будут проводиться в классных комнатах. Доступ к школам и классам для проведения наблюдений – еще одна серьезная проблема.Многие школьные округа не хотят разрешать наблюдение за учителями в своих школах, потому что считают, что это будет слишком разрушительно для учебной среды. Также известно, что учителя резко меняют свои инструкции, когда в классе присутствуют наблюдатели.

    Другая прагматическая проблема связана с неправильным использованием данных наблюдений в классе. Наблюдения в классе могут быть очень полезны в качестве формирующей процедуры оценки, но не должны использоваться для выработки итоговых решений, например, относительно увольнения или повторного найма учителя.Аналогичным образом, наблюдения в классе не следует связывать с итоговыми решениями, такими как повышение заработной платы. К сожалению, несколько школьных округов и государственных департаментов образования неправильно использовали результаты наблюдений и преобразовали полученные результаты в конкретные правила или стандарты, которые они использовали при разработке инструментов оценки. Однако эти злоупотребления являются скорее «случайностями» исследования, чем проблемами, связанными с «сущностью» исследования.

    Однако ранее упомянутые критические замечания и ограничения не обязательно умаляют ценность и полезность метода наблюдений.Многие из этих критических замечаний являются случайными аспектами некоторых наблюдательных исследований. Нейт Гейдж, Маргарет Ниделс и другие, например, опровергли многие из этих критических замечаний и представили несколько примеров того, как исследования на основе наблюдений способствовали развитию педагогических теорий. Медли также утверждал, что предыдущие методологические ограничения наблюдательных исследований были значительно уменьшены в 1990-х годах. Он указывает, например, на влияние портативного компьютера на исследования в классе.В дополнение к замене традиционных буферов обмена и секундомеров портативный компьютер поможет исследователям в точности и аккуратности записи событий, а также предоставит подробный отчет о контекстных элементах, возникающих во время наблюдения.

    Новые направления

    Важно еще раз отметить, что ни один источник данных или методология не даст достаточного ответа на все важные образовательные вопросы. Чтобы получить более полную картину того, что происходит в классах, необходимы многочисленные меры или индикаторы обучения.Некоторые из новых направлений исследований в области наблюдения в классе включают следующее: (1) сочетание качественных и количественных методов в системах наблюдения; (2) разработка инструментов наблюдения, основанных на «стандартах» педагогики; (3) использование инструментов наблюдения, ориентированных на учащихся, которые позволяют проводить сравнения между группами учащихся в классе; и (4) использование инструментов, которые оценивают аутентичные интерактивные учебные практики, которые, как было установлено, связаны с достижениями учащихся в когнитивных результатах более высокого уровня.

    БИБЛИОГРАФИЯ

    B ROPHY , J ERE E., AND G OOD , T OM L. 1974. Отношения между учителем и учеником: причины и последствия. Нью-Йорк: Холт, Райнхарт и Уинстон.

    D ELAMONT , S ARA и H AMILTON , D AVID . 1986. “Пересмотр исследования в классе: поучительная история”. В Споры в исследованиях в классе, изд. Мартин Хаммерсли.Филадельфия: Издательство Открытого университета.

    E BMEIER , H OARD и G OOD , T OM L. 1979. «Влияние инструктажа учителей о хорошем преподавании на успеваемость учащихся четвертых классов по математике». Американский журнал исследований в области образования 16: 1–16.

    E VERTSON , C AROLUN и G REEN , J UDITH . 1986. “Наблюдение как исследование и метод”. В Справочнике по исследованиям в области преподавания , 3-е издание, изд.Мерлин К. Виттрок. Нью-Йорк: Макмиллан.

    F ENNEMA , E LIZABETH и P ETERSON , P ENELOPE L. 1987. «Эффективное обучение девочек и мальчиков: одинаковое или различное?» В Беседах с учителями, изд. Дэвид К. Берлинер и Барак В. Розеншайн. Нью-Йорк: Рэндом Хаус.

    G AGE , N ATE L. и N EEDELS , M ARGARET C. 1989. «Исследование процесса-продукта в обучении? Обзор критики.” Журнал начальной школы 89: 253–300.

    G ALTON , M AURICE . 1988. “Структурированные методы наблюдений”. В Образовательные исследования, методология и измерения: международный справочник, изд. Джон П. Кивз. Оксфорд: Пергамон.

    G OOD , T OM L. 1988. «Наблюдательные исследования… Теория заземления в классах». Психолог-педагог 25: 375–379.

    G OOD , T OM L.и B ROPHY , J ERE E. 1974. «Изменение поведения учителей и учеников: эмпирическое исследование». Журнал педагогической психологии 66: 390–405.

    G OOD , T OM L. и B ROPHY , J ERE E. 2000. Looking in Classrooms, 8th edition. Нью-Йорк: Лонгман.

    G OOD , T OM L. и G ROUWS , D OUGLAS . 1979. “Проект эффективности математики Миссури: экспериментальное исследование в классах четвертых классов”.” Журнал педагогической психологии 71: 355–362.

    G OOD , T OM L .; S LAVINGS , R. L; H OBSON -H AREL , K .; и E MERSON , H. 1987. «Пассивность учащихся: исследование вопросов в классах K – 12». Социология образования 60: 181–199.

    G OOD , T OM L .; S LAVINGS , R. L .; и M ASON , D. A. 1988. «Обучение заданию вопросов: оценки и школьные эффекты».” Преподавание и педагогическое образование 4: 363–378.

    H ART , L AURIE E. 1989. «Процессы в классе, пол учащихся и уверенность в изучении математики». Журнал исследований в области математического образования 20: 242–260.

    H UANG , S HWU -Y ONG L. и W AXMAN , H ERSH C. 1996. «Наблюдения в классе за использованием технологий учащимися средних школ в математике». Школьные науки и математика 96 (1): 28–34.

    M EDLEY , D ONALD M .; C OKER , H OMER ; и S OAR , R OBERT S. 1984. Оценка работы учителя на основе измерений: эмпирический подход. Нью-Йорк: Лонгман.

    N EEDELS , M ARGARET и G AGE , N ATE L. 1991. «Сущность и случайность исследования процесса и продукта в обучении». В Эффективное обучение: Текущие исследования, изд.Херш К. Ваксман и Герберт Дж. Уолберг. Беркли: Маккатчан.

    P ADRÓN , Y OLANDA N .; W AXMAN , H ERSH C .; и H UANG , S HWU -Y ONG L. 1999. «Различия в классе и в учебной среде обучения между устойчивыми и неустойчивыми учениками начальной школы». Педагогический журнал для студентов, которым грозит отказ 4: 63–81.

    P OPKEWITZ , T OM S.; T ABACHNICK , R OBERT ; и Z EICHNER , K EN . 1979. “Притупление чувств: исследования в области педагогического образования”. Журнал педагогического образования 30: 52–60.

    R OSENSHINE , B ARAK V. 1987. «Явное обучение». В Беседах с учителями, изд. Дэвид К. Берлинер и Барак В. Розеншайн. Нью-Йорк: Рэндом Хаус.

    S IROTNIK , K EN A. 1983. «Что вы видите, то и получаете: последовательность, постоянство и посредственность в классах.” Harvard Educational Review 53: 16–31.

    S TALLINGS , J ANE A. 1980. «Пересмотр выделенного академического времени на обучение, или сверх времени на выполнение задания». Исследователь в области образования 9 (11): 11–16.

    W ALBERG , H ERBERT J. 1991. «Продуктивное преподавание и обучение: оценка базы знаний». В Эффективное обучение: Текущие исследования, изд. Херш К. Ваксман и Герберт Дж. Уолберг. Беркли: Маккатчан.

    W ALBERG , H ERBERT J.1995. “Общие практики”. В Справочнике по исследованиям по улучшению успеваемости учащихся, изд. Гордон Кавельт. Арлингтон, Вирджиния: Образовательные исследовательские услуги.

    W AXMAN , H ERSH C. 1995. «Наблюдения за эффективным обучением в классе». В Учение: теория на практике, изд. Аллан С. Орнштейн. Нидхэм-Хайтс, Массачусетс: Аллин и Бэкон.

    W AXMAN , H ERSH C. и H UANG , S HWU -Y ONG L.1996. “Различия в обучении в классе по уровню использования технологий в математике в средней школе”. Журнал образовательных компьютерных исследований 14: 147–159.

    W AXMAN , H ERSH C. и H UANG , S HWU -Y ONG L. 1997. “Различия в классе и учебной среде между эффективными и неэффективными городскими начальными школами для афроамериканских учащихся. . ” Городское образование 32 (1): 7–44.

    W AXMAN , H ERSH C., и H UANG , S HWU -Y ONG L. 1999. «Исследования по наблюдению в классе и улучшение преподавания». В Новые направления для педагогической практики и исследований, изд. Херш К. Ваксман и Герберт Дж. Уолберг. Беркли, Калифорния: Маккатчан.

    W AXMAN , H ERSH C .; H UANG , S HWU -Y ONG L .; A NDERSON , L ASELLES ; и W EINSTEIN , T HOMAS . 1997 г.«Различия в процессе обучения в городских начальных школах». Журнал исследований в области образования 91: 49–59.

    W AXMAN , H ERSH C .; H UANG , S HWU -Y ONG L .; и P ADRÓN , Y OLANDA N. 1995. «Исследование педагогики бедности в городских средних школах». Исследования в области среднего образования 8 (2): 1–22.

    Является ли культура вашей школы токсичной или позитивной?

    «Школьная культура – это совокупность норм, ценностей и верований, ритуалов и церемоний, символов и историй, составляющих« личность »школы», – говорит д-р.Кент Д. Петерсон, профессор Департамента управления образованием Университета Висконсин-Мэдисон. Education World поговорила с Петерсоном о различиях между положительной и отрицательной школьной культурой и о том, как администрация и учителя могут создать положительную культуру в своих школах. Включено: Советы по созданию позитивной школьной культуры.

    «Культура школы состоит в первую очередь из базовых норм, ценностей и убеждений, которые учителя и администрация придерживаются в отношении преподавания и обучения», – говорит доктор.Кент Д. Петерсон. Эта культура также состоит из «традиций и церемоний, которые школы проводят для создания сообщества и укрепления своих ценностей», – говорит Петерсон, профессор Департамента управления образованием Университета Висконсин-Мэдисон и соавтор книги «Формирование школьной культуры: сердце». лидерства.

    У каждой школы есть основные предположения о том, что сотрудники будут обсуждать на собраниях, какие методы преподавания работают хорошо, насколько сотрудники могут меняться и насколько важно развитие персонала, добавляет Петерсон.Этот основной набор убеждений лежит в основе общей культуры школы.

    Петерсон говорит, что в школе с позитивной культурой «существует неформальная сеть героев и героинь, а также неформальная виноградная лоза, которая передает информацию о том, что происходит в школе … [A] набор ценностей, поддерживающих профессиональное развитие. учителя, чувство ответственности за обучение учащихся и позитивная, заботливая атмосфера ».

    С другой стороны, в токсичной школьной среде «отношения учителей часто бывают конфликтными, персонал не верит в способность учеников добиться успеха, и в целом преобладает негативное отношение», – отмечает Петерсон.

    Персонал и администрация с позитивной школьной культурой верят, что они способны реализовать свои амбиции. Их коллеги, работающие в неблагоприятной школьной среде, не верят в возможность реализации своих замыслов.

    Школьная культура оказывает огромное влияние на развитие персонала. «Это влияет на отношение к тому, чтобы тратить время на улучшение обучения, мотивацию к посещению семинаров, а также на [деятельность], в которой люди хотят участвовать», – говорит Петерсон.

    Обширные ресурсы, не требующие позитивного воздействия на цветение

    В статье Положительно или Отрицательно? ( Journal of Staff Development, Summer 2002) Петерсон пишет об образцовой школьной культуре в начальной школе Ганадо (Аризона).Школа, расположенная в одном из беднейших округов США, не всегда могла похвастаться ярким профессиональным сообществом. «Со временем, – писал Петерсон, – Зигмунд Болоз, директор школы, и его сотрудники развили сильную профессиональную культуру, которая поддерживает обучение сотрудников и студентов».


    Какой термин описывает культуру вашей школы?

    Ядовитая школьная культура
    * обвиняет учеников в неуспеваемости
    * препятствует сотрудничеству
    * порождает враждебность среди сотрудников.

    Позитивная школьная культура
    * отмечает успехи
    * подчеркивает достижения и сотрудничество
    * способствует приверженности к обучению сотрудников и учащихся.

    В этой статье Петерсон описал школьную культуру, в которой персонал, студенты, директор и члены сообщества рассматриваются как учащиеся. Все учителя прошли обучение по программе вмешательства по чтению под названием CLIP (совместный проект повышения грамотности).Учителя получают поддержку в использовании программы и приглашаются на регулярные «беседы по учебной программе» для обсуждения новых идей и обмена опытом.

    В Ганадо «Наличие штатной профессиональной библиотеки символически свидетельствует о важности обучения», – продолжил Петерсон. «В школе собрано 4000 профессиональных книг и 400 видеокассет по эффективному обучению и другим профессиональным вопросам». Кроме того, ежегодно в школе работает академия для родителей, которая помогает улучшить родительские способности.

    «Сотрудники чувствуют ответственность за совершенствование своих навыков и знаний, чтобы помочь студентам учиться», – заключил Петерсон. «Они регулярно рассказывают истории успешного использования новых идей. Персонал ожидает и поощряет сотрудничество и обмен мнениями. Короче говоря, профессиональное обучение ценится в культуре».

    Согласно Петерсону, школы с отрицательной или токсичной культурой

    • Отсутствие четкого понимания цели
    • имеют нормы, усиливающие инерцию
    • винят учеников в неуспеваемости
    • препятствовать сотрудничеству
    • часто имеют активно враждебные отношения среди персонала.

    В борьбе с такой негативной культурой, говорит Петерсон Education World, «для начала персонал должен оценить основные нормы и ценности культуры, а затем в рамках группового мероприятия работать над их изменением, чтобы получить более позитивную, поддерживающую культуру. . ”

    Директорам необходимо «читать школу», – предлагает Петерсон. Они должны поговорить с рассказчиками из персонала, чтобы понять, какая у школы история. Персонал и администрация должны изучить то, что они узнали о школьной культуре, а затем они должны задать два вопроса:

    • Какие аспекты культуры положительны и должны быть усилены?
    • Какие аспекты культуры являются негативными и вредными и должны быть изменены?

    В поле «Положительно или отрицательно?» Петерсон рассказал о том, как директора и руководители персонала могут развивать положительные аспекты школьной культуры.К ним относятся следующие:

    • Отмечайте успехи на собраниях персонала и церемониях.
    • Рассказывайте истории о достижениях и сотрудничестве всякий раз, когда есть возможность.
    • Используйте понятный общий язык, созданный в процессе профессионального развития, чтобы укрепить приверженность к обучению сотрудников и студентов.

    Когда администраторы и сотрудники совместно работают над созданием среды, в которой процветает обучение, заключил Петерсон, они уменьшат такие негативные факторы, как плохое поведение учащихся и ворчание преподавателей, и создадут в целом позитивную школьную культуру с процветающим коллективом и учащимися.

    Формирование школьной культуры: сердце лидерства
    Краткое изложение этой книги, по словам авторов Терренса Э. Дила и Кента Д. Петерсона, показывает, как школьные руководители могут использовать силу школьной культуры для создания живого духа сотрудничества и сотрудничества. школьный «образ».

    Полевая книга «Формирование школьной культуры»
    Терренс Э. Дил и Кент Д. Петерсон (Джосси-Басс), эта книга предоставляет надежные методы, вопросы для размышления и групповые занятия, которые сотрудники школы могут использовать для оценки и изменения своей культуры.

    Calculus and its Applications (2 загрузки)

    % PDF-1.6 % 2 0 obj > эндобдж 6 0 obj > транслировать Acrobat Distiller 7.0.5 для Macintosh http://www.codemantra.comↂ002Cↂ0020LLC> Процесс создания этого PDF-файла составляет коммерческую тайну codeMantra, LLC и защищен законами США об авторских правах. 0020PDF> 2011-09-23T13: 01: 33 + 02: 002011-03-23T11: 55: 53 + 02: 002011-03-24T16: 40-04: 00Acrobat: pictwpstops filter 1.0uuid: 8c41f616-9770-4697-8e0b-ef049aff85dcuuid : bfec1d01-ad55-4dff-a9f2-45e7e549abd2application / pdf

  • Calculus and its Applications (2 загрузки)
  • конечный поток эндобдж 65 0 объект > транслировать q 252 0 0 322.56 0 0 см / Im0 Do Q конечный поток эндобдж 66 0 объект > транслировать

    Изучение взаимосвязи между пространственными навыками и математическими способностями: метаанализ

  • Акерман П. Л. и Вулман С. Д. (2007). Детерминанты и валидность самооценок способностей и мер самооценки. Журнал экспериментальной психологии. Заявлено , 13 (2), 57–78. https://doi.org/10.1037/1076-898X.13.2.57

    Статья PubMed Google ученый

  • Альтман, Д.Г. (1990). Практическая статистика медицинских исследований . CRC Press.

    Google ученый

  • Американское математическое общество (2020). Домашняя страница . Получено 24 ноября 2020 г. с https://www.ams.org/home/page

  • Атит К., Ганье К. и Шипли Т. Ф. (2015). Студенческие жесты способствуют проницательному мышлению. Журнал геолого-геофизического образования , 63 (1), 66–72. https: // doi.org / 10.5408 / 14-008.1

    Статья Google ученый

  • Атит, К., Пауэр, Дж. Р., Веуринк, Н., Уттал, Д.Х., Сорби, С., Пантер, Г., Мсалл, К., Фиорелла, Л., и Карр, М. (2020a) . Изучение роли пространственных навыков и математической мотивации в математической успеваемости в средней школе. International Journal of STEM Education , 7 (1), 38. https://doi.org/10.1186/s40594-020-00234-3

    Статья Google ученый

  • Атит, К., Уттал, Д. Х., & Стифф, М. (2020b). Расположение в пространстве: использование линзы, ориентированной на дисциплину, для изучения навыков пространственного мышления. Когнитивные исследования: принципы и последствия , 5 (1), 19. https://doi.org/10.1186/s41235-020-00210-z

    Статья Google ученый

  • Ауд, С., Хусар, В., Джонсон, Ф., Кена, Г., Рот, Э., Мэннинг, Э., Ван, X., и Чжан, Дж. (2012). Состояние образования 2012. NCES 2012-045. Национальный центр статистики образования . http://files.eric.ed.gov/fulltext/ED532315.pdf

  • Баттиста М. Т. (1990). Пространственная визуализация и гендерные различия в геометрии средней школы. Журнал исследований в области математического образования , 21 (1), 47–60. https://doi.org/10.2307/749456

    Статья Google ученый

  • Берг, Д. Х. (2008). Рабочая память и арифметические вычисления у детей: вспомогательные роли скорости обработки, кратковременной памяти и чтения. Журнал экспериментальной детской психологии , 99 (4), 288–308. https://doi.org/10.1016/j.jecp.2007.12.002

    Статья PubMed Google ученый

  • Берман Н. Г. и Паркер Р. А. (2002). Метаанализ: Ни быстро, ни легко. BMC Medical Research Methodology , 2 , 10. https://doi.org/10.1186/1471-2288-2-10

    Статья PubMed PubMed Central Google ученый

  • Бетелл-Фокс, К.Э. и Шепард Р. Н. (1988). Психическое вращение: эффекты сложности стимула и знакомства. Журнал экспериментальной психологии. Человеческое восприятие и производительность , 14 (1), 12–23. https://doi.org/10.1037/0096-1523.14.1.12

    Статья Google ученый

  • Бонни, Дж. У., и Лоренко, С. Ф. (2015). Индивидуальные различия в приближении детей к площади коррелируют со знанием базовой геометрии. Обучение и индивидуальные различия , 44 , 16–24. https://doi.org/10.1016/j.lindif.2015.11.001

    Статья Google ученый

  • Боренштейн, М., Хеджес, Л., Хиггинс, Дж., И Ротштейн, Х. (2005). Комплексный мета-анализ (Версия 2). Биостат.

    Google ученый

  • Браун М. В. и Кадек Р. (1993). Альтернативные способы оценки соответствия модели. Sage Focus Editions , 154 , 136-136.

    Google ученый

  • Берт, Х., Гардони, А. Л., Хаттон, А., и Тейлор, Х. А. (2017). Think3d !: Улучшение обучения математике с помощью пространственного обучения. Когнитивные исследования: принципы и последствия , 2 (1), 13. https://doi.org/10.1186/s41235-017-0052-9

    Статья Google ученый

  • Карр, М., Штайнер, Х. Х., Кайзер, Б., и Биддлкомб, Б. (2008). Сравнение предикторов ранних гендерных различий в математической компетентности. Обучение и индивидуальные различия , 18 (1), 61–75. https://doi.org/10.1016/j.lindif.2007.04.005

    Статья Google ученый

  • Кэрролл, Дж. Б. (1993). Когнитивные способности человека: обзор факторно-аналитических исследований. Издательство Кембриджского университета. https: // market.android.com/details?id=book-jp9dt4_0_cIC

    Google ученый

  • Кейси, М. Б., Наттолл, Р., Пезарис, Э., и Бенбоу, К. П. (1995). Влияние пространственных способностей на гендерные различия в результатах вступительных экзаменов в математический колледж в разных выборках. Психология развития , 31 (4), 697–705. https://doi.org/10.1037/0012-1649.31.4.697

    Статья Google ученый

  • Кейси, М.Б., Наттолл Р. Л. и Пезарис Э. (1997). Посредники гендерных различий в оценках вступительных экзаменов в математический колледж: сравнение пространственных навыков с внутренними убеждениями и тревогами. Психология развития , 33 (4), 669–680. https://doi.org/10.1037//0012-1649.33.4.669

    Статья PubMed Google ученый

  • Кейси, Б. М., Деринг, Э., Васильева, М., Гэнли, К. М., и Тайн, М. (2011).Пространственные и числовые предикторы эффективности измерения: смягчающие эффекты дохода сообщества и пола. Журнал педагогической психологии , 103 (2), 296–311. https://doi.org/10.1037/a0022516

    Статья Google ученый

  • Кейси, Б. М., Пезарис, Э., Файнман, Б., Поллок, А., Демерс, Л., и Деринг, Э. (2015). Продольный анализ ранних пространственных навыков в сравнении с арифметическими и вербальными навыками в качестве предикторов математических рассуждений девочек пятого класса. Обучение и индивидуальные различия , 40 , 90–100. https://doi.org/10.1016/j.lindif.2015.03.028

    Статья Google ученый

  • Кейси, Б. М., Ломбарди, К. М., Поллок, А., Файнман, Б., и Пезарис, Э. (2017). Пространственные навыки и арифметические стратегии девочек в первом классе как предикторы аналитического математического мышления в пятом классе. Журнал познания и развития: Официальный журнал Общества когнитивного развития , 18 (5), 530–555.https://doi.org/10.1080/15248372.2017.1363044

    Статья Google ученый

  • Кеттелл Р. Б. (1971). Способности: их структура, рост и действие 90 157. Houghton Mifflin.

    Google ученый

  • Сеси, С. Дж., И Уильямс, В. М. (2011). Понимание текущих причин недопредставленности женщин в науке. Proceedings of the National Academy of Sciences of the United States of America , 108 (8), 3157–3162.https://doi.org/10.1073/pnas.1014871108

    Статья PubMed PubMed Central Google ученый

  • Ченг, Ю. Л., и Микс, К. С. (2014). Пространственное обучение улучшает математические способности детей. Журнал познания и развития, 15 (1), 2-11.

    Google ученый

  • Cheung, M.W.L. (2015). {metaSEM}: пакет R для мета-анализа с использованием моделирования структурных уравнений. Frontiers in Psychology, 5 , 1-7. https://doi.org/10.3389/fpsyg.2014.01521

    Статья Google ученый

  • Cheung, M. W.-L., & Chan, W. (2005). Метааналитическое моделирование структурным уравнением: двухэтапный подход. Психологические методы , 10 (1), 40–64. https://doi.org/10.1037/1082-989X.10.1.40

    Статья PubMed Google ученый

  • Чирино, П.Т., Толар Т. Д., Фукс Л. С. и Хьюстон-Уоррен Э. (2016). Когнитивные и числительные предикторы математических навыков в средней школе. Журнал экспериментальной детской психологии , 145 , 95–119. https://doi.org/10.1016/j.jecp.2015.12.010

    Статья PubMed Google ученый

  • Клиффорд, Э. (2008). Визуально-пространственная обработка и математические достижения: предсказательная способность визуально-пространственных мер шкал интеллекта Стэнфорд-Бине и шкалы интеллекта Векслера для детей .Университет Южной Дакоты. http://search.proquest.com/openview/7

    3d7b16e45eca563dbc3826e3eb/1?pq-origsite=gscholar&cbl=18750&diss=y

  • College Board (2020). SAT Math Test. https://collegereadiness.collegeboard.org/sat/inside-the-test/math

  • Конвей, А. Р., Кейн, М. Дж., И Энгл, Р. У. (2003). Объем рабочей памяти и его отношение к общему интеллекту. Тенденции в когнитивных науках , 7 (12), 547–552.https://doi.org/10.1016/j.tics.2003.10.005

    Статья PubMed Google ученый

  • Корси П. М. (1972). Память человека и медиальная височная область мозга . Университет Макгилла.

    Google ученый

  • Кокс, Дж. У. (1928). Механические способности. Метуэн.

    Google ученый

  • Цуй, Дж., Чжан, Ю., Ченг, Д., Ли, Д., и Чжоу, X. (2017). Восприятие визуальной формы может быть когнитивным коррелятом математических категорий более низкого уровня для подростков. Frontiers in Psychology , 8 , 1336. https://doi.org/10.3389/fpsyg.2017.01336

    Статья PubMed PubMed Central Google ученый

  • Дири, И. Дж., Стрэнд, С., Смит, П., и Фернандес, К. (2007). Интеллект и образовательные достижения. Разведка, 35 (1), 13-21.

    Google ученый

  • Дельгадо А. Р. и Прието Г. (2004). Когнитивные посредники и половые различия в математике. Intelligence , 32 (1), 25–32. https://doi.org/10.1016/S0160-2896(03)00061-8

    Статья Google ученый

  • Эденс, К., и Поттер, Э. (2007). Взаимосвязь рисования и решения математических задач: Рисование для математических задач. Исследования в области художественного образования , 48 (3), 282–298. https://doi.org/10.1080/00393541.2007.11650106

    Статья Google ученый

  • Эггер, М., Дэйви Смит, Г., Шнайдер, М., и Миндер, К. (1997). Предвзятость в метаанализе обнаруживается с помощью простого графического теста. BMJ , 315 (7109), 629–634. https://doi.org/10.1136/bmj.315.7109.629

    Статья PubMed PubMed Central Google ученый

  • Экстрем, р.Б., Френч, Дж. У., Харман, Х., Дерман, Д. (1976). Комплект когнитивных тестов с привязкой к факторам (пересмотренное издание). Служба образовательного тестирования, Принстон, штат Нью-Джерси.

  • Эмбретсон, С. Э. (1995). Роль объема оперативной памяти и общих процессов управления в интеллекте. Интеллект , 20 (2), 169–189. https://doi.org/10.1016/0160-2896(95)

    -4

    Статья Google ученый

  • Фланаган, Д.П. и Кауфман А.С. (2004). Основы оценки WISC-IV 90 157. Джон Уайли и сыновья.

    Google ученый

  • Фрик, А. (2019). Способности к пространственному преобразованию и их связь с более поздними математическими достижениями. Психологические исследования , 83 (7), 1465–1484. https://doi.org/10.1007/s00426-018-1008-5

    Статья PubMed Google ученый

  • Фрай, А.Ф. и Хейл С. (1996). Скорость обработки, рабочая память и подвижный интеллект: свидетельства каскада развития. Психологическая наука, 7 (4), 237-241.

    Google ученый

  • Гэнли, К. М., Васильева, М. (2011). Половые различия во взаимосвязи между успеваемостью по математике, пространственными навыками и отношениями. Журнал прикладной психологии развития, 32 (4), 235–242. https://doi.org/10.1016/j.appdev.2011.04.001

  • Гири, Д. К. (2011). Когнитивные предикторы роста достижений по математике: пятилетнее лонгитюдное исследование. Психология развития, 47 (6), 1539-1552. https://doi.org/10.1037/a0025510

    Статья PubMed PubMed Central Google ученый

  • Гир, Э. А., и Гэнли, К. М. (2021). Половые различия в социальной и пространственной перспективе: повторение и расширение работы Тарампи и др., (2016). Неопубликованная рукопись.

  • Гир, Э. А., Куинн, Дж. М., и Гэнли, К. М. (2019). Связь между пространственными навыками и математической успеваемостью у детей начальной школы: продольное исследование. Психология развития , 55 (3), 637–652. https://doi.org/10.1037/dev0000649

    Статья PubMed Google ученый

  • Gilles, P.-Y., & Bailleux, C. (2001). Личностные черты и способности как предикторы академической успеваемости. Европейский журнал психологии образования , 16 (1), 3–15. https://doi.org/10.1007/BF03172991

    Статья Google ученый

  • Гиллиган, К. А., Флури, Э., и Фарран, Э. К. (2017). Вклад пространственных способностей в математические достижения в среднем детстве. Журнал экспериментальной детской психологии , 163 , 107–125. https://doi.org/10.1016/j.jecp.2017.04.016

    Статья PubMed Google ученый

  • Готтфредсон, Л.С., и Дири И. Дж. (2004). Интеллект предсказывает здоровье и долголетие, но почему? Текущие направления психологической науки , 13 (1), 1–4. https://doi.org/10.1111/j.0963-7214.2004.01301001.x

    Статья Google ученый

  • Грин, К. Т., Бунге, С. А., Брионес Чионгбиан, В., Барроу, М., и Феррер, Э. (2017). Плавное мышление предсказывает будущие математические способности детей и подростков. Журнал экспериментальной детской психологии , 157 , 125–143. https://doi.org/10.1016/j.jecp.2016.12.005

    Статья PubMed PubMed Central Google ученый

  • Грегуар Дж. И Ван Дер Линден М. (1997). Влияние возраста на размах пальцев вперед и назад. Нейропсихология, развитие и познание. Раздел B, Старение, нейропсихология и познание , 4 (2), 140–149.https://doi.org/10.1080/13825589708256642

    Статья Google ученый

  • Гундерсон, Э. А., Рамирес, Г., Бейлок, С. Л., и Левин, С. К. (2012). Связь между пространственным навыком и ранним знанием чисел: роль линейной числовой линии. Психология развития , 48 (5), 1229–1241. https://doi.org/10.1037/a0027433

    Статья PubMed Google ученый

  • Хаджиомероглу, Э.С. (2015). Роль познавательных способностей и предпочтительный способ обработки в расчетах учащихся. Евразийский журнал математики, науки и технологий Образования , 11 (5), 1165–1179. http://www.ejmste.com/pdf-51586-11492?filename=The%20Role%20of%20Cognitive.pdf

  • Haciomeroglu, E. S. (2016). Объектно-пространственная визуализация и вербальные когнитивные стили и их связь с когнитивными способностями и математической эффективностью. Образовательные науки: теория и практика , 16 (3), 987–1003.https://eric.ed.gov/?id=EJ1115147

    Google ученый

  • Хэлфорд, Г. С., Уилсон, У. Х., Филлипс, С. (1998). Способность к обработке, определяемая сложностью отношений: значение для сравнительной психологии, психологии развития и когнитивной психологии. Behavioral and Brain Sciences, 21 (6), 803-831.

    Google ученый

  • Халперн, Д. Ф., Бенбоу, К. П., Гири, Д.К., Гур, Р. С., Хайд, Дж. С., и Гернсбахер, М. А. (2007). Наука о половом различии в естественных науках и математике. Психологическая наука в интересах общества: журнал Американского психологического общества , 8 (1), 1–51. https://doi.org/10.1111/j.1529-1006.2007.00032.x

    Статья Google ученый

  • Хэнлайн М. Ф., Милтон С. и Фелпс П. С. (2010). Взаимосвязь между дошкольной блочной игрой и способностями к чтению и математике в начальной начальной школе: лонгитюдное исследование детей с ограниченными возможностями и без них. Развитие и уход за детьми в раннем возрасте , 180 (8), 1005–1017. https://doi.org/10.1080/03004430802671171

    Статья Google ученый

  • Хартер, К. А. и Ку, Х. (2008) Эффекты пространственной смежности в компьютерном обучении групповых персонализированных двухэтапных математических текстовых задач. Компьютеры в поведении человека, 24 (4), 1668-1685. https://doi.org/10.1016/j.chb.2007.06.006

  • Хос, З. и Ансари, Д. (2020). Чем объясняется взаимосвязь между пространственными и математическими навыками? Обзор данных мозга и поведения. Psychonomic Bulletin & Review, 27 , 465-482. https://doi.org/10.3758/s13423-019-01694-7

    Статья Google ученый

  • Хоуз, З., Мосс, Дж., Касуэлл, Б., & Полищук, Д. (2015). Влияние тренировки умственного вращения на пространственные и математические способности детей: рандомизированное контролируемое исследование. Тенденции в неврологии и образовании, 4 (3). 60-68.

    Google ученый

  • Хоуз, З., Мосс, Дж., Касуэлл, Б., Сео, Дж., Ансари, Д. (2019). Отношения между числовыми, пространственными и исполнительными навыками и математическими достижениями: подход с латентными переменными. Когнитивная психология, 109, 68-90.

    PubMed Google ученый

  • Хеджес, Л.В., Типтон Э. и Джонсон М. С. (2010). Надежная оценка дисперсии в мета-регрессии с оценками размера зависимого эффекта. Методы исследования синтеза , 1 (1), 39–65. https://doi.org/10.1002/jrsm.5

    Статья PubMed Google ученый

  • Хегарти, М., и Кожевников, М. (1999). Типы визуально-пространственных представлений и решение математических задач. Журнал педагогической психологии , 91 (4), 684–689.https://doi.org/10.1037/0022-0663.91.4.684

    Статья Google ученый

  • Holyoak, K. J. (2012). Аналогия и реляционные рассуждения. В книге К. Дж. Холиоака и Р. Г. Моррисона (редакторы), Оксфордский справочник по мышлению и рассуждению (стр. 234–259). Издательство Оксфордского университета.

    Google ученый

  • Ху, Л. Т., и Бентлер, П. М. (1999). Критерии отсечения для индексов соответствия в анализе ковариационной структуры: обычные критерии по сравнению с новыми альтернативами. Моделирование структурных уравнений: многопрофильный журнал , 6 (1), 1-55.

    Google ученый

  • Хаббард, Э. М., Пьяцца, М., Пинель, П., и Дехаен, С. (2005). Взаимодействие между числом и пространством в теменной коре. В журнале « Nature Reviews Neuroscience » (том 6, выпуск 6, стр. 435–448). https://doi.org/10.1038/nrn1684

  • Hyde, J. S., Fennema, E., & Lamon, S. J. (1990).Гендерные различия в успеваемости по математике: метаанализ. Психологический бюллетень , 107 (2), 139–155. https://doi.org/10.1037/0033-2909.107.2.139

    Статья PubMed Google ученый

  • Имбо, И., Вандиерандонк, А., и Де Раммелаер, С. (2007). Роль рабочей памяти в операции переноса мысленной арифметики: количество и значение переноса. Ежеквартальный журнал экспериментальной психологии, 60 (5), 708–731.https://doi.org/10.1080/17470210600762447

    Статья Google ученый

  • Джейкоб Р. и Паркинсон Дж. (2015). Потенциал школьных вмешательств, направленных на исполнительную функцию, для улучшения успеваемости: обзор. Обзор исследований в области образования, 85 (4), 512-552.

    Google ученый

  • Дженсен А. Р. (1998). Наука о умственных способностях 90 157. Издательство Praeger.

    Google ученый

  • Джонсон, К. М. (2017). Успеваемость учащихся шестого класса по математике в однополых и смешанных классах в большой городской школьной системе (Публикация № 10604090) [Докторская диссертация, Университет Гранд-Каньона]. Издание диссертаций ProQuest.

  • Кирби, Дж. Р. и Боултер, Д. Р. (1999). Пространственная способность и трансформационная геометрия. Европейский журнал психологии образования , 14 (2), 283. https://doi.org/10.1007/BF03172970

    Статья Google ученый

  • Клингберг, Т. (2006). Развитие превосходной лобно-теменной сети для зрительно-пространственной рабочей памяти. Neuropsychologia, 44 (11), 2171-2177.

    PubMed Google ученый

  • Ковач, К., И Конвей, А. Р. (2016). Теория перекрытия процессов: единый учет общего фактора интеллекта. Психологический опрос , 27 (3), 151–177. https://doi.org/10.1080/1047840X.2016.1153946

    Статья Google ученый

  • Кравчик, Д. К. (2012). Познание и нейробиология реляционных рассуждений. Brain Research, 1428, 13-23.

    PubMed Google ученый

  • Кюталля, М., & Лехто, Дж. Э. (2008). Некоторые факторы, лежащие в основе математических способностей: роль зрительно-пространственной рабочей памяти и невербального интеллекта. Европейский журнал психологии образования , 23 (1), 77. https://doi.org/10.1007/BF03173141

    Статья Google ученый

  • Кюттяла, М., Аунио, П., Лехто, Дж. Э., Ван Луит, Дж., И Хаутамяки, Дж. (2003). Визуально-пространственная рабочая память и ранние навыки счета. Педагогическая и детская психология , 20 (3), 65–76.

    Google ученый

  • Ли Ю., и Гири Д. К. (2013). Развитие зрительно-пространственной памяти предсказывает успехи в математике. В PLoS ONE (том 8, выпуск 7, стр. E70160). https://doi.org/10.1371/journal.pone.0070160

  • Линн, М. К., и Петерсен, А. К. (1985). Возникновение и характеристика половых различий в пространственных способностях: метаанализ. Развитие ребенка , 56 (6), 1479–1498. https://www.ncbi.nlm.nih.gov/pubmed/4075870

    PubMed Google ученый

  • Ломбарди, К. М., Кейси, Б. М., Пезарис, Э., Шадмер, М., и Йонг, М. (2019). Лонгитюдный анализ ассоциаций между трехмерным умственным вращением и математическими способностями рассуждения в средней школе: между полами и внутри них. Журнал познания и развития: Официальный журнал Общества когнитивного развития , 20 (4), 487–509.https://doi.org/10.1080/15248372.2019.1614592

    Статья Google ученый

  • Лоури, Т., Логан, Т., и Рэмфул, А. (2017). Визуально-пространственное обучение улучшает успеваемость учащихся начальной школы по математике. Британский журнал образовательных технологий: журнал Совета по образовательным технологиям . https://doi.org/10.1111/bjep.12142

  • Лоури, Т., Логан, Т., и Хегарти, М. (2019). Влияние тренировки пространственной визуализации на пространственное мышление и успеваемость учащихся по математике. Журнал познания и развития. https://doi.org/10.1080/15248372.2019.1653298

  • МакГрю, К. С., Вендлинг, Б. Дж. (2010). Кеттелл – Хорн – Кэрролл, отношения когнитивных достижений: что мы извлекли из исследований за последние 20 лет. Психология в школе , 47 (7), 651–675. https://doi.org/10.1002/pits.20497

  • Маккензи, Б., Булл, Р., и Грей, К. (2003). Влияние фонологической и визуально-пространственной интерференции на арифметические способности детей. Педагогическая и детская психология , 20 (3), 93–108.

    Google ученый

  • Мерриам Вебстер (нет данных) Определение МАТЕМАТИКИ . Получено 18 ноября 2020 г. с https://www.merriam-webster.com/dictionary/mat Mathematics

  • Mix, K. S. (2019). Почему связаны пространственные навыки и математика? In Child Development Perspectives (Vol. 13, Issue 2, pp. 121–126). https: // doi.org / 10.1111 / cdep.12323

  • Mix, K. S., & Cheng, Y.-L. (2012). Связь между пространством и математикой: последствия для развития и образования. Достижения в развитии и поведении детей , 42 , 197–243. https://doi.org/10.1016/b978-0-12-394388-0.00006-x

    Статья PubMed Google ученый

  • Mix, K. S., Levine, S. C., Cheng, Y.-L., Young, C., Hambrick, D. Z., Ping, R., & Константопулос, С. (2016). Отдельно, но взаимосвязано: скрытая структура пространства и математика в процессе развития. Журнал экспериментальной психологии. Общий , 145 (9), 1206–1227. https://doi.org/10.1037/xge0000182

    Статья PubMed Google ученый

  • Микс, К. С., Левин, С. К., Ченг, Ю.-Л., Янг, К. Дж., Хамбрик, Д. З., и Константопулос, С. (2017). Скрытая структура пространственных навыков и математики: воспроизведение двухфакторной модели. Журнал познания и развития: Официальный журнал Общества когнитивного развития , 18 (4), 465–492. https://doi.org/10.1080/15248372.2017.1346658

    Статья Google ученый

  • Мияке, А., и Шах, П. (1999). Модели рабочей памяти: механизмы активного обслуживания и исполнительного управления. Издательство Кембриджского университета.

    Google ученый

  • Мияке, А., Фридман, Н. П., Эмерсон, М. Дж., Витцки, А. Х., Хауэртер, А., и Вейджер, Т. Д. (2000). Единство и разнообразие исполнительных функций и их вклад в сложные задачи «лобной доли»: анализ скрытых переменных. Когнитивная психология , 41 (1), 49–100. https://doi.org/10.1006/cogp.1999.0734

    Статья PubMed Google ученый

  • Мияке А., Фридман Н. П., Реттингер Д. А., Шах П., & Хегарти, М. (2001). Как связаны зрительно-пространственная рабочая память, исполнительные функции и пространственные способности? Анализ скрытых переменных. Журнал экспериментальной психологии. Общий , 130 (4), 621–640. https://doi.org/10.1037//0096-3445.130.4.621

    Статья PubMed Google ученый

  • Moher, D., Shamseer, L., Clarke, M., Ghersi, D., Liberati, A., Petticrew, M., Shekelle, P., Stewart, L.А., & Группа ПРИЗМА-П. (2015). Предпочтительные элементы отчетности для протоколов систематического обзора и метаанализа (ПРИЗМА-П) Заявление 2015 г. Систематические обзоры , 4 , 1. https://doi.org/10.1186/2046-4053-4-1

  • Меринг В., Ньюкомб Н. С. и Фрик А. (2015). Связь пространственного мышления и пропорционального мышления у дошкольников. Журнал экспериментальной детской психологии , 132 , 213–220. https://doi.org/10.1016/j.jecp.2015.01.005

    Артикул PubMed Google ученый

  • Моросанова В. И., Фомина Т. Г., Ковас Ю., Богданова О. Ю. (2016). Познавательные и регуляторные характеристики и математическая успеваемость у старшеклассников. Личность и индивидуальные различия , 90 , 177–186. https://doi.org/10.1016/j.paid.2015.10.034

    Статья Google ученый

  • Муллис, И.В. С., Мартин, М. О., Фой, П., Арора, А. (2012). Международные результаты TIMSS 2011 по математике . Международная ассоциация оценки достижений в образовании. https://eric.ed.gov/?id=ed544554

  • Национальный центр статистики образования (2018). Программа годовых отчетов за 2018 г. https://nces.ed.gov/programs/digest/d18/figures/fig_01.asp?referrer=figures

  • Neale, M. C., & Miller, M. B. (1997). Использование доверительных интервалов на основе правдоподобия в генетических моделях. Поведенческая генетика , 27 (2), 113–120.

    PubMed Google ученый

  • Ньюкомб, Н. С. (2010). Представьте себе: улучшение изучения математики и естествознания за счет улучшения пространственного мышления. Американский педагог , 34 (2), 29. https://eric.ed.gov/?id=EJ889152

    Google ученый

  • Ньюкомб, Н. С., и Шипли, Т. Ф. (2015).Размышляя о пространственном мышлении: новая типология, новые оценки. Изучение визуального и пространственного мышления для дизайнерского творчества , 179–192. https://doi.org/10.1007/978-94-017-9297-4_10

  • Новак, М.А., Конгдон, Э.Л., Хемани-Лопес, Н., и Голдин-Мидоу, С. (2014). От действия к абстракции: использование рук для изучения математики. Психологическая наука , 25 (4), 903–910. https://doi.org/10.1177/0956797613518351

    Статья PubMed Google ученый

  • Наттолл, Р.Л., Кейси, М. Б., и Пезарис, Э. (2005). Пространственные способности как посредник гендерных различий в тестах по математике: биологические основы окружающей среды. В A. M. Gallagher (Ed.), Гендерные различия в математике: интегративный психологический подход , (Vol. 351, pp. 121–142). Издательство Кембриджского университета, xvi. https://psycnet.apa.org/fulltext/2005-04568-006.pdf

    Google ученый

  • Олвер, А. (2013). Исследование ранних пространственных и числовых навыков у детей младшего детского сада, обучающихся в игровой и исследовательской среде. [Магистерская работа, Университет Торонто].Tspace. https://tspace.library.utoronto.ca/handle/1807/42637

  • Oostermeijer, M., Boonen, A. J. H., & Jolles, J. (2014). Взаимосвязь между конструктивной игровой деятельностью детей, пространственными способностями и способностью решать математические задачи: анализ посредничества у шестиклассников. Frontiers in Psychology , 5 , 782. https://doi.org/10.3389/fpsyg.2014.00782

    Статья PubMed PubMed Central Google ученый

  • Организация экономического сотрудничества и развития (2012). Программа международной оценки студентов (PISA) Результаты PISA 2012. https://www.oecd.org/unitedstates/PISA-2012-results-US.pdf

  • Организация экономического развития (2016). Примечание для страны: основные результаты исследования PISA 2015 для США. Oecd.org/pisa/PISA-2015-United-States.pdf

  • Освальд Ф. Л., МакАби С. Т., Редик Т. С. и Хамбрик Д. З. (2015). Разработка краткого общего измерения объема рабочей памяти. Методы исследования поведения , 47 (4), 1343–1355. https://doi.org/10.3758/s13428-014-0543-2

    Статья PubMed Google ученый

  • Патерсон, Д. Г., Эллиот, Р., Андерсон, Л. Д., Тупс, Х. А., & Хайдбредер, Э. (1930). Тесты на механические способности в Миннесоте: отчет об исследовательском исследовании, финансируемом комитетом по миграции людей Национального исследовательского совета и проведенном на факультете психологии Университета Миннесоты.Университет Миннесоты Press.

    Google ученый

  • Паунонен, С. В., и Хонг, Р. Ю. (2010). Самоэффективность и прогнозирование когнитивных способностей, зависящих от предметной области. Журнал личности , 78 (1), 339–360. https://doi.org/10.1111/j.1467-6494.2009.00618.x

    Статья PubMed Google ученый

  • Пейн, К. М. (2008). Так много реформ, так мало изменений: упорство неудач в городских школах.Издательство Гарвардского Образования.

    Google ученый

  • Пэн П., Ян X. и Мэн X. (2017). Связь между приблизительной системой счисления и ранней арифметикой: посредническая роль числовых знаний. Журнал экспериментальной детской психологии , 157 , 111–124. https://doi.org/10.1016/j.jecp.2016.12.011

    Статья PubMed Google ученый

  • Пэн, П., Ван, Т., Ван, К., Лин, X. (2019). Мета-анализ связи между подвижным интеллектом и чтением / математикой: влияние задач, возраста и статуса социальной экономики. Психологический бюллетень, 145 (2), 189-236.

    PubMed Google ученый

  • Петерс, М., Лэнг, Б., Латам, К., Джексон, М., Зайюна, Р., и Ричардсон, К. (1995). Перерисованный тест мысленных вращений Ванденберга и Кузе: различные версии и факторы, влияющие на производительность. Мозг и познание , 28 (1), 39–58. https://doi.org/10.1006/brcg.1995.1032

    Статья PubMed Google ученый

  • Пустеевский, Дж. Э. (2020). clubSandwich: кластерные (сэндвич) оценки дисперсии с поправками на малую выборку. Пакет R версии 0.5.1. https://CRAN.R-project.org/package=clubSandwich

  • Пустеевский, Дж. Э., и Роджерс, М. А. (2019). Тестирование асимметрии стандартизованных разностей средних значений воронкообразного графика. Методы исследования синтеза , 10 (1), 57–71. https://doi.org/10.1002/jrsm.1332

    Статья PubMed Google ученый

  • Pustejovsky, J. E., & Tipton, E. (2021). Мета-анализ с надежной оценкой дисперсии: расширение диапазона рабочих моделей. Рукопись рецензируется. Osf.io . https://osf.io/vyfcj/download

  • Пайк, К. Л. (2003). Использование символов, слов и диаграмм в качестве индикаторов математического познания: причинная модель. Журнал исследований в области математического образования , 34 (5), 406–432. https://doi.org/10.2307/30034794

    Статья Google ученый

  • Рагхубар, К. П., Барнс, М. А., и Хехт, С. А. (2010). Рабочая память и математика: обзор подходов к развитию, индивидуальных различий и когнитивных подходов. Обучение и индивидуальные различия , 20 (2), 110–122. https://doi.org/10.1016/j.lindif.2009.10.005

    Статья Google ученый

  • Реухкала, М. (2001). Математические навыки девятиклассников: Взаимосвязь с зрительно-пространственными способностями и рабочей памятью. Обзор педагогической психологии , 21 (4), 387–399. https://doi.org/10.1080/014434101200

    Статья Google ученый

  • Родан, А., Контрерас, М. Дж., Элосуа, М.Р., и Гимено, П. (2016). Экспериментальные, но не половые различия программы тренировки умственного вращения на подростках. Frontiers in Psychology , 7 , 1050. https://doi.org/10.3389/fpsyg.2016.01050

    Статья PubMed PubMed Central Google ученый

  • Роджерс, М. А., и Пустеевски, Дж. Э. (2020). Оценка метааналитических методов для выявления выборочной отчетности при наличии зависимых размеров эффекта. Психологические методы . https://doi.org/10.1037/met0000300

  • Шмитт, С. А., Коруку, И., Наполи, А. Р., Брайант, Л. М., и Пурпура, Д. Дж. (2018). Использование блочной игры для улучшения математических и исполнительных навыков дошкольников: рандомизированное контролируемое испытание. Early Childhood Research Quarterly, 44, 181–191.

    Google ученый

  • Шнайдер У. Дж. И МакГрю К. С. (2012).Модель интеллекта Кеттелла-Хорна-Кэрролла . В Д. П. Фланаган и П. Л. Харрисон (редакторы), Современная интеллектуальная оценка: теории, тесты и проблемы (стр. 99–144). Гилфорд Пресс.

    Google ученый

  • Зейтц, К., и Шуман-Хенгстелер, Р. (2002). Фонологическая петля и центральные исполнительные процессы в умственном сложении и умножении. Psychologische Beitrage, 44 (2), 275–303.

    Google ученый

  • Шепард Р. Н. и Мецлер Дж. (1971). Мысленное вращение трехмерных объектов. Science , 171 (3972), 701–703. https://doi.org/10.1126/science.171.3972.701

    Статья PubMed Google ученый

  • Симмс, В., Клейтон, С., Крэгг, Л., Гилмор, К., и Джонсон, С. (2016). Объяснение взаимосвязи между оценкой числовой линии и математическими достижениями: роль зрительно-моторной интеграции и зрительно-пространственных навыков. Журнал экспериментальной детской психологии , 145 , 22–33. https://doi.org/10.1016/j.jecp.2015.12.004

    Статья PubMed Google ученый

  • Скагерлунд, К., и Трафф, У. (2016). Обработка пространства, времени и чисел способствует развитию математических способностей, выходящих за рамки общих когнитивных способностей. Журнал экспериментальной детской психологии , 143 , 85–101. https: // doi.org / 10.1016 / j.jecp.2015.10.016

    Статья PubMed Google ученый

  • Сорби, С. А. (2007). Развитие трехмерных пространственных навыков для студентов инженерных специальностей. Австралийский журнал инженерного образования , 13 (1), 1–11. https://doi.org/10.1080/22054952.2007.11463998

    Статья Google ученый

  • Сорби, С., Кейси, Б., Веуринк, Н., & Дулани А. (2013). Роль пространственного обучения в улучшении пространственной и вычислительной производительности у студентов инженерных специальностей. Обучение и индивидуальные различия , 26 , 20–29. https://doi.org/10.1016/j.lindif.2013.03.010

    Статья Google ученый

  • Станнард, Л., Вольфганг, К. Х., Джонс, И., и Фелпс, П. (2001). Продольное исследование взаимосвязей между строительной игрой и математическими достижениями. Развитие и уход за детьми в раннем возрасте , 167 (1), 115–125. https://doi.org/10.1080/0300443011670110

    Статья Google ученый

  • Стивенсон, Х. В., Паркер, Т., Уилкинсон, А., Хегион, А., и Фиш, Э. (1976). Лонгитюдное исследование индивидуальных различий в когнитивном развитии и успеваемости. Журнал педагогической психологии , 68 (4), 377–400. https://doi.org/10.1037 / 0022-0663.68.4.377

    Артикул Google ученый

  • Суонсон, Х. Л., и Биби-Франкенбергер, М. (2004). Взаимосвязь между рабочей памятью и решением математических задач у детей группы риска и не подверженных риску серьезных математических трудностей. Журнал педагогической психологии , 96 (3), 471–491. https://doi.org/10.1037/0022-0663.96.3.471

    Статья Google ученый

  • Тартр, Л.А. и Феннема Э. (1995). Успеваемость по математике и пол: продольное исследование выбранных когнитивных и эмоциональных переменных [6–12 классы]. Образовательные исследования по математике , 28 (3), 199–217. https://doi.org/10.1007/bf01274173

    Статья Google ученый

  • Тауб, Г. Э., Флойд, Р. Г., Кейт, Т. З., и МакГрю, К. С. (2008). Влияние общих и широких познавательных способностей на математические достижения. School Psychology Quarterly, 23, 187-198.

    Google ученый

  • Терстон, Л. Л., и Терстон, Т. Г. (1941). Факториальные исследования интеллекта. Психометрические монографии , 2 , 94. https://psycnet.apa.org/fulltext/1941-03743-001.pdf

    Google ученый

  • Типтон, Э. (2015). Корректировки небольшой выборки для надежной оценки дисперсии с мета-регрессией. Психологические методы , 20 (3), 375–393. https://doi.org/10.1037/met0000011

    Статья PubMed Google ученый

  • Толар Т. Д., Ледерберг А. Р. и Флетчер Дж. М. (2009). Структурная модель успеваемости по алгебре: беглость вычислений и пространственная визуализация как медиаторы влияния рабочей памяти на успеваемость по алгебре. Обзор педагогической психологии , 29 (2), 239–266.https://doi.org/10.1080/01443410802708903

    Статья Google ученый

  • Уттал, Д. Х., Миллер, Д. И., и Ньюкомб, Н. С. (2013). Изучение и развитие пространственного мышления. Текущие направления в психологической науке, 22 (5), 367-373. https://doi.org/10.1177/0963721413484756

    Статья Google ученый

  • Валензено, Л., Алибали, М. В., & Клацки, Р. (2003). Жесты учителей облегчают обучение учащихся: урок симметрии. Современная психология образования , 28 (2), 187–204. https://www.sciencedirect.com/science/article/pii/S0361476X02000073

    Google ученый

  • ван Гардерен, Д. (2006). Пространственная визуализация, визуальные образы и решение математических задач учащихся с разными способностями. Журнал нарушений обучаемости , 39 (6), 496–506.https://doi.org/10.1177/002221940603

    201

    Статья PubMed Google ученый

  • Ванденберг, С. Г., и Кузе, А. Р. (1978). Психические вращения, групповой тест трехмерной пространственной визуализации. Перцепционные и моторные навыки , 47 (2), 599–604. https://doi.org/10.2466/pms.1978.47.2.599

    Статья PubMed Google ученый

  • Вендетти, М.С., & Бунге, С. А. (2014). Эволюционные изменения и изменения в развитии латеральной лобно-теменной сети: небольшая часть имеет большое значение для познания более высокого уровня. Нейрон , 84 (5), 906–917. https://doi.org/10.1016/j.neuron.2014.09.035

    Статья PubMed PubMed Central Google ученый

  • Вентура, М., Шут, В., Райт, Т., и Чжао, В. (2013). Исследование достоверности оценки виртуальной пространственной навигации. Frontiers in Psychology , 4 , 852. https://doi.org/10.3389/fpsyg.2013.00852

    Статья PubMed PubMed Central Google ученый

  • Вердин, Б. Н., Голинкофф, Р. М., Хирш-Пасек, К., Ньюкомб, Н. С., Филипович, А. Т., и Чанг, А. (2014). Разборка строительных блоков: способность дошкольников к пространственной сборке связана с ранними математическими навыками. Развитие ребенка , 85 (3), 1062–1076.https://doi.org/10.1111/cdev.12165

    Статья PubMed Google ученый

  • Вердин Б. Н., Голинкофф Р. М., Хирш-Пасек К. и Ньюкомб Н. (2017). Связь между пространственными и математическими навыками в дошкольном возрасте. Монографии Общества исследований в области развития детей, 82 (1), 7–30. https://doi.org/10.1111/mono.12280 .

    Артикул Google ученый

  • Viechtbauer, W.(2010). Проведение метаанализа в R с пакетом metafor. Journal of Statistical Software, 36. https://doi.org/10.18637/jss.v036.i03https://lirias.kuleuven.be/1059637?limo=0

  • Voyer, D. (1998). Математика, пол, пространственные способности и церебральная организация: эффект подавления у талантливых учеников. Roeper Review , 20 (4), 251–258. https://doi.org/10.1080/02783199809553902

    Статья Google ученый

  • Вай, Дж., Любински Д. и Бенбоу К. П. (2009). Пространственные способности для областей STEM: более 50 лет накопленных психологических знаний укрепляют его важность. Журнал педагогической психологии , 101 (4), 817–835. https://doi.org/10.1037/a0016127

    Статья Google ученый

  • Уолберг, Х. Дж. (1984). Повышение производительности американских школ. Лидерство в образовании, 41 , 19–27.

    Google ученый

  • Ван, М.-Т., и Дегол, Дж. Л. (2017). Гендерный разрыв в науке, технологиях, инженерии и математике (STEM): текущие знания, значение для практики, политики и будущих направлений. Обзор педагогической психологии , 29 (1), 119–140. https://doi.org/10.1007/s10648-015-9355-x

    Статья PubMed Google ученый

  • Векслер, Д.(1976). Шкала интеллекта Векслера для детей, пересмотренная . Сан-Антонио, Техас: Психологическая корпорация.

  • Векслер Д. (1981). Руководство WAIS-R: пересмотренная шкала интеллекта взрослых Векслера. Психологическая корпорация.

    Google ученый

  • Векслер Д. (2012). Дошкольная и начальная шкала интеллекта Векслера – четвертое издание. Психологическая корпорация Сан-Антонио.

    Google ученый

  • Wei, W., Юань, Х., Чен, К., и Чжоу, X. (2012). Когнитивные корреляты успеваемости по высшей математике. Британский журнал педагогической психологии , 82 (1), 157–181. https://doi.org/10.1111/j.2044-8279.2011.02049.x

    Статья PubMed Google ученый

  • Уилсон, С. Дж., Поланин, Дж. Р., и Липси, М. У. (2016). Подбор метааналитических моделей структурных уравнений со сложными наборами данных. Методы исследования синтеза , 7 (2), 121–139.https://doi.org/10.1002/jrsm.1199

    Статья PubMed PubMed Central Google ученый

  • Вольфганг, К. Х., Станнард, Л. Л., и Джонс, И. (2001). Показатели блочной игры среди дошкольников как предиктор более поздних достижений в школе по математике. Журнал исследований в области детского образования: JRCE / Международная ассоциация детского образования , 15 (2), 173–180. https://doi.org/10.1080/02568540109594958

    Статья Google ученый

  • Вонг, W.И. (2017). Связь между пространством и математикой у мальчиков и девочек дошкольного возраста: важность психической трансформации, точность прицеливания и пространственная тревожность. Британский журнал психологии развития , 35 (2), 249–266. https://doi.org/10.1111/bjdp.12161

    Статья PubMed Google ученый

  • Вудкок Р. В., МакГрю К. С., Мазер Н. и Шранк Ф. А. (2001). Тесты когнитивных способностей Вудкока Джонсона III 90 157. Риверсайд Паблишинг.

    Google ученый

  • Ригли Дж. (1958). Факторный характер способностей в элементарной математике. Британский журнал педагогической психологии, 28, 61–78.

    Google ученый

  • Се, Ф., Чжан, Л., Чен, X., и Синь, З. (2019). Связаны ли пространственные способности с математическими способностями: метаанализ. Обзор педагогической психологии .https://doi.org/10.1007/s10648-019-09496-y

  • Чжан, X., и Линь, Д. (2017). Имеет ли значение темпы роста пространственных способностей при прогнозировании ранних арифметических навыков? Обучение и обучение , 49 , 232–241. https://doi.org/10.1016/j.learninstruc.2017.02.003

    Статья Google ученый

  • Чжан, X., и Линь, Д. (2018). Когнитивные предшественники чтения слов в сравнении с арифметическими способностями у маленьких китайских детей. Early Childhood Research Quarterly , 42 , 55–65. https://doi.org/10.1016/j.ecresq.2017.08.006

    Статья Google ученый

  • Чжан, X., Копонен, Т., Рясанен, П., Аунола, К., Леркканен, М.-К., и Нурми, Ж.-Э. (2014). Лингвистические и пространственные навыки предсказывают раннее развитие арифметики через знание последовательности счета. Развитие ребенка , 85 (3), 1091–1107. https://doi.org/10.1111 / cdev.12173

    Статья PubMed Google ученый

    • Математика для учителей начальной школы: современный подход, 10-е издание

    Предисловие xi

    1 Введение в решение проблем 2

    1.1 Процесс и стратегии решения проблем 5

    1.2 Три дополнительные стратегии 21

    2 Наборы, целые числа и нумерация 42

    2.1 Множества как основа для целых чисел 45

    2.2 Целые числа и нумерация 57

    2.3 Индусско-арабская система 67

    3 Целые числа: операции и свойства 84

    3.1 Сложение и вычитание 87

    3.2 Умножение и Раздел 101

    3.3 Порядок и экспоненты 116

    4 Вычисление целых чисел – мысленное, электронное и письменное 128

    4.1 Ментальная математика, оценка и калькуляторы 131

    4.2 Написанные алгоритмы для операций с целыми числами 145

    4.3 Алгоритмы в других базах 162

    5 Теория чисел 174

    5.1 Простые числа, составные части и тесты на делимость 177

    5.2 Подсчетные множители, наибольший общий множитель и наименьший общий Кратное 190

    6 дробей 206

    6.1 Набор дробей 209

    6.2 Дроби: сложение и вычитание 223

    6.3 Дроби: умножение и деление 233

    7 Десятичные дроби, отношение, пропорции и проценты 250 905

    7.1 Десятичные числа 253

    7.2 Операции с десятичными знаками 262

    7.3 Соотношение и пропорции 274

    7,4 процента 283

    8 Целые числа 302

    8.1 Сложение и вычитание 305

    8.2 Умножение, деление и порядок 9000 318 Рациональные числа, действительные числа и алгебра 338

    9.1 Рациональные числа 341

    9.2 Действительные числа 358

    9.3 Отношения и функции 375

    9.4 Функции и их графики 391

    10 Статистика 412

    10.1 Решение статистических задач 415

    10.2 Анализ и интерпретация данных 440

    10.3 Графики и статистические данные, вводящие в заблуждение 460

    11 Вероятность и простая вероятность 487

    9.1 487

    11.2 Вероятность и сложные эксперименты 502

    11.3 Дополнительные методы подсчета 518

    11.4 Моделирование, ожидаемое значение, шансы и условная вероятность 528

    12 Геометрические формы 546

    12.1 Распознавание геометрических фигур – уровень 0 549

    12.2 Анализ геометрических фигур – уровень 1 564

    12.3 Взаимосвязи между геометрическими фигурами – уровень 2 579

    12.4 Введение в формальный подход к геометрии 589

    12.5 Правильные многоугольники, мозаики и Круги 605

    12.6 Описание трехмерных форм 620

    13 Измерение 644

    13.1 Измерение с использованием нестандартных и стандартных единиц 647

    13.2 Длина и площадь 665

    13,3 Площадь поверхности 686

    13,4 Объем 696

    14 Геометрия с использованием конгруэнтности и сходства треугольников 716

    14.1 Конгруэнтность треугольников 719

    14.2 Сходство треугольников 729

    14,3

    14.4 Дополнительные евклидовы конструкции 755

    14.5 Решение геометрических задач с использованием сравнения и подобия треугольников 765

    15 Геометрия с использованием координат 780

    15.1 Расстояние и наклон в координатной плоскости 783

    15.2 Уравнения и координаты 795

    15.3 Решение геометрических задач с использованием координат 807

    16 Геометрия с использованием преобразований 820

    16.1 Преобразования 823 823

    16.3 Решение геометрических задач с использованием преобразований 863

    Эпилог: эклектический подход к геометрии 877

    Тема 1.Элементарная логика 881

    Тема 2. Арифметика часов: математическая система 891

    Ответы на упражнения / наборы задач A и B, обзоры глав, тесты глав и темы Раздел A1

    Указатель i1

    Содержание сопутствующего книжного веб-сайта

    Ресурсы для технологических проблем

    eManipulatives

    Работа с электронными таблицами

    Действия с Geometer’s Sketchpad

    Учебные пособия по технологиям

    Таблицы

    000200020002

    0002

    Графический планшет Geometer Алгебраическое мышление

    Детская литература

    Введение в теорию графов

    Дополнительные ресурсы

    Руководство по решению проблем

    Задачи для письма / обсуждения

    Научные статьи

    Web Lin ks

    Видео

    Обзор книги

    Авторские видеоролики

    Детские видеоролики

    .

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *