Задачи на логику с ответами 1 класс по математике: Логические задачи для 1 класса с ответами
Логические задачи для 1 класса
Из книги выпало несколько листов. На первой выпавшей странице стоит номер 5, а на последней номер 10.
Сколько листов выпало из книги?
——————————–
В группе 15 детей. 10 детей любят мороженое, 9 человек — конфеты. Как это может быть?
——————————–
В лесу елок больше, чем берез, а берез больше, чем осин. Чего больше: елок или осин? Почему?
——————————–
В комнате стояли табуретки и стулья. У каждой табуретки 3 ножки, а у стула — 4.
Всего табуреток и стульев было 5, а ножек у них было 18.
Сколько было табуреток и стульев?
——————————–
В книжке 12 страниц. Сколько цифр понадобилось, чтобы пронумеровать все страницы?
Сколько из них единичек? А если в книге 20 страниц?
——————————–
Полный бидон с молоком весит 10 килограммов, а наполненный до половины — 6 килограммов.
Сколько весит пустой бидон?
——————————–
У трёх девочек вместе было 20 карандашей. У Ани и Оли вместе было 15 карандашей. У Оли и Кати вместе было 12 карандашей.
У Ани и Оли вместе было 15 карандашей. У Оли и Кати вместе было 12 карандашей.
Сколько карандашей у каждой девочки?
——————————–
Нарисуй три прямых и отметь на каждой из них по две точки так, чтобы отмеченных точек было 5.
——————————–
У Маши и у Лены кукол поровну, а у Пети машинок в два раза больше, чем кукол у Лены.
Чего больше: машинок у Пети или кукол у Лены и Маши вместе?
——————————–
Коля, Вася и Боря играли в шашки. Каждый из них сыграл две партии. Сколько всего партий было сыграно?
——————————–
В квартирах 1, 2, и 3 живут белый, черный и рыжий котята. В квартире 1 — не черный.
Белый — не в квартире 1 и не в квартире 2. Кто где живет?
——————————–
У мальчика сестер и братьев поровну. Кого в семье больше: сыновей или дочерей? На сколько?
——————————–
По дороге один за другим идут 5 детей. За каждым мальчиком, кроме последнего, идёт девочка.
За каждым мальчиком, кроме последнего, идёт девочка.
Сколько девочек идут по дороге?
——————————–
Каждый из троих взрослых ведёт за руку двоих детей. Сколько детей идут со всеми взрослыми?
——————————–
Я придумала два числа. Когда я их сложила, то получила 6. Когда же из одного вычла другое, то снова получила 6.
Что же это за числа?
——————————–
В коробке 8 пирожных. Сколько пирожных надо взять из коробки, чтобы в ней осталось 5 пирожных?
——————————–
Катя задумала число, прибавила к нему 5 и получила 15. Какое число задумала Катя?
——————————–
На яблоне было 10 яблок, Садовник разрешил детям сорвать с яблони по 1 яблоку. На яблоне осталось 6 яблок.
Сколько было детей?
——————————–
Поезд состоит из 10 вагонов. Петя сел в пятый вагон от начала поезда, а Федя – в пятый вагон от конца.
В одном ли вагоне они едут?
——————————–
Плитка шоколада состоит из 6 квадратных долек.
Сколько разломов нужно сделать, чтобы разломить эту плитку на отдельные дольки?
——————————–
Пётр сын Сергея, а Сергей – сын Фёдора. Кем приходится Пётр Фёдору?
——————————–
В саду яблонь на 3 больше, чем груш. Яблонь 7. Сколько груш?
——————————–
У Зины на 4 открытки меньше, чем у Гали. У Зины 6 открыток. Сколько открыток у Гали?
——————————–
Меня зовут Иваном Сергеевичем, а моего деда (отца моего отца) – Петром Николаевичем. Запишите имя и отчество моего отца.
——————————–
Красный шнур на 1м длиннее зелёного и на 2м длиннее синего. Длина зелёного шнура 5м. Найди длину зелёного шнура.
——————————–
На вешалке висят головные уборы; шляп на 1 больше, чем беретов. Шляп 8. Сколько шапок и сколько беретов?
——————————–
Уменьшаемое больше вычитаемого на 2. Чему равна разность?
——————————–
Угадайте, сколько лет моему дедушке, если через 15 лет мы будем отмечать его семидесятилетие.
——————————–
Разность двух чисел равна вычитаемому. Придумайте такие числа и запишите пример.
——————————–
Разность двух чисел равна 0. Придумайте и запишите пример.
——————————–
Из куска проволоки согнули квадрат со стороной 6 см.
Потом проволоку разогнули и согнули из неё треугольник с равными сторонами.
Найти длину стороны треугольника.
——————————–
В первый день турист прошел 2 км, а в каждый следующий – на 2 км больше, чем в предыдущий.
Сколько он прошел в седьмой день? Сколько он прошел за 8 дней?
Математические загадки на логику с ответами. Самые сложные задачи в мире
Содержание
- Польза занятий логикой и математикой
- Уроки-игры
- Математические задачи на логику для дошкольников
- Математические задачи на логику: 1-2 класс
- Математические задачи на логику: 3-4 класс
- Занимательные математические задачи для учащихся 5-х классов с ответами
- Математические головоломки
- Визуальная тренировка для мозга
- Загадки
- Логические задачки
- ПРАВИЛЬНЫЕ ОТВЕТЫ:
- Самая сложная задача в мире
Польза занятий логикой и математикой
Элементарные математические представления помогают сформировать в детском саду. Базовые математические способности развивают в школе.
Базовые математические способности развивают в школе.
А чтобы ребёнок научился рассуждать логически, мыслить нестандартно — обычных арифметических и геометрических задач недостаточно.
Уже в дошкольном возрасте желательно выработать привычку ежедневно выполнять задания и упражнения на развитие логического мышления.
Благодаря регулярным тренировкам:
- ребёнок учится рассуждать, анализировать и делать правильные выводы;
- развивает сообразительность, память, внимание и интеллект;
- успехи повышают самооценку, интерес к обучению в школе, вдохновляют на победы в математических олимпиадах и конкурсах.
Уроки-игры
В школьных учебниках занимательного материала недостаточно. Однако опытный педагог умеет сделать привычные задания по математике интересными. В 1 классе это особенно важно, так как дети лучше откликаются на игровую форму обучения. Им скучно решать примеры, но все меняется, если учитель принесет на урок мяч и будет спрашивать верный ответ у поймавшего его.
Повысить активность детей позволяет игровой сюжет, присутствующий на занятии. Вариантов может быть множество. Например, за каждое выполненное задание ребятишки получают кусочек паззла, и в конце урока из них собирается картинка. Или класс отправляется спасать героя, попавшего в беду. На пути они встречают различных злодеев и побеждают их, решая задачки и примеры. Очень нравятся детям соревнования, когда класс делится на команды и каждая набирает жетоны за работу. Победителей можно наградить бумажными медалями. Таким образом, не всегда нужно искать занимательный материал. Иногда достаточно изменить форму его подачи.
Математические задачи на логику для дошкольников
Начиная с 3 летнего возраста малыша, родители должны понемногу заниматься тренировкой логического мышления у своих детей. Детям это очень важно, ведь для них в таком возрасте многие очевидные вещи кажутся сложными, а непонятные для восприятия взрослым, напротив, очевидными. Представим несколько вариантов логических задач для детей 3-5 лет.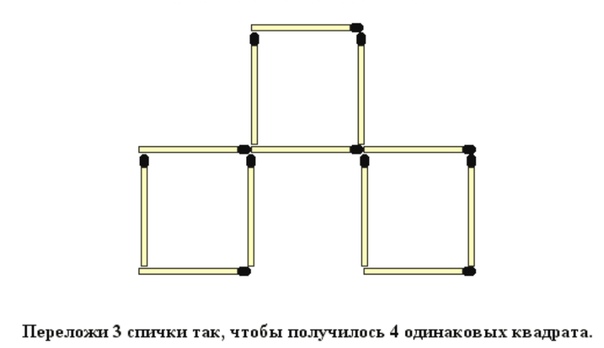
- На столе лежит 1 апельсин. Его разрезали на 2 части, сколько апельсинов лежит на столе? Ответ: 1, разрезанный.
- Собаку привязали к забору веревкой. Длина веревки составляет 10 метров, а собака прошла за день 100 метров. Как ей это удалось? Ответ: Собака ходила вдоль забора туда и обратно и «находила» целых 100 метров.
- Какой день недели соответствует числу 3? Ответ: среда, т.к. его порядковый номер в неделе – 3.Примечание: Про дни недели дошкольникам можно задавать различные варианты вопросов. Это поможет не только в развитии логического мышления, но и поможет скорее выучить дни недели.
- Посчитать, сколько людей в следующей строке: ты да я, да мы с тобой. Ответ: 2.
- Папа и сын, дедушка и внук, сын и папа. Сколько всего человек здесь отмечено? Ответ: 3, т.к. папа – сын дедушки, сын папы – внук дедушки.
- На опушке стояло 3 высоких сосны. На каждой сосне по 3 больших ветки и по 3 маленьких. На каждой маленькой ветке по яблоку. Сколько всего яблок на деревьях? Ответ: 0, на соснах яблоки не растут.

- Папу Антона зовут Андрей Викторович, а дедушку – Сергей Иванович. Какое отчество у мамы Антона? Ответ: Сергеевна, Потому что Сергей Иванович – это отец мамы Антона. Отца папы Антона зовут Виктор.
- У двух братьев по одной сестре. Сколько всего детей в семье? Ответ: 3. 2 брата и одна сестра на двоих.
- Какие камни есть в море? Ответ: мокрые.Примечание: аналогичная задача-загадка моет звучать так «Каких камней в море нет?» — ответ: сухих.
- Вася и Петя играли в морской бой и сыграли по 3 партии. Каждый выиграл по 3 раза. Это правда или ложь? Ответ: ложь. Во время одной партии выиграть может только один.
- В поле работали 5 тракторов. 2 трактора сломались и остановились. Сколько тракторов в поле? Ответ: 5, т.к. учитываются все тракторы, и рабочие, и сломанные.
- Одно яйцо варится 5 минут. Сколько времени нужно, чтобы сварить 2 яйца? Ответ: все те же 5 минут.
- Саша сидит в самолете. Впереди него машина, сзади – лошадь. Где находится Саша? Ответ: катается на карусели.

- Алена сидит, когда она встанет и уйдет, ее мама так и не сможет сесть на ее место. Где сидит Алена? Ответ: у мамы на коленях.
- Что все дети на земле делают одновременно? Ответ: взрослеют.
Опираясь на предложенные варианты заданий на развитие логического мышления, родители могут придумывать незамысловатые условия задач самостоятельно.
Математические задачи на логику: 1-2 класс
Но вот дети пошли в школу, буквально за первые месяцы учебы они начинают хорошо считать, ориентироваться в пространстве и времени. Задачки для дошкольников уже кажутся им простыми и неинтересными. Поэтому для таких деток мы приготовили несколько вариантов упражнений тренировки логики и смекалки, ориентируясь на их новые способности и возможности.
- Первоклассника попросили назвать самое большое число. Что он ответил?
Ответ: 31. Первоклассники каждый день записывают число месяца в тетрадь, самое большое число в месяце – 31. - На доске написаны два числа 4 и 5.
 Какой знак нужно поставить между ними, чтобы получился результат больше 4 и меньше 5. Ответ: запятая.
Какой знак нужно поставить между ними, чтобы получился результат больше 4 и меньше 5. Ответ: запятая. - По узкой дороге может проехать только одна машина. С одной стороны дороги находится гора. Одна машина едет с горы, другая – под гору. Как им разминуться? Ответ: обе машины едут в одном направлении и разминаться им не придется.
- Сколько раз из числа 10 можно отнять число 2? Ответ: один, т.к. уже после первого вычитания двойки останется число 8, а не 10.
- На столе стоят 6 стаканов: в первые три налили воду, вторые три – пустые. Нужно расставить стаканы так, чтобы чередовались пустые и полные стаканы, но при этом можно взять в руки только один стакан. Как поступить, чтобы выполнить условие? Ответ: Взять второй стакан и перелить из него воду в пятый стакан. Второй стакан поставить на прежнее место.
- За 10 часов 10 человек могут выкопать траншею длиной в 10 метров. Сколько нужно человек, чтобы они выкопали траншею диной в 100 метров за 100 часов? Ответ: 10 человек.
 На 1 час 10 человек выкопают 1 метр траншеи, за 10 часов они выкапывают 10 метров траншеи, а за 100 часов – 100 метров.
На 1 час 10 человек выкопают 1 метр траншеи, за 10 часов они выкапывают 10 метров траншеи, а за 100 часов – 100 метров. - Школьники участвуют в соревнованиях по бегу. Ваня занимает третью позицию, Антон занимает вторую позицию. Саша обгоняет Антона. Какую позицию занимает Саша? Ответ: вторую, т.к. впереди Антона тоже кто-то бежит и этот кто-то пока первый.
- Учитель положил на пол карандаш и попросил учеников перешагнуть через него, но никто не смог этого сделать. Почему? Ответ: карандаш лежит у стены и шагать детям некуда.
- Таня и Алиса пошли в магазин и нашли 2 рубля. Сколько бы денег они нашли, если бы с ними пошла еще и Марина? Ответ: 2 рубля, т.к. размер находки никак не зависит от количества ее нашедших.
- Из пункта А в пункт Б вышла кошка, а из пункта Б в пункт А вышла мышка. Когда они встретятся, кто из них будет ближе к пункту А, а кто к пункту Б? Ответ: они обе будут на одинаковом расстоянии от пункта А, и на одинаковом расстоянии от пункта Б.
- На столе стояли 3 чашки с чаем.
 Папа выпил чай из одной чашки и поставил ее на место. Мама выпила свой чай и тоже поставила чашку на место. Сколько чашек было на столе, когда пришел пить чай сын? Ответ: 3 чашки. Они хоть и пустые, но никуда со стола не делись.
Папа выпил чай из одной чашки и поставил ее на место. Мама выпила свой чай и тоже поставила чашку на место. Сколько чашек было на столе, когда пришел пить чай сын? Ответ: 3 чашки. Они хоть и пустые, но никуда со стола не делись. - Марина шла из дома в школу и встретила трех мужиков. У каждого за спиной был мешок. У первого мужика в мешке был один кот, у второго в мешке был один кот и один пес. У третьего в мешке было 2 пса. Сколько всего котов направлялось в школу? Ответ: один, сама Марина. Мужики с мешками шли в обратную от школы сторону.
- В классе стоял стол с четырехугольной крышкой. Ученики отпилили один угол, что стало со столом, сколько углов осталось на крышке? Ответ: 5. Если отпилить один угол, то получим на его месте 2 новых, поэтому всего 5 углов.Примечание: на самом деле количество углов может зависеть и от того, как размышляет ребенок. Если он «пилит» стол по углам диагонали, т.е. распиливает его пополам, то вполне возможно, что у стола будет 3 угла. Если же один распил приходится на угол, а второй на сторону крышки, то может остаться и 4 угла.
 Но это нюансы, которые лучше рассматривать, рисуя на листе бумаги, где ребенок собирается «пилить» стол.
Но это нюансы, которые лучше рассматривать, рисуя на листе бумаги, где ребенок собирается «пилить» стол. - На тарелке лежат 3 банана. Их нужно разделить между тремя девочками, чтобы на тарелке остался один банан. Ответ: одной девочке нужно отдать банан вместе с тарелкой.
- Какое слово зашифровано: ООО? Ответ: ТРИО, т.е. ТРИ О.
Родители тоже могут составлять свои задачи для детей, ориентируясь на предложенные варианты. Чем чаще ребенок будет заниматься упражнениями на логику, тем быстрее будет работать его мозг, тем выше будет успеваемость в школе.
Математические задачи на логику: 3-4 класс
Дальнейшее обучение в школе имеет свои особенности: дети научились складывать двузначные числа, совершать с ними различные математические операции, в том числе умножение, деление. Логические математические задачи для школьников 3-4 класса должны охватывать уже полученные знания и совершенствовать их качество.
- В кошельке лежит 15 копеек двумя монетами.
 Одна из монет не пятак, как такое может быть? Ответ: может, т.к. другая монета вполне может быть пятаком.
Одна из монет не пятак, как такое может быть? Ответ: может, т.к. другая монета вполне может быть пятаком. - Шла Маша в Волгоград, а навстречу ей 10 ребят. У каждого в руках по лукошку, в каждом лукошке по кошке, а у каждой кошки по котенку. Сколько всего ребят шло в Волгоград? Ответ: одна Маша. Все остальные, сколько бы их не перечисляли, шли навстречу девочке, а значит в противоположную сторону от Волгограда.
- Дедушка пилит бревна. Распил бревна пополам он делаем ан одну минуту. Сколько ему понадобится времени, чтобы распилить бревно на 10 частей? Ответ: 9 минут, т.к.чтобы распилить бревно на 10 частей, нужно сделать 9 распилов.
- Мальчик пришел в амбар. В каждом углу амбара стояло по 3 мешка. На каждом мешке сидело по кошке, у каждой кошки было по котенку. Сколько всего ног было в амбаре? Ответ: две, только мальчика.Примечание: Как бы долго дети не перемножали между собой числа-«ноги» кошек и котят, стоит помнить, что у кошек – лапы, а ноги – только у мальчика.
- Родители купили своим двум дочкам Маше и Лизе по коробке конфет.
 В каждой коробке было по 15 конфет. Маша съела несколько конфет и отложила коробку. А Лиза съела столько, сколько оставалось в коробке у Маши, и тоже отложила коробку. Вечером мама посчитала конфеты в коробках обеих девочек. Сколько конфет там было? Ответ: 15. Маша и Лиза съели вместе 15 конфет. Маша несколько (например, 15-х=у), а Лиза столько, сколько осталось у Маши (т.е. у конфет). Сумма х+у = 15. А у девочек было по 15 конфет, т.е. 2*15 = 30. Было 30, 15 съели, и 15 на двоих осталось. А сколько у кого – этого в задаче не уточняется.
В каждой коробке было по 15 конфет. Маша съела несколько конфет и отложила коробку. А Лиза съела столько, сколько оставалось в коробке у Маши, и тоже отложила коробку. Вечером мама посчитала конфеты в коробках обеих девочек. Сколько конфет там было? Ответ: 15. Маша и Лиза съели вместе 15 конфет. Маша несколько (например, 15-х=у), а Лиза столько, сколько осталось у Маши (т.е. у конфет). Сумма х+у = 15. А у девочек было по 15 конфет, т.е. 2*15 = 30. Было 30, 15 съели, и 15 на двоих осталось. А сколько у кого – этого в задаче не уточняется. - Из ГОРОНО в школу пришли проверяющие. Они выбрали класс для проверки, но не все дети были готовы отвечать урок. Тем не менее, на каждый вопрос учителя весь класс поднимал руку, и тот, кого учитель вызывал к доске, отвечал блестяще. Как получилось, что учитель угадывал, кого вызвать отвечать? Ответ: решением этой задачи есть небольшая хитрость. Перед уроком школьники и учитель договорились, что те, кто наверняка знают ответ на поставленный вопрос, будут поднимать правую руку.
 А те, кто не знают – левую. Благодаря маленькой хитрости класс достойно прошел проверку и никто ни о чем не догадался.
А те, кто не знают – левую. Благодаря маленькой хитрости класс достойно прошел проверку и никто ни о чем не догадался. - Что у коровы находится спереди, а у быка сзади? Ответ: буква «К». Корова, быК.
- Когда маме исполнилось 31 год, дочери было 8. Сейчас мама старше дочери ровно в 2 раза. Сколько их обеим лет? Ответ: дочке 23, маме 46. Когда дочь родилась, маме было 31-8 = 23 года. Чтобы быть старше дочки в два раза, маме должно быть 23*2 = 46 лет. За это время дочь доросла до 23 лет.
- Две одноклассницы Наташа и Лена живут в одном подъезде: Лена на втором этаже, а Наташа на четвертом. Наташа поднимается по ступенькам на четвертый этаж и проходит 60 ступенек. Сколько ступенек проходит Лена, которая поднимается на второй этаж? Ответ: 20. Чтобы подняться с первого этажа на четвертый, нужно пройти три пролета. 60_3=20 ступенек в одном пролете. А Лена поднимается с первого на второй этаж и проходит при этом только один пролет, все те же 20 ступенек.
- Может ли страус называть себя птицей? Ответ: нет, не может.
 Страусы не умеют разговаривать.
Страусы не умеют разговаривать. - Какая физическая величина не имеет ни высоты, ни глубины, ни ширины, ни длины, но ее можно измерить? Ответ: время, температура.
- Задание на логику из серии «Юный Шерлок». На вызов о самоубийстве были вызваны представители уголовного розыска. В кабинете жертвы они обнаружили диктофон и включили его. На диктофоне была записана следующая фраза: «В моей смерти прошу никого не винить, жизнь не имеет смысла…» далее раздался выстрел. Как следователи поняли, что убийство сфабриковано? Ответ: убитый не мог перемотать запись на начало, это сделал кто-то другой.
- Что не может поместиться даже в самую большую кастрюлю? Ответ: ее крышка.
- В кастрюле налита вода до самого верха. Как отмерять жидкость, не используя никаких мерительных приспособлений, чтобы в кастрюле осталась только половина жидкости. Ответ: нужно наклонить кастрюлю и выливать воду до тех пор, пока не покажется с боковой части дно. Это и будет половина кастрюли.
- Когда цифра «2» означает «10»? Ответ: на циферблате цифра «2» соответствует «10 минутам».

С каждым годом задания на развитие логики и смекалки должны становится все сложнее, иметь подвохи, хитрости, чтобы ребенок учился размышлять, уделять внимание деталям. А регулярные и систематические занятия обязательно принесут свои плоды.
Занимательные математические задачи для учащихся 5-х классов с ответами
Из гнезда вылетели три ласточки. Какова вероятность того, что через 15 секунд они будут находиться в одной плоскости? (Ответ: 100%, так как три точки всегда образуют одну плоскость)
На столе лежат две монеты, в сумме они дают 3 рубля. Одна из них — не 1 рубль. Какие это монеты? (Ответ: 2 рубля и 1 рубль. Одна то не 1 рубль, а вот другая — 1 рубль)
С какой скоростью должна бежать собака, чтобы не слышать звона сковородки, привязанной к ее хвосту? (Ответ: Если выдумаете, что ей нужно бежать со сверхзвуковой скоростью, то вы ошибаетесь — собаке достаточно стоять на месте)
Один оборот вокруг Земли спутник делает за 1 ч 40 мин, а другой — за 100 минут. Как это может быть? (Ответ: 1 ч 40 мин = 100 мин)
Как это может быть? (Ответ: 1 ч 40 мин = 100 мин)
Крыша одного дома несимметрична: один скат ее составляет с горизонталью угол 60 градусов, другой — угол 70 градусов. Предположим, что петух откладывает яйцо на гребень крыши. В какую сторону упадет яйцо — в сторону более пологого или крутого ската? (Ответ: Петухи не кладут яйца)
В 12-этажном доме есть лифт. На первом этаже живут всего 2 человека, от этажа к этажу количество жильцов увеличивается вдвое. Какая кнопка в лифте этого дома нажимается чаще других? (Ответ: Независимо от распределения жильцов по этажам, кнопка «1»)
В двух кошельках лежат две монеты, причем в одном кошельке монет вдвое больше, чем в другом. Как такое может быть? (Ответ: Один кошелек лежит внутри другого)
Сын отца профессора разговаривает с отцом сына профессора, причем сам профессор в разговоре не участвует. Может ли такое быть? (Ответ: Да, может, если профессор — женщина)
Два сына и два отца съели 3 яйца. Сколько яиц съел каждый? (По одному яйцу каждый)
На складе было 5 цистерн с горючим, по 6 т в каждой. Из двух цистерн горючее выдали. Сколько цистерн осталось? (5)
Из двух цистерн горючее выдали. Сколько цистерн осталось? (5)
Вообрази, что ты капитан футбольной команды. В районе 8 футбольных команд по 11 человек в каждой. Игроки вашей команды на 2 года моложе своего капитана, а игроки других — только на 1 год. Сколько лет капитану вашей команды? (Столько, сколько лет отвечающему)
Пара лошадей пробежала 20 км. Сколько километров пробежала каждая лошадь? (20 км)
Когда сороке исполнится 4 года, что с ней произойдет? (Будет жить пятый год)
Если в 11 часов ночи идет дождь, то возможно ли через 48 часов солнечная погода? (Нет, так как будет ночь)
Чтобы сварить 1 кг. мяса требуется один час. Сколько времени потребуется для варки ½ кг мяса? (1 час)
У Марины было целое яблоко, две половинки и 4 четвертинки. Сколько было у нее яблок? (3)
На грядке сидели 6 воробьев, к ним прилетели еще 5. Кот подкрался и схватил одного воробья. Сколько воробьев осталось на грядке? (Один, которого схватил кот. Остальные улетели)
Мальчик написал на бумажке число 86 и говорит своему товарищу: «Не производя никакой записи, увеличь это число на 12 и покажи мне ответ».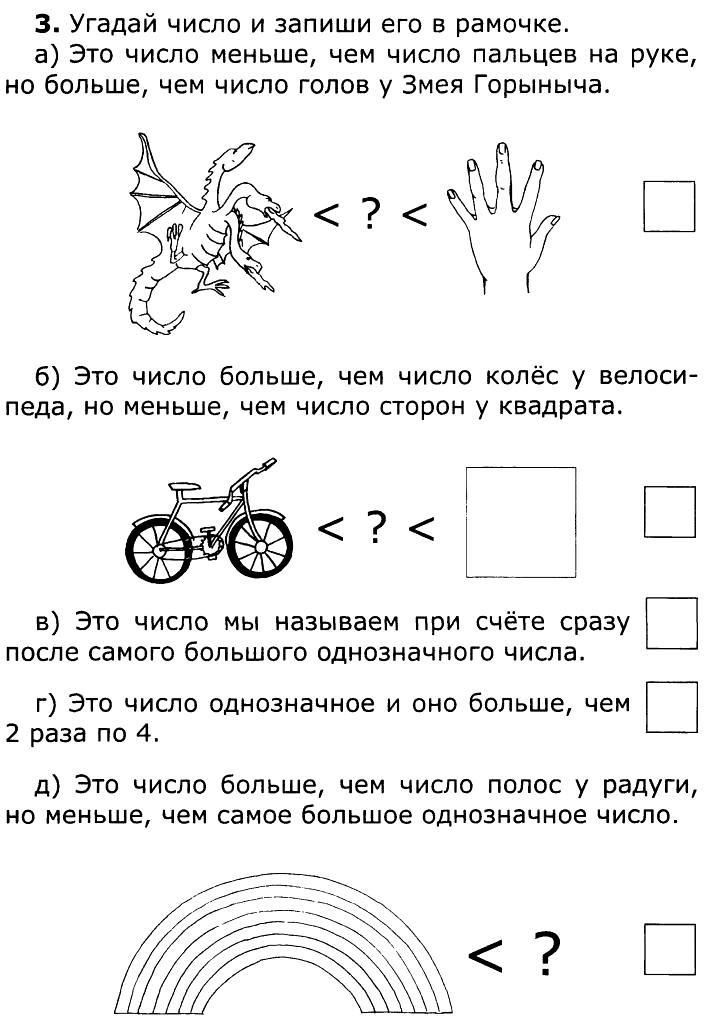 Недолго думая, товарищ показал ответ. А вы это сделать сумеете? (Перевернуть бумажку «вверх ногами»)
Недолго думая, товарищ показал ответ. А вы это сделать сумеете? (Перевернуть бумажку «вверх ногами»)
В клетке находились 4 кролика. Четверо ребят купили по одному из этих кроликов и один кролик остался в клетке. Как это могло получиться? (Одного кролика купили вместе с клеткой)
Летели утки: одна впереди и две позади, одна позади и две впереди, одна между двумя и три в ряд. Сколько всего летело уток? (Три утки, одна за другой)
У одного старика спросили, сколько ему лет. Он ответил, что ему сто лет и несколько месяцев, но дней рождения у него было всего 25. Как это могло быть? (Этот человек родился 29 февраля, т. е. день рождения у него бывает один раз в четыре года)
Что это такое: две ноги сидели на трех, а когда пришли четыре и утащили одну, то две ноги, схватив три, бросили их в четыре, чтобы четыре оставили одну? (Повар сидел на стуле, имеющем три ножки, пришла собака и утащила куриную ногу. Повар бросил стул в собаку, чтобы она оставила куриную ногу)
Часы бьют каждый час и отбивают столько ударов, сколько показывает часовая стрелка. Сколько ударов отобьют часы в течение 12 часов? (Количество ударов равняется 1+2+3+…+12…= 78. Сумма членов, равноотстоящих от концов (1+12,2+11,3+10,…) равны между собой — 13. Таких пар равноотстоящих от концов чисел имеется 6. Значит, 1+2+3+…+12=6 13=78)
Сколько ударов отобьют часы в течение 12 часов? (Количество ударов равняется 1+2+3+…+12…= 78. Сумма членов, равноотстоящих от концов (1+12,2+11,3+10,…) равны между собой — 13. Таких пар равноотстоящих от концов чисел имеется 6. Значит, 1+2+3+…+12=6 13=78)
Летели скворцы и встретились им деревья. Когда сели они по одному на дерево, то одному скворцу не хватило дерева, а когда на каждое дерево сели по два скворца, то одно дерево осталось незанятым. Сколько было скворцов и сколько деревьев? (Предположим, что после того как скворцы сели на деревья по два, с каждого дерева взлетело по одному скворцу. Один из взлетевших скворцов может сесть на незанятое дерево, тогда на каждом дереве будет сидеть по одному скворцу. По условию, если на каждое дерево сядет по одному скворцу, то один скворец останется в воздухе. Значит, взлетело 2 скворца. Тогда общее число скворцов равно 4, а число деревьев З).
Математические головоломки
Вопрос 1. Какое число зашифровано?
Вопрос 2. Как поместить шары с цифрами, чтобы получить число 30?
Как поместить шары с цифрами, чтобы получить число 30?
Вопрос 3. Какая цифра получится в конце?
Замените знак вопроса числом, соответствующим приведенным ниже уравнениям. Найдите закономерность.
Визуальная тренировка для мозга
Вопрос 4. Разделите изображение на четыре части, которые сочетали бы всех видов насекомых:
Вопрос 5. Какой вид сверху на башню: А, В, С или D?
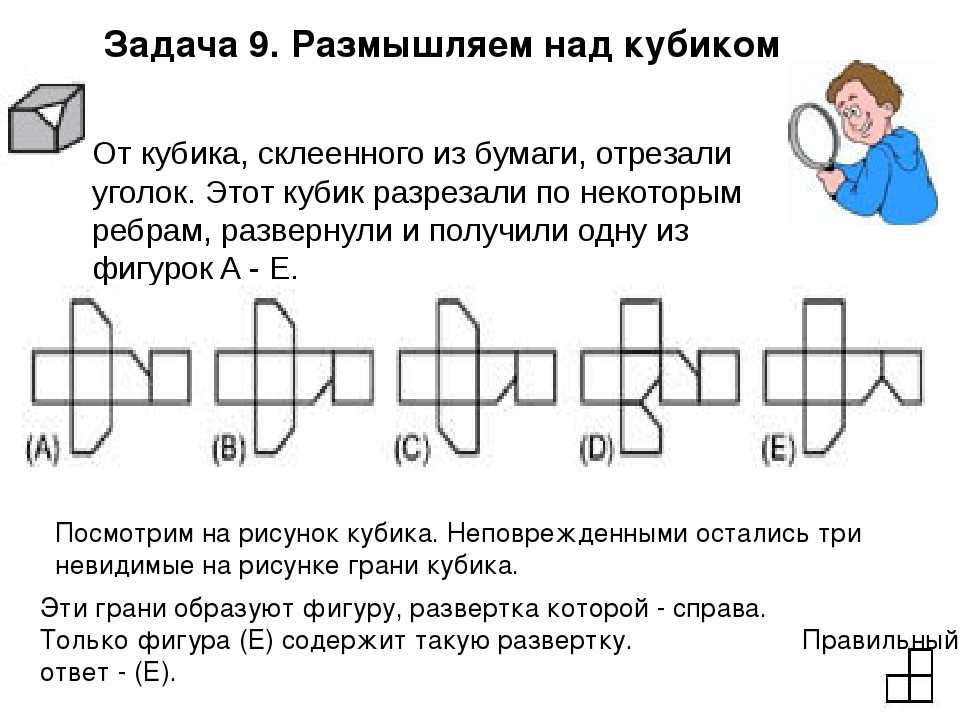
Вопрос 6. Каким образом представляются кубики для человека, который стоит в оранжевой точке и смотрит на фигуру в указанном направлении?
Вопрос 7. Быстро решите, какой фрукт необходимо добавить?
Вопрос 8. Смотрите внимательно и угадайте, кто вор?
Загадки
Вопрос 9. Примите жизненно важное решение. В комнате без света есть три двери: за первой спряталась ядовитая змея, за второй – лев, который не ел пару дней, в третьей вас ждет экзекуция на электрическом столе. Какую дверь безопаснее всего открыть?
Вопрос 10. Разминка на логику и память. В названии какого города спрятались имена ста девушек и одного парня?
Разминка на логику и память. В названии какого города спрятались имена ста девушек и одного парня?
Вопрос 11. Логическая загадка: у отца Фрэнка 5 сыновей. Имена его четырех сыновей — Фефе, Фифи, Фофо, Фуфу. Соответственно, как зовут его пятого сына?
Вопрос 12. Знаменитая загадка: по пути в Сент-Айвз я увидел мужчину с 7 женами. У каждой жены было 7 мешков. В каждом мешке было по 7 кошек. У каждого кота было 7 котят. Котенок, кошки, мешки, жены – сколько их направляются в Сент-Айвс?
Логические задачки
Вопрос 13. Как отмерить 4 литра воды, если есть 5-литровая и 3-х литровая емкости?
Вопрос 14. Как сделать цифру «4», но не сломать ни одну палочку.
Вопрос 15. В каком чайнике больше чая?
ПРАВИЛЬНЫЕ ОТВЕТЫ:
1-й Правильный ответ: 9.
2-й Правильный ответ:
Этот вопрос не может быть решен математически. Потому что сумма трех нечетных чисел не может быть четное число.
Но здесь важно ваше внимание. Если вы поместите шары с цифрами 11 и 13, то получите 24. Затем, если вы поместите шар с цифрой 9, но перевернете, то получите 24 + 6 = 30.
Если вы поместите шары с цифрами 11 и 13, то получите 24. Затем, если вы поместите шар с цифрой 9, но перевернете, то получите 24 + 6 = 30.
3-й Правильный ответ:
Если мы знаем, что каждое полученное число является степенью числа 4, получаем:
41 = 4
42 = 16
43 = 64
44 = 256
4-й Правильный ответ:
5-й Правильный ответ:
Если вы посмотрите на башню сверху, верхний слой будет оранжевым. Таким образом, ответ определенно не C.
Второй фиолетовый слой не будет виден сверху, потому что он такого же размера, как и верхний слой.
И третий слой также не будет виден, потому что он меньше, чем два верхних слоя.
Четвертый слой будет следующим, который будет виден сверху вокруг фиолетового слоя.
Последний будет самым крупным, и он оранжевый. В соответствии с этим, ответ будет A.
6-й Правильный ответ:
Пойдем шаг за шагом. Очевидно, что внизу 4 блока.
Над крайним правым блоком есть еще один. Таким образом, ответ определенно не C.
Самый высокий блок состоит из трех блоков в высоту.
Итак, ответ D.
7-й Правильный ответ:
Банан, Груша, Перец
8-й Правильные ответы:
9-й Правильные ответы:
С электрическим стулом. Палач скорее всего пойдет проверить, почему света нет, а вы сможете убежать.
10-й Правильный ответ:
Севастополь – Сева и 100 Поль.
11-й Правильный ответ:
Если у отца Фрэнка 5 сыновей, а имена 4 сыновей такие же, как указано выше, то Фрэнк уже 5-й сын.
12-й Правильный ответ:
Только я.
13-й Правильный ответ:
Налейте полную емкость в 5 литр;
Перелейте из нее в 3-х литровую емкость – получаем остаток 2 литра;
Выливаем 3 литра – остается только 2 литра воды;
Переливаем ее в 3-х литровую емкость;
Снова заполняем 5-ти литровую емкость
Переливаем в 3-х литровую емкость недостающий 1 литр воды и получаем остаток в 4 литра!
14-й Правильный ответ:
15-й Правильный ответ:
В первом. Нужно смотреть на положение носика.
Нужно смотреть на положение носика.
Самая сложная задача в мире
Самой сложной задачей в мире официально признали задание из итальянской газеты, опубликованное в 1992 году. Составил ее философ по имени Джордж Булос. Условия задачи следующие:
Имеются три божества. Одно из них ‒ покровитель правды (А), другое ‒ покровитель лжи (В), третье ‒ покровитель случайностей (С). И первый всегда отвечает исключительно правду, второй лжет, а вот третий может лгать или не лгать в произвольной последовательности. Богов нужно распознать, задав им в общей сложности 3 вопроса. Отвечать они могут лишь «нет» или «да», причем на своем собственном языке (Da и Ja), так что придется еще догадаться, которое из слов означает «да», а которое ‒ «нет». Не разрешается задавать нескольким божествам один и тот же вопрос. Зато одному можно сразу задать два или даже три вопроса, тогда остальные останутся вовсе без вопросов. Иногда ответ на какой-либо вопрос влияет на то, кому и какой следующий вопрос задать. Бог случайностей отвечает, словно в его голове подбрасывается воображаемая монетка, причем аверс ‒ правда, а реверс ‒ ложь. Запрещено задавать парадоксальные вопросы, на которые можно дать ответ как нет, так и да, или нельзя дать ответ вовсе.
Бог случайностей отвечает, словно в его голове подбрасывается воображаемая монетка, причем аверс ‒ правда, а реверс ‒ ложь. Запрещено задавать парадоксальные вопросы, на которые можно дать ответ как нет, так и да, или нельзя дать ответ вовсе.
Самая сложная логическая задача имеет следующее решение:
Первым же вопросом необходимо отыскать того, кто НЕ является божеством случайностей. Вариантов таких вопросов много, но главное условие ‒ наличие в вопросе некоторых логических связей. Например: «Если ты — божество правды, а В ‒ божество случайностей, то Da ‒ это означает да?» Можно упростить решение, применяя условные фразы, которые противоречат фактам. Суть в том, что на любой из возможных вопросов (Q), заданный божеству правды или божеству лжи («Если я задам некий вопрос Q, ответ будет звучать как Ja?»), ответят Ja в том случае, если ответ должен быть да, и Da ‒ если ответ должен быть нет. Чтобы это доказать, автор предложил целых восемь вариантов вопросов. В конце, после того, как выяснили, кто божество правды, а кто лжи, оставшийся бог будет опознан методом исключения.
Источники
- https://logiclike.com/math-logic
- https://FB.ru/article/390638/interesnyie-zadaniya-po-matematike-igryi-i-zadaniya-s-otvetami-dlya-shkolnikov
- https://ChildAge.ru/obuchenie-i-obrazovanie/nachalnaya-shkola/samostoyatelnaya-rabota/matematicheskie-zadachi-na-smekalku-s-otvetami.html
- https://ped-kopilka.ru/uchiteljam-predmetnikam/matematika/zanimatelnye-zadachi-po-matematike-s-otvetami-5-klas.html
- https://joy-pup.com/puzzle/15-novyh-zadach-na-logiku/
- https://megatopof.ru/prochee/slozhnye-zadachi.html
35 Умные математические головоломки для детей
Нет лучшего способа развить нестандартное мышление, чем математические головоломки для детей! Обычно они гораздо больше используют логику, чем математические гении, поэтому всем нужно мыслить творчески. Вот некоторые из наших любимых математических головоломок для детей, которые идеально подходят для звонарей, дополнительных баллов или для того, чтобы заполнить последние несколько минут в конце урока.
1. Используя только сложение, добавьте восемь восьмерок, чтобы получить число 1000.
Ответ: 888 + 88 + 8 + 8 + 8 = 1000
2. Два года назад я был в три раза старше моего брата. Через три года я буду вдвое старше своего брата. Сколько лет каждому из нас сейчас?
Ответ: Старшему брату 17, а младшему 7.
3. Если курица-полтора снесет полтора яйца за полтора дня, то сколько яиц снесет полдюжины куриц лежать за полдюжины дней?
Ответ: 2 дюжины или 24 яйца
4. Когда 9 + 5 = 2?
Ответ: Когда вы показываете время. 9:00 + 5 часов = 2:00.
5. У фермера было 17 овец. Все, кроме 9, убежали. Сколько овец у нее осталось?
Ответ: 9
РЕКЛАМА
6. Мальчику 2 года. Его брат вдвое моложе его. Когда первому мальчику исполнится 100 лет, сколько будет его брату?
Ответ: 99
7. Используйте числа 2, 3, 4 и 5 и символы + и =, чтобы составить истинное математическое уравнение.

Ответ: 2 + 5 = 3 + 4
8. Если 3 кошки могут поймать 3 кроликов за 3 минуты, сколько времени потребуется 100 кошкам, чтобы поймать 100 кроликов?
Ответ: 3 минуты
9. У мистера Ли 4 дочери. У каждой из его дочерей есть 1 брат. Сколько детей у мистера Ли?
Ответ: 5 (У всех дочерей один и тот же брат.)
10. Какая цифра чаще всего встречается между числами от 1 до 1000 включительно?
Ответ: 1
11. Что весит больше: 16 унций перьев или фунт чистого золота?
Ответ: Они весят одинаково. 16 унций = 1 фунт, независимо от того, какой материал взвешивается.
12. Джейк купил пару туфель и рубашку на общую сумму 150 долларов. Туфли стоят на 100 долларов дороже рубашки. Сколько стоил каждый предмет?
Ответ: Туфли стоят 125 долларов, рубашка 25 долларов.
13. У вас есть две монеты общей стоимостью 30 центов. Один из них не пятак. Какие две монеты?
Ответ: Четверть и пятак. (Только ОДНА из монет не пятицентовая!)
(Только ОДНА из монет не пятицентовая!)
14. A + B + C = D, и A x B x C = D. Какие числа делают эти два уравнения верными?
Ответ: A = 1, B = 2, C = 3 и D = 6
15. Решите это в уме (не записывая!). Возьмите 1000 и прибавьте к ней 40. Добавьте еще 1000. Теперь добавьте 30. Добавьте еще 1000. Теперь добавьте 20. Добавьте еще 1000. Теперь добавьте 10. Какова сумма?
Ответ: 4100
16. Бабушка умерла и оставила половину своих денег внучке и половину этой суммы внуку. Она оставила шестую часть своему брату, а остаток, 1000 долларов, приюту для животных. Сколько всего она оставила?
Ответ: $12,000
17. В вашем ящике для носков 18 белых и 18 синих носков. Не глядя, какое наименьшее количество носков вы должны взять, чтобы гарантированно получить совпадающую пару?
Ответ: 3
18. Вы посадили семена подсолнуха в своем саду. Каждый день количество цветов удваивается. Если цветы заполнят сад за 52 дня, то за сколько дней они заполнят половину сада?
Ответ: 51
19.
 В районе, где живут Алекс и Дев, 100 домов. Номер дома Алекса является обратным номеру дома Дева. Разница между их номерами домов заканчивается на 2. Каковы их номера домов?
В районе, где живут Алекс и Дев, 100 домов. Номер дома Алекса является обратным номеру дома Дева. Разница между их номерами домов заканчивается на 2. Каковы их номера домов?
Ответ: 19и 91
20. Что вы можете поставить между 8 и 9, чтобы результат был больше 8, но меньше 9?
Ответ: десятичная дробь (8,9 больше 8, но меньше 9.)
21. Умножьте это число на любое другое число, и каждый раз вы получите один и тот же ответ. Какой номер?
Ответ: Ноль
22. Если в корзине 6 апельсинов, а вы вынимаете 4, сколько у вас апельсинов?
Ответ: 4 (Вы взяли 4 апельсина, значит у вас 4 апельсина!)
23. В корзине 8 яблок. Восемь человек берут по 1 яблоку, но в корзине остается 1 яблоко. Как это может быть?
Ответ: Восьмой человек взял корзину с 1 яблоком.
24. Перемножьте все цифры на цифровой клавиатуре телефона. Какова общая сумма?
Ответ: Ноль (номер телефона включает цифры 0-9. )
)
25. В семье Гарсия 7 детей, каждый из которых родился с разницей в 2 года. Если старшему ребенку Гарсии 19 лет, сколько лет самому младшему ребенку Гарсии?
Ответ: 7
26. У двух матерей и двух дочерей на завтрак было по 1 яйцу, но все вместе они съели только 3 яйца. Как это может быть?
Ответ: Было всего 3 человека — бабушка, ее дочь и ее внучка.
27. 300-футовый поезд, движущийся со скоростью 300 футов в минуту, должен пройти через туннель длиной 300 футов. За какое время поезд проедет тоннель?
Ответ: 2 минуты. (Передней части поезда требуется 1 минута, а остальной части поезда потребуется еще 1 минута, чтобы пройти туннель.)
28. Я трехзначное число. Моя вторая цифра в четыре раза больше третьей цифры. Моя первая цифра на три меньше моей второй цифры. Какой я номер?
Ответ: 141
29. Тома попросили закрасить числа за пределами 100 квартир, значит, ему нужно будет закрасить числа от 1 до 100.
 Сколько раз ему придется закрасить число 8?
Сколько раз ему придется закрасить число 8?
Ответ: 20 раз (8, 18, 28, 38, 48, 58, 68, 78, 80, 81, 82, 83, 84, 85, 86, 87, 88 [две восьмерки], 89, 98 )
30. Элли работает в океанариуме. Когда она пытается поместить каждую черепаху в отдельный аквариум, у нее на одну черепаху слишком много. Но если она посадит по две черепахи на один аквариум, у нее будет на один аквариум слишком много. Сколько черепашек и сколько танков у Элли?
Ответ: У Элли 3 танка и 4 черепахи.
31. Если дюжина яиц стоит 12 центов, сколько яиц можно купить за 1 доллар?
Ответ: 100 яиц (Яйца стоят 1 пенни каждое.)
32. Если вы подбрасываете монету 100 раз и она каждый раз выпадает решкой, каков шанс, что она выпадет решкой при следующем броске?
Ответ: 50/50 (Предыдущие броски не имеют никакого значения, у вас всегда равные шансы на выпадение орла или решки.)
33. Вы посещаете магазин одежды, который имеет странный способ ценообразования.
 предметы. Жилет стоит 20 долларов, носки — 25 долларов, галстук — 15 долларов, а блузка — 30 долларов. Вы хотите купить нижнее белье. Сколько это будет стоить?
предметы. Жилет стоит 20 долларов, носки — 25 долларов, галстук — 15 долларов, а блузка — 30 долларов. Вы хотите купить нижнее белье. Сколько это будет стоить?
Ответ: 45 долларов. Предметы стоят 5 долларов за каждую букву, используемую для написания слова.
34. Как сделать это уравнение правильным: 81 x 9 = 801?
Ответ: Переверните его: 108 = 6 x 18.
35. Вы планируете потратить деньги, полученные на день рождения, сходить с друзьями в кино. Дешевле сводить 1 друга в кино дважды или 2 друзей в кино одновременно?
Ответ: Возьмите 2 друзей одновременно, так что всего вы купите только 3 билета. Если вы берете 1 друга дважды, вам нужно будет каждый раз покупать себе билет, всего 4 билета.
Мы пропустили одну из ваших любимых математических задачек для детей? Приходите поделиться своими загадками в группе WeAreTeachers HELPLINE на Facebook.
Если вам нравятся эти математические головоломки для детей, не пропустите 15 математических головоломок и числовых фокусов, которые удивят ваших учеников.

Математические головоломки 1 класса для детей (от 5 до 12 лет)
Математические головоломки 1 класса
Категория : Все категории
Класс : 1 класс 902 28
Получение…
Преимущества математических головоломок для детей 1 класса
Интерактивные математические головоломки Cuemath для детей 1 класса состоят из визуальных симуляций, которые помогают ребенку развить навыки рассуждения и сделать его логически мыслящим. Математические головоломки побуждают детей мыслить аналитически и использовать разные подходы к конкретным задачам.
Математические головоломки Cuemath для детей 1-го класса — это эффективный способ помочь ребенку увлечься математикой и развить интерес к ней. В онлайн-классах Cuemath Live математические головоломки помогают детям изучать и понимать «почему» за «что» любых математических понятий в увлекательной игровой форме.
Подробнее
Часто задаваемые вопросы
Помогают ли головоломки в математике?
Решение головоломок — отличный способ для детей познакомиться с математикой как с предметом и жизненным навыком. Это помогает им мыслить аналитически и найти разные подходы к любой проблеме. Математические головоломки для детей позволяют им повысить уровень их вовлеченности в математику и, следовательно, развить к ней интерес. На живых онлайн-классах Cuemath математические головоломки не только помогают с вышеперечисленным, но и помогают детям понять «почему» за «что» каждой математической концепции.
Это помогает им мыслить аналитически и найти разные подходы к любой проблеме. Математические головоломки для детей позволяют им повысить уровень их вовлеченности в математику и, следовательно, развить к ней интерес. На живых онлайн-классах Cuemath математические головоломки не только помогают с вышеперечисленным, но и помогают детям понять «почему» за «что» каждой математической концепции.
Как математические головоломки помогают развитию ребенка?
Математические ребусы и загадки для детей помогают развитию ребенка, подготавливая его не только к школьным экзаменам, но и к жизни. Ключевые области развития ребенка включают в себя:
- Навыки решения проблем
- Аналитическое мышление
- Навыки рассуждения
- Логический подход
- Относительно математика
- . Применение математики
- .0256
Каковы преимущества математических головоломок?
Решение математических головоломок приносит много пользы детям. Некоторые из этих преимуществ включают в себя:
- Развивает навыки рассуждения ребенка и делает его логически мыслящим
- Способствует решению проблем, связывая математику с практической ситуацией задача
- Научится понимать «почему» за «что»
- Карточки-головоломки также помогают ребенку поддерживать уровень вовлеченности и развивать интерес к математике
- Работая с карточками-головоломками, мозг ребенка развивается в гораздо большей степени, чем в его классе
В чем важность решения онлайн математических головоломок?
Во время карантина несколько школ перешли на онлайн-платформы, что позволило учащимся продолжить учебный процесс на цифровой платформе.
