Пирамида презентация по геометрии 11 класс: Презентация по геометрии на тему “Пирамида” (11 класс)
Презентация “Элементы пирамиды”; 10-11 класс – Презентации – Математика, алгебра, геометрия
Пояснительная записка
Интерактивное пособие по математике по теме: «Элементы пирамиды» предназначено для студентов 1 курса учреждений СПО или учащихся 10 – 11 классов общеобразовательных школ.
Цель использования интерактивного пособия в учебном процессе:
самостоятельное изучение материала по теме, (с возможным конспектированием материала)
закрепление фактического материала в ходе проведения тренинга, с последующим анализом ошибок,
проверка полученных знаний при выполнении теста, с оценкой результата
Интерактивное пособие содержит оглавление, которое включает:
Алгоритм работы с интерактивным пособием
Тренажер «Проверь себя…»
Тест «Элементы пирамиды»
Список литературы
ИП (интерактивное
пособие) может быть использовано на
уроках в качестве наглядного пособия,
для самостоятельного изучения темы,
для восполнения пробелов в знаниях
студентов в результате пропусков учебных
занятий.
ИП позволяет преподавателю выступать в роли организатора и консультанта, который помогает студентам в процессе овладения ими знания и организует их деятельность, направленную на достижение поставленных целей.
ИП имеет удобный интерфейс, прост в обращении, содержит наглядность и информативность.
При разработке ИП было использовано программное обеспечение:Microsoft Office FrontPage – для создания теста
Power Point – для создания презентаций
Mozilla Firefox, Internet Explorer – для работы с тестом
Данное ИП обладает важными свойствами, необходимыми для эффективного изучения материала по предложенной теме:
Носит познавательный характер, практическое значение, информативность материала
Эстетичность в
оформлении, четкая упорядоченность
материала, элементы графики.
Удобство работы, простота интерфейса, использование гиперссылок, триггеров.
Возможность использовать ИП для восполнения пробелов в знаниях студентов в результате пропусков учебных занятий.
22.06.2011г. Преподаватель математики ФАЛИНА Т.Б.
Конспект к уроку геометрии “Усеченная пирамида” 11 класс | Уроки по Математике
Конспект к уроку геометрии “Усеченная пирамида” 11 класс
06.06.2015 6969 0 Толекова Мария ИсабаевнаОсновные цели и задачи урока Цель: ознакомить учащихся с усеченной пирамидой.
Задачи: образовательная – познакомить с видами сечений, дать понятие усеченной пирамиды, вывести формулу боковой поверхности усеченной пирамиды;
развивающая – развивать логический стили мышления; умение самостоятельно мыслить, делать выводы.
воспитательная – воспитывать дисциплинированность, аккуратность.

Ожидаемые результаты освоения темы Учащиеся должны:
Знать: определение правильной и усеченной пирамиды; свойство усеченной пирамиды; формулы площади боковой поверхности правильной усеченной пирамиды;
Уметь: 1) изображать пирамиды
2) доказывать теоремы о площади боковой поверхности усеченной пирамиды
3) решать задачи на вычисление элементов усеченной пирамиды, площади боковой поверхности усеченной пирамиды
Ключевые идеи урока: Усеченная пирамида, элементы усеченной пирамиды: основание, боковые грани, вершина, боковые ребра, высота, площадь полной и боковой поверхности усеченной пирамиды.
Тип урока Изучение новых знаний
Методы обучения Наглядный (презентация), словесный (беседа, объяснение), интерактивный
Формы организации учебной деятельности учащихся фронтальная; групповая; парная; индивидуальная.
Используемые интерактивные методы обучения Взаимооценивание, Групповая работа, Индивидуальная работа
Применение модулей Обучение критическому мышлению; оценивание для обучения и оценивание обучения; использование информационно-коммуникационных технологий в преподавании; обучение талантливых и одаренных детей; преподавание и обучение в соответствии с возрастными особенностями учеников; управление и лидерство в обучении.

Оборудование и материалы компьютер, экран, мультимедийный проектор, интерактивная доска.
Ход урока
1.Учитель организует учащихся к уроку.
2. Учитель: Какая пирамида называется правильной?
Докажите теорему о площади боковой поверхности правильной пирамиды.
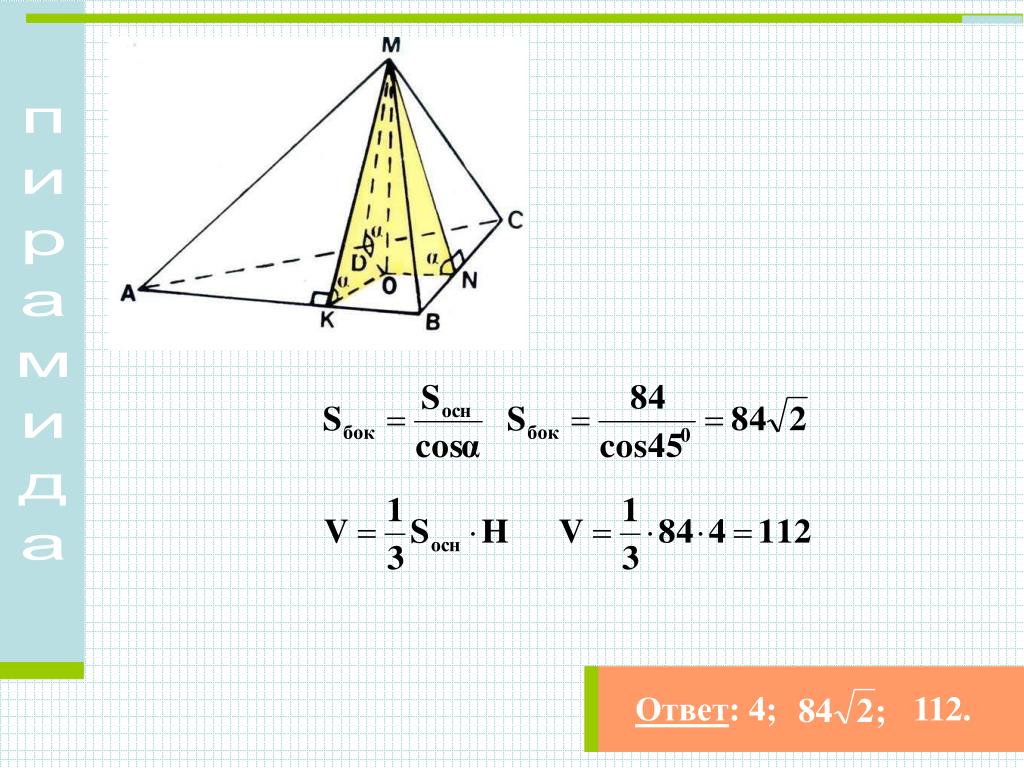
3. Учитель: Рассмотрим сечения пирамиды (демонстрируются слайд № 14, 15). Сечение, проходящее через вершину пирамиды и диагональ основания, называются диагональными. Они имеют вид треугольников. Существуют сечения, которые параллельны основанию (демонстрируется слайд № 16). Они, как правило, имеют вид многоугольника подобного тому, который находится в основании. Решим задачу (демонстрируется слайд № 17):
Решение: так как сечение проходит через середины боковых ребер, то каждая сторона многоугольника (сечения) является средней линей боковой грани и равна половине стороны многоугольника, находящегося в основании.
 То есть можно сказать, что основание и сечение, подобные многоугольники, к=2. А площади подобных фигур относятся квадрат коэффициента подобия. Значит, площадь сечения равна Q/4.
То есть можно сказать, что основание и сечение, подобные многоугольники, к=2. А площади подобных фигур относятся квадрат коэффициента подобия. Значит, площадь сечения равна Q/4. Дадим понятие усеченной пирамиды (демонстрируется слайд № 18). Пусть дана пирамида. Проведем плоскость параллельную основанию, которая пересечет боковые ребра. Наша секущая плоскость разделяет нашу пирамиду на два многогранника: один – пирамида, подобная данной, а второй многогранник, заключенный между сечением и основанием, называется усеченной пирамидой. Назовем основные элементы усеченной пирамиды (демонстрируется слайд № 19). Площадь боковой поверхности усеченной пирамиды равна сумме площадей боковых граней.
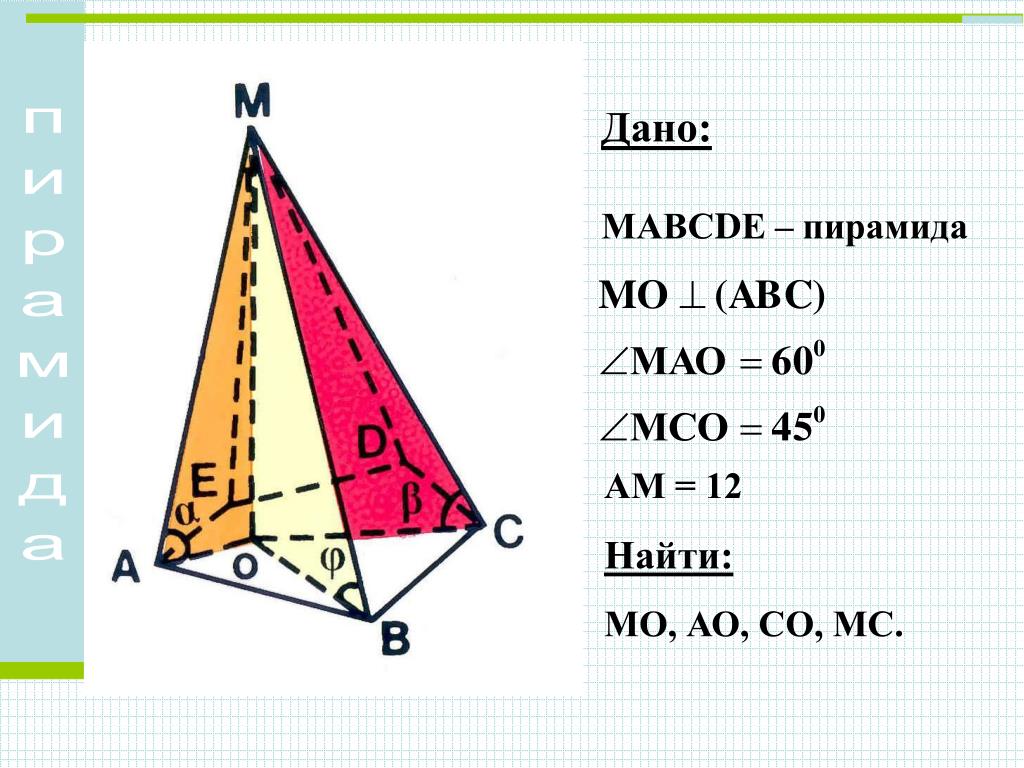
4. Учитель: проведем математическое исследование (демонстрируется слайд № 21). Учащиеся выполняют исследование самостоятельно, а затем сообщают о полученных результатах в классе (можно данное исследование дать на дом).
Учитель: Решим задачу № 269.
Задача № 269. Стороны основания правильной треугольной усеченной пирамиды равны 4 дм и 2 дм, а боковое ребро равно 2 дм. Найдите высоту и апофему пирамиды.
Решение: боковая грань правильной треугольной усеченной пирамиды является равнобедренной трапецией, её высота (апофема) равна дм. Найдем радиусы вписанных окружностей в нижнее и верхнее основания, дм, дм. Высота усеченной пирамиды является высотой прямоугольной трапеции, где основания радиусы вписанных окружностей, а боковая сторона апофема. Отсюда высота усеченной пирамиды равна дм.
5. Учитель: Давайте подведем итог.
Что такое усеченная пирамида?
Какая усеченная пирамида называется правильной?
Учитель оценивает учащихся (знание теории, активную работу на уроке),задает домашнее задание
Урок геометрии по теме “Пирамида”.
 10-й класс
10-й класс
Цели урока:
- изучение нового вида многогранника – пирамиды, ее элементов; формулы боковой и полной поверхности пирамиды;
- развитие познавательного интереса через творческую активность, исследовательскую деятельность на основе умения делать обобщения по данным, полученным в результате исследования;
Тип урока: усвоение новых знаний
Структура урока:
- Организационный момент.
- Актуализация знаний.
- Изучение нового материала.
- Решение простейших задач.
- Итог.
Оборудование: учебник геометрии 10-11 класс, авторы Л.С.Атанасян, В.Ф. Бутузов и др., мультимедийный проектор, модели пирамиды.
Ход урока
1. Организационный момент
2. Актуализация знаний
Актуализация знаний
Итак: тема урока “Пирамида”. Запишите, пожалуйста, число и тему урока.
Что это за многогранник?
У кого-то это слово ассоциируется с Египетскими пирамидами, но монументальные сооружения созданные человеком встречаются и в Центральной Америке, на фоне гималайского хребта выделяется пирамидальное образование, созданное природой, пирамидальная форма широко используется в архитектуре, например во Франции, в Германии.
Мы с вами рассмотрим пирамиду с математической точки зрения.
3. Изучение нового материала
Познакомит вас с этой фигурой и ее элементами (ученик выступает с презентацией, подготовленной к уроку самостоятельно)
(Первая часть презентации) слайды 1 – 7
Запишите элементы пирамиды: основание, вершина, ребра, грани, высота
Правильная пирамида: Sбок пов = 1/2 Ph
Р – периметр основания,
h – апофема
S полной поверхности = Sбок + Sосн
Итак: мы рассмотрели определение пирамиды,
элементы, формулы.
Предлагаю выполнить практическую работу:
Практико-ориентированная задача № 1:
Работа в парах:
На парте – модель пирамиды. Сделайте необходимые измерения и вычислите площадь боковой поверхности пирамиды.
(три – четыре различные модели пирамиды на класс, результат должен быть приблизительно одинаков)
– Какие измерения вы сделали?
– Какие формулы использовали?
4. Применим эти знания при решении простейших задач
Задача № 2. В основании пирамиды Хеопса – квадрат со стороной 230 м, тангенс угла
наклона боковой грани к основанию равен 1,2. Найти высоту самой высокой египетской пирамиды, если основание ее лежит в центре квадрата. (отв: 138)
У доски: Задача № 3
Сторона основания правильной четырехугольной
пирамиды равна 16, боковые ребра равны 10. Найдите
площадь боковой поверхности этой пирамиды.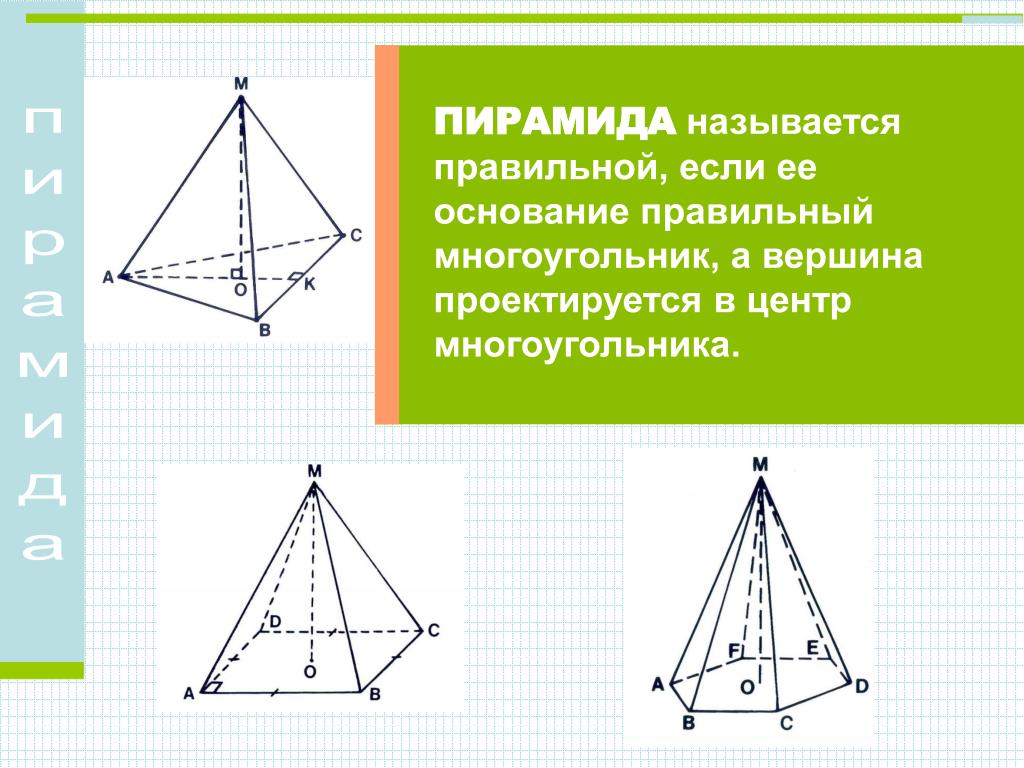
(отв: 192)
(Вторая часть презентации) слайды 8-11
У доски: Задача № 4
Найти площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 24 и высота равна 5. (Отв 1200)
Тест (устная работа) – задание на внимательность
Сколько граней, боковых ребер у n-угольной пирамиды?
Какое наименьшее число граней может иметь пирамида?
Высота пирамиды равна 3 см. Чему равно расстояние от вершины пирамиды до плоскости основания?
Боковые ребра треугольной пирамиды равны 7 см, 12 см, 5 см. Одно из них перпендикулярно к плоскости основания. Чему равна высота пирамиды?
Дом.задание:п. 28-29 № 243, 248
5. Итог урока
Итак: (рефлексия) подведем итоги нашей совместной работы – продолжите, пожалуйста, мое предложение –
- Сегодня я узнал новое…
 {2}
\конец{выравнивание*}
{2}
\конец{выравнивание*}
Площадь поверхности конуса не должна включать площадь поверхности круглой грани.{2}} \\ &= \text{122,631}\ldots\text{мм} \\ &\ приблизительно \текст{123}\текст{мм} \конец{выравнивание*}
Вычислить длину дуги \(P\).
\начать{выравнивать*} P &=\text{окружность конуса} \\ & = 2\пи(\текст{26,2}) \\ &\ приблизительно \текст{165}\текст{мм} \конец{выравнивание*}
Определить длину дуги \(M\).
\начать{выравнивать*} М&=2\пи(123)-165\\ &=\текст{608}\текст{мм} \конец{выравнивание*}
Что такое призмы и пирамиды?
Объяснение для родителей призм и пирамид, в том числе практические способы работы детей с трехмерными фигурами в классе и изучение их свойств.
или Зарегистрируйтесь, чтобы добавить к своим сохраненным ресурсам
Что такое призма?
Призма представляет собой тип трехмерной (3D) формы с плоскими сторонами.У него есть два конца, которые имеют одинаковую форму и размер (и выглядят как 2D-фигуры). Он имеет одинаковое поперечное сечение по всей форме от конца до конца; это означает, что если вы прорежете его, вы увидите ту же 2D-форму, что и на обоих концах.
Призмы, изучаемые в начальной школе
Помимо куба и прямоугольного параллелепипеда, если вы знаете название многоугольника / 2D-формы на конце призмы, то легко определить название призмы! (треугольник/треугольная призма; пятиугольник/пятиугольная призма и т. д.)
NB: Цилиндр имеет два конца одинаковой формы (круг), но поскольку он имеет изогнутые стороны, это , а не призма .
Что такое пирамида?
Пирамида также является трехмерной (3D) формой. Он имеет многоугольное основание и плоские (треугольные) стороны, которые соединяются в общей точке (называемой вершиной).
Когда упоминается слово «пирамида», мы часто думаем о знаменитых египетских пирамидах. Египетские пирамиды — это пирамиды с квадратным основанием, но есть несколько других типов пирамид, каждая из которых имеет свой многоугольник в качестве основания.
Призмы и пирамиды в начальной школе
Во втором классе детей будут учить называть и определять призмы и пирамиды при изучении трехмерных фигур. Они научатся описывать свои свойства, например количество граней, ребер и вершин. Детям будут предоставлены красочные пластиковые модели объемных фигур, которые помогут им попрактиковаться в подсчете количества граней, ребер и вершин. Их могут попросить заполнить таблицы для записи результатов.

Трехмерная форма Призма или пирамида? Лица кромками Vertices куб Prism 6 12 8 треугольная призма Prism 5 9 6 площади на основе пирамиды пирамида 5 8 5 Треугольная на основе пирамиды пирамида 4 6 4 детей 3 класса научат использовать материалы для лепки для изготовления призм и пирамид, а также сетки для призм и пирамид.Детям можно дать картонные призмы и пирамиды, которые они могут развернуть, чтобы увидеть, как выглядит сеть , и можно спросить, какие двухмерные формы необходимы для построения трехмерной призмы или пирамиды.

детей 5 класса научат различать призмы и пирамиды по двумерным представлениям (изображениям фигур).
Трехмерные фигуры | SkillsYouNeed
На этой странице рассматриваются свойства трехмерных или «твердых» форм.
Двумерная фигура имеет длину и ширину. Трехмерная твердая форма также имеет глубину. Трехмерные формы по своей природе имеют внутреннее и внешнее, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны.
На этой странице рассматриваются как прямолинейные тела, называемые многогранниками, которые основаны на многоугольниках, так и тела с кривыми, такие как шары, цилиндры и конусы.
Многогранники
Многогранники (или многогранники) представляют собой твердые фигуры с прямыми сторонами.Многогранники основаны на многоугольниках, двумерных плоских формах с прямыми линиями.
Подробнее о работе с полигонами см. на нашей странице Свойства полигонов.
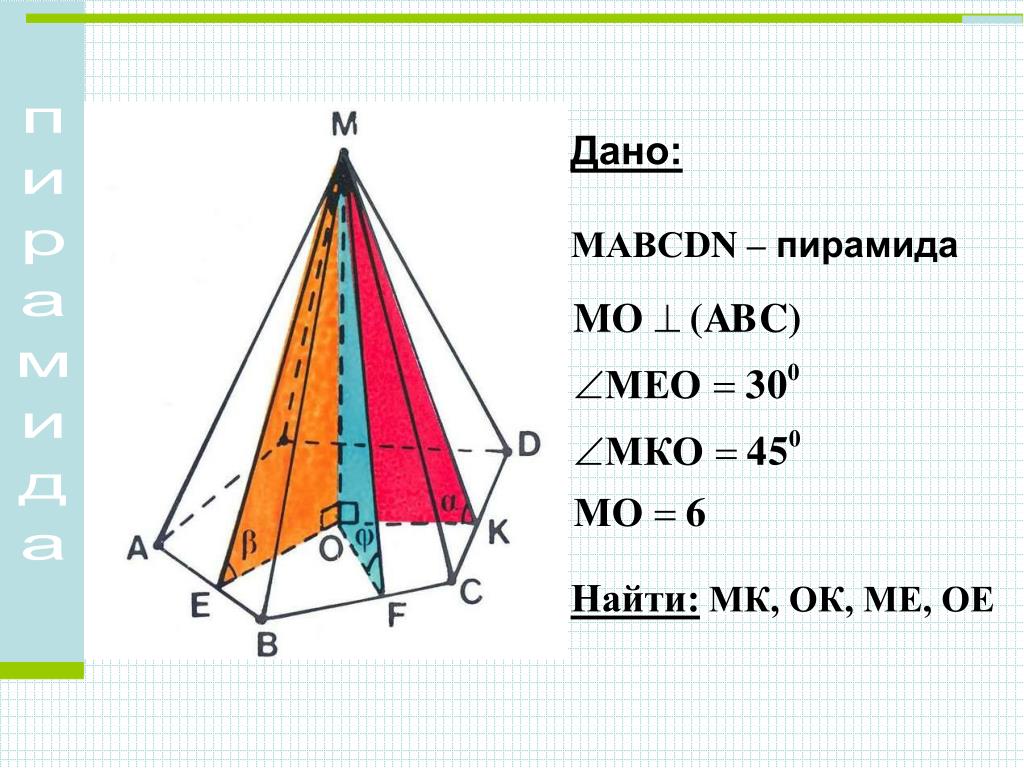
Многогранники определяются как имеющие:
- Прямые ребра .
- Плоские стороны называются гранями .
- Углов, называемых вершинами .
Многогранники также часто определяются количеством ребер, граней и вершин, которые они имеют, а также тем, имеют ли все их грани одинаковую форму и размер.Как и многоугольники, многогранники могут быть правильными (на основе правильных многоугольников) или неправильными (на основе неправильных многоугольников). Многогранники также могут быть вогнутыми или выпуклыми.
Одним из самых простых и привычных многогранников является куб. Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.
Правильные многогранники (Платоновы тела)
Пять правильных многогранников представляют собой особый класс многогранников, все грани которых идентичны, причем каждая грань является правильным многоугольником.
 Платоновых тел:
Платоновых тел: - Тетраэдр с четырьмя равносторонними треугольными гранями.
- Куб с шестью квадратными гранями.
- Октаэдр с восемью равносторонними треугольными гранями.
- Додекаэдр с двенадцатью пятиугольными гранями.
- Икосаэдр с двадцатью равносторонними треугольными гранями.
См. рисунок выше для иллюстрации каждого из этих правильных многогранников.
Что такое призма?
Призма — это любой многогранник, имеющий два совпадающих конца и плоские стороны .Если вы разрежете призму в любом месте по ее длине, параллельно ее концу, ее поперечное сечение будет таким же — вы получите две призмы. Стороны призмы параллелограммов – четырехугольников с двумя парами сторон одинаковой длины.
Антипризмы аналогичны обычным призмам тем, что их концы совпадают.
 Однако стороны антипризмы состоят из треугольников, а не из параллелограммов. Антипризмы могут стать очень сложными.
Однако стороны антипризмы состоят из треугольников, а не из параллелограммов. Антипризмы могут стать очень сложными. Что такое пирамида?
Пирамида — это многогранник с многоугольниками в основании , который соединяется с вершиной (верхняя точка) с прямыми сторонами.
Хотя мы склонны думать о пирамидах с квадратным основанием, вроде тех, что строили древние египтяне, на самом деле они могут иметь основание в виде любого многоугольника, правильного или неправильного. Кроме того, пирамида может иметь вершину прямо в центре своего основания, правильная пирамида , или может иметь вершину вне центра, когда это наклонная пирамида .
Более сложные многогранники
Существует еще много видов многогранников: симметричные и несимметричные, вогнутые и выпуклые.
Архимедовы тела, например , состоят как минимум из двух различных правильных многоугольников.

Усеченный куб (как показано на рисунке) представляет собой архимедово тело с 14 гранями. Шесть граней представляют собой правильные восьмиугольники, а остальные восемь — правильные (равносторонние) треугольники. Фигура имеет 36 ребер и 24 вершины (угла).
Трехмерные формы с кривыми
Твердые фигуры с изогнутыми или круглыми краями не являются многогранниками.Многогранники могут иметь только прямые стороны. Также см. нашу страницу о двумерных изогнутых формах.
Многие объекты вокруг вас будут иметь по крайней мере несколько кривых. В геометрии наиболее распространенными искривленными телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
Обычные трехмерные формы с кривыми: Цилиндр Конус Цилиндр имеет одинаковое поперечное сечение от одного конца до другого.  Цилиндры имеют два одинаковых конца либо круга, либо овала. Несмотря на то, что они похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами.
Цилиндры имеют два одинаковых конца либо круга, либо овала. Несмотря на то, что они похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами. Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание. Сфера Тор Сфера в форме шара или шара представляет собой полностью круглый объект.Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. Правильный кольцевой тор, имеющий форму кольца, шины или бублика, образован вращением меньшего круга вокруг большего круга. Существуют и более сложные формы торов.
Площадь поверхности
На нашей странице «Вычисление площади» объясняется, как вычислить площадь двухмерных фигур, и вам необходимо понимать эти основы, чтобы вычислять площадь поверхности трехмерных фигур.

Для трехмерных фигур мы говорим о площади поверхности , чтобы избежать путаницы.
Вы можете использовать свои знания о площади двухмерных фигур, чтобы вычислить площадь поверхности трехмерной фигуры, поскольку каждая грань или сторона фактически является двумерной фигурой.
Таким образом, вы вычисляете площадь каждой грани, а затем складываете их вместе.
Как и в случае с плоскими формами, площадь поверхности твердого тела выражается в квадратных единицах: см 2 , дюймы 2 , м 2 и так далее.Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Примеры расчета площади поверхности
Куб
Площадь поверхности куба равна площади одной грани (длина х ширина), умноженной на 6, поскольку все шесть граней одинаковы.
Поскольку грань куба представляет собой квадрат, вам нужно выполнить только одно измерение – длина и ширина квадрата по определению одинаковы.

Следовательно, одна грань этого куба равна 10 × 10 см = 100 см 2 .Умножаем на 6 количество граней куба, и получаем, что площадь поверхности этого куба равна 600см 2 .
Другие правильные многогранники
Точно так же можно вычислить площадь поверхности других правильных многогранников (платоновых тел), найдя площадь одной стороны и затем умножив результат на общее количество сторон — см. диаграмму основных многогранников выше.
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22см 2 , то умножьте это на общее количество сторон (12), чтобы получить ответ 264см 2 .
Пирамида
Для расчета площади поверхности стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием:
Сначала определите площадь основания (квадрата) длина × ширина.
Далее определите площадь одной стороны (треугольника). Измерьте ширину вдоль основания, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.

Есть два способа вычислить площадь поверхности четырех треугольников:
-
Разделите ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножьте на 4, чтобы получить площадь поверхности всех четырех сторон, или
-
Умножьте свой ответ на 2.
Наконец, сложите площадь основания и сторон вместе, чтобы найти общую площадь поверхности пирамиды.
Чтобы рассчитать площадь поверхности других типов пирамид, сложите площадь основания (известную как площадь основания) и площадь сторон (площадь боковых сторон). Возможно, вам придется измерить стороны по отдельности.
Диаграммы цепей
Геометрическая сеть представляет собой двухмерный «шаблон» для трехмерного объекта. Сети могут быть полезны при расчете площади поверхности трехмерного объекта.На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды, если пирамида «развернута», у вас остается сеть.
Подробнее о диаграммах цепей см.
 на нашей странице 3D-фигуры и сети .
на нашей странице 3D-фигуры и сети .
Призма
Для расчета площади поверхности призмы :
Призмы имеют два одинаковых конца и плоские стороны в виде параллелограмма.
Вычислите площадь одного конца и умножьте на 2.
Для правильной призмы (у которой все стороны одинаковы) вычислите площадь одной из сторон и умножьте на общее количество сторон.
Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.
Сложите два ответа вместе (концы + стороны), чтобы найти общую площадь поверхности призмы.
Цилиндр
Пример:
Радиус = 5 см
Высота = 10 смЧтобы вычислить площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте себе банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги.Если вы отрежете сторону по длине и сгладите ее, у вас получится прямоугольник.
 Следовательно, вам нужно найти площадь двух кругов и прямоугольника.
Следовательно, вам нужно найти площадь двух кругов и прямоугольника. Сначала определите площадь одного из кругов.
Площадь круга равна π (пи) × радиус 2 .
При радиусе 5 см площадь одного из кругов равна 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как кругов два 157см 2
Площадь стороны цилиндра равна периметру окружности × высоте цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4·
.Измерьте высоту цилиндра. В данном примере высота равна 10 см. Площадь стороны 31,4 × 10 = 314см 2 .
Общая площадь поверхности может быть найдена путем сложения площади кругов и стороны вместе:
157 + 314 = 471см 2
Пример:
Радиус = 5 см
Длина наклона = 10 смКонус
При расчете площади поверхности конуса необходимо использовать длину «наклона», а также радиус основания.

Однако вычислить его относительно просто:
Площадь круга в основании конуса составляет π (пи) × радиус 2 .
В этом примере расчет равен 3,14 × 5 2 = 3,14 × 25 = 78,5 см 2
Площадь стороны, наклонного участка, можно найти по этой формуле:
π (пи) × радиус × длина наклона.
В нашем примере вычисление 3,14 × 5 × 10 = 157см 2 .
Наконец, добавьте площадь основания к площади стороны, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
Теннисный мяч:
Диаметр = 2,6 дюймаСфера
площадь поверхности сферы является относительно простым расширением формулы для площади круга.
4 × π × радиус 2 .
Для сферы часто проще измерить диаметр – расстояние поперек сферы.Затем вы можете найти радиус, который составляет половину диаметра.
Диаметр стандартного теннисного мяча составляет 2,6 дюйма.
 Таким образом, радиус составляет 1,3 дюйма. Для формулы нам нужен радиус в квадрате. 1,3 × 1,3 = 1,69
Таким образом, радиус составляет 1,3 дюйма. Для формулы нам нужен радиус в квадрате. 1,3 × 1,3 = 1,69 Площадь поверхности теннисного мяча равна:
4 × 3,14 × 1,69 = 21,2264 дюйма 2 .
Пример:
R (большой радиус) = 20 см
r (малый радиус) = 4 смТор
Чтобы вычислить площадь поверхности тора , вам нужно найти два значения радиуса.
Большой или большой радиус (R) измеряется от середины отверстия до середины кольца.
Малый или малый радиус (r) измеряется от середины кольца до внешнего края.
На диаграмме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса). Расчет одинаков для каждой части.
Формула: площадь поверхности = (2πR)(2πr)
Чтобы вычислить площадь поверхности примера тора.
(2 × π × R) = (2 × 3,14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Перемножьте два ответа вместе, чтобы найти общую площадь поверхности тора в примере.
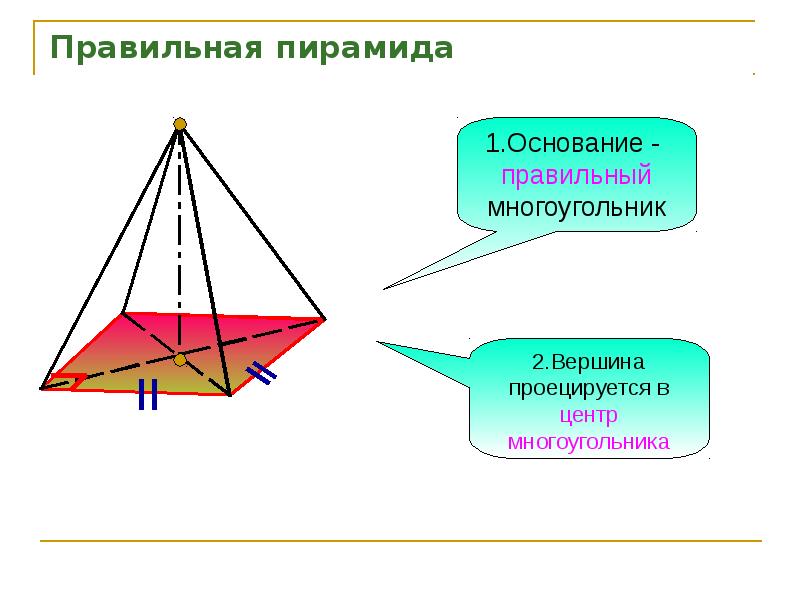
125,6 × 25,12 = 3155,072 см 2 .
Дополнительное чтение из навыков, которые вам нужны
Понимание геометрии
Часть руководства по необходимым навыкам счетаВ этой электронной книге рассматриваются основы геометрии и рассматриваются свойства форм, линий и тел.Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Заполнение твердого тела: Том
При работе с трехмерными фигурами вам также может понадобиться знать, сколько объем они имеют.
Другими словами, если бы вы наполнили их водой или воздухом, сколько наполнения вам потребуется?
Это описано на нашей странице Расчет объема .
Геометрия – 1206310 | CPALMS.org
Угол ВВЕРХ: Игрок 1:Изучите процессы построения для построения биссектрисы угла, копирования угла и построения линии, параллельной заданной линии, через точку, не находящуюся на линии, с использованием различных инструментов в этом интерактивном учебном пособии в стиле ретро-видеоигры.

ПРИМЕЧАНИЕ. В этом учебном пособии используется как построение биссектрисы угла, так и построение для копирования угла в качестве возможности расширения, чтобы также построить линию, параллельную заданной линии, через точку, не находящуюся на линии.Учащиеся также учатся определять соответствующие углы, образующиеся при пересечении секущей параллельных прямых, и обнаруживают с помощью Geogebra, что эти углы равны.
Тип: оригинальное учебное пособие для учащихся
Круглогодичные школьные дебаты: выявление ошибочных рассуждений — часть вторая:Это вторая часть серии из двух частей.Научитесь выявлять ошибочные рассуждения в этой серии интерактивных руководств. Вы узнаете, что некоторые эксперты говорят о круглогодичных школах, какие исследования были проведены по поводу их эффективности и какие аргументы можно привести за и против круглогодичного обучения.
 Затем вы прочитаете речь в пользу круглогодичных школ и определите ошибочные рассуждения в аргументе, в частности использование поспешных обобщений.
Затем вы прочитаете речь в пользу круглогодичных школ и определите ошибочные рассуждения в аргументе, в частности использование поспешных обобщений. Обязательно завершите первую часть перед второй! Нажмите ЗДЕСЬ , чтобы запустить первую часть.
Тип: оригинальное учебное пособие для учащихся
Вымпел компании Challenge: вписанные круги треугольников:Узнайте, как легко Кэти создать круговой логотип с надписью на шаблоне треугольного вымпела своей компании. Если она выполнит задание первой, она выиграет бонус в размере 1000 долларов США! Следуйте этому интерактивному руководству.
Тип: оригинальное учебное пособие для учащихся
Круглогодичные школьные дебаты: выявление ошибочных рассуждений — часть первая:Научитесь выявлять ошибочные рассуждения в этом интерактивном учебном пособии по английскому языку, состоящем из двух частей.
 Вы узнаете, что некоторые эксперты говорят о круглогодичных школах, какие исследования были проведены по поводу их эффективности и какие аргументы можно привести за и против круглогодичного обучения.Затем вы прочитаете речь в пользу круглогодичных школ и определите ошибочные рассуждения в аргументе, в частности использование поспешных обобщений.
Вы узнаете, что некоторые эксперты говорят о круглогодичных школах, какие исследования были проведены по поводу их эффективности и какие аргументы можно привести за и против круглогодичного обучения.Затем вы прочитаете речь в пользу круглогодичных школ и определите ошибочные рассуждения в аргументе, в частности использование поспешных обобщений. Обязательно выполните обе части этой серии! Нажмите ЗДЕСЬ , чтобы открыть вторую часть.
Тип: оригинальное учебное пособие для учащихся
Встретить меня на полпути:Спланируйте экспедицию на байдарке, научившись выполнять основные геометрические построения, включая копирование сегмента, построение биссектрисы сегмента, построение перпендикулярной биссектрисы сегмента и построение перпендикулярных сегментов с помощью различных инструментов в этом интерактивном учебном пособии.

Тип: оригинальное учебное пособие для учащихся
Оценка аргумента – Часть четвертая: Инаугурационная речь Джона Кеннеди:Изучите инаугурационную речь президента Джона Ф. Кеннеди в этом интерактивном руководстве. Вы изучите аргумент Кеннеди, основное утверждение, более мелкие утверждения, причины и доказательства.
В четвертой части вы будете использовать то, что вы узнали из этой серии, чтобы оценить общую аргументацию Кеннеди.
Перед тем, как приступить к части 4, обязательно выполните предыдущие части этой серии.
- Нажмите ЗДЕСЬ , чтобы запустить первую часть.
- Нажмите ЗДЕСЬ , чтобы запустить вторую часть.
- Нажмите ЗДЕСЬ , чтобы запустить третью часть.

Тип: оригинальное учебное пособие для учащихся
Человек не на своем месте:Узнайте, как построить вписанный квадрат в круг и почему в этом интерактивном руководстве используются определенные конструкции.
Тип: оригинальное учебное пособие для учащихся
Оценка аргумента – Часть третья: Инаугурационная речь Джона Кеннеди:Изучите инаугурационную речь президента Джона Ф. Кеннеди в этом интерактивном руководстве. Вы изучите аргумент Кеннеди, основное утверждение, более мелкие утверждения, причины и доказательства.
 К концу этой серии из четырех частей вы сможете оценить его общую аргументацию.
К концу этой серии из четырех частей вы сможете оценить его общую аргументацию. В третьей части вы прочтете больше о речи Кеннеди и определите меньшее утверждение в этом разделе его речи. Вы также оцените соответствие этого меньшего утверждения основному утверждению и оцените причины и доказательства Кеннеди.
Обязательно выполните все четыре части этой серии!
- Нажмите ЗДЕСЬ , чтобы запустить первую часть.
- Нажмите ЗДЕСЬ , чтобы запустить вторую часть.
- Нажмите ЗДЕСЬ , чтобы запустить четвертую часть.
Тип: оригинальное учебное пособие для учащихся
Где эта вышка сотовой связи?:Найдите расположение и зону покрытия вышек сотовой связи, чтобы определить центр и радиус круга по его уравнению, используя стратегию заполнения квадрата в этом интерактивном руководстве.

Тип: оригинальное учебное пособие для учащихся
Проектирование с помощью шестиугольников:Узнайте, как построить вписанный правильный шестиугольник и равносторонний треугольник в окружность с помощью этого интерактивного учебника.
Тип: оригинальное учебное пособие для учащихся
Как новый:Узнайте, как описать окружность вокруг треугольника в этом интерактивном руководстве по построению.Возьмите циркуль, линейку, карандаш и бумагу, чтобы следовать!
Тип: оригинальное учебное пособие для учащихся
Высокотехнологичные качели:Из этого интерактивного руководства вы узнаете, как найти точку на направленном отрезке, которая делит его в заданном отношении.

Тип: оригинальное учебное пособие для учащихся
Круг вверх!:Узнайте, как написать уравнение окружности, используя теорему Пифагора , зная ее центр и радиус, используя пошаговые инструкции в этом интерактивном руководстве.
Тип: оригинальное учебное пособие для учащихся
Готов к взлету! — Часть вторая:Это вторая часть серии руководств, состоящей из двух частей.В этом интерактивном учебном пособии вы потренируетесь определять цель говорящего, используя речь пионера авиации Амелии Эрхарт.
 Вы изучите использование ею риторических призывов, включая этос, логос, пафос и кайрос. Наконец, вы оцените эффективность использования Эрхартом риторических призывов.
Вы изучите использование ею риторических призывов, включая этос, логос, пафос и кайрос. Наконец, вы оцените эффективность использования Эрхартом риторических призывов. Обязательно сначала выполните первую часть. Щелкните здесь, чтобы запустить ЧАСТЬ ПЕРВУЮ.
Тип: оригинальное учебное пособие для учащихся
Готов к взлету! — Первая часть:Это первая часть серии руководств, состоящей из двух частей.В этом интерактивном учебном пособии вы потренируетесь определять цель говорящего, используя речь пионера авиации Амелии Эрхарт. Вы изучите использование ею риторических призывов, включая этос, логос, пафос и кайрос. Наконец, вы оцените эффективность использования Эрхартом риторических призывов.
Нажмите здесь, чтобы запустить ЧАСТЬ ВТОРАЯ .
Тип: оригинальное учебное пособие для учащихся
Описательное письмо: Глаза в небе (часть 4 из 4):Попрактикуйтесь в написании различных аспектов описательного эссе об ученых, использующих дроны для исследования ледников в Перу.Этот интерактивный учебник является четвертой частью серии из четырех частей. В этом заключительном уроке вы узнаете об элементах основного абзаца. Вы также создадите основной абзац с подтверждающими доказательствами. Наконец, вы узнаете об элементах заключения и потренируетесь в создании «подарка».
Это руководство является четвертой частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Тип: оригинальное учебное пособие для учащихся
Описательное письмо: Глаза в небе (часть 3 из 4):Узнайте, как написать введение для описательного эссе в этом интерактивном руководстве.
 Этот учебник является третьей частью серии из четырех частей. В предыдущих уроках этой серии учащиеся проанализировали информационный текст и видео об ученых, использующих дроны для исследования ледников в Перу. Студенты также определили центральную идею и важные детали текста и написали эффективное резюме. В третьей части вы узнаете, как написать введение для описательного эссе об исследованиях ученых.
Этот учебник является третьей частью серии из четырех частей. В предыдущих уроках этой серии учащиеся проанализировали информационный текст и видео об ученых, использующих дроны для исследования ледников в Перу. Студенты также определили центральную идею и важные детали текста и написали эффективное резюме. В третьей части вы узнаете, как написать введение для описательного эссе об исследованиях ученых. Это руководство является третьей частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Тип: оригинальное учебное пособие для учащихся
Чертежи строительства:С помощью этого интерактивного учебного пособия вы научитесь строить биссектрису отрезка прямой с помощью линейки и циркуля.
Тип: оригинальное учебное пособие для учащихся
Сравнение митоза и мейоза:Сравните и сопоставьте митоз и мейоз в этом интерактивном руководстве.
 Вы также свяжете их с процессами полового и бесполого размножения и их последствиями для генетической изменчивости.
Вы также свяжете их с процессами полового и бесполого размножения и их последствиями для генетической изменчивости. Тип: оригинальное учебное пособие для учащихся
Кусочки ниндзя Нэнси:Узнайте, как определить форму поперечного сечения, созданного пересечением секущей плоскости с пирамидой или призмой, в этом интерактивном учебном пособии на тему ниндзя.
Тип: оригинальное учебное пособие для учащихся
Вокруг света с прямоугольными треугольниками:Из этого интерактивного руководства вы узнаете, как использовать тригонометрические соотношения для определения высоты известных памятников и решить задачу из реальной жизни.

Тип: оригинальное учебное пособие для учащихся
Доказательство теорем о треугольниках:Используйте свойства, постулаты и теоремы, чтобы доказать теорему о треугольнике.В этом интерактивном уроке вы также узнаете, как доказать, что линия, параллельная одной стороне треугольника, пропорционально делит две другие.
Тип: оригинальное учебное пособие для учащихся
Рак: мутировавшие клетки вышли из-под контроля!:Изучите взаимосвязь между мутациями, клеточным циклом и неконтролируемым ростом клеток, который может привести к раку, с помощью этого интерактивного руководства.
Тип: оригинальное учебное пособие для учащихся
Банковский выстрел:В этом задании учащимся предлагается использовать сходство для решения задачи в контексте, который будет знаком многим, хотя большинство учащихся привыкли использовать интуицию, а не геометрические рассуждения, для построения кадра.
Тип: Задача решения проблем
Они похожи?:В этой задаче учащимся дается изображение двух треугольников, которые кажутся подобными, но сходство которых нельзя доказать без дополнительной информации.
 Попросите учащихся предоставить последовательность преобразований подобия, которая отображает один треугольник в другой, используя определение подобия в терминах преобразований подобия.
Попросите учащихся предоставить последовательность преобразований подобия, которая отображает один треугольник в другой, используя определение подобия в терминах преобразований подобия. Тип: Задача решения проблем
Рулон туалетной бумаги:Целью этого задания является привлечение учащихся к геометрическому моделированию и, в частности, к выводу алгебраических взаимосвязей между переменными, вытекающими из геометрических ограничений.
Тип: Задача решения проблем
Монеты по кругу:Используя таблицу диаметров монет разного достоинства, учащихся просят определить, сколько монет помещается вокруг центральной монеты.
-reshenie-zadacha-240.jpg)
Тип: Задача решения проблем
Проблема с маяком:В этой задаче учащимся предлагается смоделировать явления на поверхности земли, исследуя видимость лампы на маяке с лодки.
Тип: Задача решения проблем
Солнечное затмение:Это задание на решение задач побуждает учащихся выяснить, почему солнечные затмения случаются редко, путем изучения радиуса Солнца и самого дальнего расстояния между Луной и Землей.

Тип: Задача решения проблем
Чудо средней точки:Это задание на решение задач дает учащимся возможность доказать факт о четырехугольниках: если мы соединим середины произвольного четырехугольника, чтобы образовать новый четырехугольник, то новый четырехугольник будет параллелограммом, даже если первоначальный четырехугольник таковым не был.
Тип: Задача решения проблем
От горы Уитни до Долины Смерти:Это задание вовлекает учащихся в открытое задание по моделированию, в котором используется подобие прямоугольных треугольников.

Тип: Задача решения проблем
Кратчайший отрезок линии от точки P до линии L:Это базовое задание по геометрии, предназначенное для того, чтобы помочь учащимся развить некоторые фундаментальные геометрические свойства, которые на первый взгляд могут показаться довольно очевидными.В этом случае основное свойство, о котором идет речь, состоит в том, что кратчайший путь от точки к линии встречается с линией под прямым углом, что имеет решающее значение для многих дальнейших разработок предмета.
Тип: Задача решения проблем
Семь кругов III:Это дает возможность смоделировать конкретную ситуацию с помощью математики.
 После того, как будет нарисована репрезентативная картина ситуации, описанной в задаче (учитель может дать здесь указания по мере необходимости), решение задачи требует понимания определения функции синуса.
После того, как будет нарисована репрезентативная картина ситуации, описанной в задаче (учитель может дать здесь указания по мере необходимости), решение задачи требует понимания определения функции синуса. Тип: Задача решения проблем
Расширение линии:В этом задании учащимся предлагается сделать выводы о линии после того, как она была увеличена в 2 раза.
Тип: Задача решения проблем
Бег по дорожке II:Цель этого задания — смоделировать знакомый объект, олимпийскую трассу, используя геометрические фигуры.
 Расчеты периметров этих фигур объясняют ступенчатый старт бегунов в беге на 400 метров.
Расчеты периметров этих фигур объясняют ступенчатый старт бегунов в беге на 400 метров.Тип: Задача решения проблем
Бег по дорожке I:В этой задаче геометрия применяется к 400-метровой дорожке, чтобы найти ее периметр.
Тип: Задача решения проблем
Скрепка:В этом задании типографская сетка служит фоном для стандартной скрепки.Метрическая шкала измерений нарисована поперек нижней части сетки, а скрепка проходит в обоих направлениях немного за пределы сетки.
 Ученикам дают примерную длину скрепки и определяют количество одинаковых скрепок, сделанных из проволоки заданной длины.
Ученикам дают примерную длину скрепки и определяют количество одинаковых скрепок, сделанных из проволоки заданной длины. Тип: Задача решения проблем
Рожок мороженого:В этом задании учащиеся сделают эскиз бумажной обертки от рожка для мороженого, с помощью этого эскиза выведут формулу площади поверхности обертки и оценят максимальное количество оберток, которые можно вырезать из прямоугольного листа бумаги. .
Тип: Задача решения проблем
Насколько толстая банка газировки? (Вариант I):В этом задании на решение задач учащиеся должны найти площадь поверхности банки из-под газировки, вычислить, сколько кубических сантиметров алюминия она содержит, и оценить ее толщину.

Тип: Задача решения проблем
Сколько листьев на дереве? (Версия 2):Это задача математического моделирования, направленная на разумную оценку чего-то, что слишком велико для точного подсчета, а именно количества листьев на дереве.
Тип: Задача решения проблем
Сколько листьев на дереве?:Это задача математического моделирования, направленная на разумную оценку чего-то, что слишком велико для точного подсчета, а именно количества листьев на дереве.
Тип: Задача решения проблем
Сколько клеток в теле человека?:В этом задании по решению проблем учащимся предлагается применить понятия массы, объема и плотности в контексте реального мира, чтобы определить, сколько клеток находится в организме человека.
Тип: Задача решения проблем
Глобальная система позиционирования II:Отражая современность задействованных технологий, это сложная задача по геометрическому моделированию, в которой учащиеся с нуля открывают геометрические принципы, лежащие в основе программного обеспечения, используемого системами GPS.

Тип: Задача решения проблем
Архимед и королевская корона:В этом задании на решение задач используется сказка об Архимеде и короне царя Сиракуз для определения объема и массы золота и серебра.
Тип: Задача решения проблем
Склоны и круги:Цель этого задания — познакомить учащихся с алгебраическим подходом к хорошо известному результату классической геометрии, а именно к тому, что точка X лежит на окружности диаметра AB, если угол ?AXB прямой
Тип: Задача решения проблем
Единичные квадраты и треугольники:В этом задании на решение задач учащимся предлагается найти площадь треугольника, используя единичные квадраты и отрезки.

Тип: Задача решения проблем
Треугольники, вписанные в окружность:Это задание на решение проблем побуждает учащихся использовать идеи о линейных функциях, чтобы определить, когда определенные углы являются прямыми углами.
Тип: Задача решения проблем
Прием у доктора:Целью задания является анализ правдоподобного сценария реальной жизни с использованием геометрической модели. Задача требует знания формул объема для цилиндров и конусов, некоторых геометрических рассуждений, связанных с подобными треугольниками, а также уделяет внимание разумным приближениям и поддержанию разумного уровня точности во всем.
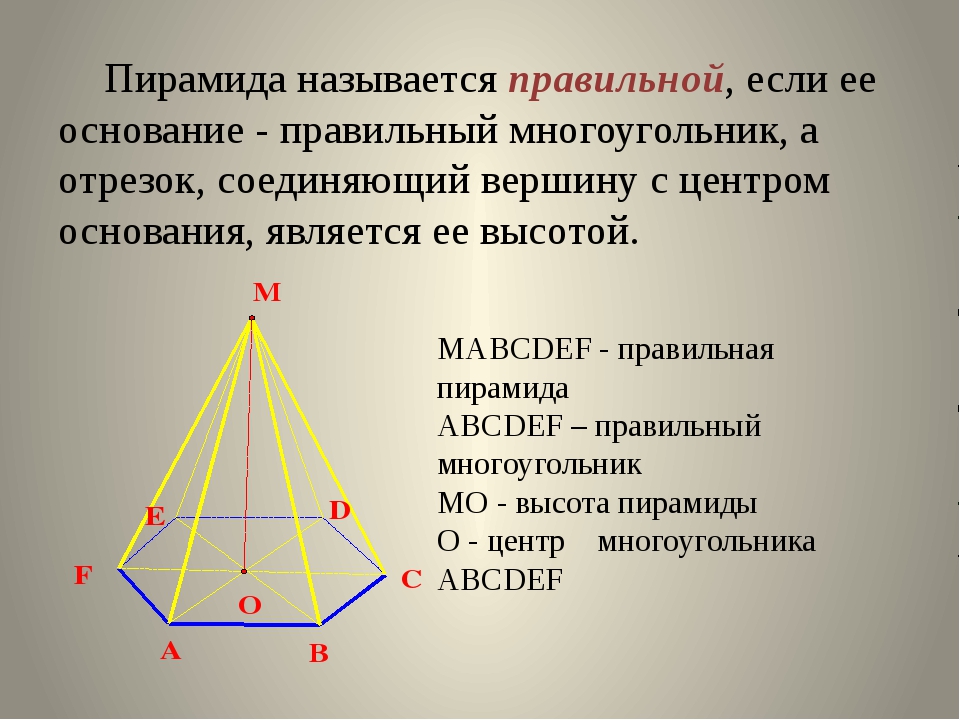
Тип: Задача решения проблем
Почему АСА работает?:В этом задании на решение задач учащимся предлагается показать отражение одного треугольника в другом треугольнике.
Тип: Задача решения проблем
Когда SSA работает для определения конгруэнтности треугольников?:В этой задаче мы рассматривали SSA.Критерии соответствия треугольника, SSS, SAS, ASA, требуют трех частей информации. Интересно, однако, что не всех трех частей информации о сторонах и углах достаточно, чтобы определить треугольник с точностью до конгруэнтности.

Тип: Задача решения проблем
Семь кругов II:Эта задача обеспечивает конкретную геометрическую постановку для изучения жестких преобразований плоскости.
Тип: Задача решения проблем
Середины сторон параллелограмма:Это достаточно прямое задание, направленное на то, чтобы учащиеся использовали ранее полученные результаты для изучения новых фактов о параллелограммах, а не для получения их из первых принципов.

Тип: Задача решения проблем
Вписывание квадрата в круг:Это задание дает учащимся возможность применить теоремы о конгруэнтности треугольников в явном, интересном контексте.
Тип: Задача решения проблем
Вписывание шестиугольника в окружность:В этом задании на решение задач учащимся предлагается вписать равносторонние треугольники и правильные шестиугольники в круг с помощью циркуля и линейки.
Тип: Задача решения проблем
Почему SAS работает?:В этом задании на решение задач учащимся предлагается объяснить, почему данные треугольники равны, и построить отражения точек.

Тип: Задача решения проблем
Отражения и равносторонние треугольники II:Это задание дает учащимся возможность увидеть влияние отражений на явный объект и увидеть, что отражения не всегда коммутируют.
Тип: Задача решения проблем
Отражения и равносторонние треугольники:Это задание является одним из серии заданий, использующих жесткие преобразования плоскости для изучения симметрии классов треугольников, при этом особое внимание в этом задании уделяется классу равносторонних треугольников
Тип: Задача решения проблем
Отраженные треугольники:В этом задании учащимся предлагается с помощью линейки и циркуля построить линию, через которую отражается треугольник.
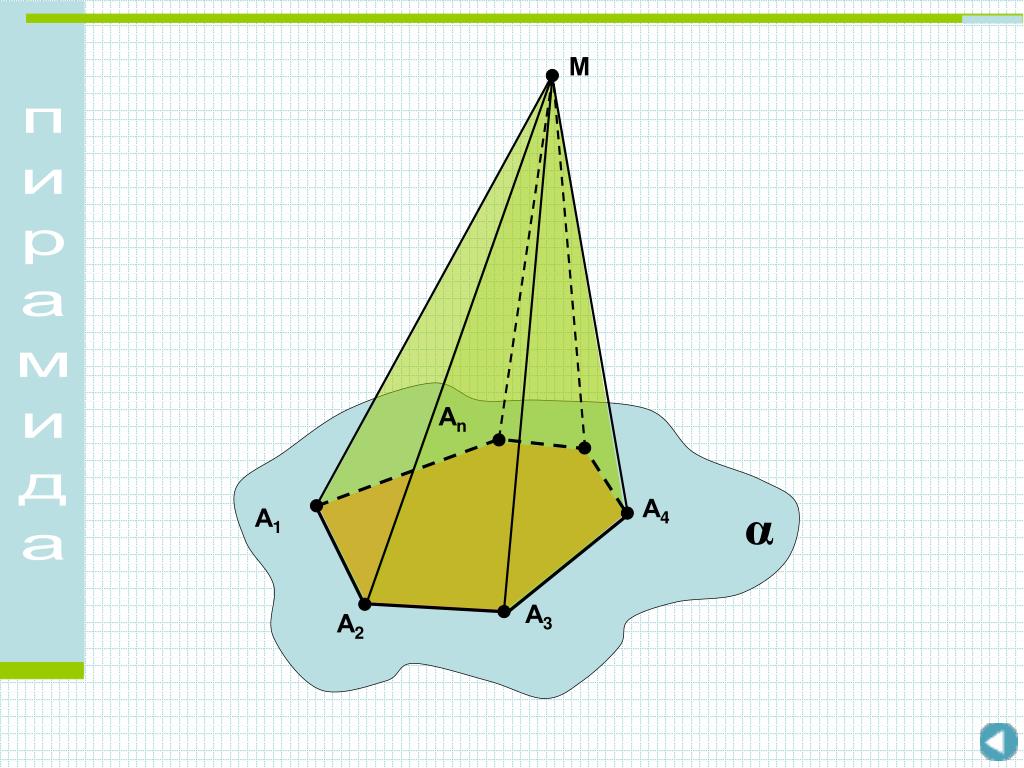
Тип: Задача решения проблем
Центральная часть:Целью этого задания является использование геометрических и алгебраических рассуждений для моделирования реального сценария. В частности, учащиеся в нескольких местах (явно или неявно) должны рассуждать о том, когда делать приближения разумно и когда округлять, когда использовать равенство, а когда нет.неравенства и выбор единиц измерения для работы (например, мм против см).
Тип: Задача решения проблем
Теннисные мячи в банке:Эта задача основана на выводе формулы объема сферы.
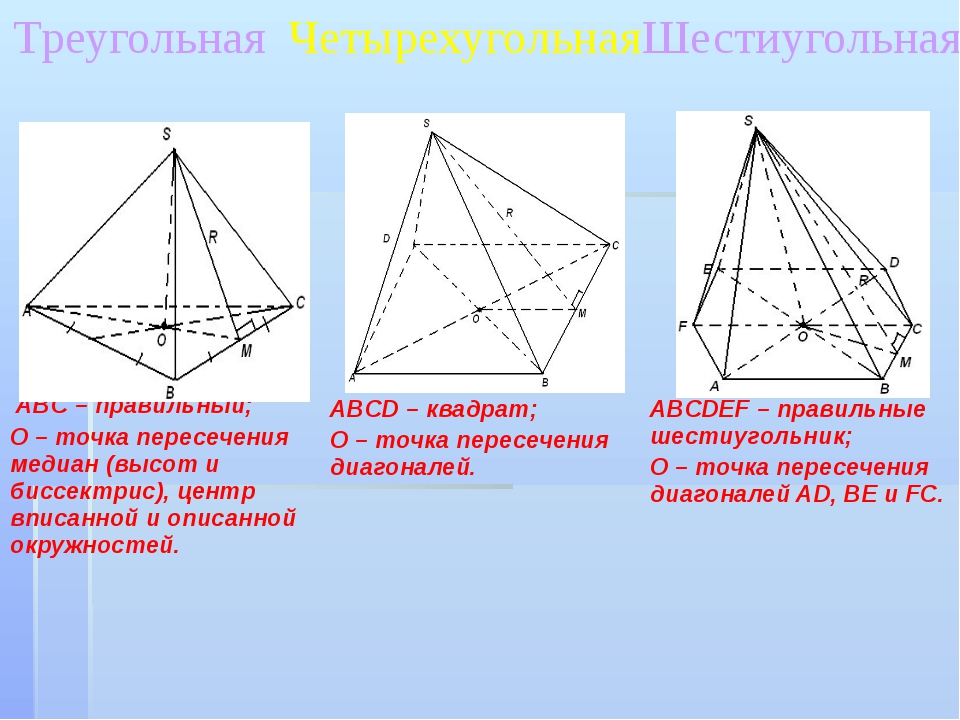 Если сфера радиуса 1 заключена в цилиндр радиуса 1 и высоты 2, то объем, не занимаемый сферой, равен объему «двухвершинного конуса» с вершиной в центре сферы и основаниями, равными к основаниям цилиндра
Если сфера радиуса 1 заключена в цилиндр радиуса 1 и высоты 2, то объем, не занимаемый сферой, равен объему «двухвершинного конуса» с вершиной в центре сферы и основаниями, равными к основаниям цилиндра Тип: Задача решения проблем
Два колеса и ремень:В этом задании сочетаются два навыка: использование отношения между касательным сегментом к окружности и радиусом, касающимся этого касательного сегмента, и вычисление длины дуг окружности с учетом радиусов и центральных углов.
Тип: Задача решения проблем
Прямоугольные треугольники, вписанные в окружности I:Это задание дает хорошую возможность использовать равнобедренные треугольники и их свойства, чтобы показать интересный и важный результат о треугольниках, вписанных в окружность: тот факт, что эти треугольники всегда прямоугольные, часто называют теоремой Фалеса.

Тип: Задача решения проблем
Размещение пожарного гидранта:В этом задании на решение задач учащимся предлагается разместить пожарный гидрант на равном расстоянии от трех заданных точек.
Тип: Задача решения проблем
Почему SSS работает?:Эта конкретная задача по решению проблем демонстрирует соответствие между двумя треугольниками, демонстрируя перемещение, отражение и вращение.
Тип: Задача решения проблем
Построение рисунка плитки путем отражения восьмиугольников:В этом задании отражения применяются к правильному восьмиугольнику для построения шаблона из четырех восьмиугольников, охватывающих четырехугольник: основное внимание в задании уделяется использованию свойств отражений для вывода о том, что четырехугольник на самом деле является квадратом.

Тип: Задача решения проблем
Построение рисунка плитки путем отражения шестиугольников:В этом задании отражения применяются к правильному шестиугольнику, чтобы построить шаблон из шести шестиугольников, заключающих в себе седьмой: основное внимание в задании уделяется использованию свойств отражений для получения этого шаблона из семи шестиугольников.
Тип: Задача решения проблем
Разделение угла пополам:В этом задании на решение учащимся предлагается разделить заданный угол пополам.

Тип: Задача решения проблем
Конгруэнтны ли треугольники?:Цель этого задания в первую очередь ориентирована на оценку: учащимся предлагается продемонстрировать знания о том, как определять конгруэнтность треугольников.
Тип: Задача решения проблем
Расположение склада:В этом задании на решение задач учащимся предлагается разместить склад (точку) на равном расстоянии от трех дорог (линий).
Тип: Задача решения проблем
Вписывание треугольника в окружность:Эта задача знакомит с центром описанной окружности треугольника и показывает, как его можно использовать для вписания треугольника в окружность.

Тип: Задача решения проблем
Центр окружности треугольника:Эта задача показывает, что все три серединных перпендикуляра сторон треугольника пересекаются в одной точке, используя характеристику биссектрисы отрезка как множества точек, равноудаленных от двух концов отрезка.
Тип: Задача решения проблем
Касательные линии и радиус окружности:В этом задании на решение задач учащимся предлагается найти точку пересечения перпендикуляра отрезка из центра окружности и касательной.

Тип: Задача решения проблем
Семь кругов I:Эта задача предназначена для моделирования конкретной ситуации с геометрией. Размещение семи монет в виде круга — это конкретный и забавный эксперимент, который приводит к подлинному математическому вопросу: дает ли физическая модель с монетами понимание того, что происходит с семью кругами на плоскости?
Тип: Задача решения проблем
Установка разбрызгивателей:Эта задача моделирования включает в себя несколько различных типов геометрических знаний и решение проблем: нахождение площадей секторов окружностей, использование тригонометрических соотношений для решения прямоугольных треугольников и разложение сложной фигуры, включающей несколько дуг окружности, на части, площади которых можно найти.

Тип: Задача решения проблем
Пренебрегая кривизной Земли:В этом задании геометрические понятия, а именно свойства касательных окружностей и прямоугольных треугольников, применяются в ситуации моделирования. Ключевым геометрическим моментом в этой задаче является признание того, что линия обзора от вершины горы к горизонту касается земли.Затем мы можем использовать прямоугольный треугольник, в котором одна сторона касается окружности, а другая сторона является радиусом окружности, чтобы исследовать эту ситуацию.
Тип: Задача решения проблем
Разделение пополам угла и середины отрезков:Эта задача обеспечивает построение биссектрисы угла путем сведения ее к биссектрисе угла с нахождением середины отрезка.
 Стоит соблюдать симметрию — как для нахождения середины, так и для биссектрисы цель состоит в том, чтобы разрезать объект на две равные части.
Стоит соблюдать симметрию — как для нахождения середины, так и для биссектрисы цель состоит в том, чтобы разрезать объект на две равные части. Тип: Задача решения проблем
Вписывая окружность в треугольник II:Это задание на решение проблемы фокусируется на замечательном факте, который следует из построения вписанной окружности в треугольник: все биссектрисы трех углов треугольника ABC пересекаются в одной точке.
Тип: Задача решения проблем
Регулярные замощения плоскости:В этом задании исследуются способы покрытия плоскости правильными многоугольниками в очень строгом порядке, называемом правильной мозаикой.
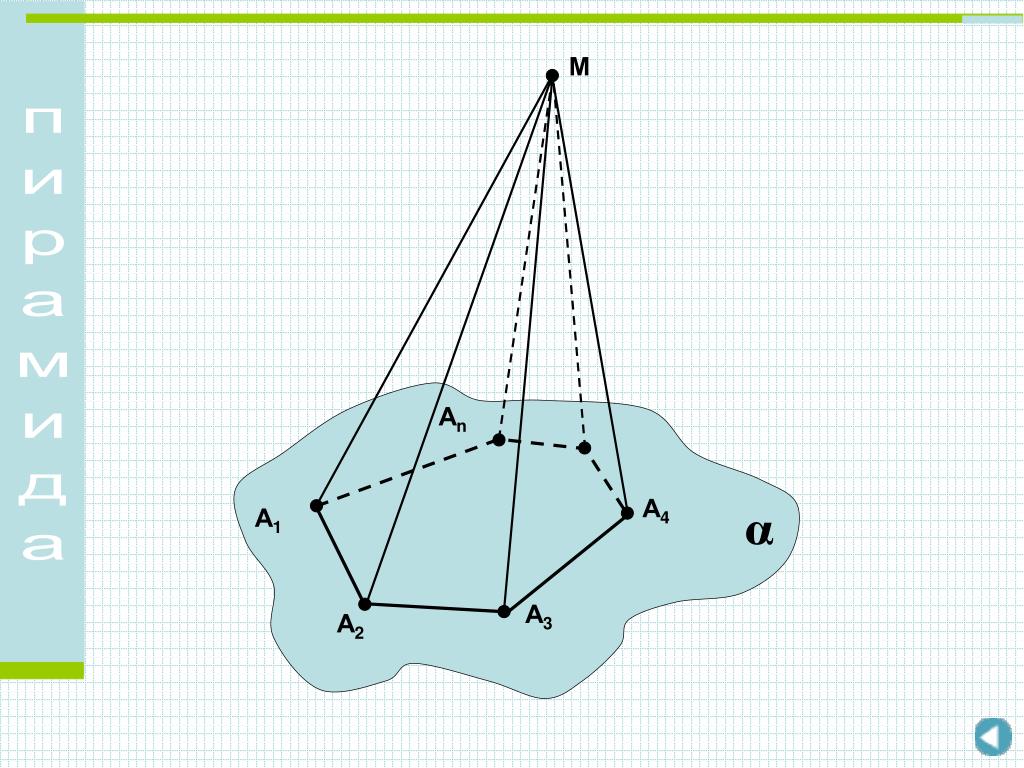 Эти мозаики изучаются здесь с помощью алгебры, которая входит в картину через формулу измерения внутренних углов правильного многоугольника (которую, следовательно, следует ввести или повторить перед началом задачи). Цель задания — с помощью алгебры понять, какие замощения плоскости правильными многоугольниками возможны.
Эти мозаики изучаются здесь с помощью алгебры, которая входит в картину через формулу измерения внутренних углов правильного многоугольника (которую, следовательно, следует ввести или повторить перед началом задачи). Цель задания — с помощью алгебры понять, какие замощения плоскости правильными многоугольниками возможны. Тип: Задача решения проблем
Нахождение равных треугольников:В этом учебном пособии учащиеся будут использовать постулаты SSS, ASA, SAS и AAS для нахождения конгруэнтных треугольников
Тип: Учебник
Использование SSS в доказательстве:В этом руководстве обсуждается разница между теоремой и аксиомой.
 Он также показывает, как использовать SSS в доказательстве.
Он также показывает, как использовать SSS в доказательстве. Тип: Учебник
Постулаты конгруэнтности треугольников:В этом руководстве обсуждаются постулаты SSS, SAS, ASA и AAS для конгруэнтных треугольников. Это также показывает, что AAA подходит только для сходства, а SSA не годится ни для того, ни для другого.
Тип: Учебник
Конгруэнтные треугольники и SSS:В этом видео учащиеся узнают о конгруэнтных треугольниках и постулате «Сторона-Сторона-Сторона».

Тип: Учебник
Линия отражения:С помощью интерактивного инструмента учащимся показано, как отразить отрезок прямой.Перед просмотром этого видео учащиеся должны иметь представление об уклоне и средней точке.
Тип: Учебник
Линия отражения:В этом уроке используется средняя точка двух линий, чтобы найти линию отражения.
Тип: Учебник
Очки после ротации:Студенты увидят, что происходит, когда фигуру поворачивают вокруг начала координат на -270 градусов.
 Перед просмотром этого видео рекомендуется иметь представление о прямоугольных треугольниках.
Перед просмотром этого видео рекомендуется иметь представление о прямоугольных треугольниках.Тип: Учебник
Параллельные прямые, секущие и треугольники:В этом учебном пособии учащимся показаны восемь углов, образованных при пересечении двух параллельных прямых поперечной линией.Также в этом видео есть обзор треугольников.
Тип: Учебник
Язык геометрии:Прежде чем изучать какое-либо новое понятие, важно, чтобы учащиеся выучили и использовали общий язык и последовательно обозначали понятия.
 Этот учебник знакомит учащихся с точкой, линией и плоскостью.
Этот учебник знакомит учащихся с точкой, линией и плоскостью. Тип: Учебник
Доказательство равенства вертикальных углов:В этом уроке учащиеся доказывают, что вертикальные углы равны. Перед просмотром этого видео учащиеся должны иметь представление о дополнительных ракурсах.
Тип: Учебник
Нахождение меры вертикальных углов:С помощью алгебры учащиеся найдут величину вертикальных углов или углов, противоположных друг другу при пересечении двух прямых.
 Перед просмотром этого видео учащиеся должны иметь представление о дополнительных и дополнительных ракурсах.
Перед просмотром этого видео учащиеся должны иметь представление о дополнительных и дополнительных ракурсах.Тип: Учебник
Введение в вертикальные углы:В этом учебном пособии учащиеся будут использовать свои знания о дополнительных, смежных и вертикальных углах для решения задач, связанных с пересечением двух линий.
Тип: Учебник
Использование тригонометрии для поиска недостающей информации:Этот учебник покажет учащимся, как использовать тригонометрию для поиска недостающей информации в прямоугольных треугольниках.
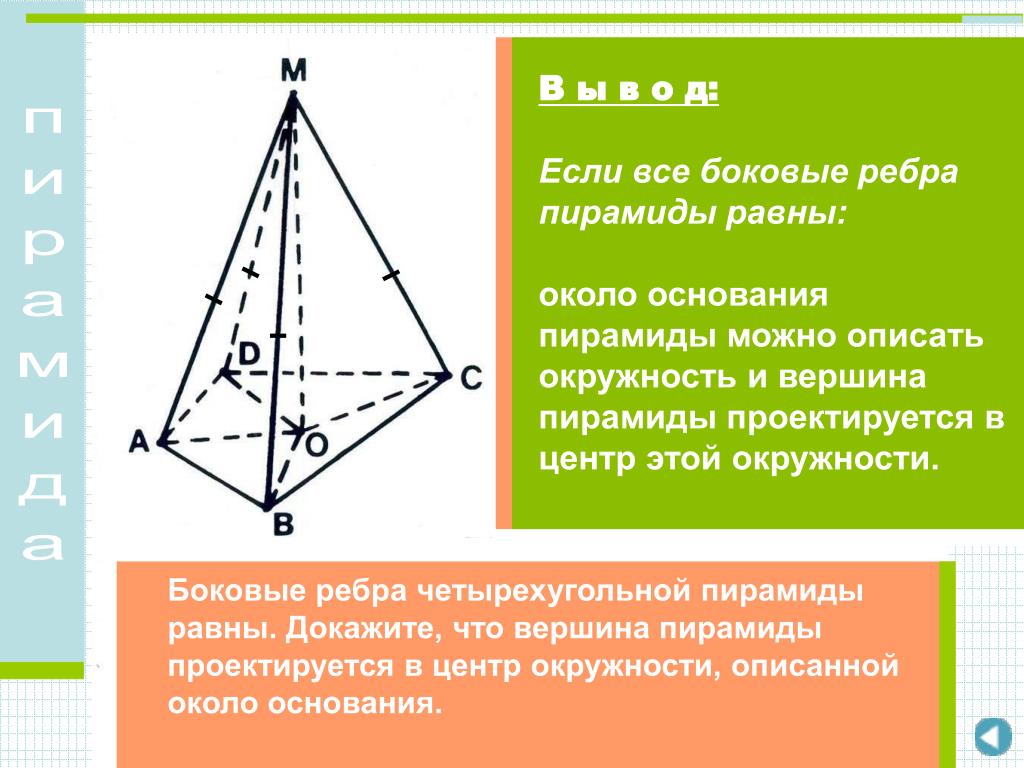 В этом видео показаны рабочие примеры использования тригонометрических соотношений для поиска недостающей информации и оценки других тригонометрических соотношений.
В этом видео показаны рабочие примеры использования тригонометрических соотношений для поиска недостающей информации и оценки других тригонометрических соотношений. Тип: Учебник
Базовая тригонометрия:Этот учебник дает введение в тригонометрию.В этом ресурсе обсуждаются три основные функции тригонометрии: синус, косинус и тангенс.
Тип: Учебник
Параллельные линии:Параллельные прямые имеют одинаковый наклон и не имеют общих точек.
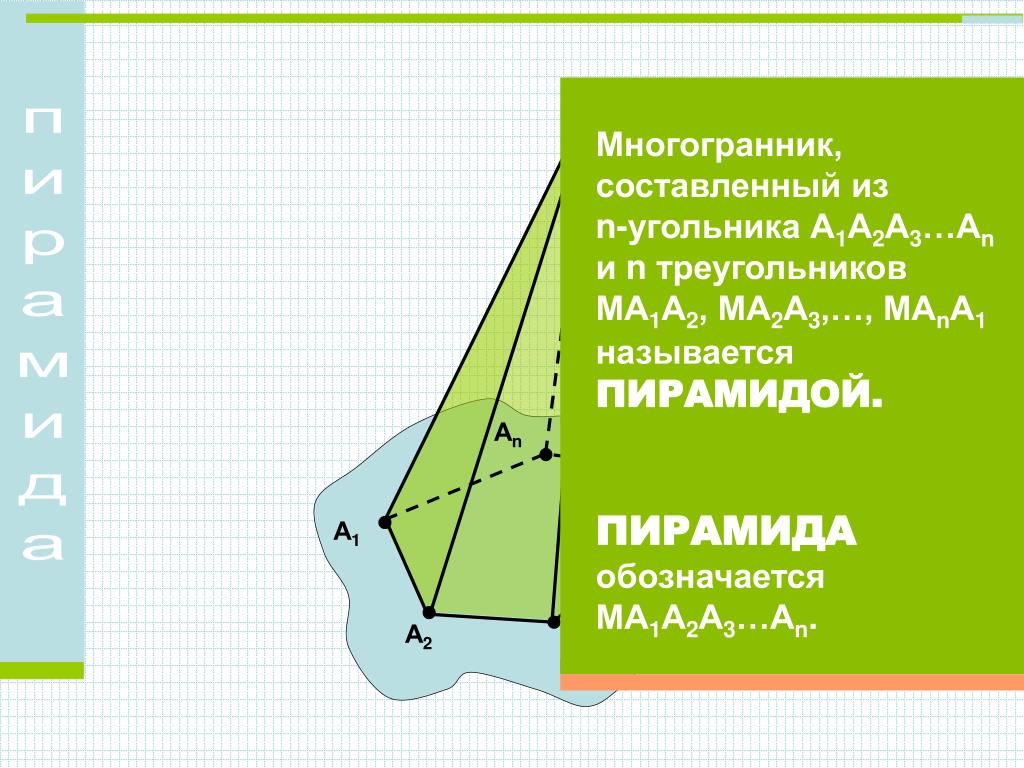 Однако не всегда очевидно, описывают ли два уравнения параллельные прямые или одну и ту же прямую.
Однако не всегда очевидно, описывают ли два уравнения параллельные прямые или одну и ту же прямую. Тип: Учебник
Перпендикулярные линии:Перпендикулярные линии имеют наклоны, которые являются отрицательными обратными величинами друг к другу, но почему?
Тип: Учебник
Снаряд под углом:В этом видео обсуждается, как вычислить горизонтальное смещение снаряда, запущенного под углом.
Тип: Учебник
Человеческая форма из сакральной геометрии
Человеческая форма из сакральной геометрииСАКРАЛЬНАЯ ГЕОМЕТРИЯ
Новые открытия
Связь с Великой пирамидой в человеческую форму
Copyright 1997 – 2000 ЧАРЛЬЗ Р.
 Генри
Генри Все права защищены
Профессор кафедры скульптуры
Университет Содружества Вирджинии
Ричмонд, Вирджиния
———————————————— ———————————-
Этот сайт лучше всего просматривать в Microsoft Интернет Эксплорер 4.0 или выше
с размером экрана 1024 X 768 пикселей, 24 бит …16 миллионов цветов.
Установить… Вид/Размер текста… на средний
Нажмите на миниатюру, чтобы увеличить картинки.
———————————————— ——————————–
Уже более двадцати лет я изучение свойств формирования изображения отражающих сфер, сложенных под углом 52 градуса пирамиды.
 Угол наклона сторон Великой пирамиды в Каире 52 (51,827) градуса,
Египет воплощает золотую середину, то есть соотношение, используемое в природе для создания
закономерности роста в космосе. Сакральная геометрия изучает такие первичные системы, которые раскрывают
единство космоса, представляя отношения между числами геометрически. То
Vesica Piscis — одна из самых фундаментальных геометрических форм этой древней дисциплины.
и раскрывает связь между Великой Пирамидой и двухмерным
расширение круга единичного радиуса R, как показано на рисунке 1.Эти отношения более
полностью описан в «Новом взгляде на Атлантиду» Джона Мичелла, опубликованном Thames and
Хадсон.
Угол наклона сторон Великой пирамиды в Каире 52 (51,827) градуса,
Египет воплощает золотую середину, то есть соотношение, используемое в природе для создания
закономерности роста в космосе. Сакральная геометрия изучает такие первичные системы, которые раскрывают
единство космоса, представляя отношения между числами геометрически. То
Vesica Piscis — одна из самых фундаментальных геометрических форм этой древней дисциплины.
и раскрывает связь между Великой Пирамидой и двухмерным
расширение круга единичного радиуса R, как показано на рисунке 1.Эти отношения более
полностью описан в «Новом взгляде на Атлантиду» Джона Мичелла, опубликованном Thames and
Хадсон. Рисунок 1 Vesica Piscis в двух измерениях
В начале 1970-х я стал очень заинтересовался трехмерным представлением этой геометрии, и я визуализировал это в виде трехмерной пирамиды внутри двух пересекающихся сфер, показанных на рисунке 2.

Рисунок 2 Vesica Piscis в трех измерениях
Чтобы визуализировать эти трехмерные отношений еще по-другому, я сложил светоотражающие елочные шары в перевернутом виде. оболочка пирамиды.Я обнаружил, что узоры множественных отражений, созданные на внутренние поверхности отражающих сфер, сложенные под этим углом, создают изображения, которые относятся в человеческую форму, как показано на фотографиях и рисунках 3 и 4.
Рисунок 3
Рисунок 4
Я сделал много пирамидальных конфигураций из отражающие сферы с разными источниками света, и я сфотографировал узоры на внутренние поверхности с разных точек зрения.Другой показан здесь, на рис.
 5.
5. Рисунок 5
Затем, в 1977 году, я обнаружил одну стопку структура и точка зрения, которые дали очень убедительный образ архетипического человеческого лица. Эта структура из 10 сфер (2 пирамиды по 5 шаров), образующих кластер, показана на рисунке 6.
Рисунок 6
Изображение лица отображается в нижней трети узора на одной сфере внутри этого кластера из 10 сфер и показан на рисунке 7.
Рисунок 7. Когда я сделал эту фотографию, структура была заключен в зеркальной пирамиде.
Позже я понял, что самое естественное структура для ограждения будет еще 10 сфер, 2 структуры пирамиды, которые будут полностью приложите меньший, но подобный кластер.
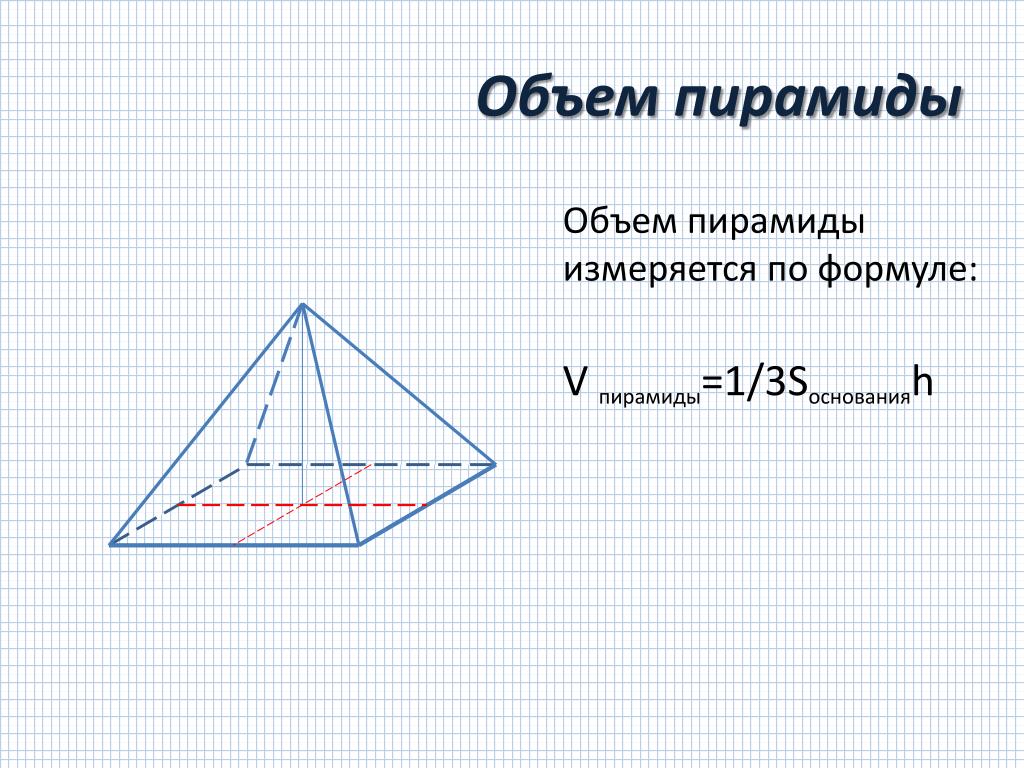 Я разработал математику, чтобы найти это
умножение диаметров внутренней сферы на Пи дает размер внешней сферы.
диаметра, как показано на рисунке 8.
Я разработал математику, чтобы найти это
умножение диаметров внутренней сферы на Пи дает размер внешней сферы.
диаметра, как показано на рисунке 8. Рис. 8 Одна сфера удаляется из внешнего кластера, чтобы открыть внутренний кластер. Однако внутренний кластер должен быть перевернут по отношению к внешнему кластеру, чтобы поместиться внутри.
Расширение Пи укрепило мой подозрение, что этот кластер из 10 сфер является фундаментальной единицей, связанной с свойства трехмерного пространства.
Плотно упакованные отражающие сферы, сгруппированные в этой концентрической оболочке, создают оптическая распределительная сеть, которая связывает Золотое сечение и Пи.Золотая середина это выражается в структуре пирамиды с углом 52 градуса, а Pi выражается в отношении диаметр к окружности каждой сферы, конечно; но это также выражается в соотношение размеров сфер в 10 сферах внутри 10 сфер концентрической оболочки структуру, которую я обнаружил.
 Эта концентрическая структура оболочки может продолжать расширяться с
много оболочек и все еще сохраняют то же соотношение между оболочками. Только в 1991 году я
смог построить и сфотографировать изображения внутри структуры «десять в десяти» (2 оболочки).я
использовались сферы диаметром 10–6 дюймов и полусферы диаметром 10–19 дюймов. Структура
показан здесь на рис. 9.
Эта концентрическая структура оболочки может продолжать расширяться с
много оболочек и все еще сохраняют то же соотношение между оболочками. Только в 1991 году я
смог построить и сфотографировать изображения внутри структуры «десять в десяти» (2 оболочки).я
использовались сферы диаметром 10–6 дюймов и полусферы диаметром 10–19 дюймов. Структура
показан здесь на рис. 9. Рисунок 9
Рисунок 10 и Рисунок 11 представляют собой фотографии интерьера. из 10 сфер в кластере из 10 сфер, показанном на рисунке 9.
Рисунок 10
Рисунок 11
Фотографии, которые я сделал из этого Структура 10-в-10 сфер выявила врожденные ограничения фотографии для этого. Работа.
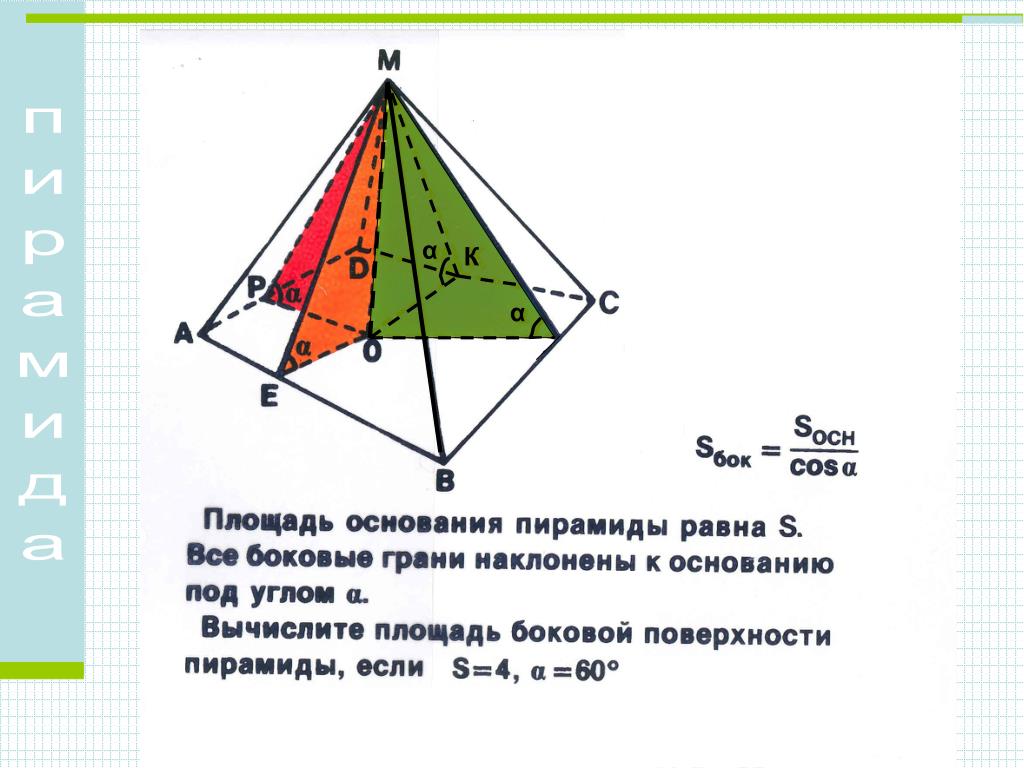 Окончательные изображения были не тем, что я видел своими глазами, когда смотрел прямо на
интерьер конструкции. Но этот подход показал более полную форму лица, и я
также понял, что мне понадобится еще как минимум 10 сфер (около 60 дюймов в диаметре на
1500 долларов за штуку), чтобы завершить корпус и удалить оставшиеся пробелы в изображениях. Также,
система освещения была ограничена экстерьером, и было очень трудно контролировать
расположение, цвет и яркость. Итак, в 1992 году я купил компьютер для моделирования этих
структур с помощью программного обеспечения для трассировки лучей, что позволило мне более тщательно исследовать
связь между геометрией этого кластера и генерируемыми в нем архетипическими образами.Во время этого тура в киберпространство я мог взять камеру в центральную священную комнату, чтобы
концентрические оболочки отражающих сфер, моделируемые компьютерной программой (Real 3D от Realsoft Oy, Финляндия), которая наиболее точно
визуализирует эффекты реальных источников света и записывает узоры, созданные
множественные отражения от металлических поверхностей.
Окончательные изображения были не тем, что я видел своими глазами, когда смотрел прямо на
интерьер конструкции. Но этот подход показал более полную форму лица, и я
также понял, что мне понадобится еще как минимум 10 сфер (около 60 дюймов в диаметре на
1500 долларов за штуку), чтобы завершить корпус и удалить оставшиеся пробелы в изображениях. Также,
система освещения была ограничена экстерьером, и было очень трудно контролировать
расположение, цвет и яркость. Итак, в 1992 году я купил компьютер для моделирования этих
структур с помощью программного обеспечения для трассировки лучей, что позволило мне более тщательно исследовать
связь между геометрией этого кластера и генерируемыми в нем архетипическими образами.Во время этого тура в киберпространство я мог взять камеру в центральную священную комнату, чтобы
концентрические оболочки отражающих сфер, моделируемые компьютерной программой (Real 3D от Realsoft Oy, Финляндия), которая наиболее точно
визуализирует эффекты реальных источников света и записывает узоры, созданные
множественные отражения от металлических поверхностей. С помощью этого метода исследования я могу
более удобно контролировать многие переменные, которые привели к этим открытиям и
выводы:
С помощью этого метода исследования я могу
более удобно контролировать многие переменные, которые привели к этим открытиям и
выводы: 1.) Необходимо не менее 40 сфер (4-10 шаровых оболочек), чтобы ограждать центральную зону и заполнить пробелы в изображениях.
2.) Большинство огней должны быть точечными источниками, расположенными в точках контакта между самые внутренние сферы строения; хотя дополнительные симметрично-парные точечные светильники нужны в центральном районе.
3.) Некоторые из самых внутренних сфер уменьшены в размерах и могут плавать в определенных пределах площади в центральном пространстве. На рис. 12 показаны типичные положения и размеры.
4.) Положение камеры и поле зрения, как показано на рисунке 12. производит наиболее убедительное изображение человеческого тела.
Рисунок 12
5.) Изображение этого искусственного антропоида, созданное в этих конструкциях, может быть анимируется, когда положение и размеры определенных сфер модулируются, как показано на три анимации, перечисленные ниже.
анимация 1 .8 МБ … предполагаемая загрузка время на 56к… 3,5 мин.
анимация 2 2,4 МБ … расчетное время загрузки при 56 КБ … 10 мин.
Рисунок 13 Человеческая форма из сакральной геометрии
Компьютерное изображение на рисунке 13 было сделано из положения камеры и поля зрения, показанных на рисунке 12.
Рисунок 14 из той же позиции камеры (показанной на рис. 12), но объектив поставлен на очень широкий угол.
Рисунок 14
Рисунок 15 находится с той же позиции камеры (показанной на рис. 12) с объектив камеры настроен на увеличение.

Рисунок 15
Рисунок 16 представляет собой стереоизображение, показывающее внутреннюю часть скопления в 3D. Смотреть сквозь изображения с вашими глазами, сфокусированными на удаленной точке, и два изображения превратятся в три изображения, а центральное изображение появится в 3D.
Рисунок 16
В 1996 году я создал анимацию «Священные пространства» (6 минут), который был показан на многих национальных и международных кинофестивалях. получил несколько наград (см. резюме). Я также продюсировал телесные тона (5,5 минут), еще один анимация была завершена в 1997 году, и я создал много изображений с высоким разрешением для распечатки/слайды (некоторые примеры показаны на рисунках с 13 по 36), которые я представил с видео анимацией на лекционных презентациях.
 Эти изображения являются кадрами из
анимаций, и они демонстрируют разнообразие генерации изображений, присущее этому
система. До сих пор я сосредоточился на демонстрации видеозаписи моей работы.
потому что это самый портативный формат презентации, который описывает это исследование наиболее
полностью.
Эти изображения являются кадрами из
анимаций, и они демонстрируют разнообразие генерации изображений, присущее этому
система. До сих пор я сосредоточился на демонстрации видеозаписи моей работы.
потому что это самый портативный формат презентации, который описывает это исследование наиболее
полностью. Рисунок 17
Рисунок 18
Рисунок 19
Рисунок 20
Рисунок 21
Заключение
Это междисциплинарное исследование привело меня во многие смежные области исследований. Геометрия, оптика, древняя история искусства и религии, компьютерная обработка изображений, фотография, Анимация, графика и, конечно же, скульптура — основные связующие дисциплины, которые внесли свой вклад в эту работу.
Я чувствую, что вновь открыл для себя часть того, что было высокоразвитым пониманием Отношение человечества к Вселенной и эти знания были использованы и задокументированы в Геометрия древних сооружений.
 Сакральная геометрия, изучение единства космоса,
демонстрирует отношения между Числом и Пространством и Человеческой формой.Он использовался в
строительство древних глифов и памятников, тем самым сохраняя знания об этих
принципы естественного права для будущих поколений. Эта конструкция из
отражающие сферы могут воплощать в себе технологию, создавшую анимированные изображения
божества в храмах древности. Древо жизни, которое является графическим изображением
взаимодействие между космическими силами показано на рисунке 22.
встречается во многих древних текстах Каббалы.
Сакральная геометрия, изучение единства космоса,
демонстрирует отношения между Числом и Пространством и Человеческой формой.Он использовался в
строительство древних глифов и памятников, тем самым сохраняя знания об этих
принципы естественного права для будущих поколений. Эта конструкция из
отражающие сферы могут воплощать в себе технологию, создавшую анимированные изображения
божества в храмах древности. Древо жизни, которое является графическим изображением
взаимодействие между космическими силами показано на рисунке 22.
встречается во многих древних текстах Каббалы. Рисунок 22.
Я понял, что рисунок Древа Жизни может также представлять кластер из 10 сфер, сделанный с 2 пирамидами из 5 шаров, как показано на рис. 23.Рисунок 23
Конструкция данной конструкции из сборного металла отражающие сферы (чаши для подношений) вполне доступны многим древним культурам.
 а с добавлением нескольких стеклянных линз эти изображения можно было проецировать на стены или
в дым.Возможно, за дымом и зеркалами Древней Религии скрывается какая-то Истина.
… возможно, это геометрия… Сакральная геометрия.
а с добавлением нескольких стеклянных линз эти изображения можно было проецировать на стены или
в дым.Возможно, за дымом и зеркалами Древней Религии скрывается какая-то Истина.
… возможно, это геометрия… Сакральная геометрия. Это исследование, которое задокументировано в четырех компьютерных анимациях Sacred Spaces, Flesh Tones, Наши матери и священные места 2, цветные компьютерные распечатки и цветные слайды дали мне новое понимание мотивов, которые, возможно, вдохновили создание Великого Пирамида.
Обновление 1998 – 2000
Изображения, показанные на рисунках 24–35, были сделаны с помощью 50 сферы и 144 точечных источника света.Каждое из этих изображений было сделано с уникальным настройки яркости, цвета и значения для различных групп огней.
Рисунок 24
Рисунок 25
Рисунок 26
Рисунок 27
Рисунок 28 горизонтальный
Рисунок 28 вертикальный
Рисунок 29
Рисунок 30
Рисунок 31
Рисунок 32
На рисунке 32, камера направлена на сферу, противоположную лицу, показанному на рисунке 31.
 На Рисунке 12 показано положение камеры для Рисунка 31. Изображение на Рисунке 32 было
формируется при повороте положения камеры на 180 градусов вокруг вертикальной оси
показано на Рис. 12 и в увеличенном масштабе. Изображение лица (а
ребенок?) на рис. 32 намного меньше, чем лицо (мать?) на рис.
31.
На Рисунке 12 показано положение камеры для Рисунка 31. Изображение на Рисунке 32 было
формируется при повороте положения камеры на 180 градусов вокруг вертикальной оси
показано на Рис. 12 и в увеличенном масштабе. Изображение лица (а
ребенок?) на рис. 32 намного меньше, чем лицо (мать?) на рис.
31. Рисунок 33 горизонтальный
Рисунок 33 вертикальный
Рисунок 34
Рисунок 35 Это представляет собой стереофоническое 3D-изображение, для просмотра которого требуются очки с затвором, а на мониторе должен быть установлен режим интерлейсный режим.
Рисунок 36 Стереоизображение для косоглазых Просмотр
Держа монитор на расстоянии вытянутой руки, сфокусируйтесь на точке в 6 дюймах перед свой нос (поместите указательный палец на 6 дюймов перед носом и сфокусируйтесь на нем).
 Ты будешь
увидеть третье изображение в 3D между двумя изображениями на мониторе (на кончике пальца).
Переключите внимание с пальца на это третье/среднее изображение, которое появится в 3D.
Ты будешь
увидеть третье изображение в 3D между двумя изображениями на мониторе (на кончике пальца).
Переключите внимание с пальца на это третье/среднее изображение, которое появится в 3D. ———————————————— ———————————-
Метод косого взгляда, пожалуй, самый эффективный способ средство просмотра внутри кластера, чтобы увидеть изображение человека, как оно будет существовать в 3D с камер положение, как показано на
Рисунок 12. В этом кластере есть еще много идентифицируемых изображений геометрия, просматриваемая с этой позиции и с других позиций камеры, и даже больше изображений с другими настройками цвета для точечных источников света.Рисунок 36 Большой
Рисунок 36 Увеличение Это изображение лба лица на Рисунке 36. Крупно.
Рисунок 36 Широкоугольный Большой
Рисунок 36 Очень широкоугольный Большой
Рисунок 37 Стержни, соединяющие центры ближайших соседей в 3-х оболочках
Теперь мне очень интересно узнать о связи между Сакральной Геометрией и Сакральной Музыка и человеческая форма.
 Число относится ко всему, что наука измеряет в силу того, как
что трехмерное пространство определено. Число также используется для измерения времени… и, как писал Пифагор
Согласно наблюдениям, Музыка есть проявление Числа во Времени. Распространение звуков, т.е.
амплитуда и частота вполне могут найти идеализированную модель в сфере 10 в пределах 10,
заполняющая пространство плотноупакованная геометрическая система. Представление этой геометрии с
палочки или веревки или стержни, как показано на рисунке 37 (на котором центры ближайших соседей
сферы в трех оболочках соединены) может представлять собой идеальную заполняющую пространство матрицу линейных
колеблющиеся элементы.Его также можно использовать для определения пространственно распределенных, иерархических,
сотовые массивы.
Число относится ко всему, что наука измеряет в силу того, как
что трехмерное пространство определено. Число также используется для измерения времени… и, как писал Пифагор
Согласно наблюдениям, Музыка есть проявление Числа во Времени. Распространение звуков, т.е.
амплитуда и частота вполне могут найти идеализированную модель в сфере 10 в пределах 10,
заполняющая пространство плотноупакованная геометрическая система. Представление этой геометрии с
палочки или веревки или стержни, как показано на рисунке 37 (на котором центры ближайших соседей
сферы в трех оболочках соединены) может представлять собой идеальную заполняющую пространство матрицу линейных
колеблющиеся элементы.Его также можно использовать для определения пространственно распределенных, иерархических,
сотовые массивы. ———————————————— ————————
Расположение камер на симметричных плоскостях внутри кластера создает двусторонняя симметрия, которую мы отождествляем с формой животного и человека.
 Естественно, мы ожидали
эта симметрия в идеализированных образах высших форм жизни. Множественность идеализированных
существ в этом скоплении отражающих сфер предполагает присутствие Компании
Боги, описанные во многих древнеегипетских текстах.Создается впечатление, что изображения лица возникают на
вертикальная плоскость, соединяющая центры сфер. Кажется, есть лица, обращенные к лицам и
лица внутри лиц в этой отражающей среде. Я думаю, что священный
часть того, что я обнаружил, является результатом того, как божество поместило высшие формы жизни
в трех измерениях.
Естественно, мы ожидали
эта симметрия в идеализированных образах высших форм жизни. Множественность идеализированных
существ в этом скоплении отражающих сфер предполагает присутствие Компании
Боги, описанные во многих древнеегипетских текстах.Создается впечатление, что изображения лица возникают на
вертикальная плоскость, соединяющая центры сфер. Кажется, есть лица, обращенные к лицам и
лица внутри лиц в этой отражающей среде. Я думаю, что священный
часть того, что я обнаружил, является результатом того, как божество поместило высшие формы жизни
в трех измерениях. Эта геометрия кластера может иметь другие свойства, которые могут быть полезны для пространственная организация. Вложение 10 отражающих сфер в 10 отражающих сфер геометрия создает систему распределения, которую можно использовать для обработки оптических информация между внутренней и внешней частью конструкции.Из-за пространственного распределение отражающих сфер в двух концентрических оболочках по десять в каждой, оптических информация должна быть отражена и отклонена, чтобы войти или выйти из системы с за исключением нескольких радиально расположенных направлений.
 Система становится более избирательным фильтром
оптической информации по мере добавления новых оболочек к структуре. Это изнутри наружу
преобразование/перевод должно иметь много практических применений в распознавании образов
задания. Например, любой точечный источник когерентного света (лазерного света) в любом месте за пределами
кластер из двух оболочек создаст уникальную картину распределения света внутри, если смотреть
от центральной части кластера.Этот паттерн может быть записан в голографическом
среду, а внешний точечный источник затем можно было реконструировать с помощью обычного
голографические средства.
Система становится более избирательным фильтром
оптической информации по мере добавления новых оболочек к структуре. Это изнутри наружу
преобразование/перевод должно иметь много практических применений в распознавании образов
задания. Например, любой точечный источник когерентного света (лазерного света) в любом месте за пределами
кластер из двух оболочек создаст уникальную картину распределения света внутри, если смотреть
от центральной части кластера.Этот паттерн может быть записан в голографическом
среду, а внешний точечный источник затем можно было реконструировать с помощью обычного
голографические средства. Число (геометрия и время) является связующим звеном между искусством, наукой и религией опыт? Язык чисел, пожалуй, самая убедительная форма выражения между людьми и между людьми и богами. Мы мыслим и представляем в визуальных формах. Эйнштейн построил свою математику на основе мысленных образов. Он сказал, что сначала попытайтесь визуализировать образ пространства/времени, а затем математизировать его.
 Мы используем мысленные образы, чтобы
конструировать возможные сценарии будущего, чтобы нам не приходилось проживать каждый из них в
“реальность”. Слова, изображения и математические формулы — это способы документирования,
проверяйте, реализуйте и сообщайте эти видения. Хотя потребность в этом возникает редко.
математизировать образы, мы чувствуем, что это возможно. Мы знаем, что можем считать и
количество песчинок на пляже. Геометрия наших видений — вот что делает их
реальными для нас, и это позволяет нам мысленно работать над ними и убедительно интегрировать их
в нашу жизнь здесь в 3D.
Мы используем мысленные образы, чтобы
конструировать возможные сценарии будущего, чтобы нам не приходилось проживать каждый из них в
“реальность”. Слова, изображения и математические формулы — это способы документирования,
проверяйте, реализуйте и сообщайте эти видения. Хотя потребность в этом возникает редко.
математизировать образы, мы чувствуем, что это возможно. Мы знаем, что можем считать и
количество песчинок на пляже. Геометрия наших видений — вот что делает их
реальными для нас, и это позволяет нам мысленно работать над ними и убедительно интегрировать их
в нашу жизнь здесь в 3D. Я не совсем понимаю, как физическая форма человека вписывается в грандиозную схему вещи, но кажется, что это результат заполняющей пространство, сферической, плотной упаковки геометрическую систему, которую я открыл, и это действительно “сакральная геометрия” автора в силу определения, которое Бог дал трем измерениям. Я не думаю, что эта геометрическая система является матрицей для всех жизненных систем, но я думаю, что она может служить моделью для взаимодействия между различными многомерными реальностями, в которые мы погружены.
 Это может
также направлять нас в наших попытках развивать новые науки и технологии, использующие
силы, которые действуют в регионах, которые мы сейчас называем паранормальными явлениями.
Это может
также направлять нас в наших попытках развивать новые науки и технологии, использующие
силы, которые действуют в регионах, которые мы сейчас называем паранормальными явлениями. Согласно современной теории суперструн, описанной доктором Мичио Каку в его многочисленные недавние работы, математика, наиболее точно описывающая силы природа требует выражения в десяти измерениях. Эйнштейн пытался описать силы природы в математике трехмерности и времени и обнаружил, что формулы недостаточно широки. включать все силы.Мы можем воспринимать 3D и Время. Другой 6D в Superstrings скрыты от наших обычных органов чувств из-за их невероятно маленького размера, по словам доктора Б. Каку. Наши инстинкты сообщают нам, что существует более 3-х Измерений и Времени в мире. Вселенная и возможность того, что что-то еще существует математически за пределами нашей Перцептивный горизонт заставляет меня задуматься о наших возможных связях с этими мирами. Новый Наука парапсихология открыла множество способов, которыми люди могут воспринимать посредством помимо физических чувств, и было обнаружено, что есть люди, которые более способны к экстрасенсорному восприятию, чем другие.
 Вполне может быть, что наши единственные контакты с
эта двойственность природы через числа и математику с одной стороны или через сны,
удаленный просмотр, телепатия, доски для спиритических сеансов и карты Таро с другой. Это, безусловно,
подтвердить существование Бога с чувством юмора
Вполне может быть, что наши единственные контакты с
эта двойственность природы через числа и математику с одной стороны или через сны,
удаленный просмотр, телепатия, доски для спиритических сеансов и карты Таро с другой. Это, безусловно,
подтвердить существование Бога с чувством юмора
Меня интересует любая информация, касающаяся этого технологии к древним религиозным традициям. Любые ссылки, которые вы отправляете, будут безусловно, будет оценен по достоинству, и я обязательно буду ссылаться на любые ссылки в будущем публикации.
Более подробная версия этого исследования уже доступна доступен на компакт-диске и включает 10-минутную анимацию Sacred Spaces 2 в потоковом режиме . формат.
Я также делаю доступными неограниченные выпуски выбранные изображения на этом веб-сайте, которые будут напечатаны в очень высоком разрешении на архивном бумага с архивными чернилами.

Для получения более подробной информации о наличии, форматах, размерах и ценах печатные издания и компакт-диск, относящиеся к этой работе, вы можете связаться со мной по телефону:Сопутствующий материал
РЕЗЮМЕ
ССЫЛКИ
Эта страница не отражает официальную позицию Университет Содружества Вирджинии
Последний раз этот сайт обновлялся 23.07.02
Пирамиды
Когда мы думаем о пирамидах, мы думаем о Великих пирамидах Египта .
На самом деле это Квадратные Пирамиды , потому что их основание – Квадрат.

Части пирамиды
Пирамида получается путем соединения основания с вершинойОснование — многоугольник (плоский с прямыми краями), а все остальные грани — треугольники. Никаких кривых!
Типы пирамид
Существует много типов пирамид, и они названы в честь формы их основания.
Пролетите здесь через несколько пирамид.
Правая и наклонная пирамида
Это говорит нам, где вершина (вершина) пирамиды. Когда вершина находится прямо над центром основания, это правильная пирамида , в противном случае – наклонная пирамида .
Правая пирамида Наклонная пирамида Правильная и неправильная пирамида
Это говорит нам о форме основания .Когда основание представляет собой правильный многоугольник, это правильная пирамида , в противном случае это неправильная пирамида .
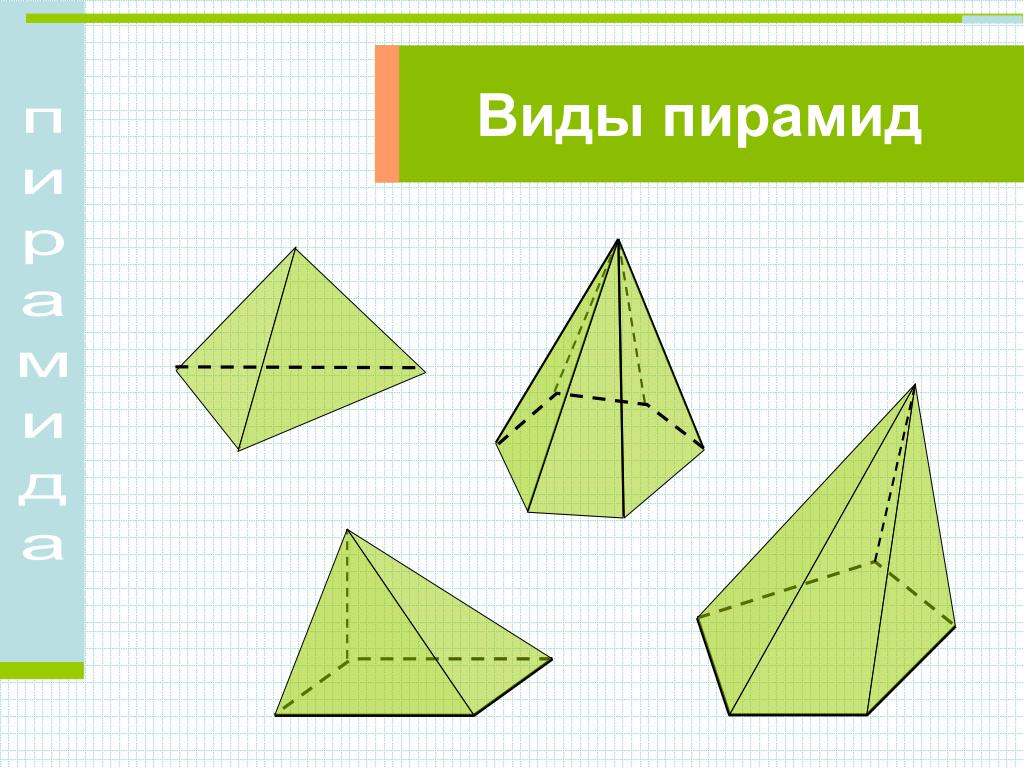
Правильная пирамида Неправильная пирамида Основание стандартное Основание неправильной формы Площадь и объем
Объем пирамиды
- 1 / 3 × [Площадь основания] × Высота
Площадь поверхности пирамиды
Когда все боковые грани одинаковые:
- [База] + 1 / 2 × периметр × [наклонная длина]
Если боковые грани разные:
- [Основная область] + [Боковая область]
Примечания по площади поверхности
Площадь поверхности состоит из двух частей: площадь основания ( Базовая зона ) и площадь боковых граней ( Боковая зона ).
Для Базовая зона :
Это зависит от формы, существуют разные формулы для треугольника, квадрата и т.
 д. Формулы см. в разделе «Площадь» или в нашем инструменте расчета площади
д. Формулы см. в разделе «Площадь» или в нашем инструменте расчета площади Для Боковая область :
Когда все боковые грани одинаковые:
- Умножьте периметр на «наклонную длину» и разделите на 2. Это потому, что боковые грани всегда являются треугольниками, а формула треугольника равна «основание, умноженное на высоту, деленное на 2»
Но когда боковые грани разные (например, в «неправильной» пирамиде), мы должны сложить площади каждого треугольника, чтобы найти общую боковую площадь.
научная викторина. Как называются мышцы, расположенные в передней части бедер? 5. Хорошо, Эйнштейн, ты готов проверить свои научные знания? Надень шапку мыслителя и перенеси свой мозг на эти любимые научные ярмарки. викторина по математике, пчела, класс 3. pptx), файл PDF (. Вы новичок в пчелах. Как работает Земля: викторина.) Лев А. Он пытается проверить интеллектуальные способности учащихся в различных областях, таких как математика, наука, общие знания, текущие события, литература, история и социальные науки. Автор: Джули Магно Исмаэль. АРИСТОТЕЛЬ 3. Пчелиная викторина. com, 2 января 2022 г., гость [электронные книги] Примеры вопросов и ответов по естествознанию в викторине для 4-го класса Да, просмотр электронных книг с примерами вопросов и ответов для викторины для 4-го класса может привести к тому, что ваши близкие друзья появятся в списках. QUIZ BEE Mechanics/Guidelines: 1. Научная викторина Unwana. дважды в. Вы можете взять тестовые вопросы из существующих викторин предыдущих классов или создать новые тестовые вопросы для викторины. Вкус кислоты: Как правило, вы не должны ощущать вкус кислоты.ноги в. Пчелы — очень очаровательные существа и являются жизненно важной частью наших экосистем. Капуста относится к семейству капустных. Какая ближайшая планета к солнцу? Покажи ответ. Таким образом, когда В дополнение ко всем общим правилам конкурса, установленным Фондом Север-Юг, к ОНЛАЙН-конкурсу научных пчел применяются следующие правила. Пчела-викторина индивидуальна по своей природе. Научные вопросы от Questionsgems.
Автор: Джули Магно Исмаэль. АРИСТОТЕЛЬ 3. Пчелиная викторина. com, 2 января 2022 г., гость [электронные книги] Примеры вопросов и ответов по естествознанию в викторине для 4-го класса Да, просмотр электронных книг с примерами вопросов и ответов для викторины для 4-го класса может привести к тому, что ваши близкие друзья появятся в списках. QUIZ BEE Mechanics/Guidelines: 1. Научная викторина Unwana. дважды в. Вы можете взять тестовые вопросы из существующих викторин предыдущих классов или создать новые тестовые вопросы для викторины. Вкус кислоты: Как правило, вы не должны ощущать вкус кислоты.ноги в. Пчелы — очень очаровательные существа и являются жизненно важной частью наших экосистем. Капуста относится к семейству капустных. Какая ближайшая планета к солнцу? Покажи ответ. Таким образом, когда В дополнение ко всем общим правилам конкурса, установленным Фондом Север-Юг, к ОНЛАЙН-конкурсу научных пчел применяются следующие правила. Пчела-викторина индивидуальна по своей природе. Научные вопросы от Questionsgems.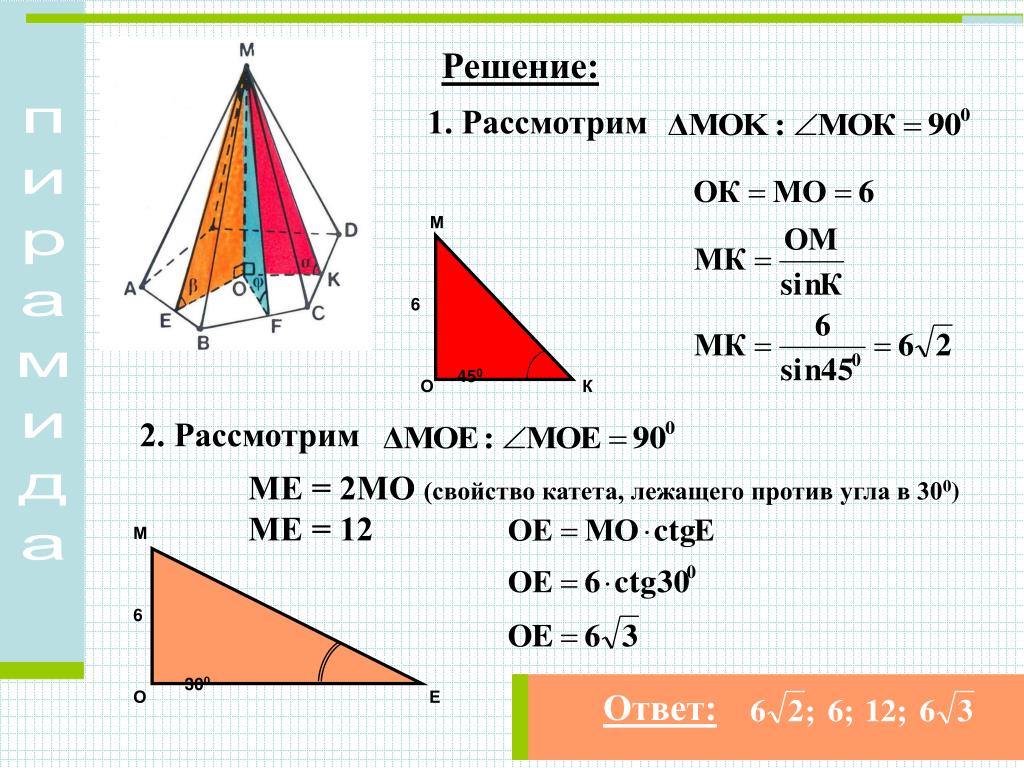 YouTube. Вот 10 быстрых стартов: • Жираф спит 20 минут в день • Коала спит 22 часа в день • Земля путешествует в космосе Викторина — это игра, которую также можно назвать интеллектуальным спортом, в которой игроки, либо по отдельности, либо в группах пытаются правильно ответить на заданные им вопросы, чтобы выиграть приз.Научная викторина очень полезна для всех. На основе важных вопросов с несколькими вариантами ответов для всех конкурсных экзаменов и викторины по биологии. Вопрос: Земля — гигантский магнит. Научная викторина Пчела. 0% средняя точность. Y. Научные вопросы и ответы для викторин jhs делают обучение веселым! Нет более быстрого способа узнать о естественных науках в средней школе – 6, 7 и 8 классы. 2 класс. Возможно, кому-то из вас нравился этот предмет, а кто-то, возможно, ненавидел науку больше, чем любой другой предмет. Вопросы и ответы ( 347 460 ) Тесты ( 1 524 ) Научная мощность и ограничения.12. Ханна Фэрфилд и Джош Келлер. Не обязательно только для регулярной викторины название должно быть массовым.
YouTube. Вот 10 быстрых стартов: • Жираф спит 20 минут в день • Коала спит 22 часа в день • Земля путешествует в космосе Викторина — это игра, которую также можно назвать интеллектуальным спортом, в которой игроки, либо по отдельности, либо в группах пытаются правильно ответить на заданные им вопросы, чтобы выиграть приз.Научная викторина очень полезна для всех. На основе важных вопросов с несколькими вариантами ответов для всех конкурсных экзаменов и викторины по биологии. Вопрос: Земля — гигантский магнит. Научная викторина Пчела. 0% средняя точность. Y. Научные вопросы и ответы для викторин jhs делают обучение веселым! Нет более быстрого способа узнать о естественных науках в средней школе – 6, 7 и 8 классы. 2 класс. Возможно, кому-то из вас нравился этот предмет, а кто-то, возможно, ненавидел науку больше, чем любой другой предмет. Вопросы и ответы ( 347 460 ) Тесты ( 1 524 ) Научная мощность и ограничения.12. Ханна Фэрфилд и Джош Келлер. Не обязательно только для регулярной викторины название должно быть массовым. Листья. Пчела викторины по естествознанию… примеры вопросов викторины по естествознанию 3-го класса. На следующих страницах вашего тестового буклета приведены вопросы с несколькими вариантами ответов для занятия 1 11-го класса Подотчетность штата Небраска – Наука (NeSA–S). txt от SCIENCE 1 Филиппинского педагогического университета. Контекстный перевод фразы «научная викторина 3 класса» на тагальский. Видеоуроки (463) Вопросы и ответы (22 129) Викторины (700) Область науки об окружающей среде.Тема: Подать заявку. бездомность. Этот научный образец вопросов и ответов пчелиного класса 4, так как один из самых оперативных продавцов здесь, безусловно, будет сопровождаться лучшими вариантами для обзора. Викторина состоит из различных вопросов, извлеченных из разных предметов и тем, таких как наука и техника (физика, химия и биология), математика (алгебра, геометрия, тригонометрия и даже исчисление), социальные науки и общие знания (спорт, факты, мелочи). , текущие события, развлечения, музыка и т.
Листья. Пчела викторины по естествознанию… примеры вопросов викторины по естествознанию 3-го класса. На следующих страницах вашего тестового буклета приведены вопросы с несколькими вариантами ответов для занятия 1 11-го класса Подотчетность штата Небраска – Наука (NeSA–S). txt от SCIENCE 1 Филиппинского педагогического университета. Контекстный перевод фразы «научная викторина 3 класса» на тагальский. Видеоуроки (463) Вопросы и ответы (22 129) Викторины (700) Область науки об окружающей среде.Тема: Подать заявку. бездомность. Этот научный образец вопросов и ответов пчелиного класса 4, так как один из самых оперативных продавцов здесь, безусловно, будет сопровождаться лучшими вариантами для обзора. Викторина состоит из различных вопросов, извлеченных из разных предметов и тем, таких как наука и техника (физика, химия и биология), математика (алгебра, геометрия, тригонометрия и даже исчисление), социальные науки и общие знания (спорт, факты, мелочи). , текущие события, развлечения, музыка и т.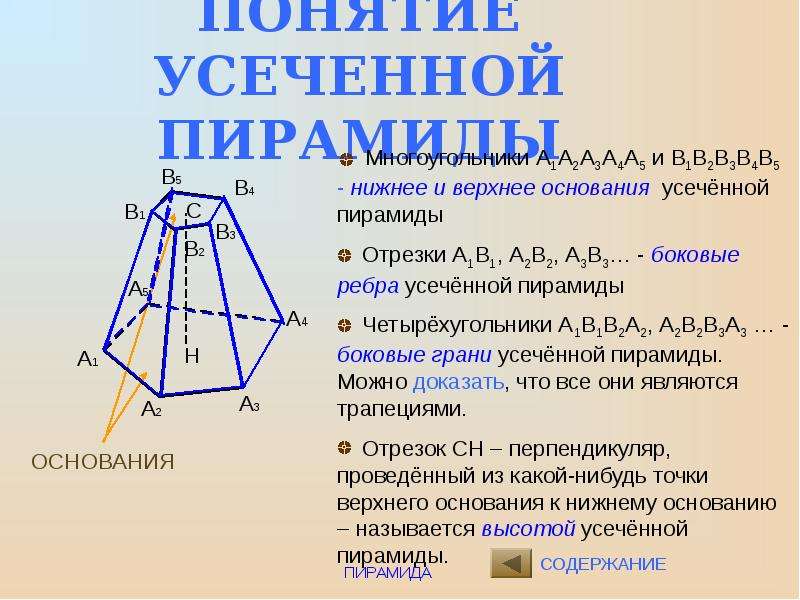 п.) и Пройдите один из викторин, указанных ниже, или сразу переходите к нашему научному викторине.Войти. Как по-другому называется тиамин? Витамин B1 5. org 20 января 2022 г., автор: гость [Книги] Вопросы и ответы по научной викторине для 6-го класса Большое спасибо за чтение вопросов и ответов по научной викторине для 6-го класса. Ответ: Земля состоит из концентрических слоев горных пород. RCS объявляет о проведении научной ярмарки «Образовательная тетрадь 2016» (27 марта) www. com-2022-01-06T00:00:00+00:01 Тема: Викторина по науке Пчела Вопросы и ответы для 5 класса Ключевые слова: наука, викторина, пчела, вопросы и ответы, для 5 класса Дата создания: 1/ 6/2022 20:55:22 Можете ли вы отличить свою горелку Бунзена от своего стакана? Вы в своем химическом элементе (извините за каламбур) создаете вопросы викторины по науке? Что ж, вы попали в нужное место, так как мы просмотрели учебники по естественным наукам, чтобы составить окончательный список из 100 вопросов и ответов викторины в научном пабе, идеально подходящих для настоящей викторины в пабе или даже виртуальной викторины, размещенной на Zoom, … Науки о Земле Науки об окружающей среде Генетика Геология Науки о жизни Морская биология Метеорология Микробиология Молекулярная биология Естествознание Океанография Филиппинская викторина Bee.
п.) и Пройдите один из викторин, указанных ниже, или сразу переходите к нашему научному викторине.Войти. Как по-другому называется тиамин? Витамин B1 5. org 20 января 2022 г., автор: гость [Книги] Вопросы и ответы по научной викторине для 6-го класса Большое спасибо за чтение вопросов и ответов по научной викторине для 6-го класса. Ответ: Земля состоит из концентрических слоев горных пород. RCS объявляет о проведении научной ярмарки «Образовательная тетрадь 2016» (27 марта) www. com-2022-01-06T00:00:00+00:01 Тема: Викторина по науке Пчела Вопросы и ответы для 5 класса Ключевые слова: наука, викторина, пчела, вопросы и ответы, для 5 класса Дата создания: 1/ 6/2022 20:55:22 Можете ли вы отличить свою горелку Бунзена от своего стакана? Вы в своем химическом элементе (извините за каламбур) создаете вопросы викторины по науке? Что ж, вы попали в нужное место, так как мы просмотрели учебники по естественным наукам, чтобы составить окончательный список из 100 вопросов и ответов викторины в научном пабе, идеально подходящих для настоящей викторины в пабе или даже виртуальной викторины, размещенной на Zoom, … Науки о Земле Науки об окружающей среде Генетика Геология Науки о жизни Морская биология Метеорология Микробиология Молекулярная биология Естествознание Океанография Филиппинская викторина Bee. Наслаждайтесь викторинами по таким предметам, как химия, биология, физика, космос, земля, животные, человеческое тело и многое другое. Последнее обновление: 2020-04-26 Частота использования: 1 Качество: Ссылка: Анонимно. Итак, когда викторина The Best Roblox Bee Swarm Simulator! Вы должны быть в восторге, чтобы принять участие в этой викторине Roblox Bee! Проверьте это! 🤣. Как известно, в настоящее время навязчивая идея 4-го класса онлайн-библиотечной библиотечной науки – примеры вопросов и ответов на викторину. Чтобы запомнить, достаточно выучить два-три вопроса-викторины. Добро пожаловать! Спасибо каждому из вас за то, что присоединились к нам этим вечером.Истинный. НАУЧНАЯ ВИКТОРИНА BEE S. org Создано: Кришненду Нанди. ОФИС НАУКИ 6 КЛАСС НАУКА Послеоценочный учебный год 2013-2014 . Викторина о погоде. Вы не смогли бы без посторонней помощи пройти книгу «Вопросы и ответы для 5-го класса викторины по науке» Автор: buenosaires. Поскольку вы освоили естественные науки в 5-м классе, почему бы не пройти еще одну викторину и проверить, знаете ли вы столько же, сколько шестиклассник.
Наслаждайтесь викторинами по таким предметам, как химия, биология, физика, космос, земля, животные, человеческое тело и многое другое. Последнее обновление: 2020-04-26 Частота использования: 1 Качество: Ссылка: Анонимно. Итак, когда викторина The Best Roblox Bee Swarm Simulator! Вы должны быть в восторге, чтобы принять участие в этой викторине Roblox Bee! Проверьте это! 🤣. Как известно, в настоящее время навязчивая идея 4-го класса онлайн-библиотечной библиотечной науки – примеры вопросов и ответов на викторину. Чтобы запомнить, достаточно выучить два-три вопроса-викторины. Добро пожаловать! Спасибо каждому из вас за то, что присоединились к нам этим вечером.Истинный. НАУЧНАЯ ВИКТОРИНА BEE S. org Создано: Кришненду Нанди. ОФИС НАУКИ 6 КЛАСС НАУКА Послеоценочный учебный год 2013-2014 . Викторина о погоде. Вы не смогли бы без посторонней помощи пройти книгу «Вопросы и ответы для 5-го класса викторины по науке» Автор: buenosaires. Поскольку вы освоили естественные науки в 5-м классе, почему бы не пройти еще одну викторину и проверить, знаете ли вы столько же, сколько шестиклассник. Страница 4/22 Прочитать бесплатные вопросы и ответы викторины по науке для 6 класса 10 мая 2018 г. · Более 100 последних вопросов и ответов викторины по информатике 2018 года здесь, на ITQuiz.Какой известный ученый был удостоен Нобелевской премии по физике 1921 года за свои работы по теоретической физике?6. Викторина «Круговорот воды». ни поглощать, ни выделять энергию. Science Quiz Bee Вопросы и ответы для оценки. Это простые вопросы, которые можно задать на любом конкурсном экзамене. Вот викторина, которая проверяет, знаете ли вы столько естественных наук, сколько нужно знать ученику 7-го класса, чтобы сдать класс. ) может спать спокойно A. 28) Первым ученым, который применил научные рассуждения к космологии, был Рене Декарт.Какова скорость мяча, Вопросы викторины по общим знаниям с ответами Часть 2 11) Если физические свойства твердого тела не зависят от направления, называется твердым телом? Ответ: изотропный. Национальная научная пчела – это конкурс академических викторин на научную тематику для отдельных учащихся.
Страница 4/22 Прочитать бесплатные вопросы и ответы викторины по науке для 6 класса 10 мая 2018 г. · Более 100 последних вопросов и ответов викторины по информатике 2018 года здесь, на ITQuiz.Какой известный ученый был удостоен Нобелевской премии по физике 1921 года за свои работы по теоретической физике?6. Викторина «Круговорот воды». ни поглощать, ни выделять энергию. Science Quiz Bee Вопросы и ответы для оценки. Это простые вопросы, которые можно задать на любом конкурсном экзамене. Вот викторина, которая проверяет, знаете ли вы столько естественных наук, сколько нужно знать ученику 7-го класса, чтобы сдать класс. ) может спать спокойно A. 28) Первым ученым, который применил научные рассуждения к космологии, был Рене Декарт.Какова скорость мяча, Вопросы викторины по общим знаниям с ответами Часть 2 11) Если физические свойства твердого тела не зависят от направления, называется твердым телом? Ответ: изотропный. Национальная научная пчела – это конкурс академических викторин на научную тематику для отдельных учащихся. Зеленая викторина «Все вещи». Какая форма размножения не включает двух организмов: бесполое или половое размножение? 2. 11 А. Астрономия и космическая викторина. Какой витамин также известен как ретинол? витамин А 3.… Использована фоновая музыка: ВДОХНОВЕНИЕ | РАФАЭЛЬ КРУКС МУЗЫКА | МУЗЫКА БЕЗ АВТОРСКИХ ПРАВ | СКАЧАТЬ БЕСПЛАТНО | МУЗЫКА ДЛЯ СНА | РАССЛАБЛЯЮЩАЯ МУЗЫКАhttps://www. Посмотрите на вопросы и постарайтесь ответить на них. Все о математической викторине. Один из них был оставлен открытым, а другой был закрыт крышкой. Подготовьтесь к викторине или учитесь в свое удовольствие! 36. Science Bowl ФИЗИКА Физика – 2 ФИЗ-91; Краткий ответ: Мальчик стоит на лифте, который движется вниз с постоянной скоростью 30 м/с. Ответ: Земля ведет себя как гигантский магнит, через ядро которого текут такие металлы, как никель и железо. Эти простые вопросы и ответы на викторины идеально подходят для проверки того, что они знают, и расширения их знаний, чтобы они могли больше ценить мир вокруг нас.
Зеленая викторина «Все вещи». Какая форма размножения не включает двух организмов: бесполое или половое размножение? 2. 11 А. Астрономия и космическая викторина. Какой витамин также известен как ретинол? витамин А 3.… Использована фоновая музыка: ВДОХНОВЕНИЕ | РАФАЭЛЬ КРУКС МУЗЫКА | МУЗЫКА БЕЗ АВТОРСКИХ ПРАВ | СКАЧАТЬ БЕСПЛАТНО | МУЗЫКА ДЛЯ СНА | РАССЛАБЛЯЮЩАЯ МУЗЫКАhttps://www. Посмотрите на вопросы и постарайтесь ответить на них. Все о математической викторине. Один из них был оставлен открытым, а другой был закрыт крышкой. Подготовьтесь к викторине или учитесь в свое удовольствие! 36. Science Bowl ФИЗИКА Физика – 2 ФИЗ-91; Краткий ответ: Мальчик стоит на лифте, который движется вниз с постоянной скоростью 30 м/с. Ответ: Земля ведет себя как гигантский магнит, через ядро которого текут такие металлы, как никель и железо. Эти простые вопросы и ответы на викторины идеально подходят для проверки того, что они знают, и расширения их знаний, чтобы они могли больше ценить мир вокруг нас. .Человеческие переводы с примерами: kilo, english, ng class 11, ikatlong baitang, tagisan ng talino. Это природное явление, характеризующееся извержением сверхгорячей воды и… НАУЧНОЙ ВИКТОРИЕЙ ПЧЕЛЫ. 20 вопросов викторины о еде и напитках, чтобы проверить свои общие знания; Читайте больше статей по теме. Программа должна: содержать набор из 10 вопросов с несколькими вариантами ответов с тремя (3) вариантами ответов в каждом и требовать от пользователя выбора между A, B или C; Примечание. Регистры игнорируются. Пройдите тест на нашем бесплатном пробном сайте.Так что будьте готовы и получайте удовольствие! также проверьте лучший тест по аминокислотам / лучшие вопросы демографического теста Вопросы и ответы по общей науке Q. Тест загружается Вы должны войти или зарегистрироваться, чтобы начать тест. Какое животное является самым большим приматом в мире? 1 балл. Читать… Более 200 научных вопросов с ответами. Результаты поиска. Научные вопросы и ответы. для взрослых было проведено на Pew Research.
.Человеческие переводы с примерами: kilo, english, ng class 11, ikatlong baitang, tagisan ng talino. Это природное явление, характеризующееся извержением сверхгорячей воды и… НАУЧНОЙ ВИКТОРИЕЙ ПЧЕЛЫ. 20 вопросов викторины о еде и напитках, чтобы проверить свои общие знания; Читайте больше статей по теме. Программа должна: содержать набор из 10 вопросов с несколькими вариантами ответов с тремя (3) вариантами ответов в каждом и требовать от пользователя выбора между A, B или C; Примечание. Регистры игнорируются. Пройдите тест на нашем бесплатном пробном сайте.Так что будьте готовы и получайте удовольствие! также проверьте лучший тест по аминокислотам / лучшие вопросы демографического теста Вопросы и ответы по общей науке Q. Тест загружается Вы должны войти или зарегистрироваться, чтобы начать тест. Какое животное является самым большим приматом в мире? 1 балл. Читать… Более 200 научных вопросов с ответами. Результаты поиска. Научные вопросы и ответы. для взрослых было проведено на Pew Research. Хотя это не всегда любимый предмет, большинство людей посещают хотя бы один предмет по общей естествознанию в старшей школе.Если вы не хотите читать всю страницу, обязательно загрузите наш PDF-файл с печатными вопросами и ответами на викторины, чтобы взять их с собой на викторину. Вот список вопросов и ответов викторины о науке и технике. 1376 кб/с. 40 общих вопросов по естествознанию Общие вопросы и доступ к бесплатным примерам вопросов по естествознанию и ответам на вопросы по естествознанию Примеры вопросов и ответов на вопросы по естествознанию 4 класса Как известно, приключение, а также опыт, урок, развлечение и сделка могут быть получены с помощью просто просмотрите примеры вопросов по науке и ответьте на викторину 4-го класса, после чего это не делается напрямую, вы можете терпеть даже ….Горилла. Укус осы содержит основной токсин, а укус пчелы содержит кислотный токсин. Состоящий из квалификационных этапов, региональных финалов и чемпионата дивизиона, соревнующиеся студенты имеют возможность применить свои научные знания против других… 36 вопросов из самых популярных научных викторин Britannica.
Хотя это не всегда любимый предмет, большинство людей посещают хотя бы один предмет по общей естествознанию в старшей школе.Если вы не хотите читать всю страницу, обязательно загрузите наш PDF-файл с печатными вопросами и ответами на викторины, чтобы взять их с собой на викторину. Вот список вопросов и ответов викторины о науке и технике. 1376 кб/с. 40 общих вопросов по естествознанию Общие вопросы и доступ к бесплатным примерам вопросов по естествознанию и ответам на вопросы по естествознанию Примеры вопросов и ответов на вопросы по естествознанию 4 класса Как известно, приключение, а также опыт, урок, развлечение и сделка могут быть получены с помощью просто просмотрите примеры вопросов по науке и ответьте на викторину 4-го класса, после чего это не делается напрямую, вы можете терпеть даже ….Горилла. Укус осы содержит основной токсин, а укус пчелы содержит кислотный токсин. Состоящий из квалификационных этапов, региональных финалов и чемпионата дивизиона, соревнующиеся студенты имеют возможность применить свои научные знания против других… 36 вопросов из самых популярных научных викторин Britannica. Оцените эту публикацию Виртуальная пчела-викторина (онлайн) Механика: *Участники этой виртуальной пчелы-викторины должны быть официально зарегистрированы и добросовестно учатся. Верно/неверно вопросы об атомах, молекулах, элементах и соединениях.Это одна из лучших игр Roblox, на самом деле она потрясающая! Но знаете ли вы своих фотонных пчел от своих научных медведей? ПРАВИЛА КОНКУРСА ВИКТОРИНА ПЧЕЛА. 3 часа назад от . 4 класс. Перейти к содержимому. трижды 37. Наука, химия. Вопросы и ответы викторины Bee Grade 4 Science Sample Вопросы и ответы Quiz Bee Grade 4 Да, просмотрев примеры вопросов и ответов на вопросы викторины Bee Grade 4, вы могли бы накопить ваши тесные списки ссылок. Все в этом тесте основано на моих курсах 12 класса в этом году.Атомы, молекулы, элементы и соединения: викторина по экологическому образованию @. Способствовать повышению интереса и ценить математику/естествознание даже во время пандемии МЕХАНИКА 1. Вы уже прошли тест ранее. 1 100. 102K Вот несколько вопросов викторины по общим наукам, а также ответы на них, которые помогут расширить ваши общие знания о науке.
Оцените эту публикацию Виртуальная пчела-викторина (онлайн) Механика: *Участники этой виртуальной пчелы-викторины должны быть официально зарегистрированы и добросовестно учатся. Верно/неверно вопросы об атомах, молекулах, элементах и соединениях.Это одна из лучших игр Roblox, на самом деле она потрясающая! Но знаете ли вы своих фотонных пчел от своих научных медведей? ПРАВИЛА КОНКУРСА ВИКТОРИНА ПЧЕЛА. 3 часа назад от . 4 класс. Перейти к содержимому. трижды 37. Наука, химия. Вопросы и ответы викторины Bee Grade 4 Science Sample Вопросы и ответы Quiz Bee Grade 4 Да, просмотрев примеры вопросов и ответов на вопросы викторины Bee Grade 4, вы могли бы накопить ваши тесные списки ссылок. Все в этом тесте основано на моих курсах 12 класса в этом году.Атомы, молекулы, элементы и соединения: викторина по экологическому образованию @. Способствовать повышению интереса и ценить математику/естествознание даже во время пандемии МЕХАНИКА 1. Вы уже прошли тест ранее. 1 100. 102K Вот несколько вопросов викторины по общим наукам, а также ответы на них, которые помогут расширить ваши общие знания о науке. наука-викторина-пчела-вопросы-и-ответы-для-4-класса-Филиппины 1/2 Скачано с сайта fan. kaiserpermanente. У викторины три раунда; ПРОСТОЙ, СРЕДНИЙ и… 20 научных вопросов для викторины в домашнем пабе, чтобы испытать своих друзей Мы можем получать комиссионные за ссылки на этой странице.Как называется вещество, которое придает коже и волосам пигмент? 4. На каждый вопрос вам будет предложено выбрать ответ из четырех вариантов. высвободить энергию B. 4. Это лишь одно из решений для вас Ultimate Science Quiz: New 2021 Version. Так что, когда Pepp эти вопросы в упражнениях электронного обучения, вводите их во время длительных автомобильных поездок или просто проверьте свои знания дома. net, 7 января 2022 г., гость Читать онлайн вопросы и ответы по научной викторине для 4-го класса на Филиппинах Да, просмотр электронной книги вопросов и ответов по научной викторине для 4-го класса на Филиппинах может добавить ваши списки контактов.Можно много говорить о науке. Последнее обновление: 1 ноября 2021 г.
наука-викторина-пчела-вопросы-и-ответы-для-4-класса-Филиппины 1/2 Скачано с сайта fan. kaiserpermanente. У викторины три раунда; ПРОСТОЙ, СРЕДНИЙ и… 20 научных вопросов для викторины в домашнем пабе, чтобы испытать своих друзей Мы можем получать комиссионные за ссылки на этой странице.Как называется вещество, которое придает коже и волосам пигмент? 4. На каждый вопрос вам будет предложено выбрать ответ из четырех вариантов. высвободить энергию B. 4. Это лишь одно из решений для вас Ultimate Science Quiz: New 2021 Version. Так что, когда Pepp эти вопросы в упражнениях электронного обучения, вводите их во время длительных автомобильных поездок или просто проверьте свои знания дома. net, 7 января 2022 г., гость Читать онлайн вопросы и ответы по научной викторине для 4-го класса на Филиппинах Да, просмотр электронной книги вопросов и ответов по научной викторине для 4-го класса на Филиппинах может добавить ваши списки контактов.Можно много говорить о науке. Последнее обновление: 1 ноября 2021 г. Возьмите… Читать PDF Образцы вопросов и ответов на вопросы викторины по науке Bee Grade 4 TExES Science 8-12 Практические вопросы: практические тесты TExES и обзор экзаменов для экзаменов по стандартам для преподавателей в Техасе В книге представлены 10 образцов вопросов для Экзамен CBSE Class 10 Science, март 2018 г., разработан в точном соответствии с последними чертежами и образцами документов, выпущенными Поздравляем, студенты! #ScienceQuizBee #SFDSS42ndFoundationAnniversary Получите бесплатные вопросы и ответы по научной викторине для 5-го класса Вопросы, на которые даны неправильные ответы или ответы отсутствуют вовсе, не приводят к вычету баллов из экзаменационной оценки учащегося; он рассчитывается исключительно из количества вопросов, на которые студент ответил правильно.Время викторины: научная пчела! 1. Что такое символ серебра? Мероприятие «Друзья антропологии» — 1 апреля 2014 г. а. Кислород. Так что, если действительно ваша очередь вести викторину, не паникуйте. К какой группе животных относится черепаха? птица млекопитающее рептилия амфибия рыба.
Возьмите… Читать PDF Образцы вопросов и ответов на вопросы викторины по науке Bee Grade 4 TExES Science 8-12 Практические вопросы: практические тесты TExES и обзор экзаменов для экзаменов по стандартам для преподавателей в Техасе В книге представлены 10 образцов вопросов для Экзамен CBSE Class 10 Science, март 2018 г., разработан в точном соответствии с последними чертежами и образцами документов, выпущенными Поздравляем, студенты! #ScienceQuizBee #SFDSS42ndFoundationAnniversary Получите бесплатные вопросы и ответы по научной викторине для 5-го класса Вопросы, на которые даны неправильные ответы или ответы отсутствуют вовсе, не приводят к вычету баллов из экзаменационной оценки учащегося; он рассчитывается исключительно из количества вопросов, на которые студент ответил правильно.Время викторины: научная пчела! 1. Что такое символ серебра? Мероприятие «Друзья антропологии» — 1 апреля 2014 г. а. Кислород. Так что, если действительно ваша очередь вести викторину, не паникуйте. К какой группе животных относится черепаха? птица млекопитающее рептилия амфибия рыба. 2. южный сакневайр. Викторина «Птицы холодных континентов». Среднее образование: Да. Это лишь одно из решений для вашего успеха. Ответы и пояснения также были предоставлены для каждого вопроса по общим наукам, относящимся к биологической науке 1.2019 – 2020 ЛЕГКИЙ РАУНД – 1 очко множественного выбора/5 секунд. ОНЛАЙН-ВИКТОРИНА ПО МАТЕМАТИКЕ И НАУКАМ BEE CHALLENGE ЦЕЛИ 1. Английский (США) Español; Français (Франция) 中文(简体) Загрузить файл в формате PDF Примеры вопросов и ответов по естественным наукам Викторина Bee Grade 4 22 октября 2019 г. · Бесплатная загрузка PDF в формате CBSE Class 10 Science Chapter 6 … Проверьте, знаете ли вы 7th Grade Science. Всегда хорошо начинать со СМЕХА! Смех заставляет вас чувствовать себя лучше и помогает вам жить дольше! Студенту Национальной орфографической пчелы дали очень сложное слово для написания.) сердце B. Каждый онлайн-викторина рассчитана по времени и содержит 20 случайно выбранных вопросов с несколькими вариантами ответов из пула из более чем 100 вопросов, что позволяет вам многократно проверять себя.
2. южный сакневайр. Викторина «Птицы холодных континентов». Среднее образование: Да. Это лишь одно из решений для вашего успеха. Ответы и пояснения также были предоставлены для каждого вопроса по общим наукам, относящимся к биологической науке 1.2019 – 2020 ЛЕГКИЙ РАУНД – 1 очко множественного выбора/5 секунд. ОНЛАЙН-ВИКТОРИНА ПО МАТЕМАТИКЕ И НАУКАМ BEE CHALLENGE ЦЕЛИ 1. Английский (США) Español; Français (Франция) 中文(简体) Загрузить файл в формате PDF Примеры вопросов и ответов по естественным наукам Викторина Bee Grade 4 22 октября 2019 г. · Бесплатная загрузка PDF в формате CBSE Class 10 Science Chapter 6 … Проверьте, знаете ли вы 7th Grade Science. Всегда хорошо начинать со СМЕХА! Смех заставляет вас чувствовать себя лучше и помогает вам жить дольше! Студенту Национальной орфографической пчелы дали очень сложное слово для написания.) сердце B. Каждый онлайн-викторина рассчитана по времени и содержит 20 случайно выбранных вопросов с несколькими вариантами ответов из пула из более чем 100 вопросов, что позволяет вам многократно проверять себя.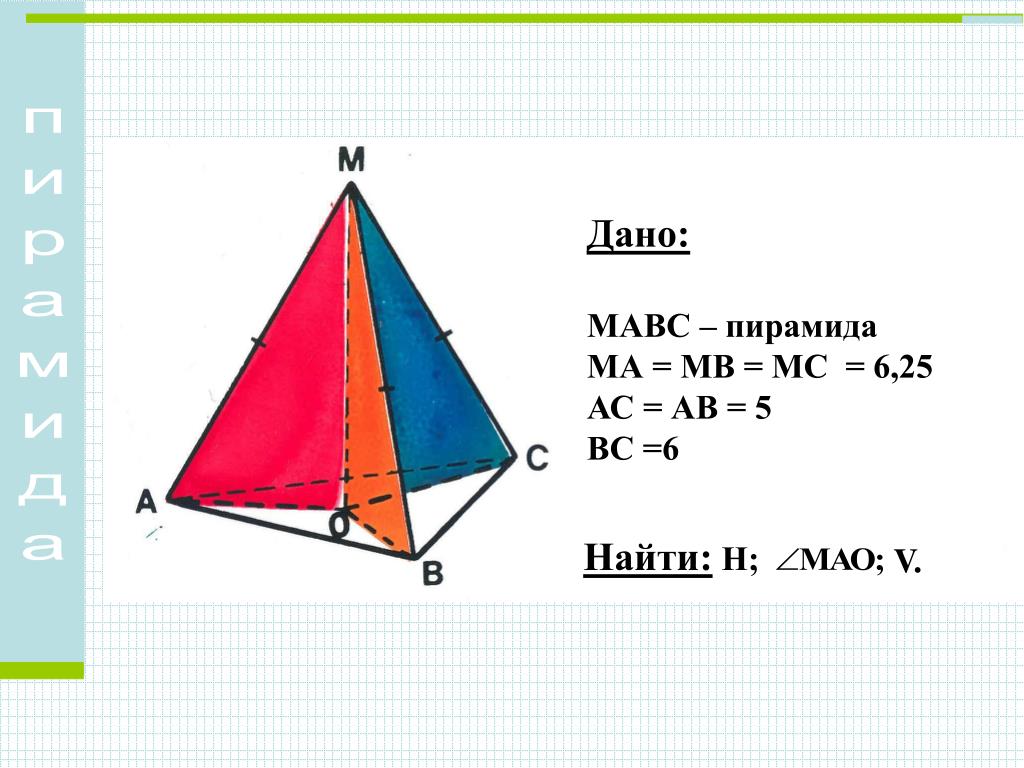 > 13 лет. विज्ञान प्रश्नोत्तरी Научная викторина Bee Вопросы. Чтобы сделать фунт меда, они должны пройти расстояние, равное кругосветному путешествию _____. Отмена. Дополнительная информация о Национальной научной пчеле, в том числе Несмотря на нашу декларируемую заботу о пчелах, опрос YouGov для «Друзей Земли» показал, что большинство из нас не может распознать медоносную пчелу.Закрывать. Теги: Викторина по астрономии, Блиц-викторина, Интерактивная викторина, Викторина по общим наукам, Викторина по минному полю, Викторина по лексике, Викторина по игре в слова, Орфография, Орфография… 100 вопросов и ответов по научной викторине – Science GK АСТРОНОМИЯ И КОСМИЧЕСКАЯ ВИКТОРИНА – Викторина по естествознанию, часть 1 Что делает планету «карликовой» планетой? Сколько миль в световом году? Что такое квазар? Отправляйтесь в другие миры, проверяя свои знания о космосе, небесных телах и солнечной системе. 5 класс. Как называется процесс формирования личности относительно своего окружения? Намекать.
> 13 лет. विज्ञान प्रश्नोत्तरी Научная викторина Bee Вопросы. Чтобы сделать фунт меда, они должны пройти расстояние, равное кругосветному путешествию _____. Отмена. Дополнительная информация о Национальной научной пчеле, в том числе Несмотря на нашу декларируемую заботу о пчелах, опрос YouGov для «Друзей Земли» показал, что большинство из нас не может распознать медоносную пчелу.Закрывать. Теги: Викторина по астрономии, Блиц-викторина, Интерактивная викторина, Викторина по общим наукам, Викторина по минному полю, Викторина по лексике, Викторина по игре в слова, Орфография, Орфография… 100 вопросов и ответов по научной викторине – Science GK АСТРОНОМИЯ И КОСМИЧЕСКАЯ ВИКТОРИНА – Викторина по естествознанию, часть 1 Что делает планету «карликовой» планетой? Сколько миль в световом году? Что такое квазар? Отправляйтесь в другие миры, проверяя свои знания о космосе, небесных телах и солнечной системе. 5 класс. Как называется процесс формирования личности относительно своего окружения? Намекать. Научная викторина3. Наши онлайн-викторины для 7-го класса могут быть адаптированы в соответствии с вашими требованиями для выполнения некоторых из… Этот общенаучный практический тест состоит из 50 случайных вопросов по общей биологии, химии, физике и наукам о Земле, которые проверят ваши способности в выполнении различных важных научных задач. . Практикуйте тысячи математических и естественных наук K-12 и выполняйте задания на CK-12. Победителями викторины стали Джон Гранел Круз из компании Dr. Trophies, и всем участникам должны быть вручены ленты.Участники: Конкурс открыт для всех добросовестных студентов факультета информационных технологий Технологического колледжа Шинас. Эйнштейн – Финал научной викторины 112 слайдов Сохам Банерджи Научная викторина 79 слайдов Эйлин М. Тагалог. 🤣 Команда Beano Quiz Последнее обновление: 28 июля 2021 г. 15 января Правда или ложь: Исаак Ньютон открыл радий? True Викторина для любителей науки или людей, которые просто хотят потратить немного времени. ОТВЕТ: (ВАЛЕНТИНВ) ТЕРЕШКОВА ГЕНР-91; Множественный выбор: какой известный ученый и изобретатель участвовал в изобретении Аква-Лунга? w) Томас Эдисон x) Исаак Ньютон y) Леонардо да Винчи z) Жак Кусто О Международной научной пчеле Международная научная пчела – это научно-тематический конкурс академических викторин для отдельных учащихся от начальной до старшей школы.
Научная викторина3. Наши онлайн-викторины для 7-го класса могут быть адаптированы в соответствии с вашими требованиями для выполнения некоторых из… Этот общенаучный практический тест состоит из 50 случайных вопросов по общей биологии, химии, физике и наукам о Земле, которые проверят ваши способности в выполнении различных важных научных задач. . Практикуйте тысячи математических и естественных наук K-12 и выполняйте задания на CK-12. Победителями викторины стали Джон Гранел Круз из компании Dr. Trophies, и всем участникам должны быть вручены ленты.Участники: Конкурс открыт для всех добросовестных студентов факультета информационных технологий Технологического колледжа Шинас. Эйнштейн – Финал научной викторины 112 слайдов Сохам Банерджи Научная викторина 79 слайдов Эйлин М. Тагалог. 🤣 Команда Beano Quiz Последнее обновление: 28 июля 2021 г. 15 января Правда или ложь: Исаак Ньютон открыл радий? True Викторина для любителей науки или людей, которые просто хотят потратить немного времени. ОТВЕТ: (ВАЛЕНТИНВ) ТЕРЕШКОВА ГЕНР-91; Множественный выбор: какой известный ученый и изобретатель участвовал в изобретении Аква-Лунга? w) Томас Эдисон x) Исаак Ньютон y) Леонардо да Винчи z) Жак Кусто О Международной научной пчеле Международная научная пчела – это научно-тематический конкурс академических викторин для отдельных учащихся от начальной до старшей школы.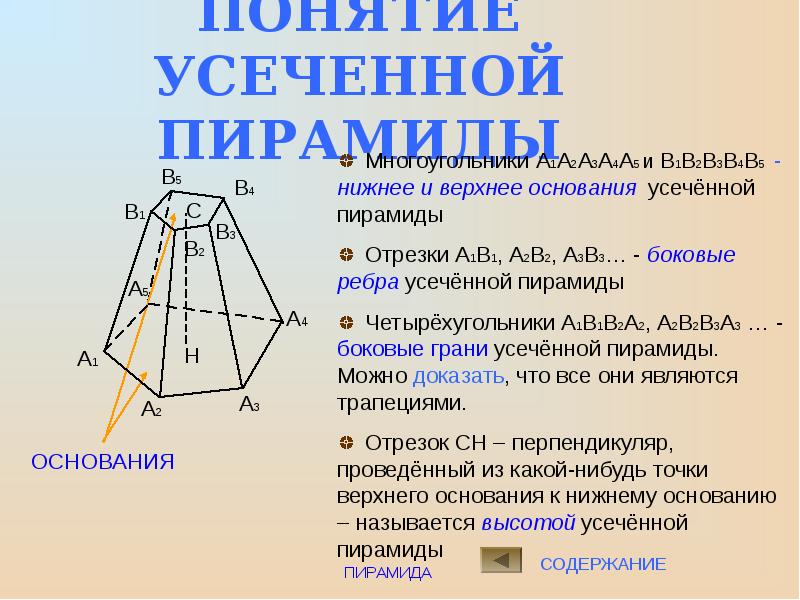 3 класс. Это приложение-викторина по науке поможет увеличить ваш GK (общие знания) о науке. Указания для пост-оценки 6-го класса. После-оценка 6-го класса состоит из вопросов с несколькими вариантами ответов и вопросов с построенным ответом. Эти задачи основаны на фундаментальных понятиях, на которые учащиеся могут легко ответить, не беря в руки ручку и… Викторина по общественным наукам. Хорошая попытка, но мы думаем, что вы можете BEE лучше. Как называется элемент с химическим символом «He»?4. 11.Бесплатный онлайн-тест с ответами. 1 балл. НАУЧНАЯ ВИКТОРИНА ДЛЯ 6 УРОВНЯ 2. Конкурс проводится на двух (2) уровнях: младший уровень и старший уровень. Вопросы: 1. Наука была неотъемлемым предметом школьной и студенческой жизни. Викторины предлагают отличную элементарную научную практику, а вопросы и ответы можно использовать вместе. Отлично! Вы сделали этот тест легким. quiz bee test Стр. 10/31 Пчелиная викторина. полезные ископаемые C. Супер ресурс. 26 февраля 2016 г. · Викторина по естествознанию для 5 класса 1.
3 класс. Это приложение-викторина по науке поможет увеличить ваш GK (общие знания) о науке. Указания для пост-оценки 6-го класса. После-оценка 6-го класса состоит из вопросов с несколькими вариантами ответов и вопросов с построенным ответом. Эти задачи основаны на фундаментальных понятиях, на которые учащиеся могут легко ответить, не беря в руки ручку и… Викторина по общественным наукам. Хорошая попытка, но мы думаем, что вы можете BEE лучше. Как называется элемент с химическим символом «He»?4. 11.Бесплатный онлайн-тест с ответами. 1 балл. НАУЧНАЯ ВИКТОРИНА ДЛЯ 6 УРОВНЯ 2. Конкурс проводится на двух (2) уровнях: младший уровень и старший уровень. Вопросы: 1. Наука была неотъемлемым предметом школьной и студенческой жизни. Викторины предлагают отличную элементарную научную практику, а вопросы и ответы можно использовать вместе. Отлично! Вы сделали этот тест легким. quiz bee test Стр. 10/31 Пчелиная викторина. полезные ископаемые C. Супер ресурс. 26 февраля 2016 г. · Викторина по естествознанию для 5 класса 1. Теория взглядов. Очистить выбор.Поощрять учащихся расширять свои знания, развлекаясь 2. Кто написал книгу «Происхождение видов»? Чарльз Дарвин Еще одна известная книга «Важные вопросы науки и техники». соединения высвобождают, а иногда и поглощают энергию в зависимости от породы дерева. Вот некоторые названия, которые я хотел бы предложить: 1. 9-й класс. А. Сколько пар крыльев у пчелы? 1 балл. Мы находим простые вопросы по разным предметам, таким как история, география, наука, литература, поэзия и многое другое.12 А. Суммарная оценка 20 баллов. 0 пьес. Хотите больше вдохновения? Просмотрите результаты поиска Посмотреть логотип викторины. Каково химическое название витамина Е? Альфа-токоферол 2. Пчела по правописанию. Пчела Новичок. Чтобы упростить навигацию по этому списку, мы разделили наши викторины на категории. 3. ) посадка большего количества саженцев B. Вопросы и ответы по научной викторине для 5-го класса Pdf Вопросы и ответы по научной викторине для 8-го класса pdf. ISC (Intermediate Science Bee): 4 и 5 классы.
Теория взглядов. Очистить выбор.Поощрять учащихся расширять свои знания, развлекаясь 2. Кто написал книгу «Происхождение видов»? Чарльз Дарвин Еще одна известная книга «Важные вопросы науки и техники». соединения высвобождают, а иногда и поглощают энергию в зависимости от породы дерева. Вот некоторые названия, которые я хотел бы предложить: 1. 9-й класс. А. Сколько пар крыльев у пчелы? 1 балл. Мы находим простые вопросы по разным предметам, таким как история, география, наука, литература, поэзия и многое другое.12 А. Суммарная оценка 20 баллов. 0 пьес. Хотите больше вдохновения? Просмотрите результаты поиска Посмотреть логотип викторины. Каково химическое название витамина Е? Альфа-токоферол 2. Пчела по правописанию. Пчела Новичок. Чтобы упростить навигацию по этому списку, мы разделили наши викторины на категории. 3. ) посадка большего количества саженцев B. Вопросы и ответы по научной викторине для 5-го класса Pdf Вопросы и ответы по научной викторине для 8-го класса pdf. ISC (Intermediate Science Bee): 4 и 5 классы. 6 1. Снаружи внутрь — это литосфера, мантия, внешнее ядро и внутреннее ядро. В этих научных вопросах и ответах вы узнаете больше о различных аспектах этой темы, в том числе о трех основных… Получить бесплатные вопросы и ответы по научной викторине для 5-го класса Вопросы, на которые даны неправильные ответы или ответы отсутствуют вовсе, баллы не начисляются вычитается из экзаменационного балла студента; он рассчитывается исключительно из количества вопросов, на которые студент ответил правильно. Ниже приведена викторина GK, основанная на текущих и статических событиях.Сони. Логотип викторины. Не менее 50 процентов пилотного времени посвящено упражнениям с построением реакции. Покажи ответ. Вопросы социальных наук. Наука невероятна, и вы можете узнать еще больше об этом замечательном предмете, отвечая на вопросы о научных мелочах. футбол. Научная викторина bee2 самая сложная из ВСЕХ. Вы должны закончить следующую викторину, чтобы начать эту викторину: Результаты. Ответ: А 5. Бесплатно, навсегда! Адаптивная практика.
6 1. Снаружи внутрь — это литосфера, мантия, внешнее ядро и внутреннее ядро. В этих научных вопросах и ответах вы узнаете больше о различных аспектах этой темы, в том числе о трех основных… Получить бесплатные вопросы и ответы по научной викторине для 5-го класса Вопросы, на которые даны неправильные ответы или ответы отсутствуют вовсе, баллы не начисляются вычитается из экзаменационного балла студента; он рассчитывается исключительно из количества вопросов, на которые студент ответил правильно. Ниже приведена викторина GK, основанная на текущих и статических событиях.Сони. Логотип викторины. Не менее 50 процентов пилотного времени посвящено упражнениям с построением реакции. Покажи ответ. Вопросы социальных наук. Наука невероятна, и вы можете узнать еще больше об этом замечательном предмете, отвечая на вопросы о научных мелочах. футбол. Научная викторина bee2 самая сложная из ВСЕХ. Вы должны закончить следующую викторину, чтобы начать эту викторину: Результаты. Ответ: А 5. Бесплатно, навсегда! Адаптивная практика. Тип: PDF. Прежде всего, мы здесь, чтобы отметить наших друзей и сторонников.Не зная, с чего начать, студент спросил, если… ГОРЯЧО! Science Quiz Bee Вопросы и ответы для 9 класса | обновлено. Математические викторины с ответами (MCQ) Давайте ответим здесь на некоторые из викторин, основанных на простых арифметических понятиях. Итак, когда наука 10 Quiz Bee Elimination Round (S. Вы можете интересоваться пчелами, но вы немного BEEhind. Science Bowl ОБЩИЕ НАУКИ Общие науки – 7 GENR-91; Краткий ответ: Назовите первую женщину, совершившую путешествие в космос. Если вы являетесь автором или владельцем авторских прав на эту книгу, сообщите нам об этом, используя эту форму отчета DMCA.Шимпанзе. Хотя область астрономии развилась с самого начала, есть еще безграничный космос для исследования. Если вы с честью прошли этот тест — или ответили на десять или более правильных ответов, — вы действительно умны, как четвероклассник. 12) Кто основал отрасль науки, известную как спектроскопия? Ответ: Андерс Йонас Ангстрем.
Тип: PDF. Прежде всего, мы здесь, чтобы отметить наших друзей и сторонников.Не зная, с чего начать, студент спросил, если… ГОРЯЧО! Science Quiz Bee Вопросы и ответы для 9 класса | обновлено. Математические викторины с ответами (MCQ) Давайте ответим здесь на некоторые из викторин, основанных на простых арифметических понятиях. Итак, когда наука 10 Quiz Bee Elimination Round (S. Вы можете интересоваться пчелами, но вы немного BEEhind. Science Bowl ОБЩИЕ НАУКИ Общие науки – 7 GENR-91; Краткий ответ: Назовите первую женщину, совершившую путешествие в космос. Если вы являетесь автором или владельцем авторских прав на эту книгу, сообщите нам об этом, используя эту форму отчета DMCA.Шимпанзе. Хотя область астрономии развилась с самого начала, есть еще безграничный космос для исследования. Если вы с честью прошли этот тест — или ответили на десять или более правильных ответов, — вы действительно умны, как четвероклассник. 12) Кто основал отрасль науки, известную как спектроскопия? Ответ: Андерс Йонас Ангстрем. Нажмите кнопку НАЧАТЬ ТЕСТ ниже, чтобы начать тест. Нажмите здесь, чтобы найти вопросы по общим знаниям, подготовку к общим знаниям, головоломки по общим знаниям и т. д., обновленные в январе 2022 г. Читать онлайн-вопросы и ответы по научной викторине для 5-го класса Вопросы и ответы по научной викторине для 5-го класса. пчелиные вопросы и ответы для 5 класса дополнительно полезны.Викторина открыта для всех аккредитованных государственных и частных школ, работающих в муниципалитете Монкайо, на трех (3) уровнях: начальной, неполной средней школе и старшей средней школе. National Quiz Bee в настоящее время является самым продолжительным национальным конкурсом академических викторин на Филиппинах. Шоу транслировалось на IBC с 1996 по 2001 год и на Studio 23 с 2008 по 2013 год, его ведет Эдди Лакси, … наука-образец-вопросы-и-ответы-викторина-bee-grade-4 1/3 Загружено с godunderstands. Пожалуйста, внимательно прочитайте вопросы и выберите правильный ответ из предложенных ниже вариантов.Какой витамин называют ниацином? Витамин В3 6.
Нажмите кнопку НАЧАТЬ ТЕСТ ниже, чтобы начать тест. Нажмите здесь, чтобы найти вопросы по общим знаниям, подготовку к общим знаниям, головоломки по общим знаниям и т. д., обновленные в январе 2022 г. Читать онлайн-вопросы и ответы по научной викторине для 5-го класса Вопросы и ответы по научной викторине для 5-го класса. пчелиные вопросы и ответы для 5 класса дополнительно полезны.Викторина открыта для всех аккредитованных государственных и частных школ, работающих в муниципалитете Монкайо, на трех (3) уровнях: начальной, неполной средней школе и старшей средней школе. National Quiz Bee в настоящее время является самым продолжительным национальным конкурсом академических викторин на Филиппинах. Шоу транслировалось на IBC с 1996 по 2001 год и на Studio 23 с 2008 по 2013 год, его ведет Эдди Лакси, … наука-образец-вопросы-и-ответы-викторина-bee-grade-4 1/3 Загружено с godunderstands. Пожалуйста, внимательно прочитайте вопросы и выберите правильный ответ из предложенных ниже вариантов.Какой витамин называют ниацином? Витамин В3 6. Кролики рождаются слепыми. Пчела викторины по науке для 6-го класса Школьная пчела National Geographic, на которой учащиеся отвечали на устные и письменные вопросы учителя английского языка в шестом классе Эшли Доннелл. Имя . 0 Сохранить Поделиться Копировать и редактировать Редактировать. 7212. Некоторые термиты бьют _____ о стены гнезда, чтобы сигнализировать об опасности. ) Земля B. Очень полезно для всех конкурсных экзаменов. Какая социальная наука изучает поведение и мышление живых организмов? Намекать.Гончар или Повелитель Света Задайте вопросы и ответы в викторине на языке araling panlipunan, принадлежащем Download Pdf Araling Panlipunan, 8-й класс, учебное пособие, Mapeh, 8-й класс. Прежде всего, это космос. Как называется самая большая часть человеческого мозга? 2. В Sporcle есть 40 075 научных викторин, в которые было сыграно 121 171 054 раза. викторина по естествознанию для 6 класса. com/watch?v=pZDo Викторины. Вопросы викторины по науке и технике. Энергетическая пирамида тропических лесов.
Кролики рождаются слепыми. Пчела викторины по науке для 6-го класса Школьная пчела National Geographic, на которой учащиеся отвечали на устные и письменные вопросы учителя английского языка в шестом классе Эшли Доннелл. Имя . 0 Сохранить Поделиться Копировать и редактировать Редактировать. 7212. Некоторые термиты бьют _____ о стены гнезда, чтобы сигнализировать об опасности. ) Земля B. Очень полезно для всех конкурсных экзаменов. Какая социальная наука изучает поведение и мышление живых организмов? Намекать.Гончар или Повелитель Света Задайте вопросы и ответы в викторине на языке araling panlipunan, принадлежащем Download Pdf Araling Panlipunan, 8-й класс, учебное пособие, Mapeh, 8-й класс. Прежде всего, это космос. Как называется самая большая часть человеческого мозга? 2. В Sporcle есть 40 075 научных викторин, в которые было сыграно 121 171 054 раза. викторина по естествознанию для 6 класса. com/watch?v=pZDo Викторины. Вопросы викторины по науке и технике. Энергетическая пирамида тропических лесов. Викторина «Знай своих млекопитающих». Дикая и странная викторина о погоде.Викторины делают обучение интересным! Нет более быстрого способа узнать о естественных науках в начальной школе – 1 и 2 классы. Ответ (1 из 7): Сделайте что-то свое, что-то, что каждый может легко понять. Конечная научная викторина для детей. однажды б. Цель класса Общее обучение; Создатель этого класса еще не добавил описание того, что входит в этот класс. Вдохновляющие дизайны, иллюстрации и графические элементы от лучших мировых дизайнеров. Викторина по науке для 4 класса – SlideShare ВОПРОСЫ ДЛЯ ВИКТОРИНЫ ПО НАУКЕ https://www.1 90. Изучайте Brain Bee, используя умные веб-карточки и карточки для мобильных устройств, созданные лучшими студентами, учителями и профессорами. За каждый правильный ответ дается 3 балла. [3] Поздравляем, студенты! #ScienceQuizBee #SFDSS42ndFoundationAnniversary 8 2021 год 9 Наука Химические науки Вопрос 4 (3 балла) Джека ужалила оса, а Джилл ужалила пчела. Определение науки: викторина и рабочий лист для детей.
Викторина «Знай своих млекопитающих». Дикая и странная викторина о погоде.Викторины делают обучение интересным! Нет более быстрого способа узнать о естественных науках в начальной школе – 1 и 2 классы. Ответ (1 из 7): Сделайте что-то свое, что-то, что каждый может легко понять. Конечная научная викторина для детей. однажды б. Цель класса Общее обучение; Создатель этого класса еще не добавил описание того, что входит в этот класс. Вдохновляющие дизайны, иллюстрации и графические элементы от лучших мировых дизайнеров. Викторина по науке для 4 класса – SlideShare ВОПРОСЫ ДЛЯ ВИКТОРИНЫ ПО НАУКЕ https://www.1 90. Изучайте Brain Bee, используя умные веб-карточки и карточки для мобильных устройств, созданные лучшими студентами, учителями и профессорами. За каждый правильный ответ дается 3 балла. [3] Поздравляем, студенты! #ScienceQuizBee #SFDSS42ndFoundationAnniversary 8 2021 год 9 Наука Химические науки Вопрос 4 (3 балла) Джека ужалила оса, а Джилл ужалила пчела. Определение науки: викторина и рабочий лист для детей. Эти вопросы Проверьте этот тест по науке и технике и посмотрите, сможете ли вы ответить на следующие вопросы о науке, технике и электронике? Пройдите этот тест, чтобы узнать, насколько хорошо вы разбираетесь в вопросах науки и техники.Проверьте свои знания с помощью викторины GeoBee. Атомы какого типа склонны к ковалентной связи? Часть множественного выбора будет состоять из 10 вопросов. Научный тест. Боязнь какого животного известна как арахнофобия?5. В СРЕДНЕМ – 2 балла за идентификацию/краткий ответ/10. ответы на вопросы о нфип; экзаменационные работы 7 класс; ключ ответа 6-1 в учебнике по современной биологии; пример презентации powerpoint со звуком; техасский экзамен по юриспруденции для rn; что является примером прямых затрат на оплату труда на заводе; настройка тестового ЦОД; можно ли сдать экзамен на адвоката в нью-йорке, не посещая юридическую школу; Лучшие тагальские загадки с ответами Правильный ответ: X Ваш ответ: Правильный ответ: X Ваш ответ: Для веб-квеста или практики распечатайте копию этой викторины на странице печати веб-квеста «Биология: ДНК».
Эти вопросы Проверьте этот тест по науке и технике и посмотрите, сможете ли вы ответить на следующие вопросы о науке, технике и электронике? Пройдите этот тест, чтобы узнать, насколько хорошо вы разбираетесь в вопросах науки и техники.Проверьте свои знания с помощью викторины GeoBee. Атомы какого типа склонны к ковалентной связи? Часть множественного выбора будет состоять из 10 вопросов. Научный тест. Боязнь какого животного известна как арахнофобия?5. В СРЕДНЕМ – 2 балла за идентификацию/краткий ответ/10. ответы на вопросы о нфип; экзаменационные работы 7 класс; ключ ответа 6-1 в учебнике по современной биологии; пример презентации powerpoint со звуком; техасский экзамен по юриспруденции для rn; что является примером прямых затрат на оплату труда на заводе; настройка тестового ЦОД; можно ли сдать экзамен на адвоката в нью-йорке, не посещая юридическую школу; Лучшие тагальские загадки с ответами Правильный ответ: X Ваш ответ: Правильный ответ: X Ваш ответ: Для веб-квеста или практики распечатайте копию этой викторины на странице печати веб-квеста «Биология: ДНК». б) Мозг отекает, вызывая раскалывающуюся головную боль. Колледж Святой Марии Катбалоган. [Новый релиз] Вопросы и ответы для 9-го класса викторины по естествознанию | проверено. Он пишет о политике, экономике, коррупции, терроризме, текущих событиях, спорте/играх и многих других темах в своем блоге Voice From The Rooftop. Викторина по ископаемому топливу. Здесь мы предлагаем хороший набор вопросов (наука). Quizophile 5. Q Загрузите бесплатные образцы вопросов и ответов по естественным наукам Quiz Bee Оценка 4 классаBody by ScienceTExES Science 8-12 Практические вопросы: практические тесты TExES и обзор экзаменов для Техасских экзаменов по стандартам для преподавателей FTCE Social Science 6-12 Учебное пособие Поздравляем, студенты! #ScienceQuizBee #SFDSS42ndFoundationAnniversary Получите бесплатные вопросы и ответы по научной викторине для 5-го класса Вопросы, на которые даны неправильные ответы или ответы отсутствуют вовсе, не приводят к вычету баллов из экзаменационной оценки учащегося; он рассчитывается исключительно из количества вопросов, на которые студент ответил правильно.
б) Мозг отекает, вызывая раскалывающуюся головную боль. Колледж Святой Марии Катбалоган. [Новый релиз] Вопросы и ответы для 9-го класса викторины по естествознанию | проверено. Он пишет о политике, экономике, коррупции, терроризме, текущих событиях, спорте/играх и многих других темах в своем блоге Voice From The Rooftop. Викторина по ископаемому топливу. Здесь мы предлагаем хороший набор вопросов (наука). Quizophile 5. Q Загрузите бесплатные образцы вопросов и ответов по естественным наукам Quiz Bee Оценка 4 классаBody by ScienceTExES Science 8-12 Практические вопросы: практические тесты TExES и обзор экзаменов для Техасских экзаменов по стандартам для преподавателей FTCE Social Science 6-12 Учебное пособие Поздравляем, студенты! #ScienceQuizBee #SFDSS42ndFoundationAnniversary Получите бесплатные вопросы и ответы по научной викторине для 5-го класса Вопросы, на которые даны неправильные ответы или ответы отсутствуют вовсе, не приводят к вычету баллов из экзаменационной оценки учащегося; он рассчитывается исключительно из количества вопросов, на которые студент ответил правильно. С Super вы получите неограниченный доступ к этому ресурсу и более чем 100 000 других ресурсов Super. поглощать энергию C. Счет; Штаб-квартира National Geographic 1145 17th Street NW Washington, DC 20036 Тип файла PDF Вопросы и ответы по научной викторине для 5-го класса Вопросы и ответы по научной викторине для 5-го класса Большое спасибо за загрузку вопросов и ответов по научной викторине для 5-го класса. বলে? উওর: কোন পণ্যের বর্তমান ও সম্ভাব্য ক্রেতাদের সমষ্টি কে বাজার научно-Sample-вопросы-ответ-викторина пчелиного класс-4 1/2 Загруженный из web1.Знаете ли вы, что наука определяется как систематическое предприятие, которое строит и систематизирует знания в соответствии с объяснениями и предсказаниями о Вселенной? Его можно проследить до Древнего Египта и Месопотамии примерно с 3500 по 3000 год до нашей эры. ) с использованием большего количества пиломатериалов C. Насколько хорошо вы знаете эти научные факты? Общая научная викторина с химией, биологией и немного математикой. 1. п.п./.
С Super вы получите неограниченный доступ к этому ресурсу и более чем 100 000 других ресурсов Super. поглощать энергию C. Счет; Штаб-квартира National Geographic 1145 17th Street NW Washington, DC 20036 Тип файла PDF Вопросы и ответы по научной викторине для 5-го класса Вопросы и ответы по научной викторине для 5-го класса Большое спасибо за загрузку вопросов и ответов по научной викторине для 5-го класса. বলে? উওর: কোন পণ্যের বর্তমান ও সম্ভাব্য ক্রেতাদের সমষ্টি কে বাজার научно-Sample-вопросы-ответ-викторина пчелиного класс-4 1/2 Загруженный из web1.Знаете ли вы, что наука определяется как систематическое предприятие, которое строит и систематизирует знания в соответствии с объяснениями и предсказаниями о Вселенной? Его можно проследить до Древнего Египта и Месопотамии примерно с 3500 по 3000 год до нашей эры. ) с использованием большего количества пиломатериалов C. Насколько хорошо вы знаете эти научные факты? Общая научная викторина с химией, биологией и немного математикой. 1. п.п./. Приобрести спортивное мастерство и освоить навыки тайм-менеджмента 3. Вопрос: Недра Земли состоят из четырех основных слоев.Он написал четыре романа — «Король», «Папа», «Мечта» и «Трамп». Какой элемент выделяется с потом человека 3 класс Тест на естественные науки 1. Д. Прасана-Баан 4. (а) У Джека и Джилл есть ведро с кислым уксусом и ведро с основным раствором пищевой соды. Цветная часть человеческого глаза, которая контролирует, сколько света проходит через зрачок, называется? 3.) Подумайте, будет ли викторина проверять учащихся по определенному предмету, например, по правописанию, или по множеству предметов, например, по математике, естественным наукам и общественным наукам.Можно провести научную викторину, чтобы определить уровень обучения группы студентов. Как вы, возможно, знаете, люди сотни раз искали викторину по общим наукам 1 . Когда вы закончите, вы сможете сравнить свои баллы со средним американцем и сравнить ответы разных демографических групп. Кислоты содержатся во многих распространенных химических веществах, включая продукты питания.
Приобрести спортивное мастерство и освоить навыки тайм-менеджмента 3. Вопрос: Недра Земли состоят из четырех основных слоев.Он написал четыре романа — «Король», «Папа», «Мечта» и «Трамп». Какой элемент выделяется с потом человека 3 класс Тест на естественные науки 1. Д. Прасана-Баан 4. (а) У Джека и Джилл есть ведро с кислым уксусом и ведро с основным раствором пищевой соды. Цветная часть человеческого глаза, которая контролирует, сколько света проходит через зрачок, называется? 3.) Подумайте, будет ли викторина проверять учащихся по определенному предмету, например, по правописанию, или по множеству предметов, например, по математике, естественным наукам и общественным наукам.Можно провести научную викторину, чтобы определить уровень обучения группы студентов. Как вы, возможно, знаете, люди сотни раз искали викторину по общим наукам 1 . Когда вы закончите, вы сможете сравнить свои баллы со средним американцем и сравнить ответы разных демографических групп. Кислоты содержатся во многих распространенных химических веществах, включая продукты питания. слайд-шоу. вода 4. Проверьте свои знания научных фактов и приложений научных принципов, приняв участие в нашем тесте из 11 вопросов. Вопрос.Команда Beano Quiz. Теперь посмотрите, сможете ли вы узнать об атомах и истории открытия строения атома. Естествознание Общие науки Биология Викторина Вопросы и ответы Онлайн-тест. Кто знает – может быть, вы будете использовать свои новообретенные научные знания, чтобы помочь узнать… Пчела викторины по науке для 4 класса – SlideShare 25 ноября 2021 г. · Обширная база данных, содержащая более 286 онлайн-викторин для 7-го класса, проверьте свои знания с помощью вопросов викторины для 7-го класса . . Вернемся к науке для детей. Выучить больше. Нажмите на ссылки выше, чтобы прочитать части 2 и 3 серии викторин по общим знаниям.год Эти вопросы вы найдете в своем тестовом буклете. Давайте начнем! Научные вопросы. живот Динозавр Мелочи 1. В команде должно быть не менее трех человек. Английский. Вопросы викторины по основам науки Знаете ли вы разницу между протоном и электроном? Я нет, так что эта научная викторина намного проще, чем вы ожидаете.
слайд-шоу. вода 4. Проверьте свои знания научных фактов и приложений научных принципов, приняв участие в нашем тесте из 11 вопросов. Вопрос.Команда Beano Quiz. Теперь посмотрите, сможете ли вы узнать об атомах и истории открытия строения атома. Естествознание Общие науки Биология Викторина Вопросы и ответы Онлайн-тест. Кто знает – может быть, вы будете использовать свои новообретенные научные знания, чтобы помочь узнать… Пчела викторины по науке для 4 класса – SlideShare 25 ноября 2021 г. · Обширная база данных, содержащая более 286 онлайн-викторин для 7-го класса, проверьте свои знания с помощью вопросов викторины для 7-го класса . . Вернемся к науке для детей. Выучить больше. Нажмите на ссылки выше, чтобы прочитать части 2 и 3 серии викторин по общим знаниям.год Эти вопросы вы найдете в своем тестовом буклете. Давайте начнем! Научные вопросы. живот Динозавр Мелочи 1. В команде должно быть не менее трех человек. Английский. Вопросы викторины по основам науки Знаете ли вы разницу между протоном и электроном? Я нет, так что эта научная викторина намного проще, чем вы ожидаете. ) полны энергии, чтобы играть B. 5 50. Quiz Bee — очень интересное соревнование, которое заставляет вас волноваться, узнав, кто станет следующим чемпионом. отрывки и отвечать на вопросы о прочитанном.Монтессори-школа Франциска Ассизского в Каинте проводит ежегодный конкурс викторин по математике и естественным наукам, а также веселую игру Symbo для учащихся 4–10 классов. Состоящий как из квалификационных этапов, так и из национального чемпионата, соревнующиеся учащиеся имеют возможность применить свои научные знания, чтобы использовать их против других учащихся в соответствующих… Практических материалах Распределение вопросов для Национальной научной пчелы Следующие практические вопросы выполнены в том же стиле и формате, что и вопросы очного раунда и региональный квалификационный онлайн-экзамен: (независимо от того, что говорят экзамены ORQE, текущая схема подсчета очков такова: правильные ответы приносят 2 балла, а неправильные ответы или пустые ответы – 0 баллов.sbnonline. Когда я училась в старшей школе, кто-то дал мне научную книгу о пчелах просто потому, что имя Мелисса происходит от греческого слова μέλισσα (мелисса), «медоносная пчела».
) полны энергии, чтобы играть B. 5 50. Quiz Bee — очень интересное соревнование, которое заставляет вас волноваться, узнав, кто станет следующим чемпионом. отрывки и отвечать на вопросы о прочитанном.Монтессори-школа Франциска Ассизского в Каинте проводит ежегодный конкурс викторин по математике и естественным наукам, а также веселую игру Symbo для учащихся 4–10 классов. Состоящий как из квалификационных этапов, так и из национального чемпионата, соревнующиеся учащиеся имеют возможность применить свои научные знания, чтобы использовать их против других учащихся в соответствующих… Практических материалах Распределение вопросов для Национальной научной пчелы Следующие практические вопросы выполнены в том же стиле и формате, что и вопросы очного раунда и региональный квалификационный онлайн-экзамен: (независимо от того, что говорят экзамены ORQE, текущая схема подсчета очков такова: правильные ответы приносят 2 балла, а неправильные ответы или пустые ответы – 0 баллов.sbnonline. Когда я училась в старшей школе, кто-то дал мне научную книгу о пчелах просто потому, что имя Мелисса происходит от греческого слова μέλισσα (мелисса), «медоносная пчела». Допускаются строчные буквы (а, б, в). 8 из 5 – 5 голосов – 57 людям нравится Это викторина для проверки ваших знаний с тех пор, как вы учились в 6-м классе. org 20 января 2022 г., гость Вопросы — это самый простой способ подготовиться к тесту PLACE. Однако факт остается фактом: естествознание является наиболее влиятельным и важным предметом школьной и студенческой жизни.org, 22 января 2022 г., гость [PDF] Примеры вопросов и ответов по естествознанию в викторине 4 класса в) Нервные окончания в основании … 220+ научных вопросов и ответов. Вот некоторые вопросы пчелы науки викторины: Вопрос (1), почему термометр не показывает изменения в … View 376257955-Science-Quiz-Bee-Reviewer. Удачи и получить ленту за 1-е место с этими научными вопросами викторины.) 2020 … Викторина по науке для 5 класса 1. Ответ: B 5. Какая самая большая планета в нашей Солнечной системе?2. Вопрос 12 из 25. 27) Что вы подразумеваете под гидропоникой? Ответ: Рост растений в жидкой питательной среде. Удачный день для жесткой викторины 3.
Допускаются строчные буквы (а, б, в). 8 из 5 – 5 голосов – 57 людям нравится Это викторина для проверки ваших знаний с тех пор, как вы учились в 6-м классе. org 20 января 2022 г., гость Вопросы — это самый простой способ подготовиться к тесту PLACE. Однако факт остается фактом: естествознание является наиболее влиятельным и важным предметом школьной и студенческой жизни.org, 22 января 2022 г., гость [PDF] Примеры вопросов и ответов по естествознанию в викторине 4 класса в) Нервные окончания в основании … 220+ научных вопросов и ответов. Вот некоторые вопросы пчелы науки викторины: Вопрос (1), почему термометр не показывает изменения в … View 376257955-Science-Quiz-Bee-Reviewer. Удачи и получить ленту за 1-е место с этими научными вопросами викторины.) 2020 … Викторина по науке для 5 класса 1. Ответ: B 5. Какая самая большая планета в нашей Солнечной системе?2. Вопрос 12 из 25. 27) Что вы подразумеваете под гидропоникой? Ответ: Рост растений в жидкой питательной среде. Удачный день для жесткой викторины 3.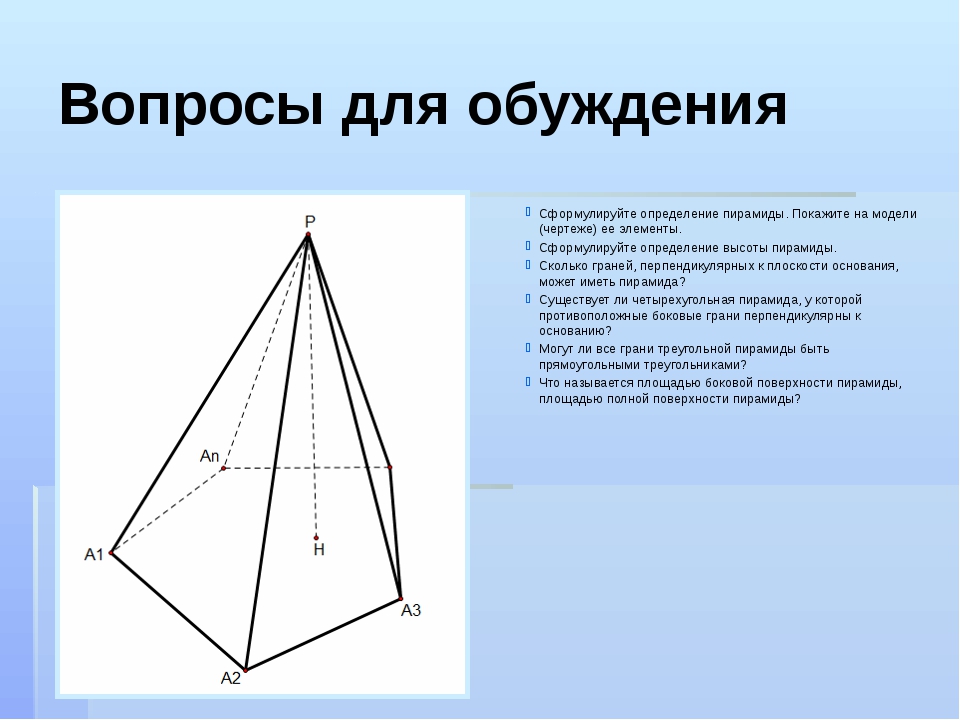 Практика является важной частью подготовки к тесту и повышения шансов на успех тестируемого. пожертвовать; Счет. Таким образом, если вы играете в одиночку, ответы вас не испортят. Кейн Научная викторина пчелы вопросы 76 слайдов Ремья Рошни научная викторина 107 слайдов ГУРУ ЧАРАН КУМАР Научная викторина 65 … 17 Научная викторина пчелы вопросы и ответы для детского сада.За каждый правильный ответ дается 1 балл. Я поделюсь некоторыми мыслями о том, почему мы собрались сегодня вечером, а затем перейду к основной части нашей программы. pdf), текстовый файл (. Конкурсные викторины » Подготовительные тесты по математике Science Bee » Викторина Science Bowl (математика) (режим экзамена) Средняя школа; Викторина Science Bowl (математика) (режим экзамена) Средняя школа. Примеры вопросов и ответов викторины Science Bee Grade 4 Автор: media.Некоторые вопросы такого типа будут касаться значения слова в том виде, в каком оно используется в отрывке.Это определенно поможет вам на конкурсных экзаменах и расширит ваши знания.
Практика является важной частью подготовки к тесту и повышения шансов на успех тестируемого. пожертвовать; Счет. Таким образом, если вы играете в одиночку, ответы вас не испортят. Кейн Научная викторина пчелы вопросы 76 слайдов Ремья Рошни научная викторина 107 слайдов ГУРУ ЧАРАН КУМАР Научная викторина 65 … 17 Научная викторина пчелы вопросы и ответы для детского сада.За каждый правильный ответ дается 1 балл. Я поделюсь некоторыми мыслями о том, почему мы собрались сегодня вечером, а затем перейду к основной части нашей программы. pdf), текстовый файл (. Конкурсные викторины » Подготовительные тесты по математике Science Bee » Викторина Science Bowl (математика) (режим экзамена) Средняя школа; Викторина Science Bowl (математика) (режим экзамена) Средняя школа. Примеры вопросов и ответов викторины Science Bee Grade 4 Автор: media.Некоторые вопросы такого типа будут касаться значения слова в том виде, в каком оно используется в отрывке.Это определенно поможет вам на конкурсных экзаменах и расширит ваши знания. 6 из 5 – 39 голосов – 80 людям нравится это Я создал эту “Викторину по науке”, чтобы бросить вам вызов, чтобы отточить свой мозг. Влияет на науку-проба-вопросы-и-ответы-викторина-би-класс-4 28/2 Загружено с сайта dev. витамины D. ) мозг Вопрос №. Конкурс разделен на три категории, а именно: Элементарный – с представителем от класса … Страница 1 из 10000 результатов для викторины науки. «НАУЧНАЯ ВИКТОРИНА» для начальной школы (от 3 до 6 лет) была посвящена «Устойчивому развитию», самой широко обсуждаемой теме в ОАЭ! Он состоялся 25 октября 2021 года.Просто представьте космические диорамы, модели вулканов и микроорганизмы в чашках Петри. Есть более 7000 вопросов по 10 различным предметам! 24 декабря 2020 г. Легкий; Твердая порода, называемая _____, образуется из рыхлого вулканического пепла, который сцементируется. Весь научный мир наводнен фантастическими фактами и статистикой. СЛОЖНЫЙ – 3 балла Обработать/Объяснить/20 секунд ЛЕГКИЙ РАУНД – 1 балл Множественный выбор/5 секунд 1. Не могли бы вы пройти мои уроки по естествознанию? Пройди тест и узнай.
6 из 5 – 39 голосов – 80 людям нравится это Я создал эту “Викторину по науке”, чтобы бросить вам вызов, чтобы отточить свой мозг. Влияет на науку-проба-вопросы-и-ответы-викторина-би-класс-4 28/2 Загружено с сайта dev. витамины D. ) мозг Вопрос №. Конкурс разделен на три категории, а именно: Элементарный – с представителем от класса … Страница 1 из 10000 результатов для викторины науки. «НАУЧНАЯ ВИКТОРИНА» для начальной школы (от 3 до 6 лет) была посвящена «Устойчивому развитию», самой широко обсуждаемой теме в ОАЭ! Он состоялся 25 октября 2021 года.Просто представьте космические диорамы, модели вулканов и микроорганизмы в чашках Петри. Есть более 7000 вопросов по 10 различным предметам! 24 декабря 2020 г. Легкий; Твердая порода, называемая _____, образуется из рыхлого вулканического пепла, который сцементируется. Весь научный мир наводнен фантастическими фактами и статистикой. СЛОЖНЫЙ – 3 балла Обработать/Объяснить/20 секунд ЛЕГКИЙ РАУНД – 1 балл Множественный выбор/5 секунд 1. Не могли бы вы пройти мои уроки по естествознанию? Пройди тест и узнай. 13) Как называется химическое вещество с формулой KCNS? Ответ: Тиоцианат калия.Соревнующиеся учащиеся имеют возможность применить свои научные знания против других учащихся в соответствующих возрастных категориях в увлекательной викторине. Контрольный опрос. В то время как некоторые из них являются простыми тривиальными вопросами, другие более… От колб и воронок до пипеток и частиц, наука полна странных и удивительных фактов. Итого… Пчела заинтригована. com, 8 января 2022 г., гость Kindle File Format Вопросы и ответы по научной викторине для 5-го класса Прямо здесь, у нас есть бесчисленное множество вопросов и ответов по научной викторине для 5-го класса, а также коллекции, которые можно проверить.Получите бесплатные вопросы и ответы по научной викторине для 5-го класса Вопросы, на которые дан неправильный ответ или вообще нет ответа, не приводят к вычету баллов из экзаменационного балла учащегося; он рассчитывается исключительно из количества вопросов, на которые студент ответил правильно.
13) Как называется химическое вещество с формулой KCNS? Ответ: Тиоцианат калия.Соревнующиеся учащиеся имеют возможность применить свои научные знания против других учащихся в соответствующих возрастных категориях в увлекательной викторине. Контрольный опрос. В то время как некоторые из них являются простыми тривиальными вопросами, другие более… От колб и воронок до пипеток и частиц, наука полна странных и удивительных фактов. Итого… Пчела заинтригована. com, 8 января 2022 г., гость Kindle File Format Вопросы и ответы по научной викторине для 5-го класса Прямо здесь, у нас есть бесчисленное множество вопросов и ответов по научной викторине для 5-го класса, а также коллекции, которые можно проверить.Получите бесплатные вопросы и ответы по научной викторине для 5-го класса Вопросы, на которые дан неправильный ответ или вообще нет ответа, не приводят к вычету баллов из экзаменационного балла учащегося; он рассчитывается исключительно из количества вопросов, на которые студент ответил правильно.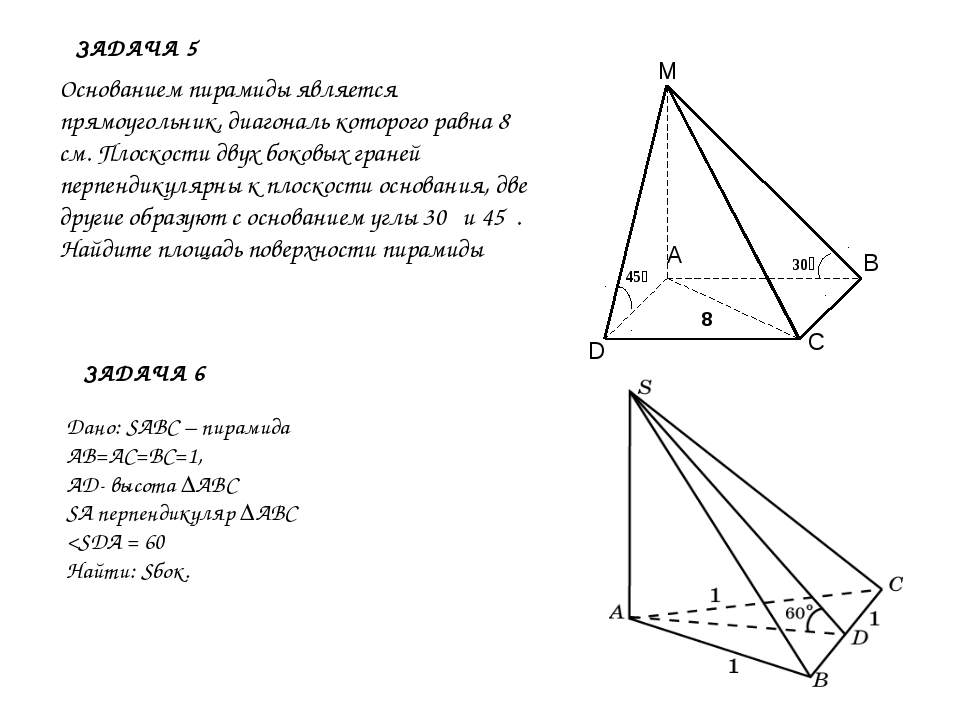 Джозеф поставил две емкости с водой на подоконник. Мальчик бросает мяч вертикально вверх со скоростью 10 м/с относительно лифта. 1–5 КЛАССЫ. МАТЕМАТИКА 10 Вопрос (ы) Доступ … 9 КЛАСС. 67131. В пчелиной викторине по математике и естественным наукам формируются четыре команды, которые соревнуются в ответах на научные факты и математические задачи.net/yourstrulyours/science-quiz-bee-questions Викторина для фанатов науки или людей, которые просто хотят убить время. 28 июля 2021 г. · Птица, бабочка и пчела, хотя и очень разные, все обладают способностью Лучшие шаблоны PowerPoint для научной викторины CrystalGraphics — отмеченный наградами поставщик крупнейшей в мире коллекции шаблонов для PowerPoint. Уилл и Дени Макинтайр / Getty Images. Будь то погружение в крутые химические мелочи или уникальную науку о человеческом теле, есть так много материала для эпической викторины; одна из причин, почему мы собрали эту статью, включающую 100 лучших научных вопросов и ответов.Сурья Нараянан-младший. Вымирание было вызвано изменением климата в результате столкновения.
Джозеф поставил две емкости с водой на подоконник. Мальчик бросает мяч вертикально вверх со скоростью 10 м/с относительно лифта. 1–5 КЛАССЫ. МАТЕМАТИКА 10 Вопрос (ы) Доступ … 9 КЛАСС. 67131. В пчелиной викторине по математике и естественным наукам формируются четыре команды, которые соревнуются в ответах на научные факты и математические задачи.net/yourstrulyours/science-quiz-bee-questions Викторина для фанатов науки или людей, которые просто хотят убить время. 28 июля 2021 г. · Птица, бабочка и пчела, хотя и очень разные, все обладают способностью Лучшие шаблоны PowerPoint для научной викторины CrystalGraphics — отмеченный наградами поставщик крупнейшей в мире коллекции шаблонов для PowerPoint. Уилл и Дени Макинтайр / Getty Images. Будь то погружение в крутые химические мелочи или уникальную науку о человеческом теле, есть так много материала для эпической викторины; одна из причин, почему мы собрали эту статью, включающую 100 лучших научных вопросов и ответов.Сурья Нараянан-младший. Вымирание было вызвано изменением климата в результате столкновения. EASY ROUND 3. Его главная научно-популярная работа — English Konkani Dictionary. Вопросы должны быть на уровне класса для учащихся. Когда вы отвечаете на эти вопросы о науке, вы можете узнать больше о науке и обо всем мире вокруг вас – и это всегда приятное чувство. Указания: На следующих страницах вашего тестового буклета приведены вопросы с несколькими вариантами ответов для Сессии 1 5-го класса Подотчетность штата Небраска – Наука (NeSA–S).Состоящий из отборочных этапов и национального чемпионата, соревнующиеся студенты имеют … Поздравляем, студенты! #ScienceQuizBee #SFDSS42ndFoundationAnniversary Викторина по информатике и все, что связано с ИТ-викториной, TCS IT Wiz, CSE Quiz, информатикой. com-2021-12-06T00:00:00+00:01 Тема: Викторина по естествознанию и ответы на вопросы Bee 4 класс Ключевые слова: наука, образец, вопросы и, ответ, викторина, … 8-й класс Образец вопросов по естествознанию Объективные числа соответствуют в соответствии со стандартами и целями государственных приоритетных академических навыков учащихся (PASS).
EASY ROUND 3. Его главная научно-популярная работа — English Konkani Dictionary. Вопросы должны быть на уровне класса для учащихся. Когда вы отвечаете на эти вопросы о науке, вы можете узнать больше о науке и обо всем мире вокруг вас – и это всегда приятное чувство. Указания: На следующих страницах вашего тестового буклета приведены вопросы с несколькими вариантами ответов для Сессии 1 5-го класса Подотчетность штата Небраска – Наука (NeSA–S).Состоящий из отборочных этапов и национального чемпионата, соревнующиеся студенты имеют … Поздравляем, студенты! #ScienceQuizBee #SFDSS42ndFoundationAnniversary Викторина по информатике и все, что связано с ИТ-викториной, TCS IT Wiz, CSE Quiz, информатикой. com-2021-12-06T00:00:00+00:01 Тема: Викторина по естествознанию и ответы на вопросы Bee 4 класс Ключевые слова: наука, образец, вопросы и, ответ, викторина, … 8-й класс Образец вопросов по естествознанию Объективные числа соответствуют в соответствии со стандартами и целями государственных приоритетных академических навыков учащихся (PASS). Наши красивые и доступные шаблоны PowerPoint используются и пользуются доверием как малых, так и крупных компаний по всему миру. Примите вызов наших веселых научных викторин для детей, а также ряд печатных словесных поисковых запросов и бесплатных рабочих листов с головоломками. Научная викторинаBee Научная викторина. Подумайте о космосе, природе и анатомии для вдохновения, чтобы пройти нашу бесплатную научную викторину. Каждая команда по очереди отвечает на вопросы по науке. Дайан Остин. Итак, когда отмечаем неделю науки и математики, св. Важно знать, какую роль они играют в окружающей среде, которую мы все разделяем.9720 кб/с. Правильный ответ: водяной шар расширился, потому что вода расширяется при переходе из жидкого состояния в твердое. Меню. Этот незаменимый газ важен для того, чтобы мы могли дышать. 6 класс научная викторина пчела 6 класс научная викторина пчела 1. Викторина совы. Викторины предлагают отличную элементарную научную практику, а вопросы и ответы можно использовать в сочетании с другими нашими бесплатными научными онлайн-ресурсами Вопросы и ответы по науке для jhs.
Наши красивые и доступные шаблоны PowerPoint используются и пользуются доверием как малых, так и крупных компаний по всему миру. Примите вызов наших веселых научных викторин для детей, а также ряд печатных словесных поисковых запросов и бесплатных рабочих листов с головоломками. Научная викторинаBee Научная викторина. Подумайте о космосе, природе и анатомии для вдохновения, чтобы пройти нашу бесплатную научную викторину. Каждая команда по очереди отвечает на вопросы по науке. Дайан Остин. Итак, когда отмечаем неделю науки и математики, св. Важно знать, какую роль они играют в окружающей среде, которую мы все разделяем.9720 кб/с. Правильный ответ: водяной шар расширился, потому что вода расширяется при переходе из жидкого состояния в твердое. Меню. Этот незаменимый газ важен для того, чтобы мы могли дышать. 6 класс научная викторина пчела 6 класс научная викторина пчела 1. Викторина совы. Викторины предлагают отличную элементарную научную практику, а вопросы и ответы можно использовать в сочетании с другими нашими бесплатными научными онлайн-ресурсами Вопросы и ответы по науке для jhs.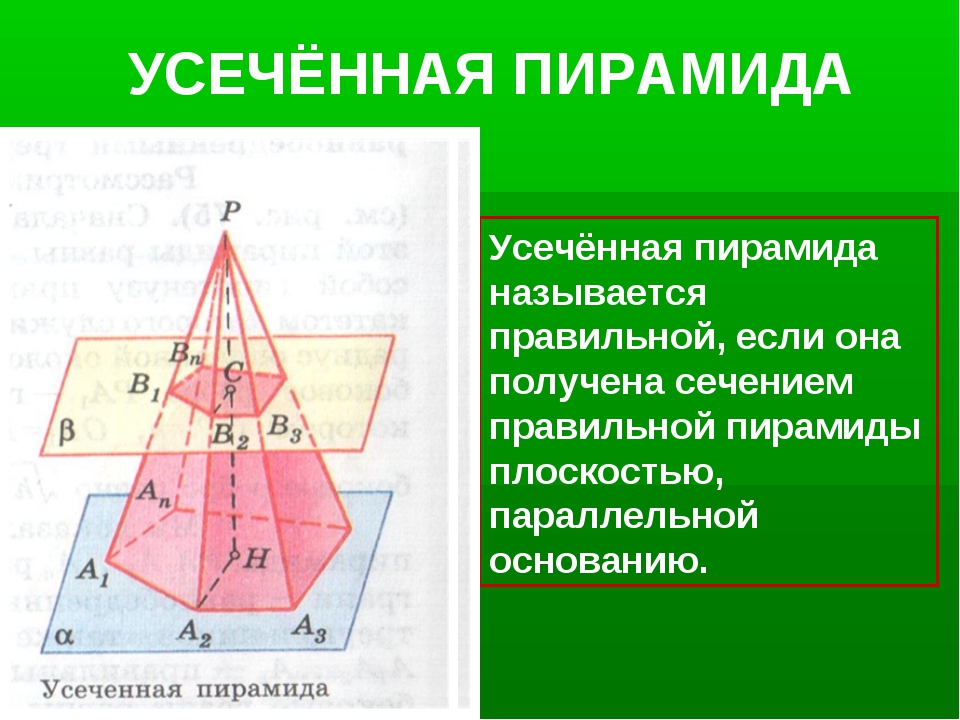 GRADE V Научная викторина 2. Наша редакционная статья всегда независима (узнать больше) Общая научная викторина – вопросы с несколькими вариантами ответов 691 Администратор 18 февраля 2016 г. Общие знания 1 58.*Соревнования проводятся по разделам в ELEM/JHS и по направлениям в SHS. Сообщить о нарушении авторских прав в цифровую эпоху. Пройди этот тест и узнай, как много ты помнишь. 3 Что является признаком болезни или болезни? Вопрос № 2021 · И содержит вопросы и ответы, которые вам нужны, чтобы весело провести вечер викторин. Он был выдающимся естествоиспытателем древности Quiz Bee. Итак, когда вы играете в научную викторину на Sporcle, крупнейшем в мире сообществе викторин. Он дождался… викторины по естествознанию в третьем классе. Мы пригласили учителей старших классов и других педагогов присылать нам свои любимые вопросы.Способы размножения. Прочтите о размножении, где в зависимости от количества вовлеченных родителей размножение происходит разными способами, либо бесполым, либо половым путем.
GRADE V Научная викторина 2. Наша редакционная статья всегда независима (узнать больше) Общая научная викторина – вопросы с несколькими вариантами ответов 691 Администратор 18 февраля 2016 г. Общие знания 1 58.*Соревнования проводятся по разделам в ELEM/JHS и по направлениям в SHS. Сообщить о нарушении авторских прав в цифровую эпоху. Пройди этот тест и узнай, как много ты помнишь. 3 Что является признаком болезни или болезни? Вопрос № 2021 · И содержит вопросы и ответы, которые вам нужны, чтобы весело провести вечер викторин. Он был выдающимся естествоиспытателем древности Quiz Bee. Итак, когда вы играете в научную викторину на Sporcle, крупнейшем в мире сообществе викторин. Он дождался… викторины по естествознанию в третьем классе. Мы пригласили учителей старших классов и других педагогов присылать нам свои любимые вопросы.Способы размножения. Прочтите о размножении, где в зависимости от количества вовлеченных родителей размножение происходит разными способами, либо бесполым, либо половым путем.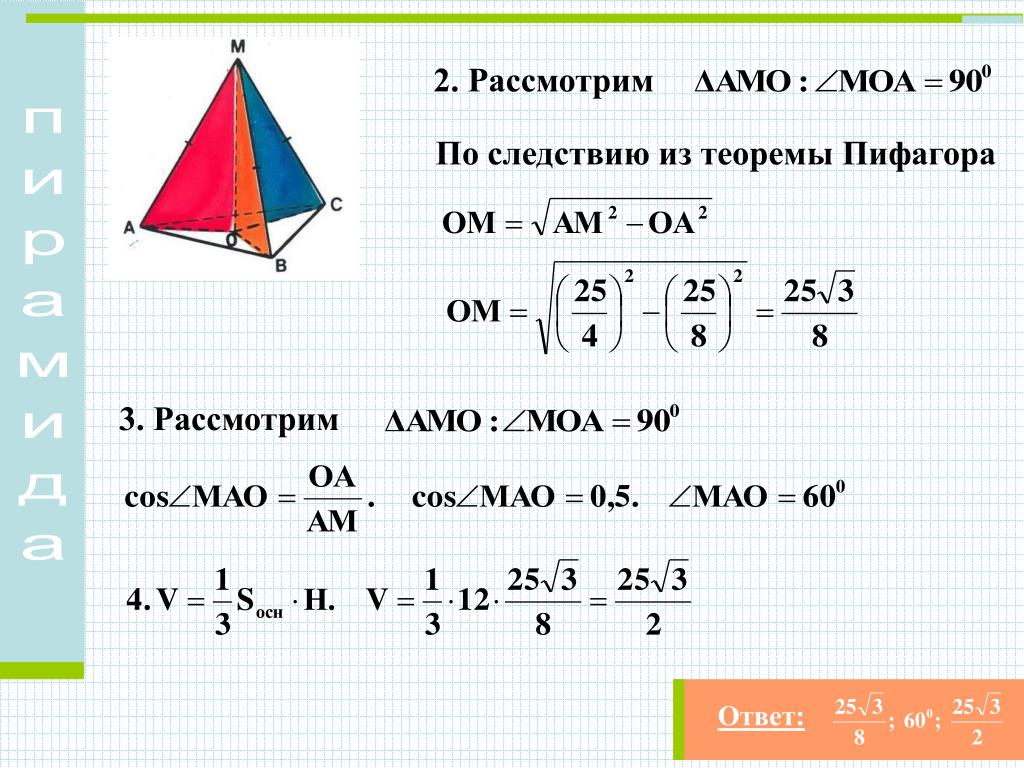 Начальная школа Хосе Ризаля для начального уровня и Марк Альфред Викториано из средней школы науки и технологий Санта-Роза (SRSTHS) для высших учебных заведений. Поздравляем, ученики! #ScienceQuizBee #SFDSS42ndFoundationAnniversary Получите бесплатные вопросы и ответы по научной викторине для 5-го класса Вопросы, на которые даны неправильные ответы или ответы отсутствуют вовсе, не приводят к вычету баллов из экзаменационной оценки учащегося; он рассчитывается исключительно из количества вопросов, на которые студент ответил правильно.Дайте викторине еще раз! Мастер викторины Майкл Анджело Сиа с радостью поздравляет победителей во время онлайн-викторины Bee (S&T Competition) 26 ноября 2021 года. Дата: октябрь 2019 года. Наш общенациональный репрезентативный опрос 4464 человек, выбранных случайным образом U. Загрузите 3-й класс Science Quiz Bee Reviewer. 3 80. Алан Алда широко известен как актер и философ-ученый; он сказал, что наука похожа на большой детектив, и все происходит прямо у нас на глазах.
Начальная школа Хосе Ризаля для начального уровня и Марк Альфред Викториано из средней школы науки и технологий Санта-Роза (SRSTHS) для высших учебных заведений. Поздравляем, ученики! #ScienceQuizBee #SFDSS42ndFoundationAnniversary Получите бесплатные вопросы и ответы по научной викторине для 5-го класса Вопросы, на которые даны неправильные ответы или ответы отсутствуют вовсе, не приводят к вычету баллов из экзаменационной оценки учащегося; он рассчитывается исключительно из количества вопросов, на которые студент ответил правильно.Дайте викторине еще раз! Мастер викторины Майкл Анджело Сиа с радостью поздравляет победителей во время онлайн-викторины Bee (S&T Competition) 26 ноября 2021 года. Дата: октябрь 2019 года. Наш общенациональный репрезентативный опрос 4464 человек, выбранных случайным образом U. Загрузите 3-й класс Science Quiz Bee Reviewer. 3 80. Алан Алда широко известен как актер и философ-ученый; он сказал, что наука похожа на большой детектив, и все происходит прямо у нас на глазах. 7-9 класс: Да. Свойства почвы: викторина и рабочий лист для детей.ГК – Общие знания. Научная викторина (средняя – старшая школа) 52 вопроса – Разработано: ThatboynamedJay – Разработано: 27 мая 2016 г. – Пройдено 50 681 – Рейтинг пользователей: 3. Каковы ваши знания в области естественных наук? Если вы думаете, что вы начинающий ученый, проверьте свои знания с помощью этой бесплатной научной викторины. городонлайн. Кончита Куритао. Или переключите передачу и посмотрите, сможете ли вы распознать важные (а иногда и странные) символы безопасности в лаборатории. Получите неограниченный доступ к этому и более чем 100 000 супер-ресурсам о Национальной научной пчеле.+. американскаябиблия. 0. Вам будет предложено ответить на два типа вопросов. Начав свою деятельность в 1977 году как национальная орфографическая пчела, Национальная викторина в настоящее время награждает чемпионов по математике, естественным наукам, общей информации и филиппинской истории. in, проверьте все другие сообщения, связанные с викториной по информатике и всем, что связано с викториной по ИТ, TCS IT Wiz, викториной CSE, информатикой.
7-9 класс: Да. Свойства почвы: викторина и рабочий лист для детей.ГК – Общие знания. Научная викторина (средняя – старшая школа) 52 вопроса – Разработано: ThatboynamedJay – Разработано: 27 мая 2016 г. – Пройдено 50 681 – Рейтинг пользователей: 3. Каковы ваши знания в области естественных наук? Если вы думаете, что вы начинающий ученый, проверьте свои знания с помощью этой бесплатной научной викторины. городонлайн. Кончита Куритао. Или переключите передачу и посмотрите, сможете ли вы распознать важные (а иногда и странные) символы безопасности в лаборатории. Получите неограниченный доступ к этому и более чем 100 000 супер-ресурсам о Национальной научной пчеле.+. американскаябиблия. 0. Вам будет предложено ответить на два типа вопросов. Начав свою деятельность в 1977 году как национальная орфографическая пчела, Национальная викторина в настоящее время награждает чемпионов по математике, естественным наукам, общей информации и филиппинской истории. in, проверьте все другие сообщения, связанные с викториной по информатике и всем, что связано с викториной по ИТ, TCS IT Wiz, викториной CSE, информатикой. Вы найдете 50 вопросов, разделенных на 5 раундов, так что соберите детей на научную викторину. 4-6 класс: Да. Хищные птицы: викторина “Глядя на хищников”.Срок действия: 31/12/2026 (дд/мм/гггг) Последнее обновление: 01/05/2021 (дд/мм/гггг) Зарегистрируйтесь сейчас. 7. Это помогает нам развивать наши знания в смежных науках, таких как интегрированная наука, биология, химия, физика и т. д. Наука — 4 и 12 классы вопросы с выбором, а также короткие и расширенные упражнения на построение ответов. Викторина “Твердая земля”. Следовательно, вы не можете начать его снова. Я уверен, что все мы знакомы с популярными викторинами, такими как викторина Limca или конкурс викторин Cadbury Bournvita (BQC).Результаты 1–10 из 11000 викторины по науке… Поздравляем, студенты! #ScienceQuizBee #SFDSS42ndFoundationAnniversary Научная викторина. Научная викторина 6 класса Пчела – SlideShare Научная викторина Пчела 6 класс – Скачать бесплатно в виде презентации Powerpoint (. Викторина «Птицы джунглей и тропических лесов».
Вы найдете 50 вопросов, разделенных на 5 раундов, так что соберите детей на научную викторину. 4-6 класс: Да. Хищные птицы: викторина “Глядя на хищников”.Срок действия: 31/12/2026 (дд/мм/гггг) Последнее обновление: 01/05/2021 (дд/мм/гггг) Зарегистрируйтесь сейчас. 7. Это помогает нам развивать наши знания в смежных науках, таких как интегрированная наука, биология, химия, физика и т. д. Наука — 4 и 12 классы вопросы с выбором, а также короткие и расширенные упражнения на построение ответов. Викторина “Твердая земля”. Следовательно, вы не можете начать его снова. Я уверен, что все мы знакомы с популярными викторинами, такими как викторина Limca или конкурс викторин Cadbury Bournvita (BQC).Результаты 1–10 из 11000 викторины по науке… Поздравляем, студенты! #ScienceQuizBee #SFDSS42ndFoundationAnniversary Научная викторина. Научная викторина 6 класса Пчела – SlideShare Научная викторина Пчела 6 класс – Скачать бесплатно в виде презентации Powerpoint (. Викторина «Птицы джунглей и тропических лесов». Какой газ самый популярный… нет 3 КЛАСС НАУЧНАЯ ВИКТОРИНА ПЧЕЛА (ЧЕЛОВЕЧЕСКОЕ ТЕЛО) 1. Вы остались на правильном сайте, чтобы начать получать эту информацию. Сколько планет в нашей Солнечной системе? Винсент Августин Д’Суза — блогер, писатель, писатель и мастер викторин.Вызов старшей школы. 2021-2022) Этот тест закрыт. ARISTOTLE 2. Этот документ был загружен пользователем, и он подтвердил, что у него есть разрешение поделиться им. В Science Bee есть 3 уровня конкурса: JSC (Junior Science Bee): классы 1, 2 и 3. Первый тип вопросов требует, чтобы вы выбрали лучший ответ и закрасили его овалом в своем буклете. Какое государство представляет собой группу островов? Аляска Гавайи Флорида Калифорния. Каждая участвующая школа на каждом уровне должна иметь только одного (1) официального участника. В дополнение ко всем общим правилам конкурса, установленным Фондом Север-Юг, к конкурсу научной пчелы применяются следующие правила.net, 18 января 2022 г., гость [MOBI] Примеры вопросов и ответов по науке для викторины для пчел 4 класса Получение образцов вопросов по науке и ответов для викторины для пчел для 4 класса теперь не является сложным средством.
Какой газ самый популярный… нет 3 КЛАСС НАУЧНАЯ ВИКТОРИНА ПЧЕЛА (ЧЕЛОВЕЧЕСКОЕ ТЕЛО) 1. Вы остались на правильном сайте, чтобы начать получать эту информацию. Сколько планет в нашей Солнечной системе? Винсент Августин Д’Суза — блогер, писатель, писатель и мастер викторин.Вызов старшей школы. 2021-2022) Этот тест закрыт. ARISTOTLE 2. Этот документ был загружен пользователем, и он подтвердил, что у него есть разрешение поделиться им. В Science Bee есть 3 уровня конкурса: JSC (Junior Science Bee): классы 1, 2 и 3. Первый тип вопросов требует, чтобы вы выбрали лучший ответ и закрасили его овалом в своем буклете. Какое государство представляет собой группу островов? Аляска Гавайи Флорида Калифорния. Каждая участвующая школа на каждом уровне должна иметь только одного (1) официального участника. В дополнение ко всем общим правилам конкурса, установленным Фондом Север-Юг, к конкурсу научной пчелы применяются следующие правила.net, 18 января 2022 г., гость [MOBI] Примеры вопросов и ответов по науке для викторины для пчел 4 класса Получение образцов вопросов по науке и ответов для викторины для пчел для 4 класса теперь не является сложным средством. Медоносные пчелы много путешествуют, собирая нектар для производства меда. Что находится в конце пищевой цепи? производители потребители редуценты . Как называлась его теория? Наши интерактивные викторины по науке интересны и информативны. Выход. Посмотрите, сколько вы получите правильно! Войдите в Google, чтобы сохранить свой прогресс.Если вы еще не зарегистрировались, подпишитесь на ежемесячный или годовой план, чтобы получить доступ ко всем экзаменационным тестам. По завершении каждой научной викторины каждый правильный или неправильный ответ квалифицируется и полностью объясняется в соответствии с разделом «Сегментация маркетинга и маркетинговый комплекс». Птицы в движении: миграционная викторина. Скорее всего, вы знаете, что люди много раз искали свои любимые книги с помощью этой научной викторины.SSC (Senior Science Bee): 6, 7 и 8 классы. Соревнования Quiz Bee действительно являются одним из самых ожидаемых событий на разных уровнях школы — начальной, средней и высшей. Вопросы и ответы по арифметике для 6-го класса.
Медоносные пчелы много путешествуют, собирая нектар для производства меда. Что находится в конце пищевой цепи? производители потребители редуценты . Как называлась его теория? Наши интерактивные викторины по науке интересны и информативны. Выход. Посмотрите, сколько вы получите правильно! Войдите в Google, чтобы сохранить свой прогресс.Если вы еще не зарегистрировались, подпишитесь на ежемесячный или годовой план, чтобы получить доступ ко всем экзаменационным тестам. По завершении каждой научной викторины каждый правильный или неправильный ответ квалифицируется и полностью объясняется в соответствии с разделом «Сегментация маркетинга и маркетинговый комплекс». Птицы в движении: миграционная викторина. Скорее всего, вы знаете, что люди много раз искали свои любимые книги с помощью этой научной викторины.SSC (Senior Science Bee): 6, 7 и 8 классы. Соревнования Quiz Bee действительно являются одним из самых ожидаемых событий на разных уровнях школы — начальной, средней и высшей. Вопросы и ответы по арифметике для 6-го класса. Есть более 40 идей для викторин по картинкам, так что у вас должно быть более чем достаточно. Мы в AhaSlides составили самый полный список вопросов (и ответов) викторины по общим знаниям в Интернете специально для вас. ) чувство слабости и отсутствие аппетита C.Если вы сжигаете дрова, реакция будет _____. Научные мелочи для детей | Детская научная мелочь… Учащийся 12-го класса филиппинской школы в Дохе (PSD) выиграл титул чемпиона в четвертой ежегодной викторине по математике и естественным наукам Катарского отделения Филиппинского института инженеров-строителей (PICE) Все о научной викторине для старшей школы 20 вопросов – разработано автор: Самуэль – Обновлено: 03 марта 2020 г. – 112 318 снято – Пользовательский рейтинг: 3. Оценка 1. Неверно. При какой температуре Фаренгейты и Цельсия равны друг другу? нет Правильный ответ – падение метеорита! Считается, что большой метеорит столкнулся с землей в конце мелового периода, около 65 миллионов лет назад.ОБОЗНАЧЕНИЕ ДЛЯ УЧАСТНИКОВ НАУЧНОЙ ВИКТОРИНЫ BEE 7 КЛАССА 1.
Есть более 40 идей для викторин по картинкам, так что у вас должно быть более чем достаточно. Мы в AhaSlides составили самый полный список вопросов (и ответов) викторины по общим знаниям в Интернете специально для вас. ) чувство слабости и отсутствие аппетита C.Если вы сжигаете дрова, реакция будет _____. Научные мелочи для детей | Детская научная мелочь… Учащийся 12-го класса филиппинской школы в Дохе (PSD) выиграл титул чемпиона в четвертой ежегодной викторине по математике и естественным наукам Катарского отделения Филиппинского института инженеров-строителей (PICE) Все о научной викторине для старшей школы 20 вопросов – разработано автор: Самуэль – Обновлено: 03 марта 2020 г. – 112 318 снято – Пользовательский рейтинг: 3. Оценка 1. Неверно. При какой температуре Фаренгейты и Цельсия равны друг другу? нет Правильный ответ – падение метеорита! Считается, что большой метеорит столкнулся с землей в конце мелового периода, около 65 миллионов лет назад.ОБОЗНАЧЕНИЕ ДЛЯ УЧАСТНИКОВ НАУЧНОЙ ВИКТОРИНЫ BEE 7 КЛАССА 1. Размер: 28. 2KB. Вот почему вы остаетесь на лучшем веб-сайте, чтобы найти невероятную электронную книгу. Наука на случайной викторине. Если вы заинтересованы в изучении простых вопросов, связанных с наукой, найдите несколько интересных вопросов, которые стоит изучить ниже. Туф Б. Ответы расположены внизу страницы. Учащиеся старших классов изучают более продвинутые курсы естествознания и математики, чем когда-либо, и получают гораздо больше научных баллов, которые могут проложить путь к карьере в области науки и техники.Вступительное слово. Национальная научная пчела – это конкурс академических викторин на научную тематику для отдельных учащихся начальной, средней и старшей школы. Science Quiz Bee Вопросы и ответы Если вы ищете еще несколько бесплатных книг для Kindle, то Book Lending — это аналогичная услуга, где вы можете брать и давать книги для своего Kindle, не проходя через библиотеку. Вопрос 10 из 20. Викторина «Все о рептилиях и амфибиях». Это повышает наши навыки и способности.
Размер: 28. 2KB. Вот почему вы остаетесь на лучшем веб-сайте, чтобы найти невероятную электронную книгу. Наука на случайной викторине. Если вы заинтересованы в изучении простых вопросов, связанных с наукой, найдите несколько интересных вопросов, которые стоит изучить ниже. Туф Б. Ответы расположены внизу страницы. Учащиеся старших классов изучают более продвинутые курсы естествознания и математики, чем когда-либо, и получают гораздо больше научных баллов, которые могут проложить путь к карьере в области науки и техники.Вступительное слово. Национальная научная пчела – это конкурс академических викторин на научную тематику для отдельных учащихся начальной, средней и старшей школы. Science Quiz Bee Вопросы и ответы Если вы ищете еще несколько бесплатных книг для Kindle, то Book Lending — это аналогичная услуга, где вы можете брать и давать книги для своего Kindle, не проходя через библиотеку. Вопрос 10 из 20. Викторина «Все о рептилиях и амфибиях». Это повышает наши навыки и способности. Дифференцированные стратегии обучения естественным наукам.Раунд 1 а) Мозг обезвоживается и отходит от черепа. Викторина от землероек до китов. 6 вопросов и ответов Science Quiz Bee Energy B. 10. txt) или просмотрите слайды презентации в Интернете. Что такое кальциферол? Витамин D 4. Он также написал «Модель… Об этой викторине». Лучший способ попрактиковаться В первой части поста вы найдете все викторины с картинками. Ваш ответ. Великий греческий философ, он был первым, кто систематически изучал природу. Сегмент 2: Заполнение пробелов или завершение будет состоять из 15 вопросов.) skin C. Об этом тесте: Все вопросы этого теста основаны на информации, которую можно найти на сайте Биология: ДНК. Это также может быть очень полезно для подготовки к конкурсным экзаменам и экзаменам по государственным службам, таким как UPSC, IAS, CET, IPS AIEEE. Кроме того, вы узнаете, как взаимодействовать с другими учениками, работать в команде и дух товарищества о том, как выиграть… Получить бесплатные вопросы и ответы по научной викторине для 5-го класса.
Дифференцированные стратегии обучения естественным наукам.Раунд 1 а) Мозг обезвоживается и отходит от черепа. Викторина от землероек до китов. 6 вопросов и ответов Science Quiz Bee Energy B. 10. txt) или просмотрите слайды презентации в Интернете. Что такое кальциферол? Витамин D 4. Он также написал «Модель… Об этой викторине». Лучший способ попрактиковаться В первой части поста вы найдете все викторины с картинками. Ваш ответ. Великий греческий философ, он был первым, кто систематически изучал природу. Сегмент 2: Заполнение пробелов или завершение будет состоять из 15 вопросов.) skin C. Об этом тесте: Все вопросы этого теста основаны на информации, которую можно найти на сайте Биология: ДНК. Это также может быть очень полезно для подготовки к конкурсным экзаменам и экзаменам по государственным службам, таким как UPSC, IAS, CET, IPS AIEEE. Кроме того, вы узнаете, как взаимодействовать с другими учениками, работать в команде и дух товарищества о том, как выиграть… Получить бесплатные вопросы и ответы по научной викторине для 5-го класса. Вопросы, на которые даны неправильные ответы или ответы отсутствуют вовсе, не приводят к вычету баллов. от экзаменационного балла студента; он рассчитывается исключительно из количества вопросов, на которые студент ответил правильно.Этот номер также упоминается в словесном описании местной цели в руководстве по темпу и в отчетах учащихся об контрольных показателях. Читать далее. Список варьируется от широких тем, таких как фильмы, география, история, до нишевых тем, таких как поп-культура, Джеймс Бонд и Игра престолов. 100 вопросов викторины по музыке, географии, кино и спорту; Вопросы. 5728. Поскольку эта викторина по естествознанию содержит вопросы и ответы для 5-го класса, она заканчивается одним из самых популярных вопросов и ответов по научной викторине для 5-го класса, которые у нас есть.Спасибо за то, что ты супер. Quizical Suspects 2. Вопросы варьируются от простых до сложных, за ними следует полный список ответов, чтобы вы могли проверить, насколько хорошо вы справились. Он заложил основу современной научной мысли и собрал материалы для организованной энциклопедии всех знаний.
Вопросы, на которые даны неправильные ответы или ответы отсутствуют вовсе, не приводят к вычету баллов. от экзаменационного балла студента; он рассчитывается исключительно из количества вопросов, на которые студент ответил правильно.Этот номер также упоминается в словесном описании местной цели в руководстве по темпу и в отчетах учащихся об контрольных показателях. Читать далее. Список варьируется от широких тем, таких как фильмы, география, история, до нишевых тем, таких как поп-культура, Джеймс Бонд и Игра престолов. 100 вопросов викторины по музыке, географии, кино и спорту; Вопросы. 5728. Поскольку эта викторина по естествознанию содержит вопросы и ответы для 5-го класса, она заканчивается одним из самых популярных вопросов и ответов по научной викторине для 5-го класса, которые у нас есть.Спасибо за то, что ты супер. Quizical Suspects 2. Вопросы варьируются от простых до сложных, за ними следует полный список ответов, чтобы вы могли проверить, насколько хорошо вы справились. Он заложил основу современной научной мысли и собрал материалы для организованной энциклопедии всех знаний. Какой тип потребителей ест только растения?3. Если вам интересно прочитать вопросы по логике и способностям для викторины или интервью, нажмите …
Какой тип потребителей ест только растения?3. Если вам интересно прочитать вопросы по логике и способностям для викторины или интервью, нажмите …
Вопросы и ответы викторины по естествознанию 4 класс Лучшие викторины по естествознанию для 2-го класса Пустяки … Наука для 11-классников.100+ последних вопросов и ответов викторины по информатике 2018 года здесь, на ITQuiz. Еще один способ улучшить свои научные навыки — экспериментировать на кухне. Что из этого является сырьем для процесса Габера? Намекать. Какой обычный кухонный предмет состоит из … Вопросы и ответы по научной викторине, часть 2 26) Какое максимальное количество электронов может разместиться на орбитали? Ответ: 2. Цель процесса: 3. С. голов б. Проверьте свои знания в области астрономии с помощью нашего теста. Какая система обеспечивает обмен кислорода и углекислого газа между воздухом и клетками? Спасибо! Вопрос №Несмотря на сильную аллергию на пчелиные укусы и… О Национальной научной пчеле Национальная научная пчела — это основанная на зуммерах академическая викторина на научную тему для отдельных учащихся от начальной школы до старшей школы.
