Геометрия 11 класс призма: Призма и её элементы — урок. Геометрия, 11 класс.
Объем прямой призмы и цилиндра 11 класс онлайн-подготовка на Ростелеком Лицей
Введение
Для решения задач потребуется вспомнить формулы для нахождения объемов куба, прямоугольного параллелепипеда и прямой треугольной призмы. (См. Рис. 1.)
Рис. 1. Объемы известных фигур
На этой базе мы сегодня выведем формулы для вычисления объемов еще двух фигур – произвольной прямой призмы и цилиндра.
Теорема 1. Объем прямой призмы
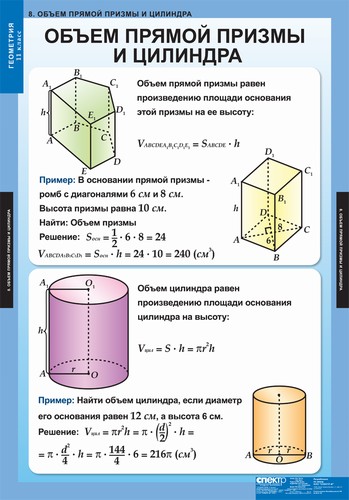
Объем прямой призмы равен произведению ее площади основания на высоту: .
Доказательство (для произвольной треугольной призмы (см. Рис. 2) и для любой призмы (см. Рис. 3)):
Рис. 2. Произвольная треугольная призма
Рис. 3. Произвольная призма
1. Рассмотрим треугольную призму (см. Рис. 4).
Рис. 4. Треугольная призма
Проведем высоты и (см. Рис. 5).
Рис. 5. Высоты и
Рис. 6. Две образовавшиеся призмы
Получается, что призма разбилась на две призмы: и . (См. Рис. 6.)
(См. Рис. 6.)
Тогда по свойству объемов объем исходной призмы будет равен сумме объемов призм разбиения .
Рис. 7. Прямоугольные треугольники в основаниях призм
Каждая из призм и является прямой призмой, в основании которой лежит прямоугольный треугольник. (См. Рис. 7.)
Рис. 8. Общая высота
Тогда и . Так как высота у этих призм одинаковая , то, складывая объемы, эту высоту можно вынеси за скобки. (См. Рис. 8.)
Таким образом, .
Что и требовалось доказать.
Рис. 9. Разбиение оснований на треугольник
2. Рассмотрим произвольную призму, т.е. -угольную, но при этом прямую. Разбиваем ее основания на треугольники. (См. Рис. 9).
Рис 10. Полученные прямоугольные призмы
Образовалось несколько треугольных призм. (См. Рис.10). Количество полученных призм не имеет значения.
Рис. 11. Площадь основания равна сумме площадей полученных треугольников
Тогда понятно, что объем исходной призмы будет равен сумме объемов полученных треугольных призм, т. е. . Поскольку каждая из полученных призм прямая и треугольная, то для данной формулы будет выполняться равенство из пункта 1 (см. Рис. 11):
е. . Поскольку каждая из полученных призм прямая и треугольная, то для данной формулы будет выполняться равенство из пункта 1 (см. Рис. 11):
(Высота у полученных призм одинаковая, т. к. эта высота является высотой исходной призмы (см. Рис. 12)).
Таким образом, для любой призмы. Теорема доказана.
Рис. 12. Общая для всех призм (полученных и исходной) высота
Пример 1
Найти объем прямой призмы (см. Рис. 13), если ; ; (где – высота ).
Рис. 13 Прямая призма
Решение. Рассмотрим . Он равнобедренный, значит, его высота совпадает с биссектрисой, то есть (см. Рис. 14).
Рис.14 Выносной рисунок
Тогда из треугольника :
. Значит, .
А тогда .
Ответ: .
Формула для вычисления объема цилиндра
Теперь найдем формулу для вычисления объема цилиндра. Как обычно, речь пойдет о прямом круговом цилиндре.
Рис.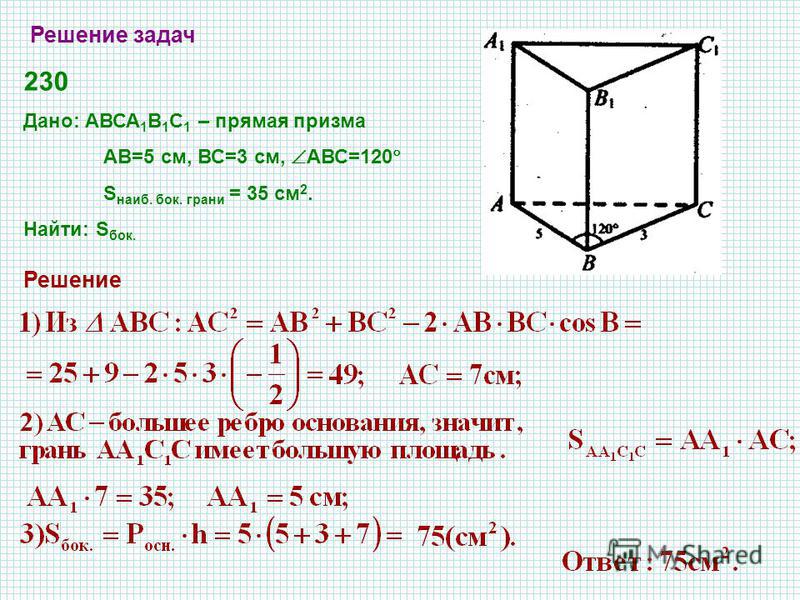 15 Комбинации цилиндра и призмы
15 Комбинации цилиндра и призмы
Напомним, что цилиндр называется вписанным в призму, если его основания вписаны в основания призмы, и наоборот, описанным – если основания описаны около оснований цилиндра. Также, напомним, что высоты у призмы и вписанного, равно как и описанного, цилиндров совпадут (см. Рис. 15).
Теорема. Объем цилиндра равен произведению площади основания на высоту. .
Формула схожа с формулой объема призмы, т. к., по сути, цилиндр – это предельный случай призмы, когда угольник в основании призмы стремится к окружности.
Рис. 16 Вписанная в цилиндр призма
Впишем в данный цилиндр радиуса и высоты правильную -угольную призму . Тогда логично, что в окружность основания цилиндра вписан правильный -угольник. Высота этой призмы будет также (см. Рис. 16).
Найдем объем призмы . Пусть – сторона основания призмы, – центр основания (см. Рис. 17). Тогда
Рис. 17 Треугольник в основании призмы
То есть
Наряду с этим опишем около данного цилиндра правильную -угольную призму .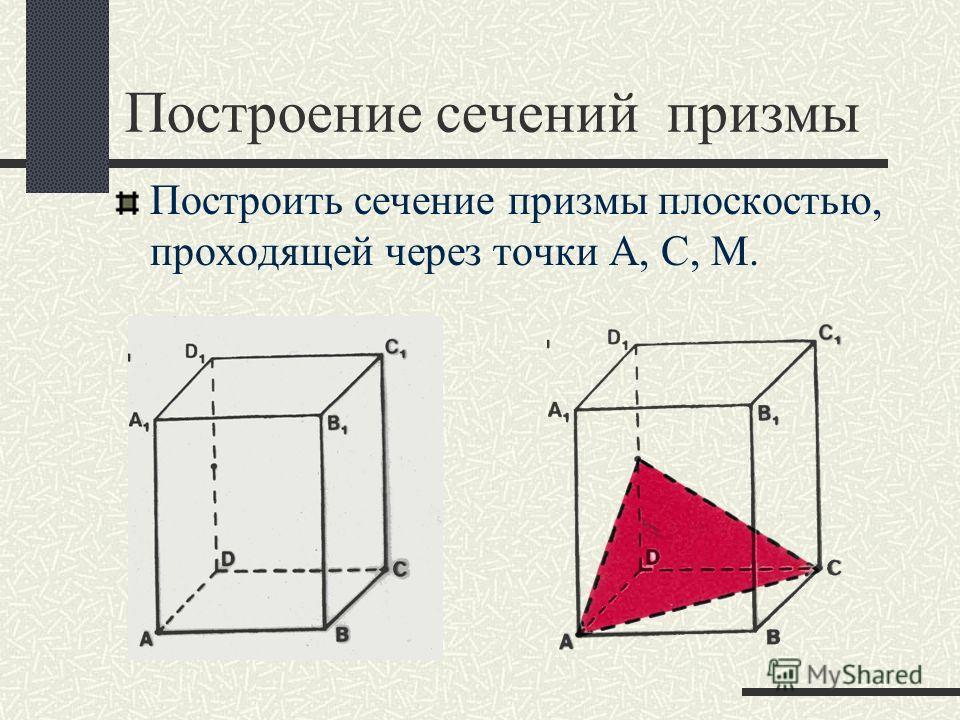 Высота этой призмы будет также (см. Рис. 18).
Высота этой призмы будет также (см. Рис. 18).
Рис. 18 Описанная около цилиндра призма
Рис. 19 Треугольник в основании )
Найдем объем призмы . Пусть – сторона основания призмы, – центр основания (см. Рис. 19). Тогда
То есть .
Таким образом, искомый объем цилиндра удовлетворяет неравенству , то есть он больше объема призмы, вписанной в него, и меньше объема призмы, описанной около него.
Устремим к бесконечности. С помощью замечательного предела можно получить, что обе площади устремятся к площади круга .
Первый замечательный предел
Вспомним замечательный предел: .
Тогда
Аналогично .
Подставляя эти результаты в формулы, получаем требуемый результат.
Значит, получаем, что , что и требовалось доказать.
Пример 2
Площадь основания цилиндра равна , а площадь осевого сечения равна . Найти объем цилиндра (См. Рис. 20).
Рис.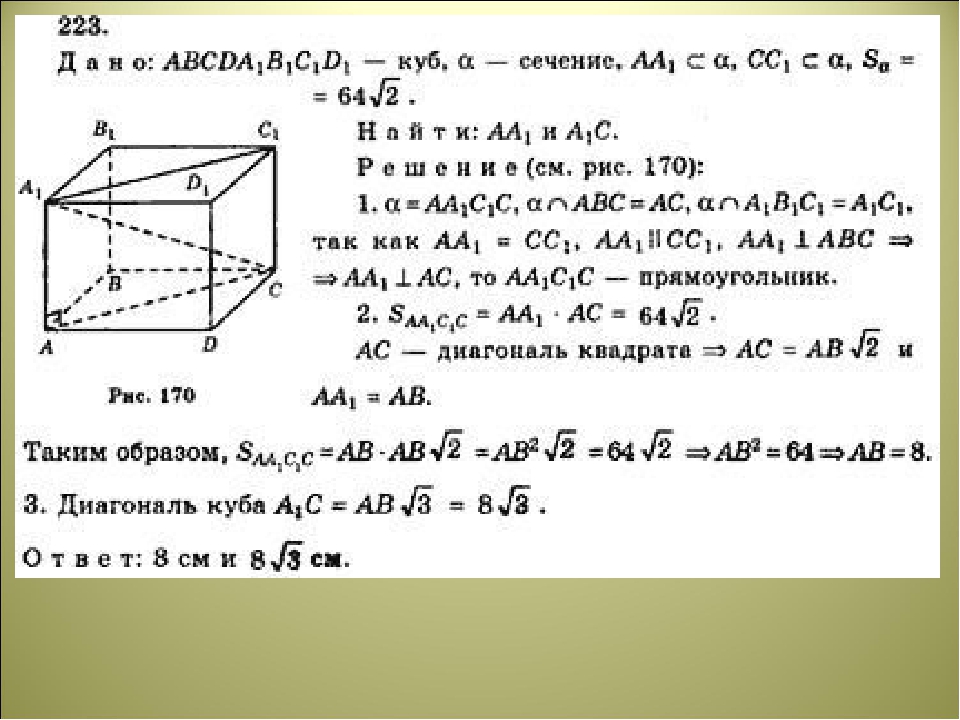 20 Искомый цилиндр
20 Искомый цилиндр
Решение., значит, .
Далее, площадь осевого сечения равна ;
Окончательно, .
Ответ: .
Задача
В цилиндр вписана призма , основанием которой является прямоугольный треугольник (), в котором , , . Найти отношение объемов призмы и цилиндра (см. Рис. 1).
Рис.1 Иллюстрация задачи
Решение.
Рис. 2 Основание призмы
Высота цилиндра равна боковому ребру призмы, т. е.. Найдем площадь основания призмы. Рассмотрим прямоугольный в основании призмы. Катет , а угол напротив этого катета , значит, гипотенуза
(см. Рис. 2).
А радиус описанной около основания окружности – это и есть радиус основания цилиндра. Кроме того, катет (по определению синуса).
Подставим данные в формулы, учитывая, что высоты у фигур совпадают, .
.
Окончательно .
Ответ: .
Заключение
Были разобраны две теоремы: две новые формулы для нахождения объемов прямой призмы и цилиндра. Выяснили, что в обоих случаях .
Выяснили, что в обоих случаях .
Список литературы
1. Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009. – 255 с.
2. А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002.
3. В.Ф. Бутузов, Ю.А. Глазков. Рабочая тетрадь по геометрии 11 класс.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт «ЯКласс» (Источник)
2. Интернет-сайт «Математика? Легко!» (Источник)
3.Интернет-сайт «ЯКласс» (Источник)
Домашнее задание
1. В цилиндр вписана правильная треугольная призма, а в призму вписан цилиндр. Найдите отношение объемов цилиндров.
2. Основание прямой призмы – ромб с острым углом 3. Диагональ боковой грани образует с плоскостью основания угол . Найдите объем призмы, если ее высота равна см.
3. Через одну образующую цилиндра проведены два сечения, угол между плоскостями которых равен , а площадь каждого из полученных сечений равна . Найдите объем цилиндра, если его высота равна см.
Найдите объем цилиндра, если его высота равна см.
| Раздел долгосрочного плана: 11.1 Многогранники | Школа: КГУ «СОШ №58, г. Караганда» | ||||||||||||||||||||||||||||
| Дата: | Учитель: Манагарова Ирина Васильевна | ||||||||||||||||||||||||||||
| Класс: 11 ЕМН | Количество присутствующих: | Количество отсутствующих: | |||||||||||||||||||||||||||
| Тема урока | Призма и ее элементы, виды призм | ||||||||||||||||||||||||||||
| Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | 11.1.3 – знать определение призмы, ее элементов, виды призм; уметь изображать их на плоскости | ||||||||||||||||||||||||||||
| Цели урока | Все: знать определение призмы, элементы призмы, виды призм, изображать треугольную и четырехугольную призмы на плоскости; Большинство: изображать разные виды призм на плоскости; Некоторые: делать развертку призмы. | ||||||||||||||||||||||||||||
| Критерии оценивания | Учащийся: – воспроизводит определение призмы, называет элементы призмы, – изображает разные виды призм на плоскости; – делает развертку призмы. | ||||||||||||||||||||||||||||
| Языковые цели | Учащиеся будут: -правильно использовать математическую терминологию для описания призмы. Предметная лексика и терминология: Призма, точка, прямая, плоскость, пространство, боковая грань, основание, диагональ, смежные грани, противоположные грани, ребро, вершина, невидимые линии, многогранник, многоугольник. Полезные фразы для диалога и письма: – Многогранной призмой называется …; – прямой призмой называется..; – наклонной призмой называется…; – параллелепипедом называется…; – в основании данной призмы лежит…; – боковая поверхность призмы состоит; – диагонали пересекаются … и в точке пересечения… | ||||||||||||||||||||||||||||
| Привитие ценностей | Умение активно учиться, анализировать ситуацию, быстро адаптироваться к новым ситуациям, ставить проблемы и принимать решения, отвечать за качество своей работы и работы группы, умение организовывать свою деятельность с соблюдением регламента. Привитие ценностей осуществляется через контент заданий, запланированных на данном уроке. | ||||||||||||||||||||||||||||
| Межпредметные связи | Изучение данного раздела расширит знания учащихся по геометрии, Учащиеся получат представление о применении стереометрии в сферах науки и техники, архитектуре и строительстве, проектировании и конструировании. Физика и химия: строение кристаллической решетки. Черчение: построение и чтение чертежей. | ||||||||||||||||||||||||||||
| Навыки использования ИКТ | Использование интерактивной доски в качестве демонстрационного средства и средства записи. Модели фигур.Поисковые системы.Справочники.Таблицы. | ||||||||||||||||||||||||||||
| Первоначальные знания | Знание аксиом планиметрии и стереометрии; понимание взаимного расположения и изображения нескольких прямых на плоскости, прямой и плоскости, плоскостей; умение находить расстояния и углы на плоскости, знание свойств плоских многоугольников. | ||||||||||||||||||||||||||||
| Ход урока | |||||||||||||||||||||||||||||
| Запланированные этапы урока | Виды упражнений, запланированных на урок: | Ресурсы | |||||||||||||||||||||||||||
| Начало урока 5 минут | Организационный момент – уточняется готовность учащихся к уроку. Целеполагание. Предлагается перечислить все геометрические фигуры, встречающиеся в видеоролике. Демонстрация видеоролика «ТОП-4 самых ярких архитектурных проектов Казахстана» – дается возможность высказать свое мнение учащимся. – Здания, какой формы чаще всего встречаются в современной архитектуре и строительстве? Учителем предлагается определить тему и цели обучения вместе с учащимися (критерии выполнения задания на уроке) Организуется определение «зоны ближайшего развития» учащихся, как ожидаемые ими результаты в конце урока. | Ютуб видео: https://youtu.be/aPS796bUoYg | |||||||||||||||||||||||||||
| Середина урока 15-20 минут Защита постеров 14 минут 1 минута | Изучение нового материала Прием активного обучения «Лото». Заполняется таблица, в шапку которой вписываются критерии оценки деятельности. ГР. Задание 1. Составьте постер о своей призме, всех ее элементах, особенностях, возможном использовании… и т.д. Итоги представьте в таблице. Учителем предлагается провести мини-исследование, как деятельность, направленную на формирование знаний и навыков, связанных с целями урока. Учащиеся объединяются в пять рабочих групп. Группы получают разные геометрические тела: непрозрачную призму прямую или наклонную.
Г Р. Критерий: воспроизводит определение призмы, называет элементы призмы Дескриптор: Обучающийся – называет элементы призмы; – определяет число и геометрическую форму каждого элемента призмы; – называет вид призмы: – формулирует определение данного вида призмы; – называет примеры возможного применения фигуры данной формы. Оценивание: Самооценивание по дескрипторам Дополнительные (возможные) вопросы группам от других групп или учителя при защите постера: Количество элементов вашей призмы… Какой фигурой может быть боковая поверхность призмы? Количество ребер, сходящихся в одной вершине? Как может выглядеть развертка. Определите вид или название призмы, используя ее элементы. На этапе защиты постеров организуется самооценивание своей и других групп, предлагается провести формативное само- и взаимооценивание по методу «Две звезды, одно пожелание» . (Примерный набор фигур) Для учащихся, работающих в более высоком темпе, предлагается дополнительные задания: Уровень В. Начертить прямую призму более крупного формата. Начертить наклонную призму более крупного формата. Критерий: изображает разные виды призм на плоскости Дескрипторы: Обучающийся: – выполняет чертеж призмы по ее развертке в каждом случае; – определяет, называет вид призмы в каждом случае; – называет элементы призмы на рисунке; – указывает невидимые линии на рисунке. Оценивание: Взаимооценивание по дескрипторам. Устные комментарии учителя Уровень С Начертите развертку многогранника (прямая шестигранная призма) по модели Критерий: делает развертку призмы Дескрипторы : Обучающийся -определяет число и форму оснований призмы; – определяет число и форму элементов боковой поверхности; – определяет вид призмы прямая или наклонная; – выполняет чертеж развертки данной призмы. Оценивание: Взаимооценивание по дескрипторам. Уровень С Объединить информацию всех 5 групп в один кластер, во время выступления групп (используя возможности интерактивной доски) Составить кластер – паучек «Призма и ее возможности» Информирование о домашнем задании: (продолжаем исследование) № 1.40, стр 22. Назовите многогранник и укажите его развертку.
2. Из плотной бумаги изготовьте одну модель призмы. Покажите и назовите все её элементы. Из трубочек соберите одну модель призмы. Сравните полученные модели. Чем они различаются? 3.Ютуб видео «Призма» и «Prizm» Видео: https://youtu.be/khl8j_F8Ytg; https://youtu.be/BHd7XLjAbro. | У 1. А. Н. Шыныбеков, Д. А. Шыныбеков, Р. Н. Жумабаев, С. С. Маделханов. Геометрия – 11, под общей редакцией М. Отелбаева, «Атамұра», Алматы, 2020. 2. А. Н. Шыныбеков, Д. А. Шыныбеков, Р. Н. Жумабаев, С. С. Маделханов. Дидактические материа- лы, «Атамұра», Алматы, 2020. 3. А. Н. Шыныбеков, С. С. Маделханов. Прикладная наглядная сте- реометрия. Дополнитель- ные электронные ресурсы: http://bilimland.kz/ru Набор деревянных непрозрачных призм Листы А-3, А-4 Карандаши, маркеры, большие линейки Интерактивная доска Листы А-3, А-4 Карандаши, маркеры, большие линейки Источник : А. Д. А. Шыныбеков, Р. Н. Жумабаев, С. С. Маделханов. Геометрия – 11, под общей редакцией М. Отелбаева, «Атамұра», Алматы, 2020. | |||||||||||||||||||||||||||
| Конец урока 5 минут | Рефлексия учеников в конце урока: «Поймай мяч», допускается «Отброшенный вопрос» Начало урока: учитель организует определение «зоны ближайшего развития» учащихся, как ожидаемые ими результаты в конце урока. Конец урока: Учитель предлагает учащимся высказаться по следующим вопросам: – Как Вы думаете, что из того, чему Вы научились на уроке, Вам пригодится в дальнейшем? – В каких современных профессиях могут пригодиться эти знания, навыки? – Где Вы встречаете призмы уже сейчас? – Что из того, чему научились сегодня, существенно важно для Вас (знания или навыки)? – Были ли на уроке вопросы, непонятные Вам? Как бы Вы хотели их закрепить? – В каком направлении необходимо работать дома? – Есть ли какие-либо мысли или мнения, которые Вы хотели бы добавить? – Как Вы можете оценивать свою работу и работу одноклассников по определенным нами вместе в начале урока критериям. | Мяч Постер с вопросами. | |||||||||||||||||||||||||||
| Дифференциация – каким способом вы хотите больше оказывать поддержку? Какие задания вы даете ученикам более способным по сравнению с другими? | Оценивание – как Вы планируете проверять уровень усвоения материала учащимися? | Охрана здоровья и соблюдение техники безопасности | |||||||||||||||||||||||||||
| Для более полного учета потребностей и продвижения каждого ученика, подобраны способы дифференциации, с учетом уровня восприятия учащихся. Поддержка осуществляется в рабочей группе и индивидуально на каждом этапе урока. На начало урока запланирована постановка учащимися целей, в формате SMART. Организуется определение «зоны ближайшего развития» учащихся, как ожидаемые ими результаты в конце урока. Цели учащихся формируют критерии заданий, выполняемых в ходе урока. Дифференциация – группировка. Учащиеся объединяются в равносильные, по уровню знаний, группы – учитывается мотивация к предмету (уровень А- слабомотивированные, В – со средним уровнем знаний, С- высоко мотивированные учащиеся) Поддержка и помощь группам оказывается учителем по запросу или при явном затруднении в продвижении. На основном этапе урока – изучении нового материала – предложено минииследование. Присутствует дифференциация по заданиям. Ученикам раздаются разные призмы: прямые и наклонные, с разным количеством граней. Создание конечного продукта: таблицы и постера, защита своей работы позволит учащимся с разным уровнем подготовки проявить свои навыки. Использется дифференциация по темпу, как выбор и выполнение индивидуального задания учащимися уровня В и С. Работа с дополнительными источниками информации, работа на интерактивной доске, поисковых системах, таблицах, справочниках. Домашнее задание дается общее, но его выполнение – по уровню знаний учащихся. | Уровень освоения учебного материала учащимися будет отслеживаться через формативное оценивание. Критерии разработают учащиеся, исходя из цели урока. Работа над заданиями с использованием дескрипторов позволит учителю понять продвижение к достижению цели урока. В ходе урока используются: формативное оценивание, устные комментарии учителя, самооценивание по дескрипторам, взаимооценивание групп и отдельных учащихся. При выполнении каждого задания запланировано самооценивание, взаимооценивание, как оценивание для обучения. Во время этапа рефлексивной деятельности учащихся запланировано самооценивание, через вопросы, побуждающие к дальнейшему продвижению, росту, мотивации учащихся. «Поймай мяч» и выскажи своё мнение, а так же, «Отброшенный вопрос», как дополнение к ответу участника группы или озвучивания собственной версии ответа. | Использование активных методов обучения, смена видов деятельности, различные приемы, стратегии – позволят учащимся быть активными на протяжении всего урока, не чувствовать усталости, продуктивно работать. С целью создания благоприятной эмоциональной среды группы формируются не случайным образом. Учитывается уровень учебной мотивации учащихся, их психологическая совместимость. Учитель оказывает поддержку, мотивирует к продвижению и успеху, организовывает позитивную формативную оценку деятельности. Выбранные формы и методы, позволяют учащимся свободно общаться, высказывать свою точку зрения; возможно, отстаивать ее. Защищать и представлять продукт совместного труда, что побуждает их к сотрудничеству, взаимообучению, повышает личную ответственность за конечный результат. | |||||||||||||||||||||||||||
| Рефлексия по уроку Была ли реальной и доступной цель урока или учебные цели? Все ли учащиеся достигли цели обучения? Если ученики еще не достигли цели, как вы думаете, почему? Правильно проводилась дифференциация на уроке? Эффективно ли использовали вы время во время этапов урока? Были ли отклонения от плана урока, и почему? | Используйте данный раздел урока для рефлексии. | ||||||||||||||||||||||||||||
| Итоговая оценка Какие две вещи прошли действительно хорошо (принимайте в расчет, как преподавание, так и учение)? 1: 2: Какие две вещи могли бы улучшить Ваш урок (принимайте в расчет, как преподавание, так и учение)? 1: 2: Что нового я узнал из этого урока о своем классе или об отдельных учениках, что я мог бы использовать при планировании следующего урока? | |||||||||||||||||||||||||||||
20 Упражнения с призмой по естественным наукам и геометрии для учащихся старших классов
Популярный тест: Что такое трехмерный объект с одинаковыми концами и параллельными сторонами? призма! С помощью призм были сделаны важные научные открытия. Например, призмы помогли продемонстрировать, что белый свет состоит из цветов радуги! Геометрические свойства призм также важно понимать, поскольку эти формы используются для создания различных технологий, включая телескопы и микроскопы. Этот список из 20 увлекательных упражнений с призмой предназначен для того, чтобы ваши ученики были в восторге от светопреломляющих и геометрических свойств призмы!
Этот список из 20 увлекательных упражнений с призмой предназначен для того, чтобы ваши ученики были в восторге от светопреломляющих и геометрических свойств призмы!
Научные занятия
1. Посмотрите Шоу доктора Бинокса
В этом анимационном видео подробно и понятно для детей объясняется, что такое призма и как она может преломлять свет, создавая радугу. Вы можете показать это видео своим детям в качестве краткого введения в призмы.
Узнать больше: Peekaboo Kidz
2. Смотреть Учителя Фредди
Вот еще одно видео, объясняющее призмы и то, как они могут создавать радужные узоры.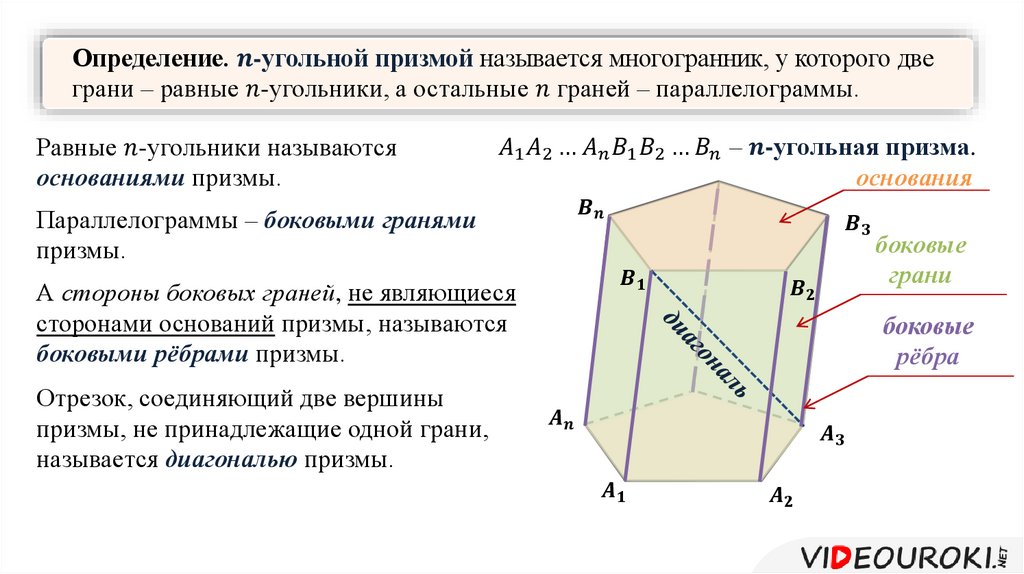 В этом видео также описывается, как процесс создания радуги из призм (преломление света) аналогичен тому, что происходит, когда радуга создается в небе после дождя.
В этом видео также описывается, как процесс создания радуги из призм (преломление света) аналогичен тому, что происходит, когда радуга создается в небе после дождя.
Узнать больше: учитель Фредди
3. Призмы и солнечный свет
Игра с треугольными или хрустальными призмами на солнце может занять некоторых учеников на несколько часов. Они заметят привлекательные радужные узоры на стене, когда свет проходит через их призму.
Узнайте больше: Маленькие корзины для маленьких ручек
4. Радуга дождя
Узнав, что капли дождя могут действовать как призмы, образуя радугу в небе, ваш класс может получить захватывающую возможность на свежем воздухе понаблюдать за природой. радуга. Когда это чудо появится в поле зрения, вы сможете вместе изучить науку о радуге!
Узнать больше: Engineering Emily
5. Эксперимент с призмой источника света
Различается ли цветовой узор радуги от призмы в зависимости от источника света? Ваши дети могут исследовать этот вопрос с помощью эксперимента, в котором сравниваются лампы накаливания, люминесцентные лампы и кадмиевый свет. Вы можете проверить ресурс ниже для списка вопросов наблюдения.
Вы можете проверить ресурс ниже для списка вопросов наблюдения.
Подробнее: NASA
6. Самодельная призма с зеркалом
Учащиеся могут сделать самодельную призму, используя зеркало, помещенное в емкость с водой. При размещении рядом с солнечным окном радужный узор преломления будет отражаться на стене.
Узнать больше: НАСА
7. Самодельная призма со стеклом
Вот еще одна самодельная призма для ваших малышей. Ваши ученики могут вырезать отверстие в куске картона и поставить его рядом со стаканом воды. Они должны разместить эти элементы таким образом, чтобы солнечный свет проходил через отверстие в стекло. Затем они могут положить лист белой бумаги и наблюдать за радугой.
Подробнее: Зал науки им. Лоуренса
8. Раскраска
Достаньте цветные карандаши, пришло время раскрашивать! Ваши ученики могут раскрасить эту картинку преломляющего призму света. Порядок цветов важен, так как их положение зависит от длины волны света.
Узнать больше: Twinkl
9. Эксперимент с призмой Ньютона
Откуда мы знаем, что белый свет состоит из этих цветов, а не что эти цвета воспроизводятся призмой? Вы можете рассказать своим детям об известных экспериментах, доказывающих это. Возможно, вы могли бы провести демонстрацию в классе.
Дополнительная информация: Khan Academy India – English
10. Интерактивный эксперимент с призмой
Если у вас нет призм под рукой, ваши ученики могут использовать этот интерактивный ресурс для управления призмами с помощью света. Он включает в себя белый свет и две призмы, чтобы ваши ученики могли воссоздать эксперименты Ньютона с призмой.
Дополнительные сведения: молекулярные выражения
Геометрические упражнения
11.
 Заполни их
Заполни их Физические демонстрации могут быть одними из наиболее эффективных методов обучения учащихся объему призм. Для этого задания попросите их собрать маленькие и пустые коробки, чтобы заполнить их кубиками. Ваши ученики узнают, как количество кубиков связано с объемом коробки.
Узнайте больше: классная комната Hooty’s
12. Соберите свои собственные коробки
Ваши ученики могут создавать 3D-коробки, используя бумагу с сеткой, ножницы и ленту. Затем они могут исследовать, как размеры их коробок соотносятся с общим объемом призм.
Подробнее: классная комната Hooty’s
13. Бумажная треугольная призма
Ваши ученики могут изучить форму треугольной призмы, соорудив ее самостоятельно с помощью этого бумажного шаблона. Они могут сделать это, сложив бумагу по пунктирным линиям и склеив или склеив края вместе.
Узнать больше: Образование
14. Цифровая квест-комната по математике
Ваши ученики были заперты в классе сумасшедшим математиком и должны использовать свои навыки решения математических задач, чтобы вырваться! Эта квест-комната содержит 3 головоломки с прямоугольными призмами.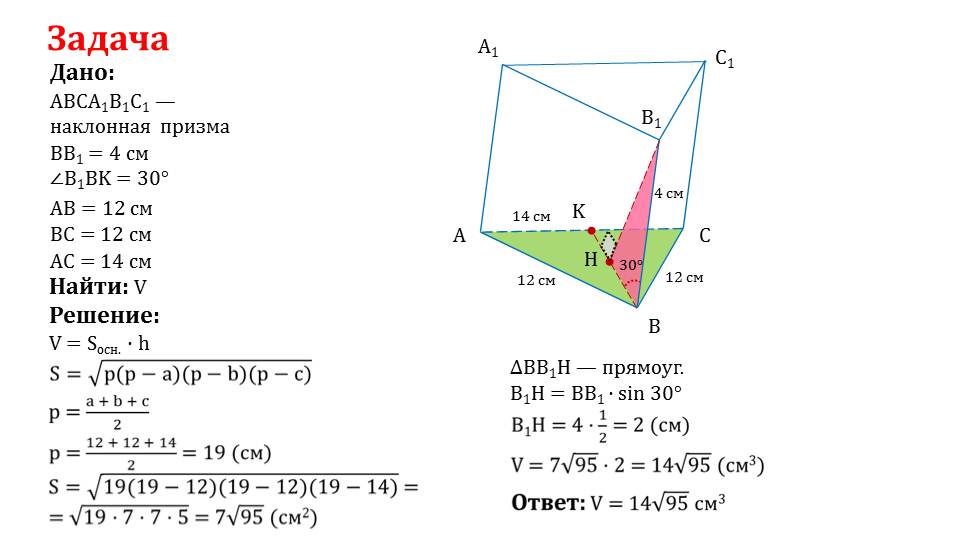 Выбирайте между печатной или онлайн-версией!
Выбирайте между печатной или онлайн-версией!
Узнать больше: Science Spot
15. Пиксель-арт с площадью поверхности
Вы не часто видите искусство на уроках математики, но эти занятия с цифровым пиксельным искусством собираются это изменить! Ваши учащиеся могут правильно ответить на вопросы о площади поверхности прямоугольных и треугольных призм, чтобы показать прекрасное цифровое произведение искусства, пиксель за пикселем.
Узнать больше: Яблоки и алгебра
16. Площадь поверхности треугольных призм Лабиринт
Включение головоломок или лабиринта может сделать решение математических задач немного веселее! В этом печатном упражнении с лабиринтом ваши ученики будут решать площадь поверхности треугольных призм, чтобы добраться до конечной точки.
Подробнее: Учителя платят учителям
17. Лабиринт с объемами призм
Ваши ученики могут попрактиковаться в решении объемов прямоугольных и треугольных призм в этом альтернативном лабиринте. Он доступен как в печатном, так и в цифровом формате!
Он доступен как в печатном, так и в цифровом формате!
Узнать больше: Учителя платят учителям
18. Площадь поверхности призмы Рабочий лист
Мне нравится использовать время в классе для практического обучения и занятий, но рабочие листы по-прежнему являются ценным ресурсом для ваших учеников, чтобы практиковать то, что они имеют научился. Этот рабочий лист посвящен решению площади поверхности треугольных призм.
Подробнее: Рабочие листы по математике 4 Kids
19. Рабочий лист «Объем призм»
Этот рабочий лист посвящен решению объема призм. На этом веб-сайте есть множество рабочих листов, с которыми вы можете ознакомиться по другим темам уроков математики.
Узнать больше: Math Worksheets 4 Kids
20. Смотреть FuseSchool
FuseSchool — отличный ресурс для уроков математики и руководств. В этом видео обсуждается нахождение объема призм. Он начинается с определения того, что такое призма, а затем проходит через формулу нахождения объема как прямоугольной, так и треугольной версий.
В этом видео обсуждается нахождение объема призм. Он начинается с определения того, что такое призма, а затем проходит через формулу нахождения объема как прямоугольной, так и треугольной версий.
Узнайте больше: FuseSchool – Глобальное образование
Похожие сообщения:
Формула призмы – объяснение, свойства, типы, формула
Призма представляет собой пятигранный многогранник с треугольным поперечным сечением. В призме два одинаковых параллельных треугольника напротив друг друга. Вместе с треугольниками наклонены друг к другу три прямоугольные поверхности. Призма — это прозрачное твердое тело, используемое для преломления. Две наклонные прямоугольные поверхности, через которые проходит свет, называются преломляющими поверхностями. Угол, образованный между этими двумя преломляющими поверхностями, называется преломляющим краем призмы. Сечение призмы, перпендикулярное преломляющему ребру, называется главным сечением призмы. Третья прямоугольная поверхность внизу является основанием призмы.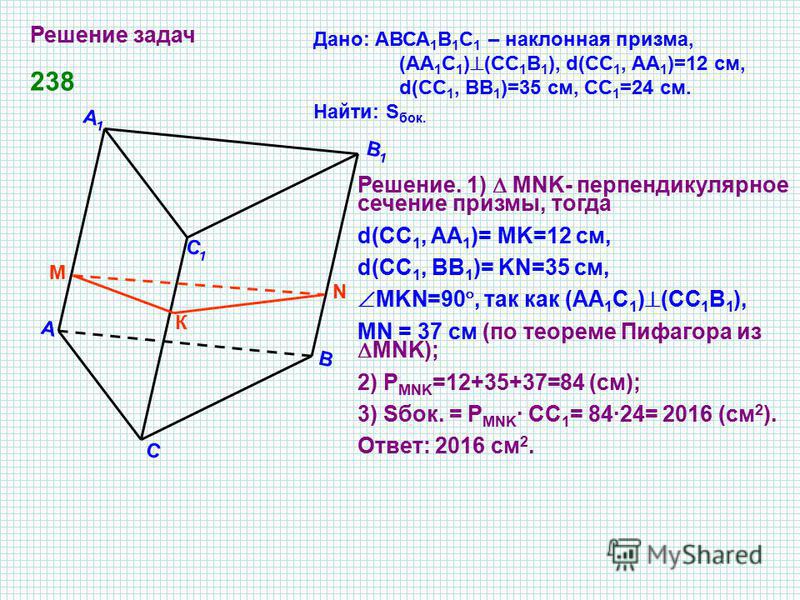
(Изображение будет загружено в ближайшее время)
Опять же, на вопрос, что такое призма, можно ответить двумя способами, поскольку ее понятие используется как в математике, так и в естественных науках. В математике призма определяется как многогранник. В физике (оптике) призма определяется как прозрачный оптический элемент с плоскими и полированными поверхностями, используемый для преломления света. Есть две формулы призмы.
-
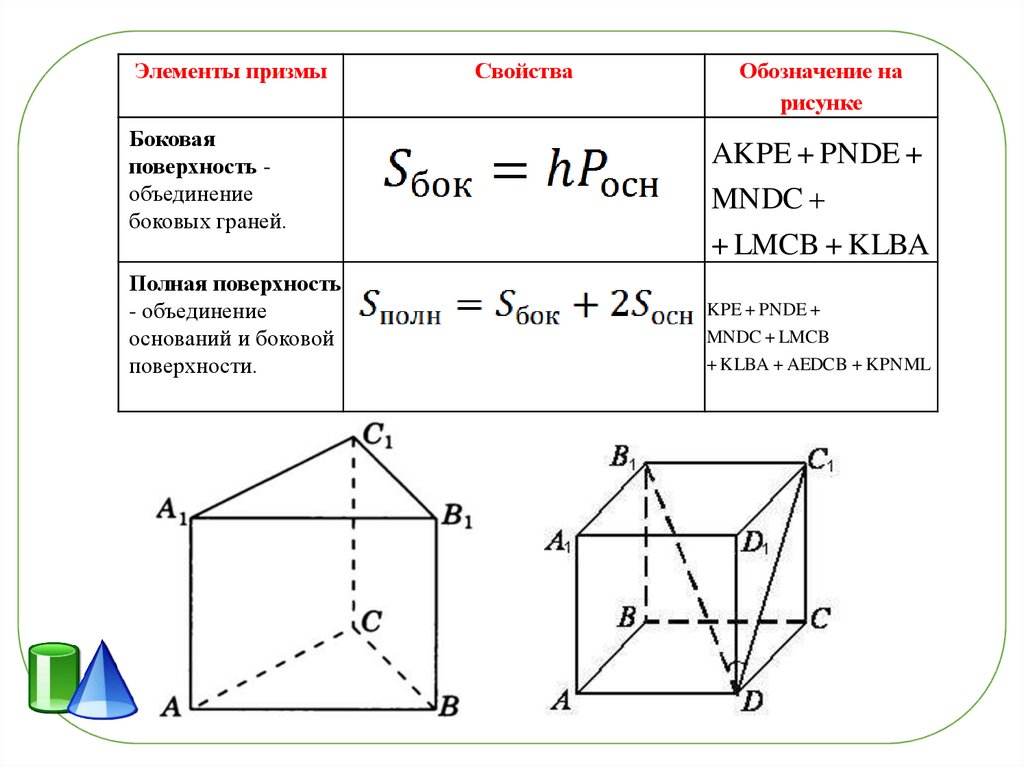
Площадь поверхности призмы = (2×BaseArea) + Площадь боковой поверхности
-
Свойства призмы
Теперь, когда мы знаем, что такое призма, мы можем легко узнать свойства призмы.
-
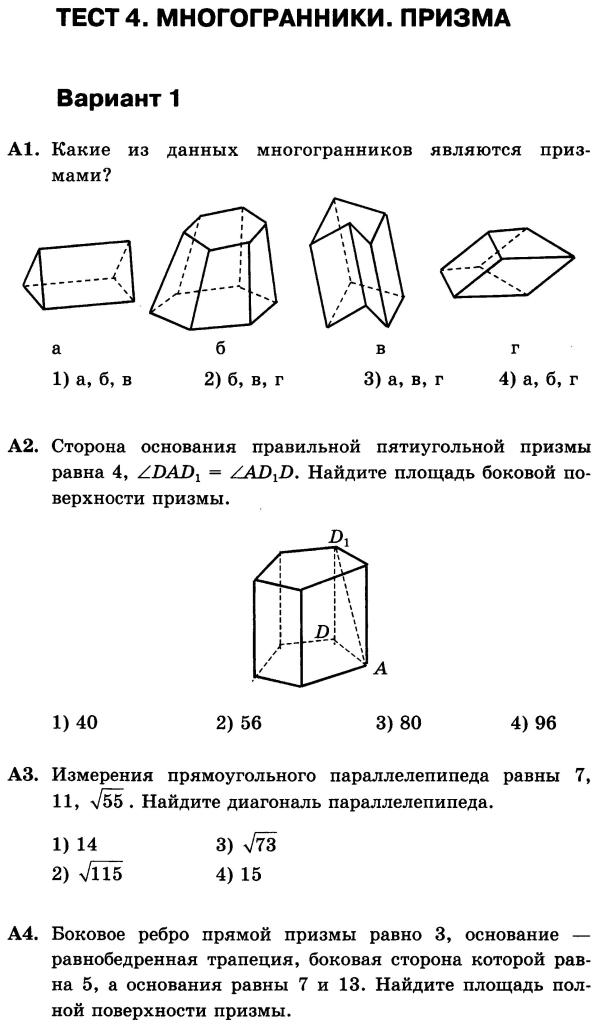
Среди всех свойств призмы самым основным является то, что основание и вершина призмы параллельны и конгруэнтны.
-
В призме, кроме основания и вершины, каждая грань представляет собой параллелограмм. Эти грани известны как боковые грани.
-
Основание и вершина имеют по одной кромке, общей с каждой боковой гранью.
-
Высота призмы в основном равна общей кромке двух смежных боковых граней.
Типы призм
Существуют различные типы призм. Вот некоторые из них:
-
Прямоугольная призма. В прямоугольной призме 2 прямоугольных основания параллельны друг другу и 4 прямоугольные грани.
-
Треугольная призма: Треугольная призма состоит из 2 параллельных треугольных поверхностей, 2 прямоугольных поверхностей, наклоненных друг к другу, и 1 прямоугольного основания.

-
Пятиугольная призма: В пятиугольной призме 2 пятиугольные поверхности параллельны друг другу и 5 прямоугольных поверхностей наклонены друг к другу.
-
Шестиугольная призма: В шестиугольной призме есть 2 шестиугольные поверхности, параллельные друг другу, и 6 прямоугольных поверхностей, наклоненных друг к другу.
Это были несколько различных типов призм.
(Изображение будет загружено в ближайшее время)
Различные типы призм
Могут быть еще два других типа призм, которые также могут быть прямой призмой и косой призмой.
(Изображение скоро будет загружено)
Площадь основания
-
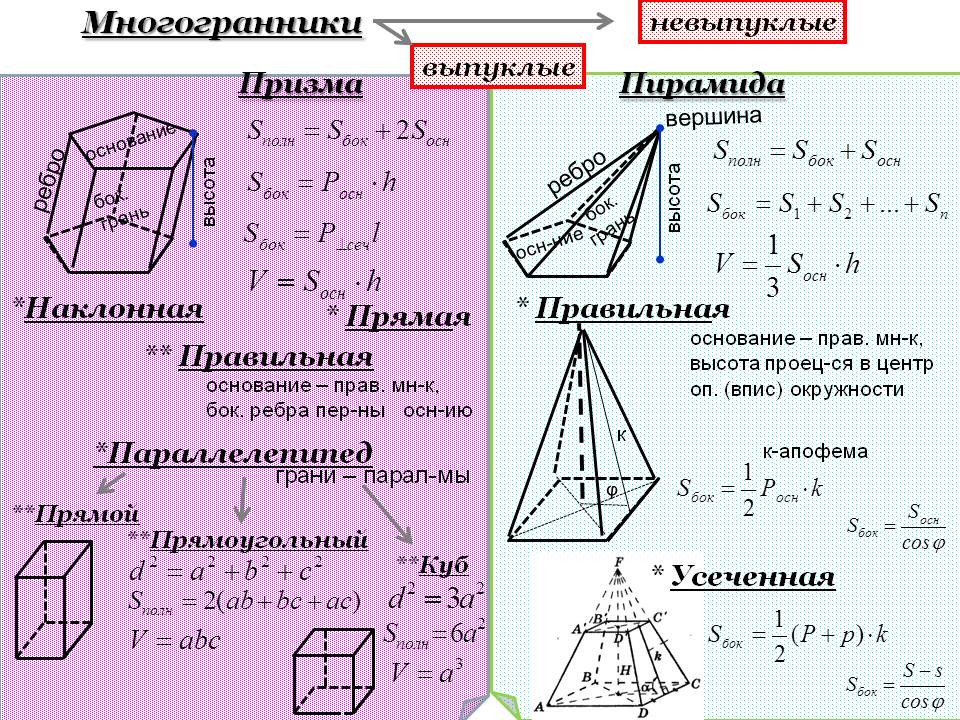
Формула площади основания прямоугольной призмы = длина основания x ширина основания.
-
Площадь основания треугольной призмы по формуле = ½ x длина апофемы x длина основания.
-
Площадь основания пятиугольной призмы формула = 5/2 x длина апофемы x длина основания.
-
Площадь основания шестиугольной призмы формула = 3 x длина апофемы x длина основания.
Площадь поверхности призмы
-
Площадь поверхности прямоугольной призмы формула = 2 x (длина основания x ширина основания) + (ширина основания x высота) + (высота x длина основания)
-
Площадь поверхности треугольной призмы по формуле = (длина апофемы х длина основания) + 3 х (длина основания х высота) +5 х (длина основания х высота)
-
Площадь поверхности шестиугольной призмы = 6 х (длина апофемы х длина основания) + 6 х (длина основания х высота)
Объем призмы А
-
Формула объема прямоугольной призмы = ширина основания x длина основания x высота
-
Формула объема треугольника = ½ x длина апофемы x длина основания x высота
Формула объема пятиугольной призмы = 5/2 x длина апофемы x длина основания x высота
-
Формула объема шестиугольной призмы = 3 x длина апофемы x длина основания x высота
Найдите объем призмы
Объем призмы можно рассчитать с помощью следующих процедур:
-
Сначала запишите размеры призмы.
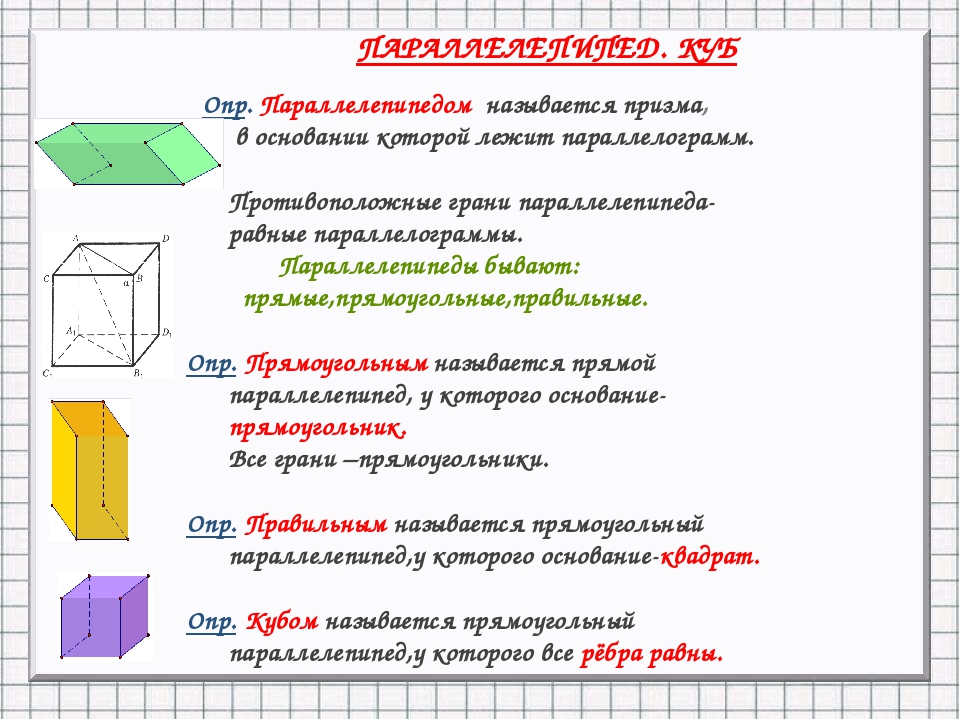
- Используя формулу V = BH, найдите объем призмы, где «V», «B» и «H» — объем, площадь основания и высота призмы соответственно.
-
После того, как вы рассчитаете объем призмы, запишите единицу объема призмы в конце (в кубических единицах).
Решенные примеры
Пример 1. Основание прямоугольной призмы, длины сторон которой равны 13 см, 20 см и 21 см. Если высота призмы 9 см. Найти:
-
Площадь полной боковой поверхности.
-
Площадь всей поверхности.
-
Объем призмы.
Решение 1. Пусть полупериметр треугольного основания призмы равен s.
Следовательно, S = (13 + 20 + 21)/2 см.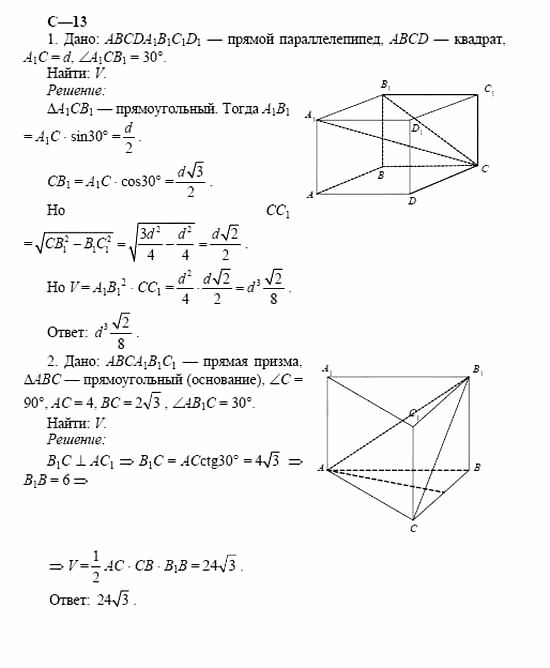
Площадь призмы = √[s(s – a)(s – b)(s – c)]
= √(27(27 – 13)(27 – 20)(27 – 21 )) кв.см.
= √(27 × 14 × 7 × 6) кв.см.
= 9×7×2 кв.см.
Площадь полной боковой поверхности призмы = (периметр основания) × высота
= (486 + 2 × 126) кв.см.
Объем призмы = площадь основания × высота
= 126 × 9 куб.см.
= 1134 куб.см.
Пример 2: Найдите площадь поверхности треугольной призмы, если длина апофемы = 5 см, длина основания = 10 см и высота = 18 см.
Решение 2: Имеем:
Длина апофемы = 5 см;
Длина основания = 10 см;
высота = 18 см
Площадь поверхности треугольной призмы = ab + 3bh
= (5 см × 10 см) + (3 × 10 см × 18 см)
= 50 см 2 + 540 см 2
= 590 см 2
Интересные факты
-
Призма способствует преломлению света.
 Он расщепляет свет на множество различных цветов, которые известны как спектр.
Он расщепляет свет на множество различных цветов, которые известны как спектр.
Разница между пирамидой и призмой
-
И пирамида, и призма представляют собой трехмерные структуры в форме многогранника, причем разница в их основаниях является наиболее существенной.
-
У призмы два основания, а у пирамиды только одно.
-
Стороны пирамиды всегда треугольные, тогда как стороны призмы всегда прямоугольные.
-
Стороны пирамиды расположены под углом к основанию, тогда как стороны призмы перпендикулярны основанию.
-
Стороны пирамиды всегда соединены вместе в одной точке; тогда как стороны призмы не всегда соединяются в одной точке.



 Навыки построения чертежей на плоскости.
Навыки построения чертежей на плоскости.
 В ходе работы у учеников формируются знания в области моделирования, сбора и обработки информации, исследования и практической работы, за счет решения поставленных проблем формируются знания и развиваются навыки самостоятельной и совместной групповой деятельности.
В ходе работы у учеников формируются знания в области моделирования, сбора и обработки информации, исследования и практической работы, за счет решения поставленных проблем формируются знания и развиваются навыки самостоятельной и совместной групповой деятельности.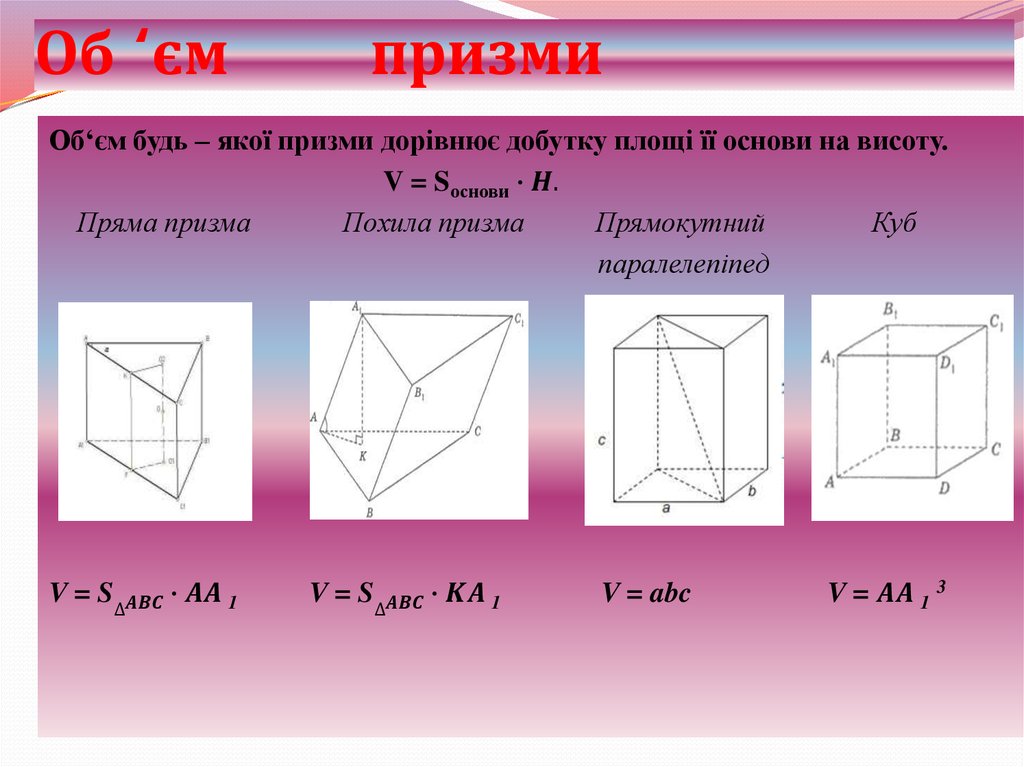 Задание 1. Составьте постер о своей призме, всех ее элементах, особенностях, возможном использовании… и т.д. Итоги представьте в таблице.
Задание 1. Составьте постер о своей призме, всех ее элементах, особенностях, возможном использовании… и т.д. Итоги представьте в таблице. 

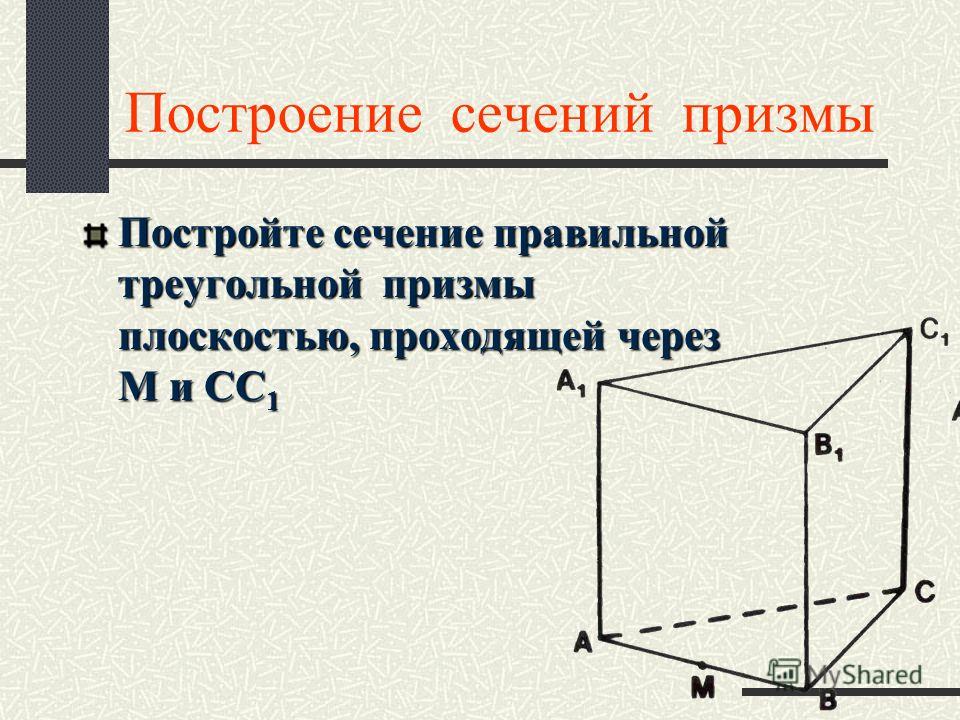 Д/З. Творческое.
Д/З. Творческое. Н. Шыныбеков,
Н. Шыныбеков,
 Вывод о сходстве и различиях призм выводит учащихся на уровень «анализ- синтез», что по силам более мотивированным в учебной деятельности. Дифференциация по заключению.
Вывод о сходстве и различиях призм выводит учащихся на уровень «анализ- синтез», что по силам более мотивированным в учебной деятельности. Дифференциация по заключению.
 Ответьте на вопросы, которые имеют важное значение в этом столбце.
Ответьте на вопросы, которые имеют важное значение в этом столбце.