Конспект занятия по формированию элементарных математических представлений в старшей группе на тему: «Геометрические фигуры».
Задачи:
Образовательные:
Закрепить знание геометрических фигур.
Совершенствовать навыки счета в пределах 10.
Учить составлять из геометрических фигур елочку и снеговика.
Формировать умение ориентироваться на листе бумаги.
Развивающая:
Воспитательная:
Демонстрационный материал: фигура котёнка из геометрических фигур на ватмане; карточки с геометрическими фигурами (круг, треугольник, квадрат, прямоугольник, овал, ромб), 2 маски, состоящие из геометрических фигур на ватмане; карточки с разными предметами для физминутки.
Раздаточный материал: математический набор для каждого ребенка; листы бумаги по количеству детей; печенье в виде любой геометрической фигуры по количеству детей.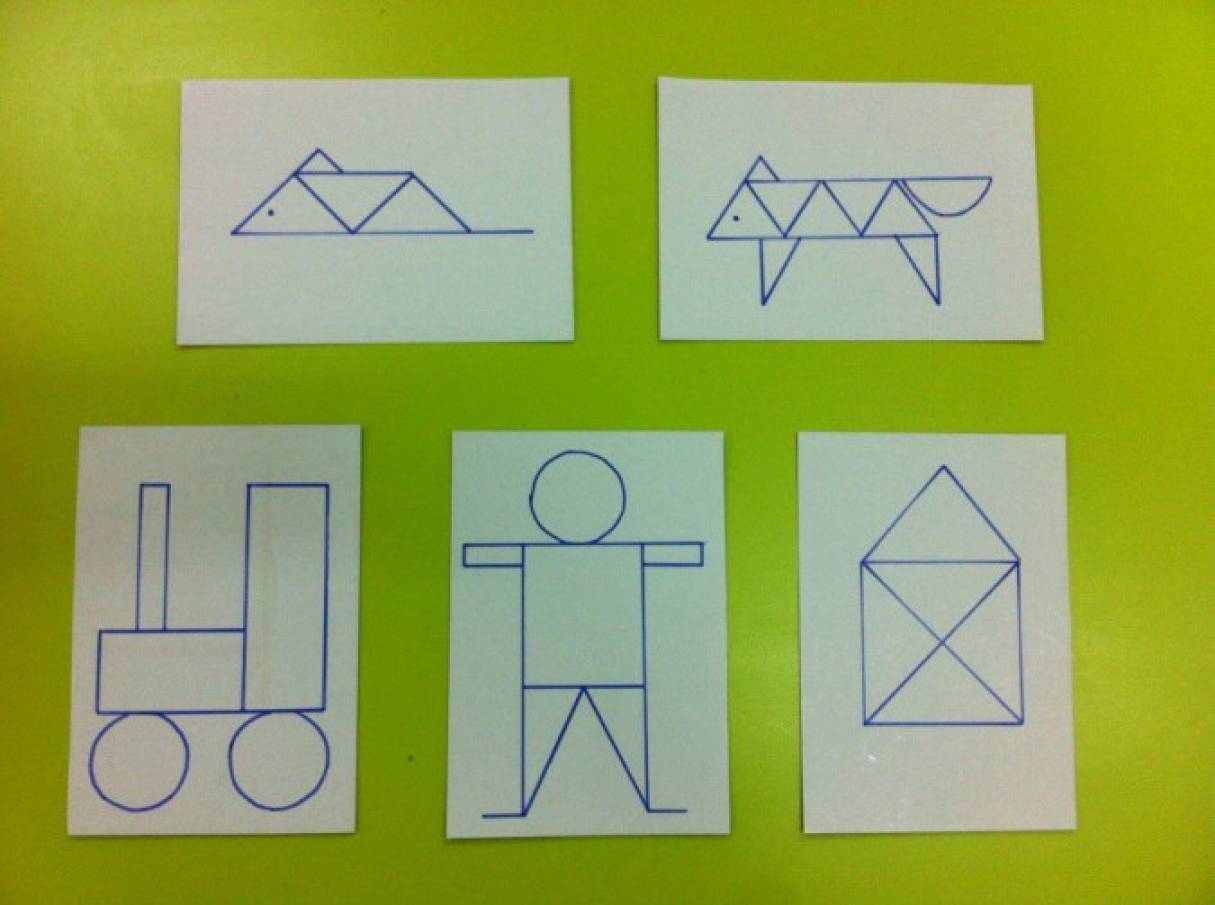
Ход занятия.
Постановка целей.
-Ребята, сегодня мы с вами отправимся в необычную страну. Что это за страна вы попробуете догадаться сами. Сначала отгадайте загадки и скажите, о каких предметах идёт речь, как одним словом их можно назвать.
1. Нет углов у меня,
И похож на блюдце я,
На тарелку и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья? ( Круг)
Три вершины, три угла,
Три сторонки – кто же я? (Треугольник)
Я фигура хоть куда,
Очень ровная всегда,
Все углы во мне равны
И четыре стороны.
Кубик – мой любимый брат,
Потому что я… (квадрат).
Растянули мы квадрат
И представили на взгляд,
На кого он стал похожим
Или с чем-то очень схожим?
Не кирпич, не треугольник –
Стал квадрат…(прямоугольник).
Это всё геометрические фигуры.
И сегодня мы побываем с вами в стране геометрических фигур. Для этого нам нужно хорошо знать геометрические фигуры и различать их. А также уметь хорошо считать и быть очень внимательными. Впереди вас ждет много интересных заданий.
Игровое упражнение «Заметь всё».
На фланелеграфе выставляются в один ряд карточки с геометрическими фигурами: круг, квадрат, треугольник, овал, прямоугольник. Детям предлагают рассмотреть их в течение 10 секунд. Затем карточки закрываются.
-Ребята, какие фигуры вы запомнили?
-Сколько их?
-Какого они цвета?
-В какой последовательности они расположены?
Затем фигуры меняются местами (дети закрывают глаза).
-Посмотрите, что изменилось?
3. Игровое задание «Назови все фигуры».
-Ребята, посмотрите внимательно на рисунок и скажите, из каких геометрических фигур состоит котёнок.
-Каких фигур больше?
4 .Игровое задание «Составь фигурку».
-Ребята, а сейчас попробуйте сами из геометрических фигурок, которые есть в ваших наборах, составить снеговика и ёлочку.
Физминутка.
Воспитатель показывает детям карточки с изображением разного количества предметов, дети считают и выполняют движения в соответствии с текстом.
1.Сколько точек будет в круге,
Столько раз поднимем руки. (3)
2.Сколько ёлочек зелёных,
Столько выполним наклонов. (5)
3. Приседаем столько раз,
Сколько бабочек у нас. (4)
4.Сколько покажу кружков,
Столько выполним прыжков. (6)
5.Ориентировка на листе бумаги.
Дети выполняют задание на листе бумаги.
-В центр листа положите круг.
-В правый верхний угол положите квадрат.
-В правый нижний угол положите треугольник.
-В левый нижний угол положите квадрат.
-В левый верхний угол положите треугольник.
6. Игровое упражнение « Какая фигура лишняя?»
На доске выставлены карточки с геометрическими фигурами.
-Ребята, как вы думаете, какая фигура здесь лишняя и почему?
7.Игровое задание «Найди отличие»
Детям предлагают найти отличие.
-Ребята, посмотрите внимательно и скажите, чем отличаются эти маски.
8. Подведение итогов.
– Вы все молодцы, отлично справились со всеми заданиями. Какое задание было для вас самым интересным? А самым сложным? У меня для вас сюрприз – вкусное печенье. Скажите, какой оно формы?
Каждый ребёнок получает по одному печенью.
Муниципальное бюджетное дошкольное образовательное учреждение «Детский сад № 151»
Конспект НОД по математике в старшей группе:
«Занимательная страна геометрических фигур»
Составила:
Воспитатель
Симакова
Екатерина
Анатольевна
Рязань, 2017
Конспект НОД по математике «Занимательная страна геометрических фигур» для старшей группы.
Интеграция образовательных областей: «Познавательное развитие»; «Социально- коммуникативное развитие»; «Физическое развитие».
Цель: учить классифицировать фигуры по разным признакам; познакомить с трапецией и ромбом.
Задачи:
Образовательные:
– упражнять детей в умении различать и называть знакомые геометрические фигуры: круг, треугольник, квадрат, прямоугольник;
– познакомить с новыми геометрическими фигурами – трапеция и ромб;
– учить находить в окружении предметы четырехугольной формы;
-упражнять в счете в пределах 6.
Развивающие:
– закреплять умение детей составлять фигуры из счетных палочек;
– способствовать развитию мелкой моторики рук;
– развивать слуховое и зрительное внимание, память, наблюдательность, любознательность и воображение;
– развивать способность у детей отгадывать загадки;
– развивать умения выполнять движения в соответствии с текстом.
Воспитательные:
– Воспитывать самостоятельность, умение планировать свою работу
– Воспитывать стремление оказывать помощь другим;
– Воспитывать дружеские взаимоотношения между детьми.
Предварительная работа: рассмотреть плакат «Геометрические фигуры», разгадывание загадок о геометрических фигурах.
Материалы: счетные палочки на каждого ребенка, плакат «Геометрические фигуры», фишки, 2 обруча, набор геометрических фигур разной формы, магнитная доска, карточки с цифрами, набор цифр на каждого ребенка.
Ход НОД:
Организационный момент:
Мы построим ровный круг,
Справа друг и слева друг.
Дружно за руки возьмемся,
И друг другу улыбнемся!
У всех хорошее настроение?
Все забыты огорчения?
Я прошу вас мне сказать
Готовы вы сейчас играть?
(ответы детей).
Воспитатель: Ну тогда вы готовы отгадать мои загадки?
Дети: Да!
Загадки про геометрические фигуры:
Каждый ребенок знает,
Что это напоминает:
Яркое солнышко,
Подсолнуха донышко,
Колеса у машины
И новый мяч у Нины! (круг).
Все четыре стороны – все ,как близнецы, равны,
И прямых угла четыре,
Как у рамки на картине.
К четырехугольникам фигуру отнесем
И …(квадратом) назовем.
Если три стороны и три угла
Вместе соединить,
То сможем тогда очень легко
(Треугольник)… получить.
Велика ли фигура или мала,
Но прямые смотри все четыре угла,
И напротив друг друга две стороны
Меж собою до миллиметра равны,-
Значит это- ….(прямоугольник),
Знает об этом каждый дошкольник!
Воспитатель: Молодцы, ребята! Все загадки отгадали! И сегодня мы отправимся в страну Геометрических фигур и познакомимся с новыми геометрическими фигурами. Послушайте стихотворения.
(Воспитатель показывает новые фигуры на плакате и зачитывает стихотворение).
Трапеция больше на крышу похожа,
Юбку трапецией рисуют тоже,
Взять треугольник и верх удалить,
Трапецию можно так получить.
Ромб -фигура непростая,
Две в себе объединяет:
Треугольник раз и два –
Фигура стала вдруг одна!
Воспитатель: Ребята, а на что похожа трапеция? А ромб? (ответы детей)
-Сколько углов у этих фигур? Подумайте и скажите, как их можно назвать одним словом?(если дети не смогут ответить, предложить им пересчитать все углы и стороны).
– Четырехугольники! Правильно! А теперь, ребята, давайте сядем за столы и выложим из счетных палочек сначала треугольник, затем квадрат, прямоугольник. (Дети выполняют задание).
Воспитатель: Из скольких палочек получился треугольник? (из трех).
А квадрат? (из четырех). А прямоугольник? (из шести). А сейчас, давайте попробуем построить из палочек новые фигуры – трапецию и ромб. Сколько нам понадобится палочек, чтобы построить трапецию? (пять палочек). А чтобы построить ромб? (четыре палочки). (Воспитатель проверяет как дети выполняют задание, помогает).
Воспитатель: Ребята, а скажите какая фигура здесь лишняя? (треугольник).
Почему? (потому что у треугольника три угла, а у всех остальных фигур по четыре угла).
Воспитатель: Ребята, пока мы с вами строили фигуры, налетел ветер и перепутал все геометрические фигуры. Поможете мне найти домики для каждой фигуры? (Проводится игра «Разложи фигуры» – треугольники, круги, квадраты лежат на ковре в беспорядке, рядом лежат три обруча – зеленый, красный и желтый). Давайте треугольники положим в красный обруч, круги – в желтый, а квадраты в зеленый. Берем по одной фигуре и несем в «домик» (Дети выполняют задание под музыку).
-Молодцы, ребята! Справились отлично! А теперь немного отдохнем и превратимся в геометрические фигуры.
Физимнутка: В математику играю
Вас в фигуры превращаю,
Раз, два, три, раз, два, три!
Геометрические фигуры на месте замри!
(игра проводится три раза).
Воспитатель: Ребята, пока мы с вами играли, цифры на нашей доске поссорились!
2 | 6 | 1 | 5 | 4 | 3 |
Случай странный, случай редкий
Цифры в ссоре! Вот те на!
Со своей стоять соседкой
Не желает ни одна!
Помири скорей ты всех,
А то будет просто смех!
(Дети выполняют задание за столами, расставляют цифры по порядку, воспитатель проверяет, как дети выполнили задание, отмечает тех детей, которые справились, помогает остальным).
Рефлексия:
Воспитатель:
Мы фигуры различали,
Мы узоры собирали,
И играли, и считали,
И совсем мы справились!
А теперь спрошу у вас:
«Задания вам понравились?»
(ответы детей)
Воспитатель: Ребята, чем мы занимались сегодня? С какими новыми фигурами познакомились? Что делали? Что было самым трудным? А что больше всего запомнилось?
Автор: Давыдова Светлана Алексеевна.
Выявить полученные знания, представления, умения, которые дети получили в течение учебного года.
Совершенствовать умение соотносить цифру с количеством, сравнивать совокупности и устанавливать между ними равенство;
Совершенствовать знания о геометрических фигурах и форме предметов;
Совершенствовать умение анализировать объекты и вычленять из представленного ряда лишний по характерному признаку;
Развивать мыслительные операции, внимание, умение ориентироваться в пространстве, сравнивать предметы по величине, понимать независимость числа.
Развивать у детей любознательность, взаимопомощь, навыки самооценки, общую и мелкую моторику.
Демонстрационный материал:
Картинки для динамической паузы, картинки «геометрические флаги», картинки «кто лишний за столом?», картинки для гимнастики для глаз.
Раздаточный материал:
Рабочие листы с заданиями «геометрические деревья», «геометрические дома», «геометрические качели», «геометрическая рыбалка».
Ножницы, клей, листы бумаги, вырезанные из цветной бумаги геометрические фигуры.
Карандаши цветные, веера с цифрами, картинки с изображением из геометрических фигур с заданным цветом каждой фигуры для раскрашивания.
Наши умные головки
Будут думать много, ловко.
Ушки будут слушать,
Ротик четко говорить.
Ручки будут хлопать,
Ножки будут топать.
Спинки выпрямляются,
Друг другу улыбаемся.
– Сегодня мы совершим путешествие в страну геометрических фигур. Какие геометрические фигуры вы знаете? Круг, овал, треугольник, прямоугольник, квадрат — это плоскостные фигуры. Еще есть фигуры объемные — куб, шар, цилиндр.
В геометрической стране геометрические фигуры везде-везде.
Перед вами деревья с кронами, похожими на геометрические фигуры. Сосчитайте, сколько всего деревьев на рисунке? Пять деревьев.
Покажите дерево, с кроной похожей на круг (овал, треугольник, прямоугольник, квадрат).
Какое по счету дерево с круглой кроной (овальной, треугольной, прямоугольной, квадратной)?
– Рассмотрите дома геометрической страны.
Как вы думаете, в каком доме живет какая геометрическая фигура?
Чей дом самый высокий (низкий)?
Чей дом самый широкий (узкий)?
К чьему дому ведет самая длинная (короткая) дорожка?
– А сейчас переверните листы бумаги на обратную чистую сторону и приготовьте для работы картонные геометрические фигуры.
Поставь квадрат в правый верхний угол.
Поставь круг в середину листа.
Поставьте треугольник в левый нижний угол.
Поставьте овал в левый верхний угол.
Поставьте треугольник в правый нижний угол.
Динамическая пауза «Сосчитай и сделай»
Сколько треугольников в елочке зеленой,
Столько ты немедленно выполни наклонов. (3)
Сколько на тарелке овальных пирожков,
Столько же немедленно выполни прыжков. (5)
Прямоугольных сколько стаканов для гостей,
Столько приседаний выполни скорей. (4)
На полке сколько круглых ваз.
Сколько квадратных флагов повесили для нас,
Столько поворотов выполни сейчас. (2)
– Как вы думаете, какая геометрическая фигура лишняя за округлым столом? Как вы думаете, какая фигура лишняя за многоугольным столом?
– Каких квадратных флагов больше, синих или красных? Их поровну.
Значит, количество флагов не зависит от их цвета.
Каких прямоугольных флагов больше, маленьких или больших? Их поровну. Значит количество не зависит от величины.
Каких треугольных флагов больше, тех что выстроили в круг, или тех, что выстроили в ряд? Их одинаковое количество. Значит количество не зависит от расположения.
– На качелях катаются геометрические фигуры. С левой стороны качелей посадите кататься три круга. А на правую сторону посадите овалов, на один меньше, чем кругов. Что можно сделать, чтобы кругов и овалов стало поровну? Добавить один овал или убрать один круг.
– Поставьте карандашом точку в середине каждой рыбки и соедините эту точку с крючками.
– Найдите глазами предмет, похожий по форме на треугольник (круг, квадрат, овал, прямоугольник).
– Как с помощью ножниц, из квадрата сделать треугольники?
Как с помощью ножниц, из прямоугольника сделать квадраты?
Как из круга сделать два полукруга?
– Составьте из получившихся у вас геометрических фигур картинку и наклейте ее на лист бумаги. Эта картинка напомнит вам о путешествии в страну геометрических фигур.
– А домой возьмите вот такую раскраску. (Картинка с изображением, составленным из геометрических фигур с заданным цветом для раскрашивания каждой фигуры).
КОНСПЕКТ ОТКРЫТОГО ЗАНЯТИЯ ПО ПОЗНАВАТЕЛЬНОМУ РАЗВИТИЮ (ФЭМП) «ПУТЕШЕСТВИЕ НА ПЛАНЕТУ ГЕОМЕТРИЧЕСКИХ ФИГУР» В СТАРШЕЙ ГРУППЕ
Лебедева Елена Борисовна Воспитатель МБДОУ ДС № 50 «Аистенок» г.
Североморск
Цель: Совершенствовать и обобщать знания детей о геометрических фигурах и форме предметов.
Задачи:
Обучающие:
Скачать конспект
Скачать презентацию
Развивающие:
Воспитывающие:
Демонстрационный материал: презентация к занятию, диск в конверте, деревья из картона, ваза для цветов, красные и желтые цветы, желтые круги и зеленые треугольники по количеству детей, юбочки с отверстиями в форме геометрических фигур, картинки жителей, сундучок с угощением.
Раздаточный материал: листы бумаги А4, набор плоскостных геометрических фигур, схема ракеты, простые карандаши по количеству детей.
Методы и приемы: объяснение, указание, пояснение, вопросы, показ, игровой прием, поощрение, педагогическая оценка.
Образовательные области:
Познавательное развитие (ФЭМП);
Речевое развитие;
Социализация (игровая деятельность).
Содержание занятия:
Ι. Вводная часть: Организационный момент.
Воспитатель: Ребята, посмотрите, сколько к вам пришло гостей, давайте поздороваемся. Подходите ко мне, встаем в круг и беремся за руки.
Я очень рада всех вас видеть. Давайте поприветствуем друг друга.
Собрались все дети в круг,
Я — твой друг и ты — мой друг!
Крепко за руки возьмитесь
И друг другу улыбнитесь!
Воспитатель: Присаживайтесь, пожалуйста, на любое место за столом (осанка).
Кто-то бросил к нам в оконце письмецо,
Может, это лучик солнца,
Что щекочет мне лицо?
Может, это воробьишко,
Пролетая, обронил?
Может, это кот, как мышку,
На оконце заманил?
На письме написано: «Детям старшей группы от правителя планеты Геометрических фигур». Ребята, смотрите, а в конверте диск, это значит, нам прислали видеописьмо. Хотите послушать?
«- Здравствуйте ребята. Я, правитель планеты Геометрических фигур услышал, что вы знаете геометрические фигуры, любите заниматься математикой. Поэтому я приготовил для вас сюрприз. Но чтобы получить его, вам необходимо совершить путешествие и выполнить мои задания.
Если вы смелые, решительные, уверенные в своих силах, тогда отправляйтесь в путь. Счастливого пути».
Воспитатель: — Ребята вы любите математику? (Ответы детей.) — Уверены в своих силах и знаниях? (Ответы детей.) — Тогда отправляемся на планету Геометрических фигур! А на чем мы будем туда полетим зашифровано у вас на листах. Посмотрите, пожалуйста, на листах изображены точки. Вася посчитай сколько их. Молодец, правильно. А сейчас вам нужно соединить точки прямыми линиями от 1 до 9. Что у вас получилось? Правильно — это ракета и мы на ней сейчас полетим на планету
Геометрических фигур – сели в ракету и полетели:
На ракете, на ракете
Мы летим к другой планете.
Воспитатель: Вот мы с вами и прилетели на планету Геометрических фигур. Но туда так просто не попасть, нужно открыть огромный замок, который висит на воротах. Посмотрите на замок, что на нем изображено? Какие геометрические фигуры вы видите? Чем эти фигуры похожи? Чем отличаются? Как вы считаете, какая фигура лишняя? Молодцы, замок открыт, и правитель планеты дарит вам в подарок — куб синего цвета.
Мы можем продолжить свой путь, где нас ждут интересные задания. Подходите ко мне. Шли мы шли и в геометрический лес пришли. Присаживайтесь на геометрическую поляну. Посмотрите, а здесь нас с вами встречает житель планеты – Квадрат. Он предлагает нам такое задание.
Задание №1 Упражнение «Геометрические деревья»
Перед вами деревья с кронами похожими на геометрические фигуры. Сосчитайте, сколько всего деревьев? (Пять деревьев). Покажите дерево, с кроной похожей на круг (овал, треугольник, прямоугольник, квадрат). Какое по счету дерево с круглой кроной (овальной, треугольной, прямоугольной, квадратной)?
Воспитатель: — Молодцы, ребята! Вы справились с заданием и квадрат нам дарит куб красного цвета.
А сейчас, ребята, давайте немного отдохнем. Вставайте и выходите ко мне.
Быстро встаньте, улыбнитесь,
Выше, выше потянитесь
Ну-ка, плечи распрямите,
Поднимите, опустите,
Влево, вправо повернитесь
Пола ручками коснитесь
Сели-встали, сели – встали
И на месте поскакали.
Воспитатель: Продолжаем наше путешествие по планете. Шли мы шли и в гости к Прямоугольнику пришли. Прямоугольник приготовил для вас следующее задание.
Задание №2 Упражнение «Расставь геометрические фигуры на листе»
– А сейчас возьмите с края стола листы бумаги и приготовьте для работы геометрические фигуры.
– Поставь квадрат в правый верхний угол.
– Поставь круг в середину листа.
– Поставьте треугольник в левый нижний угол.
– Поставьте овал в левый верхний угол.
– Поставьте треугольник в правый нижний угол.
Молодцы ребята, вы отлично справились с заданием и нам прямоугольник дарит – серебристую пирамиду.
Воспитатель: Продолжаем наше путешествие. Посмотрите, а на пути у нас с вами дом, в котором живет Круг. У него для нас такое задание:
Задание №3 Игра «Соберем крупу»
Правила игры: Дети делятся на две команды.
Нужно одной команде в миску собрать крупу круглой формы, а другой – треугольной.
Молодцы и за правильное выполнение задания нам Круг дарит желтую пирамиду.
Воспитатель: Продолжаем наше путешествие. Шли мы шли и в гости к Треугольнику пришли.
Задание №4
У него есть младшая сестренка. И у нее случилась беда, все ее юбочки порвались и на них дырки. Нужно на юбочки поставить заплатки. Я беру юбку с прямоугольной дырой и ставлю прямоугольную заплатку. А теперь ты Петя…
Воспитатель: — Молодцы, ребята! Вы справились с заданием и получаете в подарок желтую пирамиду. Присаживайтесь, пожалуйста, за столы мы с вами путешествовали по планете и нам жители планеты дарили подарки давайте посмотрим, что из них получилось. Что это ребята?
Все вы старались, внимательно слушали, поэтому и справились со всеми заданиями. Какие задания вам показались интересными? Какие сложными? С какими заданиями вы справились быстрее.
– А теперь правитель планеты Геометрических фигур предлагает вам оценить свое участие в путешествии.
«Если вы довольны своими успехами сегодня и оцениваете свою работу на «отлично» – возьмите красный цветок, а если вы считаете, что у вас что-то не получилось и вы могли бы сделать лучше – возьмите цветок желтого цвета». (Дети оценивают свою работу).
А еще жители планеты вам дарят вот этот геометрический сундучок. Давайте мы с ними попрощаемся и вернемся обратно в детский сад. До свидания!
Сели на ракету: На ракете, на ракете
В детский сад летим мы дети.
Вот мы и вернулись обратно в детский сад. Большое вам всем спасибо.
| < Предыдущая | Следующая > |
|---|
Ересектер тобындағы ұйымдастырылған оқу қызметінің конспектісі
Конспект организационной учебной деятельности в старшей группе
Өткізу күні/ Дата проведения: 3.
10.2018
Тәрбиеші/ Воспитатель: Кенжибаева Н.Н.
Білім беру саласы/Образовательная область: Познание
Пән/ Предмет: ФЭМП
Өтпелі тақырып/Сквозная тема: Здравствуй, осень золотая!
Тақырып/Тема: Геометрические фигуры (прямоугольник, овал). Знакомство с четырёхугольником, сравнение его с квадратом и прямоугольником.
Мақсаттары/Цель: Продолжать учить различать и правильно называть знакомые геометрические фигуры, познакомить с четырёхугольником. формировать умения отличать предметы по форме, величине; развивать логическое мышление, умение анализировать и выделять существенные признаки; воспитывать учебный интерес.
Русурстармен қамтамасыз ету/ Ресурсное обеспечение: набор геометрических фигур у воспитателя и каждого ребенка, набор предметных картинок, рабочие тетради
Билингвалдық компанент/Билингвальный компанент:
1.Ұйымдастырушылық кезеңі/ Организационный момент:
Организационный момент.
-Здравствуйте, ребята, присаживайтесь. С каким настроением вы пришли сегодня на занятие? Каким цветом вы бы его изобразили?
-Надеюсь, что на занятии вы не будете скучать, а ваше настроение улучшится! Приступаем к работе!
2.Негізгі бөлімі/Основная часть:
-Ребята, сегодня я вас приглашаю в страну геометрических фигур.
Кто-нибудь уже знает, что это за фигуры?
-Первая фигура – это круг. ( В-ль демонстрирует круг из набора фигур). Покажите мне такую же фигуру из своего набора. Как называется фигура, которую вы мне все сейчас показываете?
-Посмотрите внимательно на свои круги, что вы можете сказать об этой фигуре? (у круга нет углов)
-Посмотрите внимательно вокруг себя: какие предметы похожи на круг?
-Еще одна фигура – квадрат. (в-ль демонстрирует квадрат из набора фигур). Покажите мне такую же фигуру из своего набора. Как называется фигура, которую вы мне все сейчас показываете?
-Посмотрите внимательно на свои квадраты, что вы можете сказать об этой фигуре? Сколько у квадрата углов? Сколько сторон? Возьмите в одну руку квадрат, в другую – прямоугольник. Сравните их: чем они похожи, чем отличаются?
-Посмотрите внимательно вокруг себя: какие предметы похожи на прямоугольник?
-Следующая фигура – треугольник. (в –ль демонстрирует треугольник из набора фигур). Покажите мне такую же фигуру из своего набора. Как называется фигура, которую вы мне все сейчас показываете?
-Посмотрите внимательно на свои треугольники, что вы можете сказать об этой фигуре? Сколько у треугольника углов? Сколько сторон?
-Посмотрите внимательно вокруг себя: какие предметы похожи на треугольник? (аналогично производится знакомство с овалом)
Физминутка.
Хомка, Хомка, Хомячок
Полосатенький бочок
Хомка раненько встает
Шейку моет, спинку трет
Подметает Хомка хатку и выходит на зарядку
Раз, два, три, четыре, пять
Хочет Хомка сильным стать.
5.Первичное закрепление.
-Теперь я вам буду загадывать загадки про геометрические фигуры, а вы должны их отгадать.
1)Нет углов у меня,
И похож на блюдце я,
На тарелку и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья? (круг)
2)Три вершины тут видны
Три угла, три стороны,-
Ну, пожалуй, и довольно!-
Что ты видишь? (треугольник)
3)Не овал я и не круг,
Треугольнику я друг,
Прямоугольнику я брат,
Ведь зовут меня…
(квадрат)
4)Что сейчас увидим мы?
Все углы мои прямы,
Есть четыре стороны,
Но не все они равны.
Я четырехугольник
Какой? …(прямоугольник)
Работа в рабочей тетради.
3. Қорытынды / Итоговая часть:
-Ребята, наше занятие подходит к концу, вы сегодня все очень хорошо потрудились. Скажите, с какими фигурами мы сегодня познакомились? Чем отличается каждая фигура от всех остальных (круг, квадрат, треугольник, прямоугольник)?
-Какое у вас сейчас настроение? Какими красками вы бы его изобразили?
Программное содержание:
— совершенствовать умение детей считать прямым, обратным счетом в пределах 10;
— закреплять состав чисел в пределах 10, знания о плоскости, объемных геометрических фигурах, находить формы в окружающем мире;
— продолжать учить дошкольников измерять жидкие, сыпучие вещества и длину с помощью условных мерок;
— углублять знания о временах года и месяцах, календаре и часах;
— упражнять в умении составлять и решать арифметические задачи по сюжетным рисункам;
— развивать логическое мышление, творческое воображение, фантазию;
-воспитывать усидчивость, желание прийти на помощь ближнему.
Материал: ящик с орешками, письмо, карточки-билеты с геометрическими фигурами, плоскости и объемные геометрические фигуры, карточки с предметами разной формы; карты и знаки для решения примеров, цветные палочки Кюизенера, картинки-ассоциации месяцев, цветовой круг с временами года, часы, счетные палочки, перловка, манка, вода, дощечка, условные мерки для измерения.
Воспитатель. Дети, сегодня утром почтальон принесла письмо, в котором адрес нашей группы и этот ящик. Давайте прочитаем это письмо.
«ДОРОГИЕ ДЕТИ! МЫ, ЗВЕРИ ЛЕСНОЙ ШКОЛЫ, ПЕРЕДАЕМ ВАМ ЯЩИК С СЮРПРИЗОМ. А ЧТОБЫ ЕГО ПОЛУЧИТЬ НАДО ВЫПОЛНИТЬ НАШИ ЗАДАЧИ.»
Воспитатель. Дети, а вы любите сюрпризы? Тогда выполним задачи лесных зверюшек? А чтобы дальше работать нам надо разделиться на команды. Мы сделаем это с помощью карточек с изображением геометрических фигур. Каждый из вас возьмет карточку, и подойдет к столу с изображением такой геометрической фигуры, которая изображена на вашей карте.
Задача №1
Вот первое задание: На столах стоят коробки с геометрическими фигурами. Надо выбрать геометрические фигуры, которые похожи на вашу геометрическую фигуру, изображенную на карточке.
Задача №2
Решите примеры. (Дети с помощью знаков и цифр решают примеры и задачи)
1. Из-под ворот видно восемь кошачьих лап. Сколько кошек во дворе? (Две)
2. Летела стая гусей, двое впереди, одна сзади. Двое позади, одна впереди. Сколько было гусей? (Трое)
3. По небу летели воробей, ласточка и шмель. Сколько всего летело птиц? (Двое)
4. Какую посуду нельзя наполнить? (Полную)
5. Что будет с вороной, когда пройдет пять лет? (Пойдет шестой год)
Задача №3
Палочки цветовые уже ждут вас.
Числовой ряд из них нужно выложить сейчас
(Дети с помощью палочек Кюизенера выкладывают цифровой ряд, подсчитывают его прямым и обратным счетом, и выкладывают цифровой ряд)
Воспитатель. Что же, видимо, пришла пора, немного отдохнуть.
Хочу всех вас пригласить на физкультминутку и немного размяться.
Физминутка
Раз — подняли руки вверх,
Два — склонились все вниз.
Руки — в стороны!
Прыг — прыг — скок!
Наклонились, повернулись,
Друг другу улыбнулись.
Покрутились вправо — влево
Чтобы ничего не болело.
Раз, два, три, четыре!
Набираемся мы силы
Наклонились, повернулись
И товарищу улыбнулись.
Задача №4
Воспитатель.
Круг цветной дали нам зверьки,
Чтобы это значило малыши?
(Цветной круг — это четыре времени года: синий — зима, зеленый — весна, красный — лето, желтый — осень, у каждого времени года 3 месяца;)
Где еще можно увидеть месяцы? (В календаре)
Какие бывают календари? (Перекидные, настенные, настольные, отрывные)
С помощью чего еще можно определять время? (С помощью часов)
Задача №5
Чем измеряется длина? (Сантиметрами, метрами)
Объем — литрами;
Масса — килограммами.
Каждой группе нужно измерить что-нибудь условными мерками.
Итог. Рефлексия.
Воспитатель. Молодцы, дети, все задачи вы выполнили. А сейчас ящик откройте, и сюрприз получите. (Дети открывают ящик, внутри орехи)
Это орешек не простой, а очень обаятельный, «орехом знаний» его назвали, чтобы вы умными росли.
Задачи.
1. Образовательная – закрепить названия геометрических фигур, познакомить детей со способом рисования многоугольника в тетради, упражнять в счете в пределах 20, называть четные и нечетные числа, закрепить умение составлять геометрические фигуры из счетных палочек.
2. Развивающая – развивать память, логическое мышление, внимание, умение ориентироваться на листе бумаги.
3. Воспитательная – воспитывать активную любознательность.
Материалы для занятия.
Счетные палочки, простой карандаш, тетради, карточки с изображением геометрических фигур, геометрические фигуры.
Ход занятия:
1. Вводная часть
Воспитатель: Ребята, встаньте, пожалуйста, в круг.
Собрались все дети в круг,
Я твой друг и ты мой друг.
Крепко за руки возьмемся
И друг другу улыбнемся.
Воспитатель: Ребята, я очень рада видеть вас. Возьмитесь за ручки, подарите друг другу улыбку. А теперь подарите свою улыбку мне. Отлично! Сейчас у нас начнется занятие – математика, на котором мы с вами будем работать с геометрическими фигурами. Давайте все сядем на свои места.
Дети рассаживаются на свои места.
Воспитатель: Как обычно, начнем наше занятие с разминки.
Посчитаем по порядку до 20 и обратно до 1;
Назови четные числа;
Назови нечетные числа.
2 часть. Основная
Воспитатель: Как я уже сказала, мы с вами будем работать с геометрическими фигурами. А вот с какими, вам предстоит отгадать.
Игра «Узнай меня»
Я многоугольник, имею 3 стороны (треугольник)
Я многоугольник, у меня 4 равные стороны (квадрат)
Я не многоугольник, меня можно катать (круг)
У меня нет углов, но я не круг (овал)
Я четырех угольник, но у меня не все стороны равны (прямоугольник)
Воспитатель: Молодцы, все фигуры назвали правильно. Давайте еще раз перечислим, с какими геометрическими фигурами мы будем работать.
(Спросить 1-2 детей.)
Воспитатель: Ребята, а вы знаете, что геометрические фигуры можно нарисовать, начертить в тетради, вырезать из цветной бумаги. А еще их можно выложить из счетных палочек. И не одну, а сразу несколько. Давайте попробуем.
– отсчитайте три палочки и сделайте треугольник
– отсчитайте еще две палочки и сделайте еще один треугольник
– сколько треугольников получилось? (два)
– сколько палочек вы отсчитали?
– отсчитайте четыре палочки и сделайте квадрат.
– отсчитайте еще три палочки и сделайте еще один квадрат
– какая фигура у вас получилась? (прямоугольник)
– сколько четырехугольников получилось? (три)
– а сколько многоугольников получилось? (три)
– назовите их. (два квадрата и один многоугольник)
– отсчитайте еще три палочки и сделайте еще один квадрат.
– сколько палочек вы отсчитали?
– какие фигуры у вас получились?
Игра «Отгадай число».
Воспитатель: Я предлагаю отдохнуть и поиграть в игру «Отгадай число». Давайте выберем ведущего.
Шел по берегу петух,
поскользнулся,
В речку – бух.
Дети образуют круг. Ведущий, стоя в центре круга, задумывает число в пределах 10. и на ухо говорит его воспитателю. Играющие при помощи вопросов, на которые ведущий может отвечать только «Да» или «Нет», должны отгадать задуманное число. Затем ведущим становится ребенок, который отгадал число.
Дети рассаживаются на свои места.
Воспитатель: А сейчас мы будем работать с карточками. У каждого на столе лежит карточки с изображением геометрических фигур. Вы должны внимательно рассмотреть свою карточку и точно рассказать, как расположены фигуры на вашей карточке.
– Где находиться прямоугольник?
Прямоугольник находится посередине.
– Где находится овал?
Овал находится справа от прямоугольника
– Где находится круг?
Круг находится внизу, под прямоугольником
– Где находится квадрат?
Квадрат находится слева от прямоугольника
– Где находится треугольник?
Треугольник находится сверху, над прямоугольником.
(При этом карточку можно поворачивать в разные стороны, изменяя расположение фигур. И задавать те же вопросы.)
Воспитатель показывает детям пятиугольник и спрашивает, как называется эта фигура.
Воспитатель: Сегодня я покажу вам, как рисовать многоугольник в тетради. Вначале нужно решить, какой многоугольник вы будете рисовать. Я буду рисовать пятиугольник. Поставлю пять точек для вершин (показ), соединю их прямыми линиями между собой – получились стороны многоугольника (показ). Какая фигура получилась? Давайте проверим, правильно ли я нарисовала пятиугольник.
Дети проверяют, считая вершины, углы, стороны.
Воспитатель: Теперь каждый из вас нарисует любой многоугольник. А прежде давайте разомнем наши пальчики.
Пальчиковая гимнастика
Дружат в нашей группе девочки и мальчики.
Мы с тобой подружим маленькие пальчики.
1, 2, 3, 4, 5!
Начинаем счет опять: 5 4 3 2 1 –
Дружно мы в кругу стоим!
Самостоятельная работа детей.
3 часть. Итог занятия.
Воспитатель: Подошло к концу наше занятие. С чем мы сегодня работали на занятии (с геометрическими фигурами). Чему вы научились на занятии? (выкладывать геометрические фигуры из счетных палочек, рисовать многоугольники в тетради)
А теперь оцените свою работу на занятии. Если у вас хорошее настроение, вам было интересно на занятии, у вас все получалось, то поднимите руки вверх, а если вы чувствовали себя неуютно, у вас что-то не получалось, тогда опустите руки вниз.
Кэмпбелл, П.Ф. (1996). Расширение прав и возможностей детей и учителей в классах начальной математики городских школ. Городское образование , 30 , 449–475.
Карпентер, Т. (1988). Обучение как решение проблем. В Р. И. Чарльз и Э. А. Сильвер (ред.), Обучение и оценка решения математических задач (стр.187–202). Рестон, Вирджиния: Национальный совет учителей математики.
Карпентер, Т.П., Феннема, Э., и Франке, М.Л. (1996). Когнитивно управляемое обучение: база знаний для реформы начального обучения математике. Журнал начальной школы , 97 , 3–20.
Карпентер, Т.П., Феннема, Э., Франке, М.Л., Эмпсон, С.Б., и Леви, Л.В. (1999). Детская математика: познавательное обучение . Портсмут, Нью-Хэмпшир: Heinemann.
Карпентер, Т.П., Феннема, Э., Петерсон, П.Л., Чанг, К.П., и Лоэф, М. (1989). Использование знаний о математическом мышлении детей в классе: экспериментальное исследование. Американский журнал исследований в области образования , 26 , 499–531.
Карпентер, Т.П., и Леви, Л. (1999, апрель). Развитие представлений об алгебраическом мышлении в начальных классах. Документ, представленный на заседании Американской ассоциации исследований в области образования, Монреаль.
Clark, C.M., & Peterson, P.L. (1986). Мыслительные процессы учителей. В M.C.Wittrock (Ed.), Справочник по исследованиям по обучению (3-е изд., Стр. 225–296). Нью-Йорк: Макмиллан.
Кобб П., Вуд Т., Якель Э. Николлс Дж., Уитли Г., Тригатти Б. и Перлвиц М. (1991). Оценка проблемно-ориентированного математического проекта для второго класса. Журнал исследований в области математического образования , 22 , 3–29.
Коэн, Д.К., и Болл, Д.Л. (1999). Обучение, возможности и улучшение (Отчет об исследовании CPRE № RR-043). Филадельфия: Университет Пенсильвании, Консорциум исследований политики в области образования.
Коэн, Д.К., и Болл, Д.Л. (2000, апрель). Инструктивное нововведение: переосмысление истории. Документ, представленный на заседании Американской ассоциации исследований в области образования, Новый Орлеан.
Конференция Совета математических наук. (2000, сентябрь). Проект отчета по проекту «Математическое образование учителей CBMS» [On-line].Доступно: http://www.maa.org/cbms/metdraft/index.htm. [3 января 2001 г.].
Давенпорт, Л. (в печати). Учебные планы элементарной математики как инструмент реформы математического образования: проблемы внедрения и последствия для профессионального развития. В P.Smith, A.Morse и L.Davenport (Eds.), Обучение учителей и реализация учебной программы . Ньютон, Массачусетс: Центр развития образования, Центр развития обучения.
Эрлвангер, С., & Берлангер, М. (1983). Интерпретации знака равенства у младших школьников. В J.C.Bergeron & N.Herscovics (Eds.), Proceedings of the Fifth Annual Meeting of the North American Chapter International Group for the Psychology of Mathematics Education (vol. 1, pp. 250–258). Монреаль: Монреальский университет. (Услуга размножения документов ERIC № ED 289 688).
Фолкнер, К.П., Леви, Л., и Карпентер, Т. (1999). Детское понимание равенства: основа алгебры. Обучение детей математике , 6, 232–236.
Феннема, Э., Карпентер, Т.П., Франке, М.Л., Леви, Л., Якобс, В., и Эмпсон, Б. (1996). Продольное исследование обучения использованию детского мышления при обучении математике. Журнал исследований в области математического образования , 27 , 403–434.
Это означает, что новые учителя должны развивать способность «понимать педагогически рефлексивным способом; они должны не только знать свой собственный подход к дисциплине, но и знать «концептуальные барьеры», которые могут мешать другим »(McDonald and Naso, 1986: 8).Эти концептуальные барьеры различаются от дисциплины к дисциплине.
Акцент на взаимодействии между дисциплинарными знаниями и педагогическими знаниями прямо противоречит распространенным заблуждениям о том, что учителя должны знать, чтобы создавать эффективную среду обучения для своих учеников. Заблуждения состоят в том, что обучение состоит только из набора общих методов, что хороший учитель может преподавать любой предмет или что достаточно только предметных знаний.
Некоторые учителя – могут преподавать по различным дисциплинам.Однако их способность делать это требует большего, чем набор общих педагогических навыков. Рассмотрим случай Барб Джонсон, которая 12 лет проработала учителем шестого класса в средней школе Монро. По общепринятым меркам Монро – хорошая школа. Результаты стандартизированных тестов примерно средние, размер класса небольшой, здания содержатся в хорошем состоянии, администратор является сильным педагогическим руководителем, а текучесть преподавателей и персонала незначительна. Однако каждый год родители отправляют своих учеников пятого класса из местных начальных школ к жокею Монро, чтобы их дети отправляли в классы Барб Джонсон.Что происходит в ее классе, что дает ему репутацию лучшего из лучших?
В течение первой недели в школе Барб Джонсон задает своим шестиклассникам два вопроса: «Какие вопросы у вас есть о себе?» и “Какие у вас есть вопросы о мире?” Учащиеся начинают перечислять свои вопросы: «Могут ли они рассказывать о глупых мелочах?» – спрашивает один студент. «Если это ваши вопросы, на которые вы действительно хотите получить ответы, они ни глупые, ни маленькие», – отвечает учитель.После того, как ученики составят список своих индивидуальных вопросов, Барб объединяет учеников в небольшие группы, где они делятся списками и ищут общие вопросы. После долгого обсуждения каждая группа придумывает приоритетный список вопросов, упорядочивая вопросы о себе и о мире.
Снова вместе на групповом занятии Барб Джонсон выясняет приоритеты групп и работает над достижением консенсуса по объединенным спискам вопросов класса. Эти вопросы становятся основой учебной программы в классе Барб.Один вопрос: «Доживу ли я до 100 лет?» породил образовательные исследования по генетике, семейному и устному анамнезу, актуарной науке, статистике и вероятности, сердечным заболеваниям, раку и гипертонии. У студентов была возможность получить информацию у членов семьи, друзей, экспертов в различных областях, компьютерных онлайн-сервисов и книг, а также у учителя. Она описывает то, что им пришлось сделать, как стать частью «обучающегося сообщества». По словам Барб Джонсон: «Мы решаем, какие интеллектуальные проблемы являются наиболее важными, и разрабатываем способы их исследования».
Венди Петти
Кому нужны математические игры, когда их манит мир значимых реальных развлечений? На уроках математики легко и полезно подключиться к реальному миру.На информационном пути “мы можем найти онлайн-коллекции реальных математических заданий, математических заданий с конкретным фокусом на реальной жизни (включая стихийные бедствия), онлайн-источники данных, порталы для участия или запуска совместных математических и научных проектов и многое другое . Собранные здесь ресурсы из реального мира обязательно понравятся учителям и учащимся.
Перечисленные здесь сайты математической деятельности представляют собой хранилища идей уроков, которые можно изучать в автономном режиме без использования компьютеров.
Math Goodies
Их мультимедийный учебный план включает 168 углубленных уроков, организованных в учебные блоки. Для каждого блока есть соответствующий набор рабочих листов, головоломок и интерактивных обучающих игр.
Практическое использование математики и естественных наук (PUMAS)
Этот сайт предлагает 71 пример реальных приложений математики для старших классов начальной школы и выше, включая рисование / интерпретацию топографических карт, денежную математику, создание математических магических задач, измерение тепла из песка и камня; и многое другое.Коллекцию можно отсортировать по диапазону оценок, ключевому слову или названию.
Смешивание в математике
Этот набор бесплатных заданий помогает учителям, родителям и внеклассным программам добавить немного математики в повседневную жизнь учащихся. В диаграмме активности перечислены математические навыки, задействованные в каждом задании.
Реальные приложения арифметики
Эта загружаемая коллекция из 20 реальных математических проектов может быть адаптирована для учащихся старших классов начальной и средней школы.
Денежная математика: уроки для жизни
Этот бесплатный сборник из четырех уроков реальных примеров из мира финансов включает руководство для учителя с планами уроков, страницами заданий и советами для преподавателей.
National Math Trail
Студенты со всего США создавали реальные словесные задачи, связанные с их общинами. Этот трехлетний проект больше не действует, но заархивированные вопросы остаются отличным источником реальных математических задач.
Вы захотите подключиться к Интернету, чтобы изучать приведенные ниже математические задания со студентами; упражнения могут быть адаптированы для исследования в целом классе, небольшой группы или индивидуально.
Математика в реальном мире
На этом сайте представлены идеи и уроки по интеграции Google Планета Земля в учебную программу по математике; к каждому описанию деятельности прилагается соответствующий загружаемый файл Google Планета Земля. Учащиеся могут оценить большие или малые расстояния, а затем проверить фактические расстояния с помощью линейки Google Планета Земля.Они могут определять площадь таких сложных многоугольников, как поля культур необычной формы. Они могут изучать теорию сетей и обобщать правила, проводя линии, соединяющие острова. Они могут узнать о сферической геометрии, измеряя углы треугольников, построенных в глобальном масштабе. Они могут исследовать лабиринты и лабиринты, используя реальные изображения Google Планета Земля. Они могут применять формулы для определения объема твердых тел при просмотре и панорамировании Великих пирамид и других трехмерных зданий. Они могут выразить большие числа в научных обозначениях, когда они «поднимаются» на гору.Эверест. Они могут узнать о пропорциях, поскольку они используют обменные курсы, чтобы найти суммы в валюте, путешествуя по земному шару.
FEMA Disaster Master
FEMA представляет множество материалов для детей по каждому типу стихийных бедствий. В зоне бедствия простым языком передается информация и статистические данные по каждому типу бедствия.
NOAA Weather Education
Образовательные ресурсы в этой области Национальной метеорологической службы включают статистические данные и сводки суровой погоды по годам.
Math-kitecture
Студенты применяют математические навыки и концепции с помощью интерактивных и автономных мероприятий по архитектурному проектированию, в том числе «Планирование этажа в классе».
Plane Math
Интерактивные уроки и онлайн-центр проектирования самолетов объединяют математику и естественные науки.
Музыка в учебной программе
Смешайте математику и музыку, чтобы играть с ритмами и нотами, оживляя дроби.
Math приобретает новое значение, когда студенты могут сотрудничать с другими студентами и профессионалами со всего мира.
Совместные проекты CIESE
Присоединяйтесь к проектам, включающим глобальный сбор и анализ данных в Центре инноваций в области инженерии и естественнонаучного образования.
Math Forum Совместные проекты
На Math Forum перечислены различные совместные проекты по сбору данных.
Национальная ассоциация математических кружков
Этот сайт помогает собрать вместе профессионалов-математиков и студентов в неформальной обстановке для работы над интересными задачами или темами с целью увлечь учащихся математикой.
Ознакомьтесь с функциями Education World, указанными ниже, со ссылками на онлайн-источники данных или другие математические сайты из реального мира.
Отслеживание падающих температур
Учащиеся составляют график и анализируют изменения температуры во времени, используя собранные ими данные и дополнительные погодные ресурсы в Интернете.
Сколько это стоило 100 лет назад?
Студенты сравнивают изменение цен за столетие, используя онлайн-источники данных.
Обновлено 18.11.2016
Математические игры раскрывают в детях естественную любовь к числам. По мере того, как учащиеся переходят в новый учебный год, помогите им отточить свои числовые навыки с помощью некоторых из этих веселых и эффективных игр.
1. Саймон говорит: «Геометрия!»
Усовершенствуйте эту традиционную игру, предложив детям иллюстрировать следующие геометрические термины, используя только свои руки: параллельные и перпендикулярные линии; острый, прямой и тупой углы; и углы 0, 90 и 180 градусов.
Задание: Увеличьте темп команд и посмотрите, смогут ли ваши ученики не отставать!
2. ’Круглый блок
Попросите учащихся встать на площади. Дайте одному из них мяч и математическую задачу, требующую списка ответов, таких как счет по двойкам или наименование фигур с прямым углом. Прежде чем ученик ответит, он передает мяч человеку рядом с ним. Дети передают мяч по площади как можно быстрее, и ученик должен дать ответ, прежде чем мяч вернется к нему.
Задание: Когда дан правильный ответ, ребенок, у которого есть мяч, должен ответить на следующий вызов, отправив мяч обратно по кругу в противоположном направлении.
3. Отскок суммы
Покройте пляжный мяч цифрами (используйте перманентный маркер или липкие этикетки). Бросьте мяч одному ученику и попросите ее назвать номер, которого касается ее большой палец правой руки. Она бросает его следующему ученику, который делает то же самое, а затем добавляет свой номер к первому.Продолжайте в течение пяти минут и запишите сумму. Каждый раз, когда вы играете в игру, добавляйте сумму к графику. В какой день вы достигли наибольшей суммы? Низший?
Задача: Используйте дроби, десятичные дроби или сочетание отрицательных и положительных целых чисел.
4. Straw Poll
Задайте вопрос и позвольте учащимся проголосовать, поместив соломинку в один из нескольких пластиковых стаканчиков, каждый из которых имеет свой ответ. Позже ученики младшего возраста могут построить график результатов, а дети старшего возраста вычислить соотношение и процентное соотношение для каждого ответа.
Задача: Если опрошена вся школа, и если предположить, что каждый ответ получил одинаковый процент голосов, сколько голосов было бы в каждой чашке? Что, если бы ваш город был опрошен? Ваше состояние? Соединенные штаты.?
5. Уравнения для бритья
Положите ложку крема для бритья на парту каждого ученика, и они решат уравнения, «написав» крем.
Задание: Попросите учащихся сформулировать задачу. По вашему сигналу попросите их повернуться к соседнему с ними столу и решить эту проблему.Попросите детей проверить ответы на своих партах, прежде чем начинать новый раунд.
Даже 10 минут увлекательных математических игр могут ускорить обучение.
6. Классы математики
Настройте сетку классиков с макетом калькулятора. Для детей постарше вы можете использовать квадратный корень и знак отрицательного целого числа. Студенты сначала выбирают одно число, затем операцию, другое число, знак равенства и, наконец, ответ. Для двузначных ответов учащиеся могут разделить свой последний прыжок так, чтобы их левая нога попадала на цифру в разряде десятков, а правая ступня – на цифру в разряде единиц.
Задание: Ученик, выполняющий ход, бросает камень на число и должен избегать этого числа в уравнении.
7. Глобальная вероятность
Семьдесят процентов Земли покрыто водой. Проверьте эту статистику, предложив учащимся встать в круг и бросить друг другу надувной глобус. Когда ученик ловит земной шар, запишите, касается ли он большим пальцем левой руки земли или воды. Этот ученик бросает мяч однокласснику и садится.Когда все сядут, определите отношение количества раз, когда ученики касались воды большими пальцами, к количеству раз, когда они касались земли. Запишите соотношение и повторите действия в другие дни. (Со временем соотношение должно быть довольно близким к 7 к 3, или 70 процентам.)
Задача: Предскажите вероятность того, что чей-то большой палец приземлится на любом из континентов, на основе отношения площади суши каждого континента к планета в целом.
8.Сладкая математика
Смоделируйте это занятие с помощью одного пакета Skittles или M&M и документ-камеры, или позвольте каждому ученику получить свой собственный пакет. Младшие школьники могут графически отображать содержимое своих пакетов по цвету. Старшие ученики могут рассчитать соотношение каждого цвета по сравнению с общим количеством конфет в их упаковках.
Задание: Скомпилируйте результаты класса в один график, а затем попросите каждого ученика сравнить свое соотношение с соотношением для всего класса.
9. Это в карточках
Чтобы изменить традиционную карточную игру Война, присвойте значения 1 тузу, 11 валету, 12 королеве и 13 королю, а также номинал карт от 2 до 10 (для детей младшего возраста ограничьте игра только на нумерованные карты). Играя парами, каждый ученик кладет две карты лицом вверх, затем вычитает меньшее число из большего. Тот, у кого ответ больше, выигрывает все четыре карты. Если суммы совпадают, игроки переворачивают еще две карты и повторяют до тех пор, пока не будет определен победитель.
Задание: Используйте две карты, чтобы сформировать дробь, а затем сравните, чтобы увидеть, у кого дробь больше. Если они эквивалентны, повторяйте, пока кто-нибудь не выиграет раунд.
10. Бесценный стих
Дайте каждой группе из четырех или пяти студентов немного игровых денег – один доллар, два четвертака, три цента, четыре пятака и пять пенни. Прочтите стихотворение Шел Сильверстайн «Умный» и попросите студентов обмениваться деньгами в соответствии с каждой строфой.(«Мой папа дал мне однодолларовую купюру / Потому что я его самый умный сын / И я обменял ее на две блестящие четверти / Потому что два – это больше, чем один!») Спросите младших школьников, может ли человек, начавший с доллара получил хорошую сделку или нет. Старшие ученики могут подсчитать, сколько ребенок в стихотворении терял при каждом обмене.
Задача: Используйте калькулятор, чтобы определить процент потерь при каждом обмене.
Обучайте быстрой математике с помощью фруктов, кубиков и даже Twister!
11.Взвешивание
Составьте ряд фруктов и овощей, таких как апельсины, бананы, огурцы, киви, помидоры и сладкий перец. Попросите учащихся предсказать порядок продуктов от самого легкого до самого тяжелого. Используйте весы, чтобы проверить их прогнозы, а затем переставьте продукты в соответствии с их фактическим весом.
Задание: Разрежьте каждый плод пополам. Предложите студентам проанализировать, как плотность фрукта или овоща влияет на его вес.
12.String ’Em Up
Что больше – размах рук или рост? Попросите учащихся встать группами в соответствии с их предположениями: те, кто считает, что их размах рук больше, меньше или равен их росту. Дайте парам кусок веревки для проверки и измерения, а затем перегруппируйтесь в соответствии с их результатами.
Задача: Оценить отношение длины руки или ноги к росту тела, затем измерить, чтобы проверить точность оценки.
13.Твистер Математика
Наклейте этикетки с числами, формами или изображениями монет на круги коврика Twister. Дайте каждому ученику по очереди уравнение, описание формы или сумму денег, затем попросите ученика положить руку или ногу на ответ.
Задача: Пометьте коврик числами, оканчивающимися на ноль, затем позвоните по номерам и скажите детям, что они должны округлить до ближайшего ответа в большую или меньшую сторону.
14. Однометровый штрих
Раздайте группам учащихся по счетной палке, карандашу и листу бумаги.Дайте им несколько минут, чтобы записать в комнате три предмета, длина которых, по их прогнозам, составит в сумме один метр. Затем дайте им пять минут, чтобы измерить предметы, записать их длину и сложить их. Попросите группы доложить о своих результатах. Какая группа подошла ближе всего к одному метру?
Задание: Учащиеся измеряют с точностью до 1/8 дюйма, а затем переводят свои измерения в десятичные числа.
15. Количество строителей
Дайте каждой паре учеников кубик с шестью-девятью сторонами.Попросите их поставить пробелы для цифр в номере. (Их номера должны быть одинаковой длины, от четырех до девяти цифр.) Перед игрой решите, выиграет ли наибольший или наименьший номер. Учащиеся по очереди раскатывают кубик и заполняют бланки. После того, как число было написано, его нельзя изменить. Раскатайте, пока не будут заполнены все заготовки, а затем сравните числа. Если позволяет время, попросите учащихся вычесть разницу между их числами.
Задача: Вместо целого числа создайте дробную или десятичную дробь.
Математика 101 – После успешного завершения курса Математика 101 – Приветствие по специальности «Математика» студенты смогут:
Math 104 – После успешного завершения Math 104 – Mathematical Ideas учащиеся смогут:
Math 112 – После успешного завершения Math 112 – Pre-Calculus студенты смогут:
Математика 113 – После успешного завершения курса Математика 113 – Конечная математика для социальных наук студенты смогут:
Math 140 – После успешного завершения Math 140 – Mathematical Concepts for Elementary Education I, ученик сможет:
Math 141 – После успешного завершения Math 141 – Mathematical Concepts for Elementary Education II ученик сможет:
Математика 160 – После успешного завершения математики 160 – Элементы случайности ученик сможет:
Math 188 – После успешного завершения Math 188 – вводного курса Python студент сможет:
Математика 213 – По завершении курса Математика 213 – Прикладное исчисление студент сможет:
Math 221 – После успешного завершения MATH 221 – Calculus I студент сможет:
Math 222 – После успешного завершения Math 222 – Calculus II студент сможет:
Math 223 – После успешного завершения Math 223 – Calculus III студент сможет:
Математика 228 – После успешного завершения курса математики 228 – Исчисление II для биологов в контексте биологических вопросов учащийся сможет, используя ручные вычисления и / или соответствующие технологии, по телефону:
Математика 230 – После успешного завершения курса математики 230 – Программирование и решение математических задач студент сможет:
Математика 237 – После успешного завершения математики 237 – Дискретная математика студент сможет:
Math 239 – После успешного завершения Math 239 – Introduction to Mathematical Proof студент сможет:
Math 242 – После успешного завершения Math 242 – Elements of Probability and Statistics, студент сможет:
Математика 262 – После успешного завершения математики 262, прикладной статистики, студент сможет:
Math 301 – После успешного завершения Math 301 – Mathematical Logic студент сможет:
Математика 302 – После успешного завершения математики 302 – Теория множеств студент сможет:
Математика 310 – После успешного завершения курса математики 310 – Теория графов студент сможет:
Математика 315 – После успешного завершения курса Математика 315 – Комбинаторика студент сможет:
Математика 319 – После успешного завершения математики 319 – Теория чисел студент сможет:
Математика 324 – После успешного завершения математики 324 – Реальный анализ I студенты смогут:
Math 325 – После успешного завершения MATH 325 – Real Analysis II студент сможет:
Математика 326 – После успешного завершения МАТЕМАТИКИ 326 – Дифференциальные уравнения студент сможет:
Математика 328 – После успешного завершения математики 328 – Теория обыкновенных дифференциальных уравнений студент сможет:
Математика 330 – После успешного завершения курса математики 330 – Абстрактная алгебра студенты смогут:
Math 332 – После успешного завершения Math 332 – Linear Programming and Operations Research, студент сможет:
Math 333 – После успешного завершения Math 333 – Linear Algebra II, студент сможет:
Математика 335 – После успешного завершения курса Математика 335 – Основы геометрии студент сможет:
Math 338 – После успешного завершения Math 338 – Topology студент сможет:
Математика 340 – После успешного завершения курса математики 340 / биологии 340 – Моделирование биологических систем студент сможет:
Математика 341 – После успешного завершения математики 341 – Вероятность и прикладная статистика студент сможет:
Math 342 – После успешного завершения Math 342: Statistical and Machine Learning, студент сможет:
Math 343 – После успешного завершения Math 343: Advanced Applied Statistics, студент сможет:
Math 345 – После успешного завершения Math 345 – Numerical Analysis I студент сможет:
Математика 346 – После успешного завершения математики 346 – Численный анализ II студент сможет:
Математика 348 – Студенты, изучающие математику 348 – Устная презентация и исследовательский семинар:
Math 350 – После успешного завершения Math 350 – Vector Analysis, студент будет вычислять и анализировать:
Math 360 – После успешного завершения Math 360 – Probability ученик сможет:
Математика 361 – После успешного завершения математики 361 – Статистика студент сможет:
Math 366 – После успешного завершения Math 366 – Mathematical Foundations of Actuarial Science студент сможет использовать и применять следующие концепции в контексте управления рисками:
Математика 371 – После успешного завершения математики 371 – Комплексный анализ студент сможет:
Математика 372 – После успешного завершения математики 372 – Уравнения с частными производными, студент:
Математика 380 – После успешного завершения этого курса специальных тем студент:
Math 382 – После успешного завершения MATH 382 – Введение в вейвлеты и их приложения студент сможет:
Математика 383 – После успешного завершения курса математики 383 – Семинар по биоматематике студент сможет:
Math 390 – После успешного завершения MATH 390 – History of Mathematics, студент сможет:
Математика 393 – Студенты математики 393 – диплом с отличием Независимое исследование будет:
INTD 301 – После успешного завершения INTD 301 – Темы среднего образования: математика, учащиеся смогут:
INTD 302 – После успешного завершения INTD 302 – Методы и материалы: математика, студенты:
INTD 121 – После успешного завершения INTD 121 – R / Программирование студенты будут:
Заставить учащихся взаимодействовать в классе – это призыв, и в то же время это вызов при планировании уроков! Совместные занятия по математике в классе могут помочь учащимся продвигаться по их учебным траекториям… и это может быть весело! Вот почему я собрал набор из пяти загружаемых совместных математических заданий, которые вы можете использовать в своем начальном классе.
Загрузите настольные игры Math Land прямо сейчас!
Существует множество исследований, посвященных совместной игре учащихся младших классов и тому, как ее можно использовать, чтобы помочь учащимся развивать математические концепции. В недавней статье (Ramani & Eason, 2015) есть пять рекомендаций, которым следует следовать, если вы хотите собрать игры или задания для младших школьников, и я думаю, что эти действия можно распространить и на старшие классы начальной школы:
Выбирайте увлекательные учебные программы – вы увидите, что предлагаемые здесь совместные математические задания будут интересны учащимся.
Думайте вне (игровой) коробки – я использовал игру на совпадение «Концентрация» и придал ей геометрическую форму, чтобы помочь учащимся развить словарный запас. Игра, известная как «Go Fish», была изменена для усиления математического содержания.
То, что происходит в классе математики, не обязательно должно оставаться в классе математики – увязывайте игры с другими темами в учебной программе и в «реальном мире».
сверстники – ценный ресурс: учащиеся участвуют в делах и помогают друг другу, а конкуренцию можно использовать здоровым образом для мотивации учащихся.
Вовлекайте родителей и устанавливайте связи между классом и домом – совместные математические задания, описанные в этом посте, было бы здорово представить на родительском вечере.
Одна из вещей, которые вы обнаруживаете при поиске игр и занятий в Интернете, – это то, что вы получаете много просмотров о «компьютерных играх». В то время как компьютерные игры удобны и помогают студентам изучать и практиковать математику самостоятельно, совместные математические задания также помогают студентам практиковать свои социально-эмоциональные навыки во время взаимодействия друг с другом.Итак, приведенные ниже математические задания будут способствовать «старомодному» сотрудничеству между учениками, где они смогут практиковать свои социально-эмоциональные навыки:
Самосознание
Самоуправление
Социальная осведомленность
Навыки взаимоотношений
Ответственное принятие решений
Я использую эти совместные математические задания во всех ситуациях.Это самое лучшее в них! Они подходят для:
Предложите учащимся поработать вместе, чтобы попрактиковаться в сопоставлении терминов из базовой геометрической лексики с соответствующими геометрическими фигурами. Загрузите все, что вам нужно, чтобы начать играть в Geometry Concentration Game в своем классе. Это готовое задание для детей от детского сада до 3 класса содержит четыре набора карточек. В комплекте вы найдете:
Базовые наборы подходят каждому ученику младших классов.Расширенные наборы подходят для учеников 1 или 2 классов с уровнем выше среднего и для любого ученика 3-го класса.
Эта совместная игра «Go Fish» идеально подходит для младших классов, когда ученики разучивают около десяти пар. Чтобы начать играть, вам понадобится колода карт и мои распечатанные инструкции.
Загрузите Крестики-нолики Математическая игра, которая подходит для любого уровня обучения.Это увлекательный и интерактивный способ подготовиться к предстоящему экзамену или попрактиковаться в новых математических навыках! Это также способствует социально-эмоциональному обучению в классе через сотрудничество и командную работу.
Существуют различные загружаемые игровые доски Math Land для каждого класса, от 1 до 6. Учащиеся могут практиковать свои вычислительные навыки, продвигаясь по пути. Каждой группе потребуются цветные фишки и кубик, чтобы сыграть в эту настольную игру.
Загрузите это упражнение по сортировке, в котором учащиеся сортируют фракции шоколадных батончиков, сравнивая их с эталонными значениями ноль, половина и одно целое. Используйте это задание для старших классов начальной школы или в качестве дополнительного задания для младших учащихся ускоренного курса.
Эти пять простых в использовании математических заданий отлично подходят для содействия совместному обучению в вашем классе.Вы можете использовать их по-разному. Помимо того, что они веселые и увлекательные, когда используются в качестве занятий для всех классов, их можно использовать в математических центрах, как занятия для раннего финишера или на семейном вечере.
Загрузите эти задания сегодня, и вы увидите, как учащиеся взаимодействуют друг с другом в процессе обучения в вашем классе!
Sadlier Math, – новая комплексная программа по математике для классов K – 6, которая дает учителям поддержку и профессиональное развитие, необходимое для развития математически способных учеников.Загрузите бесплатный образец сегодня!
Рамани, Гита Б. и Сара Х. Исон. «Все это складывается из раннего изучения математики через игру и игры». Дельта Пхи Каппан, май 2015 г., стр. 27. Expanded Academic ASAP, http://link.galegroup.com/apps/doc/A412800569/EAIM?u=mlin_n_stevens&sid=EAIM&xid=6921eac9 . По состоянию на 14 мая 2018 г.
Что должен знать, уметь делать и / или чего должен обладать специалист по математике после окончания учебы?
*** Цели для основных математических дисциплин в формате PDF ***
Развитие математической зрелости
Логическое мышление
Эффективное общение во всех формах (письменной, устной и т. Д.))
Интеллектуальное развитие
Основы