Устройство нашей планеты, расположение на ней стран и материков привлекало внимание людей еще с давних времен. И в наши дни такая наука, как география, популярна не только среди взрослых, но и среди школьников.
Есть много интересных географических загадок, рассчитанных на то, чтобы привить ребятам интерес к географии и развить логическое мышление. Кстати, многие из них будут интересны и взрослому любознательному человеку.
Эти загадочные холодные земли до сих пор недостаточно изучены. Но определенный багаж знаний о них имеется. Кроме природных и климатических задач, придумано много географических загадок про самые белоснежные части нашей планеты. Возможно, чтобы ответить на эти несложные вопросы, понадобятся не только школьные знания, но и смекалка и остроумие.
Все мы с детства знаем названия материков, расположенных на нашей планете. Знакомы нам и названия большинства стран, даже тех, которые появились на карте совсем недавно. Однако на много ли географических загадок, основанных на программе средней школы, получится сразу найти ответ?
Две трети поверхности нашей планеты покрыты водой — океанами, морями, озерами и реками. С водными потоками непосредственно связана вся история человечества, да и жизнь на планете без воды была бы невозможной.
Поэтому специалисты в области географии так много времени уделяют изучению многочисленных водоемов планеты, как больших, так и скромных. А для детей придумано огромное количество географических загадок о морях и реках. Вот некоторые из них:
Знать названия всех городов на нашей планете просто нереально, их слишком много. Но любой образованный человек должен помнить названия столиц и других крупных городов в разных странах. А иногда можно блеснуть эрудицией в беседе, вспомнив необычный или забавный топоним. А таких странных названий очень много…
В наши дни все белые пятна на глобусе давно исследованы. Раньше было не так, когда отважные путешественники прошлого находили новые земли, они давали им названия. С точки зрения современного человека, часто они кажутся нелогичными. На этот счет существуют интересные загадки о географических открытиях, решить которые будет полезно как детям, так и взрослым. Например, такая…
Гренландия — крупнейший остров на Земле, больше 80 % территории которого покрыто ледниками. Почему же человек, открывший этот остров, дал ему название Гренландия (Зеленая земля)? Это произошло в 982 году. Скандинавский ярл Эрик Рауди стремился убедить людей поселиться на острове, поэтому и назвал его Зеленой землей.
Однако существует версия, что в Х веке климатические условия в Гренландии были более мягкими, поэтому экипаж викингов мог действительно увидеть зеленые земли юго-западной части острова. Наверно, точный ответ на эту загадку никогда не будет получен.
Изучение географии требует знания большого числа специфических терминов. Проще всего познакомить с этими понятиями детей, загадывая им забавные географические загадки. Для 7-классников и школьников постарше есть несколько интересных вариантов:
Часто для решения, казалось бы, несложных географических загадок детям нужно не только иметь определенные знания о строении планеты, но и уметь логически мыслить. Впрочем, что дети… Иногда простые вопросы способны поставить в тупик даже взрослого образованного человека.
Иногда сложно заинтересовать школьников сухими научными данными из учебников. Зато информация, переданная в веселой игровой форме, будет усвоена намного быстрее. Вот небольшая подборка стихотворных географических загадок с ответами, благодаря которым детвора сможет лучше запомнить новую информацию.
«На глобусе найдете адресок —
На талии планеты поясок».
Если представить себе «талию» земного шара, несложно догадаться, что опоясывает ее экватор.
«На ноге стоит одной,
Крутит-вертит головой.
Нам показывает страны,
Реки, горы, океаны».
Это очень простая географической загадке для 5 класса. Ответ: речь идет о макете нашей планеты — глобусе.
«Вот так чудо! Вот так диво!
Как сорвался он с обрыва,
Так уже который год
Все никак не упадет».
Речь идет о водопаде.
Рассказывая о географических загадках, сложно обойти вниманием шарады, не только помогающие запомнить новые названия и термины, но и тренирующие логическое мышление. Вот примеры нескольких несложных шарад-загадок:
«Первое можно из снега слепить,
Грязи кусок может тоже им быть.
Ну а второе — мяча передача,
Важная это в футболе задача.
Целое люди в походы берут,
Ведь без него они путь не найдут».
Ответ: Ком-пас.
«Я к углеводам отношусь,
Сластенам нужен я всегда.
Но я впустыню превращусь,
Едва ко мне прибавишь «А».
Конечно, речь идет о величайшей пустыне мира — Сахаре.
liveprosto.ru
Решение головоломок доставляет людям удовольствие: очень приятно осознавать, что именно вы только что нашли ответ на одну из самых сложных логических задач в мире. Однако это не единственная причина, почему нужно хоть иногда разгадывать головоломки. Об остальных причинах, о наиболее сложных логических задачах, пользе от их решения читайте в статье.
Наиболее трудная задача названа именно так. В народе ее именуют «Битвой людей и богов». Самая сложная логическая задача впервые была предложена философом и логиком из Соединенных Штатов Америки. Его зовут Джордж Булос. Весь свет узнал о данной головоломки после ее публикации в газете «Республика», которая издается в Италии. Это произошло в 1992 году.
Самая сложная логическая задача выглядит устрашающе с самого начала. Как записано ее условие? Допустим, существуют три бога, которые знают друг друга. Один из них является богом лжи, другой – истины, а третий – случая. Принято обозначать их буквами A, B и C, используя буквы в произвольном порядке.
Бог лжи всегда говорит только неправду, бог истины, наоборот, произносит только правдивые изречения. И наконец, бог случая может говорить как правду, так и неправду, при этом предугадать, что он сейчас скажет, нельзя.
Задача состоит в том, чтобы разобраться, кем является каждый бог. Для этого можно задать всего три вопроса. Самая сложная логическая задача подразумевает, что все эти вопросы можно адресовать как одному богу, так и каждому, но по очереди. Все зависит от полученных ответов. Вопросы должны подразумевать только утвердительный («Да») или отрицательный («Нет») ответ.
Указано, что боги понимают тот язык, на котором будут заданы вопросы, однако отвечают они на своем. Вы можете услышать либо слово Ja, либо Da. Неизвестно, какое из них означает «Нет», а какое – «Да».
Самая сложная логическая задача была опубликована вместе с несколькими подсказками к ее решению. Они звучат так:
Булос – логик и философ, который создал задачу, – в своей статье подсказал ход решения. Первое, что нужно сделать, – это вычислить бога истины или бога лжи. Для этого следует создать вопрос с комплексными логическими связями. Он должен звучать примерно так: «Будем считать, что ты – бог истины, B является богом случая, будет ли при этом Da означать «да»?» Конечно же, это не точная формулировка, это лишь приблизительный вариант. При помощи данного вопроса можно определить одного из богов. Далее все зависит от того, как задать еще два вопроса.
Многие люди знакомы с играми, ориентированными на перестановку цифр в судоку. Решение такой головоломки – отличный способ устроить 5-минутную тренировку для мозга. Возможно, у вас неплохо получается решать японские судоку. Но сможете ли вы решить самую сложную задачу в своей группе?
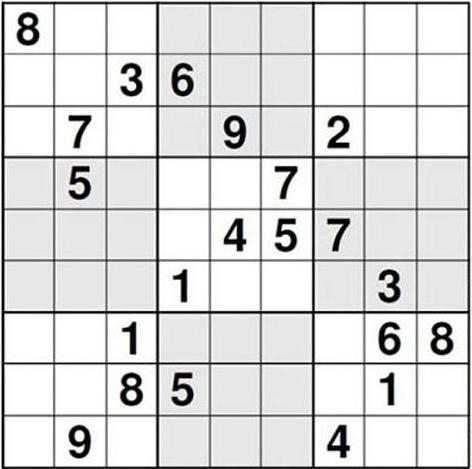
AI Sudoku – алгоритм для создания сложного судоку, построенный математиком по имени Арто Инкала в 2012 году. В последнее время появляется все больше и больше ботов, но именно этот считается самым трудным. Он называется Escargot. Наряду с основной задачей можно найти 19 других сложных судоку, которые также были созданы ботом.
Чтобы найти решение самой сложной логической задачи-судоку в мире, необходимо выделить на это достаточное количество времени. Британское издание The Telegraph сообщило, что по шкале сложности судоку «Эскаргот» оценивается в 11 баллов, при том что привычные головоломки повышенной сложности «тянут» на 5.
Михаил Моисеевич Бонгард, русский кибернетик, в 1967 году впервые опубликовал в своей книге пример логической головоломки под названием «Проблема узнавания». Однако очень сложные логические задачи Бонгарда получили популярность позже. Это случилось после того, как американский ученый Дуглас Хофштадтер написал о них в своей книге.
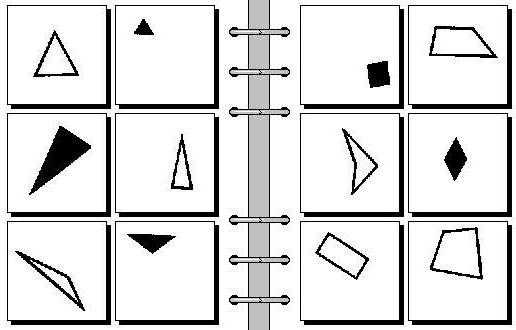
Чтобы найти решение «Проблемы узнавания», необходимо выявить определенную закономерность, или правило. Шесть изображений, которые находятся на левой странице, соответствуют этому правилу. Соответственно, изображения на правой странице не подходят под него.
Мартин Гарднер – это американский математик, который является автором большого количества различных головоломок и задач. Наиболее известная из них – это поиск «числа стойкости». Суть состоит в том, чтобы за наименьшее количество шагов свести определенное число к одной цифре. Для этого необходимо последовательно перемножать составляющие числа.
Чаще всего примером решения служит «77». Свести его к одному числу можно за несколько шагов. 7*7=49, 4*9=36, 3*6=18, 1*8=8. Действие было произведено четыре раза, это и есть «число стойкости».
На специализированных информационных ресурсах соответствующей тематики публикуется много всевозможных головоломок, в том числе и самые сложные логические задачи — с ответами, подсказками, алгоритмами решений и т. д. Они всегда вызывают живой интерес, поэтому если вы хотите занять себя или своих друзей промозглым сырым вечером, воспользуйтесь такой возможностью или даже попробуйте придумать задание самостоятельно. Поверьте, находить «числа стойкости» — весьма увлекательное занятие.
Согласно статистике, настоящие гении находят решение в течение десяти секунд. Если верить опросам, логические задачи — сложные, с подвохом — не вызывают особых трудностей у выпускников Гарварда, у них на данное задание уходит не более 40 секунд. К примеру, Билл Гейтс проходит этот тест на гениальность за 20 секунд. 15 процентов жителей Земли являются одаренными людьми, они находят решение за две минуты. А теперь посмотрите на эту картинку и догадайтесь, какая фигура здесь лишняя.
Ответ таков: фигура под номером один. Она не обладает общими признаками с остальными изображениями. Судите сами, у фигуры № 2 отсутствует белая рамка, а № 3 является единственным кругом. В то время как все остальные фигуры красные, № 4 – зеленая, а № 5 очевидно меньше других. Таким образом, только у фигуры под номером один нет ярких отличий от большинства изображений, в чем и состоит ее основное… отличие.
Другая интересная загадка тоже связана с ложью и истиной. Допустим, на острове живут сразу два племени. Лжецы всегда обманывают, а молодцы, наоборот, всегда говорят правду. Путешественник, встретивший островитянина, задал ему вопрос, чтобы узнать, кто он такой. Тот сказал, что является молодцом, и его наняли в проводники.
Во время путешествия путники увидели еще одного островитянина, который, судя по словам сопровождающего, тоже утверждал, что он молодец. Внимание, вопрос! Как определить, лжецом или молодцом был проводник?
Ответ звучит так: на этом острове все говорят, что они молодцы. Поскольку проводник правильно передал путешественнику ответ островитянина, то понятно, что он является молодцом.
Выше были представлены вашему вниманию как средние, так и очень сложные логические задачи. С ответами, прописанными в конце, решать их, конечно, проще. А чтобы напрячь мозг еще сильнее, можно создать себе дополнительные сложности: не записывать условие и попробовать найти верное решение в уме. Итак, вот еще одна головоломка.
Существует несколько футбольных команд. На турнирной таблице «Торпедо» занимает первое место, «Спартак» – пятое. «Динамо» находится посередине между этими двумя командами. Далее нужно быть очень внимательным: если «Спартак» будет опережен «Локомотивом», а «Зенит» займет место сразу после «Динамо», какая из пяти команд займет второе место? Дать ответ необходимо через 30 секунд. Он будет звучать так: «Локомотив».
Интернет можно назвать хранилищем головоломок. Но многие задачи требуют наличия простейших технических навыков, например, умения находить исходный код страницы для подсказок или изменять файлы изображений. Помните, что сложные логические задачи созданы для того, чтобы проверять ваш интеллект, а не тестировать на предмет знания компьютера.
Агентство национальной безопасности обладает не самой хорошей репутацией, поскольку оно не раз подозревалось в шпионаже за интернет-пользователями и нарушениях конфиденциальности. Если не принимать это во внимание, можно найти достаточно сложные логические задачи с ответами на официальном сайте периодических головоломок. Ежемесячно появляются новые задания. Ответ опубликовывается через несколько дней после вопроса. Периодику NSA Puzzle запустили только в прошлом году, а это значит, что уже доступна коллекция, состоящая более чем из 12 головоломок.
Очень интересно работать над решением трудной загадки в течение нескольких дней или даже недель. Терпеливым людям подойдет самая сложная логическая задача в мире под названием Blue Eyes. Согласно XKCD – лучшей веб-платформе для вундеркиндов, она развивает логическое, математическое и латеральное мышление.
Создатель головоломки услышал ее совершенно случайно и опубликовал в Интернете. При этом он не использовал даже слов. Чтобы найти ключ к ее решению, необходимо прочитать загадку, пересказать ее и попробовать мысленно найти ответ на нее. Самая сложная логическая задача в мире очень увлекательна, она занимает все свободное время.
Профессиональный психолог по имени Ричард Уайзман стал интернет-знаменитостью благодаря своему каналу на видеохостинге Youtube. Он публикует на нем различные иллюзии, фокусы и прочее. По пятницам мужчина делится в своем блоге очередной головоломкой или загадкой. Чтобы решить их, необходимо сочетать линейное, латеральное и творческое мышление. Знаменитые головоломки со спичками, а также другие загадки и задачи на основе изображений можно найти в блоге психолога.
Роберт Эббот – программист, логик и разработчик игр. Известность пришла к нему после публикации «Логических лабиринтов», которые находятся в бесплатном доступе. Суть данной головоломки состоит в том, чтобы пройти лабиринт с заданными правилами.
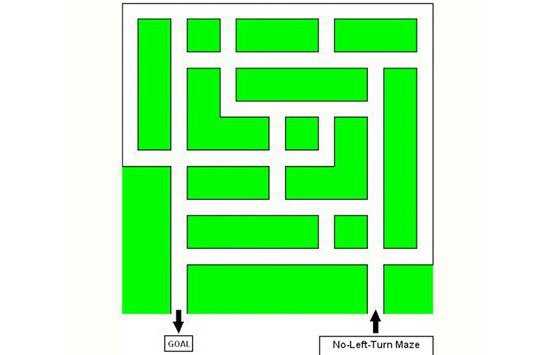
Самую первую игру, к слову, самую простую, которая называется Easy Maze 1, необходимо преодолеть, не поворачивая налево.
Головоломки и различные логические задачи обладают несколькими положительными качествами. Во-первых, они тренируют человеческий мозг, во-вторых, решать их очень интересно, а в-третьих, они позволяют развить в себе определенные черты характера.
Насколько полезными для детей могут быть головоломки?
Конечно, все самые важные качества характера закладываются в детях в раннем возрасте, и этому очень способствуют логические задачи. Однако они полезны и для взрослых людей, которые давно уже окончили школу. Мозг нужно тренировать точно так же, как и тело.
liveprosto.ru
Многие не знают например, что знаменитая и Великая теорема Ферма уже доказана, а есть ведь вообще пока не доказанные математические задачи.
В августе 1900 года в Париже состоялся II Международный Конгресс математиков. Он мог бы пройти незамеченным, если бы на нем не выступил немецкий ученый, профессор Давид Гильберт, который в своем докладе поставил 23 самые главные на тот момент, существенные проблемы, касающиеся математики, геометрии, алгебры, топологии, теории чисел, теории вероятностей и пр.
На данный момент решены 16 проблем из 23. Ещё 2 не являются корректными математическими проблемами (одна сформулирована слишком расплывчато, чтобы понять, решена она или нет, другая, далёкая от решения, — физическая, а не математическая). Из оставшихся пяти проблем две не решены никак, а три решены только для некоторых случаев.
Вот собственно весь список:
Вот как выглядят на сегодняшний день проблемы Гильберта и их статус:
1. Континуум-гипотеза. Существует ли бесконечное кардинальное число строго между кардиналами множеств целых и действительных чисел? Решена Полом Коэном в 1963 г. — ответ на вопрос зависит от того, какие аксиомы используются в теории множеств.
2. Логическая непротиворечивость арифметики. Доказать, что стандартные аксиомы арифметики не могут привести к противоречию. Решена Куртом Геделем в 1931 г.: с обычными аксиомами теории множеств такое доказательство невозможно.
3. Равносоставленность равновеликих тетраэдров. Если два тетраэдра имеют одинаковый объем, то всегда ли можно разрезать один из них на конечное число многоугольников и собрать из них второй? Решена в 1901 г. Максом Деном, ответ отрицательный.
4. Прямая как кратчайшее расстояние между двумя точками. Сформулировать аксиомы геометрии на основе данного определения прямой и посмотреть, что из этого следует. Слишком расплывчатая задача, чтобы можно было рассчитывать на определенное решение, но сделано немало.
5. Группы Ли без опоры на дифференцируемость. Технический вопрос теории групп преобразований. В одной из интерпретаций ее решил Эндрю Глисон в 1950-е гг., в другой — Хидехико Ямабе.
6. Аксиомы физики. Разработать строгую систему аксиом для математических областей физики, таких как теория вероятностей или механика. Систему аксиом для вероятностей построил Андрей Колмогоров в 1933 г.
7. Иррациональные и трансцендентные числа. Доказать, что определенные числа являются иррациональными или трансцендентными. Решена в 1934 г. Александром Гельфондом и Теодором Шнайдером.
8. Гипотеза Римана. Доказать, что все нетривиальные нули римановой дзета-функции лежат на критической линии. См. главу 9.
9. Законы взаимности в числовых полях. Обобщить классический закон квадратичной взаимности (о квадратах по определенному модулю) на более высокие степени. Частично решена.
10. Условия существования решений диофантовых уравнений. Найти алгоритм, позволяющий определить, имеет ли данное полиномиальное уравнение со многими переменными решения в целых числах. Невозможность доказал Юрий Матиясевич в 1970 г.
11. Квадратичные формы с алгебраическими числами в качестве коэффициентов. Технические вопросы решения диофантовых уравнений со многими переменными. Решена частично.
12. Теорема Кронекера об абелевых полях. Технические вопросы обобщения теоремы Кронекера. Не доказана до сих пор.
13. Решение уравнений седьмой степени при помощи функций специального вида. Доказать, что общее уравнение седьмой степени не может быть решено с использованием функций двух переменных. В одной из интерпретаций возможность такого решения доказали Андрей Колмогоров и Владимир Арнольд.
14. Конечность полной системы функций. Расширить теорему Гильберта об алгебраических инвариантах на все группы преобразований. Опроверг Масаёси Нагата в 1959 г.
15. Исчислительная геометрия Шуберта. Герман Шуберт нашел нестрогий метод подчета различных геометрических конфигураций. Задача в том, чтобы сделать этот метод строгим. Полного решения до сих пор нет.
16. Топология кривых и поверхностей. Сколько связанных компонент может иметь алгебраическая кривая заданной степени? Сколько различных периодических циклов может иметь алгебраическое дифференциальное уравнение заданной степени? Ограниченное продвижение.
17. Представление определенных форм в виде суммы квадратов. Если рациональная функция всегда принимает неотрицательные значения, то должна ли она обязательно выражаться в виде суммы квадратов? Решили Эмиль Артин, Д. Дюбуа и Альбрехт Пфистер. Верно для действительных чисел, неверно в некоторых других числовых системах.
18. Заполнение пространства многогранниками. Общие вопросы о заполнении пространства конгруэнтными многогранниками. Имеет отношение к гипотезе Кеплера, ныне доказанной (см. главу 5).
19. Аналитичность решений в вариационном исчислении. Вариационное исчисление отвечает на такие вопросы, как «найти кратчайшую кривую с заданными свойствами». Если подобная задача формулируется при помощи красивых функций, то должно ли решение тоже быть красивым? Доказали Эннио де Джорджи в 1957 г. и Джон Нэш.
20. Граничные задачи. Разобраться в решениях дифференциальных уравнений физики в определенной области пространства, если заданы свойства решения на ограничивающей эту область поверхности. В основном решена (вклад внесли многие математики).
21. Существование дифференциальных уравнений с заданной монодромией. Особый тип комплексного дифференциального уравнения, в котором можно разобраться при помощи данных о его точках сингулярности и группе монодромии. Доказать, что может существовать любая комбинация этих данных. Ответ «да» или «нет» в зависимости от интерпретации.
22. Униформизация с использованием автоморфных функций. Технический вопрос об упрощении уравнений. Решил Пауль Кебе вскоре после 1900 г.
23. Развитие вариационного исчисления. Гильберт призывал к выдвижению новых идей в области вариационного исчислении. Многое сделано, но формулировка слишком неопределенная, чтобы задачу можно было считать решенной.
Очередной раз убедился, что это слова не из «моего мира». Так что у кого то еще есть шанс прославиться …
КСТАТИ За что еще дадут миллион долларов…
В 1998 году на средства миллиардера Лэндона Клея (Landon T. Clay) в Кембридже (США) был основан Математический институт его имени (Clay Mathematics Institute) для популяризации математики. 24 мая 2000 года эксперты института выбрали семь самых, по их мнению, головоломных проблем. И назначили по миллиону долларов за каждую.
Список получил название Millennium Prize Problems.
1. Проблема Кука
Нужно определить: может ли проверка правильности решения какой-либо задачи быть более длительной, чем получение самого решения. Эта логическая задача важна для специалистов по криптографии — шифрованию данных.
2. Гипотеза Римана
Существуют так называемые простые числа, например, 2, 3, 5, 7 и т. д., которые делятся только сами на себя. Сколько их всего, не известно. Риман полагал, что это можно определить и найти закономерность их распределения. Кто найдет — тоже окажет услугу криптографии.
3. Гипотеза Берча и Свиннертон-Дайера
Проблема связана с решением уравнений с тремя неизвестными, возведенными в степени. Нужно придумать, как их решать, независимо от сложности.
4. Гипотеза Ходжа
В ХХ веке математики открыли метод исследования формы сложных объектов. Идея в том, чтобы использовать вместо самого объекта простые «кирпичики», которые склеиваются между собой и образуют его подобие. Нужно доказать, что такое допустимо всегда.
5. Уравнения Навье – Стокса
О них стоит вспомнить в самолете. Уравнения описывают воздушные потоки, которые удерживают его в воздухе. Сейчас уравнения решают приблизительно, по приблизительным формулам. Нужно найти точные и доказать, что в трехмерном пространстве существует решение уравнений, которое всегда верно.
6. Уравнения Янга – Миллса
В мире физики есть гипотеза: если элементарная частица обладает массой, то существует и ее нижний предел. Но какой — не понятно. Нужно до него добраться. Это, пожалуй, самая сложная задачка. Для ее решения необходимо создать «теорию всего» — уравнения, объединяющие все силы и взаимодействия в природе. Тот, кто сумеет, наверняка получит и Нобелевскую премию.
А помните, мы как то обсуждали Ошибку Перельмана или «что тяжелее — тонна дерева
Это копия статьи, находящейся по адресу https://masterokblog.ru/?p=47223.masterok.livejournal.com
Интересная бесплатная логическая игра головоломка. Проходите множество уровней Бурундуком в увлекательном приключении по лесным мирам.
Правильно катайте шарики и двигайте блоки – кубики по клеткам, чтобы закрывать ямы, проходить препятствия, уничтожить ловушки и опасных животных.
Помогите Бурундуку в этой бродилке с приключениями. Соберите семена и орехи к зиме. Но не думайте, что это будет так легко.
Выбирайте подходящий вариант сложности игры.
Сумеете пройти все уровни? Будет ох как не просто…
Особенности:
● Занимательные игры на логику и сообразительность.
● Много продуманных уровней для каждого режима
● Двигайте кубики – блоки и шары, проходите препятствия.
● Сложные головоломки, средней сложности и лёгкие.
● Красивая пиксельная графика. Лес, речки, животные.
● Расслабляющая музыка и звуковые эффекты.
● Интеллектуальные игры и приключения для всей семьи.
● Нет ограничения по времени. Думайте сколько угодно.
● Продумывайте Ваши шаги в прохождение игры наперёд.
● Много часов увлекательного и интересного геймплея.
● Скачайте логические игры бесплатно на русском языке.
● Головоломки для взрослых и для детей без интернета.
● Нравится Nuts, игра сокобан и двигать ящики ? Отлично!
Игра переведена на языки: * Русский * Английский * Испанский * Немецкий * Французский
☆ Мы ждем ваших отзывов и пожеланий ! ☆
ПОДРОБНЕЕ:
★ Мир 1
Режим с лёгкими детскими логическими играми. Пройти их не сложно, но они научат взаимодействию с объектами и начальной сообразительности. И подготовят к дальнейшему прохождению умной игры.
★ Мир 2
Логические задачи средней сложности. Потребуется хорошо подумать, чтобы пройти сцены с увеличивающейся запутанностью. Подойдут большинству людей и обострят соообразительность и смекалку.
★ Мир 3
Сложные головоломки для взрослых. На обдумывание и прохождение этих уровней может уйти много времени. Задачи в этом режиме очень затруднительны и замысловаты. Умный расчёт и интеллект – залог успеха!
Бонусные задания с лабиринтом, в котором бурундука преследует опасный скорпион. Пробегите лабиринт быстрее, чем он Вас схватит, соображая на ходу!
Закатывайте “лишние” кубики и шарики в ямки, или сталкивайте в воду. За это начисляются дополнительные очки (от 2-5). Имейте в виду, что иногда без этого не пройти уровень на 3 звезды.
Вас ждёт пиксельная увлекательная игра бегалка – бродилка по лесным лабиринтам по клеткам. Белка собирает орехи и семечки, а Вы проходите многие уровни. Ловушки, ямы и опасные животные: ёжики и лягушки, а также муравьи, жуки и скорпионы ждут!
Нравится игра сокобан головоломка с ящиком, или Nuts с кнопочных телефонов? Тогда наша игра на логику и смекалку тоже для Вас! Пошевелите шестерёнками и извилинами. Проверьте свою сообразительность в детских логических играх и головоломках для взрослых на русском языке. Думайте над бесплатными сложными головоломками и простыми. Решайте умные логические задачи и развивайтесь.
Выбирайте сложность игры по вкусу и вместе с белкой вперед, навстречу приключениям!
Семена
– За каждые 1000 набранных очков Вы получите 5 шт.
– Давите животных двигая от себя в лабиринте блоки и катая шарики по клеточкам. Собирайте орехи ими оставленные.
– Открывайте за них заблокированные уровни. Или проходите их по порядку.
– Покупайте в магазине семена и дополнительные жизни бурундуку, чтобы бродить и бегать дольше.
– Рестарт с чек-поинта стоит 1 семечку. Полезно на локациях с чек-поинтом, чтобы не начинать сначала.
СОХРАНЕНИЕ ВСЕГО ПРОГРЕССА В ОБЛАКЕ. Требуется авторизация в Google Play Games и интернет соединение
В СЛЕДУЮЩИХ ОБНОВЛЕНИЯХ:
– Новые сцены, больше животных, ловушек и игр на логику.
– Другие прохождения головоломок с кубиками и шариками.
– Зимнее оформление леса с новыми взаимодействиями.
– Режим редактора уровней. Постройте своё приключение.
– Ежедневные бонусные мини игры в стиле аркады и сокобан.
androspace.ru
Логические задачи по сказкам для начальной школы
Иван-царевич против Кощея Бессмертного
Иван-царевич пришел к Кощею Бессмертному, чтобы вызволить Василису Прекрасную. Показал ему Кощей три двери в темницы, а на дверях написано: на первой — «Здесь сидит Василиса Прекрасная», на второй — «Темница 3 не пустая», на третьей — «Здесь Змей Горыныч», — и сказал: «Отпущу с тобой Василису, если отгадаешь, за какой она дверью. А все надписи на дверях неверные».
Ответ: Василиса Прекрасная во второй темнице.
Как Иван-царевич Змея Горыныча победил
Собрался Иван-царевич на бой со Змеем Горынычем, трехглавым и треххвостым. «Вот тебе меч-кладенец, — говорит ему Баба- Яга. — Одним ударом ты можешь отрубить Змею либо голову, либо две головы, либо один хвост, либо два хвоста. Запомни: срубить голову — новая вырастет, срубить хвост — два новых вырастут, срубить два хвоста — ничего не вырастет». За сколько ударов Иван-царевич может срубить Змею все головы и хвосты?
Ответ: за 9.
Как Али-Баба может больше денег заработать?
Али-Баба нашел пещеру, полную золота и алмазов. Полный мешок золота весит 200 кг, полный мешок алмазов — 40 кг. Али-Баба может унести за один раз не более 100 кг. Килограмм золота стоит 200 динаров, килограмм алмазов – 60 динаров. Какую наибольшую сумму денег он может получить за золото или алмазы, унесенные в одном мешке (за один раз)?
Решение. Прежде всего, заметим, что 5 кг золота занимают тот же объем, что и 1 кг алмазов, но стоят дороже.
Сначала докажем, что Али-Баба может получить за сокровища 3000 динаров. Действительно, в мешок входит 40 кг алмазов. Если мы заменим 15 кг алмазов на 75 кг золота, то объем мешка останется прежним, а стоимость его будет равна 3000 динаров.
Докажем теперь, что 3000 динаров — это наибольшая сумма, которую можно выручить за сокровища. Если из мешка, содержащего 25 кг алмазов и 75 кг золота, убрать еще часть алмазов, то заменить их можно будет таким же количеством золота (чтобы не было превышения по массе), и общая стоимость уменьшится, так как алмазы стоят дороже. Если же убрать часть золота, то общая стоимость снова уменьшится, так как масса взятых вместо золота и алмазов будет в пять раз меньше (иначе получится превышение по объему!). Например, если взять 5х кг золота и заменить их на х кг алмазов, то стоимость сокровищ уменьшится на 40х динаров.
Ответ: 3000 динаров.
Как Кощей в печке сидел
Кощей поспорил с Бабой-Ягой, что просидит в печке 200 минут, а просидел 68 % этого времени. Сколько минут просидел Кащей в печи?
Ответ: 136 минут.
Буратино на Поле чудес
Зная, что Буратино получил золотые монеты, лиса Алиса и кот Базилио хотели их отобрать. Привели Буратино на пустырь. Лиса Алиса говорит: «Это Поле чудес. Если закопаешь золотые монеты, то наутро вырастет дерево, на котором их будет в три раза больше. Затем полученные монеты можно снова закопать в землю, и снова вырастет дерево с монетами. Так можно снять несколько урожаев. Мы можем посторожить ночью эти монеты. В награду ты будешь нам отдавать 9 монет после каждого урожая». Буратино отвечает:
«Так ведь после двух урожаев у меня совсем не останется денег. Уж лучше я сам посторожу». Сколько золотых монет было у Буратино?
Ответ: 4 монеты.
Бабушки и козлята
У трех бабушек было по одному серенькому козлику. Пошли они в лес погулять, а там их волки съели. Остались от козликов рожки да ножки. Сколько осталось рожек и сколько ножек?
Ответ: 12 ножек и 6 рожек.
Крошечка-Хаврошечка и сестры
Крошечка-Хаврошечка пошла в лес со своими сестрами — Одноглазкой, Двуглазкой и Трехглазкой. Сколько всего глаз было у этой компании?
Ответ: 8.
Неприготовленная яичница
Курочка Ряба снесла яичко, а мышка взяла и разбила. Ряба снесла еще три яичка. Мышка эти тоже разбила. Ряба поднатужилась и снесла еще пять, но бессовестная мышка разбила и эти. Из скольких яиц могли бы приготовить яичницу дед да баба, если бы они не разбаловали свою мышку?
Ответ: из 9.
Меткие стрелки
Иван-царевич и его братья пускали стрелы. Три стрелы упали на царский двор, 4 — на боярский, а 8 улетели в неизвестном направлении. Сколько всего стрел выпустили Иван-царевич и его братья?
Ответ: 15 стрел.
Грибная охота
Леший собрал 48 мухоморов, а Баба-Яга на 12 мухоморов меньше. Сколько всего съедобных грибов собрали Леший и Баба-Яга.
Ответ: ни одного
Как Иван освободил пленников
Иван — крестьянский сын освободил из темницы Змея Горыныча 20 богатырей, 10 великанов, а царских дочерей столько, сколько богатырей и великанов вместе. Сколько всего пленников освободил Иван?
Ответ: 60.
Капитан Врунгель и кенгуру
Капитан Врунгель погнался за кенгуру, в сумку которой попал мячик от гольфа. Кенгуру за 1 минуту делает 70 прыжков, каждый прыжок — 10 м. Капитан Врунгель бежит со скоростью 10 м в минуту. Догонит ли он кенгуру?
Ответ: Не догонит.
nsportal.ru
Логика у ребенка должна работать! Не превалировать над творческой активностью, но находиться с ней в гармонии и балансе. Поэтому, как и творческие способности, умение мыслить логически нужно в детях развивать.
И те загадки логические с ответами, что мы собрали для вас на этой странице, надеемся, вам в этом помогут. Некоторые из этих загадок очень просты, они для раскачки или для совсем маленьких. А другие — посложнее. Хотя, конечно, не такие сложные, как для взрослых детей. Но малышам все равно будет никак не справится с ними без вашей помощи и без ответов. Помогите же им, не будьте слишком серьезными! 🙂
Впрочем, довольно разговоров, к делу!
1)У бабушки Ани внук Сережа, кот Пушок, собака Бобик. Сколько у бабушки внуков?
Ответ:(Один)
2)Термометр показывает плюс 15 градусов. Сколько градусов покажут два таких термометра?
Ответ:(15)
3) Как правильно говорить: «не вижу белый желток» или «не вижу белого желтка»?
Ответ:(Желток не может быть белым)
4)Грузовик ехал в деревню. По дороге он встретил 4 легковые машины. Сколько машин ехало в деревню?
Ответ:(Одна)
5)Ребёнок моего отца, мне не брат. Кто это?
Ответ:(Сестра)
6)В вазе лежит 4 апельсина. Вопрос: как разделить эти 4 апельсина между четырьмя мальчиками так, чтобы каждому мальчику досталось по одному апельсину, и чтобы 1 апельсин остался в вазе?
Ответ:(Оставить четвертый апельсин в вазе)
7) Двенадцать братьев
Друг за другом бродят,
Друг друга не обходят.
Ответ: (Месяцы)
8)Знаменитый фокусник говорит, что может поставить бутылку в центре комнаты и вползти в неё. Как это?
Ответ:(Вползти в комнату может каждый)
9)Каким гребешком нельзя расчесаться?
Ответ:(Петушиным)
10) Меня зовут Миша. У моей сестры только один брат. Как зовут брата моей сестры?
Ответ:(Миша)
11) Может ли дождь лить два дня подряд?
Ответ:(Нет, между ними — ночь)
12)Какой месяц короче всех?
Ответ:(Май, так как в нём всего лишь три буквы)
13)Скажите слово, которое содержит в себе 40 гласных букв.
Ответ:(Сорока, а именно сорок «А»)
14) В парке 8 скамеек. Три покрасили. Сколько скамеек стало в парке?
Ответ:(Восемь так и осталось)
15)В коробке 25 кокосовых орехов. Обезьяна стащила все орехи, кроме 17. Сколько орехов осталось в коробке?
Ответ:(Осталось 17 орехов)
16) Какой рукой лучше размешивать чай?
Ответ:(Лучше всего чай размешивать ложечкой)
17) У каждой из 5 сестер было по двое братьев. Сколько братьев было всего?
Ответ:(Двое братьев)
18) Вы опередили лыжника, который находился на второй позиции. Какое место теперь занимаете вы?
Ответ:(Обогнав лыжника, вы становитесь на его место, а именно на второе)
19)Хозяйке необходимо испечь 6 пирожков. Как ей справиться за 15 минут, если на сковороде помещается только 4 пирожка, а с каждой стороны пирожок должен печься 5 минут?
Ответ: (сначала кладем 4 пирожка и жарим их 5 минут, далее 2 пирожка переворачиваем, а 2 снимаем, за этим кладем 2 новых пирожка и жарим еще 5 минут. После этого снимаем 2 готовых пирожка, дожариваем все остальные)
20)Где оказался Моисей, когда погасла свеча?
Ответ:(В темноте)
21) У фокусника 2 мешочка: в одном находятся карты, а в другом – шарики. Каждый из мешков подписан: один с картами — верно, другой с шариками – заведомо ложно. На 1 написано: «В этом мешке нет шариков»; на 2 – «Шарики и карты здесь». В каком мешочке карты?
Ответ:(карты в первом мешочке)
22) Что с пола за хвост не поднимешь?
Ответ:(Клубок ниток)
23) В 12-этажном доме есть лифт. На первом этаже живет всего 2 человека, от этажа к этажу количество жильцов увеличивается вдвое. Какая кнопка в лифте этого дома нажимается чаще других?
Ответ:(кнопка на первом этаже)
24) Батон разрезали на три части. Сколько сделали разрезов?
Ответ:(Два разреза)
25) Кто ходит сидя?
Ответ:(Сидя ходит шахматист)
26) На край стола поставили кастрюлю, плотно закрытую крышкой, таким образом, что две трети кастрюли свисало со стола. Через некоторое время кастрюля упала. Что в ней было?
Ответ:(В кастрюле находился лёд)
27)Чем больше из неё берёшь, тем больше становится… Что это?
Ответ:(Это яма)
28) Какое колесо не крутится при правом развороте?
Ответ:(Запасное колесо)
29) Шёл муж с женой, брат с сестрой да шурин с зятем. Сколько всех?
Ответ:(Трое)
30)На что больше всего похожа половина апельсина?
Ответ:(На вторую половину апельсина)
31) Что можно приготовить, но нельзя съесть?
Ответ:(Уроки)
32) Два мальчика играли в шашки 2 часа. Сколько времени играл каждый из мальчиков?
Ответ:(Два часа)
33) Что все люди на земле делают одновременно?
Ответ:(Становятся старше)
34) Как может брошенное яйцо пролететь четыре метра и не разбиться?
Ответ:(Нужно бросить яйцо более, чем на четыре метра, тогда первые четыре метра оно пролетит целым)
35) Что может путешествовать по свету, оставаясь в одном и том же углу?
Ответ:(Почтовая марка)
36) Известна история о маленьком мальчике, который, получив новогодний подарок, попросил маму: «Сними, пожалуйста, крышку. Я хочу подарок погладить». Что же это за подарок?
Ответ: (Этим подарком оказалась черепаха)
37) Из какой посуды не едят?
Ответ:(Из пустой.)
38) Если в 12 часов ночи идёт дождь, то можно ли ожидать, что через 72 часа будет солнечная погода?
Ответ:(Нет, через 72 часа снова будет полночь)
39) У какого слона нет хобота?
Ответ:(Хобота нет у шахматного слона)
40)За чем мы едим?
Ответ: (Мы едим за столом)
41) Росли четыре берёзы, На каждой берёзе — по четыре больших ветки, На каждой большой ветке — По четыре маленьких ветки, На каждой маленькой ветке — По четыре яблока. Сколько всего яблок?
Ответ:(Ни одного, так как на березах яблоки расти не могут.)
42) Шла бабка в Москву, навстречу ей три старика, у стариков — по мешку,
а в каждом мешке — по коту. Сколько всего шло в Москву?
Ответ:(Только бабка шла в Москву, а вот старики шли в другую сторону.)
43) Когда чёрной кошке легче всего пробраться в дом?
Ответ:(Кошке легче всего пробраться в дом, когда дверь открыта.)
44) На какой вопрос нельзя ответить «да»?
Ответ:(Да нельзя ответить на вопрос «Ты спишь?»)
45) Летела стая уток: две впереди, две позади, одна посередине и три в ряд. Сколько их всего?
Ответ:(Летело три утки)
46) Летела стая птиц, сели по двое на дерево — одно дерево осталось; сели по одной — одного недостало. Сколько птиц и сколько деревьев?
Ответ:(Три дерева и четыре птицы)
47) По какой дороге полгода ездят и полгода ходят?
Ответ:(По реке)
48)Что всегда увеличивается и никогда не уменьшается?
Ответ:(Возраст человека)
49)Как из трёх палочек сделать четыре, не ломая их?
Ответ:(Сложить из них цифру 4.)
50) Несла бабка на базар сто яиц, а дно упало. Сколько осталось в корзине яиц?
Ответ:(Ни одного не осталось: ведь дно упало)
51) Стучат, стучат – не велят скучать.
Идут, идут, а все тут как тут.
Ответ: (Часы)
52) По чему птицы летают?
Ответ:(Птицы летают по воздуху.)
53) Ирина мечтала о шоколадке, но ей на покупку не хватало 10 рублей. Леша тоже мечтал о шоколадке, но ему не доставало всего 1 рубля. Дети решили купить хотя бы одну шоколадку на двоих, но им все равно не хватило 1 рубля. Какова стоимость шоколадки?
Ответ:(Стоимость шоколадки 10 рублей. У Иры не было денег вообще)
54) Что не может увеличить лупа в треугольнике?
Ответ: (Лупа в треугольнике не может увеличить углы)
55) Что будет с вороной, когда ей исполнится 7 лет?
Ответ:(Ей пойдёт восьмой год)
56) Если бы у вас была только одна спичка, и вы вошли в комнату, где есть керосиновая лампа, камин и газовая плита, что бы вы зажгли первым делом?
Ответ:(Спичку)
57) Как правильно говорить: «не вижу белый желток» и
skhemodel.ru
Умение размышлять логически и обосновывать свои выводы необходимо всегда. Те, кто обучался в институте наверняка помнят такой наискучнейший предмет, как “Логика”. Помните одно из определений, которое давали на лекциях?
Ло́гика — раздел философии, нормативная наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых на логическом языке.
И дальше тянулись нескочнаемые лекции в течение всего семестра о “логических квадратах”, посылках и выводной информации…. “Зачем все это нужно?” – задавались многие вопросом. Вместе с тем, мне способность строить логические умозаключения пригодилась именно в той сфере в которой я трудился и продолжаю трудиться. Но…, данная способность требует постоянного совершенствования и развития. Зачем заниматься тем, что является скучным, думал я, пока друзья не подарили мне книгу:
где первое, что бросилось в глаза, это нестандартное определение “логики” по Тру-ля-ля и Тра-ля-ля
Т р у л я л я (обращаясь к Алисе). Я знаю, о чем ты думаешь, но это не так! Ни в коем разе!
Т р а л я л я. Наоборот, если было так, то так могло быть, а если бы так было, то так и было бы. Но ничего такого нет. Это и есть логика.
Книга читается не на одном дыхании, ибо это сборник задач логических задач, составленных по разделам и построенный по принципу “от простого к сложному”.
Но, вместе с тем. через всю книгу проходит одна сюжетная линия, которая затягивает читателя. Думаете, что не найдете в ней ничего интересного для себя? Тогда попробуйте решить несложные задачки:
В конце каждого раздела, естественно предоставлены решения и все логические разъяснения, почему нужно было решить так, а не иначе. Но куда интересней понять ход рассуждений самому.
Вот что написано о данной книге в аннотации:
Книга Рэймонда Смаллиана — вероятно, самый увлекательный сборник задач по логике.
Около трехсот задач различной сложности сгруппированы по разделам, герои которых Рыцари и Лжецы, Алиса в Стране Чудес, Беллини и Челлини и даже сам граф Дракула!
Если человек произносит «Я лгу» — говорит ли он неправду? Почему физики и математики по-разному решают задачи? Как вовремя распознать упыря?
Ответы на эти и более серьезные вопросы Вы найдете в этом сборнике, а может быть, и ответ на вопрос «Как же называется эта книга? ».
Для всех, кто хочет научиться рассуждать.
На мой взгляд, книга несомненно будет полезна людям связанным с юриспруденцией, правоохранительными органами и службой собственной безопасности (не путайте ССБ и физическую охрану, это несколько разные понятия, особенно раздел про “лжецов” и “говорящих правду”, а так же “рыцарей” и “простолюдинов”). Вместе с тем, я бы настоятельно рекомендовал ее родителям, кто хочет научить мыслить своих детей нестандартно, а так же, тем, кто хочет развить в себе данные способности самостоятельно.
Если заинтересовались, тогда вперед! Ведь только прочтя книгу до конца и, решив все головоломки и задачи, Вы сможете правильно ответить на вопрос: “Как же называется эта книга?”.
irecommend.ru