Конспект НОД по математике в средней группе
«Веселые друзья»
Цель:
Создание благоприятных условий для развития детей в соответствии с их возрастными и индивидуальными особенностями и склонностями.
Образовательная область: познавательное развитие.
Интеграция образовательных областей:
«Познавательное развитие», «Речевое развитие», «Физическое развитие», «Социально-коммуникативное развитие».
Виды детской деятельности: познавательная, коммуникативная, игровая.
Задачи:
Развивающие:
– развивать воображение, любознательность, память и логическое мышление детей;
– повышать речевую активность детей;
– развивать умение отвечать на вопросы.
Воспитательные:
– продолжать формировать коммуникативные навыки, умение работать в парах.
– формировать умение внимательно слушать воспитателя, отвечать на вопросы;
– вызывать эмоциональный отклик.
Образовательные:
– формировать представления о геометрических фигурах (овале, круге, треугольнике, квадрате).
– закреплять умение считать в пределах пяти.
Предварительная работа:
Проведение ООД по ознакомлению сравнения предметов на основе составления пар; организация дидактических игр по развитию математических способностей.
Материалы и оборудование: билеты – парные карточки с изображениями предметов, графических знаков и линий для обозначения мест в кинотеатре; наборы геометрических фигур – на каждого ребенка. Плакаты с изображением овощей и фруктов. Схематическое изображение животных (зайца, медведя, лисы, совы, ежа). Геометрические фигуры для фланелеграфа. Аудиозапись криков о помощи и плеска воды. Наборы пластмассовых цифр (от 1 до 5) – на каждую пару детей. Ёмкость с водой.
Организационная структура ОД:
1. Этап.
Мотивационный (проблемная ситуация).
Ход занятия.
Воспитатель.
Тай, тай, налетай.
Приглашаю на игру,
А названье не скажу.
Всех принимаем!
Никого не обижаем!
Предлагает детям разбиться на пары, ориентируясь на соответствие цветов своей одежды и одежды партнера. Каждый ребенок обосновывает свой выбор. Затем проводится пальчиковая гимнастика.
Воспитатель. Встаньте напротив друг друга и поздоровайтесь за руку.
Дети. Добрый день! (Поджимают руку, используя все пальцы.) Рад тебя видеть! (Здороваются всеми пальцами, кроме большого.) Наконец-то встретились! (Здороваются только большими пальцами.) Если что-нибудь случится, обращайся. Помогу! (Переставляют указательный и средний пальцы правой руки по левой руке партнера, «доходят» до шеи, слегка похлопывают друг друга ладонью по плечу.) Воспитатель. Вы любите сказки? (Ответы детей.) Сегодня я хочу пригласить вас в кинотеатр, где вы сможете увидеть сказку «Друзья».
2. Этап.
Планирование (реализация детского замысла)
– Давайте решим, как нам идти.
Дети. Парами, дружно, спокойно.
Воспитатель. Так не интересно, скучно. Может быть, поскачем на одной ножке, побежим или поползем?
Дети предлагают свои варианты, затем выбранным способом перемещаются к расставленным стульям.
3. Этап. Деятельностный (деятельность педагога (объяснение, показ), совместная деятельность педагога и детей (речевое развитие).
Воспитатель. Чтобы попасть на представление, надо сначала купить билет.
Дети подходят к столу, на котором разложены карточки с изображением предметов, графических знаков и линий, берут по одной и ищут стул, на котором лежит парная карточка.
Воспитатель. Если вы не уверены в правильности выбора, попросите помощи у партнера.
Перед началом сеанса контролер (один из детей) проверяет выполнение задания.
Если место ребенком выбрано правильно, он аплодисментами выражает свое одобрение, если нет – топает и помогает ребенку, допустившему ошибку, найти свое место.
Воспитатель. Внимательно смотрите на экран (фланелеграф). Быть может, вам придется помочь героям сказки.
Жили-были веселые друзья. А кто они, вы узнаете, если отгадаете загадки.
Нет углов у меня,
И похож на блюдце я,
На медаль, на блинок,
На осиновый листок.
Вы подумайте, друзья,
И скажите, кто же я? (Круг.)
Три мои стороны
Могут разной быть длины.
Где стороны встречаются –
Угол получается.
Что же вышло? Посмотри!
Ведь углов-то тоже три.
На меня вы посмотрите,
Моё имя назовите. (Треуголник.)
В ворота его не закатишь, как мяч,
И он за тобою не пустится в скач.
Четыре угла и четыре сторонки,
Похожие, точно родные сестренки,
Фигура знакома для многих ребят.
Его вы узнали? Ведь это… (Квадрат.)
Воспитатель по ходу рассказа выкладывает на фланелеграфе изображения предметов, по форме соответствующие разным геометрическим фигурам. Дети их называют.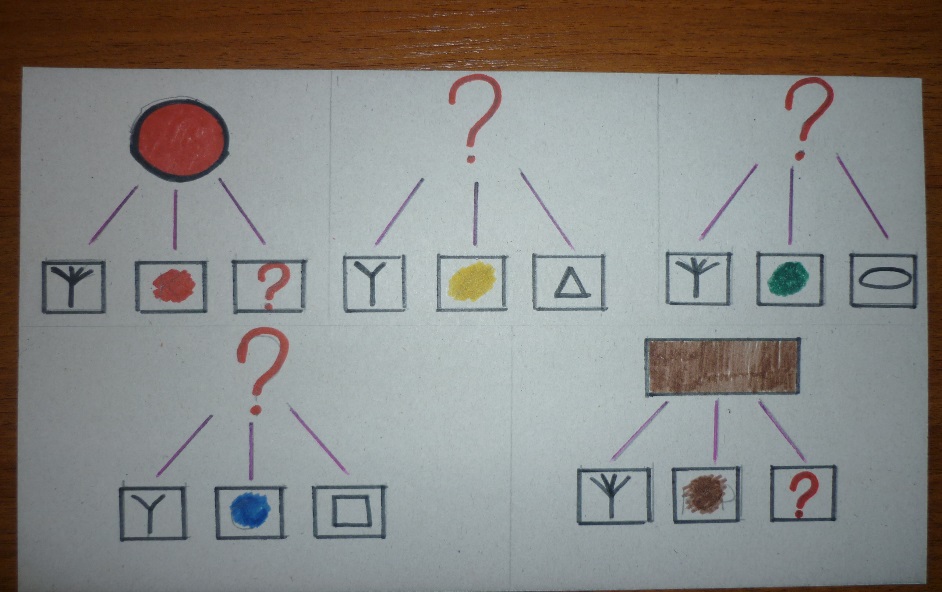
Воспитатель. Друзья жили в уютном доме (выставляет изображение дома). Какой формы были стены этого дома, его крыша, окно? (Ответы детей.)
Друзья часто сидели на стульях с удобными … (квадратными) сидениями. Стол у них был … (круглый).
Накрывая на стол, друзья ставили … (круглые) тарелки.
В чай они клали … (квадратные) кусочки сахара.
Очень любили друзья … (треугольное) печенье.
Однажды кто-то постучал в дверь их дома. Вышли друзья на порог и видят: стоит перед ними удивительная фигура, немного похожая на круг. (Выставляет на фланелеграф овал.) Стали знакомиться.
Физминутка.
1, 2, 3, 4, 5
Все умеем мы считать,
Отдыхать умеем тоже.
Руки за спину положим.
Голову подымем выше
И легко-легко подышим…
Раз, два! – выше голова,
Три, четыре – руки шире.
Пять, шесть – тихо сесть.
Воспитатель предлагает желающим детям исполнить роли геометрических фигур.
1-й ребенок (берет треугольник и говорит от его имени).
Здравствуй, друг! Я – Треугольник. У меня три стороны и три угла. Я похож на … (перечисляет предметы).
2-й ребенок (берет квадрат). А я – Квадрат, у меня четыре угла, я похож на …
3-й ребенок (берет круг). А я – Круг, у меня нет ни одного угла, я могу катиться и я похож на … Дети (хором). А ты кто?
Овал (за него говорит воспитатель).
Здравствуйте, друзья! Меня зовут Овал, я не знаю на что я похож.
Воспитатель. Дети, назовите предметы, которые по форме похожи на Овал. (Ответы детей).
Овал. Пустите меня к себе жить.
Воспитатель. Согласились фигуры. И решили отправиться на прогулку.
Дети встают, берут в руки геометрические фигуры и подходят к плакатам, на которых изображены овощи и фрукты.
Воспитатель. Проказник Овал убежал от приятелей и спрятался на огороде. Стали друзья его искать, разошлись в разные стороны. Один Квадрат остался стоять на месте. Огляделся он – вокруг никого нет. Помогите квадрату найти своих друзей. Для этого выберите овощи и фрукты, изображения которых по форме напоминают Овал (огурец, баклажан и т.
п.), Круг (помидор, яблоко, вишня и т.п.), Треугольник (морковь, клубника и т.п.).
Среди овощей и фруктов нашел Квадрат своих друзей. Пошли они дальше. Через некоторое время на их пути встал дремучий лес. Из-за деревьев навстречу вышли звери. Угадайте какие? Показывает карточки со схематическим изображением животных. Дети называют их и перечисляют геометрические фигуры, из которых составлены изображения.
Воспитатель. Давайте посчитаем, сколько зверей встретили друзья.
Один ребенок перечисляет карточки, двое-трое проверяют правильность выполнения счета.
Воспитатель. Расставьте цифры от 1 до 5 по порядку под каждым животным. А где же наши цифры?
Звучит аудиозапись плеска воды и криков «Помогите! Караул! Захлебнулся! Утонул!».
Воспитатель. Неужели что-то случилось? Дети подбегают к ёмкости с водой, в которой находятся цифры. Достают их из воды и рассказывают, кто какую спас. (Я вытащил из воды 3 и 4. мои цифры не утонули, потому что они пластмассовые.
А мои цифры 1 и 5, опустились на дно, потому что внутри пластмассы был магнит. И т.п.)
Воспитатель. Вот теперь мы можем расставить цифры по порядку под каждым животным.
Дети выполняют задание.
Воспитатель. Познакомились Круг, Овал, Треугольник и Квадрат с лесными обитателями и решили на память сделать их портреты.
Дети вновь распределяются на пары, договариваются между собой, «портрет» какого животного они будут собирать. Используя схемы-образцы и наборы геометрических фигур, выкладывают изображения.
Воспитатель. Проверьте друг у друга, похожи ли ваши животные на те, которые изображены на картинках. Дети дают оценку аккуратности и правильности выполнения работ товарищей.
4. Этап. Рефлексия.
Воспитатель. После прогулки друзья попрощались с лесными обитателями и отправились домой. Наша сказка закончилась. Возьмитесь за руки, посмотрите друг на друга и улыбнитесь.
Дети. (хором).
До свидания, сосед!
Улыбнись-ка мне в ответ.
Никогда не грусти
И улыбки всем дари!
Иллюстрированный методический журнал для воспитателей дошкольных учреждений «Ребенок в детском саду» № 2 2007 стр. 15
Итоговая НОД по математике в средней группе
Тема: «Поможем зайчику»
Цель:выявить сформированность знаний,умений,навыков по ФЭМП.
Задачи: Образовательные: -закрепить навыки количественного и порядкового счёта в пределах 5,соотнесение цифр 1-5 с количеством и порядком предметов; -закрепить умение сравнивать предметы разной высоты; -закрепить представление о геометрических фигурах: умение называть геометрические фигуры,рассказывать о них; -закрепить знания о последовательности частей суток:утро,день,вечер,ночь.
Развивающие:
-развитие у детей познавательных интересов, интеллектуальное развитие детей;
– развивать умение мыслить, рассуждать, доказывать.
Воспитывающие:
-воспитывать дружеские взаимоотношения,желание помочь тем,кто нуждается в этом.
Материал и оборудование: демонстрационный материал: сюжетная картина «Приключения снеговика»(дляопределения последовательности событий),плоскостные геометрические фигуры с изображением диких животных,иллюстрации «Части суток»,картинка реки,брёвна с цифрами от 1 до 5,картинка-подарок, три коробки.
Это ребёнок в образе Зайчика,накрытого белой тканью).
Задние 2. «Узнай и назови»
Воспитатель: Сейчас мы с вами поиграем в игру. У нас есть геометрические фигуры. В середине каждой из фигур спряталось какое-то животное. Надо назвать животное и рассказать о геометрической фигуре. (Дети становятся в круг, передают мяч из рук в руки и говорят слова: «Мячик мячик ты беги и про круг нам расскажи». У кого остался мячик тот и рассказывает о геометрической фигуре. Например: В кругу спрятался медведь, круг умеет катится, не имеет углов и сторон.
Задание 3. Дидактическая игра «Построим мостик»
Воспитатель: Путешествие наше продолжается. Следующее наше задание помочь снеговикам. Но они находятся на другой стороне реки. Чтобы пройти через реку нам надо построить мостик. У нас есть бревна с цифрами. Надо выложить их в нужной последовательности от одного до пяти. (Дети выполняют задание и получают третью часть картинки-подарка.)
Посмотрите на картинку, где они живут? ( В своих домах)Задание 5. «Назовите и разукрасьте части суток»
Воспитатель: Я уверена, что с этим заданием вы справитесь очень быстро. Назовите части суток. (Показываю картинки, дети называют)
(Двое вызванных детей соединяют пазлы в картинку.)
Автор занятия: воспитатель Нигматянова Л. З., муниципальное автономное дошкольное образовательное учреждение «Детский сад №60 «Иволга» г. Набережные Челны.
Закреплять с детьми названия геометрических фигур.
Продолжать учить определять размеры геометрических фигур (большой-маленький, толстый-тонкий, узкий-широкий).
Повторить счет от 1 до 5, и обратно.
Учить по схеме конструировать предметы при помощи логических блоков Дьенеша.
Игрушка «почтальон», посылка, геометрические фигуры, логические блоки Дьенеша, схемы, обручи.
Беседа на тему «геометрические фигуры», счет в пределах 5 и обратно.
Обратный счет.
Воспитатель:
Добрый день ребята. Сегодня у нас намечается очень интересное путешествие в страну геометрических фигур. А чтобы наше путешествие было интересным, я пригласила гостя.
(Воспроизведение шума мотороллера, стук в дверь).
Воспитатель:
К нам в гости приехал Почтальон, но не с пустыми руками, а с подарком. Хотите подарок?
Дети:
Да!
Воспитатель:
Замечательно. Но подарок надо заслужить. Подарок от почтальона можно получить только если вы выполните правильно все его задания. Готовы?
Дети:
Да!
Воспитатель:
Чтобы выполнить первое задание нужно разделиться по командам. Каждой команде я раздаю картинки-схемы и блоки Дьенеша, при помощи которых вы должны будете составить предмет, который поможет нам к приближении нашей цели.
Воспитатель:
Раз, два, три – начни! (Во время выполнения задания звучит музыка).
Почтальон:
(Воспроизводится речь почтальона). Молодцы! Вы замечательно выполнили это задание. Итак, какой предмет мы составили?
Дети:
Машины.
Воспитатель:
Правильно. С помощью этих машин мы поедем к следующему заданию. Садимся, приготовиться к старту.1-2-3-4-5,заводимся. Поехали (воспроизводится звук мотора автомобиля).
Воспитатель:
Стоп машины. Вот мы приехали к следующему заданию. Почтальон приготовил очень тяжелое задание. Я надеюсь, что вы справитесь с ним так же, как с первым.
Воспитатель:
На ковре лежат 3 обруча; красный, синий, зеленый. Внутри зеленого обруча выложены очень много геометрических фигур. Вам нужно разделить эти фигуры так, чтобы внутри красного обруча были большие и узкие фигуры, а внутри синего маленькие и толстые. Готовы? Начинаем!
Почтальон:
Я даже не предполагал, что вы такие дружные.
Молодцы!
Воспитатель:
Ребятки, садимся в машины и возвращаемся обратно. (Раздаётся звук мотора).
Теперь я убедился, что вы достойны моего подарка. (Открывает коробку, но она не открывается). Не пойму, что-то коробка не открывается.
Вспомнил. Я ведь про загадки и забыл. Если угадаете мои загадки, то посылочка моя откроется.
А братишка мой, Сережа,
Математик и чертежник –
На столе у бабы Шуры
Чертит всякие…
(Фигуры)
Три вершины тут видны,
Три угла, три стороны, –
Ну, пожалуй, и довольно! –
Что ты видишь? – …
(Треугольник)
Нет углов у меня,
И похож на блюдце я,
На тарелку и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья?
(Круг)
Не овал я и не круг,
Треугольнику я друг,
Прямоугольнику я брат,
Ведь зовут меня…
(Квадрат)
Воспитатель проводит игру используя фигурку почтальона.
Руки кверху поднимаем,
А потом их отпускаем.
А потом их развернем
И к себе скорей прижмем.
А потом быстрей, быстрей
Хлопай, хлопай веселей.
Воспитатель:
Ну что почтальон, ты доволен детьми?
Почтальон:
Да. Молодцы. Давайте еще раз попробуем открыть. (Коробка открывается почтальон раздает подарки каждому ребенку).
Почтальон:
Ребятки, что то я загостился. Меня ждут. До скорой встречи.
Дети:
До свидания.
Воспитатель:
Вот и закончилось наше путешествие. Что вам понравилось? Чтобы вы забыли это путешествие я вам раздаю рисунки–схемы, чтобы вы с родителями могли сами составлять разные предметы.
Скачать конспект занятия по математике в средней группе «Путешествие в страну геометрических фигур»
Автор занятия: Козина Людмила, воспитатель высшей квалификационной категории комунального дошкольного учебного учреждения №254 «Теремок» г.
Донецка.
Формировать умение находить равные по количеству элементов предметы, употреблять слова одинаково, столько же, поровну, учить образовывать число путем прибавления единицы, ориентироваться в пространстве используя слова «под», «над»; развивать внимание; воспитывать наблюдательность.
Демонстрационный материал: магнитная доска, три цветка (белого, голубого, красного цвета, три бабочки, карточка с цифрой 3, цветные кружочки (15 шт)
Раздаточный материал: цветные кружочки (15 шт) на каждого ребенка, карточка с цифрой 3, бумажные бабочки, карточки с двумя горизонтальными полосками, карточки с овощами (3 капусты, 3 моркови), цветные шнурки 15 см.
Дети протягивают ручки к солнышку, солнышко дало свое тепло и хорошее настроение. Затем дети берутся за руки и передают свое хорошее настроение и тепло друг другу.
Ознакомление с числом и цифрой 3Воспитатель выкладывакт на магнитной доске три цветка, две бабочки.
– Чего больше: цветков или бабочек? (Ответ детей.)
– Что надо сделать, чтобы проверить? (Каждую бабочку посадить на цветок.)
Воспитатель предлагает одному ребенку посадить бабочек на цветы.
– На сколько бабочек меньше, чем цветов? (Один)
– Что нужно сделать, чтобы их стало поровну?
Дети предлагают добавить еще одну бабочку. Воспитатель выкладывает еще одну бабочку и обращает внимание детей на принцип образования нового числа путем прибавления единицы.
– Что теперь можно сказать об количестве бабочек и цветов? (Бабочек столько, сколько цветов – три.)
– Как вы получили трех бабочек? (Добавили один.)
– Молодцы!
– А теперь взгляните перед вами лежат карточки. Что на них изображено? (Капуста, морковь).
– Как все это можно назвать одним словом? (Овощи)
– Положите три кочана капусты на верхнюю полоску, а две морковки на нижнюю полоску.
(Следить за тем, чтобы дети выкладывали карточки слева на право).
– Чего больше? (Капусты)
– Что надо сделать, чтобы овощей стало поровну? (Добавить еще одну морковку).
– Что теперь можно сказать о количестве капусты и моркови? (Капусты столько, сколько моркови — три.)
Раз, два – все присели
Затем вверх подлетели
Три, четыре – наклонились
Из ручейка умылись,
Пять, шесть – все в лес,
Ветерок нас перенес
Семь, восемь – в сад
Там цветут цветы.
– Дети, посмотрите нам ветерок принес цифру 3. Воспитатель предлагает детям рассмотреть цифру, нарисовать ее в воздухе, на столе, потом из цветных шнурочков выложить цифру 3. Если у детей возникают трудности, можно им предложить выложить цифру сначала по контуру на карточке, а уже потом – без нее.
– У Ветерка есть друзья – Солнышко и Дождик. Они решили украсить полянку: Ветерок развеял семена цветов, дождик их полив, а Солнышко согрело своими лучами.
И вот однажды…
В игре закрепляется порядковый счет, пространственные отношения. Воспитатель рассказывая, работает с демонстрационным материалом
… Проснувшись утром, Ветерок увидел, что расцвел первый цветок.
– Какого цвета первый цветок? (Голубого) За ним начали распускаться другие цветы.
– Какого цвета был следующий цветок? (Белого).
– А какой цветок расцвел третим? (Красный).
– Сколько всего цветов расцвело на лужайке? (Три).
– Какого цвета был первый, второй, третий цветок?
– Вдруг ветерок заметил, что на полянке появился еще один цветок. Он хотел подойти к нему, но лепестки цветочка зашевелились, она спорхнула и полетела.
Воспитатель раздает каждому ребенку бумажных бабочек. Дети, внимательно слушая воспитателя, показывают, где бабочка летала и пряталась.
– Бабочка летал над головой, потом села на ладошку, спряталась за спину, закапал дождик, бабочка спряталась под ладошку, Снова выглянуло солнышко, бабочка немного полетала и села на ковер.
– Молодцы ребята! Дети, сейчас мы с вами превратимся в Волшебников и начнем творить чудеса, а чудеса мы с вами будем творить из цветных кружочков.
Сначала воспитатель на ковре составляет свои рисунки из кружочков, а затем предлагает детям составить рисунки. Дети выполняют работу.
– Молодцы ребята, хорошие вы Волшебники. Такие красивые картины у вас получились!
С какой цифрой познакомились?
Какого цвета росли цветы на поляне?
Сколько было овощей?
Какое задание понравилось выполнять больше всего?
Скачать конспект занятия «Удивительное путешествие»
Возрастная группа: средняя «А» группа
Содержательные компоненты:
Познавательное развитие (развитие у детей интереса к познавательным заданиям по формированию элементарных математических представлений, любознательности)
Цель: упражнять обучающихся в составлении фигур под диктовку и по образцу, решать задачи, находить недостающий предмет.
Задачи:
Этап деятельности
Вводная часть, организация детей, мотивация к предстоящей деятельности.
Содержание деятельности
Играет лёгкая новогодняя мелодия, дети рассаживаются, педагог начинает занятие. Дети рассматривают, и читают письмо от Деда Мороза. Дед Мороз приготовил интересные задания и предлагает детям отправится в путешествие.
Деятельность воспитателя и обучающихся
Ребята, совсем скоро мы будем праздновать праздник Новый год, а кто приходит к нам на Новый год? Как вы готовитесь к новому году, как к нему готовится ваша семья? Какой подарок вы приготовили для своих родных? (ответ детей).
Знаете ребята, я получила письмо от Деда Мороза, он нам прислал увлекательные задания, к выполнению которых нужно приступить немедленно. Вы готовы отправится в путешествие по познавательным заданиям из серии «Занимательная математика»? (ответ детей).
Этап деятельности
Основная часть, непосредственная образовательная деятельность
Содержание деятельности
Первое задание:
— Без чего не встречают Новый год?
Задание от Деда Мороза.
Сделать на игре Геоконт Елочку.
Воспитатель диктует: Б — 4, Г — 4, Ж — 4 ,Ф — 2, К — 2, Ф — 1, К — 1, С — 3, О — 3, Г — 1, Ж — 1.
Обучающиеся выполняют задания: игра «Геоконт»
Второе задание:
Задания с карточками: «Какой фигуры не хватает?». Педагог предлагает детям взглянуть на карточки и запомнить фигуры и цвет фигур, затем воспитатель предлагает детям закрыть глаза и убирает одну из фигур. Дети предлагаю свои ответы на вопрос, «какой фигуры не стало?».
Воспитатель: Ребята Дедушка Мороз нам прислал интересные занимательные математические задачи. Они будут сложные, необходимо очень внимательно слушать.
1 задачка:
Два числа 1 и 3, быстро их сложите, и ответ скажите. (4).
2 задачка:
Шесть весёлых медвежат
За малиной в лес спешат.
Но один малыш устал:
От товарищей отстал.
А теперь ответ найди
Сколько мишек впереди? (5).
3 задачка:
Сколько ушей у трех мышей? (6).
Воспитатель:
Умнички! Сейчас нам пора немного отдохнуть. Педагог проводит физкультминутку: «Шёл весёлый Дед Мороз».
— Задания, которые прислал Дед Мороз мы все выполнили.
Ребята скажите вы знаете где живёт Дед Мороз? (Ответ детей, Лапландия.)
Скажите, а на каком транспорте мы можем доехать до Лапландии? (Ответ детей, самолет.)
— А нам удобнее всего доехать на поезде.
Я вам предлагаю, давайте построим поезд из палочек Кюизенера.
Воспитатель комментирует задание: выложить семь палочек, то есть семь вагончиков 1 до 7, и в каждый вагончик посадим столько пассажиров, какое число обозначает каждая палочка.
Например: в розовый вагончик посадим 2 пассажира, потому что эта палочка обозначает цифру (2) и так далее.
Воспитатель: Ребята, помните, мы с вами написали приглашение Деду Морозу, к нам на ёлку, давайте отправим его. У меня есть предложение отправить его с Вороном Метром.
Воспитатель помогает детям построить из Колумбова яйца птицу (ворон Метр).
Этап деятельности
Заключительная часть (рефлексия)
Содержание деятельности
Воспитатель предлагает детям отправить приглашение Деду Морозу.
Подводит итог занятия.
Деятельность педагога и детей
Тема: План (карта путешествий)
Программные задачи:
Материал:
Демонстрационный – игрушки, билеты в театр, таблица с планом, набор цифр от 1 до 5.
Раздаточный – счётные палочки, нитки.
Ход занятия.
1. Игра «Театр»
Воспитатель: Ребята, сегодня мы с вами отправимся в театр зверей. Вначале надо купить билеты. Как вас много желающих. Мы будем заходить группами по несколько человек, по пять.
Задание первой группе: Кто в вашей группе первый, третий, пятый? (раздаю цифры)
Задание второй группе: посчитайте от 1 до 5 (раздаю цифры)
Задание третьей группе: назовите числа по порядку, начиная с «хвоста» (раздаю цифры)
Воспитатель: Молодцы! Переверните карточку с цифрой – это приглашение-билет в театр (изображены животные).
Рассаживайтесь на стулья, согласно купленным билетам.
2. Работа с планом.
Сказка «Заяц и лиса» (с использованием игрушек)
Воспитатель: Жили-были Заяц и Лиса. Надоело им ссориться, решили они жить дружно. Пригласила Лиса Зайца в гости. Жила она далеко, не сразу дойдёшь.
Нарисовала Лиса Зайцу дорогу к своему дому (воспитатель помещает план на доске). Расскажите, как дойти до Лисы.
(Дети анализируют план совместно с воспитателем)
Воспитатель: Сколько дорог ведёт к домику Лисы?
Захотелось Зайцу искупаться. Помогите ему дойти до озера.
Решил Заяц угостить Лису грибами. Как ему попасть на грибное место?
3. Физминутка.
Воспитатель: представьте, что идём к Лисе в гости. А в лесу столько ягод. Давайте соберём Лисе земляники.
Дети шли, шли, шли
Землянику нашли!
Ах, какая ягода!
4. Игра «Составь фигуру»
У каждого ребёнка на столе по 2 верёвочки и набор счётных палочек.
Задания:
5.
Игра «Верёвочка» (Даю толстую верёвочку, связанную в кольцо)
Воспитатель: Дети, возьмитесь за верёвочку руками и образуйте Ο, 0 (овал), □, ∆.
Авторы: Торопова Ольга Владимировна, Гребенева Ольга Сергеевна
Цель:
– совершенствовать навыки счета, закреплять знание цифр;
– закреплять представления о геометрических фигурах;
– формировать навыки сотрудничества в процессе выполнения игровых заданий;
– развивать речь, слуховое и зрительное внимание, память, логическое мышление;
– воспитывать целеустремленность и настойчивость в достижении результата;
– продолжать учить работать в коллективе.
Материал: карта с Королевством королевы Математики, блюдо с конфетами, клубок, круг и треугольник из ткани голубого цвета, треугольники (для рыбок), схема построения моста, круги (цветы на полянке), треугольники (бабочки), звёздный дождь (конфетти из фольги).
Интеграция областей: «Познание», «Коммуникация», «Музыка», «Социализация».
Воспитатель: Сегодня мы отправимся и интересное путешествие в Королевство Математики. Чтобы туда попасть, нужно пройти немало испытаний, но я уверена, что вы с ними справитесь! Ну ,что, готовы?
Дети: Да!
Воспитатель: Тогда отправляемся!
Дорогу в Королевство Математики нам укажет волшебный клубок.
А вот и первое испытание. Называется «Разминка». Чтобы его пройти и отправится дальше, нужно ответить на вопросы.
– Чего у человека по одному? (Рот, нос, голова)
– Чего бывает по два? (Колена, уха, глаза)
– В каких сказках встречается цифра 3? («3 поросенка», «3 медведя»)
– Где можно встретить цифру 4? (4 времени года, 4 угла у квадрата)
Воспитатель: Молодцы! Справились с заданием. Можем продолжить путешествие.
Воспитатель катит клубок.
Воспитатель: Ребята, куда прикатился наш клубок?
Дети: К реке.
Воспитатель: И правда. Мы пришли к речке, а мостика, чтобы её перейти нет. Смотрите, ребята, кто это лежит и спит на берегу?
Дети: Черепаха Тортила.
Воспитатель: Давайте её спросим, как нам пройти в Королевство Математики.
Дети подходят и будят черепаху.
Тортила: Здравствуйте, ребята. Я черепаха Тортила. Легла отдохнуть, а вы куда направляетесь?
Дети: Мы идем в Королевство Математики.
Тортила: Молодцы. А знаете ли вы, что путь в Королевство лежит через эту речку? Я помогу вам её перейти, но для этого вы должны выполнить моё задание. Готовы?
Дети: Да.
Тортила: Посмотрите, (указывает на выложенные на полу круг и прямоугольник из ткани голубого цвета) в моём пруду нет ни одной рыбки, а мост через речку разрушен.
Запустите рыбок в пруд и постройте мост, тогда я укажу вам ваш дальнейший путь.
Воспитатель: Ну что, справимся с заданием Тортилы?
Дети: Да.
Воспитатель: Посмотрите, около пруда лежит много геометрических фигур .Как они называются?
Дети:Треугольники.
Воспитатель: Из них нужно сделать рыбок. Каждая рыбка должна состоять из четырёх треугольников одного цвета. Тут же лежит и схема, по которой вы должны построить мост. Но схема не закончена и вам нужно будет самим догадаться, как нужно достроить мост. Давайте разделимся на две группы. Первая будет выкладывать рыбок, а вторая – мост.
Дети делятся на две группы и выполняют задание. Тортила проверяет правильность выполнения.
Тортила: Молодцы! Справились с заданием! Можете отправляться дальше.
Тортила кидает волшебный клубок и указывает дальнейшую дорогу.
Воспитатель: Ребята, наш клубок прикатился на волшебную полянку. Посмотрите, как здесь много бабочек (показывает 5 треугольников), а цветов нет. Бабочки приготовили для вас очередное задание: Выложите на верхнюю полоску своих карточек столько треугольников, сколько бабочек на полянке. (5)
А сейчас их нужно посадить на цветы – выложите на нижней полоске столько кругов, сколько бабочек.
Дети выполняют задание.
Воспитатель: Молодцы, и с эти заданием справились! Отправляемся дальше. Уже видно Королевство. Последнее задание «Сладкий счет». Дети делятся на две команды, строятся в колонны по одному на некотором расстоянии от блюда с конфетами. Звучит аудиозапись веселой музыки. Участник, стоящий первым в каждой колонне, подбегает к блюду, кладет в ложку конфету, возвращается к месту старта, перекладывает конфету в тарелку своей команды и передает ложку следующему игроку . Музыка выключается. Дети пересчитывают конфеты в своей тарелке и выявляют команду-победителя.
Воспитатель: Вот мы и добрались до Королевства Математики. Воспитатель осыпает детей «звездным дождем» за успешное выполнение заданий.
В предыдущем разделе мы описали формализм теории групп применительно к графам. Здесь мы переходим к симметрии и описываем другой алгебраический объект, группоиды; это позволит нам внести больше динамики в исследование [41, 44, 45]. Очевидно, это важно для понимания динамики сетей молекулярных взаимодействий.
Напомним, что ориентированный граф кодирует динамику, задаваемую dx i / dt = f i (A , x j ), где x i – состояние молекулярных видов i , а A ij – это полная матрица смежности интерактомов.
Точнее, группа автоморфизмов сети неявно кодирует динамику. Кроме того, мы знаем, что сетевые графы, подобные интерактому, состоят из нескольких копий нескольких основных компонентов, например . Группоиды – это алгебраические объекты, похожие на группы, но обычная групповая операция не определена. Другими словами, мы распознаем симметрию, но автоморфизмы нетривиальны. Этот формализм позволит нам применять методы теории групп к сетевым графам. Большая часть этого будет сосредоточена на небольших подсетях в более крупном интерактоме, где мы наблюдаем автоморфизмы типа перестановок.
Понятие группоида наиболее прозрачно, если подойти к нему с категориальной точки зрения [46]. Стандартное определение категории C включает набор объектов A, B, … и набор морфизмов (который может быть пустым набором) для каждой пары объектов; Hom (A, B) для объектов A и B. Композиция морфизмов определена и ассоциативна, и в каждом Hom (A, A) есть единичный элемент, поэтому Hom (A, A) никогда не бывает пустым.
Но категорию C можно рассматривать как алгебраическую структуру сама по себе, наделенную бинарной операцией, что делает ее похожей на группу или полугруппу.Мы называем эту ассоциированную алгебраическую структуру G ( C ). «Элементы» (поскольку коллекция объектов не обязательно образует набор) G ( C ) – это морфизм из C , а «продукт» – это композиция, которая является ассоциативная частичная бинарная операция с элементами идентичности. Если C имеет только один объект, то можно составить любые два морфизма, и у нас будет только один элемент идентичности.Аксиомы категории гарантируют, что G ( C ) является полугруппой. Более того, если мы настаиваем на обратимости каждого морфизма в C , то G ( C ) является группой.
Теперь естественно расширить понятие группы, потребовав, чтобы объекты C образовывали набор, т.
Е. C – небольшая категория, а также попросить, чтобы каждый морфизм C обратимый.Это категоричное определение группоида. Это определение легко перевести на алгебраический язык и получить понятие, подобное определению группы [47]. Но, возможно, именно категоричное определение проливает свет на мощь группоидов. А именно, в то время как группы идеально подходят для описания симметрии объекта, группоиды могут аналогичным образом фиксировать симметрии коллекций объектов. Это прекрасно иллюстрируется современной алгебраической геометрией, когда кто-то пытается сформировать классифицирующее пространство, известное как пространства модулей, но алгебраические многообразия, которые вы хотите классифицировать (скажем, эллиптические кривые), имеют разные симметрии.Эта проблема решается на языке стеков и группоидов [48]. Необходимость в таком же мощном обобщении возникает в теории струн, где симметрии физической теории не могут быть математически реализованы в терминах топологических пространств и групп, только в терминах стеков и группоидов [49].
В группоидном подходе мы исследуем не симметрию малых подсетей и мотивов, а скорее динамику этих малых сетей, когда они представляют собой ориентированные графы и, в частности, когда эти маленькие сети соединяются вместе, чтобы образовать более крупные сети (схемы ).Симметрии, которые мы будем наблюдать, – это не симметрия сети, а симметрии в фазовом пространстве или пространстве динамики.
Интерактом, а в действительности полная сеть химических реакций, составляющая ячейку, представляет собой сложную сеть с многочисленными петлями обратной связи и цепями прямой связи. Его динамика, несомненно, сложна, и детали всей сети только сейчас выясняются; но мы можем начать размышлять о некоторых возможных динамиках, используя работу из более зрелой области – нейронных сетей.
Мы знаем, что биологические нейронные сети состоят из двух- и трехмерных массивов генераторов с частотным управлением, генераторов с управлением напряжением и логических вентилей. Инженеры построили случайные и неслучайные сети из этих компонентов и обнаружили не только то, что сеть способна хранить в памяти в виде динамических шаблонов и ограничивающих циклов (например, запоминание менуэта Баха), но и изначально случайные импульсные шаблоны, проходящие по сети.
после временной задержки для интеграции компонентов увлекает за собой другие компоненты и производит непрерывные предельные циклы.В больших массивах этих сетей предельные циклы взаимодействуют друг с другом, создавая возникающую динамику. Далее мы опираемся на работы Hasslacher и Tilden [50], Rietman et al. [51] и Ритман и Хиллис [52]. Мы утверждаем, что по аналогии аналогичная динамика будет происходить в сети молекулярных взаимодействий клетки.
На рисунке 7 представлена схема клеточного цикла. Как описано выше, циклическая группа Z 4 представляет собой простое описание клеточного цикла, но мы можем улучшить описание, включив наблюдение, что G1 и G2 являются метастабильными в одной и той же клетке.Это многоядерное состояние, аналогичным образом, могло соответствовать раковым клеткам и / или полиплоидным клеткам, в которых мы слили два ядра. Это также стабильные или, по крайней мере, метастабильные состояния клетки, и, как будет показано ниже, число стабильных состояний невелико.
Схема упрощенного клеточного цикла, который изоморфен Z 4 .
Мы можем представить один узел в этом 4-периодном цикле следующей передаточной функцией, в которую мы включаем член смещения и связанный с ним гауссов шум, θ + ε θ
, где x – входной сигнал, а β – коэффициент усиления, может быть отрицательным или положительным и включать шум.Шум центрируется вокруг среднего значения сигнала, а величина шума устанавливается примерно на одно стандартное отклонение среднего значения сигнала. Мягкие сигмоиды имеют свойство действовать как аналоговые сигналы, а не как цифровые. Кроме того, с более чем одним входом, поступающим в один и тот же узел, мы суммируем произведение входящих сигналов и их силы. Уравнение передаточной функции теперь принимает вид:
Используя эту динамику, например, четырехузловое кольцо может проявлять следующие три состояния: (0000), (0101), (0001).
Здесь мы используем нотацию, похожую на перестановку, где, например, (0001) → (0010) → (0100) → (1000) эквивалентны (0001). (Известный как эквивалентный класс 1 , где подчеркивание должно напомнить нам, что это не число, а группоид.) Интересно, что три состояния, показанные здесь, изоморфны группе слияния ядер: (0000) → мертвая клетка ; (0001) → нормальная здоровая клетка; (0101) → G1 / G2 (класс эквивалентности 5 ).
Можно спорить о том, является ли это хорошей моделью клеточного цикла, но сети с прямой связью подобных генераторов центральных паттернов (CPG) способны быстро адаптироваться к изменяющимся внешним стимулам для поддержания некоторого вовлечения или глобальной стабильности [53], и с молекулярной точки зрения это именно то, что требуется от биологических клеток.Молекулярная сеть в живых клетках состоит из очень сложной взаимосвязанной системы химических реакций с обратной связью и прямой связью. Уолхаут и его коллеги [54, 55] и другие [56, 57] заметили некоторые из этих деталей.
Они обнаружили, что обратная связь и кольцевые цепи, часто с ингибирующими связями, обычны в сетях регуляции транскрипции (сетях взаимодействия белок-ДНК). Можно предположить, что основной клеточный цикл является первичным ограничивающим циклом в динамике клетки, а динамика регулятора транскрипции используется для контроля и одновременно под контролем клеточного цикла.
Кроме того, эти кольцевые схемы могут работать в более чем одном стабильном состоянии, точно так же, как нам нужно для сложных молекулярных сетей живых клеток. Кольцевая схема с 6 узлами может иметь 5 состояний; 8-узлы могут показывать 7 состояний; 10 узлов, 16 состояний; 12 узлов, 32 состояния; 14 узлов, 64 состояния; и 16 узлов 128 состояний. Увеличение состояний следует за функцией двойного ожерелья.
где d i – делители n с d 1 = 1, d v ( n ) = n ; v ( n ) – количество делителей n ; ϕ ( n ) – общая функция, а F (.
) – последовательность Фибоначчи (где F n = (F n-1 ) + (F n-2 ) [58]). Общая функция, также называемая функцией Эйлера, представляет собой количество положительных целых чисел, меньших n , которые относительно просты с n [51].
Следовательно, даже небольшие кольца, состоящие всего из дюжины узлов, могут поддерживать большое количество стабильных состояний. Объединение этих мотивов в сети может обеспечить общую глобальную стабильность. Как отмечают Голубицкий и Стюарт [41, 44] – и как видно из большой сети на Рисунке 5 – общая сеть имеет очень низкую глобальную симметрию.
Чтобы получить более подробную информацию, рассмотрите 6-узловое кольцо только с одним активным битом (000001) как шестиугольник с одним заполненным кружком, как показано на рисунке 8. Если активный бит движется против часовой стрелки, мы можем представить переходный бит. строка следующим образом:
Рисунок 8 Схема шестузлового генератора CPG .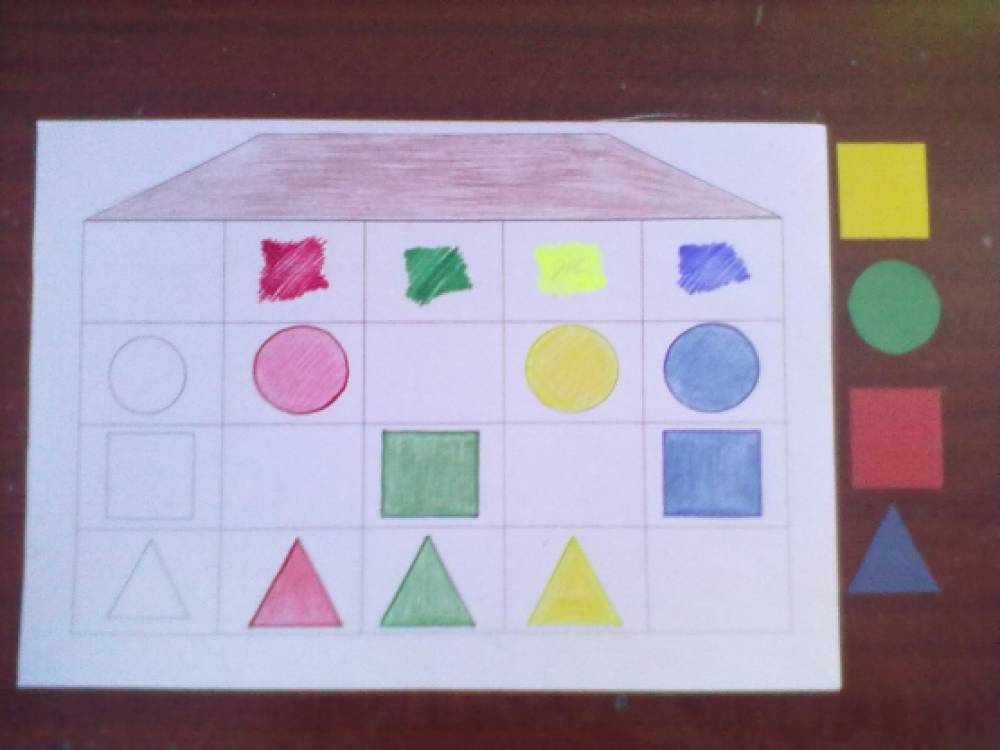
После шести оборотов, r , динамика колец находится в той же конфигурации, что и при старте.(В терминологии динамических систем это называется шестицилиндровым циклом.) Символически мы можем представить это как:
, где числа являются десятичным представлением битовой строки; они подчеркнуты, чтобы напомнить нам, что это групповые символы, и их нельзя использовать как числа. Эта строка элементов, перемежающихся операцией вращения, представляет элементы для группы и основной операции. Мы представляем эту группу тем, что верхний индекс напоминает нам, что группа предназначена для колец с шестью узлами, а нижний индекс является самым низким десятичным эквивалентом битовой строки в этой группе.
Группа описывает только одну из возможных циклических групп в 6-узловой кольцевой схеме. Поскольку в 6-узловой схеме есть четыре устойчивых колебательных состояния, всего имеется четыре группы. Полный набор всех групп представлен как:
Приведенный выше набор отображений показывает циклические перестановки из операций вращения в отдельных состояниях s , представленных как десятичный эквивалент.
Говорят, что группы и имеют порядок 6. Группа имеет третий порядок, а группа – второй порядок.Сходство между теорией групп и традиционной динамикой теперь очевидно. Две группы по 6 порядков являются 6-циклами. Одна группа третьего порядка является трехцикловой, а группа второго порядка – двухцикловой.
Оператор вращения (применяется один раз) для каждой группы разный.
По мере того, как количество оборотов, необходимых для возврата в начальное состояние, уменьшается для данной группы, периодичность увеличивается – например. два цикла быстрее, чем шесть циклов. Точно так же, когда количество оборотов, необходимых для возврата в исходное состояние, уменьшается, порядок группы уменьшается, а симметрия увеличивается.Как мы укажем позже, фазовый переход симметрии происходит во время ввода сигнала и кольцевой связи.
Эту группу можно сравнить с обычными циклическими группами. Циклическая группа C 6 состоит из десятичных чисел {0, 1, 2, 3, 4, 5} и операции
, где ρ – это оператор, который складывает два элемента в группу a, b , а затем применяет операцию модуля.
Идентификационный элемент C 6 равен 0, а обратный элемент каждого элемента a равен b = 6 – a .
Групповая таблица C 6 показана в таблице 5. В первой строке таблицы перечислены элементы группы. В первом столбце перечислены элементы группы, записанные в том же порядке, что и элементы в первой строке. Фактическое расположение элементов в первой строке / столбце не имеет значения. Первая строка – это a , первый столбец – это элемент b , для оператора ρ Элементы в таблице генерируются оператором, как и таблица умножения.
Таблица 5 Групповая таблица C 6 .Индекс p циклической группы C p задается числом
, где k | p означает k делит p ; φ ( k ) – это общая функция (как обсуждалось выше), а Z – это набор целых чисел.
Групповая таблица для группы приведена в таблице 6.
Как и в групповой таблице, элементы записываются в первой строке и первом столбце.Напомним, подчеркивание призвано напомнить нам, что это символы, а не числа. Мы определяем групповую операцию ⊗ согласно следующему отображению:
Это отображает группу CPG на первые неотрицательные целые числа в циклической группе C 6 .
С помощью определенного отображения мы установили изоморфизм между этими двумя группами
Другие изоморфизмы, которые существуют для набора групп g 6 , равны
Есть четыре подгруппы в и четыре подгруппы в C 6 : {(0), (0,3), (0,2,4), (0,1,2,3,4,5)}.
Чтобы использовать эти идеи с такими понятиями, как ввод сигнала (известный как объединение датчиков в сообществе управления) и сетевое (кольцевое) соединение для создания более крупных сетей, нам необходимо определить операторов, Φ r , которые превращают одну группу в другую.
Пусть нижний индекс оператора представляет количество оборотов при вводе сигнала. Затем мы можем записать все разрешенные операции над группами и их результаты.
Чтобы рассмотреть вход датчика и / или связь с двумя или более из этих динамических колец, мы рассмотрим пример. Это уравнение говорит, что когда в цепи CPG есть один, 1, циклически проходящий через кольцо, и если импульс длительностью, равной постоянной времени узлов, вводится при повороте 2 (индекс оператора), это будет эквивалентно инициализации кольца. схема с (000101) или десятичной 5. Следовательно, схема преобразуется в группу. Явно это будет записано как (000100) + (000001) → (000101).
Рассмотрим другой пример. Это соотношение говорит о том, что когда импульс с двумя постоянными времени вводится в положениях вращения 2 и 3 в схему с 6 узлами с сигналом, уже находящимся в положении 0 (всегда предполагаемое начальное состояние), последовательность импульсов схемы преобразуется в. Явно это будет записано как (000001) + (000110) → (0001001).
Остальные уравнения:
Эти уравнения интерпретируются следующим образом. На рисунке 8 мы видим кольцо в состоянии (000001). Если мы введем импульс короткой продолжительности (т.е., меньше времени отклика логических вентилей с соответствующими компонентами) в это кольцо в позиции 0, в то время как в этой конфигурации это не будет иметь никакого эффекта,. Если вводится в положение 1, когда кольцо находится в этом состоянии (000001), это заставит систему перейти в состояние (000101) после операции. Если мы введем короткий импульс в сеть в позиции 2, он также перейдет в (000101). С другой стороны, короткий импульс, введенный в позицию 3, заставит кольцевую схему перейти в стабильное состояние (001001) в зависимости от операции.В этом случае нижний индекс оператора указывает расстояние до узла от узла 0 в состоянии 1 (000001), в то время как верхний индекс и нижний индекс на символе напоминают нам, что кольцо является кольцом из 6 узлов и находится в состоянии (001001) . Эти правила перехода применяются либо к подаваемым импульсам, например, от внешних датчиков, либо к внутренним импульсам, например, от колец, соединенных в более крупные сети.
Число состояний, которые может выдержать кольцо, по-прежнему определяется размером кольца, заданным вышеупомянутой функцией двухрядного ожерелья.
Значение этого подхода состоит в том, что он описывает глобальную динамику и увлечение, т.е. крупномасштабную динамику молекулярной сети и реакцию окружающей среды, через динамику локальных внутренних сетей в интерактоме. Здесь нас интересует не симметрия интерактома, а симметрия локальной и глобальной динамики. В качестве примера на рисунке 9 показана диаграмма аттрактора для схемы, показанной на рисунке 8. Это схематическое изображение динамики, демонстрируемой «интерактомом», простой схемой обратной связи, показанной на рисунке 8.С точки зрения группового автоморфизма мы можем разложить график в таблице 5 на C 2 × S 2 , что сильно отличается от сети C 6 , которая дает начало динамике, показанной на рисунке 9. Это обеспечивает совершенно другое описание интерактома с точки зрения динамики, а не с точки зрения молекулярной связи. Изучение этого подхода к системной биологии – открытая проблема.
Рисунок 9Схема аттрактора, соответствующая схеме, показанной на рисунке 8 .
Метод DeepWalk выполняет случайные блуждания случайным образом, что означает, что вложения не сохраняют локальную окрестность узла хорошо. Подход Node2vec исправляет это.
Node2vec – модификация DeepWalk с небольшой разницей в случайных блужданиях. Он имеет параметры P и Q. Параметр Q определяет, насколько вероятно, что случайное блуждание обнаружит неоткрытую часть графа, а параметр P определяет, насколько вероятно, что случайное блуждание вернется к предыдущему узлу.Параметр P управляет обнаружением микроскопического изображения вокруг узла. Параметр Q управляет обнаружением большей окрестности. Он предполагает наличие сообществ и сложных зависимостей.
На рисунке показаны вероятности шага случайного блуждания в Node2vec. Мы только что сделали шаг от красного узла к зеленому. Вероятность вернуться в красный узел равна 1 / P, а вероятность вернуться в узел, не связанный с предыдущим (красным) узлом 1 / Q. Вероятность перейти к соседу красного узла равна 1.Остальные шаги внедрения такие же, как у DeepWalk.
Встраивание структурной глубокой сети (SDNE) не имеет ничего общего с двумя предыдущими подходами, поскольку не выполняет случайных обходов. Я упоминаю об этом, потому что он очень постоянен в своей работе для разных задач.
Он спроектирован таким образом, что вложения сохраняют близость первого и второго порядка. Близость первого порядка – это локальное попарное подобие между узлами, соединенными ребрами.Он характеризует структуру локальной сети. Два узла в сети похожи, если они связаны ребром. Когда одна статья цитирует другую, это означает, что они затрагивают схожие темы. Близость второго порядка указывает на сходство структур соседства узлов. Он фиксирует структуру глобальной сети. Если два узла имеют много общих соседей, они, как правило, похожи.
Авторы представляют нейронную сеть автоэнкодера, которая состоит из двух частей – см. Рисунок ниже. Автоэнкодеры (левая и правая сеть) принимают вектор смежности узлов и обучаются восстанавливать смежность узлов.Эти автоэнкодеры называются ванильными автоэнкодерами, и они изучают близость второго порядка. Вектор смежности (строка из матрицы смежности) имеет положительные значения в местах, которые указывают узлы, подключенные к выбранному узлу.
Также есть контролируемая часть сети – связь между левым и правым крылом. Он вычисляет расстояние между встраиванием левой и правой части и включает его в общую потерю сети. Сеть обучена так, что левый и правый автокодеры получают все пары узлов, которые соединены ребрами на входе.Потеря дистанционной части помогает сохранить близость первого порядка.
Суммарные потери в сети рассчитываются как сумма потерь от левого и правого автокодировщиков вместе с потерями от средней части.
Последний подход включает в себя весь граф. Он вычисляет один вектор, описывающий граф. Я выбрал подход graph3vec, поскольку он, насколько мне известно, является наиболее эффективным для встраивания графа.
Graph3vec основан на идее подхода doc2vec, который использует сеть skip-gram.Он получает идентификатор документа на входе и обучается максимизировать вероятность предсказания случайных слов из документа.
Подходы Graph3vec состоят из трех этапов:
Поскольку задачей является прогнозирование подграфов, графы с похожими подграфами и подобной структурой имеют похожие вложения.
Я представил четыре подхода, основанных на часто используемой литературе. Поскольку эта тема в настоящее время очень популярна, доступно больше подходов. Здесь я представляю список других доступных подходов:
[1] C.Мэннинг, Р. Сочер, Лекция 2 | Векторные представления слов: word2vec (2017), YouTube .
[2] Б. Пероцци, Р. Аль-Рфу, С. Скиена, DeepWalk: онлайн-обучение социальных представлений (2014), arXiv: 1403.6652 .
[3] К. Маккормик. Word2Vec Tutorial – The Skip-Gram Model (2016), http://mccormickml.com .
[4] Т. Миколов, К. Чен, Г. Коррадо, Дж. Дин, Эффективная оценка представлений слов в векторном пространстве (2013), arXiv: 1301.3781 .
[5] А. Нараянан, М. Чандрамохан, Р. Венкатесан, Л. Чен, Ю. Лю, С. Джайсвал, graph3vec: Изучение распределенных представлений графов (2017),
arXiv: 1707.05005 .
[6] П. Гоял, Э. Феррара, Методы, приложения и производительность встраивания графов: обзор (2018), Системы, основанные на знаниях .
[7] Д. Ван, П. Цуй, В. Чжу, Structural Deep Network Embedding (2016), Труды 22-й международной конференции ACM SIGKDD по открытию знаний и интеллектуальному анализу данных.
[8] А. Гровер, Дж. Лесковец, node2vec: Scalable Feature Learning for Networks (2016), Труды 22-й международной конференции ACM SIGKDD по обнаружению знаний и интеллектуальному анализу данных.
Граф – это структура данных, которая определяется двумя компонентами:
Рассмотрим приведенный ниже график,
Чтобы узнать о «Графическом представлении», щелкните здесь
Приложения:
График – это структура данных, которая широко используется в нашей реальной жизни.
Подробнее о графиках:
Характеристики графиков:
P (u, v) = (v0, v1, v2, v3 …… .vn)
Путь простой, если все узлы различны, исключение – источник и место назначения одинаковы.
Типы графов:
Доказательство для полного графа:
Рассмотрим данный граф,
// Пропустить повторяющиеся ребра
Ребра на узле A = (A, B), (A, C), (A, E), (A, C).
Кромки на узле B = (B, C), (B, D), (B, E).
Кромки на узле C = (C, D), (C, E).
Кромки на узле D = (D, E).
Ребра на узле E = EMPTY. Https://en.wikipedia.org/wiki/Graph_theory
Всего ребер = 4 + 3 + 2 + 1 + 0 = 10 ребер.
Количество узлов = 5.
Таким образом, n (n-1) / 2 = 10 ребер.
Доказано.
Читать следующий набор – Основы теории графов
Вниманию читателя! Не прекращайте учиться сейчас.Практикуйте экзамен GATE задолго до самого экзамена с помощью предметных и общих викторин, доступных в серии тестов GATE Test Series Course .
Изучите все концепции GATE CS с бесплатными живыми классами на нашем канале YouTube.
Графы, особенно сетевые графы, привлекают мое внимание.
Может быть, это интуитивная догадка, что анализ систем в виде графиков расширит мое понимание децентрализованных и централизованных сетей.Математик во мне видит, как точный сетевой анализ может принести большую пользу исследованиям систем, основанных на стимулах. Или, может быть, во мне дизайнер во многом увлечен врожденным артистизмом графиков, подобных приведенному выше – визуально привлекательным, но в конечном итоге богатым информацией.
По какой-то причине, столкнувшись с графами как деревьями в разработке программного обеспечения, как сетями в исследованиях блокчейнов или как r / datais красивой приманкой для кликов, я решил глубоко погрузиться в мир теории графов и ее подветвь. теория сети.
Статья, первоначально опубликованная на https://www.setzeus.com/Область математики – большая . Это дерево знаний разветвляется на постоянно растущее число подполей. Один из самых высокоуровневых способов разделения и описания набора ветвей – это тип , число в рамках данной проблемы. Числа в задачах могут быть дискретными , как в фиксированных, ограниченных значениях , таких как натуральные числа 1,2,3,4. Или они могут быть непрерывными , числами, которые более точно отображают нашу реальность как динамические, изменяющиеся значения , такие как скорость движения объекта.
Дискретные числа для цифровых часов старой школы – это то же самое, что непрерывные числа для современных аналоговых часов (которые скользят, а не тикают). В первом случае между 11:32 и следующей минутой 11:33 не существует чисел. В последнем случае секундная стрелка непрерывно движется , что означает, что аналоговые часы технически отображают другое значение каждый отдельный момент , когда секундная стрелка скользит от одной секунды к другой. Лучшим примером раздела математики, охватывающего дискретные числа, является комбинаторика, изучение конечных наборов объектов.Лучший пример раздела математики, основанного на непрерывных числах, – это исчисление, изучение того, как вещи меняются.
Теория графов, подраздел дискретной математики, находится на высшем уровне изучения связи между вещами. Эти вещей более формально называются вершинами, вершинами или , узлами , а сами соединения называются ребрами.
Основная идея графов была впервые представлена в 18 веке швейцарским математиком Леонардом Эйлером.Его попытки и возможное решение знаменитой проблемы Кенигсбергского моста, изображенной ниже, обычно цитируются как источник теории графов:
Статья, первоначально опубликованная на https://www.setzeus.com/Немецкий город Кенигсберг (современный Калининград, Россия) ) расположен на реке Преголе. Географическая структура состоит из четырех основных участков земли, соединенных в общей сложности семью мостами. Вопрос, заданный Эйлеру, был прост: можно ли было пройтись по городу таким образом, чтобы пересечь каждый мост один раз и только один раз (известная как прогулка Эйлера)?
Эйлер, осознавая, что соответствующими ограничениями были четыре тела суши и семь мостов, нарисовал первое известное визуальное представление современного графа.Современный граф, как видно на нижнем правом изображении C, представлен набором точек, известных как v ertices или узлов, которые соединены набором соединительных линий, известных как e dges.
Статья, первоначально опубликованная на https://www.setzeus.com/Сначала он попытался нарисовать пути в приведенном выше графе, а затем экспериментировал с несколькими теоретическими графами с чередующимся числом вершин и ребер, и в конце концов экстраполировал общее правило:
Чтобы иметь возможность идти по эйлеровому пути (иначе говоря, без повторения ребра), граф не может иметь ни одного или двух нечетных узлов?
Отсюда ветвь математики, известная как теория графов, оставалась бездействующей в течение десятилетий.Однако в наше время его применение наконец-то набирает обороты.
Приложения теории графов
Теория графов в конечном итоге является исследованием отношений . Учитывая набор узлов и соединений, которые могут абстрагироваться от всего, от макетов городов до компьютерных данных, теория графов предоставляет полезный инструмент для количественной оценки и упрощения многих движущихся частей динамических систем. Изучение графиков с помощью фреймворка дает ответы на многие проблемы компоновки, построения сетей, оптимизации, сопоставления и эксплуатации.
По мере того, как мы переходим к изучению основ набора графов и обозначений матриц (2) , не помешает повысить нашу мотивацию самоучки, охватив несколько приложений – взгляд на теорию графов в действии:
В программном обеспечении инженерии, они известны как довольно распространенные структуры данных, удачно названные деревьями решений. В мире электротехники целая дисциплина вращается вокруг создания, расчета и обслуживания электрических цепей , состоящих из нескольких частей – часто изображается в виде диаграмм в соответствии с принципами теории графов.Тем временем в области молекулярной биологии ученые экстраполируют модели прогнозов для отслеживания распространения болезней или моделей размножения. И, наконец, в противоречивом мире анализа сетей социальных сетей мы стали свидетелями того, как теория графов использовалась для создания уже стандартных функций, таких как степени разделения в LinkedIn и функции рекомендации друзей в Facebook. Давайте перейдем к следующей статье, чтобы познакомиться с общепринятыми обозначениями графов.
первоначально опубликовано на
https: // www.setzeus.com/
источников
Введение в теорию графов
Теория графов
Исследования показывают, что учителя могут интегрировать технологии, чтобы помочь учащимся понять математические процедуры и развить сложные математические задачи. навыки. Национальный совет учителей математики (NCTM) добавил, что для привлечения студентов необходимы технологические инструменты.
Какие типы технологий можно внедрить в классы математики? В следующем разделе предлагается несколько идей, которые могут помочь при обучении детей математике.
Вот несколько эффективных инструментов для обучения математике с помощью технологий.
Desmos предлагает бесплатный веб-калькулятор для построения графиков, а также цифровые задания для 6–12 классов.
Основным предложением является калькулятор, который соответствует функциональности многих калькуляторов TI стоимостью более 100 долларов. Это популярный вариант для тех, кто хочет эффективно преподавать математику с помощью технологий. Другое предложение от Desmos, центра цифровой деятельности, представляет собой несколько интерактивных уроков, которые студенты могут выполнять на своих планшетах или устройствах.Есть раздел, который позволяет учителям создавать уроки и делиться ими с другими учителями.
EquatIO – это инструмент для создания математических уравнений, формул, графиков Desmos и т. Д. На компьютерах или Chromebook.
Продукт предназначен для оцифровки математики с помощью простых методов ввода. Учителя могут печатать, писать от руки или диктовать выражения, чтобы добавить результат в документ, и есть большая библиотека, полная готовых выражений. Другими словами, это своего рода умный помощник, который может заменить ручку и бумагу, а также предложить возможности прогнозирования.Продукт работает с программным обеспечением для повышения грамотности Read & Write (платным), которое помогает сочетать доступность и обучение математике с технологиями.
EquatIO бесплатен для учителей. Платные лицензии доступны для других типов пользователей и групп.
Kahoot! это интерактивная игра, в которой учащимся в одном классе предлагаются вопросы с несколькими вариантами ответов. Этот обучающий инструмент предлагает бесплатные и платные планы.
Учителя могут искать заранее подготовленные вопросы и ответы по различным предметам или создавать свои собственные (платные).Вопросы проецируются на экран в классе, и учащиеся выбирают ответ на своих устройствах. Студенты, набравшие наибольшее количество баллов, отображаются перед следующим вопросом, создавая веселую и соревновательную атмосферу.
Kahoot! имеет базовый бесплатный план, а также два платных плана (1 или 3 доллара за учителя в месяц), которые предлагают более продвинутые функции.
Обучение детей математике с помощью онлайн-игр – популярный метод взаимодействия. Вот два бесплатных веб-сайта, на которых представлены разнообразные интерактивные игры для учащихся 1–6 классов:
Классные комнаты, оборудованные досками SMART, могут воспользоваться бесплатными занятиями и играми, доступными через Интернет.
Сайты, такие как SMART Exchange и iSmartboard.com, помогают учителям находить тысячи интересных уроков, и они организованы по классам. Многие задания и игры представлены учителями, которые уже используют их для обучения детей математике в классе.
Sumdog – это адаптивный инструмент обучения математике с использованием технологий для учащихся классов K-8. Платные планы подписки открывают доступ к премиальным инструментам для учителей.
Sumdog предлагает обучение на основе игр, которое мотивирует и увлекает студентов.На компьютерах и планшетах учащиеся отвечают на вопросы в своем собственном темпе, выполняя задания в соответствии с их уровнем навыков. Положительное подкрепление вознаграждает учеников за достижения в игре, а учителя получают оценочные данные для руководства уроками и изучения индивидуальных потребностей учеников. Исследования эффективности и тематические исследования выявили улучшения в успеваемости учащихся при использовании продукта.
Ценовые предложениядоступны на сайте Sumdog.
VmathLive предлагает онлайн-соревнования по математике для учащихся K-8 классов.Это платный продукт.
Предложение включает четыре основных компонента:
Стоимость VmathLive составляет 10 долларов США за студента или 200 долларов США за класс (до 25 студентов), согласно странице продукта компании на момент публикации.
YouTube – отличный источник интерактивных видеороликов, которые помогают студентам изучать математические концепции и применять полученные знания на практике. Вот некоторые из наиболее примечательных каналов YouTube для обучения математике:
Учителя также могут создавать свои собственные видеоролики на YouTube, чтобы получить уникальный взгляд на обучение математике с помощью технологий. Примеры варьируются от более сложного и дурацкого шоу до более простого и сфокусированного клипа в реальном мире.
Это видео по округлению было создано Mr.ДеМайо, учитель третьего класса в Юнион-Бич, штат Нью-Джерси. Здесь он и его друзья Стив и Энди занимают причудливую и забавную точку зрения на эту тему.
Это видео о ценах на продукты было создано Дженни Магиера, бывшей учительницей, которая в настоящее время работает директором программы в образовательной организации. Здесь она просит студентов математически определить, какой из трех вариантов приобретения острого сыра чеддер является лучшим.
Согласно NCTM, учителя должны хорошо разбираться в технологиях, помогающих преподавать математику.Эффективное использование некоторых из вышеупомянутых ресурсов требует стратегического подхода.
Вы можете усилить эту способность, получив онлайн-степень магистра математического образования, которая включает факультативный курс по технологиям в классах математики. В этой программе вы углубите свое понимание математических концепций и их использования во всем спектре K-12. Вы разовьете содержание математики и педагогику, необходимые для того, чтобы привить глубокий интерес к математике у следующего поколения учащихся.
Развивайте свою карьеру со степенью в Интернет-университете Аврора. Учитесь у практикующих преподавателей, которые стремятся помочь работающим профессионалам достичь своих целей. Узнайте, что значит учиться в гибкой и удобной учебной среде, получая при этом личное внимание и поддержку, которых вы ожидаете от небольшого колледжа.
Этот спонсорский контент предоставлен Интернет-службой Aurora University
Простой метод оценки релевантности вершины – вычислить ее центральность. Центральность вершины является мерой ее важности в сети в данной перспективе [7] и может быть выражена по-разному; таким образом, существует несколько типов мер центральности. Какая мера подходит в данном контексте, зависит от того, какой аспект топологии сети учитывает мера центральности.
Простейшей мерой центральности является степень вершины, также называемая центральностью градусов [7].Этот показатель предполагает, что чем лучше связана вершина, тем важнее она в сети. С точки зрения лидеров мнений кажется интуитивно понятным, что потенциал для общения и влияния больше у людей с большим количеством связей. Центральность собственного вектора пытается уловить качественный аспект связей вершины. Исходя из предпосылки, что связи с более влиятельными вершинами более важны, чем соединения с менее влиятельными вершинами, мера также принимает во внимание центральность соседей [7].Подобно собственному вектору центральность – PageRank , который оценивает важность веб-страниц в поисковой системе [8]. PageRank моделирует вероятность того, что «случайный» веб-пользователь, который начинает со случайной веб-страницы и продолжает переходить по ссылкам, посетит веб-страницу (или вершину в сети веб-страниц). Эта мера также вводит коэффициент затухания, который выражает вероятность на каждом шаге того, что пользователь не продолжит использовать ссылку, а перейдет на случайную веб-страницу. Другие меры центральности явно рассматривают косвенное соединение с другими вершинами в сети. Центральность близости является такой мерой, и она представляет собой среднее расстояние или средний кратчайший путь до всех других вершин в сети [7]. Основная идея здесь в том, что центральная вершина будет в среднем ближе, чем другие, менее центральные вершины. Это также имеет смысл с точки зрения влияния: человек, который может легко связаться с другими людьми, будет более эффективно распространять влияние. Центральность по промежуточности , с другой стороны, пытается уловить способность вершины управлять потоком коммуникации: она указывает, сколько раз вершина находилась на кратчайшем пути между двумя другими вершинами [9].Вершина, расположенная на большом количестве таких путей, имеет повышенную способность управлять связью, поскольку любая информация, проходящая через эти пути, будет проходить через вершину.
Как указывалось ранее, разные меры центральности подходят для определения наиболее важных вершин в разных контекстах, контекстах, которые соответствуют предположениям, подразумеваемым конкретной формулировкой меры. Действительно ли мера центральности отражает важность в сети, зависит от того, как информация течет в этой конкретной сети [10].Далее мы рассмотрим несколько выводов о показателях центральности как показателях лидерства. Результаты исследования лидерства мнений при принятии смартфонов предполагают, что центральность степени действительно указывает на лидерство мнений [11]. В том же исследовании было обнаружено, что, как и ожидалось, социальное влияние больше, чем более сильные связи или связи, но не было обнаружено значимого взаимодействия между силой связи и степенью центральности. Результаты [12] предполагают, что центральность степени является индикатором лидерства местного мнения, поскольку центральность высокой степени означает наличие множества связей в непосредственной среде вершины.Для оценки лидерства мирового общественного мнения лучше подходят показатели близости и промежуточности. Причина этого, по утверждению Бодендорфа и Кайзера [12], заключается в том, что люди, которые легко доступны другим, имеют больше шансов быть замеченными (центральность близости), в то время как люди, которые находятся на путях коммуникации, могут оказывать большее влияние на это общение ( центральность промежуточности). Shafiq et al. [13] в ходе экспериментов с данными, собранными из Facebook, обнаружили, что лидеры, как правило, в среднем имеют значительно более высокую степень центральности, чем другие типы людей, что подтверждает идею о том, что наличие хороших связей и высокая степень центральности выгодны для лидера мнений. положение дел.Однако они также отметили, что у большого числа лидеров нет высокой степени центральности, что предполагает, что степень центральности не охватывает все аспекты лидерства. Лучше всего близкое центральное положение наблюдается среди лидеров, особенно среди лидеров-интровертов. В их экспериментах центральность собственного вектора не могла различать лидеров и последователей, но была значительно ниже для нейтральных узлов (ни лидеров, ни последователей). PageRank, с другой стороны, был выше у лидеров, чем у подписчиков.Несмотря на эти различия в рейтинге страниц и центральном положении между лидерами и не лидерами, Shafiq et al. не рекомендуют эти меры для выявления лидеров в данных взаимодействия.
Лу и др. [14] обнаружили, что показатель PageRank менее эффективен в сетях людей, чем в сетях веб-страниц, поэтому они предлагают LeaderRank как более эффективный способ ранжирования людей в сети. LeaderRank похож на PageRank, но не содержит параметров: он вводит наземный узел, который связан со всеми другими узлами в сети, и его роль аналогична роли демпфирующего фактора в PageRank.Таким образом, этот коэффициент отсутствует, что исключает необходимость калибровки. Их эксперименты с данными из Delicious, сервиса социальных закладок, показывают, что LeaderRank превосходит PageRank в задаче выявления влиятельных пользователей. Они также обнаружили, что этот алгоритм имеет лучшую производительность, чем просто учет количества подписчиков у пользователя (то есть степень центральности).
Chen et al. [15] предложили новую полулокальную меру центральности, которая полагается на ближайших и следующих ближайших соседей для определения наиболее влиятельных узлов в неориентированной сети.Предлагаемый подход, кажется, идентифицирует влиятельные узлы лучше, чем методы, основанные на центральности на основе степени и центральности на основе промежуточности. Однако другие существующие подходы случайного блуждания, такие как PageRank и LeaderRank, кажутся лучшими индикаторами влиятельных узлов, но менее эффективны с точки зрения вычислений. Метод был протестирован в четырех различных реальных сетях: блоггеры на веб-сайте MSN Spaces (Windows Live Spaces), соавторы в области сетевых исследований, топология уровня маршрутизатора и электронные письма сотрудников университета.Метод работает по-разному в зависимости от структуры сети и рекомендуется для гетерогенных сетей и в меньшей степени для древовидных сетей. Chen et al. также проанализировали взаимосвязь между рассматриваемыми мерами центральности, показав, что, в целом, предлагаемая локальная центральность имеет сильную положительную корреляцию с центральностью по близости и слабую корреляцию с центральностью по промежуточности и центральностью по степени.
Cho et al. [16] провели систематическое исследование с использованием модели стохастических клеточных автоматов, связанной с предположением о маленьком мире, чтобы проанализировать влияние различных метрик центральности и свойств сети на скорость распространения и максимальное совокупное количество последователей в контексте распространения инноваций.Экспериментальные результаты показывают, что центральное положение на расстоянии и центральное место в рейтинге-номинация являются лучшими для максимизации совокупного числа последователей, тогда как социальность обеспечивает лучшую скорость распространения.
Эти две области математики часто упоминаются вместе, поскольку обе связаны с изучением свойств пространства. Но в то время как геометрия фокусируется на свойствах пространства, которые включают размер, форму и измерение, топология занимается менее осязаемыми свойствами относительного положения и связности.
Почти каждый ученик средней школы имел хоть какой-то контакт с евклидовой геометрией. Этот предмет оставался практически неизменным около 2000 лет, в течение которых он был жемчужиной в короне математики, архетипом логической точности и математической достоверности.
А затем, в семнадцатом веке, все изменилось во многих отношениях.
Основываясь на многовековых вычислительных методах, разработанных астрономами, астрологами, моряками и механиками в их практических занятиях, Декарт систематически ввел теорию уравнений в изучение геометрии.Ньютон и другие исследователи изучали свойства кривых и поверхностей, описываемых уравнениями, используя новые методы исчисления, точно так же, как сейчас студенты изучают текущие курсы математического анализа. Эти методы и идеи в конечном итоге привели к тому, что мы сегодня называем дифференциальной геометрией, основным инструментом теоретической физики. Например, дифференциальная геометрия была ключевым математическим ингредиентом, который Эйнштейн использовал при разработке теории относительности.
Другое событие достигло высшей точки в девятнадцатом веке в свержении евклидовой геометрии как бесспорной основы для изучения космоса.Возможны и другие геометрические формы. Это аксиоматическое исследование неевклидовой геометрии идеально сочетается с дифференциальной геометрией, поскольку последняя допускает неевклидовы модели пространства. В настоящее время нет единого мнения о том, какая геометрия лучше всего описывает вселенную, в которой мы живем.
Наконец, в восемнадцатом и девятнадцатом веках зародилась топология (или, как ее тогда называли, analysis situs), так называемая геометрия положения. Топология изучает геометрические свойства, которые остаются неизменными при непрерывной деформации.Например, независимо от того, как окружность изменяется при непрерывной деформации плоскости, точки, находящиеся внутри ее периметра, остаются внутри новой кривой, а точки снаружи остаются снаружи. Другой пример: никакая непрерывная деформация не может превратить сферу в плоскость. Таким образом, они топологически различны.
Топологию можно рассматривать как естественное дополнение к уже описанным революционным изменениям в геометрии. Ведь если кто-то осознает, что существует несколько возможных способов геометризации мира, т.е., это больше, чем просто евклидов способ измерения размеров и форм, тогда становится важным выяснить, какие свойства пространства не зависят от такого измерения. Топология, которая окончательно утвердилась в двадцатом веке, является фундаментальным предметом, который дает ответы на подобные вопросы. Это основной инструмент для физиков и астрономов, пытающихся понять структуру и эволюцию Вселенной. Действительно, недавние астрономические наблюдения вместе с основными результатами топологии открывают захватывающую перспективу того, что мы скоро будем обладать глобальной топологической структурой космоса.
.
Нарисовала Лиса Зайцу дорогу к своему дому (воспитатель помещает план на доске). Расскажите, как дойти до Лисы.