Главная › Новости
Опубликовано: 30.09.2018
СИЛА ТЯЖЕСТИ вес тела ФИЗИКА 7 класс | Романов1. Укажите, что относится к понятию «физическое тело», а что к понятию «вещество»: самолет, космический корабль, медь, авторучка, фарфор, вода, автомобиль.Физическое тело — самолет, космический корабль, авторучка.Вещество — медь, фарфор, вода.
2. Приведите примеры следующих физических тел: а) состоящих из одного и того же вещества; б) состоящих из различных веществ одинакового названия и назначения.а) Из одного вещества: стол, карандаш, стул — из дерева,б) Из различных веществ: пластиковая и стеклянная бутылка.
3. Назовите физические тела, которые могут быть сделаны из стекла, резины, древесины, стали, пластмассы.Стекло: колба лампы, бутылка.Резина: покрышка, воздушный шарик.Древесина: дверь, паркет.Сталь: резец, лезвие ножа.Пластмасса: корпус шариковой ручки, калькулятора.
4. Укажите вещества, из которых состоят следующие тела: ножницы, стакан, футбольная камера, лопата, карандаш.Ножницы — сталь; стакан — стекло; футбольная камера — резина; лопата — сталь; карандаш — дерево.
5. Начертите в тетради таблицу и распределите в ней следующие слова: свинец, гром, рельсы, пурга, алюминий, рассвет, буран, Луна, спирт, ножницы, ртуть, снегопад, стол, медь, вертолет, нефть, кипение, метель, выстрел, наводнение.
6. Приведите примеры механических явлений.Механические явления: падение тела, колебание маятника.
7.
Приведите примеры тепловых явлений.Тепловые явления: таяние снега, кипение воды.
8. Приведите примеры звуковых явлений.Звуковые явления: гром, свист милиционера.
9. Приведите примеры электрических явлений.Электрические явления: молния, искра свечи зажигания.
10. Приведите примеры магнитных явлений.Магнитные явления: взаимодействие двух магнитов, вращение стрелки компаса.
11. Приведите примеры световых явлений.Световые явления: свет лампочки, северное сияние.
12. Предлагаемую ниже таблицу начертите в тетради и впишите слова, относящиеся к механическим, звуковым, тепловым, электрическим, световым явлениям: шар катится, свинец плавится, холодает, слышны раскаты грома, снег тает, звезды мерцают, вода кипит, наступает рассвет, эхо, плывет бревно, маятник часов колеблется, облака движутся, гроза, летит голубь, сверкает молния, шелестит листва, горит электрическая лампа.
13. Назовите два-три физических явления, которые наблюдаются при выстреле из пушки.Полет снаряда, звук выстрела и взрыв пороха.
kupuk.net
Разделы: Физика
Цели урока:
Дать понятие о предмете физики. Создать представление о первичных понятиях в физике (тело, вещество, явление). Сформулировать цели изучения явлений природы. Выявить источники физических знаний, определить круг изучаемых явлений, пояснить связь физики с другими науками и техникой. Ознакомить учащихся с методами исследования физических явлений. Пробудить у детей интерес к изучению физики и развить любознательность.Оборудование: три линейки из разного материала, наклонный желоб, стальной шарик, штатив; пружина, набор грузов; электрическая лампочка на подставке электрофорная машина, электрический звонок, зеркало, детская машинка.
Ход урока
Мы приступаем с вами к изучению основ очень интересной и полезной науки – физики.
Садясь в поезд, такси, трамвай, нажимая на кнопку электрического звонка, просматривая кинофильм или наблюдая, как комбайн убирает урожай, вы едва ли задумывались над тем, какой путь прошло каждое из этих больших и маленьких достижений техники, сколько труда вложено в каждое из них. К технике мы привыкли, она стала нашим спутником.
А ведь не очень давно люди ездили в тарантасах, запряженных лошадьми, жали рожь и пшеницу серпами, сидели при свете горящих лучин в длинные зимние вечера и только в сказках мечтали о различных волшебствах. Гусли-самогуды, ковер-самолет, топор-саморуб ? вот предметы сказочных мечтаний. Вспомните, в сказке А.С.Пушкина звездочет и мудрец, подаривший царю Додону чудесного петушка, заверял его:
Петушок мой золотой Будет верный сторож твой: Коль кругом все будет мирно, Так сидеть он будет смирно; Но лишь чуть со стороны Ожидать тебе войны, Иль набега силы бранной, Иль другой беды незваной, Вмиг тогда мой петушок Приподымет гребешок, Закричит и встрепенется И в то место обернется.
И вот мечта сбылась. Современные радиолокационные установки куда лучше золотого петушка. Они позволяют мгновенно и точно обнаружить в небе самолеты, ракеты и другие объекты.
Как о чуде говорится в сказке Ершова “Конек-горбунок” о холодном свете:
Огонек горит светлее, Горбунок бежит скорее. Вот уж он перед огнем. Светит поле словно днем. Чудный свет кругом струится, Но не греет, не дымится. Диву дался тут Иван, “Что, – сказал он, – за шайтан! Шапок с пять найдется свету, А тепла и дыму нету. Эко чудо-огонек…”
И вот чудо-огонек в виде ламп дневного света проник в наш быт. Он радует людей на улицах, в магазинах, в учреждениях, в метро, в школах, на предприятиях.
Да, сказки становятся былью: гусли-самогуды воплотились в магнитофон. Электропилы за несколько секунд валят вековые деревья лучше сказочных топоров-саморубов. Не ковры, а самолеты стали широко распространенным средством транспорта. Наши ракеты выводят на орбиты искусственные спутники Земли и космические корабли с космонавтами на борту.
Трудно было человеку миллионы лет назад, Он совсем не знал природы, Слепо верил в чудеса, Он всего, всего боялся. И не знал, как объяснить Бурю, гром, землетрясенье, Трудно было ему жить.
И решил он, что ж бояться, Лучше просто все узнать. Самому во все вмешаться, Людям правду рассказать. Создал он земли науку, Кратко “физикой” назвал. Под названьем тем коротким Он природу распознал.
“Физика” – это греческое слово и в переводе означает, как вы поняли, “природа”.
Одной из древнейших наук, которая позволяет познать силы природы и поставить их на службу человеку, которая дает возможность понять современную технику и развивать ее дальше, является физика. Знания физики необходимы не только ученым и изобретателям. Без них не может обойтись ни агроном, ни рабочий, ни врач. Каждому из вас они тоже потребуются не раз, а многим, может быть, доведется сделать новые открытия и изобретения. То, что сделано трудом многих ученых и изобретателей – великолепно. Имена многих из них вы уже слышали: Аристотель, М. Ломоносов, Н. Коперник и многие другие. Но впереди еще много нерешенных задач: надо поставить на службу человеку тепло и свет Солнца, научиться безошибочно предсказывать погоду, предсказывать стихийные бедствия, надо проникнуть на огромные океанские и земные глубины, надо разведать и освоить другие планеты и звездные миры и многое другое, чего нет даже в сказках.
Но для этого надо прежде всего усвоить то, что добыто, в частности, овладеть знаниями по физике. Физика – интереснейшая наука. Ее надо изучать с большим вниманием, доходить до самой сути. Однако не рассчитывайте на легкий успех. Наука – не развлечение, не все будет весело и занимательно. Она требует настойчивого труда.
Получив некие знания, человек сформулировал закон, использовал в своей жизнедеятельности изученное явление, создал приборы и машины, прочие вспомогательные орудия, с помощью которых он может успешнее и совершеннее изучать и глубже описывать другие явления.
Сегодня на уроке нам предстоит понять и усвоить основные физические термины: физическое тело, вещество, физические явления, понять, что является предметом изучения физики и как она изучает природу.
Физика имеет дело с физическими телами. Что бы вы назвали физическим телом? (Учащиеся выдвигают свои предположения, которые я записываю на правой половине доски. Обобщая высказывания, приходим к выводу, что физическое тело – это любой предмет подлежащий рассмотрению в физике.
Назовите тела, которые вас окружают. (Приводят примеры.)
Чем отличаются друг от друга три линейки, которые у меня в руках?
Класс. Сделаны из разного материала: дерево, пластмасса, металл.
Учитель. Какой можно сделать вывод?
Класс. Тела могут различаться веществом.
Учитель. Что такое вещество?
Класс. Это то, из чего состоит физическое тело.
Учитель. Приведите примеры веществ, которые имеются у вас на столах. (Дети отвечают.)
Вещество – это один из видов материи.
Материя – это все то, что существует во Вселенной, независимо от нашего сознания.
Материя – вещество, поле.
Любой материальный предмет состоит из вещества. Мы можем его потрогать и увидеть. Сложнее с полем – мы можем констатировать последствия его действия на нас, но не можем увидеть. Например существует гравитационное поле, которое мы не ощущаем, но благодаря которому мы ходим по земле и не улетаем с нее, несмотря на то, что она вращается со скоростью 30 км/с, измерить его мы пока не можем. А вот электромагнитное поле человека не только можно ощущать по последствиям его воздействия, но и изменять.
В природе с телами происходят различные изменения. Они называются явлениями. Физическими явлениями называется. различные изменения, происходящие с физическими телами.
Какие физические явления вы наблюдали? (Учащиеся приводят примеры.)
Все явления делятся на несколько видов: механические, тепловые, звуковые, электрические, магнитные, световые.
Рассмотрим их на конкретных примерах и опытах. (Демонстрируются некоторые виды явлений.)
| Механические явления | Оптические явления | Электрические явления | Тепловые явления |
| Движение автомобиля, полет парашютиста, морская зыбь, работа пресса | Мираж: в пустыне, мерцание звезд, затмение Солнца, образование тени, радуга, игра цветов тонкой пленки, солнечный зайчик | Молнии при грозе, иллюминация, “путешествие” телеграммы из города в город, горение эл. лампы | Утренний туман, таяние снега, замерзание воды, выпаривание соли, нагревание ладоней при трении |
А сейчас подумаем вместе над таким вопросами:“Как изучают физику? Какими методами пользуются для этого?”
– Можно наблюдать за явлением, что мы и делали на уроке.
– Можно самим проводить опыты и эксперименты. При этом физики используют свое главное “оружие” – физические приборы. Назовем некоторые из них: часы, линейка, вольтметр,
– Можно применять математические знания
– Обязательно нужно делать обобщения
Задача 1. Разделите на три группы понятий следующие слова: стул, древесина, дождь, железо, звезда, воздух, кислород, ветер, молния, землетрясение, масло, компас.
| Физические тела | Вещества | Явления |
| Стул Звезда Компас Воздух | Древесина Железо Кислород Масло | Дождь Ветер Молния Землетрясение |
Задача 2. Вы случайно спрятали в карман шоколадку, и она там растаяла. Можно ли случившееся назвать явлением? (Да.)
Задача 3. Вам во сне явился добрый волшебник, подарил много мороженого, и Вы угостили им всех своих друзей. Жаль только, что это был сон. Можно ли считать появление доброго волшебника физическим явлением? (Нет.)
Задача 4. Коля ловил девчонок, окунал их в лужу и старательно измерял глубину погружения каждой девочки.
Толя только стоял рядышком и смотрел, как девчонки барахтаются. Чем отличаются Колины действия от Толиных, и как такие действия называют физики? (И физики и другие ученые назовут действия хулиганством. Но с точки зрения бесстрастной науки Толя производил наблюдения, а Коля ставил опыты).
Запись домашнего задания § 1 ? 3. Ответить на вопросы.
xn--i1abbnckbmcl9fb.xn--p1ai
В этой теме вы узнаете о:
• физические тела и вещества, из чего состоят вещества
• многообразие веществ
• физические и химические свойства веществ
• атом, его состав
• химические элементы, их названия и символы
• периодическую систему химических элементов Д. И. Менделеева, ее структура
• относительные атомные массы химических элементов и относительные молекулярные массы веществ
• химические формулы веществ, вычисления с ними относительных молекулярных масс и массовой доли элемента в сложном веществе
• валентность химических элементов
• связь между размещением элемента в периодической системе и его валентностью
• физические и химические явления
Изучение параграфа поможет вам:
· различать физические тела, вещества, материалы;
· приводить примеры физических тел, веществ, материалов
ФИЗИЧЕСКИЕ ТЕЛА И ВЕЩЕСТВА. Как вам известно из природоведения, тела, или физические тела — это все живое и неживое, что создали природа и человек на Земле. Для лучшего осознания этого понятия учтите следующее определение.
Физическое тело всегда имеет форму, ограниченную определенной, свойственной ему поверхностью, и массу.
Твердые тела, которые человек производит для своих нужд, имеют название предметов. На кухне такими предметами е тарелки, ложки, вилки, кастрюли, сковородки и много других.
Гостиную обустраивают столом, стульями, телевизором, ковром и тому подобное. То есть предметов очень много, они разнообразны, их используют для создания комфортных бытовых условий.
Ледяная сосулька, капля росы на листьях, снежинка, снеговик, ледяная скульптура (рис. 19) — это примеры физических тел. Они интересны тем, что созданы из одного вещества — воды.
Восстановите в памяти
Приведите примеры небесных тел. Опишите форму, охарактеризуйте размеры и массу одного из них по сравнению с Землей.
Рис 19. Физические тела, состоящие из воды
Рис. 20. Налив воды из делительной воронки в химический стакан
Но, согласитесь, у каждого тела — свои, присущие только ему, форма и размеры.
На рис. 20 изображен налива воды из делительной воронки в химический стакан. Будет неправильно назвать воду в этом случае физическим телом. А все потому, что она не имеет формы, которая бы хранила, как это мы видели на предыдущем рисунке. В данном случае вода — вещество, одна порция которой содержится в воронке, другая— в стакане. В каждом сосуде это вещество приобрела форму сосуда. Не проводя измерений, взглянув на рисунок, видим, что масса и объем этого вещества в воронке и стакане разные.
– Понятие вещества не связывают с конкретной формой и размерами. Веществами называют то, из чего образованы физические тела.
На примере с ледяной сосулькой, снежинкой, снеговиком видим, как из одного вещества образовалось несколько тел. Таких примеров достаточно много, и вы их можете привести самостоятельно.
Такие вещества, как кислород, углекислый газ, йод, глюкоза, етанова (уксусная) и лимонная кислоты, поваренная соль, пищевая сода, вам уже известны. В целом, веществ, которые существуют в природе и созданы человеком, очень много — более 10 млн.
Восстановите в памяти
Что вам известно об использовании названных веществ?
– Из одной и той же вещества могут образоваться или быть изготовлены различные физические тела.
Случается наоборот — предметы одного назначения изготовляют из разных веществ.
Так, скрепки бывают стальными и пластмассовыми, пакеты — полиэтиленовыми и бумажными, ложки — стальными, серебряными, деревянными.
Следует помнить, что тела живой природы (растения, грибы, животные и другие) независимо от того, они одноклеточные или многоклеточные, никогда не образуются из одного вещества.
МАТЕРИАЛЫ 1. Довольно часто к веществ или их смесей, из которых изготавливают тела, применяют название материалы.
Восстановите в памяти
Вспомните и приведите примеры одноклеточного и багатоклітинного организмов.
– Материалами называют вещества или смеси веществ, которые образовались в природе или были получены человеком и предназначенные для изготовления тел.
Вы видите примеры тел, изготовленных человеком из различных материалов (рис. 21). Так, карандаш изготовлен по меньшей мере из 4-х материалов — графита, древесины, резины, краски (нанесена на его поверхность). Кухонные ножи имеют стальные лезвия и пластмассовые или деревянные ручки. Деревья созданы природой, а деревянные изделия изготовила человек из их стволов, применив дополнительно клей, железные гвозди, краску и т. п (рис. 22).
СОВРЕМЕННЫЕ МАТЕРИАЛЫ. Сначала человек использовал природные материалы (камень, дерево, волокнистую часть стеблей льна или конопли), а со временем сама начала создавать нужные ей вещества и материалы.
Познавая вещества, человек находил им то или иное применение. В первых водопроводах вода двигалась деревянными желобами, со временем их заменили металлические трубы. На сегодня массовым является изготовление водопроводных труб из полиэтилена. Этот материал, в отличие от предыдущих, легкий и долговечный, не подвергается разрушительному воздействию внешней среды.
Сперва построенные человеком дома были без окон или имели узкие отверстия, которые закрывались на зиму. И только с изобретением способов изготовления материала под названием стекло дневное освещение домов стало привычным явлением. Сейчас впечатляющей является количество веществ, которые не существуют в природе, а изготовленные человеком искусственно.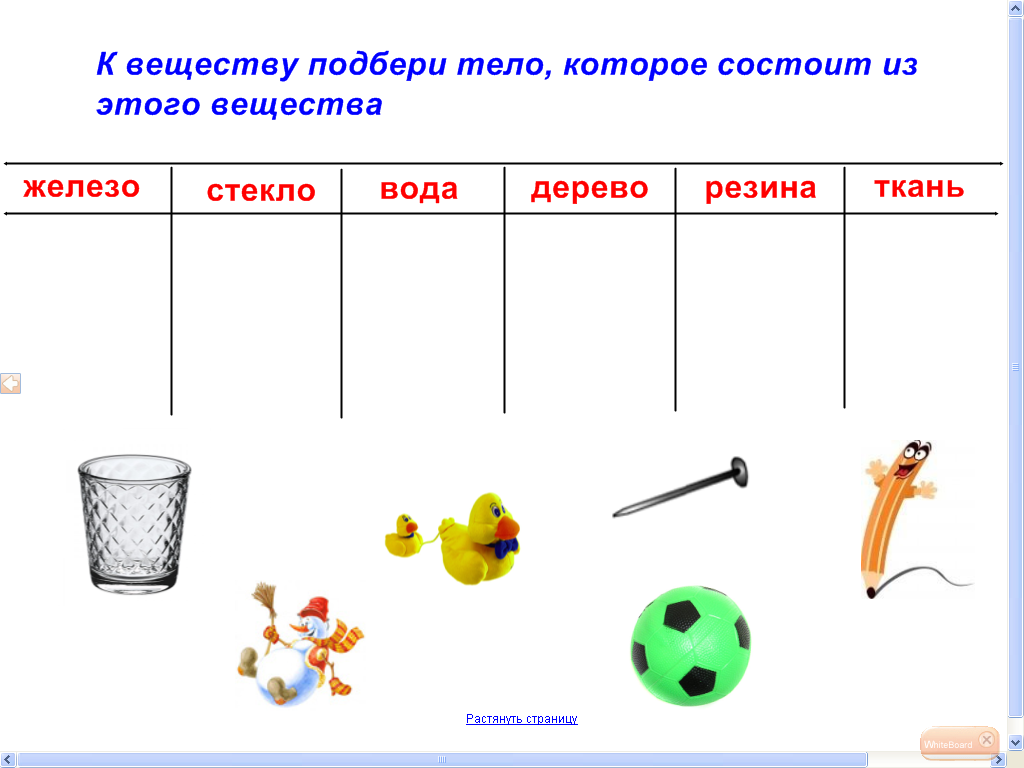
И в этом заслуга химической науки.
В повседневной жизни нас окружают различные материалы, что является веществами или смесями веществ, в основном созданными человеком благодаря достижениям химической науки. На рис. 23 изображены хорошо известные вам предметы, изготовленные из материалов, которых нет в природе. Если бы прекратилось производство этих веществ, мы лишились бы многих предметов, без которых уже не представляем своего быта.
Или еще такой пример. Материал, без которого невозможно производство покрышек для велосипедных, мотоциклетных, тракторных, автомобильных колес, называется резина. В его состав входят такие вещества, как каучук, сера, углерод.
Рис. 21. Тела, изготовленные из различных материалов
Рис. 22. Древесина — распространенный природный материал
Рис. 23. Изделия из созданных человеком материалов
Довольно часто в названии предметов звучат названия и предмета и материала, из которого он изготовлен. Например: серебряная ложка, железный гвоздь, резиновый мяч и тому подобное.
– Химические знания сделали возможным создание веществ и материалов, которых не существует в природе. Благодаря этому человек имеет возможность изготавливать множество разнообразных физических тел, или предметов.
Как видите, современная химия изучает не только вещества, что существуют в природе, но и занимается созданием новых веществ и материалов. В этих исследованиях ученые довольно часто руководствуются желанными, то есть заранее запланированными свойствами, которые отсутствуют у природных веществ.
Что же понимают под свойствами веществ? Об этом речь пойдет в следующем параграфе.
Копилка эрудита
Среди материалов большое значение приобрели сплавы. Такое название имеют твердые смеси нескольких металлов или металлов с неметаллами. Сплав бронза известный людям с III тыс. к н. е. Сейчас его тоже широко используют. В столице нашего государства (Киеве) из этого сплава построен памятник Богдану Хмельницкому (рис.
24).
Сплавы на основе алюминия появились значительно позднее бронзу. Да и сам алюминий добыли в чистом виде только в 1825 г. В XIX ст. металл был настолько дорогим. что стоил дороже золота. В настоящее время алюминий занимает второе место после железа по добыче и стоимость его умеренная. В Украине первый алюминиевый завод был построен в 1933 г. вблизи м. Запорожье.
Сплавы алюминия легкие, прочные, устойчивые к негативному воздействию окружающей среды. Такие их свойства незаменимы в самолето – и ракетостроении. Недаром алюминий называют «крылатым металлом» (рис. 25).
Рис. 24. Памятник Богдану Хмельницкому в Киеве
Рис. 25. Корпус самолета изготавливают из сплавов алюминия
?
1. Сформулируйте определения понятий: физическое тело, предмет, вещество, материал. Что характерно для тел, но отсутствует у веществ?
2. Приведите примеры современных материалов и изделий из них.
3. Изменится форма железных гвоздей, если высыпать их в ведро? Это дало основания отнести их к: а) тел; б) веществ.
4. Запишите примеры тел, изготовленных из одного вещества.
5. Заполните колонки таблицы, воспользовавшись перечнем: ложка, чашка, резина, вода, снежинка, железо, железный гвоздь, стеклянная палочка, алюминиевая проволока, сахар:
Вещества | Тела | Материалы |
6. Дополните предложения записью двух-трех собственных примеров:
а) из полиэтилена изготовлены тела:_______
б) из стекла производят:________________
7. Составьте перечень веществ, названия которых содержатся в тексте параграфа, и перечень лабораторного оборудования, на рис. 20.
8. Подумайте, чего есть больше — тел или веществ. Свой ответ обоснуйте и подтвердите примерами.
9. Расширьте свои знания о тела и вещества. Для этого поинтересуйтесь у взрослых членов вашей семьи, из каких веществ или материалов изготовлены различные предметы ежедневного обихода, инструменты их профессиональной деятельности.
О несколько новых примеров, которые станут вам известны, сделайте сообщение в классе.
schooled.ru
Тело — Тело: В математике: Тело (алгебра) множество с двумя операциями (сложение и умножение), обладающее определёнными свойствами. Тело (геометрия) часть пространства, ограниченная замкнутой поверхностью. Тело комплекса Тело (физика) … … Википедия
ФИЗИКА — ФИЗИКА, наука, изучающая совместно с химией общие законы превращения энергии и материи. В основе обеих наук лежат два основных закона естествознания закон сохранения массы (закон Ломоносова, Лавуазье) и закон сохранения энергии (Р. Майер, Джауль… … Большая медицинская энциклопедия
ФИЗИКА. — ФИЗИКА. 1. Предмет и структура физики Ф. наука, изучающая простейшие и вместе с тем наиб. общие свойства и законы движения окружающих нас объектов материального мира. Вследствие этой общности не существует явлений природы, не имеющих физ. свойств … Физическая энциклопедия
ФИЗИКА — наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, св ва и строение материи и законы её движения. Понятия Ф. и её законы лежат в основе всего естествознания. Ф. относится к точным наукам и изучает количеств … Физическая энциклопедия
Физика — Физика ♦ Physique Все, что относится к природе (от греческого physis), в частности – наука, изучающая природу (ta physika). Если природа – все, как я полагаю, значит, физика призвана вместить в себя все прочие науки. Впрочем, это… … Философский словарь Спонвиля
Физика взрыва — (a. explosion physics; н. Physik der Explosion; ф. physique de l explosion; и. fisica de explosion, fisica de estallido, fisica de detonacion) наука, изучающая явление взрыва и механизм его действия в среде. Hарушение механич.
… … Геологическая энциклопедия
ФИЗИКА ТВЕРДОГО ТЕЛА — раздел физики, изучающий структуру и свойства твердых тел. Научные данные о микроструктуре твердых веществ и о физических и химических свойствах составляющих их атомов необходимы для разработки новых материалов и технических устройств. Физика… … Энциклопедия Кольера
Физика — 1) Ф. и ее задачи. 2) Методы Ф. 3) Гипотезы и теории. 4) Роль механики и математики в Ф. 5) Основные гипотезы Ф.; вещество и его строение. 6) Кинетическая теория вещества. 7) Действие на расстоянии. 8) Эфир. 9) Энергия. 10) Механические картины,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Физика твёрдого тела — Физика твёрдого тела раздел физики конденсированного состояния, задачей которого является описание физических свойств твёрдых тел с точки зрения их атомарного строения. Интенсивно развивалась в XX веке после открытия квантовой механики.… … Википедия
Физика — I. Предмет и структура физики Ф. – наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи и законы её движения. Поэтому понятия Ф. и сё законы лежат в основе всего… … Большая советская энциклопедия
Предметом изучения многих разделов физики является поведение физических тел, их свойства и особенности взаимодействия друг с другом.
Однако, прежде чем приступать к их изучению, необходимо определить, что такое физическое тело и какими характеристиками оно обладает.
В физике, говоря о физическом теле, подразумевают некий материальный объект, обладающий формой, определённой внешней границей, отделяющей его от других тел и внешней среды, а также соответствующим этой форме объемом и массой.
Помимо вышеперечисленных базовых характеристик, физическое тело может обладать рядом других свойств – плотностью, прозрачностью, твёрдостью/упругостью и т.
д. Все предметы, которые нас окружают, являются физическими телами. Чашка, письменный стол, мяч, книга, грузовик – все они с точки зрения физики являются физическими телами.
Физики различают простые тела, обладающие простой геометрической формой, и составные, которые представляют собой скреплённые между собой комбинации простых тел. Такое представление необходимо для упрощения расчётов, особенно в случаях, когда внутреннее состояние физического тела не играет большой роли в исследуемом процессе. К примеру, тело человека можно рассматривать как совокупность шаров и цилиндров.
Помимо формы, объёма и массы, физические тела характеризуются рядом других свойств, которые могут иметь важное значение для различных ситуаций. Так, одинаковые по объёму тела нередко различаются по массе и, соответственно, по плотности. Кроме того, в ряде случаев важны и другие характеристики тел – их твёрдость, хрупкость, упругость, магнитные свойства, прозрачность, теплопроводность, однородность, электропроводность и т.д. Во многом эти свойства зависят от материалов, из которых состоят физические тела.
Так, шары, изготовленные из резины, бетона, шерсти, стекла и стали, будут иметь совершенно разные наборы физических свойств. Однако их свойства будут иметь значение лишь в том случае, когда исследуются взаимодействия тел друг с другом – например, необходимо выяснить степень деформации тех или иных тел при столкновении.
В некоторых разделах физики тела рассматриваются не в совокупности присущих им свойств, а как некие абстракции, которым присваиваются идеальные характеристики. Так в механике все тела представлены как материальные точки, без учёта их массы и других физических свойств. Эта дисциплина изучает движение материальных точек без учёта их реальных размеров и массы, поскольку для решения ряда задач эти величины не важны. Если вы рассчитываете среднюю скорость поезда на определённом интервале пути, вам совершенно не нужно знать, сколько в поезде вагонов.
Нередко физики для выполнения каких-либо расчётов используют понятие абсолютно твёрдого тела. Оно никогда не подвергается деформации, его центр массы не смещается, что позволяет без лишнего усложнения моделировать ряд процессов. Для решения термодинамических задач удобно бывает использовать абсолютно чёрное тело – абстрактный предмет, поглощающий все излучения, падающие на его поверхность.
При этом само тело может излучать электромагнитные волны, если того требует поставленная задача. В случаях, когда форма физического тела не имеет значения, подразумевается, что оно имеет форму шара.
Физика как наука возникла из-за необходимости выявления законов поведения физических тел и механизмов образования природных явлений. Фактически, все изменения в нашей среде обитания, не связанные с деятельностью человека, являются природными явлениями. Большинство из них полезны людям, но встречаются и опасные, и даже катастрофические природные явления.
Людям необходимо исследовать свойства и поведение физических тел, которые принимают в них участие, чтобы научиться предсказывать неблагоприятные явления, предупреждать их либо уменьшать наносимый ими вред. Так, пагубное действие морских волн давно научились снижать путём строительства волноломов – бетонных выступов, заходящих в море на десятки метров и разбивающих единый фронт волны.
Разрушительный эффект землетрясений преодолевается строительством сейсмоустойчивых зданий особой конструкции. Чтобы уменьшить повреждения при контакте автомобиля с твердыми объектами, несущим конструкциям его кузова придаётся особая форма. Всё это стало возможным благодаря изучению характеристик физических тел.
Содержание:
Определение
В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и
источником гравитационного взаимодействия.
{2}}}}$$
Слишком сложно?
Формула массы тела не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=\rho V$$При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной $\rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 \cdot 2=17800$ (кг)
Ответ. $m=8900 \cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
| МЕХАНИКА. | ||||||||||||||||||||
Механика– наука об общих законах движения и взаимодействия тел. Механическим движением называется изменение положения тела в пространстве относительно других тел с течением времени. Основная задача механики – определить положение тел в пространстве в любой момент времени. Разделы механики: КИНЕМАТИКА – раздел механики, изучающий способы описания движений и связь между величинами, характеризующими эти движения. СТАТИКА – раздел механики, изучающий равновесие абсолютно твердых тел. ДИНАМИКА – раздел механики, изучающий взаимное влияние тел друг на друга и изменение характера движения этих тел в результате взаимодействий тел. ЗАКОНЫ СОХРАНЕНИЯ МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. | Примеры: Ученик идет в школу. Положение ученика изменяется относительно его дома (школы, деревьев и т.п.) с течением времени. Примеры других видов движения: биологическое – рост организма; социальное – революционное | |||||||||||||||||||
Материальная точка – физическая модель тела, размерами которого в данных условиях движения можно пренебречь. | Примеры: можно пренебречь размерами автомобиля при изучении его движения по сравнению с расстоянием от Санкт-Петербурга до Москвы. Размерами этого же автомобиля нельзя пренебречь, если мы изучаем движение жука по поверхности автомобиля. | |||||||||||||||||||
Поступательное движение – движение, при котором прямая, соединяющая произвольные точки данного тела, перемещается параллельно себе самой. При этом все точки абсолютно твердого тела имеют одинаковые скорости и ускорения. | Примеры: санки скатываются с горы поступательно. | |||||||||||||||||||
Система отсчета (СО) – тело отсчета, система координат, связанная с ним, прибор для отсчета времени. | Рис. СО | |||||||||||||||||||
Траектория – воображаемая линия, вдоль которой движется тело. Примеры: лыжня, кильватерный след. Уравнение траектории – уравнение, выражающее зависимость между координатами тела. Путь – длина траектории. Путь не может быть отрицательным! | ||||||||||||||||||||
Способы описания движения. | ||||||||||||||||||||
Табличный. Достоинства: нагляден, прост, удобен при изучении периодических движений (например, таблицы координат астрономических объектов). Недостатки: не позволяет определить положение тела в любой момент времени (промежуточные значения), не позволяет предсказать характер движения. |
| |||||||||||||||||||
Словесный. Достоинства: прост, не требует научных знаний. Недостатки: слишком не точен, не является научным, не позволяет решить задачу механики. | Для того, чтобы попасть из моего дома в школу надо выйти на улицу, повернуть направо, пройти через двор, свернуть налево… | |||||||||||||||||||
Аналитический (координатный) | , где | – перемещение и радиус-вектор соответственно. | ||||||||||||||||||
Уравнение движения – уравнение, выражающее зависимость радиус-вектора (вектора перемещения, координат) от времени. Достоинства: точен, позволяет однозначно решить основную задачу механики, обладает возможностью предсказать характер движения. Недостатки: требует специальной подготовки. | ||||||||||||||||||||
Графический. Достоинства: нагляден. Недостатки: неточен, нельзя предсказать характер движения в дальнейшем. | <img alt=”Графический” top”=”” data-cke-saved-src=”/public/img/formula/image045.jpg” src=”/public/img/formula/image045.jpg”> | |||||||||||||||||||
ВЕКТОР ПЕРЕМЕЩЕНИЯ | ||||||||||||||||||||
Перемещение – направленный отрезок прямой (вектор), соединяющий начальное положение тела с его последующим положением. Обозначения: , где – радиус-вектор. В СИ измеряется в метрах. | ||||||||||||||||||||
Обозначим: x, y, z – координаты тела в любой момент времени; x0, y0, z0 – начальные координаты тела. Проекции перемещения на оси координат (иначе – координаты радиус-вектора): | ||||||||||||||||||||
Тогда: – решение основной задачи механики. Вывод: для решения основной задачи механики необходимо знать перемещение тела (проекции перемещения на оси координат. Знаки проекций: если вектор сонаправлен с осью (координата конца вектора больше координаты начала) – проекция положительна; если вектор направлен против оси (координата конца вектора меньше координаты начала) – проекция отрицательна. | ||||||||||||||||||||
СЛОЖЕНИЕ ПЕРЕМЕЩЕНИЙ
| ||||||||||||||||||||
Физика, 10 класс
Урок 14. Статика. Равновесие абсолютно твёрдых тел
Перечень вопросов, рассматриваемых на уроке:
1.
Условия равновесия тела
2.Момент силы
3.Плечо силы
4. Центр тяжести
Глоссарий по теме
Статика – раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой
Абсолютно твердое тело – модельное понятие классической механики, обозначающее совокупность точек, расстояния между текущими положениями которых не изменяются.
Центр тяжести – центром тяжести тела называют точку, через которую при любом положении тела в пространстве проходит равнодействующая сил тяжести, действующих на все частицы тела.
Плечо силы – это длина перпендикуляра, опущенного от оси вращения на линию действия силы.
Момент силы – это физическая величина, равная произведению модуля силы на ее плечо.
Устойчивое равновесие – это равновесие, при котором тело, выведенное из состояния устойчивого равновесия, стремится вернуться в начальное положение.
Неустойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, будет еще больше отклоняться от положения равновесия.
Безразличное равновесие системы — равновесие, при котором после устранения причин, вызвавших малые отклонения, система остается в покое в этом отклоненном состоянии
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017.– С. 165 – 169.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. – М.: Дрофа, 2009.
Степанова Г.Н. Сборник задач по физике. 10-11 класс. – М.: Просвещение. 1999 г. С.48- 50.
Теоретический материал для самостоятельного изучения
Равновесие – это состояние покоя, т.е. если тело покоится относительно инерциальной системы отсчета, то говорят, что оно находится в равновесии. Вопросы равновесия интересуют строителей, альпинистов, артистов цирка и многих-многих других людей.
Любому человеку приходилось сталкиваться с проблемой сохранения равновесия. Почему одни тела, выведенные из состояния равновесия, падают, а другие – нет? Выясним, при каком условии тело будет находиться в состоянии равновесия.
Раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой. Статика является частным случаем динамики. В статике твердое тело рассматривается как абсолютно твердое, т.е. недеформируемое тело. Это означает, что деформация так мала, что её можно не учитывать.
Центр тяжести существует у любого тела. Эта точка может находиться и вне тела. Как же подвесить или подпереть тело, чтобы оно находилось в равновесии.
Подобную задачу в свое время решил Архимед. Им же были введены понятие плеча силы и момента силы.
Плечо силы — это длина перпендикуляра, опущенного от оси вращения на линию действия силы.
Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.
После своих исследований Архимед сформулировал условие равновесия рычага и вывел формулу:
Это правило является следствием 2-го закона Ньютона.
Первое условие равновесия
Для равновесия тела необходимо, чтобы сумма всех сил, приложенных к телу была равна нулю.
формула должна быть в векторном виде и стоять знак суммы
Второе условие равновесия
При равновесии твердого тела сумма моментов вcех внешних сил, действующих на него относительно любой оси, равна нулю.
Не менее важен случай, когда тело имеет площадь опоры. Тело, имеющее площадь опоры, находится в равновесии, когда вертикальная прямая, проходящая через центр тяжести тела, не выходит за пределы площади опоры этого тела. Известно, что в городе Пизе в Италии существует наклонная башня. Несмотря на то, что башня наклонена, она не опрокидывается, хотя ее часто называют падающей. Очевидно, что при том наклоне, которого башня достигла к настоящему времени, вертикаль, проведенная из центра тяжести башни, все еще проходит внутри ее площади опоры.
В практике большую роль играет не только выполнение условия равновесия тел, но и качественная характеристика равновесия, называемая устойчивостью.
Различают 3 вида равновесия: устойчивое, неустойчивое, безразличное.
Если при отклонении тела от положения равновесия, возникают силы или моменты сил, стремящиеся вернуть тело в положение равновесия, то такое равновесие называется устойчивым.
Неустойчивое равновесие — это противоположный случай. При отклонении тела от положения равновесия, возникают силы или моменты сил, которые стремятся увеличить это отклонение.
Наконец, если при малом отклонении от положения равновесия тело все равно остается в равновесии, то такое равновесие называется безразличным.
Чаще всего необходимо, чтобы равновесие было устойчивым. Когда равновесие нарушается, то сооружение становится опасным, если его размеры велики.
Примеры и разбор решения заданий
1. Чему равен момент силы тяжести груза массой 40 кг, подвешенного на кронштейне АВС, относительно оси, проходящей через точку В, если АВ=0,5 м и угол α=450
Решение:
Момент силы – это величина равная произведению модуля силы на её плечо.
Сначала найдём плечо силы, для этого нам надо опустить перпендикуляр из точки опоры на линию действия силы. Плечо силы тяжести равно расстоянию АС. Так как угол равен 45°, то мы видим, что АС=АВ
Модуль силы тяжести находим по формуле:
После подстановки числовых значений величин мы получим:
F=40×9,8 =400 Н, М= 400 ×0,5=200 Н м.
Ответ: М=200 Н м.
2. Приложив вертикальную силу F, груз массой М — 100 кг удерживают на месте с помощью рычага (см. рис.). Рычаг состоит из шарнира без трения и однородного массивного стержня длиной L=8 м. Расстояние от оси шарнира до точки подвеса груза равно b=2 м. Чему равен модуль силы F, если масса рычага равна 40 кг.
Решение:
По условию задачи рычаг находится в равновесии.
Напишем второе условие равновесия для рычага:
.
После подстановки числовых значений величин получим
F= (100×9,8 ×2 + 0,5×40×9,8×8)/8=450 Н
Ответ: 450 Н.
Изучение видов равновесия.
Рассмотреть виды равновесия.
Выявить их отличия друг от друга.
Показать практическое применение описанных эффектов.
Опытным путём рассчитать зависимость вероятности падения хлеба маслом вниз от соотношения толщин хлеба и масла.
В природе всё пребывает в равновесии, нет предметов, у которых не было бы центра тяжести и зачастую его сложно определить.
Основная часть
Самая главная наука во вселенной — это физика. На физике, как на фундаменте, стоят все прочие науки. Физика — многогранна и сегодня речь пойдёт о механическом равновесии и его видах.
4.1. Что такое равновесие
Что такое равновесие? Понятие равновесия — одно из самых универсальных в естественных науках.
Равновесие — это комплекс сил, которые действуя на одну систему, компенсируют друг друга и система не получает ускорение. А система— множество элементов, находящихся в отношениях и связях друг с другом, которое образует определённую целостность, единство.
4.2. Виды равновесия
Существует 3 вида равновесия: устойчивое, неустойчивое и безразличное.
Устойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, возвращается в прежнее положение.
Неустойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, будет еще больше отклоняться от положения равновесия.
Безразличное равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, не меняет своего положения (состояния).
1 опыт: устойчивое равновесие: шарик неподвижно лежит на дне сферического углубления. При небольшом смещении тела в любом направлении от первоначального положения равнодействующая сил, действующих на тело, становится отличной от нуля и направлена к положению равновесия. Шарик возвращается в исходную точку.
2 опыт: неустойчивое равновесие: шарик неподвижно лежит на вершине сферической поверхности. При небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия. Шарик не возвращается в исходную точку.
3 опыт: безразличное равновесие: шарик неподвижно лежит на плоской поверхности. При небольших смещениях тела из первоначального положения равнодействующая приложенных к телу сил остается равной нулю. Шарик после перемещения не меняет своё положение.
4.3. Применение принципов равновесия
Принципы устойчивого равновесия используются в строительстве зданий.
Устойчивое равновесие корабля обеспечивает балласт в трюме.
Понятие устойчивости широко применяется в самолётостроении.
Устойчивость и управляемость летательного аппарата — взаимосвязанные свойства динамики полета.
Управляемость — свойство самолёта отвечать соответствующими линейными и угловыми перемещениями в пространстве на команды управления.
Устойчивость — свойство самолёта восстанавливать без вмешательства пилота кинематические параметры невозмущенного движения и возвращаться к исходному режиму полета после прекращения действия возмущений.
Устойчивое равновесие пассажирского самолёта обеспечивает верхнее расположение крыльев относительно фюзеляжа.
Неустойчивое равновесие применяется в строительстве военных самолётов.
Для достижения сверх манёвренности нужно снизить устойчивость самолёта до нулевой или даже отрицательной — ввести его в состояние неустойчивого равновесия. Например, обеспечить взаимное расположение вектора тяги ниже центра масс. И нужно увеличить тягу двигателей настолько, чтобы она превышала вес самолёта. В таком случае говорят, что удельная тяга больше единицы.
При этом управлять им вручную, когда органы управления связаны напрямую с рулями, становится невозможно. Управление берёт на себя автоматика, а лётчик, грубо говоря, только приказывает ей, что делать. Такой принцип применяется в системах управления истребителей 5-го поколения.
А все самолёты на земле находятся в состоянии безразличного равновесия.
Физику многие боятся, как огня, считая трудной.
Однако понимание зависит от способа изложения. Поехали?…
5.1. Описание системы падающего бутерброда
Распространено убеждение, что бутерброд практически всегда падает маслом вниз. Это связано с равновесием.
Лучший способ исследования в смысле объективности — поставить эксперимент. Нужно ронять на пол бутерброды до тех пор, пока вы не придете к определенному выводу. Но это негигиенично, неэкономично и неэтично. Верный результат можно получить и с помощью мысленного эксперимента. Правда, при условии, что вы умеете доводить мысленный эксперимент до конца.
Для упрощения представим себе, что бутерброд, стоит на ребре. Предположим, что стол резко убрали. Как поведёт себя бутерброд?
Принимаем, что в самом бутерброде при его падении не возникает никаких сил, которые давали бы предпочтение одной из двух ситуаций или они бесконечно малы: трение воздуха о масло и о хлеб одинаково, ветра нет.
Ну а теперь перейдём к расчётам.
5.2. Определение плотности хлеба и масла.
Для начала вычислим плотность масла и хлеба.
Размеры: 6×4,5×4см
Объём: 108 см3
Вес: 127 г
Плотность: 127 г/108 см3
ρ = 1,18 г/см3
Размеры: 7×9,5×10,5см
Объём: 698,3 см3
Вес: 318 г
Плотность: 318г / 698,3 см3
ρ = 0, 45 г/см3
5.
3. Расчет соотношения толщины хлеба и масла
Нарисуем схему бутерброда, стоящего на ребре.
Принимаем следующие обозначения:
М — толщина масла
Хл — толщина хлеба
М/2 — половина масла
М1 — расстояние от центра масс масла до центра масс бутерброда
Рм — сила, действующая на масло
Р — сила, действующая на бутерброд
Хл/2 — половина хлеба
Хл1 — расстояние от центра масс хлеба до центра масс бутерброда
Рхл — сила, действующая на хлеб
ЦМ — центр масс
Ц — центр бутерброда
Вычисляем силы, действующие на хлеб и масло:
Рм = mм * g = ρм * Vм = ρм * Sбут * М
Рхл = ρхл * Sбут * Хл
Вычисляем силы, действующие на бутерброд:
М1 * Рм = Хл1 * Рхл
Хл1 + М1 = (Хл + М) / 2 =>
Хл1 * (ρхл * Хл + ρм * М)/ρм * М = (Хл + М)/2
Вычисляем расположение центра масс:
Хл1 = (Хл + М) * ρхл * М / 2*(ρхл * Хл + ρм * М)
Хл1 =
Цм = Хл1 + Хл/2
Цм = ((Хл + М) * ρхл * М)/ (2*(ρхл * Хл + ρм * М)) + Хл/2
Вычисляем расположение центра бутерброда:
Ц = (М+Хл)/2
Сравниваем расположение центра масс и центра бутерброда.
Условия падения бутерброда маслом вниз:
Цм>Ц
Данные и формулы заносим в таблицу Exel. Полученные результаты расчётов приведены в таблице 1.
Таблица 1
|
Толщина хлеба Хл |
Толщина хлеба Хл |
Толщина хлеба Хл |
||||||
|
1 |
см |
1,5 |
см |
2 |
см |
|||
|
Толщина масла |
Центр бутерброда |
Центр масс |
Толщина масла |
Центр бутерброда |
Центр масс |
Толщина масла |
Центр бутерброда |
Центр масс |
|
М |
Ц, |
Цм |
М |
Ц, |
Цм |
М |
Ц, |
Цм |
|
см |
см |
см |
см |
см |
см |
см |
см |
см |
|
0,1 |
0,55 |
0,61 |
0,1 |
0,8 |
0,87 |
0,1 |
1,05 |
1,12 |
|
0,2 |
0,6 |
0,71 |
0,2 |
0,85 |
0,97 |
0,2 |
1,1 |
1,23 |
|
0,3 |
0,65 |
0,79 |
0,3 |
0,9 |
1,06 |
0,3 |
1,15 |
1,32 |
|
0,4 |
0,7 |
0,86 |
0,4 |
0,95 |
1,14 |
0,4 |
1,2 |
1,41 |
|
0,5 |
0,75 |
0,93 |
0,5 |
1 |
1,22 |
0,5 |
1,25 |
1,49 |
|
0,6 |
0,8 |
0,99 |
0,6 |
1,05 |
1,29 |
0,6 |
1,3 |
1,57 |
|
0,7 |
0,85 |
1,05 |
0,7 |
1,1 |
1,36 |
0,7 |
1,35 |
1,65 |
|
0,8 |
0,9 |
1,11 |
0,8 |
1,15 |
1,42 |
0,8 |
1,4 |
1,72 |
|
0,9 |
0,95 |
1,17 |
0,9 |
1,2 |
1,48 |
0,9 |
1,45 |
1,78 |
|
1 |
1 |
1,22 |
1 |
1,25 |
1,55 |
1 |
1,5 |
1,85 |
|
1,1 |
1,05 |
1,28 |
1,1 |
1,3 |
1,61 |
1,1 |
1,55 |
1,92 |
|
1,2 |
1,1 |
1,33 |
1,2 |
1,35 |
1,66 |
1,2 |
1,6 |
1,98 |
|
1,3 |
1,15 |
1,39 |
1,3 |
1,4 |
1,72 |
1,3 |
1,65 |
2,04 |
|
1,4 |
1,2 |
1,44 |
1,4 |
1,45 |
1,78 |
1,4 |
1,7 |
2,10 |
|
1,5 |
1,25 |
1,50 |
1,5 |
1,5 |
1,84 |
1,5 |
1,75 |
2,16 |
Итак, делаем следующие выводы:
Заключительная часть
Мы живём в удивительном мире, нам хочется понять то, что мы видим вокруг, ищем ответы на вопросы: почему деревья качаются, почему в дырках ничего нет, почему апельсины круглые, почему всё происходит так, а не иначе? Мы попытались приблизиться к пониманию того многообразия сил, которые действуют на тела, в том числе и на нас даже в состоянии покоя. Отличаясь по масштабам как от атомов, так и от звёзд мы раздвигаем горизонты исследований, чтобы охватить как очень маленькие, так и очень большие объекты.
Хочется закончить словами Стивена Хокинга: «И, если будут найдены ответы на все вопросы, это будет полным триумфом человеческого разума, ибо тогда нам станет понятен замысел Бога».
Литература:
Механика , наука, изучающая движение тел под действием сил, включая особый случай, когда тело остается в покое.
В первую очередь проблема движения – это силы, которые тела действуют друг на друга. Это приводит к изучению таких тем, как гравитация, электричество и магнетизм, в зависимости от природы задействованных сил. Учитывая силы, можно искать способ, которым тела движутся под действием сил; это предмет собственно механики.
Британская викторина
Викторина “Все о физике”
Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.
Исторически механика была одной из первых возникших точных наук.Его внутренняя красота как математической дисциплины и ранний замечательный успех в количественном учете движений Луны, Земли и других планетных тел оказали огромное влияние на философскую мысль и послужили толчком для систематического развития науки.
Механику можно разделить на три части: статика, которая имеет дело с силами, действующими на покоящееся тело и в нем; кинематика, описывающая возможные движения тела или системы тел; и кинетика, которая пытается объяснить или предсказать движение, которое произойдет в данной ситуации.В качестве альтернативы механику можно разделить по типу изучаемой системы. Простейшей механической системой является частица, определяемая как настолько маленькое тело, что его форма и внутренняя структура не имеют значения в данной задаче. Более сложным является движение системы из двух или более частиц, которые действуют друг на друга и, возможно, испытывают силы, действующие со стороны тел вне системы.
Принципы механики были применены к трем общим областям явлений.Движение таких небесных тел, как звезды, планеты и спутники, можно предсказать с большой точностью за тысячи лет до того, как они произойдут.
(Теория относительности предсказывает некоторые отклонения от движения в соответствии с классической или ньютоновской механикой; однако они настолько малы, что их можно наблюдать только с помощью очень точных методов, за исключением задач, затрагивающих всю или большую часть обнаруживаемой Вселенной. ) Как вторая область, обычные объекты на Земле вплоть до микроскопических размеров (движущиеся со скоростью намного ниже скорости света) правильно описываются классической механикой без значительных исправлений.Инженер, проектирующий мосты или самолеты, может с уверенностью использовать ньютоновские законы классической механики, даже если силы могут быть очень сложными, а вычислениям не хватает прекрасной простоты небесной механики. Третья область явлений включает поведение вещества и электромагнитного излучения в атомном и субатомном масштабах. Хотя вначале были достигнуты ограниченные успехи в описании поведения атомов в терминах классической механики, эти явления должным образом рассматриваются в квантовой механике.
Классическая механика занимается движением тел под действием сил или равновесием тел, когда все силы уравновешены. Этот предмет можно рассматривать как разработку и применение основных постулатов, впервые сформулированных Исааком Ньютоном в его книге Philosophiae Naturalis Principia Mathematica (1687), широко известной как Principia . Эти постулаты, называемые законами движения Ньютона, изложены ниже.Их можно использовать для предсказания с большой точностью самых разных явлений, от движения отдельных частиц до взаимодействий очень сложных систем. В этой статье обсуждается множество этих приложений.
В рамках современной физики классическую механику можно понять как приближение, вытекающее из более глубоких законов квантовой механики и теории относительности. Однако такой взгляд на место объекта сильно недооценивает его важность в формировании контекста, языка и интуиции современной науки и ученых.Наш современный взгляд на мир и место человека в нем прочно укоренен в классической механике. Более того, многие идеи и результаты классической механики выживают и играют важную роль в новой физике.
Центральными понятиями классической механики являются сила, масса и движение. Ни сила, ни масса не очень четко определены Ньютоном, и оба они были предметом многих философских спекуляций со времен Ньютона. Оба они наиболее известны своими эффектами. Масса – это мера склонности тела сопротивляться изменениям в состоянии движения.С другой стороны, силы ускоряют тела, то есть они изменяют состояние движения тел, к которым они приложены. Взаимодействие этих эффектов – основная тема классической механики.
Хотя законы Ньютона фокусируют внимание на силе и массе, три другие величины приобретают особое значение, потому что их общее количество никогда не меняется. Эти три величины – энергия, (линейный) импульс и угловой момент. Любой из них может быть перемещен из одного тела или системы тел в другое.Кроме того, энергия может менять форму, будучи связанной с единственной системой, проявляясь как кинетическая энергия, энергия движения; потенциальная энергия, энергия позиции; тепло или внутренняя энергия, связанная со случайными движениями атомов или молекул, составляющих любое реальное тело; или любая комбинация из трех. Тем не менее полная энергия, импульс и угловой момент во Вселенной никогда не меняются. Этот факт выражается в физике, говоря, что энергия, импульс и угловой момент сохраняются.Эти три закона сохранения вытекают из законов Ньютона, но сам Ньютон их не выражал. Их нужно было обнаружить позже.
Примечательно то, что, хотя законы Ньютона больше не считаются фундаментальными и даже не совсем правильными, три закона сохранения, вытекающие из законов Ньютона – сохранение энергии, импульса и углового момента – остаются в точности верными даже в квантовая механика и теория относительности. Фактически, в современной физике сила больше не является центральным понятием, а масса – лишь одним из множества атрибутов материи.Однако энергия, импульс и угловой момент по-прежнему прочно занимают центральное место. Сохраняющаяся важность этих идей, унаследованных от классической механики, может помочь объяснить, почему этот предмет сохраняет такое большое значение в современной науке.
Equilibrium , в физике, состояние системы, когда ни ее состояние движения, ни ее внутреннее энергетическое состояние не имеют тенденции меняться со временем. Говорят, что простое механическое тело находится в равновесии, если оно не испытывает ни линейного, ни углового ускорения; если его не потревожит внешняя сила, он будет оставаться в этом состоянии бесконечно.Для отдельной частицы равновесие возникает, если векторная сумма всех сил, действующих на частицу, равна нулю. Твердое тело (по определению отличающееся от частицы свойством растяжения) считается находящимся в равновесии, если в дополнение к состояниям, перечисленным для частицы выше, векторная сумма всех крутящих моментов, действующих на тело, равна нулю, так что его состояние вращательного движения остается постоянным. Равновесие считается устойчивым, если небольшие, вызванные извне смещения из этого состояния создают силы, которые стремятся противодействовать смещению и возвращать тело или частицу в состояние равновесия.Примеры включают груз, подвешенный на пружине, или кирпич, лежащий на ровной поверхности. Равновесие неустойчиво, если малейшее отклонение вызывает силы, которые увеличивают смещение. Примером может служить шарикоподшипник, балансирующий на краю лезвия бритвы.
В термодинамике понятие равновесия расширяется, чтобы включить возможные изменения внутреннего состояния системы, которое характеризуется ее температурой, давлением, плотностью и любыми другими величинами, необходимыми для полного определения ее состояния.При строгом термодинамическом равновесии температура системы однородна (в противном случае тепло текло бы), и любые градиенты в функциях состояния, таких как давление или плотность, уравновешиваются внешними силами, так что они остаются постоянными. Например, равновесное давление внизу столба воздуха выше, чем вверху из-за силы тяжести, а градиенты плотности в центрифуге уравновешиваются центробежной силой. Также полезно рассматривать квазиравновесные процессы, где, например, допускаются температурные градиенты, если скорость теплового потока слишком мала, чтобы быть значимой (адиабатические процессы), но в противном случае система находится в локальном термодинамическом равновесии.Например, адиабатическое расширение восходящего столба воздуха объясняет уменьшение температуры атмосферы с высотой.
Одна из замечательных особенностей митапов – это их способность генерировать странные обмены идеями. В конце прошлого года я продемонстрировал ThreeBody – еще одно из моих необычных приложений физики с ограниченной привлекательностью. Я упоминал, что было бы интересно посмотреть, что происходит с проблемой трех тел в сферическом пространстве – поскольку это решит проблему «выброса в бесконечность», удалив бесконечность.Это привело к обсуждению топологии игр, таких как астероиды, где верх / низ и левый / правый переплетены. Это отображение создает пространство, которое является топологическим тором. Это была искра, которая мне нужна, чтобы более тщательно обдумать, на что будет похоже движение на реальном торе.
Мне не нужен особый предлог, чтобы думать о странном физическом сценарии. Мое прошлое включает время, проведенное в перерыве в работе и на докторскую степень по искривленным пространствам-времени. Одна из проблем, возникающих в таких исследованиях как способ оттачивания навыков, – это изучение движения на искривленных 2D-поверхностях.Это отличное место, чтобы научиться использовать математический аппарат и достаточно интуитивно понятный, чтобы ответы можно было визуализировать.
Это заставило меня задуматься, насколько отличался бы космический шутер, если бы физика тора была сделана «технически правильной» ( лучший вид ). Результатом стала игра «Геодезические астероиды», которая скоро будет выпущена, в которой есть двойное представление трехмерного движения и двухмерного движения с траекториями объектов, движущихся «технически правильным образом».
Рисунок 1: Координаты тора
Сначала нам нужно математическое описание тора.Это двухмерная поверхность, поэтому для описания точки нужны только две координаты. Если мы подумаем о типичном представлении бублика, сидящем на плоскости x, y, то это угол вокруг оси z (скажем, от линии x = 0) и угол вокруг поперечного сечения тора в данном случае. Радиус центра тора равен, а радиус поперечного сечения равен.
В математике для тора все может быть описано в терминах этих координат, включая уравнения движения, которые определяют, как объект движется, когда на него нет силы.Мы привыкли думать о торе как о трехмерном объекте, но какая именно трехмерная форма получается отчасти из-за выбора, сделанного при встраивании поверхности в трехмерное пространство. На самом деле нет причин, по которым мы должны это делать, но это может помочь нашей интуиции. [Отступление: это интересный математический вопрос о том, как именно размер может потребоваться для встраивания N-мерной поверхности, мы привыкли к N + 1, например, сферы и тории, но это не общее правило!].
В нашем случае мы выбираем обычное вложение:
$$ x = (a + b \ cos {\ chi}) \ cos {\ theta} $$
$$ y = (a + b \ cos {\ chi}) \ sin {\ theta} $$
$$ z = b \ sin {\ chi} $$
Это позволяет нам отобразить координаты мира x, y, z, которые игра будет использовать, и сохранить нашу интуитивную картину тора.
А как насчет 2D-карты этого тора? Здесь я решил использовать просто как чистые 2D-координаты, то есть как если бы они были отображениями «x и y». Я делаю небольшой поворот, который объясню через минуту.
Уравнение вложения обеспечивает положение в мировом пространстве для отображения событий на торе. Какие уравнения следует использовать для расчета движения на торе? Движение происходит на торе , поэтому описание дано в терминах. Здесь есть отход от обычных уравнений, управляющих играми.В плоском трехмерном игровом мире x, y и z независимы, и нам не нужно беспокоиться о том, где в пространстве мы находимся. в начале координат такая же, как и в любой другой точке. На криволинейных поверхностях дела обстоят иначе. Чтобы прояснить это, давайте рассмотрим более простую двумерную поверхность, сферу, с долготой и широтой.
Как вы знаете из карт полетов самолетов, линии между точками представляют собой кривые на карте. Это потому, что свободный от силы (или геодезический) путь, соединяющий две точки, представляет собой большую окружность.Это означает, что если вы находитесь в Нью-Йорке и направляетесь прямо на запад, геодезический путь должен иметь диаметр окружности и вести вас в южное полушарие, пока вы не окажетесь в точке противоположности, прямо напротив Нью-Йорка, через центр Земли. [Забавный факт: очень немногие места на суше имеют противоположную точку на суше]. Вы начали только со скоростью в направлении, но в конечном итоге выбрали траекторию, которая также изменилась. Это означает, что уравнения движения связаны. Уравнение эволюции зависит от скорости в направлении.2} {(a + b \ cos {\ chi})} $$
Хорошая новость в том, что координаты на торе хорошо себя ведут. Выражение конечно. (Если вы посмотрите на уравнения для сферы, то увидите, что некоторые значения могут быть разделены на ноль. Никогда не отличная идея. Это не фундаментальная часть движения на сфере, нет специального места, где ускорение уходит в бесконечность. Это просто плохой выбор координат, и в некоторых случаях нам нужно выбрать другое начало координат. Обычно приходится покрывать поверхность несколькими пятнами координат.Для тора нам повезло, что он не нужен.)
Уравнения для искривленной поверхности взяты из раздела математики, известного как дифференциальная геометрия. «Дифференциальный», поскольку он изучает поведение поверхностей, которые достаточно гладкие, чтобы вы могли выполнять вычисления, то есть без резких ступенек или выступов. Одна из новых идей, которая входит в дифференциальную геометрию, заключается в том, что, хотя вы можете выполнять вычисления в каждой точке, вы не можете напрямую сравнивать результаты этих вычислений в разных точках.Это потому, что каждая точка имеет свою собственную касательную плоскость (в более общем смысле касательное пространство). Когда объект скользит по 2D-поверхности, локальные координаты объекта изменяются относительно координат поверхности. Возвращаясь к нашему примеру со сферой, если вы изначально направлялись на запад от Нью-Йорка, когда ваш большой круг пересекает экватор, вы больше не обращены на запад, НО вы не повернули, вы просто следовали своему геодезическому пути. Что именно представляет собой геодезический путь и как он поворачивается по мере вашего движения, можно рассчитать для поверхности.
Я не ставлю перед собой цель превратить этот пост в трактат по дифференциальной геометрии. Это очень интересный предмет, на котором разворачивается Общая теория относительности Эйнштейна. Все вводные тексты по GR начинаются с некоторой подготовки по дифференциальной геометрии, и я считаю, что их подход больше соответствует моим интересам, чем то, как книги по математике подходят к этому предмету. Тем, кто заинтересован в хорошем введении в геодезические тора и в основы дифференциальной геометрии, я рекомендую статью Янцена.Моя любимая вводная книга по GR – «Первый курс общей теории относительности» Шутца
.Космическую игру на торе можно показать в 3D, но также интересно сыграть в игру на 2D-представлении поверхности. Здесь странные траектории объектов делают очевидным влияние изогнутой поверхности. Есть некоторые компромиссы в математической чистоте, на которые я пошел, чтобы фактически закончить игру. Основная проблема заключается в том, что размер объектов в 2D и 3D виде не может быть полностью согласован (подробнее ниже).
На истинной математической поверхности расстояние, пройденное вами при обходе внешнего диаметра, отличается от внутреннего диаметра. На 2D-карте это означает, что верхний край карты не должен быть таким же широким, как середина. Поэтому наш выбор 2D-карты уязвим для эффекта, аналогичного тому, который происходит в проекции Земли Меркатора (Гренландия показана слишком большой). Я выбрал простое масштабирование в зависимости от «широты». Чтобы сохранить эту точность, необходимо изменять размер объектов по горизонтали по мере их изменения широты.Я включил это в игру как вариант, но результат выглядит немного странно. В обычном режиме игры этот режим отключен – в результате объекты на экране не совсем правильного размера. Правильный размер используется для обнаружения попаданий пуль, и в некоторых случаях очевидное попадание на карту не является «настоящим» попаданием.
Истинное масштабирование приводит к некоторым странным путям на карте. Если объект движется быстро, сжатие из-за масштабного коэффициента может превышать движение по направлению к краю, создавая впечатление, будто объект немного отступает, прежде чем продолжить.
Geodesic Asteroids доступен для Blackberry, iOS и Android. Было очень весело думать и использовать геодезическую математику, которую я выучил много лет назад. Кроме того, я впервые написал игру в стиле «видеоигры». Надеюсь, вам будет интересно.
[social4i size = “large” align = “float-right”]
В блоке законов Ньютона введена тема задач двух тел. Была обсуждена пара стратегий решения проблем, которые были применены для решения трех примеров проблем.Такие проблемы с двумя телами обычно включают решение для ускорения объектов и силы, действующей между объектами. Одна из стратегий решения задач двух тел включает использование системного анализа для определения ускорения в сочетании с анализом отдельного объекта для определения силы, передаваемой между объектами. Вторая стратегия заключалась в использовании анализа двух отдельных объектов с целью разработки системы из двух уравнений для решения двух неизвестных величин.При необходимости найдите время, чтобы просмотреть страницу о решении задач двух тел. Эта страница будет основываться на уроках, извлеченных ранее в разделе «Законы Ньютона».
В этом уроке мы проанализируем задачи о двух телах, в которых объекты движутся в разных направлениях. В этих задачах два объекта связаны цепочкой, которая передает силу одного объекта другому. Струна наматывается на шкив, который изменяет направление приложения силы без изменения величины.В качестве иллюстрации того, как работает шкив, рассмотрим схему справа. Объект A связан с объектом B строкой. Веревка наматывается на шкив в конце стола. Объект A подвешен в воздухе, а объект B лежит на столе. В этой ситуации объект А упадет вниз под действием силы тяжести, потянув вниз один конец струны, к которой он подсоединен. Согласно закону действия-противодействия Ньютона, этот нижний конец струны будет тянуть вверх на объект А.Противоположный конец нити соединен с объектом B. Этот конец нити тянет вправо за объект B. Таким образом, нить, соединяющая два объекта, тянет оба объекта с одинаковой силой, но в разных направлениях. Трос тянет вверх на объект A и вправо на объект B. Шкив изменил направление приложения силы.
Проблемы, связанные с двумя объектами, соединительными цепями и шкивами, характеризуются объектами, которые движутся (или даже ускоряются) в разных направлениях.Они движутся или ускоряются с одинаковой скоростью, но в разных направлениях. Таким образом, при решении таких задач становится важным выбрать другую систему отсчета и систему осей для каждого объекта. Следует обратить внимание на такой выбор системы осей, чтобы оба объекта ускорялись вдоль оси в положительном направлении. При правильном определении осей для каждого отдельного объекта можно построить диаграмму свободного тела. Затем к каждой диаграмме можно применить законы Ньютона, чтобы получить систему из двух уравнений для решения двух неизвестных.Этот процесс решения проблем будет продемонстрирован на трех различных примерах задач.
Пример задачи 1Масса 200,0 грамма (m 1 ) и масса 50,0 грамма (m 2 ) соединены веревкой. Струна натянута на шкив. Определите ускорение масс и натяжение струны.
Как это часто бывает, в этом примере проблема запрашивает информацию о двух неизвестных – ускорении объектов и силе, действующей между объектами.В такой ситуации, как эта, когда два объекта подвешены на шкиве, более массивный объект будет ускоряться вниз, а наименее массивный объект будет ускоряться вверх. Величина ускорения будет одинаковой для каждого объекта. Система координат, выбранная для m 1 , имеет положительную ось y, направленную вниз; система координат, выбранная для m 2 , имеет положительную ось y, направленную вверх. При таком выборе осей направление ускорения будет положительным для каждого объекта.Диаграммы свободного тела для каждой индивидуальной массы показаны ниже. Каждый объект испытывает нисходящую силу тяжести, которая рассчитывается как 1 • g и 2 • g соответственно. Каждый объект также испытывает восходящую силу натяжения, которая притягивает два объекта друг к другу.
Уравнение второго закона Ньютона (F net = m • a) можно применить к обеим диаграммам, чтобы написать два уравнения для двух неизвестных. Нетто F будет выражено как сила в направлении ускорения за вычетом силы, которая ему противодействует.Таким образом, для массы 200,0 грамм F net записывается как 1,960 N – F десятки . Для массы 50,0 грамм F net записывается как F десятки – 0,490 Н. Уравнения 1 и 2 являются результатом применения уравнения второго закона Ньютона к массам 200,0 и 50,0 граммов. (Обратите внимание, что значения массы преобразуются в стандартные килограммы перед использованием в уравнениях. Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)
1.960 – F десятки = 0,2000 • a
F десятки – 0,490 = 0,0500 • a
С этого момента несколько шагов по алгебре приведут к ответам на проблему. Уравнение 2 можно переформулировать, чтобы получить выражение для F десятков , записанное в терминах ускорения.
F десятки = 0,0500 • a + 0,490
Это выражение для F tens теперь можно подставить в уравнение 1, чтобы преобразовать его в уравнение с одним неизвестным.Это уравнение и последующие шаги алгебры, приводящие к значению ускорения, показаны ниже.
1,96 – (0,0500 • a + 0,490) = 0,2000 • a
1,96 – 0,0500 • а – 0,490 = 0,2000 • а
1,47 = 0,2500 •
a = 1,47 / 0,2500 = 5,88 м / с 2
Теперь, когда ускорение было найдено из уравнения 1, его значение можно подставить в уравнение 3, чтобы определить натяжение.
F десятков = 0.0500 • (5,88) + 0,490
F десятков = 0,784 N
Проанализированную здесь систему шкивов иногда называют машиной Атвуда. Подход к решению проблем – это стандартный подход, который будет использоваться на этой странице для решения двух неизвестных. Он будет повторен в примере проблемы 2, чтобы решить то, что обычно называют модифицированной машинной проблемой Этвуда.
Рассмотрим ситуацию с двумя телами справа.20,0-граммовый подвесной груз (m 2 ) прикреплен к 250-граммовому воздушному грейдеру (m 1 ). Определите ускорение системы и натяжение струны.
Как и в примере проблемы 1, эта система должна быть сначала проанализирована концептуально, чтобы определить направление ускорения двух объектов. Это позволит назначить оси координат для каждого объекта. Поскольку ничто не толкает m 1 влево, мы могли бы предположить, что он будет ускоряться вправо из-за натяжения струны.Висящая масса (m 2 ) будет явно ускоряться вниз под действием силы тяжести. Таким образом, система координат выбрана для m 2 имеет положительную ось y, направленную вниз; система координат, выбранная для m 1 , имеет положительную ось x, направленную вправо. При таком выборе осей направление ускорения будет положительным для каждого объекта.
Диаграмма свободного тела для каждой отдельной массы показана ниже. Каждый объект испытывает нисходящую силу тяжести (F grav ), рассчитываемую как m 1 • g и m 2 • g соответственно.Планер (m 1 ) испытывает восходящую опорную силу (воздух толкает его вверх), чтобы уравновесить силу тяжести. Планер также испытывает горизонтальную силу – силу натяжения (F десятки ) вправо. Висящая масса (m 2 ) испытывает восходящую силу натяжения (F десятки ), которая оказывает некоторое сопротивление нисходящей силе тяжести.
Уравнение второго закона Ньютона (F net = m • a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных.F net будет выражаться как сила в направлении ускорения за вычетом любой силы, которая ему противодействует. Для параплана массой 250,0 грамм (0,250 кг) F net – это просто неуравновешенная сила натяжения (F десятки ). Для подвешенной массы 20,0 г (0,020 кг) F net записывается как 0,196 N – F десятки . Уравнения 4 и 5 являются результатом применения уравнения второго закона Ньютона к 250,0-граммовому планеру и 20,0-граммовой висящей массе. (Обратите внимание, что значения массы преобразуются в стандартные килограммы перед использованием в уравнениях.Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)
F десятки = 0,2500 • a
0,196 – F десятки = 0,0200 • a
С этого момента несколько шагов по алгебре приведут к ответам на проблему. Уравнение 4 выражает значение F десятков в единицах ускорения. Это выражение для F tens можно подставить в уравнение 5, чтобы преобразовать его в уравнение с одним неизвестным.Это уравнение и последующие шаги алгебры, приводящие к значению ускорения, показаны ниже.
0,196 – 0,2500 • а = 0,0200 • а
0,196 = 0,2700 •
a = 0,196 / 0,2700 = 0,72593 м / с 2
а = ~ 0,726 м / с 2
Теперь, когда ускорение было найдено из уравнения 5, его значение можно подставить в уравнение 4, чтобы определить натяжение.
F десятков = 0,2500 • (0.72593) = 0,18148
F десятков = ~ 0,181 Н
Система шкивов, проанализированная в примере задачи 2, иногда называется модифицированной машиной Атвуда. Анализ немного сложнее, чем машина Атвуда в примере задачи 1. Последний пример задачи будет представлять собой случай модифицированной машины Атвуда с наклонной поверхностью, как показано ниже. Подход к решению проблем будет таким же.
Рассмотрим ситуацию с двумя телами справа.Ящик 2,50×10 3 кг (m 1 ) стоит на наклонной плоскости и соединен кабелем с массой 4,00×10 3 кг (m 2 ). Эта вторая масса (m 2 ) подвешена на шкиве. Угол наклона 30,0 °, поверхность не имеет трения. Определите ускорение системы и натяжение троса.
Как и предыдущая задача, первая задача включает анализ ситуации, чтобы определить, в каком направлении объекты будут ускоряться.Такой анализ позволит присвоить каждому объекту систему координатных осей. В этом случае висящая масса (m 2 ) могла ускоряться вверх или вниз. Направление его ускорения зависит от сравнения его веса (силы тяжести) с противоположной силой, действующей на другую массу (m 1 ). Масса на наклонной плоскости сталкивается с тремя силами – силой тяжести, нормальной силой и силой натяжения. Сила тяжести направлена вниз (как обычно) и рассчитывается как m 1 • g.Нормальная сила направлена перпендикулярно поверхности (как обычно). Сила натяжения направлена вверх и вправо – параллельно наклонной плоскости и в той же ориентации, что и струна, обеспечивающая эту силу. Как обсуждалось на предыдущей странице, объекты, размещенные на наклонных плоскостях, анализируются путем разделения силы тяжести на две составляющие. Один компонент направлен параллельно плоскости (и вниз под этим углом), а другой компонент направлен перпендикулярно плоскости (и вверх под этим углом).Это параллельный компонент силы тяжести, который пытается увести m 1 вниз по наклонной плоскости. Как упоминалось ранее, этот компонент может быть вычислен путем умножения веса объекта (m 1 • g) на синус угла наклона (30 °). Значение для F parallel равно
. F параллельно = м 1 • g • синус (θ) = (2500 кг) • (9,8 Н / кг) • синус (30 °)
F параллельно = 12250 Н
Этот параллельный компонент силы тяжести пытается тянуть m 1 вниз по наклонной плоскости.Поскольку m 1 прикреплен тросом к m 2 , подвесная масса будет тянуться вместе с ним. Однако есть противоположное действие силы тяжести, тянущее m 2 вниз; это противоположное действие, если оно будет доминирующим, перетащит объект m 1 вверх по наклонной плоскости. Сила тяжести на м 2 составляет
м.F grav-2 = m 2 • g = (4000 кг) • (9,8 Н / кг) = 39200 Н
Эта сила тяжести на m 2 является доминирующей силой.Таким образом, m 1 будет ускоряться вверх по наклонной плоскости, а m 2 будет ускоряться вниз. Оси координат назначаются соответственно так, чтобы каждый объект имел положительное ускорение.
На схемах ниже показаны эти оси координат и силы, действующие на два объекта. Три силы на m 1 уже обсуждались. На схеме показаны два компонента F grav . Как упоминалось на предыдущей странице, перпендикулярная составляющая силы тяжести рассчитывается как
. F перпендикуляр = m 1 • g • cosθ = (2500 кг) • (9.8 Н / кг) • cos (30 °)
F перпендикуляр = 21218 Н
Нормальная сила (F норма ), действующая на m 1 , уравновешивает F перпендикуляр , так что нет ускорения, перпендикулярного наклонной плоскости. Значение F norm также равно 21218 Н. Висящая масса (m 2 ) испытывает только две силы – силу тяжести, направленную вниз, и силу натяжения вверх.
Теперь уравнение второго закона Ньютона (F net = m • a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных.Нетто F выражается как сила в направлении ускорения за вычетом любой силы, которая ему противодействует. Для груза массой 2500 кг на уклоне (м 1 ) F net – это просто сила натяжения (F десятки ) за вычетом параллельной составляющей силы тяжести. Для подвешенной массы 4000 кг (м 2 ) F net – это сила тяжести (39200 Н) за вычетом силы натяжения (F десятки ). Уравнения 6 и 7 являются результатом применения уравнения второго закона Ньютона к m 1 и m 2 .(Обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)
F десятков – 12250 = 2500 • a
39200 – F десятки = 4000 • a
С этого момента несколько шагов по алгебре приведут к ответам на проблему. Уравнение 6 можно изменить, чтобы получить выражение для F десятков , выраженное в единицах ускорения.
F десятки = 2500 • a + 12250
Это выражение для F tens может быть подставлено в уравнение 7, чтобы преобразовать его в уравнение с одним неизвестным.Это уравнение и последующие шаги алгебры, приводящие к значению ускорения, показаны ниже.
39200 – (2500 • a + 12250) = 4000 • a
39200 – 2500 • a – 12250 = 4000 • a
26950 = 6500 •
a = 26950/6500 = 4,1462 м / с 2
а = ~ 4,15 м / с 2
Теперь, когда ускорение было найдено из уравнения 7, его значение можно подставить в уравнение 8, чтобы определить силу натяжения (F десятки ).
F десятков = 2500 • a + 12250 = 2500 • (4,1462) + 12250 = 22615 N
F десятков = ~ 2,26 x 10 4 N
Задачи с двумя телами, подобные этим трем примерам задач, могут быть довольно сложной задачей. Системный подход, применяемый к каждой проблеме, упрощает анализ. Хорошее концептуальное понимание, приверженность использованию диаграмм свободного тела и твердое понимание второго закона Ньютона – вот основные составляющие успеха.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего симулятора машины Этвуда. Вы можете найти его в разделе Physics Interactives на нашем сайте. Тренажер позволяет исследовать двухмассовые системы, ускоряемые подвешенной массой.
1. Рассмотрим ситуацию с двумя телами справа. 100,0-граммовый подвешенный груз (m2) прикрепляют к 325-граммовой массе (m1), покоящейся на столе. Коэффициент трения между 325,0-граммовой массой и столом составляет 0,215. Определите ускорение системы и натяжение струны.
2. Рассмотрим ситуацию с двумя телами справа.Ящик 3,50×10 3 кг (m 1 ) стоит на наклонной плоскости и соединен кабелем с массой 1,00×10 3 кг (m 2 ). Эта вторая масса (m 2 ) подвешена на шкиве. Угол наклона составляет 30,0 °, а поверхность имеет коэффициент трения 0,210. Определите ускорение системы и натяжение троса.
/ * * Подождите, исходники загружаются с GitHub... * * __ * ________ ________ _____ / \ _ \ * / \ \ / \ __ \ / \ / / / * / \ \ / \ \ _ \ \ __ / _ \ \ / _ / \ * / \ _______ \ / / \ \ _______ \ / \ ___ \ \ _______ \ * \ / / \ \ / / __ / \ / ___ / / __ / * \ / / \ / / _ / / \ / / \ \ / * \ / _______ / \ / _______ / \ / ___ \ \ _ \ * \ / _ / * * /Версия Phaser: 2.17.0 – Phaser CE2.16.2 – Phaser CE2.16.1 – Phaser CE2.16.0 – Phaser CE2.15.1 – Phaser CE2.15.0 – Phaser CE2.14.0 – Phaser CE2.13.3 – Phaser CE2.13.2 – Phaser CE2.13.1 – Phaser CE2. 13.0 – Phaser CE2.12.1 – Phaser CE2.12.0 – Phaser CE2.11.1 – Phaser CE2.11.0 – Phaser CE2.10.6 – Phaser CE2.10.5 – Phaser CE2.10.4 – Phaser CE2.10.3 – Phaser CE2.10.2 – Phaser CE2. 10.1 – Phaser CE2.10.0 – Phaser CE2.9.4 – Phaser CE2.9.3 – Phaser CE2.9.2 – Phaser CE2.9.1 – Phaser CE2.9.0 – Phaser CE2.8.8 – Phaser CE2.8.7 – Phaser CE2.8.6 – Phaser CE2.8.5 – Phaser CE2.8.4 – Phaser CE2.8.3 – Phaser CE2.8.2 – Phaser CE2.8.1 – Phaser CE2.8.0 – Phaser CE2.7.10 – Phaser CE2.7.9 – Phaser CE2.7.8 – Phaser CE2. 7.7 – Phaser CE2.7.6 – Phaser CE2.7.5 – Phaser CE2.7.4 – Phaser CE2.7.3 – Phaser CE2.7.2 – Phaser CE2.7.1 – Phaser CE2.7.0 – Phaser CE2.6.2 – Kore Springs2.6.1 – Caemlyn2.6.0 – Фал Моран2.5.0 – Пять королей2.4.9 – Четыре короля2.4.8 – Наблюдательный холм2.4.7 – Хиндерстэп2.4.6 – Бэрлон2.4.5 – Сенда2.4.4 – Амадор2.4.3 – Корамен2.4.2 – Альтара2.4.1 – Иониновый источник2.4.0 – Катар2.3.0 – Тарабон2.2.2 – Алькиндар2.2.1 – Данабар2.2.0 – Бетал2.1.3 – Равинда2.1.2 – Уайтбридж2.1.1 – Эйанрод2.1.0 – Кайриен2.0.7 – Амадиция2.0.6 – Джорнхилл2.0.5 – Tanchico2.0.4 – Mos Shirare2.0.3 – Allorallen2.0.2 – Ghealdan2.0.1 – Lyrelle2.0.0 – Aes Sedai1.1.6 – Shienar1.1.5 – Saldaea1.1.4 – KandorTheme: АтмосфераХаосХромОблако9 ДеньОблако9 НочьОблако9 Ночь Низкие ЦветаОблака ПолночьКобальтМалиновый РедакторРассветТкач ГрезЗатмениеGithubIdle FingersKatzenmilchKRKuroirТероядное ЖивотноеMerbivore SoftMono IndustrialMonokaiЗатра в темноте
Посмотрите код этого примера:
// github.com / photonstorm / phaser-examples / blob / master / examples / arcade Physics / body enable.js.
Получите исходный код и ресурсы для каждого примера Phaser из репозитория Phaser Examples на GitHub.
С буквально сотнями частей исходного кода это бесценный ресурс, доступный локально.
Phaser Sandbox позволяет вам программировать игры в браузере без необходимости загружать или устанавливать что-либо.
Мощный редактор включает поддержку кода Phaser, фрагменты кода JavaScript и множество функций, которые вам полюбились в таких редакторах, как Sublime и Brackets.
Matter.js – 2D движок физики твердого тела на JavaScript для Интернета
brm.io/matter-js
Демоверсии ・ Галерея ・ Возможности ・ Плагины ・ Установка ・ Использование ・ Примеры ・ Документы ・ Wiki ・ Ссылки ・ Лицензия
Посмотрите, как другие используют материю.физика js
Вы можете установить, используя менеджеры пакетов npm и Yarn, используя:
npm установить вопрос-js
В качестве альтернативы вы можете загрузить стабильную версию или попробовать последнюю экспериментальную альфа-сборку (мастер) и включить сценарий на свою веб-страницу:
Посетите вики-страницу «Начало работы», чтобы увидеть минимальный пример использования, который должен работать как в браузерах, так и в Node.js.
См. Также вики-страницы «Запуск» и «Рендеринг», на которых показано, как использовать собственную игру и циклы рендеринга.
См. Список учебных пособий.
См. Каталог примеров, который содержит исходные коды всех демонстраций.
На codepen есть еще больше примеров.
Движок можно расширить с помощью плагинов, см. Эти ресурсы:
См. Документацию по API и вики
Для сборки сначала необходимо установить node.js, а затем запустить
npm установить
Это установит необходимые зависимости сборки, затем запустит
npm run dev
для создания сервера разработки. Для получения информации о содействии см. СОДЕЙСТВИЕ.мкр.
Чтобы узнать, что нового или изменилось в последней версии, см. Журнал изменений.
См. Вики-страницу по ссылкам.
Matter.js находится под лицензией MIT License (MIT)
Copyright (c) 2014 Liam Brummitt
Эта лицензия также поставляется с выпуском и исходным кодом.
Как указано в лицензии, никаких гарантий не предоставляется.
Тип проблемы, с которой часто сталкиваются, состоит в том, что два объекта соединены вместе с силой, приложенной к одному из них.Дополнительные сложности могут возникнуть при учете сил трения. Типичной проблемой этого типа может быть один объект, лежащий на горизонтальной поверхности с заданным коэффициентом трения, связанный с другим объектом струной, проходящей через шкив. Объект, висящий на веревке, отпускается, и сила тяжести, действующая на него, заставляет оба объекта ускоряться. Чтобы решить эти проблемы, нарисуйте отдельную схему каждого объекта, показывающую все силы, действующие на него. Представьте любую неизвестную силу (часто силу между двумя объектами) с переменной.Напишите уравнение второго закона Ньютона для каждого объекта. Решите систему уравнений. Изучите пример в разделе «Образец проблемы».
Предмет весом 0,5 кг стоит на столе. Коэффициент трения между предметом и столом составляет 0,3. Он связан безмассовой струной, проходящей через безмассовый шкив без трения, с объектом весом 0,75 кг, который отпускается и падает, вытягивая за собой первую массу. Рассчитайте ускорение системы и натяжение струны.
Нарисуйте аккуратную диаграмму, показывающую как объекты, так и любые известные силы. Кроме того, нарисуйте эскиз каждого объекта отдельно, чтобы показать силы, действующие только на этот объект, как показано на рис. 2.4.1
Рисунок 2.4.1
Внимательно изучите приведенные выше схемы свободного тела. Обратите внимание, что сила, направленная вверх на B, равна силе, которая тянет вперед на A. Поскольку A и B связаны вместе, их ускорения будут одинаковыми.На самом деле это неверно в тот самый момент, когда система отпускается, поскольку струна растягивается, и степень растяжения будет немного изменяться, когда система начинает двигаться. Однако пока мы пропустим это переходное состояние.
Силу трения на объекте A можно найти, применив уравнение 4, F f = мкФ N . Нормальной силой в этой ситуации является вес объекта A. Масса объекта A составляет 0,5 кг (500 г), поэтому его вес составляет 0,5a г = 4.9 Н. Сила трения теперь составляет 1,47 Н. Вес B составляет 0,75 · 9,8 = 7,35 Н. Это больше силы трения, поэтому система будет ускоряться.
Из диаграмм свободного тела мы видим, что сила, действующая на A, равна T – 1,47, а сила, действующая на B, составляет 7,35 – T. Используя их в математической формулировке второго закона Ньютона, мы получаем:
Т – 1,47 = 0,5а (объект А)
7,35 – Т = 0,75а (объект Б)
Тщательно проанализируйте результаты. Натяжение струны меньше веса объекта B, иначе объект B не смог бы разогнаться. Напряжение больше, чем сила трения на объекте A, иначе этот объект не будет ускоряться. Также обратите внимание, что ускорение меньше ускорения свободного падения. Это необходимо, потому что на объект B действует восходящая сила T.