Задачи на логику с ответами 8 класс – Логические задачи для 8 класса с ответами
Логические задачи для 8 класса с ответами
Логические задачи для 8 класса с ответами
#1
Как вы думаете, какой предмет будет иметь одинаковое изображение при рисовании его с любой точки зрения?
Ответ?Этим свойством обладает только шар
#2
Если три десятка умножить на четыре десятка, то сколько получится?
Ответ?Получится не 12 десятков, а 120 десятков. То есть: 30 * 40 = 1200
#3
Ответьте, сколько сейчас времени, если оставшаяся часть суток в два раза превышает прошедшую?
#4
Попробуйте догадаться сколько стоит книга, если книга стоит доллар плюс пол книги.
Ответ?Книга стоит 2 доллара. Решение: полкниги стоит доллар, значит вся книга стоит 2 доллара
#5
Некий бизнесмен захотел привезти в Японию для продажи 10 000 пар первоклассных дорогих кроссовок.
Но в Японии на такие кроссовки накладываются очень большие пошлины.
Подумайте и скажите, как же хитроумный бизнесмен смог ввезти все эти кроссовки в Японию, при этом заплатил только очень небольшие деньги? Никакой коррупционной и преступной составляющей здесь нет.
Бизнесмен поступил очень хитро. Он разделил каждую пару кроссовок и отправил весь объем двумя партиями.
То есть в одной партии были только кроссовки на левую ногу, во второй только на правую ногу. Одну партию он отправил в Токио, другую в Осака.
В каждом из городов бизнесмен не заплатил пошлину и товары были конфискованы и выставлены на аукционе.
В связи с тем, что никому не была нужна партия кроссовок только на одну ногу, то бизнесмен выкупил сам обе партии за мизерные деньги.
#6
В мешке имеется 9 кг сахара. Есть также и две гири по 50г и 200г.
Подумайте, как за три взвешивания на чашечных весах отвесить 2кг сахара?
Сперва необходимо на чашечных весах разделить содержимое мешка пополам на 4,5кг в каждой чашке.
Далее одну чашу опустошаем, и снова 4,5кг делим пополам и получаем в каждой чаше весов по 2, 25кг. В третье взвешивание уже нужно опустошить обе чаши, но из одной чаши 2,25кг сахара положить в отдельный мешок.
И далее при помощи гирек в 200г и 50г (итого 250г) отвесить из пакета с 2,25кг ровно 250г. Тогда в пакете останется ровно 2 кг.
#7
5 рыбаков съели 5 карпов за 5 дней. Как вы думаете, а за сколько дней 15 рыбаков съедят 15 карпов?
Ответ?15 рыбаков съедят 15 карпов тоже за 5 дней. Если 5 рыбаков съедают 5 карпов за определенный промежуток времени, то у 15 рыбаков скорость поедания карпов в 3 раза больше, следовательно за 5 дней они съедят 15 карпов
#8
Два колхозника решили узнать, у кого больше овец.
Первый из них сказал: «если ты дашь мне свою козу, то у меня будет их в два раза больше, чем у тебя». Второй ему говорит: «А давай лучше ты мне дашь свою одну овцу, тогда у меня овец будет столько же, сколько и у тебя». Сколько же овец у каждого из колхозников? (Передачи овец пока еще не было)
У первого колхозника 7 овец, у второго только 5.
Если первый колхозник отдает одну овцу второму и их становится поровну, то значит, что изначально у первого их на 2 больше.
Если же второй колхозник отдает овцу первому, то их становится у первого в 2 раза больше, такое возможно, только если у первого изначально было 7 овец, а у второго 5
#9
Как вы думаете, сколько граней имеет шестигранный карандаш, который ни разу не затачивали?
Ответ?Шестигранный карандаш, если не подвергался заточке будет иметь 8 граней. 6 большие грани и 2 торцевые.
#10
Можете ли вы обосновать, почему почти во всех странах мира канализационные крышки у люков имеют только круглую форму? (Квадратные крышки люков бывают лишь тогда, когда они дополнительно крепятся шарнирами)
Ответ?Если крышки люков будут квадратными, то они могут легко провалиться в люк, т.к. диагональ квадрата больше стороны квадрата.
Поэтому их если и делают, то только прикрепив к люку шарнирами.
У круглых крышек люков нет диагонали и стороны, а только диаметр, который у крышки всегда больше отверстия люка
#11
Попробуйте сообразить, какой из выводов, указанных ниже, верный:
А) Здесь три ложных вывода.
Б) Здесь один ложный вывод.
В) Здесь два ложных вывода.
Г) Здесь пять ложных выводов.
Д) Здесь четыре ложных вывода.
Правильный вариант Д – здесь четыре ложных вывода. В связи с тем, что один является верным, а остальные не верные
#12
Можете ли вы записать число 1000 при помощи только восьми восьмерок и арифметических знаков суммы?
Ответ?Получится равенство: 888 + 88 + 8 + 8 + 8 = 1000
#13
В одном классе всего 36 учеников. Девочек на 3 больше, чем мальчиков. Сколько мальчиков и девочек в этом классе?
Ответ?Если разделить 36 пополам, то получим 18, т.е. две половины класса по 18 человек.
Если из первой половины добавить школьника в другую, то получится разница в 2 человека.
#14
На столе лежат 4 монеты, из которых одна сделана из другого металла и отличается по весу, хотя внешне они все одинаковые.
Как определить эту монету за 2 взвешивания на чашечных весах?
Варианты взвешиваний :
1) кладем на весы 1 и 2 монеты, если они равны по весу, то одну монету заменяем на третью.
Далее если они равны, то отличная монета 4-я, если не равны, то 3-я монета отличная от остальных.
2) кладем на весы 1 и 2 монеты, если они не равны по весу, то вместо одной монеты ложем 3-ю. Если уравновешиваются, то отличная убранная монета, если не уравновешиваются, то отличная от других монет оставшаяся на весах старая монета
#15
Как вы думаете, какой знак следует поставить между 0 и 1, чтобы было получено число больше 0, но меньше 1?
Ответ?Этот знак является запятой. То есть 0,1. Это число больше 0, но меньше 1
#16
Как так могло оказаться, что половина числа 12 стало равно 7
Ответ?Нужно написать число 12 римскими цифрами: IIX, далее провести посередине линию. Верхняя половина будет в виде VII, что соответствует цифре 7
#17
Трехлитровый сосуд полностью заполнен тремя литрами воды.
Вам необходимо за 2 переливания заполнить два пустых сосуда на 1 и 2 литра, чтобы в каждом из них было по 1 литру воды.
При этом больше нельзя пользоваться ничем, кроме этих трех сосудов.
Из полного сосуда наливаем в двухлитровый пустой ровно два литра, т.е. до краев.
Далее из этого сосуда выливаем в однолитровый ровно литр воды (т.е. до краев).
#18
На праздничном столе горят 7 свечей. 3 из них потушили. Сколько свечей останется?
Ответ?Останутся 3 потушенные свечи, т.к. остальные 4 сгорят полностью.
Как вы думаете, существуют ли линии отличные от окружности, на которых все точки будут равноудалены от какой-то одной точки?
Ответ?Равноудаленностью всех точек обладает любая линя, лежащая на поверхности шара.
aababy.ru
Логические задачи
1. Отправился человек в море и попал в шторм. Его отнесло на остров, где не было мужчин, а жили только девушки. Утром проснулся мужик на каком-то ритуале, весь обвязанный веревками, и узнал, что его хотят убить. Тогда попросил бедолага дать ему последнее слово. После того, как мужчина произнес его, девушки смастерили ему лодку, дали еду и отправили домой. Что же он сказал?
2. Эту загадку ученик первого класса решает за 5 минут, старшеклассник справляется за 15 минут, студент – за час, профессор же не решит никогда. А вот и вся головоломка: расшифруй ОДТЧПШСВДД.
3. Один поезд едет из Москвы в Санкт-Петербург с опозданием в 10 минут, а другой – в обратном направлении с опозданием в 20 минут. Какой из этих поездов будет ближе к Москве, когда они встретятся?
4. Известно, что среди девяти монет есть одна фальшивая, вес которой меньше, чем у остальных. Как с помощью чашечных весов всего за два взвешивания определить фальшивку?
5. Стоит стена из бетона высотой 3 метра, длиной 20 метров и весом 3 тонны. Как ее повалить, не имея никаких вспомогательных средств и инструментов?
6. Кошка – 3, лошадь – 5, петух – 8, ослик – 2, кукушка – 4, лягушка – 3, собака – ?
7. К реке подходят два человека. У берега стоит лодка, которая может выдержать только одного. Оба человека переправились на противоположный берег. Как?
8. Где встречается такое, что конь через коня перепрыгивает?
9. Шерлок Холмс шел по улице. И вдруг он увидел мертвую женщину, лежащую на земле. Сыщик подошел, открыл ее сумку и достал телефон. В телефонной книге нашел номер ее мужа и позвонил. Шерлок сказал: «Срочно приезжайте сюда. Ваша жена умерла». Через некоторое время приезжает муж, смотрит на жену и говорит: «Милая моя, что с тобой случилось?» Вскоре подоспела полиция. Шерлок указал пальцем на мужа женщины и промолвил: «Арестуйте этого человека, он убил свою жену». Вопрос: почему Шерлок так подумал?
10. Отец с двумя сыновьями отправился в поход. На их пути встретилась река, у берега которой находился плот. Он выдерживает на воде или отца, или двух сыновей. Как переправиться всем на другой берег?
Ответы.
1. Пусть меня убьет самая некрасивая.
2. 1, 2, 3, 4…
3. В момент встречи они будут на одинаковом расстоянии от Москвы.
4. Первое взвешивание: на каждой чаше весов по 3 монеты. Фальшивка находится в той кучке, которая меньше весит. Если равны, то фальшивая монета в третьей партии. Второе взвешивание: из тройки с наименьшим весом берем две монеты и взвешиваем. Какая чаша опуститься меньше, там и подделка. Если чаши весов равны, то фальшивка – оставшаяся монета из этой партии.
5. Толщина такой стены будет не более двух сантиметров, что позволяет толкнуть ее рукой.
6. Кошка говорит мяу (3 буквы), лошадь – и-го-го (5 букв), петух – ку-ка-ре-ку (8)… Собака, как известно, – гав, поэтому правильный ответ 3.
7. Они просто были на разных берегах.
8. В шахматах.
9. Ведь Холмс не назвал адрес, куда ехать.
10. Сперва переправляются оба сына. Один из них возвращается обратно к отцу. Папа перебирается на противоположный берег к сыну и остается на берегу, а второй сын переправляется на исходный берег за братом, после чего они оба переправляются к отцу.
1.Ответ:
Всего 5 остановок (включая конечную).
2.Ответ
На эскалаторе 280 ступеней.
Если общее количество ступеней на открытой части эскалатора обозначить через N, то при движении вниз оно будет складываться из количества ступеней, на которые опустился сам эскалатор, и количества ступеней, пройденных по нему. В первом случае время движения составило 140 : 2 = 70 секунд, во втором – 56 секунд. Для постоянной скорости эскалатора V указанные соображения приводят к уравнениям:
140 + 70*V = N
168 + 56*V = N,
решение которых N = 280 ступеней и V = 2 ступени в секунду.
3.Ответ
У кого-то может денег не быть!
1 – 1,54
2 – 1,35
3 – 0
4.Ответ:
Пусть велосипедист вёз мальчика х километров. Скорость мальчика v км/ч, скорость велосипедиста 2v км/ч. Между 12-00 и 14-00 прошло времени x/2v+a/v=(x+2a)/(2v)=2 часа. На обратную дорогу уйдёт (x+2a)/v=4 часа
5.Ответ:
12345 23456 34567 45678 56789
и обратные:
98765 87654 76543 65432 54321
и одно 55555
1.Прочитайте условие, но только один раз, и попробуйте сразу же ответить на вопрос. На конечной остановке в автобус сели четырнадцать мужчин и две женщины. На первой остановке сошли двое мужчин и вошли две женщины. На следующей остановке вышли почти все мужчины (осталось только трое), а на следующей вошли пять женщин. Проехав с полкилометра, автобус остановился, и в него вошел еще один мужчина. Сколько всего было остановок на пути следования автобуса?
2.Человек опаздывал на работу и, чтобы наверстать потерянное в пробке время, побежал вниз по эскалатору метро. Спускаясь со скоростью две ступени в секунду, он насчитал сто сорок ступеней. Через день ситуация повторилась, но теперь ему грозило большее опоздание. Естественно, по тому же эскалатору он бежал быстрее – со скоростью три ступени в секунду, а насчитал на двадцать восемь ступенек больше.
Странно получилось: чем быстрее бежишь, тем длиннее эскалатор.
Сколько же всего ступенек на нем?
3. Трое друзей хотят купить книжку. Оказалось, что двоим на покупку книги не хватает 1 копейки, третьему 2 рубля 90 копеек. Когда они сложили свои деньги, то денег на покупку книги им все равно не хватило. Зная, что денег у первого из друзей на 19 копеек больше чем у второго, найдите, сколько денег было у каждого.
4. Мальчик пошел из лагеря в город. В 12 часов, в нескольких километрах от лагеря, его догнал велосипедист и подвез его немного. Затем велосипедист высадил мальчика недалеко от города, и в 14 часов мальчик добрался до города.
Сколько времени потратит мальчик на обратную дорогу пешком, если известно, что скорость велосипедиста в два раза больше скорости мальчика?
5. На доске выписаны все пятизначные числа, у которых каждая цифра либо равна обеим соседним, либо отличается от соседних ровно на единицу – от одного в меньшую, а от другого в большую сторону.
Сколько написанных на доске чисел содержат в своей записи цифру 5?
Задачи на взвешивание и переливания.
1.Есть 10 мешков с золотом. В каждом по 10 монет. В девяти мешках монеты настоящие, а в одном – все фальшивые. Одна настоящая монета весит 5 грамм, а фальшивая – 4 грамма. Есть весы, показывающие вес в граммах.
Необходимо за одно взвешивание точно определить, в каком мешке фальшивые монеты
Мешки можно раскрывать и вытаскивать монеты
2. Как, имея пятилитровое и девятилитровое ведро, набрать из крана ровно три литра воды?
3.Винодел обычно продает свое вино по 30 и по 50 литров и использует для этого кувшины только такого размера. Один из покупателей захотел купить 10 литров. Как винодел отмерил ему 10 литров пользуясь своими кувшинами?
4.Как из полного сосуда ёмкостью в 12 л отлить половину, пользуясь двумя пустыми сосудами ёмкостью в 8 и 5 л.
5.Три человека купили сосуд, полностью заполненный 24 унциями меда. Позже они приобрели три пустых сосуда объемом 5, 11 и 13 унций. Как они могли бы поделить мед на равные части используя эти четыре сосуда? Постарайтсь решить задачу за наименьшее количество переливаний.
Восемнадцать спичек образовывают 6 одинаковых прилегающих друг к другу квадратов. Заберите 2 спички так, чтобы осталось 4 таких же квадрата.

11.Что больше: сумма всех цифр или их произведение?
12.Как разделить 5 яблок между пятью лицами так, чтобы каждый получил по яблоку и одно яблоко осталось в корзине.
13.В тот день в классе было 24 человека. Когда ученики писали контрольную работу, то они по мере завершения клали тетради в стопку одна на другую. Петя сдал тетрадь пятым по счёту. Каким по счёту его тетрадь проверят, если считать, что учитель проверяет тетрадь сверху стопки и строго по порядку?
1.Ответ:
Пронумеруем мешки от 1 до 10. Вытащим из первого 1 монету, из второго 2, из третьего 3 и так далее. Затем возьмем всю эту кучу монет и положим на весы. Если бы они все были настоящие, то общий вес составил бы 275 грамм (т.к. мы вытащили в общей сложности 55 монет). Но в одном из мешков были фальшивые. Если это был первый мешок, то вес будет на 1 грамм меньше (т.к. мы взяли оттуда 1 монету). Если фальшивые были во втором, то на 2 грамма меньше. И так далее.
2.Ответ:
Заполняем 9-литровое ведро и заливаем из него в 5-литровое ведро. (Далее 5-литровка и 9-литровка). в 9-литровке 4 литра. Выливаем воду из 5-литровки и заливаем туда 4 литра из 9-литровки. Заполняем 9-литровку и выливаем оттуда 1 литр в пятилитровку. Выливаем воду из 5-литровки, и заполняем пятилитровку из девятилитровки. Всё! В девятилитровке теперь 3 литра.
3.Ответ:
Сначала он наполнил 30-литровый кувшин и вылил его содержимое в 50-литровый. Потом опять наполнил 30-литровый и долил до полного заполнения в 50-литровый. В результате у него в кувшине останется 10 литров.
4.Ответ:
Сначала наливаете 8 литров в 8л., потом из 8л. наливаете полный 5л., в результате получается, что в 12л.- 4 литра, в 8л – 3литра, а в 5л.- 5 литров. Переливаете из 5л. в 12л. всю воду, а из 8л. переливаете все 3 литра в 5л. В результате 9 литров в 12л, 0 литров в 8л., и 3 литра в 5л. Переливаете из 12л. 8 литров в пустой 8л.,и в 12 л. остается 1 литр. Из 8л. доливаете в 5л., пока 5л. не станет полным, (в 5л. было 3л., след. долили мы еще 2литра из 8л.) Тогда в 8л. как раз остается 6л.
5.Ответ:
Сосуды могут содержать 24, 13, 11, и 5 унций соответственно:
Их начальное состояние 24, 0, 0, 0;
1 – 8, 0, 11, 5;
2 – 8, 11, 0, 5;
3 – 8, 13, 3, 0;
4 – 8, 8, 3, 5;
5 – 8, 8, 8, 0.
6. Ответ:

11.Ответ:
Больше сумма, так как произведение равно 0 (один из множителей – это цифра 0).
12.Ответ:
Один человек берет яблоко вместе с корзиной.
13.Ответ:
Подвох в том, что учитель тоже человек. Т.е. в классе было 23 ученика, и после Пети работу сдали 18 человек (23-5). Таким образом, Петину тетрадь проверят 19-ой.
videouroki.net
ВИКТОРИНА для 6-8 классов “Логические задачи”

Предлагаю учащимся 6-8 классов моей школы попробовать свои силы в дистанционной викторине. Вопросы в основном логические. А как у нас с логикой?… Правильно, тяжело! Попробуем изменить ситуацию и потренируем свое логическое мышление.
Все вопросы имеют порядковый номер. Решите как можно больше логических задачек и разместите в комментариях к этой статье ваши ответы. Обязательно указывайте номер вопроса, за ним – ваш ответ с пояснениями, если таковые требуются. Самые активные участники и наиболее интересные комментарии будут непременно отмечены учителем математики. Итак, вперед!
ВОПРОС 1. У вас в руках одна палочка. Как с её помощью образовать на столе треугольник? ВОПРОС 2. Сколько концов у двух с половиной палок? ВОПРОС 3. Когда павлин стоит на одной ноге, то он весит 4 кг. Каков будет вес павлина, когда он встанет на две ноги? ВОПРОС 4. Бывает ли такое, что снег идет два дня подряд? ВОПРОС 5. Когда у семейной пары спросили, сколько у них детей, они ответили: «У нас четыре сына, а у каждого сына есть сестра». Сколько детей в семье? ВОПРОС 6. Если разрезать три яблока и положить их на стол, то сколько яблок будет лежать на столе? ВОПРОС 7. Вирус уничтожает память компьютера. За первую минуту он уничтожил половину памяти, за вторую минуту – одну треть оставшейся памяти, за третью минуту вирус управился с четвертью того, что осталось, за четвертую минуту – с третьей частью остатка. После этого компьютер спас Антивирус. Какая часть памяти уцелела? ВОПРОС 8. Где в делении 20132013:2013=11 допущена ошибка? ВОПРОС 9. В комнате 4 угла. В каждом углу сидит кошка. Напротив каждой из этих кошек – кошка. Сколько кошек в комнате? ВОПРОС 10. Как разрезать прямоугольник прямой линией так, чтобы из двух получившихся кусочков можно было сложить треугольник? ВОПРОС 11. В школе 399 учащихся. Почему можно утвердительно сказать, что хотя бы у двоих учеников дни рождения совпадут? ВОПРОС 12. Имеем два сосуда емкостью 3 литра и 5 литров. Как с их помощью набрать из колодца 4 литра воды. ВОПРОС 13. Даны числа 9,8,7,6,5,4,3,2,1. Расположите их в клетках квадратной таблицы 3×3 так, чтобы сумма чисел в каждой диагонали, вертикали и горизонтали была одной и той же. ВОПРОС 14. Какую закономерность вы видите в данных рядах чисел? 3, 7, 11, 15, 19, 23… 9, 1, 7, 1, 5, 1… 4, 5, 8, 9, 12, 13… 1, 2, 4, 8, 16, 32… Запишите в каждом ряду пару следующих чисел. ВОПРОС 15. На одном заводе работают три друга Иванов, Петров и Сидоров. Один – инженер, другой – монтажник, третий – сварщик. У инженера нет ни братьев, ни сестер и он самый младший из друзей. Петров старше монтажника и женат на сестре Сидорова. Кто из друзей занимает должность инженера? ВОПРОС 16. Половина от половины задуманного числа равна половине. Что это за число? ВОПРОС 17. Если на прямой отметить пять точек, то сколько мы сможем рассматривать отрезков? ВОПРОС 18. На розыгрыш кубка по футболу подали заявки 48 команд. Сколько матчей будет сыграно до окончательного определения победителя? ВОПРОС 19. Если у кирпича, массой 4 кг, уменьшить в 5 раз все его размеры a, b и c, то чему будет равна масса кирпича? ВОПРОС 20. Во сколько раз путь по лестнице на 9 этаж дома длиннее пути на 3 этаж? ВОПРОС 21. Масса полного сосуда с водой 7 кг. Масса сосуда, наполненного наполовину, 4,5 кг. Сколько воды вмещает сосуд? ВОПРОС 22. Витя, Миша, Петр и Егор встретились и подружились в «Орленке». Они приехали из Краснодара, Томска, Орла и Анапы. 1. Витя и мальчик из Анапы разместились в одной комнате. Они не были раньше ни в Краснодаре, ни в Орле. 2. Миша играет в хоккей с мальчиком из Краснодара. Против них играет их приятель из Анапы. 3. Петр и мальчик из Краснодара увлекаются игрой в шахматы. Из какого города каждый ребенок?
ЗАДАЧА 23. В городе N живут три типа людей: такие, которые всегда говорят правду, всегда говорят неправду (лжецы), и шутники (они могут говорить и правду, и неправду). В этом городе кто-то угнал машину у шерифа. Полиция задержала троих человек: Джона, Джека и Билла. Полиции было известно, что один из них – лжец, один – всегда говорит правду, а про третьего точно неизвестно, говорит ли он правду или ложь. Полиция также знала, что один из них угнал машину, и что этот человек всегда говорит правду. Трое задержанных сказали следующее:
Джон: Я не виновен. Джек: Он говорит истинную правду. Билл: Я угнал машину. Кто угнал машину и кто лжец? ЗАДАЧА 24. Как без использования калькулятора найти три последние цифры произведения 1 x 2 x 3 x 4 x 5…x 17 x 18? ЗАДАЧА 25. У Петра 100 мышей. Некоторые белые, некоторые – серые. Известно, что хотя бы одна мышь серая, а из двух мышей хотя бы одна – белая. Сколько у Петра серых мышей?.
Ответы к задачам с комментариями будут непременно размещены после подведения итогов викторины. Желаю успехов в тренировке!
solodenkovagalina.blogspot.com
Сборник логических задач для школьников 8-9 классов
46. Вставить пропущенное число:
50. Вставить пропущенные числа.40
12
20
?
?
51. Вставить пропущенное число.
12
15
4
5
8
17
90
?
52. Вставить пропущенное слово.
53.Вставить пропущенное число.
3600
?
54. Вставить пропущенное число.
55. Вставить пропущенное число.
56. Вставить пропущенное число.Раздел ІІ
Решение задач
1.Пусть было х гусей, тогда по условию задачи получим уравнение x+х+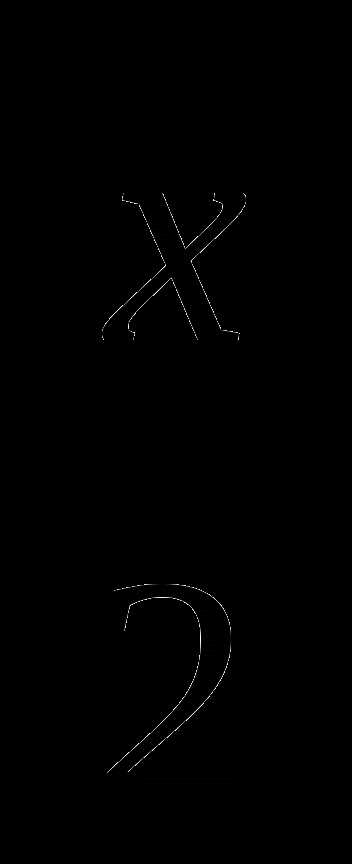 +
+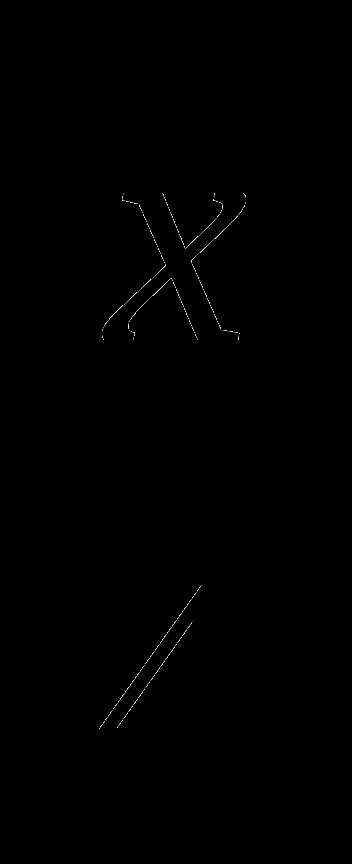 +1=100. После решения уравнения получим х=36.
+1=100. После решения уравнения получим х=36.
Итак, было 36 гусей.
Ответ: было 36 гусей.
2. Ответ: наседьмой день.
3.Ответ: число 666 нужно перевернуть и получим 999.
4.Справа – стандартный вид числа, которое записано слева, поэтому данный многочлен второй строки нужно записать в стандартном виде. Значит, получим: а3 + а2 – 3а -3.
Ответ: а3 + а2 – 3а -3.
5. Ответ:9ав – ас – вс.
6.Проанализируем данные первого ряда: 3 1058 : 5
1058 : 5 1023 = 6
1023 = 6 1034, тогда пропущенное выражение будет 63в9с : 7вс2 = 9в8с-1.
1034, тогда пропущенное выражение будет 63в9с : 7вс2 = 9в8с-1.
Ответ 9в8с-1.
7. Листопад – это опадание листьев осенью, поэтому нужно преобразовать данное выражение:
 =
= 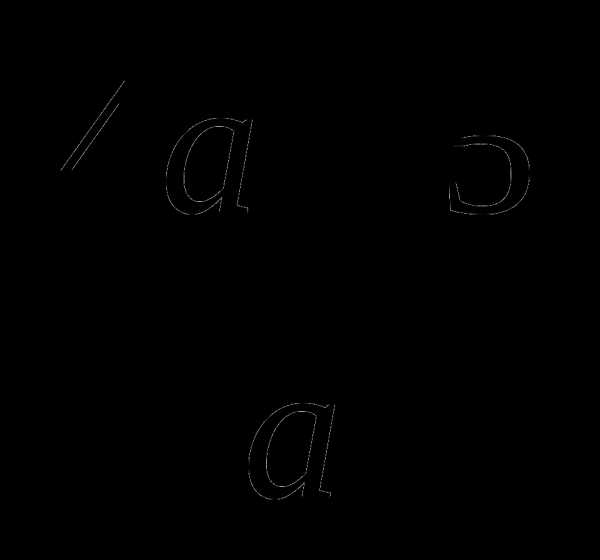 .
.
Ответ: 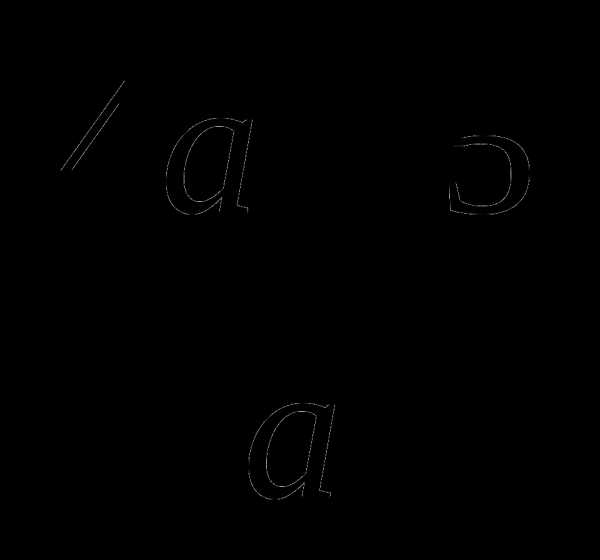 .
.
8. 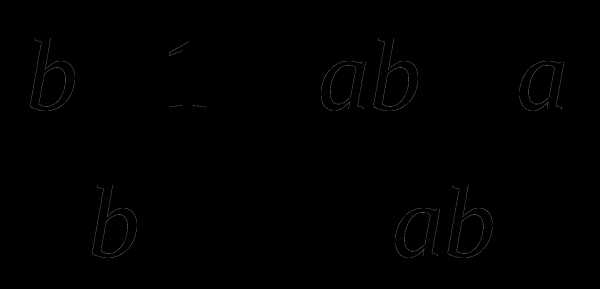 =
=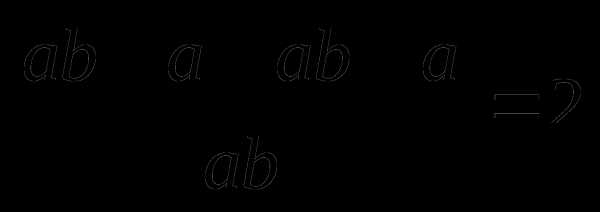 .
.
Ответ: 2.
9. Проаналируем данные первой строки: а15 : а3 = а12, тогда 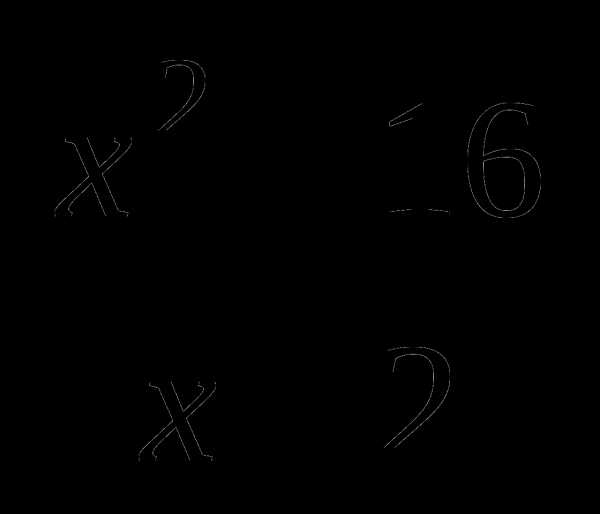 :
:  = х + 4.
= х + 4.
Ответ: х + 4.
10.х10  х8=х18, тогда найдем произведение дробей второй строки:
х8=х18, тогда найдем произведение дробей второй строки: 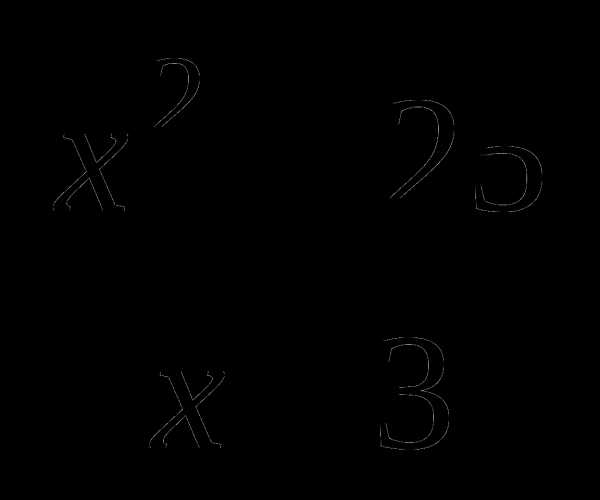

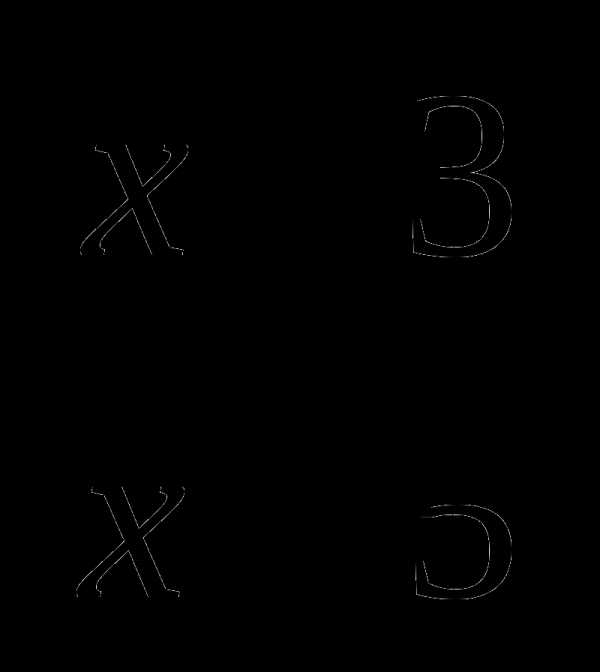 = х – 5.
= х – 5.
Ответ: х – 5.
11.В первой строке дробь 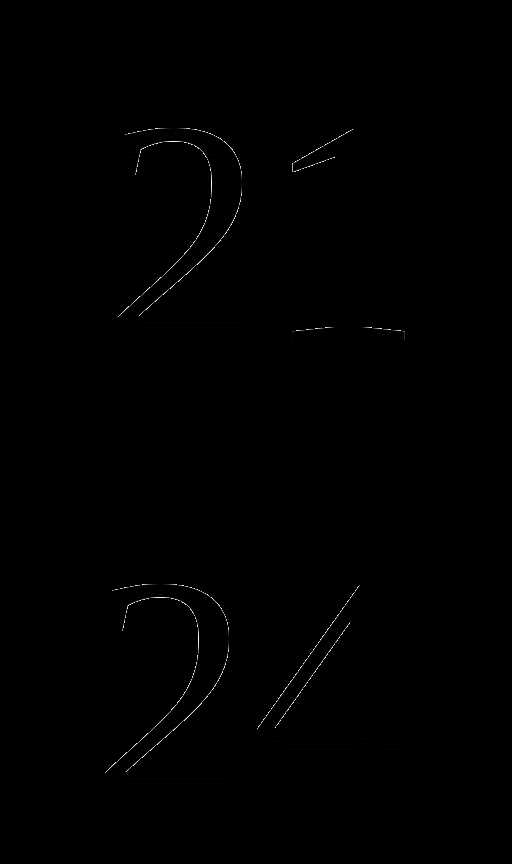 сократимая и получим
сократимая и получим  , поэтому неизвестный результат второй строки: а -3.
, поэтому неизвестный результат второй строки: а -3.
Ответ : а -3.
12.Если сократить дробь  , то получим
, то получим  , поэтому нужно сократить выражение:
, поэтому нужно сократить выражение:
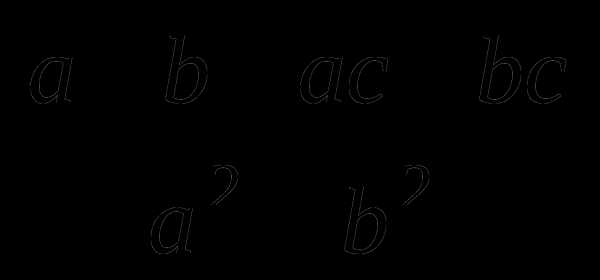 =.
=.
Ответ:  .
.
13.у(3)=4 – 32=-5, поэтому два пропущеных числа будут значениями данной функции при х=1 и х=2, значит это будут числа 0 та 3.
Ответ: 0 та 3.
14.Если воспользоваться неравенством треугольника для треугольника АВС, то получим 3<АС<13, поэтому ответом к заданию будет неравентсов 2<В1С1 <26.
Ответ: 2<В1С1 <26.
15.Воспользовавшись неравенством треугольника, имеем 2<m<12, поэтому лишним числом будет 1.
Ответ: 1.
16.Согласно свойству размещения двух окружностей на плоскости, якщо О1О2= R1 + R2, то данные окружности имеют только одну общую точку, т.е. касаются. А при другом условии имеем: О1О2>R1 + R2, тому окружности не имеют общих точек.
Ответ:
17.Корнями первого квадратного уравнения являются числа 2 и 3, а сумма их квадратов 13, аналогично сумма квадратов корней второго уравнения равна (-2)2+(-4)2=4+16=20, поэтому искомое число будет суммой корней уравнения х2+2х-3=0, т.е. (-3)2+12=10.
Ответ: 10.
18.
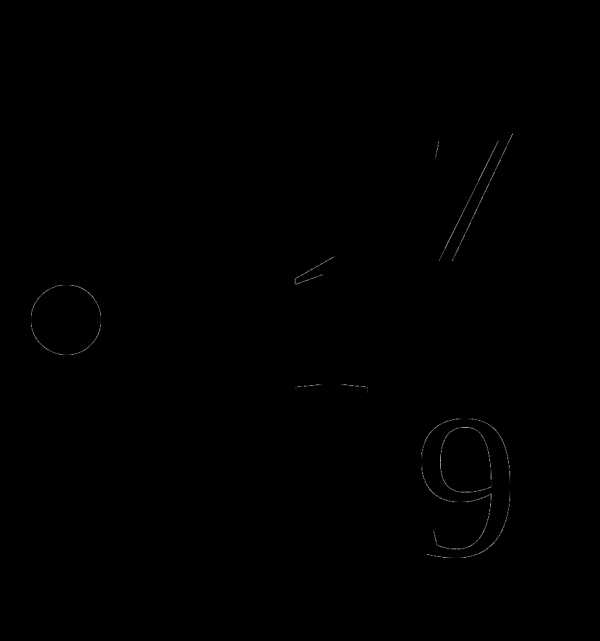 =2, поэтому нужно найти произведение двух выражений:
=2, поэтому нужно найти произведение двух выражений: 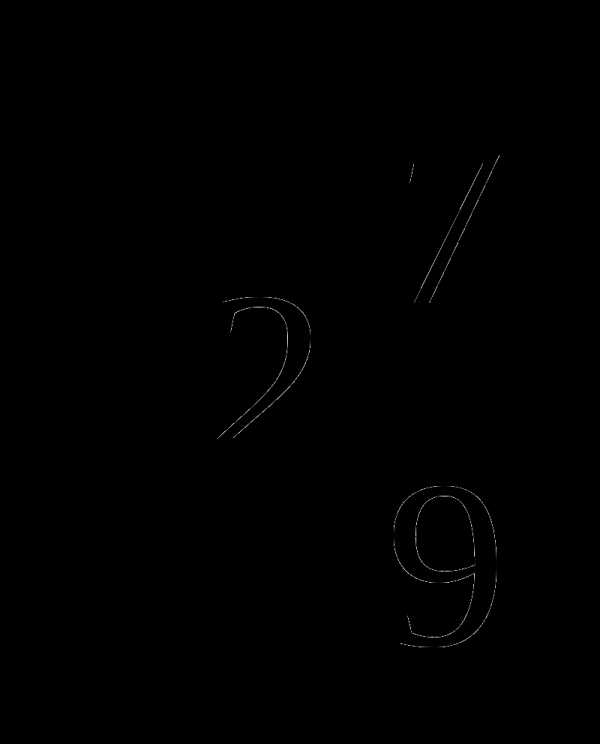
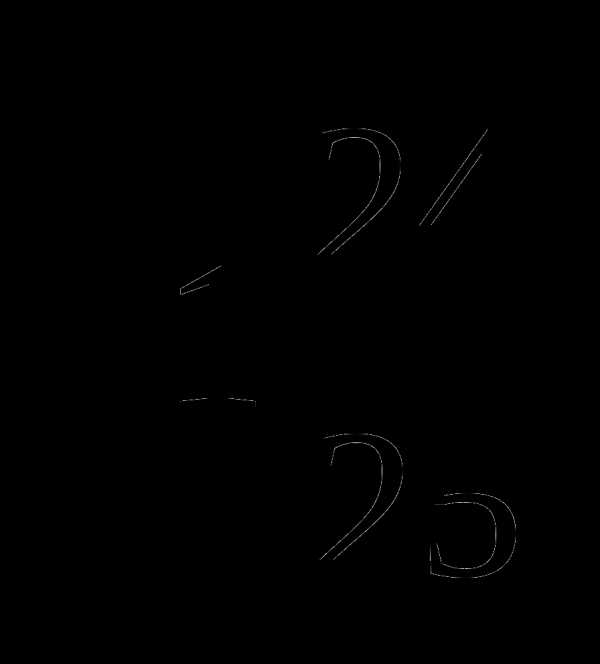 =
=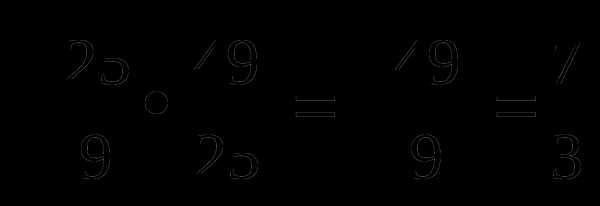 .
.
Ответ:  .
.
19.По условию первой строки: если х=4, то у=1, поэтому нужно найти целые значения х и у, удовлетворяющие данной функции. Такими значениями будут числа х=3 и у=1.
Ответ:
20. Точка А имеет координаты (3,4), поэтому расстояние до начала отсчета О(0, 0) равно . Значит, нужно вычислить ОМ=.Ответ: искомое число 13.
21. Точка А имеет координаты (4,1). Уравнение, записанное справа по теореме Виета имеет также корни х1=4 и х2=1. Поэтому нужно составить квадратное уравнение, корнями которого будут координаты точки В(-3,2).
Ответ: х2 + х -6=0.
22. 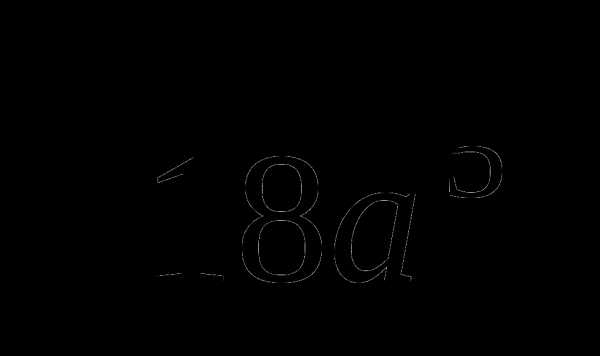 + а2
+ а2 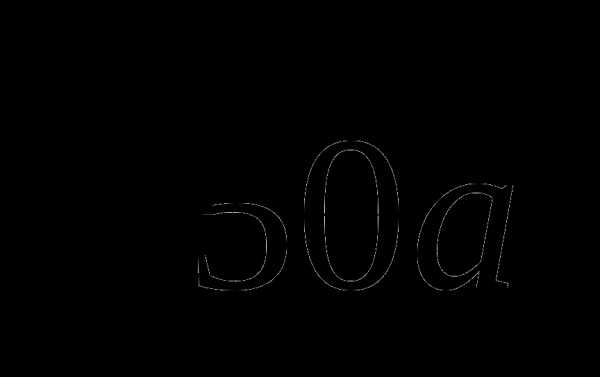 = 3а2
= 3а2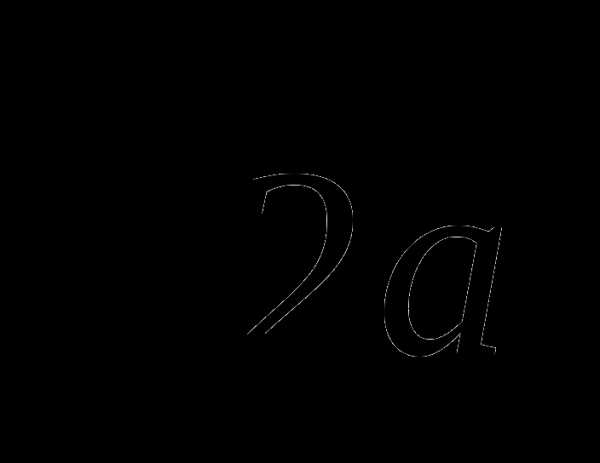 +5а2
+5а2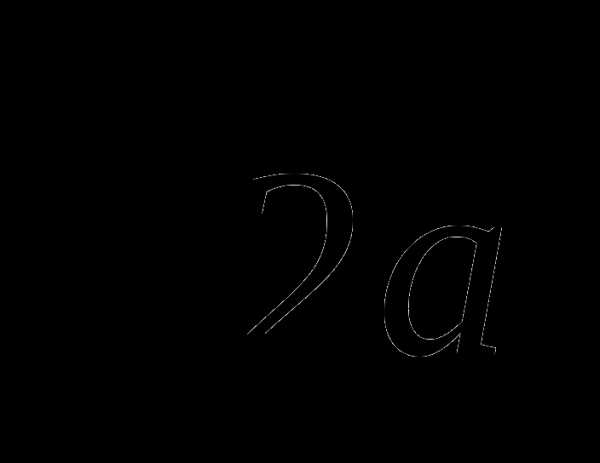 =8а2
=8а2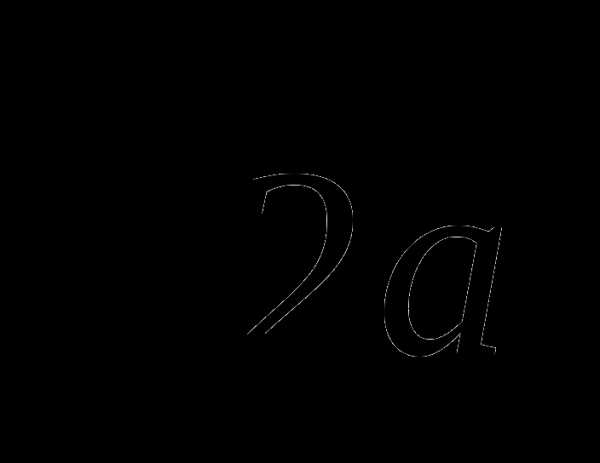 , поэтому искомое число будет равно сумме двух многочленов (
, поэтому искомое число будет равно сумме двух многочленов (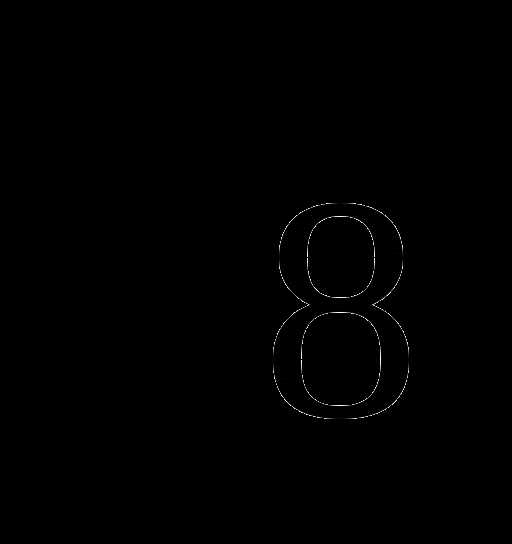 –
–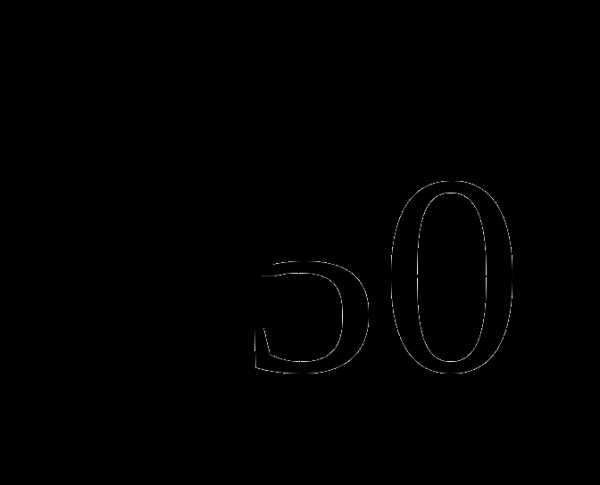 )+ (
)+ ( +
+ )=2
)=2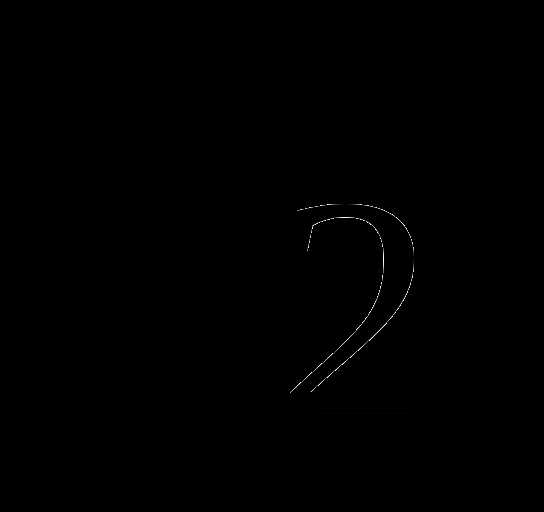 -5
-5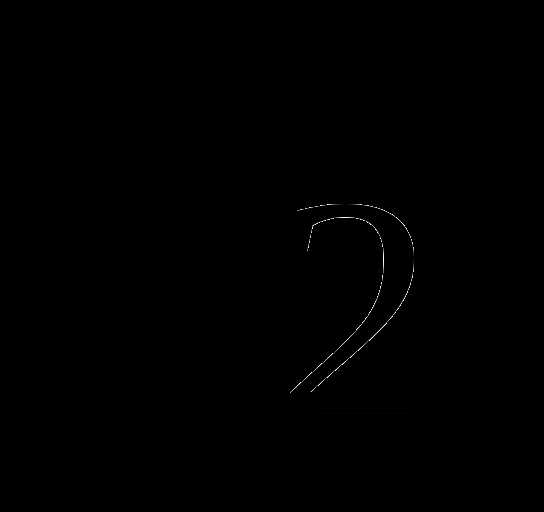 +3
+3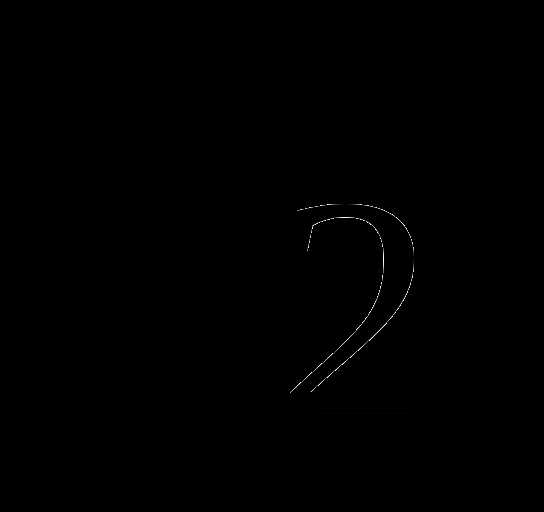 +4
+4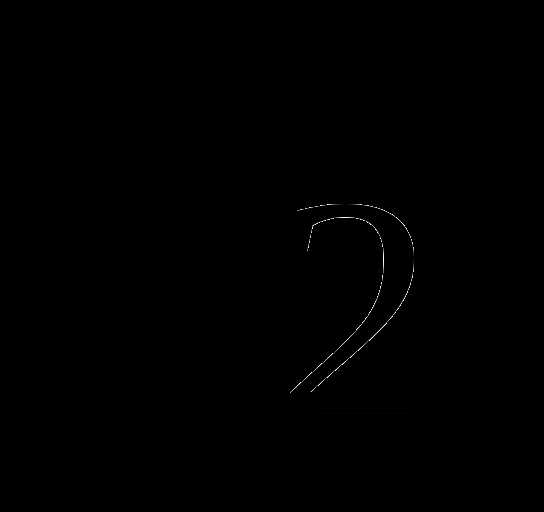 =4
=4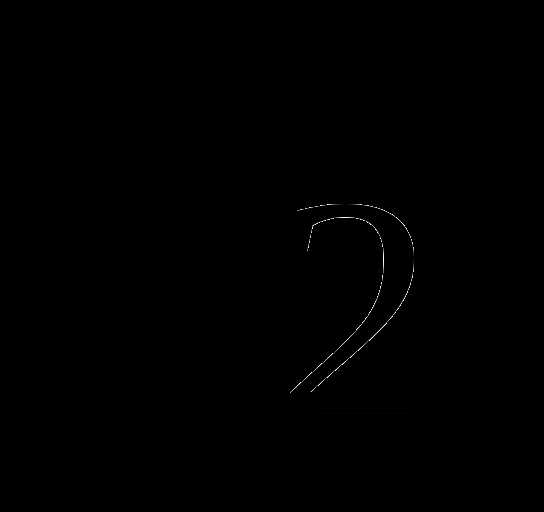 .
.
Ответ: 4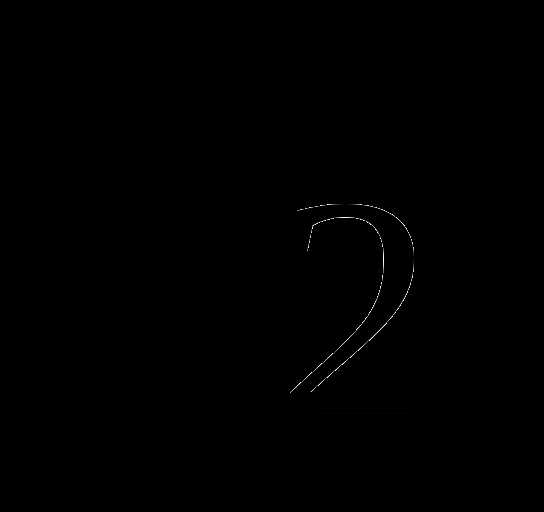 .
.
23.Произведение выражений, щвписанных в противоположных секторах, равно а21, поэтому, по часовой стрелке, получим а-3 и а18.
Ответ: а-3 и а18.
24. Произведение выражений первой и второй строк равно 1, поэтому пропущенным числом будет число, обратное к 2 , т.е.
, т.е.  .
.
Ответ:  .
.
25. Избавившись от иррациональности в знаменателе дроби  , получим
, получим 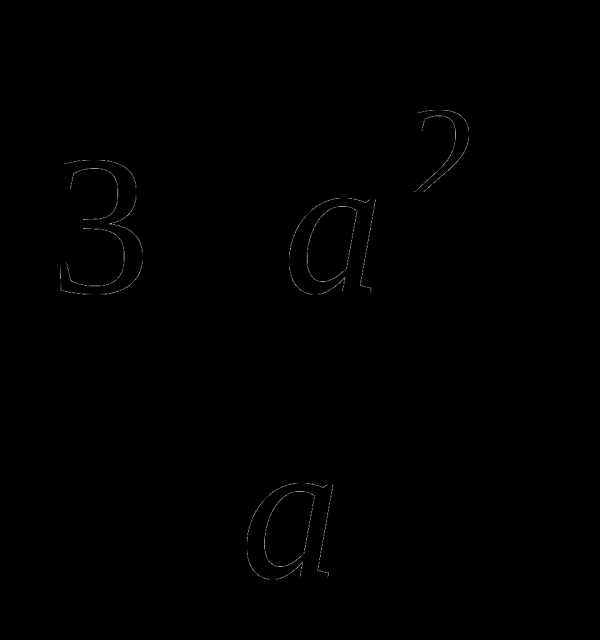 , поэтому во второй строке нужно дописать
, поэтому во второй строке нужно дописать 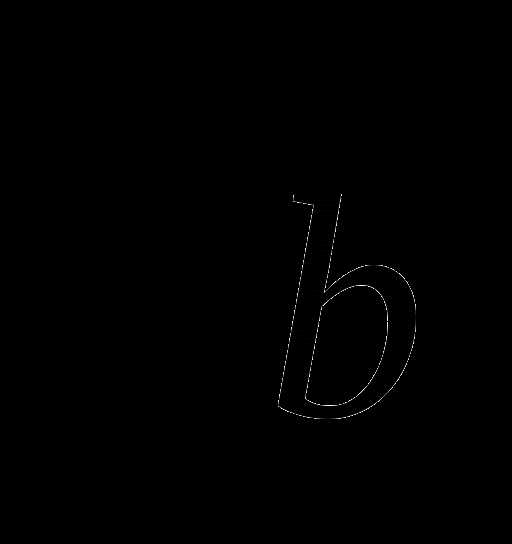 , а в третьей –
, а в третьей –  =
=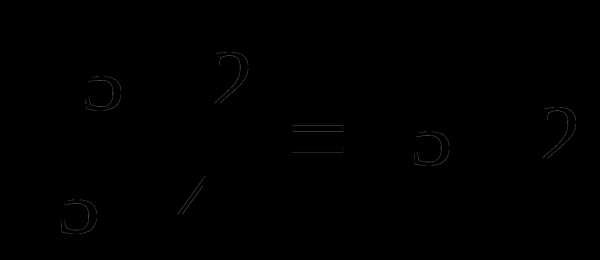 .
.
Ответ: 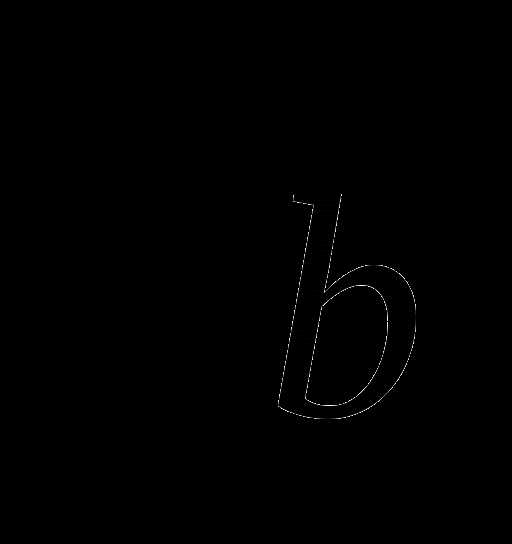 та
та  .
.
26. , поэтому искомое число будет результатом произведения .
Ответ: 24.
27.(а-7 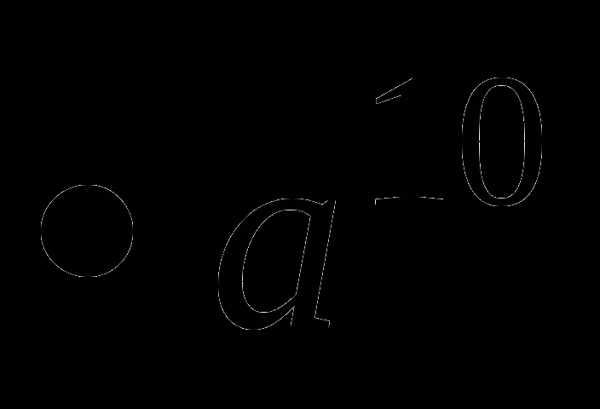 ): (а3
): (а3 а-2)=а2, поэтому искомое выражение будет равно (а-5
а-2)=а2, поэтому искомое выражение будет равно (а-5  а7): (а3
а7): (а3  а-4)=а3.
а-4)=а3.
Ответ: а3.
28. а2 – в2 =(а+в)(а-в), а3 + в3 = (а+в)(а2 – ав + в2), т.е. а+в является общим множителем в разложении многочленов. Таким образом, нужно данные многочлены разложить на множители.
Имеем: -2х2+7х-3= -2(х- )(х-3)=(1-2х)(х-3) та 10х2– х-2= 10(х-
)(х-3)=(1-2х)(х-3) та 10х2– х-2= 10(х- )(х+0,4)=(2х-1)(5х+2).
)(х+0,4)=(2х-1)(5х+2).
Ответ: 2х-1.
29.Воспользовавшись формулой расстояния между точками, ОА=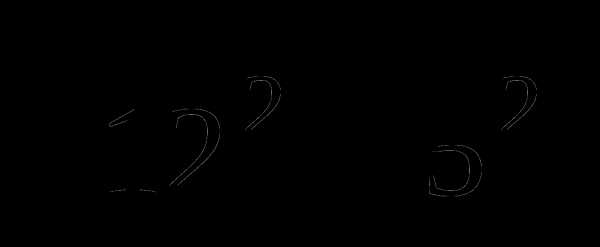 =13, поэтому нужно решить уравнение ОМ=10, т.е. х2+82=100. Таким образом, х1=6 и х2=-6.
=13, поэтому нужно решить уравнение ОМ=10, т.е. х2+82=100. Таким образом, х1=6 и х2=-6.
Відповідь: 6 и -6.
30. 6 10-7
10-7  8
8 1015=4,8
1015=4,8 109, поэтому найдем произведение выражений
109, поэтому найдем произведение выражений
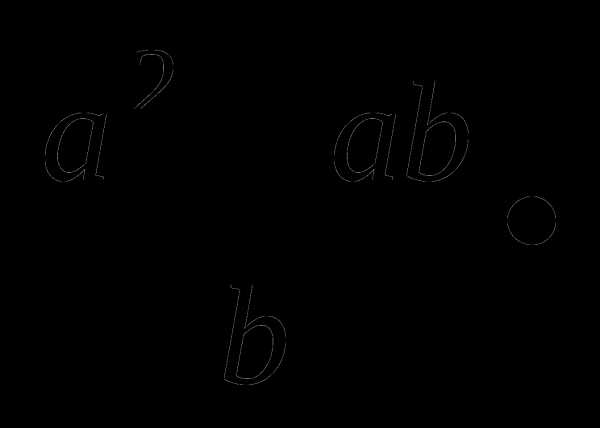
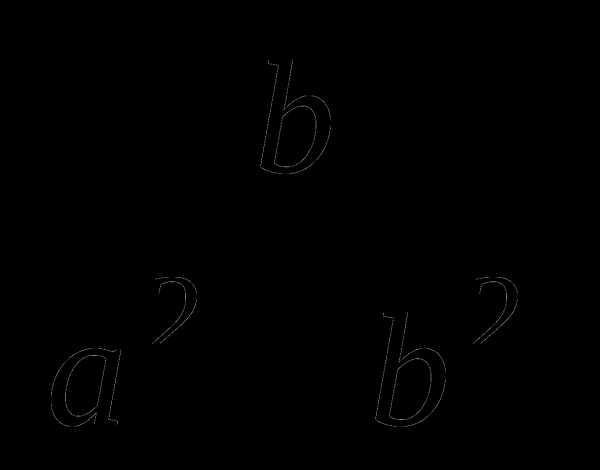 =
= .
.
Ответ:  .
.
31. Уравнение 2х-1=5 имеет корень х=3, поэтому числа 2 та -1 не являются корнями указанного уравнения, поэтому для решения задания нужно указать лишние числа, указанные на рисунке. Биквадратное уравнение х4-3х2=4 имеет два корня х1=2 и х2=-2, поэтому лишними будут числа 1 и -1.
Ответ: 1 и -1.
infourok.ru
Математические задачи на смекалку с ответами
Никто не рождается развитым и образованным. Чтобы в зрелом возрасте преуспевать, нужно немало потрудиться в детском и подростковом возрасте. Для этого родители учат с детьми стихотворения, читают книжки, развивают память, внимание, логику, тренируют мышление. Эта статья поможет вам найти упражнения и задачки для тренировки серого вещества головного мозга у детей различного возраста. Занимаясь с ребенком каждый день по 15 минут, вы подготовите отличный фундамент для его дальнейшей учебы, ведь логическое мышление – основа всех знаний и умений ребенка.
Математические задачи на логику для дошкольников
Начиная с 3 летнего возраста малыша, родители должны понемногу заниматься тренировкой логического мышления у своих детей. Детям это очень важно, ведь для них в таком возрасте многие очевидные вещи кажутся сложными, а непонятные для восприятия взрослым, напротив, очевидными. Представим несколько вариантов логических задач для детей 3-5 лет.
- На столе лежит 1 апельсин. Его разрезали на 2 части, сколько апельсинов лежит на столе? Ответ: 1, разрезанный.
- Собаку привязали к забору веревкой. Длина веревки составляет 10 метров, а собака прошла за день 100 метров. Как ей это удалось? Ответ: Собака ходила вдоль забора туда и обратно и «находила» целых 100 метров.
- Какой день недели соответствует числу 3? Ответ: среда, т.к. его порядковый номер в неделе – 3.
Примечание: Про дни недели дошкольникам можно задавать различные варианты вопросов. Это поможет не только в развитии логического мышления, но и поможет скорее выучить дни недели.
- Посчитать, сколько людей в следующей строке: ты да я, да мы с тобой. Ответ: 2.
- Папа и сын, дедушка и внук, сын и папа. Сколько всего человек здесь отмечено? Ответ: 3, т.к. папа – сын дедушки, сын папы – внук дедушки.
- На опушке стояло 3 высоких сосны. На каждой сосне по 3 больших ветки и по 3 маленьких. На каждой маленькой ветке по яблоку. Сколько всего яблок на деревьях? Ответ: 0, на соснах яблоки не растут.
- Папу Антона зовут Андрей Викторович, а дедушку – Сергей Иванович. Какое отчество у мамы Антона? Ответ: Сергеевна, Потому что Сергей Иванович – это отец мамы Антона. Отца папы Антона зовут Виктор.
- У двух братьев по одной сестре. Сколько всего детей в семье? Ответ: 3. 2 брата и одна сестра на двоих.
- Какие камни есть в море? Ответ: мокрые.
Примечание: аналогичная задача-загадка моет звучать так «Каких камней в море нет?» — ответ: сухих.
- Вася и Петя играли в морской бой и сыграли по 3 партии. Каждый выиграл по 3 раза. Это правда или ложь? Ответ: ложь. Во время одной партии выиграть может только один.
- В поле работали 5 тракторов. 2 трактора сломались и остановились. Сколько тракторов в поле? Ответ: 5, т.к. учитываются все тракторы, и рабочие, и сломанные.
- Одно яйцо варится 5 минут. Сколько времени нужно, чтобы сварить 2 яйца? Ответ: все те же 5 минут.
- Саша сидит в самолете. Впереди него машина, сзади – лошадь. Где находится Саша? Ответ: катается на карусели.
- Алена сидит, когда она встанет и уйдет, ее мама так и не сможет сесть на ее место. Где сидит Алена? Ответ: у мамы на коленях.
- Что все дети на земле делают одновременно? Ответ: взрослеют.
Опираясь на предложенные варианты заданий на развитие логического мышления, родители могут придумывать незамысловатые условия задач самостоятельно.
Математические задачи на логику: 1-2 класс
Но вот дети пошли в школу, буквально за первые месяцы учебы они начинают хорошо считать, ориентироваться в пространстве и времени. Задачки для дошкольников уже кажутся им простыми и неинтересными. Поэтому для таких деток мы приготовили несколько вариантов упражнений тренировки логики и смекалки, ориентируясь на их новые способности и возможности.
- Первоклассника попросили назвать самое большое число. Что он ответил?
Ответ: 31. Первоклассники каждый день записывают число месяца в тетрадь, самое большое число в месяце – 31. - На доске написаны два числа 4 и 5. Какой знак нужно поставить между ними, чтобы получился результат больше 4 и меньше 5. Ответ: запятая.
- По узкой дороге может проехать только одна машина. С одной стороны дороги находится гора. Одна машина едет с горы, другая – под гору. Как им разминуться? Ответ: обе машины едут в одном направлении и разминаться им не придется.
- Сколько раз из числа 10 можно отнять число 2? Ответ: один, т.к. уже после первого вычитания двойки останется число 8, а не 10.
- На столе стоят 6 стаканов: в первые три налили воду, вторые три – пустые. Нужно расставить стаканы так, чтобы чередовались пустые и полные стаканы, но при этом можно взять в руки только один стакан. Как поступить, чтобы выполнить условие? Ответ: Взять второй стакан и перелить из него воду в пятый стакан. Второй стакан поставить на прежнее место.
- За 10 часов 10 человек могут выкопать траншею длиной в 10 метров. Сколько нужно человек, чтобы они выкопали траншею диной в 100 метров за 100 часов? Ответ: 10 человек. На 1 час 10 человек выкопают 1 метр траншеи, за 10 часов они выкапывают 10 метров траншеи, а за 100 часов – 100 метров.
- Школьники участвуют в соревнованиях по бегу. Ваня занимает третью позицию, Антон занимает вторую позицию. Саша обгоняет Антона. Какую позицию занимает Саша? Ответ: вторую, т.к. впереди Антона тоже кто-то бежит и этот кто-то пока первый.
- Учитель положил на пол карандаш и попросил учеников перешагнуть через него, но никто не смог этого сделать. Почему? Ответ: карандаш лежит у стены и шагать детям некуда.
- Таня и Алиса пошли в магазин и нашли 2 рубля. Сколько бы денег они нашли, если бы с ними пошла еще и Марина? Ответ: 2 рубля, т.к. размер находки никак не зависит от количества ее нашедших.
- Из пункта А в пункт Б вышла кошка, а из пункта Б в пункт А вышла мышка. Когда они встретятся, кто из них будет ближе к пункту А, а кто к пункту Б? Ответ: они обе будут на одинаковом расстоянии от пункта А, и на одинаковом расстоянии от пункта Б.
- На столе стояли 3 чашки с чаем. Папа выпил чай из одной чашки и поставил ее на место. Мама выпила свой чай и тоже поставила чашку на место. Сколько чашек было на столе, когда пришел пить чай сын? Ответ: 3 чашки. Они хоть и пустые, но никуда со стола не делись.
- Марина шла из дома в школу и встретила трех мужиков. У каждого за спиной был мешок. У первого мужика в мешке был один кот, у второго в мешке был один кот и один пес. У третьего в мешке было 2 пса. Сколько всего котов направлялось в школу? Ответ: один, сама Марина. Мужики с мешками шли в обратную от школы сторону.
- В классе стоял стол с четырехугольной крышкой. Ученики отпилили один угол, что стало со столом, сколько углов осталось на крышке? Ответ: 5. Если отпилить один угол, то получим на его месте 2 новых, поэтому всего 5 углов.
Примечание: на самом деле количество углов может зависеть и от того, как размышляет ребенок. Если он «пилит» стол по углам диагонали, т.е. распиливает его пополам, то вполне возможно, что у стола будет 3 угла. Если же один распил приходится на угол, а второй на сторону крышки, то может остаться и 4 угла. Но это нюансы, которые лучше рассматривать, рисуя на листе бумаги, где ребенок собирается «пилить» стол.
- На тарелке лежат 3 банана. Их нужно разделить между тремя девочками, чтобы на тарелке остался один банан. Ответ: одной девочке нужно отдать банан вместе с тарелкой.
- Какое слово зашифровано: ООО? Ответ: ТРИО, т.е. ТРИ О.
Родители тоже могут составлять свои задачи для детей, ориентируясь на предложенные варианты. Чем чаще ребенок будет заниматься упражнениями на логику, тем быстрее будет работать его мозг, тем выше будет успеваемость в школе.
Математические задачи на логику: 3-4 класс
Дальнейшее обучение в школе имеет свои особенности: дети научились складывать двузначные числа, совершать с ними различные математические операции, в том числе умножение, деление. Логические математические задачи для школьников 3-4 класса должны охватывать уже полученные знания и совершенствовать их качество.
- В кошельке лежит 15 копеек двумя монетами. Одна из монет не пятак, как такое может быть? Ответ: может, т.к. другая монета вполне может быть пятаком.
- Шла Маша в Волгоград, а навстречу ей 10 ребят. У каждого в руках по лукошку, в каждом лукошке по кошке, а у каждой кошки по котенку. Сколько всего ребят шло в Волгоград? Ответ: одна Маша. Все остальные, сколько бы их не перечисляли, шли навстречу девочке, а значит в противоположную сторону от Волгограда.
- Дедушка пилит бревна. Распил бревна пополам он делаем ан одну минуту. Сколько ему понадобится времени, чтобы распилить бревно на 10 частей? Ответ: 9 минут, т.к.чтобы распилить бревно на 10 частей, нужно сделать 9 распилов.
- Мальчик пришел в амбар. В каждом углу амбара стояло по 3 мешка. На каждом мешке сидело по кошке, у каждой кошки было по котенку. Сколько всего ног было в амбаре? Ответ: две, только мальчика.
Примечание: Как бы долго дети не перемножали между собой числа-«ноги» кошек и котят, стоит помнить, что у кошек – лапы, а ноги – только у мальчика.
- Родители купили своим двум дочкам Маше и Лизе по коробке конфет. В каждой коробке было по 15 конфет. Маша съела несколько конфет и отложила коробку. А Лиза съела столько, сколько оставалось в коробке у Маши, и тоже отложила коробку. Вечером мама посчитала конфеты в коробках обеих девочек. Сколько конфет там было? Ответ: 15. Маша и Лиза съели вместе 15 конфет. Маша несколько (например, 15-х=у), а Лиза столько, сколько осталось у Маши (т.е. у конфет). Сумма х+у = 15. А у девочек было по 15 конфет, т.е. 2*15 = 30. Было 30, 15 съели, и 15 на двоих осталось. А сколько у кого – этого в задаче не уточняется.
- Из ГОРОНО в школу пришли проверяющие. Они выбрали класс для проверки, но не все дети были готовы отвечать урок. Тем не менее, на каждый вопрос учителя весь класс поднимал руку, и тот, кого учитель вызывал к доске, отвечал блестяще. Как получилось, что учитель угадывал, кого вызвать отвечать? Ответ: решением этой задачи есть небольшая хитрость. Перед уроком школьники и учитель договорились, что те, кто наверняка знают ответ на поставленный вопрос, будут поднимать правую руку. А те, кто не знают – левую. Благодаря маленькой хитрости класс достойно прошел проверку и никто ни о чем не догадался.
- Что у коровы находится спереди, а у быка сзади? Ответ: буква «К». Корова, быК.
- Когда маме исполнилось 31 год, дочери было 8. Сейчас мама старше дочери ровно в 2 раза. Сколько их обеим лет? Ответ: дочке 23, маме 46. Когда дочь родилась, маме было 31-8 = 23 года. Чтобы быть старше дочки в два раза, маме должно быть 23*2 = 46 лет. За это время дочь доросла до 23 лет.
- Две одноклассницы Наташа и Лена живут в одном подъезде: Лена на втором этаже, а Наташа на четвертом. Наташа поднимается по ступенькам на четвертый этаж и проходит 60 ступенек. Сколько ступенек проходит Лена, которая поднимается на второй этаж? Ответ: 20. Чтобы подняться с первого этажа на четвертый, нужно пройти три пролета. 60:3=20 ступенек в одном пролете. А Лена поднимается с первого на второй этаж и проходит при этом только один пролет, все те же 20 ступенек.
- Может ли страус называть себя птицей? Ответ: нет, не может. Страусы не умеют разговаривать.
- Какая физическая величина не имеет ни высоты, ни глубины, ни ширины, ни длины, но ее можно измерить? Ответ: время, температура.
- Задание на логику из серии «Юный Шерлок». На вызов о самоубийстве были вызваны представители уголовного розыска. В кабинете жертвы они обнаружили диктофон и включили его. На диктофоне была записана следующая фраза: «В моей смерти прошу никого не винить, жизнь не имеет смысла…» далее раздался выстрел. Как следователи поняли, что убийство сфабриковано? Ответ: убитый не мог перемотать запись на начало, это сделал кто-то другой.
- Что не может поместиться даже в самую большую кастрюлю? Ответ: ее крышка.
- В кастрюле налита вода до самого верха. Как отмерять жидкость, не используя никаких мерительных приспособлений, чтобы в кастрюле осталась только половина жидкости. Ответ: нужно наклонить кастрюлю и выливать воду до тех пор, пока не покажется с боковой части дно. Это и будет половина кастрюли.
- Когда цифра «2» означает «10»? Ответ: на циферблате цифра «2» соответствует «10 минутам».
С каждым годом задания на развитие логики и смекалки должны становится все сложнее, иметь подвохи, хитрости, чтобы ребенок учился размышлять, уделять внимание деталям. А регулярные и систематические занятия обязательно принесут свои плоды.
childage.ru
Логические задачи с ответами
Логические задачи для 5-6 классов.
Предисловие.
Если логическое мышление, да еще и воображение хорошо развиты у человека, то он способен творчески мыслить и творчески подходить к поставленным задачам. Развитию логического мышления необходимо учиться. Нужно уметь пользоваться логическим мышлением и воображением. Нужно также развивать и всячески способствовать развитию логического мышления. Ведь это пригодится в жизни!
Для эффективного развития логического мышления можно и нужно решать различные ситуационные задачи и загадки. Как стандартные логические задачи головоломки, так и нестандартные. Это одновременно развивает логику, интеллект, воображение, фантазию.
Это всего лишь небольшой обзор тех увлекательных логических задач, которые могут быть использованы учителями во внеурочное время, а также при проведении внеклассных мероприятий.
1.Шарики.
На столе стоят три одинаковых ящика. В одном из них 2 черных шарика, в другом 1 черный и 1 белый шарик, в третьем 2 белых шарика. На ящиках написано: “2 белых”, “2 черных”, “черный и белый”. При этом известно, что ни одна из записей не соответствует действительности. Как, вынув только один шарик, определить правильное расположение надписей?

2.Про школьников.
В класе 35 учеников, из них 20 школьников занимаются в математическом круже, 11- в литературном, 10 ребят не посещают эти кружки. Сколько литераторов увлекаются математикой?

3.Тайный поклонник.
На парту Оли упал бумажный самолет с нарисованными красными сердечками. Оля развернула его и прочитала: “Ты – лучшая девочка в классе!” Она повернулась в сидящим за ней ребятам: Ивану, Сергею, Алексею. Все три мальчика покраснели.
– Кто из вас делает мне такие комплименты? – спросила Оля.
– Это Сергей! – сказал Иван.
– Я ничего такого не делал! – сказал Сергей.
– Не имею никакого представления, о чем ты говоришь! – сказал Алексей.
Подруга Оли Маша ухмыльнулась: “Двое из них лгут!” Однако она не хочет больше ничего говорить. Кто является тайным поклонником Оли?
4.Названия птиц.
Прочитайте названия птиц в этих анаграммах. Какое слово здесь лишнее?
ВОЛИГА, НИЦАСИ, ГАЙПОПУ, РОКАСО, ВЕЙЛОСО, РЕЦСКВО, ЗАНАС, УССТРА, ЛИНФИ, БЕЙРОВО
5.Кошки-мышки.
Если пять кошек ловят пять мышей за пять минут, то сколько времени нужно одной кошке, чтобы поймать одну мышку?
6.Опасная дорога.
Есть дорога по которой может проехать только одна машина. По дороге едут две машины: одна с горы, другая под гору. Как им разъехаться?
7.Бумажные стаканчики.
Имеются три бумажных стаканчика для мороженого. Требуется разложить по этим стаканчикам 10 монет так, чтобы в каждом стаканчике было нечетное число монет. Как это сделать?
8.Трудное наследство.
Один коневладелец оставил в наследство своим сыновьям конюшню. Он завещал старшему отдать половину, среднему треть, а младшему девятую часть всех лошадей. В конюшне на момент смерти владельца осталось 17 лошадей. Как можно не нарушив завещание поделить лошадей?
9.Двенадцать.
Как разделить пополам число двенадцать, что бы получилось семь?
10.Задача про велогонку.
Петя и Вася участвовали в велогонке. Все участники стартовали одновременно и показали на финише различное время. Петя финишировал сразу после Васи и оказался на десятом месте. Сколько человек участвовало в гонке, если Вася был пятнадцатым с конца?
11.Странное вычитание.
Можно ли от 29 отнять 1, чтобы при этом получилось 30?
12.Равенство
9999999 = 100
Расставьте скобки и математические знаки так, чтобы равенство было верным.
13.Учащиеся
Из 38 учащихся 28 посещают хор и 17 лыжную секцию. Сколько лыжников посещает хор, если в классе нет учащихся , котрые не посещают хор или лыжную секицю?
14. Может ли такое быть?
Одного человека спросили:
— Сколько вам лет?
— Порядочно, — ответил он.
— Я старше некоторых своих родственников почти шестьсот раз. Может ли такое
15. Два числа.
Назовите два числа, у которых количество цифр равно количеству букв, составляющих название каждого из этих чисел.
16. Прилив.
С борта парохода был спущен стальной трап. Нижние 4 ступеньки трапа погружены в воду. Каждая ступенька имеет толщину в 5 см; расстояние между двумя соседними ступеньками составляет 30 см. Начался прилив, при котором уровень воды стал поднимается со скоростью 40 см в час. Как Вы считаете, сколько ступенек окажется под водой через 2 часа
Ответы.
1.Собственно ответ: Вытаскиваем шарик из коробки с надписью “белый и черный”. Если шарик белый, то:
в коробке “белый и черный” – 2 белых шарика;
в коробке “2 белых” – 2 черных шарика;
в коробке “2 черных” – белый и черный шарики
Если шарик черный:
в коробке “белый и черный” – 2 черных шарика;
в коробке “2 белых” – белый и черный шарики;
в коробке “2 черных” – 2 белых шарика
2. Всего 35 учеников. 10 кружки не посещают. Значит, посещают кружки 35-10=25 учеников.
25 учеников посещают кружки. 20 учеников занимаются в математическом кружке. Значит, только литературный кружок посещают 25-20=5 человек.
В литературном кружке 11 человек. Лишь 5 из них посещают только литературный кружок. Значит, 11-5 = 6 человек-литераторов посещают ещё и математический кружок.
3.Алексей.
4.Иволга, синица, попугай, сорока, соловей, скворец, страус, филин, воробей. Лишнее слово здесь – “сазан”, потому что это не птица, а рыба.
5..Пять
6.А зачем им разъезжаться? Они же обе вниз (под гору и с горы) едут.
7.Все дело в том, что один из стаканчиков можно вставить в другой. После этого в него можно положить любое нечетное число монет меньше 10. Например, 7. Оставшиеся монеты кладем в третий стаканчик.
8.Добавьте в конюшню еще одну лошадь. Теперь их получилось 18. Отдадим 9 лошадей старшему наследнику, 6 среднему и 2 младшему. Условия завещания выполнены. Можете забирать свою лошадь обратно.
9.Напишите это число римскими цифрами на листе бумаги и разрежьте его пополам.
10.Т.к. Петя финишировал сразу после Васи и оказался на 10-м месте, то Вася был девятым, т.е. перед ним было еще 8 участников. А раз известно, что Вася был пятнадцатым с конца, то всего было 15+8 = 23 участника.
11.Для того, чтобы на первый взгляд немыслимое стало естественным, нужно представить число 29 в римских цифрах. Тогда 29 – это XXIX. Отнимаем единицу, в данном случае I, и в результате получится XXX или 30.
12.(99-9):9 + (99-9) = 100
(99-99)* 999 = 10*0
999/9-99/9=100
(9*9+9)/9+99-9=100
(99-9)/9+(9-9)*9=10-0
(9*9+9)/9+(9-9)*9=10-0
99/99+(9-9)*9=1+0+0
(9*9+9)/9-9+9-9=1+0+0
13. 7 человек. Хор не посещают 10 человек, все они лыжники. Лыжников всего 17 человек, значит 7 человек надо «взять» из хора.
14.Может, например если человеку 50 лет, а его внуку или внучке 1 месяц.
15. «сто»-100 «миллион»-1000000
16.Через два часа под водой будут те же 4 ступеньки, потому что во время прилива лестница поднимается вместе с пароходом.
infourok.ru
Логические задачи, задачи на логику. С ответами.
|
Размер |
Толщина |
Фон |
||
|
Скрыть ответы |
+шрифт
–шрифт |
+жирн
–жирн |
White Cyan LGreen GYellw DpSkBl Coral DPink1 DPink2 SkBlue Orange OlivD1 OlivD2 LBlue PGreen Yellow Gold Blue Green Wheat Chocol Salmon Red HPink DPink Pink VioRed Magent Violet Plum Purple OrRed Bisque Bisqu2 LemC1 LemC2 Corns2 Honey2 Turqu1 Turqu2 SGrn1 SGrn2 Orchi1 Orang1 Gray golrod | |
В одном хлебном магазинчике есть 3 сорта булочек. На 10 рублей можно купить либо 1 булочку первого сорта, либо две булочки второго, либо 3 булочки третьего сорта. В магазин зашла группа детей, мальчиков и девочек поровну. Они сложились и получили 70 рублей. Всю сумму они потратили на покупку булочек. Каждому ребенку досталось булочек на одинаковую сумму. Сколько было куплено булочек и каких сортов, если ни одна из булочек не была поделена на части?
Ответ
Группа детей состояла из трех мальчиков и трех девочек. Каждый ребенок получил по 2 булочки 3 сорта и по 1 булочке 2 сорта.
Один не очень трудолюбивый человек устроился на работу на 30 дней. За каждый день работы он получает по 8 франков. За каждый день прогула он платит штраф в размере 10 франков. По прошествии 30 дней выяснилось, что ни работодатель, ни работник не должны друг другу нисколько денег. Подумайте и ответьте, сколько дней человек работал, а сколько было прогулов? (дни работы и прогулов не обязательно целые числа).
Ответ
Итак, ленивый человек проработал 16,(6) дня и прогулял 13,(3) дня.
Распиловщик бревен должен распилить бревно длиной 5,5 метра на бревнышки длиной 0,5 метра. Каждый распил длится 2,5 минуты. За какое время будет выполнена распиловка всего бревна?
Ответ
Распиловка бревна займет ровно за 25 минут.
Имеется стебель цветка высотой 1 метр. От земли по нему вверх начинает ползти гусеница. Днем она поднимается на 30 см, а ночью спускается на 20 см. Через какое время (в сутках) гусеница доползет до верхушки цветка?
Ответ
Гусеница доползет до верхушки цветка за 7,5 суток.
В книжном шкафу одного ученого на одной полке стоят две книги. Первая книга стоит слева от второй, рядом с ней. В первой книге 230 страниц, во второй 325 страниц. Как вы думаете, сколько всего страниц между первой страницей первой книги и последней страницей второй книги?
Ответ
Между этими страницами книг находятся только переплеты.
Солдаты выстроились в линейку на расстоянии одного метра друг от друга. Линейка растянулась на 25 метров. Сколько всего было солдат в линейке?
Ответ
Всего в линейке было 26 солдат.
Владимир и Константин живут в панельном многоквартирном доме. Владимир живет на 10 этаже, а Константин на 2 этаже этого же дома. Во сколько раз пол в квартире Владимира расположен выше от поверхности земли, чем пол в квартире Константина? (Пол на первом этаже расположен на уровне поверхности земли и все этажи по высоте одинаковые).
Ответ
Пол в квартире Владимира выше пола в квартире Константина ровно в 9 раз.
Книга с переплетом стоит 7 долларов и 60 центов. Как вы думаете, сколько стоит переплет книги, если сама книга стоит на 7 долларов дороже переплета?
Ответ
Переплет стоит 30 центов, а книга 7 долларов и 30 центов. Разница равна 7 долларам.
В двух классах одной школы всего 70 учащихся. В одном из классов всего на 5 учащихся больше, чем в другом классе. Сколько учеников в каждом классе?
Ответ
Данная задача не имеет решения.
Некоторое число было увеличено на 25 процентов. На сколько процентов нужно уменьшить новое число, чтобы получить первоначальное число?
Ответ
Новое число необходимо уменьшить на 20 процентов, чтобы получить первоначальное число.
|
Поделитесь с друзьями: |
Некоторое число было уменьшено на 25 процентов. На сколько процентов нужно увеличить результат уменьшения, чтобы получить первоначальное число?
Ответ
Новое число необходимо увеличить на 33,(3) процентов, чтобы получить первоначальное число.
У каждого из братьев есть определенное количество денег. У старшего на 25 процентов больше, чем у младшего. Сколько процентов денег должен отдать старший брат младшему, чтобы денег у них стало поровну?
Ответ
Старший брат должен отдать младшему ровно 10 процентов своих денег, тогда у них будет денег поровну.
В первом цехе одного предприятия три мастера внесли рацпредложения по сокращению расхода электроэнергии. У первого мастера экономия составила 50%, у второго мастера экономия составила 30%, у третьего мастера экономия составила 20%. На собрании было принято решение внедрить сразу все три рацпредложения. Как вы думаете, цех теперь вообще не будет нуждаться в электроэнергии или все-таки расход какой-то будет?
Ответ
После внедрения всех трех рацпредложений цех будет расходовать 28 процентов электроэнергии от первоначального объема. Расчеты следующие : 100% * 0,5 * (1 – 0,3) * (1 – 0,2) = 100% * 0,5 * 0,7 * 0,8 = 28%.
Все знают, что 2 в квадрате = 4, 10 в квадрате = 100, половина в квадрате = 1/4, треть в квадрате = 1/9. Как вы думаете, чему равен угол в квадрате?
Ответ
Угол в квадрате равен 90 градусам. Или 1/2 пи. Т.е. здесь квадрат – это фигура.
Имеется число 188. Как вы думаете, как его разделить пополам так, чтобы в результате получилась единица?
Ответ
Надо записать это число |88, далее ровно посередине провести линию. Получится дробь : 100 / 100 , которая равна единице.
Один человек принес в банк тысячу однодолларовых банкнот. И сказал, чтобы эти купюры разложили в 10 мешков таким образом, чтобы когда он в следующий раз придет и попросит выдать ему любую сумму до 1000 долларов, ему бы выдали от 1 до 10 мешков, причем нельзя перекладывать деньги из одного мешка в другой. Как банковским служащим надо разложить 1000 банкнот в 10 мешков?
Ответ
Банковские служащие должны разложить деньки в 10 мешков в следующем порядке : 1, 2, 4, 8, 16, 32, 64, 128, 256, 489. В первых девяти мешках купюры разложены в порядке геометрической прогрессии, а в последнем оставшаяся сумма. В таком виде клиенту можно выдать за один раз любую сумму до 1000 долларов.
Однажды вечером собрались семеро однокурсников, чтобы сыграть в карты по следующим правилам : кто выигрывает, тот должен выплатить каждому из шести игроков такое количество денег, которое у него имеется. Однокурсники сыграли семь партий и каждый из них выиграл по одному разу в порядке : первый, второй, третий, четвертый, пятый, шестой и седьмой однокурсник. После окончания 7-й игры у каждого из них осталось по 1 рублю и 28 копеек. Сколько денег до игр в карты было у каждого однокурсника?
Ответ
Перед началом игр в карты у однокурсников (№1, №2, №3, №4, №5, №6, №7) было денег соответственно : 4 рубля 49 копеек, 2 рубля 25 копеек, 1 рубль 13 копеек, 57 копеек, 29 копеек, 15 копеек, 8 копеек. Ответ можно получить таким способом : 7 + 1 = 8; 2*7 + 1 = 15; 4*7 + 1 = 29 и т.д. (первые множители это последовательные степени двойки : 2, 4, 8, 16, 32, 64).
На автогонках одновременно стартуют два автомобиля. Первый автомобиль каждый круг проходит за 1 минуту, второй автомобиль проходит каждый круг за 1 минуту 0,05 секунды. Определите, через сколько кругов и в каком месте круга вторая машина догонит первую?
Ответ
Так как вторая машина едет медленнее первой, то она никогда не сможет догнать первую машину.
На ярмарке тортов один покупатель приценился сразу к трем продавцам тортов. Продавцы продавали торты по двум разным ценам и каждый предлагал какой-то один торт из двух типов. Каждому из продавцов (первому, второму и третьему) покупатель задал только по одному вопросу : Дороже ли торт третьего продавца, чем торт у первого? Дороже ли торт второго, чем торт у третьего? Можете ли вы мне продать два торта за 100 рублей? На все три вопроса покупатель получил одинаковый ответ (да или нет). Как вы думаете, купил покупатель два торта за 100 рублей или нет?
Ответ
Предположим, что на первые два вопроса покупателю ответили да, тогда получилось бы, что продавцы продают торты по трем разным ценам, а не по двум. Следовательно, покупатель во всех трех случаях получил отрицательный ответ нет.
Можете ли вы назвать десятизначное число, состоящее из десяти различных цифр (цифры : 0,1,2,3,4,5,6,7,8,9), которое бы при умножении на 2 давало другое десятизначное число, также состоящее из десяти разных цифр.
Ответ
Этим числом является 4 938 271 605. Если его умножить на 2, то получим число 9 876 543 210.
|
Поделитесь с друзьями: |
www.treningmozga.com
