Прямоугольник презентация геометрия 8 класс: Презентация на тему “Прямоугольник” по геометрии 8 класс
Презентация “Прямоугольники” 8 класс – геометрия, презентации
библиотека
материалов
Содержание слайдов
Номер слайда 1
ПРЕЗЕНТАЦИЯ ПО ТЕМЕ: «ПРЯМОУГОЛЬНИК»8 КЛАССМБОУ «Красноярская средняя школа»Автор: Джелилова Лиля Энверовна,учитель математики
Прямоугольник — это четырехугольник, у которого все углы прямые (равны 90 градусам)
Номер слайда 3
Свойства прямоугольника 1.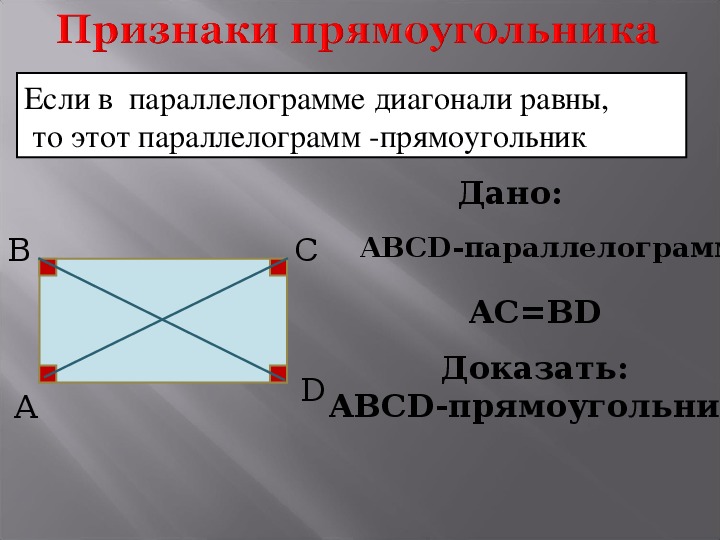 Так как прямоугольник – это параллелограмм, то все свойства параллелограмма верны и для прямоугольника. 2. Стороны прямоугольника являются его высотами.3. Диагонали прямоугольника равны.4. Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.5. Около любого прямоугольника можно описатьокружность, при этом диагональ прямоугольника равна диаметру описанной окружности.
Так как прямоугольник – это параллелограмм, то все свойства параллелограмма верны и для прямоугольника. 2. Стороны прямоугольника являются его высотами.3. Диагонали прямоугольника равны.4. Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.5. Около любого прямоугольника можно описатьокружность, при этом диагональ прямоугольника равна диаметру описанной окружности.
Номер слайда 4
Прямоугольник. Прямоугольник – это параллелограмм, у которого все углы прямые.∠A=∠B=∠C=∠D=90°
Прямоугольник.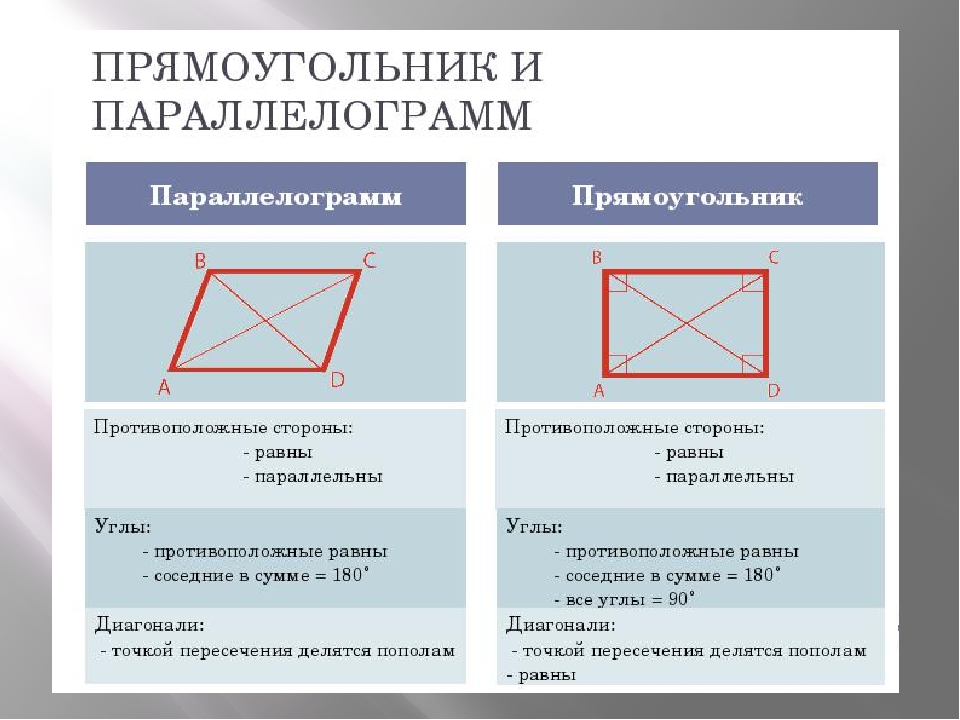 Решение задач. Задача: ABCD – прямоугольник. АК – биссектриса ∠A, СК=2,7 см, КD =4,5 см. Найти периметр ABCD. Ответ: Р=23,4 см
Решение задач. Задача: ABCD – прямоугольник. АК – биссектриса ∠A, СК=2,7 см, КD =4,5 см. Найти периметр ABCD. Ответ: Р=23,4 см
Прямоугольник. Решение задач. Задача: ABCD – прямоугольник. Найти OН, если BD=12 см, AB=6 см. Ответ: 3 см
Номер слайда 7
Площадь прямоугольника. S=a* b. S=½bh
S=a* b. S=½bh
Прямоугольник. Решение задач. Задача: ABCD – прямоугольник. Найти ∠COD, если BD=12 см, AB=6 см. Ответ: 60°
Прямоугольник
Давайте вспомним, что параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Дадим определение прямоугольнику. Итак, прямоугольник
– это параллелограмм, у которого все углы прямые.
Итак, прямоугольник
– это параллелограмм, у которого все углы прямые.
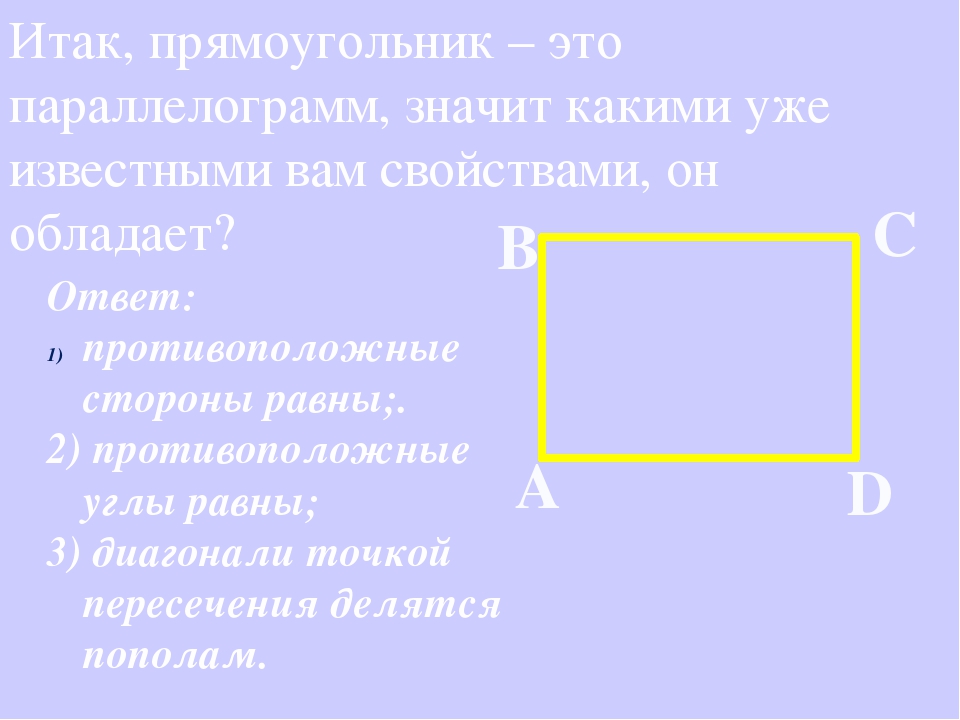
Так как прямоугольник является параллелограммом, то он обладает всеми его свойствами.
У прямоугольника противоположные стороны равны.
Диагонали прямоугольника точкой пересечения делятся пополам.
Кроме этих свойств рассмотрим ещё одно свойство – свойство диагоналей прямоугольника.
Теорема. Свойство диагоналей прямоугольника. Диагонали прямоугольника равны.
Доказательство.
Рассмотрим прямоугольные и .
Катет – общий, как противоположные стороны прямоугольника.
по двум катетам.
Следовательно, .
Что и требовалось доказать.
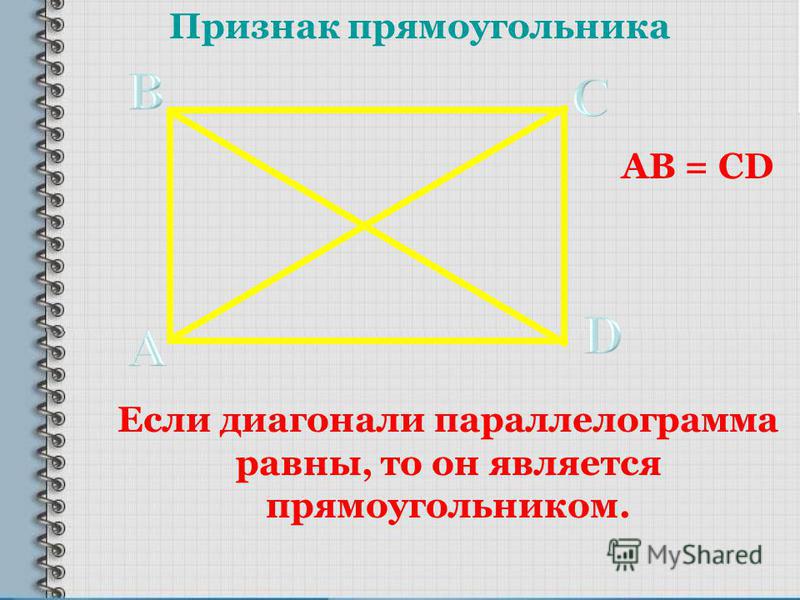
Теорема. Признак прямоугольника. Если у параллелограмма диагонали равны, то этот параллелограмм – прямоугольник.
Доказательство.
Пусть – параллелограмм,
.
Рассмотрим и .
Сторона – общая, как противоположные стороны параллелограмма,
по условию.
по третьему признаку. Следовательно, .
, .
Получаем .
.
.
Следовательно, – прямоугольник.
Теорема доказана.
Давайте решим задачу.
Задача. В прямоугольнике сторона см, а. Найдите диагональ .
Решение.
– прямоугольный.
.
(см).
,следовательно, см.
Ответ: см.
Задача. В прямоугольнике диагонали пересекаются в точке . . Найдите .
Решение.
,
следовательно, – равнобедренный.
.
,
,
,
,
.
Ответ: .
Задача. Найдите
периметр прямоугольника ,
если биссектриса делит
сторону на
отрезки см
и см.
Решение.
– прямоугольный.
.
,.
– равнобедренный,.
Так как см, то см.
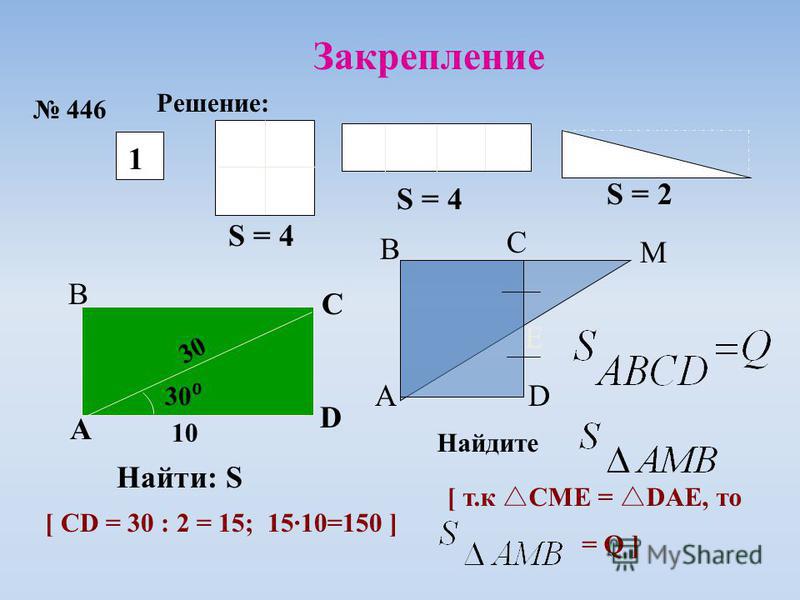
см. (см),
см.
,
(см).
Ответ: см.
Тест по теме “Прямоугольник,ромб,квадрат”
Геометрия
8 класс
Тест по теме «Прямоугольник, ромб, квадрат»
Технологическая карта контрольно-измерительного материала
Автор | Белянина С.Н.учитель математики МОУ СОШ д.Сарафаново им.Героя России Ю.П.Яковлева |
Класс | 8 |
Предмет | геометрия |
Учебник | Геометрия. |
Тема контроля | Прямоугольник, ромб, квадрат. ( п.46-47) |
Вид контроля | тематический |
Форма и методы контроля | Письменный индивидуальный тест |
Время контроля | Не более 30 минут |
Цель контроля | Проверить уровень усвоения учащимися учебного материала по данной теме. |
Формируемые результаты | Личностные результаты: – формирование ответственного отношения к учению, – формирование готовности и способности обучающегося к саморазвитию и самообразованию на основе мотивации к обучению и познанию. Метапредметные результаты: -умение осознанно выбирать наиболее эффективные способы решения учебных задач, -умение оценивать правильность выполнения учебной задачи. Предметные результаты: -овладение приемами решения геометрических задач о прямоугольнике, ромбе, квадрате; -развитие умения использовать чертежи для решения различных геометрических задач. |
Содержание теста | Тест состоит из 10 заданий. Задание №1 – на соответствие, в №2-необходимо вставить пропущенные слова, в №3 и №4 –необходимо выбрать верный ответ, в заданиях №5 и №6 нужно записать только ответ. Эти задания выполняются практически устно. |
Критерии оценивания | Оценить работу можно разными вариантами. Вариант 1: Выполнены правильно задания с №1 по №5 или №6 – «3» Выполнены правильно задания с №1 по №7 или №8- «4» Выполнены правильно с №1 по №9 или №10 – «5» Вариант 2: Если выполнено правильно от 50% до 60% – оценка «3», Если выполнено правильно от 61% до 80% – оценка «4», Если выполнено правильно от 81% до 100% – оценка «5». Вариант №3: Если ученик набрал 7-8 баллов – оценка «3», Если ученик набрал 9-13 баллов- оценка «4», Если ученик набрал 14-17 баллов- оценка «5» |
Место контроля в системе уроков | Этот тест можно провести после изучения данной темы (п.46-47). Результаты теста позволят учащимся и педагогу ещё раз обратить внимание на вопросы требующие более тщательной подготовки, устранить пробелы на последующих уроках. Тест также можно провести при подготовке выпускников к ОГЭ. |
Инструкция для выполнения теста.
Дорогой ученик!
Сейчас тебе предстоит выполнить тест по теме «Прямоугольник, ромб, квадрат». При выполнении теста будь внимательным. Обрати внимание, что в тесте проверяется знание теоретического и практического материала по теме. В тесте указано количество баллов за каждое задание.
В тесте указано количество баллов за каждое задание.
Ответы вноси в специальный бланк для ответов. Пиши аккуратным, разборчивым почерком.
Тест содержит 10 заданий. Задание №1 на соответствие, в №2 нужно вставить пропущенные слова, в №3 и №4 необходимо указать верный ответ, №5 и №6 решаются практически устно, но можно использовать для записи решения, черновик, в №7,8,9 нужно решить задачу по готовому чертежу. Можно делать краткие записи в черновике. Решение и ответ задания №10 нужно оформить в бланке.
Справочным материалом пользоваться запрещается.
Время выполнения теста – не более 30 минут.
Желаю успехов!
Тест по теме «Прямоугольник, ромб, квадрат»
№ | Текст задания | Максимальное количество баллов |
1 | Установите соответствие между четырёхугольниками и их названиями. Ответ запишите в таблицу. 1)ромб 2)параллелограмм 3)прямоугольник 4)квадрат 5)трапеция | 1б. |
2 | Вместо многоточия вставить пропущенные слова: А) Прямоугольником называется параллелограмм, у которого все углы ……… Б) Прямоугольник, у которого все стороны равны называется …………. В) Все углы квадрата ……… Г) Параллелограмм, у которого все стороны равны называется ………. Д) Если в параллелограмме диагонали равны, то этот параллелограмм……….. Е) Диагонали ромба …………….. и делят его углы ………… | Каждый ответ по 0,5 балла. Максимальный балл за вопрос -3б. |
3 | Квадрат сложили из четырёх равных треугольников. Какие это треугольники? А) равносторонние Б) равнобедренные В) разносторонние | 1б. |
4 | Четырёхугольник является ромбом, если обладает следующими свойствами: А) диагонали равны Б) диагонали точкой пересечения делятся пополам В) диагонали перпендикулярны и точкой пересечения делятся пополам Г) диагонали перпендикулярны | 1б. |
5 | Решить задачу. Сторона ромба равна 8 см. Найти периметр ромба. | 1б. |
6 | Диагонали параллелограмма 4дм и 5дм. | 1б. |
7 | Решить задачу по готовому чертежу. В ромбе KMNP MP=8 см, MPN = 60.Найти периметр ромба KMNP. | 2б. |
8 | Решить задачу по готовому чертежу. Дан прямоугольник AMKP. Найти угол АОМ. | 2б. |
9 | Решить задачу по готовому чертежу. PNMK – прямоугольник, AP = 6 см. Найти периметр ABCD. | 2 б. |
10 | Решить задачу. Решение записать в отведенное для этого место на бланке ответов. Через вершину С прямоугольника АВСД проведена прямая, параллельная диагонали ВД и пересекающая прямую АВ в точке М. Через точку М проведена прямая, параллельная диагонали АС и пересекающая прямую ВС в точке N. Найти периметр четырёхугольника АСМN, если диагональ ВД равна 8 см. | 3 б. |
Бланк ответов
Ф.И.ученика______________________________________________
№ задания | Ответ | Кол-во баллов |
1 | ||
2 | Ответ: А)____________________________________________ Б)____________________________________________ В)____________________________________________ Г)____________________________________________ Д)____________________________________________ Е)____________________________________________ | |
3 | Ответ:_____________________ | |
4 | Ответ:_____________________ | |
5 | Ответ:_____________________ | |
6 | Ответ:_____________________ | |
7 | Ответ:_____________________ | |
8 | Ответ:_____________________ | |
9 | Ответ:____________________ | |
10 | Решение: Ответ:______________________ | |
Общее количество баллов | ||
Оценка | ||
Ключ к тесту:
№ задания | Ответ |
1 | |
2 | Ответ: А) прямые или 90 Б) квадратом В) прямые или 90 Г) ромбом Д) прямоугольник Е) взаимно перпендикулярны, пополам |
3 | Б |
4 | В |
5 | 32 см |
6 | Нет |
7 | 32 см |
8 | 40 |
9 | 48 см |
10 | 32 см |
Литература:
Геометрия. 7-9 классы: учеб.для общеобразоват. организаций /Л.С.атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – М.:Просвещение,2017
7-9 классы: учеб.для общеобразоват. организаций /Л.С.атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – М.:Просвещение,2017
Поурочные разработки по геометрии .8 класс. М:ВАКО,2004
Иллюстративная математика
Задача
Четырехугольник с вершинами $(-6, 2)$, $(-3,6)$, $(9, -3)$, $(6,-7)$ Прямоугольник? Объяснять.
Комментарий IM
Цель этого задания — дать учащимся возможность применить широкий спектр идей из геометрии и алгебры, чтобы показать, что данный четырехугольник является прямоугольником. Здесь потребуется творческий подход, поскольку единственной имеющейся информацией являются декартовы координаты вершин четырехугольника.Использование этой информации для демонстрации того, что четыре угла являются прямыми, потребует некоторых вспомогательных построений. Студентам потребуется достаточно времени, и для некоторых
методы, представленные ниже, руководство. Награда за тщательное выполнение этого задания должна оправдать усилия, потому что это дает учащимся возможность увидеть несколько геометрических и алгебраических конструкций, объединенных для достижения общей цели.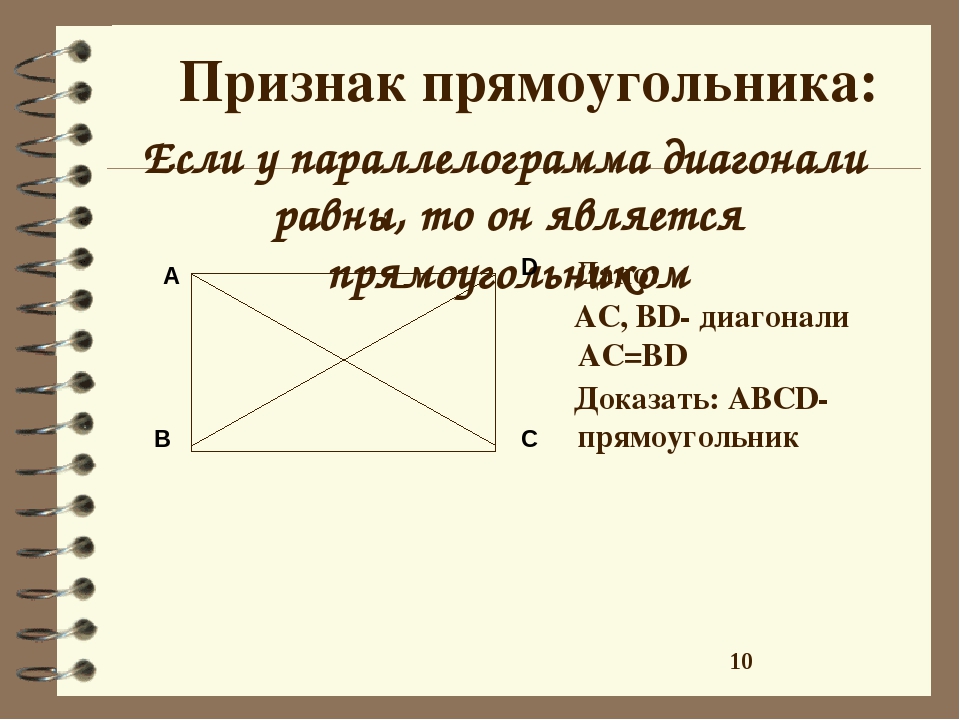
Эта задача была сформулирована так, чтобы поддерживать широкий спектр подходов, которые помогают связать стандарты геометрии восьмого класса со стандартами геометрии (и алгебры) средней школы. Важно учитывать разные методы решения, потому что это выявляет связи между разными стандартами. Чтобы решить эту задачу, учащиеся должны показать, что все четыре угла в четырехугольнике прямые. Один из способов добиться этого на уровне восьмого класса — это теорема Пифагора и ее обращение.Также на уровне восьмого класса к четырехугольнику можно применить жесткие движения плоскости, чтобы его углы были равны углам, образованным горизонтальными и вертикальными линиями сетки.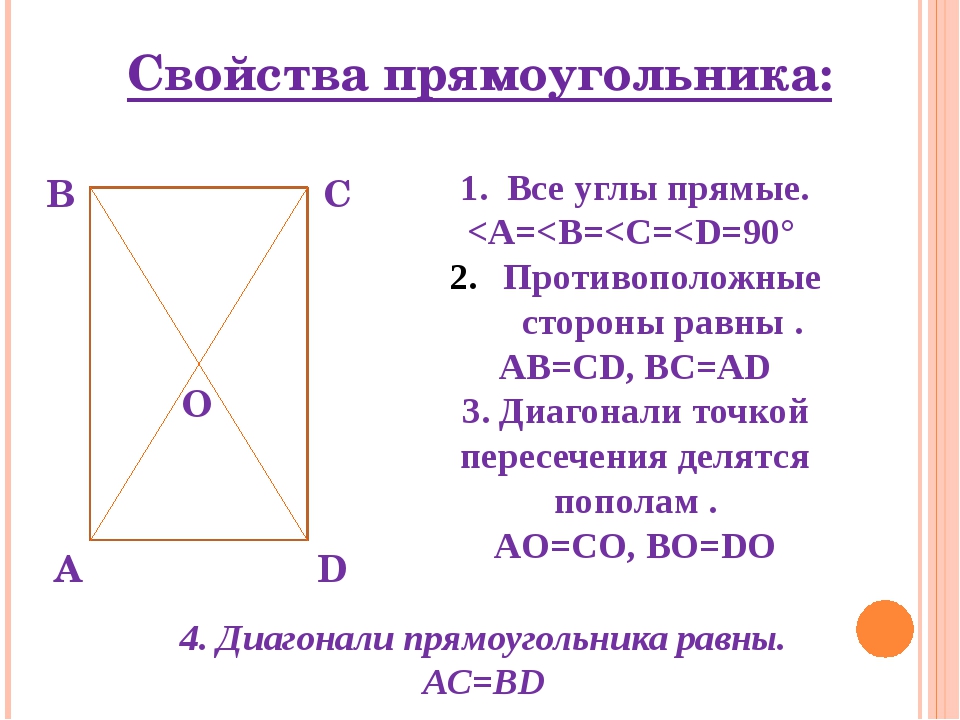
Одним из преимуществ открытых задач, подобных этой, является то, что они допускают несколько творческих решений и тем самым показывают, как связаны между собой различные направления учебной программы. Эта задача очень сильно поддерживает трансформационный подход к геометрии, адаптированный в CCSS: второе решение использует повороты и перемещения фундаментальным образом, в то время как четвертое решение требует понимания подобных треугольников и, следовательно, растяжений плоскости. В то же время это дает возможность связать эти новые идеи с классическими подходами, используя теорему Пифагора и наклоны прямых.
В то же время это дает возможность связать эти новые идеи с классическими подходами, используя теорему Пифагора и наклоны прямых.
Это задание предназначено только для учебных целей. Открытый характер задачи делает ее идеально подходящей для расширенной работы и обсуждения, включая обмен идеями и различными подходами. Два решения подходят для восьмого класса, в то время как остальные четыре требуют знания содержания средней школы, поэтому в идеале учащиеся будут работать над этим как в средней школе, так и позже в старшей школе.
Учителя, работающие с учащимися 8-х классов, могут предложить предварительные задания в виде шаблонов, которые представляют координаты четырех вершин четырехугольника с центром в точке (0,0), чтобы использовать одно жесткое движение (вращение), а затем отдельный набор координаты четырех вершин, образующих четырехугольник со стороной, параллельной линиям сетки. Затем учащиеся могут рассмотреть как эти предварительные задачи, так и стратегии, полезные для их решения, когда им будет представлен этот элемент задачи в том виде, в котором он написан.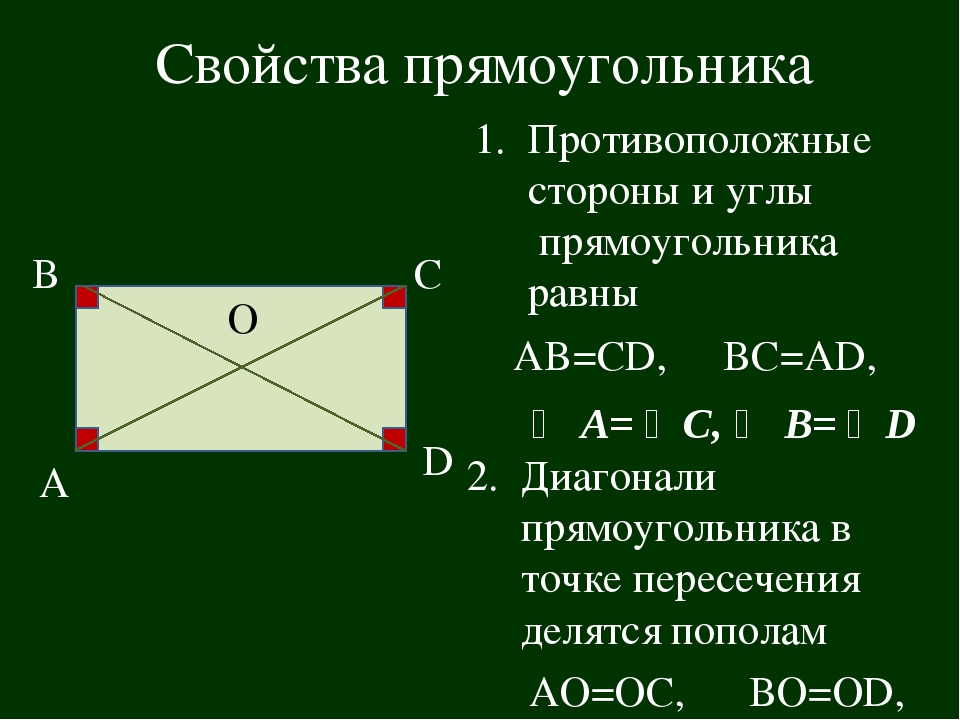 Существует также более директивная версия этой задачи, в которой учащимся предлагается использовать теорему Пифагора: 8.G Прямоугольник в координатной плоскости
Существует также более директивная версия этой задачи, в которой учащимся предлагается использовать теорему Пифагора: 8.G Прямоугольник в координатной плоскости
Решение 6 — это версия решения 2 для старшей школы. Остальные решения представляют разные подходы, поскольку они концептуально сильно отличаются друг от друга.
Решения
Решение: Теорема Пифагора и ее обращение (8.G.7 и 8.G.8)
Ниже приведено изображение четырехугольника, обозначенного $PQRS$, с двумя добавленными диагоналями, а также точками $M$ и $N$, которые помогут вычислить длину двух диагоналей $\overline{PR}$ и $\ overline{QS}$ с помощью теоремы Пифагора.2 \end{выравнивание}
Все длины справа можно рассчитать с помощью координат. Например, $|PM| = 5$ и $|MR| = 15$, так как $P = (-6,2)$, $M = (-6,-3)$, и $R = (9,-3)$. Аналогично $|SN| = 13$ и $|NQ| = 9$. Подставляя эти значения в приведенные выше уравнения, мы находим $$ |PR| = |КВ| = \sqrt{250}. $$
Чтобы показать, что $PQRS$ — прямоугольник, нам нужно показать, что четыре угла
являются прямыми углами. 2$.2$.
2$.2$.
Решение: Жесткие движения самолета (8.G.2 и 8.G.3)
Цель здесь состоит в том, чтобы сначала переместить четырехугольник так, чтобы его центр находился в $(0,0)$, а затем примените поворот вокруг $(0,0)$ так, чтобы линии, содержащие стороны прямоугольника, были параллельны линиям сетки. Обратите внимание, что $(-3,6)$ — это точка прямоугольника с наибольшей координатой $y$, а $(6,-7)$ — точка с наименьшей координатой $y$. Точка с наибольшей координатой $x$ равна $(9,-3)$, а точка с наименьшей координатой $x$ равна $(-6,2)$.Нам нужно перевести влево на $1,5$ единиц и вверх на $0,5$ единиц, чтобы центрировать этот прямоугольник вокруг $(0,0)$. Вершины перенесенного прямоугольника: $(-7,5,2,5)$, $(-4,5,6,5)$, $(7,5,-2,5)$, $(4,5,-6,5)$. Переведенный прямоугольник с вершинами $A = (-7,5,2,5)$, $B = (-4,5,6,5)$, $C = (7,5,-2,5)$, $D = (4,5,-6,5)$ равен на фото ниже:
Обратите внимание, что четырехугольник является параллелограммом: мы можем убедиться в этом, вычислив наклоны прямых, содержащих противоположные стороны параллелограмма.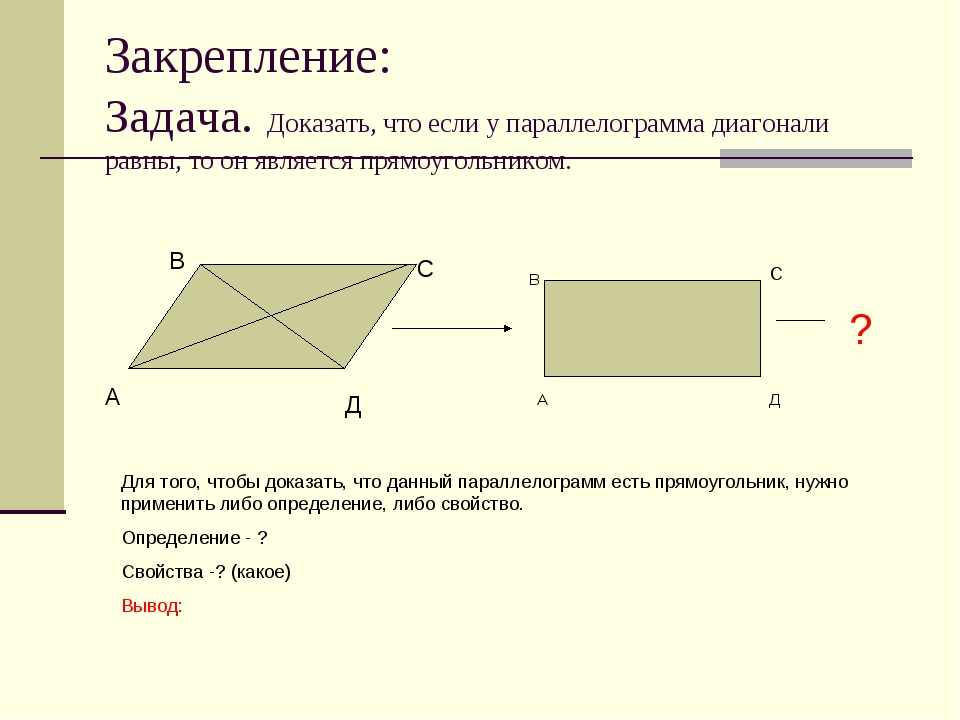 За
пример
$$
\text{наклон}\влево(\overleftrightarrow{AB}\вправо) =
\frac{2,5-6,5}{-7,5 -(-4,5)} = \frac{-2,5-(-6,5)}{7,5 – 4,5} =
\текст{наклон}\влево(
\overleftrightarrow{CD}\вправо)
$$
что мы можем видеть без оценки, так как правое выражение является левым
выражение руки, умноженное на $\frac{-1}{-1} = 1$. так же
$$
\text{наклон}\влево(\overleftrightarrow{BC}\вправо) =
\ гидроразрыва {6,5-(-2,5)} {-4,5-7,5} = \ гидроразрыва {-6,5-2,5} {4,5-(-7,5)} =
\text{наклон}\влево(\overleftrightarrow{DA}\вправо).
$$
Обратите внимание, что диагонали $\overline{AC}$ и $\overline{BD}$ четырехугольника $ABCD$ проходят через $(0,0)$.2}$ который
— расстояние от $B$ до $(0,0)$.
За
пример
$$
\text{наклон}\влево(\overleftrightarrow{AB}\вправо) =
\frac{2,5-6,5}{-7,5 -(-4,5)} = \frac{-2,5-(-6,5)}{7,5 – 4,5} =
\текст{наклон}\влево(
\overleftrightarrow{CD}\вправо)
$$
что мы можем видеть без оценки, так как правое выражение является левым
выражение руки, умноженное на $\frac{-1}{-1} = 1$. так же
$$
\text{наклон}\влево(\overleftrightarrow{BC}\вправо) =
\ гидроразрыва {6,5-(-2,5)} {-4,5-7,5} = \ гидроразрыва {-6,5-2,5} {4,5-(-7,5)} =
\text{наклон}\влево(\overleftrightarrow{DA}\вправо).
$$
Обратите внимание, что диагонали $\overline{AC}$ и $\overline{BD}$ четырехугольника $ABCD$ проходят через $(0,0)$.2}$ который
— расстояние от $B$ до $(0,0)$.
Предположим, мы вращаем $ABCD$ около $(0,0)$, пока не найдем новый четырехугольник $EFGH$ с $\overleftrightarrow{FG}$ и $\overleftrightarrow{EH}$ оба параллельны оси $x$. Диагонали $\overline{EG}$ и $\overline {FH}$ по-прежнему пересекаются в точке $(0,0)$ и конгруэнтны, как показано ниже:
Глядя на картинку, предположим, что мы фиксируем $E$ и $G$, а затем выбираем $x$ и $y$ с
$x$ на верхней синей линии, $y$ на нижней синей линии, так что $(0,0)$ содержится в $\overline{xy}$.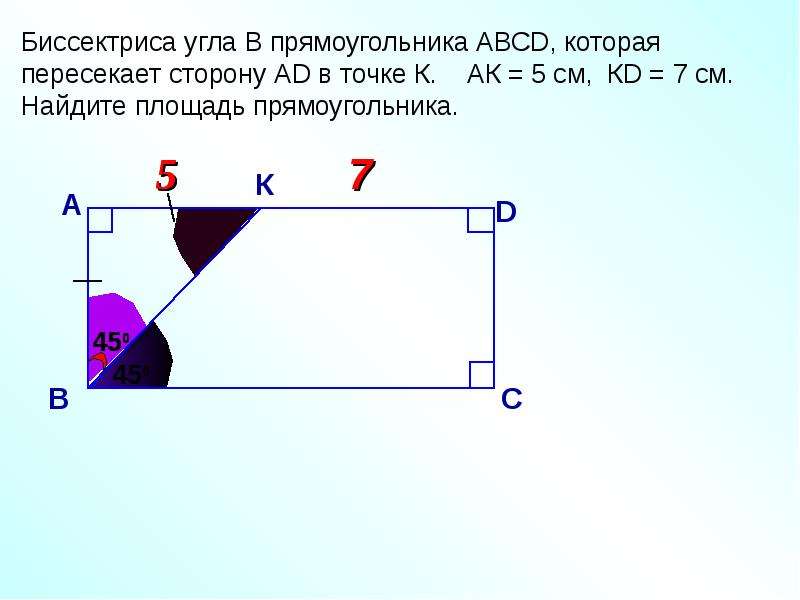 Если $x$ находится слева от $F$ или справа от $G$, то $|xy| \gt
|EG|$. Если $x$ находится между $F$ и $G$, то $|xy| \lt |EG|$. Итак, если $|xy| = |EG|$, то $x = F, y = H$, где $EFGH$ — прямоугольник.
Если $x$ находится слева от $F$ или справа от $G$, то $|xy| \gt
|EG|$. Если $x$ находится между $F$ и $G$, то $|xy| \lt |EG|$. Итак, если $|xy| = |EG|$, то $x = F, y = H$, где $EFGH$ — прямоугольник.
Решение: Наклоны линий (G.GPE.4 и G.GPE.5)
Обозначим вершины четырехугольника следующим образом: $P = (-6,2)$, $Q = (-3,6)$, $R = (9,-3)$, $S = (6,- 7)$:
Идея этого подхода состоит в том, чтобы рассмотреть линии, содержащие четыре стороны четырехугольника $PQRS$ и по критерию наклона показать, что они удовлетворяют в прямых углах.Напомним, что критерий наклона гласит, что если линия $L_1$ имеет наклон $s_1 \neq 0$ и линия $L_2$ имеет наклон $s_2 = \frac{-1}{s_1}$, тогда $L_1$ и $L_2$ перпендикулярны (в единственной точке их пересечения). Вычислим наклоны линий, содержащих смежные вершины $PQRS$:
\начать{выравнивать} \text{наклон}\left(\overleftrightarrow{PQ}\right) &= \frac{2-6}{-6-(-3)} = \frac{-4}{-3}\\ \text{наклон}\left(\overleftrightarrow{QR}\right) &= \frac{6-(-3)}{-3-9} = \frac{9}{-12} \\ \text{наклон}\left(\overleftrightarrow{RS}\right) &= \frac{-3-(-7)}{9-6} = \frac{4}{3} \\ \text{наклон}\left(\overleftrightarrow{SP}\right) &= \frac{-7-2}{6-(-6)} = \frac{-9}{12} \end{выравнивание}
Поскольку $\frac{-4}{-3}$ и $\frac{9}{-12}$ являются обратными величинами разных знаков,
$\overleftrightarrow{PQ}$ пересекается с $\overleftrightarrow{QR}$ перпендикулярно в точке $Q$.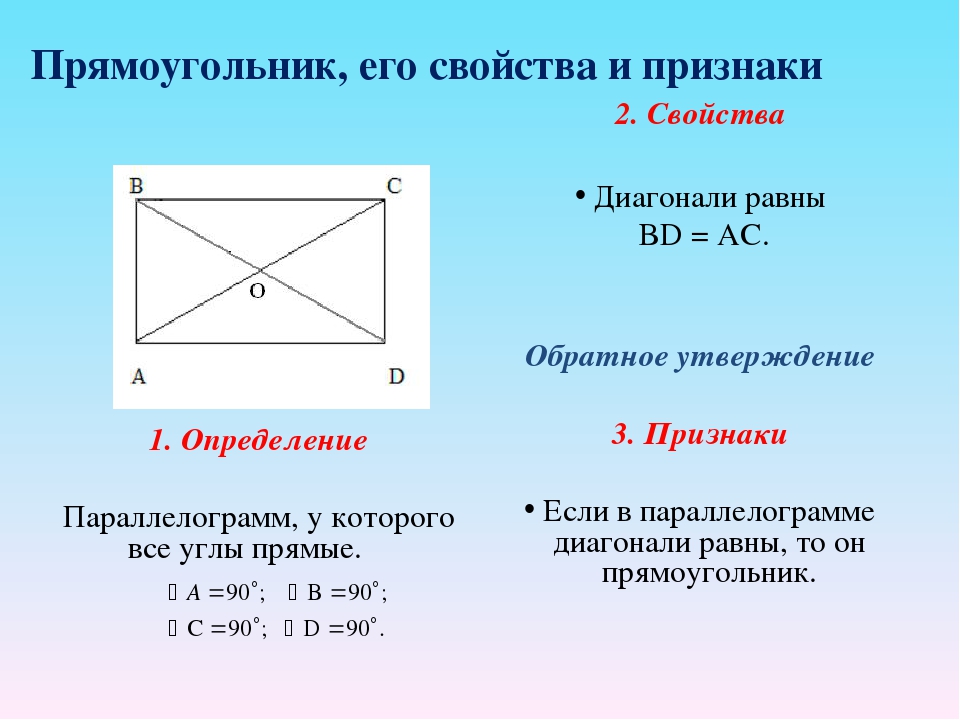 Так как $\frac{9}{-12}$ и $\frac{4}{3}$ являются обратными величинами разных знаков,
$\overleftrightarrow{QR}$ пересекается с $\overleftrightarrow{RS}$ перпендикулярно в точке $R$. Так как $\frac{4}{3}$ и $\frac{-9}{12}$ являются обратными величинами противоположных знаков,
$\overleftrightarrow{RS}$ пересекается с $\overleftrightarrow{SP}$ перпендикулярно в точке $S$. Поскольку $\frac{-9}{12}$ и $\frac{-4}{-3}$ являются обратными величинами разных знаков,
$\overleftrightarrow{SP}$ пересекается с $\overleftrightarrow{PQ}$ перпендикулярно в точке $P$. Поскольку в четырехугольнике $PQRS$ все четыре угла прямые, $PQRS$ — прямоугольник.
Так как $\frac{9}{-12}$ и $\frac{4}{3}$ являются обратными величинами разных знаков,
$\overleftrightarrow{QR}$ пересекается с $\overleftrightarrow{RS}$ перпендикулярно в точке $R$. Так как $\frac{4}{3}$ и $\frac{-9}{12}$ являются обратными величинами противоположных знаков,
$\overleftrightarrow{RS}$ пересекается с $\overleftrightarrow{SP}$ перпендикулярно в точке $S$. Поскольку $\frac{-9}{12}$ и $\frac{-4}{-3}$ являются обратными величинами разных знаков,
$\overleftrightarrow{SP}$ пересекается с $\overleftrightarrow{PQ}$ перпендикулярно в точке $P$. Поскольку в четырехугольнике $PQRS$ все четыре угла прямые, $PQRS$ — прямоугольник.
Решение: Подобные треугольники (G.SRT.5)
Этот подход начинается с добавления прямоугольника, стороны которого лежат на линиях координатной сетки, в которую вписан данный прямоугольник, как показано на рисунке. ниже:
Данный четырехугольник был помечен $PQRS$, а описывающая его
прямоугольник был помечен $ABCD$. Сейчас мы изучим следующие четыре
треугольники: $\треугольник APS$, $\треугольник BQP$, $\треугольник CRQ$ и $\треугольник DSR$.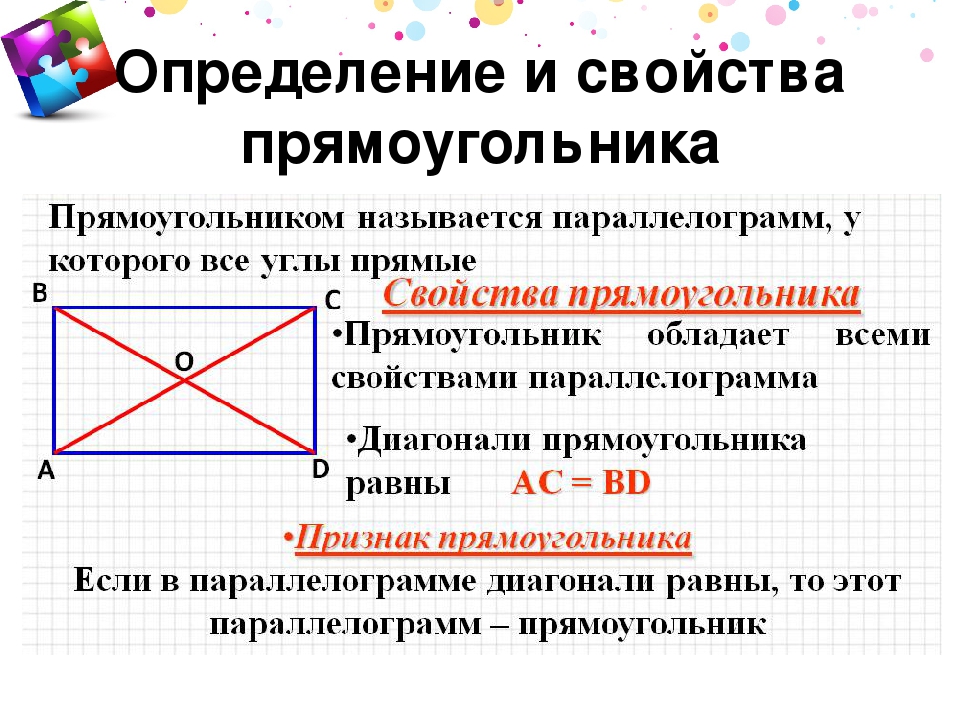 Заметим, что $\треугольник APS$ сравним с $\треугольником CRQ$ по формуле
САС:
Заметим, что $\треугольник APS$ сравним с $\треугольником CRQ$ по формуле
САС:
- $|АП| = |CR| = 9$,
- $|КАК| = |CQ| = 12$,
- $m(\угол A) = m(\угол C) = 90$.
Аналогичные рассуждения показывают, что $\треугольник BQP$ конгруэнтен $\треугольнику DSR$:
- $|БК| = |ДС| = 3$,
- $|БП| = |ДР| = 4$,
- $m(\угол B) = m(\угол D) = 90$.
Теперь мы сравним по одному треугольнику из каждой из наших конгруэнтных пар, $\triangle
Например, APS$ и $\triangle BQP$. Обратите внимание, что $|AP| = 3 \times |BQ|$
и $|КАК| = 3 \times |BP|$. Так как оба угла $A$ и $B$ прямые
отсюда следует, что $\triangle APS$ подобен $\triangle BQP$.\circ$, чтобы показать, что каждый угол
в четырехугольнике $PQRS$ — прямой угол. Мы предоставляем подробный аргумент для $\angle QPS$; другие случаи можно сделать таким же образом. Обратите внимание, что
$$
m(\угол BPQ) + m(\угол (QPS) + m(\угол APS) = 180
$$
потому что эти три угла вместе образуют прямую линию. Поскольку $\triangle APS$ подобен $\triangle BQP$, мы знаем, что $m(\angle BPQ) = m(\angle
АСП)$. Имеем $m(\угол APS) + m(\угол ASP) + m(\угол PAS) = 180$.
Но $m(\angle PAS) = 90$, так как этот угол образован пересечением осей координат $x$ и $y$.Таким образом, мы заключаем, что
Поскольку $\triangle APS$ подобен $\triangle BQP$, мы знаем, что $m(\angle BPQ) = m(\angle
АСП)$. Имеем $m(\угол APS) + m(\угол ASP) + m(\угол PAS) = 180$.
Но $m(\angle PAS) = 90$, так как этот угол образован пересечением осей координат $x$ и $y$.Таким образом, мы заключаем, что
\начать{выравнивать} m(\угол (QPS) &= 180 – m(\угол APS) – m(\угол BPQ) \\ &= 180 -m(\угол APS) + m(\угол ASP) \\ &= 180 – 90 \\ & = 90. \end{выравнивание}
Аналогичное рассуждение показывает, что остальные четыре угла в четырехугольнике $PQRS$ прямые, а значит, это прямоугольник.
Решение: Конгруэнтные треугольники (G-CO.9, G-CO.11)
Это решение является вариантом первого решения, подходящего для старшеклассников.Каждая из двух диагоналей прямоугольника делит прямоугольник на два треугольника, и мы покажем, используя критерий $SSS$ конгруэнтности треугольников, что все четыре из этих треугольников конгруэнтны. Это означает, что все четыре треугольника прямоугольные, а четырехугольник — прямоугольник.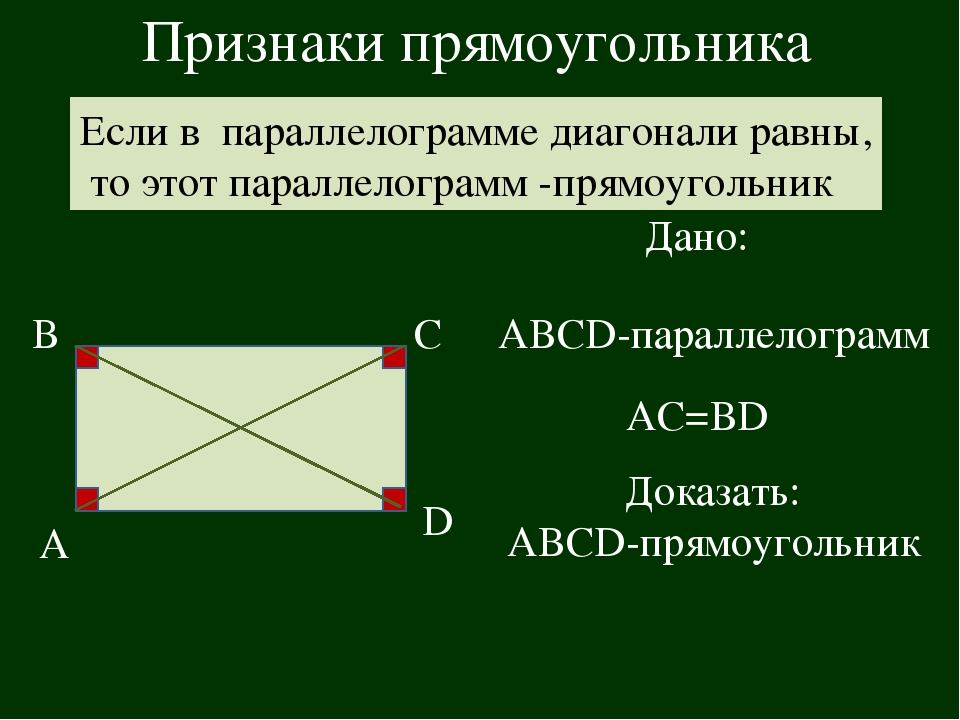
Используя координаты $P = (-6,2)$, $Q = (-3,6)$, $R = (9,-3)$, $S = (6,-7)$ и формулу расстояния для точек на плоскости имеем
\начать{выравнивать} |ПК| &= \sqrt{25} = 5\\ |QR| &= \sqrt{225} = 15\\ |РС| &= \sqrt{25} = 5\\ |СП| &= \sqrt{225} = 15.\circ$ и $PQRS$ — прямоугольник.
Решение: Параллелограммы и прямоугольники (G-CO.11)
Это решение следует той же логике, что и второе решение, но использует важный критерий прямоугольника, разработанный в старшей школе: параллелограмм является прямоугольником тогда и только тогда, когда его диагонали равны. Сначала покажем, что четырехугольник является параллелограммом. Наклон линии, содержащей $(-6, 2)$ и $(-3,6)$, равен
$$
\frac{6-2}{-3-(-6)} = \frac{4}{3}.
$$
Наклон линии, содержащей $(9,-3)$ и $(6,-7)$, равен
$$
\frac{-7-(-3)}{6-9} = \frac{-4}{-3}.$$
Поскольку эти прямые имеют одинаковый наклон, они параллельны. Точно так же
наклон линии, содержащей $(-6,2)$ и $(6,-7)$, равен
$$
\frac{-7-2}{6-(-6)} = \frac{-9}{12}.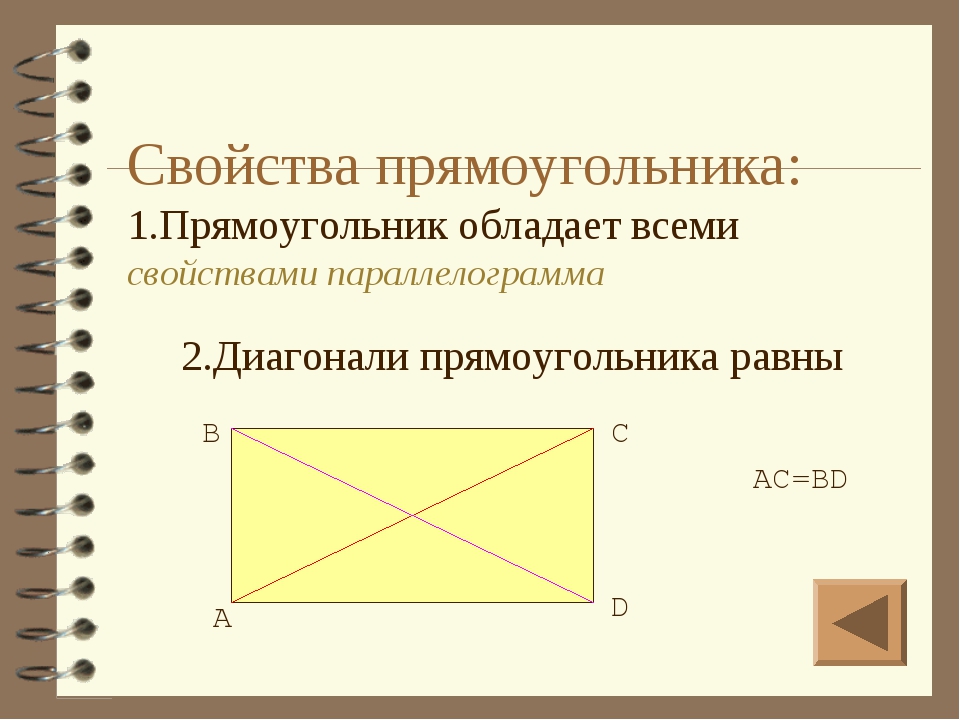 $$
Наклон линий, содержащих $(-3,6)$ и $(9,-3)$, равен
$$
\frac{-3-6}{9-(-3)} = \frac{-9}{12}.
$$
Эти две линии имеют одинаковый наклон, поэтому они также параллельны и
четырехугольник является параллелограммом.
$$
Наклон линий, содержащих $(-3,6)$ и $(9,-3)$, равен
$$
\frac{-3-6}{9-(-3)} = \frac{-9}{12}.
$$
Эти две линии имеют одинаковый наклон, поэтому они также параллельны и
четырехугольник является параллелограммом.
Чтобы показать, что две диагонали четырехугольника имеют одинаковую длину, мы можем использовать формулу расстояния для точек на плоскости.2} = \sqrt{250}. $$ Эти две диагонали параллелограмма имеют одинаковую длину, поэтому четырехугольник, образованный этими четырьмя точками, является прямоугольником.
Что такое прямоугольник? – [Определение, факты и примеры]
Что такое прямоугольник?
Прямоугольник — это двухмерная фигура в геометрии, имеющая 4 стороны и 4 угла. Две его стороны сходятся под прямым углом. Таким образом, у прямоугольника 4 угла по 90° каждый. Противоположные стороны прямоугольника имеют одинаковую длину и параллельны.Две стороны называются параллельными, если расстояние между ними остается одинаковым во всех точках.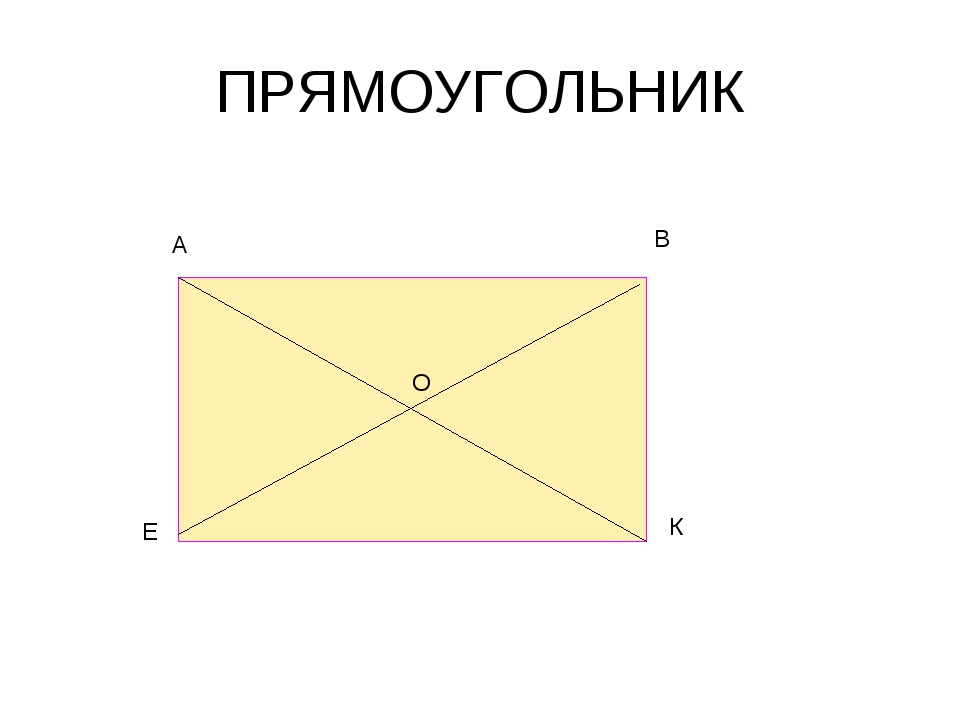
Другие названия прямоугольника
-
Поскольку все углы прямоугольника равны, мы также называем его равноугольным четырехугольником.
-
Поскольку у него параллельные стороны, мы также можем назвать его параллелограммом. Параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны.
Равноугольный четырехугольник
Параллелограмм
Свойства прямоугольника:
Площадь прямоугольника:
Площадь прямоугольника равна произведению двух его смежных сторон
Площадь прямоугольника = длина × ширина
Периметр :
Периметр прямоугольника равен сумме длин его четырех сторон.Так как параллельные стороны прямоугольника имеют одинаковую длину, то формула периметра прямоугольника равна
.
Периметр прямоугольника = Длина + Ширина + Длина + Ширина
= 2 длина + 2 ширина
2 (длина + ширина)
Диагонали прямоугольника :
Отрезки, соединяющие противоположные углы прямоугольника, называются его диагоналями.На данном рисунке две диагонали прямоугольника AC и BD. Диагонали прямоугольника имеют одинаковую длину. Следовательно, AC = BD
.
Прямоугольник, являющийся наиболее распространенной формой, является частью нашей повседневной жизни. Некоторыми реальными примерами прямоугольника являются столешницы, книги, мобильные телефоны, телевизор и т. д.
д.
| Интересные факты
|
Руководство по математике UnboundEd
Что содержится в Руководстве по содержанию и как его использовать?
Получите ответы на все свои вопросы о Руководстве по содержанию, в том числе о том, что содержится в каждой части и как их можно использовать в вашей роли в вашей школе.
Просмотр часто задаваемых вопросов8.Г.А | Понимание конгруэнтности и сходства с использованием физических моделей, прозрачных пленок,
или программное обеспечение для геометрии.
8.GB | Поймите и примените теорему Пифагора.
Добро пожаловать в серию руководств по математике UnboundEd! Эти руководства предназначены для того, чтобы объяснить, что говорят новые высокие стандарты математики о том, что учащиеся должны изучать в каждом классе, и что они означают для учебной программы и обучения. Это руководство, первое для 8 класса, состоит из трех частей. В первой части представлен «экскурсия» по стандартам в первых двух кластерах области геометрии (касающихся конгруэнтности, сходства и теоремы Пифагора) с использованием свободно доступных онлайн-ресурсов, которые вы можете использовать или адаптировать для своего класса.Во второй части показано, как эти стандарты соотносятся с другими понятиями в 8 классе. А в третьей части объясняется, какое место занимают конгруэнтность, сходство и теорема Пифагора в процессе обучения от начальных классов до старших классов.
Конгруэнтность и сходство
Стандарты для 8-го класса полны важных идей, так зачем начинать эту серию с конгруэнтности и подобия? Во-первых, эти стандарты являются частью «основной работы» 8-го класса, а это означает, что они заслуживают большей части учебного времени в течение учебного года. 1 Приоритизация основной работы в течение года гарантирует, что этим стандартам будет уделено должное внимание. Соответствие и сходство также необходимы учащимся для понимания других важных понятий в 8 классе, в частности наклона линии. (8.EE.B.6) Следовательно, работа с конгруэнтностью и подобием должна предшествовать линейным уравнениям, что является еще одной важной частью работы.
1 Приоритизация основной работы в течение года гарантирует, что этим стандартам будет уделено должное внимание. Соответствие и сходство также необходимы учащимся для понимания других важных понятий в 8 классе, в частности наклона линии. (8.EE.B.6) Следовательно, работа с конгруэнтностью и подобием должна предшествовать линейным уравнениям, что является еще одной важной частью работы.
Конгруэнтность и сходство также являются отличным способом начать год, потому что они включают практический подход через преобразования, что делает их доступными для любого учащегося с базовым пониманием линий и углов.Более того, стандарты соответствия и сходства напрямую связаны со стандартами геометрии средней школы (в частности, с предметами «Конгруэнтность», «Сходство и правильные треугольники»), поэтому они важны для будущих успехов учащихся. Так что, если вам интересно, с чего начать год, конгруэнтность и сходство — это надежная ставка.
В 8 классе стандарты, касающиеся конгруэнтности и сходства, сгруппированы в один кластер (называемый 8. G.A, так как это первый кластер стандартов по геометрии в классе).Несмотря на то, что он содержит только пять стандартов, этот кластер объединяет ряд математических идей, в том числе три, которые не часто рассматриваются как связанные: конгруэнтность и подобие, преобразования и отношения углов. Давайте посмотрим, что говорят эти стандарты, а затем рассмотрим каждый из них более подробно.
G.A, так как это первый кластер стандартов по геометрии в классе).Несмотря на то, что он содержит только пять стандартов, этот кластер объединяет ряд математических идей, в том числе три, которые не часто рассматриваются как связанные: конгруэнтность и подобие, преобразования и отношения углов. Давайте посмотрим, что говорят эти стандарты, а затем рассмотрим каждый из них более подробно.
8.Г.А | Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для создания геометрии.
Порядок стандартов не указывает порядок, в котором они должны преподаваться.Стандарты — это всего лишь набор требований к тому, что учащиеся должны знать и уметь делать к концу каждого года; они не предписывают точную последовательность или учебный план. В этом случае имеет смысл сначала познакомить учащихся со свойствами отражений, переносов и поворотов (8.G.A.1), а затем использовать эти преобразования для установления понятия конгруэнтности (8. G.A.2). После этого учащиеся должны быть готовы к расширению и понятию сходства (8.G.A.4). Решение задач с преобразованиями на координатной плоскости (8.G.A.3) можно интегрировать вместе с работой с этими первыми тремя стандартами, а применения трансформаций (8.G.A.5) также можно преподавать в сочетании с другой работой или их можно оставить напоследок.
G.A.2). После этого учащиеся должны быть готовы к расширению и понятию сходства (8.G.A.4). Решение задач с преобразованиями на координатной плоскости (8.G.A.3) можно интегрировать вместе с работой с этими первыми тремя стандартами, а применения трансформаций (8.G.A.5) также можно преподавать в сочетании с другой работой или их можно оставить напоследок.
Прежде чем мы начнем работать с этими стандартами, давайте на мгновение остановимся и подумаем, почему они так важны. В прошлом геометрия в классах K-8, как правило, фокусировалась на широком круге тем, ни одна из которых не преподавала слишком глубоко. Студенты могли выучить термины «конгруэнтный» и «похожий» в очень общем виде (возможно, как «одинаковая форма, тот же размер» и «такая же форма, разный размер»), но это была степень их знакомства с этими двумя важными понятиями. .Преобразования рассматривались как совершенно отдельная идея — если они вообще были освещены — с упором только на выполнение преобразований (без описания их свойств). С другой стороны, геометрия в старших классах посвящала много времени преподаванию критериев соответствия и подобия треугольников, что не имело ничего общего с тем, что ученики делали раньше. Однако теперь стандарты для 8-го класса и старшей школы используют преобразования, чтобы помочь учащимся понять конгруэнтность и сходство и согласовать их ожидания в отношении обучения учащихся.Их внимание сосредоточено не столько на выполнении преобразований, сколько на том, как они улучшают понимание учащимися взаимосвязей между фигурами. Мы хотим, чтобы учащиеся не просто могли выполнить, скажем, отражение прямоугольника над линией, но и объяснить, чем изображение этого прямоугольника похоже или отличается от оригинала. Что мы знаем об изображении этого прямоугольника на основании того, что мы знаем об исходной фигуре и свойствах преобразований?
С другой стороны, геометрия в старших классах посвящала много времени преподаванию критериев соответствия и подобия треугольников, что не имело ничего общего с тем, что ученики делали раньше. Однако теперь стандарты для 8-го класса и старшей школы используют преобразования, чтобы помочь учащимся понять конгруэнтность и сходство и согласовать их ожидания в отношении обучения учащихся.Их внимание сосредоточено не столько на выполнении преобразований, сколько на том, как они улучшают понимание учащимися взаимосвязей между фигурами. Мы хотим, чтобы учащиеся не просто могли выполнить, скажем, отражение прямоугольника над линией, но и объяснить, чем изображение этого прямоугольника похоже или отличается от оригинала. Что мы знаем об изображении этого прямоугольника на основании того, что мы знаем об исходной фигуре и свойствах преобразований?
Отражения, переносы и повороты: основы
Прежде чем двигаться дальше, давайте остановимся и определим, что мы подразумеваем под отражением, перемещением и вращением.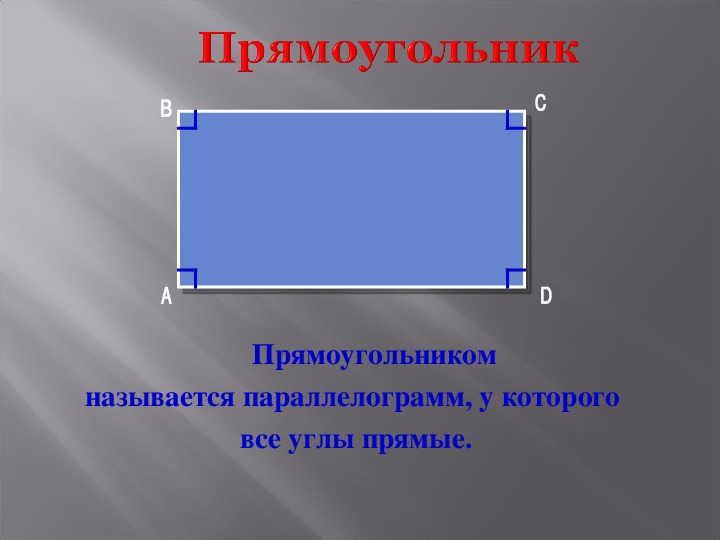 Это сложные идеи для описания словами, поэтому мы начнем с некоторых приблизительных определений, а затем посмотрим на некоторые иллюстрации. 2
Это сложные идеи для описания словами, поэтому мы начнем с некоторых приблизительных определений, а затем посмотрим на некоторые иллюстрации. 2
- Грубо говоря, отражение переносит фигуру (такую как точка, линия, отрезок, многоугольник или окружность) с одной стороны линии (называемой линией отражения) на другую сторону. Например, на приведенной ниже диаграмме △ABC переходит в △A’B’C’ путем отражения через линию DE.
- Грубо говоря, перевод перемещает фигуру по определенному вектору.Например, на приведенной ниже диаграмме △ABC теперь преобразуется в △A’B’C’ путем переноса вдоль вектора DE.
- Грубо говоря, при повороте фигура вращается вокруг точки (называемой центром вращения) на фиксированный угол. В качестве последнего примера на приведенной ниже диаграмме △ABC превращается в △A’B’C’ путем поворота на 90° по часовой стрелке.
-
В совокупности эти три преобразования иногда называют основными жесткими движениями из-за того, что они «жестко» перемещают фигуру по плоскости, сохраняя длины сегментов и .
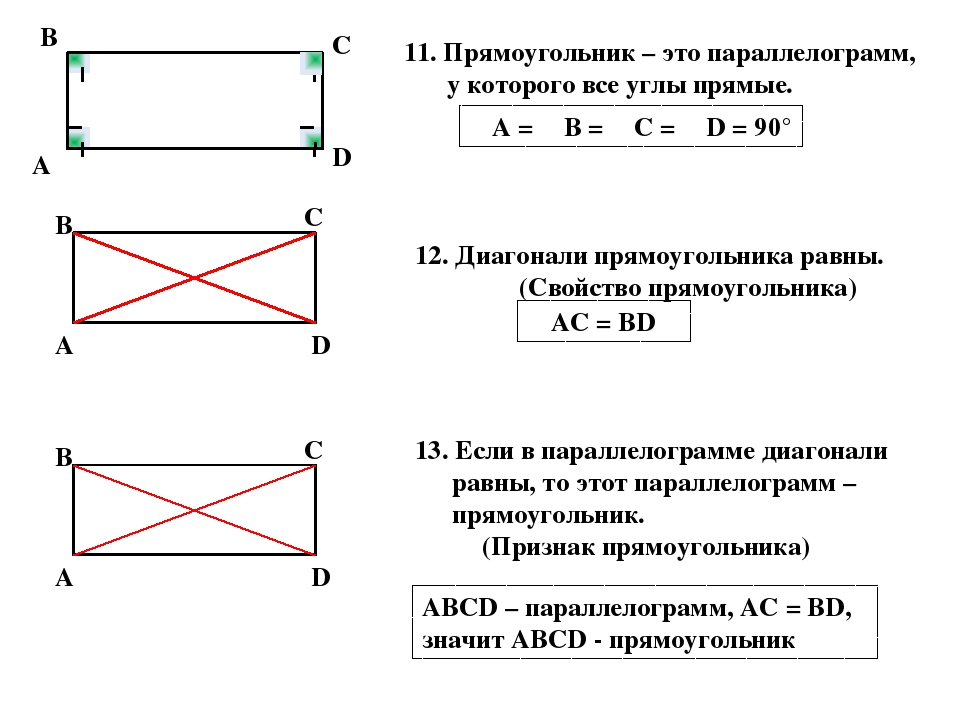 (Позже в этом руководстве мы обсудим нежесткое преобразование: расширение.)
(Позже в этом руководстве мы обсудим нежесткое преобразование: расширение.)
Запоминание точного определения каждого преобразования не имеет значения. Будет лучше, если учащиеся попробуют каждое из преобразований, а затем разработают свои собственные определения как способ обработки свойств каждого из них. Сначала следует ожидать таких слов, как «flip», «slide» и «turn». Однако они не охватывают все идеи, указанные в стандарте, и вскоре учащимся потребуется пересмотреть их более подробно.Все учащиеся должны уметь сказать, например, что отражение сохраняет расстояния вдоль линий и отрезков и меры углов. Они также должны заметить, что расстояние между каждой точкой фигуры и линией отражения остается неизменным при отражении фигуры. На проработку всех трех жестких движений может уйти несколько дней — хорошей идеей может быть сосредоточение внимания на одном из них в день, — но это время будет потрачено с пользой, если учащиеся смогут определить и четко сформулировать свойства каждого преобразования.
Понимание свойств отражений, переводов и вращений
Учащиеся должны начать изучение конгруэнтности с практического опыта: самостоятельно пробовать отражения, переводы и повороты и описывать свойства фигур при этих преобразованиях. (8.G.A.1) Лучшие инструменты для этого — прозрачные пластиковые пленки (для кодоскопов) или калька — могут показаться старомодными, но они хорошо справляются со своей задачей. Существуют программные пакеты, которые также позволяют учащимся легко экспериментировать с трансформациями (GeoGebra — один из популярных продуктов, доступный бесплатно в Интернете), но многие учителя на собственном опыте убеждаются, что для учащихся лучше сначала провести тактильное ознакомление со всеми неподвижными движениями. .
Давайте взглянем на пример плана урока, чтобы увидеть, как может выглядеть введение одного типа преобразования. Этот план урока имеет дело с размышлениями, но базовая структура будет работать так же хорошо для переводов или поворотов.
8 класс, модуль 2, урок 4: пример 1
Отражение через линию определяется с помощью следующего примера.
- Пусть 𝐿 — вертикальная линия, а 𝑃 и 𝐴 — две точки, не лежащие на 𝐿, как показано ниже. Кроме того, пусть 𝑄 будет точкой на 𝐿.(Черный прямоугольник обозначает границу бумаги.)
- Ниже приводится описание того, как отражение перемещает точки 𝑃, 𝑄 и 𝐴 за счет использования прозрачности.
- Проведите линию 𝐿 и ровно три точки на прозрачной пленке, используя красный цвет. (Обязательно используйте прозрачную пленку того же размера, что и бумага.)
- Удерживая бумагу неподвижной, отразите прозрачность по вертикальной линии (поменяв местами левую и правую), сохраняя при этом вертикальную линию и точку 𝑄 поверх их черных изображений.
-
Положение красных фигур на прозрачной пленке теперь представляет собой отражение исходной фигуры. Отражение (𝑃) — это точка, представленная красной точкой слева от 𝐿, Отражение (𝐴) — красная точка справа от 𝐿, а точка Отражение (𝑄) — это сама точка 𝑄.

- Обратите внимание, что точка не меняется при отражении.
8 класс, модуль 2, урок 4. по состоянию на 29 мая 2015 г.Copyright © 2015 Великие умы. UnboundEd не связан с правообладателем этой работы.
СкрытьПоказать
При чтении помните, что этот урок является частью раздела, в котором для преобразований используются формальный язык и обозначения (включая обозначения функций). Стандарты не требуют обозначения функций в 8 классе, и вы можете не захотеть знакомить учащихся с формальными терминами в первый день — это нормально. Что мы действительно хотим подчеркнуть, так это то, как этот урок знакомит учащихся с концепцией отражения:
-
Урок начинается с практического упражнения с диапозитивами.Студенты могут видеть, как отражение определяет точки изображения, и, вероятно, сразу же начнут замечать взаимосвязь между каждой точкой и ее изображением. Вероятно, лучше, чтобы их первая попытка была не на координатной плоскости; условности построения графиков могут отвлекать учащихся от понимания основных свойств отражений.
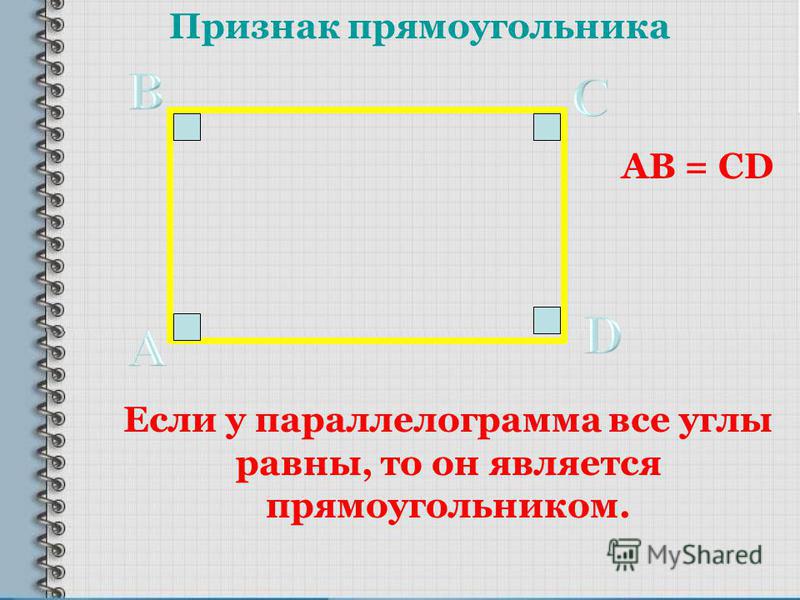
- Учащиеся пробуют выполнить несколько других упражнений. Прозрачность все еще ожидается на этом этапе. В одном упражнении используется горизонтальная линия отражения, а в другом — фигура с вершиной на линии отражения — оба варианта хороши для учащихся.
- Упражнения 3–5 задают несколько важных вопросов, которые побуждают учащихся сформулировать ключевые идеи стандарта. Их просят сравнить величины углов и длины отрезков и заметить, что они конгруэнтны. Это поможет им формализовать эти свойства на следующем этапе урока. (Эти идеи могут быть записаны на «привязке», которая висит в классе до конца урока.)
- В других примерах учащиеся используют новые концепции.
Ожидайте, что учащиеся будут регулярно использовать свои диапозитивы в течение первых нескольких дней. В конце концов, они начнут интуитивно понимать, как будет выглядеть каждое преобразование, и будут все меньше и меньше полагаться на прозрачность. Это «шестое чувство» того, как будет выглядеть изображение фигуры, и есть то, для чего вы снимаете, и оно позволит учащимся в дальнейшем представлять решения всевозможных проблем.
Конгруэнтность
После того, как учащиеся изучат свойства каждого жесткого движения отдельно, они могут перейти к размышлению о конгруэнтности и случаях, когда одна фигура переходит в другую с помощью последовательности жестких движений.(8.G.A.2) Оглядываясь назад на стандарт, мы видим, что он состоит из двух частей:
- Учащиеся должны понимать, что одна фигура конгруэнтна другой, если одну можно перевести в другую серией жестких движений.
- Студенты должны быть в состоянии описать последовательность жестких движений, которые переводят одну фигуру в другую.
Первая часть означает, что учащиеся должны разработать определение конгруэнтности, основанное на преобразованиях, и должны быть в состоянии объяснить, почему две фигуры конгруэнтны на основе свойств неподвижных движений.(Обратите внимание, что это отличается от традиционного определения конгруэнтности «такая же форма, тот же размер».) Вторая часть означает в значительной степени то, что она говорит: учащиеся должны быть в состоянии описать в некоторых деталях преобразования, которые переводят одну фигуру в другую.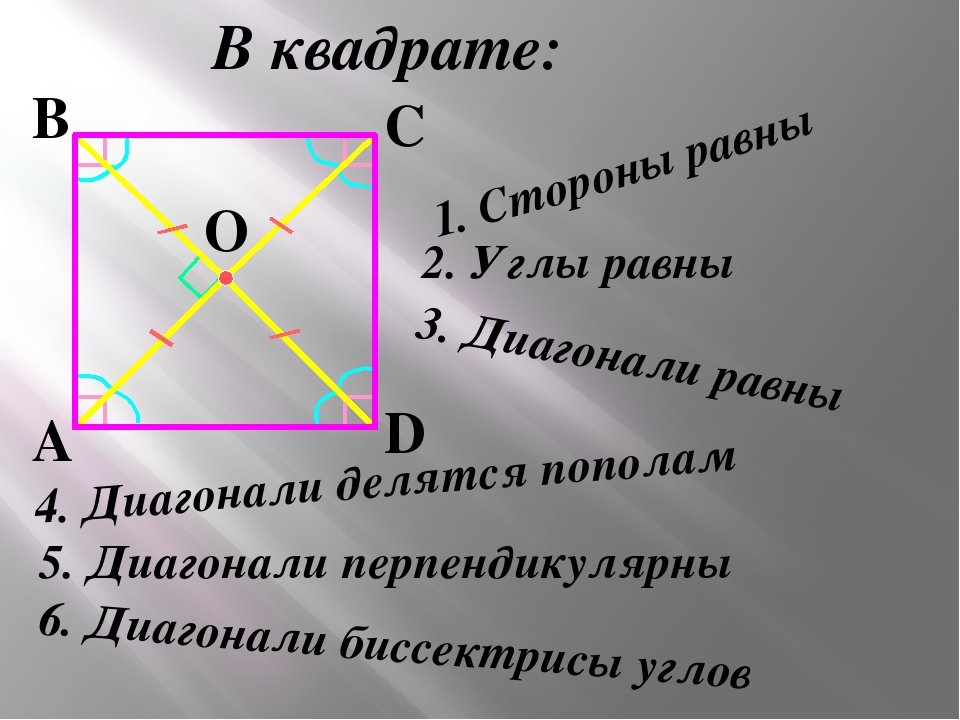 . Эта задача является примером:
. Эта задача является примером:
Конгруэнтные треугольники
Два треугольника на картинке ниже равны:
- Укажите последовательность вращений, перемещений и/или отражений, которая переводит △𝑃𝑅𝑄 в △𝐴𝐵𝐶.
- Можно ли показать конгруэнтность в части (а), используя только переносы и повороты? Объяснять.
«Конгруэнтные треугольники» компании Illustrative Mathematics распространяется под лицензией CC BY 4.0.
СкрытьПоказать
Это задание носит обучающий характер и служит началом урока и приводит к новым идеям по мере его прохождения учащимися. Дайте его учащимся после того, как они познакомятся с твердыми движениями, и они быстро заметят, что ни одно преобразование не поможет — им придется использовать более одного.Поощряйте учащихся быть точными в своих объяснениях. Если вы видите отражение, где должна быть линия отражения? Если видите перевод, то по какому вектору? Может возникнуть большая дискуссия, когда учащиеся делятся несколькими решениями проблемы.
После того, как учащиеся решат задачу, вы можете рассказать о том, что PQR точно отображается на ABC посредством перевода и отражения (или других, более сложных последовательностей) без пробелов или перекрытий. Поскольку они использовали только жесткие преобразования (которые не изменяют меры углов или длины отрезков) для получения одной фигуры из другой, мы можем сказать, что они конгруэнтны.С этого момента вы хотите, чтобы учащиеся использовали это определение конгруэнтности, и если их попросят продемонстрировать конгруэнтность двух фигур, они должны делать это посредством преобразований.
Расширения
Для закрепления жестких преобразований и их связи с конгруэнтностью потребуется некоторое время. Затем пришло время ввести понятие подобия, которое включает в себя еще одно преобразование — расширение. (8.G.A.4) Как и выше, мы начнем с приблизительного определения, а затем уточним его с помощью некоторых иллюстраций.Грубо говоря, расширение — это преобразование фигуры (например, точки, линии, отрезка, многоугольника или круга) в другую фигуру с определенным коэффициентом масштабирования. При расширении расстояние между фиксированной точкой (называемой центром расширения) и расширяемым объектом становится больше или меньше пропорционально масштабному коэффициенту. Примеры ниже показывают два расширения △ABC с центром в точке P, одно с масштабным коэффициентом больше 1, а другое с масштабным коэффициентом меньше 1.
При расширении расстояние между фиксированной точкой (называемой центром расширения) и расширяемым объектом становится больше или меньше пропорционально масштабному коэффициенту. Примеры ниже показывают два расширения △ABC с центром в точке P, одно с масштабным коэффициентом больше 1, а другое с масштабным коэффициентом меньше 1.
Как мы видим, цифры при расширении могут быть увеличены или уменьшены, в зависимости от коэффициента масштабирования.Это поднимает важный момент: «Расширение» имеет особое математическое значение, отличное от его значения в повседневном английском языке (где оно означает просто увеличение, а не сокращение). Учащимся может потребоваться некоторое время, чтобы приспособиться к этому новому использованию знакомого слова, но просмотр примеров с масштабными коэффициентами разной величины поможет этому процессу.
Так же, как и в случае жестких движений, учащиеся должны иметь некоторый практический опыт дилатации и использовать этот опыт для выработки все более точных определений дилатации. Вы можете использовать прозрачные пленки для такого занятия, но лучшими инструментами могут быть линейка или циркуль: учащиеся могут измерить расстояние от каждой точки на фигуре до центральной точки. Затем они могут попытаться, например, умножить эти длины на масштабный коэффициент 2, чтобы получить расширение. (Аналогичным образом они могут попробовать использовать масштабный коэффициент 1/2.) Этот план урока знакомит учащихся с упражнением, которое выполняется с помощью компаса.
Вы можете использовать прозрачные пленки для такого занятия, но лучшими инструментами могут быть линейка или циркуль: учащиеся могут измерить расстояние от каждой точки на фигуре до центральной точки. Затем они могут попытаться, например, умножить эти длины на масштабный коэффициент 2, чтобы получить расширение. (Аналогичным образом они могут попробовать использовать масштабный коэффициент 1/2.) Этот план урока знакомит учащихся с упражнением, которое выполняется с помощью компаса.
8 класс, модуль 3, урок 2: пример 1
Вернитесь к своей догадке или взгляните на наш список классов.Какие предположения оказались верными? Откуда вы знаете?
- Ответы могут различаться в зависимости от предположений, сделанных классом. Учащиеся должны определить, что гипотеза о том, что линия отображается в линию под расширением, верна.
Как вы думаете, что произойдет, если мы выберем другое расположение центра или точек 𝑃 и 𝑄?
- Точки 𝑂, 𝑃 и 𝑄 являются произвольными точками.
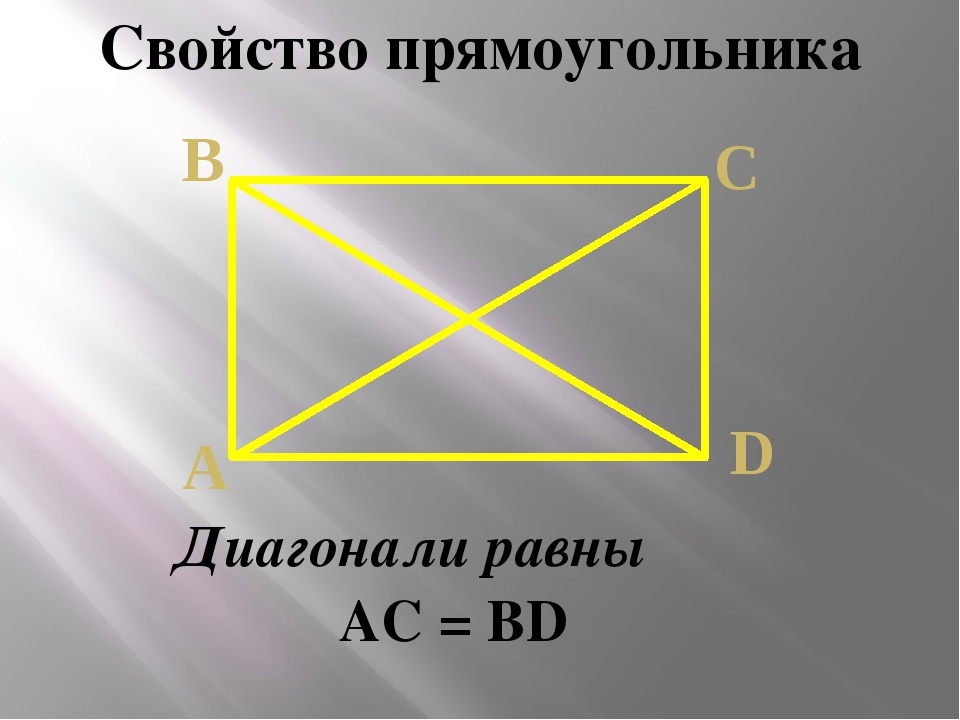 Это означает, что они могли быть где угодно в самолете. По этой причине результаты будут одинаковыми; то есть расширение по-прежнему будет давать линию, и линия будет параллельна оригиналу.
Это означает, что они могли быть где угодно в самолете. По этой причине результаты будут одинаковыми; то есть расширение по-прежнему будет давать линию, и линия будет параллельна оригиналу.
Посмотрите еще раз на рисунок и представьте, что с помощью нашей прозрачности можно перевести отрезок 𝑂𝑃 по вектору 𝑂𝑃 в отрезок 𝑃𝑃 ’ и отрезок 𝑂𝑄 по вектору 𝑂𝑄 в отрезок 𝑄𝑄’. Располагая этой информацией, можете ли вы сказать что-нибудь еще о линиях 𝐿 и 𝐿’?
- Поскольку 𝑃 и 𝑄 являются произвольными точками на прямой 𝐿, а переводы отображают прямые в параллельные прямые, когда вектор не параллелен исходной прямой или не является ее частью, мы можем сказать, что 𝐿 параллелен 𝐿’.
8 класс, модуль 3, урок 2.орг/ресурс/класс-8-математика-модуль-3-тема-урок-2; по состоянию на 29 мая 2015 г. Copyright © 2015 Великие умы. UnboundEd не связан с правообладателем этой работы.
СкрытьПоказать
Опять же, вы можете использовать любые инструменты, которые у вас есть, для подобной деятельности. Учащиеся могут использовать линейки для измерения расстояний от центра расширения или они могут использовать прозрачные пленки для отслеживания расстояний. В результате у них развивается интуиция о том, как работает дилатация, и они могут отвечать на различные дополнительные вопросы.Например, как изменение масштабного коэффициента влияет на изображение фигуры? Как перемещение центра расширения влияет на изображение фигуры? Что произойдет, если центр расширения окажется внутри, на или за пределами фигуры? Что даст расширение с коэффициентом масштабирования 1? Любой из них может вызвать интересную дискуссию и помочь учащимся лучше понять, как дилатации ведут себя в различных условиях.
Учащиеся могут использовать линейки для измерения расстояний от центра расширения или они могут использовать прозрачные пленки для отслеживания расстояний. В результате у них развивается интуиция о том, как работает дилатация, и они могут отвечать на различные дополнительные вопросы.Например, как изменение масштабного коэффициента влияет на изображение фигуры? Как перемещение центра расширения влияет на изображение фигуры? Что произойдет, если центр расширения окажется внутри, на или за пределами фигуры? Что даст расширение с коэффициентом масштабирования 1? Любой из них может вызвать интересную дискуссию и помочь учащимся лучше понять, как дилатации ведут себя в различных условиях.
Сходство
Когда у учащихся появится интуитивное представление о том, как работает расширение, они смогут определить сходство и описать серию преобразований подобия.(8.G.A.4) Как и в случае с конгруэнтностью, здесь преследуется двоякая цель; студенты должны:
-
Поймите сходство с точки зрения жестких движений и расширений.
- Опишите последовательность преобразований подобия.
Задача, подобная этой, может быть хорошим началом:
Вы можете использовать это задание в том виде, в котором оно есть, или использовать его как учебное задание, чтобы представить идею сходства посредством неподвижных движений и растяжений. В этом случае мы могли бы немного упростить вопрос: «Не могли бы вы сопоставить маленькую стрелку с большой, используя жесткие движения и расширения? Поясните свой ответ.” Есть несколько способов сделать это, как показано в разделе решения задачи, и это возможность для содержательного обсуждения. Как только несколько методов будут установлены, вы можете объяснить учащимся, что они только что показали, что эти фигуры похожи, потому что мы смогли перевести одну фигуру в другую посредством отражений, перемещений, поворотов и расширений. Это становится определением подобия. (Обратите внимание, что это отличается от определения подобия «одинаковая форма, разный размер», с которым учащиеся могут быть знакомы.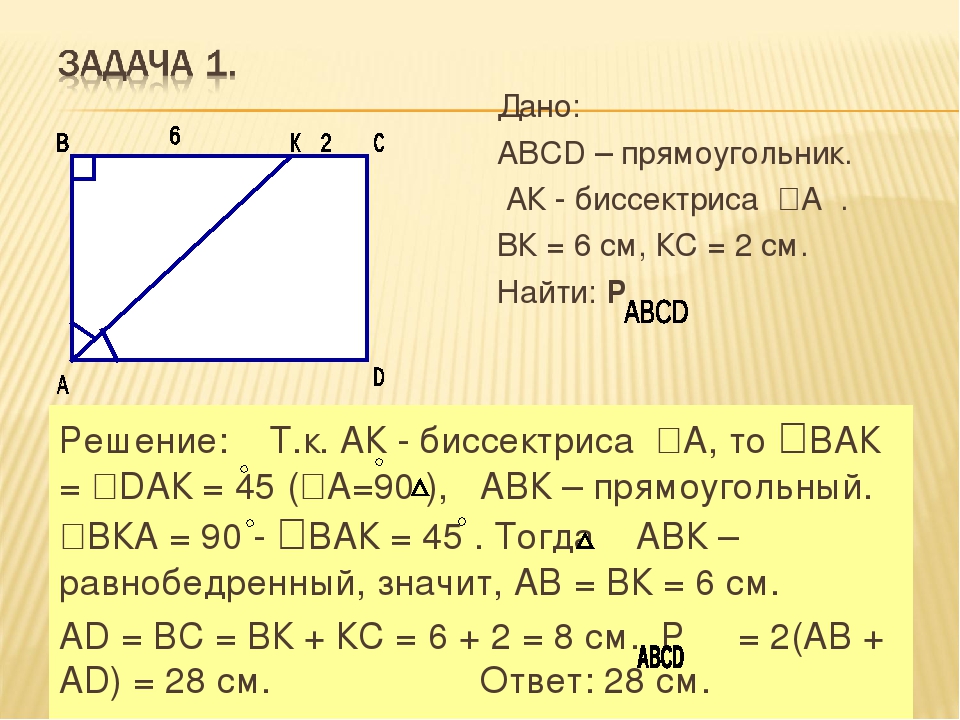 Дело не в том, что эти две фигуры связаны серией трансформаций и оказываются похожими; скорее, они похожи, потому что связаны серией преобразований. Другими словами, как только мы установили трансформационную последовательность, мы установили сходство.)
Дело не в том, что эти две фигуры связаны серией трансформаций и оказываются похожими; скорее, они похожи, потому что связаны серией преобразований. Другими словами, как только мы установили трансформационную последовательность, мы установили сходство.)
Конгруэнтны, похожи или и то, и другое?
Учащимся важно понять, что конгруэнтность и сходство не исключают друг друга; это не тот случай, когда две фигуры являются одним, но никогда не являются другим. На самом деле, если две фигуры конгруэнтны, они также подобны.Чтобы понять почему, вспомните определение сходства: одна фигура похожа на другую, если она может быть получена последовательностью отражений, перемещений, вращений и расширений. Любое из преобразований конгруэнтности, которые мы рассмотрели выше, также подходит под это определение — две задействованные фигуры будут конгруэнтны, но также будут соответствовать критериям сходства.
Переход к координатной плоскости
Начальные встречи учащихся с каждым преобразованием (включая расширение) не обязательно должны происходить на координатной плоскости.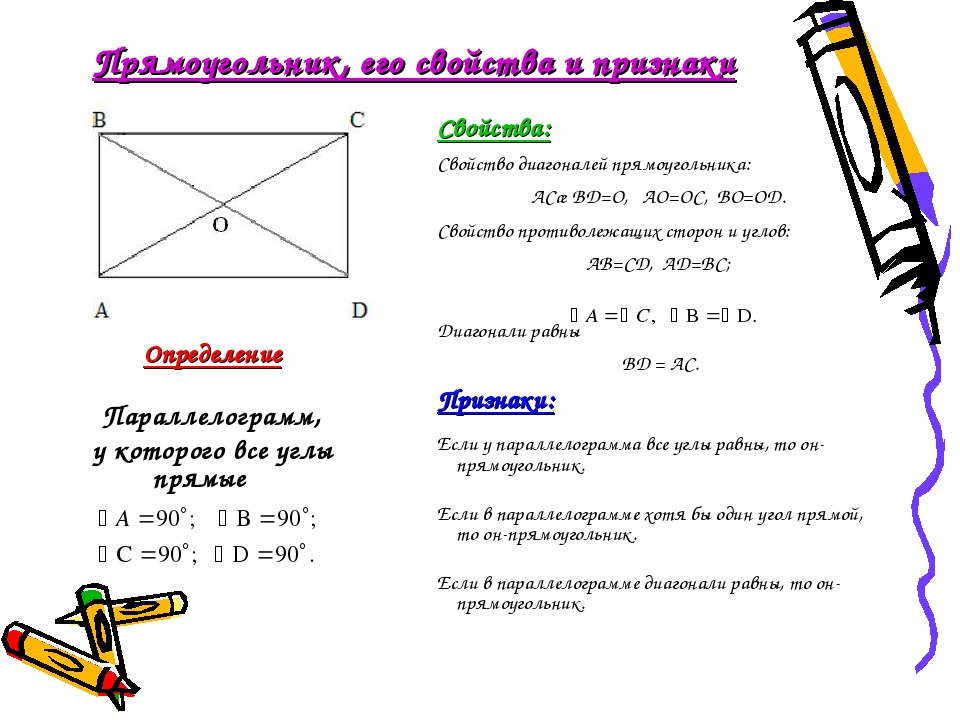 На самом деле введение каждого преобразования в «синтетический» контекст (без использования координат, как в приведенных выше примерах) часто позволяет учащимся сосредоточиться на свойствах самих преобразований, не беспокоясь об условностях координатной плоскости. Это также хорошее напоминание о том, что вселенная преобразований — это гораздо больше, чем просто подмножество, которое мы можем описать с помощью целочисленных координат. (Студенты также склонны разрабатывать «правила» для выполнения преобразований на координатной плоскости — например, «поменять местами значения x и y» для поворота на 180 градусов — на самом деле это не должно быть акцентом в раннем обучении.Вспомните, как наш вводный план урока по вращению не включал никаких координатных сеток.)
На самом деле введение каждого преобразования в «синтетический» контекст (без использования координат, как в приведенных выше примерах) часто позволяет учащимся сосредоточиться на свойствах самих преобразований, не беспокоясь об условностях координатной плоскости. Это также хорошее напоминание о том, что вселенная преобразований — это гораздо больше, чем просто подмножество, которое мы можем описать с помощью целочисленных координат. (Студенты также склонны разрабатывать «правила» для выполнения преобразований на координатной плоскости — например, «поменять местами значения x и y» для поворота на 180 градусов — на самом деле это не должно быть акцентом в раннем обучении.Вспомните, как наш вводный план урока по вращению не включал никаких координатных сеток.)
Однако в какой-то момент учащиеся должны уметь работать с преобразованиями на координатной плоскости и ясно описывать эффекты определенных преобразований, используя координаты. (8.G.A.3) По сути, этот стандарт предназначен для того, чтобы взять все, что учащиеся узнали о преобразованиях в целом, и применить это к задачам на координатной плоскости. Разнообразие проблем, подразумеваемых здесь, огромно, и представить исчерпывающую выборку просто невозможно.Но давайте в качестве примера того, как ученики совершают прыжок на координатную плоскость, рассмотрим одну задачу:
Разнообразие проблем, подразумеваемых здесь, огромно, и представить исчерпывающую выборку просто невозможно.Но давайте в качестве примера того, как ученики совершают прыжок на координатную плоскость, рассмотрим одну задачу:
Опять же, это только один пример, но давайте рассмотрим его внимательно. В дополнение к твердому пониманию свойств преобразований и базового понимания координатной плоскости учащиеся также должны быть знакомы с уравнениями горизонтальных линий. (Если вы еще не достигли этого на своем курсе, ничего страшного; учащиеся все еще могут выполнить аналогичное задание, включающее отражение по оси X.) Если у них все это есть, они могут начать решать. Не нужно много времени, чтобы понять, что эта проблема устойчива к грубой силе; даже если бы лист миллиметровой бумаги размером 2000 х 2000 квадратов существовал, потребовалась бы целая вечность, чтобы нарисовать соответствующую точку и отразить ее. Вместо этого им придется применить некоторые идеи об отражениях: в частности, что расстояние между точкой и линией отражения равно расстоянию между ее изображением и линией отражения.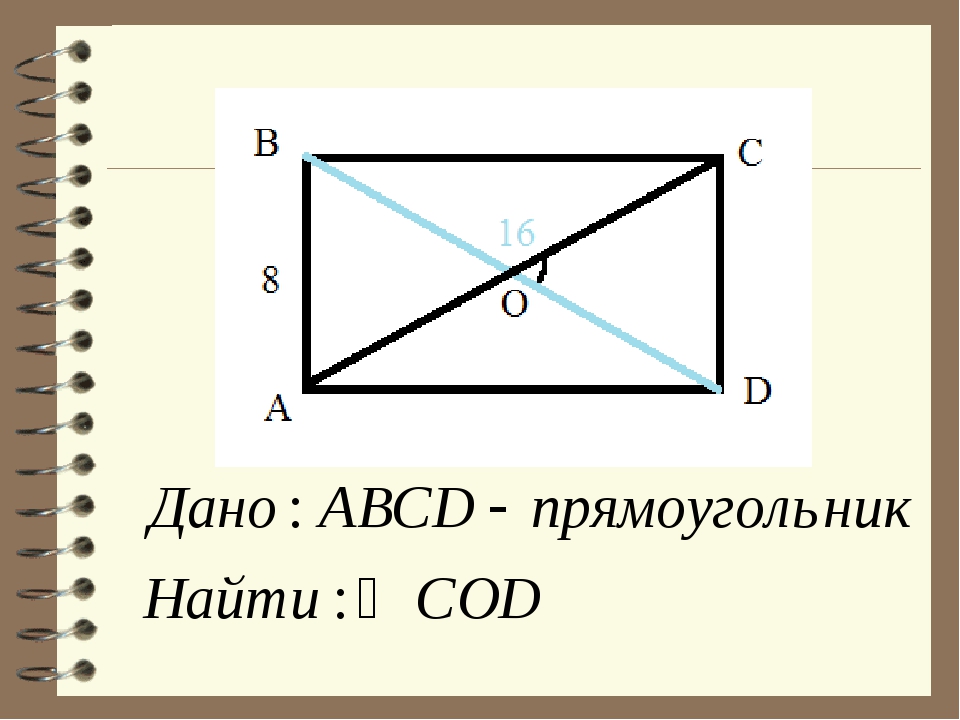 Две стратегии, которые вы могли бы предложить ученикам попробовать:
Две стратегии, которые вы могли бы предложить ученикам попробовать:
- Попросите их создать грубый набросок координатной плоскости или части плоскости, чтобы помочь им визуализировать ситуацию.Тогда они смогут увидеть, что (1000, 2012) на 12 единиц выше y = 2000, поэтому точка отражения будет на 12 единиц ниже y = 2000. Более того, отражение вообще не сдвинет изображение влево или вправо. , поэтому координата x обеих точек будет одинаковой. Эти две подсказки должны позволить им собрать решение вместе.
- Попросите их подумать о более простом случае, например, отразив точку (1, 10) на линии y = 8. Затем предложите им связать решение более простой задачи с исходным вопросом.Цифры будут немного другими, но процесс будет таким же.
В обоих случаях учащиеся получают гибкое представление о том, как работают преобразования, и применяют их к определенным точкам и расстояниям на координатной плоскости.
Частные случаи конгруэнтности: трансверсали и треугольники
На первый взгляд последний стандарт в кластере 8.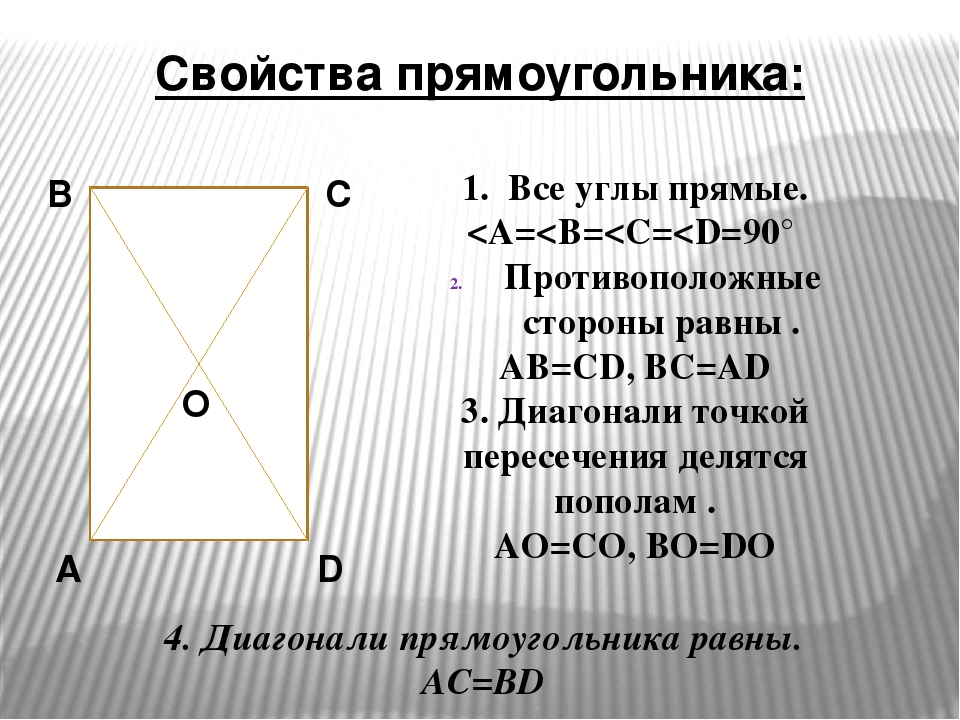 G.A может показаться неуместным. Как мы перешли от преобразований к трансверсалям? И какое отношение все это имеет к углам треугольника? Эти идеи — преобразования, трансверсали и треугольники — долгое время рассматривались и преподавались как отдельные идеи.Но теперь все они понимаются как связанные. (8.G.A.5) Чтобы увидеть, как преобразования связаны с трансверсалями, давайте взглянем на этот урок:
G.A может показаться неуместным. Как мы перешли от преобразований к трансверсалям? И какое отношение все это имеет к углам треугольника? Эти идеи — преобразования, трансверсали и треугольники — долгое время рассматривались и преподавались как отдельные идеи.Но теперь все они понимаются как связанные. (8.G.A.5) Чтобы увидеть, как преобразования связаны с трансверсалями, давайте взглянем на этот урок:
8 класс, модуль 2, урок 12: исследовательское задание 2
На рисунке ниже ‖ и 𝑚 — это трансверсаль. С помощью транспортира измерьте углы 1–8. Назовите углы, равные по величине.
∠1 = ∠3 = ∠5 = ∠7 = и ∠2 = ∠4 = ∠6 = ∠8
а. Что вы заметили в измерениях ∠1 и ∠5? Как вы думаете, почему это так? (При необходимости используйте прозрачность.)
∠𝟏 и ∠𝟓 равны по мере. Мы можем перенести ∠𝟏 вдоль вектора на линии 𝒎 так, чтобы вершина ∠𝟏 отображалась на вершину ∠𝟓. Переводы сохраняют угол, поэтому два угла совпадут.
б. Что вы заметили в измерениях ∠3 и ∠7? Как вы думаете, почему это так? (При необходимости используйте прозрачность. ) Существуют ли другие пары углов с такими же отношениями? Если да, перечислите их.
) Существуют ли другие пары углов с такими же отношениями? Если да, перечислите их.
∠𝟑 и ∠𝟕 равны по мере. Мы можем перенести ∠𝟑 вдоль вектора на линии 𝒎 так, чтобы вершина ∠𝟑 отображалась на вершину ∠𝟕.Переводы сохраняют угол, поэтому два угла совпадут. Другими парами углов с таким же отношением являются ∠𝟒 и ∠𝟖 и ∠𝟐 и ∠𝟔.
с. Что вы заметили в измерениях ∠4 и ∠6? Как вы думаете, почему это так? (При необходимости используйте прозрачность.) Есть ли другая пара углов с таким же соотношением?
Меры ∠𝟒 и ∠𝟔 равны. Вращение на 𝟏𝟖𝟎° вокруг центра отобразит ∠𝟒 в ∠𝟔. Повороты сохраняют угол, поэтому мы знаем, что ∠𝟒 и ∠𝟔 равны.∠𝟑 и ∠𝟓 имеют одинаковые отношения.
8 класс, модуль 2, урок 12. по состоянию на 29 мая 2015 г. Copyright © 2015 Великие умы. UnboundEd не связан с правообладателем этой работы.
СкрытьПоказать
Как мы видим, учащиеся используют транспортир для измерения и определения взаимосвязей между углами. Затем они возвращаются к знакомому инструменту (прозрачности) из работы с трансформациями, чтобы понять, почему существуют эти отношения. Последующее обсуждение особенно интересно: учащиеся должны обратить внимание на то, как соотносятся соответствующие углы при переводе одного угла в другой. Точно так же чередующиеся внутренние углы связаны поворотом одного угла на 180 градусов к другому. Это, по сути, математическая основа для идей, которые когда-то часто давались учащимся средней школы только как постулаты («альтернативные внутренние углы конгруэнтны» и т. д.). Потратив время на изучение причин этих угловых взаимосвязей, учащиеся с большей вероятностью запомнят их и будут опираться на свои знания в будущем.
Последующее обсуждение особенно интересно: учащиеся должны обратить внимание на то, как соотносятся соответствующие углы при переводе одного угла в другой. Точно так же чередующиеся внутренние углы связаны поворотом одного угла на 180 градусов к другому. Это, по сути, математическая основа для идей, которые когда-то часто давались учащимся средней школы только как постулаты («альтернативные внутренние углы конгруэнтны» и т. д.). Потратив время на изучение причин этих угловых взаимосвязей, учащиеся с большей вероятностью запомнят их и будут опираться на свои знания в будущем.
В прошлом другой идеей, которую часто преподавали изолированно и давали студентам в качестве постулата, была сумма внутренних углов треугольника. Но после того, как учащиеся поймут углы, образованные секущими в свете преобразований, они смогут объяснить, откуда взялась эта идея. Чтобы понять, как это сделать, давайте рассмотрим эту задачу.
Как поясняет решение задачи, учащиеся могут разработать неформальный аргумент в пользу того, что a + b + c = 180, используя альтернативные отношения внутренних углов, чтобы установить, что три смежных угла на диаграмме имеют размеры a, b и c, и что вместе они три угла образуют прямой угол.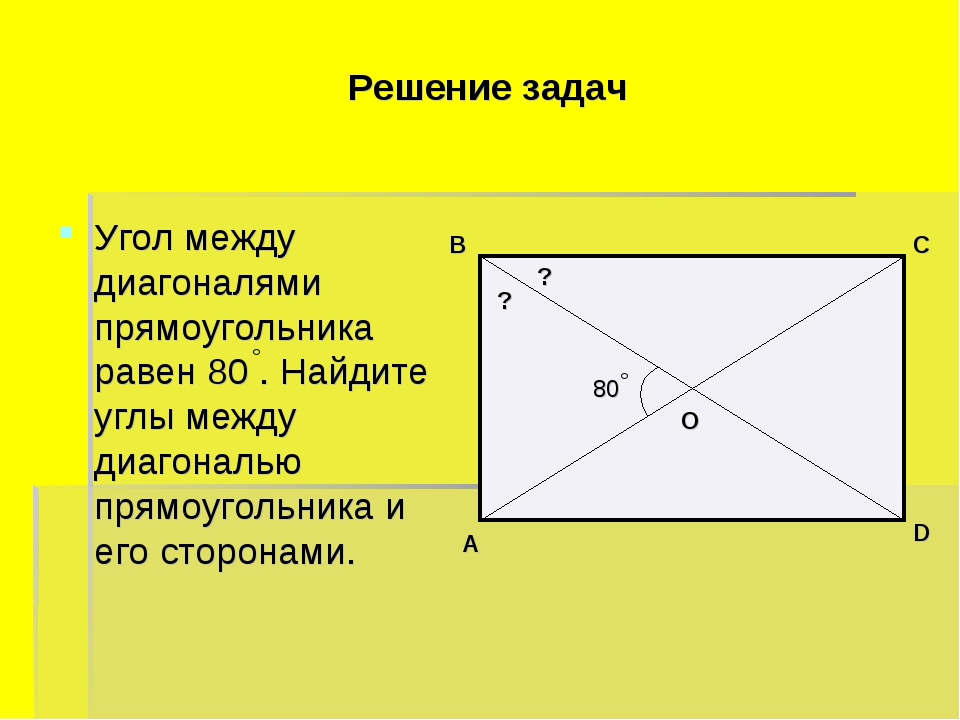 Это не простой аргумент, но он доступен учащимся 8-го класса. Если ваши учащиеся имеют ограниченный опыт выполнения заданий, требующих рассуждений и объяснений такого типа, несколько подмостков могут быть полезны, чтобы помочь им полностью усвоить идеи. вовлеченный. Например, если у ваших учеников возникают проблемы с мерами углов, заданными в виде переменных, вы можете начать с треугольника с целочисленными мерами углов. Вы также можете попросить их повторить ту же технику (удлинить одну сторону, а затем построить параллельную линию через противоположную вершину) на другом треугольнике с целыми числами углов, а затем перейти к «обычному» треугольнику, показанному выше.А во второй части задания учащиеся, не привыкшие объяснять свои мысли, могут извлечь пользу из одного или двух вводных предложений, чтобы начать свои ответы.
Это не простой аргумент, но он доступен учащимся 8-го класса. Если ваши учащиеся имеют ограниченный опыт выполнения заданий, требующих рассуждений и объяснений такого типа, несколько подмостков могут быть полезны, чтобы помочь им полностью усвоить идеи. вовлеченный. Например, если у ваших учеников возникают проблемы с мерами углов, заданными в виде переменных, вы можете начать с треугольника с целочисленными мерами углов. Вы также можете попросить их повторить ту же технику (удлинить одну сторону, а затем построить параллельную линию через противоположную вершину) на другом треугольнике с целыми числами углов, а затем перейти к «обычному» треугольнику, показанному выше.А во второй части задания учащиеся, не привыкшие объяснять свои мысли, могут извлечь пользу из одного или двух вводных предложений, чтобы начать свои ответы.
Последняя идея, которую учащиеся готовы объяснить посредством преобразований, — это критерий угла-угла для сходства треугольников. Это задание знакомит учащихся с серией вопросов, предназначенных для того, чтобы привести их от конкретного случая к более общему утверждению.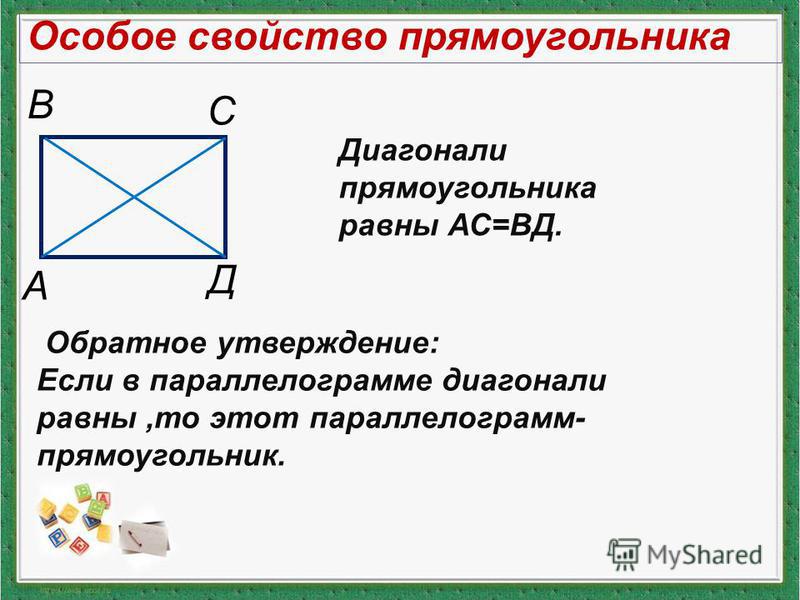
Подобные треугольники II
Треугольники 𝐴𝐵𝐶 и 𝑃𝑄𝑅 имеют две пары конгруэнтных углов, как указано:
- Объясните, используя расширения, переводы, отражения и/или повороты, почему △𝑃𝑄𝑅 похоже на △𝐴𝐵𝐶.
- Углы 𝐶 и 𝑅 равны?
- Можете ли вы показать сходство в части а, не используя отражение? Как насчет того, чтобы не использовать дилатацию? Объяснять.
- Предположим, 𝐷𝐸𝐹 и 𝐾𝐿𝑀 — два треугольника с 𝑚(∠𝐷)=𝑚(∠𝐾) и 𝑚(∠𝐸)=𝑚(∠𝐿). Подобны ли треугольники 𝐷𝐸𝐹 и 𝐾𝐿𝑀?
«Similar Triangles II» компании Illustrative Mathematics находится под лицензией CC BY 4.0.
СкрытьПоказать
Части (a), (b) и (c) этой задачи основаны на понимании учащимися преобразований подобия.Затем часть (d) просит их, так же как и в двух предыдущих заданиях, обобщить. Имея «общую» пару треугольников с двумя парами конгруэнтных углов, могут ли они показать сходство? Опять же, учащиеся, не привыкшие объяснять свои мысли, могут нуждаться в поддержке. Им могут быть полезны некоторые возможные диаграммы DEF и KLM, чтобы увидеть, что точные задействованные преобразования не так важны, как тот факт, что некоторая последовательность жестких движений и расширений приведет к переходу одного треугольника в другой.Одно или два начала предложения также могут быть полезными. Как и в случае с любым из этих заданий, цель состоит не в том, чтобы избавиться от необходимых рассуждений, а в том, чтобы дать учащимся другой способ увидеть, о чем их просят подумать и объяснить.
Им могут быть полезны некоторые возможные диаграммы DEF и KLM, чтобы увидеть, что точные задействованные преобразования не так важны, как тот факт, что некоторая последовательность жестких движений и расширений приведет к переходу одного треугольника в другой.Одно или два начала предложения также могут быть полезными. Как и в случае с любым из этих заданий, цель состоит не в том, чтобы избавиться от необходимых рассуждений, а в том, чтобы дать учащимся другой способ увидеть, о чем их просят подумать и объяснить.
Теорема Пифагора
Еще одна важная идея, дебютировавшая в геометрии для 8-го класса, — теорема Пифагора. Стандарты, связанные с теоремой Пифагора, также являются частью основной работы класса. Учитывая уравнения, с которыми учащиеся столкнутся при решении задач с теоремой Пифагора, например, c2 = 25 и a2 = 17, может иметь смысл преподавать эти стандарты после того, как учащиеся освоятся с квадратными и кубическими корнями (8.EE.A.2) и работать с иррациональными числами. (8.NS.A.1) (Подробнее о взаимосвязи между стандартами см. в Части 2 данного руководства.) Независимо от того, какую последовательность вы выберете для обучения, важно понимать, что ряд стандартов средней школы зависит от знания теоремы Пифагора, поэтому учащиеся обязательно должны получить это содержание в 8 классе.
(8.NS.A.1) (Подробнее о взаимосвязи между стандартами см. в Части 2 данного руководства.) Независимо от того, какую последовательность вы выберете для обучения, важно понимать, что ряд стандартов средней школы зависит от знания теоремы Пифагора, поэтому учащиеся обязательно должны получить это содержание в 8 классе.
Стандарты, связанные с теоремой Пифагора, сгруппированы в другую группу (называемую 8.G.B, так как это вторая группа стандартов по геометрии в 8 классе).Давайте посмотрим, что они говорят.
8.GB | Поймите и примените теорему Пифагора.
Опять же, порядок стандартов не указывает порядок, в котором они должны преподаваться. Но в этом случае имеет смысл начать с доказательства теоремы Пифагора (8.G.B.6), а затем перейти к решению разного рода задач (8.G.B.7 и 8.G.B.8).
Прежде чем мы начнем говорить о стандартах в этом кластере, давайте выдвинем на первый план две важные идеи.
-
Теорема Пифагора гласит: если треугольник прямоугольный, длины катетов равны a и b, а длина гипотенузы равна c, то a2 + b2 = c2.
- Обратное утверждение теоремы Пифагора также верно: если треугольник имеет длины сторон a, b и c и a2 + b2 = c2, то этот треугольник прямоугольный.
В прошлом эта тема часто вводилась студентам, давая им формулу (упомянутую выше: a2 + b2 = c2) и объясняя, что обозначают переменные.Затем обучение вращалось вокруг относительно простых задач, в которых учащимся давались длины двух сторон прямоугольного треугольника, и они должны были найти третью. Такое решение задач все еще имеет место, но Стандарты начинаются с того, что студентов просят объяснить доказательство теоремы Пифагора и ее обращение. (8.G.B.6) При этом они узнают две важные вещи:
-
Теорема Пифагора описывает отношения между сторонами прямоугольного треугольника (а не просто формулу). Когда учащиеся понимают природу взаимосвязи и могут выразить ее устно (а также в алгебраических терминах), они настроены на применение ее в более широком диапазоне ситуаций и расширение своего обучения в дальнейшем.

- Обратная теорема Пифагора так же полезна, как и сама теорема. Студенты узнают, что они могут использовать теорему не только тогда, когда они знают, что у них есть прямоугольный треугольник, но также и тогда, когда им нужно установить, что треугольник является прямоугольным.
Итак, откуда взялась теорема Пифагора? На самом деле существует много разных доказательств, некоторые из них сложнее, чем другие. Эти разные доказательства основаны на разных методах и приводят разные причины истинности теоремы Пифагора.В этом уроке используется доказательство «квадрат внутри квадрата» с использованием площади, начинающееся так:
8 класс, модуль 2, урок 15: обсуждение
Первое доказательство теоремы Пифагора требует знания некоторых основных фактов о геометрии.
- Конгруэнтные треугольники имеют равные площади.
- Все соответствующие части конгруэнтных треугольников конгруэнтны.
- Теорема суммы треугольника.
 (∠ сумма △)
(∠ сумма △)
- В прямоугольных треугольниках сумма двух непрямых углов равна 90°.(∠ сумма рт. △)
Далее мы рассмотрим то, что называется квадратом внутри квадрата. Внешний квадрат имеет длины сторон (a+b), а внутренний квадрат имеет длины сторон c. Наша цель — показать, что +=
Для достижения этой цели мы сравним общую площадь внешнего квадрата с частями, из которых он состоит, то есть с четырьмя треугольниками и меньшим внутренним квадратом.
8 класс, модуль 2, урок 15. по состоянию на 29 мая 2015 г.Copyright © 2015 Великие умы. UnboundEd не связан с правообладателем этой работы.
СкрытьПоказать
Остальная часть доказательства, которую вы видите в плане урока, помогает учащимся понять, что внутренняя фигура на самом деле является квадратом, а затем использует вычисление площади для вывода формулы. Если вы собираетесь использовать этот план урока, подумайте о степени поддержки, которую вы хотите оказать — возможно, учащиеся смогут сами пройти часть проверки и закончить под вашим руководством, или, может быть, им нужно больше структурированности. (Одно предупреждение: алгебра, используемая в этом последнем вычислении, включает в себя умножение двух биномов, что не требуется до старшей школы. Возможно, вам придется помочь учащимся применить распределительное свойство новым способом.) В любом случае, они понимают. что теорема Пифагора включает в себя аспект площади, который полезен для интерпретации определенных типов прикладных задач.
(Одно предупреждение: алгебра, используемая в этом последнем вычислении, включает в себя умножение двух биномов, что не требуется до старшей школы. Возможно, вам придется помочь учащимся применить распределительное свойство новым способом.) В любом случае, они понимают. что теорема Пифагора включает в себя аспект площади, который полезен для интерпретации определенных типов прикладных задач.
Применение теоремы Пифагора для решения задач
Как только учащиеся понимают происхождение теоремы Пифагора, они приступают к решению задач.(8.G.B.7) Сначала учащиеся могут решать задачи только с целыми числами, чтобы сосредоточиться на интерпретации ситуации с точки зрения прямоугольного треугольника и проведении точных расчетов. (Вышеприведенный план урока включает несколько примеров таких задач начального уровня.) Это задание требует более подробной интерпретации.
Бег на футбольном поле
Во время игры плей-офф дивизиона 2005 года между «Денвер Бронкос» и «Нью-Инглэнд Пэтриотс» игрок «Бронко» Чемп Бэйли перехватил Тома Брэди у линии ворот (см. обведенную букву B).Он довел мяч почти до чужой линии ворот. Бен Уотсон из «Патриотов Новой Англии» (см. обведенную W) погнался за Чемпом и выследил его прямо перед другой линией ворот.
обведенную букву B).Он довел мяч почти до чужой линии ворот. Бен Уотсон из «Патриотов Новой Англии» (см. обведенную W) погнался за Чемпом и выследил его прямо перед другой линией ворот.
На изображении ниже каждая решетка равна одному ярду: также обратите внимание, что ширина поля составляет 53 ярда.
- Как вы можете использовать диаграмму и теорему Пифагора, чтобы примерно определить, сколько ярдов пробежал Бен Уотсон, чтобы выследить Чэмпа Бейли?
- Воспользуйтесь теоремой Пифагора, чтобы приблизительно определить, сколько ярдов пробежал Ватсон в этой пьесе.
- Кто из игроков пробежал дальше во время этой игры? Примерно на сколько еще ярдов?
«Бег по футбольному полю» от Illustrative Mathematics под лицензией CC BY 4.0.
СкрытьПоказать
Учащимся может потребоваться прочитать задачу несколько раз, чтобы понять, что представляет собой каждая часть диаграммы. И, как вы можете видеть, некоторые оценки в порядке. Учитывая, что все поле имеет длину 100 ярдов и ширину 53 1/2 ярда, какова длина сторон этого почти треугольника? Как только учащиеся смогут увидеть прямоугольный треугольник и его размеры, эта проблема станет очень решаемой.
И, как вы можете видеть, некоторые оценки в порядке. Учитывая, что все поле имеет длину 100 ярдов и ширину 53 1/2 ярда, какова длина сторон этого почти треугольника? Как только учащиеся смогут увидеть прямоугольный треугольник и его размеры, эта проблема станет очень решаемой.
Нахождение расстояний на координатной плоскости
Студенты также должны использовать теорему Пифагора, чтобы найти расстояния в координатной плоскости. (8.G.B.8) На самом деле это специфический вариант проблем, которые мы только что обсуждали; студенты учатся интерпретировать две точки на координатной плоскости как определяющие гипотенузу прямоугольного треугольника. Эта проблема исходит из вводного урока по этой идее.
8 класс, модуль 7, урок 17: пример 1
Какое расстояние между двумя точками на координатной плоскости? Округлите ответ до десятых.
8 класс, модуль 7, урок 17. по состоянию на 29 мая 2015 г. Copyright © 2015 Великие умы. UnboundEd не связан с правообладателем этой работы.
Прежде чем перейти к этой задаче, учащиеся сталкиваются с последовательностью вопросов, в которых они находят длины некоторых горизонтальных и вертикальных отрезков, понимая, что длина отрезка на координатной плоскости — это просто количество квадратов, которые он покрывает.Более того, они видят, что невозможно найти расстояние диагонального отрезка, считая квадраты. Затем эта конкретная проблема ставится как задача, и у учащихся есть время поработать над ней. (Возможно, что в контексте раздела по теореме Пифагора некоторые учащиеся решат применить здесь свои новые знания. В идеале учащиеся должны быть в состоянии объяснить своим сверстникам, как построить прямоугольный треугольник из этих точек. и решить для рассматриваемой длины.)
После решения такой задачи учащиеся должны потренироваться в нахождении расстояния между точками в разных квадрантах координатной плоскости, а также расстояния между двумя точками, заданными упорядоченными парами и не нанесенными на плоскость.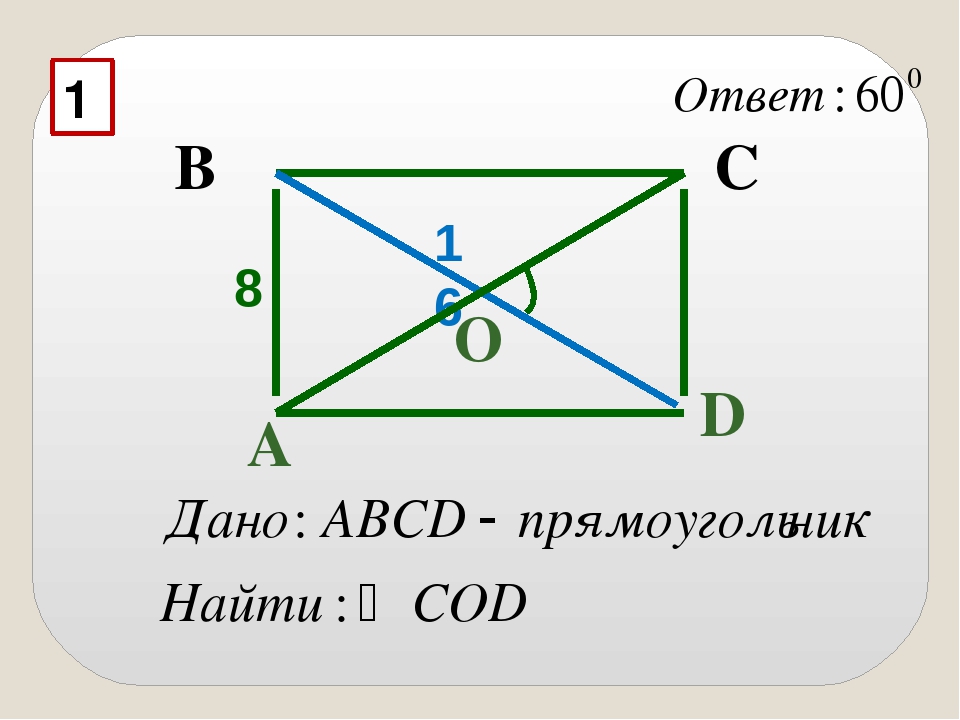 (Если вас интересует задание, которое может помочь им в этом, ознакомьтесь с разделом «Нахождение расстояния между точками» из «Иллюстративной математики». Комментарии и решения дают некоторые идеи о том, как учащиеся могут перейти от нахождения расстояния между двумя точками. конкретные, пронумерованные точки указывают на общий случай любых двух пар координат.)
(Если вас интересует задание, которое может помочь им в этом, ознакомьтесь с разделом «Нахождение расстояния между точками» из «Иллюстративной математики». Комментарии и решения дают некоторые идеи о том, как учащиеся могут перейти от нахождения расстояния между двумя точками. конкретные, пронумерованные точки указывают на общий случай любых двух пар координат.)
Роль математических практик
Стандарты включают не только знания и навыки; они также признают необходимость того, чтобы учащиеся занимались некоторыми важными практиками математического мышления и общения.Эти «Математические практики» имеют свой собственный набор стандартов, которые содержат те же основные цели для классов K-12. 3 (Идея состоит в том, что учащиеся должны с годами развивать одни и те же привычки мышления все более изощренными способами). на глубоком концептуальном понимании, необходимом в каждом классе. Другими словами, Практики помогают учащимся усвоить содержание.В таблице ниже приведены несколько примеров того, как математические практики могут помочь учащимся понять и применить геометрические понятия в 8 классе.
Подкаст-клип: Важность математических практик с Эндрю Ченом и Питером Коу (начало 30:33, конец 43:39)
Преобразования: связь с выражениями и уравнениями
Преобразования имеют решающее значение для понимания еще одной основной работы для 8 класса: наклона. 4 Студенты впервые сталкиваются с наклоном на графиках пропорциональных отношений, понимая его как единичную скорость отношения. (Это понятие впервые было разработано в 7 классе.) Почему же наклон линии постоянен? Этот вопрос часто заметают под ковер. Один из способов понимания — применение подобия: каждая линия на координатной плоскости подразумевает любое количество подобных «треугольников наклона» с пропорциональными сторонами. (8.EE.B.6) Это задание показывает пример того, как учащиеся могут подойти к этой концепции.
Уклоны между точками на линии
Наклон между двумя точками вычисляется путем нахождения изменения значений y и деления на изменение значений x. Например, наклон между точками (7, -15) и (-8, 22) можно вычислить следующим образом:
Например, наклон между точками (7, -15) и (-8, 22) можно вычислить следующим образом:
- Разница в значениях y составляет −15 − 22 = −37.
- Разница в значениях x составляет 7 − (−8) = 15.
- Разделив эти две разности, мы находим, что наклон равен −.
Ева, Карл и Мария вычисляют наклон между парами точек на линии, показанной ниже.
Ева находит наклон между точками (0,0) и (3,2). Карл находит наклон между точками (3,2) и (6,4). Мария находит наклон между точками (3,2) и (9,6). Каждый из них нарисовал треугольник, чтобы облегчить свои расчеты (показано ниже).
- Какой треугольник нарисовал учащийся? Завершите расчет уклона для каждого ученика. Как можно геометрически интерпретировать различия в значениях x и y в нарисованных ими картинках?
-
Рассмотрим любые две точки (, ) и (, ) на линии, показанной выше.Нарисуйте треугольник, подобный треугольникам, нарисованным Евой, Карлом и Марией.
 Каков наклон между этими двумя точками? Почему этот наклон должен быть таким же, как наклоны, рассчитанные тремя студентами?
Каков наклон между этими двумя точками? Почему этот наклон должен быть таким же, как наклоны, рассчитанные тремя студентами?
«Наклоны между точками на линии» от Illustrative Mathematics под лицензией CC BY 4.0.
СкрытьПоказать
Как указано в решении, треугольники в этом задании сконструированы таким образом, чтобы учащиеся могли легко определить их как похожие, используя серию жестких движений и растяжений.Поскольку любой треугольник на прямой можно перевести в другой больший или меньший треугольник путем переноса и расширения, они должны быть подобны. Таким образом, учащиеся могут продемонстрировать, что наклон между любыми двумя точками на любой заданной линии будет одинаковым. (Это более дедуктивный и математически обоснованный способ понимания наклона линии, чем простое наблюдение за тем, чтобы наклон между несколькими парами точек на одной конкретной линии был одинаковым.)
Теорема Пифагора: связь с выражениями и уравнениями и системой счисления
Теорема Пифагора тесно связана с работой в области системы счисления (NS) и выражений и уравнений (EE)..jpg) Стандарты ЭЭ являются частью основной работы 8-го класса, в то время как стандарты NS обозначены как «вспомогательные» работы, поскольку они могут усилить и расширить основные темы.
Стандарты ЭЭ являются частью основной работы 8-го класса, в то время как стандарты NS обозначены как «вспомогательные» работы, поскольку они могут усилить и расширить основные темы.
В 8-м классе стандарты NS знакомят учащихся с иррациональными числами (числа типа √2, которые не могут быть выражены в виде дробей), (8.NS.A.1), а стандарты EE знакомят учащихся с простыми уравнениями, такими как x2 = 8 и y3 = 27, которые включают решение с квадратными и кубическими корнями. (8.EE.A.2) Поскольку применение теоремы Пифагора естественным образом приводит к уравнениям этого типа, решение задач в контексте прямоугольных треугольников представляет собой сходимость двух стандартов.Возьмем, к примеру, нашу задачу из стандарта 8.G.B.8 выше:
Когда учащиеся решают, они получают уравнение 22 + 62 = c2, и их решение выглядит примерно так:
22 + 62 = с2
4 + 36 = с2
40 = с2
√40 = с
На основе работы со стандартом 8.NS.A.1 учащийся 8-го класса должен уметь сказать, что √40 — это число от 6 до 7, потому что 40 — это число от 36 (62) до 49 (72).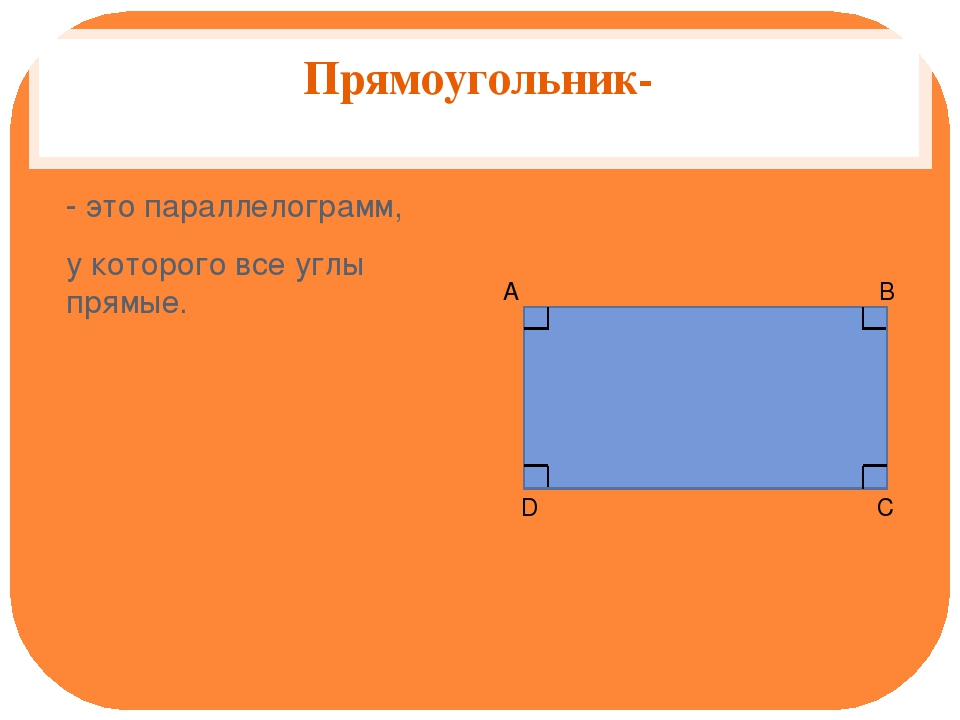 Отсюда они могут сделать вывод, что это меньше 6.5, потому что 40 ближе к 36, чем к 49, и используйте последовательные приближения, чтобы найти, что это примерно 6,3. Оглядываясь назад на задачу, которая включает расстояния в 2 единицы и 6 единиц для катетов, можно сказать, что это разумная длина для гипотенузы.
Отсюда они могут сделать вывод, что это меньше 6.5, потому что 40 ближе к 36, чем к 49, и используйте последовательные приближения, чтобы найти, что это примерно 6,3. Оглядываясь назад на задачу, которая включает расстояния в 2 единицы и 6 единиц для катетов, можно сказать, что это разумная длина для гипотенузы.
Откуда берутся сходство и сходство?
В то время как конгруэнтность и сходство начинаются в 8 классе, более фундаментальные понятия геометрии должны развиваться в начальных и средних классах. Уже в детском саду они начинают думать о длине и классифицировать формы.(К.Г.А.2) 4 класс оказывается решающим для работы с конгруэнтностью и подобием: Определяется понятие меры угла, (4.МД.С.5) а также точки, прямые, отрезки и лучи. (4.G.A.1) В 5 классе учащиеся узнают о координатной плоскости и точках графика в первом квадранте. (5.G.A.1) Затем, в 6 классе, учащиеся расширяют свои знания о системе счисления, включая отрицательные числа, тем самым открывая всю координатную плоскость. (6.NS.C.8) Работа над координатной плоскостью продолжается в 7 классе, (7.RP.A.2), а учащиеся решают задачи на чертежи в масштабе. (7.G.A.1) Хотя эти задачи не требуют формального понимания подобия с точки зрения преобразований, они дают учащимся возможность работать с парами похожих фигур и масштабных коэффициентов.
(6.NS.C.8) Работа над координатной плоскостью продолжается в 7 классе, (7.RP.A.2), а учащиеся решают задачи на чертежи в масштабе. (7.G.A.1) Хотя эти задачи не требуют формального понимания подобия с точки зрения преобразований, они дают учащимся возможность работать с парами похожих фигур и масштабных коэффициентов.
Подкаст-клип: Важность согласованности с Эндрю Ченом и Питером Коу (начало 9:34, конец 26:19)
Откуда взялась теорема Пифагора?
Теорема Пифагора также является новой для 8 класса.Хотя это не требует длительного обучения, некоторые базовые условия все же применяются:
- Учащиеся должны быть знакомы с экспоненциальной записью с 6 класса, чтобы понимать алгебраическую формулу. (6.EE.A.1)
-
Как отмечалось выше, учащимся необходим опыт решения уравнений 6, 7 и 8 классов, чтобы решать задачи с теоремой Пифагора. (6.EE.B.7, 7.EE.
 B.4, 8.EE.A.2)
B.4, 8.EE.A.2)
- Точно так же, как и преобразования, четкое понимание теоремы Пифагора опирается на такие элементарные понятия геометрии, как мера длины и угла.(4.G.A.1)
Предложения для учащихся, отстающих от
Если, приступая к разделу о конгруэнтности и сходстве, вы знаете, что ваши ученики не имеют четкого представления о названных выше идеях (или вообще не сталкивались с ними), что вы можете сделать? Нецелесообразно (и даже нежелательно) преподавать заново все, что ученики должны были выучить в 4–7 классах; в 8 классе есть много нового материала для изучения, поэтому основное внимание должно быть уделено стандартам для данного класса. В то же время существуют стратегические способы подведения итогов «незавершенного обучения» предыдущих оценок в рамках модуля конгруэнтности.Вот несколько идей для адаптации вашей инструкции, чтобы восполнить пробелы.
-
Если значительное число учащихся не полностью понимают углы или другие элементарные понятия, вы можете запланировать один или два урока, посвященных этим идеям, прежде чем приступить к преподаванию материалов для своего класса.
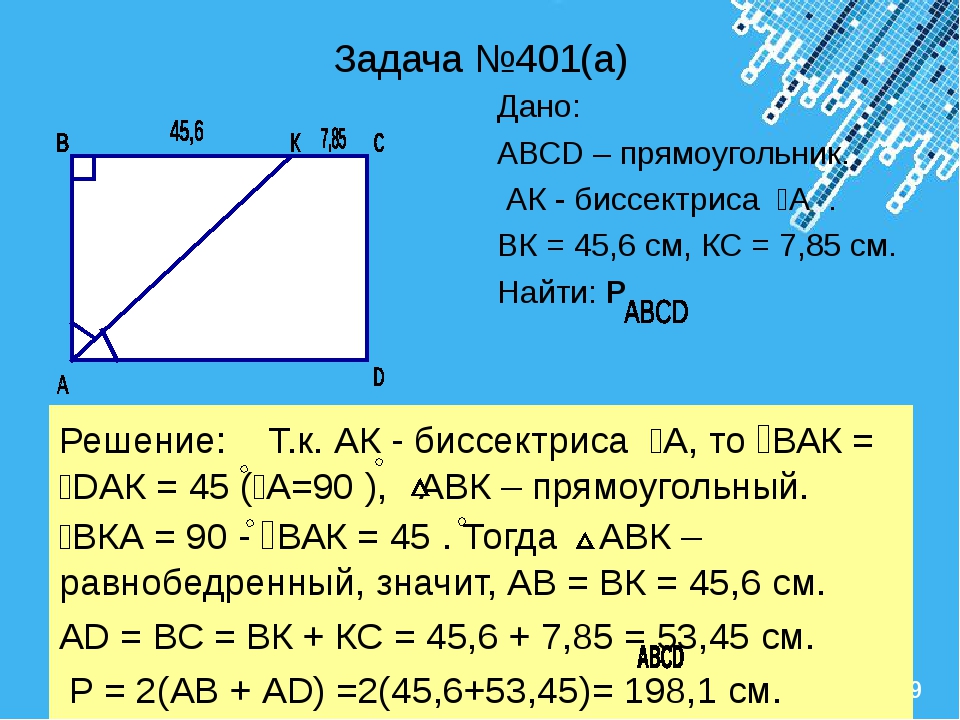 (Здесь могут оказаться полезными два урока 4-го класса: один по измерению угла, а другой по различению длины и меры угла.) Если вы считаете, что весь урок — это слишком много, вы можете спланировать краткий «мини-урок» или использовать некоторые задачи, связанные с этими идеями, в качестве разминки перед вашими первыми уроками конгруэнтности.
(Здесь могут оказаться полезными два урока 4-го класса: один по измерению угла, а другой по различению длины и меры угла.) Если вы считаете, что весь урок — это слишком много, вы можете спланировать краткий «мини-урок» или использовать некоторые задачи, связанные с этими идеями, в качестве разминки перед вашими первыми уроками конгруэнтности. - Если у значительного числа учащихся нет опыта работы с координатной плоскостью или они еще не умеют точно наносить точки, вы можете запланировать урок или серию разминок по этой идее перед началом работы с преобразованиями на координатной плоскости. (Этот урок для 6 класса по рисованию многоугольников на координатной плоскости может быть хорошим источником проблем для этого типа урока.)
-
Если значительное количество учащихся не умеет свободно идентифицировать и описывать геометрические фигуры (точки, прямые, отрезки и т.), вы можете запланировать мини-урок или серию разминок, чтобы повторить их в течение первых нескольких дней модуля, связанного с трансформациями.
 (Этот урок для 4 класса, который знакомит с только что упомянутыми терминами, содержит простое введение в эти идеи, и задачи, которые следуют за уроком, также могут быть полезны.)
(Этот урок для 4 класса, который знакомит с только что упомянутыми терминами, содержит простое введение в эти идеи, и задачи, которые следуют за уроком, также могут быть полезны.)
Куда идут эти понятия?
Конгруэнтность и сходство долгое время были важными идеями в старшей школе, и, как объяснялось выше, преобразования теперь играют центральную роль в понимании этих идей.Один из первых опытов, которые учащиеся получат в средней школе по геометрии, — разработка точных определений твердотельных движений. (G-CO.A.4) Использование преобразований позволяет учащимся устанавливать критерии конгруэнтности треугольников (G-CO.B.8) и дает им инструмент для использования при доказательстве теорем. (G-CO.C) Как только учащиеся поймут конгруэнтность, они будут готовы решать задачи, связанные с конгруэнтными фигурами, (G.SRT.B.5) исследовать отношения внутри треугольников, (G-C.A.2) и доказывать утверждения, используя координаты. (Г-ГПЭ.Б.4) В дальнейшем они столкнутся с более специализированными приложениями конгруэнтности; Принцип Кавальери, например, зависит от знания того, что означает конгруэнтность поперечных сечений двух разных фигур. (G-GMD.A.1) Сходство включает в себя аналогичный процесс и ведет к изучению тригонометрии. G-SRT.C.9 Последняя последовательность показывает, как работа в 8-м классе ведет в старшую школу.
(G-GMD.A.1) Сходство включает в себя аналогичный процесс и ведет к изучению тригонометрии. G-SRT.C.9 Последняя последовательность показывает, как работа в 8-м классе ведет в старшую школу.
Если вы только что закончили это руководство, поздравляем! Надеюсь, это было информативно, и вы можете вернуться к нему в качестве справочного материала при планировании уроков, создании модулей или оценке учебных материалов.Для получения дополнительных руководств из этой серии посетите нашу страницу Enhance Instruction. Чтобы узнать больше о том, как вы можете использовать эти руководства в своей повседневной практике, посетите нашу страницу часто задаваемых вопросов. И если вы хотите узнать больше о конгруэнтности, сходстве и теореме Пифагора в 8 классе, не забудьте эти ресурсы:
Партнеры по достижениям учащихся: внимание в 8 классе
Хунг-Хси Ву: Преподавание геометрии в соответствии с общими базовыми стандартами
EngageNY: 8 класс, материалы модуля 2 (конгруэнтность)
EngageNY: класс 8, модуль 3, материалы (сходство)
EngageNY: 8 класс, материалы модуля 7 (теорема Пифагора)
Иллюстративные задачи по математике для 8 класса
1.
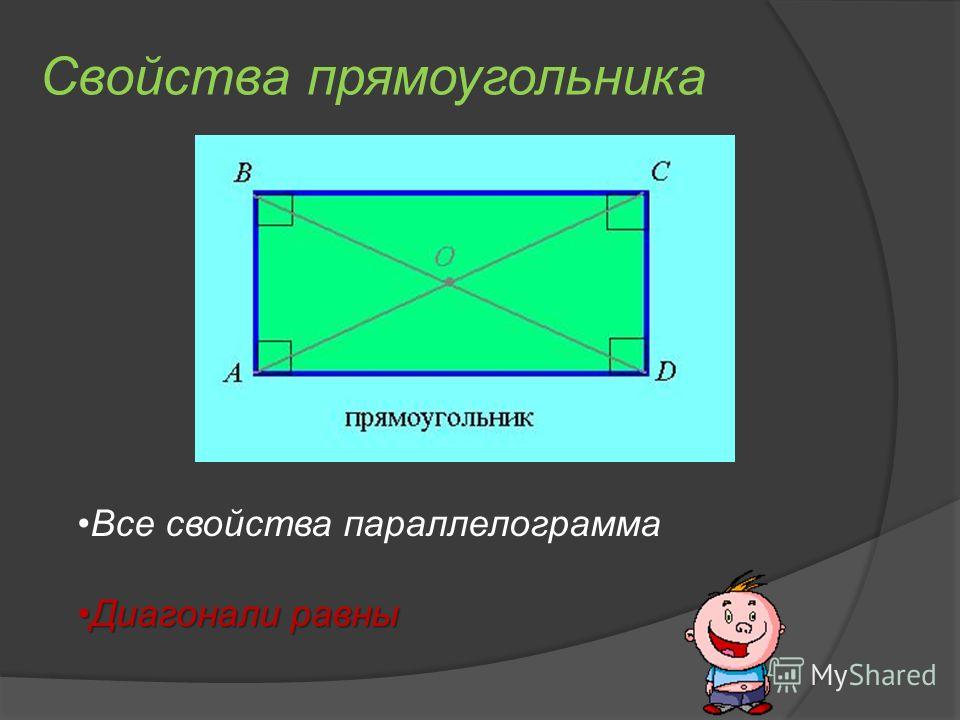 Что такое руководство по содержанию?
Что такое руководство по содержанию?
В нашей работе с высокими академическими стандартами мы часто слышим, как преподаватели спрашивают: «Как выглядит обучение в соответствии со стандартами?» Наши руководства по содержанию призваны ответить на этот вопрос, подробно рассматривая одну или несколько групп математических стандартов одновременно. Справочники по содержанию предназначены для каждого класса и предметной области, и есть руководства для каждого класса или курса, от детского сада до алгебры II. Если вы хотите узнать больше о преподавании пропорций и пропорциональных отношений в 6 классе, например, наше соответствующее Руководство по содержанию даст вам исчерпывающее, но доступное объяснение этих стандартов, несколько примеров открытых образовательных ресурсов (ООР), которые соответствуют стандартам, и конкретные предложения по поддержке преподавания пропорций и пропорциональных рассуждений в 6 классе.
Наша цель при создании Руководства по содержанию заключалась в том, чтобы предоставить занятым учителям практичный и удобный для чтения ресурс о том, что говорят стандарты математики на уровне класса, а также примеры учебных материалов, которые поддерживают концептуальное понимание, решение задач, и процедурные навыки и беглость для студентов.
Важно отметить, что руководства по содержанию не предназначены для использования в качестве учебного плана (или любого другого документа для учащихся), руководства или исходного материала для действий по подготовке к экзаменам или какого-либо инструмента оценки учителей.
2. Что содержится в руководстве по содержанию?
Каждое руководство по содержанию ориентировано на определенную группу стандартов. Большинство руководств по содержанию имеют одну и ту же структуру, состоящую из трех частей:
.- Часть 1 разъясняет навыки и понимание учащихся, описываемые этой группой стандартов. Этот раздел иллюстрирует стандарты с использованием нескольких студенческих заданий из свободно доступных онлайн-источников. Учителя могут использовать или адаптировать эти задания для своих учеников.
-
Часть 2 объясняет, как эта группа стандартов связана с другими стандартами того же класса.Мы подчеркиваем, как эти связи влияют на планирование и преподавание, и как эта согласованность внутри класса может расширить доступ для учащихся.
 Часть 2 также включает несколько студенческих заданий из свободно доступных онлайн-источников.
Часть 2 также включает несколько студенческих заданий из свободно доступных онлайн-источников. -
Часть 3 отслеживает избранные этапы обучения, ведущие к содержимому уровня класса, описанному в конкретном Руководстве по содержанию. Это обсуждение переходит в серию конкретных и практических предложений о том, как учителя могут использовать прогрессии для обучения учащихся, которые могут быть не готовы к математике на уровне класса.Наконец, в части 3 прослеживается переход к содержанию в более высоких классах.
3. Как я могу использовать руководства по содержанию?
Учителя, прочитавшие наши Руководства по содержанию, говорят, что видят преимущества для всех преподавателей. Вот несколько советов о том, как их могут использовать разные педагоги.
Учителя могут использовать справочники по математике по адресу:
- Повысить или освежить свои знания о стандартах и требованиях к тому, что учащиеся должны знать к концу года.
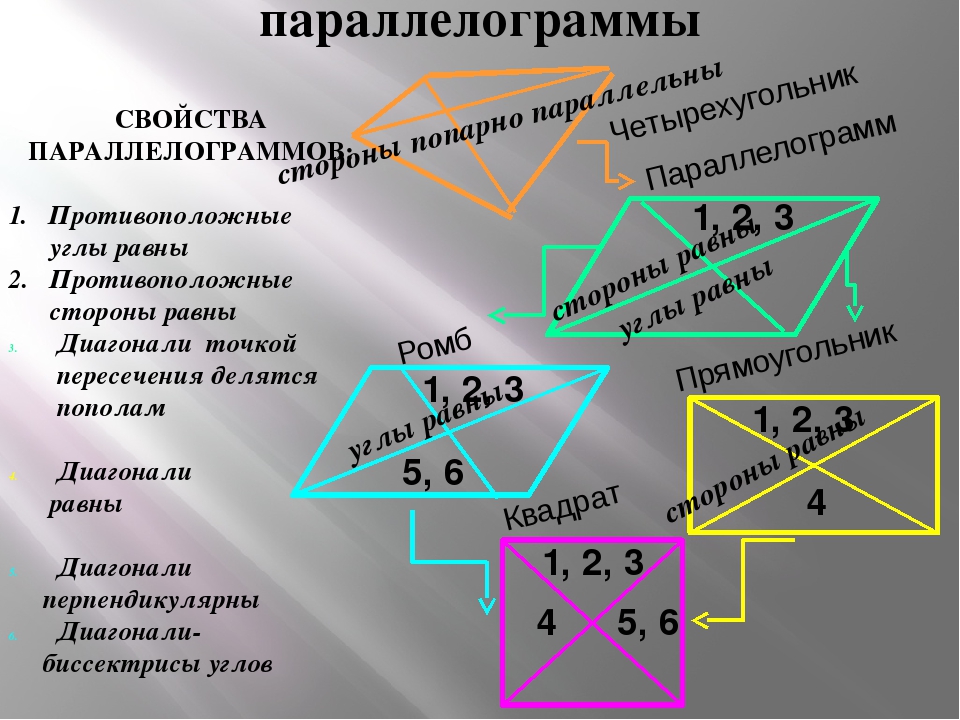
- Адаптируйте уроки и модули, используя соответствующие предварительные условия, чтобы помочь учащимся, отстающим в классе.
- Получите доступ к лучшим доступным ООР по математике, чтобы использовать их для введения и/или закрепления понятий
- Убедитесь, что их учебный план и/или разделы:
- Сосредоточьтесь на основной работе класса и соответствующей глубине каждого стандарта.
- Нацельтесь на соответствующие аспекты строгости — процедурные навыки и беглость, моделирование и применение, а также концептуальное понимание, описанное в стандартах.
- Помогите учащимся установить согласованные связи внутри и между классами.
- Создайте или пересмотрите свои уроки и вопросы, чтобы сосредоточиться на важных понятиях в стандартах.
Преподаватели и руководители школ могут использовать руководства по математике по адресу:
- Обновить или расширить свои знания о стандартах и требованиях к тому, что учащиеся должны знать к концу года.

- Разрабатывайте и сообщайте о согласованных требованиях к планированию уроков и обучению в соответствии со стандартами.
- Дайте ссылку при планировании и/или обсуждении обучения с учителями.
- Получите представление о том, как должны выглядеть инструкции и работа учащихся, чтобы соответствовать требованиям стандартов.
- Разработка и разработка контента и сессий/семинаров по повышению квалификации на основе стандартов.
- Поощряйте содержательные, основанные на стандартах обсуждения среди сотрудников и расширяйте их знания.
- Разработать и/или пересмотреть планы улучшения школы, чтобы поддержать и включить содержание и основанное на практике преподавание и обучение.
4. Зачем нужны руководства по содержанию?
Переход к более высоким стандартам заставил учителей по всей стране внести существенные изменения в свое планирование и обучение, но только одна треть учителей считает, что они готовы помочь своим ученикам пройти более строгие оценки, соответствующие стандартам (Kane et. др., 2016). Этого следовало ожидать, поскольку новые высокие стандарты представляют собой значительный отход от ранее существовавших стандартов. Стандарты требуют более глубокого понимания математического содержания, которое они преподают; различная последовательность того, что учащиеся должны усвоить, к какому классу; а также другая педагогика, которая делает упор на концептуальное понимание учащихся, решение проблем и беглость процедур с одинаковой интенсивностью.
др., 2016). Этого следовало ожидать, поскольку новые высокие стандарты представляют собой значительный отход от ранее существовавших стандартов. Стандарты требуют более глубокого понимания математического содержания, которое они преподают; различная последовательность того, что учащиеся должны усвоить, к какому классу; а также другая педагогика, которая делает упор на концептуальное понимание учащихся, решение проблем и беглость процедур с одинаковой интенсивностью.
Однако поддержка учителей в обеспечении высоких стандартов в их классах отстает. Исследования показывают, что подготовка учителей в США в настоящее время недостаточна для подготовки учителей к преподаванию требовательных новых стандартов (Центр исследований в области математики и научного образования, 2010 г.). И хотя существуют некоторые ресурсы, которые «распаковывают» стандарты, мало, если они вообще есть, объясняют , а иллюстрируют стандарты. «Распаковка» стандартов один за другим также может привести к бессвязному представлению, пренебрегающему структурой и последовательностью стандартов. Создавая Руководства по содержанию, мы стремились предоставить занятым учителям практичный, легкий для чтения ресурс о стандартах для их классов и о том, как помочь всем учащимся изучить их. Существует множество эмпирических данных о том, что, когда учителя обладают как хорошими знаниями математического содержания, которое они преподают, так и педагогическими знаниями, помогающими учащимся освоить эти содержательные знания, их ученики узнают больше (Baumert et. al., 2010; Hill, Rowan and Ball). , 2005; Rockoff и др., 2008). Мы надеемся, что, имея в руках Руководства по содержанию, учителя добьются большего успеха, помогая своим ученикам продвигаться к подготовке к колледжу и карьере.
Создавая Руководства по содержанию, мы стремились предоставить занятым учителям практичный, легкий для чтения ресурс о стандартах для их классов и о том, как помочь всем учащимся изучить их. Существует множество эмпирических данных о том, что, когда учителя обладают как хорошими знаниями математического содержания, которое они преподают, так и педагогическими знаниями, помогающими учащимся освоить эти содержательные знания, их ученики узнают больше (Baumert et. al., 2010; Hill, Rowan and Ball). , 2005; Rockoff и др., 2008). Мы надеемся, что, имея в руках Руководства по содержанию, учителя добьются большего успеха, помогая своим ученикам продвигаться к подготовке к колледжу и карьере.
5. Какая связь между руководствами по содержанию и последовательностями?
Документы Progressions описывают развитие понимания математики от класса к классу. Они были основаны на исследованиях когнитивного развития детей, а также на логической структуре математики. Прогрессии объясняют, почему стандарты расположены именно так. Руководства по содержанию часто выделяют ключевые идеи из прогрессий, но не добавляют новых стандартов и не меняют ожиданий в отношении того, что учащиеся должны знать и уметь; они стремятся объяснить и проиллюстрировать группу стандартов одновременно, используя свободно доступные онлайн-источники.Хотя задания и уроки ООР в Руководствах по содержанию являются одним из способов соответствовать стандартам для каждого класса, они не являются единственными средствами для этого.
Руководства по содержанию часто выделяют ключевые идеи из прогрессий, но не добавляют новых стандартов и не меняют ожиданий в отношении того, что учащиеся должны знать и уметь; они стремятся объяснить и проиллюстрировать группу стандартов одновременно, используя свободно доступные онлайн-источники.Хотя задания и уроки ООР в Руководствах по содержанию являются одним из способов соответствовать стандартам для каждого класса, они не являются единственными средствами для этого.
6. Как отбирались ресурсы?
Для иллюстрации Стандартов мы выбрали примеры заданий и уроков из свободно доступных онлайн-источников, таких как EngageNY, Illustrative Mathematics и Student Achievement Partners. Эти источники выбраны потому, что они полностью соответствуют новым высоким стандартам на основе национального обзора учебных программ K-12 или созданы организациями, возглавляемыми авторами новых высоких стандартов.Кроме того, поскольку они являются открытыми образовательными ресурсами (ООР), они свободно доступны для всех видов использования.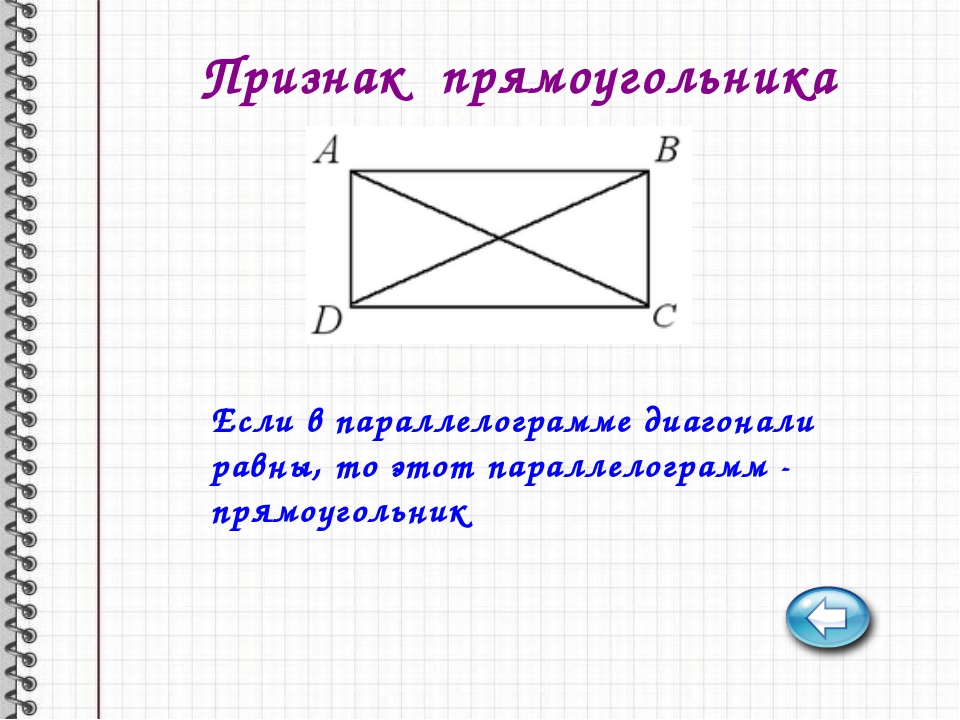 Все материалы UnboundEd также являются ООР, что является частью нашего стремления сделать высококачественный и согласованный контент доступным для всех преподавателей.
Все материалы UnboundEd также являются ООР, что является частью нашего стремления сделать высококачественный и согласованный контент доступным для всех преподавателей.
7. Почему Руководства по содержанию касаются лишь нескольких стандартов? Где остальные стандарты?
Каждое руководство по содержанию относится к подмножеству стандартов для оценки. Стандарты, рассматриваемые в первом наборе руководств по содержанию для каждого класса, обычно относятся к высокоприоритетному содержимому; эти стандарты также часто являются хорошим выбором для обучения в начале года.Дополнительную информацию о выборе стандартов можно найти во введении к каждому Руководству по содержанию. Со временем мы разработаем дополнительные Руководства по содержанию для каждого класса и обновим существующие. Мы планируем иметь четыре руководства по содержанию для каждого класса или курса, от детского сада до алгебры II. Руководства будут публиковаться волнами, каждая волна будет состоять из одного руководства для каждого класса. Мы планируем выпустить второй набор руководств по содержанию для каждого класса к концу 2016-17 учебного года.
Мы планируем выпустить второй набор руководств по содержанию для каждого класса к концу 2016-17 учебного года.
8.Как я могу быть в курсе новых руководств по содержанию?
Если вы хотите получать обновления контента и событий от UnboundEd, включая новые руководства по контенту, подпишитесь на объявления UnboundEd здесь.
Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для создания геометрии. Поймите и примените теорему Пифагора. Используйте подобные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для прямой, проходящей через начало координат, и уравнение y = mx + b для прямой, пересекающей вертикальную ось в точке b.Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для создания геометрии. Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для создания геометрии.
Экспериментально проверьте свойства поворотов, отражений и переводов:
Линии превращаются в прямые, а отрезки прямых в отрезки прямой одинаковой длины.Углы принимаются равными углам.
Параллельные прямые переводятся в параллельные прямые.
Поймите, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.Опишите эффект расширения, перевода, поворота и отражения на двухмерных фигурах, используя координаты.
Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.
Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для создания геометрии.
Экспериментально проверьте свойства поворотов, отражений и переводов:
Линии превращаются в прямые, а отрезки прямых в отрезки прямой одинаковой длины.Углы принимаются равными углам.
Параллельные прямые переводятся в параллельные прямые.
Поймите, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.Опишите эффект расширения, перевода, поворота и отражения на двухмерных фигурах, используя координаты.
Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними. Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников.
Экспериментально проверьте свойства поворотов, отражений и переводов:
Поймите, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.
Опишите эффект расширения, перевода, поворота и отражения на двухмерных фигурах, используя координаты.
Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников.
Экспериментально проверьте свойства поворотов, отражений и переводов:
Поймите, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.
Опишите эффект расширения, перевода, поворота и отражения на двухмерных фигурах, используя координаты.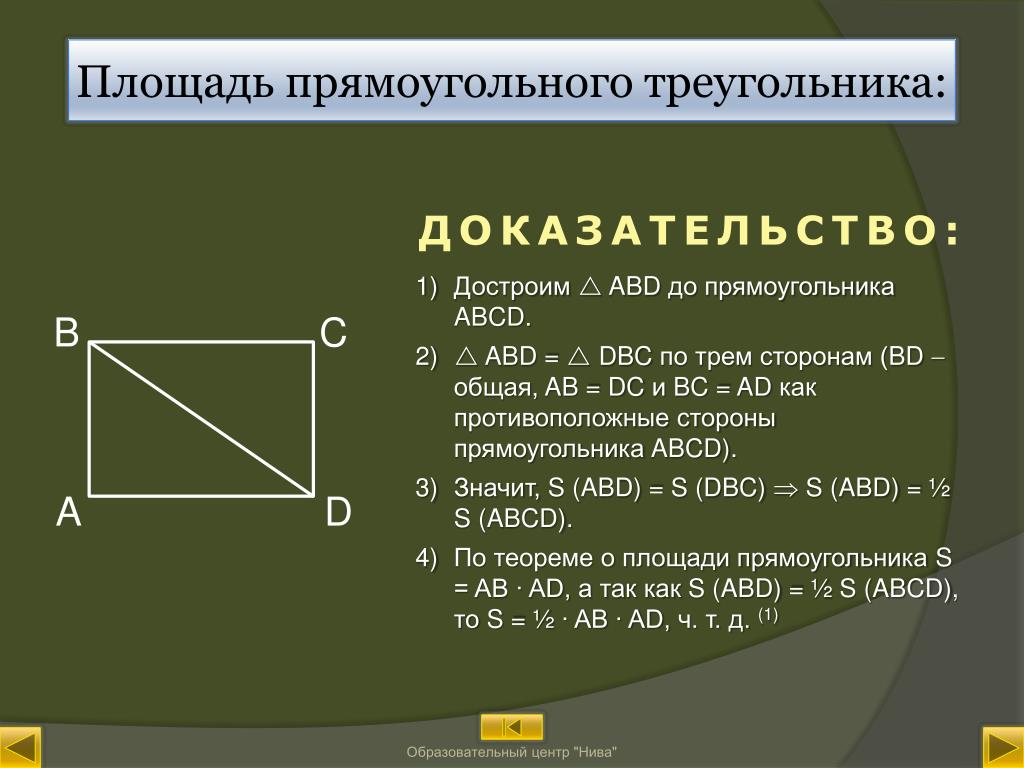 Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников.
Экспериментально проверьте свойства поворотов, отражений и переводов:
Поймите, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.
Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.
Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников.
Экспериментально проверьте свойства поворотов, отражений и переводов:
Поймите, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.
Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними. Опишите эффект расширения, перевода, поворота и отражения на двухмерных фигурах, используя координаты.
Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для создания геометрии.
Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников.Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x² = p и x³ = p, где p — положительное рациональное число. Вычислите квадратные корни из маленьких совершенных квадратов и кубические корни из маленьких совершенных кубов. Знайте, что √2 иррационально.
Знайте, что числа, которые не являются рациональными, называются иррациональными.
Опишите эффект расширения, перевода, поворота и отражения на двухмерных фигурах, используя координаты.
Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для создания геометрии.
Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников.Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x² = p и x³ = p, где p — положительное рациональное число. Вычислите квадратные корни из маленьких совершенных квадратов и кубические корни из маленьких совершенных кубов. Знайте, что √2 иррационально.
Знайте, что числа, которые не являются рациональными, называются иррациональными.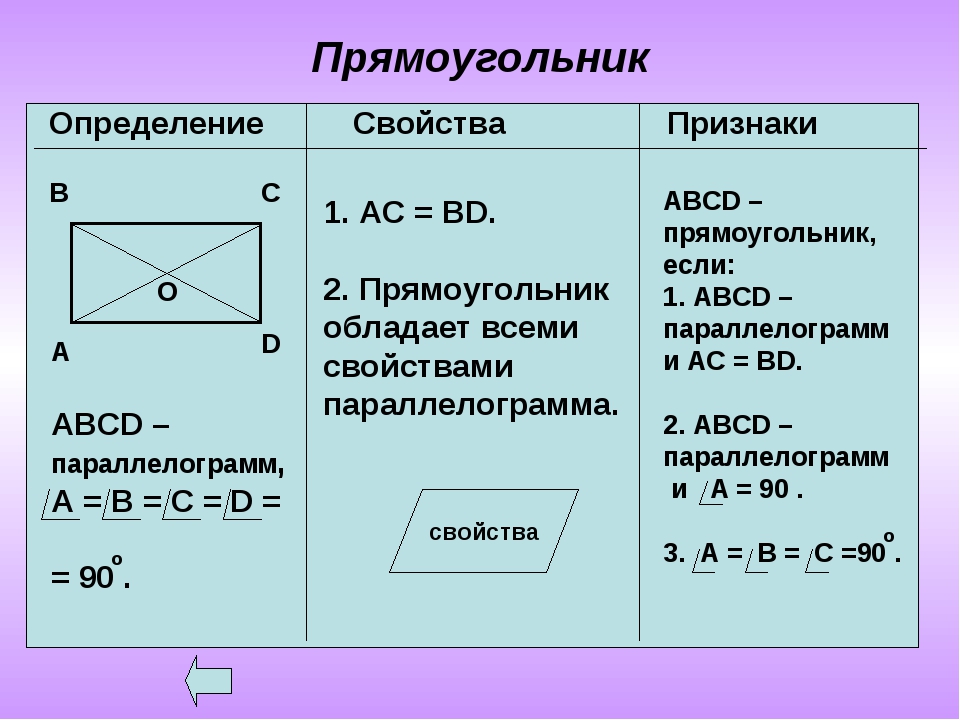 Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.Поймите и примените теорему Пифагора.
Поймите и примените теорему Пифагора.
Объясните доказательство теоремы Пифагора и ее обращения.
Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальном мире и математических задач в двух и трех измерениях.Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.
Объясните доказательство теоремы Пифагора и ее обращения.
Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальном мире и математических задач в двух и трех измерениях.
Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.Поймите и примените теорему Пифагора.
Поймите и примените теорему Пифагора.
Объясните доказательство теоремы Пифагора и ее обращения.
Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальном мире и математических задач в двух и трех измерениях.Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.
Объясните доказательство теоремы Пифагора и ее обращения.
Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальном мире и математических задач в двух и трех измерениях.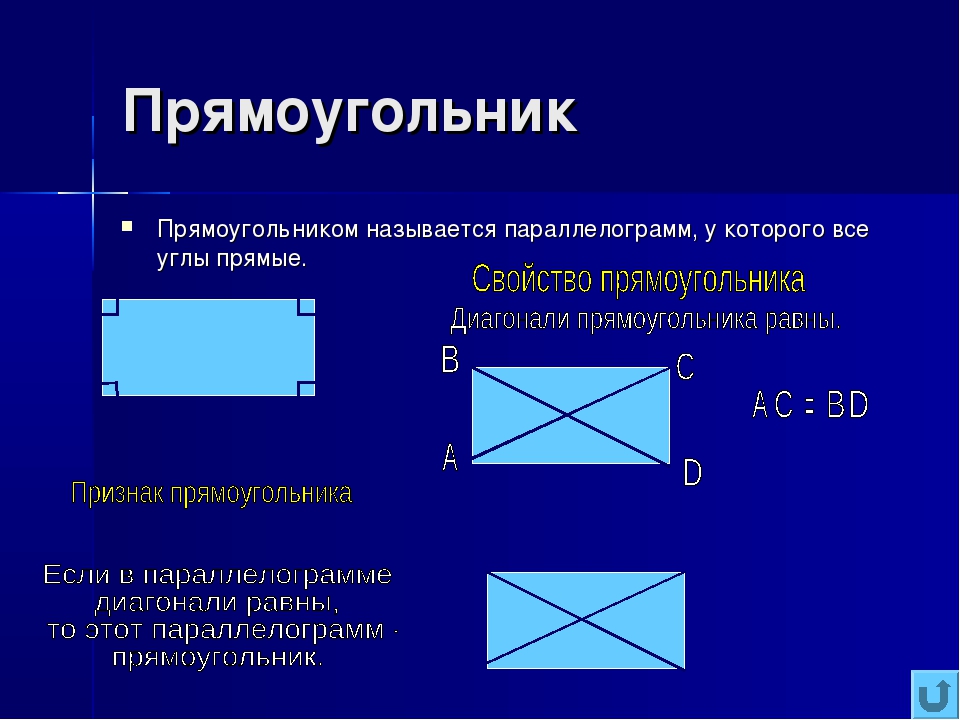 Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.Объясните доказательство теоремы Пифагора и ее обращения.
Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальном мире и математических задач в двух и трех измерениях.
Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.
Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.Ищите и используйте структуру.
Рассуждайте абстрактно и количественно.
Используйте подобные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для прямой, проходящей через начало координат, и уравнение y = mx + b для прямой, пересекающей вертикальную ось в точке b.
Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.Объясните доказательство теоремы Пифагора и ее обращения.
Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальном мире и математических задач в двух и трех измерениях.
Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.
Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.Ищите и используйте структуру.
Рассуждайте абстрактно и количественно.
Используйте подобные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для прямой, проходящей через начало координат, и уравнение y = mx + b для прямой, пересекающей вертикальную ось в точке b. Знайте, что числа, которые не являются рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.
Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x² = p и x³ = p, где p — положительное рациональное число.Вычислите квадратные корни из маленьких совершенных квадратов и кубические корни из маленьких совершенных кубов. Знайте, что √2 иррационально.
Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.
Знайте, что числа, которые не являются рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.
Знайте, что числа, которые не являются рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.
Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x² = p и x³ = p, где p — положительное рациональное число.Вычислите квадратные корни из маленьких совершенных квадратов и кубические корни из маленьких совершенных кубов. Знайте, что √2 иррационально.
Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.
Знайте, что числа, которые не являются рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.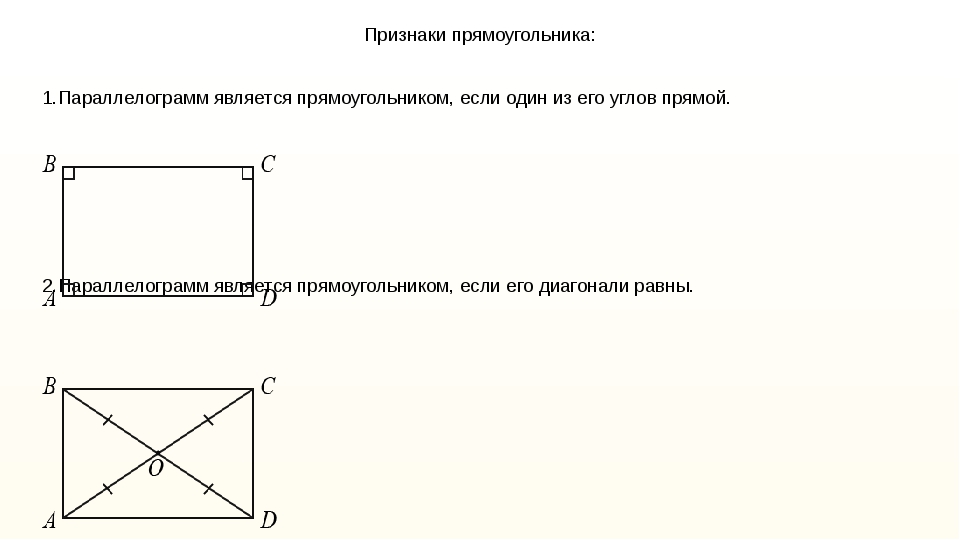 Правильно называйте фигуры независимо от их ориентации или общего размера.
Распознавать углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку, и понимать принципы измерения углов:
Рисовать точки, прямые, отрезки, лучи, углы (прямые, острые, тупые), перпендикулярные и параллельные прямые. Определите их на двумерных фигурах.Используйте пару перпендикулярных числовых линий, называемых осями, для определения системы координат, где пересечение линий (начало координат) расположено так, чтобы совпадать с 0 на каждой линии, и заданной точкой на плоскости, расположенной с помощью упорядоченной пары координат. числа, называемые его координатами. Поймите, что первое число указывает, как далеко нужно пройти от начала координат в направлении одной оси, а второе число указывает, как далеко нужно пройти в направлении второй оси, при условии, что имена двух осей и координаты соответствовать (т.
Правильно называйте фигуры независимо от их ориентации или общего размера.
Распознавать углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку, и понимать принципы измерения углов:
Рисовать точки, прямые, отрезки, лучи, углы (прямые, острые, тупые), перпендикулярные и параллельные прямые. Определите их на двумерных фигурах.Используйте пару перпендикулярных числовых линий, называемых осями, для определения системы координат, где пересечение линий (начало координат) расположено так, чтобы совпадать с 0 на каждой линии, и заданной точкой на плоскости, расположенной с помощью упорядоченной пары координат. числа, называемые его координатами. Поймите, что первое число указывает, как далеко нужно пройти от начала координат в направлении одной оси, а второе число указывает, как далеко нужно пройти в направлении второй оси, при условии, что имена двух осей и координаты соответствовать (т. г., ось x и координата x, ось y и координата y).
Решайте реальные и математические задачи, отображая точки во всех четырех квадрантах координатной плоскости. Включите использование координат и абсолютного значения для нахождения расстояний между точками с одной и той же первой координатой или одной и той же второй координатой.
Распознавать и представлять пропорциональные отношения между величинами.
Решение задач, связанных с чертежами геометрических фигур в масштабе, включая вычисление фактических длин и площадей по чертежу в масштабе и воспроизведение чертежа в масштабе в другом масштабе.Напишите и оцените числовые выражения, включающие целые числа.
Решайте реальные и математические задачи, записывая и решая уравнения вида x + p = q и px = q для случаев, когда p, q и x являются неотрицательными рациональными числами.
г., ось x и координата x, ось y и координата y).
Решайте реальные и математические задачи, отображая точки во всех четырех квадрантах координатной плоскости. Включите использование координат и абсолютного значения для нахождения расстояний между точками с одной и той же первой координатой или одной и той же второй координатой.
Распознавать и представлять пропорциональные отношения между величинами.
Решение задач, связанных с чертежами геометрических фигур в масштабе, включая вычисление фактических длин и площадей по чертежу в масштабе и воспроизведение чертежа в масштабе в другом масштабе.Напишите и оцените числовые выражения, включающие целые числа.
Решайте реальные и математические задачи, записывая и решая уравнения вида x + p = q и px = q для случаев, когда p, q и x являются неотрицательными рациональными числами.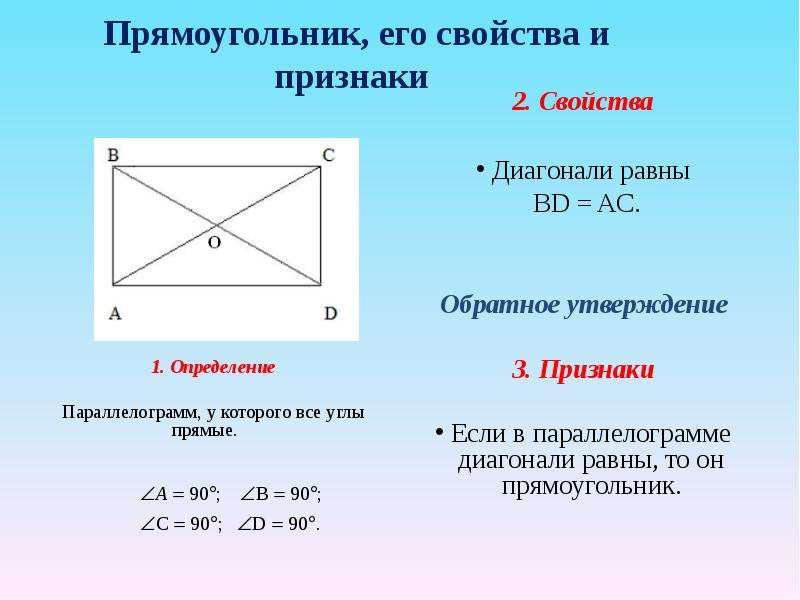 Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах.Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x² = p и x³ = p, где p — положительное рациональное число. Вычислите квадратные корни из маленьких совершенных квадратов и кубические корни из маленьких совершенных кубов. Знайте, что √2 иррационально.
Рисовать точки, прямые, отрезки, лучи, углы (прямые, острые, тупые), перпендикулярные и параллельные прямые. Определите их на двумерных фигурах.Разработайте определения поворотов, отражений и перемещений с точки зрения углов, окружностей, перпендикулярных линий, параллельных линий и отрезков.
Объясните, как критерии конгруэнтности треугольников (ASA, SAS и SSS) следуют из определения конгруэнтности в терминах жестких движений.
Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах.Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x² = p и x³ = p, где p — положительное рациональное число. Вычислите квадратные корни из маленьких совершенных квадратов и кубические корни из маленьких совершенных кубов. Знайте, что √2 иррационально.
Рисовать точки, прямые, отрезки, лучи, углы (прямые, острые, тупые), перпендикулярные и параллельные прямые. Определите их на двумерных фигурах.Разработайте определения поворотов, отражений и перемещений с точки зрения углов, окружностей, перпендикулярных линий, параллельных линий и отрезков.
Объясните, как критерии конгруэнтности треугольников (ASA, SAS и SSS) следуют из определения конгруэнтности в терминах жестких движений.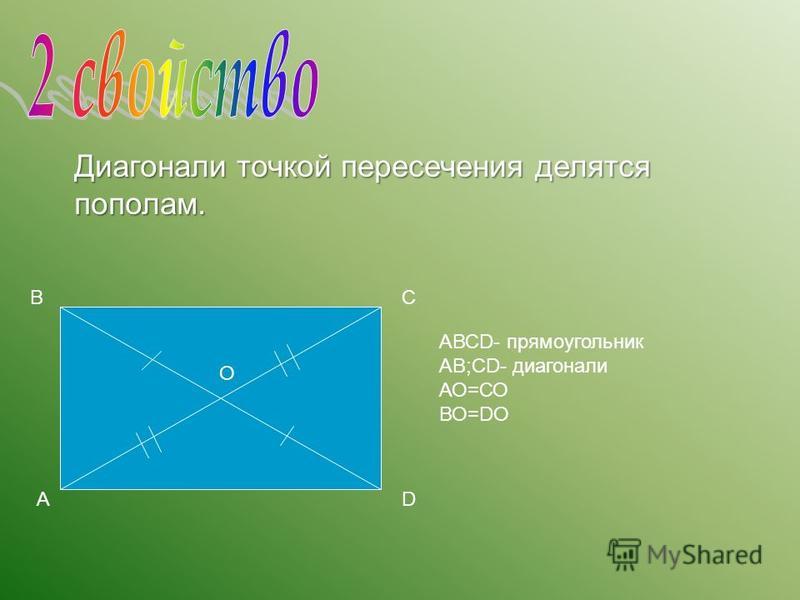 Докажите геометрические теоремы
Используйте критерии конгруэнтности и подобия для треугольников, чтобы решать задачи и доказывать отношения в геометрических фигурах.Определите и опишите отношения между вписанными углами, радиусами и хордами.
Используйте координаты для алгебраического доказательства простых геометрических теорем.
Приведите неформальные аргументы в пользу формул длины окружности, площади круга, объема цилиндра, пирамиды и конуса.
Докажите геометрические теоремы
Используйте критерии конгруэнтности и подобия для треугольников, чтобы решать задачи и доказывать отношения в геометрических фигурах.Определите и опишите отношения между вписанными углами, радиусами и хордами.
Используйте координаты для алгебраического доказательства простых геометрических теорем.
Приведите неформальные аргументы в пользу формул длины окружности, площади круга, объема цилиндра, пирамиды и конуса.
Геометрия и измерение — проект «Подключенная математика»
Естественные и искусственные объекты окружающего нас мира очерчены, поддерживаются и украшаются бесконечным разнообразием геометрических форм.Главной целью модулей в разделе Connected Mathematics 3 (CMP3) «Геометрия и измерения» является развитие понимания учащимися связей между формой и функцией обычных форм. Например, треугольники обеспечивают структурную устойчивость фермам моста, потому что они являются жесткими фигурами. Шестиугольники – это распространенная форма декоративной плитки из-за их множества симметрий и того факта, что их можно использовать для покрытия плоских поверхностей без нахлеста или зазоров. Строители используют 3-4-5 треугольников для проверки перпендикулярности каркаса, потому что каждый такой треугольник должен быть прямоугольным.
Например, треугольники обеспечивают структурную устойчивость фермам моста, потому что они являются жесткими фигурами. Шестиугольники – это распространенная форма декоративной плитки из-за их множества симметрий и того факта, что их можно использовать для покрытия плоских поверхностей без нахлеста или зазоров. Строители используют 3-4-5 треугольников для проверки перпендикулярности каркаса, потому что каждый такой треугольник должен быть прямоугольным.
В цепочке «Геометрия и измерения» есть шесть модулей, а также связи с темами «Геометрия и измерения» во многих модулях других ветвей контента. Центральными целями цепочки являются:
- Расширить понимание и навыки геометрических измерений периметра и площади многоугольников и кругов, а также площади поверхности и объема прямых призм, цилиндров, конусов и сфер;
- Развить понимание сходства и соответствия геометрических фигур, используя как концепции преобразований, так и условия, связанные с измерениями сторон и углов, для установления этих отношений;
- Разработка связей пропорциональности между линейными измерениями, измерениями площади и объема для подобных фигур;
- Расширение понимания построения координатных графиков до четырех квадрантов; и
- Разработайте теорему Пифагора для прямоугольных треугольников и связанную с ней формулу расстояния для точек на координатной сетке.

Процессы обучения, направленные на достижение каждой из этих широких целей, описаны в следующих разделах.
Расширение знаний и навыков с помощью геометрических измерений
Учащиеся шестого класса, скорее всего, знают, как найти площадь прямоугольника и объем прямоугольной призмы. Модуль «Покрытие и окружение » для шестого класса рассматривает основные идеи периметра, площади и объема, но расширяет основную идею покрытия (и заполнения) фигуры копиями единиц длины (сегмента), площади (квадрата) или объем (куб) несколькими способами.Во-первых, он выделяет и помогает учащимся увидеть разницу между периметром и площадью, задавая вопрос: «Каковы размеры прямоугольника с фиксированным периметром и максимальной площадью?» и «Каковы размеры прямоугольника с фиксированной площадью и минимальным периметром?» Например, на следующем изображении показаны два прямоугольника площадью 16 квадратных единиц, но с разными периметрами.
Площадь ABCD = 16 квадратных единиц Площадь EFGH = 16 квадратных единиц Периметр ABCD = 16 квадратных единиц Периметр EFGH = 20 квадратных единиц
Во-вторых, Покрытие и окружение использует принцип, согласно которому фигуры можно разрезать на части и собирать в новые формы без изменения площади, чтобы логически вывести формулы площади треугольников и параллелограммов. Этот принцип проиллюстрирован ниже.
Этот принцип проиллюстрирован ниже.
Площадь параллелограмма слева равна сумме двух площадей, трапеции и треугольника. Площадь прямоугольника справа также является суммой тех же двух площадей. В обоих случаях A = bh квадратных единиц. Учащиеся связывают геометрическую идею, площадь с алгебраической идеей, отношениями.
Наконец, Покрытие и окружение закладывает основу для расчета объема в любой призме, подчеркивая тот факт, что такую призму можно рассматривать как стопку из нескольких слоев единичных кубов и что количество таких кубов в каждой стопке равно площадь основания призмы.
Те же самые общие принципы измерения применяются в блоке для наполнения и упаковки класса 7 . Filling and Wrapping расширяет возможности вычисления площади и объема для кругов, многоугольных призм, цилиндров, конусов и сфер. В каждом случае учащиеся распространяют основные идеи, которые очень хорошо применимы к прямоугольным фигурам, на аппроксимацию других, более сложных фигур.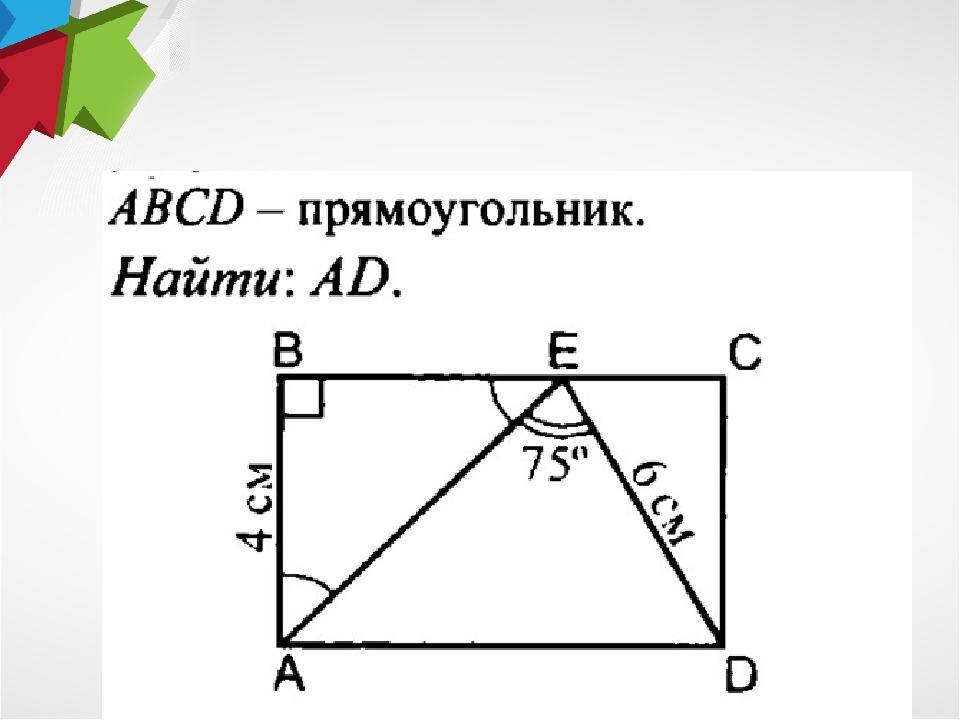 Площадь круга аппроксимируется путем покрытия круга квадратами радиуса, как показано здесь.
Площадь круга аппроксимируется путем покрытия круга квадратами радиуса, как показано здесь.
Площадь и длина окружности связаны рассечением. Окружность внизу разрезана на восемь секторов, а затем эти сектора переставлены так, чтобы получился примерный параллелограмм. По мере того как мы делим круг на все большее и большее количество секторов, основание параллелограмма приближается к половине окружности C круга, а высота параллелограмма приближается к радиусу r круга. Площадь параллелограмма примерно равна 0,5Cr или 0.5(2π r ) r или π r 2 .
А объем цилиндра рассчитывается по принципу «площадь основания умножить на высоту», введенному с прямоугольными призмами. Площадь поверхности и объем цилиндров, конусов и сфер пересматриваются в «Скажи это с помощью символов» в 8 классе.
В 7 классе, Формы и конструкции рассматривает и расширяет измерение углов. Несколько проблем приводят к фундаментальным результатам о мерах углов в многоугольниках: вывод формулы для внешних и внутренних угловых мер любого многоугольника и развитие отношений между мерами углов, образованных пересекающимися прямыми и параллельными прямыми, пересекаемыми секущими. В совокупности эти расширения понятий и навыков измерения закладывают прочную основу для развития понятий подобия и соответствия в 7 и 8 классах.
В совокупности эти расширения понятий и навыков измерения закладывают прочную основу для развития понятий подобия и соответствия в 7 и 8 классах.
Развитие понимания конгруэнтности и сходства
С неформальной точки зрения две геометрические фигуры называются конгруэнтными, если они имеют одинаковую форму и размер. Две фигуры называются подобными, если они имеют одинаковую форму, но, возможно, разные по размеру. Есть по крайней мере два стандартных способа сделать это неформальное понимание математически точным: один статический, а другой динамический.
Стандартный способ установления конгруэнтности для фигур, подобных двум треугольникам, состоит в том, чтобы сказать, что существует соответствие между вершинами фигур, при котором соответствующие пары сторон и углов равны по размеру. Более динамичный подход к конгруэнтности состоит в том, чтобы сказать, что существует сохраняющее расстояние преобразование (отражение, вращение, перенос или скользящее отражение), которое отображает одну фигуру точно поверх другой.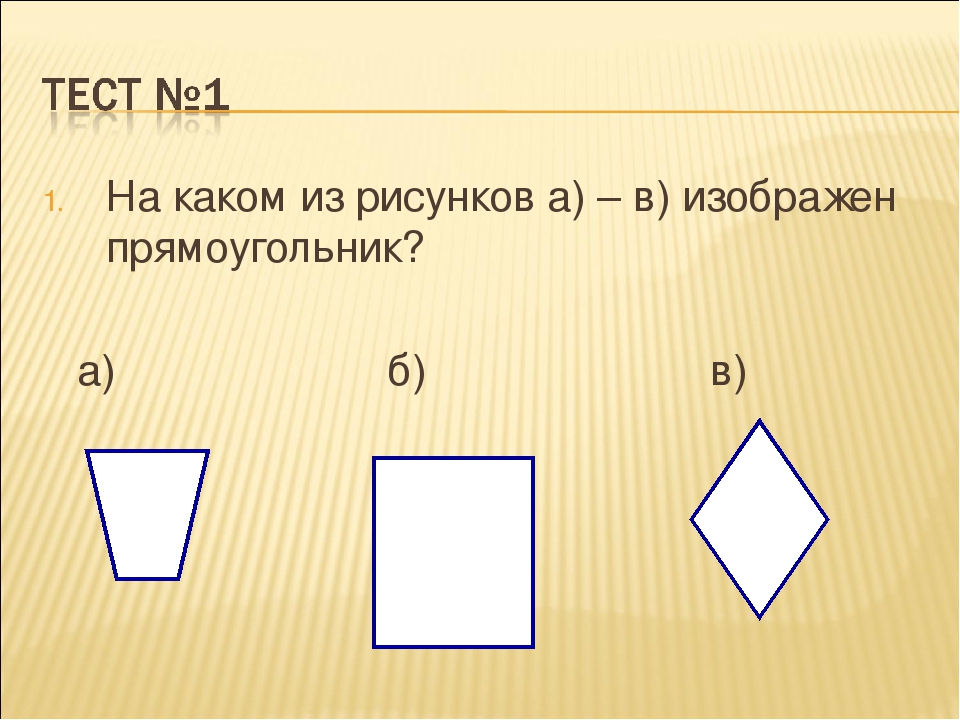
Статический критерий подобия говорит, что два треугольника подобны, если существует соответствие между вершинами, такое что соответствующие углы равны по мере и отношения длин соответствующих сторон равны.Более динамичный, но математически эквивалентный подход к сходству начинается с концепции преобразований растяжения и коэффициентов масштабирования. Например, расширение с масштабным коэффициентом 3 / 2 и центральной точкой P сопоставляет каждую точку X с точкой изображения X’, , так что PX’ = 3 / 2 пикс. Тогда две геометрические фигуры подобны с масштабным коэффициентом k , если существует некоторая комбинация преобразований растяжения и жесткого движения, которая отображает одну фигуру точно поверх другой.
Как со статической, так и с динамической точек зрения в конце концов нужно получить ответы на вопрос: «Какая минимальная информация о сторонах и углах двух фигур (особенно треугольников) гарантирует, что они конгруэнтны или подобны?» Для конгруэнтности треугольников есть несколько знакомых критериев: наиболее распространенными являются сторона-угол-сторона, сторона-сторона-сторона и угол-сторона-угол. Для подобия треугольников есть сравнимые результаты. Например, два треугольника подобны, если отношения длин соответствующих сторон одинаковы или отношения двух пар сторон равны и углы между ними равны по размеру.Для подобия есть еще один критерий, подчеркивающий значение измерения углов: два треугольника подобны, если существует соответствие между вершинами, так что соответствующие углы равны по мере. Фактически, этот критерий может быть установлен с конгруэнтностью только двух пар соответствующих углов (поскольку постоянная сумма углов 180 ° в каждом треугольнике заставляет третью пару углов быть конгруэнтной).
Для подобия треугольников есть сравнимые результаты. Например, два треугольника подобны, если отношения длин соответствующих сторон одинаковы или отношения двух пар сторон равны и углы между ними равны по размеру.Для подобия есть еще один критерий, подчеркивающий значение измерения углов: два треугольника подобны, если существует соответствие между вершинами, так что соответствующие углы равны по мере. Фактически, этот критерий может быть установлен с конгруэнтностью только двух пар соответствующих углов (поскольку постоянная сумма углов 180 ° в каждом треугольнике заставляет третью пару углов быть конгруэнтной).
Развитие конгруэнтности и подобия в CMP3 делает упор на более динамичный подход посредством преобразований и начинается с концептуально более богатой концепции подобия.Модуль 7 класса «Растягивание и сжатие» вовлекает учащихся в различные практические действия по расширению, которые растягивают и уменьшают размер простых фигур (и связаны с функциями увеличения и уменьшения копировальных аппаратов).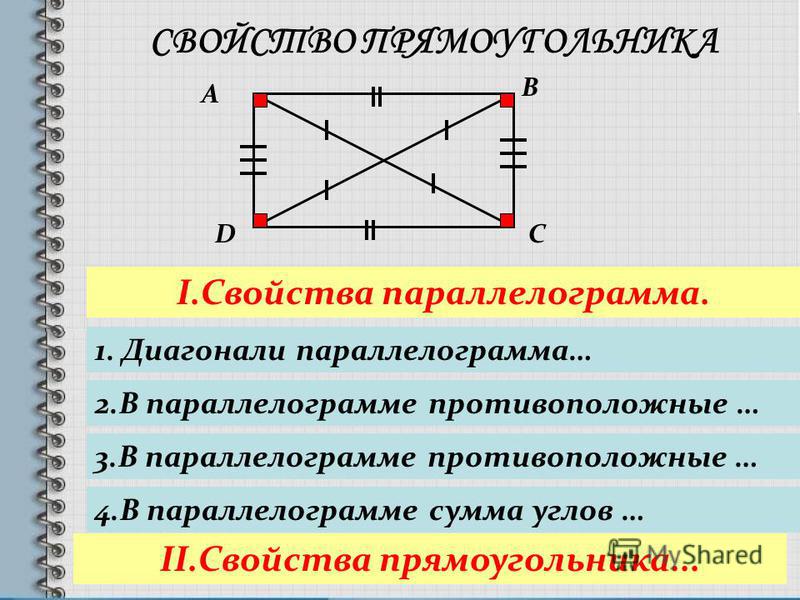 Этот опыт показывает, как изменяется размер, но не форма расширенных фигур, и как размеры углов сохраняются при преобразованиях подобия.
Этот опыт показывает, как изменяется размер, но не форма расширенных фигур, и как размеры углов сохраняются при преобразованиях подобия.
История конгруэнтности и подобия, начатая несколько неформально и визуально в Формы и конструкции и Растягивание и сжатие , завершается в модуле Бабочки, вертушки и обои 8 класса , в котором динамика (включая трансформации) и статические подходы объединяются и применяются к множеству стандартных задач.
Разработка пропорциональности соединений подобных фигур
В задании «Растягивание и сжатие» учащихся просят сравнить отношения длин сторон на аналогичных фигурах, чтобы получить визуальную основу для рассуждений о пропорциях. Затем сравнение периметров и площадей подобных фигур вводит принципиально важный вопрос: «Как масштабные коэффициенты расширения связаны с изменениями периметра и площади фигур?» Общий принцип, согласно которому линейные размеры изменяются на коэффициент расширения k , а площади изменяются на k 2 , пересматривается и расширяется в последующих задачах измерения. В задании «Заполнение и упаковка » в 7-м классе учащиеся обнаруживают, что если объемную фигуру увеличить в масштабе k , объем изменится в k 3 коэффициенте.
В задании «Заполнение и упаковка » в 7-м классе учащиеся обнаруживают, что если объемную фигуру увеличить в масштабе k , объем изменится в k 3 коэффициенте.
Расширение понимания координатных методов и теоремы Пифагора
Повсеместное использование компьютерных инструментов для графических задач, таких как архитектурное черчение, роботизированное производство и производство фильмов, сделало методы координат в геометрии фундаментальными навыками для многих современных рабочих.Эта тенденция отражена в задачах CCSSM по математике для средних классов и в модулях геометрии CMP3, которые соответствуют этим ожиданиям.
Первый модуль 6-го класса, Prime Time , просит учеников построить пары факторов, чтобы найти визуальную закономерность в этих числах. Связанное задание в Покрытие и окружение предлагает учащимся показать шаблоны длины и ширины, которые дают постоянную площадь, но другой периметр, и постоянный периметр, но другую площадь.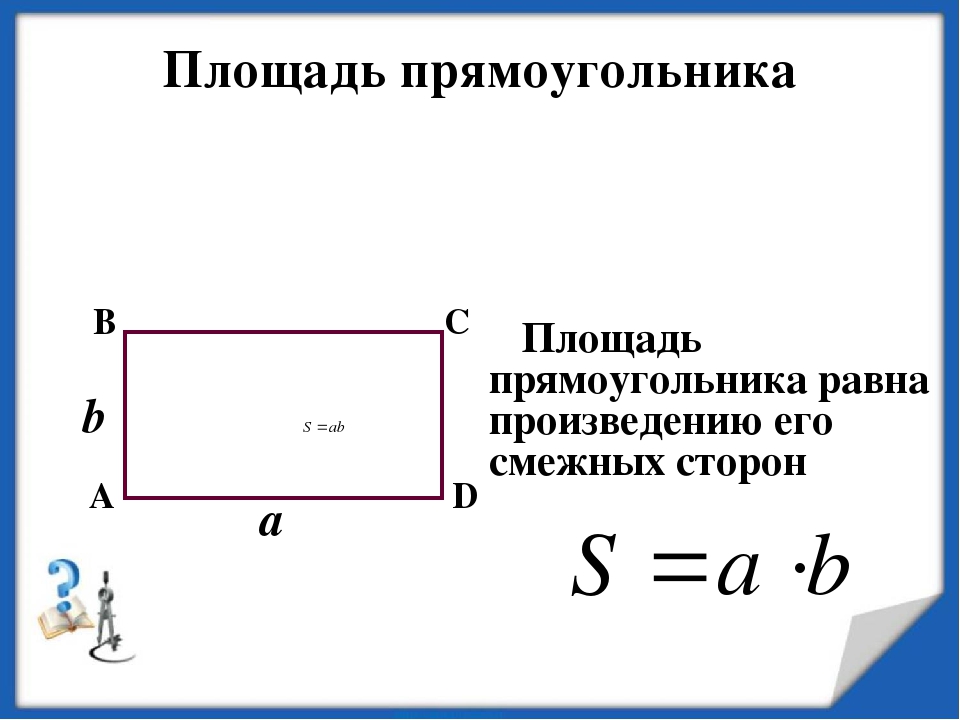 Эти связи с алгебраическими отношениями переменных снова исследуются в разделе «Переменные и шаблоны» , где основное внимание уделяется выражениям и функциям в разделе «Алгебра и функции». Переменные и закономерности и Подчеркните отрицательное в начале 7 класса расширьте графическое представление на все четыре квадранта.
Эти связи с алгебраическими отношениями переменных снова исследуются в разделе «Переменные и шаблоны» , где основное внимание уделяется выражениям и функциям в разделе «Алгебра и функции». Переменные и закономерности и Подчеркните отрицательное в начале 7 класса расширьте графическое представление на все четыре квадранта.
Учащиеся могут находить расстояния в координатных сетках, используя неформальные методы из Покрытие и окружение и формальные методы из В поисках Пифагора . Последний модуль развивает теорему Пифагора и стандартную формулу расстояния. Кроме того, в В поисках Пифагора учащиеся разрабатывают уравнение окружности, идею геометрии, выраженную алгебраически.Координаты и формула расстояния снова объединяются в Бабочки, Вертушки и Обои , чтобы разработать правила координат для конгруэнтности и преобразования подобия.
Соединения
В духе Connected Mathematics эти геометрические идеи и методы применяются и улучшаются при работе над задачами во многих других модулях. Наиболее заметная и мощная связь геометрии и измерений с другими направлениями учебной программы CMP3 – это взаимодействие концепций рационального числа и пропорциональности в разделе «Числа и операции» со сходством.Однако, поскольку подход CMP3 к алгебре делает упор на функциональные отношения между количественными переменными, геометрические методы построения координатных графиков также занимают видное место в каждом модуле алгебры. Эта визуализация взаимосвязей между переменными также занимает центральное место в нашей разработке темы математического моделирования в анализе данных, а модели областей обеспечивают мощную поддержку работы с дробями, десятичными знаками и вероятностью. Наконец, концепции геометрии и измерения в CMP3 предоставляют бесценные визуальные ресурсы для решения проблем и абстрактных рассуждений обо всех аспектах математики.
Наиболее заметная и мощная связь геометрии и измерений с другими направлениями учебной программы CMP3 – это взаимодействие концепций рационального числа и пропорциональности в разделе «Числа и операции» со сходством.Однако, поскольку подход CMP3 к алгебре делает упор на функциональные отношения между количественными переменными, геометрические методы построения координатных графиков также занимают видное место в каждом модуле алгебры. Эта визуализация взаимосвязей между переменными также занимает центральное место в нашей разработке темы математического моделирования в анализе данных, а модели областей обеспечивают мощную поддержку работы с дробями, десятичными знаками и вероятностью. Наконец, концепции геометрии и измерения в CMP3 предоставляют бесценные визуальные ресурсы для решения проблем и абстрактных рассуждений обо всех аспектах математики.
Применение теоремы Пифагора для определения неизвестных длин сторон в прямоугольных треугольниках в реальных и математических задачах в двух и трех измерениях.
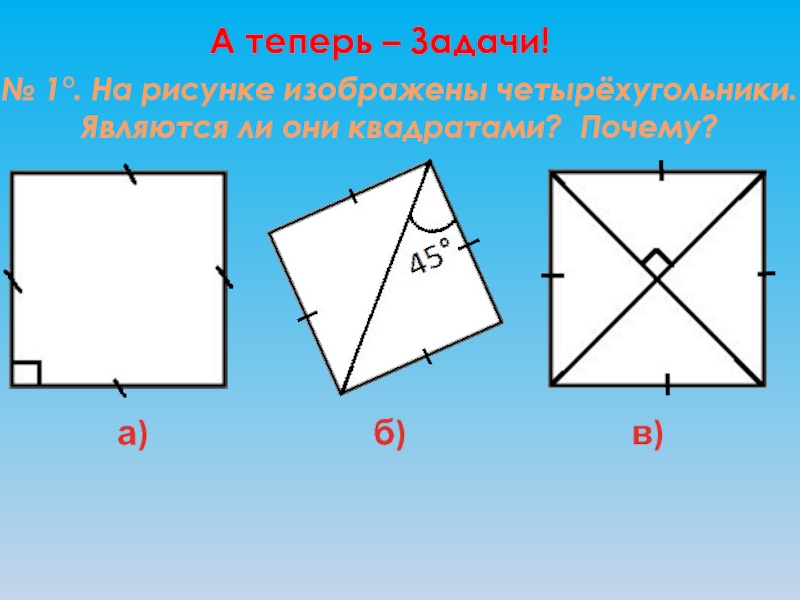 Очки:
Очки:
В этом пособии учащиеся определят объем трех стаканов различной формы. Им потребуются предварительные знания формул объема для цилиндров, конусов и сфер, а также опыт решения уравнений, упрощения квадратных корней и применения теоремы Пифагора.
Тип: Задача решения проблем
Прямоугольник в координатной плоскости: Это задание дает возможность применить теорему Пифагора к кратным треугольникам, чтобы определить длину гипотенузы; обратная теорема Пифагора также требуется, чтобы заключить, что определенные углы являются прямыми углами.
Тип: Задача решения проблем
Гонки птиц и собак:Цель этого задания состоит в том, чтобы учащиеся использовали теорему Пифагора в качестве инструмента решения задач для вычисления расстояния между двумя точками на сетке.В этом случае сетка также является картой, а названия улиц можно рассматривать как определяющие систему координат (хотя для решения задачи система координат не нужна).
Тип: Задача решения проблем
Это прямоугольник?: Цель этого задания — предоставить учащимся возможность применить широкий спектр идей из геометрии и алгебры, чтобы показать, что данный четырехугольник является прямоугольником.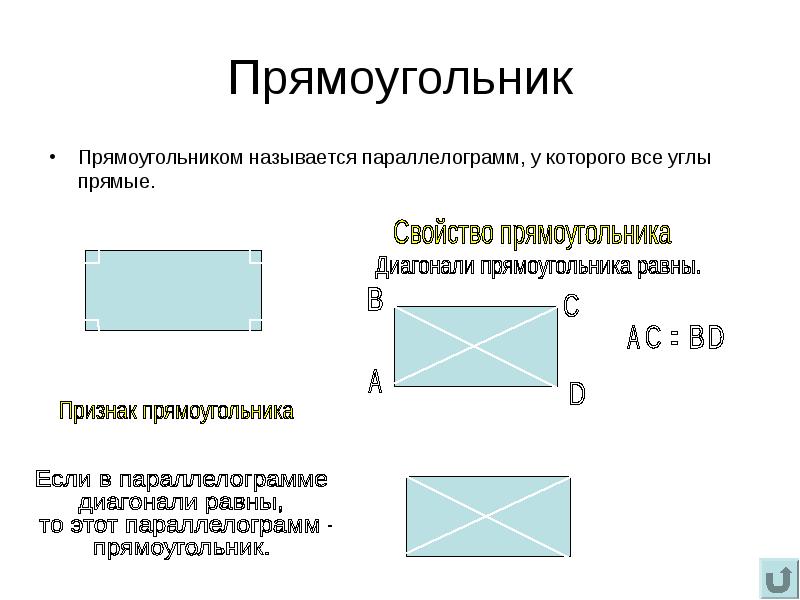 Здесь потребуется творческий подход, поскольку единственной имеющейся информацией являются декартовы координаты вершин четырехугольника. Использование этой информации для демонстрации того, что четыре угла являются прямыми, потребует некоторых вспомогательных построений. Учащимся потребуется достаточно времени, а для некоторых методов, описанных ниже, – руководство. Награда за тщательное выполнение этого задания должна оправдать усилия, потому что это дает учащимся возможность увидеть несколько геометрических и алгебраических конструкций, объединенных для достижения общей цели.Преподаватель может пожелать, чтобы учащиеся сначала провели мозговой штурм, чтобы найти способы показать, что четырехугольник является прямоугольником (прежде чем представить им явные координаты прямоугольника для этой задачи): в идеале, они могут затем разделиться на группы и сразу же приступить к работе, как только им будут представлены координаты четырехугольника для этой задачи.
Здесь потребуется творческий подход, поскольку единственной имеющейся информацией являются декартовы координаты вершин четырехугольника. Использование этой информации для демонстрации того, что четыре угла являются прямыми, потребует некоторых вспомогательных построений. Учащимся потребуется достаточно времени, а для некоторых методов, описанных ниже, – руководство. Награда за тщательное выполнение этого задания должна оправдать усилия, потому что это дает учащимся возможность увидеть несколько геометрических и алгебраических конструкций, объединенных для достижения общей цели.Преподаватель может пожелать, чтобы учащиеся сначала провели мозговой штурм, чтобы найти способы показать, что четырехугольник является прямоугольником (прежде чем представить им явные координаты прямоугольника для этой задачи): в идеале, они могут затем разделиться на группы и сразу же приступить к работе, как только им будут представлены координаты четырехугольника для этой задачи.
Тип: Задача решения проблем
Площадь трапеции: Цель этого задания состоит в том, чтобы учащиеся использовали теорему Пифагора, чтобы найти неизвестные длины сторон трапеции, чтобы определить площадь. Эта задача потребует творчества и настойчивости, так как учащиеся должны разложить заданную трапецию на другие многоугольники, чтобы найти ее площадь.
Эта задача потребует творчества и настойчивости, так как учащиеся должны разложить заданную трапецию на другие многоугольники, чтобы найти ее площадь.
Тип: Задача решения проблем
Применение теоремы Пифагора в математическом контексте:Три прямоугольных треугольника окружают заштрихованный треугольник; вместе они образуют прямоугольник размером 12 на 14 единиц.Используемый рисунок показывает некоторые размеры, но не в масштабе. Поймите и примените теорему Пифагора.
Тип: Задача решения проблем
Площади геометрических фигур с одинаковым периметром: Эта задача является частью очень богатой традиции задач, направленных на максимизацию площади, ограниченной фигурой с фиксированным периметром.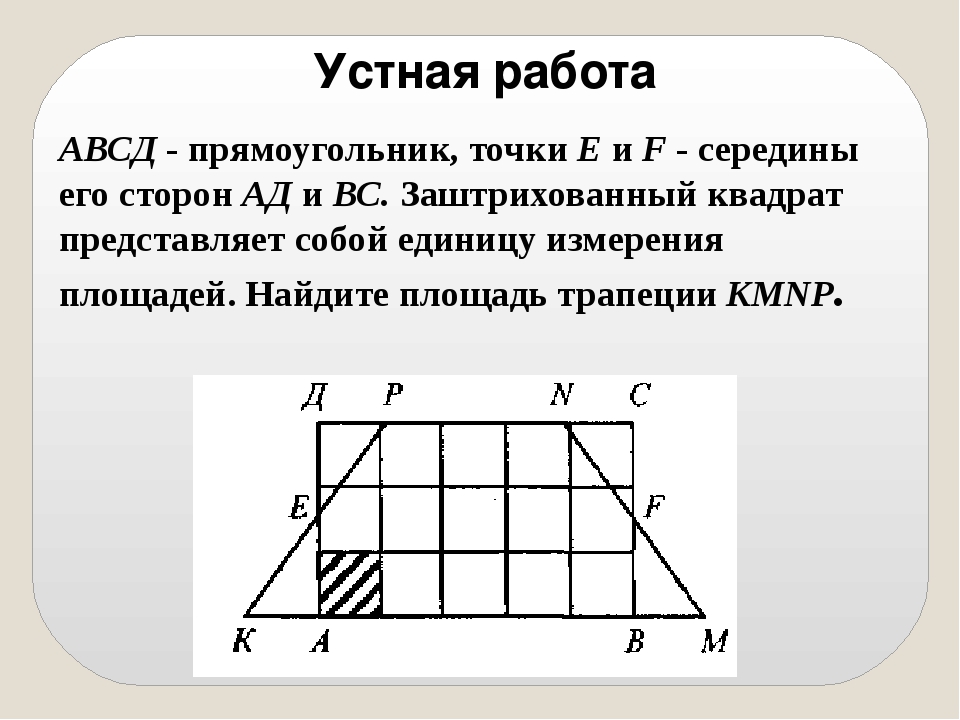 Здесь рассматриваются только три формы, потому что задача более сложная для более неправильных форм. Например, из всех треугольников тот, у которого фиксированный периметр P и наибольшая площадь, — это равносторонний треугольник, все длины сторон которого равны P3, но это трудно показать, потому что нелегко найти площадь треугольника с точки зрения длин трех сторон. (хотя формула Герона достигает этого). Не так просто сравнить площади двух треугольников с одинаковым периметром, не зная их отдельных площадей.Для четырехугольников возникает аналогичная задача: показать, что из всех прямоугольников с периметром P наибольшей площадью является квадрат, длина стороны которого равна P4, — хорошая задача, над которой должны подумать учащиеся. Но сравнить квадрат с четырехугольником неправильной формы с равным периметром будет сложно.
Здесь рассматриваются только три формы, потому что задача более сложная для более неправильных форм. Например, из всех треугольников тот, у которого фиксированный периметр P и наибольшая площадь, — это равносторонний треугольник, все длины сторон которого равны P3, но это трудно показать, потому что нелегко найти площадь треугольника с точки зрения длин трех сторон. (хотя формула Герона достигает этого). Не так просто сравнить площади двух треугольников с одинаковым периметром, не зная их отдельных площадей.Для четырехугольников возникает аналогичная задача: показать, что из всех прямоугольников с периметром P наибольшей площадью является квадрат, длина стороны которого равна P4, — хорошая задача, над которой должны подумать учащиеся. Но сравнить квадрат с четырехугольником неправильной формы с равным периметром будет сложно.
Тип: Задача решения проблем
Бег на футбольном поле: Учащиеся должны обдумать, как они могут использовать теорему Пифагора, чтобы найти расстояния, пройденные Беном Уотсоном и Чемпом Бейли.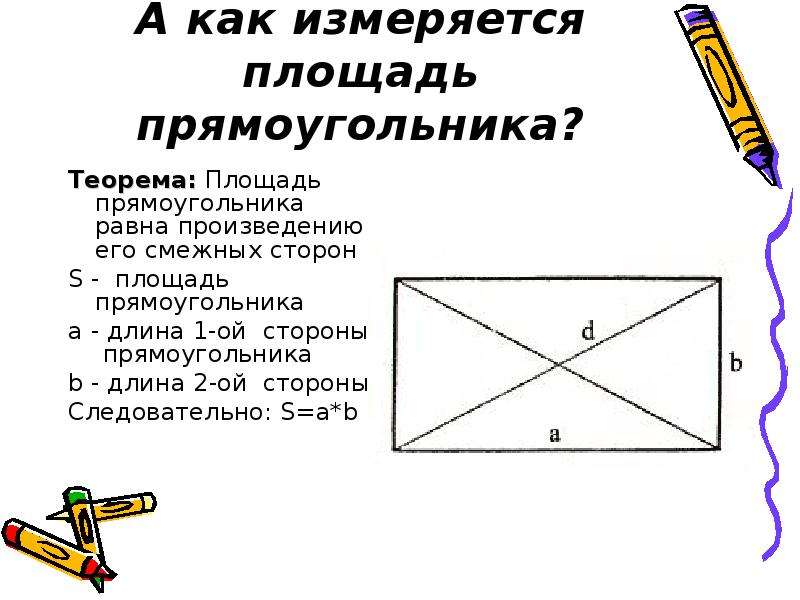 Здесь следует сосредоточиться не на том, кто пробежал большее расстояние, а на том, как построить прямоугольные треугольники, чтобы применить теорему Пифагора к этой проблеме. Учащиеся должны использовать свои навыки измерения и делать разумные оценки, чтобы построить треугольники и правильно применить теорему.
Здесь следует сосредоточиться не на том, кто пробежал большее расстояние, а на том, как построить прямоугольные треугольники, чтобы применить теорему Пифагора к этой проблеме. Учащиеся должны использовать свои навыки измерения и делать разумные оценки, чтобы построить треугольники и правильно применить теорему.
Тип: Задача решения проблем
Расширение в координатной плоскости — видео и расшифровка урока
Пример расширения 1
Нарисуйте прямоугольник ABCD с координатами A(-2, 1), B(1, 1), C(1, -1), D(-2, -1).Затем расширьте изображение с коэффициентом масштабирования 2, используя исходную точку в качестве центра расширения.
Сначала мы наносим точки для прямоугольника ABCD.
Далее берем все координаты и умножаем их на 2:
A'(-4, 2), B'(2, 2), C'(2, -2), D’ (-4, -2)
Теперь мы сопоставляем новое изображение с исходным изображением.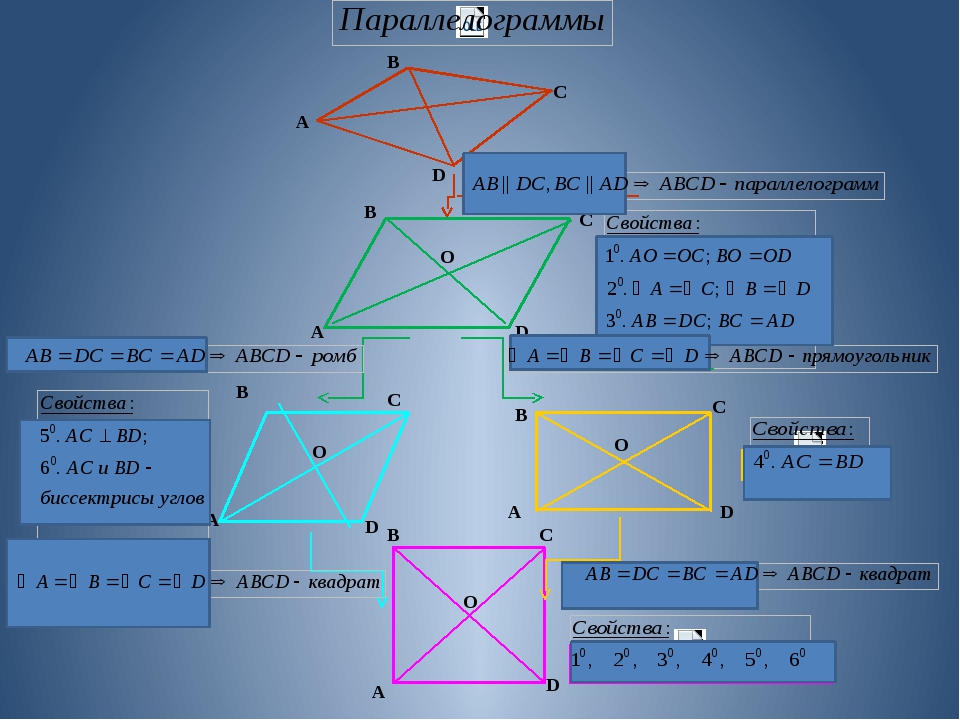
Является ли новая цифра увеличением или уменьшением исходного изображения?
Поскольку новая фигура больше, а коэффициент масштабирования больше 1, новое изображение является увеличенным.
Пример расширения 2
Нарисуйте треугольник ABC с координатами A(2, 6), B(2, 2), C(6, 2). Затем расширьте изображение с коэффициентом масштабирования 1/2, используя исходную точку в качестве центра расширения.
Сначала мы наносим исходный треугольник на координатную плоскость:
Далее мы умножаем каждую координату на масштабный коэффициент 1/2. Умножение на 1/2 равносильно делению каждой координаты на 2:
A'(1, 3), B'(1, 1), C'(3, 1)
Затем мы рисуем новое изображение с исходное изображение:
Является ли новое изображение увеличением или уменьшением исходной фигуры?
Поскольку коэффициент масштабирования был на долю меньше 1, а новый треугольник меньше исходного, это сокращение.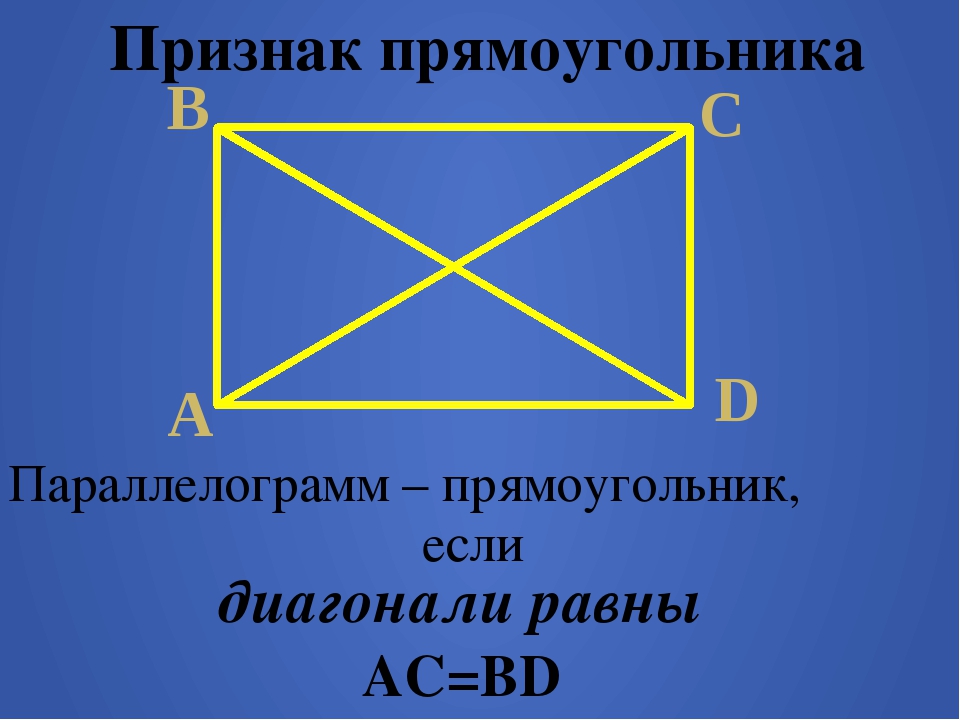
Пример расширения 3
Учитывая исходный прямоугольник ABCD и увеличенное изображение A’B’C’D’, определите масштабный коэффициент и произошло ли увеличение или уменьшение.
Сначала перечислим координаты исходной фигуры и координаты новой фигуры:
A(0, 2), B(3, 2), C(3, 0), D(0, 0 )
A'(0, 4), B'(6, 4), C'(6, 0), D'(0,0)
Увеличенное изображение больше, чем исходное изображение, поэтому увеличение произошло.
Итак, на что был умножен первый набор координат, чтобы получить увеличенное изображение? Поскольку все координаты были умножены на 2, масштабный коэффициент равен 2.
Итоги урока
Хорошо, давайте на минутку повторим то, что мы узнали. Расширение — это увеличение или уменьшение изображения с помощью масштабного коэффициента. Мы также узнали, что центр расширения — это точка, относительно которой мы расширяем объект. Масштабный коэффициент — это число, на которое умножается каждая координата для получения нового изображения. Увеличение — это когда коэффициент масштабирования больше 1, а новое изображение больше исходного. Уменьшение — это когда коэффициент масштабирования меньше 1, а новое изображение меньше исходного.
Увеличение — это когда коэффициент масштабирования больше 1, а новое изображение больше исходного. Уменьшение — это когда коэффициент масштабирования меньше 1, а новое изображение меньше исходного.
Чтобы построить график изображения и найти увеличенное изображение, выполните следующие шаги:
- Нарисуйте исходный рисунок.
- Умножьте исходные координаты на масштабный коэффициент.
- Нарисуйте увеличенное изображение, нанеся новые точки.
Прямоугольная система координат
Точка, которая делит пополам отрезок, образованный двумя точками (x1, y1) и (x2, y2), называется средней точкой. Учитывая две точки, (x1, y1) и (x2, y2), середина — это упорядоченная пара, заданная формулой (x1+x22, y1+y22). и определяется по следующей формуле:
Средняя точка представляет собой упорядоченную пару, образованную путем нахождения среднего значения x и среднего значения y заданных точек.
Пример 8: Вычислите среднюю точку между (−1, −2) и (7, 4).
Решение: Сначала вычислите среднее значение x и y заданных точек.
Затем сформируйте среднюю точку в виде упорядоченной пары, используя усредненные координаты.
Чтобы убедиться, что это действительно средняя точка, вычислите расстояние между двумя заданными точками и убедитесь, что результат равен сумме двух равных расстояний от конечных точек до этой средней точки. Эта проверка предоставляется читателю в качестве упражнения.
Попробуйте! Найдите среднюю точку между (−6, 5) и (6, −11).
Тематические упражнения
Часть A: заказанные пары
Дайте координаты баллов A , , , C , D и E .
1.
2.
3.
4.
5.
6.
Нарисуйте график заданного набора упорядоченных пар.
7. {(−4, 5), (−1, 1), (−3, −2), (5, −1)}
8.{(−15, −10), (−5, 10), (15, 10), (5, −10)}
9. {(−2, 5), (10, 0), (2, −5), (6, −10)}
10. {(−8, 3), (−4, 6), (0, −6), (6, 9)}
11. {(−10, 5), (20, −10), (30, 15), (50, 0)}
12. {(−53, −12),(−13, 12),(23, −1),(53, 1)}
13. {(−35, −43),(25, 43),(1, −23),(0, 1)}
14. {(−3,5, 0), (−1,5, 2), (0, 1,5), (2,5, −1,5)}
15. {(−0,8, 0,2), (−0,2, −0,4), (0, −1), (0,6, −0,4)}
16. {(−1,2, −1,2), (−0,3, −0,3), (0, 0), (0,6, 0,6), (1,2, 1,2)}
Укажите квадрант, в котором находится данная точка.
17. (−3, 2)
(−3, 2)
18. (5, 7)
19. (−12, −15)
20. (7, -8)
21. (−3,8, 4,6)
22. (17.3, 1.9)
23. (−18, −58)
24.(34, −14)
25. х>0 и у<0
26. х<0 и у<0
27. х<0 и у>0
28. х>0 и у>0
Средняя цена галлона обычного неэтилированного бензина в городах США представлена на следующем линейном графике. Используя график, ответьте на следующие вопросы.
Источник: Бюро трудовой статистики.
29. Какова была средняя цена галлона неэтилированного бензина в 2004 г.?
30. Какова была средняя цена галлона неэтилированного бензина в 1976 г.?
31. В какие годы средняя цена галлона неэтилированного бензина составляла 1,20 доллара США?
32. На сколько выросла цена галлона бензина с 1980 по 2008 год?
На сколько выросла цена галлона бензина с 1980 по 2008 год?
33. На сколько процентов увеличилась цена галлона неэтилированного бензина с 1976 по 1980 год?
34.На сколько процентов увеличилась цена галлона неэтилированного бензина с 2000 по 2008 год?
Средняя цена на белую муку общего назначения в городах США с 1980 по 2008 год представлена на следующем линейном графике. Используйте график, чтобы ответить на следующие вопросы.
Источник: Бюро трудовой статистики.
35. Какова была средняя цена фунта муки в/с в 2000 г.?
36.Какова была средняя цена фунта муки в/с в 2008 г.?
37. В каком году средняя цена муки составляла 0,25 доллара за фунт?
38. В какие годы средняя цена муки составляла 0,20 доллара за фунт?
39. На сколько процентов увеличилось количество муки с 2000 по 2008 год?
40. На сколько процентов увеличилось количество муки с 1992 по 2000 год?
На сколько процентов увеличилось количество муки с 1992 по 2000 год?
Используя следующие данные, постройте линейный график.
41. Доля выпускников средней школы, поступивших в колледж.
| Год | Процент |
|---|---|
| 1969 | 36% |
| 1979 | 40% |
| 1989 | 47% |
| 1999 | 42% |
Источник: Сборник статистики образования.
42. Среднесуточная температура в градусах Фаренгейта в мае.
| Экзамен | Температура |
|---|---|
| 8:00 | 60 |
| 12:00 | 72 |
| 16:00 | 75 |
| 20:00 | 67 |
| 00:00 | 60 |
| 4:00 | 55 |
Вычислите площадь фигуры, образованной путем соединения следующего набора вершин.
43. {(0, 0), (0, 3), (5, 0), (5, 3)}
44. {(−1, −1), (−1, 1), (1, −1), (1, 1)}
45.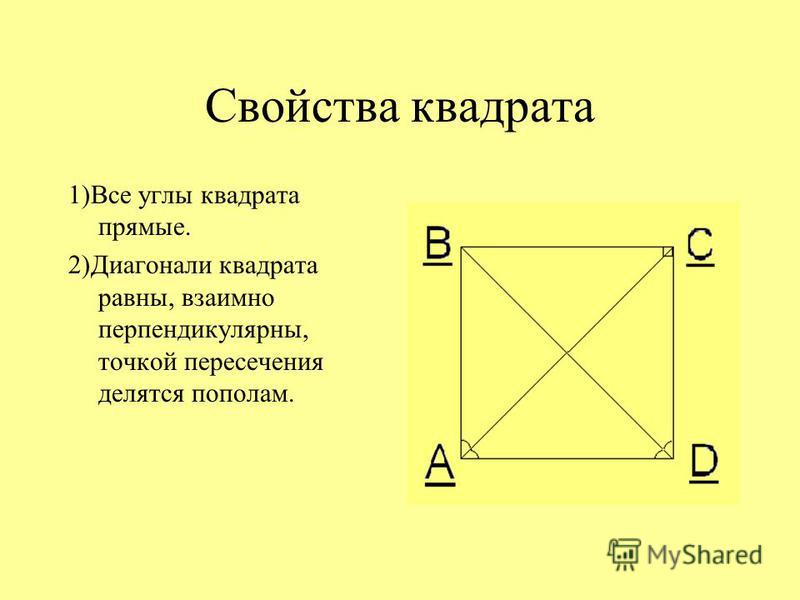 {(−2, −1), (−2, 3), (5, 3), (5, −1)}
{(−2, −1), (−2, 3), (5, 3), (5, −1)}
46. {(−5, −4), (−5, 5), (3, 5), (3, −4)}
47. {(0, 0), (4, 0), (2, 2)}
48. {(-2, -2), (2, -2), (0, 2)}
49. {(0, 0), (0, 6), (3, 4)}
50. {(−2, 0), (5, 0), (3, −3)}
Часть B: Формула расстояния
Вычислить расстояние между заданными двумя точками.
51. (−5, 3) и (−1, 6)
52. (6, -2) и (-2, 4)
53. (0, 0) и (5, 12)
54. (−6, −8) и (0, 0)
55. (−7, 8) и (5, –1)
56. (-1, -2) и (9, 22)
57. (−1, 2) и (–7/2, −4)
58. (−12, 13) и (52, −113)
59. (−13, 23) и (1, −13)
60. (12, −34) и (32, 14)
61.(1, 2) и (4, 3)
62. (2, –4) и (–3, –2)
63. (−1, 5) и (1, −3)
(−1, 5) и (1, −3)
64. (1, -7) и (5, -1)
65. (-7, -3) и (-1, 6)
66. (0, 1) и (1, 0)
67. (−0,2, −0,2) и (1,8, 1,8)
68. (1.2, –3.3) и (2.2, –1.7)
Для каждой задачи покажите, что три точки образуют прямоугольный треугольник.
69.(−3, −2), (0, −2) и (0, 4)
70. (7, 12), (7, –13) и (–5, –4)
71. (−1,4, 0,2), (1, 2) и (1, −3)
72. (2, -1), (-1, 2) и (6, 3)
73. (-5, 2), (-1, -2) и (-2, 5)
74. (1, -2), (2, 3) и (-3, 4)
Равнобедренные треугольники имеют две катеты одинаковой длины. Для каждой задачи покажите, что следующие точки образуют равнобедренный треугольник.
75.(1, 6), (−1, 1) и (3, 1)
76. (−6, −2), (−3, −5) и (−9, −5)
77. (−3, 0), (0, 3) и (3, 0)
78.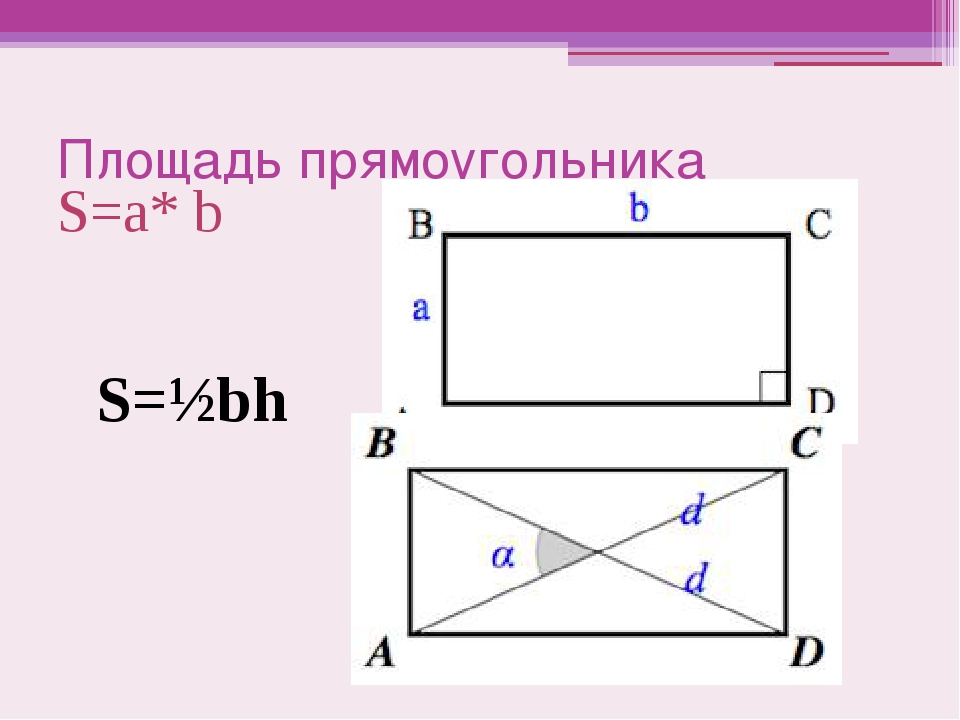 (0, −1), (0, 1) и (1, 0)
(0, −1), (0, 1) и (1, 0)
Вычислите площадь и периметр треугольников, образованных следующим набором вершин.
79. {(-4, -5), (-4, 3), (2, 3)}
80. {(−1, 1), (3, 1), (3, −2)}
81. {(−3, 1), (−3, 5), (1, 5)}
82.{(−3, −1), (−3, 7), (1, −1)}
Часть C: Формула средней точки
Найдите среднюю точку между данными двумя точками.
83. (-1, 6) и (-7, -2)
84. (8, 0) и (4, −3)
85. (−10, 0) и (10, 0)
86. (−3, −6) и (−3, 6)
87. (−10, 5) и (14, −5)
88. (0, 1) и (2, 2)
89. (5, -3) и (4, -5)
90.(0, 0) и (1, 1)
91. (-1, -1) и (4, 4)
92. (3, -5) и (3, 5)
93. (−12, −13) и (32, 73)
94. (34, −23) и (18, −12)
(34, −23) и (18, −12)
95. (53, 14) и (−16, −32)
96. (−15, −52) и (710, −14)
97. Дан прямоугольный треугольник, образованный вершинами (0, 0), (6, 0) и (6, 8), покажите, что середины сторон образуют прямоугольный треугольник.
98. Дан равнобедренный треугольник, образованный вершинами (−10, −12), (0, 12) и (10, −12), покажите, что середины сторон также образуют равнобедренный треугольник.
99. Вычислите площадь треугольника, образованного вершинами (−4, −3), (−1, 1) и (2, −3). (Подсказка: вершины образуют равнобедренный треугольник.)
100. Вычислите площадь треугольника, образованного вершинами (−2, 1), (4, 1) и (1, −5).
Часть D: Темы на доске обсуждений
101.Исследуйте и обсуждайте жизнь и вклад Рене Декарта в математику.
102. Исследуйте и обсудите историю прямоугольного треугольника и теоремы Пифагора.

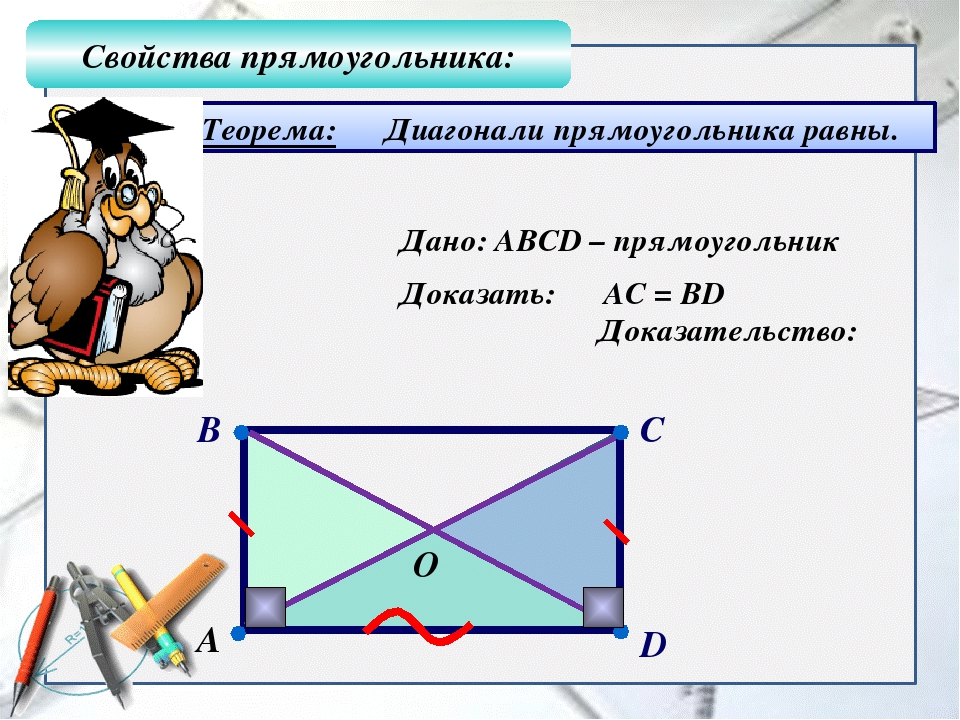 7-9 классы: учеб.для общеобразоват. организаций /Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – М.:Просвещение,2017
7-9 классы: учеб.для общеобразоват. организаций /Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – М.:Просвещение,2017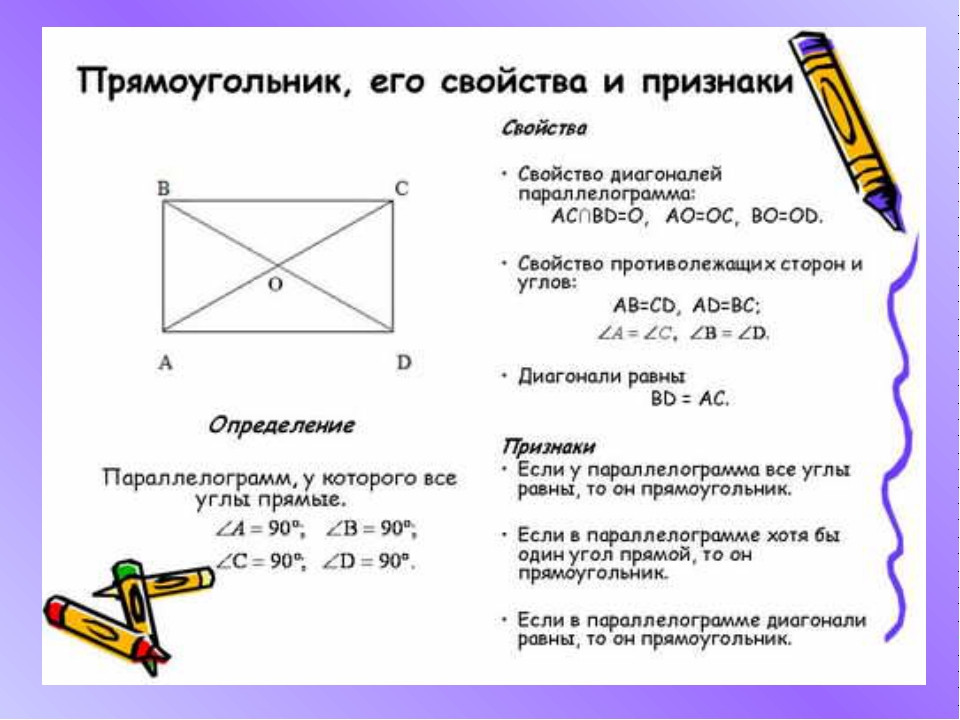
 Задачи №7-№9 выполняются по готовым чертежам. Решение можно записать в тетрадь, но в бланк вносится только ответ. Задание №10 повышенного уровня. Оценивается в 3 балла. Чертеж, решение и ответ необходимо записать в отведенное для этого место на бланке ответов. Тест предназначен для учащихся общеобразовательных классов, может быть использован для профильных классов как периодического, так и промежуточного контроля. Учащиеся должны записать ответ в специальном бланке ответов. При выполнении ученик может пользоваться черновиком. Справочные материалы запрещаются. С критериями можно познакомить учеников в начале урока. Вариант оценивания учитель выбирает самостоятельно.
Задачи №7-№9 выполняются по готовым чертежам. Решение можно записать в тетрадь, но в бланк вносится только ответ. Задание №10 повышенного уровня. Оценивается в 3 балла. Чертеж, решение и ответ необходимо записать в отведенное для этого место на бланке ответов. Тест предназначен для учащихся общеобразовательных классов, может быть использован для профильных классов как периодического, так и промежуточного контроля. Учащиеся должны записать ответ в специальном бланке ответов. При выполнении ученик может пользоваться черновиком. Справочные материалы запрещаются. С критериями можно познакомить учеников в начале урока. Вариант оценивания учитель выбирает самостоятельно. 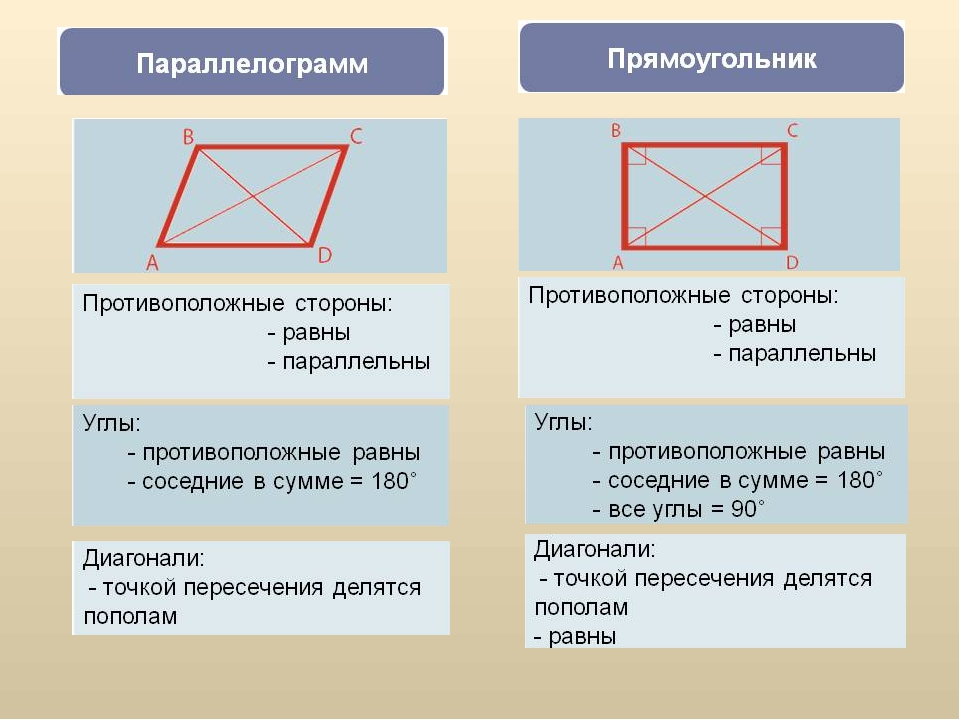

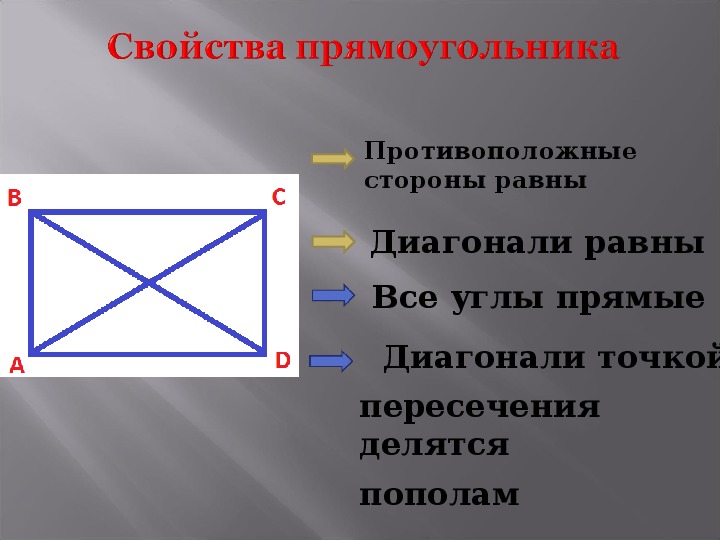
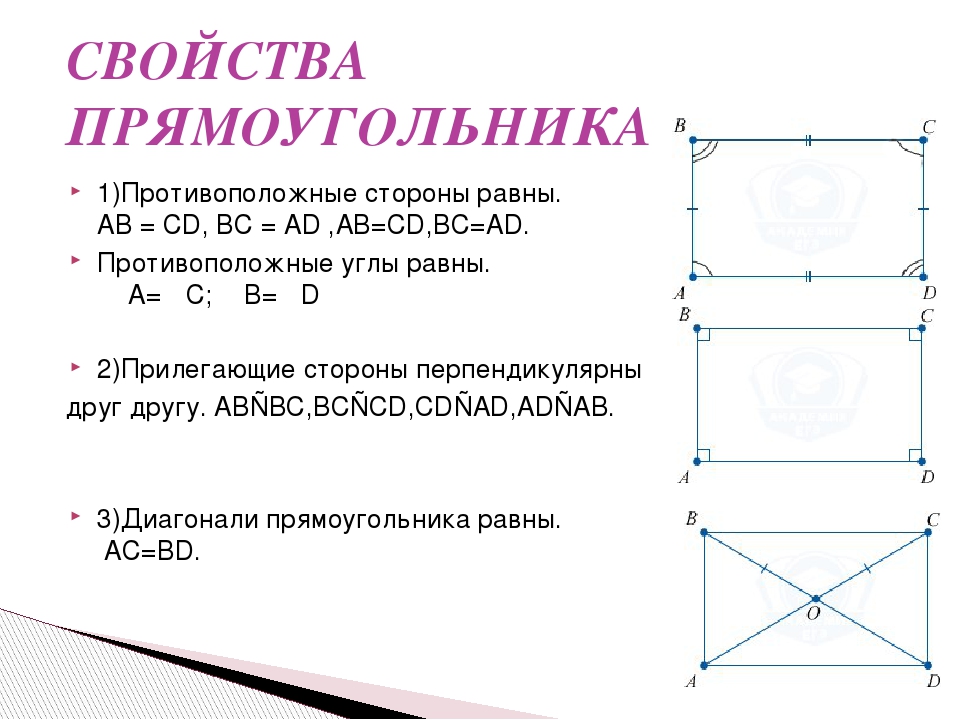 Является ли этот параллелограмм прямоугольником? (Ответить на вопрос словом «да» или «нет»)
Является ли этот параллелограмм прямоугольником? (Ответить на вопрос словом «да» или «нет»)