40
II раунд
Продолжить игру
СВОЯ
СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ
ТРЕУГОЛЬНИК
50
10
20
30
40
ОКРУЖНОСТЬ
50
40
30
20
10
ЗАВЕРШИ ВЫСКАЗЫВАНИЕ
50
40
20
30
10
II раунд
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются …
СМЕЖНЫМИ
Продолжить игру
II раунд
20
a
1
2
b
3
Найти:
II раунд
Продолжить игру
30
Сформулируйте свойство внешнего угла треугольника
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним
Продолжить игру
II раунд
40
в пять раз меньше
Найдите
II раунд
Продолжить игру
50
a
1
2
b
3
Найти:
II раунд
Продолжить игру
10
В треугольнике MKN провели отрезок КР так, что угол KРN прямой. Как называется отрезок КР?
Высота
Продолжить игру
II раунд
20
В треугольнике АВС середину стороны ВС соединили с вершиной А. Как называется этот отрезок?
Медиана
Продолжить игру
II раунд
30
Периметр треугольника АВС равен 63 см. Найдите сторону АВ, если ВС в два раза больше стороны АВ, а АС на 5см меньше стороны АВ.
АВ=17 см
Продолжить игру
II раунд
40
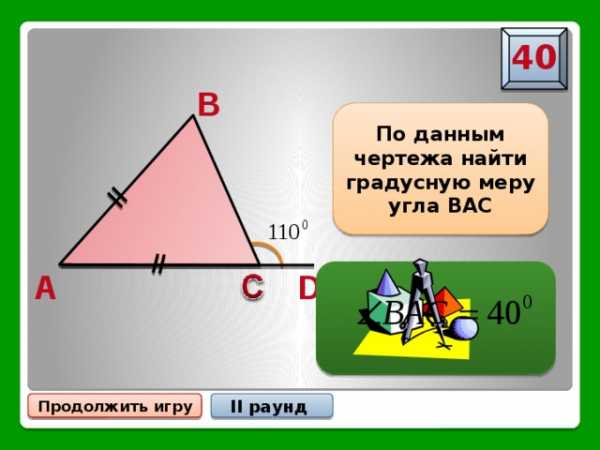
B
По данным чертежа найти градусную меру угла ВАС
A
D
Продолжить игру
II раунд
50
C
Найдите:
A
B
II раунд
Продолжить игру
10
Отрезок, соединяющий центр окружности с какой-либо точкой окружности, называется …
Радиусом окружности
Продолжить игру
II раунд
20
Хорда, проходящая через центр окружности, называется …
Диаметром окружности
Продолжить игру
II раунд
30
A
Найти:
O
II раунд
Продолжить игру
40
О – центр окружности.
Найдите углы треугольника OBD
A
B
O
II раунд
Продолжить игру
50
Почему древние греки называли геометрию пыльной работой?
Потому что все чертежи чертились на пыли
Продолжить игру
II раунд
10
Пересекающиеся прямые имеют …
… одну общую точку
Продолжить игру
II раунд
20
Внешний угол треугольника равен …
… сумме двух углов треугольника, не смежных с ним
Продолжить игру
II раунд
30
Гипотенузой прямоугольного треугольника называется …
… сторона, лежащая против прямого угла
Продолжить игру
II раунд
40
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, …
… лежащий против этого катета,
равен
Продолжить игру
II раунд
50
В прямоугольном треугольнике медиана, проведенная из вершины прямого угла, …
… равна половине гипотенузы
Продолжить игру
II раунд
СВОЯ
РАВНОБЕДРЕННЫЙ И ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИКИ
60
20
80
100
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
20
60
80
100
ВЫБЕРИ ВЕРНОЕ УТВЕРЖДЕНИЕ
20
60
80
ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ
40
80
20
100
ФИНАЛ
Если гипотенуза в прямоугольном треугольнике равна 13 см и один из острых углов равен 30º, то какова тогда длина катета лежащего против этого угла
20
6,5 см
Продолжить игру
ФИНАЛ
40
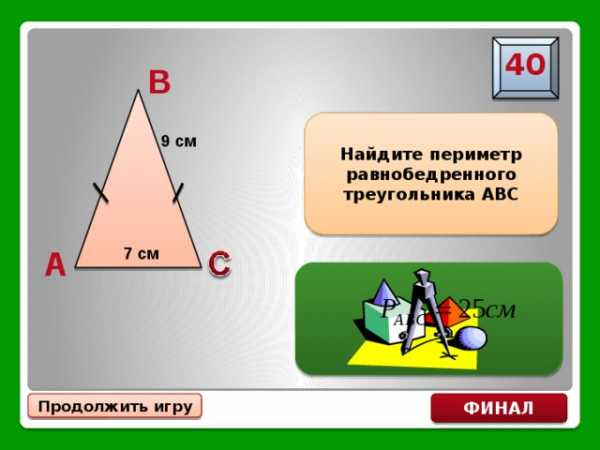
B
Найдите периметр равнобедренного треугольника АВС
9 см
A
7 см
ФИНАЛ
Продолжить игру
А
60
В
Найдите
С
Продолжить игру
ФИНАЛ
80
Найдите
ФИНАЛ
Продолжить игру
BH=4 см
Найти: АН
АН=12 см
Продолжить игру
ФИНАЛ
20
Прямые a и b пересечены секущей так, что внутренние односторонние углы составили в сумме 190 0 . Сколько общих точек имеют прямые a и b?
ОДНУ
Продолжить игру
ФИНАЛ
40
Параллельны ли прямые a и b?
ДА
ФИНАЛ
60
Найти:
Продолжить игру
ФИНАЛ
80
Автор книги, которая называется «Начала». В этой книге он сформулировал основные принципы построения геометрии.
Евклид
Продолжить игру
ФИНАЛ
A
100
Найти:
D
ФИНАЛ
Продолжить игру
В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
А) в любом;
Б) в равнобедренном;
В) в равностороннем.
20
Б) в равнобедренном
Продолжить игру
ФИНАЛ
Если в треугольнике два угла равны, то этот треугольник:
А) равнобедренный;
Б) равносторонний;
В) прямоугольный.
40
А) равнобедренный
Продолжить игру
ФИНАЛ
Как изображается хорда на чертеже окружности?
А) прямой линией;
Б) дугой окружности;
В) отрезком с концами, лежащими на окружности.
60
В) отрезком с концами, лежащими на окружности
Продолжить игру
ФИНАЛ
Какое наибольшее число лучей можно провести из одной точки, чтобы все углы, ограниченные соседними лучами, были тупыми?
80
А) 3 ; Б) 2; В) 4.
А) 3
Продолжить игру
ФИНАЛ
Через точку, не лежащую на данной прямой, проходит:
А) только одна прямая, параллельная данной;
Б) всегда проходит прямая, параллельная данной;
В) только одна прямая, не пересекающиеся с данной.
100
А) только одна прямая, параллельная данной
Продолжить игру
ФИНАЛ
6+7 Продолжить игру ФИНАЛ “
20
Существует ли данный треугольник?
A
C
Нет, т.к.146+7
Продолжить игру
ФИНАЛ
40
По данным на чертеже найдите длину отрезка КМ
9 см
7 см
КМ=9 см
ФИНАЛ
Продолжить игру
60
Стороны одного треугольника 50 см; 60 см; 0,7 м. Стороны другого треугольника 5 дм; 6 дм; 7 дм. Равны ли эти треугольники?
Да, по трем сторонам
Продолжить игру
ФИНАЛ
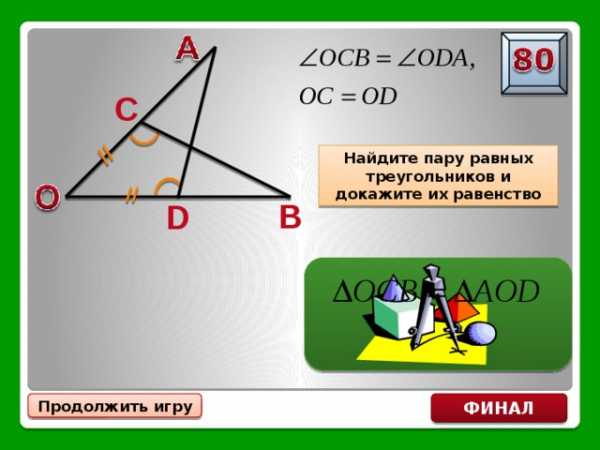
C
Найдите пару равных треугольников и докажите их равенство
B
D
по стороне и двум прилежащим к ней углам
ФИНАЛ
Продолжить игру
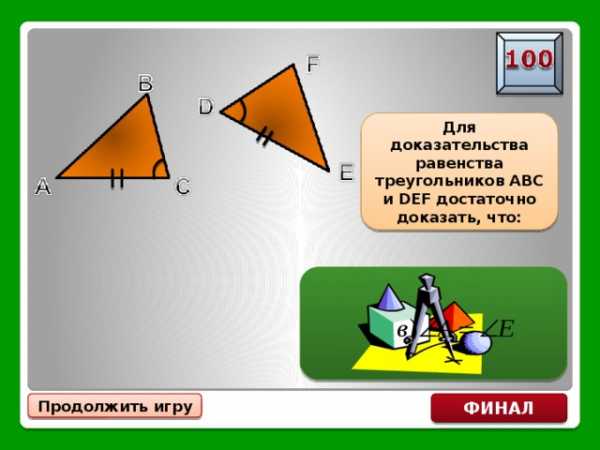
Для доказательства равенства треугольников ABC и DEF достаточно доказать, что:
Продолжить игру
ФИНАЛ
4.
5.
финал
Найдите расстояние от точки М до прямой АВ
АМ=14 см
B
M
MD=7 см
M
финал
A
C
AC// BD, AC=AB
B
multiurok.ru
Викторина по геометрии для учащихся 7-9 классов
«Геометрия вокруг нас»
Цель викторины: Развитие интереса детей к математике.
Задачи:
1. Развивать математические способности детей.
2. Развивать познавательные способности, память, внимание, эрудицию.
3. Расширять кругозор учащихся.
1. Луч Солнца – это
Неограниченная прямая
Прямая, ограниченная с одного конца
Прямая, ограниченная с двух концов
2. Угол учебника «Геометрия»:
Развернутый
Прямой
Острый
Тупой
3. Две пересекающиеся прямые под столом, образующие четыре прямых угла:
Параллельные
Скрещивающиеся
Перпендикулярные
4. Расстояние от дома до школы измеряют:
штангенциркулем
масштабной миллиметровой линейкой
рулеткой
астролябией
5. Стандартной международной единицей измерения длины выбран:
Метр
Километр
Сантиметр
Миллиметр
6. Треугольник с двумя равными сторонами:
1) Равносторонний
2) Разносторонний
3) Равнобедренный
7. Сумма длин сторон тетради это:
Площадь
Периметр
Объем
8. Сколько признаков равенства треугольников:
2
3
4
5
9. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны:
Биссектриса
Высота
Медиана
Радиус
10. В равнобедренном треугольнике биссектриса, проведенная к основанию, является:
Медианой
Высотой
Медианой и высотой
11. Чему равен соседний угол забора к углу 740:
2860
1060
160
1160
12. Объем комнаты – это
Вместимость комнаты
Периметр комнаты
Площадь комнаты
13. Для строительства забора на участке вычисляют:
Периметр
Площадь
Объем
14. Для покрытия пола линолеумом вычисляют:
Периметр
Площадь
Объем
15. Сумма углов треугольника равна:
900
1800
2700
3600
16. Треугольник Пифагора:
Тупоугольный
Остроугольный
Прямоугольный
17. Арена цирка имеет форму:
Квадрата
Окружности
Трапеции
Ромба
18. Что не является параллелограммом:
Квадрат
Ромб
Трапеция
Прямоугольник
19. Какую фигуру называют «скошенный квадрат»:
1) Квадрат
2) Ромб
3) Трапеция
4) Прямоугольник
20. Колесо велосипеда сколько имеет осей симметрии:
1
2
4
Бесконечно много
21. Самое распространенное геометрическое тело в портфеле школьника:
Куб
Параллелепипед
Конус
Шар
22. Какой отрезок «бегает по углам и делит угол пополам»
1) Биссектриса
2) Высота
3) Медиана
4) Радиус
23. «Колесо обозрения» и колесо велосипеда – фигуры:
Равные
Подобные
Неподобные
24. Новогодняя елка имеет форму:
Пирамиды
Параллелепипеда
Конуса
Цилиндра
25. Кремлевская звезда сколько имеет осей симметрии:
1
2
4
Бесконечно много
26. Какие линии на Земном шаре никогда не пересекутся:
параллели
меридианы
№
Ответ
1
2
2
2
3
3
4
3
5
1
6
3
7
2
8
2
9
3
10
3
11
2
12
1
13
1
14
2
15
2
16
3
17
2
18
3
19
2
20
4
21
2
22
1
23
2
24
3
25
1
26
1
infourok.ru
Викторина по геометрии для учащихся 7-9 классов
«Геометрия вокруг нас»
Цель викторины: Развитие интереса детей к математике.
Задачи:
1. Развивать математические способности детей.
2. Развивать познавательные способности, память, внимание, эрудицию.
3. Расширять кругозор учащихся.
1. Луч Солнца – это
2. Угол учебника «Геометрия»:
3. Две пересекающиеся прямые под столом, образующие четыре прямых угла:
4. Расстояние от дома до школы измеряют:
5. Стандартной международной единицей измерения длины выбран:
6. Треугольник с двумя равными сторонами:
1) Равносторонний
2) Разносторонний
3) Равнобедренный
7. Сумма длин сторон тетради это:
8. Сколько признаков равенства треугольников:
9. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны:
10. В равнобедренном треугольнике биссектриса, проведенная к основанию, является:
11. Чему равен соседний угол забора к углу 740:
12. Объем комнаты – это
13. Для строительства забора на участке вычисляют:
14. Для покрытия пола линолеумом вычисляют:
15. Сумма углов треугольника равна:
16. Треугольник Пифагора:
17. Арена цирка имеет форму:
18. Что не является параллелограммом:
19. Какую фигуру называют «скошенный квадрат»:
1) Квадрат
2) Ромб
3) Трапеция
4) Прямоугольник
20. Колесо велосипеда сколько имеет осей симметрии:
21. Самое распространенное геометрическое тело в портфеле школьника:
22. Какой отрезок «бегает по углам и делит угол пополам»
1) Биссектриса
2) Высота
3) Медиана
4) Радиус
23. «Колесо обозрения» и колесо велосипеда – фигуры:
24. Новогодняя елка имеет форму:
25. Кремлевская звезда сколько имеет осей симметрии:
26. Какие линии на Земном шаре никогда не пересекутся:
№ | Ответ |
1 | 2 |
2 | 2 |
3 | 3 |
4 | 3 |
5 | 1 |
6 | 3 |
7 | 2 |
8 | 2 |
9 | 3 |
10 | 3 |
11 | 2 |
12 | 1 |
13 | 1 |
14 | 2 |
15 | 2 |
16 | 3 |
17 | 2 |
18 | 3 |
19 | 2 |
20 | 4 |
21 | 2 |
22 | 1 |
23 | 2 |
24 | 3 |
25 | 1 |
26 | 1 |
nsportal.ru
2 балла
4 балла
6 баллов
8 баллов
2
4
3
1
8
6
7
5
12
9
11
10
13
14
15
16
Какой угол называется прямым?
Угол, равный 90 градусов.
Чему равна сумма углов треугольника?
180 градусов.
Как называются стороны прямоугольного треугольника?
Катет, гипотенуза.
Каким свойством обладают вертикальные углы?
Вертикальные углы равны.
Что называется медианой треугольника?
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Каким свойством обладают углы при основании в равнобедренном треугольнике?
Равны.
Каким свойством обладают прямые, если при пересечении двух прямых секущей накрест лежащие углы равны?
Параллельны.
Какие углы называются смежными?
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.
Что называется биссектрисой треугольника?
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Каким свойством в равнобедренном треугольнике обладает биссектриса, проведённая к основанию?
Является медианой и высотой.
Чему равна сумма острых углов прямоугольного треугольника?
90 градусов.
Что используется для измерения углов?
Транспортир, астролябия, угломер.
Какие утверждения называются аксиомами?
Утверждения, не требующие доказательств.
Каким свойством обладает катет прямоугольного треугольника, лежащий против угла в 30 градусов?
Равен половине гипотенузы.
Что такое окружность?
Геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.
Что такое геометрия?
Наука, занимающаяся изучением геометрических фигур.
multiurok.ru
Геометрия.
Аксиома.
3 аксиомы планиметрии о взаимном расположении точек и прямых.
IV аксиома планиметрии о трех точках прямой.
V аксиома планиметрии о точке прямой.
VI аксиома планиметрии о прямой на плоскости.
Отрезок.
Луч.
Угол.
Развернутый угол.
Равные фигуры.
Середина отрезка.
Биссектриса угла.
Измерение отрезков.
Свойства измерения отрезков.
Измерение углов.
Свойства измерения углов.
Прямой угол.
Острый угол.
Тупой угол.
Смежные углы.
Свойство смежных углов.
Вертикальные углы.
Свойство вертикальных углов.
Перпендикулярные прямые.
Свойство перпендикулярных прямых.
Треугольник.
Периметр треугольника.
Равные треугольники.
Теорема, доказательство теоремы.
Первый признак равенства треугольников.
Второй признак равенства треугольников.
Третий признак равенства треугольников.
Теорема о единственности опущенного перпендикуляра.
Медиана треугольника.
Биссектриса треугольника.
Высота треугольника.
Свойство о пересечении медиан, биссектрис и высот треугольников.
Равнобедренный треугольник.
Равносторонний треугольник.
Свойства равнобедренного треугольника.
Определение.
Определение окружности.
Хорда окружности.
Диаметр окружности.
Дуга окружности.
Круг.
Определение параллельных прямых.
Параллельные отрезки.
Секущая.
Углы при параллельных прямых и секущей.
3 признака параллельности двух прямых.
Аксиома параллельных прямых.
2 следствия из аксиомы параллельных прямых.
Обратная теорема.
Свойства параллельных прямых.
Свойство прямой, перпендикулярной к одной из двух параллельных прямых.
Сумма углов треугольника.
Внешний угол треугольника.
Свойства внешнего угла треугольника.
Виды треугольников.
Элементы прямоугольного треугольника.
Теорема о соотношениях между сторонами и углами треугольника.
2 следствия из теоремы о соотношениях между сторонами и углами треугольника.
Неравенства треугольника.
Свойства прямоугольных треугольников.
Признаки равенства прямоугольных треугольников.
Свойство двух параллельных прямых о равноудаленности точек.
Расстояние между параллельными прямыми.
Замечательные точки треугольника.
А2: Имеются по крайней мере 3 точки, не лежащие на одной прямой.
А3: Через любые 2 точки проходит прямая, и притом только одна.
А4: Из трех точек прямой одна и только одна лежит между двумя другими.
А5: Каждая точка О прямой разделяет её на 2 части (два луча) так, что любые две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.
А6: Каждая прямая а разделяет плоскость на две части (две полуплоскости) так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а.
Отрезок – это часть прямой, ограниченная двумя точками. Точки, ограничивающие отрезок, называются его концами. Отрезок обозначается двумя заглавными латинскими буквами. Например, АВ или ВА.
Луч – это часть прямой, ограниченная одной точкой. Эта точка называется началом луча. Луч обозначается двумя заглавными латинскими буквами или одной строчной латинской буквой. Например, луч АВ или луч m.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало – вершиной угла. Угол обозначается тремя заглавными латинскими буквами или одной заглавной латинской буквой или двумя строчными латинскими буквами. Например, 
или
или 
.
Угол называется развернутым, если обе его стороны лежат на одной прямой.
Две геометрические фигуры называются равными, если их можно совместить наложением.
Середина отрезка – это точка отрезка, делящая его пополам, т.е. на два равных отрезка.
Биссектриса угла – это луч, исходящий из вершины угла и делящий его на два равных угла.
Измерение отрезков. Выбрав единицу измерения, можно измерить любой отрезок, т.е. выразить его длину некоторым положительным числом.
Свойства измерения отрезков. 1) Равные отрезки имеют равные длины. 3) Меньший отрезок имеет меньшую длину. 3) Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
Измерение углов. Градусной мерой угла называется положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.
Свойства измерения углов. 1) Равные углы имеют равные градусные меры.2) Меньший угол имеет меньшую градусную меру. 3) Развернутый угол равен 180 градусам. 4Неразвернутый угол меньше 180 градусов. 5) Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
Прямой угол – угол, градусная мера которого равна 90 градусов.
Острый угол – угол, градусная мера которого меньше 90 градусов.
Тупой угол – угол, градусная мера которого больше 90 градусов, но меньше 180 градусов.
Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.
Свойство смежных углов. Сумма смежных углов равна 180 градусов.
Вертикальные углы. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов. Вертикальные углы равны.
Перпендикулярные прямые. Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
Свойство перпендикулярных прямых. Две прямые, перпендикулярные к третьей, не пересекаются.
Треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, соединенных отрезками. Три точки называются вершинами, а отрезки – сторонами треугольника.
Периметр треугольника – это сумма длин трех сторон треугольника.
Равные треугольники – треугольники, которые при наложении совмещаются. Если два треугольника равны, то элементы одного треугольника соответственно равны элементам другого треугольника.
Теорема, доказательство теоремы. Утверждение, справедливость которого устанавливается путем рассуждения, называется теоремой, а сами рассуждения называются доказательством теоремы.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения также пересекаются в одной точке.
Треугольник называется равнобедренным, если его две стороны равны. Эти стороны называются боковыми, а третья – основанием.
Треугольник, все стороны которого равны, называется равносторонним.
В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Предложение, в котором разъясняется смысл того или иного выражения или названия, называется определением.
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, - радиусом окружности.
Отрезок, соединяющий две точки окружности, называется её хордой.
Хорда, проходящая через центр окружности, называется диаметром.
Часть окружности, ограниченная двумя точками, называется дугой окружности.
Часть плоскости, ограниченная окружностью, называется кругом.
Две прямые на плоскости называются параллельными, если они не пересекаются.
Два отрезка называются параллельными, если они лежат на параллельных прямых.
Прямая с называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.
Углы при параллельных прямых и секущей:
2)Если две прямые параллельны третьей прямой, то они параллельны.
2) обратно, против большего угла лежит большая сторона.
multiurok.ru
Викторина – это игра, у которой нет границ, потому ее можно проводить в любом классе и по любому предмету. Особенно интересны викторины по математике с ответами, провести которые можно вместо контрольной, или самостоятельной работы на неделе математике в школе. В ходе викторины ученикам можно предложить устно и письменно предложить решить задачи, начертить несколько геометрических фигур и провести логическое расследование, основываясь на рациональном мышлении и логике.
В первом туре викторины по математике с ответами ученики должны быстрее всех остальных устно решить ряд задач.
Задача № 1. Блокнот стоил 60 рублей, книга стоит столько же плюс 1/3 к этой сумме. Вопрос: сколько стоит книга?
(90 рублей)
Задача № 2. На сколько увеличиться дробь, если ее числитель будет увеличен на знаменатель.
(ответ: увеличиться в 1 раз)
Задача № 3. 10 рабочих роют яму за 10 часов, выкапывают 10 метров ямы. Сколько рабочих понадобиться, чтобы выкопать 100 метров за 100 часов.
(10)
Задача № 4. Самолет тратит на перелет из аэропорта А в аэропорт Б ровно 1.20 минут, но на обратный путь он тратит всего 80 минут. Как у него это выходит. (в часе 60 минут, то есть 80 минут – это ровно 1.20 минут)
Задача №5. 3 птицы ловят за 1 минуту каждая по одной мухе, но за три минуты, у них получается поймать 3 мухи. Сколько нужно птиц, чтобы поймать за 1 час 60 мух.
(3 птицы)
Задача № 6. Как с помощью пяти двоек записать число 11, используя при этом все имеющиеся в математике знаки математических действий?
(22/2 +2-2)
Ученикам предлагается начертить на доске следующие геометрические фигуры:
Тот, кто быстрее всех справится с заданием — объявляется победителем. От каждой команды участвует только по одному человеку, чертить нужно с использованием линейки и циркуля.
Далее ученики должны ответить на такие вопросы как:
(90, 45, 45)
(360)
(90)
(линия, противостоящая прямому углу треугольника, расположена напротив катета)
5.Что такое биссектриса в треугольнике?
(линия, проведенная из прямого угла прямоугольного треугольника к гипотенузе и делящая треугольник пополам)
(5 братьев и 1 сестра)
(1250 метров)
(105)
(24 года, 29 февраля)
Проведенная с использованием вышеприведенных задач и вопросов викторина для 6-7 классов будет интересной, занимательной, а главное, проверит знания учеников не только по только что пройденному материалу, но и по ранее изученным темам. Вопросы являются весьма примерными, их с легкостью можно заменить любыми другими, как касающимися непосредственно темы урока, так и весьма обширного материала по математике и геометрии, которую ученики как раз начинают изучать в 7 классе.
razvitiedetei.info
Разделы: Математика, Конкурс «Презентация к уроку»
Загрузить презентацию (10,6 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель урока: Развитие исследовательского и ассоциативного мышления учащихся.
Задачи:
Тип урока: урок-соревнование (урок-игра).
Форма проведения: викторина, построенная по сюжетам известной телевизионной игры «Своя игра».
Технология: групповая и индивидуальная работа.
Оборудование: презентация «Своя игра», два компьютера (один для показа мультимедийной презентации, другой для оперативного подсчета результатов в программе Microsoft Excel), мультимедийный проектор, интерактивная доска, сигнальные карточки, канцелярские принадлежности, 3 листа (А4) для финального раунда
Участвуют три команды.
План урока:
Подготовительная работа:
“Своя игра” состоит из 2 раундов и финального раунда. Каждый раунд состоит из 4 тем по 5 вопросов в каждой (20 вопросов). Вопросы располагаются слева направо, по возрастанию степени сложности:
I раунд – стоимость вопросов (от 10 до 50),
II раунд – стоимость вопросов (от 20 до 100).
Игра начинается с жеребьёвки. Выбор темы и стоимости вопроса осуществляет капитан. Ведущий (учитель) зачитывает вопрос. Команда ведет обсуждение и, если готова, поднимает сигнальную карту. Команде, первой поднявшей сигнальную карту, предоставляется возможность ответа на вопрос. Обсуждение на этом заканчивается. Капитан указывает на игрока, который будет отвечать (или отвечает сам).
Если команда отвечает правильно, то ей предоставляется право выбора следующего вопроса, если она отвечает неверно, то право ответить на этот же вопрос предоставляется другой команде. Правильный ответ прибавляет количество очков к общей сумме команды. Неверный ответ уменьшает общее количество очков. Кроме того, в игре имеется “Кот в мешке”. Если команда попадает в выборе вопроса на “Кота в мешке”, то она автоматически передает его другой команде.
Правильный ответ на вопрос “Кота в мешке” увеличивает общее количество очков команды на стоимость данного вопроса, неправильный – уменьшает. Каждый следующий раунд начинает команда, набравшая меньшее количество очков.
Финальный раунд (“Своя игра”) представляет пять возможных тем раунда. К финалу допускаются команды, набравшие положительное количество очков. Команды одна за другой убирают темы, которые им не нравятся (начинает убирать команда, набравшая меньшее количество очков), до тех пор, пока не останется одна тема. Далее команды делают ставку в пределах своей накопленной суммы (записывают на бумаге и сдают жюри). Задается вопрос. Команды думают над ним в течении 60 секунд, записывают ответ на бумаге, и зачитывают его. Правильный ответ в финальном раунде увеличивает общую сумму команды на сделанную ставку, а неправильный – уменьшает. Подсчет очков производится автоматически в программе MS Excel независимым экспертом (учителем). Выигрывает команда, набравшая наибольшее количество очков.
(см. Приложение 2)
Учитель суммирует все баллы в электронной таблице MS Excel и проектирует результаты на экране (см. Приложение 1). Объявляет победителей. Далее разбирается весь ход игры. Учитель акцентирует внимание на удачных решениях, разбираются задания, с которыми не справились команды.
Итоги урока.
21.04.2013
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai