Урок
Дата:
Класс: 7
Тема: Линейное уравнение с одной переменной
Цель урока:
1. Познакомить учащихся с тем, что такое линейное уравнение с одной переменной, что называется корнем уравнения, как решать уравнения с помощью алгоритма решения уравнений с одной переменной;
2.Способствовать развитию памяти, речи, логического мышления, внимания.
3. Способствовать воспитанию интереса к математике, упорства в достижении поставленной цели, трудолюбия, аккуратности.
Предметные: знать понятие линейного уравнения, равносильности уравнений, корней уравнения; уметь применять полученные знания при решении упражнений
Метапредметные: уметь устанавливать причинно – следственные связи, строить логическое рассуждение, умозаключение. Умение действовать в соответствии с предложенным алгоритмом.
Личностные: готовность к жизненному и личностному самоопределению, знания моральных норм, умения выделять нравственный аспект поведения и соотносить поступки и события с принятыми этическими нормами, ориентация в жизненных ролях и межличностных отношениях (формируются во время выполнения заданий, в которых школьникам предлагается дать собственную оценку)
Регулятивные: уметь поставить учебную цель, задачу на основе того, что уже известно и усвоено; уметь планировать последовательность своих действий для достижения конечного результата.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками; постановка вопросов.
Оборудование: учебник алгебры 7 кл., конспект, мел, доска, указка.
Ход урока.
I Организационный момент.
Здравствуйте, ребята! Садитесь! Проверьте свою готовность к уроку, проверьте принадлежности ,чтоб на парте у каждого были учебник ,тетрадь ,дневник, письменные принадлежности.
II Актуализация знаний.
Д.з к доске два человека, остальные работают на повторении. Прежде чем перейдём к изучению нового материала, давайте с вами немного повторим ( привидение подобных слагаемых, раскрытие скобок) . Посмотрите на доску, по очереди раскроем скобки, приведём подобные слагаемые:
a-(3+b)=
c-b(3c-c+2b)=
3d+4(c-3b+d)=
– Молодцы ребята!
III Сообщение темы и цели урока.
А сейчас запишите число, 8.09.11. на полях, классная работа и тему урока « Линейное уравнение с одной переменной». Мы познакомимся с вами: Что называется л.
у. с одной переменной, что называется корнем уравнения, познакомимся с алгоритмом решения уравнения.
IV Изучение нового материала.
-Давайте приведём примеры линейных уравнений с одной переменной. ( учащиеся говорят, записываю на доске) 3x=12, 5y=10, 2a+7=0….
_ Как вы думаете, что значит решить уравнение? (ответ уч-ся: решить уравнение значит найти все те значения переменных, при которых уравнение обращается в верное равенство) Молодцы! Так вот каждое значение переменной называют корнем уравнения. Так какие корни имеют ,написанные нами на доске уравнения? (ответ учащихся: 3x=12, имеет корень x=4,т.к. 3*4=12 и т.д.)
_ на доску вешаю плакат. Посмотрите, ребята, давайте дадим определение линейному уравнению с одной переменной: Линейным уравнением с одной переменной x наз-ся уравнение вида ax+b=0 ,где a и b любые числа( коэффициенты). Если a=0 , b=0 , т.е. уравнение имеет вид 0x+0=0 , то корнем уравнения является любое число (бесконечное множество ) . Если a=0 ,b=0, уравнение имеет вид 0x+b=0.
, то ни одно число этому уравнению не удовлетворяет, т.е. корней нет.
Рассмотрим наиболее распространённый вид уравнения, когда a=0 ,
1) ax+b=0 = ax=-b (слагаемое перенесли вправо с противоположным знаком)
2) x=- b/a.
Фактически мы выработали определённый порядок действий, т.е. алгоритм .( стр. 20 учебника )
Алгоритм решения линейного уравнения ax+b=0 в случае, когда a=0 |
1. Преобразовать уравнение к виду ax=-b. 2. Записать корень уравнения в виде x=( – b) : a , или , что тоже самое , x=-b/a. |
А как же быть ,если уравнение имеет такой вид, например: 2x-2=10-x? (пробуют ответить уч-ся) . Рассуждаем так: Два выражения равны тогда и только тогда, когда их разность равна 0. т.е. ( 2x-2)- (10-x)=0. Что делам дальше?(ответ уч-ся: Раскрываем скобки, приводим подобные слагаемые) К доске идёт ученик, остальные записывают в тетрадях.
Нашли x=4.
А можем мы всё это решение обобщить в алгоритм? Конечно. ( стр.21 учебника)
Алгоритм решения уравнения ax+b=cx=d ( a=c) |
1. Перенести все члены уравнения из правой части в левую с противоположными знаками. 2. Привести в левой части подобные слагаемые , в результате чего получится уравнение вида kx+m=0, где k=0. 3. Преобразовать уравнение к виду kx=-m и записать его корень : x=-m/k. |
Попробуем решить такое уравнение: (3x-4)/5=( 2x+1)/ 2. Давайте вспомним основное свойство пропорции? ( ответ уч-ся: произведение крайних членов равно произведению средних членов). После преобразований можем решить уравнение по алгоритму? (да) К доске вызываю ученика. Остальные работают самостоятельно в тетрадях. Не забывайте, ребята писать каждый раз с новой строчки, ставить запятые, записать ответ. Молодцы!
V Первичное закрепление.
Откройте задачник на стр.
22 устно по цепочке решаем № 4.1, 4.2(письменно, на доске )
VI Подведение итогов урока.
Итак, ребята, что на уроке вы узнали нового? ( что наз-ся уравнением с одной переменной) , А что называется коэффициентом?( число при неизвестном ,или переменной)Что есть корень уравнения? ( Значение переменной, при котором уравнение переходит в верное равенство) Чему научились ? ( решать линейные уравнения с помощью алгоритма). Оценки за урок…Молодцы, ребята!
VII Дача домашнего задания.
Откройте дневники, запишите задание на дом. С. 20-21 учебника, выучить алгоритмы , В задачнике № 4.5,№4.7.
Спасибо за урок, все свободны!
Урок № 6
Тема. Линейное уравнение с одной переменной
Цель: повторить, углубить и расширить знания учащихся о видах уравнений с одним неизвестным, сводящиеся к линейным уравнениям с одной Переменной (уравнение с модулем и уравнения, содержащие дроби), и способы равносильных преобразований таких уравнений.
Тип урока: углубление знаний, усвоения умений.
Ход урока
I. Организационный момент
II. Проверка домашнего задания
@ Поскольку целью выполнения домашнего задания было формирование устойчивых навыков решения линейных уравнений ах = b с одной переменной при различных значениях а и b, то № 1 и 2 следует тщательно проверить и еще раз прокомментировать способ решения уравнений.
№ 1. Решите уравнение:
1) 15(х + 2) – 30 = 12х 15x + 30 – 30 = 12x 15x = 12х 15x – 12x = 0 3x = 0 х = 0 |
2) 6(1 + 5х) = 5(1 + 6х) 6 + 30x = 5 + 30x 30x – 30x = 5 – 6 0x = -1 корней нет |
3)3у + (у-2) = 2(2у-1) 3у + у – 2 = 4у – 2 4у – 2 = 4у – 2 4у – 4у = -2 + 2 0y = 0 в – любое число |
4) 6у – (у – 1) = 4 + 5у 6у – у + 1 = 4 + 5у 5у + 1 = 4 + 5у 5у – 5у = 4 – 1 0у = 3 корней нет |
№ 2.
Найдите корни уравнений:
1) 7(х – 8,2) = 3x + 19 7x – 57,4 = 3x + 19 7x – 3x = 19 + 57,4 4х = 76,4 х = 76,4 : 4 x = 19,1 |
2) 0,2(5x – 6) + 4x = 3,8 x – 1,2 + 4x = 3,8 5х – 1,2 = 3,8 5х = 3,8 + 1,2 5x = 5 x = 5 : 5 x = 1 |
3) 0,4(2x – 7) + 1,2(3x + 0,7) = 1,6x 0,8x – 2,8 + 3,6x + 8,4 = 1,6x 4,4x + 5,6 = 1,6x 4,4x – 1,6x = -5,6 2,8x = -5,6 x = -5,6 : 2,8 x = -2 |
III. Актуализация опорных знаний
@ Во время математического диктанта повторяем теоретический материал и способы действий, рассмотренные на предыдущем уроке.
Математический диктант
1. Придумайте и запишите любое линейное уравнение с одним неизвестным х [у].
2. Как называется уравнение-2х = 17 [17х = -2]?
3. При каких условиях уравнение ах = 5 [ау = 3] имеет единственный корень (не имеет корней)? Запишите этот корень.
4. Решите уравнение 0,2 х = -1 [-0,3х = 1].
5. Решите уравнение 2х + 1 = 3х – x [х + 3 = 5 + х – 2].
6. Решите уравнение 5 – х = 2x + 2 [2 – 2х = -2х + 3].
По завершении работы ответы проверяются, корректируются и повторяются определение линейного уравнения с одной переменной и схема решения линейных уравнений.
IV. Систематизация, углубление и расширение знаний
1. Работа с опережающим заданием
Рассмотрите уравнение: | х | = 3; | х | =0; | х | = -3.
По известному алгоритму выполните сравнение (приложение 2).
Выводы: 1) Все приведенные уравнения можно записать в виде одного уравнения | х | = а, где а – любое число.
2) Способ решения и число корней этого уравнения зависит от знака числа а, а именно:
2. Расширение знаний
Как было уже сказано на предыдущем уроке, решение многих уравнений, имеющих одну переменную, сводится к решению линейных уравнений с одной переменной. Среди таких уравнений можно выделить:
а) уравнения с модулем;
б) уравнения, содержащие дроби.
Далее разбираем решения уравнений названных видов.
а) . @ Прежде чем начинать объяснения, следует активизировать мышление учащихся, предложив сравнить уравнение с уравнением вида | х | = а. Чем отличается данное уравнения от уравнения | х | = а? Чем похожи эти уравнения? Чем похож способ решения (первый шаг) и чем будет отличаться решение? После этого делаем записи в тетрадях (проводим устные замечания): . 1) 2x – 3 = 3 или 2) 2x – 3 = -3. (Поскольку 3 > 0, | x | = а, а > 0, то x = a или x = -а. Решаем линейные уравнения.) 2х = 6, 2х = 0. х = 3, х = 0. Ответ. 3; 0 |
б) . @ Прежде чем решать уравнение, следует сравнить его с другими уравнениями, которые были решены ранее. Провести беседу, рассмотрев такие вопросы: Чем отличается данное уравнения от уравнения № 1 в домашнем задании? Что общего? Какое свойство равносильных уравнений можно использовать, чтобы избавиться от дробей? Свойство дробей используется при этом? После этого можно записать решение, добавив устные комментарии. . (Найдем НСК (18; 12; 9) = 36 и умножим на него обе части уравнения. . (Выполним умножение.) 2(2х – 1) = 3х + 4х; 4х – 2 = 3х + 4. (Выполним равносильные преобразования, сведем уравнение к линейному и решим его.) 4х – 3х = 4 + 2, х = 6 Ответ. 6 |
Выводы. Разобрав примеры а) и б) мы убедились в том, что некоторые уравнения с модулем, так же как и некоторые уравнения с дробями (не все!!!), путем выполнения равносильных преобразований и использования свойств чисел могут быть сведешь к линейных уравнений с одной переменной.
V. Усвоение умений
Выполнение письменных упражнений
1. Решите уравнения, содержащие переменную под знаком модуля:
1) |х| = 3;
2. 2) |х| + 1 = 7;
3. 3) |x| – 2 = -3;
4. 4) |х – 3| = 2;
5. 5) |х – 4| = 0;
6) |х + 3| = -4;
6.
7) 3|x| – 1 = 0;
7. 8) |3х + 2| – 4 = 0;
8. 9) |2(x – 3)(х + 4)| = 2.
9. Решите уравнение:
1) ;
2) ;
3) ;
4) ;
5) .
10. * Логическое упражнение.
Найдите пропущенный рисунок:
3х – 8 = 8x – 28 |
? |
VI. Итоги урока. Рефлексия
Игровой момент «Найдите ошибку»
Ученик 7 класса Петрик Тяпляпкін сказал, что очень хорошо научился решать уравнения, сводящиеся к линейным, и показал, как он решает уравнения. Вот его решения.
а) , х – 3 = 2х – 1, х – 2х = -1 + 3, -x = 2, х = -2 |
х – 3 = 2, х = 5 |
Согласны ли вы с такими решениями? Как бы вы оценили успехи Петрика?
VII.
Домашнее задание
№ 1. Решите уравнение:
1) |2х – 3| = 5;
2) |2х – 1| + 7 = 8;
3) |5х – 4(2х + 3) | = 6;
4)* (опережающее домашнее задание) 2(|x| – 3) – 4(2|х| + 9) = -48;
5) ;
6) .
№ 2. При каком значении а уравнение ах = 42:
1) имеет корень -7;
2) корней не имеет;
3) имеет бесконечное множество корней?
| Назад | Содержание | Вперед |
Линейное уравнение — это уравнение, в котором наивысшая степень переменной всегда равна 1. Оно также известно как уравнение одной степени. Стандартная форма линейного уравнения с одной переменной имеет вид Ax + B = 0. Здесь x — переменная, A — коэффициент, B — постоянная. Стандартная форма линейного уравнения с двумя переменными имеет вид Ax + By = C.
| 1. | Что такое линейное уравнение? |
| 2. | Формула линейного уравнения |
| 3. | График линейных уравнений |
| 4. | Часто задаваемые вопросы о линейных уравнениях |
Уравнение, имеющее наивысшую степень 1, называется линейным уравнением. Это означает, что ни одна переменная в линейном уравнении не имеет показатель степени больше 1. График линейного уравнения всегда образует прямую линию.
Линейное уравнение Определение: Линейное уравнение — это алгебраическое уравнение, где каждый член имеет показатель степени 1, и когда это уравнение изображается на графике, оно всегда приводит к прямой линии. Вот почему оно называется «линейным уравнением».
Существуют линейные уравнения с одной переменной и линейные уравнения с двумя переменными.
Давайте научимся определять линейные уравнения и нелинейные уравнения с помощью следующих примеров.
| Уравнения | Линейный или нелинейный |
|---|---|
| у = 8х – 9 | Линейный |
| у = х 2 – 7 | Нелинейный, степень переменной x равна 2 |
| √у + х = 6 | Нелинейный, степень переменной y равна 1/2 |
| у + 3х – 1 = 0 | Линейный |
| г 2 – х = 9 | Нелинейный, степень переменной y равна 2 |
Формула линейного уравнения — это способ выражения линейного уравнения. Это можно сделать разными способами. Например, линейное уравнение может быть выражено в стандартной форме, в форме точки пересечения или в форме точка-наклон. Теперь, если мы возьмем стандартную форму линейного уравнения, давайте узнаем, как оно выражается.
Мы видим, что оно варьируется от случая к случаю в зависимости от количества переменных, и следует помнить, что наивысшая (и единственная) степень всех переменных в уравнении должна быть 1.
Стандартная форма или общая форма линейных уравнений с одной переменной записывается как Ax + B = 0; , где A и B — действительные числа, а x — единственная переменная. Стандартная форма линейных уравнений с двумя переменными выражается как Ax + By = C; , где A, B и C — любые действительные числа, а x и y — переменные.
График линейного уравнения с одной переменной x образует вертикальную линию, параллельную оси y, и наоборот, тогда как график линейного уравнения с двумя переменными x и y образует прямую линию. Построим график линейного уравнения с двумя переменными с помощью следующего примера.
Пример: Постройте график линейного уравнения с двумя переменными, x – 2y = 2.
Построим график линейного уравнения, выполнив следующие шаги.
| х | 0 | 2 | 4 | -2 |
|---|---|---|---|---|
| у | -1 | 0 | 1 | -2 |
Так линейное уравнение изображается на графике.Линейное уравнение с одной переменной — это уравнение, в котором присутствует только одна переменная. Оно имеет форму Ax + B = 0, где A и B — любые два действительных числа, а x — неизвестная переменная, имеющая только одно решение. Это самый простой способ представить математическое утверждение. Это уравнение имеет степень, которая всегда равна 1. Линейное уравнение с одной переменной решается очень просто. Переменные разделяются и подводятся к одной стороне уравнения, а константы объединяются и подводятся к другой стороне уравнения, чтобы получить значение неизвестной переменной.
Пример: Решить линейное уравнение с одной переменной: 3x + 6 = 18.
Чтобы решить данное уравнение, подносим числа в правой части уравнения и сохраняем переменную в левая сторона. Это означает, что 3x = 18 – 6. Затем, когда мы решим для x, мы получим 3x = 12.
Наконец, значение x = 12/3 = 4.
Линейное уравнение в Две переменные имеют вид Ax + By + C = 0, где A, B, C — действительные числа, а x и y — две переменные, каждая из которых имеет степень 1. Если мы рассмотрим два таких линейных уравнения, они называются одновременными линейными уравнениями. Например, 6х + 2у + 9= 0 — линейное уравнение с двумя переменными. Существуют различные способы решения линейных уравнений с двумя переменными, такие как графический метод, метод подстановки, метод перекрестного умножения, метод исключения и метод определителя.
Уравнение похоже на весы с одинаковыми весами с обеих сторон. Если мы прибавим или вычтем одно и то же число из обеих частей уравнения, оно останется верным. Точно так же, если мы умножаем или делим одно и то же число в обеих частях уравнения, это правильно. Мы подносим переменные к одной стороне уравнения, а константу к другой стороне, а затем находим значение неизвестной переменной.
Это способ решения линейного уравнения с одной переменной. Давайте разберемся в этом с помощью примера.
Пример: Решите уравнение, 3x – 2 = 4.
Выполняем математические операции с левой (левой) и правой (правой) частями так, чтобы равновесие не нарушалось. Итак, давайте добавим 2 с обеих сторон, чтобы уменьшить LHS до 3x. Это не нарушит баланс. Новая левая сторона равна 3x – 2 + 2 = 3x, а новая правая сторона равна 4 + 2 = 6. Теперь давайте разделим обе части на 3, чтобы уменьшить левую часть до x. Таким образом, мы имеем х = 2 . Это один из способов решения линейных уравнений с одной переменной.
Советы по линейным уравнениям:
☛ Статьи по теме:
Пример 1: Сумма двух чисел равна 44. Если одно число на 10 больше другого, найдите числа, составив линейное уравнение.
Решение:
Пусть число равно x, значит, другое число равно x + 10. Мы знаем, что сумма обоих чисел равна 44. Следовательно, линейное уравнение можно представить в виде x + x + 10. = 44. В результате получается 2x + 10 = 44. Теперь давайте решим уравнение, изолируя переменную с одной стороны и вводя константы с другой стороны. Это означает, что 2x = 44 – 10. Упрощая RHS, мы получаем 2x = 34, поэтому значение x равно 17. Это означает, что одно число равно 17, а другое число равно 17 + 10 = 27,
Ответ: Следовательно, эти два числа — 17 и 27.
Пример 2: Число, умноженное на шесть, равно 48. Составьте линейное уравнение и найдите неизвестное число.
Решение: Пусть неизвестное число равно x. Шесть раз это число равно 48, значит 6x = 48. Итак, это линейное уравнение можно решить, чтобы найти значение x, которое является неизвестным числом. 6x = 48 означает, что x = 48/6 = 8.
Ответ: Следовательно, неизвестное число равно 8.
Пример 3: Решение данного линейного уравнения: 5x – 95 = 75.
Решение: Данное уравнение составляет 5x – 95 = 75.
⇒ 5x = 75 + 95
9000 29. = 170
⇒ x = 34
Ответ: Следовательно, значение x равно 34.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила.
Узнайте, почему стоит математика, с нашими экспертами Cuemath
Запишитесь на бесплатный пробный урок
перейти к слайдуперейти к слайду
Линейное уравнение — это уравнение, в котором наивысшая степень переменной всегда равна 1. Оно также известно как уравнение одной степени. Когда это уравнение изображается на графике, оно всегда приводит к прямой линии. По этой причине его называют «линейным уравнением». Существуют линейные уравнения с одной переменной, с двумя переменными, с тремя переменными и так далее. Стандартная форма линейного уравнения с одной переменной имеет вид Ax + B = 0. Уравнение вида Ax + By = C называется линейным уравнением с двумя переменными. Вот несколько примеров линейных уравнений: 5x + 6 = 1, 42x + 32y = 60, 7x = 84 и т. д.
Формула линейного уравнения — это способ выражения линейного уравнения.
Это может быть выражено в стандартной форме, в форме пересечения наклона или в форме точка-наклон. Стандартная форма линейного уравнения с одной переменной имеет вид Ax + B = 0. Здесь x — переменная, A — коэффициент при x, а B — константа. Стандартная форма линейного уравнения с двумя переменными имеет вид Ax + By = C. Здесь x и y — переменные, а A, B и C — любые действительные числа.
Линейное уравнение называется линейным, потому что когда мы пытаемся построить график данной линейной функции, получается прямая линия.
Мы можем решить линейное уравнение с одной переменной, переместив переменные в одну часть уравнения, а числовую часть — в другую. Например, x – 1 = 5 – 2x можно решить, переместив числовые части в правую часть уравнения, оставив переменные в левой части. Следовательно, мы получаем x + 2x = 5 + 1. Таким образом, 3x = 6. Это дает x = 2,
Да, линейные уравнения могут иметь дроби только до тех пор, пока знаменатель в дробной части является постоянной величиной.
Переменные не могут быть частью знаменателя любой дроби в линейном уравнении.
Линейное уравнение с одной переменной — это уравнение, в котором присутствует только одна переменная. Оно имеет форму Ax + B = 0, где A и B — любые два действительных числа, а x — неизвестная переменная, имеющая только одно решение. Например, 9x + 78 = 18 — линейное уравнение с одной переменной.
Линейное уравнение с двумя переменными имеет форму Ax + By + C = 0, где A и B — коэффициенты, C — постоянный член, а x и y — две переменные, каждая со степенью 1 Например, 7x + 9y + 4 = 0 — это линейное уравнение с двумя переменными. Если мы рассмотрим два таких линейных уравнения, они называются одновременными линейными уравнениями.
Линейные уравнения не имеют степени, отличной от 1, в любом члене. Общая форма линейного уравнения выражается как Ax + By + C = 0, где A, B и C — любые действительные числа, а x и y — переменные.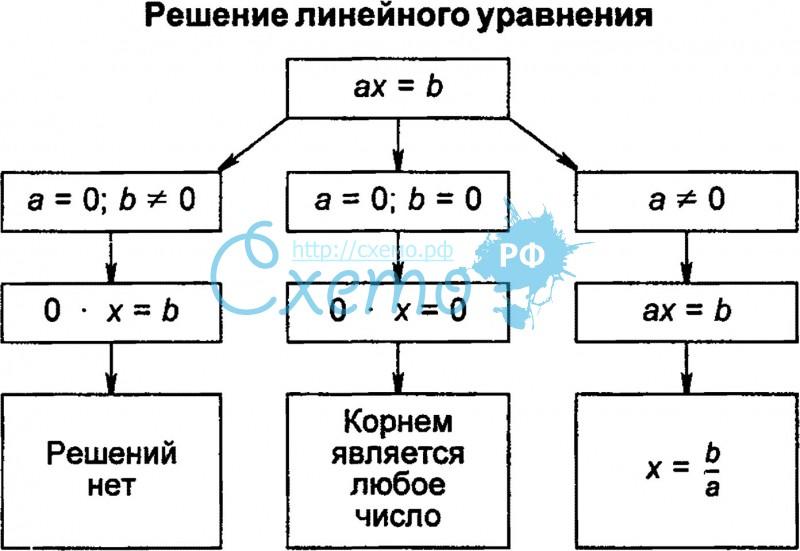
Принимая во внимание, что квадратные уравнения имеют по крайней мере один член, содержащий переменную, которая возведена во вторую степень. Общая форма квадратного уравнения выражается как ax 2 + bx + c = 0. Другое различие между двумя типами уравнений заключается в том, что линейное уравнение образует прямую линию, тогда как квадратное уравнение образует на графике параболу.
Когда мы рисуем линейные уравнения, они образуют прямую линию. Чтобы построить график уравнения формы Ax + By = C, мы получаем два решения, которые соответствуют точкам пересечения x и y. Преобразуем уравнение к форме y = mx + b. Затем мы заменяем значение x другими числами и получаем значение y, которое создает набор координат (x, y). Эти координаты можно нанести на график, а затем соединить линией.
Линейные уравнения с дробями решаются так же, как мы решаем обычные уравнения. Нам нужно ввести переменную с одной стороны и константы с другой стороны и найти переменную.
Например, давайте решим уравнение (2a/3) – 10 = 12.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист по линейным уравнениям
В этой статье рассказывается все, что вам нужно знать о том, как преподавать линейные уравнения.
Представь это. Вы открываете пособие для учителя, чтобы заглянуть в следующий блок: « Линейные уравнения ».
Ах, да! Линии графика, определение наклона, изменение формы! На вашем лице появляется тонкая улыбка, когда вы с удовольствием вспоминаете, как научились строить графики этих уравнений, которые кажутся вам такими простыми. Прочитав немного дальше, вы задаетесь вопросом, испытают ли ваши ученики такую же радость обучения.
Вам это кажется достаточно простым, но будет ли это достаточно просто для них? Есть ли способ сделать этот опыт приятным даже для неуверенных в себе учеников?
Вы задаетесь вопросом: «С чего мне начать?»
Больше не удивляйтесь. Читайте дальше, поскольку мы обсуждаем не только с чего начать изучение модуля линейных уравнений, но и необходимые навыки, определение линейного уравнения, примеры линейных уравнений, приложения линейных уравнений, математические стандарты линейных уравнений, советы о наклоне, распространенные заблуждения и идеи для вас!
Что мы рассматриваем
Когда мы думаем о начале подразделения, мы должны начать с конца. В конце концов, как мы узнаем, с чего начать, если не установили свои цели?
Во-первых, давайте начнем со стандартов, которые нам необходимо охватить. Имейте в виду, что эти стандарты могут отличаться в зависимости от вашего конкретного уровня обучения или государственных стандартов. После того, как вы определили основные стандарты, которые необходимо охватить, вы можете ставить цели обучения. Продолжайте читать, и мы далее предоставим список некоторых важных основных стандартов линейных уравнений.
Давайте начнем с этого важного общего базового стандарта для восьмиклассников:
CCSS.MATH.CONTENT.8.EE.B.5
«Нарисуйте пропорциональные отношения, интерпретируя единичную скорость как наклон графика. Сравните два разных пропорциональных отношения, представленных по-разному. Например, сравните график «расстояние-время» с уравнением «расстояние-время», чтобы определить, какой из двух движущихся объектов имеет большую скорость».
Мы можем сосредоточиться на интерпретации уклона. Мы можем создать цель обучения, используя удобный для учащихся язык. Вот пример цели обучения, основанной на этом стандарте:
| «Учащиеся смогут сравнивать наклоны на графиках с наклонами в уравнениях и объяснять свои ответы в контексте». |
Чтобы узнать больше о сравнении уклонов, ознакомьтесь с этой статьей о параллельных и перпендикулярных линиях.
Теперь, когда мы выбрали одну из целей для нашего модуля, мы знаем, что нам нужно спланировать конкретные уроки, включающие словесные задачи и письменные ответы. Мы знаем, что учащиеся должны уметь не только определять наклоны в уравнениях и графиках, но и объяснять наклон в контексте. Постановка целей в начале раздела позволяет нам использовать время занятий для эффективной подготовки учащихся к достижению целей обучения. Цели обучения становятся мишенью .
Не только яблочко для вас, но и для ваших учеников. Презентация целей обучения учащимся в начале раздела обеспечивает учащимся концентрацию и способность к самоанализу. Перед экзаменационным днем учащиеся могут спросить себя: «Знаю ли я, как объяснить уклон?» или «Знаю ли я, как объяснить наклон в контексте ?» Вы можете предоставить учащимся возможность обдумать свои новые навыки в классе на протяжении всего модуля и отстаивать свои интересы, если им нужна помощь в достижении конкретных целей.
У сильного отряда должно быть около от трех до пяти целей обучения . Постановка слишком большого количества учебных целей дает нам слишком много для выполнения за время, обычно отведенное на единицу. Слишком малое количество затрудняет соблюдение всех стандартов. Помните, что одна цель обучения может касаться основных компонентов более чем одного стандарта. Помните об академическом календаре и о том, сколько времени отведено на этот модуль. Лучше успешно выполнить три цели, чем быстро пробежать пять целей.
После того, как цели обучения определены, мы можем сосредоточиться на планировании урока. Какие навыки нужны учащимся для поддержки задач, которые мы просим их выполнить?
Вернуться к оглавлению
Существует несколько обязательных навыков, которые укрепят уверенность учащихся, когда они отправляются в путешествие по линейным уравнениям. Мы обсудим три важных предпосылки для обучения линейным уравнениям: свойство дистрибутивности, решение уравнений для переменной и построение графиков.
Студенты должны будут использовать распределительное свойство при изменении формы точка-наклон на форму наклон-пересечение.
Обязательно найдите время, чтобы оценить, насколько хорошо учащиеся могут распределять материалы, прежде чем приступить к изучению модуля или, по крайней мере, в самом начале модуля. Вы можете быть приятно удивлены их способностями или шокированы пробелами в их знаниях. В любом случае, использование оценивания в классе важно для обучения навыкам, в которых учащиеся больше всего нуждаются в помощи. Хотя у вас может быть время для обзорного дня, может быть лучше включать небольшое количество практики распределения собственности каждый день. Подумайте о том, чтобы использовать время класса «Разминка»/«Сделать сейчас» или включить несколько задач на раздачу в свои уроки и домашнюю работу.
Начните заниматься алгеброй 1 на Альберте прямо сейчас!
Учащиеся должны решить для y при изменении стандартной формы на форму с пересечением наклона (иногда называемую «буквенными уравнениями»).
Например, получив 6x+19y=2 и попросив представить его в форме пересечения наклона, учащиеся должны решить, как изолировать переменную y.
В начале этого модуля предоставьте учащимся широкие возможности для решения переменной в простых уравнениях, например, для решения b в уравнении A=bh. Разминка и формативное оценивание — отличные места для постановки подобных практических задач.
Мы еще вернемся к этой теме, когда будем рассматривать заблуждения.
Ознакомьтесь с лицензиями школы Альберта !
Существует широкий спектр графических возможностей. Некоторые учащиеся легко усваивают графики и любят представлять уравнения в графической форме. Другие учащиеся увязают в понимании новых обозначений и того, как работает координатная плоскость.
При графическом отображении уравнения обязательно формулируйте важные элементы обозначений. Например, при построении уравнения в виде точки-наклона, такого как y-7=\frac{1}{2}(x+4), обязательно запишите точку как (-4, 7) и объясните учащимся что координата x всегда записывается первой, а координата y всегда записывается второй.
Объясните, как вы знаете, где разместить точку на основе оси x и оси y.
При обучении у нас редко бывает достаточно времени, чтобы провести весь обзор, который мы хотели бы сделать. При построении графиков вместо того, чтобы тратить день на повторение, постарайтесь сделать акцент на ключевых графических обозначениях и обзоре, когда вы преподаете новые концепции. Подчеркните, что такое точка пересечения с осью y и как подъем и бег связаны с осью x и осью y. Даже отличники, изучающие графики, получат пользу от повторения процесса.
Для помощи в ознакомлении со всеми основными навыками построения графиков, которые потребуются учащимся, вот пост о построении графиков линейных уравнений.
Вернуться к оглавлению
Линейное уравнение: определение« Линейное уравнение » — это особый тип уравнения, описывающего прямую линию.
Помните, линейное уравнение не может описать любой случайный график. Наклон графика должен оставаться постоянным, поскольку линейные уравнения описывают только прямые линии (а не кривые).
Вернуться к оглавлению
3 Примеры линейных уравненийЧтобы узнать, как преподавать линейные уравнения, давайте начнем с нескольких примеров.
Линейные уравнения могут быть записаны в трех формах: форма точки пересечения, форма точка-наклон и стандартная форма.
Форма пересечения наклона: y=mx+b
Пример: y=7x+\frac{13}{2}
Форма точки-наклона: y-y_1=m(x-x_1)
Пример: y-7=\frac{1}{2}(x+4)
Стандарт От: ax+by=c
Пример: 2x+6y=7
Дополнительные обзоры и примеры всех трех форм линейных уравнений можно найти в этой статье, в которой показаны различия и преобразования между всеми формами.
Вернуться к оглавлению
3 Применение линейных уравнений в реальной жизниПотребление бензина знакомо учащимся. Чувствовали ли студенты запах бензина в большом желтом автобусе или ждали в машине, пока их родители заливали бензин, в некоторых случаях студенты испытывали бензин.
Мы можем просто найти транспортное средство. В этом примере мы будем использовать Chrysler Pacifica. Chrysler Pacifica имеет топливную экономичность 22 \text{миль на галлон} при совмещении расхода топлива по городу и шоссе (источник). Бензобак Chrysler Pacifica вмещает 19\text{ галлонов} бензина (источник).
Теперь мы можем составить уравнение, связывающее количество бензина с количеством миль, пройденных после заправки.
Пусть x представляет количество пройденных миль, а y представляет собой количество бензина, оставшегося в автомобиле. Мы знаем, что точка пересечения по оси Y равна 19, потому что это количество бензина в автомобиле до того, как оно уедет с заправочной станции.
Определение уклона требует немного больше усилий. Наш график показывает, сколько миль вы можете проехать на каждом галлоне бензина. Однако эффективность использования топлива описывает количество бензина, сожженного на определенное количество миль. Мы можем обсудить взаимное. Обратная величина \frac{ 22 \text{ миль}}{1 \text{ галлон}} равна \frac{1 \text{ галлон}}{22 \text{ миль}} . Автомобиль будет сжигать один галлон бензина на каждые пройденные 22 мили. Поскольку мы описываем количество бензина, оставшегося в автомобиле, наш наклон отрицателен. Когда газ сгорает, его больше нет в бензобаке. Наклон нашего уравнения равен \frac{-1}{22}.
Как только мы получим уравнение:
y=\frac{-1}{22}x+19
… мы можем ответить на любые вопросы!
Вернуться к оглавлению
Многие учащиеся могут пользоваться роскошью мобильного телефона без бремени счетов. Попросить студентов рассчитать счет за мобильный телефон на основе может быть чем-то вроде откровения!
Давайте посмотрим на поставщика услуг, такого как T-Mobile. Их тарифный план Essentials стоит $30\text{ в месяц}. Это отличное место для обсуждения связи с «подъемом по сравнению с пробегом». Однако мы не можем платить \$30\text{ в месяц}, пока у нас не будет телефона. Существует такое разнообразие типов телефонов, но мы можем использовать Galaxy A11, который стоит 180 долларов. Это будет наша начальная стоимость.
Теперь мы можем составить уравнение:
y=30x+180
…чтобы представить сумму денег, потраченную на телефон и использование телефона.
С этого момента мы можем задавать различные вопросы, например: «Сколько времени прошло, прежде чем мы заплатили более тысячи долларов за использование телефона?» Мы также могли бы предложить учащимся построить график или сравнить эту стоимость со стоимостью другого тарифного плана и комбинации телефонов.
Вернуться к оглавлению
Замечательный создатель строительных лесов поделился проектом, в котором ученики сами выращивают траву. Студенты измеряют рост каждый день, чтобы построить график. Созданная линия не является линейным уравнением. Однако учащиеся могут составлять линейные уравнения, используя две точки на графике. Эти линейные уравнения могут позволить учащимся предсказать будущий рост травы.
Этот проект может привести к содержательным дискуссиям о реальных данных.
При обучении математике мы иногда избегаем примеров, нарушающих шаблоны. Хотя иногда это уместно, учащимся также полезно видеть данные, которые делают , а не соответствует модели, о которой мы учим.
Студенты могут увидеть, как навыки, которые они изучают, могут помочь им понять и интерпретировать данные, даже если они не совсем соответствуют примерам текущего модуля.
Вернуться к оглавлению
Ранее мы обсуждали важность стандартов при обучении линейным уравнениям. Ниже приведен полный список стандартов, связанных с линейными уравнениями.
Наш список начинается с трех стандартов для восьмого класса, а также включает два стандарта по математике для средней школы. Гиперссылки направляют вас на веб-сайт инициативы Common Core State Standards Initiative, где некоторые стандарты разбиты на некачественные. Обратите внимание, что конкретные стандарты для вашего подразделения могут отличаться в зависимости от уровня обучения и государственных стандартов.
Нарисуйте пропорциональные отношения, интерпретируя удельную скорость как наклон графика.
Сравните два разных пропорциональных отношения, представленных по-разному. Например, сравните график «расстояние-время» с уравнением «расстояние-время», чтобы определить, какой из двух движущихся объектов имеет большую скорость.
Решение линейных уравнений с одной переменной.
Анализ и решение пар одновременных линейных уравнений.
Решение линейных уравнений и неравенств с одной переменной, включая уравнения с коэффициентами, представленными буквами.
Точно и приблизительно решать системы линейных уравнений (например, с помощью графиков), ориентируясь на пары линейных уравнений с двумя переменными.
Вернуться к оглавлению
Советы, которые помогут учащимся понять уклон Уклон — это понятие, которое снова и снова будет всплывать в математическом будущем наших учащихся.
Это, однако, не должно давать вам повода приукрашивать уклон. Наклон — это фундаментальная часть понимания, на которую должны опираться учащиеся. Понимание наклона поможет учащимся усвоить более сложные функции с изменяющимся наклоном, понять такие понятия, как ускорение, и понять, как определить производную функции.
Чтобы построить прочную основу для понимания наклона, мы должны использовать визуальные, устные и кинестетические методы. Помните, что все учащиеся получают пользу от всех методов. Это образовательный миф, что учитель должен изменить свой стиль преподавания, чтобы достичь определенного типа обучения. Вместо этого учитель всегда должен использовать все три метода, особенно при подготовке основы для такого важного понятия, как наклон.
Вернуться к оглавлению
Первый: визуальные методы. Наглядно покажите учащимся, как «выглядит» склон. Что такое подъем над пробегом? Где на графике «рост»? Где находится «бег» на графике? Как выглядит уравнение с наклоном \frac{1}{3}? Как выглядит уравнение с наклоном 17?
Прочтите эту обзорную статью , чтобы узнать о прекрасном взаимодействии контента и графических изображений.
Чтобы пойти еще дальше, покажите им, что моделирует это уравнение. Если вы создаете уравнение, моделирующее скорость объекта, покажите им объект, движущийся с этой скоростью. Сделайте визуальные связи с тем, что моделирует график, чтобы помочь учащимся понять, что означает наклон. Продолжайте читать, чтобы увидеть Turtle Time Trials , который делает это очень хорошо.
Вернуться к оглавлению
Для устных методов не забывайте использовать как можно больше словарного запаса каждый раз, когда вы объясняете построение графика или расчет наклона.
Укажите, когда вы считаете подъем, когда считаете пробежку, когда делаете новую точку, когда рисуете линию с нулевым наклоном и т. д. недостаточно , чтобы показать учащимся график и изображение. Вы должны явно указать все связи с уравнениями.
Кроме того, включите моменты, когда вы говорите, определяя наклон, как с визуальным изображением, так и без него.
Позвольте учащимся озвучить, как определить уклон и как его рассчитать. Учащимся будет полезно слушать друг друга, а учащимся будет полезно поделиться своими процессами решения. Акт выражения того, как найти наклон, заставляет студента более полно обрабатывать свой метод и увеличивает его способность сохранять и вспоминать информацию.
Вернуться к оглавлению
Что касается кинестетических методов, помните, что вы не можете «переусердствовать». Дайте учащимся как можно больше разнообразных задач на уклон.
Пусть они запишут свою работу. Кинестетическое обучение не должно быть сложным. Студенты могут идти шаг за шагом с партнером, чередуя, кто пишет какой шаг. Вы можете попросить одного учащегося проговаривать шаги, пока другой учащийся записывает то, что говорит его партнер, а затем поменяться ролями. Учащиеся могут использовать свои руки, чтобы визуально показать, как выглядят различные склоны. Учащиеся могут использовать магниты, чтобы создать большой график на доске в классе.
Есть столько разных способов!
Некоторые учителя любят сумасшествие и энергию и заставляют своих учеников двигаться и общаться, в то время как другие хотят мира и спокойствия. Оба учителя могут эффективно использовать кинестетическое обучение. Где бы вы ни находились в этом спектре, крайне важно предоставить вашим ученикам возможность самим попрактиковаться в наклоне и заставить их написать его или физически продемонстрировать свое понимание.
Вернуться к оглавлению
Распространенные заблуждения учащихся о линейных уравненияхПосле небольшой практики учащиеся обычно достаточно уверенно используют:
y=mx+b
Учащиеся сияют от гордости, поскольку они легко определяют наклон 5 и точку пересечения y 2 в уравнении y=5x+2.
Затем следует уравнение, которое делает не совсем подходящим шаблону . Учащиеся поднимают руки, и вы знаете, что они смотрят на такое уравнение, как:
x=6
Хотя горизонтальные и вертикальные линии могут показаться более простыми, чем построение графика в виде точек и наклонов, эти линии не соответствуют шаблону, который мы привили нашим ученикам.
Мы должны найти время, чтобы объяснить, почему эти уравнения различны. Как указывалось выше, крайне важно предоставить визуальные связи с уравнениями и указать, как вы знаете, как должен выглядеть график.
Возможно, вы почувствуете, что учащиеся быстро усваивают эту тему. Затем вы можете быть разочарованы, когда они плохо справятся с этой темой на итоговой оценке. Помните, что если учащиеся не будут часто повторять информацию, они ее забудут. Требуется время, прежде чем информация попадет в долговременное хранилище памяти, и еще больше практики, чтобы упростить извлечение этой информации. Не забудьте включить несколько практических вопросов с горизонтальными и вертикальными линиями во время занятий в классе и во время домашней работы с высокой частотой.
Для получения дополнительной информации у нас есть целый пост, посвященный горизонтальным и вертикальным линиям.
Вернуться к оглавлению
Иногда мы, учителя математики, забываем о умственных проблемах, с которыми сталкиваются ученики при изучении новых навыков.
Нам решение для одной переменной кажется достаточно простым, независимо от того, есть ли какие-либо дополнительные переменные.
Для многих молодых студентов, изучающих математику, решение переменной означает «получение ответа». Они хотят число, и когда вы красиво заканчиваете менять стандартную форму на форму с пересечением наклона и пишете:
y=\frac{-6}{19}+\frac{2}{19}
…и с гордостью восклицают: «Я решил уравнение для y», некоторые учащиеся могут показаться озадаченными. Этим студентам вы не могли решить для y, потому что у вас нет «ответа».
Это очень простое умственное препятствие, которое можно преодолеть с помощью объяснений, примеров и практики. Скажите своим ученикам, что решение — это не число , а уравнение. Объясните, что их ответы будут отличаться от того, к чему они привыкли. Как было сказано выше, определение решения для переменной в качестве необходимого навыка может помочь вам легче перейти к решению для y. Предоставьте учащимся широкие возможности для решения переменных в простых уравнениях.
Конечно, заблуждения у ваших учеников могут быть разными. Существует множество других причин, по которым ваши ученики могут иметь определенные пробелы в своих знаниях. Вот почему формативное оценивание так важно. Потратьте время, чтобы получить обратную связь от ваших студентов. Задавайте им вопросы, и учащиеся отвечают на доске, в Kahoot, через случайный вызов.
Если учащиеся не могут правильно ответить на вопросы, выясните, какие ошибки они допускают. Исправьте ошибку и предоставьте частые возможности правильно использовать новые математические навыки!
Вернуться к оглавлению
Идеи для занятий по линейным уравнениям На сайте Albert.io вы найдете полезную информацию и тысячи практических вопросов. Эти практические вопросы — отличный способ убедиться, что все учащиеся получают содержательную обратную связь. Albert.io не только объясняет все ответы на свои вопросы, но и объясняет, почему не должны были быть выбраны неправильные ответы.
Эти объяснения могут помочь учащимся выявить свои ошибки и извлечь из них уроки.
Если вам нравится объединять науку и STEM-образование, это занятие превосходно!
Это уникальная игра, в которой учащиеся должны провести космический шаттл через препятствия. Единственное предостережение заключается в том, что вам необходимо иметь MATLAB, но вы можете скачать MATLAB в виде 30-дневной пробной версии бесплатно. Упражнение обеспечивает полезную практику определения местоположения точек, определения наклона и использования наклона для решения точки пересечения по оси Y в форме точки пересечения наклона.
Этот интерактивный опыт под названием «Испытания на время черепах» наверняка понравится учащимся.
(Упрощаем выражение под знаком модуля.) .
)
Сравните два разных пропорциональных отношения, представленных по-разному. Например, сравните график «расстояние-время» с уравнением «расстояние-время», чтобы определить, какой из двух движущихся объектов имеет большую скорость.