Интересные задачи по математике 6 класс – 6
Логические задачи для 6 класса
Логические задачи для 6 класса с ответами
#1
В магазин доставили 6 бочонков с квасом, в них было 15, 16, 18, 19, 20 и 31 литр.
В первый же день нашлось два покупателя: один купил два бочонка, другой – три, причем первый купил вдвое меньше кваса, чем второй.
Не пришлось даже раскупоривать бочонки. Из шести бочонков на складе остался всего лишь один. Какой?
#2
Банка с медом весит 500 граммов. Та же банка с керосином весит 350 граммов. Керосин легче меда в 2 раза. Сколько весит пустая банка?
Ответ? Пустая банка весит 200 граммов#3
Товар на 10% подорожал, потом на 10% подешевел. Когда цена его была ниже: до подорожания или после подешевления?
Ответ? После подешевления товар стал на 1% дешевле, чем до подорожания#4
За 5 рублей куплено 100 штук разных фруктов.
Сколько фруктов каждого рода было куплено? Ответ? 1 арбуз (50 копеек), 39 яблок (3 рубля 90 копеек), 60 слив (60 копеек)
#5
Изделие весит 89,4 грамма. Сообразите в уме, сколько тонн весит миллион таких изделий
Ответ? Миллион изделий весит 89,4 тонны#6
Круглое бревно весит 30 килограммов. Сколько бы оно весило, если бы било вдвое толще, но вдвое короче?
Ответ? Бревно весило бы 60 килограммов#7
На чашечных весах 3 кубика и 1 морская раковина уравновешиваются 12 бусинами, а 1 раковина уравновешивается 1 кубиком и 8 бусинами.
Сколько бусин надо положить на свободную чашку весов, чтобы уравновесить раковину на другой чашке?
#8
В Древнем Риме философы-законники любили задавать друг другу такую задачу.
Вдова обязана оставшееся после мужа наследство в 3500 золотых разделить с ребенком, который должен родиться.
Если родится дочь, то мать получает двойную долю дочери.
Но случилось так, что родились близнецы – сын и дочь.
Как следует разделить наследство, чтобы были выполнены все требования закона? Ответ? Вдова должна получить 1000 золотых, сын – 2000 золотых, дочь – 500 золотых. Тогда требования закона будут выполнены, потому что вдова получит вдвое меньше сына и вдвое больше дочери.
#9
Четыре кошки и 3 котенка весят 15 килограммов, а 3 кошки и 4 котенка весят 13 килограммов.
Предполагается, что все взрослые кошки весят одинаково и котята также весят одинаково.
Сколько весит каждая кошка и каждый котенок в отдельности?
#10
Чтобы сжить с белого света Змея Горыныча, которому исполнилось 40 лет, Кощей Бессмертный придумал приучить его к курению.
До скольких лет доживет Змей Горыныч, если он не будет курить? Ответ? Некурящий Змей Горыныч проживет до 130 лет.
#11
Три яблока и 1 груша весят столько же, сколько 10 персиков, а 6 персиков и 1 яблоко весят столько же, сколько 1 груша.
Сколько же персиков надо взять, чтобы уравновесить 1 грушу?
#12
Напишите по порядку девять цифр: 1 2 3 4 5 6 7 8 9.
Сможете ли вы, не меняя порядка цифр, вставить между ними знаки плюс и минус таким образом, чтобы в результате получилось ровно 100?
#13
Как составить из четырех троек числа 1, 2, 3, 4, 6.
Ответ? Решение:1 = 33/33
2 = 3/3 + 3/3
3 = (3 + 3 + 3)/3
4 = (3*3 + 3)/
6 = (3 + 3)*3/3.
#14
Вы, конечно, знаете, что пятью тройками и знаками математических операций можно записать число 100: 33 – 3 + 3/3 = 100. Но можно ли записать пятью тройками число 10?
Ответ?Решение:
33/3 – 3/3 = 10
(3*3*3 + 3)/3 = 10
33/3 + 3/3 = 10.
#15
В вашем распоряжении пять двоек и любые знаки математических операций.
Вы должны с помощью только этого цифрового материала, используя его полностью и применяя знаки математических операций, выразить числа 15, 11, 12321
Решение:
(2 + 2)2 – 2/2 = 15
(2 * 2)2 – 2/2 = 15
22 + 2 – 2/2 = 15
22/2 + 2 * 2 = 15
22/2 + 22 = 15
22/2 + 2 + 2 = 15
22/2 + 2 – 2 = 11
(222/2)2 = 1112 = 12321.
aababy.ru
Игра «Занимательная математика» для учащихся 6-7 классов – TOП
Игра «Занимательная математика» для учащихся 6-7 классов
Автор: Чибизова Ольга Васильевна,
учитель математики в 5-11 классах
ГБОУ СОШ пос. Кировский,
Самарская обл, Красноармейский р-н, п. Кировский
Внеклассное мероприятие – игра “Занимательная математика” предназначено для учащихся 6-7 классов. Игру можно использовать при проведении недели математики между учащимися одного класса или между командами разных классов. Интересные задания на внимание, смекалку, воображение. В ходе конкурса принимают участие не только команды, но и болельщики. Игра развивает логическое мышление, учит принимать быстрое решение в нестандартной обстановке, воспитывает умение работать в команде.
Цель игры: закрепить знание по математике, развить догадку, эрудицию, пробудить математическую любознательность; развивать математические способности, сообразительность, логическое мышление, укреплять память учащихся.
| баллы | ||||||||||
| Задания | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Алгебраические задачи |
||||||||||
| Задачи на разрезание | ||||||||||
| Комбинаторные задачи |
||||||||||
| Логические задачи | ||||||||||
Учащиеся разбиваются на команды. Каждая команда выбирает капитана, придумывают название команды, связанное с математикой. Выбирают по очереди вопросы. Если одна команда затрудняется, то на помощь приходит вторая команда. Возможна помощь зала. Все очки суммируются. Команда, набравшая больше очков – ПОБЕДИТЕЛЬ.
Алгебраические задания
- Какое число делится без остатка на любое целое число, отличное от нуля?
- Чему равно произведение всех цифр?
- Три разных числа сначала сложили, а затем их же умножили. Сумма и произведение оказалась равными. Какие это числа?
- Слово, которым обозначается эта фигура, в переводе с греческого означает «натянутая тетива». Что это?
- В древности такого термина не было. Его ввел в XVII в. Французский математик Франсуа Виет, в переводе с латинского он означает «спица колеса». Что это?
- Баба – Яга варит волшебное зелье: к 1,5 кг мёда она добавила 100г волчьих когтей, 100г дёгтя и 300 г слёз кикиморы? Сколько % слёз кикиморы в этом зелье?
- Древнеегипетская задача.
Количество и его четвертая часть дают вместе 15. Найти количество. - В доме 6 этажей. Во сколько раз путь по лестнице на 6 этаж длиннее, чем на 3, если лестницы имеют одинаковое число ступенек?
- Найдите последнюю цифру в записи числа 250.
- Можно ли, имея два сосуда ёмкостью 3 л и 2 л, набрать из водопроводного крана 4 л воды?
Ответы на алгебраические задания
1) 0
2) 0
3) 1, 2, 3.
4) гипотенуза
5) радиус
6) 15 %
7) 12
8) в 2 раза
9) 4
10) Можно. Набираем 3 литра воды и переливаем в 2-литровый сосуд, затем выливаем 2л и переливаем 1 л в 2-литровый сосуд. Снова наполняем 3-литровый сосуд, получаем 4 л.
Логические задания
- Нильс летел в стае на спине гуся Мартина. Он обратил внимание, что построение стаи напоминает треугольник: впереди вожак, затем 2 гуся, в третьем ряду 3 гуся и т.д. Стая остановилась на ночлег на льдине. Нильс увидел, что расположение гусей на этот раз напоминает квадрат, состоящий из рядов, в каждом ряду одинаковое количество гусей, причём число гусей в каждом ряду равно числу рядов. Гусей в стае меньше 50.Сколько гусей в стае?
| 1. 35 | 2. 36 | 3. 37 | 4. 38. |
- Человек рассеянный лёг спать в 7.00 вечера в квартире на улице Бассейной, предварительно заведя будильник на 8.00 с тем, чтобы встать утром. Сколько часов он спал, пока его не разбудил будильник?
- В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 – в спортивном, а 10 ребят не посещают кружков вообще. Сколько тех, кто посещают оба кружка?
- Портной имеет кусок сукна в 16 метров, от которого он отрезает ежедневно по 2 метра. По истечении скольких дней он отрежет последний кусок?
- У мальчика сестер столько же, сколько и братьев, а у девочки братьев в три раза больше, чем сестёр. Сколько в семье братьев и сколько сестер?
- Пять друзей, встретившись, обменялись рукопожатиями. Сколько было всего сделано рукопожатий?
- Встретились три мальчика: Белов, Чернов, Рыжов.
– Вы только посмотрите, – воскликнул Белов,- у нас у всех разные волосы, и их цвет не совпадает с фамилией.
– Ты прав,- ответил ему черноволосый мальчик.
Определите цвет волос каждого мальчика?
- В семье четверо детей, им 5,8,13 и 15 лет. Детей зовут Аня, Боря, Вера, Галя. Сколько лет каждому ребёнку, если одна девочка ходит в детский сад, Аня старше Бори и сумма лет Ани и Веры делится на 3?
- У Иванова было несколько одинакового веса поросят и несколько ягнят также одинакового веса. Мальчик спросил Иванова, сколько весит один поросенок и один ягнёнок. Иванов ответил, что 3 поросёнка и 2 ягнёнка весят 22 кг, а 2 поросёнка и 3 ягнёнка весят 23кг. Как узнать, сколько весит один поросенок и один ягнёнок?
- Мама купила коробку кускового сахара. Дети съели верхний слой, состоящий из 77 кусочков. Затем они съели боковой слой, состоящий из 55 кусочков. Сколько кусочков сахара осталось в коробке?
Ответы на задания по логике
1) 2
2) 2
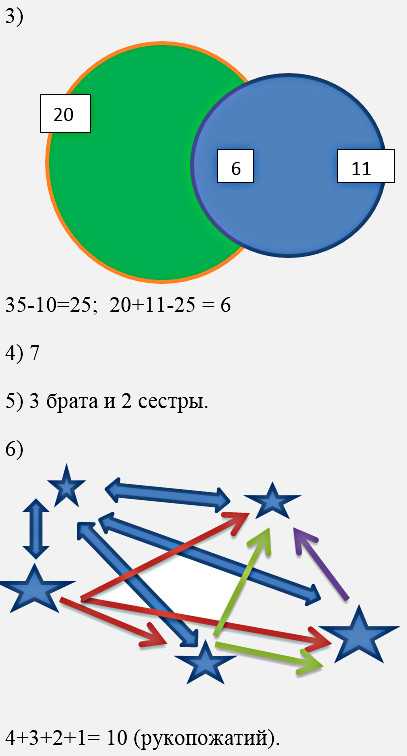
7) Белов –рыжий, Чернов –белый, Рыжов – черный.
8) Так как девочка ходит в детский сад, то Боре не 5 лет. Так как Аня старше Бори, то Ане 13 лет или 15 лет. Но сумма лет Ани и Веры делится на 3, поэтому Ане 13 лет, тогда Вере 5лет. Тогда так как Аня старше Бори, то Боре 8 лет. Гале остаётся 15 лет.
9) 3 поросёнка и 2 ягнёнка весят 22 кг,
а 2 поросёнка и 3 ягнёнка весят 23кг.
5 поросят и 5 ягнят весят 45 кг
1 поросёнок и 1 ягнёнок весят 9 кг
2 поросёнка и 2 ягнёнка весят 18 кг,
1 поросёнок – 4 кг
1 ягнёнок весит 5 кг
10) верхний слой: 7х11; боковой слой (оставш.) 11х5. Всего 7х11х6 = 462. Передний слой (оставш.): 5х6 = 30.
Осталось: 462-77-55-30= 300.
Комбинаторные задания
1) Турнир по боксу проходил по «олимпийской системе» (в каждом круге: проигравшие выбывают, отдыхающих нет). Сколько боксёров участвовало в турнире, если по окончании турнира выяснилось, что 32 человека выиграли боёв больше, чем проиграли?
2) Делится ли число 9! На 90?
3) В квадратном зале для танцев надо поставить вдоль стен 10 кресел так, чтобы у каждой стены стояло кресел поровну.
4) На столе лежат 3 спички. Добавьте к ним ещё 2, чтобы получилось 8.
5) На столе лежат 3 спички. Сделайте из них четыре.
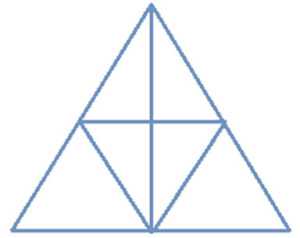
6) Сколь треугольников изображено на рис.
7) Плотники пилят брёвна на метровые куски. Отпиливание одного такого куска занимает одну минуту. За сколько минут распилят бревно длиной пять метров?
8) Один сапфир и два топаза
ценней, чем изумруд, в три раза.
А семь сапфиров и топаз
его ценнее в 10 раз.
Определить мы просим Вас,
Сапфир ценнее или топаз?
9) В фигуре, изображенной на рис., закрасьте некоторые клетки черным цветом, а остальные оставьте белыми так, чтобы у каждой белой клетки было ровно две черные соседки (по стороне), а у каждой черной клетки было ровно две белые соседки.
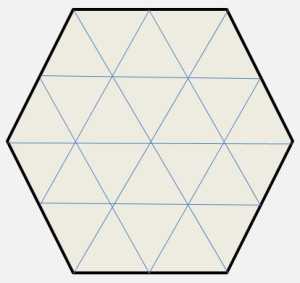
10) Какие числа являются делителем числа 21348?
Ответы на комбинаторные задания
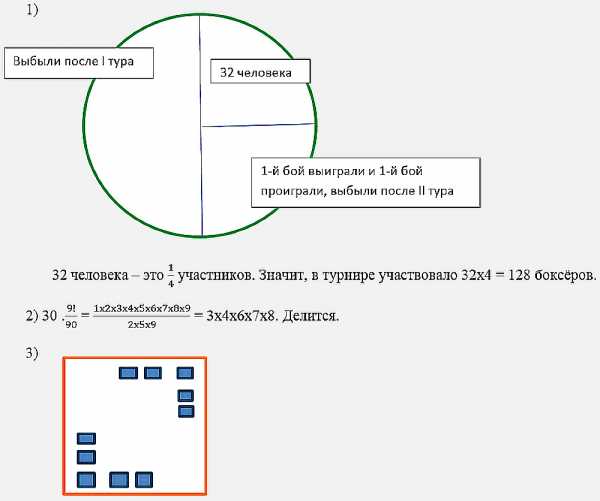
По два кресла у каждой стены и по одному в противоположных углах.
4) III – VIII.
5) III – IV .
6) 13 треугольников.
7) За 4 минуты.
8)Так как один сапфир и два топаза равны по стоимости 3 изумрудам,
то 8 сапфиров и 16 топазов равноценны по стоимости 24 изумрудам.
Так как семь сапфиров и топаз равны по стоимости 8 изумрудам,
то 21 сапфир и 3 топаза равноценны по стоимости 24 изумрудам.
А тогда, получается, что 13 сапфиров равноценны 13 топазам. А это означает, что сапфир и топаз равноценны.
9)

10) 21348-чётное, делится на 2. 2+1+3+4+8=18, по признакам делимости на 9 и на 3, 21348 – делится на 9 и на3. Отсюда следует, что оно обязательно делится 21348:2=10674, 7116, 2372.
Задачи на разрезание
1. Квадрат содержит 16 клеток. Разделите квадрат на две равные части так, чтобы линия разреза шла по сторонам клеток. (Способы разрезания квадрата на две части будем считать различными, если части квадрата, полученные при одном способе разрезания, не равны частям, полученным при другом способе). Сколько всего решений имеет задача?
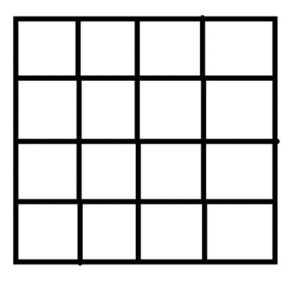
2. Разделить фигуру на четыре равные части так, чтобы линия разреза шла по сторонам квадратов.

- На что больше пойдёт краски: на окрашивание квадрата или этого необычного кольца?

- Арбуз разрезали на 4 части и съели. Получилось 5 корок. Может ли такое быть?
- На какое наибольшее число частей можно разрезать блин тремя прямолинейными разрезами? Сколько частей может получиться при трёх разрезах каравая хлеба?
- Какое наибольшее число полосок размерами 1х5 клеток можно вырезать из квадрата клетчатой бумаги 8х8 клеток?
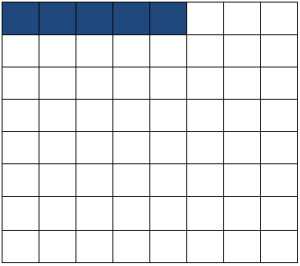
- Можно ли сложить квадрат какого-либо размера из деревянных плиток указанного на рис. вида, используя плитки обоих видов?


Ответы на задания: разрезания фигур
1.

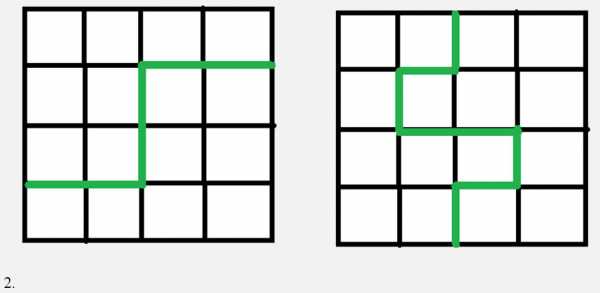
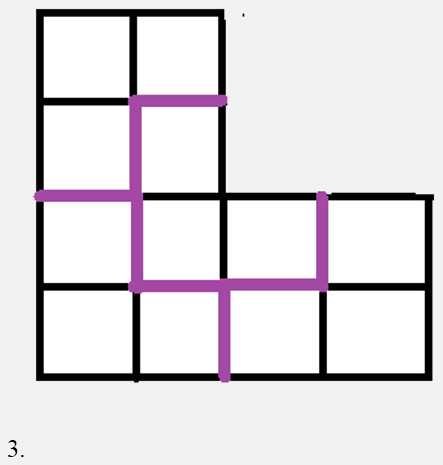


Если разрезать кольцо на части и сложить их, то получится квадрат. Поэтому краски на окрашивание квадрата пойдёт столько же, что и на окрашивание кольца.
- Да, если одна часть вырезана в виде «столбика», идущего через весь арбуз. У этого куска две корки, соединенные мякотью. Остальной арбуз можно разрезать на «нормальные»
- Блин можно разрезать на 7 частей (рис. а)
Каравай хлеба на 8 частей (рис. б)

6. 12 полосок

Да. Вначале составим прямоугольники 2х3, 2х4, затем полоску 2х7, а затем полоску 2х14. Семь таких фрагментов дают квадрат 14х14.
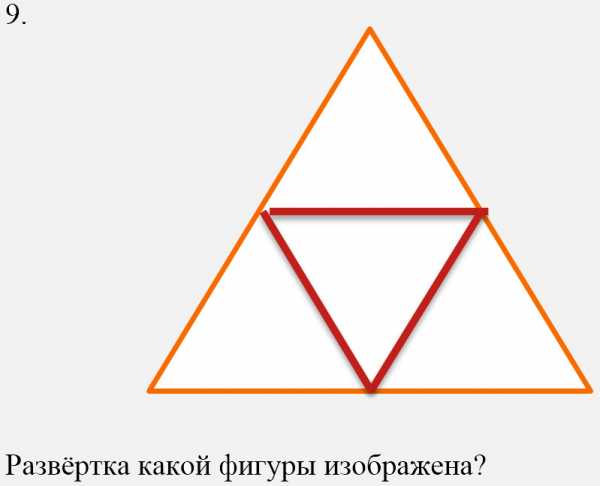
- Куб (гексаэдр).
- Пирамида (тетраэдр).
- Октаэдр.
xn—-8sb3aemcew1d.xn--p1ai
Решение занимательных задач по математике в 5–6-х классах с использованием дидактической игры
Разделы: Математика, Внеклассная работа
Класс:
#}Цель занятия:
- Реализация принципа умственного развития лицеистов;
- Развитие познавательной и творческой деятельности учащихся.
Задачи обучения:
- привить навыки самостоятельного поиска новых закономерностей;
- пробуждать их любознательность;
- формировать и развивать интерес лицеистов к занятиям математикой.
Задачи воспитания: содействовать эстетическому, трудовому воспитанию лицеистов, воспитывать сознательную дисциплину.
Задачи развития: развивать логическое мышление, память, учить грамотно проводить рассуждения, развивать культуру коллективного умственного труда.
Ход занятия1. Вступительное слово ведущего-учителя.
2. Игра “Счастливый случай”, состоящая из 5 геймов.
3. Подведение итогов игры, награждение
Оборудование:
- Плакат с названием геймов:
1 гейм “Дальше… дальше… дальше”
2 гейм “Заморочки из бочки”
3 гейм “Темная лошадка”
4 гейм “Гонка за лидером”
5 гейм “Лирическая мозаика” - Секундомер
- Бочка с бочонками
- Магнитофон с записью мелодии “Счастливый случай” (включается перед началом игры и каждым геймом)
- Плакат “Обдумай цель раньше, чем дело начать”
- Плакат “Видит око далеко, а ум еще дальше”
- Плакат “Математика + удача = Счастливый случай”
Вступление
Дорогие ребята и уважаемые взрослые! Я рада приветствовать вас всех на игре “Счастливый случай”.
Мой юный друг!
Сегодня ты пришел в этот класс,
Чтоб посидеть, подумать отдохнуть,
Умом своим на все взглянуть.
Пусть ты не станешь Пифагором,
Каким хотел бы, может быть,
Но будешь ты рабочим, а может быть ученым,
И будешь математику любить.
Вы не раз, ребята, принимали участие в разных играх, но в математической викторине “Счастливый случай” участвуете впервые. И для того, чтобы выиграть сегодня, не нужно забывать как говорят пословицы: “Обдумай цель раньше, чем дело начать”, “Видит око далеко, а ум дальше”.
Наши команды приготовились идти по нелегкому пути к победе. И сегодня они будут бороться не только за победу, но и за счастливый случай. И пусть Математика + удача принесут вам Счастливый случай.
Две команды, у каждой есть свое название.
- Разыграть, какая из команд начнет отвечать первой.
- В конце каждого гейма счетная комиссия объявляет итоговый результат каждой команды.
1 гейм “Дальше… дальше… дальше”
Каждая команда поочередно бросает игровой кубик (на пяти гранях кубика нанесены единицы, на одной грани – подкова):
1 – 1 балл за правильный ответ;
подкова – 3 балла за правильный ответ;
Каждая команда бросает кубик 6 раз.
Вопросы 1 команде:
- За 3 мин. бревно распилили на полуметровые бревна, причем каждая распиловка занимала 1 мин. Найти длину бревна. (2 мин)
- Тройка лошадей бежит со скоростью равной 15 км/ч. С какой скоростью бежит каждая лошадь? (15 км/ч)
- Во сколько раз путь по лестнице на 16-й этаж дома длиннее пути на 4-й этаж дома? (В 5 раз)
- Может ли сумма 4-х последовательных натуральных чисел быть простым числом? (Нет, она делится на 2)
- Лена произнесла предложение, которое являлось верным. Коля его в точности повторил, но оно уже было неверным. Какое предложение произнесла Лена? (Меня зовут Лена)
- 3 курицы за 3 дня снесут 3 яйца. Сколько яиц снесут
9 кур за 9 дней? (27 яиц)
3 куры за 1 день – 1 яйцо
9 кур за 1 день 9 яиц
9 кур за 3 дня – 27 яиц
Вопросы 2 команде:
- Пять ворохов сена и семь ворохов сена свезли вместе. Сколько получилось ворохов сена? (Один)
- Какими нотами можно измерить расстояние? (Ми-ля-ми)
- Волк и лиса соревновались в беге. Кто какое место занял, если известно, что волк был одним из первых, а лиса последней? (Лиса – 1, волк – 2)
- Какой цифрой заканчивается произведение всех нечетных двухзначных чисел? (Цифрой 5)
- За книгу заплатили 1 рубль и еще половину стоимости книги. Сколько стоит книга? (2 рубля)
- Если из одной стопки тетрадей переложить в другую 10 штук, то тетрадей в стопках будет поровну. На сколько в одной стопке тетрадей было больше, чем в другой? (На 20 штук)
2 гейм “Заморочки из бочки”
Шесть пронумерованных бочонков. Тянуть бочонки (3 раза). Начинает команда, у которой на данный момент меньше очков.
Ведущий зачитывает команде вопрос, номер которого указан на бочонке. За правильный ответ - 2 балла.
- Половина от половины равна половине. Найдите число (2)
- Число 30 легко выразить тремя пятерками 5*5+5=30. А как можно это число выразить другими тремя цифрами? (6*6-6=30, 33-3=30, 33+3=30)
- В коробке лежат карандаши: 4 красных и 3 синих. В темноте берут карандаши. Сколько нужно взять карандашей, чтобы в них было не менее 1 синего? (5)
- Известно, что один носорог весит 1 т 700 кг. Сколько носорогов сможет увезти машина грузоподъемностью 5 тонн? А сколько крокодилов сможет увезти все та же машина, если один крокодил 170 кг? (2 носорога, 9 крокодилов, т.к. 2 носорога уже в машине)
- Математик, оказавшись случайно в небольшом городке и желая хоть как-то убить время, решил подстричься. В городе имелось лишь два мастера, у каждого из них своя парикмахерская. Заглянув к одному мастеру, математик увидел, что в салоне грязно, сам мастер одет неряшливо, небрежно подстрижен. В салоне другого мастера было идеально чисто, а владелец был безукоризненно одет и аккуратно подстрижен. Поразмыслив, математик отправился к первому парикмахеру. Не могли бы вы объяснить причину столь странного на первый взгляд решения математика? (Поскольку в городе лишь два парикмахера, то каждый мастер вынужден стричься у другого. Математик выбрал того из мастеров, кто лучше подстриг своего конкурента.)
- Представьте число “2” в виде суммы четырех различных дробей, числители которых 1, а знаменатели натуральные числа. (1/1+1/2+1/3+1/6)
3 гейм “Темная лошадка”
Игра с командами. Им предлагается угадать, кто проведет этот гейм.
- она учитель лицея
- на “отлично” закончила среднюю школу
- на “отлично” закончила Уральский педагогический институт
- общительна
- любит петь
- умеет решать наитруднейшие задания по математике
- принимает участие, как член жюри, на городских олимпиадах, турнирах городов
(Лариса Степановна Тарасова)
Гость объясняет правила 3-го гейма.
Он загадывает имена великих математиков, читает наиболее известные факты из их биографии.
1 команде: Человек, который хотел быть и юристом, и философом, и офицером, но стал математиком. Он первый ввел в математику прямоугольную систему координат. (Декарт)
2 команде: Ученый, который нашел отношение длины окружности к диаметру. (Архимед)
1 команде: Кто написал знаменитое произведение “Начало”, которое сделало имя этого математика бессмертным? (Евклид)
2 команде: Ученый, который известен как создатель школы математиков. Он открыл замечательное свойство прямоугольных треугольников. (Пифагор)
На доске вывешиваются портреты великих математиков
Архимед Декарт
Пифагор Лобачевский
Евклид С. Ковалевская
Лицеистам заранее сообщают фамилии этих ученых для ознакомления с биографиями.
В 3-м гейме команды получают 5 баллов за правильный ответ.
4 гейм “Гонка за лидером”
Каждой команде задаются вопросы. За каждый правильный ответ команда получает один балл. Если в течение 3-х секунд после прочтения вопроса команда не дает никакого ответа, ведущий зачитывает правильный ответ и задает следующий вопрос. Вопросы задавать начинают той команде, у которой на данный момент меньше очков.
Вопросы для 1-ой команды:
- Какая разница между числом и цифрой? (10 цифр, чисел много.)
- Что называют биссектрисой угла? (Луч, выходящий из вершины угла и делящий угол пополам.)
- Сколько музыкантов в квартете? (4)
- Наименьшее натуральное число? (1)
- Как называется дробь, у которой числитель меньше знаменателя? (Правильная)
- Соперник нолика. (Крестик)
- Наука о числах, их свойствах и действиях над ними. (Арифметика)
- Сколько дней в летних каникулах? (92)
- Сотая доля числа. (Процент)
- Есть у уравнения и растения. (Корень)
- То, на что делят. (Делитель)
- Сколько получится десятков, если два десятка умножить на три десятка? (60)
- Делится ли число 111*121*131*141-151 на 10? (Да, т.к. оно оканчивается на ноль.)
- На лесопильном заводе каждую минуту машина отпиливает от бревна кусок в 1 м. Через сколько она распилит кусок в 6 м? (5 минут)
- Петух, стоя на одной ноге, весит 3 кг. Сколько он весит, стоя на двух ногах? (3 кг)
- Найдите модуль числа (-6). (6)
- 41 – это простое число? (Да)
- Какие прямые пересекаются под прямым углом? (Перпендикулярные)
- Формула для периметра квадрата. (Р=4а)
Вопросы для 2-ой команды:
- Излишек при нахождении частного. (Остаток)
- Записывается с помощью цифр. (Число)
- Отрезок, делящий круг пополам. (Диаметр)
- Он бывает натуральным. (Ряд)
- Число 666 увеличили в 1,5 раза, не производя над ним никаких арифметических действий. Какое число получили? (999)
- Какая мера длины была распространена на Руси? (Локоть, сажень)
- Сколько будет 52, 62, угол в квадрате? (90° )
- Сумма длин всех сторон треугольника. (Периметр)
- Трудный путь от условия к ответу. (Решение)
- Сколько пьес во временах года П. И. Чайковского? (12)
- Число противоположное 5. (-5)
- Другое название угломера. (Транспортир)
- Место, на котором стоит цифра в записи числа. (Разряд)
- Метод Эратосфена, в котором простые числа “отсеиваются” от составных. (Решето)
- Число, обратное 2. (1/2)
- Как называется верхняя часть дроби? (Числитель)
- Сколько концов у 3,5 палок? (8)
- Назовите число, “разделяющее” положительные и отрицательные числа. (0)
- Как называются прямые, которые не пересекаются? (Параллельные или скрещивающиеся)
5 гейм “Лирическая мозаика”
Каждой команде дается задание придумать четверостишие на заданные рифмы:
Остаток – недостаток
Свойство – устройство
Копейка – линейка
Число – весло
Куб – дуб
Скобка – коробка
Закон – дракон
2 балла за одно придуманное четверостишие.
В конце 5-го гейма подсчитывается общий итог игры. Победителям – медали в форме подковы. Другой команде – призы.
7.02.2005
urok.1sept.ru
Занимательные задачи – Математика – 6 класс
Урок №64 Класс: 6А,Б,В Дата:
Тема: Занимательные задачи по теме «Целые числа».
Цель: Привитие интереса к математике; популяризация среди учащихся занимательных задач, развитие познавательного интереса, интеллекта.
Задачи:
образовательные: закрепить ранее полученные знания по математике в новых условиях;
коррекционно- развивающие: развитие и коррекция внимания, логического мышления,
воспитательные: воспитание положительной мотивации к предмету, дисциплинированности, быстроты реакции.
Оборудование:
плакаты с названием команд, карточки с заданиями.
Ход занятия:
Учитель:– Добрый день, дорогие друзья! Сегодня у нас урок занимательной математики. Принимают участие 2 команды. В каждой команде есть капитан, есть названия команд.
Ученик 1.
Начинаем мы опять
Решать, отгадывать, смекать
Учитель:
Счётный конкурс открываю
Добрый день мои друзья!
Две команды на турнире
Их сейчас представлю я:
– Вот команда «Отличники» (хором говорит команда)
Девиз: Пусть узнает каждый школьник
Будут нам, сказать хочу,
Все заданья по плечу.
Учитель: Про команду № 2 (хором говорит команда)
Девиз: Разошлась уже молва
Называемся «Квадрат»
Нам любой учёный рад.
Учитель: Для подведения итогов игры требуется жюри в составе 3 учителей.
1конкурс. «Смекни-ка»
Для каждой команды приготовлено задание. Команды начинают считать одновременно. Жюри внимательно смотрит: кто быстрее справится и поднимет карточку, проверяют выполнение.
Задача 1:
Чтобы подняться на каждый этаж дома, надо пройти 30 ступенек лестницы. Сколько ступенек нужно пройти, чтобы подняться на третий этаж?
Ответ:60 ступенек.
Задача 2:
Шестиметровое бревно надо распилить на части, длина которых по 1 м. На отпиливание одной части тратится 2 мин. За сколько минут будет распилено все бревно?
Ответ: за 10 минут.
.
2 конкурс: « Веселые вопросы и тесты.
1.Каких камней на дне моря не найдешь?
(Сухих)
2. Какую ленту в косу не вплетешь?
( Пулеметную.)
3.На каких полях трава не растет?
( На шахматных )
4.Какую ветку не найдешь на дереве?
( Железнодорожную. )
5. Какие числа употребляются при счете? Ответ: С
природные;
естественные;
натуральные;
искусственные.
6. Какими бывают современные фотоаппараты? Ответ: А
цифровые;
числовые;
формульные;
дробные.
7. Что выкидывает человек, совершая какой-нибудь предосудительный, странный, смешной поступок? Ответ: С
цифру;
число;
номер;
формулу.
8. Что получается при делении чисел? Ответ: В
личное;
частное;
общественное;
коллективное
3 конкурс «Пословицы и поговорки.
Вставить нужные числительные в пословицы.
На семь бед ___ ответ. (1)
Одна голова хорошо, а ___ лучше. (2)
Семь раз отмерь, ___ отрежь. (1)
Один пашет, а ___семеро руками машут. (7)
Кто скоро помог, тот дважды___ помог. (2).
Не узнавай друга в три дня, узнавай в ___ года. (3).
Один с сошкой, а __семеро_ с ложкой. (7)
Сам не дерусь, __семерых_ боюсь. (7)
4 конкурс « Задачи- смекалки».
1. Сколько получается, если из наименьшего двузначного числа вычесть наибольшее однозначное?(1)
2. На сколько единиц меньше наибольшее однозначное число, чем наибольшее двузначное число? (90)
3. Произведение каких однозначных чисел дает число 5?( 1 и 5)
4. Назови два таких числа, чтобы их произведение и частное равнялось бы 17.
(1 и 17)
5.Две сардельки варятся 6 минут. За сколько сварятся 8 таких же сарделек?(За 6 минут)
6.Какие часы показывают верное время только два раза в сутки? ( Часы, которые остановились)
7.Самолет летит от Москвы до Санкт-Петербурга 1 час, а обратно то же расстояние пролетает за 60 минут. Почему такая разница? ( 1ч=60 мин)
8.В клетке находилось 4 кролика. Четверо ребят купили по одному из этих кроликов и один кролик остался в клетке. Как такое могло случиться?(Один кролик куплен с клеткой).
9.Сколько концов у десяти палок? А у десяти с половиной?(22)
10.Два отца и два сына съели три апельсина. По сколько съел каждый ?(по одному)
5 конкурс : «Найди пропавшие буквы»
Задание для 1 команды:
1.СММ (Сумма)
2.РДС (Радиус)
3.ЗДЧ (Задача)
Задание для 2 команды:
1.ГМТР (Геометрия)
2.КЛМТР (Километр)
3.ЧСТН (Частное)
6 конкурс «Блиц опрос».
Вопросы для 1 команды
Как называется результат сложения? (Сумма)
Наименьшее натуральное число. (Один)
Сколько минут в часе? (60)
Как называется треугольник, у которого две стороны равны? ( Равнобедренный)
Может ли в треугольнике быть два тупых угла? (Нет)
Как называется прибор для измерения углов? ( Транспортир)
На что похожа половина персика?( На вторую половину)
Как называется дробь, у которой числитель равен знаменателю? (Одна целая)
Чему равна сумма углов треугольника?(180 градусов)
Назовите наименьшее двухзначное число. (99)
Как называются прямые, которые не пересекаются на плоскости? ( Параллельные)
Сколько козлят было у многодетной козы? (7)
Соперник нолика. (Крестик)
Вопросы для 2 команды
1.Как называется треугольник, у которого все стороны равны? (Равносторонний)
2.Может ли в треугольнике быть два прямых угла?(Нет)
3.Как называется прибор для измерения отрезков? (Линейка)
4.Как называется часть дроби над чертой? (Числитель)
5.Чему равна сумма смежных углов? (180)
6.Как называется число, делящееся без остатка на 2? (Четное)
7.Как называются прямые, которые пересекаются под прямым углом? (Перпендикулярные)
8.Сколько музыкантов в квартете? (4)
9.Как называется сотая часть числа? (Процент)
10.Разделите 100 на половину. (50)
11.Как называется результат вычитания?(Разность)
12.Одна десятая дециметра равна 1…(1см)
13.При умножении любого числа на 1 получается 0? (Нет)
Конкурс 6: « Составь слова»
Задание для команд, из слова АРИФМЕТИКА составить другие слова, побеждает команда, составившая большее количество слов.
Жюри подводит итоги, а в это время задачи в стихах для зрителей:
1.Любит порядок мальчик Егорка.
Книги свои он расставил на полки
Девять книжек на одной и четыре на другой.
Сколько на двух полках книжек у Егорки?(13)
2.На лыжах в поход ребятишки идут
По полю и роще проходят маршрут.
Смотрите , какая кругом красота!
Весь путь прошагали за три часа.
Двенадцать всего километров прошли.
С какой они скоростью шли? (4 км)
Подведение итогов. Самые активные получают «5». Рефлексия (понравился ли урок, нарисуйте смайлик на полях).
Учитель: Слово жюри.
На этом наш урок завершается. Поздравляем команду с победой.
Но победителями оказались все, потому что каждый узнал что-то новое.
Спасибо всем участникам! И удачи в изучении математики!
Д/з.414, 415, 416.
multiurok.ru
Занимательные задачи для внеурочной деятельности 5-6 класс.
Занимательные задачи для внеурочной деятельности 5-6 класс.
Можно ли три яблока разделить между двумя отцами и двумя сыновьями так, что бы каждому досталось по одному яблоку?
Решение: Можно, т. к. их всего трое: дед (отец) – отец(сын) – сын.
Найти последние три цифры произведения всех натуральных чисел от 1 до 18.
Решение: 1*2*3*4*5*…*10*11*12*13*14*15*16*17*18 оканчивается тремя нулями, т. к. при умножении 2и5, 12и 15 в конце получается два нуля и ещё есть множитель 10.
В двух комнатах было 76 человек. Когда из одной комнаты вышло 30, а из второй 40 человек, то людей в комнатах осталось поровну. Сколько человек было в каждой комнате первоначально?
Решение: 76-(30+40)=6(чел.) – осталось в двух комнатах. 6:2=3(чел.) – осталось в каждой из двух комнат.
30+3=33(чел.) – было в одной комнате.
40+3=43(чел.) – было в другой комнате.
Электропоезд длиною 18 метров проезжает мимо километрового столба за 9с. Сколько времени ему понадобится, чтобы проехать мост длиною 36 метров?
Решение: 1) за 9 с. поезд проходит расстояние, равное своей длине, т. е. 18 метров. 18:9=2(м/с) – скорость поезда.
2) Чтобы проехать мост длиной 36 метров, поезд должен пройти: 36+18=54(м) 54:2=27(с)
Ответ: 27 секунд.
В классе учатся менее 50 обучающихся. За контрольную работу 1/7 учеников получили пятёрки, 1/3 – четвёрки, 1/2 – тройки. Остальные работы оказались неудовлетворительными. Сколько было таких работ?
Решение: Число учеников в классе меньше 50 и кратно 7 и 2 и 3. Это число 42.
1/7+1/3+1/2=14/42+6/42+21/42=41/42(всех учащихся) получили удовлетворительные оценки. Значит 1/42 всех учащихся получили неудовлетворительные оценки.
1/42 от 42: 1/42*42=1(ученик)
Ответ: одна неудовлетворительная работа.
Витя сказал своему другу Коле:
«Я придумал пример на деление, в котором делимое, делитель, частное и остаток оканчиваются соответственно на 1, 3, 5 и 7». Подумав, Коля ответил: «Что-то ты путаешь». Прав ли Коля?
Решение: Чтобы найти делимое при делении с остатком, нужно частное умножить на делитель и прибавить остаток. Т. к. делитель оканчивается на 3, а частное – на 5, то при умножении на конце будет цифра 5, и если к этому числу прибавить 7, то делимое будет оканчиваться на 2, а по условию на конце делимого стоит 1. Значит Коля прав.
Цифру 9, с которой начиналось трёхзначное число, перенесли в конец число. В результате получилось число на 216 меньше. Какое число было первоначальным?
Решение: Искомое число имело вид 900+а, после перестановки цифры 9 в конец числа, оно стало иметь вид 10а+9. По условию (10а+9) меньше (900+а) на 216. Составим уравнение:
(900+а) – (10а+9)=216
– 9а=-216 – 891
а=75. Искомое число 975.
-Однажды грибов я набрал! – Ели дотащил. Но тащил-то почти одну воду – в свежих грибах её 90%. А когда грибы высушили, то они стали на 15 кг легче. Теперь в них было 60% воды. Сколько грибов я принес домой?
Решение: х (кг) – грибов принёс из леса.
0,9 х (кг) – воды в грибах
(х-15)(кг) –грибов стало после сушки
(0,9 х-15)(кг) воды осталось в грибах
0,9 х-15(кг) составляет 60% от (х-15)(кг)
0,6(х- 15)=0,9х-15, х=20
Ответ: 20 кг грибов принёс я из леса.
На олимпийских играх наши спортсмены завоевали 96 медалей, из них 65 золотых и бронзовых, а золотых и серебряных – 61. Сколько золотых, серебряных и бронзовых медалей получили они в отдельности?
Решение: 96-65=31-серебряных медалей.
61-31=30- золотых медалей
65-30=35-бронзовых медалей
kopilkaurokov.ru
Занимательные задачи для 5-6 классов по математике
РЕШЕНИЕ ЗАНИМАТЕЛЬНЫХ ЗАДАЧ ПО МАТЕМАТИКЕ В 5–6-Х КЛАССАХ
Цель занятия:
Реализация принципа умственного развития лицеистов;
Развитие познавательной и творческой деятельности учащихся.
Задачи обучения:
привить навыки самостоятельного поиска новых закономерностей;
пробуждать их любознательность;
формировать и развивать интерес лицеистов к занятиям математикой.
Задачи воспитания: содействовать эстетическому, трудовому воспитанию лицеистов, воспитывать сознательную дисциплину.
Задачи развития: развивать логическое мышление, память, учить грамотно проводить рассуждения, развивать культуру коллективного умственного труда.
Ход занятия
1. Вступительное слово ведущего-учителя.
2. Игра “Счастливый случай”, состоящая из 5 геймов.
3. Подведение итогов игры
Бочка с бочонками
Магнитофон с записью мелодии “Счастливый случай” (включается перед началом игры и каждым геймом)
Плакат “Обдумай цель раньше, чем дело начать”
Плакат “Видит око далеко, а ум еще дальше”
Плакат “Математика + удача = Счастливый случай”
Вступление
Дорогие ребята и уважаемые взрослые! Я рада приветствовать вас всех на игре “Счастливый случай”.
Мой юный друг!
Сегодня ты пришел в этот класс,
Чтоб посидеть, подумать отдохнуть,
Умом своим на все взглянуть.
Пусть ты не станешь Пифагором,
Каким хотел бы, может быть,
Но будешь ты рабочим, а может быть ученым,
И будешь математику любить.
Вы не раз, ребята, принимали участие в разных играх, но в математической викторине “Счастливый случай” участвуете впервые. И для того, чтобы выиграть сегодня, не нужно забывать как говорят пословицы: “Обдумай цель раньше, чем дело начать”, “Видит око далеко, а ум дальше”.
Наши команды приготовились идти по нелегкому пути к победе. И сегодня они будут бороться не только за победу, но и за счастливый случай. И пусть Математика + удача принесут вам Счастливый случай.
Две команды, у каждой есть свое название.
Разыграть, какая из команд начнет отвечать первой.
В конце каждого гейма счетная комиссия объявляет итоговый результат каждой команды.
1 гейм “Дальше… дальше… дальше”
Каждая команда поочередно бросает игровой кубик (на пяти гранях кубика нанесены единицы, на одной грани – подкова):
1 – 1 балл за правильный ответ;
подкова – 3 балла за правильный ответ;
Каждая команда бросает кубик 6 раз.
Вопросы 1 команде:
За 3 мин. бревно распилили на полуметровые бревна, причем каждая распиловка занимала 1 мин. Найти длину бревна. (2 мин)
Тройка лошадей бежит со скоростью равной 15 км/ч. С какой скоростью бежит каждая лошадь? (15 км/ч)
Во сколько раз путь по лестнице на 16-й этаж дома длиннее пути на 4-й этаж дома? (В 5 раз)
Может ли сумма 4-х последовательных натуральных чисел быть простым числом? (Нет, она делится на 2)
Лена произнесла предложение, которое являлось верным. Коля его в точности повторил, но оно уже было неверным. Какое предложение произнесла Лена? (Меня зовут Лена)
3 курицы за 3 дня снесут 3 яйца. Сколько яиц снесут 9 кур за 9 дней? (27 яиц)
3 куры за 1 день – 1 яйцо
9 кур за 1 день 9 яиц
9 кур за 3 дня – 27 яиц
Вопросы 2 команде:
Пять ворохов сена и семь ворохов сена свезли вместе. Сколько получилось ворохов сена? (Один)
Какими нотами можно измерить расстояние? (Ми-ля-ми)
Волк и лиса соревновались в беге. Кто какое место занял, если известно, что волк был одним из первых, а лиса последней? (Лиса – 1, волк – 2)
Какой цифрой заканчивается произведение всех нечетных двухзначных чисел? (Цифрой 5)
За книгу заплатили 1 рубль и еще половину стоимости книги. Сколько стоит книга? (2 рубля)
Если из одной стопки тетрадей переложить в другую 10 штук, то тетрадей в стопках будет поровну. На сколько в одной стопке тетрадей было больше, чем в другой? (На 20 штук)
2 гейм “Заморочки из бочки”
Шесть пронумерованных бочонков. Тянуть бочонки (3 раза). Начинает команда, у которой на данный момент меньше очков.
Ведущий зачитывает команде вопрос, номер которого указан на бочонке. За правильный ответ – 2 балла.
Половина от половины равна половине. Найдите число (2)
Число 30 легко выразить тремя пятерками 5*5+5=30. А как можно это число выразить другими тремя цифрами? (6*6-6=30, 33-3=30, 33+3=30)
В коробке лежат карандаши: 4 красных и 3 синих. В темноте берут карандаши. Сколько нужно взять карандашей, чтобы в них было не менее 1 синего? (5)
Известно, что один носорог весит 1 т 700 кг. Сколько носорогов сможет увезти машина грузоподъемностью 5 тонн? А сколько крокодилов сможет увезти все та же машина, если один крокодил 170 кг? (2 носорога, 9 крокодилов, т.к. 2 носорога уже в машине)
Математик, оказавшись случайно в небольшом городке и желая хоть как-то убить время, решил подстричься. В городе имелось лишь два мастера, у каждого из них своя парикмахерская. Заглянув к одному мастеру, математик увидел, что в салоне грязно, сам мастер одет неряшливо, небрежно подстрижен. В салоне другого мастера было идеально чисто, а владелец был безукоризненно одет и аккуратно подстрижен. Поразмыслив, математик отправился к первому парикмахеру. Не могли бы вы объяснить причину столь странного на первый взгляд решения математика? (Поскольку в городе лишь два парикмахера, то каждый мастер вынужден стричься у другого. Математик выбрал того из мастеров, кто лучше подстриг своего конкурента.)
Представьте число “2” в виде суммы четырех различных дробей, числители которых 1, а знаменатели натуральные числа. (1/1+1/2+1/3+1/6)
3 гейм “Темная лошадка”
Игра с командами. Им предлагается угадать, кто проведет этот гейм.
она учитель лицея
на “отлично” закончила среднюю школу
на “отлично” закончила Уральский педагогический институт
общительна
любит петь
умеет решать наитруднейшие задания по математике
принимает участие, как член жюри, на городских олимпиадах, турнирах городов
(Лариса Степановна Тарасова)
Гость объясняет правила 3-го гейма.
Он загадывает имена великих математиков, читает наиболее известные факты из их биографии.
1 команде: Человек, который хотел быть и юристом, и философом, и офицером, но стал математиком. Он первый ввел в математику прямоугольную систему координат. (Декарт)
2 команде: Ученый, который нашел отношение длины окружности к диаметру. (Архимед)
1 команде: Кто написал знаменитое произведение “Начало”, которое сделало имя этого математика бессмертным? (Евклид)
2 команде: Ученый, который известен как создатель школы математиков. Он открыл замечательное свойство прямоугольных треугольников. (Пифагор)
На доске вывешиваются портреты великих математиков
Архимед Декарт
Пифагор Лобачевский
Евклид С. Ковалевская
Лицеистам заранее сообщают фамилии этих ученых для ознакомления с биографиями.
В 3-м гейме команды получают 5 баллов за правильный ответ.
4 гейм “Гонка за лидером”
Каждой команде задаются вопросы. За каждый правильный ответ команда получает один балл. Если в течение 3-х секунд после прочтения вопроса команда не дает никакого ответа, ведущий зачитывает правильный ответ и задает следующий вопрос. Вопросы задавать начинают той команде, у которой на данный момент меньше очков.
Вопросы для 1-ой команды:
Какая разница между числом и цифрой? (10 цифр, чисел много.)
Что называют биссектрисой угла? (Луч, выходящий из вершины угла и делящий угол пополам.)
Сколько музыкантов в квартете? (4)
Наименьшее натуральное число? (1)
Как называется дробь, у которой числитель меньше знаменателя? (Правильная)
Соперник нолика. (Крестик)
Наука о числах, их свойствах и действиях над ними. (Арифметика)
Сколько дней в летних каникулах? (92)
Сотая доля числа. (Процент)
Есть у уравнения и растения. (Корень)
То, на что делят. (Делитель)
Сколько получится десятков, если два десятка умножить на три десятка? (60)
Делится ли число 111*121*131*141-151 на 10? (Да, т.к. оно оканчивается на ноль.)
На лесопильном заводе каждую минуту машина отпиливает от бревна кусок в 1 м. Через сколько она распилит кусок в 6 м? (5 минут)
Петух, стоя на одной ноге, весит 3 кг. Сколько он весит, стоя на двух ногах? (3 кг)
Найдите модуль числа (-6). (6)
41 – это простое число? (Да)
Какие прямые пересекаются под прямым углом? (Перпендикулярные)
Формула для периметра квадрата. (Р=4а)
Вопросы для 2-ой команды:
Излишек при нахождении частного. (Остаток)
Записывается с помощью цифр. (Число)
Отрезок, делящий круг пополам. (Диаметр)
Он бывает натуральным. (Ряд)
Число 666 увеличили в 1,5 раза, не производя над ним никаких арифметических действий. Какое число получили? (999)
Какая мера длины была распространена на Руси? (Локоть, сажень)
Сколько будет 52, 62, угол в квадрате? (90° )
Сумма длин всех сторон треугольника. (Периметр)
Трудный путь от условия к ответу. (Решение)
Сколько пьес во временах года П. И. Чайковского? (12)
Число противоположное 5. (-5)
Другое название угломера. (Транспортир)
Место, на котором стоит цифра в записи числа. (Разряд)
Метод Эратосфена, в котором простые числа “отсеиваются” от составных. (Решето)
Число, обратное 2. (1/2)
Как называется верхняя часть дроби? (Числитель)
Сколько концов у 3,5 палок? (8)
Назовите число, “разделяющее” положительные и отрицательные числа. (0)
Как называются прямые, которые не пересекаются? (Параллельные или скрещивающиеся)
5 гейм “Лирическая мозаика”
Каждой команде дается задание придумать четверостишие на заданные рифмы:
Остаток – недостаток
Свойство – устройство
Копейка – линейка
Число – весло
Куб – дуб
Скобка – коробка
Закон – дракон
2 балла за одно придуманное четверостишие.
В конце 5-го гейма подсчитывается общий итог игры. Победителям – медали в форме подковы. Другой команде – призы.
Занимательные задачи по математике 1.В каждом из 4 углов комнаты сидит кошка. Напротив каждой из этих кошек сидят три кошки. Сколько всего в этой комнате кошек? 2. У отца шесть сыновей. Каждый сын имеет сестру. Сколько всего детей у этого отца? 3. В мастерской по пошиву одежды от куска сукна в 200 м ежедневно, начиная с 1 марта, отрезали по 20 м. Когда был отрезан последный кусок? 4. В клетке находятся 3 кролика. Три девочки попросили дать им по одному кролику. Каждой девочке дали кролика. И все же в клетке остался один кролик. Как так получилось? 5. 6 рыбаков съели 6 судаков за 6 дней. За сколько дней 10 рыбаков съедят 10 судаков? 6. На одном дереве сидело 40 сорок. Проходил охотник, выстрелил и убил 6 сорок. Сколько сорок осталось на дереве? 7.Два землекопа за 2 часа работы выкопают 2 м канавы. Сколько нужно землекопов, чтобы они за 100 часов работы выкопали 100 м такой же канавы? 8. Два отца и два сына разделили между собой 3 апельсина так, что каждому досталось по одному апельсину….
kopilkaurokov.ru
Подборка занимательных задач для 6
Занимательные задачи по математике 6 — 7 класс. Переправы и разъезды
Автор: Колпаков А.Н. on 10 августа 2011
Предлагаю небольшую подборку задач на реки и мосты, переправы и разъезды. Они не привязаны к программам 6 и 7 класса, поэтому репетитор по математике может использовать их в 5-ом и даже в 4-oм классе. Но все-таки совсем маленьким ученикам (даже олимпиадникам) большинство задач покажутся слишком трудными (из-за большого перебора вариантов). Я ориентировался на уровень развития среднестатистического шести — семиклассника с математическим и логическим складом ума. Для него задачи репетитора по математике покажутся и не только интересными, но и более доступными. Тренируйте мозги у своих учеников!
1) Знаменитая задача про волка, козу и капусту:
Фермеру необходимо переправить через широкую реку капусту, козу и волка. Но беда в том, что в лодке с человеком есть одно место или для капусты или для козу или для волка. Если фермер оставит козу с волком, то волк может съесть козу, а если оставить капусту с козой, то она съесть капусту. В присутствии фермера никто никого не ест. Подскажите ему способ переправы на другой берег?
2) Отряд солдат подошел к реке и задумал через нее переправиться. Однако мост оказался сломанным, а река очень глубокой. Рядом с берегом в лодке сидят 2 мальчика, но их лодка настолько маленькая, что на ней можно переправиться на другой берег или только одиному солдату или только двум мальчикам — не больше. Как им переправиться?
3) Три рыцаря у каждого из которых был свой оруженосец съехались на берегу реки, к которому была привязана двухместная лодка. Их лошади переправились вплавь, а людей ждала лодка. Но оруженосцы, словно сговорившись, не захотели оставаться на берегу в компании незнакомых рыцарей. Иговоры и угрозы не помогли. Тогда оруженосцы подумали и нашли способ переправиться не нарушая требование оруженосцев. Как они это сделали?
4) Можно ли рыцарям переправиться при этих же условиях, если съедутся 4 рыцаря и 4 оруженосца?
5) К реке подошли 4 рыцаря и 4 оруженосца, но лодка оказалась трехместной. Можно ли осуществить переправу с теми же условиями оруженосцев?
6) К берегу реки подошли 3 контрабандиста с двумя мешками золота каждый. У берега нашлась трехместная лодка в которую помещались любые три мешка, или контрабандист + 2 мешка, или 2 контрабандиста + 1 мешок или 3 контрабандиста. Каждый из преступников не может оставить ни один из своих мешков наедине с другими преступниками, но может их оставить на безлюдном берегу. Могут ли все они переправиться через реку?
7) Четыре рыцаря с оруженосцами хотят переправиться через глубокую реку на лодке без гребца, вмешающая не более двух человек. Недалеко от места переправы есть островок, на котором можно высаживаться. Как можно переправиться с условием, что нигде (ни на берегах, ни в лодке, ни на острове) ни один оруженосец не находился в компании чужих для него рыцарей?
8) Поезд M приближается к железнодорожной станции и его обгоняет быстро едущий поезд из города N, который нужно пропустить вперед. От главного пути, около станции, отходит боковая ветка — тупик, на которую временно можно оттащить вагоны с главного пути, но она так мала, что может вместить весь поезд M. Как можно пропустить поезд N вперед?
9) По речному каналу один за другим плывут три парохода: M;N и K. Навстречу им плывут еще три парохода, идущие также один за другим: P;H и E. Канал такой ширины, что два парохода не могут в нем разъехаться, но в конце одной из сторон канала есть карман в виде залива. В него можно отвести только один из пароходов. Могут ли эти пароходы разъехаться около этого кармана?
Дети с удовольствием решаю задачи предложенные репетитором математики, над которыми можно «думать рисунком». Объяснительные тексты к ним писать нет смысла, так как не хватит тетрадного листа. Достаточно нарисовать. К олимпиадным задачам они не относятся, а больше рассчитаны на развлечение и тренировку памяти, внимания и смекалки. Рисуйте и думайте на здоровье!
Колпаков Александр Николаевич. Репетитор по математике, Строгино
Задачи на разъезды прислал мой коллега Александров Григорий Павлович репетитор по математике. Москва, Митино.
Автор: Колпаков А.Н. on 18 декабря 2010
На этой странице сайта «профессиональный репетитор по математике» вы найдете подборку задач на логику высказываний, на перебор и сортировку вариантов, на доказательство и на рассуждение. Такие задачи учат ребенка анализировать условия и делать выводы, обосновывать факты и явления. Репетитор по математике может использовать эти материалы в своей работе с учениками не младше 5-6 класса. Список задач будет постепенно пополняться.
1) Имеется 25 городов. Известно, что из каждого города в другие города ведут как минимум 12 дорог. Докажите, что из каждого города можно проехать в каждый.
2) В марсианском метро 101 станция и 5000 перегонов между ними. Докажите, что можно добраться с любой станции до любой станции.
3) В соревнованиях по лыжным гонкам участвовали 3 лыжника: Антонов, Володин и Степанов. Перед дистанцией один зритель сказал, что первым придет Антонов, второй зритель сказал, что Степанов не будет последним, а третий зритель предсказал, что Володин не будет последним. После забега выяснилось, что угадал всего лишь один зритель, а другие ошиблись. В каком порядке лыжники пришли к финишу?
4) Варя сказала, что на ее день рождения пришли больше шести подруг. А ее сестра сказала, что подруг было больше пяти. Сколько подруг пришло к Варе, если из двух этих утверждений одно истинное, а другое ложное?
Здесь представлены примеры логических задач для 5-го, 6-го и 7-го класса. Это рекомендуемый возраст для знакомства с приемами их решения, так как в более ранний период жизни ребенок чаще всего еще не способен ни анализировать информацию на несколько шагов вперед, ни мыслить абстрактно. Вместе с этим критический вид деятельности у него не является основным средством познания. В 8-ом классе и старше я бы не советовал репетиторам увлекаться такими задачами из-за их очевидного отклонения от содержания программы. Есть куда более важные направления для развития ученика.
Колпаков Александр Николаевич, репетитор по математике Москва, Строгино.
Автор: Колпаков А.Н. on 15 ноября 2010
Репетиторам по математике, а также ученикам, проявляющим интерес к математике, предлагается подборка задач олимпиадного уровня на часы, даты и календарь. Список задач регулярно пополняется. Большинство из этих задач отобрано мной именно для работы с шести-семиклассниками, однако некоторые из них репетитор по математике может предложить ученикам уже 5-ом классе. У задач нет четкой возрастной принадлежности и единственным требованием к пониманию их решения, кроме способностей удерживать в голове все расуждения, является умение выполнять действия с дробями. Уровень задач соответствует уровню малого мехмата МГУ, второй математической школы, Курчатовской школы и др.
1) Найдите самое большое количество пятниц в году?
2) Может ли в каком-либо месяце быть 5 понедельников и 5 четвергов?
3) В одном месяце три сестры пришлись на четные числа. Какого числа в этом будет второе воскресенья?
4) Какой сегодня день недели, если известно, что когда послезавтра станет вчера, то сегодня будет также далеко от воскресенья, как тот день, который был сегодня, когда вчера было завтра?
5) Человек родился 7 января 40 года до нашей эры, а умер 7 января 50 года нашей эры. Сколько лет он прожил?
6) Найдите угол в градусах между минутной и часовой стрелкой в 8ч 30мин.
7) Найдите угол в градусах между минутной и часовой стрелкой в 18ч 15мин.
8)*Совешание у директора завода началось между 6 и 7 часами вечера, завершилось между 9 и 10 часами. Требуется найти точное время начала и окончания этого совещания, если за его время часовая и минутная стрелки
поменялись местами.
9)*Дима начал выполнять домашнее задание репетитора по математике между 4 и 5 часами вечера, когда его часов совпадали, а закончил работу, когда часовая стрелка оказалась напротив минутной (по одной прямой). Надите сколько минут Дима выполнял задание репетитора и в котором часу он его сделал?
Автор: Колпаков А.Н. on 7 ноября 2010
Вашему вниманию предлагается подборка задач на определение фальшивых монет путем взвешивания на чашечных весах без гирь. Данный тип задач очень распространен и обычно используется репетиторами по математике на развивающих занятиях со способными школьниками разного возраста. Никакой математической нагрузки задачи на взвешивание не несут. Их назначение — развитие абстрактного мышления, тренировка памяти, внимания, обучение построению алгоритмов и планов решений не отягощенных математикой. Учитывая оторванность задач от программ учебников, репетитор по математике может предлагать работать с монетами произвольно и в любой период учебы ребенка. Единственный критерий их отбора — количество взвешиваний, необходимых репетитору для демонстрации решений. В данном списке большинство задач требует более двух взвешиваний и поэтому редко доступны для самых маленьких.
1) Имеется 6 одинаковых настоящих монет и еще одна фальшивая, которая легче остальных. Как на чашечных весах без гирь найти эту фальшивую менету? Опишите порядок взвешиваний.
2) Теперь у нас 7 настоящих монет и еще одна фальшивая, также более легкая остальных. Как найти фальшивую монету за два взвешивания ?
3) Как из 10 монет, среди которой тоже есть фальшивая определить ее за три взвешивания?
4) А теперь попробуйте из 16 монет обнаружить фальшивую не более чем за 3 взвешивания.
5) Задача усложняется и теперь перед нами 17 монет, а количество взвешиваний опять не более чем три.
6) А вот у нас уже 20 монет вместе с фальшивой, как всегда более легкой. Нужно потратить не более 3-х взвешиваний для ее вывления. Как надо их выполнить?
7) Монет 26 штук, одна фальшивая. Взвешиваний опять не более трех. Как найти эту фальшивую монету?
8) Из 27 монет одна фальшивая. как ее найти снова за три взвешивания?
9) Теперь у нас всего 28 монет вместе с одной фальшивой. Как ее найти за 4 взвешивания?
10) Имеется 40 монет среди которых какие-то две монеты фальшивые. Определите за 2 взвешивания 20 настоящих монеты.
11) А сможете ли вы из 82 монет среди которых одна более легкая (фальшивая) найти наименьшее число взвешиваний, которое потребуется для ее определения?
12) И наконец перед нами 11 настоящих монет и еще одна фальшивая. Надо потратить не более четырех взвешиваний.
infourok.ru
