4.4
Средняя оценка: 4.4
Всего получено оценок: 394.
4.4
Средняя оценка: 4.4
Всего получено оценок: 394.
Луч – это одно из основных базовых построений наравне с точкой и прямой. Изучение луча в курсе математики 5 класса дает начало другим важным темам: системам координат и углам на плоскости.
Луч это прямая, ограниченная с одной стороны. Это определение лучше усвоится, если выучить свойства луча:
Правильное обозначение луча спорный вопрос. Наиболее правильный вариант это две точки, например ОА. Причем первой точкой обозначают начало луча. Но также обозначают отрезки и прямые, поэтому чаще пишут луч с началом в точке О.
Рис. 1. Луч.Углы – это единственные фигуры, состоящие из лучей.
Что такое угол? Это геометрическая фигура, состоящая из двух лучей, начало которых лежит в одной точке. В фигурах углы состоят из отрезков, а не из лучей.
Может случиться ситуация, когда оде стороны угла будут совпадать, тогда говорят, что величина угла равна 0 градусов. Может получиться и так, что обе стороны угла образуют прямую, тогда говорят, что угол равен 180 градусам. Такой угол называют развернутым, а лучи основным и дополнительным.
Величина угла отражает поворот одного луча относительно другого.
Еще одно применение лучей это различные системы координат. В математике 5 класса первой темой идет изучение координатной прямой. Это два луча с углом поворота в 180 градусов. Начало лучей обозначается за нулевую точку или начало отчета. Влево от начала отчета откладываются отрицательные координаты, в право-положительные. Другое название координатной прямой: числовой луч.
Рис. 2. Координатный луч.С помощью координатного луча удобно сравнивать дроби и таким образом решать неравенство.
С помощью координатных лучей создается и координатная плоскость. Так называемая декартова система координат состоит из двух координатных прямых или 4 лучей. Подобная система позволяет определять положение точки на плоскости, вычерчивать графики функций и графически решать разного рода уравнения.
Помимо декартовой системы существует полярная система координат. В полярной системе используются понятия угла и координатной прямой. Координатная прямая определяет положение точки, а угол степень ее подъема над осью.
Полярная система координат одна из самых древних в истории человечества. Так сложилось, что именно пользуясь этой системой, древние мореплаватели покоряли неизвестные просторы нашего мира. Декартова система появилась гораздо позднее. Но она более удобна для ориентации на местности. Декартову систему проще использовать как в разделах математики, так и других дисциплинах: физике, теплотехнике, гидравлике и программировании.
Декартовая система четырьмя лучами делиться на 4 четверти, положение точки в каждой из которых определяется знаком координат.
Координаты подразделяют на абсциссы и ординаты. Проще говоря на х и у. Например точка (3, 4) имеет две положительные координаты, а значит она будет находиться в первой четверти. Обе отрицательные координаты соответствуют третьей четверти, положительный у при отрицательном х это вторая четверть, а отрицательный у при положительном х – четвертая.
Чтобы построить точку в декартовых системах координат необходимо от деления числового луча, соответствующего координате, поднять перпендикуляр. Координаты две, значит и перпендикуляров будет два. Точка их пересечения и будет искомой точкой.
Числовая прямая – это луч, с нанесенными на него числами или интервалами чисел. Числовую прямую используют для сравнения дробей, рисунков к задаче и нахождения ОДЗ функции. Последнее встречается чаще всего.
Фигурной скобкой на прямой обозначается область, в которую не могут попадать корни. После решения уравнения, найденные корни наносятся на числовую прямую. Попавшие в фигурную скобку недопустимых значений корни исключаются из решения.
Мы узнали, что такое луч и числовая прямая. Поговорили о фигурах, составленных из лучей и системах координат, где применяются числовые прямые. Проработали вопрос наглядности изображения нужных точек и разобрались с тем, как правильно проставлять координаты на координатном луче.
Доска почёта
Чтобы попасть сюда – пройдите тест.
Артём Закутний
8/10
Антон Кабашный
8/10
Дария Петроченко
9/10
Валик-Ти Кукурузов
7/10
Виктор Финякин
7/10
Александр Барсов
10/10
Юля Александрова
8/10
Вова Свистельников
7/10
Наталия Левина
8/10
Марина Молодцова
6/10
4.4
Средняя оценка: 4.
4
Всего получено оценок: 394.
А какая ваша оценка?
Рейтинг: 5 / 5
Оценок: 1
Тестовые задания для 5 класса по теме: Прямая, отрезок, луч.
Правильный вариант ответа отмечен знаком +
1. Сколько существует отрезков, соединяющих две точки?
1) 0 –
2) 1 +
3) 2 –
4) бесконечное множество –
2. Какое количество отрезков с началом в точке A можно провести на данном рисунке?
1) 1 –
2) 3 –
3) 5 +
4) 7 –
3.
Выберите правильно обозначенную прямую на рисунке:
1) 1 –
2) 2 –
3) 3 +
4) 4 –
4. На плоскость нанесена точка E. Сколько прямых можно провести через эту точку?
1) 0 –
2) 1 –
3) 2 –
4) бесконечное множество +
1) MK, ML, NM, KN, LK, NL +
2) MK, KL, LN, NM –
3) KM, LL, NM, MK, MN, KN –
4) ML, KN, LM, NK –
6. Выберите вариант, где верно перечислены все отрезки, изображённые на рисунке:
1) KS, ST, TO –
2) KS, TK, SO, ST –
3) SK, SO, TS, KT, OT –
4) SK, SO, TK, OT, TS, OK +
7. На сколько частей две параллельные прямые делят плоскость?
1) 1 –
2) 2 –
3) 3 +
4) бесконечное множество –
8. Сколько точек пересечения у прямых a и b, изображённых на рисунке?
1) 0 +
2) 1 –
3) 2 –
4) бесконечное множество –
9.
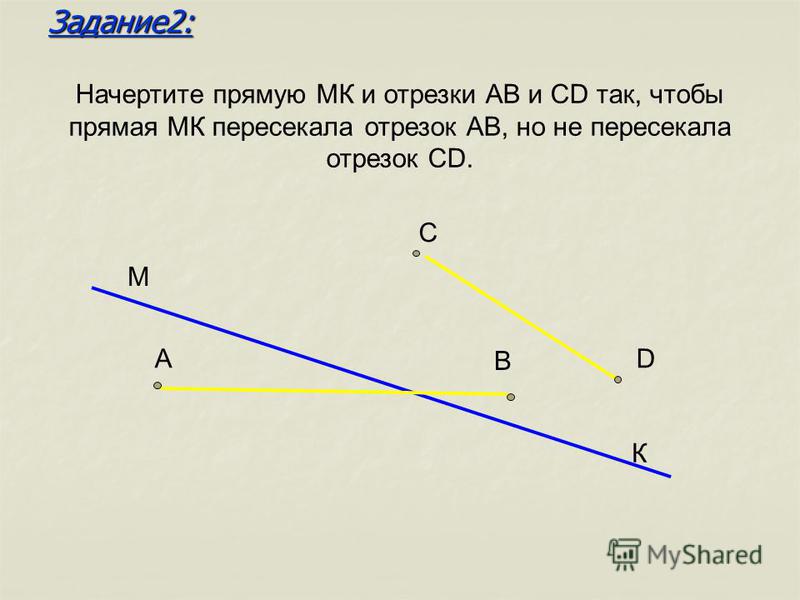На прямой отмечены три точки: D, K, P. Какое название прямой невозможно в этом случае?
1) PK –
2) DP –
3) KP –
4) DD +
тест 10. На данном рисунке пересекаются:
1) луч и отрезок –
2) луч и прямая +
3) отрезок и отрезок –
4) луч и луч –
11. Выбери вариант, где верно рассчитано число отрезков, изображённых на рисунке:
1) 4 –
2) 5 –
3) 8 –
4) 10 +
12. Выберите рисунок, на котором представлен луч:
1) 1 –
2) 2 –
3) 3 –
4) 4 +
13. На сколько частей прямая делит плоскость?
1) 0 –
2) 1 –
3) 2 +
4) бесконечное множество –
14. Выберите вариант ответа, в котором верно записаны все лучи, получившиеся при пересечении прямых AB и CD.
1) AB, CD –
2) OA, OD, AB –
3) OA, OC, OB, OD +
4) BO, AD, DO, CO –
15.
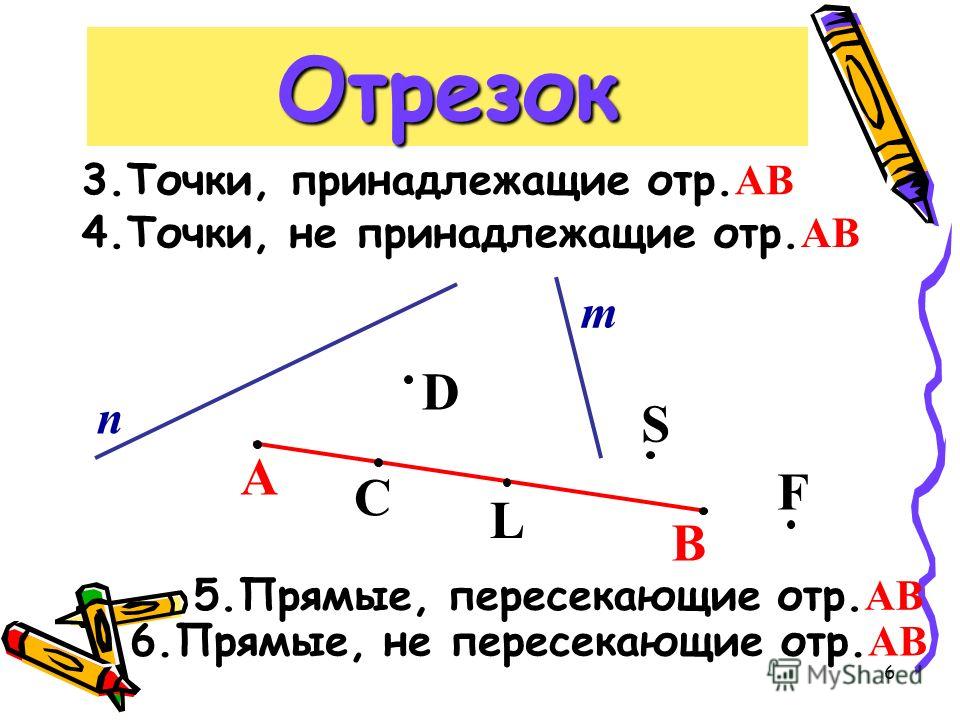Рассмотрите рисунок. Выберите луч, который не выходит из точки O.
1) TO –
2) EO –
3) EL +
4) OK –
16. Пусть на плоскости проведены две пересекающиеся прямые. На сколько частей разделилась плоскость?
1) 1 –
2) 2 –
3) 4 +
4) бесконечное множество –
17. Как много отрезков выходит из точки E судя по рисунку?
1) 1 –
2) 2 –
3) 4 +
4) бесконечное множество –
18. Найдите точку, принадлежащую лучу AM:
1) P –
2) K +
3) N –
4) Z –
19. Сколько букв необходимо для обозначения отрезка?
1) 1 –
2) 2 +
3) 3 –
4) обозначается словом –
тест-20. Сколько лучей представлено на рисунке?
1) 1 –
2) 2 –
3) 4 +
4) бесконечное множество –
21. На рисунке изображены прямые. Найдите количество точек их пересечения.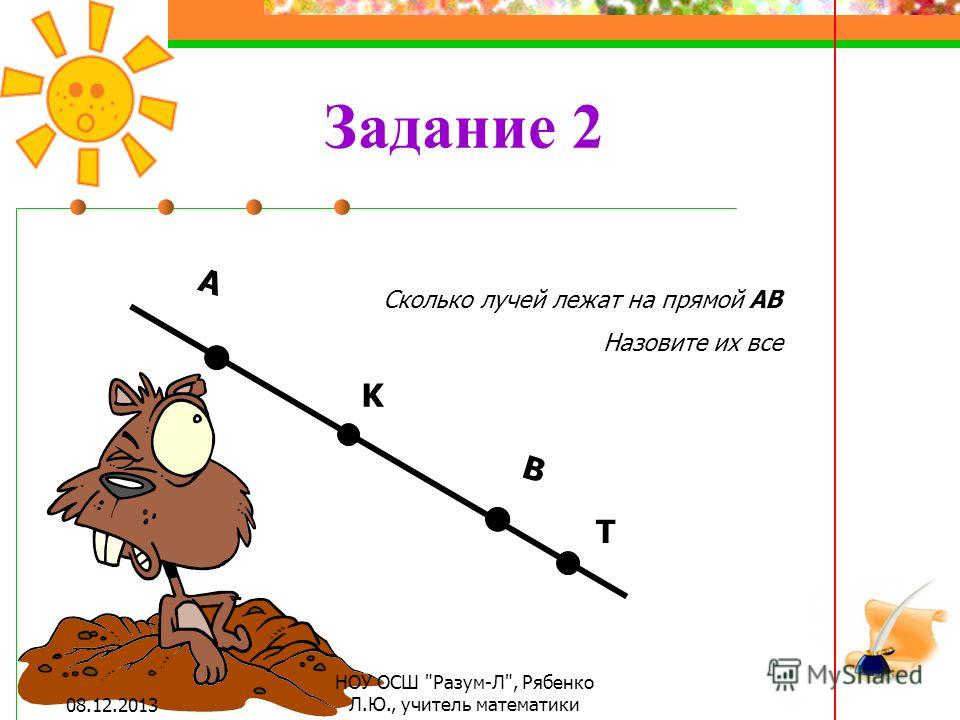
1) 1 –
2) 2 –
3) 3 +
4) 4 –
22. Сколько образуется лучей, если поставить на прямой точку?
1) 0 –
2) 1 –
3) 2 +
4) бесконечное множество –
23. Из скольких отрезков состоит данная фигура?
1) 3 –
2) 4 –
3) 6 +
4) 8 –
24. Какая геометрическая фигура представлена на рисунке?
1) луч +
2) прямая –
3) отрезок –
4) ломаная –
25. Сколько точек пересечения имеют две пересекающиеся прямые?
1) 0 –
2) 1 +
3) 2 –
4) бесконечное множество –
26. Какой вариант ответа верно описывает отрезки TS и PS на рисунке?
1) равные –
2) параллельные –
3) острые –
4) пересекающиеся +
27. Какая из точек, обозначенных на рисунке, лежит на прямой KM?
1) Z –
2) D –
3) P +
4) E –
тест_28.
Какое количество точек лежит на произвольной прямой?
1) 0 –
2) 1 –
3) 2 –
4) бесконечное множество +
OBISHIKEIKI
OBISHIKEIKI
[Характеристики]
· Это широкий продукт, который можно использовать с уровнем или чем-то подобным, расположенным сверху.
· В качестве эталонной поверочной линейки оптимально подходит для параллельных и прямых измерений.
· Для проверки точности работы машин, сборки прецизионных машин, эталона по установке турбин электростанций, проверки и т. д.
· Этот продукт имеет прямолинейность и параллельность (неравная высота JIS), соответствующие стандартам JIS (JIS B 7514) для прямые правители.
· Незатвердевший продукт.
· Прочный ящик для хранения, который также можно использовать для транспортировки
| Номер детали |
|---|
| ЭД201 |
| Номер детали | Скидка за объем | Дней до отгрузки |
|---|---|---|
| 9003 30 дней |
Загрузка. ..
| Модель продукта | Линейка | Угол (°) | 180 | Длина (мм) | 1000 |
|---|---|---|---|---|---|
| Ширина (мм) | 50 | Высота (мм) | 85 | Прямолинейность/параллельность (мкм) | 6 |
| Масса (кг) | 16 | Функция | Для проверки точности работы механизмов, сборки прецизионных машин, установки турбин электростанций и т. д. Этот продукт имеет прямолинейность и параллельность (неравная высота JIS), соответствующие стандарту JIS (JIS B 7514) для прямых линеек. | Дополнение | Прочный ящик для хранения, который также можно использовать для транспортировки. |
Примечания к продукту: Пожалуйста, ознакомьтесь со спецификацией продукта, чтобы узнать номер детали ED201 на балочной линейке класса A. Модель ED201 включена в наши предложения для станочных угольников OBISHIKEIKI и в нашу полную линейку продуктов OBISHIKEIKI.
RIKENKEISOKUKI
RIKENKEISOKUKI
[Характеристики]
· Высокоточная линейка, которую можно использовать для проверки плоскостности, прямолинейности, параллельности и т. д. прецизионный уровень (ширина уровня 30-50 мм).
· Quenched product (quenched hardness of 60 Hs or greater)
| Part Number |
|---|
| RSHW-1000Y |
| RSHW-1500Y |
| RSHW-2000Y |
| Номер детали | Скидка за объем | Количество дней до отгрузки | Общая длина (мм) | Высота (мм) | Прямолинейность (мм) | Масса (кг) |
|---|---|---|---|---|---|---|
5 дней | 1000 | 80 | ±0,006 | 13 | ||
| 6 | 1500 | 100 | ±0,008 | 30 | ||
5 Days | 2000 | 120 | ±0.010 | 45 |
Loading…
| Product Type | Линейка | Угол (°) | 180 | Ширина (мм) | 50 |
|---|
MISUMI использует файлы cookie для предоставления вам услуг и улучшения этого веб-сайта.