Тема: Плоскость. Прямая. Луч. ( Дата 19.09 Класс 5а )
Тип урока: изучение нового материала
Цели:
Предметные
– познакомить учащихся с геометрическими фигурами : плоскость. прямая. луч ;
– научить распознавать на рисунках эти фигуры, а в окружающем мире – объекты, для которых плоскость. прямая. луч являются моделями.
Личностные
– проявлять интерес к изучению темы и желание применять приобретённые знания и умения.
Метапредметные
– формировать умение видеть математическую задачу в контексте проблемной ситуации, в окружающей жизни.
Планируемые результаты: учащиеся научаться распознавать на чертежах геометрические фигуры: плоскость. прямая. луч.
Основные понятия: плоскость. прямая. луч.
Организационная структура урока.
1.
Ну-ка, проверь, дружок!
Готов ли ты начать урок?
Всё ль на месте? Всё ль в порядке?
Книжка, ручка и тетрадка…
Проверили? Вот здорово!
К уроку всё готово!
2 Активизация знаний обучающихся.
Верным помощником на уроке у нас будет самая маленькая геометрическая фигура
“Весёлая точка”.
№1 Прочитайте числа: 180000509, 300001700, 608600005003(фронтально)
№2 Какое число нужно вписать в последнюю клетку?(индивидуально по цепочке)
№3 Выразите в дециметрах: 50 см, 230 см, 67 м, 800 м. (фронтально)
Выразите в метрах : 600
см, 30 дм, 2 км, 12000 мм.
3. Мотивация урока. Анаграммы. Просмотр презентации.
Расшифруйте слова: КОСТЬПЛОС, МАЯПРЯ, РЕЗООТК, КАТОЧ, ЧУЛ, ТКИНИ.
-Это слова”плоскость”, «прямая», «отрезок», «точка», «луч», «нитки».
-Все ли расшифрованные слова вам знакомы?
-А где вы с ними встречались?
(На уроке математики, а нитки на уроке труда).
-Какое слово лишнее?
(Нитки. Они не относятся к уроку математики).
-Но все эти слова сегодня помогут нам сделать открытие.
Сообщение темы и цели урока.
-Рассмотрите фигуры на доске.
– Какую из этих фигур вы уже знаете?(отрезок)
– В какие группы фигуры можно объединить?
(В ходе рассуждения можно разбить на 3 группы: мы рассмотрим «отрезки» )
-Но возникает проблема: куда можно отнести фигуры 1, 3 и 4?
4. Изучение нового материала.
– понятие плоскости (с. 27-28 рассмотреть на окружающих примерах)
– Сравните фигуры с уже известными нам отрезком
-Что можно сказать?
-Можно ли эту фигуры назвать отрезком? Почему?
-Тогда давайте выполним одну операцию.
-В руках у меня 2 катушки тесьмы. Мы раздвигаем их в разные стороны.
-Что заметили?
(Это прямая линия, только в воздухе)
-Можно ли её продолжить в обоих направлениях?
-А эту прямую можно изобразить на доске?
(Чертим на доске, а дети в тетради).
А
а
В
Без начала и без края линия прямая,
Хоть 100 лет по ней идти,
Не найдёшь конца пути.
(Эта геометрическая фигура – прямая)
– У людей есть имена, у животных клички.
-А прямую линию можно обозначить одной или двумя буквами.
– Предложите имя прямой линии.
Вывод: У прямой линии нет ни начала, ни конца.
Мы можем изобразить только маленькую часть прямой линии. Её можно продолжить.
-Наша Весёлая Точка поможет нам ещё
поработать с прямой линией.
-Поставьте точку, проведите через неё прямую линию.
-Можно ещё провести линию через эту точку?
-Сколько прямых линий можно провести через одну точку?
-Поставьте 2 точки. Через эти точки проведите прямую линию. Можно ли ещё провести?
А К
Вывод: Через одну точку можно провести сколько угодно линий, а через 2 точки – только одну.
-Теперь нашу прямую линию я разрежу.
(К месту разреза прикреплю Солнышко).
-Что получилось?
-На что похоже?
(Луч солнца)
О новой фигуре разносится весть
Конца пусть в ней нет,
Начало-то есть!
И солнце, тихонько взойдя из-за туч,
Сказало: «Друзья, назовём его луч!»
-Можно ли продолжить луч со стороны разреза?
(Нет, мешает круг и нечего продолжать)
-А с другой стороны?
(Можно продолжить до бесконечности)
СРАВНИТЕ: Луч и прямую линию.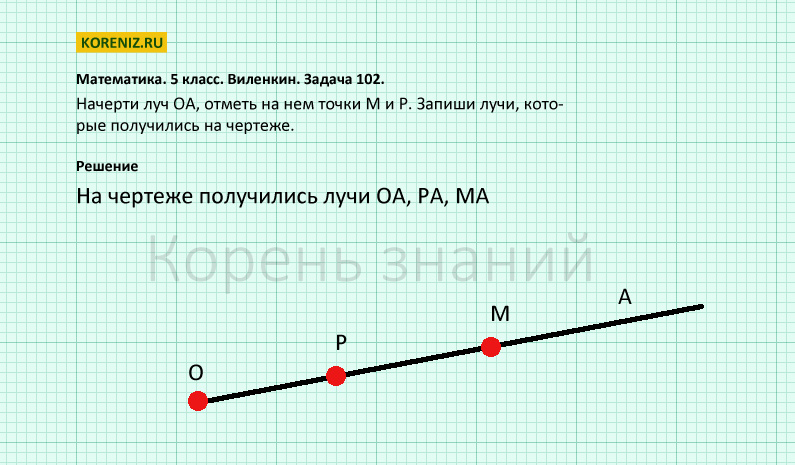
(Прямую линию можно продолжить в обе стороны, а луч только в одну. Луч имеет начало)
-Начертите луч на доске и в тетради
-Луч обозначается двумя прописными буквами.
На первом месте всегда указывается начало луча.
-Поставьте точку, проведите луч, а ещё можно провести из этой точки, ещё…
-Какие лучи бывают?
(Солнечные лучи, лампа, фонарик и т.д.)
Вывод: Луч – это прямая линия, ограниченная с одной стороны. Из одной точки можно провести бесконечное множество лучей.
-У луча я отрезаю ту часть, которую можно продолжить…и прикреплю ещё одну точку.
-Что получилось?
(Отрезок)
-Линия, ограниченная с двух сторон.
СРАВНИТЕ: Луч и отрезок.
-У луча есть только начало, а отрезок имеет и начало и конец.
-Можно отрезок изобразить на доске и в тетради?
Точки две поставь в тетради,
Чтоб потом нарисовать между ними
Под линеечку – прямую,
И окажется, мой друг,
Что отрезок вышел вдруг,
Только точкам имена дать ты
Не забудь!
-Отрезок обозначается двумя буквами,
но порядок при чтении и записи не имеет значения.
Вывод: Отрезок – это прямая, ограниченная с двух сторон.
-Что нового узнали об этих фигурах?
Вывод: Луч, прямая – это геометрические фигуры.
Работа с учебником $ 4 с.17-28.
5. Физкультминутка.
Раз, два, три, четыре, пять,-
Все умеем мы считать,
Отдыхать умеем тоже,
Руки за спину заложим,
Голову поднимем выше
И легко – легко подышим,
Раз – подняться, потянуться,
Два – согнуться, разогнуться,
Три – в ладоши три хлопка,
На четыре – руки шире,
Пять – руками помахать,
Шесть – за парту тихо сесть.6. Первичное закрепление нового материала.
(На доске изображены геометрические фигуры)
-Найдите отрезок, луч, прямую.
-Обоснуйте свой ответ.
-Можно ли сказать, что они пересекающиеся?
-А могут ли они пересечься?
Учебник: №85, 87(устно), 88(устно), 90, 91 – фронтально
Рабочая тетрадь: № 32, 34, 35, 36 – индивидуально(обучающая самостоятельная работа)
№ 33- работа в парах
Повторение: № 105
7.
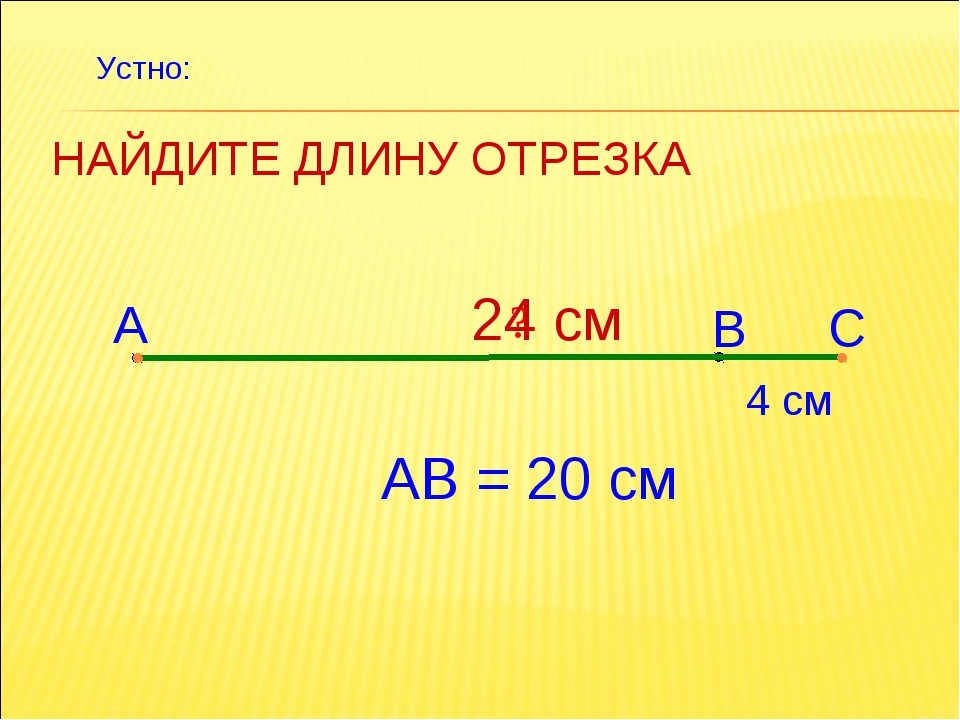Обучающая самостоятельная работа.
8. Домашнее задание.
На дом вам будет дано следующее задание: $ 4, № 86, 89, 106, доп. № 111.
9. Подведение итогов урока. Рефлексия.
Вопросы : 1-7 с. 29.
– Соедините названия фигуры с фигурой.
Подберите правильное название.
ОТРЕЗОК ЛУЧ ПРЯМАЯ линия ПЛОСКОСТЬ
ПРЯМАЯ линия – не имеет начала и конца; можно обозначать одной или двумя буквами; через одну точку можно провести сколько угодно линий, через две – только одну.
ЛУЧ– прямая, ограниченная с одной стороны; продолжать можно только в одну сторону; из одной точки можно провести сколько угодно лучей; лучи бывают разные.
ОТРЕЗОК – прямая линия, ограниченная с двух сторон; на одной прямой может быть несколько отрезков; любую прямую можно превратить в отрезок.
ПЛОСКОСТЬ – воображаемая
геометрическая модель; модели части плоскости: тетрадь, крышка стола, пол,
стены, поле, море и т.
д. Плоскость бесконечна, её нельзя изобразить.
Нарисовать свое настроение в виде солнышка в конце урока. «Лестница успеха».
-Вы сегодня дружно и творчески работали (Оценивается работа обучающихся).
-Спасибо всем! Урок окончен.
Технологическая карта урока
Предмет | Математика |
Класс | 5 класс |
Тема урока, место в изучаемой теме, разделе | «Плоскость, прямая, луч» (Урок из раздела «Натуральные числа», 10 урок из раздела) |
Тип урока | Урок открытия новых знаний |
Цели урока | предметные – познакомить учащихся с геометрическими фигурами: плоскость, прямая, луч; научить распознавать на рисунках эти фигуры, а в окружающем мире – объекты, для которых плоскость, прямая, луч являются моделями. личностные – проявлять интерес к изучению темы и желание применять приобретенные знания и умения метапредметные: формировать умение видеть математическую задачу в контексте проблемной ситуации, в окружающей жизни. |
Задачи урока | образовательные: продолжить работу по формированию у учащихся пространственного воображения; научить различать простые геометрические фигуры развивающие: создать условия для развития учебно-познавательной деятельности; вести работу по развитию математической речи, логического мышления, умения анализировать, делать выводы; воспитательные: содействовать формированию положительного отношения к урокам, понимания необходимости знаний; показать практическую значимость математики при решении задач из повседневной жизни; воспитывать культуру поведения учащихся во время работы. |
Планируемые результаты | Учащийся научится распознавать на чертежах геометрические фигуры: плоскость, прямая, луч |
Основные понятия | Плоскость, прямая, свойство прямой, луч |
Формы организации образовательного пространства на уроке | Фронтальная и индивидуальная работы; работа с учебником. |
Средства обучения | Учебник, письменные принадлежности, презентация, компьютер, интерактивная доска, листы самоконтроля; ресурсы сети Интернет: http://school-collection.edu.ru; http://www.mathvaz.ru Методическое пособие по математике 5 класс/Е.В.Буцко, А.Г.Мерзляк, В.Б.Полонский, М.С.Якир/ ФГОС /Алгоритм успеха/ |
Используемые технологии | Здоровьесберегающая, информационно-коммуникационная, технология сотрудничества |
Базовый учебник | Учебник 5 класс /А.Г. Мерзляк, В.Б. Полонский, М.С.Якир /М.: Вентана-Граф, 2016 |
План – конспект урока
Этап урока, продолжительность | Деятельность учителя | Деятельность учащихся | Методы, приёмы, средства обучения | Формируемые УУД |
1. 1 мин | Приветствует учащихся, оценивает их готовность к учебной деятельности, мобилизирует внимание. Создать благоприятный психологический настрой на работу. | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. «Ребята, проверьте пожалуйста, все ли у вас готово к уроку?» Выполняют необходимые действия, демонстрируют готовность для работы. | Словесный | Регулятивные: прогнозирование своей деятельности; Коммуникативные: планирование учебного сотрудничества с учителем и одноклассниками Личностные: умение выделять нравственный аспект поведения; самоопределение |
2. Мотивация учебной деятельности, 1 мин | – Предлагает послушать строки из стихотворения С. и каждый час – Как вы понимаете эти строки? – Ребята, я желаю вам успешной работы на уроке и думаю, что мы все с вами справимся с заданиями | Слушают, объясняют смысл прочитанного четверостишия; смотрят на доску, определяют смысл предстоящего поиска, излагают свои мысли. | Метод стимулирования положительной самооценки | Познавательные: умение извлекать информацию, обобщать, делать выводы. Коммуникативные: умение слушать, анализировать, излагать свои мысли в устной форме и понимать речь других; Личностные: умение проявлять познавательную инициативу |
3. Актуализация знаний, 7 мин | – Предлагает решить устно примеры поочередно и вписать правильность ответов в листы самоконтроля в дневнике достижений – Предлагает решить задачу: http://school-collection. – ставит проблему
| -Актуализируют необходимые установки; -выполняют задания и вписывают результаты в листы самоконтроля; -проводят подсчёт баллов за устную работу – анализируют, отвечают на вопросы учителя, предлагают способы решения проблемы | Фронтальный опрос с элементами тестирования с применением листа самоконтроля (приложение № 1) (слайды №2-5) из презентации «Устный счет. Арифметические действия» Частично поисковая, исследовательская деятельность; | Познавательные: поиск и выделение необходимой информации; строит свои высказывания, формулирует вывод на основе анализа Регулятивные: выделение и осознание того, что уже пройдено, фиксация индивидуального затруднения, пути решения проблемы; удерживать цель деятельности до получения ее результата; планировать решение учебной задачи; корректировать деятельность: вносить изменения в процесс с учетом возникших трудностей и ошибок, намечать способы их устранения; Коммуникативные: умение выражать свои мысли, аргументация; формирование умений совместно с другими детьми оценивать способы решения и делать выводы; находить решение задачи и оценивать полученные результаты. Личностные: применять правила делового сотрудничества: сравнивать разные точки зрения; считаться с мнением другого человека; проявлять терпение и доброжелательность в споре, дискуссии, доверие к собеседнику. |
4. Изучение нового материала, 10 мин | – Как вы думаете, какую тему мы сегодня с вами будем изучать? – Организует высказывания, предположения учащихся в отношении того, что и как исследовать; -подводит к тому, что плоскость бесконечна – Предлагает начертить прямую через одну точку, две точки, три точки, 4 точки и сделать вывод -вызывает к интерактивной доске учеников, чтобы продемонстрировать получившееся изображение – дает понятие луча; отрабатывается взаимное расположение изучаемых фигур: пересекаются (не пересекаются) две прямые, прямая и луч, луч и отрезок, отрезок и прямая; точка принадлежит (не принадлежит) прямой, лучу, отрезку. | – находят в окружающих предметах плоскость -свободно обмениваются мнениями, делают выводы – в тетрадях чертят прямую, проходящую через две точки, 3 точки, 4 точки делают самостоятельные выводы – Смотрят, выполняют задания , оценивают, делают выводы | Частично поисковая, исследовательская деятельность; Презентация «Дм 3 Плоскость. | Познавательные: поиск и выделение необходимой информации; структурирование знаний; анализ объектов; Регулятивные: формирование умений ставить личные цели деятельности, оценивать полученные результаты; делать выводы; самостоятельное создание способов решения проблем творческого и поискового характера. Личностные: проявление внимания, интереса, желания больше узнать Коммуникативные: умение слушать, анализировать, излагать свои мысли в устной форме согласно речевому этикету и понимать речь других; |
5. Физминутка, 2 мин | Даёт рекомендации по выполнению. Ведёт счёт. | Выполняют гимнастику | Здоровьесберегающие | Коммуникативные: умение работать по заданию Личностные: формирование ЗОЖ |
6. 6 мин | Выявление пробелов первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу. -организует работу с учебником: предлагает устно ответить на вопросы на стр. 29 – решение №85 в тетрадях; к интерактивной доске вызывается 1 ученик – №87, 88 решают всем классом устно – №90,91 – работа в парах | – Отвечают на вопросы – Выполняют задания; – учащиеся, которые справились с заданием, записывают своё решение на доске – записывают решение в тетрадь, советуются с соседом по парте – результаты решения записывают в листы самоконтроля | Фронтальная работа с классом Индивидуальная работа Работа в парах | Познавательные: рефлексия способов и условий действия. Анализ и синтез объектов. Коммуникативные: сотрудничество в поиске и сборе информации; умение точно и грамотно выражать свои мысли; выслушивать мнение членов команды, не перебивая; принятие коллективного решения. Регулятивные: |
7. Закрепление (обеспечение осознанности формируемых знаний и умений), 5 мин | Самостоятельная работа (по вариантам) с самопроверкой | Выполняют работу; Сверяются с ответами на доске, выставляют баллы в дневнике достижений в листах самоконтроля | Индивидуальная самостоятельная работа | Познавательные: рефлексия способов и условий действия. Анализ и синтез объектов. Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения; саморегуляция. Коммуникативные: умение выражать свои мысли, аргументация; формирование умений совместно с другими детьми оценивать способы решения и делать выводы; находить решение задачи и оценивать полученные результаты. |
8. Рефлексия 2 мин | – Дать качественную оценку работы класса и отдельных обучаемых Какая была сегодня тема урока? Какую цель ставили? Достигли цели? Расскажите по схеме, чему научились на уроке: я – знаю я – запомнил я – смог И поставьте себе смайлик – один из 4 | Учащиеся отвечают | Фронтальная работа с классом | Коммуникативные: умение выражать свои мысли, аргументация Личностные: умение оценить свои знания и возможности |
9. Домашнее задание, 1 мин | Завершается урок. Он пошёл ребятам впрок? Постарались все понять? Учились тайны открывать? Ответы полные давали? На уроке не зевали?» Учитель предлагает дозированное домашнее задание §4, вопросы, №86, 89, 93. | Учащиеся записывают в дневники домашнее задание | Личностные: формирование самооценки на основе критерия успешности учебной деятельности |
Приложение № 1
Лист самоконтроля
Вид задания | Количество правильных ответов | Шкала баллов | Суммарный балл за задание |
Тест | |||
1 слайд | 5 | ||
2 слайд | 5 | ||
3 слайд | 8 | ||
4 слайд | 5 | ||
Задача № 85 | 1 | ||
Задача №87 | 1 | ||
Задача №88 | 1 | ||
Задача №89 | 1 | ||
Задача №90 | 1 | ||
Задача №91 | 1 | ||
Самостоятельная работа | |||
Задание 1 | 1 | ||
Задание 2 | 1 | ||
Задание 3 | 1 | ||
Суммарный балл за работу |
Критерии оценок: 27-32б-«5»; 20-26б- «4»; 16-19б – «3»; меньше 16 б- «2»
Приложение № 2
Всё отлично! Было трудно, Старался, Было скучно…
но я разобрался.
но многое не понятно.
Приложение 3
Самостоятельная работа
«Геометрические фигуры»
Вариант 1
Самостоятельная работа
«Геометрические фигуры»
Вариант 2
Перейти к:
Операции и алгебраическое мышление | Числа и операции с основанием десять | Число и операции-дроби | Измерения и данные | Геометрия
5.OA.A.1
Используйте круглые и фигурные скобки в числовых выражениях и оценивайте выражения с этими символами.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
5.OA.A.2
Напишите простые выражения, которые записывают вычисления с числами, и интерпретируйте числовые выражения без их вычисления.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
5.OA.B.3
Сгенерируйте два числовых шаблона, используя два заданных правила. Определите очевидные отношения между соответствующими терминами. Сформируйте упорядоченные пары, состоящие из соответствующих терминов из двух шаблонов, и отобразите упорядоченные пары на координатной плоскости.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
5.
НБТ.А.1
Знайте, что в многозначном числе цифра на одном месте представляет в 10 раз больше, чем она представляет на своем правом месте, и 1/10 того, что она представляет на своем левом месте.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
5.NBT.A.2
Объясните закономерности в количестве нулей произведения при умножении числа на степень 10 и объясните закономерности в расположении десятичной точки когда десятичная дробь умножается или делится на степень 10. Используйте целые числа в степени для обозначения степеней 10.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
5.NBT.A.3
Читать, писать и сравнивать десятичные дроби с тысячными.
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков.
5.NBT.B.5
Свободно умножайте многозначные целые числа по стандартному алгоритму.
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
5.NBT.B.6
Нахождение целых чисел в частных с до четырехзначными делимыми и двузначными делителями, используя стратегии, основанные на разрядном значении , свойства операций и/или связь между умножением и делением. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
5.NBT.B.7
Сложение, вычитание, умножение и деление десятичных долей до сотых с использованием конкретных моделей или рисунков и стратегий, основанных на разрядности, свойствах операций и/или отношений между сложением и вычитанием; свяжите стратегию с письменным методом и объясните используемую аргументацию.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
5.NF.A.1
Сложение и вычитание дробей с разными знаменателями (включая смешанные числа) путем замены данных дробей эквивалентными дробями таким образом, чтобы получить эквивалентную сумму или разность дробей с одинаковыми знаменателями.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
5.NF.A.2
Решать словесные задачи на сложение и вычитание дробей, относящихся к одному и тому же целому, включая случаи разных знаменателей, например, с помощью визуальные дробные модели или уравнения для представления проблемы. Используйте эталонные дроби и числовой смысл дробей для мысленной оценки и оценки обоснованности ответов.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
5.NF.B.3
Интерпретировать дробь как деление числителя на знаменатель (a/b = a ÷ b). Решайте текстовые задачи на деление целых чисел, чтобы получить ответы в виде дробей или смешанных чисел, например, используя визуальные модели дробей или уравнения для представления задачи.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
5.NF.B.5
Интерпретировать умножение как масштабирование (изменение размера) по:
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
5 .NF.B.6
Решайте реальные задачи, связанные с умножением дробей и смешанных чисел, например, используя визуальные модели дробей или уравнения для представления задачи.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
5.NF.B.7
Примените и расширите прежнее понимание деления, чтобы разделить единичные дроби на целые числа и целые числа на единичные дроби.
См. соответствующие рабочие листы, рабочие тетради
5.MD.A.1
Преобразование между стандартными единицами измерения разного размера в заданной системе измерений (например, преобразование 5 см в 0,05 м) и использование этих преобразований при решении многоэтапных задач реального мира.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
5.MD.B.2
Постройте линейный график для отображения набора данных измерений в долях единицы (1/2, 1/4, 1/8). Используйте операции над дробями для этого класса, чтобы решить задачи, связанные с информацией, представленной в линейных графиках.
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
5.MD.C.3
Распознавать объем как атрибут объемных фигур и понимать принципы измерения объема.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
5.MD.C.4
Измерение объемов путем подсчета кубических единиц, используя кубические сантиметры, кубические дюймы, кубические футы и импровизированные единицы измерения.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
5.
MD.C.5
Свяжите объем с операциями умножения и сложения и решите реальные и математические задачи, связанные с объемом.
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
5.G.A.1
Используйте пару перпендикулярных числовых линий, называемых осями, для определения системы координат, где пересечение линий (начало координат) расположено так, чтобы совпадать с 0 на каждой линии и заданной точкой в плоскость расположена с помощью упорядоченной пары чисел, называемой ее координатами. Поймите, что первое число указывает, как далеко нужно пройти от начала координат в направлении одной оси, а второе число указывает, как далеко нужно пройти в направлении второй оси, при условии, что имена двух осей и координаты соответствуют (например, ось x и координата x, ось y и координата y).
См. соответствующие рабочие листы, рабочие тетради, планы уроков
5.
Организационный,
Маршака. Пусть каждый день
edu.ru/catalog/rubr/608887c4-68f4-410f-bbd4-618ad7929e22/113925/?interface=pupil&class=47&subject=16
Прямая. Луч»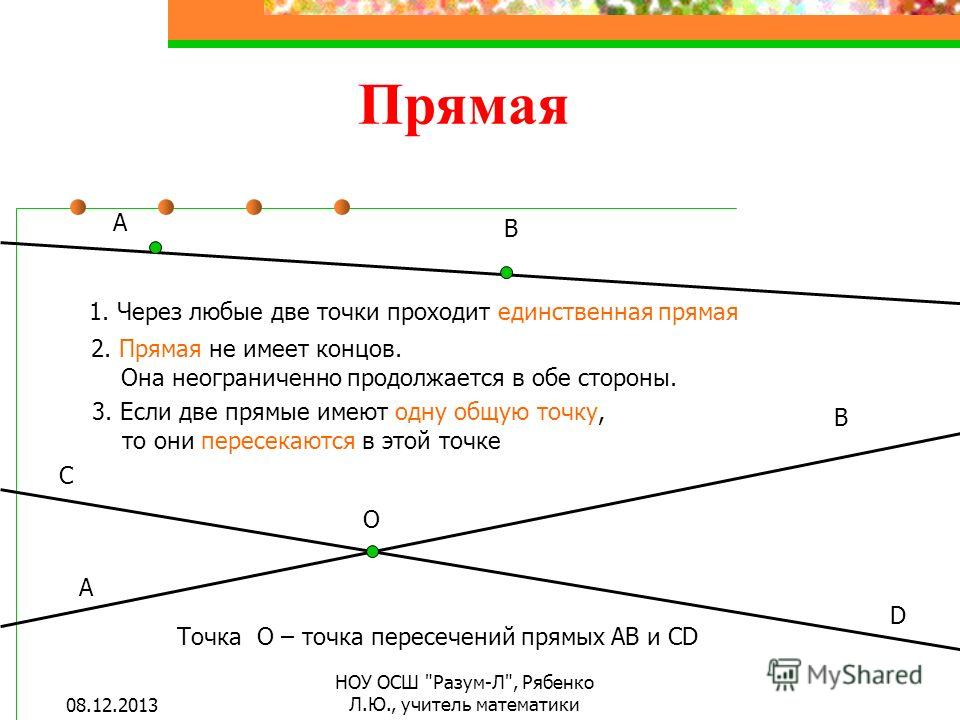
Первичное закрепление изученного материала
