Связь умножения и сложения 3 класс конспект урока: “Связь умножения и сложения” – 3 класс | План-конспект урока по математике (3 класс) на тему:

“Связь умножения и сложения” – 3 класс | План-конспект урока по математике (3 класс) на тему:

Тема: Связь умножения и сложения

Цели: вспомнить смысл действия умножения; закреплять вы-числительные навыки, умение решать задачи и уравнения изученных видов.

Планируемые результаты: учащиеся научатся заменять сложение умножением; решать задачи на умножение и обратные им задачи; анализировать и делать выводы; работать самостоятельно.

Планируемые метапредметные результаты:

Личностные:

формировать положительное отношение к учению,

развивать интерес к различным видам решения поставленной учебной задачи и к расширению математических знаний.

Регулятивные:

уметь определять и формулировать цель на уроке;

учиться совместно с учителем обнаруживать и формулировать учебную проблему;

планировать свои действия в связи с поставленной задачей.

понимать, принимать и сохранять учебную задачу; осуществлять самооценку учебных действий.

Познавательные:

уметь ориентироваться в своей системе знаний;

ориентироваться в предложенном материале, находить нужную информацию.

Коммуникативные:

уметь с достаточной полнотой и точностью выражать свои мысли;

слушать и понимать речь других;

уметь работать в паре, группе;

Оборудование урока: персональный компьютер, мультимедиа-проектор; карточки для работы в группах, рабочие тетради.

Методы: практический, проблемный, частично-поисковый, словесный.

Время реализации занятия: 45 минут.

Ход урока

1. Организационный момент.        Психологический настрой

  – Ребята, у нас сегодня открытый урок математики и  к нам на урок  пришли гости.

  Давайте с ними поздороваемся.   Садитесь.

 – Посмотрите друг на друга, улыбнитесь, пожелайте успешной работы себе, соседу,  всему классу.

  (Учащиеся)  – Пожелаем всем удачи –      (Слайд)

                       За работу! В добрый час!

– Что необходимо нам для успешной работы на уроке? (Мы должны внимательно  слушать учителя,  думать и правильно отвечать на вопросы). 

– Покажите своей посадкой, что вы готовы работать.

II.         Актуализация знаний

1. Индивидуальная работа

– Ребята сегодня Буратино прислал вам задания и просит вас их выполнить. И первое задание –  помочь ему выиграть лотерею. У каждого из вас есть карточки. Выиграет тираж только тот, кто правильно вычеркнет все числа. Сколько заданий, столько вычеркнутых чисел.  (Слайд)

	11		40
3		21		50	68		80
7	15			54			90
		29	45			70
8	19			30		76

1. Увеличить 9 на 6. ( 15)

2.Уменьшить 13 на 5. ( 8)

3.Найти сумму чисел 6 и 5. (11)

4.Найти разность чисел 70 и 20. ( 50)

5.К 70 прибавить 6. (76)

6.От 84 отнять 4. ( 80)

7.В каком числе 4 десятка и 5 единиц? (45)

8.Какое число следует за числом 69? ( 70)

9.Какое число предшествует числу 30? (29)

10. Увеличьте 50 на 4. (54)

11.К 45 прибавьте такое же число. (90)

12. Назовите сумму чисел 60 и 8. (68)

13. Из 11 вычесть 8. (3)

14. Из каких одинаковых чисел можно составить число 14. (Из 7.)

– Нашу работу мы продолжим  с оформления тетради.

– Откройте свои тетради. Вспомним правила посадки при письме, правильное расположение тетради, наклон головы. Запишите в тетрадях число, классная работа.

2.Минутка чистописания

– Ребята, какую бы вы сегодня за урок хотели  получить отметку? (5)

– Я предлагаю вам, записать цифру 5 соблюдая правильный алгоритм написания.

– Внимание на экран.   Начинают писать наклонную палочку немного правее середины верхней стороны клетки и ведут её почти до центра клетки. Затем пишут полуовал. Сверху от палочки пишут вправо волнистую линию.

III.        Самоопределение к деятельности

– Посмотрите на данные выражения.

28 + 26 + 22+ 4 =

35+ 17 + 13 + 5 =

46+ 22+14 +8 =  

З+З+З+З+З

— Какая сумма лишняя и почему? (Последняя, так как складываются одинаковые числа, а в остальных — разные.)

– Вычислите 3 первых выражения с каждого ряда по 1 человеку. (3 учащихся.)

– Я положила на стол  по 3 кружка 5 раз. Сколько всего кружков я положила? Как узнали?    

 (3 + 3 + 3 + 3+ 3 = 15.)

– Запишем эту сумму (записывает на доске). Какие слагаемые в этой сумме?  (Одинаковые.)

– Сколько одинаковых слагаемых?  (5.)

 —Каким действием можно заменить сложение одинаковых чисел? (Умножением.)

– Как записывают пример на умножение?    (Записывают так: 3 · 5 = 15.) 

– Точка – знак умножения. Число 3 показывает, какое брали слагаемое, а число 5 показывает, сколько взяли одинаковых слагаемых. Читают этот пример так: 3 умножить на 5, получится 15.

 

—Что показывает первое число? (Какое число является слагаемым.)

—Что показывает второе число? (Сколько раз повторяется слагаемое.)

– Как вы думаете, чем мы будем заниматься на уроке? (Говорить о  связи умножения и сложения.)

– Правильно. О  связи умножения и сложения.

-Какие цели мы поставим на урок? (1. Научиться  заменять сумму одинаковых слагаемых умножением. 2. Научиться,  решать задачи  действием  …………. (умножения)

-Правильно.

IV.         Работа по теме урока

Работа по учебнику    (Карточка)

—         Прочитайте задание рядом с красной стрелкой на с. 18 учебника. Что обозначает каждое число в записи 3•4  (3-какое число повторяется , 4 – сколько раз оно повторяется.)

 6 • 3?  (6— какое число повторяется,  3 — сколько раз оно повторяется.)

— Замените произведение суммой и вычислите.   (6 + 6 + 6=18.)

— Сделайте вывод: что такое умножение? (Сложение одинаковых чисел.)

№ 1 (с. 18).    (Устное выполнение. )

– Почему во всех примерах сложение можно заменить умножением? (Все слагаемые одинаковые.)

– Что показывает каждое число в записи умножения? (Первое число — какое число повторяется, второе число — сколько раз оно повторяется.)

По сколько взяли? (по 2.)

Сколько раз по два  взяли? (8.)

№2 (с. 18).

– Посмотрите на № 2. Сформулируйте задание. Что нужно сделать?  (Сравнить выражения.)

– Чем интересны эти записи? (Слева записаны суммы, справа – произведения.)

–  Что нужно сделать, чтобы сравнить выражения? (Заменить умножение сложением или наоборот.)

(Проверка. Учащиеся по очереди называют знаки и доказывают свой выбор.)

Примерные рассуждения учеников: 4 + 4 + 4 04-5. Заменим умножение сложением:

4 + 4 + 4 0 4 + 4 + 4 + 4 + 4. Слева число 4 повторяется 3 раза, а справа — 5 раз, значит, ставим знак

Слева число 8 повтор 3 раза, а справа 8+8  – 2 раза.

(Для тех кто выполнил №2 –   Решают уравнения.)

– У Буратино сложности с решением уравнений. Это индивидуальные задания на карточках.

67 —х = 39                                    35+  х=72                                               х + 28 = 73

V.         Физкультминутка

– Буратино предлагает провести физкультминутку.

Буратино потянулся  (сидя за партой, руки к плечам, поднимание и опускание локтей),

Раз – нагнулся. Два – нагнулся  (наклоны к левой и правой ноге),

Руки в стороны развел,

Ключик, видно, не нашел  (руки в стороны, повороты направо, налево).

Чтобы ключик нам достать,

Нужно на носочки встать.  (встают на носки, руки поднимают вверх и медленно садятся за парты. Повторить 2–3 раза).

VI.        Закрепление изученного материала

Работа по учебнику.  №4 (с. 18).

             Рассматривание рисунка. 
-Что изображено на рисунке? Расскажите, о чём должны помнить, когда в природе видим похожую картину?  (Не трогать птиц руками.)
– Итак, продолжаем.

– Какие задачи называются обратными? (Когда известное становится неизвестным, а то, что нужно было узнать, — известным. )

— Составьте задачу, которая решается умножением. (В 4 гнездах по 2 птенца. Сколько всего птенцов?)

— Сделайте схематический рисунок и решите задачу. Обозначьте каждое гнездо кружочком, в каждом кружочке напишите цифру 2.

   2    2    2    2

 Решение: 2•4 = 8 (п.).   Ответ: всего 8 птенцов.

— Составьте задачу, в которой нужно узнать, сколько было гнезд. (Вывелись 8 птенцов, по 2 в каждом гнезде.  В скольких гнездах вывелись птенцы ?)

—Каким действием решается задача? (Делением.)

— Сделайте схематический рисунок и решите задачу.

ОО/ ОО/ОО/ОО

 Решение: 8:2 = 4 (г.).  Ответ: птенцы вывелись в 4 гнездах.

– Буратино предлагает вам следующую обратную задачу  решить в группах.

 (Формируются в группы.)

– Составьте задачу, в которой нужно узнать, сколько птенцов было в каждом гнезде. (В 4 гнёздах вывелись 8 птенцов, причём в каждом гнезде птенцов было поровну. Сколько птенцов было в каждом гнезде?

– Каким действием решается задача? (Делением. )

– Сделайте схематический рисунок и решите задачу.

ОООО/ ОООО  8:4 = 2 (п.)  Ответ: в каждом гнезде было 2 птенца.

 (Задачи на карточках.)

VII.         Рефлексия

– Оцените свою работу на уроке.

–  Карточки с решениями вложите в свои тетради.

VIII.         Подведение итогов урока

—         Что такое умножение? (сложение одинаковых слагаемых.)

—         Что показывает первое число в записи умножения? Что показывает второе число?

—         Чем был полезен урок для вас?

– Спасибо за урок!

Домашнее задание: Учебник: № 5 (с. 18).

3 класс. Математика. Урок 10. ТЕМА. СВЯЗЬ УМНОЖЕНИЯ И ДЕЛЕНИЯ

Цель деятельности учителя	Способствовать развитию умений по заданному примеру на умножение составлять два выражения на деление, объяснять, как получили результат, используя математическую терминологию
Тип урока	Закрепление знаний и способов действий
Планируемые образовательные результаты	Предметные: научатся называть компоненты и результаты умножения и деления, устанавливать взаимосвязь между результатом и компонентами умножения, составлять карточки-схемы, читать математические выражения. Метапредметные: овладеют умениями понимать учебную задачу урока, отвечать на вопросы, обобщать собственные представления; научатся слушать собеседника и вести диалог, оценивать свои достижения на уроке, пользоваться учебником. Личностные: проявляют положительное отношение к урокам математики, к учебе
Оборудование	Интерактивная доска (экран), компьютер, проектор
Этапы урока	Задания и упражнения	Деятельность учителя	Деятельность учащихся
I. Мотивация к учебной деятельности	Подготовка к усвоению изучаемого материала	– Начнем урок с пожелания друг другу добра. Я желаю тебе добра, ты желаешь мне добра, мы желаем друг другу добра. Если будет трудно – я тебе помогу.	Демонстрируют готовность к уроку, организуют рабочее место
II. Актуализация знаний	1. Проверка домашнего задания.	Проверяет наличие домашней работы в тетрадях.	Показывают выполненную домашнюю работу.
	2. Целеполагание.	– Откройте учебник на с. 19, определите тему и цель урока.	Формулируют тему и цель урока.
	3. Устный счет	– Найдите «лишние» числа: а) 90, 20, 25, 50, 70; б) 42, 24, 48, 45, 49; в) 76, 32, 18, 4, 27.	Выполняют задания
		– Сравните: 27 … 29 5 дм … 50 см 76 … 56 3 дм 2 см … 2 дм 3 см 94 … 49 7 дм 4 см … 48 см
		– Решите занимательные задачи:  6 рыбаков съели 6 судаков за 6 дней. За сколько дней 10 рыбаков съедят 10 судаков?  На одном дереве сидели 40 сорок. Проходил охотник, выстрелил и убил 6 сорок. Сколько сорок осталось на дереве?  2 землекопа за 2 ч работы выкопают 2 м канавы. Сколько нужно землекопов, чтобы они за 100 ч работы выкопали 100 м такой же канавы?  2 отца и 2 сына разделили между собой 3 апельсина так, что каждому досталось по одному апельсину. Как это могло получиться?
III. Изучение нового материала		– Определите взаимосвязь между множителями и произведением. Записывает на доске: 7 · 4. Записывает ответ, названия компонентов и результата.	Читают пример с использованием терминов «первый множитель», «второй множитель», вычисляют с помощью сложения произведение.
		1 множитель 2 множитель произведение 7 · 4 = 28 28 : 7 = 4 28 : 4 = 7	Выясняя, как получены второй и третий примеры из первого, приходят к выводу, что, разделив произведение (28) на первый множитель (7), получили второй множитель (4), а разделив произведение (28) на второй множитель (4), получили первый множитель (7).
		– Посмотрите на запись второго примера. Как его получили из первого?	– Произведение (28) разделили на первый множитель (7) и получили второй множитель (4).
		– Как получили третий пример из первого?	– Произведение (28) разделили на второй множитель (4) и получили первый множитель (7).
		Аналогичная работа проводится по рисункам и записям, данным в учебнике на с. 19, в задании 1. При этом полезно попросить объяснить записи с использованием данных рисунков.
		4 · 2 = 8 3 · 6 = 18 5 · 4 = 20 8 : 2 = 4 18 : 6 = 3 20 : 5 = 4 8 : 4 = 2 18 : 3 = 6 20 : 4 = 5 Объяснения будут такими же, как и в предыдущем примере.
		– Сформулируйте вывод. Учитель подчеркивает, что этот вывод следует запомнить.	– Если произведение двух множителей разделить на один из них, то получится другой множитель.
	Физкультминутка	Организует проведение физкультминутки	Выполняют движения согласно инструкции учителя
IV. Практическая деятельность	1. Решение задач.	№ 2. Разбирается под руководством учителя, можно показать, как записать краткое условие к такой задаче.	Читают задачу. Один ученик у доски выполняет иллюстрацию в виде схематического рисунка с точками: … | … | … | … | …
			Решение: 1 этаж – 3 м. 5 этажей – ? м. Затем вызванный ученик записывает решение и ответ задачи: 3 · 5 = 15 (м) – всего. Ответ: 15 метров – высота дома.
		– Составьте теперь к этой задаче обратную.	– Высота дома – 15 м, а высота каждого этажа – 3 м. Сколько в доме этажей? Вызванный ученик выходит к доске, записывает условие, решение и ответ задачи: … | … | … | … | … Решение: 15 : 3 = 5 (эт.) – всего. Ответ: в доме 5 этажей.
		Аналогичная работа проводится по еще одной обратной задаче.	Решают задачу.
		№ 4. Задача разбирается с учителем.
		– Прочитайте задачу. Что в ней известно?
		– Прочитайте внимательно, на сколько равных частей надо разделить эти орехи. – Почему вы так решили?	– На 3 равные части.
			Вызванный ученик решает задачу у доски: … | … | … Решение: 12 : 3 = 4 (ор.) – у каждого. Ответ: 4 ореха получил каждый.
	2. Самостоятельная работа.	– Выполните самостоятельно задания № 3, 5, 6.	Решают самостоятельно.
	3. Работа с геометрическим материалом.	– Какая фигура «лишняя»? (На полях учебника.) – Выполните задание № 8, проверьте друг друга	Выполняют устно. Выполняют самостоятельно с последующей взаимопроверкой
V. Итоги урока. Рефлексия деятельности	Обобщение полученных на уроке сведений. Заключительная беседа. Выставление оценок	– Ребята, что нового узнали сегодня на уроке? – Какую же связь мы установили? – Что еще повторяли на уроке? – Где могут пригодиться эти знания в жизни?	Отвечают на вопросы
VI. Домашнее задание	Инструктаж по выполнению домашнего задания	Учебник, с. 19, № 7. Рабочая тетрадь, с. 9, № 5, 6	Задают уточняющие вопросы

3.OA.A.3 Планы уроков — Common Core Math

Умножение R.A.C.E.

План урока

Умножение R.A.C.E.

Научите своих учеников использовать различные представления при создании и решении текстовых задач. Простые аббревиатуры и наглядные пособия упрощают обучение умножению.

3 класс

Математика

План урока

Раздели это!

План урока

Раздели это!

Оживите деление с помощью этого практического вводного урока по работе с делением! Студенты будут использовать настоящие проблемы и манипулятивные методы, чтобы испытать разделение в действии.

3 класс

Математика

План урока

Рассказы об умножении

План урока

Истории умножения

Математику можно превратить в короткие истории! Вдохновите своих учеников проявить творческий подход с помощью этого плана урока, который поможет им попрактиковаться в составлении и решении текстовых задач.

2 класс

Математика

План урока

Ты в ударе! Практика умножения фактов

План урока

Ты в ударе! Практика умножения

Ваши ученики изо всех сил пытаются запомнить таблицу умножения? Мы все знаем, что единственный способ запомнить математические факты — это практиковаться! Этот практический урок — увлекательный способ для вашего класса попрактиковаться, чтобы освоить факты умножения.

3 класс

Математика

План урока

Заказы книг: деньги

План урока

Заказы на книги: Деньги

Не выбрасывайте все эти лишние копии бланков заказов на книги! Они являются отличным трамплином для уроков математики. В этом уроке они объединяются в упражнения, призванные помочь юным ученикам разобраться в денежной математике.

3 класс

Математика

План урока

Домино Умножение

План урока

Умножение домино

Не опрокинуть костяшки домино! На этом уроке ваши ученики будут практиковаться в умножении на 2 костяшек домино.

2 класс

Математика

План урока

Модели массивов в умножении

План урока

Модели массивов в умножении

Этот урок позволяет учащимся изучить концепцию умножения на практике. Дети также поймут, почему умножение важно, а также как решать задачи на умножение, используя модели массивов.

3 класс

Математика

План урока

Задачи на разделение слов

План урока

Проблемы со словами на деление

Освежите свое понимание задач со словами на деление с делением в длину и однозначными делителями! Используйте этот урок, чтобы помочь учащимся определить ключевые термины деления и решить текстовые задачи.

3 класс

Математика

План урока

Пришло время отпраздновать Китайский Новый год!

План урока

Пришло время отпраздновать Китайский Новый год!

Празднование китайского Нового года — это весело для семьи и друзей! Используйте этот урок, чтобы рассказать своим ученикам о некоторых праздничных традициях и мероприятиях, когда они будут практиковаться в решении текстовых задач, требующих времени и всех четырех математических операций.

3 класс

Математика

План урока

Партнерское сложение и умножение

План урока

Объединение сложения и умножения

Умножение больше не является загадкой, когда оно связано с сложением! Помогите своим ученикам установить связь между умножением и повторяющимся сложением с помощью этого практического урока, который включает в себя несколько типов конкретных примеров.

3 класс

Математика

План урока

Решение задач на умножение и деление

План урока

Решение задач на умножение и деление

Научите своих учеников четырем простым шагам, которые помогут им уверенно решать задачи на умножение и деление.

3 класс

Математика

План урока

Умножить на 5

План урока

Умножить на 5

Помогите своим учащимся обнаружить закономерности при умножении на пять.

3 класс

Математика

План урока

Детали отдела

План урока

Details of Division

Научите своих учеников словарным запасам, чтобы правильно обсуждать уравнения деления, а затем предложите им написать свои собственные текстовые задачи! Используйте этот урок самостоятельно или в качестве предварительного урока для

Разделите это!

3 класс

Математика

План урока

Размышление над задачами на умножение и деление

План урока

Размышление над задачами на умножение и деление

Научите своих учеников размышлять над информацией в задачах на умножение и деление перед их решением. Используйте этот урок отдельно или в качестве предварительного урока к Шаги через задачи на умножение и деление .

3 класс

Математика

План урока

Стратегии сделать умножение легким

План урока

Стратегии упрощения умножения

На этом уроке ваши ученики увидят, как порядок множителей не влияет на произведение в выражении умножения. Используйте это отдельно или вместе с

Ты в ударе! Практика умножения фактов.

3 класс

План урока

Дополнительные планы для третьего класса

План урока

Дополнительные планы для третьего класса

Планирование замены в классе никогда не было проще, чем с этим недельным дополнительным пакетом для третьего класса! Ваш заместитель может дополнить обучение уроками о том, как мы все связаны, которые будут обучать и вдохновлять учащихся!

3 класс

Чтение и письмо

План урока

Математика 3 класс | Умножение и деление, часть 1

Краткое содержание модуля

---

Модуль 2 открывает глаза учащихся на некоторые из наиболее важных тем, которые учащиеся изучают в 3 классе, — умножение и деление.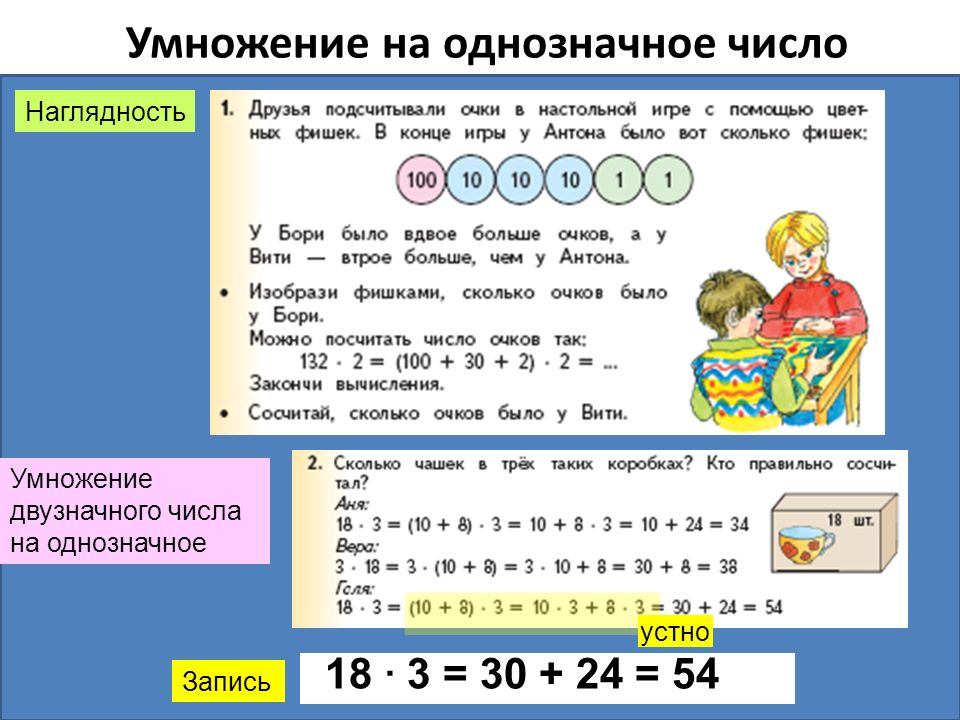 В этом разделе «учащиеся начинают развивать эти понятия, работая с числами, с которыми они более знакомы, такими как 2, 5 и 10, в дополнение к числам, которые легко пропустить, таким как 3 и 4», что позволяет познавательный спрос на значение самих умножения и деления, а не вычисления (CCSS Toolbox, Sequenced Units for the Common Core State Standards in Mathematics Grade 3). Затем в Блоке 3 учащиеся будут работать над более сложными блоками 0, 1, 6–9., и кратное 10. 

Во 2-м классе учащиеся научились считать объекты в массивах, используя многократное сложение (2.OA.4), чтобы получить основу для умножения. Они также проделали большую работу над одно- и двухэтапными задачами на сложение и вычитание, освоив все типы задач, включающие эти операции (2.OA.1). Учащиеся будут полагаться на это основополагающее понимание и ориентацию равных групп при решении контекстуальных проблем в этом модуле.

В начале этого раздела учащиеся получают представление об умножении и делении в контексте задач на равные группы и массивы в теме A. Удерживать внимание на концептуальном понимании умножения и деления (3.OA.1, 3 .OA.2), Тема A не обсуждает конкретные стратегии решения, поэтому учащиеся могут пересчитать все объекты (стратегия 1-го уровня) или вспомнить свой пропуск и повторное сложение (стратегии 2-го уровня) из 2-го класса, чтобы найти неизвестное. продукт. Однако в темах B и C основное внимание уделяется разработке более эффективных стратегий для решения задач умножения и деления, включая пропуск счета и многократное сложение (стратегии уровня 2), а также «просто знание» фактов, которое работает для достижения цели. «к концу 3 класса [учащиеся] знают наизусть все произведения двух однозначных чисел и связанные с ними факты деления» (3.OA.7). Как говорится в книге «Операции и алгебраическое мышление», «освоение этого материала и достижение беглости в умножении однозначных чисел и связанном с ним делении может занять довольно много времени, потому что не существует общих стратегий умножения или деления всех однозначных чисел, как для сложения или вычитание» (OA Progression, стр. 22). Таким образом, поскольку «существует много шаблонов и стратегий, зависящих от конкретных чисел», они сначала работают с факторами 2, 5 и 10 в Теме B, поскольку они выучили эти последовательности с пропуском счета во 2-м классе. Затем в Теме C они работать с новыми множителями 3 и 4. Только тогда, когда учащиеся лучше познакомятся с этими множителями, учащиеся будут решать с ними более сложные и/или абстрактные задачи, в том числе определение неизвестного целого числа в уравнении умножения или деления, связывающем три целые числа (3.OA.4) и решение двухэтапных текстовых задач с использованием всех четырех операций (3.OA.3, 3.OA.8), оценивая обоснованность их ответов для различных типов задач по теме D. Наконец, модуль завершается сосредоточением внимания на категориальных данных, где учащиеся рисуют и решают задачи, связанные с масштабированными графическими изображениями и масштабированными гистограммами, что является хорошим приложением основной работы по умножению и делению. Как отмечают Прогрессии, «эти изменения связаны с упором на умножение в этой степени» (MD Прогрессия, стр. 7). Учащиеся также решают одно- и двухэтапные текстовые задачи, связанные с данными на этих графиках, опираясь на обширную работу, которую учащиеся проделали с текстовыми задачами в течение года. Таким образом, этот поддерживающий стандарт кластера значительно улучшает основную работу, над которой они работали во всем подразделении.

На протяжении всего раздела учащиеся выполняют различные математические упражнения. Модуль уделяет особое внимание абстрактным и количественным рассуждениям, поскольку учащиеся начинают понимать значение умножения и деления и абстрактных символов, используемых для их представления (MP.2). Кроме того, учащиеся моделируют математические модели с этими новыми операциями, решая одно- и двухэтапные текстовые задачи с их участием (MP.4).

Введение в умножение и деление углубляется в Разделе 3, когда учащиеся изучают более сложные множители 0, 1, 6–9.и кратны 10. Затем, в Разделе 4, учащиеся изучат область и ее связи с этими операциями. В 4 классе их понимание умножения и деления станет еще более богатым, когда они начнут понимать мультипликативное сравнение и решать текстовые задачи с ним (4. ОА.1, 4.ОА.2). Кроме того, они будут решать многоэтапные текстовые задачи, включающие все четыре операции, иногда с необходимостью интерпретации остатка в контексте задачи (4.OA.3). Наконец, учащиеся расширят свое вычислительное мастерство до многозначных чисел, умножая целое число до четырех цифр на однозначное целое число и два двузначных числа, а также делят до четырехзначных дивидендов на единицу. -разрядный делитель (4.NBT.5, 4.NBT.6). Умножение и деление обеспечивают основу для множества алгебраических и геометрических тем, от линейных функций до тригонометрии, и, таким образом, это содержание имеет решающее значение для всего будущего изучения математики.

Темп: 24 учебных дня (21 урок, 2 гибких дня, 1 день оценки)

Fishtank Plus для математики

Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.

Узнать больше

Оценка

---

Следующие оценки сопровождают Модуль 2.

Предварительный модуль

Перед началом модуля учащиеся должны пройти предварительную оценку и самооценку учащихся. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.

Промежуточный модуль

Предложите учащимся выполнить оценку промежуточного модуля после урока 9.

Послемодуль

Используйте приведенные ниже ресурсы для оценки усвоения учащимися содержания модуля и плана действий для будущих модулей.

• Постмодальная оценка

• Ключ к ответам после модульной оценки

• Руководство по анализу послемодульной оценки

  92F25A3F-8529-4314-9899-6EE68694E3D0

• Самооценка студентов после окончания обучения

Расширенный пакет оценивания

Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить уровень владения учащимися базовыми навыками и понятиями, а также их прогресс в изучении содержания модуля.

Скачать образец

Подготовка блока

---

Интеллектуальная подготовка

Предложения по подготовке к обучению данного модуля

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Запуск модуля

Подготовьтесь к преподаванию этого модуля, погрузившись в стандарты, большие идеи и связи с предыдущим и будущим содержанием. Запуск модулей включает в себя серию коротких видеороликов, целевую литературу и возможности для планирования действий.

Обновление до Plus

Интеллектуальная подготовка для всех модулей

• Прочтите и прокомментируйте разделы «Сводка модуля» и «Основные сведения» плана модуля.
• Выполните все целевые задачи и снабдите их комментариями, учитывая «Сводку модуля» и «Основные сведения».
• Пройти итоговую оценку.

Интеллектуальная подготовка для конкретных модулей

• Прочтите статью «Моделирование с помощью математики» на канале Teaching Channel и посмотрите видеоролики о трехактных задачах.
• Прочитайте документ «Типы ситуаций для операций в задачах Word» от Achieve the Core для умножения и деления. Определите типы словесных проблем любых применимых оценочных вопросов.
• (необязательно) Прочтите стр. 22–28 документа «Операции и алгебраическое мышление» («OA») Progressives о 3 классе.
• Прочтите следующую таблицу, в которой указаны модели, используемые во всем устройстве.

Равные группы	Пример:  4 равные группы по 3 звезды
Массив	Пример: 4 ряда по 3
Ленточная схема один к одному	Пример:  Есть 10 команд по 4 ученика в каждой. Сколько учеников во всех командах?
Диаграмма ленты	Пример: В каждом 4 мешка по 3 сливы. Сколько всего слив?
График
Гистограмма

Основные понятия

Основные математические понятия, которые учащиеся поймут в этом модуле

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

• В Соединенных Штатах принято представлять уравнение $$3\times 6 = \square$$ в виде 3 групп по 6 элементов в каждой: 3 шестерки (в отличие от 6 групп).
  из 3). «Но в других странах уравнение 3 × 6 = □ означает, сколько будет 3 вещей, взятых 6 раз (6 групп по 3 вещи в каждой): шесть троек. Некоторые учащиеся приносят эту интерпретацию уравнений умножения в класс. Поэтому полезно обсудите различные интерпретации и позвольте учащимся использовать то, что используется у них дома» (OA Progression, стр. 25).
• Уравнение $$20\div 4 = \square$$ можно интерпретировать двумя способами: есть 20 объектов, которые нужно разделить на группы по 4, и мы хотим знать, сколько групп мы можем составить (модель измерения деления), или есть 20 объектов, которые нужно разделить на 4 группы, и мы хотим знать, сколько объектов находится в каждой группе (разделительная модель разделения).
• Осмысление задач и настойчивость в их решении — важная практика при решении текстовых задач. Ключевые слова не всегда указывают на правильную работу.
• Задачи на умножение можно решать с помощью различных стратегий возрастающей сложности, включая создание и подсчет всех величин, участвующих в умножении или делении (стратегия уровня 1), повторный счет заданного числа (уровень 2) и использование свойства операций составления и разложения неизвестных фактов на известные (уровень 3).

Материалы

Материалы, изображения и инструменты, которые потребуются преподавателям и учащимся для этого раздела

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

• Счетчики (максимум 20 на одного учащегося или небольшую группу) – вместо этого учащиеся могут использовать обычный материал для занятий, например скрепки

Словарный запас

Термины и обозначения, которые учащиеся изучают или используют на уроке

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

массив

символ деления, $${\div}$$

деление/деление 2 делимое

делимое 3

9000 или

равные группы

коэффициент

ключ

символ умножения, $${\times}$$

умножение/умножение

произведение

частное

строка/столбец

масштаб

3 Чтобы увидеть весь словарный запас для модуля 2, просмотрите наш глоссарий лексики для 3-го класса.

Модульная практика

---

Словесные задачи и упражнения на беглость речи

Получите доступ к ежедневной практике со словесными задачами и нашим ориентированным на содержание упражнениям на беглость речи, созданным, чтобы помочь учащимся укрепить свои навыки применения и беглости речи.

Предварительный просмотр

Узнать больше

Схема урока

---

Тема A: Значение умножения и деления

Определите и создайте ситуации с участием равных групп и опишите эти ситуации, используя язык и обозначения умножения.

3.ОА.А.1

Идентифицируйте и создавайте ситуации, связанные с массивами, и описывайте эти ситуации, используя язык и нотацию умножения.

3.ОА.А.1

Идентифицируйте и создавайте ситуации с неизвестным размером группы и находите размер группы в ситуациях.

3.ОА.А.1 3.ОА.А.2 3.ОА.А.3

Определить и создать ситуации с участием неизвестного количества групп и найти количество групп в ситуациях.

3.ОА.А.1 3.ОА.А.2 3.ОА.А.3

Свяжите умножение и деление и поймите, что деление может представлять ситуации неизвестного размера группы или неизвестного количества групп.

3.ОА.А.1 3.ОА.А.2 3.ОА.А.3 3.OA.B.6

Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.

Уже есть учетная запись? Войти

Тема B: Умножение и деление на 2, 5 и 10

Добейтесь беглости с фактами умножения, используя единицы 2, 5 и 10.

3.ОА.А.1 3.ОА.С.7

Докажите коммутативность умножения.

3.OA.B.5

Добейтесь беглости с фактами деления, используя единицы 2, 5 и 10.

3.ОА.А.2 3.OA.B.6 3.ОА.С.7

Решить одношаговые текстовые задачи на умножение и деление с использованием единиц 2, 5 и 10.

3.ОА.А.1 3.ОА.А.2 3.ОА.А.3

Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.

Уже есть учетная запись? Войти

Тема C: Умножение и деление на 3 и 4

Развивайте беглость с умножением и делением, используя единицы измерения 3.

3.ОА.А.1 3.ОА.А.2 3.OA.B.5 3.OA.B.6 3.ОА.С.7

Развивайте беглость с умножением и делением, используя единицы 4.

3.ОА.А.1 3.ОА.А.2 3.OA.B.5 3.ОА.С.7

Решите одношаговые текстовые задачи на умножение и деление, используя единицы 3 и 4.

3.ОА.А.1 3.ОА.А.2 3.ОА.А.3

Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.

Уже есть учетная запись? Войти

Тема D: Более сложные задачи на умножение и деление

Определите неизвестное целое число в умножении или уравнении деления, связывающем три целых числа, включая уравнения с буквой, обозначающей неизвестную величину.

3.ОА.А.4 3.ОА.С.7 3.OA.D.8

Решайте одношаговые текстовые задачи на умножение и деление и записывайте контексты задач, чтобы сопоставить выражения и уравнения.

3.ОА.А.1 3.ОА.А.2 3.ОА.А.3

Решите двухэтапные текстовые задачи на умножение и деление.

3.OA.D.8

Решите двухэтапные текстовые задачи, включающие все четыре действия.

3.OA.D.8

Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.

Уже есть учетная запись? Войти

Тема E: масштабированное изображение и гистограммы

Создавайте масштабированные графические изображения, где предусмотрен масштаб.

3.МД.Б.3

Создавайте масштабированные графические изображения, масштаб которых необходимо определить.

3.МД.Б.3

Создавайте гистограммы с масштабированием, где предусмотрен масштаб.

3.МД.Б.3

Создайте гистограммы с масштабированием, где необходимо определить масштаб.

3.МД.Б.3

Решите одно- и двухэтапные задачи со словами, используя информацию, представленную в масштабированном изображении и гистограммах.

 

3.МД.Б.3 3.OA.D.8

Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.

Уже есть учетная запись? Войти

Общие базовые стандарты

---

Ключ

Основной кластер

Вспомогательный кластер

Дополнительный кластер

Основные стандарты

Стандарты содержания, рассматриваемые в этом модуле

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Измерения и данные

• 3. МД.Б.3 — Нарисуйте диаграмму в масштабе и гистограмму в масштабе, чтобы представить набор данных с несколькими категориями. Решайте одно- и двухэтапные задачи «насколько больше» и «на сколько меньше», используя информацию, представленную в масштабированных гистограммах. Например, нарисуйте гистограмму, в которой каждый квадрат гистограммы может представлять 5 домашних животных.

Операции и алгебраическое мышление

• 3.ОА.А.1 – Интерпретируйте произведения целых чисел, например, интерпретируйте 5 × 7 как общее количество объектов в 5 группах по 7 объектов в каждой. Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7.

• 3.ОА.А.2 — Интерпретировать целочисленные частные целых чисел, например, интерпретировать 56 ÷ 8 как количество объектов в каждой доле, когда 56 объектов разделены поровну на 8 долей, или как количество долей, когда 56 объектов разделены на равные доли по 8 объекты каждый. Например, опишите контекст, в котором количество долей или количество групп можно выразить как 56 ÷ 8.

• 3.ОА.А.3 – Используйте умножение и деление в пределах 100 для решения текстовых задач в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например, используя рисунки и уравнения с символом для неизвестного числа для представления проблемы.

• 3.ОА.А.4 — Определить неизвестное целое число в умножении или делении уравнения, связывающего три целых числа. Определите неизвестное целое число в умножении или делении уравнения, связывающего три целых числа. Например, определите неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ?

• 3.ОА.Б.5 — Применение свойств операций как стратегий умножения и деления. Студентам не нужно использовать формальные термины для этих свойств. Пример: зная, что 8 × 5 = 40 и 8 × 2 = 16, можно найти 8 × 7 как 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. ( Распределительное свойство.) Пример: если известно 6 × 4 = 24, то известно и 4 × 6 = 24 (перестановочное свойство умножения). 3 × 5 × 2 можно найти из 3 × 5 = 15, тогда 15 × 2 = 30 или на 5 × 2 = 10, тогда 3 × 10 = 30. (Ассоциативное свойство умножения.)

• 3.ОА.Б.6 — Понимайте деление как проблему неизвестного фактора. Например, найдите 32 ÷ 8, найдя число, которое дает 32 при умножении на 8.

• 3.ОА.С.7 — Свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная, что 8 × 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.

• 3.OA.D.8 — Решите двухэтапные текстовые задачи, используя четыре операции. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените обоснованность ответов, используя вычисления в уме и стратегии оценки, включая округление. Этот стандарт ограничивается задачами, поставленными с целыми числами и имеющими целочисленные ответы; учащиеся должны знать, как выполнять операции в общепринятом порядке, когда нет скобок для указания определенного порядка (порядок операций).

Основополагающие стандарты

Стандарты, описанные в предыдущих единицах или классах, которые важны для текущей единицы

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Измерения и данные

• 2.МД.Д.10

Числа и операции в десятичной системе счисления

• 2. НБТ.А.2

• 3.НБТ.А.2

Операции и алгебраическое мышление

• 2.ОА.А.1

• 2.OA.C.3

• 2.ОА.С.4

Будущие стандарты

Стандарты будущих классов или разделов, которые связаны с содержанием данного раздела

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Числа и операции в десятичной системе счисления

• 4.НБТ.Б.5

• 4.НБТ.Б.6

Числа и операции — дроби

• 4.NF.B.4

• 5.NF.B.3

• 5. NF.B.4

• 5.NF.B.5

• 5.NF.B.6

• 5.NF.B.7

Операции и алгебраическое мышление

• 4.ОА.А.1

• 4.ОА.А.2

• 4.ОА.А.3

• 4.ОА.Б.4

Стандарты математической практики

• CCSS.MATH.PRACTICE.MP1 – Разбираться в проблемах и настойчиво решать их.

• CCSS.MATH.PRACTICE.MP2 — Рассуждайте абстрактно и количественно.

• CCSS.MATH.PRACTICE.MP3 — Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.

• CCSS.MATH.PRACTICE.

  Добавить комментарий Отменить ответ

  Ваш адрес email не будет опубликован. Обязательные поля помечены *

  Комментарий *

  Имя *

  Email *

  Сайт