Конспект урока таблица пифагора 3 класс: Разработка урока по математике на тему: “Таблица Пифагора” (3класс)

Таблица умножения и деления с числом 4. Таблица Пифагора

Кхе-кхе… А вот и я, Матюша.

Соскучились? Сегодня я познакомлю вас с таблицей умножения и деления с числом четыре. Я наслышан, что таблицу умножения и деления с числами два и три вы уже знаете. Да и умножение на один, надеюсь, труда для вас не составляет. Но, всё-таки, повторить умножение на эти числа стоит. Повторение – мать учения. Итак, друзья, за работу.

Четыре умножить на один – один. Один умножить на четыре – один.

Четыре умножить на два – восемь. Два умножить на четыре – восемь.

Четыре умножить на три – двенадцать. Три умножить на четыре – двенадцать.

Ну а дальше будем составлять. Смотрите-ка на ответы – четыре, восемь, двенадцать.

Как только второй множитель увеличивается на один, произведение увеличивается на четыре.

Следующий пример у нас – четыре умножить на четыре. А ответ будет на четыре больше двенадцати, то есть шестнадцать. И во втором столбике – то же самое.

Четыре умножаем на пять. Ответ на четыре больше шестнадцати – двадцать. Ну и пять умножить на четыре, конечно, тоже двадцать.

От перестановки множителей произведение не меняется.

Четыре умножаем на шесть. Ответ на четыре больше двадцати – двадцать четыре. Шесть умножить на четыре – тоже двадцать четыре.

Четыре умножить на семь – двадцать восемь. Семь умножить на четыре двадцать восемь.

Четыре умножить на восемь – тридцать два. Восемь умножить на четыре – тридцать два.

Четыре умножить на девять – тридцать шесть. Девять умножить на четыре – тридцать шесть.

Ну а уж четыре умножить на десять – конечно сорок, как и десять умножить на четыре – сорок.

Вот таблицу умножения мы и составили.

А теперь посмотрите, сколько вы уже знаете и сколько осталось выучить.

Ну что, с умножением справились, пора приниматься за деление. А ведь, как известно, деление – это действие обратное умножению. И сейчас самое время вспомнить правило. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. То есть, таблицу деления мы будем составлять на основе таблицы умножения.

Вот эти примеры мы уже знаем.

Ну а шестнадцать разделить на четыре? Конечно, четыре.

Двадцать разделить на четыре? Пять. А двадцать разделить на пять – четыре.

Двадцать четыре разделить на четыре – шесть. Двадцать четыре разделить на шесть – четыре.

Двадцать восемь разделить на четыре – семь. Двадцать восемь разделить на семь – четыре.

Тридцать два разделить на четыре – восемь. Тридцать два разделить на восемь – четыре.

Тридцать шесть разделить на четыре – девять. Тридцать шесть разделить на девять – четыре.

Сорок разделить на четыре – разумеется, десять. А сорок разделить на десять – четыре.

Ого, сколько примеров получилось. А выучить-то надо гора-аздо меньше.

Но я чувствую, что вы немного устали. Впрочем, как и я. Поэтому я предлагаю вам совершить маленькую экскурсию в древние века.

Оказывается, старейшая известная таблица умножения обнаружена в Древнем Вавилоне и имеет возраст примерно 4000 лет.

В древнем Китае примерно 2000 лет назад пользовались таблицей умножения, более похожей на современную.

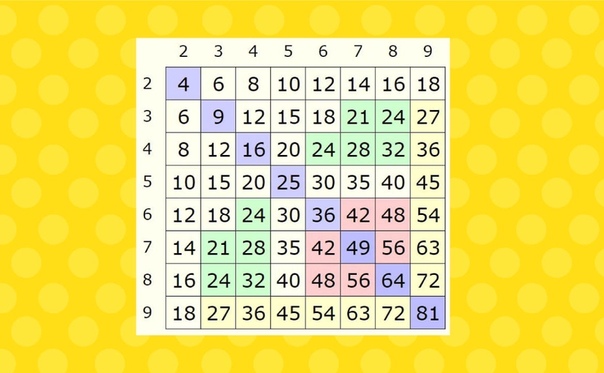
Но сейчас часто пользуются такой таблицей умножения, которую называют «

Таблица Пифагора». Считают, что древнегреческий ученый и математик Пифагор Самосский, живший примерно полторы тысячи лет назад, составил эту таблицу умножения. Вот как она выглядит:

И сегодня я научу вас пользоваться этой таблицей.

Посмотрите, как в ней расположены числа. Сначала в горизонтальной строчке и в первом столбике числа от одного до десяти. Потом – все результаты умножения на два, то есть четные числа, Дальше – результаты умножения на три. Потом на четыре. И так далее.

Вот, например, вам надо умножить три на четыре. Находим в первом столбике число три. В верхней строчке число четыре. Ведем от них навстречу друг другу линии, или стрелки. Число на месте встречи и будет результатом умножения этих чисел, то есть, произведением. Произведение чисел три и четыре равно двенадцати.

Но можно было и наоборот – в верхней строчке найти число три, а в первом столбике – четыре. Всё равно место встречи стрелок – число двенадцать. Неважно – первый множитель выбирать в первом столбце или в первой строке; второй множитель в первой строке или в первом столбце. Ведь вы помните, что от перестановки множителей произведение не меняется.

А теперь попробуем умножить число четыре на семь. Вот четыре, вот семь. Стрелки бегут навстречу. Произведение чисел четыре и семь равно двадцати восьми.

А как вы думаете, делить можно при помощи этой таблицы? Конечно, можно.

Например, двадцать четыре надо разделить на шесть. Теперь первое число выражения, двадцать четыре, мы ищем не в крайних рядах таблицы, а в её середине. Э, да здесь два числа двадцать четыре!

Какое из них выбрать? Посмотрите,

одно из чисел находится на перекрестке линий от чисел три и восемь. Второе – на перекрестке чисел шесть и четыре. Так как нам надо найти частное чисел двадцать четыре и шесть, то конечно, мы выберем второе число. Так как это произведение чисел шесть и четыре, значит, двадцать четыре разделить на шесть, равно четыре.

А если, к примеру, надо найти частное чисел двадцать один и три? Находим в середине таблицы число двадцать один. От него можно провести стрелки к числам три и семь. Значит, двадцать один разделить на три, равно семь!

Ну что, вы поняли, как пользоваться таблицей Пифагора? Правда здорово? Это я Пифагору на ушко про эту таблицу рассказал. Не верите? Дело ваше.

А я свое дело сделал. Теперь вам осталось только таблицы умножения и деления с числом четыре наизусть выучить, да ещё потренироваться в работе с

таблицей Пифагора. И перед тем, как нам сегодня распрощаться, я хочу вам сказать слова великого Пифагора:

Не делай никогда того, чего ты не знаешь, но научись всему, что следует знать, и тогда ты будешь вести спокойную жизнь….

Ну всё. Пойду я немного прогуляюсь, а потом спать. Всем пока!

Разработка урока математики на тему «Таблица умножения», 2 класс

№ п/п	Этап урока	Содержание
1	Орг.момент	Открытий путь – нелёгкий путь, но человеку не свернуть… Что? Почему? – за ним следят, чтоб шёл вперёд, а не назад. Вот почему из года в год наука движется вперёд! Желаю и вам успеха в продвижении вперед!
1	Актуализация опорных знаний Устный счет.	1) -Чтобы открыть новую математическую тайну, проведём разминку: -Откройте тетради. Запишите число, классная работа. -Какое сегодня число? -Дадим математическую характеристику числа 21. Какое это число? (двузначное, нечетное, 2д.1ед.) Назовите соседей числа? (20, 22) -На минутке чистописания запишите это число (21) и продолжите запись числового ряда в порядке уменьшения на 4. 21, 17, 13, 9, 5, 1 -Молодцы! Посмотрите на доску и проверьте себя. -У кого все правильно, поставьте + на полях. Если есть ошибки – исправьте. (слайд 1)   2. -Как называется эта фигура? (квадрат, прямоугольник, многоугольник, четырехугольник) (слайд 2)   (представлен квадрат со стороной 5 см) -Какое бы вы задание дали по этой фигуре? (Найти периметр, площадь) -Что называется периметром? (Сумма длин всех сторон) – Как найти периметр? ( сложить все стороны, 5+5+5+5=20 см) -Каким действием можем заменить эту сумму? (умножением) -Почему? ( одинаковые слагаемые берём несколько раз) -Какое выражение получится? (5*4=20 см) На 3 слайде: 3 5+5+5+5=20см 5•4=20 см – Чем похожи эти записи? -Чем отличаются? -Что показывает первое число при умножении? (какое число складываем) -Что показывает второе число? (сколько раз складываем первое число) -Что такое умножение? (замена суммы одинаковых слагаемых)
2	Постановка учебной задачи. (Самоопределение к деятельности)	4. На доске написаны слова: «Сумма», «Множитель», «Множитель», «Произведение». Слайд 4 -Прочитайте слова, написанные на доске, и найдите среди них «лишнее» слово. (Сумма). – Объясните свой ответ. ( Так называются числа при умножении, а само действие называется…(умножение) -Что связывает между собой действия «сложения» и «умножения»? ( умножение это сложение одинаковых чисел) -Решите следующие выражения. Слайд 5 16-7                12+3      3+3+3+2+3 4+4+4+4          8+8+8+8+8+8+8+8+8 – Какое из них сложнее решить? (последнее) -Каким действием нам было легче считать? ( умножением 8*9) А чтобы быстро считать нужно научиться пользоваться таблицей умножения, а затем выучить её.
3	Открытие новых знаний   Знакомство с таблицей умножения  Физминутка	-Что такое умножение? Это умное сложение. Ведь умней умножить раз, Чем слагать всё целый час! -А вот эта таблица вам знакома? -Где вы её видели? ( на обложке в тетради) -Правильно! А вы знаете как она называется? Да ребята, это таблица умножения. Слайд 6 1х1=1 2х1=2 3х1=3 4х1=4 5х1=5 1х2=2 2х2=4 3х2=6 4х2=8 5х2=10 1х3=3 2х3=6 3х3=9 4х3=12 5х3=15 1х4=4 2х4=8 3х4=12 4х4=16 5х4=20 1х5=5 2х5=10 3х5=15 4х5=20 5х5=25 1х6=6 2х6=12 3х6=18 4х6=24 5х6=30 1х7=7 2х7=14 3х7=21 4х7=28 5х7=35 1х8=8 2х8=16 3х8=24 4х8=32 5х8=40 1х9=9 2х9=18 3х9=27 4х9=36 5х9=45 1х10=10 2х10=20 3х10=30 4х10=40 5х10=50 6х1=6 7х1=7 8х1=8 9х1=9 10х1=10 6х2=12 7х2=14 8х2=16 9х2=18 10х2=20 6х3=18 7х3=21 8х3=24 9х3=27 10х3=30 6х4=24 7х4=28 8х4=32 9х4=36 10х4=40 6х5=30 7х5=35 8х5=40 9х5=45 10х5=50 6х6=36 7х6=42 8х6=48 9х6=54 10х6=60 6х7=42 7х7=49 8х7=56 9х7=63 10х7=70 6х8=48 7х8=56 8х8=64 9х8=72 10х8=80 6х9=54 7х9=63 8х9=72 9х9=81 10х9=90 6х10=60 7х10=70 8х10=80 9х10=90 10х10=100
		-А теперь рассмотрите внимательно две таблицы. Слайд 7 – Одинаковые ли они? (нет) -Как называется первая таблица? (таблица сложения) -С какой целью вы знакомились с таблицей сложения? (чтобы быстро находить суммы) -Как вы думаете, для чего нам нужна таблица умножения? (чтобы находить произведение) -Правильно! -Правильно! А вторая таблица называется -таблица умножения, или еще её называют таблицей Пифагора. -Интересно, почему Пифагора? Это слово еще написано с заглавной буквы. Наверное, он и есть имя создателя этой таблицы. -Давайте убедимся в том, что эта таблица отличается от таблицы сложения. -Найдите число, которое стоит на пересечении столбца с номером 5 и строки с номером 2. ( 10) -А почему число 10? ( потому что 5•2=10) – А в таблице сложения, какое число стоит на пересечении этих столбца и строки? (7 т. к. 5+2=7) Слайд 8 Справочный материал Табли́ца умноже́ния, она же табли́ца Пифаго́ра — таблица, где строки и столбцы озаглавлены множителями, а в ячейках таблицы находится их произведение. Используется для обучения школьников умножению. А вот когда была создана эта таблица умножения? Узнаем из видеофрагмента. (включить видео) Слайд 9
4	Первичное закрепление	6) Работа по учебнику – А теперь давайте поучимся работать по этой таблице. – Откройте учебник на с 52 – В таблице умножения стоят произведения чисел от 1 до 10. Например, произведение чисел 3 и 5 можно найти двумя способами. 1-й способ: нужно найти тройку в левом столбце и пятерку в верхней строке, провести от 3 горизонтальную линию и от 5 вертикальную. Клетка, на которой линии встречаются, является произведением (в данном случае 15) – Кто может назвать 2-й способ? Давайте проверим. Слайд 10
6	Закрепление изученного материала	7. Работа над темой урока. 1) Фронтальная работа. – Сейчас мы потренируемся решать примеры, используя таблицу умножения. Положите перед собой листочки с таблицей умножения, найдите №1, читаем задание и найденные произведения раскрашиваем синим карандашом. Кто справится первый поднимите руку, я подойду, оценю 3 человека. 3∙ 8, 5 ∙ 7, 6 ∙ 6 , 4 ∙ 9 , 7 ∙ 4 , 10 ∙ 3 – В каких строчках или столбцах стоят только четные числа? – Там, где множители четные числа
7	Включение нового знания в систему знаний	А сейчас мы поработаем в парах. Давайте вспомним как нужно работать в паре Слайд 11 Сначала 1 вариант выписывает в тетрадь любое двузначное число из таблицы, а 2 вариант находит в таблице и записывает произведение равное этому числу. Меняемся ролями. Молодцы! Оценить 1 пару. № 3, с.54 У доски и в ноутбуках выполняют 4 выражения. -Назовите числа в строчке, которая начинается с числа 4.  (4,8,12,16,20,24,28,32,36,40) -Как они изменяются? (увеличиваются на 4) -Как изменяются числа в столбце таблицы, который начинается с числа 8? ( увеличиваются на 8) Сформулируйте правило для строки, которая начинается с числа 7 ( каждое следующее число увеличивается на 7) Работа по слайду. Восстановите спрятанные числа. Слайд 12)
8	Самостоятельная работа	Индивидуальная работа -А теперь вы попробуете самостоятельно выполнить задание с помощью таблицы умножения. Карточки каждому ученику 4•3=              6•5+18= 5•8=              9•4+60=          или задание  со с. 54, №3 выполняется в персональных ноутбуках.
9	Итог урока	9) Итог урока. -Как называется новая таблица, с которой вы познакомились на уроке? (умножения, Пифагора) -Что такое умножение? (сложение одинаковых чисел) – Что записано в клетках таблицы (произведения чисел) Давайте прочитаем и попробуем закончить предложения: Незаконченное предложение. Слайд №13 Я познакомился … Я научился… Я вспомнил… Рефлексия: Оцените свою работу на уроке. (дети выбирают смайлики и показывают) Оценивание
		8) Домашнее задание: 1)подготовить сообщение о Пифагоре;  2) с.53, №6

Конспект открытого урока математики по теме Умножение на двузначное и трехзначное число

Тема урока: «Умножение на двузначное и трехзначное число».

Цели:

Образовательные: продолжить работу по отработке вычислительных навыков, повторить связь между величинами (скорость, время, расстояние), знание порядка выполнения действий; Коррекционные: упражнять учащихся в умении умножать многозначное число на двузначное и трёхзначное, развивать функции анализа и синтеза в процессе мыслительных операций, развивать математическую речь учащихся, познавательную активностьВоспитательные: способствовать развитию интереса к предмету, воспитывать самостоятельность в учебной работе, коммуникабельность.

Тип урока: закрепление

Оборудование:

учебник М.И.Моро “Математика 4 класс”, мультимедийный проектор, ПК, экран, презентация, карточки для индивидуальной работы, тесты.

ХОД УРОКА

1. Организационный момент.

Слайд 1

Очень строгая наука,

Очень точная наука,

Интересная наука –

Это____________

Математика любит внимательных, организованных людей. Сейчас проверим, кто уже настроился на хорошую работу.

2. Актуализация знаний.

-Что у вас на партах? (таблица Пифагора). Я называю табличные случаи умножения, а вы закрашиваете квадрат с правильным ответом.

4х7, 6х6, 8х5, 4х5, 8х7, 6х5, 5х5, 6х7,8х6, 7х7, 4х6, 7х5. Слайд 2

–Какая цифра у вас получилась? – Какое это число? (Четное).

Допишите любые две цифры, чтобы у вас получилось трехзначное число.

Запишите число, классная работа и пропишите полученное трехзначное число всю строку. Это и есть минутка чистописания.

3. Работа по теме урока.

– Что мы делали на предыдущем уроке?

-Сегодня мы с вами продолжим работу по данной теме

– Давайте вспомним алгоритм умножения на двузначное число. Слайд 3

46 ∙ 73

(1 ученик решает у доски с подробным объяснением, дети записывают в тетрадь).

– А теперь давайте повторим алгоритм умножения на трёхзначное число Слайд 4

∙ 134 (1 ученик решает у доски с подробным объяснением).

4.Решение задачи. Слайд 6

Стр.43 №149

Прочитайте задачу.

Экскаватором можно выкопать за 1 час канаву длиной 20 м. Одну канаву копали 10 часов, а другую 12 часов. Найди общую длину канав, которые выкопали за это

время. Реши задачу разными способами. Сравни их и выбери удобный способ.

-Что нам известно в задаче?

-Что нам дает число 10? Число 12?

-Что необходимо найти?

-Как найти общую длину?

-Кто пойдет к доске?

10 ∙ 20 = 200 (м) – за 10 часов

12 ∙ 20 = 240 (м) – за 20 часов200 + 240 = 440 (м) – за все время.

– Каким еще способом можно решить эту задачу?

(10 + 12) ∙ 20 = 440 (м) – за все время.

-Запишите самый удобный вариант.Проверка Слайд 7

5. Физкультминутка (танец с музыкальным сопровождением).

«Веселая зарядка»

6. Самостоятельная работа учащихся.

-Работаем самостоятельно! Что это: пример, уравнение, выражение?

Перед вами математические выражения Слайд 8

25 ∙ (364 + 242)= 15150

702 ∙ 69 + 702 ∙ 18 = 71074

(78213-75209) ∙ 207-5 ∙ 308 = 620288

Выберите то выражение, которое вам по силам.

Проверка: Поднимите руки, кто выбрал первое выражение. Проверьте правильно ли вы решили своё выражение. Поднимите руки, кто выбрал для решения второе выражение. Проверяем. Проверка третьего выражения. (Проверка по шаблону)

7. Работа в парах Слайд 9, 10

Для работы в парах мы используем задачи, знания которых нам пригодятся на проверочной работе.

-Как мы находили площадь и периметр квадрата?

S = а · b

Р = а · 4

Задание для 1 ряда:

Периметр квадрата равен 36 см. Найдите его площадь.

Взаимопроверка. Проверка по шаблону:

36 : 4 = 9 (см) – сторона квадрата

9 · 9 = 81 (см²) – площадь квадрата

2 ряд:

Длина стороны квадрата 6 см.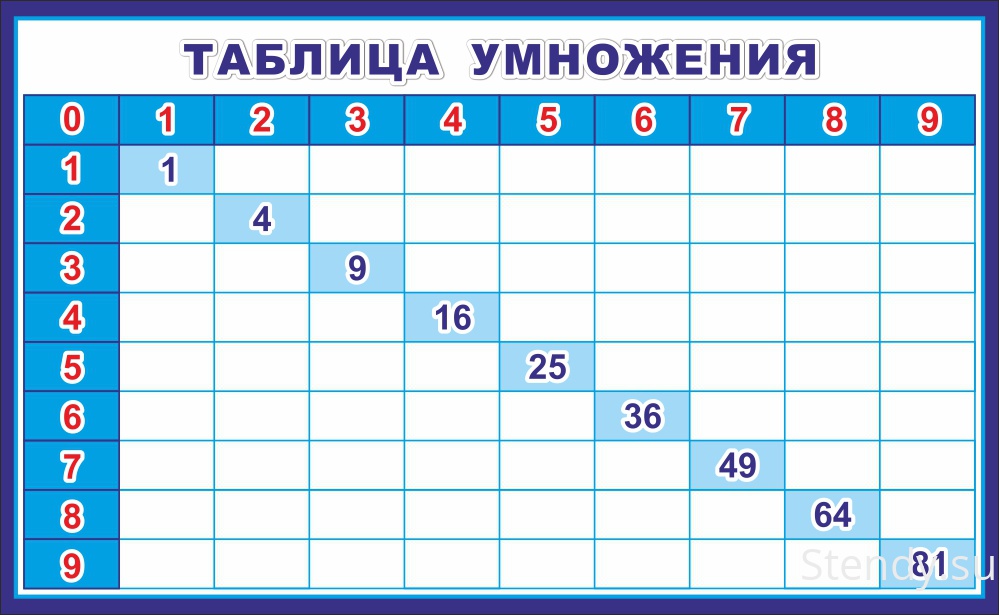 Узнайте площадь и периметр квадрата.

Взаимопроверка. Проверка по шаблону:

1) 6 ∙ 6 = 36

2) 6 ∙ 4 = 24

Ответ: площадь квадрата 36 см², периметр квадрата 24 см.

3 ряд:

Найти площадь и периметр квадрата, длина сторон которого 7см

Взаимопроверка. Проверка по шаблону.

S = 7 · 7=49 (cм²)

Р = 7 · 4=28 (cм)

8. Работа по учебнику: Стр. 43 № 146 Слайд 11

2 примера решить у доски.

9. Тест по изученной теме.

У вас на парте лежат тесты. Подпишите их. Сосредоточьтесь. Начинайте выполнять задания теста.

ТЕСТ. Слайд 12

1. Чему равно число, содержащее 149 единиц I класса и 37 единиц II класса?

1) 37149 3) 149037

2) 370149 4) 14937

2. Выбери запись, где умножение выполнено без ошибок.

1) 237 2) 490

105 360

____ ____

1185 294

+ 237 +147

176400

4. Ширина прямоугольника 2см, длина -7 см. Найди площадь.

1) 9 см² 3) 14 см²

2) 14 см² 4) 5 см²

4. С какой скоростью должен ехать автомобиль, чтобы проехать за 7 часов 560 км?

1) 60 км/ч 3) 80 км/ч

2) 90 км/ч 4) 80 км

Взаимопроверка (поменяйтесь тестами).

Проверка по шаблону Слайд 13

1) 1 2) 4 3) 2 4) 3

10. Домашнее задание: Слайд 14

1 вариант – стр.43 № 148

2 вариант – стр.43 № 153

Стр.44 №157 – по желанию.

11. Итог урока.

Выставление оценок.

Вот и кончился урок. Давайте подведем итоги нашего сегодняшнего урока. Чем сегодня занимались? (ответы детей)

В чём немножко затруднялись? (ответы детей)

Вам понравился урок?

Пусть урок пойдёт вам впрок!

12. Рефлексия. Слайд 15

Для рефлексии мы будем использовать прием «Паровозик»: На каждой парте лежат по два жетона: один – с улыбающимся личиком, другой – с грустным. Я на доске приклею поезд с вагончиками, на которых обозначены этапы урока. Я предлагаю вам опустить «веселое личико» в тот вагончик, который указывает на то задание, которое вам было интересно выполнять, а «грустное личико» в тот, который символизирует задание, которое показалось не интересным. Можно использовать только один жетон по вашему усмотрению.

Дети берут жетоны и опускают в вагончики.

Ребята, на этом наш урок окончен.

Спасибо за работу на уроке. Слайд 16.

Приложения

ТЕСТ.

1. Чему равно число, содержащее 149 единиц I класса и 37 единиц II класса?

1) 37149 3) 149037

2) 370149 4) 14937

2. Выбери запись, где умножение выполнено без ошибок.

1) 237 2) 490

105 360

____ ____

11 85 29 4

+ 237 +147

355 176400

Ширина прямоугольника 2см, длина -7 см. Найди площадь.

1) 9 см23) 14 см2

2) 14 см2 4) 5 см2

4. С какой скоростью должен ехать автомобиль, чтобы проехать за 7 часов 560 км?

1) 60 км/ч 3) 80 км/ч

2) 90 км/ч 4) 80 км

ТЕСТ.

1. Чему равно число, содержащее 149 единиц I класса и 37 единиц II класса?

1) 37149 3) 149037

2) 370149 4) 14937

2. Выбери запись, где умножение выполнено без ошибок.

1) 237 2) 490

105 360

____ ____

11 85 29 4

+ 237 +147

355 176400

Ширина прямоугольника 2см, длина -7 см. Найди площадь.

1) 9 см23) 14 см2

2) 14 см2 4) 5 см2

4. С какой скоростью должен ехать автомобиль, чтобы проехать за 7 часов 560 км?

1) 60 км/ч 3) 80 км/ч

2) 90 км/ч 4) 80 км

Если Вы являетесь автором этой работы и хотите отредактировать, либо удалить ее с сайта – свяжитесь, пожалуйста, с нами.

Конспект урока математики в 1 классе УМК «Начальная школа XXI века»Тема урока «Сложение с числом 0»

Саженкова Наталья Владимировна , учитель начальных классов
Смоленская область г.Смоленск

Цель овладение умением прибавлять число 0. Ожидаемые результатыУметь прибавлять число 0, уметь находить значение сумм по линейке Регулятивные – принимать и сохранять цель учебной деятельности – самооценка, взаимооценка Познавательные – формулировать обобщенные выводы на основании сравнения Коммуникативные – умение работать в группах, парах, мотивация к изучению нового материала способность к самооценке на основе критерия успешности учебной деятельности уважение к мыслям другого человека, доброжелательность Задачи урока 1. Сделать вывод о прибавлении нуля к числу.2. Организовать самооценивание обучающимися работы на уроке.

(справка о публикации находится на 2 листе в файле со свидетельством)

План-конспект урока математики по теме

«Сложение с числом 0»

Предмет: математика, 1 класс УМК: «Начальная школа XXI века»

Тема урока «Сложение с числом 0»

Тип урока: открытие новых знаний

Цель: овладение умением прибавлять число 0.

Ожидаемые результаты:Уметь прибавлять число 0,

уметь находить значение сумм по линейке

Регулятивные:

– принимать и сохранять цель учебной деятельности;

– самооценка, взаимооценка;

Познавательные:

– формулировать обобщенные выводы на основании сравнения;

Коммуникативные:

– умение работать в группах, парах, мотивация к изучению нового материала;

способность к самооценке на основе критерия

успешности учебной деятельности; уважение к мыслям другого человека, доброжелательность

Задачи урока:

1. Сделать вывод о прибавлении нуля к числу.2. Организовать самооценивание обучающимися работы на уроке.

Оборудование: Рудницкая Н.Ф. Математика: Учебник для 1 класса: в 2 частях. Издательский центр «Вентана – Граф» 2011г; презентация, мультимедийный проектор, сигнальные карточки

Ход урока:

1.Организационный момент:

– Ну, ребята, был звонок.

Начинается урок.

Повернитесь все назад,

Гости там у нас сидят.

Мило улыбнитесь,

Обратно повернитесь.

И тихонечко садитесь.

Снег летает и сверкает

В золотом сиянии дня,

Словно пухом устилает

Все дороги и дома.

Сыплет, сыплет снег – снежок,

Начинаем наш урок.

Мы с вами продолжаем изучать математику. Гостем на нашем уроке будет ещё одна наука, а какая вы узнаете разгадав ребус.

Кто знает, что изучает эта наука?( изучает прошлое).Так вот мы сегодня узнаем интересные сведения из истории математики.

2.Минутка чистописания: Обратите внимание на доску. Прочитайте числа 5 2 7 18 9 .Найдите лишнее число, почему оно лишнее?( двузначное) Именно в этом веке был издан первый учебник по арифметике, так раньше называли математику.(Прописываем в тетради число 18.)Что вы можете сказать об этом числе? Какие цифры мы используем для его записи. Как правильно записываются двузначные числа?

3.Устный счёт: Посмотрите на картину Богданова-Бельского Н.П. «Устный счёт» ,ясно, что это время старой школы более ста лет назад. Эта картина хранится в Третьяковской галерее.

Чем заняты дети? (Считают в уме).

1.Работа в парах

1 пара Поставь + или –

5 0 =5 7 0 =7

6 0=6 15 0=15

13 0=13

2 пара Вставь пропущенное число:

5+ =5 7+ =7

6+ =6 15+ =15

13+ =13

3 пара

Число	1	4	2	3	5	6	7
Увеличь на 0

4 пара «Математический футбол»

2. Индивидуальная работа

Соедини выражения с их значениями.

8+2 7 6-2

10

7-1 8 4+3

6

8-3 3 2+1

5

4-2 4 5+3

10-3 2 9-3.

3.Работа с классом

Решить математическую цепочку

2 команды «Кто быстрее?»

-8 +3 +4 -2 -1 +0 =

+3 +4 -1 -4 +0 =

Устный счёт с остальными

– Какое число при счёте следует за числом 8?

– Назовите число, предыдущее 8. Назовите число, следующее за 3.

– Покажите соседей числа 9; 3; 7.

– Какое число больше на 1, чем 8?

– Какое число меньше на 1, чем 4?

– Увеличьте 6 на 1 и еще раз на 1.

– Увеличьте 8 на 1.

– Уменьшите 7 на 1.

– Уменьшите 9 на 1 и еще раз на 1.

3. Задачи в стихах.

Семь рассерженных гусей,

Семь отчаянных друзей,

Ходят-бродят: «Га-га-га!»

Тут хозяйка позвала:

– Есть хотите?

– Да-да-да!

И пошли ватагой всей

Семь рассерженных гусей.

Семь гусей ушли кормиться.

Сколько же осталось птицы? (Нисколько.)

Три мартышки – три соседки –

С ветки прыгали на ветку.

Расшумелись, раскричались.

Дождь пошел – все разбежались.

– Сколько мартышек на ветке осталось? (0.)

– Сколько мартышек домой разбежалось? (3.)

4.Работа по теме урока

Проверка работы в парах

1 пара . Поставь + или –

5 + 0 =5 7 +0 =7

6 + 0=6

15 + 0=15

Какой знак был пропущен при решении примеров?( сложения) +

На доске появляется карточка со знаком +

2 пара Вставь пропущенное число: Какое число пропущено?(0)

5+ 0 =5 7+ 0 =7

6+ 0 =6 15+ 0 =15

13+ 0 =13

Давайте подумаем над чем мы будем работать на уроке.

«Сложение с числом 0»

Попробуйте продолжить

Узнаю

Научусь

Обратите внимание на последнюю запись математической цепочке

Что вы заметили?

+0= +0 =

3 пара Изменилось ли число ?

Число	1	4	2	3	5	6	7
Увеличь на 0	3	4	2	3	5	6	7

Нет. Какой вывод можно сделать?

Вывод по теме: если к числу прибавить нуль, получится то же число.

Ведущий :Рано утром, как только солнце косыми лучами коснулось земли, цифры двинулись в путь. Долго шли они под палящим солнцем и наконец добрались до реки Сложение.Цифры бросились к реке, чтобы напиться, но река сказала:

Сложение «Превратитесь в числа, встаньте парами и сложитесь! Тогда дам вам напиться». Ведущий :Все исполнили приказание реки. Ноль тоже встал в пару с одним из чисел. Но число, с которым он сложился, осталось недовольно: ведь река давала столько воды, сколько единиц получилось при сложении.

Сложение А от участия нуля число ни на сколько не увеличилось: сколько ни прибавляй ноль, больше не станешь

Давайте создадим модель правила

Представим что это число

Получаем модель правила

5.Первичное закрепление

Исследовательская работа по учебнику

Найдем на шкале линий число 0 и отсчитаем от него вправо 3 шага по единице. Придем к числу 3.)

Найдем на шкале линейки число 3 и сделаем от него вправо 0 шагов. Это означает, что мы остались на месте, не сделали ни одного шага, и ответ получился 3. Значит, 3 + 0 = 3.)

Повторите, какой вывод можно сделать.

Если к числу прибавить нуль, получится то же число.

Какой предмет вы использовали чтобы помочь цыплёнку шагать?(линейку)

Линейке исполнилось больше 200 лет. В средневековье монахи использовали вместо линейки тонкие свинцовые пластинки.

Работа по учебнику стр .12 № 2,3 устно 13 №4 №6( в тонкой тетради и у доски)

1) Решение задачи 3.

Задание. Составьте и решите задачу, ответ запишите, используя правило.

– Сколько карандашей в I коробке? (8.)

– Сколько карандашей во II коробке? (0.)

– Сколько карандашей в двух коробках? (8.) Почему?

– Как записать решение? (8 + 0 = 8.)

Учащиеся проверяют правило: если к числу прибавить 0, получится это же число.

2) Аналогичное решение задачи 4.

№6( в тонкой тетради и у доски)

Работа в рабочей тетради стр. 9 №1, 2,3

6.Физкульминутка

7.Закрепление

Работа в группе 1 Расшифруйте запись

3+4= А 8-4= М

12-2= И 5+0= К

6+3= Ц 9-1= Е

10+9= Т 5-3= Р

10-7= Н 8-2= У

4	7	19	8	4	7	19	10	5	7
м	а	т	е	м	а	т	и	к	а

Работа в группе 2 «Мозаика»

Решить примеры и собрать мозаику. Собрав мозаику, вы узнаете об одном великом математике всего мира

9+0	12+0	14+0
6+0	17+0	5+0
4+0	0+8	0+11

Работа в группе 3 «Мозаика» Соберите мозаику, и вы узнаете

об одном великом открытии

9+0	12+0	14+0
6+0	17+0	5+0
4+0	0+8	0+11

Самостоятельная работа с остальными учащимися

Работа по учебнику стр 12 №2

Проверка

Отчёт 1 группы –известный математик Пифагор

Отчёт 2 группы известное открытие -это таблица Пифагора или таблица умножения

Отчёт 3 группы

Математика –царица наук

Мы сегодня получили много знаний на уроке это маленькие зёрнышки . Я благодаря вам тоже сегодня сделала много открытий. И бросаю в этот сосуд зёрна знаний которыми поделилась с вами. Вы работали отлично поэтому я бросаю 5 зёрнышек.

Я узнал

Я научился

Мне понравилось

Итог урока

Презентация на тему “Таблица умножения на 2”

Это умное сложение. Ведь умней умножить раз, Чем слагать всё целый час! Столбик таблицы умножения. Давайте сравним наш столбик со столбиком на доске.

Путешествие в таблицу умножения

Что заметили? А как нам записать такую же? Поменять множители местами Самостоятельная работа. Проверка записи примеров. Квадрат А что вы знаете о квадрате? У квадрата все стороны равны 1 способ: Тогда в путь!

Презентация на тему “Таблица умножения на 2” по математике

Слайд 1 – Летим в путешествие на ракете. Заведем мотор. Встаньте, выйдите из-за парт. Наш девиз: В космос полетим отважно, Чтоб открыть секреты важные!

Аннотация к презентации

Выйдем из ракеты, оглядимся. Посмотрим направо, налево, вперед. Слайд 2 Читает слова Умняша Здравствуйте, ребята! Я — Умняш.

Добро пожаловать на планету Умножения! Здесь вас ждет много интересного Слайд3 – Ну, что, начнем знакомство с планетой Умножения. Слайд 4. Впереди нас ждут интересные задания. А за правильные ответы Умняш будет дарить вам пятерки. Слайд 5 Встаньте из-за парт. Раз, два, три, четыре, пять, Продолжаем мы играть! Слайд 6 Давайте назовем некоторых из них.

Найдите лишних обитателей планеты. Замените произведение чисел суммой, найдите значение выражений. Слайд 7 А теперь снежинки нам подскажут нужное направление. Сосчитайте всю снежную цепочку, запишите конечный результат. Слайд 8 – Молодцы, ребята! Слайд 9 Поставьте себе 5, если все выполнили Правильно и без ошибок. Умяш все видит и контролирует. За правильные ответы получают пятёрки. Нас ждет улица Сезам.

Слайд 10 Речевка. Ходьба на месте Раз, два, три, четыре, пять, Продолжаем мы играть! Слайд 11 Сравните произведения. Остаются два произведения 4 х 1; 4 х 0 – Прочитайте оставшиеся произведения. Гражданско- патриотические. Здоровый образ жизни.

Профессии Профориентация. Предметно- тематические. Жизнь замеча- тельных людей. Города, страны, столицы. Обучающий тренажер по математике позволяет изучать таблицу деления двузначных чисел на числа от 2 до 9 поэтапно с. Музыка внедрена в презентацию. Пригодится ли в жизни знание таблицы умножения? Урок математики 3 класс Разработал: Дашамолонова Г. Слайд 2.

Презентация на тему “Таблица умножения на 2”

Презентация по математике на тему “Знакомство с таблицей умножения”. Столичный учебный центр г. Москва. Дистанционные курсы. Оборудование: презентация по теме «Первичное знакомство с таблицей умножения. Умножение на 2», карточки для проверки.

Закрепление знания таблицы умножения и деления Цели:. Презентация “Таблица умножения и деления на 3” 2 класс. Уменьшаемое 41, а разность — Чему равно вычитаемое? Ресурс предназначен для закрепления таблицы умножения в 3 классе. Презентацию рекомендую использовать в индивидуальной работе. . ШУМО учителей математики: Россия, Санкт-Петербуг. Презентации Power Point математика для начальных классов скачать.

Тренажер школьникам: Таблица умножения Образовательные игры для детей и.

Таблица деления Разгони тучки Игра. Таблица Пифагора.

УМК “Школа. Презентация урока математики, 3 класс, программа “Гармония”. На уроке происходит знакомство с таблицей умножения и деления с числом 9 в занимательной форме, с применением мультимедиа-презентации,. Презентация по математике 3 класс таблица умножения играть. Задания на закрепление таблицы умножения и деления на 8 3 класс. Отец поймал 9 окуней, это в 3 раза больше, чем поймал сын..

Проверка знания таблицы умножения скачать бесплатно Социальная. К плану занятия прилагается презентация “Скоро каникулы”. Значит тема нашего урока: Урок 2. Сообщение темы урока: Деление на 9. Поэтому для всех педагогов является актуальным повышение квалификации по этому направлению! Подать заявку на курс. Скачать материал. Попробовать бесплатно. Презентация по русскому языку словарные слова , фронтальный опрос 2 класс. Конспект урока по русскому языку на тему: Презентация к уроку обучения грамоте в 1 классе” Фабрика букв”.

Индивидуальное обучение программа по математике для 4 класса. Презентация “Планирование досуговой деятельности”. Выступление на школьном методическом объединении. Не нашли то что искали? Вам будут интересны эти курсы: Оставьте свой комментарий Авторизуйтесь , чтобы задавать вопросы. Найдите подходящий для Вас курс.

Как ребенку быстро и легко выучить таблицу умножения?

Таблицу умножения обычно начинают проходить уже во втором классе, когда дети уверенно освоили сложение. Педагоги обычно говорят, что таблицу нужно учить наизусть, чтобы «отлетала от зубов». Казалось бы, это не так уж и необходимо. Например, умножить 7 на 6 — это то же самое, что просто взять 6 раз по 7 и сложить, не запоминая лишних цифр… Но мало того, что эти сложные операции затянут выполнение контрольных работ, — в обычной жизни, за пределами школы, знание таблицы умножения требуется постоянно. В магазине, дома, а в будущем — и на работе… Так что же, каждый раз строить длинные цепочки вычислений или доставать калькулятор? Нет, выучить таблицу все же придется — зато раз и навсегда.

Как помочь ребенку выучить таблицу умножения?

Помочь ребенку выучить таблицу умножения не так уж сложно, если правильно подойти к обучению. Вот несколько рекомендаций.

Заинтересуйте

У ребенка должна появиться мотивация. Не конфета и прогулка, хотя на усмотрение родителей можно использовать и эти методы, а что-то более значимое и долгосрочное. Сначала продемонстрируйте, в каких случаях, кроме урока в школе, таблица умножения необходима. Например, он хочет угостить пятерых друзей любимыми конфетами — каждому раздать по три, — и сколько же всего конфет принести? Или на день рождения к ребенку собираются три семьи, в каждой по три человека — сколько пар столовых приборов надо приготовить?

Нарисуйте школьнику печальную перспективу: вот в магазине его, доверчивого неуча, обманывает продавец. А вот он на работе не может умножить две цифры и достает калькулятор, а коллеги поднимают его на смех. Вот, в конце концов, он спустя годы решает в классе куда более длинные и сложные примеры, чем предлагают ему пока, и «плавает», потому что не знает основ. Без таблицы умножения в математике дальше не продвинуться! А без математики — не окончить школу и не пойти учиться на того, кем ребенок сейчас мечтает быть…

А чтобы избежать всех этих проблем, надо-то всего лишь взять и выучить эту таблицу! И уж с каким восхищением будут смотреть учителя и одноклассники, которым умножение пока не дается

Объясните суть таблицы умножения

В умножении второе число обозначает, сколько раз нужно сложить первое с самим собой. Это базовый момент, который должен усвоить ребенок, и заодно подстраховка, если он все-таки в ответственный момент забыл какой-то один результат в таблице умножения. Но, как мы уже заметили, постоянно на метод последовательного сложения вместо умножения полагаться не стоит.

Чтобы школьник лучше понял смысл, продемонстрируйте ему, что, например, 4 х 3 — это три ряда по 4 клеточки в каждом. Пусть сосчитает число клеточек — это и будет произведение цифр.

Успокойте и упростите

Наверняка ребенок ужаснется, увидев столбцы примеров на умножение сзади на обложке своей тетради: «И это все я должен знать назубок?!» Объясните, что все не так ужасно, как выглядит, ведь от перемены мест множителей произведение не меняется. То есть достаточно запомнить, сколько будет 3 х 4, чтобы понять, сколько — 4 х 3. А значит, учить придется не столь и много.

Используйте таблицу Пифагора

Вместо длинных рядов чисел продемонстрируйте таблицу Пифагора. В ее строках и столбцах — множители, а на пересечении — произведение. Покажите ребенку, как с ней работать, лучше всего — с карандашом: ищешь первое число по вертикали, второе — по горизонтали, а там, где они «встречаются», и есть значение произведения. Какую цифру искать в столбце, а какую — в строке, совершенно неважно, ведь перемена мест множителей роли не играет.

Эта таблица наглядна, и учиться по ней гораздо приятнее, особенно если у школьника хорошо развита визуальная память. Да и знания по ней можно проверить за пару секунд.

Чтобы заинтересовать ребенка, можно рассказать, что таблице умножения почти 4 тыс. лет, и нашли ее в Древнем Вавилоне. Только та таблица была гораздо более сложной и громоздкой — 60-ричной, а не десятичной, какую используют в России. Между прочим, в Великобритании таблица заканчивается не на 10 х 10, как у нас, а на 12 х 12, потому что там другие система мер длины и денежное обращение (фут равен 12 дюймам, шиллинг — 12 пенсам). И в английском образовании на изучение таблицы умножения ребенку дают время аж до 11 лет.

Не перегружайте

Дети хорошо усваивают информацию, в том числе для долговременной памяти. Но переутомлять ребенка не стоит. Выделите по одному-два дня на каждый кусок таблицы умножения — например, сегодня мы выучим таблицу на 2, завтра закрепим, послезавтра начнем — на 3, и так далее.

Важно начинать с простого. Разделавшись с таблицей на 3 и 4, младшеклассник уже усвоит основные принципы таблицы умножения, и дальше будет легче.

Повторяйте

Чем чаще, тем лучше: если учить таблицу умножения с разбросом в пять дней, толку не будет. Для создания нейронных связей в мозгу нужны регулярность и привычка. Пусть ребенок не только отвечает на ваши вопросы, но и регулярно натыкается на таблицу. Например, можно повесить красочный плакат в его комнате.

Проверяя знания ребенка, также двигайтесь от простого к более сложному: вначале, задавая ему вопрос «Сколько будет 3 х 2?», давайте ему больше времени на размышление. На первых порах следом за «3 х 2» спрашивайте «3 х 3», а со временем, когда школьник усвоит таблицу умножения лучше, предлагайте примеры вразнобой.

Укажите на закономерности

Некоторые принципы умножения помогут сократить время на лишние вычислительные операции:

1. Умножив на 0, мы получим 0, на 1 — то же число, а на 10 — то же число, но с ноликом на конце.
2. Умножить на 2 — это сложить число с самим собой.
3. Умножить на 4 — это умножить на 2 и еще раз на 2. Поскольку ребенок пока не научился умножать двузначные числа, но уже хорошо умеет складывать, ему будет проще умножить на 2 и прибавить к получившемуся числу такое же. Например, 6 х 4 = 6 х 2 + 6 х 2 = 12 + 12 = 24.
4. При умножении на 5 произведение (результат умножения) заканчивается на 5 или 0, причем поочередно — например, 1 х 5 = 5, 2 х 5 = 10, 3 х 5 = 15.
5. При умножении на 9 проще умножить на 10 (то есть приставить к исходному числу 0), а потом вычесть это исходное число: 9 х 9 = 9 х 10 — 9 = 81.
6. Кстати, когда ребенок чуть освоится с умножением и начнет решать примеры подлиннее, объясните: там, где есть умножение, сложение и вычитание, по умолчанию сначала выполняется умножение. Если только нет скобок — действие в них как раз должно быть совершено первым. Так, в примере 9 х (10 — 9) результат будет уже другой: сначала решается то, что в скобках, а потом уже выполняется умножение: 9 х 1 = 9.
7. При умножении на 11 (такие операции пригодятся ребенку чуть позже) изначальная цифра удваивается: 6 х 11 = 66, 8 х 11 = 88. Если речь о двухзначных числах, тоже можно обойтись без калькулятора: возьмите умножаемое число и между двумя его цифрами вставьте их сумму. Например: 12 х 11 = 132 (между 1 и 2 — 3).

Запоминание закономерностей таблицы умножения — еще один способ успокоить ребенка. Если он что-то и забудет, результат можно будет «вывести».

5 эффективных способов выучить таблицу умножения

Не ограничивайтесь одним методом объяснения и запоминания. Научить можно разными способами:

1. На пальцах и палочках

С этого стоит начинать знакомство с таблицей умножения. Легче всего показать «два раза по два» на пальцах или каких-то предметах. Правда, с более сложными вычислениями — например, с таблицей на 8 — будет труднее. муторнее.

Но при этом по пальцам легко освоить умножение на 9. Расположите руки вниз ладонями и мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните палец, которому соответствует число, на которое нужно умножить 9. Например, если пример звучит как «9 х 5», это будет большой палец левой руки. Теперь считайте, что все пальцы слева (4) — десятки, а справа (5) — единицы. Таким образом, ответ — 45.

2. Через приложения на телефоне

Современным школьникам, возможно, больше понравится изучать таблицу умножения на экране любимого гаджета. Упражняться можно не только в учебное время, но и на каникулах или в транспорте по дороге в школу — скорее всего, такую тренировку ученик будет воспринимать скорее как игру, чем как домашнее задание, и ему самому будет интереснее.

Приложений немало: в некоторых ребенку одновременно предлагается решить пример, уложиться в предложенное время и накопить баллы/призы. Азарт, как известно, — отличный стимул.

3. По карточкам

Это более «древний», но тоже близкий к игровому способ запоминания. Распечатайте примеры из таблицы умножения на карточках: на одной стороне — пример, на другой — ответ (только проследите, чтобы цифры в ответе не просвечивали, лучше взять плотный картон). Разложите карточки в ряд и предложите ребенку выбрать пример. Если он отвечает верно, убирайте карточку с поля, если нет — перекладывайте ее в конец ряда. Игра заканчивается, когда карточек на столе не остается. Эту игру можно проводить и на время — пусть ребенок соревнуется сам с собой или с другими детьми.

4. По стихам

Стишки про таблицу умножения есть в интернете — в такой форме любая теория запоминается лучше. Например: «Осьминоги шли купаться: дважды восемь ног — шестнадцать», «Два атлета взяли гири, это — дважды два — четыре». Этот способ лучше использовать как вспомогательный, в дополнение к остальным — не будешь же придумывать стишок на каждый пример. Впрочем, были бы желание и фантазия.

5. По играм и мультикам

Одна из популярных игр — «Математическое лото». В нее стоит играть группой детей, находящихся примерно на одном уровне знаний таблицы умножения. Механика примерно та же, что с карточками, только на одних карточках пишутся примеры, на других — ответ. Раздайте детям те, что с ответами, — например, по 4 числа-ответа на каждой карточке, — а те, что с примерами, оставьте себе и поочередно показывайте группе. Пусть тот, кто найдет в карточке ответ, зачеркнет это число и назовет вслух. Например, ведущий говорит: «9 х 9». Тот, у кого в карточке есть число 81, зачеркивает его и называет вслух. Выигрывает тот, кто первым зачеркнул все числа в своей карточке и при этом решил примеры верно.

Еще больше ребенка может заинтересовать игра «Золотоискатели». У нее интересная «легенда»: искатели сокровищ нашли остров, где спрятан клад, но должны тщательно просчитывать ходы, чтобы первыми находить лучшие тайники. Для игры требуются поле — незаполненная таблица Пифагора (можно нарисовать квадрат с ячейками самостоятельно, десяток произвольно выбранных клеток раскрасьте желтым цветом), игровой кубик и ручка.

Первый игрок бросает кубик — сколько ему выпало, столько шагов от старта в любую сторону (но в одном направлении) он может сделать. В клетку, на которой остановился, игрок вписывает произведение чисел, на пересечении которых находится. Это будет количество монет, которые он нашел. Если удалось остановиться на желтой клетке — игрок нашел сундучок, и сумма удваивается. Причем если на этой клетке остановится потом другой игрок (а по правилам он имеет на это право), монет из сундучка он уже не получит.

Следующий игрок, бросая кубик, отсчитывает шаги уже от той клетки, где остановился соперник. Игра заканчивается, когда остается пять пустых клеток. Естественно, выигрывает тот, кто собрал больше монет.

Увлекательна и «Борьба прямоугольников». Это игра на двоих. Нужны только лист бумаги в клеточку, два фломастера, два кубика и по одному цветному карандашу для обоих участников. Каждый игрок по очереди бросает по два кубика. Выпавшие цифры — множители. Игрок рисует на листке со своей стороны прямоугольник или квадрат, стороны которого по количеству клеток равны числам на кубиках. В середине фигуры записывается ее площадь, то есть произведение чисел. Когда на листе не остается места для новых фигур, игру можно завершить. Выиграл тот, кому повезло заполнить фигурами больше клеточек на бумаге.

Другая, менее творческая игра, предлагает участникам из написанных на плакате чисел от 1 до 90 назвать те, что встречаются в таблице умножения на то или иное число. Можно устроить соревнование на время — раздать плакаты нескольким детям и предложить каждому вычеркивать или подчеркивать числа.

Можно заказать в интернете или найти в магазине уже готовые настольные игры на тему умножения — «Много-много» или «Цветариум».

Онлайн-игры для запоминания таблицы умножения, которые можно свободно отыскать в Сети, ничего не скачивая, схожи механикой с играми в мобильных приложениях. Ребенку даются все те же примеры на умножение, но в картинках (вместо 3 х 2 на «доске» рисуется три звездочки, а потом «х 2»), или тренажер на время с результатами: игрок решает сгенерированные компьютером примеры и видит в табличке, сколько дал правильных и неправильных ответов.

По тому же принципу построены развивающие «арифметические» мультфильмы: на экране появляется то или иное, меняющееся количество птичек/зверюшек/конфет, фоном идет веселая тематическая песенка. Но это, опять же, скорее для закрепления уже усвоенного материала, чем для его изучения.

Итак, ничего сложного и ужасного — чередуя разные методы освоения материала, вы постепенно достигнете успеха. Не настраивайтесь на быстрый результат — вероятно, до того, как школьник сможет уверенно отвечать на любой вопрос по таблице, пройдет не меньше месяца. Зато результат будет приносить плоды всю жизнь.

Математика и логика для детей 7-13 лет

Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате

узнать подробнее

Теорема Пифагора – объяснение и примеры

Теорема Пифагора, , также известная как « теорема Пифагора, », возможно, самая известная математическая формула , которая определяет отношения между сторонами прямоугольного треугольника.

Приписывают теорему греческому математику и философу по имени Пифагор (569-500 до н. Э.). Он внес большой вклад в математику, но теорема Пифагора является наиболее важной из них.

Пифагору приписывают несколько вкладов в математику, астрономию, музыку, религию, философию и т. Д. Одним из его заметных вкладов в математику является открытие теоремы Пифагора. Пифагор изучил стороны прямоугольного треугольника и обнаружил, что сумма квадрата двух более коротких сторон треугольников равна квадрату самой длинной стороны.

В этой статье e будет обсуждаться, что такое теорема Пифагора , ее обратная формула и формула теоремы Пифагора .Прежде чем углубляться в тему, вспомним прямоугольный треугольник. Прямоугольный треугольник – это треугольник, внутренний угол которого равен 90 градусам. В прямоугольном треугольнике две короткие ножки встречаются под углом 90 градусов. Гипотенуза треугольника противоположна углу в 90 градусов.

Что такое теорема Пифагора?

Теорема Пифагора – это математический закон, который гласит, что сумма квадратов длин двух коротких сторон прямоугольного треугольника равна квадрату длины гипотенузы .

Теорема Пифагора алгебраически записывается как:

a ² + b ² = c ²

Как выполнить теорему Пифагора?

Рассмотрим прямоугольный треугольник выше.

Учитывая, что:

∠ ABC = 90 °.

Пусть BD – прямая, перпендикулярная стороне AC.

Подобные ∆s:

∆ADB и ∆ABC – подобные треугольники.

Из правила подобия

⇒ AD / AB = AB / AC

⇒ AD × AC = (AB) ² —————– (i)

Аналогично;

∆BDC и ∆ABC – подобные треугольники.Следовательно;

⇒ DC / BC = BC / AC

⇒ DC × AC = (BC) ² —————– (ii)

Комбинируя уравнения (i) и (ii), мы получаем
AD. × AC + DC × AC = (AB) ² + (BC) ²

⇒ (AD + DC) × AC = (AB) ² + (BC) ²

⇒ (AC) ² = (AB) ² + (BC) ²

Следовательно, если мы положим AC = c; AB = b и BC = b, тогда;

⇒ c ² = a ² + b ²

Существует множество демонстраций теоремы Пифагора , приведенных разными математиками.

Другая распространенная демонстрация – это нарисовать 3 квадрата таким образом, чтобы они образовывали прямоугольный треугольник между ними, а площадь большего квадрата (в гипотенузе) равна сумме площадей меньшего. два квадрата (те, что с двух сторон).

Рассмотрим 3 квадрата ниже:

Они нарисованы таким образом, что образуют прямоугольный треугольник. Мы можем записать их площади в форме уравнения:

Площадь квадрата III = Площадь квадрата I + Площадь квадрата II

Предположим, что длина квадрата I , квадрата II, и квадрат III – это a, b и c соответственно.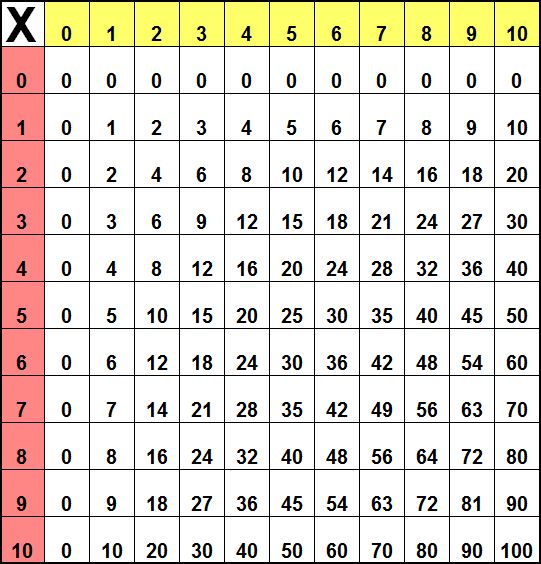

Тогда

Площадь квадрата I = a ²

Площадь квадрата II = b ²

Площадь квадрата III = c ²

Следовательно, мы можем написать это как:

a ² + b ² = c ²

, что является теоремой Пифагора.

Обращение теоремы Пифагора

Обращение теоремы Пифагора – это правило, которое используется для классификации треугольников как прямоугольный, острый или тупой.

Учитывая теорему Пифагора, a ² + b ² = c ² , затем:

• Для острого треугольника c ² 2 + b ² , где c равно сторона, противоположная острому углу.
• Для прямоугольного треугольника c ² = a ² + b ² , где c – сторона угла в 90 градусов.
• Для тупого треугольника c ² > a ² + b ² , где c – сторона, противоположная тупому углу.

Пример 1

Классифицируйте треугольник с размерами; a = 5 м, b = 7 м и c = 9 м.

Решение

Согласно теореме Пифагора, a ² + b ² = c ² тогда;

a ² + b ² = 5 ² + 7 ² = 25 + 49 = 74

Но, c ² = 9 ² = 81
Сравните: 81> 74

Отсюда c ² > a ² + b ² (тупой треугольник).

Пример 2

Классифицируйте треугольник, длина сторон которого a, b, c равна 8 мм, 15 мм и 17 мм соответственно.

Решение
a ² + b ² = 8 ² + 15 ² = 64 + 225 = 289
Но, c ² = 17 ² = 289
Сравните: 289 = 289

Следовательно, c ² = a ² + b ² (прямоугольный треугольник).

Пример 3

Классифицируйте треугольник с длинами сторон: 11 дюймов, 13 дюймов и 17 дюймов.

Решение
a ² + b ² = 11 ² + 13 ² = 121 + 169 = 290
c ² = 17 ² = 289
Сравните: 289 <290

Следовательно, c ² 2 + b ² (острый треугольник)

Формула теоремы Пифагора

Формула теоремы Пифагора имеет вид:

⇒ c ² = a ² + b ²

где;

c = длина гипотенузы;

a = длина одной стороны;

b = длина второй стороны.

Эту формулу можно использовать для решения различных задач, связанных с прямоугольными треугольниками. Например, мы можем использовать формулу для определения третьей длины треугольника, когда известны длины двух сторон треугольника.

Применение формулы теоремы Пифагора в реальной жизни

• Мы можем использовать теорему Пифагора, чтобы проверить, является ли треугольник прямоугольным или нет.
• В океанографии формула используется для расчета скорости звуковых волн в воде.
• Теорема Пифагора используется в метеорологии и авиакосмической сфере для определения источника звука и его дальности.
• Мы можем использовать теорему Пифагора для расчета электронных компонентов, таких как телевизионные экраны, компьютерные экраны, солнечные панели и т. Д.
• Мы можем использовать теорему Пифагора для вычисления градиента определенного ландшафта.
• В навигации теорема используется для вычисления кратчайшего расстояния между заданными точками.
• В архитектуре и строительстве мы можем использовать теорему Пифагора для расчета уклона крыши, дренажной системы, плотины и т. Д.

Рабочие примеры теоремы Пифагора:

Пример 4

Две короткие стороны прямоугольного треугольника равны 5 см и 12 см. Найдите длину третьей стороны

Решение

Дано a = 5 см

b = 12 см

c =?

Из формулы теоремы Пифагора; c ² = a ² + b ² , имеем;

c ² = a ² + b ²

c ² = 12 ² + 5 ²

c ² = 144 + 25

√c ² = √169

c = 13.

Следовательно, третий равен 13 см.

Пример 5

Длина диагонали и одной стороны треугольной стороны составляет 25 см и 24 см соответственно. Каков размер третьей стороны?

Решение

Используя теорему Пифагора,

c ² = a ² + b ² .

Пусть b = третья сторона

25 ² = 24 ² + b ²
625 = 576 + b ²
625 – 576 = 576 – 576 + b ²
49 = b ²
b ² = 49

b = √49 = 7 см

Пример 6

Найдите размер экрана компьютера, размеры которого составляют 8 дюймов и 14 дюймов.

Подсказка: диагональ экрана соответствует его размеру .

Решение

Размер экрана компьютера совпадает с его диагональю.

Используя теорему Пифагора,

c ² = 8 ² + 15 ²

Решите относительно c.

c ² = 64 + 225

c ² = 289

c = √289

c = 17

Следовательно, размер экрана компьютера составляет 17 дюймов.

Пример 7

Найдите площадь прямоугольного треугольника, учитывая, что диагональ и основания составляют 8,5 см и 7,7 см соответственно.

Решение

Используя теорему Пифагора,

8,5 ² = a ² + 7,5 ²

Решите для a.

72,25 = a ² + 56,25

72,25 – 56,25 = k ² + 56,25 – 56,25

16 = a ²

a = √16 = 4 см

Площадь прямоугольного треугольника = ( ½) x основание x высота

= (½ x 7.7 x 4) см ²

= 15,4 см ²

Практические вопросы

1. Канат длиной 20 м протягивается от вершины 12-метрового дерева до земли. Какое расстояние между деревом и концом веревки на земле?
2. К стене прислонена лестница длиной 13 м. Если расстояние от основания лестницы до стены составляет 5 м, какова высота стены?

Предыдущий урок | Главная страница | Следующий урок

Теорема Пифагора (Пифагора) – формула, доказательство, примеры

Теорема Пифагора, которую также иногда называют теоремой Пифагора, является наиболее важной формулой в области геометрии.Согласно Пифагору, квадрат гипотенузы равен сумме квадратов двух других сторон треугольника. В этом уроке вы узнаете о теореме Пифагора, ее выводах и уравнениях, за которыми следуют решения реальных задач о треугольнике и квадратах теоремы Пифагора.

Что такое теорема Пифагора?

Теорема Пифагора утверждает, что если треугольник прямоугольный (90 градусов), то квадрат гипотенузы равен сумме квадратов двух других сторон. В данном треугольнике ABC, имеем BC ² = AB ² + AC ² . Здесь AB – основание, AC – высота или высота, а BC – гипотенуза.

Теорема Пифагора Уравнение

Уравнение теоремы Пифагора поможет вам решить задачи с прямоугольным треугольником, используя уравнение Пифагора: c ² = a ² + b ² (‘c’ = гипотенуза прямоугольного треугольника, тогда как ‘a’ и ‘b ‘- две другие ноги.). Следовательно, любой треугольник с одним углом, равным 90 градусам, сможет создать треугольник Пифагора. Мы можем использовать это уравнение Пифагора: c ² = a ² + b ² .

История теоремы Пифагора

Теорема Пифагора была введена греческим математиком Пифагором из Самоса. Он был древнегреческим ионийским философом. Он основал группу математиков, которые религиозно работали с числами и жили как монахи.Наконец, греческий математик сформулировал теорему, поэтому она названа по его имени «теоремой Пифагора». Хотя он был введен много веков назад, его применение в нынешнюю эпоху обязательно в прагматических ситуациях.

Хотя Пифагор ввел и популяризировал эту теорему, существует достаточно свидетельств, доказывающих ее существование в других цивилизациях, за 1000 лет до рождения Пифагора. Самые старые известные свидетельства датируются 20-16 веками до нашей эры.C в древневавилонский период.

Теорема Пифагора Формула

Формула теоремы Пифагора утверждает, что в прямоугольном треугольнике ABC квадрат гипотенузы равен сумме квадратов двух других катетов. Если AB, BC и AC – стороны треугольника, то: BC ² = AB ² + AC ² . Если a, b и c – стороны треугольника, то c ² = a ² + b ² . В этом случае мы можем сказать, что AB – основание, AC – высота или высота, а BC – гипотенуза.

Доказательство теоремы Пифагора

Теорема Пифагора может быть доказана многими способами. Некоторые из наиболее распространенных и наиболее широко используемых методов заключаются в использовании доказательства алгебраического метода и использовании аналогичного метода треугольников для их решения. Давайте рассмотрим оба этих метода по отдельности, чтобы понять доказательство этой теоремы.

• Алгебраический метод Доказательство теоремы Пифагора
• Доказательство теоремы Пифагора с использованием подобных треугольников

Алгебраический метод Доказательство теоремы Пифагора

Доказательство теоремы Пифагора алгебраическим методом поможет нам получить доказательство теоремы Пифагора, используя значения a, b и c (значения мер длин сторон, соответствующих сторонам BC, AC и AB соответственно).Рассмотрим четыре прямоугольных треугольника ABC, где b – основание, a – высота и c – гипотенуза. Расположите эти четыре равных прямоугольных треугольника в данном квадрате со стороной a + b.

Площадь квадрата, образованного таким образом из четырех треугольников, равна c ² . Площадь квадрата со стороной (a + b) = Площадь четырех треугольников + Площадь квадрата со стороной c. Отсюда следует (a + b) ² = 4 × 1/2 × (a × b) + c ² , a ² + b ² + 2ab = 2ab + c ² .Следовательно, a ² + b ² = c ² . Следовательно, доказано.

Доказательство теоремы Пифагора с использованием подобных треугольников

Два треугольника называются подобными, если их соответствующие углы имеют одинаковую меру и их соответствующие стороны находятся в одинаковом соотношении. Кроме того, если углы имеют одинаковую меру, то мы можем сказать, используя закон синуса, что соответствующие стороны также будут в одинаковом соотношении. Следовательно, соответствующие углы в подобных треугольниках приведут нас к равному соотношению сторон.

В треугольнике ABD и треугольнике ACB:

• ∠A = ∠A (общий)
• ∠ADB = ∠ABC (оба прямые углы)

Таким образом, треугольник ABD и треугольник ACB равноугольны, что означает, что они подобны по критерию сходства AA. Точно так же мы можем доказать треугольник BCD аналогично треугольнику ACB. Поскольку треугольники ABD и ACB подобны, имеем AD / AB = AB / AC. Таким образом, мы можем сказать, что AD × AC = AB ² . Точно так же похожи треугольники BCD и ACB.Это дает нам CD / BC = BC / AC. Таким образом, мы также можем сказать, что CD × AC = BC ² . Теперь, используя оба этих уравнения подобия, мы можем сказать, что AC ² = AB ² + BC ² . Следовательно, доказано.

Теорема Пифагора Треугольники

Правые треугольники подчиняются правилу теоремы Пифагора и называются треугольниками теоремы Пифагора. Длина всех трех сторон вместе называется троек Пифагора. Например, 3, 4 и 5 можно назвать одним из наборов таких треугольников.Есть намного больше прямоугольных треугольников, которые называются треугольниками Пифагора. Все такие треугольники подчиняются одному общему правилу: c ² = a ² + b ² .

Теорема Пифагора Квадраты

Согласно теореме Пифагора Гипотенуза ² = Перпендикуляр ² + База ² или c ² = a ² + b ² , , что дополнительно подтверждает, что площадь квадрата, построенного на гипотенузе прямоугольного треугольника, будет равна сумме площадей квадратов, построенных на двух других сторонах.И эти квадраты известны как квадраты Пифагора.

Приложения теоремы Пифагора

Хотя необходимо изучить основные концепции, такие как формулировки теорем и их математическое представление, нам было бы более любопытно понять приложения теоремы Пифагора, с которыми мы сталкиваемся в повседневных жизненных ситуациях.

Вот некоторые из приложений теоремы Пифагора

• Инжиниринг и строительство

Большинство архитекторов используют технику теоремы Пифагора, чтобы найти значение, а также, когда длина или ширина известны, очень легко вычислить диаметр конкретного сектора. В основном он используется в двух измерениях в инженерных областях.

• Распознавание лиц в камерах видеонаблюдения

Сегодня мы больше знакомы с распознаванием лиц, оно снижает беспорядок при расследовании преступлений в зонах безопасности. Он подчиняется концепции теоремы Пифагора, то есть расстояние между камерой наблюдения и местом, где заметили человека, хорошо проецируется через объектив с использованием этой концепции.

• Деревообработка и дизайн интерьеров

Поскольку основная концепция указывает, что если квадратные картоны могут быть легко превращены в треугольник, разрезая их по диагонали, то концепция Пифагора может быть очень легко применена.Большинство деревянных работ выполняется по стратегии, которая упрощает работу дизайнеров.

Это очень удивительный факт, но люди, путешествующие по морю, используют эту технику, чтобы найти кратчайшее расстояние и путь к интересующим их местам.

Обычно геодезисты используют эту технику для поиска крутых горных областей, зная горизонтальную область, им было бы легче вычислить остальную часть, используя концепцию Пифагора. Фиксированное и изменяющееся расстояние может быть просмотрено геодезистом в телескоп, что облегчает путь.

☛ Статьи по теме

Если вы хотите получить больше концептуальных знаний с помощью практических иллюстраций, попробуйте Рабочие листы теорем Пифагора. Кроме того, для лучшего понимания ознакомьтесь с еще несколькими интересными статьями, связанными с теоремой Пифагора.

Часто задаваемые вопросы по теореме Пифагора

Что такое теорема Пифагора в математике?

Правые треугольники подчиняются правилу теоремы Пифагора и называются треугольниками теоремы Пифагора.Все такие треугольники подчиняются одному общему правилу: c ² = a ² + b ² .

Что такое обратная теорема Пифагора?

Обратное к теореме Пифагора: если сумма квадратов любых двух сторон треугольника равна квадрату третьей (наибольшей) стороны, то он называется прямоугольным треугольником.

Какая польза от теоремы Пифагора?

Теорема Пифагора работает только для прямоугольных треугольников.Когда известны любые два значения, мы можем применить теорему Пифагора и вычислить другое.

Как найти теорему Пифагора для прямоугольного треугольника?

Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов двух других сторон. Когда известны любые два значения, мы можем применить теорему и вычислить другое.

Каковы применения теоремы Пифагора в реальной жизни?

Теорема Пифагора помогает в

• Вычисление расстояния между точками на плоскости.
• Расчет периметра, площади поверхности, объема геометрических фигур и т. Д.
• В архитектуре и строительстве.
• В опросах

Как найти квадрат плюс B в квадрате, равный C в квадрате, используя теорему Пифагора?

Квадрат плюс B в квадрате равен C в квадрате означает c ² = a ² + b ² , что является формулой теоремы Пифагора для определения гипотенузы в прямоугольном треугольнике, когда две другие стороны равны данный.

Можно ли применить теорему Пифагора к любому треугольнику?

Нет, вы не можете применить теорему Пифагора или теорему Пифагора к любому треугольнику. Это должен быть прямоугольный треугольник, только тогда можно использовать теорему Пифагора и получить соотношение, в котором сумма двух квадратов сторон равна квадрату третьей стороны.

Теорема Пифагора [видео] Формула, определение, примеры и доказательство

Теорема Пифагора – очень удобный способ найти длину любой одной стороны прямоугольного треугольника, если вы знаете длину двух других сторон.

Содержание

1. Что такое теорема Пифагора?
2. Формула теоремы Пифагора
3. Как использовать теорему Пифагора

Теорема Пифагора с квадратными корнями

Задачи со словами по теореме Пифагора

Примеры теорем Пифагора

Пифагорейские тройки

Доказательство теоремы Пифагора

Что такое теорема Пифагора?

Теорема Пифагора утверждает, что в прямоугольных треугольниках сумма квадратов двух катетов (a и b) равна квадрату гипотенузы (c).

История теорем Пифагора

Теорема Пифагора названа в честь греческого математика Пифагора и написана им. Пифагор произносится ( «пи-таг-у-рус», с коротким звуком «я» в первом слоге; пи как в булавке), но теорема была описана во многих цивилизациях по всему миру. Теорема произносится как «пи-тхаг-у-ри-ун».

Теорема в геометрии – доказуемое утверждение. Теорема Пифагора была доказана очень давно.

Формула теоремы Пифагора

В любом прямоугольном треугольнике ABC самая длинная сторона – это гипотенуза, обычно обозначаемая c и противоположная ∠C. Две ветви, a и b, противоположны ∠A и ∠B. ∠C – прямой угол, 90 °, а ∠A + ∠B = 90 ° (дополнительный).

Три стороны всегда поддерживают такое соотношение, что сумма квадратов катетов равна квадрату гипотенузы. По математике это выглядит так:

Как пользоваться теоремой Пифагора

Теорема Пифагора может использоваться, чтобы найти длину гипотенузы, если вам известны длины катетов a и b.

Решить относительно c

Предположим, у вас нога a = 5 сантиметров и b = 12 сантиметров:

Объяснение шагов теоремы Пифагора

Начнем с нашей формулы:

а2 + Ь2 = с2

Затем подставляем длину каждой ножки:

52 + 122 = c2

Умножьте каждое число на себя:

25 + 144 = c2

Затем прибавляем:

169 = c2

Теперь извлекаем квадратный корень из обеих частей:

169 = c2

Итак, вы берете главный корень с обеих сторон и получаете:

13 = с

Решите относительно a или b

Вы можете знать длину гипотенузы и одного катета и по-прежнему пользоваться теоремой Пифагора.Предположим, вы знаете, что c = 40 футов, а короткая нога a = 24 фута.

Шаг за шагом

Наша формула:

а2 + Ь2 = с2

Сначала подключите то, что вы знаете:

242 + b2 = 402

Умножьте каждое число на само себя, затем добавьте:

576 + b2 = 1600

Затем вам нужно вычесть длину a2 с обеих сторон, чтобы выделить b2:

(576 – 576) + b2 = (1600 – 576)

С левой стороны остается только b2.

b2 = 1024

Теперь извлеките квадратный корень из обеих частей:

.

b2 = 1024

Возьмите главный корень с обеих сторон и получите:

б = 32

Проверяю ваш ответ

Итак, наш прямоугольный треугольник имел катеты a = 24, b = 32 и гипотенузу c = 40. Если вы не верите своему ответу, вставьте все три числа обратно в теорему Пифагора:

242 + 322 = 402

Проверим, складываются ли числа:

576 + 1024 = 1600

Все проверено; мы были правы! И наши числа были хорошими, целыми числами, что облегчало работу.

Теорема Пифагора с квадратными корнями

Вы можете использовать теорему Пифагора для решения относительно любой длины, если вам известны длины двух других сторон.

Предположим, вам нужна длина гипотенузы c. Тогда вам просто нужен квадратный корень из суммы a2 + b2, например:

с = a2 + b2

Если вам нужно найти короткую ножку a, измените формулу, чтобы она выглядела следующим образом:

а = с2 – в2

И если вам нужно найти более длинную ветвь b, вы переписываете формулу, чтобы она выглядела так:

б = с2 – а2

Проблемы со словами по теореме Пифагора

Выдвижная лестница пожарного опирается на здание, так что ее верхняя часть едва касается желоба по краю крыши. Вы знаете, что длина лестницы составляет 41 фут, и она находится в 9 футах от стены здания. Насколько высоко здание?

Лестница – гипотенуза, 41 ‘, а отрезок a – короткий отрезок, 9’. Вставьте то, что вы знаете, в любую формулу, которую вы хотите использовать для решения длинной ноги b:

Начнем с нашей формулы:

а2 + Ь2 = с2

Сначала подключите то, что вы знаете:

92 + b2 = 412

Умножьте каждое число на само себя, затем добавьте:

81 + b2 = 1681

Затем вам нужно вычесть длину a2 с обеих сторон, чтобы выделить b2:

(81 – 81) + b2 = (1681 – 81)

С левой стороны остается только b2.

b2 = 1600

Теперь извлеките квадратный корень из обеих частей:

.

b2 = 1600

Возьмите главный корень с обеих сторон и получите:

б = 40

Давайте решим это по-другому!

Если вам нужно найти более длинный отрезок b, вы переписываете формулу, чтобы она выглядела так:

б = с2 – а2

б = 412 – 92

б = 1681 – 81

б = 1600

б = 40

Примеры теорем Пифагора

Найдите ответы на эти пять задач теоремы Пифагора:

Пример # 1

Найдите гипотенузу c прямоугольного треугольника с длиной короткого отрезка a = 6 и длиной длинного отрезка b = 8:

а2 + Ь2 = с2

62 + 82 = c2

36 + 64 = c2

100 = c2

100 = c2

10 = с

Пример # 2

Найдите короткий катет a для прямоугольного треугольника с длиной длинного катета b = 24 и длиной гипотенузы c = 25:

а2 + Ь2 = с2

а2 + 242 = 252

а2 + 576 = 625

a2 + (576 – 576) = (625 – 576)

а2 = 49

а2 = 49

а = 7

Пример # 3

Найдите длинный катет b прямоугольного треугольника с длиной короткого катета a = 65 и длиной гипотенузы c = 97:

а2 + Ь2 = с2

652 + b2 = 972

4,225 + b2 = 9,409

(4,225 – 4,225) + b2 = (9,409 – 4,225)

b2 = 5 184

b2 = 5 184

б = 72

Пример # 4

Найдите короткий катет a для прямоугольного треугольника с длиной длинного катета b = 60 и длиной гипотенузы c = 68:

а = с2 – в2

а = 682–602

а = (68 + 60) (68 – 60)

б = (128 × 8)

а = 10242

а = 32

Пример # 5

Найдите длинный катет b прямоугольного треугольника с длиной короткого катета a = 60 и длиной гипотенузы c = 100:

б = с2 – а2

б = 1002–602

б = (100 + 60) (100-60)

б = (160 × 40)

б = 6,4002

б = 80

Пифагорейская троица

Причина, по которой наши примеры задач закончились красивыми, аккуратными, целыми числами, заключается в том, что мы использовали тройки Пифагора или три целых числа, которые работают для выполнения теоремы Пифагора.

Наименьшая тройка Пифагора – 3, 4, 5 (прямоугольный треугольник с катетами 3 и 4 единицы и гипотенузой 5 единиц). Все , кратные из этой тройки, будут , также будут тройками:

6, 8, 10

9, 12, 15

12, 16, 20

Список никогда не заканчивается, и включает в себя один из наших примеров: 24, 32, 40. Существуют и другие тройки Пифагора:

5, 12, 13 (мы использовали это в нашем примере!)

8, 15, 17

9, 40, 41

И этот список никогда не заканчивается!

Узнайте, как идентифицировать и классифицировать тройки Пифагора как примитивные или импримитивные (не примитивные), а также научитесь использовать теорему Пифагора для поиска троек Пифагора.

Доказательство теоремы Пифагора

Существуют тысячи доказательств этой теоремы, в том числе одно, сделанное президентом США Джеймсом Гарфилдом (до того, как он стал президентом). Одно доказательство легко сделать с миллиметровой бумагой, линейкой, карандашом и ножницами.

Постройте △ ABC с участками a и b слева и снизу и гипотенузой c справа вверху. Катет a противоположен A, катет b противоположен B, а гипотенуза c противоположна прямому углу C.

Пусть длина a = 3, b = 4 и гипотенуза c = 5.

Как доказать теорему Пифагора

Постройте квадрат, используя ногу a в качестве правой стороны квадрата. Это будет 9 квадратных единиц (а2). Постройте квадрат, используя ногу b в качестве верхней стороны его квадрата, так что это будет 16 квадратных единиц (b2). Вырежьте еще один квадрат 5 x 5 и совместите его с гипотенузой c, так что квадрат будет c2.

Подумайте: что такое 9 квадратных единиц + 16 квадратных единиц? Это 25 квадратных единиц, площадь c2.

площадь = а × а = а2

площадь = b × b = b2

площадь = c × c = c2

a2 + b2 = c2

Краткое содержание урока

Если вы работали аккуратно, теперь вы должны знать, что такое теорема Пифагора, узнавать ее, когда вы ее видите, и применять ее для решения задач в геометрии. Вы можете использовать его, чтобы найти длину любой одной стороны прямоугольного треугольника, если вы знаете длины двух других сторон. Мы также узнали, как доказать теорему Пифагора.

Следующий урок:

Обращение теоремы Пифагора

Теорема Пифагора

Теорема Пифагора

---

Департамент математического образования
Дж. Уилсон, EMT 669

---

Теорема Пифагора
по
Стефани Дж.Моррис

---

Теорема Пифагора была одной из самых ранних теорем, известных древнему миру. цивилизации. Эта знаменитая теорема названа в честь греческого математика. и философ Пифагор. Пифагор основал пифагорейскую школу Математика в Кортоне, греческом морском порту на юге Италии. Ему приписывают со многими вкладами в математику, хотя некоторые из них, возможно, действительно были работой его учеников.

Теорема Пифагора – самый известный математический труд Пифагора.Согласно легенде, Пифагор был так счастлив, когда открыл теорему что он принес в жертву волов. Позднее открытие, что квадрат корень из 2 иррационален и, следовательно, не может быть выражен как отношение два целых числа, сильно обеспокоившие Пифагора и его последователей. Они были набожными в их убеждении, что любые две длины были целыми кратными некоторой единице длина. Было предпринято много попыток подавить знание о том, что квадрат корень из 2 иррационален.Говорят даже, что человек, разгласивший секрет утонул в море.

Теорема Пифагора – это утверждение о треугольниках, содержащих правую угол. Теорема Пифагора утверждает, что:

«Площадь квадрата, построенного на гипотенузе правой стороны. треугольник равен сумме площадей квадратов на оставшихся стороны »

Рисунок 1

Согласно теореме Пифагора, сумма площадей двух красные квадраты, квадраты A и B, равны площади синего квадрата, квадрата С.

Таким образом, теорема Пифагора, сформулированная алгебраически:

для прямоугольного треугольника со сторонами длиной a, b и c, где c – длина гипотенузы.

Хотя Пифагору приписывают знаменитую теорему, вполне вероятно, что вавилоняне знали результат для некоторых конкретных треугольников по крайней мере на тысячелетие раньше, чем Пифагор. Неизвестно, как греки изначально продемонстрировал доказательство теоремы Пифагора.Если методы Book II Евклида элементов , вероятно, что это было доказательство рассечения, аналогичное следующему:

“Большой квадрат со стороной a + b разделен на два меньших квадрата стороны a и b соответственно, и два равных прямоугольника со сторонами a и b; каждый из этих двух прямоугольников можно разделить на два равных прямоугольных треугольника нарисовав диагональ c. Четыре треугольника можно расположить внутри другого. квадрат стороны a + b, как показано на рисунках.

Площадь квадрата может отображаться двумя способами:

1. Как сумма площадей двух прямоугольников и квадратов:

2. Как сумма площадей квадрата и четырех треугольников:

Теперь, установив два выражения в правой части этих уравнений равными, дает

Следовательно, квадрат на c равен сумме квадратов на a и b.(Burton 1991)

Есть и других доказательств теоремы Пифагора. Один пришел из современной китайской цивилизации, найденной в древнейших сохранившихся китайских текст, содержащий формальные математические теории, Arithmetic Classic Гномана и Круговых Пути Небес.

Доказательство теоремы Пифагора, основанное на фигуре из этого книга была включена в книгу Виджаганита, (Корневые вычисления), индуистский математик Бхаскара.Единственное объяснение Бхаскары своего доказательства было просто “вот” .

Эти доказательства и геометрическое открытие теоремы Пифагора привело к одной из самых ранних проблем теории чисел, известной как Пифгорейская проблема.

Проблема Пифагора :

Найдите все прямоугольные треугольники, стороны которых имеют целую длину, таким образом найдя все решения в натуральных числах уравнения Пифагора:

Три целых числа (x, y, z), удовлетворяющие этому уравнению, называются пифагоровыми. тройной.

Некоторые тройки Пифагора :

x y z

3 4 5

5 12 13

7 24 25

9 40 41

11 60 61

Формула, которая будет генерировать все тройки Пифагора, впервые появилась в Книга X элементов Евклида :

где n и m – натуральные числа противоположной четности и m> n.

В своей книге Arithmetica Диофант подтвердил, что он мог получить право треугольников, используя эту формулу, хотя он пришел к ней под другим цепочка рассуждений.

Теорема Пифагора может быть представлена ​​студентам в середине школьные годы. Эта теорема становится все более важной во время высоких школьные годы. Недостаточно просто сформулировать алгебраическую формулу для Теорема Пифагора. Студентам необходимо видеть геометрические связи. также.Обучение и изучение теоремы Пифагора можно обогатить и улучшены за счет использования точечной бумаги, геодорсов, фальцовки бумаги и компьютерная техника, а также многие другие учебные материалы. Через использование манипуляторов и других образовательных ресурсов, пифагорейский Теорема может значить для студентов гораздо больше, чем просто

и подставляя числа в формулу.

Ниже приведены различные доказательства теоремы Пифагора, включая один Евклидом.Эти доказательства, наряду с манипуляциями и технологиями, могут значительно улучшить понимание студентами теоремы Пифагора.

Ниже приводится итог доказательства Евклида, одного из самых известных математики. Это доказательство можно найти в Книге I Евклида Элементов .

Предложение: В прямоугольных треугольниках квадрат на гипотенузе. равна сумме квадратов на ногах.

Рисунок 2

Евклид начал с пифагорейской конфигурации, показанной выше на рисунке. 2.Затем он построил перпендикулярную линию от C до отрезка DJ на квадрат на гипотенузе. Точки H и G являются пересечением это перпендикуляр со сторонами квадрата на гипотенузе. Это ложь по высоте до прямоугольного треугольника ABC. См. Рисунок 3.

Рисунок 3

Затем Евклид показал, что площадь прямоугольника HBDG равна площади квадрата на BC и что площадь прямоугольника HAJG равна площади площади на AC.Он доказал эти равенства, используя понятие подобия. Треугольники ABC, AHC и CHB подобны. Площадь прямоугольника HAJG равна (HA) (AJ) и поскольку AJ = AB, площадь также (HA) (AB). Сходство треугольников ABC и AHC означает

и, следовательно,

или, как требуется, площадь прямоугольника HAJG такая же, как у площадь квадрата на стороне AC. Таким же образом треугольники ABC и CHG похожий. Итак

и

Так как сумма площадей двух прямоугольников равна площади квадрата на гипотенузе это завершает доказательство.

Евклид очень хотел как можно скорее включить этот результат в свою работу. Однако, поскольку его работа над подобием не должна была начаться до Книг V и VI, ему необходимо было придумать другой способ доказать пифагорейский Теорема. Таким образом, он использовал результат, что параллелограммы являются двойными треугольниками. с таким же основанием и между одинаковыми параллелями. Нарисуйте CJ и BE.

Площадь прямоугольника AHGJ в два раза больше площади треугольника JAC, и площадь квадрата ACLE – это двойной треугольник BAE.Два треугольника совпадают пользователя SAS. Тот же результат аналогичным образом следует для другого прямоугольника. и квадрат. (Кац, 1993)

Нажмите здесь для анимации GSP чтобы проиллюстрировать это доказательство.

---

Следующие три доказательства являются более заметными доказательствами Теорема Пифагора и была бы идеальной для школьников-математиков. Фактически, это доказательства того, что учащиеся умеют конструировать сами. в какой-то момент.

---

Первое доказательство начинается с прямоугольника, разделенного на три части. треугольники, каждый из которых содержит прямой угол.Это доказательство можно увидеть с помощью компьютерных технологий или чего-то столь же простого, как Карточка 3х5 разрезана на прямоугольные треугольники.

Рисунок 4


Рисунок 5

Видно, что треугольники 2 (зеленый) и 1 (красный) полностью исчезнут. треугольник перекрытия 3 (синим цветом). Теперь мы можем дать доказательство пифагорейского Теорема с использованием тех же треугольников.

Проба:

I. Сравните треугольники 1 и 3.

Рисунок 6

Углы E и D, соответственно, являются прямыми углами в этих треугольниках. Сравнивая их сходство, получаем

и на Рисунке 6 BC = AD. Итак,

Путем перемножения получаем:

II. Сравните треугольники 2 и 3:

Рисунок 7

Сравнивая сходство треугольников 2 и 3, получаем:

На рисунке 4 AB = CD.По замене,

Перекрестное умножение дает:

Наконец, сложив уравнения 1 и 2, мы получим:

Из треугольника 3,

AC = AE + EC

т.

Рисунок 8

Мы доказали теорему Пифагора.

---

Следующее доказательство – это еще одно доказательство теоремы Пифагора, которое начинается с Прямоугольник.Он начинается с построения прямоугольника CADE с BA = DA. Следующий, построим биссектрису угла
Рисунок 9

Далее, поскольку m m

По теореме подобия AA треугольник EBF подобен треугольнику CAB.

Теперь пусть k будет коэффициентом подобия между треугольниками EBF и CAB.

.

Рисунок 10

Таким образом, треугольник EBF имеет стороны с длинами ka, kb и kc.Поскольку FB = FD, FD = kc. Кроме того, поскольку противоположные стороны прямоугольника совпадают, b = ka + kc и c = a + kb. Решая для k, мы имеем

а также

Таким образом,

Путем перекрестного умножения,

Следовательно,

, и мы завершили доказательство.

---

Следующее доказательство теоремы Пифагора, которое будет представлено тот, который начинается с прямоугольного треугольника. На следующем рисунке треугольник ABC – прямоугольный треугольник.Его прямой угол равен C.

Рисунок 11

Затем нарисуйте CD перпендикулярно AB, как показано на следующем рисунке.

Рисунок 12

Треугольник 1

Сравните треугольники 1 и 3 :

Треугольник 1 (зеленый) – это прямоугольный треугольник, с которого мы начали до построения. CD. Треугольник 3 (красный) – один из двух треугольников, образованных конструкцией CD.

Рисунок 13
Треугольник 1.Треугольник 3.

Сравнивая эти два треугольника, мы видим, что

Сравните треугольники 1 и 2 :

Треугольник 1 (зеленый) такой же, как указано выше. Треугольник 2 (синий) – другой треугольник, образованный построением CD. Его прямой угол – это угол D.

Рисунок 14
Треугольник 1. Треугольник 2.

Сравнивая эти два треугольника, мы видим, что

Складывая уравнения 3 и 4, получаем:

Из рисунков 11 и 12 для CD имеем (p + q) = c.Путем подстановки получаем

---

---

Следующее доказательство теоремы Пифагора, которое будет представлено, это одно в котором будет использоваться трапеция.

Рисунок 15

По конструкции, которая была использована для формирования этой трапеции, все 6 треугольники, содержащиеся в этой трапеции, являются прямоугольными. Таким образом,

Площадь трапеции = сумма площадей 6 треугольников

И, используя соответствующие формулы для площади, получаем:

Мы завершили доказательство теоремы Пифагора с использованием трапеции.

---

Следующее доказательство теоремы Пифагора, которое я представлю, является доказательством можно научить и доказать с помощью головоломок. Эти головоломки можно составить используя конфигурацию Пифагора, а затем разбивая ее на разные формы.

Перед тем, как представить доказательство, важно изучить следующий рисунок. поскольку это напрямую относится к доказательству.

Рисунок 16

В этой пифагорейской конфигурации квадрат на гипотенузе был разделен на 4 прямоугольных треугольника и 1 квадрат MNPQ в центре.С МН = АН – АМ = а – б. Каждая сторона квадрата MNPQ имеет длину a – b. Этот дает следующее:

Площадь квадрата на гипотенузе = Сумма площадей четырех треугольников. и Площадь квадрата MNPQ

Как упоминалось выше, это доказательство теоремы Пифагора может быть исследованы и доказаны с помощью головоломок, составленных из пифагорейской конфигурации. Студенты могут составить эти пазлы, а затем использовать кусочки квадратов на катеты прямоугольного треугольника покрывают квадрат гипотенузы.Этот может быть отличной связью, потому что это «практическое» занятие. Затем учащиеся могут использовать головоломку, чтобы доказать теорему Пифагора на своих собственный.

Рисунок 17

Чтобы создать эту загадку, дважды скопируйте квадрат на BC, один раз поместив его под квадрат на AC и один раз справа от квадрата на AC, как показано на рисунке 17.

Доказательство с использованием рисунка 17:

Треугольник CDE конгруэнтен треугольнику ACB по участку-участку.

В треугольнике ACB m

В треугольнике CDE m

Треугольник EGH конгруэнтен треугольнику ACB по участку-участку. M

(Примечание: детали 4 и 7, а также части 5 и 6 не разделены.)

Посчитав площадь каждой части, можно показать, что

Площадь 1:

Площадь 2:

Площадь 3:

Зона 6 (и Зона 5):

Зона 7 (и Зона 4):

Сложив все эти области вместе, мы получим следующий результат:

и

Таким образом, мы доказали теорему Пифагора для головоломки.

---

Представленные здесь доказательства – это лишь некоторые из многих доказательств Теорема Пифагора. Теорема Пифагора – очень важное понятие. чтобы студенты учились и понимали. Нельзя не подчеркнуть, что студенты должны понимать геометрические концепции, лежащие в основе теоремы, как а также его алгебраическое представление. Этого можно добиться с помощью использование технологий, манипуляторов и доказательств. Студенты, которым преподают Теорема Пифагора, использующая эти методы, увидит связи и, таким образом, получить большую пользу.

---

Библиография

Beamer, Джеймс Э. Использование головоломок для обучения теореме Пифагора: Учитель математики. Май 1989 г .; NCTM: Рестон, Вирджиния.

Бертон, Дэвид М. История математики Бертона: Введение (Третий выпуск) . 1991; Уильям С. Браун Издатели: Dubuque, IA.

деЛемос, Джейми. Теорема Пифагора: Учитель математики. Январь 1995; NCTM: Рестон, Вирджиния.

Хоэн, Ларри. Новое доказательство теоремы Пифагора: Математика Учитель. Февраль 1995 г .; NCTM: Рестон, Вирджиния.

Кац, Виктор Дж. История математики. 1993; Харпер Коллинз: Нью Йорк, Нью Йорк.

Луфкин, Дан. . Невероятная карта три на пять! : Математика Учитель. Февраль 1996: Рестон, Вирджиния.

---

Вернуться к Стефани Моррис ЕМТ 669 стр.

---

Теорема Пифагора с использованием опыта сначала, формализовать позже (EFFL)

Моей дочери 11 лет, и в настоящее время она усердно работает в 6-м классе.Ей всегда интересно узнать больше о математике, и она иногда становится пилотным тестером для уроков EFFL, которые мы разрабатываем. Недавно мы гуляли, и она спросила:

«Не было бы быстрее, если бы мы просто прорезали диагональ по этому полю?»

Я ответил, спросив ее, думает ли она, что он будет короче, и сколько времени мы могли бы сэкономить, выбрав ее сокращенный путь. Когда мы приехали домой, я начал разрабатывать уроки, которые помогли бы ответить на эти вопросы. Через несколько часов я тестировал уроки с дочерью и 8-летним сыном.2 !!! Я думаю, что слышал об этом раньше »

Она открыла теорему Пифагора! Это один из моментов, которыми я больше всего горжусь отцом.

Каковы учебные цели этих уроков?

Обучение Цели День 1

• Уметь определять гипотенузу и катеты прямоугольного треугольника.

• Поймите, что гипотенуза – это самая длинная сторона прямоугольного треугольника, но она короче суммы двух других сторон.

Учебные цели, день 2

Учебные цели, день 3

Самая большая разница, которую вы заметите в этих уроках по сравнению с более традиционным уроком по теореме Пифагора, заключается в том, что учащиеся немного обдумывают и переживают, чтобы прийти к Теорема Пифагора, а не учитель, просто рассказывающий ученикам о взаимосвязи, а затем просящий их применить ее. Это лежит в основе философии преподавания : сначала опыт, формализация позже, (EFFL).

На каком уровне следует преподавать эти уроки?

Стандартные математические стандарты Common Core требуют, чтобы учащиеся познакомились с теоремой Пифагора в 8-м классе, но этот урок достаточно низкопрофильный, чтобы его можно было использовать раньше.

Обучая этому учащихся средней школы, важно не пропустить День 1. День 1 дает нам причину, по которой нам может понадобиться теорема Пифагора. Вы, безусловно, можете объединить День 1 и День 2 в одно занятие.

День 2 и 3 можно было бы использовать в классе геометрии средней школы, но, вероятно, их нужно будет расширить. Расширение, вероятно, будет включать примеры с нецелочисленными решениями, а также доказательство теоремы Пифагора.

Не стесняйтесь поделиться этими уроками со своими коллегами, которые могут преподавать теорему Пифагора. Попросите их ответить на это сообщение в блоге с любыми отзывами или идеями, которые могут помочь другим учителям.

Действия: Действительно ли ярлык короче?

Рабочий день 1: DOCX / PDF

Рабочий день 2: DOCX / PDF

Рабочий день 3: DOCX / PDF

26 PDF

6 Ключи ответа

29 Теорема Пифагора с примерами

Теорема Пифагора – это способ соотнести длины катетов прямоугольного треугольника с длиной гипотенузы, которая является стороной, противоположной прямому углу.Несмотря на то, что он написан в этих терминах, его можно использовать для поиска любой стороны, если вам известны длины двух других сторон. В этом уроке мы рассмотрим несколько различных типов примеров применения этой теоремы.

Содержание

1. Примеры использования теоремы Пифагора
2. Решение прикладных задач (текстовых задач)
3. Решение алгебраических задач
4. Сводка

реклама

Применение теоремы Пифагора (примеры)

В приведенных ниже примерах мы увидим, как применить это правило, чтобы найти любую сторону прямоугольного треугольника.Как и в приведенной ниже формуле, пусть a и b будут длинами катетов, а c – длиной гипотенузы. Однако помните, что вы можете использовать любые переменные для представления этих длин.

В каждом примере обращайте пристальное внимание на предоставленную информацию и на то, что мы пытаемся найти. Это поможет вам определить правильные значения для использования в различных частях формулы.

Пример

Найдите значение \ (x \).

Решение

Сторона, противоположная прямому углу, – это сторона с меткой \ (x \).2 \)

Следовательно, можно написать:

\ (\ begin {align} x & = \ sqrt {100} \\ & = \ bbox [граница: сплошной черный 1 пиксель; отступ: 2 пикселя] {10} \ end {align} \)

Возможно, вы помните, что в таком уравнении \ (x \) также может быть –10, поскольку –10 в квадрате также равно 100. Но длина любой стороны треугольника никогда не может быть отрицательной, и поэтому мы рассматриваем только положительный квадратный корень.

В других ситуациях вы будете пытаться найти длину одного из катетов прямоугольного треугольника.2 = 80 \)

Следовательно:

\ (\ begin {align} y & = \ sqrt {80} \\ & = \ sqrt {16 \ times 5} \\ & = \ bbox [граница: 1 пиксель сплошной черный; отступ: 2 пикселя] {4 \ sqrt {5 }} \ end {align} \)

В этом последнем примере мы оставили ответ в точной форме вместо того, чтобы находить десятичное приближение. Это обычное дело, если вы не работаете над прикладной проблемой.

Приложения (проблемы с текстом) с теоремой Пифагора

Существует множество различных типов реальных проблем, которые можно решить с помощью теоремы Пифагора.Самый простой способ увидеть, что вы должны применять эту теорему, – это нарисовать картину любой описанной ситуации.

Пример

Два туриста покидают хижину одновременно: один направляется на юг, а другой – на запад. Через час турист, идущий на юг, преодолел 2,8 мили, а пешеход, идущий на запад, – 3,1 мили. Какое в данный момент самое короткое расстояние между двумя туристами?

Решение

Сначала нарисуйте изображение предоставленной информации.2 \)

Теперь воспользуйтесь калькулятором, чтобы извлечь квадратный корень. Вероятно, вам придется округлить свой ответ.

\ (\ begin {align} x & = \ sqrt {17,45} \\ & \ приблизительно 4,18 \ text {миль} \ end {align} \)

Как видите, вам решать, что прямой угол является частью ситуации, заданной в слове «проблема». Если это не так, то вы не можете использовать теорему Пифагора.

Задачи в стиле алгебры с теоремой Пифагора

Есть еще один тип проблем, с которыми вы можете столкнуться, когда вы используете теорему Пифагора для написания некоторого типа алгебраических выражений.Это то, что вам не нужно будет делать на каждом курсе, но оно возникает.

Пример

Прямоугольный треугольник имеет гипотенузу длины \ (2x \), катет длины \ (x \) и катет длины y. Напишите выражение, которое показывает значение \ (y \) через \ (x \). 2 \)

Когда в задаче написано «значение \ (y \)», это означает, что вы должны решить для \ (y \).2} \)

Наконец, это упрощает выражение, которое мы ищем:

\ (y = \ bbox [граница: сплошной черный 1 пиксель; отступ: 2 пикселя] {x \ sqrt {3x}} \)

объявление

Сводка

Теорема Пифагора позволяет вам найти длину любой из трех сторон прямоугольного треугольника. Это одна из тех вещей, которые вам следует запомнить, поскольку она встречается во всех областях математики, и, следовательно, вы, вероятно, пройдете множество различных математических курсов.Не забывайте избегать распространенной ошибки, заключающейся в том, чтобы путать ноги в формуле с гипотенузой, и всегда рисовать картинку, если она не указана.

Подпишитесь на нашу рассылку новостей!

Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.

Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!

Связанные

Пифагор – обзор | Темы ScienceDirect

4.Математика и божественное в пифагорейцах: предположение

Что сделало пифагорейцев пифагорейцами ? То есть, что заставляло древних усматривать связь между мыслями, скажем, Филолая и Архита, и историями, связанными с личностью Пифагора? В этом вопросе много неизвестного. Похоже, что для того, чтобы называться «пифагорейцем», древний автор должен был приехать с греческого Запада (где происходила большая часть деятельности Пифагора). Но означает ли это, что между пифагорейцами шестого и четвертого веков существовала историческая преемственность? Мы просто не знаем.Поэтому лучше сосредоточиться на образце верований и обычаев, которые имя «Пифагор» вызвало у греков. Каким-то образом Филолай и Архит соответствовали этому образцу. Почему так было?

В этом вопросе тоже нужно размышлять. Итак, говоря несколько догматически, мы можем предложить следующее описание «Пифагора», представленного греческому воображению.

Похоже, что Пифагора в первую очередь помнили как харизматического религиозного лидера особого рода.Он предложил образ жизни, гарантирующий некоторую форму избавления от боли и смерти. Если это действительно так, то Пифагор олицетворял греческий тип – обычно, однако, исполнялся мифическими фигурами. Орфей был другой такой фигурой-спасителем, как и другие герои и боги, такие как сам Дионисий. Вокруг таких фигур-спасителей сформировались особые практики, мистических культов. ¹⁷ Они сыграли важную роль в греческом воображении. Поэтому, вероятно, в связи с такими мистическими практиками мы должны понять, что вызвал термин «пифагорейский».

Рис. 3. Пифагор.

Предоставлено Капитолийским музеем в Риме.

Следование мистической практике значило бы выделиться из общедоступной греческой религии группы граждан в городе-государстве. В спасении есть что-то исключительное: как бы идея спасения подразумевает, что есть другие, которых нет. В лодке не так много места. Таким образом, проводится различие между теми, кто принадлежит к спасенному внутреннему кругу, и теми, кто не принадлежит. Переход во внутренний круг – посвящение – происходит через участие в деятельности, свойственной группе, будь то аскетический ритуал орфиков или пифагорейцев или какой-то особый ритуал, выполняемый в ритуальном центре.

Короче говоря, суть таких практик – это переход от мирского к божественному через процесс становления другим. Именно эту формулу мы получили для пифагорейцев пятого и четвертого веков (за вычетом роли, данной математике и, в частности, музыке, и ее пропорциям в качестве агента в посвящении). Это могло быть причиной для греков в четвертом веке. века, чтобы представить Филолая, например, пифагорейцем. Такие авторы, как Филолай, предложили путь от здесь повседневного до там божественного, проходя через странную форму жизни.

Как греки преодолевают разрыв между мирским и божественным? Мы можем проследить структуру, в соответствии с которой мост все больше и больше оказывается, так сказать, оккупированным людьми.

Религиозный ритуал как таковой направлен на преодоление разрыва между мирским и божественным: но традиционный ритуал Города – будучи посвящен как ритуал – в некотором смысле принадлежит богам. Поэтому требуется дальнейший, более личный ритуал – культ мистерий. Здесь человек делает выбор в пользу совершения обряда и, таким образом, берет на себя контроль над своей судьбой, помимо того, что предусмотрено предписанным ритуалом повседневной религии.Пифагор, явно установив новый мистический культ г., приблизил божественное: утверждалось, что практика, установленная смертным, может выйти за пределы смертности. Даже в этом случае иррациональность первоначальной пифагорейской практики подразумевает, что эта практика либо бесполезна, либо богодухновенна. Чтобы сделать это утверждение правдоподобным – о преобразовании в трансцендентное человеческими средствами – преобразующей силе следует дать некоторую рациональную основу. Таким образом, пифагорейцы пятого и четвертого веков продолжили, рационализируя тайну, создав систематический философский аналог опыта тайны.Есть важные различия между четырьмя стадиями – традиционный ритуал, мистический культ, Пифагор и пифагорейская философия – но есть основная преемственность, которая объясняет, я полагаю, почему пифагорейцев называли «пифагорейцами». Короче говоря, из всего интеллектуального разнообразия, предложенного в конце пятого века, пифагорейцы предлагали жизнь, наиболее напоминающую жизнь мистического культа. Отсюда их особая абсурдность, а также их особая перспективность.

Почему математика? То есть, почему пифагорейцы взяли математику как средство преобразования к трансцендентному? Я полагаю, что мы можем это объяснить.Чтобы обрисовать это предположение, давайте более внимательно рассмотрим практику мистического культа.

В мистическом культе, скажем, в знаменитом Элевсинском культе, посвященный должен следовать долгому и особому обряду: жертвоприношения, шествия, посты, и все это приводит к особой церемонии, проводимой в атмосфере тайны, ужаса и экстаза; секреты ведут к секретам, пока не будут раскрыты высшие секреты. Все это, наконец, должно дать посвященному лучшую загробную жизнь и отменить ожидаемые в противном случае адские наказания.Секреты при тщательном изучении (иногда их раскрывали в древности, несмотря на строгие правила, запрещающие их разглашение) кажутся разочаровывающими. В чем высота тайны Элевсина? Священник объявляет: «Хозяйка родила священного мальчика, Бримо Бримосу», а затем выставляется кукурузный початок и молча режется.

Любое конкретное изображение экстаза неизбежно покажется разочаровывающим, и при соответствующей подготовке и постановке обряд, несомненно, был бы достаточно эффективным.Но сосредоточиться на эффектах постановки – значит упустить более важный момент, а именно, что любое рациональное утверждение было бы неуместным в данном контексте. Любой текст можно инсценировать, но одни тексты больше подходят для экстаза, чем другие. Сама иррациональность текста Brimo-to-Brimos наделяет его преобразующей силой. Текст требует интерпретации (Кто такая Бримо? Может быть, она богиня Элевсина, а именно Деметра? И кто ее мальчик?). Таким образом, такие иррациональные тексты предоставляют нам словесный аналог основной теме ритуала, которой является тема становления другим.Сам текст, так сказать, захвачен актом становления другим: это метафорическое высказывание, неметафорическое значение которого остается непрозрачным. Точно то же самое относится и к срезанному початку кукурузы: мы сразу же видим этот акт как богатый метафорическим значением, но нам не дается указаний, которые указывали бы на уникальную буквальную интерпретацию метафоры, так что срезанная кукуруза остается как бы , метафора, висящая в воздухе. (Кстати, именно поэтому тайна, окружающая тайны, была так важна: с раскрытым ритуалом утверждения и действия приобрели бы стандартные интерпретации и, таким образом, превратились бы в мертвых метафор.)

Принцип следующий. Определенное «загадочное» заявление – или действие – само по себе бессмысленно, но оно предполагает смысл, который, однако, отличается от его поверхностного значения. Если мы назовем утверждение P, то выражение будет иметь форму «P is not P». Погружаясь в систему такого рода выражений, вы становитесь не-собой, и это является основой преобразующей силы мистической практики. Если идентичность ставится под сомнение, то и самоидентичность ставится под сомнение.

Переход, совершенный в мистической практике, опосредован странностями. Таким образом, мы можем начать применять то, что мы видели в мистических культах, к самим пифагорейцам. Мы отметили стремление к различию ради различия, характерное как для раннего Пифагора, так и для самих пифагорейцев. Мы также отметили чувство возвышенного и смешного, каким-то образом объединенное, присущее обоим. Воздержание Пифагора от бобов или интерес пифагорейцев к трем символам Ξ, Ψ и Z столь же абсурдны и столь же значимы, как кукурузный початок: они предлагают способы преобразования, будь то личность в исправившегося, аскетичного человека. , или мира в музыкальную структуру.

Мы можем быть более конкретными. Давайте еще раз рассмотрим задачу, стоящую перед пифагорейцами. Они ищут рациональное основание для загадочного опыта: то есть они больше не могут полагаться на выражение типа Бримо-Бримо. Им нужно какое-то буквальное утверждение, сохраняющее метафорический смысл вещи-бытия-чего-то-другого. Выше мы предложили формулу для описания пифагореизма: Инаковость, основанная на пропорции, ведет к потустороннему. Теперь я предполагаю, что это можно вывести из задачи пифагореизма: рационализировать тайну.

Лучшей отправной точкой для рационализации тайны было бы то, что буквально есть что-то еще : объект, который является одновременно двумя радикально разными вещами, поэтому парадоксальное утверждение «X не X» может быть буквально действительный.

Музыка в своей математической интерпретации предлагает именно это и в особенно подходящей форме: это конкретная вещь, музыкальный инструмент, и одновременно, согласно математической интерпретации, это абстрактная вещь – система пропорций.В основе обоих лежит единая формула, так что можно буквально сказать «соотношение породило гармонию» – Бримо породило Бримос, – и поэтому мир струн и инструментов (мир смертных, в котором мы живем) одновременно является чем-то другим. : другой, нематериальный мир. Вот одна из причин, по которой музыка могла бы быть очевидным способом для систематического пифагореизма: она воплощает непрерывность мирского и потустороннего.

Это можно обобщить. Ибо что делает эту преемственность вообще возможной? Как можно буквально сказать, что «X не X»? Это потому, что мы имеем дело с операторами пропорции: «эта строка соответствует этой строке, как 3 – 4».Это пропорция: самый простой способ буквально сказать, что два отдельных домена в определенном смысле являются одним и тем же. Они разные; и тем не менее они олицетворяют одни и те же отношения. Таким образом, пропорции – наиболее естественный путь пифагорейцев. Их проект состоял в том, чтобы предложить интеллектуально систематизированный коррелят мистической практики – как бы буквальный перевод метафоры без потери ее метафорической силы. Именно это и есть утверждения о пропорциях. Мы вспоминаем, как Аристотель жаловался на пифагорейскую тенденцию обосновывать все, соответственно, в числовой и музыкальной сфере: ¹⁸ ‘Они даже говорят, что Ξ, Ψ и Z являются согласными, и поскольку существует три согласования, двойные согласные также являются три.… Некоторые говорят, что таких случаев много, например, что средние строки представлены девятью и восемью, а эпический стих состоит из семнадцати слогов, что равно количеству… никому не было трудно ни сформулировать такие аналогии, ни найти их в вечном, так как они могут быть найдены даже в бренных вещах ». Из такой критики становится ясно, что пифагорейские предположения выражались такими утверждениями, как «как X в области A, так Y в области B» – общая форма утверждений о пропорции или аналогии или, действительно, общая форма метафоры.Аристотель критикует пифагореизм за его метафорический язык, но метафоры иногда верны – когда они являются истинными утверждениями аналогии, то есть пропорциями. Таким образом, например, если мы возьмем гармонию сфер как утверждение пропорции (как движение звезд друг к другу, то есть движение струн по октаве), мы получим утверждение, которое в принципе могло бы быть просто истинным. . В то же время это все еще – как сказал бы Аристотель – «поэтическое». Действительно, это утверждение имеет соответствующий эффект «таинственности», отчуждая нас от обыденного мира вокруг нас и заставляя его казаться более «божественным» просто в силу того, что оно обладает двойственностью или метафорой, присущей его механизму.Если нас одновременно окружают звезды и музыкальные гармонии, тогда земной мир не просто приземленный.

Подводя итог, можно сказать, что есть два свойства греческой математики – и, в частности, греческой музыкальной теории, – которые сделали бы ее подходящей для пифагорейского проекта. Во-первых, соотношение конкретного и абстрактного. (Это наиболее очевидно в математической музыкальной теории, но это также более широкая черта греческой математики с ее уравнением конкретной диаграммы и общей нематериальной теоремой.Во-вторых, греческая математика в основном полагалась на инструмент пропорции , который является общим инструментом корреляции отдельных областей. Таким образом, эти две, казалось бы, несовместимые области – математика и тайна – тоже могут быть объединены. Греческая математика могла быть загадкой, сделанной буквально.

Приведенный выше отчет, конечно, был просто догматическим утверждением спекулятивного предположения. Возможно, это не подходит для исторического исследования, и поэтому в заключение я повторю сделанное здесь предположение как философское утверждение относительно математики и божественного.

Возможно, мы удивимся, что между ними существует какая-то связь. Это потому, что сегодня мы часто думаем о математике как о сфере буквально par excellence. Мы считаем, что метафора больше подходит для обсуждения божественного, и что математика не дает нам метафор. В математике – мы склонны думать – все есть то, что есть, и единственное допустимое отношение – это отношение логического следования, то есть тождество. Таким образом, математика задумана как область утверждений формы «X есть X».Как же он может вести нас в потустороннее – в область, так сказать, не-X?

Но, в конце концов, это не единственный способ увидеть математику и, возможно, даже не самый естественный способ увидеть ее. В конце концов, почему Рассел так не любил Пифагора? Не из-за его абсурдности, а из-за его убедительности: Рассел сам видел, что его собственное философское развитие уводит от пифагореизма. ¹⁹ Рассел, по его собственным словам, когда-то был пифагорейцем.

Описывая таким образом свой философский рост, Рассел имел в виду следующее.В ранний период своей логики Рассел считал, что математика информативна, то есть открывает неочевидные истины. Позже, основываясь на том, что он понимал как аргумент «Трактата» Витгенштейна, Рассел начал думать о математике как о простой системе тавтологий. То есть это была не более чем система полезных сокращенных выражений формы «X есть X». Информацию можно было получить только путем эмпирического исследования, и математика придала этому исследованию не более чем форму.

Этот более поздний взгляд был одним из стандартных описаний отношений между математикой и наукой в ​​20 веке, и он может вызвать наше собственное удивление при встрече с отношениями между математикой и божественным. Он был основан на такой точке зрения, что в своей книге «История западной философии » Рассел сказал, что пифагореизм оказал влияние на философию «как глубокое, так и неудачное». Пифагореизм для Рассела был источником его собственной юношеской ошибки – взгляда на математику как на выходящую за рамки тавтологии, то есть утверждение, что «X не есть X».

Так вот, является ли математика информативной или нет – это вопрос, который я здесь не буду вдаваться, но сам факт, во что верил молодой Рассел Рассел, представляет интерес. Эту позицию занимал Рассел , когда все еще занимался математикой (если, то есть, именно так мы должны называть «Principia Mathematica»). Для практикующего математика эта интуиция о том, что математика имеет дело с «X есть не X», является непреодолимой. Проще говоря, «X есть X» никогда не утверждается ни в одном математическом тексте.То есть: в математике нет утверждений вида «Квадраты на сторонах прямоугольного треугольника равны квадратам на сторонах прямоугольного треугольника». Математические утверждения всегда имеют форму «Квадраты на сторонах прямоугольного треугольника равны квадрату на гипотенузе». Математика утверждает тождество разных, а не одного и того же. По сути, это то, чем он является: инструмент для того, чтобы сделать действительными и утверждениями очевидной формы «X не X».

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт