Задачи для детей 2 класса логические: Логические задачи для 2 класса
Логические задачки для 2 класса
Материал опубликовал
3
#2 класс #Математика #ФГОС #Учебно-дидактические материалы #Тест (специальный формат) #Все учителя #Школьное образование #УМК «Школа России»
Конкурсная работа Всероссийский конкурс педагогического мастерства для учителей начальных классов «Логические задачи для учащихся 1–4 классов» |
Логические задачи для активизации мыслительной деятельности учащихся начальной школы на уроках математики.
Можно использовать и для проведения дополнительных занятий, а также для внеклассных мероприятий по математике.
1.10 насосов за 10 минут выкачивают 1 тонну воды. За сколько минут 20 таких насосов выкачивают 2 тонны воды?
Решение: 10нас/10мин=1мин/10:10=1 (одна минута)1*20=20 (20 минут) Ответ: 20 минут
2.На участке дороги длиной 90 м. Школьниками поручено посадить деревья так, чтобы между ними были расстояния в 9 метров.
Решение: 90:9=10(д.) Ответ: школьники должны посадить 10 деревьев.
3.На столе лежали три линейки. Жёлтая была длиннее зелёной на 2 см. Синяя короче зелёной на 3 см. Найти длину жёлтой линейки, если длина синей – 15 см.
Ответ:Синяя линейка- 15см Зеленая линейка -18 см Жёлтая линейка-20 см
4.К числу 67 прибавить 2 однозначных числа и получить 75. Какие числа прибавили?
Решение: 5-67=8 8/2=4 два по четыре Ответ: 4 и 4
5.В море плавало 9 пароходов. 2 парохода пристали к пристани. Сколько пароходов в море? (9).
6.Неожиданно пошел сильный дождь. Но Таня, Саша, Лена не промокли. Почему?(Они наблюдали из окна; у них были плащи, зонты).
7.В реке купались дети. Они постоянно ныряли в воду и невозможно их было пересчитать. На берегу были разбросаны кеды, всего 12 штук. Сколько детей купалось в реке? (6).
8. Какой знак нужно поставить между 4-мя и 5-ю, чтобы результат оказался больше 4-х и меньше 5-ти? (Запятую)
9. Брату и сестре вместе 10 лет. Сколько лет им будет вместе через пять лет? (20 лет)
Брату и сестре вместе 10 лет. Сколько лет им будет вместе через пять лет? (20 лет)
10. По улице шли два отца и два сына, да дедушка с внуком. Сколько всего человек шло по улице? (3 человека)
11. Если один петух закукарекает, то человек проснётся. Сколько петухов должны закукарекать, чтобы проснулись три человека? (Один петух)
12. На сколько больше наименьшее двузначное число, чем наибольшее однозначное? (На 1)
13. В автобусе ехало7 человек. На первой остановке вышло 3 пассажира, а село 12. Наследующей — вышли 9 человек, зашли 5. Далее — вышли 7, зашли 8. Сколько было остановок? (3 остановки)
14. На уроке физкультуры дети выстроились в одну шеренгу с интервалом 1 м. Шеренга растянулась на 20 м. Сколько детей было на уроке? (21 ученик).
15. Карина гуляла и видела у реки 4 уток, 2 гусей, жука, 4 бабочки и соседскую собаку. Сколько птиц видела Карина? (6 птиц)
Опубликовано в группе «Учителя начальных классов»
Чтобы написать комментарий необходимо авторизоваться.
Задачи на логику 2 класс по математике с ответами
-
Логические задачи на предположения для 2 класса – с ответами и решением
-
Логические задачи на метод извлечения
-
Задачи на логику с использованием методов предположения и метода извлечения с ответами и подробным решением
-
Логические задачи для юного сыщика – увлекательная книга с заданиями для второклассников и детей постарше
-
Задачи и задания на логику и математику
]]>Логические задачи на предположения для 2 класса – с ответами и решением
Задача № 1.
Сергей, Игорь, Мишка и Юра играли во дворе в футбол и разбили окно.
— Кто разбил стекло? – спросила тетя Дарья.
— Оконное стекло разбил Юра или Мишка, – ответил Сергей.
— Я оконное стекло не разбивал, – отнекивался Юра.
— Это сделал Мишка, – сказал Игорь.
— Нет, Игорь, ты ошибся, — возразил Мишка.
Кто из ребят разбил оконное стекло, если трое футболистов всегда говорят только правду, а четвертый может и обмануть? Проверь свое внимание и наблюдательность.
Решение и ответ
1) Предположим, что Сергей обманул. Высказывания со соединителем ” или ” ложно, когда все его части ложны. Поэтому из этого следует, что ни Юра, ни Мишка не разбивали, тогда высказывания Игоря, который, как и все остальные, должен был говорить правду, противоречит тому, что Мишка не разбивал. Поэтому предположение неправильное.
2) Предположим, что обманул Юра, поэтому следует, что он разбил стекло. Учитывая, что высказывания других детей правдивы, а значит и
Игоря. Мы приходим к тому, что Мишка тоже разбил, что противоречит условию задачи, так как оконное стекло разбил только один из парней.
3) предположим, что Игорь сказал неправду, то есть, Мишка не разбивал оконное стекло. Тогда вторая часть суждения Сергея ошибочна.
Тогда вторая часть суждения Сергея ошибочна.
Учтя, что оно правильное и имеет союз «или», делаем вывод, что другая его составляющая должна быть истинной. То есть, оконное стекло разбил Юра, и это противоречит правильному суждению Юрки, который утверждает, что он ее не разбивал. Поэтому предположение неправильное.
4) предположим, что неправду сказал Мишка, а значит Игорь не ошибся «Это сделал Мишка». При этом условии суждения и Сергея и
Юрка тоже прав.
Ответ: Мишка разбил оконное стекло.
Задание № 2
Трое друзей – Николай, Олег и Петр во дворе играли в футбол, и один из них случайно разбил мячом оконное стекло. Когда жители квартиры, в которой разбили стекло, спросили, кто это сделал, Николай признался:”это я разбил оконное стекло”. Олег сказал:”это не Петр”.Позже выяснилось, что одно из этих утверждений правильное, а одно – ложное. Кто из этих мальчиков разбил оконное стекло?
Решение и ответ:
1) Предположим, что признание Николая правильное, то есть, он разбил стекло. Тогда Олег по условию задачи сказал неправду. Это
Тогда Олег по условию задачи сказал неправду. Это
означает что оконное стекло разбил Петр, а это противоречит тому, что только один из парней разбил стекло.
2) допустим, Олег сказал правду – оконное стекло не разбил Петр, тогда выражение Николая не является правдой и Николай стекла не разбивал.
Итак, стекло разбил Олег.
Задача № 3
Журналист приехал на аэродром, чтобы пообщаться с пилотом, штурманом и бортинженером одного самолета, фамилии которых – Дубов, Гришко и Солдатенко. Пока журналист разыскивал экипаж, ему пришлось услышать от людей, что:
- Дубов – не пилот;
- Солдатенко – не бортинженер;
- Дубов – бортинженер;
- Солдатенко – не пилот.
Во время беседы с экипажем журналист выяснил, что из четырех суждений соответствует действительности только одно. Какую специальность имеет
каждый член экипажа?
Ответ и решение
1) Предположим, что правильным является суждение первое: “Дубов не пилот”, тогда другие суждения неправильные и следует что Солдатенко
бортинженер и Солдатенко пилот. Итак мы пришли к противоречию, ибо каждый член экипажа имеет только одну специальность. Поэтому наше
Итак мы пришли к противоречию, ибо каждый член экипажа имеет только одну специальность. Поэтому наше
предположение неверно.
2) Предположим, что правильным является следующее суждение: “Солдатенко не бортинженер», тогда остальные три суждения ошибочны. Это означает, что Дубов – пилот и Солдатенко – пилот. Снова пришли к противоречия.
3) предположим, что правильным является суждение ” Дубов бортинженер”, тогда аналогично ко второму случаю получаем, что Дубов и Солдатенко являются пилотами.
4) предположим, что является правильным суждение ” Солдатенко не пилот”, а все остальные неправильные.
Отсюда получаем что: “Дубов – пилот», «Солдатенко – бортинженер», «Гришко – штурман.»
Задача №4
Трех друзей – одноклассников зовут Володя, Слава и Никита. Кто-то из них потерял дневник. Их другу Вадиму сказали:
- Дневник потерял не Володя.
- Дневник потерял Слава.
Но выяснилось, что одно из этих сообщений правильное, а другое – ложное.
Решение и ответ
В этой задаче надо предполагать возможность, что каждый парень мог потерять свой дневник.
Предположим, что сообщение “дневник потерял не Володя” правильное. Тогда другое суждение ложно, то есть Слава дневника не потерял. Это значит, что его потерял Никита.
Ответ: дневник потерял Никита.
Задача № 5
Во время сбора металлолома Дмитрий, Борис и Богдан нашли большую и тяжелую деталь. Дети начали обсуждать вес детали и из какого она металла.
– Нам повезло, – сказал Дмитрий по дороге в школу. – Эта штука из чистой меди и весит килограммов 30.
— Какая там медь, – возразил Борис. – Это самое обычное железо, а весит оно, видимо, килограммов 100.
— Да, это точно не медь, — вмешался в разговор Богдан, — а весит деталь, я полагаю, килограммов 50.
На школьном дворе все сразу выяснилось. Учительница, которая принимала металлолом, сказала:
– Не огорчайтесь, каждый из вас прав только вполовину.
Определи, из какого металла находка и каков ее вес.
Решение и ответ
Для удобства основные суждения можно записать следующим образом:
- Дмитрий: эта штука из чистой меди и весит 30 кг.
- Борис: это железо и весит 100 кг.
- Богдан: это медь и весит 50 кг.
1) Предположим, что в суждении Дмитрия первая часть неправильная, а вторая – правильная. Это означает, что деталь не из чистой
меди и вес ее 30 кг. Тогда в суждении Бориса вторая часть будет ложной, а значит первая – истинной, ибо каждый ответ по условию
задача наполовину правильная. А это значит, что деталь изготовлена из железа. В этом случае обе части суждения Богдана ложны, а
его ответ, как и других детей, должен быть наполовину правильный. Поэтому наше предположение неверно.
2) Предположим, что в суждении Дмитрия первая часть правильная, а вторая – нет, то есть, деталь из чистой меди и вес ее не 30 кг. Тогда в суждении Бориса первая часть будет ложной, а значит вторая – истинной.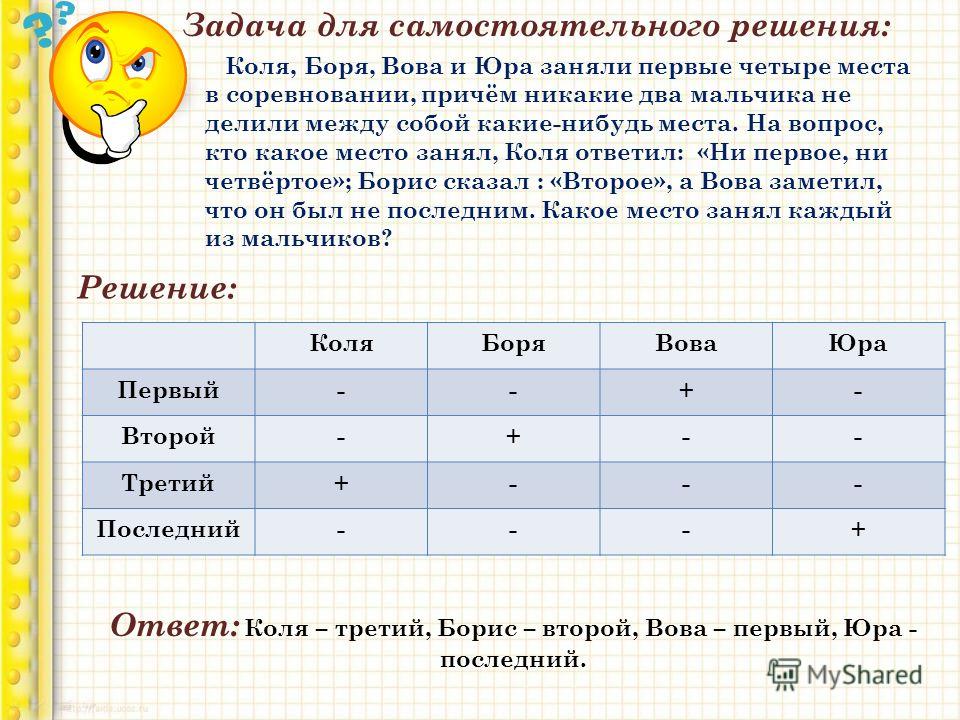
Из этого следует, что, вес найденного предмета 100 кг. Тогда в утверждении Богдана первая часть будет истинной, а вторая ложной, что соответствует условию задачи.
Ответ: деталь из меди и весит 100 кг.
Задание № 6
Одиннадцатиклассник и Николай, Василий и Сергей –призеры городской математической олимпиады, руководили математическим кружком второклассников. На одном из занятий они предложили детям логическую задачу, которую составил один из них. Второклассникам задача понравилась, и они спросили, кто составил задачу. Ребята ответили так:
Сергей : “я задачу не составлял. Василий тоже не сочинял”.
Василий : “Сергей задачу не составлял. Задачу составил Николай”.
Николай : “Я задачу не составлял. Задачу составил Сергей”.
Еще и добавили, что один из них дважды сказал правду, второй- дважды неправду, а третий сказал правду только наполовину. Они предложили малышам самостоятельно определить, кто из них составил задачу. Определи это и ты.
Ответы и решение
1). Предположим, что Сергей дважды правду сказал. Это означает, что ни Сергей, ни Василий задачу не составляли. Тогда в ответе Василия
Предположим, что Сергей дважды правду сказал. Это означает, что ни Сергей, ни Василий задачу не составляли. Тогда в ответе Василия
первая часть суждения правильная. Это значит что вторая должна быть ложной (правду наполовину сказал). Из этого следует, что и Николай не составлял задачу, противоречащую условию: никто из этих ребят задачи не сочиняли.
2) Допустим, Сергей дважды сказал неправду, то это значит, что задачу составили оба парня: Сергей и Василий, что снова противоречит
условию задачи.
3)Предположим, что Сергей правду сказал только наполовину:
а) пусть, первая часть суждения Сергея правильная, тогда вторая – ложная: это значит, что Василий составлял задачу. Исходя из предположения получаем, что и вторая часть суждения Василия правильная , потому что, первая правильная то и вторая должна быть правильная, то есть, задачу составил Николай. Пришедший в противоречие Николай сочинял задачу и Василий.
б) предположим, что первая часть суждения Сергея – неправильная, то есть, задачу составил Сергей. Тогда, вторая является правильной,
Тогда, вторая является правильной,
то есть, Василий не составлял задачу. Исходя из этого, первая часть суждение Василия неправильное то и второе по условию должно быть
неправильная (дважды неправду сказал). То есть Николай не составлял задачи.
В суждении Николай первая часть тогда будет правильная, то и вторая должно быть правильной (дважды правду сказал). То есть, Сергей составил задачу. В этом случае противоречия не встретили.
Итак, задачи составил Сергей.
Логические задачи на метод извлечения
Задание № 1
Татьяна и Тамара имеют фамилии Иваненко и Сидоренко. Какая фамилия у каждой девочки, если Татьяна живет на одной улице с Сидоренко?
Решение и ответ:
Если Таня живет на одной улице с Сидоренко, то фамилия Сидоренко не Танина, а значит Тамарина, а Татьяна имеет другую из данных двух фамилий: Иваненко.
Задание № 2
Трое друзей: Алексей, Борис и Виктор учатся в одном классе. Один из них ездит домой из школы троллейбусом, один — трамваем, один — автобусом. Как-то после уроков Алексей проводил своего друга до остановки автобуса. Когда мимо них проезжал троллейбус, третий друг крикнул из окна: “Борис, ты забыл в школе тетрадь по математике! “Кто каким видом транспорта ездит домой?
Как-то после уроков Алексей проводил своего друга до остановки автобуса. Когда мимо них проезжал троллейбус, третий друг крикнул из окна: “Борис, ты забыл в школе тетрадь по математике! “Кто каким видом транспорта ездит домой?
Решение и ответ:
Решая задачу, будем заполнять таблицу:
| троллейбус | трамвай | автобус | |
| Алексей | |||
| Борис | |||
| Виктор |
Пользуясь суждением условия задачи «Алексей проводил своего друга до остановки автобуса», делаем вывод, что Алексей автобусом
не ездит, потому что каждый из них ездит разным видом транспорта. Ставим в колонке таблицы «автобус» напротив Алексея прочерк. Если с
троллейбуса третий друг обратился к Борису, это значит, что Алексей шел с Борисом и ни один из них ездит троллейбусом. Ставим в колонке
Ставим в колонке
«Троллейбус» нашей таблицы прочерки напротив Алексея и Бориса и делаем вывод, что троллейбусом ездит Виктор. Ставим «+» в
колонке «Троллейбус» напротив Виктора, а в других колонках напротив него прочерки.
| троллейбус | трамвай | автобус | |
| Алексей | – | – | |
| Борис | – | ||
| Виктор | + | – | – |
Рассмотрев внимательно таблицу, видим, что Алексей не ездит троллейбусом и автобусом. Так что он ездит трамваем . Отметим это знаком”+”. Тогда напротив Бориса в колонке «трамвай» ставим прочерк.
| троллейбус | трамвай | автобус | |
| Алексей | – | + | – |
| Борис | – | – | |
| Виктор | + | – | – |
В таблице отметим, что Борис не ездит ни троллейбусом, ни трамваем. Это значит, что Борис ездит автобусом.
Это значит, что Борис ездит автобусом.
| троллейбус | трамвай | автобус | |
| Алексей | – | + | – |
| Борис | – | – | + |
| Виктор | + | – | – |
Итак, Алексей ездит трамваем, Борис-автобусом, Виктор – троллейбусом.
Задание № 3
Внимательно прочитай текст и дай точный ответ на вопрос. Кондратенко, Давыдов и Сидоренко живут на одной улице. Один из них работает маляром, второй — плотником, третий — водопроводчиком. Однажды маляр обратился к плотнику, чтобы тот починил дверь в его квартире, но ему сказали, что он помогает Сидоренко ремонтировать пол. Определи профессию каждого, если известно, что водопроводчик никогда не видел Давыдова.
Ответ и решение
Решая задачу, заполним таблицу
| маляр | плотник | водопроводчик | |
| Кондратенко | |||
| Давыдов | |||
| Сидоренко |
Из того, что маляр обратился к плотнику за помощью и плотник сказал, что помогает Сидоренко ремонтировать пол, следует, что Сидоренко
не является маляром и не является плотником. В таблице напротив Сидоренко в колонках прочерки и делаем вывод, что Сидоренко водопроводчик и это отмечаем знаком «+» в таблице, а напротив Кондратенко и Давыдова в колонке «водопроводчик» ставим прочерки.
В таблице напротив Сидоренко в колонках прочерки и делаем вывод, что Сидоренко водопроводчик и это отмечаем знаком «+» в таблице, а напротив Кондратенко и Давыдова в колонке «водопроводчик» ставим прочерки.
| маляр | плотник | водопроводчик | |
| Кондратенко | – | ||
| Давыдов | – | ||
| Сидоренко | – | – | + |
Из того, что водопроводчик никогда не видел Давыдова, означает, что Давыдов не плотник, потому что плотник водопроводчика знает, потому что ему
ремонтирует пол. Итак, ставим в колонке «плотник» напротив Давыдова прочерк.
| маляр | плотник | водопроводчик | |
| Кондратенко | – | ||
| Давыдов | – | – | |
| Сидоренко | – | – | + |
Разглядев таблицу, делаем выводы, что Давыдов не плотник и не водопроводчик, следовательно он маляр и ставим ” + ” в соответствующей клеточке.
| маляр | плотник | водопроводчик | |
| Кондратенко | – | – | |
| Давыдов | + | – | – |
| Сидоренко | – | – | + |
Если плотником не является Давыдов и Сидоренко то им является Кондратенко. Завершаем заполнение таблицы. Итак, Кондратенко-плотник, Давыдов – маляр, Сидоренко – водопроводчик.
| маляр | плотник | водопроводчик | |
| Кондратенко | – | + | – |
| Давыдов | + | – | – |
| Сидоренко | – | – | + |
Логические задачи на предположение и метод извлечения для 2 класса
Задание № 1
Николай, Саша и Алексей ловили рыбу. Каждый из них поймал разное количество рыб. Саша и коля поймали вместе 6 рыбин, а Алексей и Николай — 4 рыбины. Сколько Рыбин поймал каждый мальчик?
Саша и коля поймали вместе 6 рыбин, а Алексей и Николай — 4 рыбины. Сколько Рыбин поймал каждый мальчик?
Задание на предположение.
1. Предположим, что Алексей поймал 1 рыбину, а Николай тогда поймал три (4 – 1 = 3), потому что вместе они поймали 4 рыбины. Из того, что
Саша и коля поймали вместе 6 рыб, следует, что Саша поймал тоже 3 рыбины, а это противоречит тому, что они поймали разное количество
Рыбин. Так что предположение ложное.
2. Предположим, что Алексей поймал 3 рыбины, тогда Николай – 1 рыбу (4 – 3 = 1) . Если Саша с Николаем поймали 6 Рыбин, то Саша поймал 6 – 1 = 5 рыбин.
Задание № 2
Ученики Володя, Саша и Мишка после исполнения контрольной работы сказали:
Володя : “Я написал контрольную на двенадцать баллов”.
Саша : “Я написал на десять баллов”.
Мишка : “Я написал не на двенадцать”.
После проверки выяснилось, что один из мальчиков получил 12 баллов, второй – 11, третий – 10. Какую оценку получил каждый, если известно, что двое из них правильно назвали свою оценку, а один ошибся?
Ответ и решение
Задача на предположение. Исходим из того, что по условию задачи, один из мальчиков ошибся.
Исходим из того, что по условию задачи, один из мальчиков ошибся.
1) Предположим, что ошибся Володя, то есть, он контрольную написал не на 12 баллов. Если Саша написал на 10 баллов контрольную, а Мишка, как и Володя, не на 12 баллов, то мы получили, что ни один из учеников не выполнили контрольную работу на 12 баллов, что противоречит условию задачи.
2) Предположим, что ошибся Саша. Это значит, что Саша написал контрольную не на десять баллов. Если Володя и Мишка сказали правду, то Володя написал контрольную на 12 баллов, из того, что Саша не на 10 баллов написал, следует, что он получил 11 баллов. Тогда Мишка написал контрольную на 10 баллов.
Ответ: Володя – на 12 баллов, Саша – на 11 баллов, Мишка – на 10 баллов.
Задание № 3
В велогонках участвовали пятеро школьников. После завершение соревнований пятеро болельщиков заявили:
— Николай занял первое место, а Иван – четвертое.
— Сергей занял второе место, а Иван – четвертое.
—Сергей занял второе место, а Николай – третье.
— Анатолий занял первое место, а надежда – второе.
— Надежда заняла третье место, а Анатолий – пятое.
Зная, что в заявлениях каждого болельщика одна часть правильная, а вторая – ложная, найди правильное распределение мест.
Эта задача на предположение.
1) Предположим, что первая часть первого утверждения правильная, а вторая ошибочная, то есть Николай занял первое место, а Иван не четвертое. Тогда во втором утверждении вторая часть тоже ложна (ибо она такая же как и вторая часть в первом утверждении). Поэтому первая часть этого суждения должна быть правильной, то есть Сергей занял второе место.
В следующем утверждении первая часть такая же, как и первая в втором утверждении, значит она правильная, тогда вторая часть то есть Николай третьего места не занял. В четвертом суждении: “Анатолий занял первое место, а Надежда-второе”, – ни одна из частей не может быть правильной, потому что по предположению первое место занял Николай, а из второго суждения мы сделали вывод, что второе место занял Сергей. Итак, мы пришли к противоречию, поэтому предположение неправильное.
Итак, мы пришли к противоречию, поэтому предположение неправильное.
2) Предположим, что в первом утверждении первая часть ложная, а вторая правильная. Это значит, что Николай не занял первого места, а Иван занял четвертое. Во втором утверждении вторая часть такая как и вторая в первом. Значит она правильная, поэтому первая его часть ложная. Это значит, что Сергей не занял второго места. В третьем утверждении первая часть такая, как и первая во втором, поэтому она ошибочна, значит вторая его часть истинна, то есть Николай занял третье место.
Если Николай занял третье место, то первая часть пятого утверждение: “Надежда заняла третье место, а Анатолий-пятое” – ложная, а значит вторая его часть правильная. То есть Анатолий занял пятое место. Поэтому первая часть четвертого суждения: «Анатолий занял первое место» а Надежда – второе – ложная, а это значит, что вторая егочасть правильная. Итак, Надежда заняла второе место. Осталось не занятым первое место. Поэтому его занял Сергей.
Ответ: первое место – Сергей, второе место – Надежда, третье место – Николай, четвертое место – Иван, пятое место – Анатолий.
Задание № 4
Татьяна, Ирина и Иван живут в одном доме. Каждый из них занимается музыкой: пением, игрой на фортепиано или на скрипке.
Известно, что:
- Ирина живет на том же этаже, что и певец.
- Пианист с Иваном учатся в разных классах.
- Татьяна и певец учатся в одном классе.
Чем занимается каждый из них?
Решение и ответ
Задача на метод извлечения, поэтому удобно решать, заполняя таблицу:
| пение | игра на фортепиано | игра на скрипке | |
| Татьяна | |||
| Ирина | |||
| Иван |
С первого утверждения: «Ирина живет на том же этаже, что и певец ” – следует, что Ирина пениями не занимается. Ставим в колонке
Ставим в колонке
“пение” напротив Ирины прочерк. Из утверждения: “пианист с Иваном учатся в разных классах» – следует, что Иван не является пианистом. Ставим в
таблицы напротив Ивана в колонке «Игра на фортепиано» прочерк. Из следующего утверждения: “Татьяна и певец учатся в одном классе» –
следует, что Татьяна не занимается пением и ставим в таблице напротив нее в колонке «пение» – прочерк.
| пение | игра на фортепиано | игра на скрипке | |
| Татьяна | – | ||
| Ирина | – | ||
| Иван | – |
Осталась в этой колонке одна пустая ячейка напротив Ивана. Это значит, что Иван занимается пением. Ставим знак ” + ” в этой клеточке, а в другой напротив Ивана – прочерк
| пение | игра на фортепиано | игра на скрипке | |
| Татьяна | – | ||
| Ирина | – | ||
| Иван | + | – |
Возвращаемся снова ко второму и третьему утверждению и делаем вывод, что если Татьяна и певец Иван учатся в одном классе, а пианист с Иваном в разных классах, то Татьяна не является пианистом и ставим прочерк напротив Татьяны в колонке «игра на фортепиано».
| пение | игра на фортепиано | игра на скрипке | |
| Татьяна | – | – | |
| Ирина | – | ||
| Иван | + | – | – |
Тогда в этой колонке осталась пустая клеточка напротив Ирины, то есть она является пианистом и ставим знак ” + ” в этой ячейке и прочерк напротив Ирины в колонке «Игра на скрипке». Теперь в последней колонке осталась одна пустая клеточка напротив Татьяны. Итак, она играет на скрипке.
| пение | игра на фортепиано | игра на скрипке | |
| Татьяна | – | – | + |
| Ирина | – | + | – |
| Иван | + | – | – |
Ответ: Татьяна – на скрипке, Ирина играет на фортепиано, Иван занимается пением.
Логические задачи для юного сыщика
Эта увлекательная книга поможет ребенку почувствовать себя настоящим детективом и помощь следователю в раскрытии преступлений.
Всего в книге 25 увлекательных задач, которые 2 – классник может решать дома, вместе с родителями. К каждой задаче есть ответ.
Скачать книгу с логическими задачами]]>
Задачи на логику и математику для 2 класса
План урока по логическому мышлению в математике во втором классе
Название урока : Логическое мышление в математике во втором классе
Цели урока :
Материалы :
Введение (5 минут) :
 понятие логического мышления. Объясните, что логическое мышление — это способность думать и принимать решения на основе доказательств и фактов.
понятие логического мышления. Объясните, что логическое мышление — это способность думать и принимать решения на основе доказательств и фактов. Занятие 1 (10 минут):
Занятие 2 (15 минут):

Занятие 3 (20 минут):
Заключение (5 минут):
Оценка :
Примечание : Распределение времени и мероприятия могут быть скорректированы в зависимости от размера класса, потребностей учащихся и доступных ресурсов.
https://www.fractions4kids.com/wp-content/uploads/2023/02/fractions-for-kids-55.jpg 853 1280 дроби4kids https://www.fractions4kids.com/wp-content/uploads/2023/01/logo-2.png Fractions4kids2023-02-04 18:11:422023-02-05 04:52:03План урока по логическому мышлению во втором классе математикиО
Fractions 4 kids — это бесплатный сайт, предлагающий множество материалов для детей, учителей и родителей. Этот веб-сайт ломает понятие дробей, предлагая различные методы обучения. Есть фракционные рабочие листы, онлайн-интерактивные тесты и игры разных разновидностей. Проверьте меню для лучшего пользовательского опыта.
Проверьте меню для лучшего пользовательского опыта.
© Авторское право – Математические дроби. Занятия для детей 2-го, 3-го, 4-го, 5-го, 6-го и 7-го классов, игры, викторины, рабочие листы
25 логических упражнений для средней школы
Вы учите логике или она приходит сама собой? На самом деле этому можно научиться! Логика и критическое мышление — одни из самых важных навыков, которым учатся в средней школе, но как учить логике? Учащиеся средней школы изучают логику посредством рассуждений и дедукции. Обладая этими навыками, учащиеся могут использовать критическое мышление и рассуждения, чтобы сделать рациональный вывод. С помощью этого списка из 25 логических упражнений учащиеся могут развить навыки, необходимые им для использования этих навыков и использования логики для решения задач!
1. Игры для мозга!
С помощью этих игр для мозга учащиеся решают головоломные головоломки, которые подталкивают их к поиску решений, для решения которых требуется немного больше размышлений. Эти забавные головоломки служат практикой для учащихся средней школы, которые учатся использовать свои логические рассуждения.
Эти забавные головоломки служат практикой для учащихся средней школы, которые учатся использовать свои логические рассуждения.
Подробнее: Лаура Рандаццо
2. Пропаганда и критическое мышление
Обучение учащихся логике является одним из самых важных навыков, которым они должны научиться. Используйте эту деятельность, пропаганду и критическое мышление, чтобы показать учащимся, как стать критически мыслящими с помощью поп-культуры.
Подробнее: Просто добавьте учащихся
3. Квест-комнаты
Квест-комнаты предлагают учащимся увлекательную и увлекательную деятельность, которая позволяет им практиковать свое логическое мышление и критическое мышление. В этом упражнении учащиеся работают вместе, чтобы решить головоломки и проблемы, которые бросают вызов их логике.
Подробнее: Beyond the Worksheet
4. Загадки
Хотите интересный и простой способ улучшить навыки логики и критического мышления учащихся? Ученые доказали, что загадки делают именно это. Решите эти хитрые головоломки и улучшите свою логику.
Решите эти хитрые головоломки и улучшите свою логику.
Узнайте больше: AdMe.ru
5. Устройте дебаты
Учащиеся средней школы — отличные спорщики, им просто нужно что-то интересное, чтобы бросить вызов их мышлению. Используйте эти темы для дебатов, чтобы помочь учащимся задействовать свои навыки логического мышления и бросить вызов своим сверстникам.
Узнайте больше: Игры 4 ESL
6. Проведите пробное испытание
Ничто так не заставит ваших учеников средней школы использовать свои логические рассуждения, как пробное испытание. В имитационном судебном процессе учащиеся используют свои навыки критического мышления для защиты своих дел. Развивайте командообразование, критическое мышление и логику с помощью этого веселого занятия.
Дополнительная информация: Право для детей
7. Логические ошибки
Иногда бывает сложно вовлечь учащихся средней школы в процесс обучения. В этом упражнении учащиеся играют разных персонажей, используя творческое мышление и логику. Наблюдайте, как ваши ученики сияют от волнения в этом увлекательном логическом задании.
В этом упражнении учащиеся играют разных персонажей, используя творческое мышление и логику. Наблюдайте, как ваши ученики сияют от волнения в этом увлекательном логическом задании.
Подробнее: Обучение между строк
8. Головоломки
Заставить наших учащихся мыслить нестандартно и использовать свои навыки критического мышления может быть непросто. Заинтересуйте своих учеников обучением и логикой с помощью этих увлекательных головоломок, которые бросают вызов мышлению вашего ученика.
Узнайте больше: GCF Learn Free.org
9. Обучение умозаключениям
Когда дело доходит до логики, очень важно научить учащихся пользоваться умозаключениями. Учащиеся используют выводы, чтобы «читать между строк» и развивать навыки составления подсказок. Используя выводы и критическое мышление, учащиеся могут развивать свои логические рассуждения.
Используя выводы и критическое мышление, учащиеся могут развивать свои логические рассуждения.
Узнайте больше: Любите, смейтесь, учите
10. Логические головоломки
Отточите логику своих учеников, используя творческие логические головоломки. Воспитывайте и развивайте критическое мышление вашего ученика, бросая вызов его мышлению с помощью этих головоломок. Анализируйте, делайте выводы и решайте!
Узнайте больше: Кристин Наннини
11. Головоломки
Хотите простой способ добавить время логике в день вашего ученика? Используйте эти головоломки, чтобы бросить вызов логике вашего ученика в течение дня. Учащиеся развивают логику, многократно практикуясь. Эти забавные головоломки — отличный способ добавить больше логики в день вашего ученика.
Подробнее: Научи маму
12. Игры, головоломки и головоломки
У каждого учителя есть ученики, которые успевают закончить раньше всех. Вместо того, чтобы заставлять их сидеть за партой в ожидании следующего урока, предоставьте им доступ к головоломкам, головоломкам и упражнениям на критическое мышление, которые помогут развить их логические навыки.
Вместо того, чтобы заставлять их сидеть за партой в ожидании следующего урока, предоставьте им доступ к головоломкам, головоломкам и упражнениям на критическое мышление, которые помогут развить их логические навыки.
Подробнее: Научи маму
13. Иллюзии
Наш мозг может заставить нас увидеть то, чего на самом деле нет, или скрыть изображение, чтобы оно выглядело так, как будто его нет. Эти забавные иллюзии бросят вызов мозгу вашего ученика и подтолкнут его логику к нестандартному мышлению. Что ты видишь?
Подробнее: Странности разума
14. Страшные истории для развития логики
Не секрет, что большинство учащихся средней школы любят страшные истории. Почему бы не использовать эти страшные истории, чтобы помочь построить логику вашего ученика? Эти забавные короткие, страшные истории заставят ваших учеников развить критическое мышление и логику.
Подробнее: Hey Natayle
15. Головоломка с треугольником
Создать головоломку, бросающую вызов логике учащихся, очень просто! В этой творческой логической головоломке учащиеся используют квадратный лист бумаги, чтобы создать треугольник. Это не так просто, как кажется, и вашему ученику потребуется дополнительное критическое мышление, чтобы решить эту проблему!
Подробнее: Чем мы занимаемся весь день
16. Взгляд с точки зрения
Использование перспективы — отличный способ заставить учащихся задуматься над собственной логикой. Может быть сложно увидеть вещи с другой точки зрения, но это важный навык для учащихся, особенно когда речь идет о логике. Проверьте эти действия от Secondary English Coffee Shop.
Подробнее: The Secondary English Coffee Shop
17. Принудительные аналогии
Пытались ли вы когда-нибудь сравнить две вещи, которые, казалось бы, не связаны друг с другом? Что ж, в этом задании именно это и просят студентов сделать! Это может показаться проще, чем есть на самом деле, но сравнение двух не связанных между собой вещей требует большого логического мышления.
Подробнее: Тэмми Де Шоу Учитель-сова
18. STEM Challenges
Неудивительно, что наука, технология, инженерия и математика полны логических действий. В этом задании, основанном на STEM, учащиеся используют логическое мышление и рассуждения для разработки экспериментов.
Подробнее: Brain Ninjas
19. Поощряйте критическое мышление
Критическое мышление, развивающее логику, можно добавить к любому уроку. Добавьте несколько творческих и сложных заданий к урокам чтения и письма вашего ученика. Поощряйте учащихся использовать логику в повседневных задачах.
Подробнее: Bespoke Classroom
20. Шестиугольное мышление
Эта новая и креативная стратегия составления карт разума — отличный способ помочь учащимся развить свои логические навыки. Учащиеся изучают набор идей, записанных в виде шестиугольников. Они создают головоломку, используя логику и критическое мышление.
Узнайте больше: Now Spark Creativity
21. Задача «Зефирка»
Когда нужно помочь учащимся развить логику, зефирка — это то, что им понравится. Из зефира и спагетти ученики строят башни.
Подробнее: Миссис Э. Преподает математику
22. Решение задач
Каждое утро или урок начинайте с простой задачи. Студенты используют логику и критическое мышление, чтобы решать проблемы, которые бросают вызов их навыкам.
Дополнительная информация: Mosswood Connections
23. Углубление вопросов
Знаете ли вы, что существуют разные уровни вопросов? Каждый из четырех уровней вопросов помогает учащимся глубже обдумать содержание, которое они изучают. Используйте эти четыре уровня вопросов, чтобы помочь учащимся развить навыки логики и критического мышления.
Подробнее: Patheos
24. Логические игры
Изучение логики с помощью игр — это увлекательный и увлекательный способ помочь учащимся приобрести навыки, необходимые им для критического мышления.
