Тема: Приёмы вычислений для случаев 26+4, 95+5
Ход урока
I. Орг. момент.
Здравствуйте, ребята. Сейчас у нас урок математики. А чтобы у вас было хорошее настроение я прочту вам стихотворение.
Встало солнышко давно,
Заглянуло к нам в окно.
На урок торопит нас –
Математика сейчас.
Ребята, с каким настроением вы пришли сегодня на урок? Я надеюсь, что это бодрое и радостное настроение сохранится у вас на протяжении всего урока – путешествия.
II. Актуализация знаний.
Мы пришли сюда у…(учиться)
Не лениться, а тру…(трудиться)
Только тот кто много з…(знает)
В жизни что-то до…(достигает)
Согласны вы с этим? Что же мы сегодня будем делать? А в гостях у нас сегодня 2 маленькие пчёлки. Они нас приглашают в математическую пчелиную страну.
1.Устный счёт.
а) Повторение состава числа 10. (карточки) б) Игра «Помоги каждой пчёлке найти свой цветок»
2.
Минутка чистописания Какое число лишнее? Что это за число? Из каких цифр оно состоит?(4,7)
Какие ещё числа можно составить из этих цифр? (44, 74, 77) Замени число суммой разрядных слагаемых.
3. Матем. диктант.
-Запишите число, в котором 6дес., и 7 ед. -Чему равна сумма чисел 30 и 30 -От какого числа надо отнять 1, чтобы получить 19. Запишите сумму чисел 9 и 9.
-Миша и Маша пошли в лес по грибы. Миша нашел 15 грибов, а Маша – 4 гриба. Сколько грибов собрали дети? -Мама купила 14 апельсинов. 2 апельсина она отдала дочке. Сколько апельсинов осталось у мамы? -50 увеличьте на 7 -78 уменьшите на 70 -Задуманное число уменьшили на 8 и получили 10. Какое число задумали? Обведите два числа – близнеца, подчеркните лишнее число.
Проверка: 67,60,20,18,19,12,57,8,18
III. Изучение нового материала.
1. Постановка проблемы. Теперь пчёлка приглашает нас к Озеру новых знаний. Чтобы попасть к озеру надо распределить примеры на группы: 26+4, 95+5, 54-2, 67-30.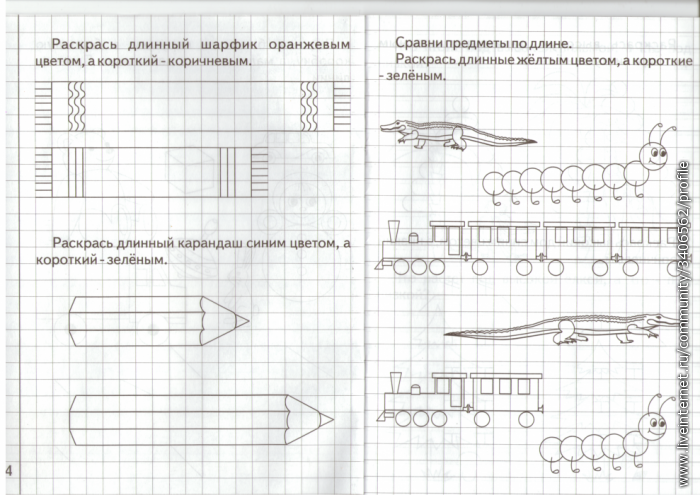
На какие группы распределили?
54-2 26+4
67-30 95+5
Давайте попробуем решить эти примеры. Первый столбик получилось. А как же второй? Сформулируйте тему урока: Приёмы вычислений для случаев 26+4, 95+5
– Чему мы должны научиться на уроке? Решать примеры на сложение? Как это делать? Проблема поставлена, её надо решить.
Есть ли у кого предположение, как решать эти примеры? Снова будем использовать наши слова: заменяю число…(суммой разрядных слагаемых), получится пример…, вычисляю удобным способом.
26+4= 20+(6+4)=30; 95+5=90+(5+5)=100
IV. Закрепление новых знаний.
1. Работа с учебником.
С. 60 № 1 (письменно с комментированием) Потренируемся в решении новых числовых выражений, найдём и запишем сумму чисел. А пчёлки за нами понаблюдают.
2. Физкультминутка. Молодцы, ребята, вы, наверное, устали? Пчёлка предлагает нам немного отдохнуть и приглашает нас на берег реки «Физкультурной»
Пчёлка утречком проснулась.
Потянулась 1,2,3, улыбнулась 1,2,3.
Раз – росой умылась.
Два – изящно покружилась,
Три – нагнулась и присела,
На четыре – полетела,
И на стул тихонько села.
3. Решение задач. С. 60 № 3 Посмотрите, теперь наши пчёлки на Острове задач. А до нас этот остров посетили две девочки Лена и Света. Там они уже успели поиграть в игру «Угадай мелодию» А что у них получилось, мы узнаем из задачи №3 с. 60
4. Работа с геометрическим материалом. Всем известно, что пчёлы живут в улье. А улей имеет квадратную сторону, длиной 10 дм. Пчёлки просят посчитать периметр улья, чтобы его утеплить на зиму. Ответ запишите в метрах.
5. Работа с логическими задачами.
а) На две мухи можно поймать двух рыбок. Сколько рыбок можно поймать на семь мух. (Можно совсем не поймать, а можно и семь).
б) У Сени восемь пар носков. Сколько носков на правую ногу? (Восемь).
6. Блиц – турнир (если останется время)
Сколько раз отжался Миша?V. Рефлексия. Итог урока. Наше путешествие подошло к концу.
Закончите предложения:
Оцените свою работу на уроке и давайте посмотрим, с каким настроением вы уходите с него. На столе у каждого из вас лежат 3 смайлика зеленого, жёлтого и красного цвета.
Если вы довольны собой, то покажите зелёный смайлик, если вы допускали неточности, то жёлтый смайлик, если для достижения хорошего результата вам надо ещё постараться, то красный смайлик.
VI. Домашнее задание. С. 60 № 2,6
Минута. Определение времени по часам» | Начальная школа | Журнал «Педмастерство»Автор: Чанкова Анастасия Андреевна
Организация: МБОУ «Школа № 32»
Населенный пункт: Кемеровская область, г. Прокопьевск
«Час, минута. Определение времени по часам».
Цель урока: сформировать представление о единицах времени (час, минута), уметь определять время по часам, прививать интерес к уроку математики.
Задачи урока:
обучающие: познакомить учащихся с новыми единицами времени, научить учащихся определять время по часам, уметь представлять двузначное число в виде разрядных слагаемых, уметь составлять и решать обратные задачи.
развивающие: умение делать выводы, сравнивать, анализировать, наблюдать, расширять кругозор, расширять словарный запас.
воспитательные: воспитание уважения друг к другу, умения работать в парах и в коллективе в целом, уметь признавать свои ошибки, умение слушать друг друга.
Планируемые результаты:
предметные:
– развивать у учащихся умение определять время по часам;
личностные:
– проявлять интерес к новому материалу;
– оценивать работу себя и своих одноклассников;
– устанавливать связи между целью деятельности и мотивом;
Универсальные учебные действия:
регулятивные:
– определять цель на уроке с помощью учителя;
– учиться работать по плану;
– учиться планировать свою деятельность;
– высказывать свои предположения;
– уметь адекватно воспринимать оценку;
коммуникативные:
– слушать друг друга;
– владеть речью, которая соответствует нормам русского языка;
– искать общее решение в совместной учебной деятельности с одноклассниками;
познавательные:
– ориентироваться в своей системе знаний;
– сравнивать, анализировать;
– делать выводы о результатах совместной учебной деятельности;
– ориентироваться в учебнике;
– умение искать необходимую информацию;
Тип урока: комбинированный урок
Оборудование: учебник по математике М.
И. Моро 2 класс, в двух частях (первая часть), модель часов.
I. Организационный момент
-Здравствуйте, ребята! С началом нового учебного дня! И сегодня у нас очередной урок математики. И как всегда, перед началом урока, я проверяю ваше рабочее место. Ничего лишнего у вас не должно быть на партах. Учебники и тетради должны аккуратно лежать на краю стола.
-Садитесь, ребята!
– Откройте ваши тетради и запишите число. Дату мы записываем на полях, не забудьте от домашней работы отступить четыре клетки. Дальше запишем «Классная работа». Не забывайте ставить точку.
II. Минутка чистописания
– Ребята, отгадайте загадку. О какой цифре идет речь в этой загадке?
Кошка в кубики играла,
Кошка кубик потеряла.
Закружилась голова…
Было три, осталось…
(Два)
– Ребята, когда я проверяла Ваши работы, я увидела, что у многих не получается цифра 2. Давайте еще раз напишем эту цифру.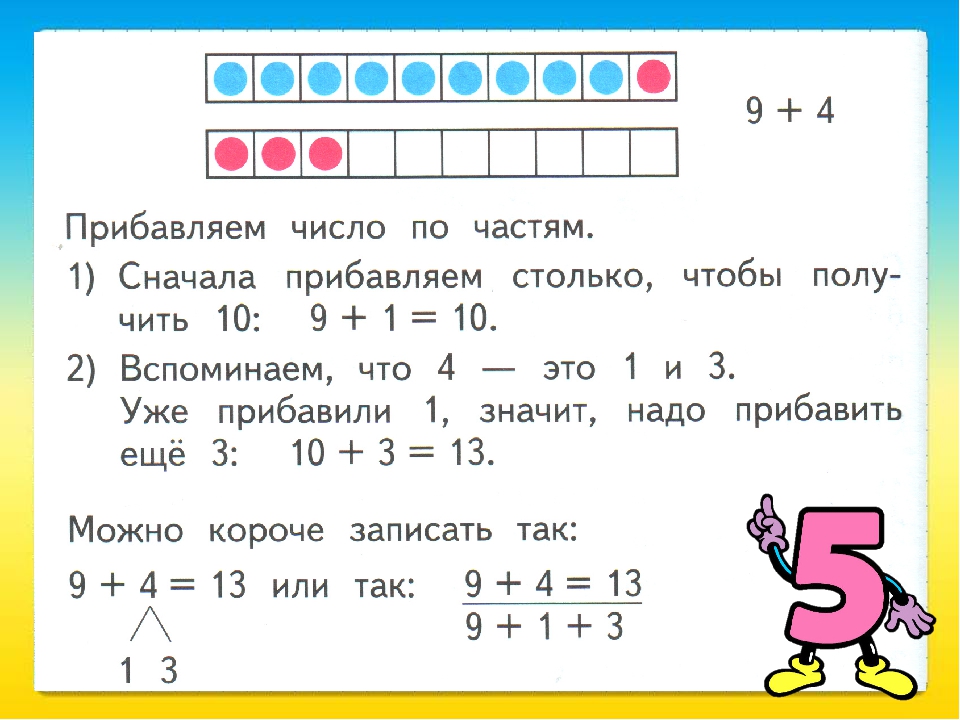
222222….
20202020…..
– Что вы хотите сказать?
– Какова роль цифры 2 в числе 2?
– Какова роль цифры 2 в числе 20?
III. Актуализация знаний
1. Устный счет
– Давайте посчитаем от 1 до 20 и обратно.
– А теперь посчитаем в пределах 100. Посчитайте все вместе числа в пределах 100, сначала в порядке возрастания, а затем в порядке убывания. Молодцы!
2. Проверка домашнего задания на с.30 (№ 6, № 7).
IV. Постановка учебной задачи
– Ребята, пожалуйста, отгадайте загадку:
Ног нет, а хожу,
Рта нет, а скажу,
Когда спать,
Когда вставать,
Когда работу начинать!
– Кто догадался, о чем мы сегодня будем говорить на уроке?
– Пожалуйста, сформулируйте тему урока.
V. Открытие нового знания
– Ребята, как вы думаете, для чего нужны часы?
– Какие часы вы знаете?
– Ребята, посмотрите на модель часов.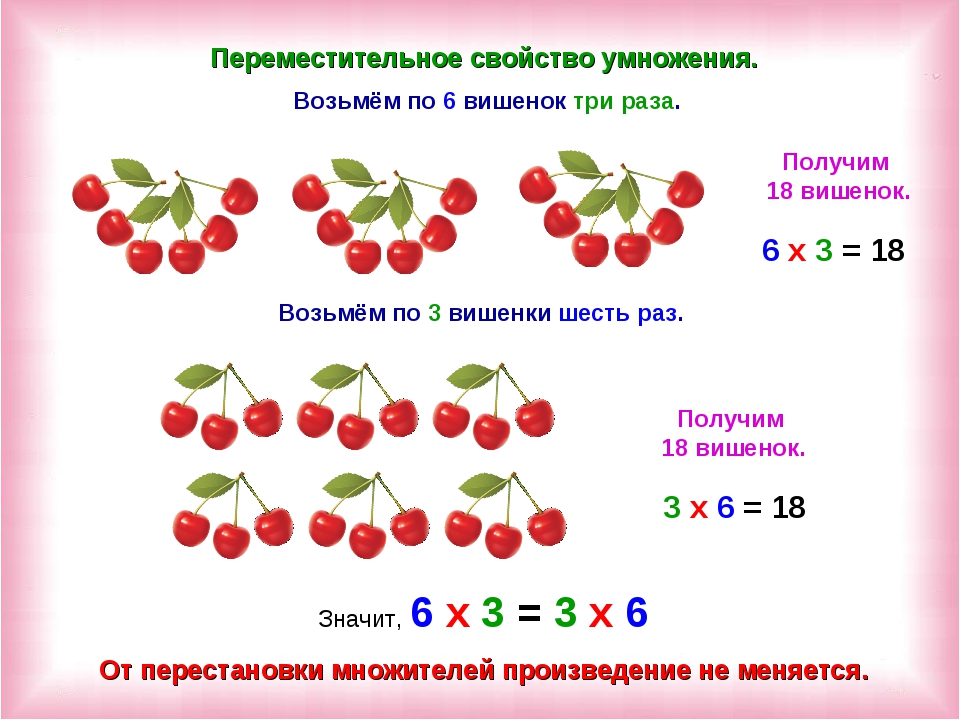
(Учитель показывает классу заранее подготовленную модель часов). Числа, которые вы видите на часах, называются циферблатом. (Дети повторяют вместе с учителем новое слово «циферблат»). Что еще вы видите на часах? (Две стрелки).
– Ребята, а почему на часах две стрелки? Откройте, пожалуйста, учебник на с.31. Прочитайте правило, которое дано у вас в учебнике.
– Итак, расскажите мне, ребята, как называется часовая стрелка и как она выглядит? (Часовая стрелка – это самая маленькая стрелка, движется она от одной большой черточки до другой).
– А минутная? (Минутная – это большая стрелка, движется она от маленькой черточки до другой).
– Пока маленькая стрелка (часовая) подвинется от одной цифры до другой, большая (минутная) проходит весь круг.
– Ребята, сколько маленьких черточек на циферблате, посчитайте. (60)
– Расстояние от одной маленькой черточки до другой называется минута. А весь круг, который проходит маленькая стрелка, называется час.
– Ребята, скажите, сколько в одном часе минут? (60)
– Итак, ребята, запишите в своих тетрадях следующее: 1ч=60 мин.
Обведите это правило в рамочку и выучите его.
– Вы сегодня тоже приготовили свои модели часов. Давайте потренируемся показывать время. Я буду вам называть время, а вы будете его показывать на часах. (три часа ровно, 8 часов ровно, девять тридцать и тд.)
Работа с моделью часов: дети определяют время.
– Найдите в учебнике № 1 на с.31 (до какого числа ты можешь посчитать в течение минуты?)
Засекается время, дети считают.
Далее выполняется упражнение в определении времени по часам. Рассматриваются рисунки в задании 2 (с. 30 учебника, часть 1).
– Какое время показывают часы?
– Как будут расположены стрелки часов, когда пройдет 1 час? (Предлагает показать на модели часов.)
– На сколько минут спешат каждые из этих часов, если на самом деле сейчас 7 часов 25 минут?
Затем дети показывают на модели часов различное время (перед тем как начать работу, учитель должен напомнить детям, что расстояние от одного большого деления до другого минутная стрелка проходит за 5 минут.
-Стр. 31 №2. (Дети проговаривают устно).
VI. Физкультминутка
Мы ходить умеем так:
Тик-так, тик-так!
Головой качаем так:
Тик-так, тик-так!
Наклоняемся вот так:
Тик-так! Тик-так!
VII. Закрепление нового материала
Учащиеся разбирают задачу № 3 на с.31 под руководством учителя.
Прочитайте задачу. (Один ученик читает, остальные внимательно следят за ним).
– Ребята, о чем говорится в этой задаче? ( О времени, которое мальчики потратили на игру в шахматы) Что такое партия? Сколько времени заняла первая партия? А вторая? Какой вопрос задачи? Что нужно найти? Это простая или составная задача? (простая, она решается одним действием, почему вы так решили?). С чего мы начинаем решать задачу? (Сначала мы пишем краткую запись). Коллективно составляется краткая запись, затем дети самостоятельно в тетради записывают решение и ответ. После проверки задачи учитель просит учащихся изменить вопрос так, чтобы задача решалась двумя действиями, то есть, чтобы она стала составной.
1 п. – 30 мин
2п. – ? на 10 мин
Измените вопрос, чтобы задачу нельзя было решить одним действием. Как изменится краткая запись? (Добавится фигурная скобка со знаком вопроса.)
1 п. – 30 мин
2п. – ? на 10 мин
30-10=20 (мин) – 2 п.
30+20=50 (мин)-всего
Ответ: 50 минут.
VIII. Самостоятельная работа
В учебнике ребята решают № 5. Вспоминают, как представить двузначное число в виде суммы разрядных слагаемых. (С последующей взаимопроверкой).
IX. Итог урока
– С какими единицами времени познакомились сегодня на уроке (час, минута)
– Сколько минут в одном часе? (60)
– Как называются стрелки на часах?
– Как они движутся?
X. Рефлексия
Сегодня на уроке:
– мне понравилось….
– вызвало затруднения….
– было интересно выполнять….
– что было непонятно на уроке….
XI. Домашнее задание
Выучить правило на с.31, дома еще раз потренироваться показывать время на модели часов, выполнить № 4 на с.31 (решить задачи, составить и решить задачи обратные данной)
Спасибо за урок, дорогие ребята!
Список используемой литературы и источников
1. ФГОС «Школа России». Моро М.И., Бантова М.А. «Математика». Учебник для 2 класса. Часть 1,2. М., Просвещение
2. https://nsportal.ru/nachalnaya-shkola/matematika/2014/09/18/konspekt-uroka-po-matematike-chas-minuta-opredelenie-vremeni
3. https://nsportal.ru/nachalnaya-shkola/matematika/2018/03/10/chas-minuta-opredelenie-vremeni-po-chasam-2-klass
4. https://infourok.ru/konspekt-uroka-po-matematike-na-temu-chas-minuta-2-klass-4561749.html
Опубликовано: 09.11.2020Учащиеся, обладающие математическими способностями, понимают величины и их отношения в проблемных ситуациях.
Они привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентирующими символами так, как будто они живут собственной жизнью, не обязательно обращая внимание на свои референты — и способность контекстуализировать, делать паузы по мере необходимости в процессе манипулирования, чтобы исследовать референты для задействованных символов. Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов. — СССС
Эта формулировка звучит очень по-школьному, но такую же математическую практику можно развить и в начальной школе. Второклассникам, которые учатся писать числовые выражения, может быть предложено написать числовые выражения, описывающие количество плиток на этом рисунке
различными способами.
Имея опыт решения подобных задач, чтобы они знали, что от них требуется, учащиеся могут написать 1+2+3+4+3+2+1 (высоты ступенек слева направо) или 1+3+5+. 7 (ширина слоев сверху вниз) или 10+6 (количество каждого цвета) или различные другие выражения, которые фиксируют то, что они видят. Все это деконтекстуализации — репрезентации, которые частично сохраняют первоначальную структуру отображения, но только числом, а не формой или другими особенностями изображения. Имеет смысл не всякое выражение, которое дает в сумме 16 — например, трудно было бы оправдать 2+14, — но ребенок, который пишет, например, 8+8 и объясняет как «бутерброд» — количество блоков в двух средних слоях плюс количество блоков в верхнем и нижнем — взял абстрактную идею и добавил к ней контекстное значение.
В более общем плане, Математическое занятие № 2 требует, чтобы учащиеся смогли перевести проблемную ситуацию в числовое предложение (с пробелами или без них) и, решив арифметическую часть (любым способом), распознать связь между всеми элементами предложения и исходной проблемой.
Это включает в себя проверку того, что единицы (объекты!) в задачах имеют смысл. Так, например, в деконтекстуализация задача на вопрос, сколько автобусов нужно для 99 детей, если в каждом автобусе 44 места, ребенок может написать 99÷44. Но после вычисления 2r11, или 2¼, или 2,25 учащийся должен реконтекстуализировать : контекст требует целочисленного ответа, а не, в данном случае, только ближайшего целого числа. Успешная реконтекстуализация также означает, что учащийся знает, что ответ — 3 автобуса, а не 3 ребенка или просто 3.
Конкретно-репрезентативно-абстрактный учебный подход
Что такое конкретно-репрезентативный-абстрактный (CRA) учебный подход?
Учебный подход CRA — это «вмешательство в обучение математике, которое, как показывают исследования, может улучшить успеваемость учащихся по математике».
(Хаузер) Подход представляет собой «учебную стратегию, состоящую из трех частей, каждая из которых основывается на предыдущей инструкции, чтобы способствовать обучению и удержанию учащихся, а также использовать концептуальные знания». (Хаузер) Три части следующие:
Учитель использует символы операций (+, –, x, /) для обозначения сложения, умножения или деления. Это «символический» этап, на котором учащиеся могут использовать абстрактные символы для моделирования задач (Хаузер).В классе этот подход помогает учащимся создавать значимые связи между конкретным, репрезентативным и абстрактным уровнями мышления и понимания. Обучение учащихся начинается с визуального, осязаемого и кинестетического опыта для установления базового понимания, а затем учащиеся могут расширить свои знания с помощью графических представлений (рисунков, диаграмм или набросков) и, наконец, могут перейти на абстрактный уровень понимания. мышление, при котором учащиеся используют исключительно математические символы для представления и моделирования задач (Хаузер).
Исследования показали, что «учащиеся, которые используют конкретные материалы, развивают более точные и полные мысленные представления, часто демонстрируют большую мотивацию и поведение при выполнении задания, понимают математические идеи и лучше применяют эти идеи в жизненных ситуациях» (Хаузер).
.
Какова цель подхода CRA?
Главной целью учебного подхода CRA является «обеспечить учащимся четкое понимание математических концепций/навыков, которые они изучают». (Special Connections, 2005) Используя свой конкретный уровень понимания математических концепций и навыков, учащиеся могут позже использовать эту основу и добавлять/связывать свое концептуальное понимание с абстрактными проблемами и обучением. Прохождение учащимися этих трех шагов дает учащимся более глубокое понимание математических концепций и идей и обеспечивает отличную основополагающую стратегию для решения проблем в других областях в будущем. (Особые связи, 2005).
Как реализовать подход CRA в моем классе?
Одним из первых и наиболее важных шагов к внедрению подхода CRA в классе является «использование подходящих конкретных объектов для обучения определенным математическим понятиям/навыкам. Отдельные материалы (например, предметы для счета, такие как бобы, чипсы, кубики unifix, палочки от эскимо и т.
д.) особенно полезны, поскольку учащиеся могут видеть и чувствовать свойства предметов, которые они используют». (Особые связи, 2005).
После того, как учащиеся овладели конкретным уровнем исполнения, введите соответствующие процедуры рисования, в которых учащиеся решают задачи, рисуя простые изображения конкретных объектов, которые они использовали ранее (например, числа, точки и круги). «Повторяя движения, которые учащиеся ранее использовали с конкретными материалами, рисование простых изображений этих объектов поддерживает развивающееся абстрактное понимание учащимися концепции/навыка» (Special Connections, 2005).
Наконец, после того, как учащийся продемонстрирует полное понимание репрезентативного уровня, используйте соответствующие стратегии, чтобы помочь учащимся перейти от этого репрезентативного уровня к более абстрактному уровню. Если учащимся трудно перейти к абстрактному, «повторно обучите математическую концепцию/навык, используя соответствующие конкретные материалы, а затем явно покажите взаимосвязь между конкретными материалами и абстрактным представлением материалов».
(Special Connections, 2005 г.) Если учащиеся уже имеют определенный уровень понимания этой концепции/навыка, «предоставьте учащимся возможность использовать свой язык для описания своих решений и своего понимания математической концепции/навыка, который они изучают» (Special Connections). , 2005).
На этом рисунке показано, как использовать обучающий подход CRA к задаче 4+5=9.
Советы учителю по использованию математических манипулятивных инструментов в классе
Что такое математические манипулятивные инструменты?
Манипулятивные материалы — это конкретные модели или объекты, включающие математические понятия. Наиболее эффективными инструментами являются те, которые воздействуют на несколько органов чувств, к которым учащиеся могут прикасаться и перемещать их (а не демонстрация материалов учителем). Манипулятивные материалы должны относиться к реальному миру учащихся (Хедденс, 19 лет).97).
Список/использование рекомендуемых математических инструментов (манипуляции)
Некоторые распространенные инструменты, используемые при обучении элементарной математике.
Фото: Лиза де Гарсия
Базовые 10 блоков
· Базовые 10 блоков поставляются в виде единиц (один куб), длинных (состоящих из 10 единиц), плоских (состоящих из 10 длинных или 100 единиц), и кубы (состоящие из 10 плоских или 1000 единиц).
· Блоки с основанием 10 можно использовать для многих математических процедур:
o Знакомство с понятием разрядности
o Чтение и запись чисел
o Ноль в качестве заполнителя
o Сложение
o Вычитание
o Умножение
o Деление
o Дроби
o Десятичные числа/операции с десятичными знаками
o Расширенная нумерация
o Счет/пропуск счета
o Геометрия (площадь и периметр)
o Вероятность, отношения, пропорции
· См.
: http://www.susancanthony.com/Resources/base10ideas.html для более подробной информации и идей
Палочки Кюизенера 9002 9
· Палочки Куизенера цветные деревянные или пластиковые стержни со значениями от одного до десяти, окрашенные в соответствии с номером, который они обозначают:
o Белый стержень = 1 см.
Красный стержень = 2 см.
Светло-зеленый стержень = 3 см.
Лавандовый стержень = 4 см.
Желтый стержень = 5 см.
Темно-зеленый стержень = 6 см.
Черный стержень = 7 см.
Коричневый стержень = 8 см.
Синий стержень = 9 см.
Оранжевый стержень = 10 см.
· Палочки Кюизенера можно использовать для:
o Вероятности и статистики
o Соотношения, пропорции
o Дроби
o Сложение
o Вычитание
Блоки шаблона
· Блоки шаблона составляют один сантиметр толстые разноцветные блоки шести форм: шестиугольники, квадраты, трапеции, треугольники, параллелограммы и ромбы.
Каждая форма имеет свой цвет.
· Блоки шаблонов можно использовать для:
o Дробей
o Шаблонов
o Геометрии
o Симметрии
o Сложение
o Умножение
o Уравнения
o Соотношения
· См. следующий веб-сайт для дополнительная информация и подробности: http://www.netrox.net/~labush/nctm.htm#Pattern
Кубы Unifix
· Кубы Unifix — это разноцветные взаимосвязанные кубы, которые соединяются только одним способом. Они представлены в десяти однотонных цветах, что делает их достаточно наглядными для демонстрации и позволяет легко создавать узоры и сортировать.
· Кубы Unifix можно использовать для:
o Подсчет/пропуск счета
o Сложение
o Вычитание
o Умножение
o Деление
o Образцы
o Смысл числа
o Равенство
o Факт семейства
o Совершенные квадраты
o Графики
o Разрядное значение
o Дроби
o Измерение
o Вероятность
· Более подробные сведения см.
на следующем веб-сайте: http://www.netrox.net/~labush/nctm.htm#Unifix
Hundred Chart t
· Сотня ряд из 100 квадратов в расположении 10 x 10, который образует больший квадрат. Маленькие квадраты пронумерованы от 1 до 100.
· Таблицу сотен можно использовать для:
o Визуальный счет/пропуск счета
o Визуальное сложение и вычитание
o Дроби
o Десятичные числа
o Проценты
· Более подробные сведения см. на следующем веб-сайте: http://www.christiancottage.com/articles/HundredChart.html 900 06
Snap Cubes
· Snap Кубы похожи на кубы Unifix, но они связаны со всех сторон (шестью способами). Они бывают разных цветов
· Кубики Snap можно использовать для:
o Подсчет/пропуск счета
o Сложение
o Вычитание
o Умножение
o Деление
o Шаблоны
o Смысл чисел
o Равенство
o Семейства фактов
o Совершенные квадраты
o Графики
o Разрядное значение 9 0006
о Дроби
o Измерение
o Вероятность
o Геометрия
o Трехмерные фигуры
Дробные столбцы
· Дробные столбцы представляют собой цветные кубы или плитки, пропорциональные и представляющие собой целое, половинки, трети, четверти, пятые, шестые, восьмые, десятые и двенадцатые доли.
· В комплект обычно входят:
o один красный целый
o две розовые половинки
o й красный оранжевый терции
o четыре желтые четверти
o пять зеленый квинты
o шесть бирюзовых (сине-зеленых) сексты
o восемь синие восьмые
o десять фиолетовые 9 0041 десятых
o двенадцать черных двенадцатых
· Могут использоваться для
o Дроби
§ Смысл числа дробей
§ Равные дроби
§ Операции с дробями
§ Смешанные числа
o Пропорция
o Соотношения
Цветные плитки размером 1 дюйм
· Это цветные квадратные плитки размером 1 x 1 дюйм. Обычно их можно купить со смесью четырех цветов.
· Они могут использоваться для:
o Счет и пропуск счета
o Образцы
o Умножение
o Деление 900 06
o Сложение
o Вычитание
o Геометрия (периметр и площадь)
o Местное значение
o Измерение
o Графики и вероятность
· Дополнительные сведения и идеи см.
ниже: http://www.learningresources.com/text/pdf/2218book.pdf
Двусторонние жетоны
· Двусторонние жетоны обычно представляют собой круглые фишки с разными цветами на каждой стороне.
· Может использоваться для:
o Целые числа
o Дополнение
o Вычитание
o Умножение
o Деление
o Вероятность
o Отношения
o Проценты
10 кадров
· Десять кадров представляют собой прямоугольник, состоящий из десяти квадратов (5 на 2). На них могут быть точки, представляющие значения от 1 до 10, или они могут быть пустыми.
· Они могут использоваться для:
o Сложение
o Вычитание
o Группировка
o Подсчет
o Разрядное значение
100 бусин
9000 5 · 100 бусин получается путем нанизывания 100 бусин на нить.
Они состоят из 2 цветов, которые чередуются через каждые десять.· Их можно использовать для
o Счет и пропуск счета
o Основные математические операции
Бобы и чашка 9 0006
· Бобы и чашка состоят из чашки и бобов. Учитель решает, сколько фасоли положить в чашку для обозначенных задач.
· Они могут использоваться для:
o Счета
o Сложения
o Вычитания
o Умножения
9 0005 o Подразделение
Другие полезные математические инструменты, которые можно использовать в классе:
Где купить математические инструменты
http://www.
eaieducation.com/?gclid=COb69aTk35kCFRwwawodjSVyWA
http://www.enasco. com
http://lakeshorelearning.com
http://gamblersgifts.com (карты и кости)
eManipulatives
http://www.wiley.com/college/musser/CL_0471263796_S/emanipulatives/nav/met-index.html
http://www.mathplayground.com/math_manipulatives.html 90 006
http://nlvm.usu.edu/
Полезные ссылки
Бетонный уровень Инструкция: http://coe.jmu. edu/mathvidsr
Вопросы и ответы о манипуляторах С Мэрилин Бернс: http://teacher.scholastic.com/products/instructor/burnsqa.htm
7 Обязательных условий для использования манипуляций: http://content.scholastic.com/browse/article.jsp?id=4003
Подробнее о математических манипуляциях: http://www.iched.org/cms/ scripts/page.
Они привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентирующими символами так, как будто они живут собственной жизнью, не обязательно обращая внимание на свои референты — и способность контекстуализировать, делать паузы по мере необходимости в процессе манипулирования, чтобы исследовать референты для задействованных символов. Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов. — СССС