Точки и линии конспект урока 1 класс перспектива: Конспект+презентация по математике на тему “Точки и линии” (1 класс)
Конспект+презентация по математике на тему “Точки и линии” (1 класс)
Модель урока математики в 1 классе
Урок-сказка на тему « Точки и линии»
Автор: Власова Марина Владимировна, учитель начальных классов
МОБУ лицей № 4 муниципального района Давлекановский район
Республика Башкортостан
Учебно-методическое обеспечение: Л.Г. Петерсон, Математика, 1 класс (1 часть), Москва, « Ювента» /Учебник 2009.
Необходимое оборудование и материалы: учебники, тетради, компьютер, проектор, экран.
Время реализации занятия: 35 минут.
Авторский медиапродукт:
1. Опрерационная среда Word, Power Point.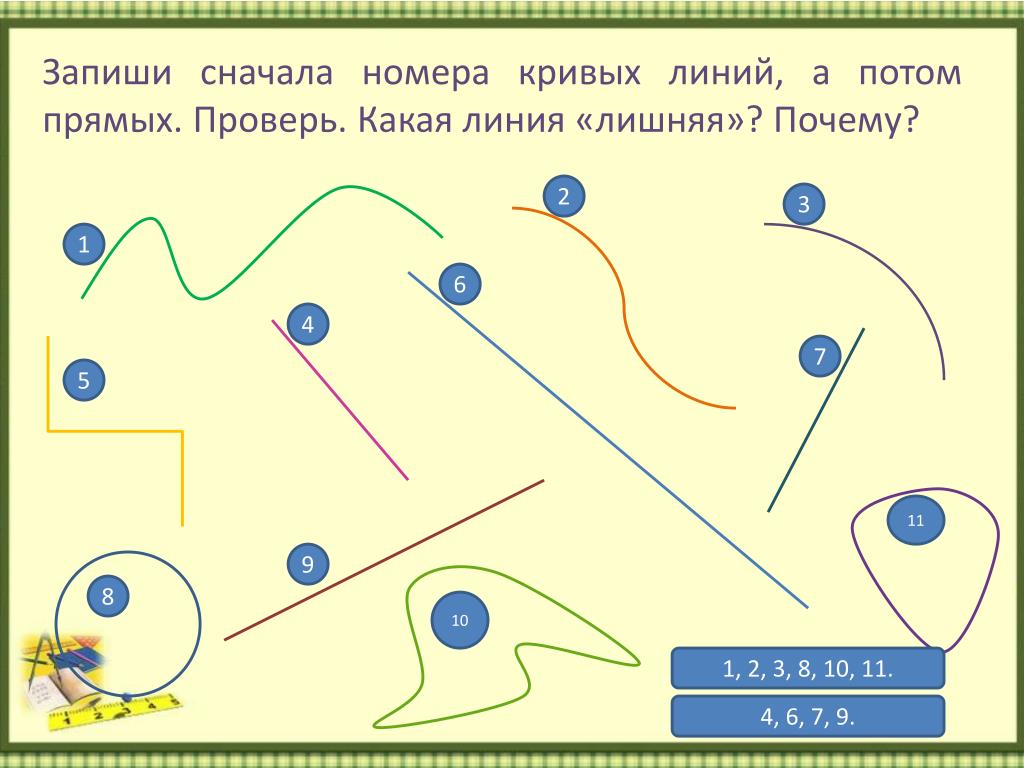
2. Наглядная презентация учебного материала .
3. Технологический сценарий: модель урока.
Целесообразность использования медиапродукта на занятии:
1. Недостаточное количество наглядного материала.
2. Развитие наглядно-образного мышления за счет повышения уровня наглядности.
3. Привитие интереса к предмету математики за счет игровой формы занятия.
Распределение времени на блоки занятия
Части – блоки занятия
Временная реализация (в минутах)
Организационный момент.
1 минута
Психологический настрой
1 минута
Постановка цели
1 минуты
Физкультминутка – 2 шт.
4 минуты
Устный счет
8 минут
Постановка проблемной ситуации и поиск ее решения
6 минут
Актуализация, повторение, закрепление и отработка полученных знаний.
12 минут
Итог урока.
2 минуты
Задачи занятия:
Образовательные:
Формировать представление о точке и линии, способность к их различению;
Совершенствовать вычислительные навыки, тренировать мыслительные операции обучающихся, уточнить названия компонентов сложения и вычитания и формировать способность к правильному использованию в речи.
Развивающие:
Развитие логического мышления, творческого воображения, внимания памяти, познавательной деятельности и творческих способностей обучающихся.
Воспитательные:
Воспитывать положительное отношение к учебному процессу, интерес к предмету и литературе.
Воспитывать взаимопонимание, взаимопомощь, культуру поведения на уроке, аккуратность, самостоятельность, терпение друг к другу.
Модель урока совмещена с презентацией.
Слайд 1
Ход урока
I. Организационный момент.
Прозвенел звонок на урок. – Добрый день, ребята! Мне приятно вас всех видеть. Давайте подарим друг другу хорошее настроение:
На части не делится солнце лучистое
И вечную землю нельзя поделить,
Но искорку счастья луча золотистого
Ты можешь, ты в силах друзьям подарить.
– Ребята, я улыбаюсь вам, вы улыбнитесь мне. Улыбка может согреть других своим теплом, показать ваше дружелюбие и улучшить всем настроение. Хорошее настроение всегда помогает справиться с любой задачей и добиться хороших результатов.
Хорошее настроение всегда помогает справиться с любой задачей и добиться хороших результатов.
II. Психологический настрой.
Слайд 2
Сегодня необычный урок математики. На нём все ученики класса отправятся в волшебный мир.
Наш урок будет похож на сказку,
Нам без знаний никуда.
Взяв с собой тетрадь, учебник, ручку и указку,
Отправляемся туда.
И так, готовы вы отправиться в сказку?
III. Постановка цели.
Целью нашего путешествия будут испытания, которые ждут нашего героя и нас, так как мы должны б
IV. Актуализация, повторение, закрепление и отработка полученных знаний.
Слайд 3.
Задание 1. Перед вами числа: 5, 3, 9, 7, 1, 13, 11
Расположите их в порядке возрастания: 1, 3,5,7,9,11,13
Мы узнали название сказки – «Колобок»
Название сказки узнали, главного героя тоже, а кто написал? (русский народ)
Слайд 4
А теперь, давайте представим , что мы оказались в этой сказке, и вспомним, как все началось.
Слайд 5,6
Итак, в домике с резными окнами жили – поживали дедушка да бабушка.Вот дедуля и просит: “Испеки мне жёнушка колобок как в сказке, благо, что муки у нас вдоволь. Пошла старушка за мукой в кладовую, взяла муки, замесила тесто на сметане, скатала колобок, изжарила его в масле и поставила на подоконник остывать.
Колобок, на удивление, получился необычный. Мало того, что непоседа, еще и любознательный. Лежит колобок на подоконнике, смотрит на небо и звезды считает. Поможем ему.
Слайд 7
Полежал колобок, посмотрел по сторонам, а потом скатился на завалинку, с завалинки на травку, с травки на дорожку и покатился по дорожке
Слайд 8, 9
Катится, катится , а навстречу ему …
Слайд 10.
Зачитывается загадка
– Привет, Зайчишка!
– Привет, какая встреча, я тебя Колобок сейчас съем. Ты такой румяненький!
Ты такой румяненький!
– Нет, ты меня не съешь, я тебе нужен. Ведь смотрю ты задание выполнить не можешь. А задания то в Лесной школе не простые, а я могу тебе помочь.
Слайд 11.
Делим на группы. Составляем буквенные выражения, а затем числовые выражения. При этом повторяем название компонентов при сложении и вычитании, а также их взаимосвязь.
Обрадовался Зайка, поблагодарил Колобка за помощь и пожелал ему счастливого пути.
Покатился колобок дальше Прикатился в Лесную школу. А там урок начался . Сел он за парту, открыл тетрадь и так увлёкся, что не заметил как подошёл к нему
Слайд 12.
-Здравствуй, Колобок. Вот ты мне и попался.
-А зачем я тебе?
-Съесть хочу, проголодался малость.
–Ничего у тебя не получится. Ты плохо в математике разбираешься, а я со своими друзьями могу тебе помочь.
–Это верно, задали мне задание не простое.
Слайд 13.
Молодцы! Снова мы выручили колобка и помогли волку.
Волк доволен остался, а колобок покатился дальше.
Катится и видит, сидит…
Слайд 14.
Сидит медведь и пытается помочь лесным животным грибочки поделить. Но не просто поделить, а по-честному разделить.
Слайд 15.
Увидел Мишенька колобка, забыл про грибочки и говорит:
– Здравствуй, колобок, уж больно ты аппетитный, съем я тебя!
– Где тебе, косолапому, съесть меня, грибы разделить, и то не можешь. Давай лучше я тебе помогу.
Поможем, ребятки?
Молодцы, опять помогли колобку, спасли его.
Покатился наш колобок дальше. А навстречу ему (загадка).
Слайд 16.
Конечно лиса. Хитро, ласково так заговорила: “Здравствуй колобок, румяненький бочок. Слышала, по лесу гуляешь, зверушкам помогаешь, задачки медведю решаешь. А вот сможешь ли моё задание выполнить? Я ведь в лесу лучший математик. А не выполнишь я тебя съем”. Делать нечего, испугался колобок рыжей лисы. Пришлось ему соглашаться. Поможем и мы колобку.
Слайд 17.
Чтобы лиса не съела колобка, давайте вместе поможем ему. Надо самостоятельно пройти через 3 столбика чисел так, чтобы, сложив их, в сумме получилось 10.
Расстроилась лиса, что осталась без обеда, да делать нечего. Колобок остался цел и невредим, все задания выполнены.
Остановился колобок. Не знает, колобок, куда лучше дальше катиться.
Слайд 18
(дети объясняют решение)
VII. Физ. минутка для глаз
Покатился колобок дальше. Давайте понаблюдаем за дорожкой, по которой покатился колобок.
Слайд 19.
Вы – молодцы!
V. Физ. минутка
Вы устали, засиделись?
Вам размяться захотелось?
Приступаем мы к зарядке.
Раз – подняться, потянуться,
Два – согнуться, разогнуться,
Три – в ладоши три хлопка, головою три кивка,
На четыре – руки шире,
Пять – руками помахать,
Шесть – за парту тихо сесть.
Семь, восемь – лень отбросим.
Слайд 20.
V1. Постановка проблемной ситуации и поиск ее решения.
А что же было дальше?
Остановился колобок, оглянулся назад и задумался :
– А почему следы на земле остаются разные?
Слайд 21.
Выслушиваются ответы детей
Формулируется вывод
Точка – коснуться бумаги острием карандаша
Линия – провести острием карандаша по листу бумаги
Точки обозначаются буквами
V11. Х. Работа с учебником (стр. 56 – урок 35)
Задания 1, 2 – выполняются с коллективным обсуждением.
– назовите точки, изображенные на рисунке?
– какая из точек самая верхняя?
– какая из точек самая нижняя?
– какая из точек самая правая?
– какая из точек самая левая?
Соедините красной линией точки А и Б, поставьте на ней точку К.
Соедините синей линией точки Д и М так, чтобы линия прошла через точку В
Проведите желтую линию, которая начинается и заканчивается в точке Е.
Слайд 22
А все ли линии одинаковые? – задумался колобок и вспомнил свой путь.
Выслушиваются ответы детей.
Слайд 23,24
Выводы: Линии – прямые и кривые
Слайд 25
И все? – задумался колобок. Пришлось ему опять вспомнить свой путь.
Выслушиваются ответы детей.
Слайд 26
Выводы: Линии – замкнутые и незамкнутые.
V111. Актуализация и отработка полученных знаний
Работа в учебнике
Задания 3,4 выполняются коллективно
3. Если мы выйдем из точки А и пойдем по этой линии, то вернемся обратно в точку А. Проводим практическую работу, обводим линии красным карандашом. Эти линии замкнутые, у них нет ни начала, ни конца. Учащиеся убеждаются в этом и дорисовывают свою замкнутую линию, которая проходит через точку К.
С аналогичным рассуждением выполняется задание 4.
Незамкнутые линии имеют начало и конец.
Задание 5 –самостоятельно, с последующим обсуждением и взаимопроверкой.
Слайд 27
Х. Физкультминутка
Руки подняли и покачали –
Это деревья в лесу.
Руки согнули, кисти встряхнули —
Ветер сбивает росу.
В стороны руки, плавно помашем —
Это к нам птицы летят.
Как они тихо садятся, покажем —
Крылья сложили назад.
Х1. Отработка навыков полученных знаний в парах, группах.
Задание 6,7,8,9 выполняются в парах, затем проверяются в группах
Слайды 28,29,30,,31
Х111. Подведение итогов урока. Оценивание. Обобщение.
Оценивание. Обобщение.
Слайд 32
– Давайте оценим свою работу. Вспомним, что удалось повторить за урок?
– Что показалось трудным?
– Какое задание было самым интересным?
– А с каким настроением вы уходите с урока, выразите на лице колобка и поместите на доску.
Я вам тоже хочу сказать за такое удивительное общение спасибо. Спасибо, что вы дружно помогали друг другу и героям сказки.
Слайд 33
В мире много сказок грустных и смешных
Нам нельзя без дружбы.
Пусть герои сказок дарят нам тепло.
Пусть добро навеки побеждает зло!
А теперь, давайте отдохнем, послушаем и потанцуем под чудесную песню, которая подходит к нашему сегодняшнему занятию.
Дети танцуют под музыку «Дорога добра»
|
Этап урока |
Действия учителя |
Деятельность обучающихся |
|
1.
|
Здравствуйте, ребята! Долгожданный дан звонок Ты готов начать урок? Все ль на месте Все ль в порядке: Ручка, книжка и тетрадка, Карандаш, линейка, ластик? Все ли правильно сидят? Все ль внимательно глядят? И так, начинаем наш урок.
|
|
|
2. 2. Эмоционально-волевая регуляция. Актуализация знаний
|
Давайте , ребята, повторим материал прошлого урока. Что такое множество? Как называется каждый предмет из группы?
Придумай название для предметов и животных, собранных вместе.
Сравни элементы множеств в первом и во втором рядах. Есть ли в первом ряду элемент, которого нет во втором? Есть ли во втором ряду элемент, которого нет в первом? Значит эти множества какие? Сравни множества в верхнем и нижнем рядах. |
Группа предметов.
Элемент множества.
Коллекция марок, набор карандашей, стая птиц, чайный сервиз, букет цветов, стая коров.
Они одинаковые.
Равные.
Во втором, мышь. |
|
3. 3. Мотивационно-целевой этап. Постановка учебной задачи
|
Если возьмём карандаш и прикоснёмся им к бумаге, остаётся след. Что это? Правильно. Это точка. Мы будем сегодня говорить о точках и линиях. Значит, как называется тема нашего урока? |
Точка.
«Точки и линии.» |
|
4.
|
Подсчитай точки. А из точек состоят линии. Линии
бывают разные. Еще раз по-внимательнее! Посмотрите как чертят прямую линию. Для этого берут карандаш и линейку. Прижимают линейку к бумаге. Проведут карандашом линию. Это прямая.
|
10,8,7,5. |
|
5. 5. Первичное формирование умений на основе самоконтроля.
|
Работа с учебником (стр.38) Найди на рисунке прямые линии.
Найди кривые линии.
Молодцы! Множество точек на рисунке раздели на части по цвету. Сколько получилось частей? Какую фигуру напоминает тебе множество красных точек? Множество зелёных? Множество синих? Сколько элементов в множестве оранжевых точек? Правильно.
Переходим к следующему заданию. Восстанови на рисунках равные множества по их частям, если в каждом было по три элемента.
Где на рисунках элементов больше: в множестве ромашек или в множестве пчел? На сколько больше?
Где больше: в множестве кругов или в множестве квадратов? На сколько больше?
Физкультминутка. Руки в
стороны — в полет |
Крыша, стены дома, окно, забор, лучи солнца, ствол ели.
Тропинка, верёвка для игры с котёнком, кусты у дома, орнамент на крыше.
4
Круг
Треугольник
Квадрат
7
1)
2) 3)
Во множестве ромашек.
На один.
В множестве кругов. На один. |
|
6. Самостоятельная работа с проверкой по эталону. Самоанализ и самоконтроль.
|
№1.Открыли тетради и работаем в тетрадях Сколько линий ты видишь на рисунке? Сколько прямых линий? Сколько кривых линий? А теперь отметим это точками, как показано в образце. Взяли красный карандаш и обведите прямые линии красным карандашом. Молодцы! №2. Дорисуйте веревки на каждом рисунке. Назовите линии, которые получились?
№3. Посмотрите, ребята, на данные множества. Сколько множеств вы видите? Назовите элементы первого множества.
Среди данных множеств есть множество равное первому множеству? Назовите элементы второго множества.
Среди данных множеств есть множество, равное этому множеству? Обведите
линии, их выделяющие, одним цветом. №4. Выдели на рисунке множества по указанным меткам. Какую метку забыл нарисовать художник? Добавь её и обведи красной линией соответствующее множество. №5. Нарисуй справа такую же мышку, но так, чтобы она смотрела в противоположную сторону.
|
6
2 4
Прямая, кривая,кривая, прямые.
4 Ромашка, ёжик, чашка.
Нет. Чашка, ромашка, птичка, треугольник. Да, последнее.
Треугольник. |
|
7. 7. Включение нового знания в систему знаний и повторение. |
А теперь, внимание на экран. Слайд 1. Посмотрите на рисунок. По реке проходит прямая линия. Кто оказался справа от прямой, а кто слева? Слайд 2.
Еще ребята очень важно знать: Слайд 3. Изображение прямой можно продолжать в обе стороны бесконечно? Прямая линия не имеет ни начала, ни конца.
|
Слева: бабочка. Справа: лягушка, пчела, рыба.
Слева: лось, медведь,лиса, лисёнок, заяц, змея. Справа: мышь, ящерица, бобёр, олень, кабан. |
|
8. 8. Рефлексия деятельности
|
– Что нового было сегодня на уроке?
– Какие задания понравились вам больше всего?
Ребята! Оцените свою работу на уроке с помощью сигнальной ленты «Светофор» |
О точках и линиях.
Найти и рисовать линии. |
Конспект урока с мультимедиа «Точка и линии»
ТЕМА: «Точка и линии»
Класс: 1 класс
Предмет: математика
УМК (авторы): «Перспектива». Г. В. Дорофеев, Т. Н. Миракова, Т. Б. Бука.
Тип урока : ОНЗ
Цель: формирование представлений о точке, прямых и кривых линиях.
Планируемые результаты(предметные):
- учащиеся научатся различать и называть точку, прямую линию, кривую линию;
- использовать математическую терминологию при выполнении заданий разного вида.
Метапредметные:
Регулятивные:
- принимать и сохранять учебную задачу, соответствующую этапу обучения;
- совместно с учителем оценивать действия, вносить соответствующие коррективы;
- в сотрудничестве с учителем, классом находить варианты решения учебной задачи.
Познавательные:
- устанавливать аналогии и причинно-следственные связи, делая выводы;
- давать характеристики изучаемым математическим объектам на основе их анализа;
- строить небольшие математические высказывания в устной форме.

Коммуникативные:
- принимать участие в работе фронтальной, индивидуальной, в парах;
- воспринимать мнение других людей и их позицию;
- уметь аргументировать.
Личностные:
- осознавать математические составляющие окружающего мира;
- проявлять интерес к учебному материалу;
- давать оценку своей работе на основе заданных критериев успешности учебной деятельности.
Формы и методы обучения
Формы: фронтальная, индивидуальная, работа в парах
Методы: словесные, наглядные, практические, ЭОР
Образовательные ресурсы
- Математика. 1 класс. Учебник, для общеобразоват. организаций с прил. на электрон, носителе. В 2 ч. Ч. 1/ Г. В. Дорофеев, Т. Н. Миракова, Т. Б. Бука; Рос. акад. наук. Рос. акад. образования, изд-во «Просвещение». — 6-е изд. — М. : Просвещение, 2018. — 128 с.
- Математика. 1 класс. Рабочая тетрадь. В 2 ч.
 Ч. 1/ Г. В. Дорофеев, Т. Н. Миракова, Т. Б. Бука. изд-во «Просвещение». — 5-е изд. — М. : Просвещение, 2018. — 95 с.
Ч. 1/ Г. В. Дорофеев, Т. Н. Миракова, Т. Б. Бука. изд-во «Просвещение». — 5-е изд. — М. : Просвещение, 2018. — 95 с. - Ситникова Т.Н. Поурочные разработки по математике. 1 класс.- 2-е изд. – М.: ВАКО, 2017. – 840 с.
- ММП (с использованием ЭОР – фрагмент видеофильма”Занимательная математика” Р. Саакянц)
- Доска SMART Board, проектор;
- Математика. 1 класс. Электронное приложение к учебнику Г.В. Дорофеева, Т.Н. Мираковой /1CD/ (В комплекте с учебником)ü аудио запись песни Е. Железновой “Мы кружок нарисовали”
- Индивидуальный комплект у каждого учащегося: карта самоотчёта – карточка с рисунком, 3 смайла, таблица с числами и буквами. Рисунок карандаша, прямой и кривой линий, точки
Конспект урока с мультимедиа приложением
RAR / 33.39 Мб
ТЕМА: «Точка и линии»
Класс: 1 класс
Предмет: математика
УМК (авторы): «Перспектива». Г. В. Дорофеев, Т. Н. Миракова, Т. Б. Бука.
Тип урока : ОНЗ
Цель: формирование представлений о точке, прямых и кривых линиях.
Планируемые результаты(предметные):
- учащиеся научатся различать и называть точку, прямую линию, кривую линию;
- использовать математическую терминологию при выполнении заданий разного вида.
Метапредметные:
Регулятивные:
- принимать и сохранять учебную задачу, соответствующую этапу обучения;
- совместно с учителем оценивать действия, вносить соответствующие коррективы;
- в сотрудничестве с учителем, классом находить варианты решения учебной задачи.
Познавательные:
- устанавливать аналогии и причинно-следственные связи, делая выводы;
- давать характеристики изучаемым математическим объектам на основе их анализа;
- строить небольшие математические высказывания в устной форме.
Коммуникативные:
- принимать участие в работе фронтальной, индивидуальной, в парах;
- воспринимать мнение других людей и их позицию;
- уметь аргументировать.

Личностные:
- осознавать математические составляющие окружающего мира;
- проявлять интерес к учебному материалу;
- давать оценку своей работе на основе заданных критериев успешности учебной деятельности.
Формы и методы обучения
Формы: фронтальная, индивидуальная, работа в парах
Методы: словесные, наглядные, практические, ЭОР
Образовательные ресурсы
- Математика. 1 класс. Учебник, для общеобразоват. организаций с прил. на электрон, носителе. В 2 ч. Ч. 1/ Г. В. Дорофеев, Т. Н. Миракова, Т. Б. Бука; Рос. акад. наук. Рос. акад. образования, изд-во «Просвещение». — 6-е изд. — М. : Просвещение, 2018. — 128 с.
- Математика. 1 класс. Рабочая тетрадь. В 2 ч. Ч. 1/ Г. В. Дорофеев, Т. Н. Миракова, Т. Б. Бука. изд-во «Просвещение». — 5-е изд. — М. : Просвещение, 2018. — 95 с.
- Ситникова Т.Н. Поурочные разработки по математике.
 1 класс.- 2-е изд. – М.: ВАКО, 2017. – 840 с.
1 класс.- 2-е изд. – М.: ВАКО, 2017. – 840 с. - ММП (с использованием ЭОР – фрагмент видеофильма”Занимательная математика” Р. Саакянца)
- Доска SMART Board, проектор;
- Индивидуальный комплект у каждого учащегося: карта самоотчёта – карточка с рисунком, 3 смайла, таблица с числами и буквами,
- Рисунок карандаша, прямой и кривой линий, точки
Ход урока:
І. Этап мотивации: (1 – 2 мин)
Цель: создание таких условий, чтобы ученик внутренне собрался, подготовился и нацелился на «покорение новых вершин».
Мы -умные, мы – дружные,
Мы – внимательные,
Мы – старательные.
Мы – отлично учимся,
У нас всё получится!
– Урок математики.
– Присаживайтесь, называя по цепочке числа натурального ряда
– Обратите внимание у каждого из вас на столе – лист, с одной стороны которого карта самоотчёта, а с другой – рисунок для работы на уроке. Как всегда на уроке для самооценивания нам понадобятся смайлы. Зелёный – всё получилось, было понятно, собой доволен; жёлтый – было интересно, но некоторые задания вызывали затруднения; красный – было трудно, есть над чем поработать.
Как всегда на уроке для самооценивания нам понадобятся смайлы. Зелёный – всё получилось, было понятно, собой доволен; жёлтый – было интересно, но некоторые задания вызывали затруднения; красный – было трудно, есть над чем поработать.
СЛАЙД 2
ІІ. Актуализация и фиксирование индивидуального затруднения в пробном действии: (5 – 6 мин)
Цель: внутреннее осознание учащимися потребности открытия новых знаний и умений. Активизация мыслительных процессов.
– Сосчитайте с соседом по парте от 1 до 10 по очереди, друг за другом и от 10 до 1. Оцените с помощью смайла свою работу.
– Работаем с таблицей. Возьмите красный карандаш.
– Отметьте букву, с числом предыдущим для числа 6
– число, которое находится между числами 16 и 18
– Предыдущее числа 3
– Последующее числа 18
– число, которое в натуральном ряду находится между числами 11 и 13
– Число следующее за числом 17
– Число, которое при счёте идёт перед числом 9
– Проверяем, назовите ответы 5, 17, 2, 19, 12, 18, 8. Оцените свою работу с помощью смайлов.
Оцените свою работу с помощью смайлов.
– Мы получили множество чисел. Что такое множество?
– На какие подмножества можно разбить множество этих чисел? ( однозначные и двузначные; чётные и нечётные)
-А какое же слово у нас получилось? (МОЛОДЕЦ)
-Вы действительно, молодцы. Чему учились? ( совершенствовали вычислительные навыки, буквы складывали в слово) СЛАЙД 3
III. Этап выявления места и причины затруднений: (4 – 5 мин)
Цель: осознание учащимися, в чем именно состоит затруднение, каких знаний, умений и навыков им не хватает для решения пробного задания.
-Отгадайте загадку:
Чертят им или рисуют.
Грифель по листку танцует.
Он большой помощник наш,
Мой волшебный … (карандаш)
Учитель держит в руках карандаш.(вывесить на доску картинку)
– Это не простой Карандаш, а волшебный. Он знает много нового, и вместе с ним мы отправляемся в увлекательное путешествие в одну замечательную страну. Какую, давайте узнаем, выполнив действия.
Какую, давайте узнаем, выполнив действия.
СЛАЙД 4
– Карандаш нас знакомит со страной Геометрия.
– Может быть кто-нибудь знает, что это за страна такая?
Геометрия – это раздел математики, который изучает фигуры и их свойства. Это слово греческого происхождения и состоит из двух греческих слов: ГЕО – «земля», МЕТРЕО – «измеряю».
– Давайте посмотрим видеофильм, который поможет нам больше узнать о геометрии.
– Что вы запомнили? Оцените свою работу на этом этапе с помощью смайлов.
Физминутка для глаз
Глаза поднять вверх-вниз, влево-вправо. Повторить по 4 раза.
Нарисуйте глазами окружность влево, вправо. Повторить по 4 раза.
Крепко зажмурить глаза, сосчитать до 10 про себя, а затем открыть их на такое же время. Повторить 4-6 раз.
Быстро моргать в течение 10-12 секунд, открыть глаза, отдыхать 10-12 секунд. Повторить 3 раза.
-Разгулялся как-то наш карандаш и оставил на бумаге следы своего присутствия.
-Посмотрите, что же получилось?
– Что вы видите?
СЛАЙД 5
– Со всеми ли фигурами вы знакомы? Какие геометрические фигуры можно объединить во множество?
-В чём ваше затруднение? (Как точно называются оставшиеся геометрические фигуры)
– Какова тема нашего урока? ( Точки и линии)
– Какие задачи мы перед собой поставим? (разобраться как называются геометрические фигуры, больше узнать о них, научиться их различать, правильно рисовать.)
IV. Этап построения проекта выхода из создавшейся ситуации: (3 – 4 мин)
Цель: выбор способа разрешения проблемы, выбор метода и средств. Выбирается способ, который позволит получить новое знание: способ уточнения, способ дополнения.
– Раскрою вам один секрет, а вы внимательно послушайте и посмотрите. Это берег большой реки. Солнышка еще нет, но уже светает. Тепло, спокойно. Мысленно оглядитесь вокруг, посмотрите вдаль, туда, где река смыкается с небом. Это линия горизонта – прямая линия. Она тянется далеко-далеко влево и вправо. У прямой линии нет ни начала, ни конца.
Это линия горизонта – прямая линия. Она тянется далеко-далеко влево и вправо. У прямой линии нет ни начала, ни конца.
Солнышко встает из-за горизонта. Оно поднимается выше, становится светло. Прилетела птичка, клюнула что-то на песке у озера. От клюва остался след – это точка. Проползла маленькая змейка. След от змейки на песке – кривая линия. Солнце уже высоко, наступил день. Все растения тянутся к солнышку. Наше мысленное путешествие заканчивается.
СЛАЙД 6
– Вы узнали секрет. Давайте попробуем применить секрет для определения названия новых геометрических фигур.
– Как называется линия, где море смыкается с небом? (линия горизонта).
– Какая она? ( прямая)
– Как называется след от клюва птички на песке? (точка)
– Какую линию оставила змейка? (Кривая)
V. Реализация построенного проекта: (5 – 6 мин)
Цель: создание проекта выхода и проба применить его на практике.
– Сейчас волшебными стали и ваши карандаши. У каждого из вас есть карточка с рисунком. Возьмите свой волшебный карандаш и поставьте точку в левом верхнем углу. Как вы это сделали? (лёгким прикосновением карандаша)
– …, выйди, покажи, пожалуйста, как ты это сделал на интерактивной доске.
– А чем точка отличается от ягодки земляники? (Ягодка большая, а точка маленькая)
– Нарисуйте путь точки по рассказу: “Точка пошла в лес. Сначала она дошла до молодой берёзки, обогнула её слева и пошла к земляничке, дошла до неё и плавно повернула к озеру.
– Какая линия получилась? (Кривая)
– А можно ли было быстрее, короче дойти до озера сразу? Каким образом? (прямо)
– Какая линия в результате может получиться? (Прямая)
– Кто догадался, как это можно сделать? (Под линейку)
– Начертите прямую линию от точки до озера с помощью линейки. Оцените свою работу с помощью смайлов. СЛАЙД 7
Физминутка
– Поднимитесь, пожалуйста. Выполняйте движения по заданию. Показываю прямую линию – руки поднимите вверх, кривую – бежим на месте, точка – приседайте
Выполняйте движения по заданию. Показываю прямую линию – руки поднимите вверх, кривую – бежим на месте, точка – приседайте
VI. Этап первичного закрепления с проговариванием во внешней речи: (5 – 6 мин)
Цель: решение типовых задач по новой теме.
– А теперь давайте проверим, правильно ли мы сделали вывод по теме.
Точка получается одним прикосновением карандаша к листу. Точка самая основная и простая геометрическая фигура.
Прямую линию можно начертить с помощью линейки, а кривую можно чертить как угодно.
У прямых и кривых линий нет концов. Их можно продолжить. СЛАЙД 8-9
– Прямые линии можно найти и в окружающей обстановке. Попробуйте их назвать.
Игра «Угадай, что это за линия?» (хорошо читающие дети снимают с сенсорного креста и читают загадки)
– Отгадайте загадки, но при этом не забывайте, с какими понятиями мы сегодня познакомились.
1. Крашеное коромысло над рекой повисло. (Радуга, чтобы нарисовать её, необходимо провести кривые линии.)
– Сколько нужно провести кривых линий, чтобы получилась радуга? Кто знает стихотворение о том, в какой последовательности идут цвета радуги?
2. Кто всю ночь по крыше бьёт да постукивает, и бормочет, и поёт, убаюкивает? (Дождь, состоит из прямых линий.)
3. Ежедневно по утрам
Он в окошко входит к нам.
Если он уже вошел —
Значит, день пришел.
(Солнечный луч, состоит из прямой линии.)
4. Висит сито – не людьми свито. (Паутина, в ней есть и прямые и кривые линии.)
Оцените свою работу с помощью смайлов.
VII. Этап работы в парах и самостоятельной работы с проверкой по эталону: (6 – 7 мин)
Цель: самостоятельное выполнение типовых заданий, проверка их по предложенному эталону сначала сами, затем друг у друга. Создание ситуации успеха для каждого ученика.
– Откройте учебник на с. 38. Найдите на рисунке прямые и кривые линии. Поработайте в паре, показывая и называя друг другу по очереди.
– Как можно с помощью линейки проверить, прямая линия или нет? ( Приложить линейку, если линия с ней совпадает, то линия прямая)
-Множество точек разделите по цвету. Сколько получилось частей? 4
– Какую фигуру напоминают красные точки? круг
– А зеленые точки? треугольник
-Сколько синих точек в этом множестве? 8
– Сколько оранжевых? 7
Физминутка для мелкой мускулатуры пальцев рук Е. Железнова “Мы кружок нарисовали” аудиозапись песни
Рисуем на ладони кружочек, черточку, волну, точки, а потом – встряхиваем кистями рук.
– Откройте Рабочую тетрадь на с. 30 №1. Выполните задание самостоятельно, отмечая точками количество линий.
– Сколько линий на рисунках? (6)
– Сколько прямых линий? (2)
– Какого они цвета? ( синего и красного)
– Сколько кривых линий ? ( 4)
– Рассмотрим №2. Дорисуйте верёвочки.
Дорисуйте верёвочки.
– Какие линии получились?
– Покажите соседу по парте прямые линии, что это? ( верёвки для белья и качелей)
– Назовите кривые линии, что это? ( Скакалка и лента гимнастки) Оцените свою работу на этом этапе с помощью смайлов.
VIII. Этап включения в систему знаний и повторения: (6 – 3 мин)
Цель: фиксация полученных знаний, рассмотреть, как новое знание укладывается в систему ранее изученного, при возможности довести полученный навык до автоматизированности использования и подготовить учеников к дальнейшему погружению в тему.
– Как вы думаете, можем ли мы применить новые знания в жизни? Где и как?
– Почему у нас возникла необходимость изучить данную тему?(этот материал войдет в нашу копилку знаний, пригодится в жизни).
– Как вы думаете, какие задания нам дальше нужно выполнять?( задания на повторение изученного).
В зависимости от оставшегося времени можно выполнить фронтально, индивидуально (возможность работы на отдельном ноутбуке, самостоятельно)
* https://learningapps. org/view7597771Проверь себя. 1 класс. Точка и линии. Восстановите текст.
org/view7597771Проверь себя. 1 класс. Точка и линии. Восстановите текст.
* Помочь карандашу разбить линии на группы и сравнить их число.
* Выполнить задания на Электронном приложении к учебнику Г.В. Дорофеевой, Т.Н. Мираковой 1CD
СЛАЙД 10 -11
Оцените свою работу с помощью смайлов.
— В какую страну путешествовали? Над чем работали на уроке?
IX. Промежуточный этап, на котором формулируется домашнее задание: (1 – 2 мин)
Цель: рекомендации к выполнению домашнего задания.
– А тем ребятам, кто захочет проверить и закрепить свои знания по теме нужно будет зайти на образовательную платформу Учи.ру в предмет Математика, раздел Геометрия Точка, линия и выполнить предлагаемые задания. СЛАЙД 12
X. Этап рефлексии учебной деятельности на уроке: (2 – 1 мин)
Цель: соотнесение задач, которые учащиеся ставили на уроке и результатов своей деятельности.
– Заполните карту самоотчёта
– Кто доволен сегодняшним уроком? Оцените свою работу с помощью смайлов.
– Спасибо за работу, молодцы!
/data/files/e1566804199.doc (Пояснительная записка к приложениям)
/data/files/y1566804119.ppt (Точка и линии)
/data/files/j1566804139.mp4 (Занимательная геометрия)
/data/files/v1566804179.mp3 (Мы кружок нарисовали)
/data/files/s1566804243.doc (Приложения к уроку)
Урок 7. формы. многообразие форм окружающего мира. изображение объёма на плоскости и линейная перспектива – Изобразительное искусство – 6 класс
«Изобразительное искусство»
«6» класс
Урок № 07. Формы. Многообразие форм окружающего мира. Изображение объёма на плоскости и линейная перспектива
Перечень вопросов, рассматриваемых в теме:
Пространственная форма и её геометрические виды.
Выявление конструкции предмета через соотношение простых геометрических фигур и изображение сложной формы предмета (силуэта) как соотношения простых геометрических фигур при соблюдении их пропорций.
Построение изображения простых предметов по правилам линейной перспективы.
Определение и использование в рисунке понятия «линия горизонта», «точка зрения», «точка схода», «вспомогательные линии», «взгляд сверху, снизу, сбоку».
Связь между новым представлением о человеке в эпоху Возрождения и задачами художественного познания и изображения явлений реального мира.
Глоссарий по теме:
Слово конструкция (от лат. constructio) переводится как «составление, построение», то есть взаимное расположение частей предмета, их соотношение.
Точка зрения предполагает взгляд на предметы из одной неподвижной точки при построении перспективного изображения. На предметы можно смотреть сверху, снизу и сбоку, меняя точку зрения.
Линейная перспектива – это способ представления трёхмерных объектов в двухмерном изображении. Рассмотрим построение перспективы: изображения вспомогательных линий сходятся в одной точке – это точка схода.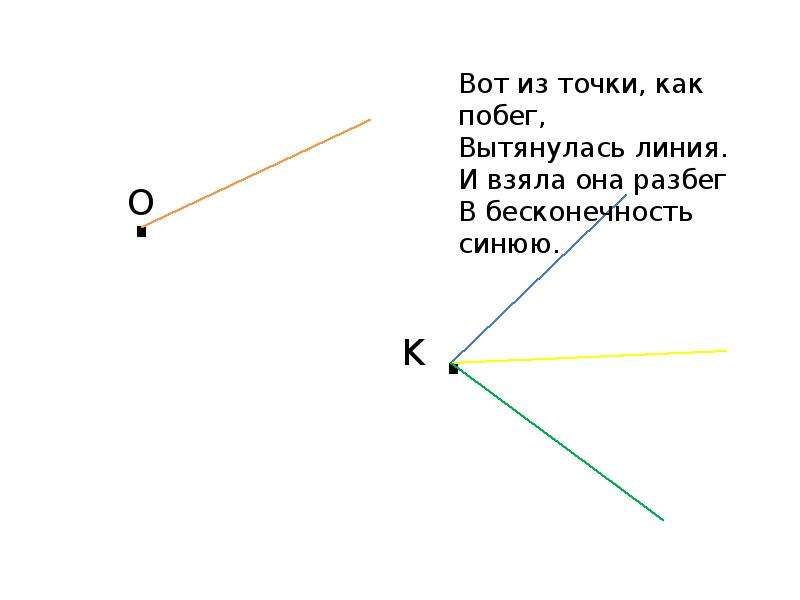 Она лежит на линии горизонта – уровне наших глаз.
Она лежит на линии горизонта – уровне наших глаз.
Если уходящие вглубь линии перпендикулярны условной линии глаз наблюдателя, то построение называется центральной линейной перспективой.
Основная и дополнительная литература по теме урока:
1. Неменская Л. А. Изобразительное искусство. Искусство в жизни человека. 6 класс: учеб. для общеобразоват. организаций / Л. А. Неменская; под ред. Б. М. Неменского. – 10-е изд. перераб. и доп. – М.: Просвещение, 2019. – 191 с.: ил. – ISBN 978-5-09-071640-6 – С. 62-67.
Открытые электронные ресурсы по теме урока:
1. Леонардо да Винчи. Трактат о живописи. О живописи и перспективе [Электронный ресурс]. – Режим доступа: https://litra.pro/traktat-o-zhivopisi/da-vinchi-leonardo/read/5 (дата обращения: 14.08.19)
2. Зрительные теории итальянского Возрождения [Электронный ресурс]. – Режим доступа: https://art-life.biz/rus/files/glava-21.pdf (дата обращения: 14.08.19).
Теоретический материал для самостоятельного изучения
Изображения всех объектов предметного мира и окружающей природы можно построить на основе простых геометрических фигур и тел. Чтобы научиться рисовать, необходимо научиться видеть внутреннюю структуру каждого предмета – его конструкцию.
Чтобы научиться рисовать, необходимо научиться видеть внутреннюю структуру каждого предмета – его конструкцию.
Слово конструкция (от лат. constructio) переводится как «составление, построение», то есть взаимное расположение частей предмета, их соотношение.
В жизни все тела объёмны, они имеют три измерения – длину, ширину и высоту. Объёмная конструкция любого предмета может быть рассмотрена как сложение геометрических тел: шара, куба, конуса, пирамиды, цилиндра.
Одним из важнейших правил изображения на плоскости объёмных предметов является перспектива – система отображения на плоскости глубины пространства. Мы видим удаленные предметы меньшими, чем они есть на самом деле.
На изображениях эпохи Средневековья мы видим в основном сюжеты, связанные с духовной жизнью. В тот период взгляд на мир можно назвать вертикальным – от земли к небу. Но со временем вследствие развития техники и науки взгляды на жизнь и место человека в ней претерпели изменения. Вслед за изменениями жизни пришло изменение и видения мира, его можно назвать горизонтальным – вглубь пространства, и вглубь жизни человека. Художники эпохи Возрождения, черпали своё вдохновение в вере в человека и в его силы. Именно человек стал центром интересов изобразительного искусства. Первое письменное изложение правил перспективы появилось в 1435 г. в книге «О живописи» Леона-Баттисты Альберти, итальянского художника, архитектора, учёного и литератора.
Вслед за изменениями жизни пришло изменение и видения мира, его можно назвать горизонтальным – вглубь пространства, и вглубь жизни человека. Художники эпохи Возрождения, черпали своё вдохновение в вере в человека и в его силы. Именно человек стал центром интересов изобразительного искусства. Первое письменное изложение правил перспективы появилось в 1435 г. в книге «О живописи» Леона-Баттисты Альберти, итальянского художника, архитектора, учёного и литератора.
Точка зрения предполагает взгляд на предметы из одной неподвижной точки при построении перспективного изображения. При её перемене и очертания предметов на плоскости могут существенно измениться. На предметы можно смотреть сверху, снизу и сбоку, меняя точку зрения. Если смотреть на предмет прямо, так чтобы наши глаза были на середине высоты предмета, то мы увидим его плоским, то есть только одну его сторону. Во всех остальных случаях мы видим сразу три стороны предмета.
Но те стороны предмета, которые уходят в глубину, мы видим по законам линейной перспективы. Линейная перспектива – это способ представления трёхмерных объектов в двухмерном изображении. Рассмотрим построение перспективы: изображения вспомогательных линий сходятся в одной точке – это точка схода. Она лежит на линии горизонта – уровне наших глаз. Обозначая эту линию в своём рисунке, художник сразу обретает систему отсчёта. Линия горизонта может быть выше или ниже в зависимости от точки зрения.
Линейная перспектива – это способ представления трёхмерных объектов в двухмерном изображении. Рассмотрим построение перспективы: изображения вспомогательных линий сходятся в одной точке – это точка схода. Она лежит на линии горизонта – уровне наших глаз. Обозначая эту линию в своём рисунке, художник сразу обретает систему отсчёта. Линия горизонта может быть выше или ниже в зависимости от точки зрения.
Если уходящие вглубь линии перпендикулярны условной линии глаз наблюдателя, то построение называется центральной линейной перспективой. При угловой перспективе линии контуров и плоскостей уже не сходятся в единой точке, а расходятся к двум точкам схода – слева и справа от наблюдателя
Примеры и разбор решения заданий тренировочного модуля:
1. Решите кроссворд:
3У | |||||||||||
2З | Г | ||||||||||
1Ц | Е | Н | Т | Р | А | Л | Ь | Н | А | Я | |
Е | О | ||||||||||
Н | В | ||||||||||
И | А | ||||||||||
Я | Я | ||||||||||
По горизонтали:
1 – тип линейной перспективы, когда уходящие вглубь линии перпендикулярны условной линии глаз наблюдателя
По вертикали:
2 – эта точка предполагает взгляд на вещи из одной неподвижной точки при построении перспективного изображения
3 – при этом типе перспективы линии контуров и плоскостей уже не сходятся в единой точке, а расходятся к двум точкам схода – слева и справа от наблюдателя
Правильные ответы:
По горизонтали: 1. центральная.
центральная.
По вертикали: 2. зрения. 3. угловая
2. Рассортируйте по категориям рисунки. Для этого перенесите изображения по столбцам.
Перспектива | |
Линейная | Угловая |
Правильный вариант:
Перспектива | |
Линейная | Угловая |
Линейная перспектива презентация по изо. Основные положения теории линейной перспективы
Болгарская средняя общеобразовательная школа №1
с углубленным изучением отдельных предметов.
Районный семинар учителей
художественно – эстетического цикла по теме
Урок ИЗО в 6 «А» классе
по теме:
«Перспектива»
Учитель ИЗО
II квалификационной категории
г. Болгар 2009г.
Перспектива.
Цель: Научить передавать пространство на плоскости изображения.
Развивать навыки рисования перспективы.
Воспитывать интерес и наблюдательность к окружающему миру.
Оборудование и материалы:
1.Картины художников,
2.Схемы построения перспективы в рисунке (слайды)
3.Для учеников: альбом, карандаш, ластик.
Ход урока
Орг. Момент.
Пейзаж (слайд 1.)
Ребята скажите, что изображено на этой картине? (пейзаж)
Что художник хочет показать в пейзаже? (природу, пространство)
Да. Сегодня нам понятно, что пейзаж – это прежде всего изображение пространства. Но понимание способов изображения пространства было разным в различные эпохи.
В эпоху Древнего Египта изображения никогда не создавали иллюзию прорыва стены, а следовали вдоль ее плоскости, располагаясь рядами, подобно строкам письма. Изображения словно мерно шествовали, ритмически повторяя жесты. Изображение переносилось на плоскость не в том виде, в котором оно предстает глазу, а в том, которое наиболее выражает ее суть.
Изображение переносилось на плоскость не в том виде, в котором оно предстает глазу, а в том, которое наиболее выражает ее суть.
1.Настенная роспись. Древний Египет. (слайд 2.)
Древние египтяне совмещали в одном изображении вид сверху, вид спереди и вид в профиль.
2.Сад и пруд. Древний Египет. (слайд 3.)
Искусство Средних веков сосредотачивается на духовной и эмоциональной жизни людей. Изображения несут символический и рассказывающий, повествовательный смысл.
3.Чудо Архангела Михаила о флоре и лавре. Икона. Россия. 15 век. (слайд 4.)
У пространства иконы свои законы построения. Икона будто открывается навстречу стоящему перед ней человеку. Линии в иконе, если их продолжить, сходятся впереди – на молящемся человеке, как бы замыкаются им.
В эпоху Возрождения в искусстве возобладал интерес к изучению реально наблюдаемого мира и личности человека. И вот появилось «окно», через которое художник посмотрел вдаль, и родилось понятие – перспектива, линия горизонта, точка схода.
Что же такое перспектива?
Перспектива – это средство отобразить глубину рисунка, передать пространство на плоскости изображения.
Пример: представим себе железную дорогу. Все знают, что рельсы лежат параллельно , а это значит, что они нигде не пересекаются. (слайд 5.)
Но если мы встанем на пути и посмотрим вдаль, то будет казаться, что с удалением от нас, рельсы сходятся ближе, ближе, пока, наконец, не сольются в одну точку. (слайд 6.)
То же самое можно увидеть, если выйти на прямой участок обычной дороги. Только здесь, вместо рельс будут сходиться края дороги. Точку, где рельсы или края дороги соединяются, называют “точкой схода” . Эта точка всегда лежит на линии горизонта .(слайд 7.)
Слово «горизонт» всем конечно, знакомо. Этим словом мы называем линию, отделяющую видимое небо от видимой земли.
Линия горизонта бывает высокой и низкой, это средство выразительности. Для передачи земных далей нужна высокая точка зрения, а когда линия горизонта расположена у нижнего края картины, мы видим просторы небес. (слайды 8-9.)
(слайды 8-9.)
А, что же происходит с предметами по мере их удаления? (слайд 10.)
Они уменьшаются, меняется цвет…
Давайте назовем основные правила линейной и воздушной перспективы:
1. Прямые, параллельные линии, на рисунке сходятся в одной точке.
2. Предметы, уходящие вдаль, уменьшаются в размере.
4. По мере удаления предметов цвет теряет свою насыщенность и контрастность, светлеет.
5. Ближний план – теплый и контрастный, средний – тона мягче, дальний – светлый, обобщенный, все сливается в общей воздушной дымке.
Практическая работа:
Сегодня мы с вами будем рисовать улицу по всем правилам перспективы, но сначала построим ее на доске.
(работа учеников у доски, построение улицы, обсуждение каждого шага)
1. Располагаем лист горизонтально.
2. Проводим линию горизонта (высокую)
3. Рисуем дорогу с точкой схода на линии горизонта.
4. Дома, начиная с первого плана.
5. Работаем простым карандашом.
Работаем простым карандашом.
Итог урока:
Анализ работ – лучшие показываю всему классу.
Работа красками на следующем уроке.
Домашнее задание:
Наблюдение линейной и воздушной перспективы.
Принести краски, баночку, кисти.
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Точки схода Основы линейной перспективы
Вступление. Фронтальная перспектива. Угловая перспектива. Трехточечная перспектива. Заключение. План
В изобразительном искусстве объект, в основе формы которого лежит прямоугольный параллелепипед, имеет 1, 2 или 3 точки схода в зависимости от его расположения относительно взгляда наблюдателя и плоскости картины
Одна (главная) точка схода используется во фронтальной перспективе, когда плоскости, формирующие каркас объекта, расположены либо параллельно плоскости катины, либо – перпендикулярно ей, то есть объект расположен «прямо» по отношению к взгляду наблюдателя. Фронтальная перспектива
Фронтальная перспектива
В этой ситуации линии, параллельные плоскости картины, остаются параллельными, а линии, перпендикулярные ей, сходятся в одной точке на линии горизонта. Такая точка и называется главной точкой схода. Главная точка схода
Р Фронтальная перспектива куба
Фронтальная перспектива комнаты
Перспектива улицы
Возможно различное положение объекта относительно линии горизонта.
Косоугольная (угловая) перспектива Угловая перспектива объекта возникает, когда объект расположен на горизонтальной плоскости, но повернут относительно плоскости картины.
Косоугольная (угловая) перспектива В косоугольной перспективе только вертикальные линии сохраняют параллельность, в то время как остальные сходятся к горизонту. В результате получается два пучка сходящихся линий в соответствующие две точки схода.
Здесь также возможно различное положение объекта относительно линии горизонта.
Точки схода находятся на линии горизонта. Расстояни между ними зависит от расстояния от наблюдателя до плоскости картины. Чем дальше находится наблюдатель, тем дальше точки схода.
Чем дальше находится наблюдатель, тем дальше точки схода.
От расстояния между точками схода зависит восприятие объектов
1. Если размещать дистанционные точки схода достаточно близко друг к другу создается ощущение, что объекты угрожают вам – впечатление скорее драматическое. 2. Более “нормальный” вид создается, если одна из точек схода (или обе) выходит за пределы рисунка. 3. Чем дальше точки схода расходятся в стороны, тем меньше видимых искажений зритель увидит на законченном рисунке. Пояснение к предыдущему слайду
Угловая перспектива интерьера
Угловая перспектива улицы
В реальном рисовании обычно встречатся смешанные варианты: одни объекты расположены фронтально, другие под различным углами
В таких ситуациях используюся различные вспомогательные точки схода для конкретного объекта
Три точки схода Такая перспектива используетя, когда объект находится не только под углом к наблюдателю, но и на наклонной поверхности относительно направления взгляда наблюдателя (либо взгляд наблюдателя под углом к поверхости земли).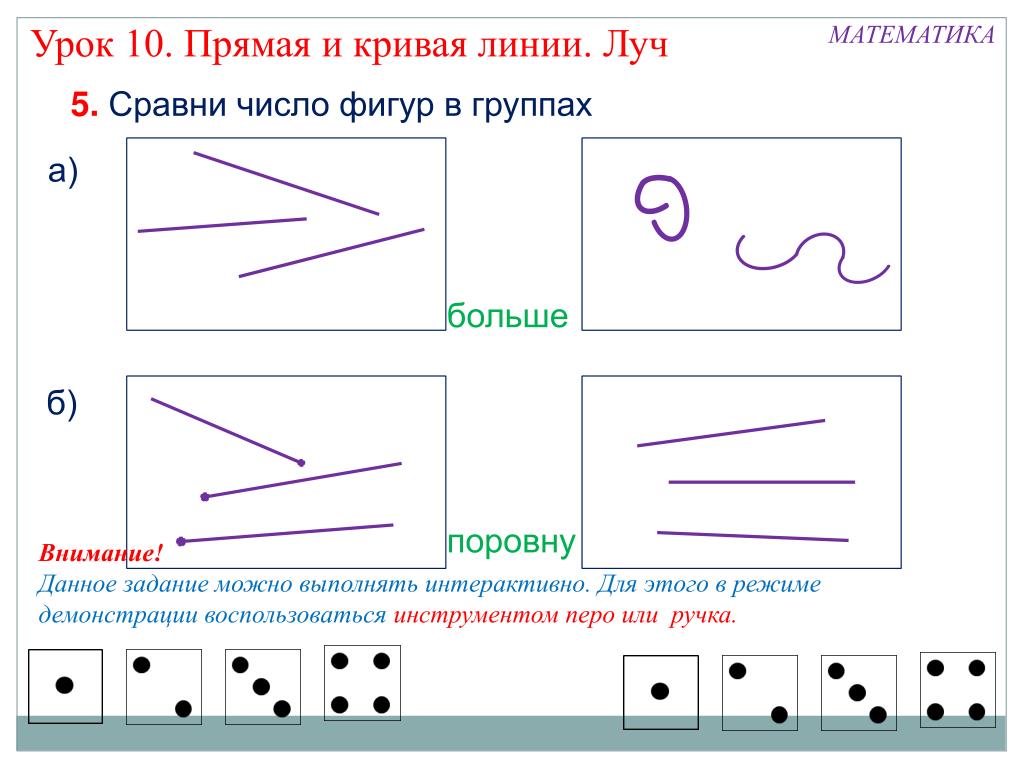
Часто третья точка схода необходима для изображения высотных зданий снизу или с «высоты птичьего полета».
Такую перспективу называют трехточечной. В английском языке, когда третья точка схода находится вверху, используется термин Worm”s Eye perspective . Worm”s Eye (дословно) – взгляд червяка. Сравните: в русском языке есть термин «лягушачья перспектива», означающий изображение с очень низкой линией горизонта, когда объекты «возвышаюся» над наблюдателем.
В изобразительном искусстве объект, в основе формы которого лежит прямоугольный параллелепипед, имеет 1, 2 или 3 точки схода в зависимости от его расположения относительно взгляда наблюдателя и плоскости картины. Во фронтальной и угловой перспективе точки схода лежат на линии горизонта, в трёхточечной – одна из точек находится наверху или внизу картины (обычно за ее пределами). При изображении различных объектов обычно встречатся смешанные варианты: одни объекты расположены фронтально, другие под различным углами В таких ситуациях используюся различные вспомогательные точки схода для конкретного объекта. Подводим итоги
Подводим итоги
Спасибо за внимание!
По теме: методические разработки, презентации и конспекты
Разработка к уроку изобразительного искусства на тему “Правила линейной и воздушной перспективы” включает себя подробный план-конспект урока и презентацию с наглядным материалом….
Терминологический диктант “Изображение объема на плоскости и линейная перспектива.Освещение”(6 класс)
Терминологический диктант для 6 класса по изобразительному искусству состоит из 20 вопросов освещающие темы по линейной перспективе, освещение….
Перспектива (от лат. perspicere ясно видеть, постигать) в изобразительном искусстве система способов изображения пространства на плоскости. Перспектива в рисунке – способ изображения объемных фигур, передающий их собственную пространственную структуру и расположение в пространстве. В изобразительном искусстве перспектива используется как одно из художественных средств для усиления выразительности образов.
Перспектива бывает линейная, воздушная и обратная. Линейная перспектива это способ изображения окружающей действительности на плоскости с передачей объема и глубины. Линейная перспектива наиболее традиционна, т.к. отвечает естественному восприятию окружающего мира.
Линейная перспектива это способ изображения окружающей действительности на плоскости с передачей объема и глубины. Линейная перспектива наиболее традиционна, т.к. отвечает естественному восприятию окружающего мира.
Обратная перспектива способ изображения, при котором линии схода направлены не вглубь картины, а на зрителя. Этот вид перспективы использовали древнерусские живописцы в иконописи и фресках. Центр мира при этой проекции помещался внутрь художника и зрителя и параллельные линии сходились не снаружи, а внутри наблюдателя. Из двух одинаковых предметов большим при изображении пространства на плоскости в этой системе оказывался тот. который располагается дальше от зрителя.
Все предметы, находящиеся ниже этой плоскости, ниже горизонта, мы видим сверху; все предметы, находящиеся выше горизонта,- видим снизу. У всякой горизонтальной плоскости, находящейся ниже горизонта, мы видим верхнюю поверхность; у плоскости, находящейся выше горизонта, мы видим нижнюю поверхность. Все горизонтальные линии, находящиеся ниже перспективного горизонта, то есть видимые сверху, при удалении как бы поднимаются и приближаются к нему, но никогда его не пересекают. Все линии, расположенные выше горизонта, удаляясь, кажутся опускающимися и приближающимися к нему. Они не пересекают его.
Все горизонтальные линии, находящиеся ниже перспективного горизонта, то есть видимые сверху, при удалении как бы поднимаются и приближаются к нему, но никогда его не пересекают. Все линии, расположенные выше горизонта, удаляясь, кажутся опускающимися и приближающимися к нему. Они не пересекают его.
Cлайд 1
Основные положения теории линейной перспективы Выполнила: Заморина Марина 303 гр. Руководитель: кандидат педагогических наук, доцент С.И.Гудилина Все, что фиолетовым – гиперссылкиCлайд 2
Перспектива Предметы в окружающей нас действительности находятся в пространстве, то есть одни из них расположены к нам ближе, другие –дальше. Если, например, смотреть на удаляющиеся от наблюдателя электромачты или телеграфные столбы, то можно увидеть, как они кажутся уменьшающимися по высоте, хотя в действительности имеют одинаковый размер. рисунок крупнееCлайд 3
Cлайд 4
Кажущееся уменьшение величины предметов, находящихся на разном удалении от зрителя, можно проследить и на примере домов, расположенных вдоль улицы. Таким образом, чем дальше от зрителя находятся предметы, тем меньшими они кажутся. Если на один и тот же предмет смотреть с разных мест или изменять его положение по отношению к зрителю, то каждый раз он будет зрительно восприниматься по-разному. Примеры: Круг Книга
Таким образом, чем дальше от зрителя находятся предметы, тем меньшими они кажутся. Если на один и тот же предмет смотреть с разных мест или изменять его положение по отношению к зрителю, то каждый раз он будет зрительно восприниматься по-разному. Примеры: Круг Книга
Cлайд 5
Круг ОБРАТНО При изменении положения круга по отношению к наблю- дателю можно видеть, как меня- ются его очертания. В одном случае круг можно увидеть в виде правильной окружности (если он расположен фронталь- но), в другом случае -в виде эл- липса, в третьем – в виде пря- мой линии. Это зависит от того, какое положение занимает круг по отношению к уровню зрения (линии горизонта) и к плоскости картины. ВЫВОДCлайд 6
Книга ОБРАТНО Изменение очертаний предмета в зависимости от его положения по отношению к рисующему можно проследить на книге. Книгу можно расположить по отно- шению к зрителю так, что в одном случае мы будем видеть две, а в другом случае – три ее плоскости. ВЫВОДCлайд 7
Вывод ОБРАТНО На основе этого примера можно сделать такой вывод – вид предмета меняется в зависимости от его расположения относительно наблюдателя.
Cлайд 8
Линейная перспектива Разработка теории линейной перспективы как метода изображения пространственных форм на плоскости занимались такие видные художники эпохи Возрождения, как Пьетро делла Франческа, Паоло Учелло, Леон Баттиста Альберти, Леонардо да Винчи, Альбрехт Дюрер и многие другие. Гравюра Альбрехта ДюрераCлайд 9
Одна из гравюр Дюрера дает представление о принципе получения перспективного изображения, который положен в основу и современной теории линейной перспективы. Здесь мы имеем следующие основные элементы: объект изображения, единую неподвижную точку зрения(художник смотрит на предмет одним глазом через трубу), прозрачную плоскость, расположенную между предметом и глазом наблюдателя, на котором выполняется рисунок. Показать рисунокCлайд 10
Cлайд 11
Возможность получения изображения на прозрачной плоскости предмета объясняется законами излучения, распространения и поглощения света. Отраженные лучи света, идущие в глаз от предмета, встречая на своем пути прозрачную плоскость, оставляют на ней как бы следы в виде множества точек. Если эти воображаемые точки соединить, то мы и получим на этой плоскости контур видимого предмета. Его величина будет меньше действительного размера наблюдаемого предмета. Посмотреть рисунок
Если эти воображаемые точки соединить, то мы и получим на этой плоскости контур видимого предмета. Его величина будет меньше действительного размера наблюдаемого предмета. Посмотреть рисунок
Cлайд 12
ОБРАТНО Подобные изображения следует рассматривать как перспективное изображение предметов, полученное методом центрального проецирования, так как все проецирующие лучи проходят через одну точку – оптический центр глаза(зрачок). Высота этой точки на практике определяется горизонтальной плоскостью, проходящей на уровне глаз рисующего, которая изображается горизонтальной прямой и называется линией горизонта. А прямоугольная проекция точки зрения на плоскость называется главной или центральной точкой.Cлайд 13
Наблюдение натуры через прозрачную плоскость и легло в основу термина Перспектива. Прозрачную вертикальную плоскость, через которую художник наблюдает предметы, в теории перспективы принято называть плоскостью картины или картиной Наблюдая предметы через прозрачную плоскость картины, мы как бы видим их изображение на ней и даже можем получить реальный рисунок, если обведем видимые сквозь эту плоскость контуры предмета, о чем уже отмечалось выше. Причем этот рисунок будет отвечать всем правилам линейной перспективы.
Причем этот рисунок будет отвечать всем правилам линейной перспективы.
Cлайд 14
Перспектива ОБРАТНО (от лат. Perspectus – увиденный сквозь что-либо, ясно увиденный) – один из способов изображения объемных тел на плоскости или на какой-либо другой поверхности в соответствии с кажущимися изменениями их величины, формы и четкости, вызванными расположением в пространстве и степенью удаленности от наблюдателя.Cлайд 15
Картинная плоскость ОБРАТНО Эта плоскость является как бы посредником между рисовальщиком и наблюдаемым предметом, с одной стороны, между натурой и плоскостью листа бумаги, на которой строится изображение – с другой.Cлайд 16
На практике дело обстоит совсем иначе. Рисуют не на прозрачных плоскостях, а на обычной плотной бумаге, и перед натурой не устанавливают прозрачную плоскость. Разговор о прозрачной плоскости при рисовании с натуры может идти как о возможности увидеть через нее предметы с учетом явлений перспективы или же как о воображаемой плоскости картины с как бы увиденным на ней лежащий перед рисовальщиком лист бумаги. Вопросы Литература
Вопросы Литература
Пейзаж
Сравните два пейзажа.
Сад в пруду. Древний Египет. 2 тыс.до н.э.
Щедрин С. Вид из грота. 1827 г.
Пейзаж
ИЗОБРАЖЕНИЕ ПРОСТРАНСТВА В
ПЕЙЗАЖЕ.
Правила построения перспективы
Задачи урока:
Пейзаж
– передача пространства в
пейзаже;
– развитие воображения;
– воспитание эстетических
чувств к природе и бережного
отношения к ней.
Основные элементы пейзажа:
Пейзаж
– земная поверхность
– растительность
– постройки
– водоёмы (озера, моря, реки)
– фауна
– люди
– облака, дождь
1. Назовите виды
(мотивы) пейзажа.
Пейзаж
2. Определите, какой
характер имеет
каждый пейзаж.
Репродукции картин находятся на доске.
Виды искусства:
Живопись
Саврасов А. Сухаревская башня
Графика
И.Шишкин. Лес
Настенная роспись. Древний Египет
Этрусский мастер. Два танцора роспись. Около 400 г. до н.э.
Бог виноделия Вакх у подножия вулкана Везувий. Фреска. 1 в. н.э.
Архангел Михаил. Икона. Россия.
Иоахим Патинир. Бегство в Египет. 1515-1524
П. Брейгель Старший «Охотники на снегу».Нидерланды. 16 в.
Леон Баттиста Альберти
«Перспектива
есть не что иное,
как наблюдение
местности сквозь
прозрачное стекло,
на поверхности
которого рисуются
лежащие за ним
предметы»
Художник представляет себе картинную плоскость как бы прозрачной, а
все, что изображается на ней, – расположенным позади этой плоскости. Линия горизонта – это воображаемая прямая, условно
находящаяся в пространстве на уровне глаз наблюдателя.
Линии схода – это линии, образующие края формы объекта
и показывают положение объекта в перспективе.
Точка схода – точка, в которой соединяются линии схода.
Линия горизонта
Точка
схода
Линейная перспектива – это изменение
масштабов изображения на плоскости.
Правила линейной перспективы:
Предметы,
уходящие в даль,
уменьшаются
в размере
Параллельные линии
сходятся в точке
схода на линии
горизонта
(линии наших глаз)
Вид Большой Немецкой улицы. М. И. Махаева. 1751. Тушь, перо
Изменение высоты линии горизота
– низкая линия горизонта
– линия горизонта на уровне роста человека
– высокая линия горизонта
Н.Рерих. Ведущая
Вид Неаполя. С.Щедрин. 1827 г.
Сильвестр Щедрин. Веранда, обвитая виноградом, 1828
Золотая осень. В.Д.Поленов
Воздушная перспектива – изменение
предмета в цвете и тоне. Воздух редко
бывает идеально прозрачным: дым, пыль,
водяные пары часто создают дымку, которая
изменяет цвет объектов вдалеке.
Линия горизонта – это воображаемая прямая, условно
находящаяся в пространстве на уровне глаз наблюдателя.
Линии схода – это линии, образующие края формы объекта
и показывают положение объекта в перспективе.
Точка схода – точка, в которой соединяются линии схода.
Линия горизонта
Точка
схода
Линейная перспектива – это изменение
масштабов изображения на плоскости.
Правила линейной перспективы:
Предметы,
уходящие в даль,
уменьшаются
в размере
Параллельные линии
сходятся в точке
схода на линии
горизонта
(линии наших глаз)
Вид Большой Немецкой улицы. М. И. Махаева. 1751. Тушь, перо
Изменение высоты линии горизота
– низкая линия горизонта
– линия горизонта на уровне роста человека
– высокая линия горизонта
Н.Рерих. Ведущая
Вид Неаполя. С.Щедрин. 1827 г.
Сильвестр Щедрин. Веранда, обвитая виноградом, 1828
Золотая осень. В.Д.Поленов
Воздушная перспектива – изменение
предмета в цвете и тоне. Воздух редко
бывает идеально прозрачным: дым, пыль,
водяные пары часто создают дымку, которая
изменяет цвет объектов вдалеке.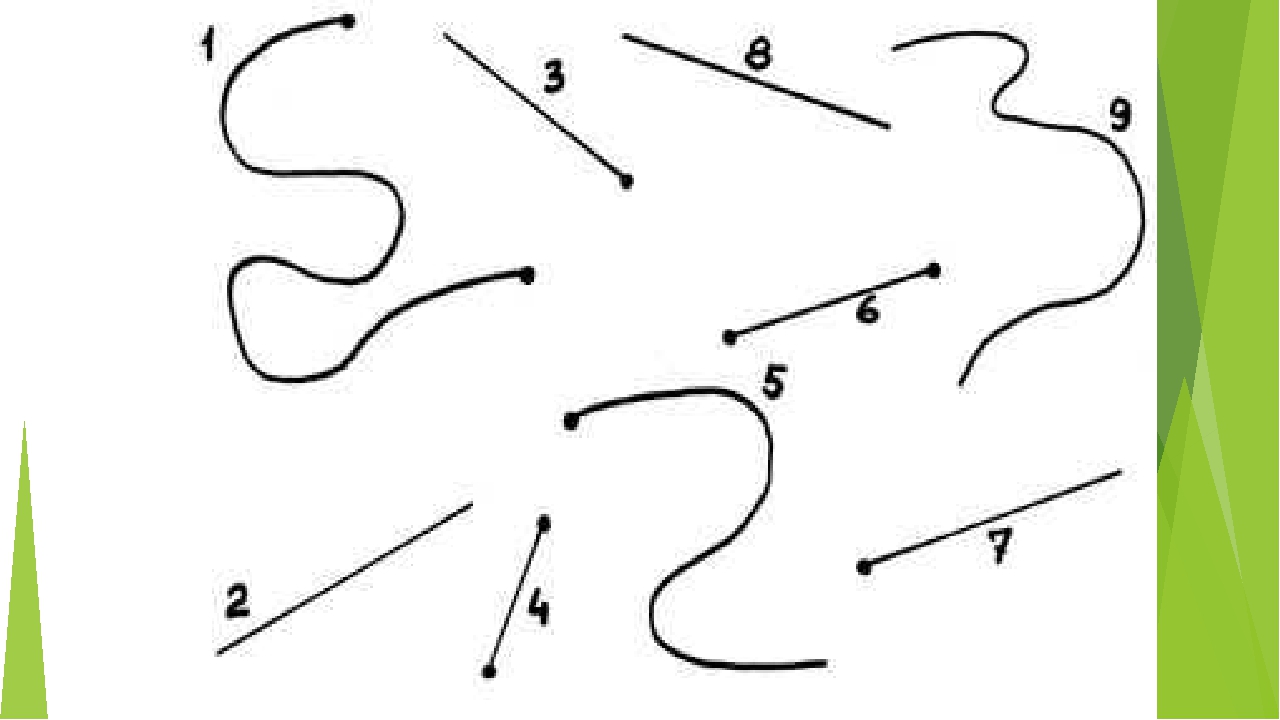 Правила воздушной перспективы:
Ближние предметы
надо изображать объёмно,
а дальние – плоско.
Все ближние предметы
надо изображать детально,
а дальние – обобщённо.
Ближние предметы изображать
ярко окрашенными,
а удалённые – бледными.
Контуры ближних
предметов изображать
резче, а удалённых – мягче.
Ближние предметы
надо изображать
многоцветными, а удалённые
–одноцветными.
Порядок работы над пейзажем:
Приступая к выполнению самостоятельной
работы, первое выберите тему для пейзажа.
Прежде всего, определите в пейзаже
плоскость земли и неба.
Затем уточните положение линии горизонта.
Относительно ее определи место основных
элементов композиции.
Дальний план – 3 план
Средний план – 2 план
Ближний план – 1 план
И.Левитан. На озере
Этапы выполнения пейзажа:
1.
2.
3.
1.Выполнение рисунка карандашом
2. Нанесение основных цветовых пятен
3. Проработка деталей, обобщение
Гимнастика для глаз
Упражнение 1. Закрой глаза и дай им отдохнуть.
Упражнение 2. Несколько раз посмотри попеременно
вверх-вниз, влево-вправо.
Правила воздушной перспективы:
Ближние предметы
надо изображать объёмно,
а дальние – плоско.
Все ближние предметы
надо изображать детально,
а дальние – обобщённо.
Ближние предметы изображать
ярко окрашенными,
а удалённые – бледными.
Контуры ближних
предметов изображать
резче, а удалённых – мягче.
Ближние предметы
надо изображать
многоцветными, а удалённые
–одноцветными.
Порядок работы над пейзажем:
Приступая к выполнению самостоятельной
работы, первое выберите тему для пейзажа.
Прежде всего, определите в пейзаже
плоскость земли и неба.
Затем уточните положение линии горизонта.
Относительно ее определи место основных
элементов композиции.
Дальний план – 3 план
Средний план – 2 план
Ближний план – 1 план
И.Левитан. На озере
Этапы выполнения пейзажа:
1.
2.
3.
1.Выполнение рисунка карандашом
2. Нанесение основных цветовых пятен
3. Проработка деталей, обобщение
Гимнастика для глаз
Упражнение 1. Закрой глаза и дай им отдохнуть.
Упражнение 2. Несколько раз посмотри попеременно
вверх-вниз, влево-вправо. Упражнение 3. Несколько раз зажмурься и снова
открой глаза.
Упражнение 4. Часто поморгай глазами.
Упражнение 5. Посмотри в окно – сначала на предмет,
находящийся в непосредственной близи, потом
переведи взгляд вдаль.
Вывод:
Для передачи пространства в
пейзаже необходимо знать
правила перспективы.
Линейная перспектива –
изменение масштабов изображения на
плоскости.
Воздушная перспектива –
изменение предмета в цвете и тоне.
Упражнение 3. Несколько раз зажмурься и снова
открой глаза.
Упражнение 4. Часто поморгай глазами.
Упражнение 5. Посмотри в окно – сначала на предмет,
находящийся в непосредственной близи, потом
переведи взгляд вдаль.
Вывод:
Для передачи пространства в
пейзаже необходимо знать
правила перспективы.
Линейная перспектива –
изменение масштабов изображения на
плоскости.
Воздушная перспектива –
изменение предмета в цвете и тоне.
Конспект урока математики по теме “Равные фигуры” с презентацией. 1-й класс
УМК: “Перспектива” (авт. учебника Л.Г.Петерсон).
Класс: 1.
Цели:
- Формирование у учащихся представления о равных фигурах как фигурах совпадающих при наложении, способности к различным способам обоснования равенства фигур.
- Совершенствование навыка счета в пределах 9.
- Развитие пространственного мышления, речи и логических операций: анализа, синтеза, сравнения, обобщения.

- Привитие интереса к изучению математики.
Оборудование: компьютер, проектор.
Ход урока
1. Оргмомент. Психологический настрой учащихсяРебята, мы продолжаем наше путешествие по увлекательной стране математике.
- из каких геометрических фигур состоит этот паровоз?
- сколько их? (13)
- на какие группы можно разбить фигуры? (по цвету: красные и синие; по размеру: большие и маленькие; по форме: треугольники, круги, прямоугольники)
- сколько красных фигур? (5)
- сколько синих фигур? (8)
- сколько прямоугольников? (4)
- на какие части можно разбить прямоугольники? (красные и синие; большие и маленькие).
Слайды № 2–3
– На страницах нашего учебника нас очень часто сопровождает Веселый гном. Но сегодня он пришел к нам за помощью, чтобы мы помогли ему сравнить фигуры.
– Рассмотрите геометрические фигуры, изображенные на рисунке? Давайте, попарно сравним фигуры, расположенные рядом. Но, для начала вспомним, что значит «сравнить» фигуры? (Найти сходства и различия).
– Чем же различаются фигуры? (Выделяются три признака, по которым различаются фигуры, – форма, цвет, размер. Причем на слайде №3 фигуры различаются только по одному признаку. На слайде № 4 задание усложняется:
- 1 пара – цвет, размер;
- 2 пара – размер, форма;
- 3 пара – размер, форма, цвет;
- 4 пара – размер;
- 5 пара – размер, форма, цвет.
Фронтальная работа с классом.
Слайд № 4– Ещё вчера Гному было дано очень сложное задание, с которым ему справиться не удалось. А задание было следующим: найти среди предложенных фигур, фигуру равную фигуре а, и сделать вывод о том, как можно определить равенство фигур?
– Поскольку Гном с этим заданием не справился, сегодня на уроке мы с вами этим и займемся.
– Посмотрите внимательно на рисунок. Как вы считаете, какие фигуры являются равными?
(Вполне вероятно, что часть детей ответит, чторавны фигуры а и б, другие – вспомнят смысл понятия равенства – совпадение и выберут одинаковые по размеру желтый и зеленый круги.)
– Как вы думаете, как можно проверить равенство кругов? (Совместить их друг с другом)
Проверка высказанных учащимися предположений
– Итак, давайте сделаем вывод о том, какие фигуры мы можем назвать равными?
(Равными являются те фигуры, которые можно совместить наложением)
Далее с помощью моделей устанавливается свойство равных фигур: если первая фигура равна второй, а вторая – третьей, то первая фигура тоже равна третьей.
Слайд № 5.
– У Гнома три треугольника. Треугольник а равен треугольнику б, а треугольник б равен треугольнику в.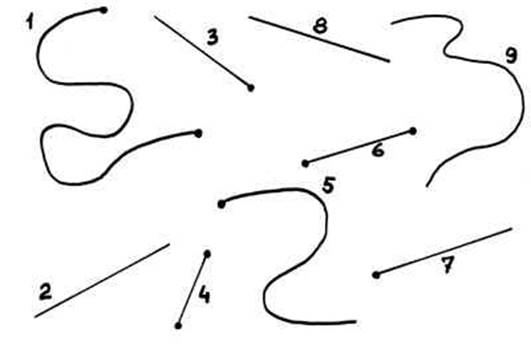 Как вы думаете, будут ли равны треугольники а и в? Как это проверить?
Как вы думаете, будут ли равны треугольники а и в? Как это проверить?
Далее делается вывод о свойстве равных фигур.
5. Первичное закрепление нового материалаВыполнение № 1, стр. 36.
Слайд № 6.
– Что нужно сделать в задании № 1? (Найти равные фигуры и раскрасить их одним цветом)
– Рассмотрите фигуры, как вы думаете, какие фигуры равны? Как это можно проверить? (Путем пересчета клеток)
– Какие фигуры останутся незакрашенными? Назовите попарно равные фигуры? (Проверка по слайду № 7)
ФИЗКУЛЬТМИНУТКА (Слайд № 8)
Чтобы вырасти нам с Гномом,
Нужно сильно потянуться-
Чтобы солнышка коснуться,
Наклониться, повернуться
И друг другу улыбнуться.
Выполнение № 2, стр. 36. Слайд № 9.
– Что нужно сделать в задании № 2? (Для каждой геометрической фигуры, изображенной справа, найти равную ей часть рисунка, изображенного слева, и раскрасить их так, чтобы равные части были закрашены одним цветом)
6. Работа над ранее пройденным материалом
Работа над ранее пройденным материалом
Выполнение № 3, стр. 36. Слайд № 10.
– Что здесь нужно сделать? (Нарисовать точки так, чтобы на обеих половинках их было поровну, а сумма равнялась данному числу.)
Учащиеся в течение 1-2 минут выполняют задание самостоятельно, затем оно проверяется фронтально по образцу.
Выполнение № 4, стр. 37. Слайд № 11.
– Почему под первым рисунком записано выражение 2+3? (К трем синим треугольника добавили два красных треугольника.)
– Сколько треугольников получилось? (5 треугольников.)
– Запишите ответ, а остальные задачи выполните так же.
После самостоятельного решения примеров в течение 1-2 мин учитель ставит вопросы:
– Какое равенство записали под вторым рисунком? (5+3=8)
– Что нужно нарисовать в третьем мешке? (Ответы могут быть различными 4 треугольника, 4 кружка и т. д.)
д.)
– Какой получился ответ? (2+4=6)
В последнем примере этого задания возможны несколько вариантов решения: 6+0=6, 6+1=7, 6+2=8, 6+3=9 и т.д. Несколько из этих вариантов следует обсудить с детьми.
Выполнение № 5, стр. 37. Слайд № 12
– Почему под первым рисунком записано 8-3? (Было 8 кружков, а три кружка зачеркнули, то есть вычли.)
– Какой ответ надо записать? (5)
– Сделайте остальные задания так же.
При проверке решения после 1-2 мин самостоятельной работы учитель спрашивает:
– Что нужно сделать на втором рисунке? (Зачеркнуть 3 треугольника.)
– Какое равенство получилось? (7-3+4.)
– Какое равенство надо записать под третьим рисунком? (9-4=5)
Затем разбираются различные варианты решения четвёртого примера: 6-0=6, 6-1=5 и т.д.
ЗРИТЕЛЬНАЯ ФИЗКУЛЬТМИНУТКА
(Слайд № 13)
Выполнение № 6, стр. 37. Слайд № 14
37. Слайд № 14
– У Гнома, возникло очередное затруднение. Давайте поможем ему решить примеры и проверим правильность с помощью числового луча.
3 + 1 + 5 |
9 – 7 + 4 |
9 – 8 + 3 + 2 |
8 – 2 + 1 |
6 + 3 – 1 |
5 + 2 – 6 + 7 |
В данном задании повторяется сложение и вычитание на числовом луче. Учащиеся решают примеры, а затем с помощью числового луча делают проверку. Так, как примеров много, то на отрезке стрелки не рисуются, а лишь отсчитывается соответствующее число единиц направо (при сложение) или налево (при вычитании).
7. Самостоятельная работаСлайд № 15. (Работа по Прописям)
– Для того чтобы вы смогли выполнить задание по прописям, Гном решил напомнить вам, как правильно писать цифры, которые встретятся в задании.
Слайд № 16
– Давайте напомним Гному, чем мы занимались сегодня на уроке?
– Что нового узнали?
– Какие фигуры мы можем назвать равными?
– С каким свойством равных фигур мы познакомились сегодня на уроке?
Урок 2. Линейная перспектива. Как нарисовать коробок и книгу
Мы знаем, что параллельные линии не пересекаются, расстояние между ними не меняется, но часто наблюдаем противоположное. Например, расстояние между параллельными краями дороги или рельсов, уходящих вдаль, постепенно сокращается, пока они не сойдутся в одной точке на горизонте.
Такое визуальное искажение носит название «линейная перспектива». Это зрительное изменение форм и размеров предметов по мере их отдаления, а также принципы создания иллюзии 3D-пространства на плоскости. Разберем ее важные составляющие: линию горизонта, точки и линии схода.
Содержание:
Линия горизонта
Линия горизонта совпадает с уровнем глаз зрителя (художника).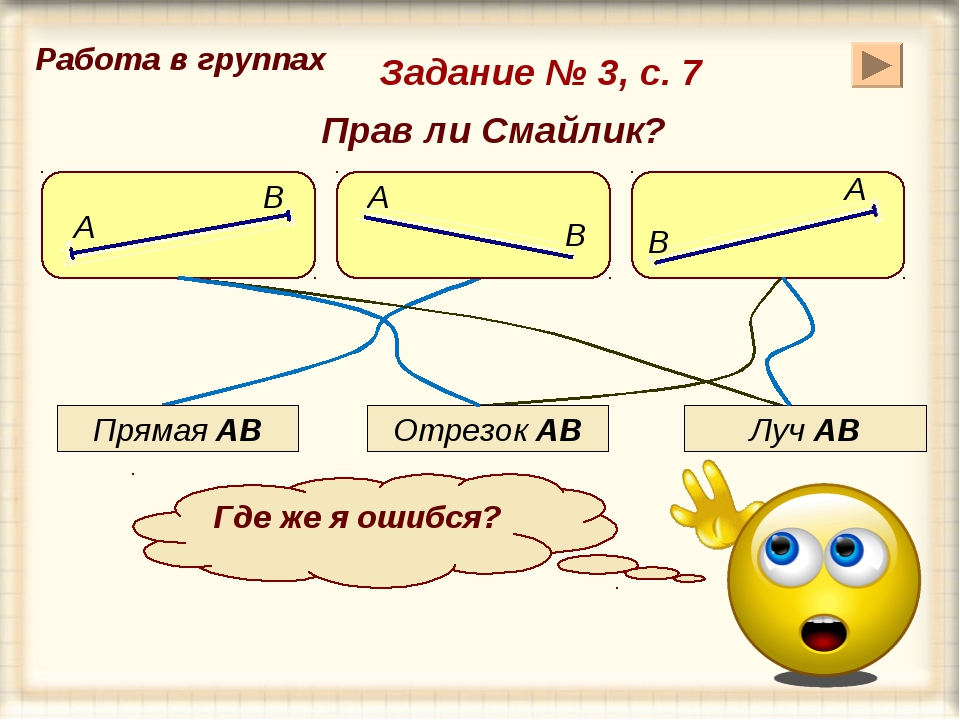 То, с какого положения мы смотрим на предметы, определяет их вид. Взгляните на вещи вокруг. С разных положений: сидя на стуле, стоя на полу. Рассмотрите полки книжного шкафа на фотографии. У тех из них, которые находятся примерно на уровне наших глаз, мы видим только переднюю грань. Для тех, которые расположены выше, – еще и нижнюю плоскость. Опустите взгляд – теперь видны передняя и верхняя плоскости полок.
То, с какого положения мы смотрим на предметы, определяет их вид. Взгляните на вещи вокруг. С разных положений: сидя на стуле, стоя на полу. Рассмотрите полки книжного шкафа на фотографии. У тех из них, которые находятся примерно на уровне наших глаз, мы видим только переднюю грань. Для тех, которые расположены выше, – еще и нижнюю плоскость. Опустите взгляд – теперь видны передняя и верхняя плоскости полок.
Точки схода
В точках схода пересекаются параллели, уходящие вглубь рисунка. Они называются линиями схода. Это края дороги, длинного моста, верхние и нижние границы ряда фонарей или опор ЛЭП, а также направленные вдаль продолжения ребер куба, книги, коробка, стола и так далее.
Линия горизонта, точки и линии схода с помощью этих элементов будем строить предметы в перспективе.
Будем рассматривать в этом уроке наиболее распространенные случаи: точек схода одна или две, они лежат на линии горизонта.
Одна точка схода
В этом случае предмет расположен строго перед нами. То есть мы видим его переднюю грань, горизонтальные стороны которой строго горизонтальны. Все вертикали строго вертикальны. Дальняя стенка параллельна передней. В этом случае мы можем видеть еще нижнюю или верхнюю плоскость предмета.
То есть мы видим его переднюю грань, горизонтальные стороны которой строго горизонтальны. Все вертикали строго вертикальны. Дальняя стенка параллельна передней. В этом случае мы можем видеть еще нижнюю или верхнюю плоскость предмета.
Две точки схода
Точек схода будет две, если предмет расположен не прямо, а несколько развернут. Обычно мы видим две боковые грани и центральное ребро, а также верхнюю или нижнюю грань. В том случае, когда нам видна передняя плоскость (а не две боковых), она находится под некоторым углом, то есть ее горизонтальные стороны не строго горизонтальны, как в случае с одной точкой схода.
Давайте разберемся с основными принципами линейной перспективы:
| 1 | Чем дальше расположен один и тот же предмет, тем меньше он будет выглядеть. Это же распространяется и на его части. Например, представьте, что нам надо нарисовать коробок. Если при его построении будем исходить из факта, что противоположные грани одинаковы по размеру, то рисунок будет больше похож на чертеж.  Если нарисовать дальнюю грань меньше ближней – это будет больше соответствовать тому, как видим предметы в реальности. Если нарисовать дальнюю грань меньше ближней – это будет больше соответствовать тому, как видим предметы в реальности. |
| 2 | Углы искажаются в пространстве. Например, если мы рисуем куб в перспективе, не все его углы останутся прямыми. У граней, направленных вдаль, углы между сторонами больше или меньше 90°. Однако вертикали сохранят прямой угол в наиболее распространенных случаях. |
| 3 | Линия горизонта в рисунке одна. |
Рисуем коробок с одной точкой схода
Шаг 1. Нарисуем линию горизонта и прямоугольник – переднюю плоскость коробка. Представим, что он расположен прямо перед нами, при этом не смещен ни вправо, ни влево. Поэтому точку схода (ТС) нарисуем примерно по центру прямоугольника.
Шаг 2. Из углов прямоугольника проведем линии к точке схода. На этих линиях схода лежат ребра граней, направленных вдаль (к линии горизонта).
Шаг 3. Перейдем к рисованию дальней стенки коробка. Мы изображаем условный коробок, поэтому можем произвольно выбрать расстояние от передней до дальней грани. Начинаем с любого ребра. Например, проведем нижнее. Оно заключено между ранее нарисованными линиями схода и параллельно линии горизонта.
Шаг 4. От точек пересечения этого ребра с линиями схода проведем вертикальные стороны дальней грани. А потом верхнее ребро. Сформировали дальнюю стенку коробка, параллельную передней.
Шаг 5. Чтобы форма лучше читалась, смягчим линии схода, которые выходят за пределы дальней грани. Наш первый коробок готов. Чтобы увидеть, как меняется его вид в зависимости от положения относительно линии горизонта, нарисуем еще два таких же по размерам прямоугольника. Один выше первого, другой – ниже.
Шаг 6. От углов двух новых прямоугольников проведем линии к первой точке схода.
Шаг 7. Мы рисуем три одинаковых коробка. Их расстояние до нас не меняется, смещение происходит только по вертикальной оси. Размеры дальних стенок будут одинаковы. И чтобы их найти, продлим вертикали боковых сторон дальней стенки первого коробка.
Мы рисуем три одинаковых коробка. Их расстояние до нас не меняется, смещение происходит только по вертикальной оси. Размеры дальних стенок будут одинаковы. И чтобы их найти, продлим вертикали боковых сторон дальней стенки первого коробка.
Шаг 8. Нарисуем стороны дальних стенок новых коробков по точкам пересечения вспомогательных вертикалей и линий схода.
Шаг 9. А теперь аккуратно удалим вспомогательные линии и смягчим невидимые глазу ребра. Самые ближние линии (стороны передних граней) выделим более насыщенной линией. Это усилит ощущение пространства в работе. Три коробка готовы!
Порисуйте самостоятельно коробки разных размеров с одной точкой схода. Попробуйте нарисовать коробок, немного смещенный относительно точки схода по горизонтальной оси.
Рисуем коробок с двумя точками схода
Шаг 1. Начинаем с линии горизонта. Нарисуем произвольно ребро коробка. Чем длиннее ребро, тем дальше должны располагаться от него точки схода.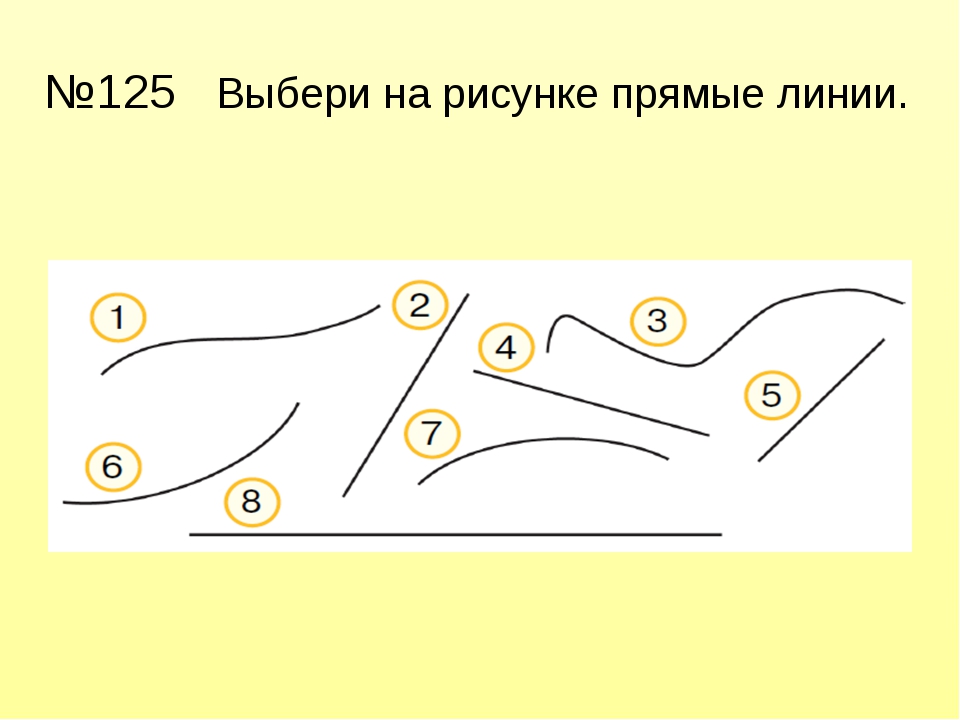 Поэтому сделаем его небольшим, чтобы уместиться в листе со всем построением. Отметим точки схода на линии горизонта. Если разместить их слишком близко к ребру, искажение формы коробка будет сильнее, чем требуется. Не стоит размещать их и слишком далеко.
Поэтому сделаем его небольшим, чтобы уместиться в листе со всем построением. Отметим точки схода на линии горизонта. Если разместить их слишком близко к ребру, искажение формы коробка будет сильнее, чем требуется. Не стоит размещать их и слишком далеко.
Шаг 2. Соединим концы этого ребра с точками схода.
Шаг 3. Нарисуем вертикали двух других видимых нам ребер. Здесь тоже произвольно выбираем их расположение.
Шаг 4. Дорисуем недостающие стороны нижней грани. Соединим нижнюю точку пересечения правого ребра с линией схода с левой точкой схода. А от нижней точки пересечения левого ребра с линией схода проведем прямую в правую точку схода. У нас образовалась нижняя стенка коробка.
Шаг 5. То же самое проделаем для верхней стенки. А затем проведем заднее вертикальное ребро, соединив дальние углы верхней и нижней граней.
Шаг 6. Выделим чуть сильнее верхнюю грань. Еще сильнее – ближние боковые стенки коробка. Так ближнее будет казаться ближе, а дальнее – дальше. Смягчим линии построения. Коробок готов!
Еще сильнее – ближние боковые стенки коробка. Так ближнее будет казаться ближе, а дальнее – дальше. Смягчим линии построения. Коробок готов!
Будет полезно нарисовать несколько таких коробок разной высоты и с разным положением точек схода. Где-то форма коробка получится неестественно искаженной (из-за выбранного положения точек схода), где-то наоборот – удачной. Благодаря сравнению результатов таких попыток мы учимся чувствовать оптимальное соотношение, и оно зависит от размеров изображаемого объекта, от расстояния до зрителя.
Рисуем книгу по фото
Изображая реальный предмет в перспективе, для более точного построения удобно сначала нарисовать для него коробок соответствующих параметров. Потом что-то отсечем, что-то добавим, чтобы получить необходимую форму. Именно это мы сейчас и проделаем.
Шаг 1. Наметим общие габариты книги. Оставим место над книгой для линий схода и горизонта. Проверим, сколько раз ее высота укладывается в ширине. А затем найдем, сколько раз высота передней грани блока страниц укладывается во всей высоте. Обозначим центр книги.
А затем найдем, сколько раз высота передней грани блока страниц укладывается во всей высоте. Обозначим центр книги.
Шаг 2. Зная ширину книги и высоту передней грани, нарисуем прямоугольник фронтальной плоскости коробка. После этого нарисуем боковые грани нижней плоскости (обложки), уходящие вдаль, определяя их наклон методом визирования. Продлим их до пересечения и получим точку схода.
Шаг 3. От точки схода проведем линии к верхним углам прямоугольника передней плоскости. Нарисуем верхнюю границу книги через ранее найденную точку до пересечения с только что намеченными линиями схода. От этих точек пересечения опустим вертикали до первых линий схода – боковые стороны дальней стенки коробка для книги. Дорисуем нижнюю сторону этой стенки.
Шаг 4. Смягчим линии построения и невидимые грани. Коробок готов. Поставим метки ближних верхних уголков страниц, измерив визированием, насколько они удалены от краев книги.
Шаг 5. Через эти метки проведем верхние боковые границы блока страниц, уходящие вдаль. То же проделаем и для нижних границ этого блока. Уточняем их наклон и положение методом визирования. Проведем центральную линию книги.
Шаг 6. Визуально разобьем контур разворота на несколько основных отрезков. Определяем их наклон методом визирования. Схематично наметим их в рисунке.
Шаг 7. Проведем более плавную линию разворота. Наметим корешок книги. Сотрем вспомогательные линии, чтобы они не отвлекали.
Шаг 8. Уточним детали. Слегка скруглим углы обложки, отделим ее линиями от блока страниц. Нарисуем закладку слева. Ее край делаем неровным, чтобы подчеркнуть характер. Легкими линиями кое-где наметим отдельные страницы и наличие текста. Этого будет достаточно, ведь зритель дорисовывает в своем воображении недостающие повторяющиеся детали. Слегка смягчаем ластиком дальние линии, а ближние к нам выделяем более сильным нажимом, чтобы создать иллюзию глубины пространства.
Книга готова!
Не всегда удобно делать подобное построение через горизонт, линии и точки схода. Последние могут выходить за пределы листа. В этом случае ради более точного построения можно увеличить лист, приклеив бумагу по бокам. Еще один вариант – перед началом работы сделать маленький набросок коробка для предмета, схему-подсказку соответствующих пропорций и в нужном ракурсе. Такая схема рисуется со всеми вспомогательными линиями и точками. Важно сделать это построение как можно точнее, чтобы затем перенести на чистовик в нужном масштабе найденные соотношения размеров и наклоны ребер, но уже без точек и линий схода, без обозначения горизонта. Затем предмет вписывается в коробок, как это сделали мы.
После определенной практики можно обойтись совсем без линии горизонта и точек схода. Вместо этого можно опираться на метод из первого урока – измерение углов и пропорций карандашом.
Как при этом добиться большей точности изображения:
| 1 | Следует рисовать все линии предмета, даже невидимые (скрытые).  Так проще понять, насколько убедительно выглядит форма, есть ли в ней ошибки. Так проще понять, насколько убедительно выглядит форма, есть ли в ней ошибки. |
| 2 | Хорошо немного продлевать ребра. Так лучше видно, соблюдается ли принцип постепенного сокращения расстояний между параллелями по мере их отдаления. |
| 3 | Сравнивайте длины вертикальных ребер. Чем они дальше, тем меньше должны быть в рисунке. |
Порисуйте книги по фото, а еще лучше с натуры, потому что фотографии могут искажать форму. Это будет очень полезной практикой изображения реальной объемной формы на плоскости листа.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
План урока «Перспектива в одной точке»
Цели обучения
После этого урока учащиеся смогут:
- Объяснять одноточечную перспективу
- Определить ключевые детали в картине, использующей одноточечную перспективу
- Сравните идеи, представленные на картине, с идеями, представленными в стихотворении
Продолжительность
Приблизительно 60-90 минут
Стандарты учебной программы
- CCSS.ELA-Literacy.RL.9-10.7 Проанализируйте изображение предмета или ключевой сцены в двух разных художественных средствах, включая то, что подчеркивается или отсутствует в каждой трактовке (например, «Музей изящных искусств» Одена и «Пейзаж с падением» Брейгеля). Икара).
Ключевой словарь
- Одноточечная перспектива
- точка схода
- линия горизонта
Необходимые материалы
Инструкции
Начните с направления учащихся к изучению. com урок по рисованию в одной точке. Напишите на доске следующие текстовые коды:
com урок по рисованию в одной точке. Напишите на доске следующие текстовые коды:
- подчеркивание = информация, которую я считаю важной
- ? = непонятная мне информация
- ! = информация, которую я уже знал
Воспроизвести видео. Предложите учащимся прочитать и использовать текстовый код.
Когда видео закончится, пусть они встретятся с партнерами по локтям (парами). Они должны сначала объяснить, что они уже знали из видео. Затем они должны поделиться частями, которые они закодировали со знаком вопроса.Если они могут ответить на вопросы друг друга, они должны это сделать. Наконец, попросите их выбрать одну важную информацию, чтобы поделиться с классом.
Перейдите к обсуждению видео всем классом, призывая пары поделиться своими важными фактами и оставшимися вопросами.
Далее проект картины Ван Гога Спальня в Арле. Лучшее место для проецирования — интерактивная доска или белая доска. Попросите добровольцев выйти к доске и попытаться определить линию горизонта и точку схода картины. Объясните классу, что, находя точку схода или линию горизонта на картине, они критически относятся к ней, что поможет им ее интерпретировать.
Объясните классу, что, находя точку схода или линию горизонта на картине, они критически относятся к ней, что поможет им ее интерпретировать.
Теперь пора предложить учащимся пройти анализ картины. Техника, которая будет использоваться, представляет собой подход, основанный на мозге, который начинается с эмоций и заканчивается критическим анализом. Хотя первые несколько шагов могут показаться бесполезными, подумайте об этом как о попытке «разогнать» мозг ваших учеников. Попытка раскрыть смысл картины — это изощренное мышление, за которое мозг не готов взяться, пока не справится с более легкими задачами.Этот метод обсуждения/письма проведет студентов через эти ранние этапы и заставит их мозги быть готовыми к решению более сложных аналитических задач.
Для рисования выполните следующие шаги со своими учениками, попросив их сначала поговорить со своими партнерами, а затем призвать их поделиться со всем классом. Вы также должны поделиться, чтобы смоделировать тип мышления, который вы хотели бы видеть у своих учеников.
- Шаг первый: Эмоции. Что вы чувствуете, когда смотрите на эту картину?
- Шаг второй: подключение.Что вам напоминает эта картина? Видели ли вы что-нибудь подобное раньше? Заставляет ли это вас думать о телешоу, фильме, другой картине, воспоминании, поездке в музей или о чем-то еще из вашего прошлого?
- Шаг третий: Детализация. Выберите один небольшой участок картины. Опишите это партнеру как можно подробнее. Ваш партнер должен выбрать другой раздел, чтобы описать вам.
- Шаг четвертый: соединение деталей. Что общего между этими двумя небольшими частями? (Когда вы дойдете до этой части обсуждения, постарайтесь установить связи или написать заметки на доске, чтобы представить разнообразие идей, которые будут генерироваться вашим классом.)
- Шаг пятый: смысл. Что вы получаете от этой картины? Вы не пытаетесь найти Смысл, просто подумайте о том, что вы вынесете из картины. Что это говорит вам?
На этом уроке ваши ученики только что проанализировали известное произведение искусства! У них могут быть не самые глубокие интерпретации, но они успешно использовали технику, чтобы прийти к смыслу, который можно было бы аргументировать и подтвердить доказательствами. Пришло время познакомить их со стихотворением.Раздайте экземпляры и попросите учащихся сначала прочитать его про себя, а затем пригласите не менее двух добровольцев прочитать стихотворение вслух. Вы также можете попросить каждого ученика прочитать стихотворение своим партнерам по обсуждению. Вы также должны прочитать стихотворение, чтобы смоделировать этот навык для класса. После чтения учащиеся будут использовать версию описанной выше техники для интерпретации стихотворения. Это должно быть сделано путем того, чтобы учащиеся писали индивидуально и тихо.
Пришло время познакомить их со стихотворением.Раздайте экземпляры и попросите учащихся сначала прочитать его про себя, а затем пригласите не менее двух добровольцев прочитать стихотворение вслух. Вы также можете попросить каждого ученика прочитать стихотворение своим партнерам по обсуждению. Вы также должны прочитать стихотворение, чтобы смоделировать этот навык для класса. После чтения учащиеся будут использовать версию описанной выше техники для интерпретации стихотворения. Это должно быть сделано путем того, чтобы учащиеся писали индивидуально и тихо.
- Шаг первый: Эмоции. Какое чувство у вас вызывает это стихотворение?
- Шаг второй: подключение.Что вам напоминает это стихотворение? Вы когда-нибудь видели что-нибудь подобное? Заставляет ли это вас думать о телешоу, фильме, другом стихотворении, воспоминании, книге, которую вы читали, или о чем-то в вашем прошлом?
- Шаг третий: Детализация. Выберите один небольшой момент из стихотворения. Опишите его в письменной форме как можно подробнее.
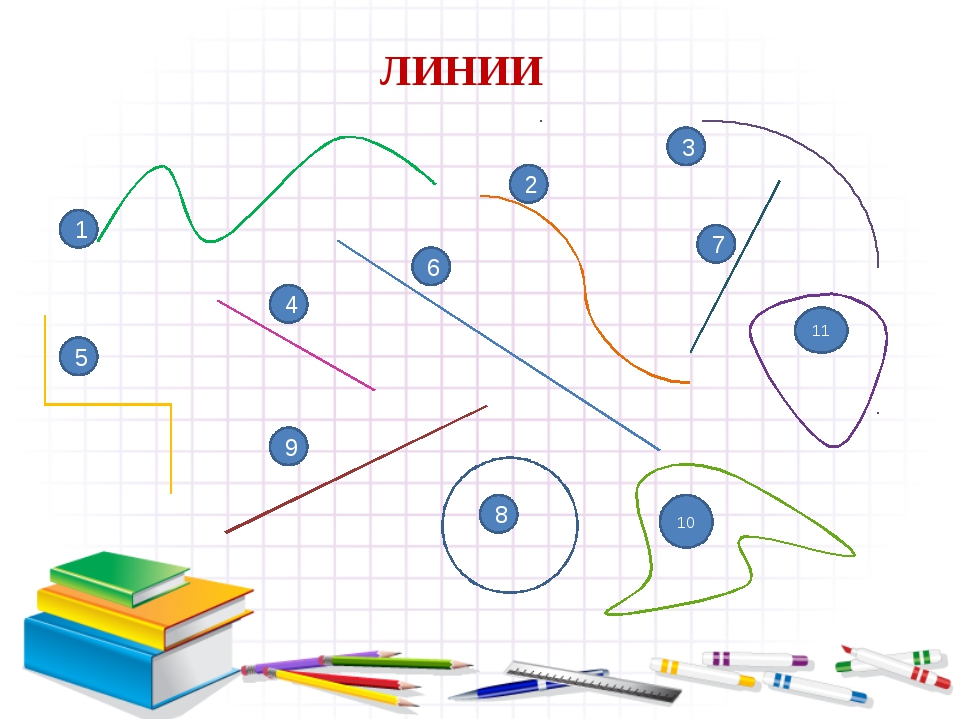 Представьте сцену в своем воображении и добавьте детали, чтобы заполнить то, что вы рисуете в своей голове.
Представьте сцену в своем воображении и добавьте детали, чтобы заполнить то, что вы рисуете в своей голове. - Шаг четвертый: Теперь выберите еще один небольшой момент из стихотворения. Подробно опишите этот момент.
- Шаг пятый: соединение деталей. Что общего между этими двумя небольшими частями? Напишите о связях, которые вы находите между двумя выбранными вами моментами.
- Шаг шестой: смысл. Что вы почерпнули из этого стихотворения? Вы не пытаетесь найти Смысл, просто подумайте о том, что вы вынесете из стихотворения. Что это говорит вам?
Соберите идеи класса на доске, сосредоточив внимание на шагах пять и шесть.
Завершите урок формирующей оценкой.Дайте каждому ученику каталожную карточку. Они будут использовать пространство на одной стороне для создания диаграммы Венна. В левом круге они будут включать детали и идеи из картины, которые появляются только на картине. Справа они отметят идеи и детали, которые появляются только в стихотворении. В центре они покажут, что у них общего. Используйте эти каталожные карточки, чтобы оценить понимание учащимися вашего урока.
В центре они покажут, что у них общего. Используйте эти каталожные карточки, чтобы оценить понимание учащимися вашего урока.
Расширения урока
- Используйте различные произведения изобразительного искусства и литературы с одной и той же техникой, начиная с определения линии горизонта и точки схода, чтобы сориентировать учащегося в искусстве, затем переходите к письму и обсуждению.
- Написать аналитическое эссе, используя диаграмму Венна в качестве схемы
- Предложите учащимся интерпретировать картину и стихотворение либо в письменной форме, либо в виде презентации, и попросите их использовать детали, которые они отметили, в качестве доказательства, подтверждающего их интерпретацию.
- Используйте это как отправную точку для изучения перспективы. Теперь, когда учащиеся имеют опыт рассмотрения перспективы в изобразительном искусстве, они могут лучше понимать точку зрения в литературе. Вот четыре связанных исследования.ком уроки с точки зрения.

Цикл 1 Чертеж | Inside The Lines Lessons
Чтобы завершить первые шесть недель цикла 1, мы будем рисовать китайских воздушных змеев. План урока касается рисования в зеркальном отображении, одноточечной перспективы и абстрактного дизайна. Это много, но я надеюсь, что дети будут чувствовать себя уверенно в своих знаниях и получат удовольствие от рисования своей последней работы.
Многие историки считают, что родиной воздушного змея является Китай, и первое зарегистрированное использование воздушного змея было в Китае в 196 г. до н.э.У воздушных змеев было много целей: их использовали для доставки сообщений, для празднования особых случаев и даже в качестве оружия на войне! Марко Поло приписывают первое известие о воздушных змеях в Европу после своего путешествия по Азии в тринадцатом веке. Там такая интересная и уникальная история! Продолжить чтение →
Нравится:
Нравится Загрузка…
На этой неделе учащиеся будут практиковать концепцию одноточечного перспективного рисунка. Это трудно вписать в наш раздел, посвященный древнему искусству, потому что ранние цивилизации, как правило, создавали плоские изображения с небольшой глубиной или без нее.Фактически, использование перспективы в живописи не было замечено до 15-го века в Италии. Но, конечно, идеи путешествуют…
Это трудно вписать в наш раздел, посвященный древнему искусству, потому что ранние цивилизации, как правило, создавали плоские изображения с небольшой глубиной или без нее.Фактически, использование перспективы в живописи не было замечено до 15-го века в Италии. Но, конечно, идеи путешествуют…
Первое использование математической перспективы в японском искусстве можно легко увидеть в гравюрах на дереве Хокусая и Хиросигэ в 1800-х годах. Они используют очень сильные, четкие линии, которые создают динамическую глубину и перспективу. Вы можете использовать следующие изображения, чтобы показать своим ученикам раннюю японскую живопись с некоторой глубиной, но без одноточечной перспективы, а также более поздние отпечатки с одноточечной перспективой.(Я часто помещаю изображения в презентацию Powerpoint и использую свой ноутбук, чтобы представить изображения в классе, а не распечатывать их все) Хотя искусство и этнические группы Африки огромны, одной общей чертой является изготовление масок. Даже в рамках этой общности африканские маски могут иметь широкий спектр от репрезентативных до полностью абстрактных. В этом уроке мы рассмотрим абстрактные маски из регионов Древнего Мали и Ганы (предложение истории и географии недели 14), а также других культур, окружающих эти области.Несмотря на то, что мы будем учиться и черпать вдохновение из их проектов, студенты ни в коем случае не должны их копировать.
Даже в рамках этой общности африканские маски могут иметь широкий спектр от репрезентативных до полностью абстрактных. В этом уроке мы рассмотрим абстрактные маски из регионов Древнего Мали и Ганы (предложение истории и географии недели 14), а также других культур, окружающих эти области.Несмотря на то, что мы будем учиться и черпать вдохновение из их проектов, студенты ни в коем случае не должны их копировать.
Что мы хотим, чтобы учащиеся узнали из этого урока:
- Что означает термин «абстракция»
- Как сделать акцент в абстрактном дизайне
- Как черпать вдохновение из другой работы, но изменить ее, чтобы сделать ее лучше наш собственный
Надеюсь, вам и вашим ученикам понравится урок!
Продолжить чтение →
Нравится:
Нравится Загрузка…
Как и у древних египтян, у майя была письменность, основанная на символах и изображениях. Образы, используемые в их написании, сложны, и на самом деле для их создания требовались художники. Таким образом, писцы всегда должны были быть художниками, и их слово «писец» отражало это: т’зиб означает и художник , и писец! (Это заставляет меня думать о современной каллиграфии: слиянии письменности и искусства).
Таким образом, писцы всегда должны были быть художниками, и их слово «писец» отражало это: т’зиб означает и художник , и писец! (Это заставляет меня думать о современной каллиграфии: слиянии письменности и искусства).
Для перевернутого рисунка на этой неделе я использовал майяский символ шоколада.В этой статье и великолепном видео рассказывается о языке майя, а также расшифровывается символ “шоколад”. Это супер весело и интересно! Продолжить чтение →
Нравится:
Нравится Загрузка…
Руководство по основам предлагает использовать греческие вазы для рисования в зеркальном отображении, и что вы знаете! Это отлично работает для Цикла 1 и древних цивилизаций.
Мы знаем, что греки использовали симметрию в архитектуре, и мы можем видеть ту же любовь к порядку и равновесию в их искусстве.Большая часть их керамики была симметричной формы и украшена геометрическими узорами, цветочными мотивами и сценами из жизни или мифологии. Если возможно, принесите несколько книг по греческому искусству или цивилизации, чтобы учащиеся могли просматривать их по мере завершения своих рисунков.
Этот урок посвящен рисованию в зеркальном отображении с использованием контура вазы, но также включает использование OiLS путем добавления геометрических рисунков. Каждый план урока включает в себя несколько примеров традиционных греческих узоров, но варианты безграничны! Продолжить чтение →
Нравится:
Нравится Загрузка…
В этом году вышло новое Руководство по основам, но вы заметите, что рисунки для недель 1-6 такие же, как и в прошлом. Поскольку Цикл 1 посвящен истории древних королевств, я буду сочетать концепции рисования с искусством древних цивилизаций.
Неделя 1 начинается с основных элементов рисования с использованием концепции OiLS. Мы будем использовать египетские символы, чтобы попрактиковаться в изучении того, что мы видим, и копировании этого на своей бумаге. Помните, что это уроки рисования: суть в том, чтобы научиться хорошо рисовать, а не обязательно проявлять творчество.Как только навыки рисования развиты, учащиеся могут легче выражать свои мысли, потому что у них есть необходимые для этого навыки! Можно попросить учащихся замедлиться, точно следовать указаниям и даже переработать рисунок, чтобы улучшить его. Это будет очень эффективно в долгосрочной перспективе, и студенты увидят, что результаты того стоят.
Это будет очень эффективно в долгосрочной перспективе, и студенты увидят, что результаты того стоят.
Ниже вы найдете планы уроков с видео для детей 4–6, 7–9 и 10–11 лет. Если у вас есть дополнительные вопросы, пожалуйста, не стесняйтесь обращаться ко мне. Удачного рисования!
Продолжить чтение →
Нравится:
Нравится Загрузка…
Линии и углы – определения, свойства, типы, практические вопросы
Древние математики ввели понятие линий для представления прямых объектов, ширина и глубина которых пренебрежимо малы. Линии, рассматриваемые Евклидом как ширина за вычетом длины, составляют основу евклидовой геометрии.
Когда два луча (часть прямой) пересекаются в одной плоскости, они образуют угол. Точка пересечения называется вершиной.
В этой статье мы рассмотрим основные свойства, определения и типы линий и углов, связанных с геометрией.Мы также рассмотрим несколько примеров, чтобы вы лучше поняли свойства линий и углов. Прежде чем мы двинемся дальше, взгляните на пятиэтапный план подготовки к GMAT, чтобы набрать 700+ на GMAT:
Определение строки
Линия не имеет конечных точек. Он имеет бесконечную длину.
Определение сегмента линии
Отрезок — это отрезок прямой, или, другими словами, можно сказать, что отрезок — это линия с двумя концами.
Например, , На диаграмме показана линия L, и один сегмент этой линии — AB.
На плоскости может быть много линий или отрезков.
И эти линии можно разделить на несколько типов в зависимости от относительного расположения одной строки относительно другой строки.
Типы линий
Пересекающиеся линии
Две прямые пересекаются, если они пересекаются в одной точке.
Например, L 1 и L 2 являются пересекающимися линиями на приведенной ниже диаграмме
.
Параллельные линии
Пара прямых параллельна, если они никогда не пересекаются.
Например, L 1 , L 2 и L 3 являются параллельными линиями на приведенной ниже диаграмме.
Поперечная линия
Поперечная линия пересекает две или более линий в разных точках.
Например, линия L 3 является поперечной линией на приведенной ниже диаграмме.
Далее мы рассмотрим углы и их свойства.
Набрав Q50-51 на GMAT, вы получите 700+ баллов GMAT. Начните свой путь к получению Q50-51 на GMAT с помощью онлайн-курса подготовки e-GMAT на основе искусственного интеллекта.Наш xPERT не только выбирает наиболее оптимизированный путь обучения, но и отслеживает ваши улучшения, гарантируя, что вы быстро и надежно достигнете целевого показателя Quant. Посмотрите это видео, чтобы узнать больше:
Угол – что это такое?
Угол образуется при пересечении двух прямых. Обозначим угол символом ∠.
Обозначим угол символом ∠.
Угол состоит из двух катетов и одной общей вершины, в которой сходятся две прямые.
Например, ∠AOD образуется при пересечении прямых AB и CD.
Кроме того, между ветвями AO и OD образуется ∠AOD, поэтому мы включаем A, O и D в название угла.
Знаете ли вы, что положение точек катетов не имеет значения, если их общая вершина является средней буквой в названии угла
Измерение угла
Угол измеряется в градусах.
Угол может измеряться от нуля (0) градусов до 360 градусов. На основании измерения угла они делятся на четыре типа:
- Острый угол
- Прямой угол
- Тупой угол
- Рефлекторный угол
Острый угол
Когда измерение угла находится в диапазоне от 0 до 90 градусов.
Прямой угол
Когда измерение угла составляет ровно 90 градусов.
- Если между двумя прямыми имеется прямой угол, то говорят, что эти две прямые перпендикулярны друг другу .

Тупой угол
При измерении угла между 90 и 180 градусами.
Прямая линия имеет угол 180 градусов.
Угол рефлекса
При измерении угла между 180 и 360 градусами.
Мы обсудили основные типы углов.
Теперь обсудим углы, образованные при пересечении двух прямых.
Если вы планируете сдавать GMAT, мы можем предоставить вам доступ к качественному онлайн-контенту для подготовки. По состоянию на 4 октября 2021 года мы являемся самой популярной компанией по подготовке к GMAT на gmatclub: на 4 октября 2021 года мы получили более 2200 отзывов.
Углы, образованные между двумя пересекающимися прямыми
Вертикально противоположные углы
При пересечении двух прямых получается 4 угла.
- И углы , которые противоположны друг другу в точке пересечения , известны как вертикально противоположные углы .

- Вертикально противоположные углы всегда равны.
Теперь обсудим углы, образованные при пересечении двух прямых третьей прямой, т. е. поперечной линией.
Углы, образованные поперечной линией
Когда поперечная линия пересекает две прямые, образуются восемь углов, как показано на рисунке.
Теперь из этой диаграммы получается несколько специальных пар углов.
Например: если вы заметили , что (∠1, ∠3), (∠2, ∠4), (∠5, ∠7) и (∠6, ∠8) являются вертикально противоположными углами.
Аналогично получаем еще несколько видов углов. Давайте обсудим их.
Другие типы уголков
Внутренние и внешние уголки
Внутренние углы — это углы, находящиеся внутри области между двумя линиями.
- И внешние углы – это те, которые присутствуют внутри этой области.
Например:
- ∠2, ∠3, ∠5 и ∠8 — внутренние углы.
- А, ∠1, ∠4, ∠6 и ∠7 — внешние углы.
Соответствующие углы
Два угла называются соответственными, если они лежат по одну сторону от поперечной линии так, что:
- Один угол внутренний, а
- Другой угол внешний
Например:
(∠4, ∠8), (∠3, ∠7), (∠1, ∠5) и (∠2, ∠6) — 4 пары соответствующих углов
Альтернативные внутренние углы
Два внутренних угла, находящихся по разные стороны от поперечной линии, называются параллельными внутренними углами.

Например:
- (∠2, ∠8) и (∠3, ∠5) — альтернативные внутренние углы.
Альтернативные наружные углы
Два внешних угла, находящихся по разные стороны от поперечной линии, называются альтернативными внешними углами.
Например:
- (∠1, ∠7) и (∠4, ∠6) — альтернативные внешние углы.
Примечание: Если поперечная линия пересекает две параллельные прямые, то соответствующие углы, альтернативные внутренние углы и альтернативные внешние углы равны.
Итак, мы рассмотрели все типы углов.
Давайте теперь узнаем о некоторых свойствах углов.
Свойства углов
Сумма углов одной стороны прямой
Сумма всех углов по одну сторону прямой всегда равна 180 градусов.
Например, сумма ∠1, ∠2 и ∠3 составляет 180 градусов.
Сумма углов вокруг точки
Сумма всех углов вокруг точки всегда равна 360 градусам.
Например, сумма углов (∠1, ∠2 и ∠3) вокруг точки O составляет 360 градусов.

Если вам понравилась эта статья, вот еще несколько статей, которые могут вам понравиться:
Применение свойств линий и углов в вопросах
Линии и углы – Вопрос 1
На приведенной выше диаграмме линия CD параллельна линии EF. Если ∠AHD и ∠JIE равны 118° и 30° соответственно, то какова мера угла GIB?
- 30
- 32
- 34
- 40
- 62
Раствор
Шаг 1: Дано
- линия CD параллельна линии EF.
- ∠AHD =118°
- ∠JIE = 30°
Шаг 2: найти
Этап 3: Подход и разработка
Нам нужно найти меру угла GIB.
- Итак, по заданной информации мы знаем, что прямая CD параллельна прямой EF, а прямая AB им перпендикулярна.
- Следовательно, ∠DHI = ∠FIB, так как оба угла являются соответствующими.
- Мы можем найти ∠dhi или ∠fib как
- ∠AHD + ∠dhi = 180 °
- 118 ° + ∠fib = 180 °
- ∠fib = 62 °
- Теперь, ∠fib = ∠fig + ∠GIB
- Судя по диаграмме, ∠FIG = ∠JIE, так как это вертикально противоположные углы между EF и JG.

- ∠fib = ∠fig + ∠gib
- 62 ° = ∠jie + ∠gib
- 62 ° = 30 ° + ∠GIB
- ∠GIB = 32 °
Следовательно, правильный ответ вариант Б.
Линии и углы — Вопрос 2
На приведенной выше диаграмме угол DFE и угол BFC представлены X и Y соответственно. Если ∠AFC = 100° и ∠BFE = 45°, то каково значение Y-X?
- 20
- 25
- 30
- 35
- 40
Раствор
Шаг 1: Дано
- ∠DFE = X
- ∠BFC = Y
- ∠AFC = 100°
- ∠BFE = 45°
Этап 3: Подход и разработка
Чтобы найти Y-X, нам нужно сначала найти Y и X.
Мера угла Y:
противоположен указанному cross-start .
- Нам дано ∠AFC = 100° и
- ∠AFC + ∠BFC = 180°, так как сумма углов на одной стороне прямой равна 180°
- 100° + ∠BFC = 180°
Мера угла X:
- Нам дано ∠BFE = 45° и,
- ∠DFE + ∠BFE + ∠BFC = 180° , так как сумма углов на одной боковой прямой составляет 180°.

- X + 45° +80°= 180°
Следовательно, Y – X = 80° – 55° = 25°.
Таким образом, правильный ответ — вариант Б.
Если вы планируете сдавать GMAT, мы можем предоставить вам доступ к качественному онлайн-контенту для подготовки. По состоянию на 4 октября 2021 года мы являемся самой популярной компанией по подготовке к GMAT на gmatclub: на 4 октября 2021 года мы получили более 2200 отзывов.
Урок рисования с видом с земли для детей
Этот рисунок с видом с земли для учащихся средней школы является отличным инструментом для обучения одноточечной перспективе, а также может использоваться для обучения теории цвета. Этот проект охватывает общие базовые стандарты по математике для 4-8 классов, которые можно найти в конце урока.
Уровни обучения
4-й, 5-й, 6-й, 7-й и 8-й классы. Показанные примеры были сделаны 4-м классом.

Объектив
На этом уроке «Искусство перспективы с видом с земли» учащиеся продемонстрируют одноточечную перспективу, создав линию горизонта города, видимую с уровня земли.
Время
4 урока по 60 минут
Материалы
- Карандаши
- Линейки (аршина и одна лапка)
- Ножницы
- Клей
- Мелки
- 12×18 Акварельная бумага – Canson XL Series Watercolor Textured Paper Pad for Paint, Pencil, Pencil Acrylic, Fold Over, 140 фунтов, 12 x 18 дюймов, 30 листов
- Кисти – Набор кистей для акриловых красок, 1 упаковка / 10 шт. Нейлоновые кисти для волос для всех целей Профессиональные наборы для художников масляной акварели
- Жидкие акварельные краски – Sargent Art 22-6010 Набор акварельных красок, 8 унций, 10 штук
- Салфетки для промокания краски
- Маркер Sharpie – Перманентный маркер Sharpie, Fine Point, черный, упаковка из 5 шт.
Строительная бумага Ray Sulfite, 12 x 18 дюймов, черная, 50 листов – 054150
Inspiration/Artist
Я получил идею этого проекта с этого сайта — нажмите здесь
Инструкция с вопросами
День 1
Используйте эту теорию цвета для детей, вдохновленную презентацией Disney PowerPoint: нажмите здесь
Посмотрите видеоролики и обсудите принципы создания перспективы.
Игры для мозга: «Что ты видишь?» – Нажмите здесь
Игры для мозга: «Подсказки перспективы, линейная перспектива и размерный контраст» — нажмите здесь
способа создать иллюзию пространства — нажмите здесь
Одноточечная перспектива – нажмите здесь
Обсудить со студентами:
- В каком направлении направлены линии во всех примерах? (вертикальная, горизонтальная, перспективная (диагональная))
- Горизонтальная, вертикальная, перспективная, параллельная лексика.
Попросите учеников использовать свои руки, чтобы показать вам, что есть что.
- Последовательны ли они? Видите ли вы какие-либо линии, которые не следуют правилу этих линий? (пс… ответ – нет)
На самом деле я проецирую фотографию в одноточечной перспективе на белую доску. С помощью аршина я буквально прослеживаю линии на доске. Когда я выключаю проектор, ученики видят, что «наука», стоящая за этой техникой, действительно работает. Горизонтальные линии остаются горизонтальными.Вертикальные линии именно такие. Несмотря на то, что наш мозг хочет сделать вертикальные линии «стройными», на самом деле они остаются вертикальными.
День 2
Студенты смотрят это видео на Youtube.
Как нарисовать город с драматической перспективой: шаг за шагом: Нажмите здесь
Если вы не очень хорошо знакомы с One Point Perspective или ваши ученики не учатся в более высоких средних классах, я рекомендую держаться подальше от боковых сторон зданий для этого проекта и позволять показывать только фасад здания.
Самое замечательное в этом уроке то, что он действительно закрепляет правила одноточечной перспективы.
Основные моменты: Линии либо параллельны вертикали, либо параллельны горизонтали, либо находятся на линии перспективы. Для этого урока ВСЕ СТОРОНЫ ЗДАНИЙ ЯВЛЯЮТСЯ ЛИНИЯМИ ПЕРСПЕКТИВЫ. Это включает в себя стороны окон и дверей. Верх и низ каждого здания, каждого окна и каждой двери горизонтальны по отношению к вам. Это означает, что когда вы переворачиваете бумагу, и перед вами стоит здание, линии горизонтальны.
#1
Учащиеся используют квадратный лист акварельной бумаги размером 12×12. Я использовал этот круг в форме пирога в качестве шаблона, чтобы нарисовать большой круг. Подойдет и большая тарелка. Я сложил этот шаблон и нашел центр, который я использовал, чтобы проткнуть отверстие и найти свою точку для перспективы с одной точкой.
#2
Затем, используя линейку, начните рисовать линии здания.
Всегда касайтесь правилом точки в центре. Я показываю своим ученикам, как держать край линейки, по которому вы проводите, на той стороне, где легче всего провести его той рукой, которая у них ведущая.Другими словами, вам не нужно пересекать верхнюю часть и усложнять отслеживание бокового края линейки. Обратите внимание, что линия, которую я нарисовал, не имеет какой-либо определенной длины, но она не доходит до середины.
#3
Здесь я показываю, как две линии были нарисованы на линиях перспективы. Бумага обращена ко мне, поэтому я рисую верх здания горизонтально.
#4
Повторяйте этот процесс для каждого здания по мере движения по кругу.Стороны находятся в перспективе с точкой… вершины горизонтальны, если смотреть на вас. Когда вы добавляете окна и двери, их стороны также должны быть в перспективе, а верх и низ — горизонтальными.
Будет ученик, который захочет добавить сторону здания, которая не касается точки.
Или то, что, помоги мне небеса, не использует линейку. Я говорю им, что я фея-линейка, и хожу с линейкой, чтобы проверить их работу. Они думают, что это весело, и почему-то думают, что их линии будут такими же прямыми, как линейка.Вставьте забавные закатывающиеся глаза. Не произойдет. Я позволяю одному зданию коснуться точки, но только после того, как они освоятся с процессом. Я прошу их решить проблему, почему существует это правило. Наконец они обнаруживают, что это будет означать, что более чем одно здание касается вершины другого здания. Гении. Я также позволяю им исследовать включение мостов и отверстий, подобных Эйфелевой башне.
День 3/4
Время следующих шагов зависит от класса.Я жду до 3-го дня, чтобы хоть кто-нибудь из учеников прикоснулся к шулеру. Иногда некоторым ученикам нужно исправить некоторые строки. Перерыв в этот момент позволяет мне перепроверить работу каждого ребенка, прежде чем он продолжит. Если вы чувствуете, что они могут перейти на маркер, во что бы то ни стало, сделайте это.

Я говорю им рассмотреть окна. Они хотят, чтобы они были желтыми или белыми? Вспоминаем волшебную природу белых мелков как резистов при работе акварелью. Перед тем, как начать рисовать, наносят карандаш, чтобы линии оставались четкими и четкими.
Ваш рисунок с видом на землю почти готов! Наконец, я добавляю несколько жидких акварельных станций по комнате. Это также отличная поддержка цветового круга. Я призываю их использовать сначала красный, желтый и синий цвета, распределенные по третям. Остальные цвета хорошо сочетаются между собой. Другая идея состоит в том, чтобы заранее пометить акварельную бумагу каждым цветом. После нанесения краски они вырезаются, поэтому любые следы будут срезаны. Затем бумага приклеивается к листу черной плотной бумаги размером 12×12.Виола!
Вот некоторые готовые Вид с земли Перспектива Произведения искусства !
Общие базовые стандарты
4 класс – Математика – Геометрия
Рисуйте и идентифицируйте линии и углы, а также классифицируйте формы по свойствам их линий и углов.
(3)
5 класс – Математика – Геометрия
Графические точки на координатной плоскости для решения реальных и математических задач.(1-2)
6 класс – Математика – Геометрия
Решайте реальные и математические задачи на площадь, площадь поверхности и объем. (1-4)
7 класс – Математика – Геометрия
Рисовать, строить и описывать геометрические фигуры и описывать отношения между ними. (1-2)
Решайте реальные и математические задачи, связанные с измерением угла, площади, площади поверхности и объема. (5)
8 класс – Математика – Геометрия
Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для геометрии.(1-4)
Основы класса пространственных объектов—ArcGIS Pro | Документация
Классы объектов — это однородные наборы общих объектов, каждый из которых имеет одинаковое пространственное представление, например точки, линии или полигоны, и общий набор столбцов атрибутов, например класс линейных объектов для представления осевых линий дорог.
Четыре наиболее часто используемых класса пространственных объектов — это точки, линии, полигоны и аннотации (термин для текста карты).
На приведенном ниже рисунке они используются для представления четырех наборов данных для одной и той же области:
На этой диаграмме вы также можете увидеть потенциальную потребность в моделировании некоторых дополнительных свойств объектов.Например, канализационные линии и расположение люков составляют ливневую канализационную сеть, систему, с помощью которой можно моделировать стоки и потоки. Также обратите внимание на то, что соседние участки имеют общие границы. Большинство пользователей участков хотят поддерживать целостность границ общих объектов в своих наборах данных, используя топологию .
Как упоминалось ранее, пользователям часто необходимо моделировать такие пространственные отношения и поведение в своих наборах географических данных. В этих случаях вы можете расширить эти базовые классы пространственных объектов, добавив ряд расширенных элементов базы геоданных, таких как топологии, наборы сетевых данных и ландшафты.

Типы классов объектов
Векторные объекты (географические объекты с векторной геометрией) — это универсальные и часто используемые типы географических данных, хорошо подходящие для представления объектов с дискретными границами, таких как улицы, штаты и участки. Объект — это объект, который хранит свое географическое представление, которое обычно представляет собой точку, линию или полигон, в качестве одного из своих свойств (или полей) в строке. В ArcGIS классы объектов представляют собой однородные наборы объектов с общим пространственным представлением и набором атрибутов, хранящихся в таблице базы данных, например, класс линейных объектов для представления осевых линий дорог.
При создании класса объектов вас попросят установить тип объектов, чтобы определить тип класса объектов (точка, мультиточка, полилиния или мультипатч).
Обычно классы пространственных объектов представляют собой тематические наборы точек, линий или полигонов, но существует несколько типов классов пространственных объектов.
Первые три поддерживаются в базах данных и базах геоданных. Последние четыре поддерживаются только в базах геоданных.
- Точки — объекты, которые слишком малы для представления в виде линий или полигонов, а также в виде точечных местоположений (например, GPS-наблюдения).
- Линии — отображают форму и расположение географических объектов, таких как осевые линии улиц и ручьи, слишком узкие, чтобы изображать их в виде областей. Линии также используются для представления объектов, имеющих длину, но не имеющих площади, таких как горизонтали и границы.
- Полигоны — набор многогранных пространственных объектов, представляющих форму и расположение однородных типов объектов, таких как штаты, округа, участки, типы почв и зоны землепользования.
- Аннотация — текст карты, включая свойства того, как текст отображается.Например, в дополнение к текстовой строке каждой аннотации включены другие свойства, такие как точки формы для размещения текста, его шрифт и размер точек, а также другие свойства отображения.
Аннотация также может быть связана с функциями и может содержать подклассы.
- Размеры — особый вид аннотаций, показывающих определенные длины или расстояния, например, для указания длины стороны здания или границы земельного участка или расстояния между двумя объектами. Измерения широко используются в приложениях проектирования, инженерии и объектов для ГИС.
- Мультиточки — объекты, состоящие из более чем одной точки. Мультиточки часто используются для управления массивами очень больших коллекций точек, таких как кластеры лидарных точек, которые могут содержать буквально миллиарды точек. Использование одной строки для такой геометрии точек невозможно. Кластеризация их в многоточечные строки позволяет базе геоданных обрабатывать массивные наборы точек.
- Мультипатчи — трехмерная геометрия, используемая для представления внешней поверхности или оболочки объектов, занимающих дискретную область или объем в трехмерном пространстве.
Мультипатчи состоят из плоских трехмерных колец и треугольников, которые используются в сочетании для моделирования трехмерной оболочки. Вы можете использовать мультипатчи для представления чего угодно, от простых объектов, таких как сферы и кубы, до сложных объектов, таких как изоповерхности и здания.
- Трехмерный объект — трехмерная геометрия, специализирующаяся на представлении дополнительной поддержки формата, такой как материалы, вдоль внешней поверхности или оболочки элементов, занимающих дискретную область или объем в трехмерном пространстве.Вы можете использовать 3D-объекты для представления материалов с высоким уровнем детализации для поддержки эстетики, такой как глянец или шероховатость. Вы можете использовать их на простых или сложных объектах, таких как сферы и кубы, а также на сложных структурах, таких как изоповерхности и строительные материалы. 3D-объекты используют расширенные связанные таблицы для хранения нескольких компонентов материалов.
Эти таблицы вместе с плоскими трехмерными кольцами и треугольниками используются для моделирования трехмерной оболочки.
Геометрия объектов и координаты объектов
Классы объектов содержат как геометрическую форму каждого объекта, так и описательные атрибуты.Геометрия каждого объекта в первую очередь определяется его типом объекта (точка, линия или полигон). Но также могут быть определены дополнительные геометрические свойства. Например, объекты могут состоять из одной части или состоять из нескольких частей, иметь трехмерные вершины, иметь линейные меры (называемые m-значениями) и содержать параметрически определенные кривые. В этом разделе представлен краткий обзор этих возможностей.
Линии и полигоны, состоящие из одной и нескольких частей
Классы линейных и полигональных объектов могут состоять из отдельных или нескольких частей.Например, штат может состоять из нескольких частей (Гавайские острова), но считается объектом одного штата.
Вершины, сегменты, высоты и измерения
Геометрия объектов в основном состоит из координатных вершин.
Сегменты линий и полигонов охватывают вершины. Сегменты могут быть прямыми ребрами или параметрически определенными кривыми. Вершины в пространственных объектах также могут включать z-значения для представления мер высоты и m-значения для представления измерений вдоль линейных объектов.
Типы сегментов линейных и полигональных объектов
Линии и полигоны определяются двумя ключевыми элементами: упорядоченным списком вершин, определяющих форму линии или полигона, и типами сегментов линий, используемых между каждой парой вершин. Каждая линия и многоугольник представляют собой упорядоченный набор вершин, которые можно соединить, чтобы сформировать геометрическую фигуру. Другой способ представить каждую линию и многоугольник — это упорядоченная серия соединенных сегментов, где каждый сегмент имеет тип: прямая линия, дуга окружности, эллиптическая дуга или кривая Безье.
Тип сегмента по умолчанию — прямая линия между двумя вершинами. Однако, когда вам нужно определить кривые или параметрические формы, у вас есть три дополнительных типа сегментов, которые можно определить: дуги окружности, эллиптические дуги и кривые Безье.
Эти формы часто используются для представления застроенной среды, такой как границы участков и дороги.
Вертикальные измерения с использованием значений z
Координаты объектов могут включать вершины x,y и x,y,z. Z-значения чаще всего используются для представления высот, но они могут представлять и другие измерения, такие как годовое количество осадков или качество воздуха.
Объекты могут иметь координаты x,y и, опционально, дополнительные значения высоты по оси z.
Линейные измерения с использованием m-значений
Вершины линейных объектов также могут включать m-значения. Некоторые ГИС-приложения используют систему линейных измерений для интерполяции расстояний вдоль линейных объектов, таких как дороги, ручьи и трубопроводы. Вы можете присвоить m-значение каждой вершине объекта. Типичным примером является система измерения километровых столбов на шоссе, используемая транспортными управлениями для регистрации состояния дорожного покрытия, ограничений скорости, мест аварий и других происшествий на автомагистралях.
Двумя широко используемыми единицами измерения являются расстояние в милях от заданного местоположения, такого как линия округа, и расстояние от опорного маркера.
Вершины для измерений могут быть либо x,y,m, либо x,y,z,m.
Поддержка этих типов данных часто упоминается как линейная ссылка . Процесс геолокации событий, происходящих в этих измерительных системах, называется динамической сегментацией .
Измеренные координаты составляют основу этих систем.В реализации линейной привязки в ArcGIS термин «маршрут» относится к любому линейному объекту, такому как городская улица, шоссе, река или труба, который имеет уникальный идентификатор и общую систему измерения вдоль каждого линейного объекта. Набор маршрутов с общей системой измерения может быть построен на линейном классе объектов.
Допуски элементов
Точность местоположения и поддержка высокоточной структуры управления данными имеют решающее значение в управлении данными ГИС. Ключевым требованием является возможность хранения информации о координатах с достаточной точностью.
Точность координат описывает количество цифр, которые используются для записи местоположения. Это определяет разрешение, с которым собираются и управляются пространственные данные.
Поскольку базы геоданных и базы данных могут записывать высокоточные координаты, пользователи могут создавать наборы данных с высоким уровнем точности и с большим разрешением, поскольку инструменты сбора данных и датчики улучшаются с течением времени (ввод данных из геодезии и гражданского строительства, сбор кадастровых данных и данных COGO, увеличение разрешение изображений, лидар, планы зданий из САПР и т. д.).
ArcGIS записывает координаты, используя целые числа, и может обрабатывать местоположения с высокой точностью. В различных операциях ArcGIS координаты объектов обрабатываются и управляются с помощью некоторых ключевых геометрических свойств. Эти свойства определяются во время создания каждого класса пространственных объектов или набора пространственных данных.
Следующие геометрические свойства помогают определить разрешение координат и допуски обработки, используемые в различных пространственных обработках и геометрических операциях:
- Разрешение X,y: точность, с которой записываются координаты в классе пространственных объектов
- Допуск X,y: A Кластерный допуск, используемый для кластеризации объектов с совпадающей геометрией; используется в топологии, наложении объектов и связанных операциях
- Z-допуск и z-разрешение: Свойства допуска и разрешения для измерения вертикальной координаты в наборах 3D-данных (например, мера высоты)
- M-допуск и m-разрешение : Свойства допуска и разрешения для измерений вдоль линейных объектов, используемых в наборах данных линейной привязки (например, расстояние вдоль дороги в метрах)
Разрешение X,y
Разрешение x,y класса объектов или набора данных объектов — числовая точность, используемая для хранения значений координат x,y.
Точность важна для точного представления объектов, анализа и картирования.
Разрешение x,y определяет количество десятичных разрядов или значащих цифр, используемых для хранения координат объекта (как по x, так и по y). Вы можете думать о разрешении как об определении очень мелкой сетки, к которой привязаны все координаты. Значения координат фактически хранятся и обрабатываются как целые числа в ArcGIS. Поэтому иногда эту сетку сетки называют целочисленной сеткой или координатной сеткой.
Разрешение определяет расстояние между сетками в координатной сетке, на которое укладываются все координаты.Разрешение x,y выражается в единицах данных (в зависимости от системы координат), таких как футы штата, метры UTM или метры Альберса.
Разрешение x,y по умолчанию для классов пространственных объектов составляет 0,0001 метра или его эквивалент в единицах системы координат набора данных. Например, если класс пространственных объектов хранится в футах состояния, точность по умолчанию составляет 0,0003281 фута (0,003937 дюйма).
Если координаты указаны в широте-долготе, разрешение x,y по умолчанию составляет 0,000000001 градуса.
На приведенном ниже рисунке представлен концептуальный вид координатной сетки, на которой все значения координат привязаны к сетке сетки. Сетка охватывает экстент каждого набора данных. Мелкость этой сетки (расстояние между линиями в сетке) определяется разрешением x,y, которое очень мало.
При необходимости вы можете переопределить значение разрешения x,y по умолчанию и установить другое значение для каждого класса объектов или набора данных объектов. Установка меньшего значения разрешения x,y потенциально может увеличить время хранения и обработки наборов данных по сравнению с теми, которые используют более высокие значения разрешения x,y.
Допуск X,Y
Когда вы создаете класс пространственных объектов, вас попросят установить допуск X,Y. Допуск x,y используется для установки минимального расстояния между координатами в операциях кластеризации, таких как проверка топологии, создание буфера и наложение полигонов, а также в некоторых операциях редактирования.
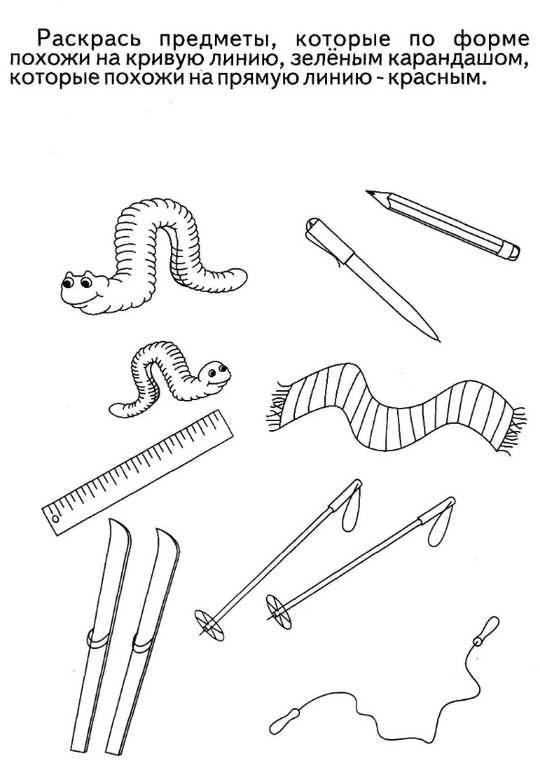
На операции обработки объектов влияет допуск x,y, который определяет минимальное расстояние, разделяющее все координаты объектов (узлы и вершины) во время этих операций.По определению, он также определяет расстояние, на которое координата может перемещаться по x или y (или по обоим) во время операций кластеризации.
Допустимое отклонение по осям x,y — очень маленькое расстояние (по умолчанию 0,001 метра в наземных единицах измерения). Он используется для разрешения неточных мест пересечения координат во время операций кластеризации. При обработке классов пространственных объектов с использованием геометрических операций координаты, расстояние по оси x и расстояние по y которых находятся в пределах допусков x,y друг друга, совпадают (другими словами, имеют одно и то же местоположение x,y).Таким образом, сгруппированные координаты перемещаются в общее место.
Как правило, менее точная координата перемещается в место более точной координаты или новое местоположение вычисляется как средневзвешенное расстояние между координатами в кластере.
В этих случаях средневзвешенное расстояние основано на рангах точности сгруппированных координат.
Для получения дополнительной информации о том, как задаются ранги точности для каждого класса пространственных объектов, см. раздел Топология в ArcGIS.
Процесс кластеризации работает путем перемещения по карте и определения кластеров координат, которые находятся в пределах допуска x,y друг друга.ArcGIS использует этот алгоритм для обнаружения, очистки и управления общей геометрией объектов. Это означает, что координаты совпадают (и привязаны к одному и тому же общему местоположению координат). Это является основополагающим для многих операций и концепций ГИС.
Максимальное расстояние, на которое координата может переместиться в новое место во время таких операций, равно квадратному корню из двух значений допуска x,y. Алгоритм кластеризации является итеративным, поэтому в некоторых случаях координаты могут смещаться больше, чем это расстояние.
Допуск x,y по умолчанию установлен на 0,001 метра или его эквивалент в единицах реальной системы координат набора данных (другими словами, 0,001 метра на земле).
Например, если ваша система координат записана в футах государственной плоскости, допуск x,y по умолчанию составляет 0,003281 фута (0,03937 дюйма).
Значение по умолчанию для допуска x,y в 10 раз превышает разрешение x,y по умолчанию, и это рекомендуется для большинства случаев. У вас есть возможность установить большее значение допуска для данных с меньшей точностью координат или меньшее значение для набора данных с очень высокой точностью.
Важно отметить, что допуск x,y не предназначен для использования для обобщения геометрических форм. Вместо этого он предназначен для интеграции работы с линиями и границами во время топологических операций. Это означает интегрирование координат, которые находятся на очень малых расстояниях друг от друга. Поскольку координаты могут смещаться как по x, так и по y на величину допуска x,y, вы можете решить многие потенциальные проблемы, обрабатывая наборы данных с помощью команд, использующих допуск x,y. К ним относятся обработка очень малых перелетов или недолетов, автоматическое удаление дубликатов сегментов и координированное прореживание вдоль граничных линий.

Вот несколько полезных советов:
- Как правило, вы можете использовать допуск x,y, который в 10 раз превышает разрешение x,y, и ожидать хороших результатов.
- Чтобы перемещение координат было небольшим, оставьте малым допуск x,y. Однако слишком малый допуск x,y (например, в 3 раза больше разрешения x,y или меньше) может неправильно интегрировать линейную работу с совпадающими границами и координатами.
- И наоборот, если ваш допуск x,y слишком велик, координаты объектов могут накладываться друг на друга.Это может поставить под угрозу точность представления границ объекта.
- Допустимое отклонение x,y никогда не должно приближаться к разрешению захвата данных. Например, при масштабе карты 1:12 000 1 дюйм равен 1000 футам, а 1/50 дюйма равен 20 футам. Сохраняйте перемещение координат, используя допуск x, y, значительно ниже этих значений. Помните, что допуск x,y по умолчанию в этом случае равен 0,0003281 фута, что является разумным значением по умолчанию для допуска x,y; на самом деле лучше всего использовать значения допуска x,y по умолчанию во всех случаях, кроме крайних.

- В топологиях можно установить ранг координат для каждого класса пространственных объектов. Установите ранг координат ваших наиболее точных объектов (например, обследованных объектов) на 1, а менее точные объекты на 2, 3 и т. д. по убыванию уровня точности. Это приводит к тому, что другие координаты объектов с более высоким номером ранга точности (и, следовательно, с более низкой точностью координат) подстраиваются под более точные объекты с более низким номером ранга.
Хранение классов объектов
Каждый класс объектов управляется в одной таблице.Столбец формы в каждой строке используется для хранения геометрии или формы каждого объекта.
В таблице классов пространственных объектов верно следующее:
- Каждый класс пространственных объектов представляет собой таблицу.
- Отдельные объекты хранятся в виде строк.
- Атрибуты объектов записываются в столбцах.

- Столбец shape содержит геометрию каждого объекта (точка, линия, многоугольник и т. д.).
- Столбец ObjectID содержит уникальный идентификатор для каждой функции.
Если вы создаете класс линейных объектов в базе геоданных, в класс объектов автоматически добавляется дополнительное поле для записи длины линии.Если вы создаете класс полигональных объектов, автоматически добавляются два дополнительных поля для записи длины (периметра) и площади каждого полигонального объекта. Единицы измерения этих значений зависят от пространственной привязки, заданной для класса пространственных объектов. Имена этих полей различаются в зависимости от используемой базы данных и пространственного типа. Это обязательные поля, и вы не можете их изменить.
Расширение классов пространственных объектов
Каждый класс пространственных объектов представляет собой набор географических объектов с одинаковым типом геометрии, одинаковыми атрибутами и одинаковой пространственной привязкой.
Вы можете расширить классы пространственных объектов, хранящиеся в базах геоданных, чтобы добавить поведение или целостность данных. Ниже показано, как вы можете расширить классы пространственных объектов с помощью базы геоданных и почему.
Работа с классами пространственных объектов в базе геоданных
Опция Описание Подтипы
Вы можете использовать подтипы для управления набором подклассов объектов в одном классе объектов.Это часто используется в таблицах классов объектов для управления различным поведением подмножеств объектов одного типа.
Домены атрибутов
Домены атрибутов можно использовать для указания списка допустимых значений или диапазона допустимых значений для столбцов атрибутов.
Используйте домены, чтобы обеспечить целостность значений атрибутов. Домены часто используются для принудительной классификации данных (например, класса дорог, кодов зонирования и классификаций землепользования).
Управление версиями
Управление версиями можно использовать для управления рядом ключевых рабочих процессов ГИС для управления данными; например, поддерживать длительные транзакции обновления, исторические архивы и многопользовательское редактирование.
flex-wrap — CSS: каскадные таблицы стилей
Свойство CSS
flex-wrapустанавливает, будут ли flex-элементы принудительно помещаться в одну строку или могут переноситься на несколько строк. Если перенос разрешен, он устанавливает направление, в котором строки располагаются друг над другом.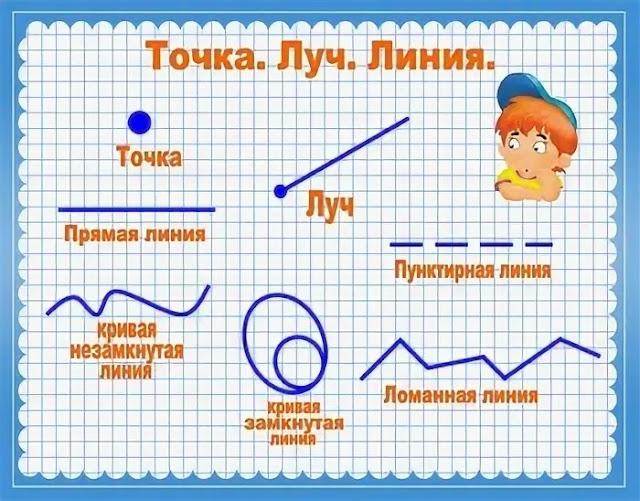
Дополнительные свойства и информацию см. в разделе Использование гибких блоков CSS.
flex-wrap: nowrap; flex-wrap: обернуть; flex-wrap: обернуть-обратно; flex-wrap: наследовать; flex-wrap: начальный; flex-wrap: вернуться; flex-wrap: не установлено;Свойство
flex-wrapуказано как одно ключевое слово, выбранное из списка значений ниже.Значения
Допустимы следующие значения:
сейчасЭлементы Flex расположены в одну строку, что может привести к переполнению контейнера Flex. cross-start либо эквивалентен start , либо перед в зависимости от значения
flex-direction. Это значение по умолчанию.оберткаЭлементы Flex разбиваются на несколько строк. cross-start либо эквивалентен start , либо перед в зависимости от значения
flex-direction, а cross-end
обратная сторонаВедет себя так же, как
обертка, но перекрестный начальный и перекрестный конец переставлены.сейчас | обернуть | wrap-reverseУстановка значений переноса гибкого контейнера
HTML
Это пример для flex-wrap:wrap
<дел> <дел>1 <дел>2 <дел>3
Это пример для flex-wrap:nowrap
<дел> <дел>1 <дел>2 <дел>3Это пример для flex-wrap:wrap-reverse
<дел> <дел>1 <дел>2 <дел>3УСБ
.содержание,
.content1,
.content2 {
цвет: #fff;
шрифт: 100 24px/100px без засечек;
высота: 150 пикселей;
ширина: 897 пикселей;
выравнивание текста: по центру;
}
.контент раздел,
.content1 раздел,
.content2 раздел {
высота: 50%;
ширина: 300 пикселей;
}
.красный {
фон: оранжево-красный;
}
. зеленый {
фон: желто-зеленый;
}
.синий {
фон: стальной синий;
}
.содержание {
дисплей: гибкий;
flex-wrap: обернуть;
}
.content1 {
дисплей: гибкий;
гибкая обертка: nowrap;
}
.content2 {
дисплей: гибкий;
flex-wrap: обернуть-обратно;
}
зеленый {
фон: желто-зеленый;
}
.синий {
фон: стальной синий;
}
.содержание {
дисплей: гибкий;
flex-wrap: обернуть;
}
.content1 {
дисплей: гибкий;
гибкая обертка: nowrap;
}
.content2 {
дисплей: гибкий;
flex-wrap: обернуть-обратно;
}
Результаты
Таблицы BCD загружаются только в браузере
Линии в геометрии — типы, примеры
В геометрии распространенной ошибкой является утверждение, что отрезок и линия — это одно и то же.
Сегмент имеет определенное начало и определенный конец, причем каждый конец представлен точкой.
Примеры отрезков включают длину стола, расстояние прямой дороги и т. д.
С другой стороны, линия не имеет определенного начала или конца.
Сегмент является частью линии, но линия не является частью сегмента.
Вокруг нас так много прямых линий, краев зданий, дорог, по которым мы путешествуем.
Давайте подробно изучим линии.
Линия – это фигура, образованная двумя точками, соединенными на минимальном расстоянии между ними, и оба конца которых уходят в бесконечность.
Хотя линии не имеют определенного начала или конца, в нашей повседневной жизни они представлены такими примерами, как железнодорожные пути или автострады.
Луч — это часть прямой, которая имеет только одну фиксированную точку, а другая точка не имеет конца.
Хотя лучи имеют фиксированное начало и не имеют определенного конца, в нашей повседневной жизни они представлены такими примерами, как солнечный свет или свет факела.
Отрезок — это часть линии фиксированной длины, или можно сказать, что оба конца отрезка фиксированы. Сегменты, иногда также называемые линейными сегментами.
Хотя оба сегмента линии имеют фиксированные концы, в нашей повседневной жизни они представлены такими примерами, как край стола, провод или столб.
Аналитический центр
- Предположим, вы привязали веревку к одной точке Земли и начали ходить с другим концом веревки в руке.Вы идете по прямой, спустя столько месяцев вам каким-то образом удалось вернуться в ту же точку, откуда вы начали.
 Один из ваших друзей отмечает, что пока вы шли по линии, фигура, полученная с помощью веревки, не была линией. Какой ответ вы дадите своему другу?
Один из ваших друзей отмечает, что пока вы шли по линии, фигура, полученная с помощью веревки, не была линией. Какой ответ вы дадите своему другу?
Что такое параллельные линии?
Две прямые называются параллельными, если они лежат в одной плоскости и никогда не пересекаются.
Или мы можем сказать, что если две прямые не имеют точки пересечения, они называются параллельными прямыми.{\circ}\), то они перпендикулярны друг другу.
Исследуйте типы линий в симуляции ниже.
Горизонтальные и вертикальные линии
Линии классифицируются на основе их выравнивания.
Горизонтальные линии
Линии, нарисованные горизонтально, называются горизонтальными линиями.
Вертикальные линии
Линии, нарисованные вертикально, называются вертикальными линиями.
Наклонные или наклонные линии
Линии, проведенные в наклонном положении или образующие угол, отличный от 0, 90, 180, 270, 360 градусов с горизонтальными или вертикальными линиями, называются наклонными или наклонными линиями.
Важные примечания
- Линия не имеет конечных точек.
- Луч имеет только одну фиксированную точку.
- Отрезок линии — это часть линии фиксированной длины.
- Перпендикулярные линии имеют угол 90 градусов между собой.
- Параллельные линии не пересекаются.
Решенные примеры
Сэм хочет найти фигуры, состоящие только из отрезков. Помогите ему выбрать правильные цифры из следующих.
Раствор
Давайте обсудим каждый вариант по порядку:
Вариант А состоит из 5 сегментов линии.
Вариант B состоит из 3 прямых сегментов и изогнутой части.
Вариант C представляет собой круг, поскольку он состоит только из изогнутых частей.
Вариант D состоит из 4 сегментов линии.
|
\(\следовательно\) Варианты A и D верны. |
Найдите правильные типы линий на рисунке ниже.
Раствор
Вариант А представляет собой пару параллельных линий
Вариант B — это пара непараллельных линий или линий пересечения.
Вариант C является примером перпендикулярных линий.
Том выбирает точки пересечения линий, указанных на рисунке ниже, он заметил, что есть 5 точек пересечения. Он прав?
Раствор
Точки, в которых пересекаются любые из этих прямых: \(\text{A, B, C, D, E, F}\)
Следовательно, всего 6 точек пересечения.
| \(\поэтому\) Том не прав |
Интерактивные вопросы
Вот несколько упражнений для практики.
Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Надеемся, вам понравилось узнавать о строках с интерактивными вопросами. Теперь вы сможете легко решать задачи на линии.
О Куэмате
Наша команда экспертов по математике в Cuemath стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, это логическое мышление и разумный подход к обучению, в которые мы в Cuemath верим.
Часто задаваемые вопросы по линиям
1. Что такое уравнение прямой?
Общее уравнение прямой может быть задано как \(ax + by + c= 0\).
Где \(a, b, c\) — константы, а \(x, y\) — переменные.
2. Чему равен угол между двумя перпендикулярными прямыми?
Угол между двумя перпендикулярными линиями равен 90 градусов.
3. Что такое секущая?
Секущая – это прямая, пересекающаяся в двух точках с окружностью.
Прямая AB является секущей окружности.
4. Что такое касательная?
Касательная линия — это линия, которая касается окружности в одной точке.
Прямая \(L\) является касательной к окружности в точке \(P\).
5. Какие прямые параллельны?
Две прямые называются параллельными, если они лежат в одной плоскости и никогда не пересекаются.
.

 1. Самоопределение
к деятельности. Организационный момент
1. Самоопределение
к деятельности. Организационный момент 
 4.
«Открытие нового знания»(построение проекта выхода из затруднения)
4.
«Открытие нового знания»(построение проекта выхода из затруднения)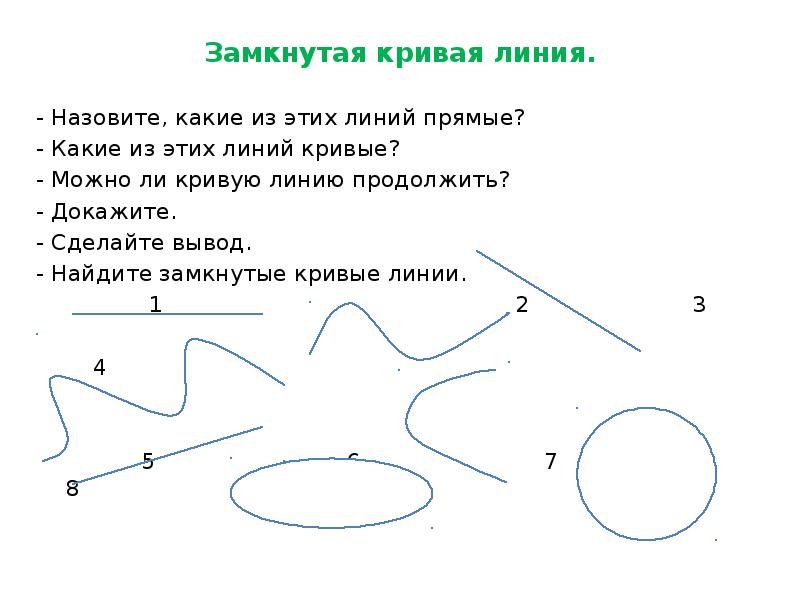 Молодцы!
Молодцы!

 Тропинка похожа на кривую линию. Кто справа от
кривой, а кто слева?
Тропинка похожа на кривую линию. Кто справа от
кривой, а кто слева?
