03.05.2023| | 0 Comment
Логика в 1 классе: Логические задачи для 1 класса с ответами и решениями, развивающие задания на логику для детей 7-8 лет
Логические задачи для 1-го класса: тренируем счёт, смекалку и даже чувство юмора
Логические задачи — важная составляющая развития ребенка. Рассказываем, как лучше браться за такие задачи вместе с детьми, и делимся подборкой развивающих заданий.
Зачем детям логические задачи
Детям с малых лет важно развивать логическое мышление. Это важно не только для того, чтобы хорошо учиться в школе, но и для всей дальнейшей жизни ребенка. Логика, умение последовательно рассуждать — инструмент, который необходим во всех повседневных и профессиональных ситуациях и которым ребенок, однажды усвоив, будет пользоваться всю жизнь.
Развитая логика помогает ребенку:
- Разбираться в огромном количестве новой информации и отсеивать недостоверную.
- Строить рассуждения и последовательно мыслить.
- Принимать продуманные решения, основанные на разных «за» и «против».
- Формулировать свои мысли и выступать публично.
Какую бы профессию ни выбрал ребенок и каким трудом он бы ни занимался, даже если это будет далеко о математики или программирования, ему будут нужны эти навыки.
Логика — это основа критического мышления, которое жизненно необходимо любому человеку, — думаем, с этим никто спорить не станет.
В хороших школах логические задачки дети решают с самого первого класса, но это не отменяет необходимость решать их и дома самостоятельно. В конце концов такой тренировки никогда не бывает мало.
Какие задачи давать первоклассникам
Уже в дошкольном возрасте, 4–5 лет, большинство могут понять простые логические операции, такие как сравнение или классификация. В первом классе школы особенно важно уделять достаточно внимания решению логических задач — это обеспечит успешное освоение школьной программы в целом. Как и любой навык, логическое рассуждение поддается тренировке.
Первоклассников особенно важно обучать правильной работе с силлогизмами. Силлогизм — это логическое умозаключение, в котором из двух данных суждений (или из посылок) получается третье суждение (вывод). Классическим силлогизмом, который обычно разбирают на уроках логики, является следующий:
- Всякий человек смертен (посылка 1).
- Сократ — человек (посылка 2).
- Следственно, Сократ смертен (заключение, выведенное из посылок).
Конечно, с детьми подобные логические рассуждения стоит тренировать на более близких им предметах — например, на задачках и загадках про игрушки или сладости.
В решении логических задач вместе с ребенком не забывайте хвалить его за правильные ответы и поддерживать. Важно, чтобы у ребенка было позитивное подкрепление и решение логических задач он связывал с удовольствием и игрой, а не с обязаловкой.
Задания для детей 7–8 лет
1. Ты гуляешь по лесу и видишь, что за одним из деревьев спрятались медвежата. Видно всего 8 лапок. Сколько всего медвежат за деревом?
Ответ: 2
2. В многоквартирном доме живет много кошек. На первом этаже живет две кошки, на втором в два раза больше, на третьем — столько же, сколько на втором, плюс еще одна. Сколько всего кошек живет в доме?
Ответ: 11
3. Маша, Ваня и Лиза решили полакомиться мороженым и купили эскимо, фруктовый лед и вафельный стаканчик.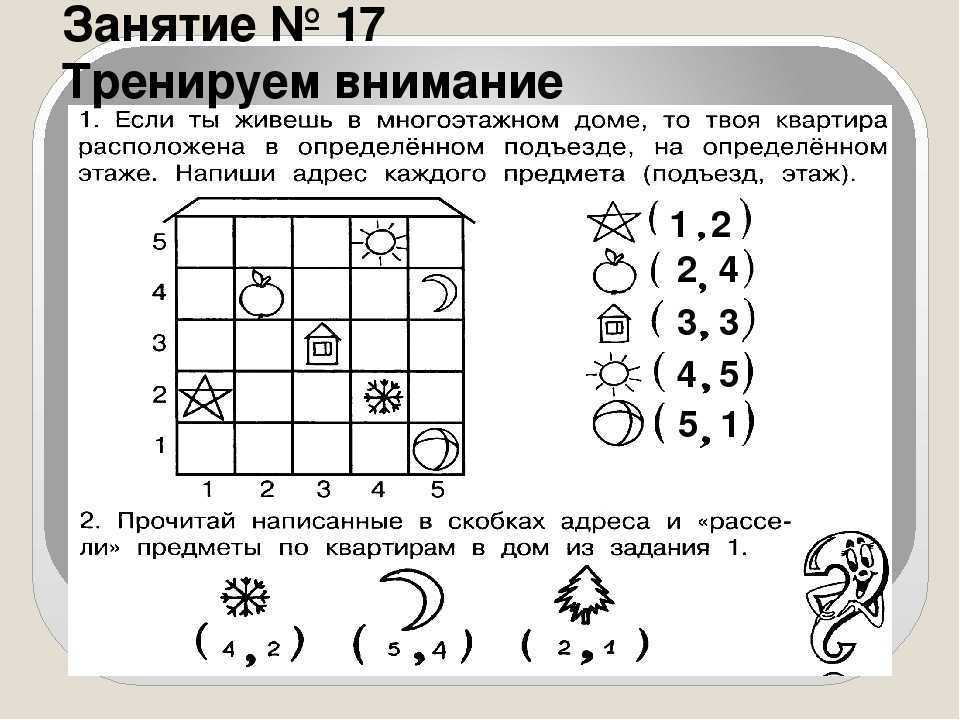
Ваня выбрал фруктовый лед, а Маша не любит эскимо. Кто из ребят какое мороженое ест?
Ответ: Ваня — фруктовый лед, Маша — вафельный стаканчик, Лиза — эскимо
4. В одном цветочном горшке растут 6 маленьких кактусов. Мама решила рассадить их в разные горшки, чтобы кактусам было посвободнее. Сколько ей нужно купить горшочков, чтобы в каждом было по 2 кактуса?
Ответ: 3
5. Человек выпрыгнул из самолета без парашюта и приземлился на твердую землю. При этом он ничего себе не повредил. Как так получилось?
Ответ: Он прыгал из самолета, который стоял на земле
6. Лестница в твою квартиру состоит из 9 ступенек. Какая ступенька находится на середине?
Ответ: Пятая
7. Два брата-близнеца помогали маме готовить обед. Вместе они трудились 4 часа. Сколько часов работал каждый?
Ответ: 4
8. В корзине лежат яблоки. Известно, что их можно разделить поровну между 2 или 3 детьми. Сколько яблок в корзине, если их меньше 10?
Ответ: 6 яблок
9.
Какие часы показывают верное время только два раза в сутки?
Ответ: Исправные часы со стрелками
10. Брат старше сестры на 1 год. На сколько лет он будет старше сестры через 5 лет?
Ответ: На 1 год
11. Мальчик идет из школы домой 30 минут. За сколько минут эту же дорогу пройдут 3 мальчика?
Ответ: За 30 минут
12. Мальчика, в которым ты познакомилась на детской площадке, зовут Юра. У его сестры только один брат. Как зовут брата его сестры?
Ответ: Юра
13. К тебе пришли гости, а в холодильнике — бутылка колы, пакет с яблочным соком и 1 кг торта. Что откроешь в первую очередь?
Ответ: Холодильник
14. Мужчина ехал в машине. Фары у него не работали, луны на небе не было, фонари вдоль дороги не светили. Прямо перед машиной дорогу стал перебегать щенок, но водитель вовремя затормозил, и аварии не произошло. Как водителю удалось разглядеть щенка?
Ответ: На улице был день
15.
У тебя есть три одинаковые коробки, в которых лежат конфеты: в одной ананасовые, во второй — мятные, а в третьей — смесь ананасовых и мятных. Этикетки на коробках наклеены неправильно, то есть то, что написано на этикетке, и то, что внутри, не совпадает. Можете ли взять 1 конфету из любой коробки и точно определить, в какой из них какие конфеты?
Ответ: Нет
16. Из каюты капитана пиратского корабля исчезла бочка, в которой было 3 литра ямайского рома. Подозрение пало на пиратов Гарри, Тома и Одноглазого Чарли. Подозреваемые заявили:
Гарри: «Не трогал я Вашего рома. Том тоже ни при чём».
Том: «Ручаюсь головой, сэр, Гарри невиновен. Ром стянул Одноглазый».
Чарли: «Бутылочку Вашу взял Гарри. А я в этом не замешан».
Капитану удалось выяснить, кто взял ром. Оказалось, что один из подозреваемых дважды солгал, другой — дважды сказал правду, а третий один раз солгал, а в другой раз сказал правду. Вор действовал в одиночку. Кто же вор?
Ответ: Ром украл Гарри
17.
Ваня решил купить 2 конфеты для себя и 8 груш для двух младших сестер. Но в результате купил в четыре раза больше конфет для себя и не купил ничего сестрам. Дома его начала мучить совесть, и он поделился конфетами с сестрами. 4 конфеты оставил себе, а оставшиеся распределил между ними. По сколько конфет получила каждая сестра?
Ответ: По 2 конфеты
18. Лиза пришла в магазин за фруктами и решила купить 4 груши. В магазине было все перепутано, пришлось искать по всем отделам. По 1 груше Лиза нашла в двух ящиках у входа в магазин, 4 груши лежали на полке рядом с сахаром. Половина этих груш оказались плохими, поэтому Лиза решила купить 3. Сколько всего груш было в магазине?
Ответ: 6
19. В 1-м классе у всех мальчиков 2 одинаковых имени (половину мальчиков зовут Ваня, а половину — Илья) и 4 одинаковые фамилии (всех мальчиков зовут либо Иванов, либо Петров, либо Галкин, либо Палкин). Может ли быть в классе мальчик по имени Ваня Палкин? А Илья Галкин?
Ответ: Да
20.
Папа попросил тебя сходить в магазин и купить 2 пакета молока и 7 яблок. Ты зашел в магазине и смог купить 1 пакет молока, а вместо яблок взял 3 кг. печенья и 5 конфет. Как сильно расстроится папа?
Ответ: Зависит от его характера
Загадки от известных писателей1. Загадка Корнея Чуковского из журнала «Еж» (№ 1, 1928)
Шел Кондрат
В Ленинград,
А навстречу — двенадцать ребят.
У каждого по три лукошка,
В каждом лукошке — кошка,
У каждой кошки — двенадцать котят.
У каждого котенка
В зубах по четыре мышонка.
И задумался старый Кондрат:
«Сколько мышат и котят
Ребята несут в Ленинград?»
Ответ: Глупый, глупый Кондрат!
Он один и шагал в Ленинград,
А ребята с лукошками,
С мышами и кошками
Шли навстречу ему —
В Кострому.
2. Загадка из книги Льюиса Кэрролла «Логическая игра» (1887)
Элизабет, Лиззи,
Бэтси и Бэсс
Весною с корзинкой
Отправились в лес.
В гнезде на березе,
Где не было птиц,
Нашли они пять
Розоватых яиц.
Но всем четверым
По яичку досталось,
И все же четыре на месте осталось.
Ответ:
Хоть разные
Названы здесь имена
(Элизабет, Лиззи,
Бэтси и Бэсс),
Но так называлась
Девчонка одна.
Она и ходила с корзинкою в лес.
Перевод английской загадки Самуила Маршака (журнал «Мурзилка», № 1, 1960)
3. Ни одно ископаемое животное не может быть несчастно в любви.
Устрица может быть несчастна в любви.
Какое заключение из этого можно сделать?
Ответ: Устрица — не ископаемое животное
Задания на логику в картинках
Задание 1
Ответ: 2, так как из всех животных в предложенных ответах только лиса смотрит влево
Задание 2
Выясни, какие цифры должны быть вместо звездочек и гриба.
Ответ: Звездочка — это 6, гриб — 8
Логические задачи по математике для 1 класса с ответами, решениями
Логические задачи по математике для 1 класса
Логические задачи по математике для 1 класса позволяют развить у ребенка способность последовательно мыслить, а также умение думать в целом.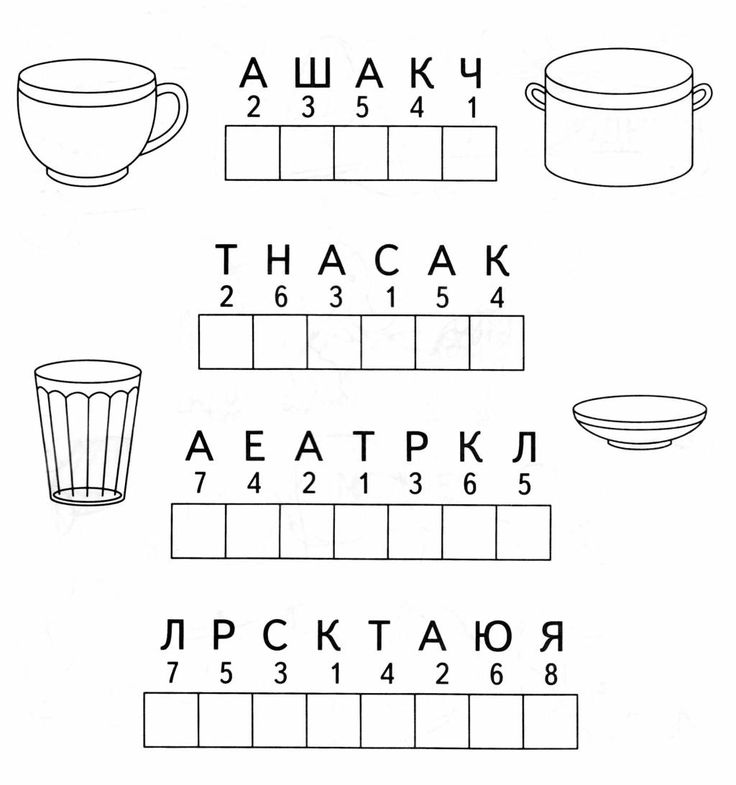
Однако иногда случается так, что у ребенка пропадает желание заниматься математикой в школе, хотя в процессе подготовки к поступлению в первый класс он проявлял большой интерес к логическим задачкам. Случается это по той причине, что ребенку очень быстро надоедают похожие задания. Чтобы школьнику было действительно интересно, его все время нужно стараться заинтересовывать чем-то новым.
Виды математических задач для детей 1 класса
Как показывает практика, среди наиболее интересных задач для учеников первых классов обычно выделяют следующие:
•логические – на сложение и вычитание;
•составные – в несколько действий;
•текстовые – логические и математические.
Интересно! Кроссворды для детей 6 лет
Ребенок будет с удовольствием решать поставленные перед ним задачи, если чередовать их и придумывать к ним условия, которые будут интересны детям.
Логические задачи на сложение и вычитание
В рамках учебного процесса в школе чаще всего встречаются обычные задачи на сложение и вычитание.
Однако ребенку будет куда интереснее заниматься математикой, если задачи будут побуждать его к логическим размышлениям, а не просто машинально вычитать и прибавлять цифры. Приведем несколько наглядных примеров логических задач по математике для 1 класса с ответами и картинками.
Пример №1
Условие. Три подружки взяли в каждую руку по 1 воздушному шарику. Сколько всего шариков есть у девочек?
Решение и ответ. У девочек имеется 6 шариков, так как каждая подружка взяла по одному шару, как в левую, так и в правую руку.
Пример №2
Условие. На тарелке лежит 1 пирожное, 2 конфеты и 3 груши. Сколько всего фруктов находится на тарелке?
Решение и ответ. Количество фруктов в тарелке – 3 штуки. Потому что только груши являются фруктом, а пирожное и конфеты – нет.
Пример №3
Условие. У фермера была 12-литровая бочка, в которой находилось 7 литров воды, а также полностью наполненное водой ведро, объемом 8 литров. Бочку дополнили доверху из ведра. Сколько литров воды осталось в ведре?
Решение и ответ.
В ведре осталось 3 литра воды. В бочке не хватало 5 литров (12-7=5), которые фермер взял из ведра, где изначально находилось 8 литров жидкости (8-5=3).
Как видите, задачи составлены таким образом, чтобы помимо работы с цифрами ребенку приходилось проявлять смекалку.
Однако, как показывает практика, в возрасте 7 лет дети могут иметь разный уровень подготовки. Следовательно, приведенные выше задачи могут показаться для кого-то из малышей слишком сложными. В этом случае имеет смысл предложить ему более простые задачки на сложение и вычитание. Однако суть остается прежней – задания должны быть интересными. Зная, чем увлекается ребенок, можно составить задачу, которая будет интересна конкретно ему.
Пример
Условие. У Маши было 2 яблока, а у ее подруги Леры – 3. Сколько всего яблок у девочек?
Решение и ответ. Всего у девочек 5 яблок (2+3=5).
Составные – в несколько действий
Такие задачи в два или три действия ученикам 1 класса наверняка понравятся.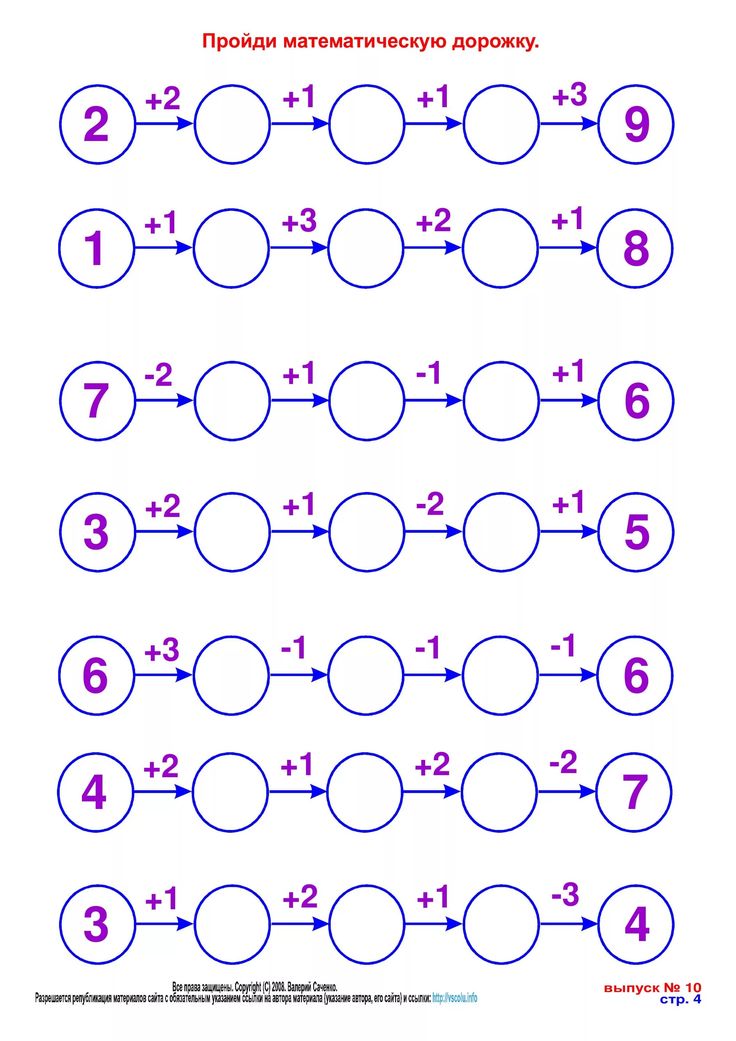
Кроме того, с их помощью у ребенка будет очень хорошо развиваться логика и память.
Пример №1
Условие. Монстрик фиолетового цвета скушал 4 целых апельсина. А его друг – красный монстрик, съел 7 половинок таких же апельсинов. Кто из них скушал больше апельсинов?
Решение и ответ. Фиолетовый монстрик съел больше, чем его друг. 1 целый апельсин – это 2 половинки. Значит, 4 целых апельсина можно записать, как 2+2+2+2=8 половинок. 8>7, значит фиолетовый монстрик скушал больше, чем его друг.
Пример №2
Условие. На столе у Светы было 8 пирожных. К ней пришло 5 гостей, и каждый из них скушал по 1 пирожному. Хозяйка подумала, что нужно добавить вкусностей, поэтому достала из холодильника еще 4 пирожных и добавила их на стол к оставшимся сладостям. Однако гости сказали, что уже сыты и не стали брать добавку. Сколько всего пирожных осталось на столе?
Решение и ответ. На столе осталось 7 пирожных. 8-5=3 пирожных, осталось на столе после того, как гости взяли себе по 1 штуке.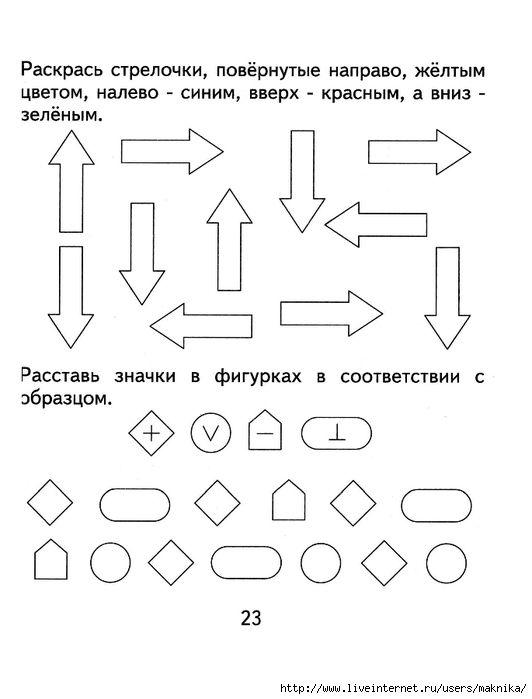
3+4=7 пирожных оказалось на столе, когда хозяйка добавила вкусностей из холодильника.
Интересно! Умение детей по возрастам
Текстовые – логические и математические на сообразительность
Такие задачи очень хорошо развивают у детей 7 лет умение логически мыслить. Далее мы рассмотрим несколько примеров таких заданий с их решением.
Пример №1
Условие. У Фёдора есть две сестры и два брата. Кого в семье больше: женщин или мужчин?
Ответ. Мужчин в этой семье на 1 человека больше, потому что Федор тоже мужчина.
Пример №2
Условие. Ира, Надя, Коля и Аня решили заняться спортом. У них есть 2 скакалки и 2 мяча. Известно, что у Ани в руках скакалка, а у Коли и у Нади – одинаковые предметы. Какие предметы в руках у Коли, Нади и Иры?
Ответ. У Коли и Нади в руках мячи, а у Иры – скакалка.
Пример №3
Условие. Учитель выдал ученикам картинку, на которой изображены различные фигуры разных цветов, и загадал одну из них.
Чтобы у детей была возможность назвать правильную фигуру, преподаватель дал им несколько подсказок:
•фигура точно не синяя и не квадратная;
•она треугольная или круглая.
Ответ. Глядя на картинку, методом исключения мы можем определить, о какой именно фигуре идет речь. Учитель загадал оранжевый треугольник.
Такие математические задания-головоломки способствуют развитию логики и тренирует навыки владения основными приемами мышления в целом. Обобщение, сравнение, выделение определенных признаков – всему этому ребенка учат задания такого типа.
Пример №4
Условие. Найдите закономерность и продолжите ряд подходящими цифрами: 5,6,8,11,15,…
Ответ. …20,26,33 и так далее. В ряду вышеуказанных чисел мы видим определенную закономерность. Сначала мы прибавили 1, потом 2, затем 3, после этого 4, затем 5, потом 6 и так далее. То есть, с каждым шагом мы прибавляем число на единицу больше, чем предыдущее.
Усложненные задачи по математике на логику
Некоторые дети довольно легко справляются с обычными математическими задачами и показывают очень хорошие результаты в школе.
Таких преуспевающих учеников нередко отправляют на олимпиады.
Далее приведем примеры логических задач по математике, с которыми ученик первого класса может столкнуться на олимпиаде.
Пример №1
Условие. Известно, что кролик легче, чем щенок на 2 килограмма. Если посадить щенка на левой чаше весов, а кролика на правой, то какая чаша весом будет располагаться выше? Каким образом после этого нужно использовать две имеющиеся гири, чтобы уравновесить весы?
Решение и ответ. Исходя из условий задачи, мы можем быть уверены, что щенок тяжелее кролика, а, значит, правая сторона весов, на которой сидит кролик, будет находиться выше. Чтобы весы уравновесились, гиря, находящаяся в чаше с кролем, должна быть тяжелее на 2 килограмма, чем гиря, которую мы разместим в чашу с щенком (3-1=2). Таким образом, получается, что в чашу к щенку нам нужно поставить гирю весом 1 килограмм, а к кролику – утяжелитель в 3 килограмма.
Пример №2
Условие. Рассмотрите картинку и определите стоимость медвежонка, исходя из имеющихся данных.
Решение и ответ. В первом ряду мы видим уточку и вертолет, общая стоимость которых составляет 4 условных единицы. Во втором ряду мы наблюдаем те же игрушки, но рядом с ними расположен еще и медвежонок. При этом нам известно, что общая стоимость этих трех предметов – 10 условных единиц. Так мы можем вычислить цену медвежонка (10-4=6).
Математика действительно очень интересная наука, знание которой очень помогает человеку в повседневной жизни. Поэтому важно прививать ребенку любовь к ней с самых малых лет. Как это сделать вы уже знаете, главное – чтобы малышу было интересно.
Интересно! Поделки из ватных дисков
Надеемся, что приведенные в статье логические задачи по математике для 1 класса окажутся вам полезными, и ваш ребенок достигнет успеха в школе.
LOGIC PRO: однократное посещение класса 1, в прямом эфире или по запросу (включает бесплатный 90-D
- ДОМАШНЯЯ
- ОБ
- ТЕКУЩИЕ КУРСЫ
- ПРОПУСК ГОСТЯ
- Отзывы
- Часто задаваемые вопросы
- КЛАССЫ
- ТЕКУЩИЙ КАЛЕНДАРЬ КУРСА
- ПРОПУСК ГОСТЯ В 9 КЛАСС0004
- Как это работает
- Зачисление на полный семестр
- УРОКИ
- ОНЛАЙН
- Онлайн-классы
- Онлайн уроки
- МОЛОДЕЖНЫЙ
- ЗАПИСЬ
- Информация о студии
- Записаться на сеанс
- Производство
- ЛОГИК ПРО Х
- СОБЫТИЯ
- ПРЕДСТОЯЩИЕ СОБЫТИЯ
- ПРЕДЫДУЩИЕ СОБЫТИЯ
- ПРОПУСК ГОСТЯ
- РЕСУРСЫ
- Новости
- Открытый микрофон в Лос-Анджелесе
- Архив новостей
- Полезные ссылки
- Сервисные возможности
- КОНТАКТЫ
- Подписаться
- Войти
- ␡
- Ваша корзина пуста
Дом Продукты LOGIC PRO: одно посещение класса 1, в прямом эфире или по запросу (включая бесплатную 90-дневную пробную версию Logic Pro)
shopify.com/s/files/1/0879/6900/products/LogicProSingleClassVisitatTheSongwritingSchool_5e41a49a-6f86-4405-8fb4-3d2e59e2545f_1024x1024.png?v=1674252033″ data-title=”LOGIC PRO: Class 1 Single Visit, Live or On-Demand (Includes Free 90-Day Trial of Logic Pro)”>
Хотите изучить Logic Pro и решить, как лучше всего это сделать?
Присоединяйтесь к нам для Class 1 of Logic Pro Level 1 , по запросу за единовременную плату и получите 3 часа вводного обучения.
Видео полностью снабжено подписями со всеми ключевыми командами и терминами для дополнительного понимания и обучения.
Вам понравился класс, и вы хотите записаться на полный курс из 6 занятий, чтобы научиться записывать, редактировать, аранжировать и микшировать свои песни? Вы можете применить эту разовую плату к полному курсу обучения.
- Если у вас еще нет программного обеспечения для записи и создания на базе Mac, получите
- Не уверены, что ваш компьютер совместим? Ознакомьтесь с требованиями к системе Logic .
Полный курс проходит по субботам с 10:00 до 13:00 по тихоокеанскому времени в течение 6 недель, 18 часов общего обучения , с видеокурсами, доступными по запросу. Чтобы узнать больше о полном курсе или зарегистрироваться, перейдите сюда.
Занятия с инструктором Джей Ашер , автор 5 книг по логике, многолетний руководитель группы пользователей Лос-Анджелеса.
Джей преподает логику в Школе написания песен с 2009 года (во времена Logic 9!).
Классы:
Тип класса: Неизвестный тип
1.1 Логические операции
Математика обычно включает в себя объединение истинных (или гипотетически истинных) утверждения различными способами для получения (или доказательства) новых истинных утверждений. Начнем с разъяснения некоторых из этих фундаментальных идей.
Под предложением мы подразумеваем утверждение, имеющее определенное истинностное значение , истина (T) или ложь (F) — например,
«В 1492 году Колумб плыл по синему океану». (T)
«Наполеон выиграл битву при Ватерлоо». (Ф)
В общем, на 92+y = 12$”, то $P(2,8)$ и $P(3,3)$ верно, а $P(1,4)$ и $P(0,6)$ ложны. Если $Q(x,y,z)$ равно “$x+y
Является ли предложение истинным или ложным, обычно зависит от того, что мы
говорят о том, что одно и то же предложение может быть истинным или ложным в зависимости от
по контексту; например, формула $x|y$ означает, что `$x$ делит
$у$’.
Вселенная дискурса для конкретной области математики представляет собой набор, который содержит все, что представляет интерес для этой темы. Когда мы изучение математических формул типа «$x$ делит $y$» на переменные предполагается, что они принимают значения в любом дискурсивном универсуме подходит для конкретного предмета. Вселенная дискурса обычно ясно из обсуждения, но иногда нам нужно будет идентифицируйте его явно для ясности. Вселенная дискурса обычно обозначается $U$.
Сложные предложения и формулы составляются из более простых,
используя небольшое количество логических операций .
Просто горстка
этих операций позволит нам сказать все, что мы должны сказать в
математика.
Если $P$ — это формула, то «не $P$» — это другая формула. формула, которую мы символически запишем как $\lnot P$. Конечно, $\lне P$ ложно, если $P$ истинно, и наоборот, например,
«6 не простое число» или «Неверно, что 6 премьер” или “$\lnot(\hbox{6 простое число})$” (T)
«Рональд Рейган не был президентом». (Ф)
Предположим, что $P$ и $Q$ — формулы. Затем «$P$ и $Q$» — это формула, записанная символически как $P\land Q$, называемое соединением из $P$ и $Q$. Чтобы $P\land Q$ были истинными как $P$, так и $Q$ должно быть истинным, иначе оно ложно, например,
«5 долларов = 6 долларов и 7 долларов = 8 долларов». (F)
«Сиэтл находится в Вашингтоне, а Бойсе — в Айдахо». (T)
«Толстой был русским, а Диккенс был Французский.” (Ф)
Если $P$ и $Q$ являются формулами, то формула “$P$ или $Q$” записывается символически как $P\lor Q$, называемая дизъюнкция $P$ и $Q$.
Это
важно отметить, что это включительно или, то есть, “либо
или оба”. Таким образом, если $P$, $Q$ или оба $P$ и $Q$ истинны,
то же самое и с $P\lor Q$. Единственный случай, когда $P\lor Q$ может быть ложным, состоит в том, что оба $P$
и $Q$ ложны, например,
«Вашингтон в Канаде или Лондон в Англии». (T)
“$5
«Ленин был испанцем или Ганди был итальянцем». (Ф)
Если $P$ и $Q$ – формулы, то “если $P$, то $Q$”
или “$P$ означает, что $Q$” написано
$P\подразумевает Q$, используя условное обозначение ,
$\подразумевает$. Не очевидно (по крайней мере, для большинства людей), под чем
обстоятельства $P\имеет Q$ должно быть правдой. Отчасти это потому, что
«if… then» используется в обычном английском языке более чем одним способом, однако
нам нужно исправить правило, которое позволит нам точно знать, когда $P\ подразумевает
Q$ верно. Конечно, если $P$ истинно, а $Q$ ложно, $P$ не может
подразумевают $Q$, поэтому $P\implis Q$ в этом случае ложно.
Чтобы помочь нам с
в других случаях рассмотрим следующее утверждение:
«Если $x$ меньше 2, то $x$ меньше 4».
Это утверждение должно быть верным независимо от значения $x$. (при условии, что вселенная дискурса является чем-то знакомым, например целые числа). Если $x$ равно 1, оно оценивается как $\rm T\имплицитно T$, если $x$ равно 3, оно становится $\rm F\implis T$, а если $x$ равно 5, становится $\rm F\ подразумевает F$. Таким образом, оказывается, что $P\implis Q$ истинно, если только $P$ истинно, а $Q$ ложно. Это правило, которое мы принимаем.
Наконец, biconditional , написанный $\Leftrightarrow$, соответствует фраза «если и только если» или «если» для краткости. Таким образом, $P \Leftrightarrow Q$ истинно, когда и $P$, и $Q$ имеют одинаковое истинностное значение, иначе оно ложно.
Пример 1.1.2 Предположим, что $P(x,y)$ равно “$x+y=2$” и $Q(x,y)$
равно “$xy>1$”. Тогда, когда $x=1$ и $y=1$,
$\lnot P(x,y)$, $P(x,y)\land Q(x,y)$, $P(x,y)\lor Q(x,y)$,
$P(x,y)\имеет Q(x,y)$ и $P(x,y)\Leftrightarrow Q(x,y)$
имеют значения истинности F, F, T, F, F соответственно, а когда
$x=2$ и $y=3$ имеют истинностные значения
Т, Ф, Т, Т, Ф соответственно.
$\квадрат$
Используя операции $\lnot$, $\land$, $\lor$, $\implies$,
$\Leftrightarrow$, мы можем построить составных выражений, таких как
$$
(P\land (\lnot Q))\ подразумевает ((\lnot R)\lor ((\lnot P)\land Q)).
$$
Как показывает этот пример, иногда необходимо
включать много круглых скобок, чтобы группировать термины
в формуле ясно. Как и в алгебре, где
умножение имеет приоритет перед сложением, мы можем
убрать некоторые скобки
согласование определенного порядка, в котором логически
операции выполняются. Мы
будет применять операции в этом порядке, начиная с
от первого к последнему: $\lnot$, $\land$, $\lor$, $\implies$
и $\Leftrightarrow$. Так
$$A\подразумевает B\или C\land\lnot D
$$
сокращение от
$$A\подразумевает (B\или (C\land (\lnot D))).
$$
Как и в алгебре, часто разумно включать
несколько дополнительных скобок, чтобы убедиться, что предполагаемый смысл понятен.
Большая часть информации, которую мы обсудили, может быть резюмирована в таблицы истинности .
Например, таблица истинности для
$\lnot P$:
| $P$ | $\lnot P$ |
|---|---|
| Т | Ж |
| Ф | Т |
В этой таблице две строки, потому что есть только две возможности для истинное значение $P$. Другие логические операции используют две переменные, поэтому им требуется 4 строки в их таблицах истинности.
| $P$ | $Q$ | $P\land Q$ | $P\lor Q$ | $P\Rightarrow Q$ | $P\Leftrightarrow Q$ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Т | Т | Т | Т | Т | Т | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ф | Т | Ф | Т | Т | Ф | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Т | Ж | Ж | Т | Ж | Ж | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ф | Ф | Ф | Ф 9п$
строки в таблице, потому что есть много разных способов назначить
T и F для $n$ простых формул в составном выражении.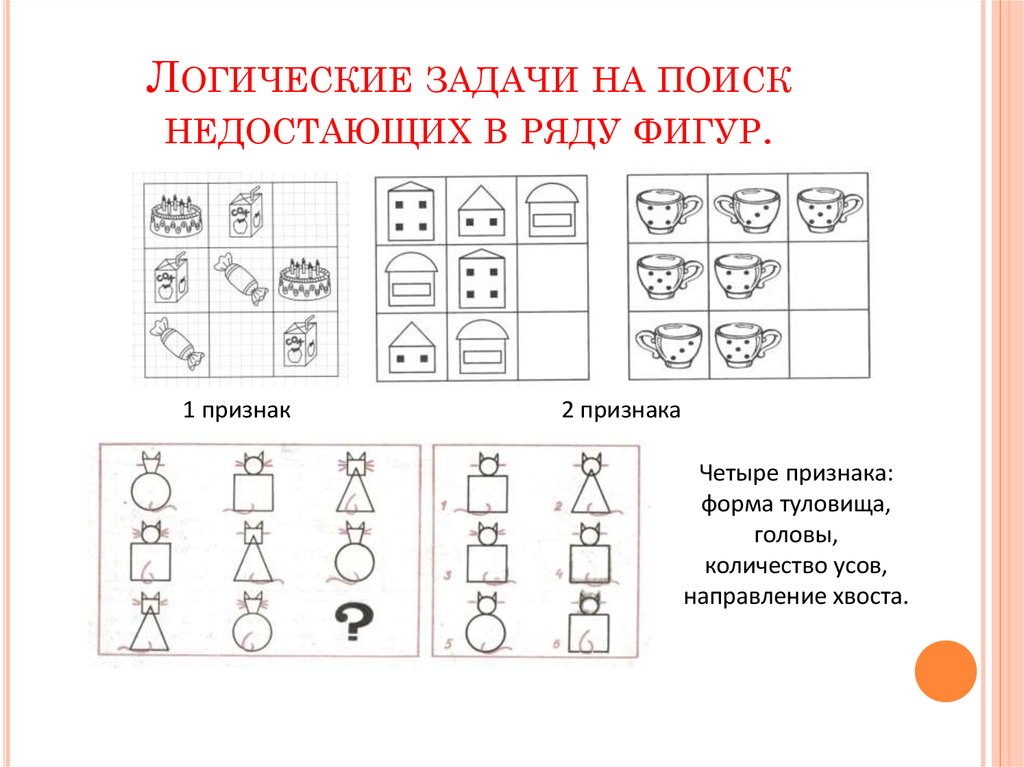 Таблица истинности для $(P\land Q)\lor \lnot R$ такова:
Обратите внимание, как включение промежуточных шагов облегчает работу с таблицей. Тавтология — это логическое выражение, которое всегда оценивается как T, то есть последний столбец его таблицы истинности состоит только из Т. Иногда говорят, что тавтология равна 9.0122 действительный ; хотя «действительный» используется в других контекстах как ну, это не должно вызывать путаницы. Например, $(P\land Q)\lor P\Leftrightarrow P$ является тавтологией, поскольку ее таблица истинности такова:
Мы перечисляем несколько важных тавтологий в следующей теореме. Теорема 1.1.3. Справедливы следующие утверждения. а) $P\стрелка влево \lnot\lnot P$ б) $P\lor Q\Leftrightarrow Q\lor P$ c) $P\land Q\Стрелка влево Q\land P$ d) $(P\land Q)\land R\Стрелка влево P\land(Q\land R)$ e) $(P\lor Q)\lor R\Стрелка влево P\lor(Q\lor R)$ f) $P\land (Q\lor R)\Leftrightarrow (P\land Q)\lor (P\land R)$ g) $P\lor (Q\land R)\Стрелка влево (P\lor Q)\land (P\lor R)$ h) $(P\подразумевает Q)\Стрелка влево (\lnot P\lor Q)$ i) $P\имеет (P\или Q)$ j) $P\land Q\имплицит Q$ k) $(P\стрелка влево Q)\стрелка влево ((P\подразумевает Q)\land (Q\подразумевает P))$ l) $(P\подразумевается Q)\стрелка влево (\lnot Q\подразумевается \lnot P)$ Доказательство. Доказательства оставлены в качестве упражнений. $\qed$ Заметим, что (b) и (c) — коммутативные законы, (d) и (e) —
ассоциативные законы и (е) и (ж) говорят, что $\land$
и $\lor$ распределяются друг над другом. Если две формулы всегда принимают одно и то же истинностное значение независимо от того, элементы из вселенной дискурса, которые мы заменяем различными переменные, то мы говорим, что они эквивалентны . Стоимость эквивалента формулы в том, что они говорят одно и то же. Это всегда правильный шаг в доказательстве заменить некоторую формулу эквивалентной. Кроме того, многие тавтологии содержат важные идеи для построения доказательств. Для например, (k) говорит, что если вы хотите показать, что $P\Leftrightarrow Q$, это можно (и часто целесообразно) разбить доказательство на два части, одна из которых доказывает импликацию $P\implis Q$, а вторая доказывая обратное , $Q\имеет P$. При чтении теоремы 1.1.3 у вас может возникнуть
заметил, что $\land$ и $\lor$ обладают многими схожими свойствами. Джордж Буль. Буль
(1815–1864) имел только обычное школьное образование, хотя и выучил
Греческий и латынь самостоятельно. Он начал свою карьеру в качестве элементарного
школьным учителем, но решил, что ему нужно больше узнать о
математики, поэтому он начал изучать математику, а также
языки, необходимые ему для чтения современной литературы на
математика. В 1847 году он опубликовал короткую книгу «Математический анализ».
Анализ логики , который, можно справедливо сказать, лег в основу исследования.
математической логики. Ключевой вклад работы заключался в
переопределить «математику» так, чтобы она означала не просто «изучение чисел и
величина», но изучение символов и манипулирование ими в соответствии с
к определенным правилам. В «Исследовании законов мысли» , опубликованном в 1854 г.,
Буль установил настоящую формальную логику, развивая то, что сегодня называется
Булева алгебра или иногда алгебра множеств . Он использовал символы для
сложение и умножение как операторы, но в совершенно абстрактном
смысл. Сегодня эти символы все еще иногда используются в булевых выражениях.
алгебре, хотя символы `$\land$’ и `$\lor$’, и `$\cap$’ и
`$\cup$’ также используются. Буль применил алгебраическую манипуляцию к
процесс рассуждения. Вот простой пример типа
манипуляцию, которую он проделал: уравнение $xy=x$ (которое сегодня можно было бы записать
$x\land y = x$ или $x\cap y = x$) означает, что «все вещи, удовлетворяющие
$x$ удовлетворяет $y$’, или, говоря нашим языком, $x\имеет y$. Если также $yz=y$ (что
есть $y\implis z$), то подстановка $y=yz$ в $xy=x$ дает
$x(yz)=x$ или $(xy)z=x$. Информация здесь взята из A History of Mathematics, by Карл Б. Бойер, Нью-Йорк: John Wiley and Sons, 1968. Подробнее информацию см. в Lectures on Ten British Mathematics , by Александр Макфарлейн, Нью-Йорк: John Wiley & Sons, 1916. Пример 1.1.1 Постройте таблицы истинности для следующих логических выражений: а) $(P\land Q)\или \lnot P$ б) $P\имеет (Q\land P)$ c) $(P\land Q)\Стрелка влево (P\lor \lnot R)$ d) $\lnot P\имеет в виду \lnot(Q\lor R)$ Пример 1.1.2 Проверьте тавтологии в теореме 1.1.3. Пример 1.1.3 Предположим, что $P(x,y)$ — это формула «$x+y=4$», а $Q(x,y)$ — это формула “$x $P(x,y)\land Q(x,y)$, $\lnot P(x,y)\lor Q(x,y)$, $P(x,y)\подразумевает \lnot Q(x,y)$, $\lnot(P(x,y)\Leftrightarrow Q(x,y))$, , используя значения:
Пример 1. |
посчитай и прочитай.
Это говорит о том, что существует
форма алгебры для логических выражений, аналогичная алгебре
для числовых выражений. Этот предмет называется Булева алгебра и имеет множество применений.
особенно в информатике.
Они называются «двойственными» понятиями — для любого свойства
один, есть почти идентичное свойство, которому удовлетворяет другой,
экземпляры двух операций поменялись местами. Это часто
означает, что когда мы доказываем результат, включающий одно понятие, мы получаем
соответствующий результат для своего двойственного без дополнительной работы.
Важность этого уровня абстракции для
будущее математики трудно переоценить. Вероятно, на
Благодаря этой работе он перешел на должность в Куинс-колледж в Корке.
Заменив $xy$ на $x$, получим $xz=x$, или
$x\подразумевает z$. Этот простой пример логического рассуждения используется более
и далее по математике.
92+bD+c=0$, обработка
$D$ как номер , предоставляет информацию о решениях для
дифференциальное уравнение.