Программа факультатива
«ЛОГИКА»
« Логика – наука о законах и формах мышления; ход рассуждений и умозаключений; разумность, внутренняя закономерность чего – нибудь».
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Направленность программы:
Востребованость развития функциональной грамотности школьника и формирование основ логического мышления.
ВВЕДЕНИЕ
Слово «логика» происходит от древнегреческого logos, обозначающего мысль, слово, понятие, закон, рассуждение. Этимология слова «логика» показывает, что это наука, имеющая отношение к языку и мышлению в целом. Действительно, логика рассуждений – и в математике, и в повседневной жизни – теснейшим образом связана с языком, с его коммуникативным аспектом. Человек, который не в состоянии проанализировать важную для него лично информацию, становиться подчас жертвой демагогии, политических и юридических спекуляций, недобросовестной рекламы.
Некоторые концепции современного подхода к организации математического образования.
В связи с наметившейся тенденцией общества на гуманизацию среднего образования, с ориентацией процесса обучения на индивидуальные интересы личности главной задачей обучения математике становится не изучение основ математической науки, а общеинтеллектуальное развитие, т.е. развитие функциональной грамотности. Таким образом, методическая система обучения математике должна быть переориентирована с увеличения объема информации, «обязательной для усвоения», на формирование умений анализировать, продуцировать и использовать информацию.
Несомненно, изучение математики вносит определяющий вклад в умственное развитие ребёнка. В процессе обучения в арсенал приёмов и методов человеческого мышления естественным образом включается индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование, аналогия.
ЦЕЛИ И ЗАДАЧИ КУРСА.
Цель
Задачи курса – учащиеся углубляют стихийно складывающуюся логическую интуицию, накапливают практический опыт овладения основными логическими приёмами: сравнением, обобщением, способностью выделять существенное, конкретизацией, классификацией, аналогией, абстрагированием; вырабатывают навыки последовательного и доказательного мышления, формируют умения аргументированно обосновывать, отстаивать свои взгляды и убеждения; развивают языковую культуру, учатся умению адекватно понимать или выражать предлагаемую информацию.
ДИДАКТИЧЕСКИЕ ПРИЕМЫ
Особое внимание уделено осуществлению дидактической функции, которую принято называть мотивационно – стимуляционной. Это делается, во – первых, по ходу занятия, во – вторых, в начале каждой новой темы. Первый уровень можно назвать мотивацией локального значения: это постановка естественных вопросов, текущих гипотез и т. д.. Второй уровень можно назвать мотивацией глобального значения: это формулирование ближайших целей, которых нужно достичь, а также краткий анонс того, чему будет посвящена тема. Промежуточный уровень мотиваций состоит в достаточном числе занятий – игр. Упомянутые приёмы проблемного обучения настраивают ученика на осмысление поставленных целей, стимулируют его внимание и способствует выработке столь необходимого оценочного отношения к получаемым сведениям.
1) Теоретический материал.
Все понятия в этом курсе вводятся естественным образом при рассмотрении соответствующих примеров из реальной жизни, а не с помощью формальных определений, т.
е. преподавание ведется на уровне, максимально приближенному к ученику.
2)Задачи.
Теоретический материал должен осознавать и усваиваться преимущественно в процессе решения задач и различных заданий, предлагающихся в форме интеллектуальных игр.
Задачи этого курса – логические. Для их решения, как правило, не требуется большого запаса математических знаний. Они требуют от ученика умения применять знакомые ему логические операции, т. е. их решение развивает логическое мышление. Во- первых, логические задачи почти всегда носят занимательный характер и этим привлекают даже тех, кто не любит математику. Логические задачи разбиты по группам, каждая группа имеет свое название и ориентирована на определенный возрастной уровень.
Уникальная польза, которую приносят ребенку логические игры, отражена в высказывании Чарлза Лютвиджа Додгсона /Л. Кэрролла /: « В процессе игры вы овладеваете такими методами, которые позволяют вам обрести ясность мысли, способность вырабатывать у вас привычку к систематическому мышлению и, что особенно ценно, умение обнаруживать логические ошибки и находить изъяны и пробелы тех, кто не пытался овладеть увлекательным искусством логики».
Особенности психологического развития младших школьников.
Психолог Л. С. Выготский отмечал интенсивное развитие интеллекта в младшем школьном возрасте. Чтобы развитие было успешным, нужна помощь со стороны учителя (в данном случае и настоящего курса). Для этого требуется знание особенностей психологического развития младших школьников, а также понимание конечных целей.
Ребенок 7-8 лет обычно мыслит конкретными категориями, часто поднимает аргументацию и доказательство простым указанием на реальный факт или опираться на аналогию, далеко не всегда правомерную. К моменту перехода в среднее звено школьники должны научиться сопоставлять, сравнивать, анализировать, находить частное и общее, устанавливать простые закономерности. Необходимо показать ребенку дифференцированный подход к признакам предмета ( существенным и несущественным), научить его давать обоснованное доказательство, понимать причинно- следственные связи.
В связи с преобладанием деятельности первой сигнальной системы у младших школьников более развита наглядно – образная память.
Они склонны к механическому запоминанию без осознания смысловых связей. К переходу в среднее звено у учащихся должна сформироваться способность к запоминанию и воспроизведению материала, аргументации, логических схем рассуждения.
В начальной школе необходимо не только закладывать основу знаний учащихся, но следует учить самостоятельно мыслить и творчески работать. На развитие этих качества и направлен курс внеурочной деятельности учащихся по « Логике».
Срок реализации
Программа курса разработана на 1 года обучения.
Формы занятий
Ведущими формами организации обучения является парная и групповая. Наряду с вышеназванными формами работы, осуществляется индивидуализация процесса обучения и применение дифференцированного подхода к учащимся, так как в связи с их индивидуальными способностями, результативность в усвоении учебного материала может быть различной. Дифференцированный подход поддерживает мотивацию к предмету и способствует творческому росту учащихся.
ОЖИДАЕМЫЙ РЕЗУЛЬТАТ:
В процессе обучения должен формироваться опыт самопознания и личностной самооценки, то есть обучающиеся должны учиться иметь свою точку зрения на ту или иную ситуацию, уметь отстаивать её при необходимости, активно сотрудничать со взрослыми, совместно с другими учащимися решать те или иные задачи, уметь слушать учителя, слушать товарища, не перебивать высказывания других, вырабатывать умение задавать вопросы на понимание уточнение.
Коммуникативные УУД – умение работать в группе со сверстником, аргументировать свой выбор, уметь участвовать в диалоге, используя вербальные и не вербальные способы коммуникативности.
Познавательные УУД – обучающих должны учиться работать с информацией, понимать речь учителя, выполнять логические операции(сравнение, анализ, обучение, классификации, установление аналогий, логические цепочки.)
Регулятивные УУД – уметь оформлять свою деятельность, быть инициотивным, самостоятельным, корректировать свою деятельность.
Личностные УУД: формировать учебную мотивацию, осознанность учения и личной ответственности
Регулярные занятия логическими упражнениями позволят научить детей:
описывать признаки предметов, слов и чисел;
узнавать предметы по заданным признакам;
определять различные и одинаковые свойства предметов, слов, чисел;
выделять существенные признаки предметов;
сравнивать предметы, слова, числа;
определять последовательность событий;
определять отношения между предметами типа род – вид;
давать определения тем или иным понятиям;
устанавливать причинно – следственные связи;
высказывать суждения, делать выводы;
уметь производить простейший анализ и синтез;
формируется речь, находчивость, сообразительность.
Формируется интерес к содержанию учебной деятельности, приобретению знаний.
Формами проверки результативности занятий являются:
выпуск книг-самоделок собственных логических заданий
подготовка и проведение детьми « Минуток смекалки» на уроках в
своём классе
Формами подведения итогов реализации программы могут быть – конкурсы знатоков, викторины, интеллектуальные марафоны, КВНы, олимпиады.
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ЗАНЯТИЙ
1 класс (33 ч)
№
Тема
Задачи
Содержание
Дата
1
«Логика.
Что это такое?»
Познакомить детей с предметом логики. Дать представление о познании человеком окружающего мира, об основных формах чувственного познания и абстрактного мышления. Формировать умения детей активно включаться выполнить поставленную задачу самостоятельно, точно.
1 Знакомство с предметом «логика».
2 Игра «Я знаю…» (с мячом)
3 Упражнение «Кто наблюдательнее?»
4 Беседа о временах года.
5 Дидактическая игра «Что сначала, что потом» (коллективная)
6 Графическое упражнение.
2
Загадки. Анализ построения.
Учить детей отгадывать загадки, уметь объяснить по какому признаку они догадались, о чём идёт речь. Упражнять в умении выделять главное, отвлекаясь от второстепенного. Познакомить детей с загадкой, как одной из единиц познания окружающего мира.
1 Беседа о загадках.
2 Классификация загадок.
3 Упражнение «Отгадай загадку – нарисуй отгадку»
4 Игра «Где игрушка?»
5 Беседа о временах года «Когда это бывает?»
6 Графическое упражнение.
3
Анализ. Синтез. Признаки предметов.
Познакомить детей с понятием «признак предмета», упражнять в умении вычленять отдельные признаки предметов. Развивать у детей умение мыслить с помощью разнообразных логических приёмов, проводить простейший анализ и синтез.
1 Беседа о предметах которые нас окружают.
2 Упражнение «Определи предмет на ощупь»
3 Упражнение «Узнавание предмета по заданным признакам»
4 Игра «найди отличия»
5 Упражнение «Определи время года по перечисленным признакам»
6 Графическое упражнение.
4
Цвет. Форма. Размер.
Учить детей вычленять в предметах данные признаки, обосновывать его выбор, доказывать его целесообразность. Развивать сенсорное восприятие, умение выполнять задание по инструкции. Активизировать речь детей, учить детей рассуждать вслух.
1 Повторение предыдущей темы, вычленение первых трёх признаков предметов: цвет, форма, размер.
2 Упражнение «Кто наблюдательнее?»
3 Игра «Круг, треугольник, квадрат»
4 Игра «Определи фигуру»
5 Игра «Цвет»
6 Графическое упражнение.
5
Вкус. Запах. Материал.
Познакомить детей с ещё некоторыми признаками предметов, характерных не для всех предметов, а только для специфических. Упражнять детей в соотношении предмета с материалом, из которого он изготовлен. Поощрять и поддерживать интерес детей к выполнению заданий.
1 Вычленение специфических признаков предмета (вкус, запах)
2 Игра «Угадай на вкус»
3 Игра «Определи по запаху»
4 Упражнение «Что из чего?»
5 Упражнение на выделение признаков предметов.
6 Графическое упражнение на тренировку памяти.
6
Живое – неживое. К какой группе относится. Использование человеком.
Учить детей определять по существенным признакам отношение предмета к определённой группе.
Выяснить значение каждого из предметов для использования человеком. Упражнять детей в установлении причинно – следственных связей, в умении видеть результат, полученный в ходе определённой работы.
1 Беседа по теме. Знакомство со способами группировки предметов по какому – либо признаку.
2 Игра «Живое – неживое»
3 Упражнение «Предметное лото»
4 Упражнение «Продолжи предложение»
5 Закрепление знаний о сезонных явлениях.
6 Графическое упражнение.
7
Сравнение. Сериация.
Вид – род.
Формировать и развивать у детей основные операции мышления. Учить находить сходства и различия между предметами и явлениями. Формировать умения устанавливать наиболее часто встречающиеся отношения между понятиями, такими как вид – род. Развивать зрительное и слуховое восприятие.
1 Закрепление всех признаков предметов.
2 Упражнение «Цепочка слов»
3 Изучение и знакомство с новыми понятиями.
Игра «Сравнение». Как нужно сравнивать. Как нельзя сравнивать.
4 Игра «Найди родню»
5 Упражнение «Доскажи словечко»
6 Графическое упражнение на тренировку памяти.
8
Отрицание.
Ограничение.
Учить детей видеть существующие противоречия: уметь применять в ходе упражнений различные категории. Упражнять в умении видеть корень проблемы. Формировать способность отстаивать свою точку зрения, доказывать истинность своего ответа.
1 Закрепление видовых и родовых понятий. Игра «Рыбы – птицы – звери»
2 Упражнение «Наоборот»
3 Работа с предметами. Игра «Что загадали?»
4 Игра «Определи фигуру»
5 Отгадывание загадок (с использованием ограничения, отрицания)
6 Графическое упражнение.
9
Обобщение. Классификация.
Познакомить детей с классификацией предметов и её существенными признаками (естественными и основными) и не существенными (вспомогательными).
Учить обобщать и распределять предметы по группам, где каждая группа, каждый класс имеет своё постоянное место. Упражнять детей в умении находить и использовать свойства объектов для достижения поставленной цели.
1 Упражнение «Продолжи ряд»
2 Знакомство с понятиями «классификация», «обобщение».
3 Работа в малых группах на классификацию предметов и явлений.
4 Игра «Подбери по смыслу»
5 Игра «Круг – кружочек»
6 Графическое упражнение.
10
Что лишнее?
Чего не хватает?
На основе полученных знаний, учить детей видеть противоречия, устранять ошибку, которую они считают допущенной. Развивать внимательность, наблюдательность, умение анализировать предложенный материал.
1 Беседа по прошлой теме, закрепление приёмов обобщения и классификации.
2 Упражнение «Пропущенные фигуры»
3 Игра «Чего без чего не бывает»
4 Работа в парах по карточкам «Чего без чего не бывает»
5 Игра «Что лишнее? Кто Лишний?»
6 Графическое упражнение по образцу «Закономерность»
11
Придумывание загадок.
Упражнять детей в придумывании загадок, отражая в них характерные признаки предмета, о котором идёт речь. Развивать абстрактное мышление, воображение . Формировать творческую активность, развивать речь.
1 Работа с различными видами загадок.
2 Разгадывание ребусов, шарад
3 Беседа по теме. Определение структуры и плана построения загадки.
4 Придумывание загадок детьми. Анализ результатов.
5 Игра «Лото загадок»
6 Упражнение на ориентировку «Красный, жёлтый, зелёный»
12
Алгоритм отгадывания.
Упражнять детей в умении анализировать, выдвигать идеи и проверять их истинность на практике. Развивать умственную активность детей, способность мыслить логично, использовать умение оперировать полученными знаниями.
1 Упражнение «Узнай предмет по заданным признакам»
2 Установление алгоритма отгадывания.
3 Упражнение «Шумно, вкусно, кругло, красно»
4 Работа в группах по карточкам (одна группа загадывает предмет, другая, используя алгоритм, отгадывает)
5 игра «Цепочка слов»
6 Диктант «Замени название предмета геометрической фигурой»
13
Суждения.
Упражнять детей в умении утверждать или отрицать признаки предметов или их отношений. Учить детей не только выдвигать идеи, но и развивать умение тщательно и детально разрабатывать их. Формировать активность и личное участие в выдвижении тех или иных суждений.
1 Игра «Хорошо – плохо»
2 Закрепить времена года и их признаки. Высказать своё суждение о них.
3 Упражнение «Вопрошайка»
4 Игра «Интеллектуальный теннис»
5 Упражнение «Закончи предложение – выскажи суждение»
6 Графический диктант.
14
Умозаключения.
Учить детей делать выводы, опираясь на факты обследования; получать заключение по определённым правилам вывода. Упражнять в установлении связи между различными явлениями, легко переходить от одних связей к другим.
1 Игра «Что сначала, что потом»
2 Природные явления и времена года: взаимосвязь, смена, признаки.
3 Упражнение «Вывод»
4 Упражнение «По какому признаку?»
5 Весёлая игра на внимание и мышление «Он – она»
6 Графический диктант.
15
Ожившие фигуры. Преобразования.
Учить детей тщательно и детально обследовать фигуры, делать выводы. Во время преобразования фигур формировать умения учитывать все факторы преобразования. Развивать мышление, сосредоточенность на поставленной задаче.
1 Упражнение «Из каких фигур состоит предмет»
2 Игра «Танграм», «Колумбово яйцо»
3 Знакомство с «Фабрикой преобразований»
4 Игра «Ожившие фигуры»
5 Упражнение «Пропавшие буквы в весёлых стихах»
6 Упражнение на тренировку памяти.
16
Чего на свете не бывает?
Формировать у детей образное мышление, фантазию, умение логично высказывать своё суждение. Развивать творческую и речевую активность, лингвистическое мышление.
1 Беседа по теме «Так бывает или нет?»
2 Упражнение «Нелепицы»
3 Игра «Слова, которых не бывает»
4 Упражнение «Чего на свете не бывает?»
5 Игра «Исправь ошибку»
6 Графическое упражнение «Фантазия».
17
Логика в математике.
Учить детей мыслить логически и творчески выражать свои мысли, используя математические термины. Развивать всестороннее восприятие конкретного.
1 Упражнения «Лишнее число», «Математические бусы», «Ошибки – невидимки»
2 Игра «Путешествие» (по ориентировке на плоскости листа).
3 Упражнение «Сосчитай фигуры»
4 Упражнение «Форма. Размер. Цвет»
5 Игра «Ошибка художника»
6 Диктант на внимание и мышление.
18
Логика и наша речь.
Упражнять детей в умении выражать свои мысли, слушать и понимать других. Развивать навыки речевого общения, умение правильно и логично строить фразы.
1 Игра «Назови слово»
2 Коварная викторина про слова.
3 Игра «Цепочка слов»
4 Упражнение «Продолжи рассказ»
5 Ребусы и анаграммы «Зашифрованное слово»
6 Расшифруй и напиши слово.
19
Логика в окружающем мире.
Учить детей находить и вычленять логические связи в окружающем мире, делать выводы. Учить устанавливать связи между предметами и явлениями. Развивать познавательную активность детей.
1 Упражнение «Сравним картинки»
2 Игра «Что где лежит?»
3 Игра «Из отдельных частей собери предмет скорей»
4 Упражнение «Придумай название»
5 Чтение произведения о временах года.
6 Графическое упражнение.
20
Ощущение.
Восприятие.
Представления.
Упражнять детей в познании окружающего мира с помощью чувственных форм. Учить детей пользуясь своими ощущениями судить о предмете в целом. Развивать внимательность и сосредоточенность.
1 Беседа по теме.
2 Игра «Чудесный мешочек»
3 Упражнение «Узнаем предмет по заданным признакам»
4 Задания с палочками.
5 Упражнение «Соедини картинки и слова»
6 Графическое упражнение.
21
Понятие. Абстрагирование.
Учить детей мысленному выделению одного из признаков предмета и отвлечение от других, т.е выделение существенных признаков и отвлечение от несуществующих, второстепенных. Развивать умственную активность.
1 Упражнение «Объясните понятие»
2 Упражнение «Найдём предмет не похожий на другие»
3 Игра «Что на что похоже»
4 Упражнение «Поиск предметов обладающих сходными свойствами»
5 Упражнение «Поиск предметов с противоположными свойствами»
6 графическое упражнение «Мозаика» (абстрактный рисунок).
22
Слова. Определения.
Развивать у детей мыслительные операции анализа и синтеза; формировать умения и навыки в составлении определений. Развивать связную речь, умение логично выстраивать свой ответ.
1 Беседа по теме.
2 Упражнение «Дай определение»
3 Игра «Закончи предложение»
4 Упражнение «Соедини слова»
5 Упражнения «Вставь в определение нужное слово», Проверка определений»
6 Графическое упражнение.
23
Часть – целое. Причина – следствие.
Продолжать учить детей классифицировать предметы, но не только по видовым иродовым понятиям, но и по составляющим каждого отдельного предмета. Развивать наблюдательность, стремление к самостоятельному умозаключению.
1 Отгадывание загадок.
2 Игра «Рассеянный художник»
3 Упражнение «Кому, что?»
4 Коллективная работа «Подбери заплатки к коврикам»
5 Упражнение «Установи причину событий»
6 Графическое упражнение «Закончи рисунок»
24
Последовательность
Противоположность
Формировать у детей понятийное мышление, стремление к овладению основными операциями логического мышления; умение исключать неясность, двусмысленность.
1 Игра «Круглый год»
2 Упражнение «Последовательность»
3 Творческое задание «Проектировщики и строители»
4 Упражнение «После, потом, сейчас»
5 Упражнение «Знакомим с противоположными понятиями»
6 Графическое упражнение «Закончи узор»
25
Количественные и качественные соотношения предметов.
Учить детей понимать количественные и качественные соотношения предметов, уметь понимать их категории. Познакомить детей более подробно с группой парных понятий. Развивать умение делать самостоятельные выводы.
1 Беседа по теме.
2 Игра «Где игрушка»
3 Упражнение «Прочитаем сказку»
4 Упражнение «Отгадываем загадки, ответим на вопросы»
5 Объяснение смысла пословиц.
6 Графическое упражнение «Разноцветные бусы»
26
Логические пары.
Логические цепочки.
Учить детей составлять логические пары, учитывая какой – либо общий признак, уметь объяснить свой выбор. Упражнять детей в составлении логических цепочек с учётом признака последнего предмета в цепочке. Развивать логическое мышление, умение давать чёткие ответы.
1 Упражнение «Найди пару»
2 Игра «Цепочка слов»
3 Игра «Что сначала, что потом»
4 Упражнение «Найди сходство»
5 Игра «Логические цепочки»
6 Графическое упражнение «Укрась кубики»
27
Сочинение на заданную тему.
Предложить детям придумать, как можно больше предложений на заданную тему, как реалистичных, так и фантастических. Учить детей прослеживать логическую связь между ними.
1 Беседа по теме.
2 Игра «Угадай героя сказки»
3 Игра «Зашифрованное слово»
4 Упражнение «Сочиняем наоборот»
5 Сочиняем сказку «Загадочный ящик»
6 Графическое упражнение «Два Замка»
28
Чего только не
услышишь.
Учить детей видеть и понимать неожиданные нестандартные оттенки и нюансы ситуаций, выделять логические несоответствия. Развивать внимательность, творческую активность.
1 Беседа по теме «Звуки вокруг нас»
2 Игра «Испорченный телефон»
3 Игра «Переведите с детского языка»
4 Упражнение «Каскад слов»
5 Разучивание и повторение скороговорок.
6 Графическое упражнение «переведи язык звуков, на язык линий»
29
Взгляд с позиции другого.
Учить воспринимать одни и те же события по-разному, поощрять в детях не только результат, но и саму попытку решения ситуации. Развивать у детей желание обсуждать ситуацию, делать свои выводы.
1 Игра «Фотограф»
2 Упражнение «Сыщики»
3 Весёлая этимологическая викторина.
4 Игра «Хорошо – плохо»
5 Взгляд с позиции другого.
6 Графическое упражнение «Зеркало»
30
Нелогичные ситуации.
Учить детей отличать нелогичные ситуации от других, привычных. Упражнять в умении самим, создавать такие ситуации. Развивать внимание, творческую активность.
1 Игра «Кто что делает?»
2 Игра «Чепуха»
3 Игра «Бывает – не бывает»
4 Упражнение «Найди ошибку в рисунках»
5 Игра «определи, что здесь изображено?»
6 Графическое упражнение «Нарисуй по точкам»
31
Поиск способов применения предметов.
Развивать у детей способность концентрировать мышление на одном предмете, рассматривать практически все свойства предмета.
Развивать умение вводить предметы в самые разные ситуации и взаимосвязи.
1 Игра «Поиск общих свойств»
2 Игра «Поиск предметов обладающих сходными свойствами»
3 Игра «Поиск предметов с противоположными свойствами»
4 Упражнение «Новая жизнь старых вещей»
5 Игра «Как это можно использовать?»
6 Графический диктант.
32
Логические задачи.
Развивать у детей логическое мышление, умение применять полученные знания для решения нестандартных задач. Упражнять в умении мыслить разносторонне.
1 Логические задачи.
2 Весёлые задачки для маленьких умников.
3 Упражнение «Найди закономерность»
4 Коварная викторина про слова.
5 Игра «логический домик»
6 Графическое упражнение «Штриховки»
Список использованной литературы
Т.К. Жикалкина «Игровые и занимательные задания по математике. 1 класс», М.,: Просвещение, 1986.
– 47с.: ил.
«Занимательные задачи для маленьких», М., Омега, 1994. – 256с.: с ил.
Г.В. Керова «Нестандартные задачи по математике», М.: ВАКО, 2008. – 240с.
Л.В. Лазуренко «Занимательные материалы к урокам математики в 1-2 классах», Волгоград: Учитель – АСТ, 2005. – 96с.
Г.Г. Левитас «Нестандартные задачи на уроках математики в 1 классе», – М.: Илекса, 2008, – 56с.
Т.Н.Максимова «Интеллектуальный марафон: 1-4 классы», М.: ВАКО, 2009. – 208с.
Л.Г.Петерсон Программа «Учусь учиться» по математике для 1-4 классов начальной школы по образовательной системе деятельностного метода обучения «Школа 2000…». – М.: УМЦ «Школа 2000…», 2007. – 112с.
В.Н. Русанов «Математические олимпиады младших школьников: Кн. Для учителя: Из опыта работы (в сел. р-нах). – М.: Просвещение, 1990. – 77с.: ил.
Л.Ф. Тихомирова, А.В.Басов А.В. «Развитие логического мышления детей. Популярное пособие для родителей и педагогов», – Ярославль: «Академия развития», 1997.
– 240с. илл.
В.М.Туркина «400 развивающих заданий по математике. 1 класс: Практическое пособие. – М.: АРКТИ, 2008. – 64с.
|
Логика классов — это раздел математической логики (см. Логика математическая), основным предметом рассмотрения в котором служат классы (множества) предметов, задаваемые характеризующими их свойствами, общими для всех входящих в данный класс элементов. В рамках математической логики логика классов может пониматься, с одной стороны, как такое расширение логики высказываний (см. Логика высказываний), при котором «элементарные высказывания» уже не рассматриваются только как нерасчленяемое далее «целое», а каждое из них имеет субъектно-предикатную форму (то есть может рассматриваться на содержательном уровне как нераспространённое повествовательное предложение, в котором различаются подлежащие [subjects] и сказуемые [predicates]). Другая трактовка логики классов, — отличающаяся от указанной по форме, но эквивалентная по существу, — состоит в истолковании её как частного случая логики предикатов (см. Имеется ещё одна, изоморфная первым двум, интерпретация логики классов, в соответствии с которой объектами её рассмотрения являются множества (классы) каких-либо предметов — вне зависимости от каких бы то ни было свойств, общих для их элементов, — и операции над множествами. Таким образом, логика классов в этом случае рассматривается как формализованная теория множеств, отождествляемая с алгеброй множеств (см. Алгебра логики), в которой рассматриваются произвольные множества и обычные теоретико-множественные операции. Сопоставляя (взаимно-однозначно) множествам (классам) высказывания о принадлежности какого-либо предмета данному множеству, пересечению множеств — конъюнкцию соответствующих высказываний, объединению — дизъюнкцию, а дополнению — отрицание, получают указанный выше изоморфизм алгебры высказываний и алгебры множеств. |
Образование всегда использовало элементы игры чтобы мотивировать учащихся, нагляднее оценивать их результатов и больше увлекать в процесс обучения. Школьная система оценок — это, по сути, игровая схема. Формулировки из задачника по математике про поезд, идущий из точки А в точку Б, с одной стороны, во-первых, показывают связь науки с реальной жизнью, а с другой — делают её ближе и понятнее для детей.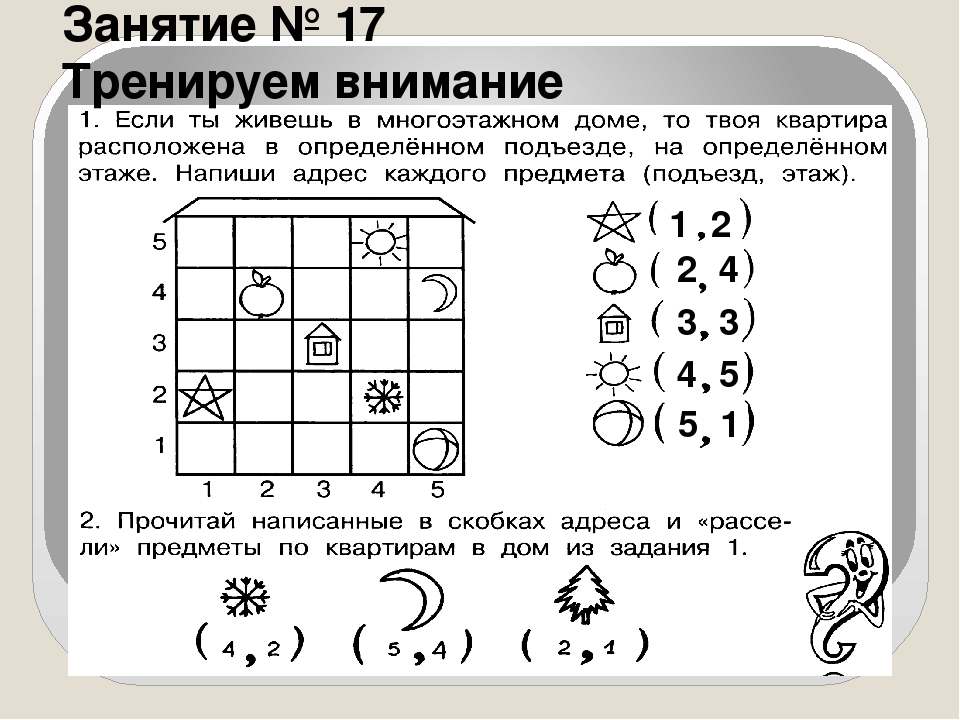
Игровые приёмы используют и в корпоративном образовании, курсы ДПО, школы, вузы и особенно — EdTech-проекты, некоторые из которых перешагнули от геймифицированного обучения к основанному на играх обучения или game-based learning.
Главное, что EdTech перенял у многочисленных стратегий, квестов и бродилок — это принцип game-based learning (GBL). По подсчетам аналитиков, к 2025 году объем рынка решений для GBL составит $28,8 млрд — это один из самых быстрорастущих сегментов во всей образовательной индустрии.
Обучение по принципу GBL отличается от геймифицированных форматов. В таком обучении игра из метода усвоения нового материала превращается в самоцель — но при этом она косвенно развивает необходимые навыки. В GBL-проектах, как и в видеоиграх, обязательно есть роль, хотя персонажа может и не быть, если речь идет, скажем, о симуляторе. Эта роль влияет и на цель: если в геймифицированном обучении в итоге нужно освоить новый материал или получить некий аттестат, то в GBL-игры мы играем, чтобы победить монстров, построить империю или спасти галактику.
Только для решения этой задачи мы должны применить навыки из какой-то предметной области.
Логично, что в game-based learning за счет погружения в вымышленный мир пользователь намного больше вовлекается в процесс. Однако полностью построить обучение — например, весь школьный курс математики или программу по освоению Python — на принципах GBL не получится, поэтому в образовании эксплуатируются отдельные его элементы. Game-based learning — дополнительный инструмент в освоении нового материала, но никак не основной.
GBL может использоваться для развития как предметных навыков, так и метапредметных. В первом случае в игру встраиваются задания, для выполнения которых требуется применить определенные знания — например, в области программирования. Существует множество компьютерных игр для разработчиков, где для перехода на следующий уровень нужно писать код. Одна из наиболее известных — Robocode: пользователь в ней должен управлять армией роботов и сражаться с врагами, используя для своих действий языки Java, Scala и C#.
Обучающие игры применяются и во многих других предметных областях. Так, в этом году на платформе Учи.ру появилась RPG-игра «Магическая математика». По сюжету герой, обычный школьник, приходит в новый класс, где с первого же дня начинают происходить странные вещи: в школе пропадает электричество, учитель дает странное домашнее задание, ведущее к запертой двери, а на следующий день бесследно пропадает. Чтобы открыть дверь и выяснить, что стоит за таинственным исчезновением педагога, игроку нужно решать головоломки, используя знания из курса математики.
Материал из Wiki – Факультет компьютерных наук
Приветствуем Вас на странице факультатива “Неклассические логики”, который прошёл на факультете компьютерных наук в феврале-марте 2020 года.
Курс знакомит с многообразием существующих логических систем. Основное внимание будет уделяться “нестандартным” логикам, тому, как логический способ мышления применяется к решению задач лингвистики, философии и информатики.
Курс направлен на студентов ФКН академических программ бакалавриата “Программная инженерия” и “Прикладная математика и информатика”, но может быть интересен и студентам других программ, интересующихся логикой.
Официальная страница факультатива на сайте ФКН
1. Понятие логики. Логика vs риторика. Формальный язык (на примере исчисления высказываний). Семантика. Система вывода. Корректность. Полнота. Дополнительно: пресуппозиция и импликатура. Постулаты Грайса. Перформативы. Слайды
2. Исчисление предикатов. Арифметика Пеано. Теория множеств. Слайды
3. Модальные логики. Логика контрафактивных условных предложений. Модальность в естественном языке. Слайды
4. Интуиционизм. Темпоральная логика. Динамическая логика. Слайды
5. Эпистемическая логика. Динамическая эпистемическая логика. Синтаксическая динамическая эпистемическая логика. Логика обоснования (justification logic). Слайды
6. Логики, ориентированные на естественный язык.
Формальная семантика. Обобщённые кванторы. Сдвиг типов. Продолжения. Динамическая логика предикатов. Слайды
7. Субструктурные логики. Линейная логика. Категориальные грамматики. Слайды
8. Логики, ориентированные на доказательство корректности компьютерных программ. Системы типов. Логика Хоара. Логика разделения (separation logic). Слайды
Главы 1, 2, 4, 7.1-5.
Русский перевод: Бенджамин Пирс. Типы в языках программирования. Лямбда пресс, 2012.Время занятий: 18:10 – 19:30 по понедельникам.
Предварительный график:
1, 8, 15, 22 февраля; 1, 15, 22, 29 марта.
Итоговая_оценка_за_курс = 0.5*оценка_за_работу_на курсе + 0.5*оценка_за_экзамен_либо_реферат.
Это актуальная формула!
В ходе курса студентам будет предложено одно или несколько заданий по теме курса.
Нужно будет разобраться в новом для себя материале, а также подготовить эссе, основанное на материалах исследовательских работ.
Шкала оценки – десятибалльная. Округление – стандартное арифметическое.
Георгий Бронников – программист, лингвист, разработчик компании JetBrains. georgy.bronnikov собака jetbrains.com
Факультатив проходит при поддержке компании JetBrains.
Программа
кружка «Мир логики»
(Возрастной состав: 7 – 10 лет.
Срок реализации: 4 года)
Составитель: Нигириш С.В.
учитель начальных классов
первой квалификационной
категории
Содержание:
Введение
1. Пояснительная записка
2. Учебно-тематическое планирование занятий
3. Содержание дополнительной образовательной программы
4. Методическое обеспечение дополнительной образовательной программы
5.Список литературы
6. Приложение
Введение
Кто с детских лет занимается математикой,
тот развивает внимание, тренирует свой мозг,
свою волю, воспитывает настойчивость
и упорство в достижении цели.
(А. Маркушевич)
«Что значит владеть математикой? Это есть умение решать задачи, причём не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности». Это слова известного математика Д. Пойа, которые отражают одну из задач, стоящих перед преподавателями: воспитание творческой активности учащихся.
Важнейшим периодом в развитии и формировании человека является обучение его в начальной школе. В это время закладываются основы умственного развития детей, создаются предпосылки для подготовки самостоятельно мыслящего, критично оценивающего свои действия человека, способного сопоставлять, сравнивать, выдвигать несколько способов решения проблемы, оценивать их и выбирать наиболее рациональный, выделять главное и делать обобщенные выводы, применять полученные знания на практике. Необходимым условием достижения таких результатов выступает развитие у ребенка логического мышления как важнейшего фактора, обеспечивающего эффективность его дальнейшего обучения в школе, успешность в профессиональной подготовке и жизни.
Пояснительная записка
Умение мыслить логически, выполнять умозаключения без наглядной опоры, сопоставлять суждения по определенным правилам – необходимое условие успешного усвоения учебного материала. Широкие возможности в этом плане дает кружок “Мир логики”. Данный курс способствует развитию познавательной активности, формирует потребность в самостоятельном приобретении знаний и в дальнейшем индивидуальном обучении. В ходе решения задач на смекалку, головоломок дети учатся планировать свои действия, обдумывать их, догадываться в поисках результата, проявляя при этом творчество. Эта работа активизирует не только мыслительную деятельность ребенка, но и развивает у него качества, необходимые для профессионального мастерства.
Программа математического кружка создана для занятий с учащимися 1-4 классов (дети с высокой учебной мотивацией).
Основная цель программы – всестороннее развитие ребенка, становление самосознания, формирование у него способностей к самоизменению и саморазвитию, интеллектуальное развитие личности.
Достижение этой цели обеспечено посредством решения следующих задач:
1. Пробуждение и развитие устойчивого интереса учащихся к математике.
2. Оптимальное развитие математических способностей у воспитанников и привитие учащимся определенных навыков научно-исследовательского характера.
3. Воспитание высокой культуры математического мышления.
4. Развитие у воспитанников умения самостоятельно и творчески работать с учебной и научно-популярной литературой.
6. Расширение и углубление представлений воспитанников о практическом значении математики.
7. Воспитание у воспитанников чувства коллективизма и умения сочетать индивидуальную работу с коллективной.
развитие математического кругозора, мышления, исследовательских умений учащихся при решении текстовых задач;
формирование представлений о математике как части общечеловеческой культуры;
повышение математической культуры ученика;
воспитание трудолюбия, терпения, настойчивости, инициативы.
Основными педагогическими принципами, обеспечивающими реализацию программы, являются:
• доступность;
• системность;
• научность;
• учет возрастных и индивидуальных особенностей каждого ребенка;
• доброжелательный психологический климат на занятиях;
• личностно-деятельный подход к организации учебно-воспитательного процесса;
• подбор методов занятий соответственно целям и содержанию занятий и эффективности их применения;
• оптимальное сочетание форм деятельности;
Данная программа позволяет воспитанникам ознакомиться со многими интересными вопросами математики на данном этапе обучения, выходящими за рамки школьной программы, расширить целостное представление о проблеме данной науки. Решение математических задач, связанных с логическим мышлением закрепит интерес детей к познавательной деятельности, будет способствовать развитию мыслительных операций и общему интеллектуальному развитию.
Не менее важным фактором реализации данной программы является и стремление развить у воспитанников умений самостоятельно работать, думать, решать творческие задачи, а также совершенствовать навыки аргументации собственной позиции по определенному вопросу.
Программа математического кружка содержит в основном традиционные темы занимательной математики: арифметику, логику, комбинаторику и т.д. Включает в себя всевозможные разнообразные нестандартные виды математических заданий, направленных на развитие математических способностей учащихся, логического нестандартного мышления, творческого подхода к решению учебных задач. Дает возможность воспитанникам работать как под руководством учителя, так и проявить свои способности на занятиях и при самостоятельной работе дома с родителями.
Обучение по программе осуществляется в виде теоретических и практических занятий для учащихся. В ходе занятий ребята выполняют проекты, готовят рефераты, выступления, принимают участия в конкурсных программах.
Основное содержание занятий составляет материал арифметического и геометрического характера. Большая роль отведена решению задач. Задачи рекомендуется решать арифметическим способом по вопросам или с пояснениями, что позволяет отчетливо выявлять логическую схему рассуждения. Поэтому на занятиях математического кружка рассматриваются задачи, формирующие умение логически рассуждать, применять законы логики.
В практике работы кружка возможны следующие формы работы: решение занимательных и комбинаторных задач, конкурсы знатоков, КВНы, игровые занятия, знакомство с научно-популярной литературой, с учением великих математиков, участие в математической олимпиаде, различных математических конкурсах, выпуск математических газет.
Освоение содержания программы кружка способствует интеллектуальному, творческому, эмоциональному развитию учащихся. При реализации содержания программы учитываются возрастные и индивидуальные возможности младших школьников, создаются условия для успешности каждого ребёнка.
Ожидаемые результаты:
По окончании обучения воспитанники должны знать:
• нестандартные методы решения различных математических задач;
• логические приемы, применяемые при решении задач;
• историю развития математической науки, биографии известных ученых-математиков.
По окончании обучения воспитанники должны уметь:
• рассуждать при решении логических задач, задач на смекалку, задач на эрудицию и интуицию;
• систематизировать данные в виде таблиц при решении задач, при составлении математических кроссвордов, шарад и ребусов;
Учебно-тематическое планирование занятий
Первый год обучения
Тема раздела | Общее кол-во часов | В том числе | |
Теоретические | Практические | ||
Пространственные представления | 2 | 1 | 1 |
Закономерности | 2 | 1 | 1 |
Геометрия | 2 | 2 | |
Комбинаторика | 1 | 1 | |
Логика | 4 | 4 | |
Нестандартные задачи | 2 | 2 | |
Математические игры | 5 | 5 | |
Итого | 18 | 3 | 15 |
Второй год обучения
Тема раздела | Общее кол-во часов | В том числе | |
Теоретические | Практические | ||
Закономерности | 2 | 1 | 1 |
Геометрия | 3 | 1 | 2 |
Комбинаторика | 2 | 1 | 1 |
Логика | 5 | 1 | 4 |
Нестандартные задачи | 3 | 3 | |
Математические игры | 3 | 3 | |
Итого | 18 | 4 | 14 |
Третий год обучения
Тема раздела | Общее кол-во часов | В том числе | |
Теоретические | Практические | ||
Закономерности | 2 | 2 | |
Геометрия | 2 | 2 | |
Комбинаторика | 1 | 1 | |
Логика | 4 | 1 | 3 |
Нестандартные задачи | 3 | 2 | 1 |
Математические игры | 6 | 6 | |
Итого | 18 | 6 | 12 |
Четвёртый год обучения
Тема раздела | Общее кол-во часов | В том числе | |
Теоретические | Практические | ||
Многозначные числа | 2 | 2 | |
Геометрия | 2 | 2 | |
Комбинаторика | 3 | 1 | 2 |
Логика | 3 | 3 | |
Нестандартные задачи | 3 | 1 | 2 |
Математические игры | 5 | 5 | |
Итого | 18 | 2 | 16 |
Содержание образовательной программы
Первый год обучения
Пространственные представления Графические диктанты. Взаимное расположение предметов. При изучении данной темы уточняются представления детей о пространственных отношениях «справа-слева», «перед-за», «между», «над-под», «выше-ниже», «дальше-ближе».
Закономерности Выявление закономерности расположения предметов и фигур.
Геометрия Поверхности. Линии. Точки. Луч. Отрезок. Ломаная линия. Замкнутые и незамкнутые ломаные линии. У детей формируются первые представления о кривой и плоской поверхностях, умение проводить на них линии и изображать их на рисунках.
Комбинаторика, логика, нестандартные задачи Задания на развитие памяти, мышления, логики, внимания. Изучение правил шифровки.
Математические игры Задачи-шутки, решение задач на материале сказок.
Второй год обучения
Закономерности Использование ритма при составлении закономерности по форме, размеру, цвету, количеству.
Геометрия Углы. Многоугольники. Многогранники. Применяются сформированные в первом классе представления о линиях, поверхностях и точках для выполнения различных заданий с геометрическими фигурами: кривая, прямая, луч, ломаная. Уточняются представления об угле, многоугольнике; при знакомстве второклассников с многоугольниками используются их представления о поверхности; продолжается работа по формированию умения читать графическую информацию, дифференцировать видимые и невидимые линии.
Комбинаторика, логика, нестандартные задачи Задания на развитие мышления, памяти, логического рассуждения. Решение нетрадиционных задач путём сравнения исходных данных и рассуждений.
Математические игры Правила решения ребусов; разгадывание ребусов на основе знания правил.
Третий год обучения
Закономерности Закономерность расположения чисел; продолжение ряда чисел, на основе закономерности их расположения. Наблюдения над изученными видами закономерностей в ряду чисел, геометрических фигур; сравнение, обобщение, вывод.
Геометрия Кривые и плоские поверхности. Объёмные предметы (призма, пирамида, цилиндр, конус, шар). Окружность. Круг. Продолжается работа, начатая в первом и втором классах. Формируется представление о пересечении фигур на плоскости и в пространстве, умение читать графическую информацию и конструировать геометрические фигуры. Дается представление о круге как сечении шара, о связи круга с окружностью как его границей, о взаимном расположении окружности и круга на плоскости.
Комбинаторика, логика, нестандартные задачи Задания на развитие мышления, памяти, логического рассуждения. Решение задач нетрадиционными способами;
Математические игры Математическая грамматика, викторины, кроссворды, олимпиады.
Четвёртый год обучения
Многозначные числа Упражнения с многозначными числами.
Геометрия Равносоставленные фигуры. Цилиндр. Конус. Шар. (Тела вращения). Пересечение фигур. Продолжается работа по формированию представления о взаимосвязях плоскостных и пространственных фигур. Цилиндр, конус, шар рассматриваются как тела вращения плоской фигуры вокруг оси; устанавливаются соответствия новых геометрических форм с известными детям предметами; учащиеся знакомятся с развертками конуса, цилиндра, усеченного конуса; продолжается работа по формированию умений читать графическую информацию и изображать на плоскости объемные фигуры. Обобщаются представления учащихся о различных геометрических фигурах на плоскости и в пространстве и их изображениях.
Комбинаторика, логика, нестандартные задачи ) Задания на развитие мышления, памяти, логического рассуждения. Решение комбинаторных задач, задач на «просеивание»; истинные и ложные умозаключения. Задачи, связанные со временем.
Математические игры Ребусы, занимательные конкурсы, олимпиады, интеллектуальный марафон.
1 класс
№ п/п | Тема занятий | |||
1. | Организационное занятие. | |||
2. | Цвет, форма, размер, материал. | |||
3. | Выше-ниже, больше-меньше, слева-справа. | |||
4. | Раньше-позже. | |||
5. | Совокупность предметов. | |||
6. | Расположение предметов в пространстве. | |||
7. | Решение задач на развитие пространственных представлений. | |||
8. | Сказочные поезда. | |||
9. | Цепочки. | |||
10. | Последовательность событий. | |||
11. | Шифровка. | |||
12. | Задачи – шутки. | |||
13. | Точка. Прямая. Кривая. | |||
14. | Луч, отрезок. | |||
15. | Угол. Стороны, вершины углов. | |||
16. | Ломаная линия. Замкнутые и незамкнутые ломаные линии. | |||
17. | Математическая викторина. | |||
18. | Решение логических задач. | |||
2 класс
№ п/п | |
1. | Страна Геометрия. |
2. | Преобразование фигур на плоскости. |
3. | Город Четырёхугольников. |
4. | Числовые ребусы. |
5. | Соединение и пересечение фигур. |
6. | Симметрия фигур. |
7. | Логические задачи |
8. | Логический ряд чисел. |
9. | Логические задачи. |
10. | Праздник числа. |
11. | Решение логических задач. |
12. | Нетрадиционные задачи. |
13. | Решение комбинаторных задач |
14. | Познавательные математические цепочки. |
15. | Старинные задачи. |
16. | Задачи, решаемые с конца. |
17. | Примеры с зашифрованным словом. |
18. | Зашифрованные примеры. |
3 класс
№ п/п | Тема занятий |
1. | Поиски закономерностей. |
2. | Нестандартные задачи. |
3. | Задачи в стихах. |
4. | Логические задачи. |
5. | Меры длины. |
6. | Логические задачи. |
7. | Логические задачи. |
8. | Конструирование предметов из геометрических фигур. |
9. | Логические задачи. |
10. | Математический кроссворд |
11. | Задачи в стихах. |
12. | Объём фигур. |
13. | Логические задачи. |
14. | Нестандартные задачи. |
15. | Занимательный диктант. |
16. | Задачи с геометрическим содержанием. |
17. | Задачи в стихах. |
18. | Логические задачи. |
4 класс
№ п/п | Тема занятий |
1. | Упражнения с многозначными числами |
2. | Числа-великаны и числа малютки. |
3. | Числовые ребусы. |
4. | Загадки- смекалки. |
5. | Решение комбинаторных задач |
6. | Арифметические задачи, требующие особого решения. |
7. | Математические ребусы. |
8. | Геометрия в пространстве. |
9. | Кривые и плоские поверхности. |
10. | Задачи, связанные с прямоугольным параллелепипедом. |
11. | Решение комбинаторных задач |
12. | Решение математических задач с помощью рассуждений. |
13. | Математическая викторина. |
14. | Решение комбинаторных задач |
15. | Конкурс знатоков |
16. | Проектная деятельность «Великие математики» |
17. | Интеллектуальный марафон. |
18. | Задачи, связанные со временем. |
Список литературы
Агаркова Н.В. Нескучная математика. 1 – 4 классы. Занимательная математика. Волгоград: Учитель, 2009
Белякова О. И. Занятия математического кружка. 3 – 4 классы. – Волгоград: Учитель, 2011.
Дьячкова Г.Т. Математика: 2 – 4 классы: олимпиадные задания. Волгоград: Учитель, 2007
Евтюкова Т. Поиграем в эрудитов? Сибирское университетское издательство, 2009
Зак. А.З. Интеллектика. 3 класс. Тетрадь для развития мыслительных способностей. Интеллект-центр, 2010.
Малофеева Н. Развиваем интеллект. Лучшие логические игры. Эксмо, 2010.
Мищенкова Л.В. 50 развивающих занятий с младшими школьниками. Феникс. Школа развития, 2012.
Интернет – ресурсы:
Единая коллекция цифровых образовательных ресурсов http://school- collection.edu.ru /
Интернет учителю начальной школы http://mmc.rightside.ru/links/66- nachalka.html
Педагогическая библиотека http://www.pedlib.ru
Математический бой. Цель: Способствовать проявлению индивидуальных способностей учащихся, активизации их познавательной деятельности. Задачи: Уметь применять полученные на уроках знания в нестандартной ситуации; Развивать математическое мышление, внимание, память, воображение; Воспитывать чувство взаимопомощи, умение работать в сотрудничестве; Прививать интерес к математике. Оборудование: Девиз урока: Одна голова – хорошо, а две лучше. Дерево оценивания, ребусы, маршрутный лист у каждого ребёнка. Ход урока: 1. Орг.момент Мы умные – мы – дружные; Мы – внимательные, мы – старательные; Мы отлично учимся, всё у нас получится. 2. Вступительное слово учителя. Учитель: Математика самая интересная и занимательная наука в мире. С древнейших времен известно, что математика учит нас мыслить, логически рассуждать. Кто с детских лет занимается математикой, тот развивает свой ум, внимание, воспитывает волю и настойчивость. А эти качества нужны всем: и врачу, и артисту, и учителю, и художнику. 3. Сообщение цели и задач урока. Чему мы учились на уроках математической логики? Отгадывать ребусы, головоломки, отвечать на хитрые вопросы, логические ряды, магические квадраты, задачи в стихах. Какие задачи мы для себя поставим? РАССУЖДАТЬ АНАЛИЗИРОВАТЬ; ДОКАЗЫВАТЬ; А теперь определим формулу успеха: СТАРАНИЕ + ВНИМАНИЕ + СООБРАЗИТЕЛЬНОСТЬ = УСПЕХ А ЧТОБЫ закрепить наш УСПЕХ, мы будем фиксировать свои результаты на маршрутном листе. Каждое выполненное задание будем отмечать + или , если задание очень трудное, то ставим знак ?, а если лёгкое ! рядом со знаком. Итак, мы начинаем Математический бой! Вы принимаете мои условия? Тогда подписываем договор! Дети пишут свою фамилию и имя. 4. Основная часть 1. А вот и первое испытание: Чтобы проверить вашу готовность к работе, я прочитаю стихотворение, а вы внимательно слушайте и запоминайте . А ответ запишите рядом с цифрой 1. Василиса в узелочек, завязала свой платочек, А в платочке спрятала зёрнышко от яблока. Чтоб надёжным был секрет, уложила всё в конверт. А потом конверт в коробку, Вася бросила так ловко. Но, в коробке мало толку, место ей на верхней полке.! И теперь никто на свете не узнает о секрете. Что спрятала в конверт Василиса? (Зёрнышко от яблока) А раз мы такие внимательные, то легко справитесь и со следующим заданием 2. Шифрованное письмо: У вас зашифрована фраза, определённой букве соответствует цифра. А В Г Д Е Л Н О Р У Х Ч Ш 1 2 3 4 5 6 7 8 9 10 11 12 13 ОДНА ГОЛОВА ХОРОШО, А ДВЕ ЛУЧШЕ.( девиз урока) 8 4 7 1 3 8 6 8 2 1 11 8 9 8 13 8 1 4 2 5 6 10 12 13 5 Вместе работать легче? Тогда за работу! 3. Работа в парах: Логический ряд. 2, А, 4, Б, 6, В, …, …, …, … . Как называются числа которые вставили? 15, 8, 13, 6, 11, …, …, …, … . (четные, нечетные). И с этим заданием вы справились. Оцените свой труд. А вы умеете отгадывать ребусы? 4. Ребусы. Работа в группе Время выполнения: 2минуты Кто больше разгадает ребусов. Отметить +/ 5. Ребус Физ минутка « Дракончик» ПЕРЕМЕНА Ребус: 6. Головоломка: КВАДРАТ Индивидуально и у доски. 7. Логическая задача. Петя Задачкин задумал число Х и к нему прибавил 12. Сумма получилась на 1 меньше чем 16. Какое число задумал Петя? Х + 12 = 15 Х = 3 8. Рефлексия: Мы справились со всеми заданиями. И нам открылось дерево Яблонька. Какие плоды растут на яблоне? Давайте вспомним, какие задания мы выполняли, что было интересно, легко, что далось не просто, пришлось подумать. В своём листе подчеркните нужную фразу: Было интересно! Было трудно, но я справился! Было очень трудно! Если вам было легко и со всеми заданиями справились, то на яблоньку поместите плод – яблоко, трудно – цветок. Я – принимаю бой! ______________________ 1. 2. 1 А Загадка: __________________________________ Шифрованное письмо: 2 В 3 Г 4 Д 5 Е 6 Л 7 Н 8 О 9 Р 10 У 12 13 11 Х Ч Ш 8 4 7 1 3 8 6 8 2 1 11 8 9 8 13 8 1 4 2 5 6 10 12 13 5 ____________________________________________________________ 3.Логический ряд: работа в парах 2, А, 4, Б, 6, В, …, …, …, … . 15, 8, 13, 6, 11, …, …, …, … . 4.Ребус ________________________________________________________ 5.Головоломка Убери 4 палочки, чтобы осталось 5 квадратов 6.Логическая задача. Петя Задачкин задумал число Х и к нему прибавил 12. Сумма получилась на 1 меньше чем 16. Какое число задумал Петя?______________ Рефлексия: Было интересно! Было трудно, но я справился! Было очень трудно! Самоанализ урока Факультатив « Математическая логика» Тип : Урок игра Вид : Закрепление полученных знаний Цель: Способствовать проявлению индивидуальных способностей учащихся, активизации их познавательной деятельности. Задачи: Уметь применять полученные на уроках знания в нестандартной ситуации; Развивать математическое мышление, внимание, память, воображение; Воспитывать чувство взаимопомощи, умение работать в сотрудничестве; Прививать интерес к математике. Оборудование: Девиз урока: Одна голова – хорошо, а две лучше. Дерево оценивания, ребусы, маршрутный лист у каждого ребёнка. В классе 29 учащихся, 14 девочек и 15 мальчиков. Класс со средним уровнем обученности, разноуровневый, уровень мотивации от среднего до высокого. Планировала урок с учётом возрастных особенностей учащихся, по принципу от простого к сложному. Данный урок 18по счету по учебному плану. На предыдущих уроках ребята учились разгадывать ребусы, головоломки, логические ряды, решали логические задачи. Все запланированное на уроке выполнили, ребята были активны, выполняли задания по силе своих возможностей. На уроке проводилась индивидуальная, парная и групповая форма работы. В начале урока учащиеся в листах самооценки на лестнице знаний оценили свои возможности и определили, справятся ли они с предложенными заданиями. В маршрутных листах учащиеся фиксировали степень выполнения каждой работы: +! Легко; +? – Подумал и решил; ? Трудно. В конце урока проведена Рефлексия. Дети сравнили свои ожидания с реальными результатами, и поняли, что некоторые ожидали, будет легко, а оказалось, столкнулись с определёнными трудностями. И итогом урока было дерево успеха: Кому было интересно и легко на дерево поместил спелое яблоко. А кому было трудно – цветок.
Курс «Логика и критическое мышление», рассчитанный на один семестр, направлен на то, чтобы помочь учащимся познакомиться с ключевыми аспектами здравого мышления. Курс включает еженедельные чтения, записанные лекции и домашние задания; ежемесячные экзамены и завершаются короткой дипломной работой.
Прежде чем обсуждать затронутые темы, многие ученики и родители оценят краткое введение в логику и критическое мышление.
Логика – это частично понимание прочитанного и частично математика, но более практичное и увлекательное (если вы уже не любитель математики).
Подобно тому, как мы решаем математические уравнения, мы анализируем аргументы с помощью логики, чтобы определить, приводит ли данная информация к хорошему выводу.
Нам необходимы навыки критического мышления, чтобы помочь нам интерпретировать информацию, которую мы читаем в новостях или слышим в наших повседневных разговорах. Критическое мышление помогает нам найти логику среди риторики, предвзятости, неопределенности и других заблуждений, которые могут затруднять понимание или затруднять рассуждение.
Почти половина курса посвящена аспектам критического мышления, таким как
Наряду с этими аспектами студенты изучают такие аспекты логики, как
В ходе этого процесса мы будем читать и обсуждать короткие христианские чтения по логике. Мы подходим к логике как к важной структуре в творении Бога. Логика позволяет рассуждать, что помогает нам понимать мир и хорошо функционировать в нем.
Слово Бога ясно показывает, что Он взаимодействует с нами как мыслящими существами. Поэтому хорошо думать особенно важно для христиан.
Заявление об ограничении ответственности: Обратите внимание, что мы будем проводить время в классе, анализируя спорные темы и реальные дебаты.Мы не уклоняемся от этих тем, поскольку студентам важно научиться интерпретировать идеи, которые они услышат в новостях и в повседневных разговорах. Тем не менее, мы делаем все возможное, чтобы рассматривать все темы с учетом библейских взглядов на студентов.
Логические рассуждения необходимы в большинстве областей человеческого исследования. Дисциплина логики рассматривает логическое рассуждение как объект изучения. Логика была одной из основных ветвей философии со времен Аристотеля; он произвел революцию в основах математики в 20 веке; и его назвали «вычислением информатики», имеющим приложения во многих областях.Логика также сыграла важную роль в исследовании языка и разума как основа формальной семантики в лингвистике и автоматизированных рассуждений в искусственном интеллекте. Благодаря этим междисциплинарным связям, логика служит мостом между гуманитарными науками и областями STEM (наука, технология, инженерия и математика). Изучение логики улучшает способности студентов рассуждать и строго аргументировать, читать и писать аналитически, различать закономерности среди сложности и понимать абстрактные структуры.Второстепенная логика (предлагается на факультете философии) состоит из трех основных курсов по символической логике, которые могут проходить параллельно в рамках философии или математики, плюс выбор из трех факультативов для старших классов из ряда курсов философии, математики, лингвистики. , и компьютерные науки.
Посетить веб-сайт отдела
Logic Minor в Беркли состоит из трех основных курсов по символической логике, которые могут проходить параллельно в рамках философии или математики, плюс выбор из трех факультативов для старших классов из списка курсов по философии, математике, лингвистике , и компьютерные науки.
Все несовершеннолетние должны быть заявлены не позднее, чем за один семестр до ожидаемого окончания срока обучения студента (EGT). Если семестр перед EGT выпадает на осень или весну, крайний срок – последний день недели RRR. Если семестр перед EGT – летний, крайний срок – последняя пятница летних сессий. Чтобы объявить несовершеннолетнего, свяжитесь с консультантом отдела для получения информации о требованиях и процессе декларирования.
Пожалуйста, обратите внимание: согласно политике Колледжа литературы и наук в вашу второстепенную и основную программу может быть включено не более одного курса высшего образования.
+ Указывает, что этот преподаватель является лауреатом награды «Выдающиеся преподаватели».
Уэсли Х. Холлидей, Доцент . Философия, логика.
Профиль исследования
Джон Макфарлейн, Профессор . Античная философия, философская логика, философия языка, эпистемология.
Профиль исследования
Паоло Манкосу, Профессор . Философия, философия математики и ее история, философия логики, математическая логика.
Профиль исследования
Антонио Монтальбан, Профессор . Математическая логика.
Профиль исследования
Стюарт Рассел, Профессор . Искусственный интеллект, вычислительная биология, алгоритмы, машинное обучение, принятие решений в реальном времени, вероятностные рассуждения.
Профиль исследования
Томас Скэнлон, Профессор . Математика, теория моделей, приложения к теории чисел.
Профиль исследования
Санджит Сешиа, Профессор . Автоматизация электронного проектирования, теория, компьютерная безопасность, программный анализ, надежные вычисления, вычислительная логика, формальные методы.
Профиль исследования
Пьер Симон, Доцент .
Теодор А. Сламан, Профессор . Математика, теория рекурсии.
Профиль исследования
Ханс Слуга, Профессор . Политическая философия, новейшая европейская философия, история аналитической философии, Фреге, Витгенштейн, Фуко.
Профиль исследования
Джон Стил, Профессор . Математика, описательная теория множеств, теория множеств, тонкая структура.
Профиль исследования
Умеш Вазирани, Профессор . Квантовые вычисления, гамильтонова сложность, анализ алгоритмов.
Профиль исследования
Сет Ялчин, Профессор . Философия языка, логика, философия разума, когнитивная наука, семантика, метафизика.
Профиль исследования
Джон У. Аддисон, Почетный профессор . Математика, теория определимости, описательная теория множеств, теория моделей, теория рекурсивных функций.
Профиль исследования
Роберт Андерсон, Почетный профессор . Финансы, теория вероятностей, математическая экономика, нестандартный анализ.
Профиль исследования
Чарльз С. Чихара, Почетный профессор .
Код Алана Д., Почетный профессор .
Лео А. Харрингтон, Почетный профессор . Математика, теория моделей, теория рекурсии, теория множеств.
Профиль исследования
+ Ричард Карп, Почетный профессор . Вычислительная молекулярная биология, геномика, молекулы ДНК, структура генетических регуляторных сетей, комбинаторные и статистические методы.
Профиль исследования
Пол Кей, Почетный профессор . Лингвистика, социолингвистика, лингвистическая антропология, прагматика, синтаксис, семантика, лексика, грамматика, обозначение цветов, лексическая семантика, грамматические вариации, межъязыковое обозначение цветов, кодирование контекстных отношений в правилах грамматики.
Профиль исследования
Ральф Н. Маккензи, Почетный профессор . Математика, логика, универсальная алгебра, общая алгебра, теория решеток.
Профиль исследования
У. Хью Вудин, Почетный профессор . Математика, теория множеств, большие кардиналы.
Профиль исследования
Лотфи А. Заде, Почетный профессор . Искусственный интеллект, лингвистика, теория управления, логика, нечеткие множества, анализ решений, нейронные сети экспертных систем, мягкие вычисления, вычисления со словами, вычислительная теория восприятия и точный естественный язык.
Профиль исследования
PHI 2010.Введение в философию (3). Введение в некоторые из центральных проблем философии. Студенты также узнают, как строить и критиковать аргументы и развивать свои собственные философские позиции.
PHI, 2016. Философия через фильм (3). Этот курс представляет собой введение в широкий круг философских тем с использованием фильма в качестве средства обсуждения. Философские темы могут включать вопросы этики, философии разума, метафизики, эпистемологии, философии религии и / или политической философии.Различные фильмы используются для того, чтобы поднять важные философские вопросы и помочь в понимании основных философских текстов, которые пытаются ответить на эти вопросы.
PHI 2100. Рассуждение и критическое мышление (3). Вводный курс логики, предназначенный для того, чтобы дать студентам понимание и практику использования аргументов для обоснования выводов и решений. Курс подчеркивает приобретение навыков, необходимых для составления четких, убедительных аргументов, и особенно полезен для тех, кто планирует продолжить обучение в таких областях, как право или бизнес.
PHI 2620. Экологическая этика (3). Исследование прошлых и настоящих экологических проблем и их влияния на современное общество. Также анализируется историческое развитие экологических перспектив и этических теорий, которые были созданы этими подходами.
PHI 2630. Этические вопросы и выбор жизни (3). Курс, основанный на этических теориях для изучения основных этических проблем, с которыми человек сталкивается при принятии решений о видах деятельности, которыми он должен заниматься, и о том, какой образ жизни вести.Будут изучены такие вопросы, как вопросы жизни и смерти (например, аборты, эвтаназия, права животных) и социальной справедливости (например, дискриминация, ответственность перед будущими поколениями).
PHI 2635. Биоэтика (3). Этот курс представляет собой изучение философских основ биоэтической теории и исследование острых вопросов современной биоэтики с упором на обсуждение расы, пола и уязвимых групп населения (например, бедных, иммигрантов).Мы будем использовать инструменты этической теории, философского анализа и аналитического письма для изучения ряда моральных проблем, возникающих в сфере здравоохранения, включая справедливость в здравоохранении, эксперименты и исследования на людях, репродуктивные технологии, старение, донорство органов и эвтаназию. На протяжении всего курса мы будем изучать предположения о правах, людях и этических принципах, которые используются при принятии медицинских решений.
IDS 3358 Создание аргумента: символическая логика и формы правильного рассуждения (3). Изучение основ современной символической логики (исчисления высказываний и предикатов) с особым вниманием к оценке символизированных аргументов с использованием методов естественной дедукции. Темы включают валидность, обоснованность, доказательство, символизацию, таблицы истинности, деревья истинности, а также функциональный и количественный вывод истинности.
PHI 3162. Логика и закон (3). Этот курс представляет собой углубленное изучение применения логики в правовом контексте, с особым упором на методы индуктивного мышления, такие как рассуждения по аналогии и причинно-следственные связи.Курс фокусируется на построении и представлении письменных аргументов, а также на оценке аргументов как исторических, так и современных юридических решений.
PHI 3220. Введение в философию языка (3). Исследование основных философских вкладов в понимание языка и его функций в общении. Обсуждение концепций значения, истины, ссылки, понимания и интерпретации. Чтения включают классику философии ХХ века.
PHI 3300. Знание и вера (3). Критический анализ современных теорий об основах человеческого знания: что следует считать знанием; как мы это получаем; роли уверенности, сомнения и скептицизма; и средства, с помощью которых мы могли бы максимизировать его.
PHI 3320. Философия разума (3). Анализ центральных вопросов философии разума. Темы могут включать: проблема разума и тела, единство разума, природа сознания, искусственный интеллект и свобода воли.
PHI 3330. Свобода воли (3). Свобода воли важна для нас по разным причинам. Например, нас может волновать свобода воли, потому что мы хотим контролировать свои действия. Мы также можем заботиться о свободе воли, потому что мы считаем, что люди не несут моральной ответственности за свои действия, если у них нет свободы воли. Мы можем подумать, что без свободы воли никто не заслуживает похвалы, порицания, награды или наказания за все, что он сделал. Этот курс будет охватывать ряд различных философских позиций о свободе воли и моральной ответственности, а также некоторые аргументы за и против этих позиций.
PHI 3400. История и философия науки (3). Пристальный взгляд на некоторые из важнейших философских проблем наук по мере их развития на протяжении всей истории, от Аристотеля до Галилея, Пастера и Эйнштейна, включая то, какие методы считаются научными, а также рассмотрение того, как наука изменила мир и роль ценностей.
PHI 3452. Философия биологии (3) . Этот курс знакомит с основными дискуссиями в философии биологии, включая те, что связаны с расширенным эволюционным синтезом, законами эволюции, единицами отбора, адаптационизмом, спецификацией и т. Д.Этот курс объединяет биологические науки и инструменты аналитической философии, чтобы лучше понять некоторые теоретические проблемы биологии.
PHI 3641. Деловая этика (3). Определение и обсуждение оправданных решений моральных и этических проблем, возникающих при ведении деловых и экономических операций. Рассмотрены международные деловые условия и этические проблемы, возникающие из-за необходимости разрабатывать продукты и услуги, которые нравятся различным национальным и мировым группам населения.
PHI 3670. Этическая теория (3). Исследование природы морали и морального рассуждения посредством критического анализа работ классических и современных теоретиков этики, направленных на ответы на вопросы: «Что такое хорошо?» и “Что мне делать?”
PHI 3700. Философия религии (3). Анализ основных вопросов философии религии. Темы могут включать рациональность религиозных убеждений, веры, религиозного опыта, религиозного языка, зла и отношения между религией и моралью.Также предлагается Департаментом религии.
PHI 3800. Философия искусств (3). Введение в основные вопросы философии искусства и эстетики. Темы могут включать природу красоты, природу искусства, реализм в живописи, интерпретацию в литературе, природу танца и выразительность в музыке. Литература включает как исторические, так и современные источники.
PHI 3881. Философия музыки (3). Введение в современную литературу по философии музыки.Задаваемые вопросы включают: Что такое музыка? Выражает ли музыка эмоции? Как оценивать музыку? Как «понять» музыку? Почему кросс-культурное понимание музыки может быть трудным? Что представляет собой аутентичный спектакль?
PHI 3882. Философия в литературе (3). Исследование того, как метафизические и моральные идеи функционируют в структуре избранных романов в пьесах.
ФИ 3930р. Избранные темы (1-3). (Только для класса S / U). Можно повторять максимум до трех часов в семестр.
PHI 4134. Современная логика I (3). Предварительное условие: IDS 3358 или эквивалент или разрешение преподавателя. Промежуточный курс современной символической логики с особым вниманием к семантической оценке символизируемых аргументов. Темы включают схемы и интерпретацию, модели, выполнимость, нормальные формы, выразительную полноту, процедуры доказательства, металогические законы, а также теоремы о разумности и полноте.
PHI 4137. Современная логика II (3). Необходимое условие: PHI 4134.Продвинутый курс современной символической логики. Обсуждаемые темы включают теорему компактности, логику тождества, имен и описаний, логику второго порядка, теорию типов, наследственность, определение натурального числа Фреге-Рассела и результаты Геделя о неполноте.
PHI 4500. Метафизика (3). Критическое рассмотрение недавних философских работ с различных точек зрения на вопрос о том, что существует; например, материя, разум, время, пространство, универсальные свойства, причины и сущности.
PHI 4905r. Направленное индивидуальное исследование (1-3). Можно повторять максимум шесть часов в семестр.
PHI 4912r. Работа с отличием (3). Можно повторять максимум до двенадцати часов в семестр.
PHI 4930r. Философские проблемы (3). Изучение избранных философских проблем с продвинутой точки зрения. Может повторяться максимум девять часов в семестр.
PHI 4938r. Семинар для майоров (3). Семинар с переменным содержанием для профильных специалистов для углубленной работы по выбранным философским темам / областям и практики написания содержательной философской работы.Может быть повторен один раз с разрешения преподавателя максимум до шести часов в семестр.
PHI 4999r. Учебник по философии (1-3). Критическое прочтение и обсуждение важных классических и современных философских текстов. Переменный контент. Переменный кредит: от одного до двух семестровых часов на курс чтения; два-три семестровых часа для курса чтения с основательным письмом. Повторяется с разрешения преподавателя максимум до двенадцати семестровых часов.
ПНХ 3061.Философия Средневековья и Возрождения (3). Обзор западной философии с третьего по шестнадцатый век, начиная с работ христианских, еврейских и арабских философов, а затем обращаясь к расцвету гуманизма, индивидуализма и науки.
PHH 3130. Платон и его предшественники (3). Древнегреческая философия от ее истоков до работ одного из величайших практиков. Задаваемые вопросы включают: Что там? Что я могу об этом знать? Что я должен делать?
ПНХ 3140.Аристотель Августину (3). Философия от «Учителя тех, кто знал» (Аристотель) до конца античного мира и господства христианства. Темы включают: устройство мирового порядка, Бог, место человека.
PHH 3400. Современная философия (3). Критическое исследование теорий западных философов 17-18 веков посредством тщательного изучения репрезентативных текстов как эмпирических, так и рационалистических традиций.
ТНХ 3500.Философия XIX века (3). Исследование разнообразных стилей, идей и систем таких философов, как Гегель, Кьеркегор, Шопенгауэр, Маркс, Милль, Брэдли и Ницше.
PHH 3700р. Американская философия (3). Исследование основных тенденций в американской философии от Джонатана Эдвардса до американского идеализма 19 и 20 веков и прагматического движения с акцентом на Пирса, Джеймса и Дьюи. Может быть повторен один раз с разрешения преподавателя максимум шесть семестровых часов.
PHH 4600р. Современная философия (3). Основные современные философские движения исследуются через избранных центральных представителей. Среди рассмотренных могут быть Фреге и его предшественники, Рассел и Мур, ранний Витгенштейн, логические позитивисты и их преемники, Гуссерль и его феноменология, Хайдеггер, Сартр, позднее Витгенштейн и его преемники. Может повторяться с разрешения преподавателя максимум девять часов в семестр.
ПНМ 2121.Философия расы, класса и пола (3). Концентрация на современных философских обсуждениях расы, класса и пола. Темы включают анализ ключевых институтов (например, работа, экономика, семья, образование) и социальных вопросов (например, идентичность, сексуальность, насилие и социальные изменения).
PHM 2300. Введение в политическую философию (3). Введение в основные вопросы политической философии: обоснование политической власти, роль закона, политическое обязательство, неоколониализм, неповиновение, революция, права, соответствующие цели правительства, модели распределения и справедливость.
PHM 3020. Философия секса (3). Этот курс представляет собой исследование современных философских дебатов о сексе и сексуальных отношениях. Темы включают, помимо прочего, определение пола, различие между «нормальным» и «ненормальным» сексом, сексуальную эксплуатацию и объективацию, сексуальное согласие, взаимосвязь между сексом и смыслом жизни и природу романтической любви.
PHM 3123. Философия феминизма (3). Всесторонний обзор наиболее важных школ мысли и проблем феминистской философии с акцентом на феминистскую политику и этику.Обсуждаются либеральный, социалистический, марксистский и радикальный феминизм и их различные взгляды на равенство и подчинение. Проанализирована критика ставших традиционными теорий со стороны цветных женщин и теоретиков “различия”. Также рассматриваются проблемы, вызывающие особую озабоченность у феминисток: семья, сексуальность, профессиональная свобода, домогательства, изнасилования, порнография и домашнее насилие.
PHM 3331r. Современная политическая мысль (3). Основные политические идеи современного мира, подчеркнутые в исследованиях избранных политических теоретиков, таких как Макиавелли, Гоббс, Локк, Руссо, Юм, Берк, Гегель, Маркс, Энгельс, Бентам, Милль, Джефферсон, Мэдисон, Ленин и Муссолини.Может повторяться максимум девять часов в семестр. Также предлагается кафедрой политологии.
PHM 3351. Философия прав человека (3). Этот курс представляет собой обзор философского обсуждения прав человека и моральных и политических вопросов, возникающих в результате их нарушений. Мы исследуем философские основы заявлений о правах человека, а также о правах человека женщин, политическом зле и массовых злодеяниях. Мы анализируем вопросы справедливости и прощения в контексте социального исцеления и демократизации.
PHM 3400. Философия права (3). Всесторонний обзор наиболее важных школ мысли, традиционных проблем и текущих вопросов англо-американской философии права. Основными обсуждаемыми теориями являются естественное право, позитивизм, реализм (включая движение за право и экономику) и критические юридические исследования (включая теорию расы и гендера). Также исследуются различные взгляды на толкование закона и роль судебной власти в американской политике. Включает анализ юридических дел и рассмотрение таких вопросов, как справедливость, равенство, свобода, неприкосновенность частной жизни и наказание.
PHM 4340р. Современная политическая мысль (3). Исследование ряда вопросов, направления или школы мысли в современной политической философии. Может повторяться максимум девять часов в семестр. Также предлагается кафедрой политологии.
PHP 3510. Введение в марксистскую философию (3). Критический обзор предпосылок и тезисов марксизма относительно понимания истории, экономических реалий, политической борьбы и идеологий, содержащихся в основных трудах его основателей.
PHI 3786r. Экзистенциализм (3). Введение в экзистенциальную философию посредством подробного и критического анализа избранных основных работ в этой области с особым вниманием к Хайдеггеру и / или Сартру. Может повторяться максимум девять часов в семестр.
PHP 4930р. Исследования основных философов (3). Подробное исследование крупного философа (например, Платона, Аристотеля, Канта и т. Д.) Или философской школы (например, стоиков, марксистов). Может повторяться максимум девять часов в семестр.
IFS 2031. Кто такой человек? Культура, гендер и права человека (3). Язык прав человека сформировал международный политический дискурс после окончания Второй мировой войны. Но кто считается человеком? В 1979 году международное сообщество впервые приняло Конвенцию против всех форм дискриминации в отношении женщин, которая неофициально считается международным биллем о правах женщин. В 1995 году Пекинская декларация особо признала права женщин как права человека и гендерное равенство как предмет серьезной международной озабоченности, который должен рассматриваться как отвечающий всеобщим интересам.Целью многих международных документов тогда и с тех пор, а также анализа глобального гендерного неравенства были в первую очередь аргументы, исходящие из обычаев и традиций, как ключевых источников, формирующих теорию и практику гендерной жизни женщин во всем мире. Не все обращения к обычаям и традициям сами по себе проблематичны. Тем не менее, некоторые из них одновременно проблематичны и являются предметом оспаривания универсалистскими и культурными релятивистами в отношении прав человека. В этом курсе мы исследуем допущения, лежащие в основе этих аргументов, и оценим призывы к «культуре» по существу.В частности, мы обсудим апелляции к обычаям и традициям, включая религиозные традиции, которые часто используются для изоляции групп женщин и девочек от внутренней и международной защиты прав человека. Мы рассмотрим глобальное систематическое явление насилия в отношении женщин в мирное и военное время, глобальную систему торговли женщинами и девочками и такие «культурные» обычаи, как калечащие операции на половых органах и детские браки. Наконец, мы обсудим вопросы, которые по-разному влияют на жизнь женщин в худшую сторону, как в случае с женщинами-беженками, или в лучшую сторону, как на пути к свободе через личное и экономическое развитие.
IFS 2047. Философия и кино (3). Этот семинар основан на примерно пятнадцати великих фильмах 20-го века, используя их как средство для исследования важных философских вопросов о природе реальности, смысле жизни, правильном моральном образе действий, корнях великого искусства и намного больше. Каждую неделю мы будем смотреть один фильм с последующим обсуждением, а затем каждый студент напишет короткое (500 слов) эссе о фильме, его философском значении и важности.Эссе будут оцениваться незамедлительно, и студентам будет предоставлена обратная связь. Предварительный список включает «Шейн», «Некоторым нравится погорячее», «Триумф воли», «Искатели», «Район 9», «Баллада о солдате», «Седьмая печать», «Страсть Жанны». д’Арк »,« Bell de Jour »,« Четыреста ударов »,« Великая иллюзия »и другие. Нет текста и нет выпускного экзамена. Оценки будут основываться на успеваемости в классе и письменной работе.
IFS 2048. Мир без Бога? (3). В этом курсе рассматриваются три основных вопроса: (1) Можем ли мы объяснить существование нашей Земли и Вселенной в целом, не обращаясь к Богу? (2) Может ли существовать объективный моральный кодекс, которому все мы должны следовать, даже если Бога нет? (3) Можем ли мы иметь духовное или религиозное отношение к миру без веры в Бога? До недавнего времени большинство людей считало, что ответ на каждый из этих вопросов был отрицательным.Но эти ответы открыты для сомнений. Ученые заявили, что мы можем получить полное и удовлетворительное объяснение существования и природы всего, не обращаясь к разумному замыслу. Философы морали утверждали, что добро и зло полностью независимы от воли Бога. Действительно, некоторые думали, что религия задерживает этическое развитие и понимание. Наконец, что, пожалуй, наиболее интригующе, многие мыслители теперь предполагают, что агностики и атеисты могут иметь религиозное отношение трепета и благоговения ко Вселенной и находить жизнь полностью осмысленной без какой-либо веры в сверхъестественных существ.
IFS 2065. Природа человека: современные и современные перспективы (3). Какую форму принимает правильно прожитая жизнь? Это основной вопрос, с которым мы все сталкиваемся. Сократ придерживался особого подхода к этому вопросу, и с тех пор философы занимаются им: чтобы знать, как нам жить, нам нужно знать, кто мы есть. Знание того, кем мы являемся, говорит нам, какой образ жизни подходит для нас. Этот курс исследует и оценивает описания человеческой природы, которые ключевые исторически влиятельные философы дали на этот вопрос, а также способы, которыми их ответы отражаются в современных дебатах о том, кто мы есть.
IFS 2079. Девочки-фантазии: философские исследования женщин и девочек в научной фантастике и фэнтези (3). «Человек не рождается, но становится женщиной». Симона де Бовуар. Представления женщин и девочек в популярной культуре формируют общее представление о женственности, девичестве, красоте и сексуальности. В течение семестра мы будем использовать традиционные философские тексты, а также нетрадиционные материалы, такие как фильмы, литература, телевидение и комиксы, для изучения вопросов о женской природе, девичестве, красоте, насилии, угнетении и сексуальной активности.
IFS 2106. Познай себя: философское исследование самопознания (3). Это курс о самопознании, а именно о том, что значит «познать себя» и что отличает знание о себе от знаний других видов. Мы прочитаем ряд философских и литературных работ, в которых исследуются эти вопросы, а студенты напишут работы и подготовят творческие работы, чтобы продемонстрировать свое собственное мнение о них.
IFS 3130. Создание аргумента: символическая логика и формы правильного рассуждения (3). Почему одни аргументы хороши, а другие – плохи? Как отличить? В этом курсе вы ответите на эти вопросы и тем самым улучшите свою способность различать хорошие и плохие рассуждения, критически относиться к любому предмету и приводить убедительные аргументы по этому поводу.
Вернуться к философии и религии | Указатель курсов
1301 ФИЛОСОФИЯ ДЛЯ ЖИЗНИ Базовый курс УЦА, удовлетворяющий трехчасовым требованиям по запросу и анализу в качестве факультатива по гуманитарным дисциплинам.Развивает базовые навыки критического мышления, уделяя особое внимание разъяснению личных ценностей, основных взглядов на человеческую природу и вопросов философской мысли. Сочетает в себе лекционный и дискуссионный методы. [АКТЫ: PHIL1103]
1330 МИРОВЫЕ ФИЛОСОФИИ Основной факультатив УЦА, отвечающий требованиям разнообразия мировых культур. Развивает базовые навыки критического мышления, подчеркивая глобальный характер философствования и прояснение личных и социальных ценностей посредством межкультурного понимания.Сочетает в себе лекционный и дискуссионный методы.
1373 FYS: HUMANITIES FYS (семинар первого года) по гуманитарным наукам предоставляет студентам небольшую классную среду, предназначенную для развития сообщества, развития навыков, необходимых для успеха, и повышения важности письменного и устного общения. Темы будут отличаться в зависимости от преподавателя.
1375 FYS: РАЗНООБРАЗИЕ В МИРОВЫХ КУЛЬТУРАХ Этот курс представляет собой небольшую классную среду для учащихся, предназначенную для развития сообщества и осознания разнообразия человеческого опыта, а также для усиления важности критического мышления, а также устного и письменного общения.
2300 СУЩЕСТВУЮЩИЕ ПРОБЛЕМЫ В ФИЛОСОФИИ Факультативный курс для студентов специальностей и несовершеннолетних по философии и религиоведению. Критическое вводное исследование экзистенциальных проблем философии. Для студентов, которые хотят более углубленное введение в философию. Сочетает в себе лекционный и дискуссионный методы.
2305 КРИТИЧЕСКОЕ МЫШЛЕНИЕ Базовый курс УЦА, удовлетворяющий трехчасовым требованиям по запросу и анализу в качестве факультатива по гуманитарным дисциплинам. Предназначен для улучшения способности человека рассуждать ясно и правильно и принимать рациональные решения на основе понимания стратегий принятия решений, знания того, как использовать информацию, и способности избегать ошибочного мышления.Сочетает в себе методы лекции, обсуждения и критического письма. [АКТЫ: PHIL1003]
2310 ВВЕДЕНИЕ В ЛОГИКУ Обязательный курс для всех специальностей философии и несовершеннолетних (может заменить PHIL 3310) и факультатив для несовершеннолетних по лингвистике. Курс для любого студента, желающего улучшить свои мыслительные способности. Вводное изучение правильного вывода в дедуктивном, научном и повседневном контекстах. Включены классическая и современная логика, логика науки, принципы определения и распространенные ошибки рассуждений.В первую очередь лекция и целевое обучение.
2325 СОВРЕМЕННЫЕ НРАВСТВЕННЫЕ ПРОБЛЕМЫ Основной факультатив УЦА, отвечающий требованиям к ответственному образу жизни. Введение в основные моральные и этические проблемы, с которыми сталкиваются люди 21 века, такие как аборты, эвтаназия, права животных и голод в мире. Сочетает в себе лекционный и дискуссионный методы.
2360 ПОЛ, РАСА И КЛАСС: ФИЛОСОФСКИЕ ВОПРОСЫ Основной факультатив УЦА, отвечающий требованиям к ответственному образу жизни.Введение в философские вопросы, касающиеся пола, расы и класса, с акцентом на то, как эти вопросы влияют на нашу идентичность и образ жизни с другими людьми. Сочетает в себе лекционный и дискуссионный методы.
3300 ГРЕЧЕСКАЯ И РИМСКАЯ ФИЛОСОФИЯ Одна из последовательностей истории философии. Требуется для всех специальностей философии, но открыт для других студентов, интересующихся античной философией. Поощряется в качестве факультатива по философии для несовершеннолетних. Ранняя западная философия от Фалеса до Плотина.Особый упор на Платона и Аристотеля. Сочетает в себе лекционный и дискуссионный методы. [UD UCA Core: I, C]
3301 СРЕДНЕВЕКОВАЯ ФИЛОСОФИЯ Одна из последовательностей истории философии; факультатив для специальностей и несовершеннолетних по философии и религиоведению. Основные мыслители и проблемы средневекового периода. Упор на Августина, Ансельма, Аквинского, Скотта и Оккама. Сочетает в себе лекционный и дискуссионный методы.
3302 СОВРЕМЕННАЯ ФИЛОСОФИЯ Одна из последовательностей истории философии.Обязателен для всех специальностей философии, но открыт для всех студентов, интересующихся современной философией. Поощряется в качестве факультатива по философии для несовершеннолетних. Основные философские деятели от Возрождения до Канта. Упор на Декарта, Спинозу, Локка, Беркли, Юма и Канта. Сочетает в себе лекционный и дискуссионный методы.
3303 ФИЛОСОФИЯ ДЕВЯТНАДЦАТОГО ВЕКА Одна из последовательностей истории философии; факультатив для специальностей и несовершеннолетних по философии и религиоведению. Основные проблемы и философы девятнадцатого века, включая Гегеля, Ницше, Кьеркегора, Конта, Маха, Шопенгауэра и Милля.Сочетает в себе лекционный и дискуссионный методы.
3304 АМЕРИКАНСКИЙ ПРАГМАТИЗМ Одна из последовательностей истории философии. Изучение основных американских философов и движений с колониальных времен до наших дней с упором на прагматизм. Сочетает в себе лекционный и дискуссионный методы.
3310 СИМВОЛИЧЕСКАЯ ЛОГИКА Может служить обязательным или факультативным курсом философии для основных и несовершеннолетних, но открыт для всех студентов, интересующихся современными системами символической логики.Темы курса включают перевод английских предложений в логику, построение таблиц истинности для проверки логических свойств и естественные выводы (доказательства) как в логике высказываний, так и в логике предикатов. Сочетает лекционный метод с задачами по решению проблем. [UD UCA Core: I]
3320 ЭТИКА Требуется для всех специальностей и несовершеннолетних в области философии (может быть заменен требованием PHIL 3325). Фундаментальные этические теории в истории философии, включая теории Платона, Аристотеля, Канта и Милля.Также будут изучены современные теории морали. Сочетает в себе лекционный и дискуссионный методы. [UD UCA Core: I, R]
3325 ПОЛИТИЧЕСКАЯ ФИЛОСОФИЯ Элективный курс философии для основных и несовершеннолетних (может быть заменен требованием PHIL 3320). Либо обзор избранных основных политических теорий от Платона до Маркса, либо тщательное изучение исторических и современных дискуссий по такой базовой теме, как справедливость, права или политическая власть. Сочетает в себе лекционный и дискуссионный методы.[UD UCA Core: I, R]
3330 ФИЛОСОФИЯ ПРАВА Этот курс будет посвящен основным традициям и вопросам философии права и теории права. Темы, которые будут охвачены, будут включать: мораль и закон, верховенство закона, права и конституционализм. По выбору для студентов, изучающих философию или несовершеннолетних. Рекомендуется для студентов дошкольного образования. Лекция и обсуждение.
3331 ФИЛОСОФИЯ РЕЛИГИИ Факультатив для основных и несовершеннолетних по философии и может служить требованием или факультативом для студентов, изучающих религию, но открыт для любого студента, интересующегося данной темой.Природа религиозных переживаний, веры и разума, теистические аргументы, проблема зла, бессмертия и проблемы религиозного языка. Сочетает в себе лекционный и дискуссионный методы. [UD UCA Core: I]
3340 КРИТИЧЕСКИЕ ТЕОРИИ ГОНКИ Факультативный курс для основных и несовершеннолетних специальностей по философии и афро-афроамериканским исследованиям. Попытки понять историю, значение и ценность афроамериканского опыта. Ключевые проблемы включают идентичность, отчуждение, справедливость и расизм.Сочетает в себе лекцию и дискуссию. [UD UCA Core: D, R]
3341 ТЕОРИИ ЗНАНИЙ Элективный курс философии для основных и несовершеннолетних, открытый для других с интересом. Систематическое изложение и критический анализ некоторых из следующих проблем теории познания: концепции истины, теории восприятия, личная идентичность и знание других умов, а также альтернативные концепции природы и границ знания, включая рационализм, эмпиризм, и интуиционизм.Сочетает в себе лекционный и дискуссионный методы.
3343 ФИЛОСОФИЯ СЕКСА И ЛЮБВИ Факультативный курс для студентов, изучающих философию или религию, а также факультатив для несовершеннолетних и других заинтересованных студентов, изучающих гендерные вопросы. Этот курс посвящен ряду философских трактатов по вопросам секса, любви и отношений между ними. Сочетает лекции и дискуссии.
3345 ФЕМИНИСТИЧЕСКАЯ ФИЛОСОФИЯ Элективный курс для студентов специальностей и несовершеннолетних по философии, а также для несовершеннолетних и других заинтересованных студентов.Исследование отношений между феминизмом и философией. Курс будет сравнивать и противопоставлять различные типы феминистской теории, например, либеральный, экзистенциалистский, радикальный, социалистический, психоаналитический и мультикультурный феминизм. Сочетает в себе лекционный и дискуссионный методы. [UD UCA Core: D, R]
3352 АЗИАТСКАЯ ФИЛОСОФИЯ И РЕЛИГИЯ Факультативный курс философии или религиоведения для студентов специальностей и несовершеннолетних, а также обязательный базовый курс для младших классов востоковедения. Основные религии и философские идеи Азии с акцентом на индуизм, буддизм, конфуцианство и даосизм.Сочетает в себе лекционный и дискуссионный методы. [UD UCA Core: D, C]
3360 ФИЛОСОФИЯ ИСКУССТВ Факультативный курс философии для основных и несовершеннолетних, но открытый для всех студентов, интересующихся искусством. Изучение природы и цели искусства и переживания смысла и ценности посредством художественного творчества и признательности. Сочетает в себе лекционный и дискуссионный методы. [UD UCA Core: C]
3370 МЕТАФИЗИКА Элективный курс для всех студентов, изучающих философию или религиоведение или специализирующихся на нем, и факультатив для других заинтересованных студентов.Этот курс представляет собой обзор того, что Аристотель называл «первой философией». Метафизика – это область исследования, в которой человек пытается ясно и систематически решать широкий круг философских вопросов, ответы на которые лежат в основе нашего фундаментального понимания природы реальности. Формат лекции и обсуждения.
3375 ФИЛОСОФИЯ РАЗУМА Элективный курс для всех студентов, изучающих философию, и факультатив для других заинтересованных студентов. Этот курс представляет собой введение в философию разума, которая сочетает в себе обзор исторических позиций в этой области с соответствующими современными проблемами в изучении сознания, эволюционной психологии и искусственного интеллекта.Лекция и обсуждение.
3380 ФИЛОСОФИЯ НАУКИ Факультативный курс философии для основных и несовершеннолетних, но открытый для студентов, интересующихся наукой. Изучение методов научного объяснения и подтверждения в логическом и историческом контекстах. Сочетает в себе лекционный и дискуссионный методы. [UD UCA Core: I, C]
3390 СТАЖИРОВКА В ФИЛОСОФИИ Для основных и несовершеннолетних для выполнения выборных требований в одной из четырех обязательных областей: история, социальная и политическая, ценностная или метафизика и эпистемология.Какой выбор он может выполнить, зависит от содержания программы стажировки и по усмотрению заведующего кафедрой философии и религии. Каждая стажировка адаптирована к потребностям работодателя и интересам студента. Стажировка требует 120-150 часов работы с работодателем на 3 часа факультативного кредита. Предпосылки: младшее или старшее звание и согласие координатора ведомственной стажировки.
3395 ТЕМА В ФИЛОСОФИИ Углубленное изучение выбранной основной проблемы философии или работ отдельных философов или групп философов.Изменения содержания могут быть повторены для кредита. См. Описание содержания в расписании семестра.
4300 ЧТЕНИЯ ПО ФИЛОСОФИИ Независимое исследование, предназначенное для углубленного изучения конкретных проблем и отдельных людей в философии. Условие: согласие инструктора.
4301 PHILOSOPHY FOR HONORS TUTORIAL Независимое исследование, предназначенное для того, чтобы дать выдающимся студентам возможность провести углубленное философское исследование. Может засчитываться в пользу майора. Условие: Приглашение от философского факультета.
4305 КОНТИНЕНТАЛЬНАЯ ФИЛОСОФИЯ Одна из последовательностей истории философии. Целенаправленное изучение одной или двух областей континентальной философии. Эти области включают феноменологию, экзистенциализм, герменевтику и постмодернизм. Изученные философы могут включать Гуссерля, Хайдеггера, Сартра, Гадамера, Деррида и Фуко. Сочетает в себе лекционный и дискуссионный методы.
4306 АНАЛИТИЧЕСКАЯ ФИЛОСОФИЯ Одна из последовательностей истории философии. Изучение эмпирической метафизики и эпистемологии с участием таких философов, как Рассел, Витгенштейн, Эйер, Льюис, Райл, Куайн и Дэвидсон.Сочетает в себе лекционный и дискуссионный методы.
4310 БОЛЬШИЕ РАБОТЫ ПО ФИЛОСОФИИ Курс Capstone. Внимательное чтение крупного философского труда, ведущее к написанию философской статьи. Факультативное направление по направлению «История философии» для специальностей. [UD UCA Core: Z]
4320 ПРИКЛАДНАЯ ЭТИКА В этом курсе особое внимание уделяется практике философской этики посредством применения этических теорий и рассуждений к различным проблемам или темам. Акцент делается на применении этических теорий и рассуждений к различным аспектам современной частной и общественной жизни.Темы могут включать, помимо прочего, этику и бизнес, окружающую среду, международную политику или гендер. Этот курс является факультативным и охватывает область социальных, политических и ценностей для основных и второстепенных философских факультетов. Содержание меняется в зависимости от изучаемой области. Может быть повторено до шести часов кредита с согласия председателя. Лекция и обсуждение. [UD UCA Core: D, R]
4330 ФИЛОСОФИЯ ЯЗЫКА Факультативный курс для основных или младших специалистов по философии или лингвистике, но открытый для всех, кто интересуется данной темой.Исследование природы языка в его отношении к сознанию, логике, социальному поведению и реальности. Сочетает в себе лекцию и дискуссию.
4340 ЗНАЧЕНИЕ ЖИЗНИ Курс Capstone. Курс по выбору для студентов специальностей и несовершеннолетних по философии и религиоведению. Исследование классических и современных попыток ответить на вопрос «В чем смысл жизни?» Ключевые вопросы включают личную идентичность, источники значимости, смертность и религиозные убеждения. Сочетает в себе лекционный и дискуссионный методы.[UD UCA Core: Z]
4350 ЭТИКА ЗДРАВООХРАНЕНИЯ Элективный курс, предназначенный в первую очередь для студентов, изучающих медицинские науки, но также будет засчитан в качестве основного или дополнительного по философии. Изучение вопросов и принципов этики, связанных со здоровьем. Темы включают этическое мышление, биоэтику и индивидуальные тематические исследования проблем, возникающих в практике различных областей здравоохранения.
Специальность состоит из девяти курсов.
| Код | Название | Кредиты |
|---|---|---|
| PHIL 2111 | 1 | Древняя философия |
| PHIL 2223 | Логика | 1 |
| 6 | ||
Минор состоит из пяти курсов.
| Код | Название | Кредиты |
|---|---|---|
| PHIL 2111 | 1 | Древняя философия |
| 1 | ||
| 1 | ||
| 1 | ||
Вы не просматриваете текущий курс, перейдите на вкладку текущего года.
Курс с отличием и продвинутый уровень Примечание: Академическая строгость – это больше, чем просто поручать студентам больший объем работы. Благодаря применению, анализу, оценке и созданию сложных идей, которые часто бывают абстрактными и многогранными, учащимся предлагается критически мыслить и совместно работать над изучаемым содержанием.
Содержание должно включать, но не ограничиваться, следующее:
Особые примечания:
Развитие английского языка Особые примечания по стандартам ELD:
Учителя требуются для обучения аудированию, устной речи, чтению и письму, которое позволяет изучающим английский язык (ELL) обмениваться информацией, идеями и концепциями для академического успеха в предметной области языковых искусств.Для заданного уровня владения английским языком и с визуальной, графической или интерактивной поддержкой учащиеся будут взаимодействовать со словами, выражениями, предложениями и речами на уровне своего класса, чтобы обрабатывать или воспроизводить язык, необходимый для академической успеваемости. Стандарт ELD должен определять соответствующую концепцию области содержания или тему исследования, выбранную разработчиками учебных программ и учителями, которая максимизирует потребность ELL в коммуникативных и социальных навыках. Чтобы получить доступ к вспомогательному документу ELL, в котором описаны определения и дескрипторы производительности, щелкните следующую ссылку: https: // cpalmsmediaprod.blob.core.windows.net/uploads/docs/standards/eld/la.pdf
Сокращенное название: СЕМАНТИКА – ЛОГИКА HON
Количество кредитов: Половина кредита (.5)
Продолжительность курса: семестр (S)
Тип курса: Курс по выбору
Уровень курса: 3
Статус курса: Утверждено Государственным советом
Уровень (и): 9,10,11,12
Для преподавания этого курса требуется один из этих вариантов сертификации для преподавателей.
Проверенные ресурсы, которые студенты могут использовать для изучения концепций и навыков в этом курсе.
Проверенные ресурсы, которые могут использовать опекуны, чтобы помочь студентам изучить концепции и навыки этого курса.
Логика – это теория разумного рассуждения.Этот модуль знакомит студентов с некоторыми типами рассуждений, которые регулярно используются в повседневной жизни, в философии и во многих других областях. Студенты познакомятся с множеством мощных методов проверки достоверности аргументов и построения самих аргументов. По пути мы также сделаем паузу, чтобы рассмотреть некоторые философские проблемы и парадоксы, которые порождает логика. Этот блок будет интересен всем, кто интересуется природой здравого смысла. Он особенно полезен для студентов, изучающих математику или информатику, и должен серьезно рассматриваться как факультатив для всех, кто специализируется на философии.
| Название агрегата | Введение в логику |
|---|---|
| Код единицы | HPh303 |
| Кредитные пункты | 12,5 |
| Колледж / школа | Колледж искусств, права и образования Гуманитарный факультет |
| Дисциплина | Философия и гендерные исследования |
| Координатор | Доктор Ричард Корри |
| Доступен как факультатив для студентов? | Есть |
| Уровень | Средний |
Этот блок в настоящее время недоступен.
Пожалуйста, убедитесь, что ваш компьютер соответствует минимальным системным требованиям, если вы посещаете дистанционное обучение / вне кампуса.
Единицы предлагаются в режиме посещения, если не указано иное (то есть присутствие требуется в указанном кампусе). Подразделение, определенное как предлагаемое по дистанции, то есть отсутствие требований к посещаемости, идентифицируется с номинальным зачислением в университетский городок. Подразделение, предлагаемое как посещающим студентам, так и удаленным от одного и того же кампуса, идентифицируется как имеющее оба режима обучения.
* Конечная дата выхода – это последняя дата, с которой вы можете выйти из подразделения без академического штрафа, однако вы все равно будете нести финансовое обязательство (см. Объяснение дат выхода для получения дополнительной информации).
Даты переписи единиц, отображаемые в настоящее время на 2022 год, являются ориентировочными и могут быть изменены. Окончательные даты переписи на 2022 год будут доступны с 1 октября 2021 года.
О датах переписи
| Область образования | Начало взноса учащегося 1 | Взнос старого ученика 1 | Взнос студента, утвержденного на подготовительном курсе 2 | Полная внутренняя пошлина |
|---|---|---|---|---|
| не применимо |
1 Подробнее о размерах взносов студентов см. Здесь.
2 Информацию о праве на участие и утвержденных курсах Pathway можно найти здесь
3 Пожалуйста, обратитесь сюда, чтобы узнать о праве на HECS-HELP
4 Пожалуйста, обратитесь сюда для получения права на FEE-HELP
Если у вас есть какие-либо вопросы относительно сборов, свяжитесь с UConnect или дополнительную информацию можно найти на StudyAssist.
Обратите внимание: иностранных студентов должны обратиться к этой странице, чтобы узнать ориентировочную стоимость курса.
Вы не можете записаться в этот блок, а также в следующие:
HPA291-A И HPA391-A| Схема преподавания | На территории кампуса: еженедельные лекции (2 часа) и учебные пособия (1 час) |
|---|---|
| Оценка | Заключительный экзамен (60%) | Задание (10%) | Задание (15%) | Задание (15%) |
| Расписание | Посмотреть расписание лекций | Посмотреть полное расписание занятий |
Университет оставляет за собой право изменять или удалять курсы и доступные единицы в зависимости от обстоятельств.
Если в логике высказываний отвлекаются от связей между субъектом и предикатом высказывания, то в логике классов эти связи учитываются. В число классов в логике классов включается и пустой класс (0), содержащий нулевое множество элементов, и универсальный класс (1), включающий все объекты рассматриваемой области. С классами можно производить операции пересечения, объединения и дополнения. К алфавиту логики высказываний в логике классов добавляются переменные a, b, c, … для классов; знаки, обозначающие операции с классами; постоянные термы 0 и 1 и знаки для обозначения отношений между классами. Далее даётся индуктивное определение терма и класса. Вводятся отношение включения класса в класс (ab) (a включается в класс b), отношение равенства двух классов (a = b). Оба эти отношения могут быть определены через отношение принадлежности элемента классу (aab).
Логика предикатов), а именно логики одноместных предикатов, точнее логики, оперирующей с объёмами понятий, содержания которых выражаются соответствующими одноместными предикатами.
Рассматривая реализацию логики классов на одноэлементной области, сводят вопрос об истинности (ложности) формул логики классов к соответствующим вопросам для логики высказываний, подобно которой логика классов оказывается, таким образом, разрешимой. Отсюда нетрудно получить и разрешимость логики одноместных предикатов; а поскольку, как было указано, она по существу совпадает с логикой классов, последнюю в настоящее время уже не рассматривают в виде специальной теории, трактуя её как частный случай логики предикатов (где ей соответствует логика одноместных предикатов).